IN VITRO VALIDATION OF FINITE ELEMENT MODEL OF AAA HEMODYNAMICS INCORPORATING REALISTIC OUTLET BOUNDARY CONDITIONS

Abstract

Purpose

To validate numerical simulations of flow and pressure in an abdominal aortic aneurysm (AAA) using phase-contrast MRI (PCMRI), and an in-vitro phantom under physiological flow and pressure conditions.

Materials and Methods

We constructed a 2-outlet physical flow phantom based on patient imaging data of an AAA, and developed a physical Windkessel model to use as outlet boundary conditions. We then acquired PCMRI data in the phantom while it operated under conditions mimicking a resting and a light exercise physiological state. Next, we performed in-silico numerical simulations, and compared experimentally measured velocities, flows, and pressures in the in-vitro phantom to those computed in the in-silico simulations.

Results

There was a high degree of agreement in all of the pressure and flow waveform shapes and magnitudes between the experimental measurements and simulated results. The average pressures and flow split difference between experiment and simulation were all within 2%. Velocity patterns showed good agreement between experimental measurements and simulated results, especially in the case of whole-cycle averaged comparisons.

Conclusion

We demonstrated methods to perform in-vitro phantom experiments with physiological flows and pressures, showing good agreement between numerically simulated and experimentally measured velocity fields and pressure waveforms in a complex, patient-specific AAA geometry.

INTRODUCTION

Hemodynamic parameters such as the three-dimensional blood flow and pressure fields, as well as the stress and strain in blood vessels, have direct effects on the initiation and development of cardiovascular diseases such as atherosclerosis and aneurysms (1-5). The hemodynamic forces within blood vessels also directly affect biological adaptation of vessel diameter and wall thickness (6,7). The design and evaluation of implantable medical devices such as stents and stent grafts require knowledge of how the in-vivo forces and tissue motions will interact with the devices. Medical imaging can be used to investigate these hemodynamic parameters, but with limited temporal and spatial resolutions. As computing resources increase, image-based computational fluid dynamics (CFD) methods are becoming powerful tools to quantify these hemodynamic conditions. The ability of CFD techniques to finely resolve time and space enables the study of disease mechanisms (8-12), and can aid in the design and evaluation of medical devices (13-16). The ease of applying variations in geometry and flow conditions in the computational domain also motivates the use of CFD in the planning and prediction of surgical procedures (17,18). However, much work remains to provide proper input parameters to CFD simulations, and to validate CFD methods against experimental data. Phase contrast MRI (PCMRI) is a versatile in-vivo technique (19,20) that can provide velocity data to be used as input parameters at discrete locations, and to validate numerical computations at other locations.

Previous In-vitro experiments have been performed to compare CFD computed velocity fields with those measured with PCMRI. However, these prior studies did not include realistic outflow boundary conditions (BC), which are required to represent physical properties of downstream vasculature not modeled in the numerical domain, and to produce physiologic levels of pressure. For example, previous in-vitro CFD validation studies have implemented simple zero pressure BC in the physical setup (phantom outlets connect directly into a fluid reservoir) (21,22), and many also employed steady flow (23,24). In the computational domain, flow velocity BC were commonly prescribed (25,26), but this type of BC is difficult to employ in patient-specific CFD studies, since obtaining flow velocity data for all of the outlets of a major blood vessel in a patient is very difficult. In addition, realistic patient-derived abdominal aortic aneurysm (AAA) geometry under pulsatile flow has not been considered in in-vitro validation models. Complex or even turbulent flows within AAA geometries have commonly been reported in literature (27,28), making patient-derived AAA geometries more challenging targets for validation studies.

In this study, we present results from a complex AAA geometry under physiological flows, and Windkessel BC (a practical BC prescription method in CFD simulations to provide physiologically realistic impedances (29-31)), to achieve validation of the numerical method. We built a 2-outlet physical model (flow phantom) of a patient-specific AAA, and constructed physical analogs of a Windkessel lumped-parameter model which we attached to the outlets of the flow phantom to provide physiologically-realistic outlet flow impedances. We then used a 1.5T MRI system to acquire PCMRI data in multiple 2D planes in the AAA phantom while it was under pulsatile, and physiologically-realistic flow and pressure conditions. The use of PCMRI in this study allows us to follow a similar protocol for future in-vivo validations. Next, we performed in-silico numerical CFD simulations using a finite-element analysis (FEA) technique, and prescribed outlet BC using analytical models of the Windkessel directly corresponding to its physical construction. We then compared experimentally measured velocities, flows, and pressures in the in-vitro AAA phantom to those computed in the in-silico CFD simulations.

MATERIALS & METHODS

Anatomical Model Construction

From a gadolinium-enhanced MR angiography scan of an AAA patient (Figure 1a), we constructed a 3D computational anatomical model (Figure 1b) that includes the AAA, and the renal and common iliac arteries(28). The anatomical domain extends from about 4cm superior to the first renal branches to 4cm inferior to the aortic bifurcation, and includes a few centimeters of the renal arteries. The final computational model shown in Figure 1b includes extensions we added to the anatomical domain vessels to accommodate the two-outlet connections to the rest of the flow loop. Finally, we used this computational model to physically construct a rigid AAA phantom for the in-vitro experiment using a stereolithography technique (Viper™ si2 stereolithography machine, 3D Systems Corporation, Rock Hill, SC) and MR-compatible resin (WaterShed® XC 11122, DSM Somos®, Elgin, IL) (32) (Figure 1c).

Figure 1.

Anatomical Phantom Model a) MR Imaging data from an AAA patient. b) 3D computer model constructed based on patient imaging data. c) Physical phantom constructed from 3D computer model.

Outlet Boundary Condition

We used a four-element Windkessel model consisting of an inductance (L), proximal resistance (Rp), capacitance (C), and distal resistance (Rd), as outlet BC (Figure 2 & Figure 3a). Physically, we designed the Windkessel modules such that physiologically realistic flows and pressures were achieved in the phantom, and that the resistance and capacitance values of the lumped-parameters remained reasonably constant over the whole operating range of the flow conditions (33).

Figure 2.

In-vitro Experiment Flow System Setup Diagram

Figure 3.

a) The physical Windkessel module assembly and the corresponding analytical representation b) The resistance module c) The capacitance module

Resistance

In order to obtain significant flow resistance while keeping the flow laminar (which is required to obtain a resistance value that is independent of flow rate), we constructed the resistance module by placing a large number of thin-walled glass capillary tubes (Sutter Instrument, CA) in parallel with each other inside a plexiglass cylinder (Figure 3b). Using Poiseuille's law and the equation for parallel resistances, the resistance of the module can be calculated by:

$$\text{Resistance}=8\mu 1∕\left(\mathrm{N}\pi {\mathrm{r}}^4\right)$$ (1)

where μ is the dynamic viscosity of the working fluid, l is the length of the capillary tubes, r is the inside radius of each individual capillary tube, and N is the total number of capillary tubes in parallel (34). Table 1 shows the list of resistance modules we used in the experiment with their construction details and resulting resistances.

Table 1.

List of resistance modules used in the experiment. Resistances values are calculated using a fluid viscosity of 0.0457 dynes-s/cm² as measured from the working fluid.

Resistance Module	Cylinder Diameter	Capillary Tubes Length (cm)	Capillary Tubes ID/OD* (mm)	# of Capillary Tubes	Resistance (dynes-s/cm5)
Rp1	1″	10	1.1 / 1.5	233	549
Rd1-1**	3/8″	10	0.78 / 1	71	7132
Rd1-2**	0.71cm	5	1.1 / 1.5	16	4000
Rp2	5/8″	10	0.75 / 1	194	3053
Rd2	3/8″	10	0.9 / 1.2	48	5951

^*ID/OD stands for inside diameter/outside diameter

^**Rd1-1 and Rd1-2 are placed in parallel, and together act as the “Rdl” shown in Figure 2. A valve turns Rd1-2 on and off for the light exercise and resting flow conditions to change the effective resistance value of “Rdl”.

Capacitance

The capacitance of a fluid system is define as C=ΔV/ΔP where ΔV and ΔP are the changes in volume and pressure. In a closed system at constant temperature, an ideal gas exhibits the behavior PV=(P+ΔP)(V-ΔV), where P and V are the reference pressure and volume. The capacitance of a column of air is then:

$${\mathrm{C}}_{\mathrm{a}}=(\mathrm{V}-\Delta \mathrm{V})∕\mathrm{P}$$ (2)

For small changes in volume relative to the reference volume, a reasonably constant capacitance can be obtained with an air column. We constructed the capacitance module with a plexiglass box that can trap a precise amount of air, which acts as a capacitance in the system (Figure 3c). The capacitance box has an inlet and an outlet, and as the fluid enters and exits the box, the fluid level in the box rises and falls slightly. The varying fluid level also contributes to a capacitance that is in series with the capacitance due to air compression. The pressure change in the fluid due to the varying fluid level “Δh” is:

$$\Delta \mathrm{P}=\rho \mathrm{g}\Delta \mathrm{h}=\rho \mathrm{g}\Delta \mathrm{V}∕\mathrm{A}$$ (3)

where ρ is the fluid density, g is the gravitational constant, and A is the area of the fluid/air interface (assuming a constant cross-sectional area column of fluid). The capacitance due to the varying fluid level is then:

$${\mathrm{C}}_{\mathrm{v}}=\mathrm{A}∕\left(\rho \mathrm{g}\right)$$ (4)

Since C_v is in series with C_a, if C_v>>C_a the overall capacitance can be approximated by C_a alone. In the actual construction of the capacitance module, we designed the box to be large enough so that such approximation is true. We also designed a smooth contour for the inlet of the module in order to minimize flow turbulences and thus avoid parasitic resistances (Figure 3c).

Inductance

The flow inductance results from the fluid momentum, and can be calculated from the geometry of the physical system. The flow inductance in a fluid conduit is:

$$\mathrm{L}=\rho 1∕\mathrm{A}$$ (5)

where l and A are the length and the cross-sectional area of the conduit.

In-vitro Experiment

Flow Loop Setup

We placed the flow phantom and the outlet impedance modules in a flow system as shown in Figure 2. The experiment mimicked two different physiological conditions: a resting condition, and a light exercise condition. We computed the resting, supra-renal level aortic flow waveform by summing the infra-renal blood flow velocity previously acquired by PCMRI in the same AAA patient, and published data of renal flow (35). For the light exercise condition, we increased the average flow to two times that of resting, increased the heart rate from 60 bpm to 80 bpm, and decreased the downstream resistance of the aortic outlet Rd1 (by turning on a valve to allow flow through Rd1-2 which is in parallel with Rd1-1) to mimic vasodilation of the lower extremity vessels. This mimics a very mild exercise condition such as light walking. We then used a custom-built, MR-compatible, and computer-controlled pulsatile pump (36), in parallel with a 1/12 horse-power, 3100RPM, steady flow pump (Model 3-MD-HC, Little Giant Pump Co., OK) with a ball valve attached at its outlet for flow rate control, to physically reproduce the supra-renal flow waveforms as the input flow to the phantom. At the inlet of the phantom we placed one meter of straight, rigid tubing, a honeycomb flow straightener, and two pressure-stabilization grids, in order to provide sufficient entrance conditioning to generate a stable and fully-developed Womersley flow profile at the phantom inlet. We tested this entrance flow conditioning method in a separate phantom using PCMRI, and observed that a Womersley velocity profile was achieved at the end of the entrance length. The working fluid in the flow system was a 40% glycerol solution with a dynamic viscosity similar to that of blood, and contained 0.5% Gadolinium.

Flow & Pressure Probe Measurements

We used an MR-compatible ultrasonic transit-time flow sensor to monitor the total input flow to the phantom. We placed the externally clamped flow probe (8PXL, Transonic Systems, NY) around a short section of Tygon tubing R3603 immediately upstream of the one-meter flow conditioning rigid tubing, and sent the signals from the probe into a flowmeter (TS410, Transonic Systems, NY) with its low pass filter setting at 160Hz. For pressure measurements, we inserted MR-compatible catheter pressure transducers (“Mikro-Tip” SPC-350, Millar Instruments, Houston, TX) through small ports on the sides of the phantom to capture pressure waveforms at the phantom outlets, and also immediately downstream of the parallel impedance modules to record the pressure to be used as reference ground pressure. Note that the pressure data presented in the results section is relative to the reference ground pressure. We sent the signals from each catheter pressure transducer into a pressure control unit (TCB-600, Millar Instruments, TX) which produces an electrical output of 0.5V per 100mmHg of pressure. We recorded the data from the flow meter and the pressure control units at a sample rate of 96 Hz using a data acquisition unit (USB-6259, National Instruments, Austin, TX) and a LabVIEW program (LabVIEW v.8, National Instruments, Austin, TX). We acquired pressure and flow data intermittently (approximately every 0.5~1 hour) throughout the experiment in between MR scans. We averaged approximately 50 cycles of flow rate and pressure data to obtain one averaged cycle for each acquisition. We then averaged the measurements from all the acquisition throughout the experiment to obtain one cycle of flow rate and pressure data that represents each of the two flow conditions. The cycles of flow rate and pressure measurements were stable both in between the cycles of one acquisition, and between the different acquisitions throughout the experiment.

MRI

We acquired flow velocity data at different slice locations within the phantom (Figure 2) using a cardiac-gated 2D 3-component cine PCMRI sequence in a 1.5T GE MR scanner (Signa, GE Medical Systems, Waukesha, WI) and an 8-channel cardiac coil. The slice locations represent the mid-aneurysm location for each lobe of the bilobed aneurysm anatomy, and also a location directly downstream of the renal branches where flow is likely to be complex. The imaging parameters were: 256×192 acquisition matrix reconstructed to 256×256, 24×24 cm² field of view, 5mm slice thickness, TR=~13 ms, TE=~5.5 ms, 20 degree flip angle, and NEX=2. The through-plane velocity encoding (Venc) for slices 1-3 were 100, 50, and 50 cm/s, respectively, for the resting flow condition, and 100, 75, 50 cm/s, respectively, for the light exercise flow condition. The in-plane Venc for slices 1-3 were 30, 30 and 50 cm/s, respectively, for the resting flow condition, and 30, 40, and 50 cm/s, respectively, for the light exercise flow condition. The LabVIEW program which controlled the pulsatile pump produced a trigger signal that was converted by an electrocardiogram (ECG) simulator (Shelley Medical Imaging Technologies, London, Ontario, Canada) into an ECG signal used by the MRI system for gating, and 24 time points per cardiac cycle synchronized to this ECG signal were reconstructed. The temporal resolution of the velocity data was two times the TR (~26ms). We placed vitamin E capsules (Schiff Nutrition Group, Inc, Salt Lake City, UT) as well as saline bags around the flow region of each slice to produce the reference signals of stationary fluids, which we then used for baseline eddy current correction with a linear correction algorithm in the analysis of the PCMRI data.

In-silico Simulation

We performed the numerical simulation of flow and pressure using a custom stabilized finite-element method to solve the incompressible Navier-Stokes equations, assuming rigid walls and a Newtonian fluid with a density of 1.1 g/cm³ and dynamic viscosity of 0.0457 dynes-s/cm² as measured from the working fluid (37). We discretized the 3D anatomical model in Figure 1b into an isotropic finite-element mesh with a maximum edge size of 0.1 cm and containing 3.2 million linear tetrahedral elements using commercial mesh generation software (MeshSim, Simmetrix, Inc., NY). For each of the two flow conditions, we first ran a steady flow simulation with the mean probe-measured flow prescribed at the inlet, and the sum of the proximal and distal resistances in each of the outlet Windkessel models as the resistance BC for each of the outlets. For the steady flow simulation, we used a timestep size of 0.001 second and ran the simulation for 0.5 second, which was sufficient for the pressure inside the domain to stabilize. We then used the pressure and velocity results from the steady simulation as the initial condition for the pulsatile flow simulation. For the pulsatile flow simulation, we mapped the inflow waveform (the averaged representative cycle of flow probe measurement) to the inlet face using a Womersley velocity profile. For the BC at the 2 outlets, we prescribed a Windkessel model with the lumped-parameter component values (Table 2) calculated from their physical constructions. We used an augmented lagrangian method to constrain the shapes of velocity profiles at the outlets to prevent divergence (38). This technique has been shown to have very little effect to the flow and pressure calculations in the numerical domain (38). We used a timestep size of 0.0004 second, and simulated 11 cardiac cycles for each of the two flow conditions. The first cycle of the simulation result was discarded, and the last 10 cycles where the pressures had stabilized were included in the final analysis. The cycle-to-cycle variations in the velocity pattern of the numerical simulation results indicate the presence of aperiodic features in the velocity pattern. Since the PCMRI technique combines measurements acquired over multiple cycles into one cycle of velocity data, we averaged the simulation results from corresponding time points in the last 10 successive cycles to mimic the PCMRI data acquisition method (36). The aperiodic features in the velocity patterns tend to also be the higher spatial frequency features which cannot be resolved by MR imaging due to its limited spatial resolution. Cycle to cycle averaging of the simulation results removes these high spatial frequency features, making the comparisons to MR data more meaningful.

Table 2.

Values of lumped-parameter components in the Windkessel outlet BC prescribed to the FEA simulations.

	Resting Condition		Light Exercise Condition
	Aortic outlet	Renal outlet	Aortic outlet	Renal outlet
L (dynes-s2/cm5)	7	16	7	16
Rp (dynes-s/cm5)	549	3053	549	3053
C (cm5/dynes)	0.0003253	0.0001644	0.0003222	0.0001590
Rd (dynes-s/cm5)	7132	5951	2563	5951

RESULTS

PCMRI Flow Measurements at Different Slice Locations

In the case of a rigid phantom and flow conservation, the total flow across any arbitrary axial section of the phantom is theoretically identical at any instant in time. Figure 4 shows the flow through the abdominal aorta as measured with PCMRI at the three different slice locations, for the resting and light exercise conditions. We found that the flows measured at the different locations agree well. The average flow measured at S1, S2, and S3 are 24.1, 24.0, and 24.5 cc/s respectively (2% maximum difference) for the resting condition, and 68.4, 68.5, and 68.7 cc/s respectively (0.4% maximum difference) for the light exercise condition. For the resting condition, however, the flow waveform acquired from S1 was temporally shifted by one sampling point compared to S2 and S3. In Figure 4, we have shifted the S1 waveform to align it to the S2 and S3 waveforms.

Figure 4.

PCMRI Measured Flow Through the Abdominal Aorta at Different Slice Locations (S1-S3) for a) Resting condition, and b) Light exercise condition.

PCMRI vs. Flow Probe Measured Inlet Flow Waveforms

PCMRI flow measurements were validated against ultrasonic flow probe measurements. Figure 5 shows flow comparisons between the PCMRI measurements (the sum of the aortic and renal branches at S3), and the flow probe measurements at the inlet of the phantom, for the resting and light exercise flow conditions. Figure 5 shows close agreement between the PCMRI and flow probe measured flow waveforms both in their magnitudes and shapes. The shapes of the waveforms agree well including the small features of local peaks and troughs. Slight disagreement between the first data point in the PCMRI measured flow and the flow probe data could be due to the retrospective reconstruction of the PCMRI data. For the resting condition, the average flows were 42 cc/s and 46 cc/s as measured by the flow probe and PCMRI respectively. For the light exercise condition, the average flows were 88 cc/s and 96 cc/s as measured by the flow probe and PCMRI respectively. For both flow conditions, the averaged flow measured by PCMRI was 8-9% higher than that measured by the flow probe.

Figure 5.

PCMRI vs. Ultrasonic Flow Probe Measured Total Inlet Flow for a) Resting condition, and b) Light exercise condition.

Measured vs. FEA Flow & Pressure Waveforms

Figure 6 shows comparisons between in-vitro, MR measured, and in-silico, simulated flow waveforms, and comparisons between in-vitro, catheter probe measured, and in-silico, simulated pressure waveforms, for each of the two flow conditions. We used the PCMRI data at S3, which included both the aortic and the renal branch outlets, to construct the aortic and renal flow waveforms. There is excellent agreement between the experimental data and simulated results for the pressure and flow waveforms. The pressure and flow waveforms are physiologic in shape and magnitude. Specifically, the renal flow is always antegrade (35), but the abdominal aortic flow is retrograde during part of the cardiac cycle in resting condition. The flow split ratios between the aortic and renal branches are 54:46 (predicted by the simulation) and 53:47 (measured by MR) for the resting condition, and 74:26 (predicted) and 72:28 (measured) for the light exercise condition. The predicted and measured root mean square pressures are 132 mmHg and 130 mmHg respectively (1.8% difference) for the resting condition, and 154 mmHg and 160 mmHg respectively (3.8% difference) for the light exercise condition.

Figure 6.

Measured In-vitro (Solid lines) vs. Simulated In-silico (dashed lines) Pressure & Flow Waveforms for a) Resting condition, and b) Light exercise condition

PCMRI vs. FEA Instantaneous Time Point Velocity Patterns

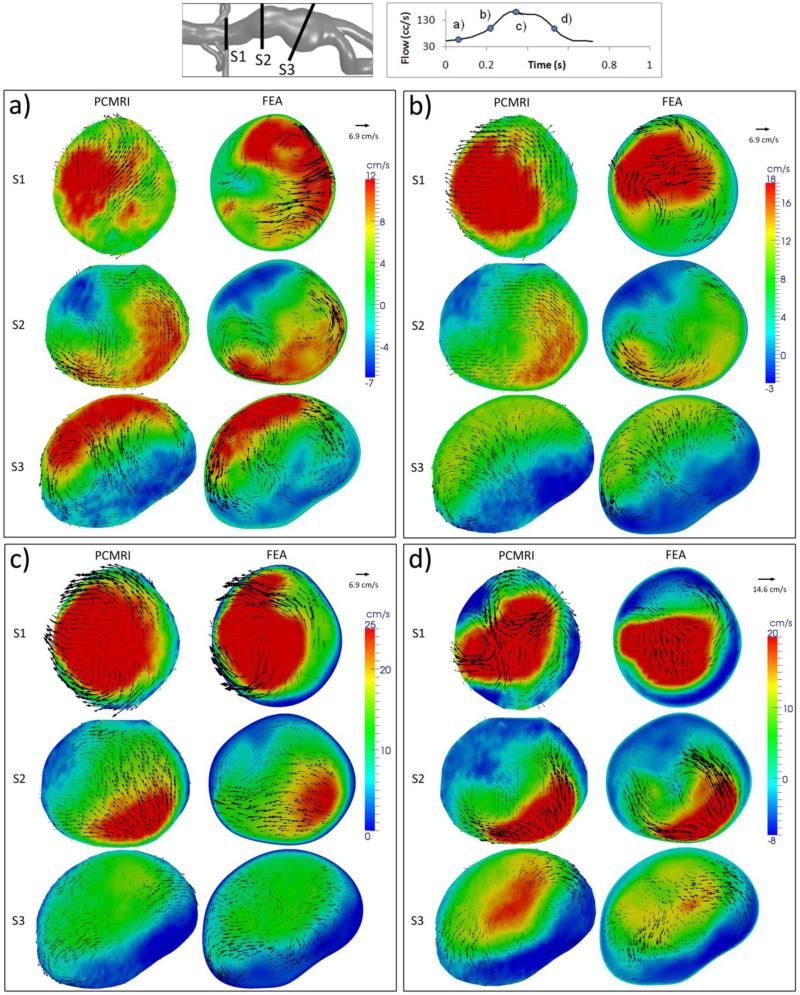
Figures 7 and 8 show through-plane and in-plane velocity comparisons between the cycle-to-cycle ensemble-averaged simulation results, and 3-component PCMRI velocity data. For each of the flow conditions, the comparisons are made at four different time points of the cardiac cycle (diastole, acceleration, systole, and deceleration), and at three slice locations within the abdominal aorta (S1, S2, and S3). For both flow conditions, we found reasonable agreement between the simulation results and PCMRI data in all of the comparisons at the systole and deceleration time points, and also in the S3 location at all time points.

Figure 7.

Resting Condition Flow Velocity Comparisons: Between MR Measurements and FEA Results at the a) Diastole, b) Acceleration, c) Systole, and d) Deceleration time point, at three different slice locations (S1-S3). Colour map and arrows correspond to through-plane and in-plane velocities, respectively.

Figure 8.

Light Exercise Flow Velocity Comparisons: Between MR Measurements and FEA Results at the a) Diastole, b) Acceleration, c) Systole, and d) Deceleration time point, at three different slice locations (S1-S3). Colour map and arrows correspond to through-plane and in-plane velocities, respectively.

For the resting condition in Figure 7, flow velocities are very low at the diastole time point, leading to low signal-to-noise in the MR data, and also poor agreement with simulation results; however, diastolic velocities measured with PCMRI at the S3 location still agreed well with simulation under such a circumstance. Many in-plane velocity comparisons at the S1 location showed patterns that seem to mismatch at first glance, but contained features in common upon more careful examination. One such example is deceleration at S1 under the resting condition, where the MR data show a counter-clockwise vortex in the upper half of the slice and a clockwise vortex in the bottom half, and the FEA results show a less prominent, but existing counter-clockwise vortex at the top of the slice, and downward velocities along the bottom right wall forming a clockwise vortex structure with the right-ward velocities near the center of the slice.

For the light exercise condition in Figure 8, S2 at deceleration is an example of how the detailed flow features can be matched in the comparisons: Positive and negative through-plane velocities along two opposite walls of the vessel are shown in both the simulation and PCMRI results with similar magnitudes and shapes, and in-plane velocities moving away from the high through-plane flow area creating two vortices towards the center are also shown in both results. The less favorable comparisons occurred at S1 and S2 at the acceleration time point, and also at S1 at the diastole time point. For these same slices and time points, we also observed significant cycle-to-cycle velocity pattern variations in the simulation results.

PCMRI vs. FEA Whole-cycle Averaged Velocity Patterns

Figure 9 shows velocities averaged over all of the time points in the cardiac cycle at the three different slice locations for each of the two flow conditions. There is good agreement between the PCMRI measurements and FEA results in all of the slices for both flow conditions and for both the through-plane and in-plane velocities. Complex patterns of in-plane velocities at the S1 location match between the simulation results and experimental data. For the resting condition, even though the orientations of the S1 in-plane velocities are slightly different between the comparisons, upon closer examination it is clear that both contain the clockwise and counter-clockwise vortices in the lower left and upper right parts of the slice.

Figure 9.

Whole-cycle Averaged Flow Velocity Comparisons: Between MR measurements and FEA results at three different slice locations (S1-S3) for a) Resting condition and b) Light exercise condition.

DISCUSSION

The purpose of this study was to produce a set of in-vitro experimental data that can be used to compare against FEA results of flow and pressure within a complex and realistic anatomy, and under physiological flow and pressure conditions. We have built a well controlled and characterized experimental setup consisting of a precisely constructed, patient-derived flow phantom, well-defined BC modules, and highly periodic cardiac cycles, in order to acquire such experimental data. We used PCMRI, an imaging method that could be employed in-vivo. We also used a two-outlet, patient-specific AAA anatomy under two physiological conditions – resting and light exercise. We demonstrated that with the methods described in this paper, we were able to construct and characterize lumped parameter impedance modules with predictable component values and behaviors, which enabled us to accurately prescribe corresponding analytical models at the outlet boundaries of the numerical simulations, and predict the flows through the two outlets of the phantom and the pressures within the phantom. In addition, the complex impedances provided by the impedance modules are important in achieving flows through the aortic and renal outlets that are dramatically different in their shapes and phases.

The close agreement between PCMRI volumetric flow measurements at different slice locations indicated the precision of the PCMRI measurements. The close agreement between the PCMRI and ultrasonic flow probe measured flow waveform shapes showed that the PCMRI measurements had sufficient temporal resolution to capture the various frequency components in the flow waveforms. A discrepancy of <10% in the mean flow was both within the specified absolute accuracy of the ultrasonic flow probe, as well as consistent with the anticipated accuracy of PCMRI flow measurements (39,40).

We found instantaneous flow velocity pattern agreements between MR and FEA results in the complex and realistic AAA geometry. The S1 location exhibited more complex flow and cycle-to-cycle variations compared to the other slice locations, possibly due to the fact that it was immediately downstream of the renal branches, and because it had a small cross-sectional area resulting in high flow velocity and high Reynold's number. The S3 location, on the other hand, exhibited less complex flow and aperiodicity due to its lower flow velocities. Since PCMRI is acquired over multiple cardiac cycles, data accuracy depends heavily on periodicity. Cycle-to-cycle variations in simulation results are likely due to flow turbulence (28), and previous studies have shown that flow turbulence causes MR signal loss (41,42) which also contributes to measurement challenges. Large amounts of cycle-to-cycle variations also require a large number of cycles in the FEA simulation to be averaged in order to obtain a representative and stable ensemble average. Thus, the effects of complex flow and aperiodicity are detrimental to both the MR measurements and simulation result interpretations, leading to poorer comparisons. We indeed found less favorable comparisons at the S1 location, and consistently good comparisons at the S3 location as expected. Another interesting finding was that the presence of complex flow and aperiodicity upstream did not seem to affect the downstream flow stability and predictability, which is consistent with the findings of Les et al (28). At the diastolic time point in the light exercise condition, even though there was significant aperiodicity in the S1 location, stable and periodic flow resumed downstream at S2 and S3, where good agreements were obtained between the PCMRI and FEA results. At the acceleration time point in the light exercise condition, there was also much aperiodicity at both S1 and S2, and yet further downstream at S3, the flow features agreed well.

The PCMRI data contained approximately 600, 1200, and 1900 voxels within the flow region of S1, S2, and S3, respectively. The poorer comparison observed at S1 could also be a consequence of the lower number of voxels in the flow region at that location compared to the other slice locations.

The velocity encoding (Venc) of the PCMRI acquisition is typically set to a value that is able to capture the highest flow velocities during systole without aliasing. However, such Venc setting may not be appropriate for obtaining high signal-to-noise data during diastole if the flow velocities are near zero during that period of the cardiac cycle. If one needs to obtain more accurate flow velocity data during diastole, a separate acquisition with a lower Venc assignment may be called for. It is useful to note that the volumetric flow measurements was not affected by the lower signal-to-noise ratio: the MR measured volumetric flow waveform agreed closely with the flow probe measured waveform even during the resting condition diastolic period when the flow was very low and the MR measured velocity pattern appeared noisy.

When the flow velocities were averaged over all of the time points within the cardiac cycle, the S1 comparison for the light exercise condition was slightly better than that of the resting condition, likely due to the lack of backflow through the abdominal aorta. During parts of the cardiac cycle under resting condition where backflow occurred through the abdominal aorta, and continuous forward flow persisted through the renal branch, complex and aperiodic flow at the nearby S1 location was likely to occur and contribute to the slight differences in the comparison. The ability to predict whole-cycle averaged flow velocities is clinically useful, as many studies have correlated parameters such as mean blood flow and mean shear stress to blood vessel adaptation behavior and disease progression (4-6,43). In general, the good comparisons of the whole-cycle averaged velocity patterns we found at all of the three slice locations for both flow conditions bode well for the application of CFD in cardiovascular studies.

Previous validation studies that have used zero-pressure (21,36,44) or flow split ratio (45) BC have shown good velocity pattern comparisons between measurement and simulation under pulsatile flow conditions. Those studies, however, did not operate under physiologic pressures, and in the cases involving multiple outlets, could not achieve outflow waveforms of different shapes and phases through the different outlets. For example, the work presented by Zhao et al. featured flow waveforms through the two outlets of the phantom that were nearly identical (45). Such a limitation may be acceptable while mimicking a small subset of anatomical locations such as the coronary bifurcation, but it severely hampers the ability to realistically mimic many parts of the anatomy such as the aorta with renal branches where drastically different flow waveforms should exit the different outlets. While not possessing physiologic pressures, and different flow waveforms through multiple outlets, the levels of agreements between the measured and simulated results in previous validation studies were comparable to those presented in this study. The advantage of employing the Windkessel BC in this study is that physiological pressure and flow relationships, as well as physiological outflow waveforms through multiple outlets are possible, allowing the comparisons of pressure and flow under holistically physiological conditions.

In regards to the sources of errors in this study, we found that the segmentation and baseline correction variabilities in processing the MR data seemed to have little effect on the results. The geometric tolerance of the phantom manufacturing from the CAD model could also influence results, although it has been shown that slight geometric variations have minimal impact on simulated flow and pressure (36). Slight variations in the cyclic pump output could affect the PCMRI data integrity, but in general we were able to obtain highly periodic flows from the flow pumps. The values of the lumped parameter components, especially of the resistance modules, also have a large impact on the resultant pressure waveforms in the experiment. The slight differences between the measured and simulated pressures could be possibly attributed to small differences between the theoretical and the actual resistance values of the resistance modules. The inlet flow prescription can affect FEA simulation results, and slight differences in the numerical prescription of the input flow compared to that in the physical experiment could introduce errors in the simulation results. The numerical simulation also assumed fluid behaviors that must be precisely matched by the actual fluid used in the experiment. The mesh size we used for this problem was likely sufficient to solve the problem domain with reasonable fidelity, yet a larger mesh would certainly provide better mesh convergence. Since each set of the PCMRI data was acquired over hundreds of cardiac cycles, an ensemble average of the simulation results over a larger number of cycles might also provide better comparisons to the MR data. The PCMRI data was acquired using a 0.5cm slice thickness, where the simulation was run on a 0.1cm maximum edge size mesh, and the data was projected onto the analysis planes by linear interpolation from the nearest nodes. Examinations of the simulation data showed no significant qualitative differences in the velocity contours between slice planes that are offset approximately 0.3cm toward each direction. We thus concluded that the 0.5cm acquisition thickness of the PCMRI measurements does not significantly affect the qualitative comparison results. This is consistent with the findings of Ku et al. (36) who concluded that spatial averaging of CFD simulation results across a distance mimicking the PCMRI acquisition slice thickness produced little difference in the velocity contours. Finally, we estimate that the uncertainties in identifying the slice locations in the simulation data corresponding to the PCMRI measurements were within approximately 3mm.

The lumped parameter BC modules we developed in this study can provide the necessary tool to perform further in-vitro studies incorporating additional physiologically realistic aspects, such as compliance of the blood vessel. The ability to reproduce physiological pressures is absolutely essential for obtaining physiological deformation in an in-vitro experimental setup, allowing the investigations of behaviors mimicking in-vivo tissue motion and wave propagation. The effects on flow velocities and pressure due to vessel wall motion can be captured computationally by prescribing at the fluid-solid interface non-zero fluid velocities that are based on solid domain calculations (46). By prescribing accurate vessel wall properties for the solid domain calculations, we expect the computational simulation to be capable of predicting flow and pressure in a deformable geometry.

In conclusion, we have demonstrated the capabilities of numerical simulations to predict flow and pressure in a complex AAA geometry, and we have developed the necessary methods towards further validations of the numerical technique, which could eventually show that the numerical method can be applied clinically to make accurate predictions of pressure and flow in the vasculatures of a real patient.