Abstract
Background
A nonlinear isotropic finite element (FE) model of a 29 year old human crystalline lens was constructed to study the effects of various geometrical parameters on lens accommodation.
Methods
The model simulates dis-accommodation by stretching of the lens and predicts the change in the lens capsule, cortex and nucleus surface profiles at select states of stretching/accommodation. Multiple regression analysis (MRA) is used to develop a stretch-dependent mathematical model relating the lens sagittal height to the radial position of the lens surface as a function of dis-accommodative stretch. A load analysis is performed to compare the FE results to empirical results from lens stretcher studies. Using the predicted geometrical changes, the optical response of the whole eye during accommodation was analysed by ray-tracing.
Results
Aspects of lens shape change relative to stretch were evaluated including change in diameter (d), central thickness (T) and accommodation (A). Maximum accommodation achieved was 10.29 D. From the MRA, the stretch-dependent mathematical model of the lens shape related lens curvatures as a function of lens ciliary stretch well (maximum mean-square residual error 2.5×10−3 µm, p<0.001). The results are compared with those from in vitro studies.
Conclusions
The FE and ray-tracing predictions are consistent with EVAS studies in terms of load and power change versus change in thickness. The mathematical stretch-dependent model of accommodation presented may have utility in investigating lens behaviour at states other than the relaxed or fully-accommodated states.
Keywords: Crystalline lens, Accommodation, Presbyopia, Finite Element Method
Background
Accommodation is an opto-mechanical physiological process by which the eye alters its optical power to achieve clear vision from distance to near. The main components of the accommodative system consist of the lens that effects the change in optical focus, suspended at its equator by the zonules to the ciliary body containing the annular ciliary muscle.
The empirical study of the characteristics and behaviour of the accommodative system presents technical challenges due to the small dimensions (millimetres to microns), difficulty in measuring mechanical properties of the zonular fibres and the ciliary body in vivo, fine forces (milli-Newtons) involved in the intricately organized ocular tissues, and the inaccessible location of the lens inside an intact eye surrounded by the aqueous and vitreous. Despite these challenges, in vivo and ex vivo investigations have been carried out, with various levels of precision, to lend insight into the optical and mechanical aspects of accommodation. While in vivo investigations would be most preferred, these are hindered by additional physical limitations; for example, the view of the peripheral lens (towards its equator) is obscured by the iris. To some extent, these limitations may be circumvented by taking advantage of advanced techniques including ultrasound biomicroscopy (UBM) (1, 2) and MRI (3–7) although these imaging devices do require further improvements in resolution (6). Other limitations include the inaccuracy of physical experimental techniques due to the short period of viability of the post-mortem lens (8). One remaining unmet need is an in vivo method for directly investigating the forces involved in accommodation.
An alternative to empirical study is theoretical investigation, of which one approach is the finite element method (FEM). Finite element (FE) models (9–12) have been constructed and used to investigate lens behaviour during accommodation. Some have been used to evaluate certain theories of accommodation (9–13); to estimate the required dis-accommodative force exerted by the ciliary muscle (11); to study the age-dependence of the zonular forces as a proposed cause for presbyopia (14); to verify the effectiveness of proposed treatments for presbyopia (12); to investigate the effects of changing the lens material properties (15); to examine the importance of including the influence of the vitreous in accommodation (16) and to perform sensitivity analyses on the crystalline lens and accommodation (17). While other parameters such as the internal refractive index gradient (18) of the lens may also be involved, the principal parameter that determines lens optical power change during accommodation is the change in its surface curvatures. These surfaces include the anterior and posterior interfaces between aqueous, lens capsule, lens cortex, lens nucleus and vitreous. Previous FE models typically report the resultant optical power or load at particular instances or stretching steps during dis-accommodation (i.e. ciliary muscle relaxation leading to stretching of the zonules and lens). A few FE modelling studies have investigated the relationship between the progression of lens stretch and the resultant change in various aspects of lens surface profiles in terms of curvature or slope. However, although some studies have reported the force-dependent variation in certain geometrical parameters (e.g. the apical/central curvature radii of lens surfaces) (19–21), none of these studies have described the lens shape in terms of point-by-point profile across a substantial extent of the lens as a continuous function of the amount of ciliary stretch. A stretch-dependent model of lens surface shape and subsequently, lens optical power, would be of value as it could provide greater understanding of the mechanics and optics of the lens during the process of accommodation.
FE models to date have been constructed using lens shapes, forces and optical properties based on ‘typical’ values in the literature. Thus, individual or individualised values are not represented. The objective of the present study is to explore the stretch-dependent changes in terms of various geometrical parameters using numerical modelling and to develop a mathematical model of the surface profiles of the lens whose predictions can be validated against corresponding results obtained from direct ex vivo lens stretching experiments (22). As lens-stretcher systems are capable of providing results for individual eyes, we hope that this approach would provide firstly, a method for direct validation of the model and secondly, a basis for developing individualised models for a specific eye.
Methods
Base model: The Burd FE Model
For FE modelling, the procedure developed by Burd et al (9), henceforth referred to as the “Burd Model”, was replicated with some modifications/assumptions that are summarized in Table 1. The Burd Model is well-established and much-cited, providing predictions for 11, 29 and 45 years of age, and is reasonably straightforward to implement. This model has been verified to be able to portray most of the lens behaviour during accommodation and has been widely used (10–13, 16) to investigate aspects of accommodation and presbyopia.
Table 1.
Key modifications in the present model from the Burd Model.
| Category | Details | Reason |
|---|---|---|
| Discretisation | Quadratic quadrilateral 8-node element |
|
| Use of contact elements | To prevent sliding of contacting bodie | |
| Refined Elements towards the equatorial region | Accuracy/convergence | |
| Loading steps | Lens is gradually stretched in 10 steps with results at each step outputted | To facilitate investigation of relationship between progression of lens stretch and change in profiles of lens surfaces |
| Optical modelling | Optical performance evaluated using Ray-tracing Method | Paraxial calculations does not give an accurate lens optical power over a wider aperture |
In this study, we assumed the 29 year-old model of Burd as a starting point. Modifications were made to the model for achieving the objective of our study. For brevity, the remainder of the methods section will describe only key features and differences between the two models. The reader is encouraged to refer to Burd et al (2002) for full details of the original model.
Lens deformations during accommodation are known to be dependent on the material properties distribution (12). In the present model, the lens geometry and material properties from Burd et al. (2002) were adopted as the starting point. While different elastic moduli were assigned to the cortex and nucleus, the materials within each of the cortex and nucleus ‘compartments’ were considered to be isotropic and linear elastic. Time-dependent mechanical phenomena such as creep are beyond the scope of this study and were not taken into account.
The model in this study was implemented using the commercial FE software ANSYS (ANSYS® Academic Research, Release 13.0, ANSYS Inc., PA, USA) and the model was solved using ANSYS® Mechanical APDL (ANSYS Parametric Design Language).
Modelling the reference geometry: Discretisation of the model
To model the stretch-dependency of lens surface profiles, a higher data density for each position of stretch than the original Burd Model was instituted to improve precision. In an attempt to assure convergence and improve precision of solution, to discretise the model, quadratic quadrilateral 8-node elements were used instead of triangular elements to increase the number of calculation nodes. This element type is appropriate for the axi-symmetric analysis of nearly incompressible materials and should produce a more realistic portrayal of the lens. Surface-to-surface 3-node contact elements with “bonded” option set were placed in the nucleus-cortex and cortex-capsule contact boundary to prevent the contacting bodies from sliding or being detached. From the clinical macro-observation stand-point, it is familiar to most surgeons that significant manipulations are required to remove clumps of cortex or nucleus (even after phaco-emulsification) and to strip lens epithelial cells from the internal surface of the capsule. These observations imply a degree of ‘cohesiveness’ between layers of the lens that would prevent sliding between layers. Hence contact elements are used in this model.
The geometry is meshed using 9,766 elements (corresponding to 30,577 nodes). The meshed model of the entire lens, the zonular fibres and the ciliary anchoring point is shown in Figure 1.
Figure 1.
Discretised FE model of the accommodative system with boundary conditions applied; A: single-point ciliary body, accommodative stretch is applied to this point; B and D: anchoring points of the anterior and posterior zonules, respectively; Point C: Anchoring point of the equatorial zonules and the lens equator; The brighter areas represent the lens nucleus and cortex respectively; Elements are gradually refined as they approach the lens capsule; The lens polar axis is fixed (shown by roller support symbols) in the horizontal direction due to the lens axi-symmetry (i.e. no x-translation of the lens polar axis during stretch).
Boundary conditions and loading process
Employing the conventional assumption that the lens, when fully accommodated, is free of stresses; no pre-stresses are applied to the lens in the baseline (unstretched) configuration. As the lens is rotationally symmetric, the lens polar axis is permitted only one degree of freedom (i.e. translation in axial (Y) direction, see Figure 1) and the required pull (ciliary stretch) for dis-accommodation is applied as displacement in the horizontal (X) direction through a single-point ciliary body (Point A in Figure 1). It should be noted that the model in actuality simulates dis-accommodation (i.e. radially stretching, as opposed to releasing the lens). The initial, unstretch position represents the maximally accommodated (near focus) state of the lens while the maximally (end-point) stretched lens represents the distance focus state. In order to provide ease of comparability and consistency with previous studies, results are reported here in terms of accommodation and accommodative amplitude; that is, the difference in optical power from the maximally stretched, distance focus state, to the other states of stretch. The difference in power between maximally stretched and unstretched represents the maximum amplitude of accommodation.
In the Burd Model, the 29-year-old lens ciliary body was stretched to a maximum of 0.36 mm. In this study, the radial ciliary stretch was applied to the single-point ciliary starting from zero as the reference geometry to a maximum value of 0.49 mm in 10 steps with increments of approximately equal size ranging from 39 µm to 61 µm. This greater amount of stretch is commensurate with results of experiments on fresh donor tissues using a lens stretcher apparatus, the Ex Vivo Accommodation Simulator (EVAS) that showed human and non-human primate crystalline lenses can be stretched reversibly when the inner ciliary ring diameter is increased by up to approximately 0.8 mm in diameter (22,23) which is an equivalent of 0.4 mm half-diameter change in the axisymmetric FE model. The value of 0.49 mm (corresponding to a ciliary ring diameter increase of 0.98 mm) was chosen in order to maximise overlap of induced lens changes (as opposed to ciliary stretching) in the FE model with EVAS results for comparison purpose, while also ensuring convergence of the FE model.
FE analysis
A static structural analysis is carried out and the numerical model is solved using the ANSYS® FE package. Literature on FE modelling reports that changes in the lens to either the equatorial force or displacement does not follow a linear response (10, 12, 15, 25). Thus, a large deflection nonlinear solution was performed using the ANSYS APDL®.
Surface profiles fitting
The FE analysis generates the deformed profiles of the anterior and posterior capsule, cortex and nucleus at each step of ciliary body stretch. For each of the eleven steps (reference and ten stretching steps) and each of the six lens surfaces (i.e. aqueous-capsule, capsule-cortex, cortex-nucleus, nucleus-cortex, cortex-capsule, capsule-vitreous), Cartesian (X, Y) coordinates are extracted for 24 data points that are located approximately equally spaced from the lens axis (i.e. X = 0 mm) to 2.53 mm radial distance.
To satisfy identified requirements for functions describing lens surface curvatures (25), 6th-order even polynomials (Equation 1) were used to describe each of the six surfaces at each of eleven states of stretch. Even polynomial was used given the assumed symmetry of the profiles. Values for the polynomial coefficients (a through d) of Equation 1 were determined using a least-squares curve-fitting method to each set of points.
| (1) |
In Equation 1, Y represents the sagittal height (distance along Y-axis) of the surface in millimetres at the radial distance (from the axis) X in millimetres. During preliminary studies, 4th-order and 8th -order even polynomial fittings were also attempted. However, errors of estimate for the 4th -order curves (maximum residuals of 50 µm) were consistently higher (especially for points towards the lens equator) than those for the 6th -order polynomial (maximum residuals of 10 µm). Conversely, errors of estimate for the 8th -order fitting (maximum residuals of 9 µm) were consistently similar to those of the 6th -order suggesting possible redundancy, or at least numerical inefficiency.
Optical power calculation
For each of the eleven stretching steps, the optical power of the lens was calculated using an eye model constructed in an optical ray-tracing software (Zemax version 12, Radiant Zemax, Redmond WA, USA). Table 2 provides the prescription of this optical model eye for the initial (unstretched reference) 29-year-old lens.
Table 2.
Prescription of the optical eye model used for calculating change in optical power accommodation) at each step of stretch. The values shown are for the unstretched maximally accommodated) 29-year-old lens.
| Even Polynomial Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|
| Surface no. |
Surface Type | Component | Thickness (mm) |
Index | 2nd-Order (mm−1) |
4th-Order (mm−3) |
6th-Order (mm−5) |
Power (D) |
| 0 | Standard | Visual Object | Infinity | 1.000 | ||||
| 1 | Paraxial | Accommodation | 0.000 | 1.000 | 0.00† | |||
| 2 | Paraxial | Cornea (ideal) | 3.000 | 1.3374 | 42.00 | |||
| 3 | Even Asphere | Capsule Front | 0.721 | 1.381 | 8.991E-02 | −1.697E-03 | −5.404E-05 | |
| 4 | Even Asphere | Nucleus Front | 2.680 | 1.406 | 1.342E-01 | 2.053E-03 | 1.649E-04 | |
| 5 | Even Asphere | Nucleus Back | 0.733 | 1.381 | −1.408E-01 | −2.421E-03 | 4.750E-04 | |
| 6 | Even Asphere | Capsule Back | 15.718‡ | 1.336 | −1.371E-01 | −2.017E-03 | −2.004E-04 | |
| 7 | Standard | Retina | 1.336 | |||||
is the distance from the posterior lens to the retina set by optimisation of the most-stretched state (distance focus) in the first stage of computation.
is the optical power of the surface representing accommodation that is set by optimisation for all other stretched states in the second stage of computation
We assumed that the capsule does not contribute to the optical power of the lens. Thus, the refractive interfaces between aqueous-lens and lens-vitreous were considered to be the anterior aqueous-capsule (Surface 3) and posterior capsule-vitreous (Surface 6) surfaces while the capsule-cortex surfaces were ignored. In this way, the 6th -order even polynomials fitted to the four lens surfaces (anteriorly aqueous-capsule, cortex-nucleus, and posteriorly nucleus-cortex and capsule-vitreous) at each stretch step, together with the position of the vertex of the surfaces, were used to define the refracting surfaces (Surfaces 3 to 6) of the lens. The 6th -order even polynomial surfaces were implemented by using the “even asphere” surface type in Zemax.
The natural lens receives light rays that have already been refracted by the cornea – i.e. it does not operate at infinite conjugate ratio. We included this effect in the optical model by including an ideal thin lens (Surface 2) to represent corneal refraction, modelled using the “Paraxial” surface type in Zemax. This thin lens ‘cornea’ has focal length in air of 23.8 mm; approximately equivalent to the typical corneal power of 42 D, and is placed 3 mm in front of the anterior capsule surface of the lens to represent the distance from the cornea to the lens (i.e. the anterior chamber). To avoid confusion, it is worth noting that the “Paraxial” lens type in Zemax is a full-aperture lens (i.e. not limited to paraxial rays) that has ideal optical characteristics. In particular, its equivalent focal length at any ray-height is the same as its paraxial focal length (hence its name). Thus, ray-tracing is conducted at finite ray-heights, not just paraxially. This surface type was used to direct positive vergence incident rays onto the lens surface without introducing any aberrations.
The refractive indices assumed for the lens components were based on recent studies (27) while refractive indices for the aqueous and vitreous were values adopted from an established eye model (28). The lens equivalent index has been shown by recent studies to remain constant during accommodation (29, 30). Figure 2 shows the layout of the eye model in the unstretched state.
Figure 2.
Layout of the accommodative system optical model. Numbered surfaces corresponds to those of Table 2 together with their relative position (thickness column of the table). Surfaces 1 and 2 are co-located surfaces representing the optical power provided by accommodation and the idealized cornea. Surface 3 is the anterior capsule; Surfaces 4 and 5 the anterior and posterior cortex-nucleus interfaces, and Surface 6 the posterior capsule. During optical analysis, four rings of light rays are traced from distant object (left) to the retina (7 at far right).
A merit function system was constructed for optimisation of the model eye to determine the refractive power of the eye model at each lens stretch step. This merit function system is based on minimizing the RMS distance of four rings of light rays assuming axial symmetry. An entrance pupil diameter of 5 mm was used throughout. The above criteria for best focal position (RMS spot size) and pupil diameter were selected to provide comparability with the lens stretching system (22) against which the model’s predictions may be validated. Thus, it should be noted that the model portrays the opto-mechanical response of the lens itself and not ocular accommodation, as it does not include the influences of such known phenomena as Stiles-Crawford effect, polychromatic response of the eye (as are incorporated in, e.g. the Visual Strehl Ratio (20) and pupil miosis.
The amount of optical accommodation corresponding to each step of lens stretch was computed by placing an additional ideal thin lens (Surface 1) in the same plane as the idealized cornea. Thus with this arrangement, the calculated optical power, and subsequent accommodation amplitude, are referenced to the corneal surface.
The computation involved two stages. At the first stage, the maximally stretched condition (i.e. 0.49 mm of stretch) is assumed to correspond to distance focus (i.e. unaccommodated). We thus set the optical power of the paraxial thin lens (Surface 1) representing accommodation amplitude to zero (i.e. infinite focal length). Next we optimized the optical model using the merit function system to find the best position (vitreous to retina distance, thickness for Surface 6) for the retina. The retina position is then fixed for the remainder of the optical computation.
In the second stage, for each stretching step including the initial unstretched state in turn, we optimized the optical model using the merit function system by varying the power of the paraxial thin lens (Surface 1) representing accommodation amplitude. The negative of the value for the optical power found by optimisation represented the accommodative power for that stretch state.
Stretch-dependent function for surface profiles
Examination of the coefficients from the 6th -order polynomial fit of the lens surfaces plotted against ciliary body stretch suggested that a reasonable fit of surface profile against amount of stretch may be achieved using a 4th -order function of stretch.
Thus, a stretch-dependent function relating sagittal height, Y and radial distance X to amount of ciliary stretch S (in millimetres) was constructed according to Equation 2.
| (2) |
The coefficients for this function were computed using a least-squares multiple linear regression model.
Results
Figure 3 shows the vertical deformation (i.e. surface profile change) in the lens at four steps of stretch. Consistent with the Helmholtzian theory (31), when ciliary stretch is transmitted to the lens equator via the zonules (i.e. during dis-accommodation) the central lens curvatures become flatter resulting in the central lens thickness to reduce and the lens diameter to increase (see Figure 3). Maximum accommodation achieved was 10.29 D (referred at the corneal plane).
Figure 3.
Surface profile change of the lens at four accommodative steps: a) baseline geometry; b) S=200 µm, c) S=360 µm, d) S=490 µm.
By least-squares (bivariate) curve-fitting, changes in diameter (d), central thickness (T) and accommodation (A) can be described as an approximately linear function of lens stretch (S in mm) with standard error of estimate < 0.6 µm, respectively (Equations 3, 4 and 5).
| (3) |
| (4) |
| (5) |
The anterior and posterior zonules, which do not pull in an exactly vectorally radial direction. In addition, their zonules points of insertion at the capsule, together with the configuration of the lens and the elasticity of the lens cortex at the region of zonular insertion, renders the response slightly curvilinear. A second-order fit to the response provides a substantially improved fit with standard error of estimates of less than 0.2 µm (Equations 6, 7 and 8).
| (6) |
| (7) |
| (8) |
Figure 4 shows the variation in the lens total, nuclear and cortical thickness distribution versus accommodative stretch. Results show that the change in the nuclear thickness accounts for approximately 70% of the change in the total lens thickness at any amount of stretch.
Figure 4.
Change in nucleus, cortex and total thickness versus accommodative stretch. Approximately 70% of the change in total lens thickness is due to the change in nucleus thickness.
The profile changes of individual surfaces with ciliary stretch are plotted in Figure 5. The polynomial coefficients based on Equation 1 are found at each state of the ciliary stretch. Equation 1 fitted to each of the six surfaces returned a worst-case mean-squared residual error of 2.5×10−3 µm (for posterior cortex, p<0.001). These coefficients were then used as the input to the optical model. Surface fitting coefficients for the 3D stretch-dependent function (Equation 2) are listed in Table 3. The bolded values with asterisks are coefficients that contributed statistically significantly (p<0.01) to the surface profile with stretching.
Figure 5.
Profile changes of each surface with ciliary stretch. In all diagrams, the steepest profile (greatest sagittal height) corresponds to the unstretched (accommodated) lens.
Table 3.
Surface fitting coefficients for Equation 2.
| k2i,j | Anterior lens | Posterior lens | |||||
|---|---|---|---|---|---|---|---|
| j | i | Capsule | Cortex | Nucleus | Capsule | Cortex | Nucleus |
| 0 | 0 | 2.0397* | 2.0302* | 1.3193* | −2.0942* | −2.0784* | −1.3610* |
| 0 | 1 | −0.0900* | −0.0903* | −0.1343* | 0.1408* | 0.1409* | 0.1371* |
| 0 | 2 | 0.0017* | 0.0016* | −0.0021* | 0.0024* | 0.0027* | 0.0020* |
| 0 | 3 | 0.0001 | 0.0001 | −0.0002* | −0.0005* | −0.0005* | 0.0002* |
| 1 | 0 | −1.9014* | −1.9005* | −1.5980* | 0.3091* | 0.3007* | 0.1813* |
| 1 | 1 | 0.1887* | 0.1919* | 0.2828* | −0.0432 | −0.0348 | −0.0903* |
| 1 | 2 | −0.0035 | −0.0039 | −0.0093 | −0.0124 | −0.0159 | −0.006 |
| 1 | 3 | −0.0006 | −0.0006 | 0.0006 | 0.0008 | 0.0012 | −0.0008 |
| 2 | 0 | 4.7737* | 4.7830* | 4.8869* | 3.5111* | 3.5668* | 3.5231* |
| 2 | 1 | −0.2309 | −0.2522 | −0.4925* | −0.0456 | −0.1204 | −0.0433 |
| 2 | 2 | −0.0132 | −0.0087 | 0.0272 | −0.0066 | 0.0227 | −0.0110 |
| 2 | 3 | 0.0032 | 0.0031 | 0.0003 | 0.002 | −0.0015 | 0.0047 |
| 3 | 0 | −7.5634* | −7.5837* | −7.9770* | −7.0496* | −7.2100* | −7.184* |
| 3 | 1 | 0.0001 | 0.0583 | 0.4356 | −0.1050 | 0.1191 | −0.0206 |
| 3 | 2 | 0.0562 | 0.0426 | −0.0166 | 0.0637 | −0.0277 | 0.0637 |
| 3 | 3 | −0.0071 | −0.0068 | −0.005 | −0.0083 | 0.003 | −0.0113 |
| 4 | 0 | 5.1571* | 5.1749* | 5.4763* | 5.1669* | 5.3205* | 5.2335* |
| 4 | 1 | 0.1733 | 0.119 | −0.1138 | 0.1616 | −0.0577 | 0.0950 |
| 4 | 2 | −0.0534 | −0.0403 | −0.0101 | −0.0629 | 0.029 | −0.064 |
| 4 | 3 | 0.0055 | 0.0051 | 0.0063 | 0.0078 | −0.0036 | 0.0094 |
Bolded coefficients with asterisks are statistically significant at p<0.01.
The values for j represent orders for stretch (S) while 2i represents the orders for radial distance from axis (X)
A note regarding interpretation of Figure 5 and many of the subsequent figures: the curves plotted are for the absolute position of the surface points at their state of stretch. Since during stretching, the radial position of any given point changes (increases), points with the same radial distance but at different states of stretch are not corresponding points. That is, they are not from the same original unstretched point.
Figure 6 shows the plots for the anterior and posterior lens surfaces using the resultant 3D stretch-dependent mathematical model (Equation 2).
Figure 6.
Plot of the 3D stretch-dependent mathematical model (Equation 2) relating sagittal height of the six lens surfaces as a function of radial distance from geometrical axis and amount of stretch. The lens equatorial plane is at zero sagittal height. A 2D (plane) slice at a select stretch value provides the predicted profile for the six surfaces at that stretch state. Note that due to its thinness, the capsule thickness (upper-most and bottom-most surfaces) cannot be resolved in this plot.
Figure 7 shows the distribution of surface slope in the lens versus radial position. In all lens profiles, increasing the ciliary stretch causes the absolute slope at any point to decrease.
Figure 7.
Local slope variation across the lens at different ciliary stretch for the six lens surfaces.
From the surface slope and radial distance, the tangential and sagittal radii of curvature of the lens are calculated as a function of radial distances. The tangential radius (rt) is the instantaneous radius of curvature along the profile of the surface at a given point and is calculated using Equation 6.
| (6) |
The sagittal radius (rs) is the radius of curvature in a plane perpendicular to the profile. Geometrically, it is the distance from the given point to the intersection of the normal at that point and the lens axis. It is calculated using Equation 7.
| (7) |
Figures 8 and 9 show respectively the local distribution of the instantaneous (tangential) and axial (sagittal) radius of curvature for each surface. These two radius definitions are relevant to the optical power contribution of the lens surfaces. For example, the sagittal radius is inversely related to the on-axis power of the lens at a given radial distance from the axis (which optically equates to the ray-height).
Figure 8.
Distribution of instantaneous (tangential) radius of curvature across the lens at different ciliary stretch for the six lens surfaces.
Figure 9.
Distribution of axial (sagittal) radii of curvature across the lens at different ciliary stretch for the six lens surfaces.
The tangential radii of curvature in the capsule and cortex surfaces increase with increase in the radial position. This is similar to the geometry of the initial lens shape (i.e. flatter near the poles and steeper near the equatorial region). In the anterior nucleus, the radius of curvature undergoes a dramatic decrease with increase in radial position. In contrast, the radius of curvature in the posterior nucleus first increases slightly and then decreases with increase in the radial position (except for the s=0.00 mm profile which has constant radius of curvature since the nucleus was initially modelled as a circular curve).
Discussion
An FE model of the crystalline lens based on previous numerical studies has been constructed to predict quantitatively the changes in the surface profiles of the lens capsule, cortex and nucleus. Using these predictions, optical power calculations were performed with ray-tracing to determine the amount of accommodation with lens stretch. An additional advantageous feature of FE modelling is that it facilitates predicting the accommodative response for designing an accommodating IOL when a mechanical lens stretcher such as EVAS is not available (40, 41).
A novel 3D mathematical model relating the lens surface profile to lens stretch was developed and fitted to the results of the FE analysis.
Results suggest that even with an idealised, purely horizontal ciliary stretch, a small posterior shift occurs during dis-accommodation. This can be seen in the slight posterior shift in the equatorial plane of the lens in Figure 3 and suggests that, in the converse direction, a concomitant anterior shift occurs during accommodation, although the vertical component of this shift in the FE prediction is small, at around 80 µm. While in the correct direction, the predicted shift is small compared to literature values (9, 10, 13, 16). It is worth emphasising that the antero-posterior movement of the model on stretching is in ‘free space’, constrained only by the anchoring point of the zonules at the ciliary body. This is to maintain comparability with lens stretching systems which also do not substantially constrain the motion of the lens in the axial direction. To further improve the modelling of the antero-posterior movement of the lens on accommodation may require additional components and/or parameters in the FE model. This becomes a necessity if modelling the operation of certain designs of “accommodating intraocular lenses” (32).
The results shown in Figure 4, that the predicted change in nuclear thickness accounts for approximately 70% of the change in the total lens thickness at any amount of stretch, is close to the experimental results of Patnaik (1967) (33) and Dubbelman et al (2003) (34). Using Scheimpflug imaging, Dubbelman et al (2003) found that there were no measurable changes in the cortex thickness during accommodation, while the cortex accounts for 30% of the thickness change in the FEM. The reason for this difference could be that in their experimental study on real lenses, the gradient mechanical properties of the cortex and nucleus are included, whereas in our FEM we assign uniform Young’s moduli to the lens. It could also be that the optical and mechanical cortex and nucleus do not correspond to exactly the same definition of the anatomical regions as seen in vivo by Scheimpflug imaging.
It can be seen from Figure 7 (c, f) that the ciliary stretch substantially alters the slope of the nucleus profiles near the equator, it only changes the nucleus slope near the polar region slightly. Further, Figure 8 shows that while the radii of curvature at the pole steadily increase with stretch, the radii of curvature near the equatorial region first decreases very slightly before increasing. The results show that there is a 53% and 25% reduction in the central anterior and posterior surface curvatures, respectively, when the lens is dis-accommodated with 0.49 mm stretch.
While it has been well-established, and reproduced by the present model, that the lens continuously flattens in curvature over its central region (the most optically relevant region) during dis-accommodation, .
Figure 8 and Figure 9 also show that both the tangential and sagittal radii increases at all points on dis-accommodation, with only the exception of the anterior lens capsule and cortex. These latter decrease in tangential radius on stretching at radial distances above about 2 mm.
Reconciliation with lens stretcher results
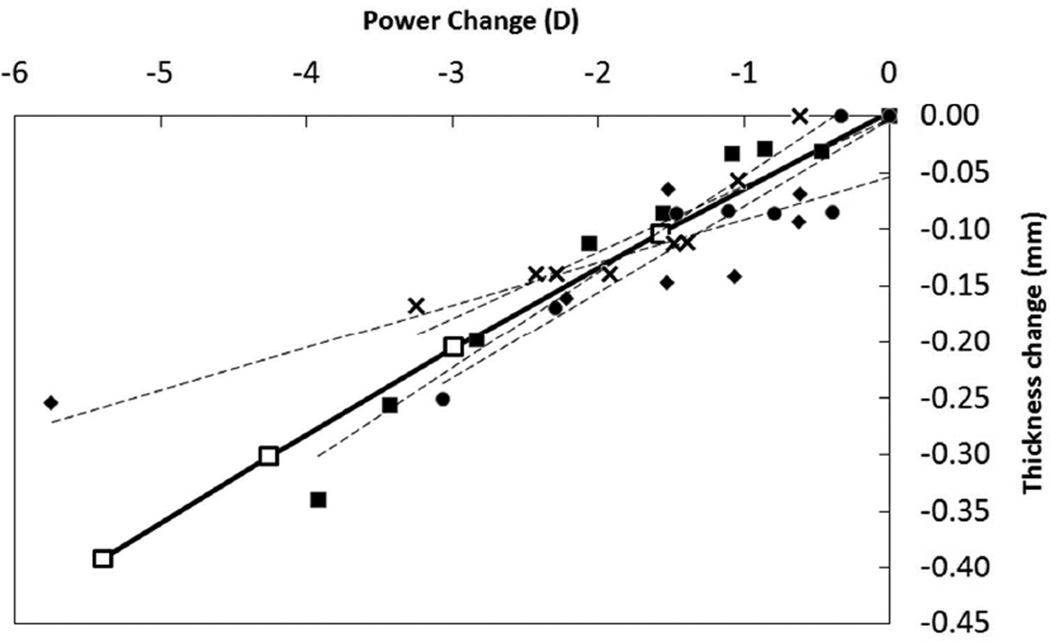
At corresponding states of stretch, the surface profiles predicted with the current model compare well with those of the Burd Model verifying that our model with the modifications is behaving appropriately. This study extends on the work of Burd et al by using a 3D surface-fitting mathematical model to relate lens surface profiles to state of stretch, thereby realizing a model from which surface shapes may be interpolated for any desired state of stretch. This extension from an FE model, predicting lens changes against amount of stretch, enables the comparison of the model against published empirical data on lens shape versus stretch – in particular, those produced from lens stretcher apparatuses (22, 23). Figure 10 compares various responses of the EVAS experiments on eyes from donors of age around 30 years (23) to our numerical modelling results that assumed a 29 year old lens. The FE results show a thickness change per dioptre of accommodation of 0.08 mm/D which is favourably comparable with a value of 0.06 mm/D found in the literature (23). Also, the FE model is consistent with literature which found a linear relationship between the accommodative force and the lens diameter. In particular, Augusteyn et al found approximately a diameter change of 4 microns per milli-Newtons force which is in close agreement to the value of 6.25 microns of diameter change per milli-Newtons force from our model (23).
Figure 10.
Comparison of FE modelling predictions with individual eye results from EVAS studies. In all graphs, the hollow square marks the FEM data. Dashed lines are linear trends for each of the five sets of EVAS results. a) Load versus change in lens diameter, b) Load versus change in lens thickness c) Thickness change versus accommodation.
There are a number of factors which could explain the difference between the FEM and EVAS results:
Firstly, the zonular arrangement in the model does not portray the natural arrangement observed by scanning electron microscopy and confocal microscopy in both adult human and young non-human primates. In addition, the zonules do not all terminate at one point at the ciliary body as the model approximates; instead the anterior zonules pass through the ciliary processes and have branches that are attached to the ciliary processes while the posterior zonules are part of and surrounds the hyaloid membrane (35) that encases the vitreous body. In addition, recent ultrasound biomicroscopy studies performed in rhesus monkeys show posterior zonules that seem to connect directly to the pars plana of the ciliary. In reality, anterior and posterior zonules terminate at the pars plana–pars plicata region (36). The distribution of zonular attachments to the lens capsule and ciliary body are complex. Moreover, these fibres exhibit varied directionality and interlacing (37) making a faithful model difficult to construct. Further, it is known that the positions of distribution of zonular attachment changes with continuous lens growth as a result of aging (38). A model that reproduces the effect of zonular transmission of forces from the ciliary to the lens at that microscopic level remains a key challenge.
Figure10a and Figure 10b compare the load versus diameter-change and load versus thickness-change response from the FE model and EVAS experiments for selected individual eyes between 29 to 31 years old. It may be seen that although the experimental data on thickness change suffer from a relatively large amount of scatter, the response found from our model is qualitatively consistent with the EVAS measurements in terms of magnitude of change and linearity; both the FE model and EVAS measurements of Augusteyn et al (2011) suggest a linear response with the accommodative load. The discrepancy could be due to less accurate input data on the lens material properties. But it should be noted also that lens diameter is not the most robust parameter by which to assess accommodative response - diameter change is a relatively small amount and lens diameter measurements in EVAS have limited precision. Additionally, due to scarcity of data, the vitreous and hyaloid membrane were not modelled in this study which could affect the outcomes as they are directly in contact with the lens. Discrepancy in the predicted load may also be due to the possible difference between the modelled zonular architecture and reality. Modelling the exact zonular geometry is not possible due to at least two reasons; first, the zonular architecture is not known accurately and also a natural randomness exists and different eyes have different zonular geometry. Second, the limitations inherent in FE modelling reduce the similarity of the modelled zonules and the real architecture to some extent. From another point of view, in the FE model, due to local deformations and stress concentration at the zonular insertion points (equatorial region) the outputted diameter is not exact and may be affected by the stress concentration at the zonules tip. It could be seen from Figure 10c that the thickness-change versus accommodation response (power change) of the FE model compares very well with that of EVAS. It should be noted that the accommodation amplitude calculated in the current model is referred to the corneal plane while the lens stretch (EVAS) optical calculations are referred to the mid-plane (approximately equatorial plane) of the lens sample. The difference in effectivity due to the difference reference plane positions (around 5 mm maximum), at the largest accommodation found (around 10 D), amounts to a maximum discrepancy in power of less than 0.5 D which is negligible.
Doubtlessly, further enhancements to the model are needed. Experimental data demonstrated that core (nucleus and cortex) elasticity is not constant in the lens but varies from the lens centre to the outer lens (18, 34). This gradient in mechanical properties may need to be modelled in unison with the known gradient refractive index of the lens. To fully model the opto-mechanical behaviour of the lens, their effects should be taken into account. Future models could combine the stretch-dependency of the current model with age-dependency to construct a comprehensive stretch and age-dependent mathematical model capable of covering the effect of ciliary stretch with aging to provide an improved basis for understanding presbyopia.
With further refinement of the model, the ability for validation of model predictions against direct empirical results of individual lenses, will hopefully, provide a platform from which individualised models for specific lens and eyes may be developed. From this, new knowledge founded on understanding the finer, individual differences may ensue.
Conclusions
A numerical finite element model based on a previous model has been constructed and used to characterize the stretch-dependent changes in the surface profiles of the anterior and posterior lens capsule, cortex and nucleus. A function relating the profiles of the capsule, cortex and nucleus to the amount of ciliary stretch was obtained by multiple linear regression of the model output. The results of the study are in agreement with recent ex vivo studies in terms of load and power change versus change in thickness, however, more work is needed to improve the prediction relating load and diameter. This model can then provide the basis for a quasi-analytical solution for the optics of accommodation.
Acknowledgements
The authors dedicate this study to the memory of Jerry Chen (1978–2009) who initiated much of our program in FE modelling that led to this work. The authors gratefully acknowledge Profs Jean-Marie Parel (University of Miami) and Robert Augusteyn (Brien Holden Vision Institute) for their encouragement, guidance and constructive comments on the manuscript, Dr Thomas John Naduvilath for assistance with statistical analyses, and Dr Ashik Mohamed (LV Prasad Eye Institute) for providing us with the EVAS data. The study was supported in part by National Eye Institute Grants 2R01EY014225 and 1R01EY021834, and P30EY014801 (Center Grant); an unrestricted grant from Research to Prevent Blindness.
Footnotes
Competing interests
The authors declare that they have no competing interests.
References
- 1.Schachar RA, Kamangar F. Computer image analysis of ultrasound biomicroscopy of primate accommodation. Eye. 2006;20(2):226–233. doi: 10.1038/sj.eye.6701838. [DOI] [PubMed] [Google Scholar]
- 2.Urs R. PhD Thesis. University of Miami; 2010. Investigation of Accommodation and Presbyopia using Ultrasound Imaging during Ex Vivo Simulated Accommodation. [Google Scholar]
- 3.Kasthurirangan SM, Atchison DA, Pope JM. MRI study of the changes in crystalline lens shape with accommodation and aging in humans. Journal of Vision. 2011;11(3):1–16. doi: 10.1167/11.3.19. [DOI] [PubMed] [Google Scholar]
- 4.Strenk SA, Semmlow JL, Strenk LM, Munoz P, Gronlund-Jacob J, DeMarco JK. Age-related changes in human ciliary muscle and lens: A magnetic resonance imaging study. Investigative Ophthalmology and Visual Science. 1999;40(6):1162–1169. [PubMed] [Google Scholar]
- 5.Strenk SA, Strenk LM, Guo S. Magnetic resonance imaging of aging, accommodating, phakic, and pseudophakic ciliary muscle diameters. Journal of Cataract & Refractive Surgery. 2006;32(11):1792–1798. doi: 10.1016/j.jcrs.2006.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Strenk SA, Strenk LM, Guo S. Magnetic resonance imaging of the anteroposterior position and thickness of the aging, accommodating, phakic, and pseudophakic ciliary muscle. Journal of Cataract & Refractive Surgery. 2010;36(2):235–241. doi: 10.1016/j.jcrs.2009.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Langner SM, Terwee T, Koopmans SA, Krüger PC, Hosten N, Schmitz K, Guthoff RF, Stachs O. 7.1 t MRI to assess the anterior segment of the eye. Investigative Ophthalmology & Visual Science. 2010;51(12):6575–6581. doi: 10.1167/iovs.09-4865. [DOI] [PubMed] [Google Scholar]
- 8.Augusteyn RCR, Borja D, Ziebarth NM, Parel JM. Biometry of primate lenses during immersion in preservation media. Molecular Vision. 2006;12:740–747. [PubMed] [Google Scholar]
- 9.Burd HJ, Judge SJ, Cross JA. Numerical modelling of the accommodating lens. Vision Research. 2002;42(18):2235–2251. doi: 10.1016/s0042-6989(02)00094-9. [DOI] [PubMed] [Google Scholar]
- 10.Judge SJ, Burd HJ. Modelling the mechanics of accommodation and presbyopia. Ophthalmic and Physiological Optics. 2002;22(5):397–400. doi: 10.1046/j.1475-1313.2002.00065.x. [DOI] [PubMed] [Google Scholar]
- 11.Hermans EA, Dubbelman M, van der Heijde GL, Heethaar RM. Estimating the external force acting on the human eye lens during accommodation by finite element modelling. Vision Research. 2006;46(21):3642–3650. doi: 10.1016/j.visres.2006.04.012. [DOI] [PubMed] [Google Scholar]
- 12.Van de Sompel D, Kunkel GJ, Hersh PS, Smits AJ. Model of accommodation: Contributions of lens geometry and mechanical properties to the development of presbyopia. Journal of Cataract & Refractive Surgery. 2010;36(11):1960–1971. doi: 10.1016/j.jcrs.2010.09.001. [DOI] [PubMed] [Google Scholar]
- 13.Martin H, Guthoff R, Terwee T, Schmitz KP. Comparison of the accommodation theories of Coleman and of Helmholtz by finite element simulations. Vision Research. 2005;45(22):2910–2915. doi: 10.1016/j.visres.2005.05.030. [DOI] [PubMed] [Google Scholar]
- 14.Hermans EA, Dubbelman M, van der Heijde GL, Heethaar RM. Change in the accommodative force on the lens of the human eye with age. Vision Research. 2008;48(1):119–126. doi: 10.1016/j.visres.2007.10.017. [DOI] [PubMed] [Google Scholar]
- 15.Schachar RA, Abolmaali A, Le T. Insights into the age-related decline in the amplitude of accommodation of the human lens using a non-linear finite-element model. British Journal of Ophthalmology. 2006;90(10):1304–1309. doi: 10.1136/bjo.2006.100347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ljubimova D, Eriksson A, Bauer S. Aspects of eye accommodation evaluated by finite elements. Biomechanics and Modeling in Mechanobiology. 2008;7(2):139–150. doi: 10.1007/s10237-007-0081-2. [DOI] [PubMed] [Google Scholar]
- 17.Abolmaali A, Schachar RA, Le T. Sensitivity study of human crystalline lens accommodation. Computer Methods and Programs in Biomedicine. 2007;85(1):77–90. doi: 10.1016/j.cmpb.2006.08.005. [DOI] [PubMed] [Google Scholar]
- 18.Weeber H, Eckert G, Pechhold W, Heijde RL. Stiffness gradient in the crystalline ens. Graefes Archive of Clinical and Experimental Ophthalmology. 2007;245(9):1357–1366. doi: 10.1007/s00417-007-0537-1. [DOI] [PubMed] [Google Scholar]
- 19.Lanchares E, Navarro R, Calvo B. Hyperelastic modelling of the crystalline lens, Accommodation and presbyopia. Journal of Optometry. 2012;05(03):110–120. [Google Scholar]
- 20.Rosales P, Wendt M, Marcos S, Glasser A. Changes in crystalline lens radii of curvature and lens tilt and decentration during dynamic accommodation in rhesus monkeys. Journal of Vision. 2008;8(1) doi: 10.1167/8.1.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ni YLX, Wu MX, Lin Y, Sun YY, He C, Liu YZ. Objective evaluation of the changes in the crystalline lens during accommodation in young and presbyopic populations using Pentacam HR system. International Journal of Ophthalmology. 2011;4(6):611–615. doi: 10.3980/j.issn.2222-3959.2011.06.07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Manns F, Denham D, Billotte C, Ziebarth N, Borja D, Fernandez V, Aly M, Arrieta E. Optomechanical response of human and monkey lenses in a lens stretcher. Investigative Ophthalmology & Visual Science. 2007;48(7):3260–3268. doi: 10.1167/iovs.06-1376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Augusteyn RC, Mohamed A, Nankivil D, Veerendranath P, Arrieta E, Taneja M, Manns F, Ho A, Parel JM. Age-dependence of the optomechanical responses of ex vivo human lenses from India and the USA, and the force required to produce these in a lens stretcher: The similarity to in vivo disaccommodation. Vision Research. 2011;51(14):1667–1678. doi: 10.1016/j.visres.2011.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Borja DM, Manns F, Ho A, Ziebarth NM, Acosta AC, Arrieta-Quintera E, Augusteyn RC, Parel JM. Refractive power and biometric properties of the nonhuman primate isolated crystalline lens. Investigative Ophthalmology & Visual Science. 2010;51(4):2118–2125. doi: 10.1167/iovs.09-3905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chien HM, Huang T, Schachar RA. Analysis of human crystalline lens accommodation. Journal of Biomechanics. 2006;39(4):672–680. doi: 10.1016/j.jbiomech.2005.01.017. [DOI] [PubMed] [Google Scholar]
- 26.Chien HM, Huang T, Schachar RA. A mathematical expression for the human crystalline lens. Compr Ther. 2003;29(4):244–258. doi: 10.1385/comp:29:4:244. [DOI] [PubMed] [Google Scholar]
- 27.Hermans EA, Dubbelman M, Kuijer JPA, van der Heijde RGL, Heethaar RM. Constant volume of the human lens and decrease in surface area of the capsular bag during accommodation: An MRI and Scheimpflug study. Investigative Ophthalmology & Visual Science. 2009;50(1):281–289. doi: 10.1167/iovs.08-2124. [DOI] [PubMed] [Google Scholar]
- 28.Navarro RS, Bescós J. Accommodation-dependent model of the human eye with aspherics. Journal of the Optical Society of America A, Optics and Image science. 1985;2(8):1273–1281. doi: 10.1364/josaa.2.001273. [DOI] [PubMed] [Google Scholar]
- 29.Hermans EA, Dubbelman M, van der Heijde RGL, Heethaar RM. Equivalent Refractive Index of the Human Lens upon Accommodative Response. Optometry & Vision Science. 2008;85(12):1179–1184. doi: 10.1097/OPX.0b013e31818e8d57. [DOI] [PubMed] [Google Scholar]
- 30.Maceo BM, Manns F, Borja D, Nankivil D, Uhlhorn S, Arrieta E, Ho A, Augusteyn RC, Parel JM. Contribution of the crystalline lens gradient refractive index to the accommodation amplitude in non-human primates: in vitro studies. Journal of Vision. 2011;11(13):23. doi: 10.1167/11.13.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Helmholtz H. Physiological optics. Vol. 1. New York: Dover; 1962. von. (1909) pp. 143–172. English translation by JPC Southall for the Optical Society of America (1924) 603 from the 3rd German edition of Handbuch der Physiologischen Optik. Hamburg: Voss. [Google Scholar]
- 32.Hancox J, Spalton D, Heatley C, Jayaram H, Marshall J. Objective measurement of intraocular lens movement and dioptric change with a focus shift accommodating intraocular lens. Journal of Cataract & Refractive Surgery. 2006;32(7):1098–1103. doi: 10.1016/j.jcrs.2006.01.092. [DOI] [PubMed] [Google Scholar]
- 33.Patnaik B. A photographic study of accommodative mechanisms: changes in the lens nucleus during accommodation. Investigative Ophthalmology & Visual Science. 1967;6(6):601–611. [PubMed] [Google Scholar]
- 34.Dubbelman M, van der Heijde GL, Weeber HA, Vrensen GFJM. Changes in the internal structure of the human crystalline lens with age and accommodation. Vision Research. 2003;43(22):2363–2375. doi: 10.1016/s0042-6989(03)00428-0. [DOI] [PubMed] [Google Scholar]
- 35.Bernal A, Parel JM, Manns F. Evidence for posterior zonular fiber attachment on the anterior hyaloid membrane. Investigative Ophthalmology and Visual Science. 2006;47(11):4708–4713. doi: 10.1167/iovs.06-0441. [DOI] [PubMed] [Google Scholar]
- 36.Lütjen-Drecoll EK, Wasielewski R, Ting-Li L, Croft MA. Morphology and accommodative function of the vitreous zonule in human and monkey eyes. Investigative Ophthalmology & Visual Science. 2010;51(3):1554–1564. doi: 10.1167/iovs.09-4008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Glasser A, Campbell MCW. Presbyopia and the optical changes in the human crystalline lens with age. Vision Research. 1998;38(2):209–229. doi: 10.1016/s0042-6989(97)00102-8. [DOI] [PubMed] [Google Scholar]
- 38.Farnsworth PN, Shyne SE. Anterior zonular shifts with age. Experimental eye Research. 1979;28(3):291–297. doi: 10.1016/0014-4835(79)90091-5. [DOI] [PubMed] [Google Scholar]
- 39.Wilde GS, Burd HJ, Judge SJ. Shear modulus data for the human lens determined from a spinning lens test. Experimental Eye Research. 2012;97(1):36–48. doi: 10.1016/j.exer.2012.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McLeod SD, Vargas LG, Portney V, Ting A. Synchrony dual-optic accommodating intraocular lens: Part 1: Optical and biomechanical principles and design considerations. Journal of Cataract and Refractive Surgery. 2007;33(1):37–46. doi: 10.1016/j.jcrs.2006.09.020. [DOI] [PubMed] [Google Scholar]
- 41.Sheppard AL, Bashir A, Wolffsohn JS, Davies LN. Accommodating intraocular lenses: a review of design concepts, usage and assessment methods. Clinical and Experimental Optometry. 2010;93(6):441–452. doi: 10.1111/j.1444-0938.2010.00532.x. [DOI] [PubMed] [Google Scholar]