Rate of evolutionary change in cranial morphology of the marsupial genus Monodelphis is constrained by the availability of additive genetic variation

Abstract

We tested the hypothesis that the rate of marsupial cranial evolution is dependent on the distribution of genetic variation in multivariate space. To do so, we carried out a genetic analysis of cranial morphological variation in laboratory strains of Monodelphis domestica and used estimates of genetic covariation to analyze the morphological diversification of the Monodelphis brevicaudata species group. We found that within-species genetic variation is concentrated in only a few axes of the morphospace and that this strong genetic covariation influenced the rate of morphological diversification of the brevicaudata group, with between-species divergence occurring fastest when occurring along the genetic line of least resistance. Accounting for the geometric distribution of genetic variation also increased our ability to detect the selective regimen underlying species diversification, with several instances of selection only being detected when genetic covariances were taken into account. Therefore, this work directly links patterns of genetic covariation among traits to macroevolutionary patterns of morphological divergence. Our findings also suggest that the limited distribution of Monodelphis species in morphospace is the result of a complex interplay between the limited dimensionality of available genetic variation and strong stabilizing selection along two major axes of genetic variation.

INTRODUCTION

A fundamental question in studies of morphological evolution is whether the genetic architecture of traits is capable of influencing the amount and rate of evolutionary change in morphology at a macroevolutionary level (Agrawal & Stinchcombe, 2009). While genetic variation for individual traits is abundant, the presence of genetic correlations implies that some multivariate combinations will hold more genetic variation than others. This uneven distribution of genetic variation in multivariate space should affect the rate at which a population evolves along the different dimensions (Marroig & Cheverud, 2005). Estimating the geometry of genetic variation in high dimensional systems, like the mammalian skull, is a difficult task given the large breeding designs and sampling efforts necessary to accurately estimate genetic variance/covariance matrices (G) (Steppan et al., 2002). Therefore, studies of phenotypic covariation have become increasingly used as proxies for studies of genetic covariation.

Phenotypic studies have shown that morphological traits tend to be organized into distinct clusters of highly intercorrelated traits, termed modules (Marroig & Cheverud, 2001; Goswami, 2007; Porto et al.,2009; Koyabu et al., 2014). The mammalian skull is composed of two major modules: the face and neurocranium (Cheverud, 1996). Interestingly, highly altricial mammalian clades, such as marsupials, have a less overt modular structure (Porto et al., 2013), marked by strong between-module integration. As a consequence, the overall level of association among cranial morphological elements in marsupials is much higher than in eutherian mammals (Porto et al., 2009; Shirai & Marroig, 2010). Variation in one trait is often strongly associated with variation in the whole structure, resulting in some marsupial species presenting as much as 85% of their total morphological variation concentrated along a single allometric size axis (Porto et al., 2009). If genetic in origin, this strong covariation among traits within populations has the potential to produce strong microevolutionary constraints on evolution along any dimension other than overall size, the only dimension with abundantly available variation in marsupials (Porto et al., 2009). These microevolutionary constraints, in turn, would provide us with a proximate cause for the long standing observation that the occupation of morphospace by marsupials is much more restricted than by eutherians, even when fossils are taken into account (e.g., Sears, 2004; Cooper & Steppan, 2010; Kelly & Sears, 2011; Bennett & Goswami, 2013).

Still, evolutionary inferences based on phenotypic covariation among traits rely on several assumptions (Ackermann & Cheverud, 2002). A major assumption is that patterns and magnitudes of integration observed at the level of the phenotype (P) are reflective of the underlying genetic covariance structure (G). This assumption has never been empirically tested for marsupials.

Evolutionary inferences based on trait covariation also rarely tackle the issue of whether strong genetic covariation will effectively facilitate the evolutionary diversification of the group along certain morphological dimensions at the expense of others and, consequently, that failure to incorporate information about trait integration will lead to incorrect inferences regarding the evolutionary processes that led to species diversification. Part of the difficulty lies in predicting how the potentially complex structure of G will affect the evolutionary change in morphology (Arnold et al., 2001). Marsupials, however, represent a unique opportunity in which to test hypotheses relating G to the pattern of between-species divergence, due to the simple expectations that can be drawn from their broadly shared within-population covariance structure (Porto et al., 2009; Shirai & Marroig, 2010). In particular, the concentration of morphological variation along a single allometric size axis allows us to hypothesize that morphological evolution should proceed at a fast pace when occurring along the allometric size dimension and at a slow pace whenever it occurs along other dimensions.

Here we take advantage of the Texas Biomedical Research Institute (Texas Biomed) strains of the gray short-tailed opossum (VandeBerg & Williams-Blangero, 2010), Monodelphis domestica, to carry out a quantitative genetic analysis of cranial morphological variation in this species, coupled with an analysis of the evolutionary diversification of the Monodelphis brevicaudata species group. We focus on the brevicaudata group given the group’s well resolved taxonomy and systematics (Voss et al., 2001; Pavan et al., 2012; Pavan et al., 2014). We start by estimating G and showing that it shares not only the overall pattern but also the high level of morphological integration observed in the phenotype. We then use G to analyze patterns of between-species divergence in the brevicaudata group. The analysis of between-species divergence is divided into two main approaches. First, we test the prediction that the rates of morphological evolution along the branches of the phylogeny are strongly associated with whether divergence occurs in size. Second, we test the hypothesis that incorporating information about genetic covariation increases our ability to detect the selective regimes underlying species diversification. To measure the impact of genetic covariances on our inferences, we here follow Agrawal & Stinchcombe (2009) and carry out tests of neutral evolution under two different scenarios. In the first scenario genetic covariances are taken into account, while in the second covariances are set to zero. By comparing the two scenarios, we hope to show that failure to take genetic covariances into account in studies of morphological evolution of this group can lead to fundamentally different conclusions regarding the nature of the evolutionary processes that operated throughout the diversification of the group.

METHODS

Samples

We measured 468 Monodelphis skulls in this study. Of these, 199 correspond to laboratory specimens of Monodelphis domestica, belonging to 16 partially inbred strains raised at the Texas Biomed (Table S1). All laboratory specimens are 400 days of age and are mid-aged adults. The mean inbreeding coefficient of individuals within strains is approximately 0.7. Strains are closely related relative to natural populations and present an average between-strain coefficient of kinship of 0.1. To maintain consistency, strain names correspond to the strain identifications at Texas Biomed (VandeBerg & Williams-Blangero, 2010).

The remaining 269 individuals correspond to adult specimens belonging to six different species from the brevicaudata species group (Pavan et al., 2014) (Table S1). We chose the brevicaudata species group as the focus of the analysis of morphological diversification for several reasons. The brevicaudata group’s taxonomy and systematics were the focus of recent studies (Voss et al., 2001; Pavan et al., 2012). Museum availability in Brazilian/US collections and detailed osteological descriptions (Wible, 2003) also contributed to this decision. We follow the taxonomic arrangement proposed by Pavan et al.(2014) throughout this study. Our samples of M. brevicaudata are restricted to northern Guyana and Venezuela, south of the Orinoco river; samples of M. palliolata are from northern Venezuela; samples of M. arlindoi are from Suriname and northern Brazil (Pará); samples of M. touan are from northern Brazil (Amapá); and samples of M. glirina are from the Brazilian Amazon, south of the Amazon river. Wild-caught samples of M. domestica are from Bolivia, Paraguay, and central and northeastern Brazil. A complete list of measured specimens is available as Appendix S1.

Measurements

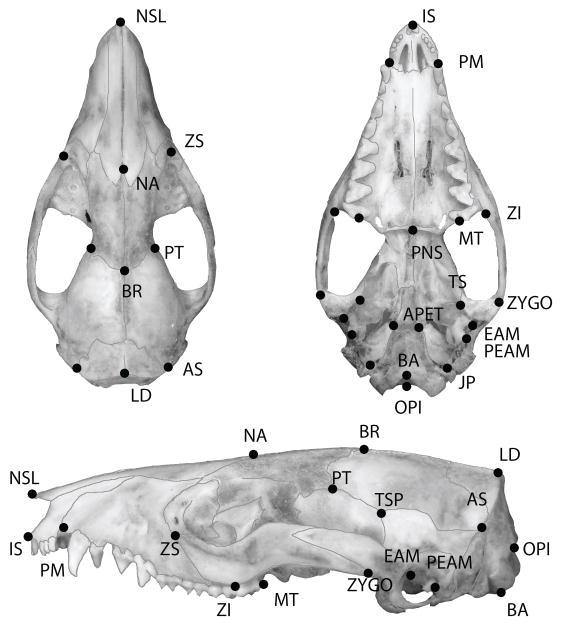
We recorded three-dimensional coordinates for thirty-four cranial landmarks (Figure 1) using a Microscribe digitizer (MX/3DX models). From this landmark dataset, we extracted a set of 30 linear measurements that represent skull morphology without much redundancy caused by measurement colinearity in 3D space (Table S2). This procedure for measuring specimens is detailed in Marroig & Cheverud (2001). We measured all specimens twice. Since repeatabilities were high (>0.9) (Lessells & Boag, 1987), we used the average of the repeated measurements in the subsequent analyses.

Figure 1.

Thirty four landmarks on the dorsal, ventral and lateral view of a Monodelphis domestica cranium. Landmarks are placed at the intersection of cranial sutures and other identifiable features.

Estimation of a high-dimensional G

In this study, our main strategy was to use the between-strain differences in cranial traits to estimate G and then draw evolutionary inferences from it. Estimating high-dimensional G matrices represents a challenge to any researcher interested in the evolution of complex phenotypes. Unconstrained G-matrices for 30 traits require that 30(30+1)/2 parameters be estimated (Kirkpatrick & Meyer, 2004) This number largely overwhelms the effective number of individuals that we were able to sample. While small effective sample sizes are the norm in the G-matrix literature (Steppan et al., 2002), classical unconstrained estimates of such high dimensional G are bound to be swamped by sampling error (Marroig et al. 2012). Constrained estimators, by reducing the number of relevant underlying parameters, offer a possible alternative to this problem (Runcie & Mukherjee, 2013). Our knowledge of the determinants of complex phenotypes suggests that these are the result of a limited number of underlying factors (e.g., developmental/functional processes). For the mammalian skull, these underlying factors are often modular in nature (Koyabu et al., 2014), meaning that each of these developmental processes affects only a few traits. Therefore, here we used a recently described Bayesian sparse factor model (BSFG) to estimate G (Runcie & Mukherjee, 2013). This model represents an extension of the animal model to high-dimensional data, using two main constraints. Firstly, the model assumes that a limited number of factors underlie most of the variation in the complex phenotype. It does so not by constraining the number of factors per se but by assuming that the majority of them are relatively unimportant. So, instead of attempting to identify the number of existent latent factors (k), the model uses information on the decline in the influence of successive latent factors and, during the model fitting procedure, retains only the first k*factors. In our case, we only kept the latent factors that explain at least 1% of the phenotypic variance. The second main constraint of the model is that it assumes that each of these factors affects a limited number of traits. The main advantage of using such a model is that it constrains estimation of G to a space that is biologically realistic, therefore preventing sampling error from dominating the genetic signal. The other major advantage of such a model, in our case, is that its priors assume that most factors have modular effects, implying that G matrices derived from it are expected to be highly modular. The major disadvantage of using constrained estimators is the possibility of overly constraining the covariance structure, generating apparent genetic signal where there is only noise. To evaluate the extent to which the BSFG model constrains G’s covariance structure, we compared our estimate of G to one in which individuals are randomly assigned to strains (G_noise). The general form of the BSFG is:

$$\mathbf{G}=\mathbf{\Lambda }{{\mathbf{\sum }}_{\mathbf{h}}}^{\mathbf{2}}{\mathbf{\Lambda }}^{\mathbf{t}}+{\mathbf{\psi }}_{\mathbf{a}}$$ (2)

where Λ is the matrix of trait loadings on each factor, Σ_h² is the diagonal matrix of factor heritabilities (broad-sense), and ψ_a is the diagonal matrix of trait-specific genetic variances. The model required four main inputs: a n x p matrix of phenotypic observations (Y), a b x n fixed effect design matrix (X), a r x n random effect design matrix (Z₁) and a r x r additive genetic relationship matrix (A), where n is the number of individuals sampled, r is the number of strains (random effect), b is the number of sex categories (fixed effect) and p is the number of traits. We calculated the additive genetic relationship matrix as twice the coefficient of coancestry among strains (Falconer & Mackay, 1996). The diagonal of this matrix is proportional to the average inbreeding coefficient within each strain and, therefore, it takes into account the fact that strains are not completely inbred. The off-diagonal elements are proportional to the coefficients of coancestry among strains, which were calculated based on representative individuals from each strain using the KINSHIP program implemented in PEDSYS 2.0 (Dyke, 1999).

We ran the Gibbs sampler for 40,000 iterations, discarded the first 20,000 as burn-in, and collected 1000 posterior samples with a thinning rate of 20. We calculated the posterior means of our model parameters and used them as our estimates. We used the standard deviation of the model parameters in the posterior as a measurement of uncertainty in the parameters estimates. As a general rule, we used the coefficient of determination (average pairwise r_g² estimates) of the genetic correlation matrix as a measurement of overall genetic integration among traits (Marroig & Cheverud, 2001).

One of the potential pitfalls of estimating G based on inbred lines is that it gives us an estimate of the total genetic variance, rather than the additive genetic variance (e.g., Runcie & Mukherjee, 2013). For that reason, the accuracy of our estimate of G depends on the ratio between these two variances (V_A/V_G). Opportunely, both data and theory suggest that additive variance should often account for close to 100% of the total genetic variance in complex traits under the current design (Hill et al., 2008). Therefore, our use of inbred strains should not significantly impact the estimates of genetic covariances among traits.

Finally, we also evaluated the extent to which sampling error affects our estimates of G and its eigenvalues. Our assessment of the effects of sampling error over overall matrix structure can be found in Appendix S2, and the effects of sampling error over the eigenvalues of G can be found in Appendix S3.

Rate of skull evolution

We drew a very simple hypothesis from our knowledge of marsupial cranial integration patterns to test the assumption that strong genetic covariation facilitates the evolutionary diversification of the group along a specific morphological dimension. If most of the within-species genetic variation is concentrated on a single allometric size axis, morphological diversification should occur fastest when occurring along this LLR (Schluter, 1996). We tested this hypothesis using the trait means of the six Monodelphis species. In particular, we used the fastAnc function implemented in phytools v.0.4–21 (Revell, 2012) to obtain maximum likelihood estimates for the ancestral states for all nodes of the group’s phylogeny (Pavan et al., 2014). For each branch, we calculated a column vector representing the difference in trait means between each node pair. We then extracted information on orientation and amount of divergence. We measured orientation in terms of the degree to which each mean difference vector was correlated with an allometric size vector (PC1_G) (Marroig & Cheverud, 2005). High correlation with size indicates that most of the between-species divergence occurred along size, and vice versa. Since PC signs (+/−) are arbitrary, we use the squared correlation coefficient as a measurement of overall alignment with size.

We measured the amount of divergence as the vector norm. Long vectors indicate substantial morphological divergence, while short vectors indicate a relative lack of divergence. We then plotted the amount of divergence against branch length estimates in order to test whether the amount of morphological diversification depends on time since divergence. Finally, we calculated the overall rate of morphological evolution by dividing the amount of divergence along each branch by the corresponding branch length. If morphological evolution is dependent on the geometric distribution of genetic variation, we expect the rate of evolution to be highly and positively correlated to how closely the morphological divergence is aligned with the LLR (Marroig & Cheverud, 2005). To put our results in a broader context, we also calculated PC-specific rates of evolution measured in haldanes (Pitchers et al., 2014).

Evolutionary inference when dealing with a highly integrated skull

Our second hypothesis was that failure to incorporate information about trait integration can lead to fundamentally different inferences regarding the evolutionary processes that led to species diversification. Here we follow the suggestion by Agrawal & Stinchcombe (2009) and compare evolutionary inferences drawn from our cranial data under two different scenarios: one in which genetic covariances are taken into account and one in which covariances are set to zero (i.e., using the diagonal of G). We use evolutionary inference here to mean the test of the null hypothesis that evolutionary change in skull morphology in the brevicaudata group is compatible with genetic drift. We can model between-population morphological divergence under drift as:

$$\mathbf{B}=(\mathrm{t}/{\mathrm{N}}_{\mathrm{e}})\mathbf{G}$$ (4)

where B is the between-population covariance matrix in generation t, G is the additive genetic covariance matrix of the ancestral population, and N_e is the effective population size (Ackermann & Cheverud, 2002). Since t/N_e is a constant for each comparison, we can expect B to be proportional to G when morphological diversification occurs by genetic drift. In order to test for proportionality, we decomposed G into its eigenvalues and eigenvectors using a Principal Component Analysis (PCA). With that, we obtained a diagonal matrix whose elements represent the genetic variances along each of principal components (PC). We divided the elements of this diagonal by 2F, since the additive variance (V_A) calculated based on inbred lines tends to overestimate the V_A of the ancestral population by two times the average inbreeding coefficient within strains (Falconer & Mackay, 1996). We then projected each of the six Monodelphis species into this new space by calculating their PC scores and estimated B as the variance among these (Ackermann & Cheverud, 2002). We tested the proportionality of G and B in terms of a linear regression:

$$ln({\mathrm{B}}_{\mathrm{i}})=ln(\mathrm{t}/{\mathrm{N}}_{\mathrm{e}})+\mathrm{\beta }\text{ln}({\mathrm{G}}_{\mathrm{i}})$$ (5)

where β is the slope of the regression, B_i is the variance of species mean scores along G’s principal component i, and G_i is the genetic variance along principal component i. We can consider G and B proportional when β equals one. A value significantly different from one indicates that the observed morphological differentiation among species did not occur solely by drift (Ackermann & Cheverud, 2002). We considered β as significantly different from one whenever the 95% confidence interval (CI) of the regression slope did not include the value of one. We calculated confidence intervals for the regression slope using two main approaches. The first approach does not directly take into account the uncertainty in G and estimates the 95% CI of the slope as +/−1.96 *SE _(β), where SE_(β) equals:

$${\text{SE}}_{(\mathrm{\beta })}=\sqrt{\mathit{\sum }{(y_i-{\widehat{\mathrm{y}}}_i)}^2/(n-2)}/\sqrt{\mathit{\sum }{(x_i-\overline{x})}^2}$$ (6)

where y_i is the value of the dependent variable for PC i, ŷi is the predicted value of the dependent variable for PC i, x_i is the observed value of the independent variable for PC i, x̄ is the mean of the independent variable, and n is the number of observations. The second approach uses the 1,000 estimates of G in the posterior to estimate 1,000 posterior estimates of β and derives the 95% CI as the interval into which 95% of the posterior estimates of β fall.

The main drawback of such test is that it does not allow us to distinguish between directional and stabilizing selection, as both can alter β (Ackermann & Cheverud, 2002). Also, this test cannot properly be applied to nodes encompassing less than four terminal taxa, restricting our tests to the three most basal nodes of the Monodelphis phylogeny (following Marroig & Cheverud, 2004). For that reason, we also carried out exact tests of neutrality (see Test of neutral evolution using N_e).

Regardless of the test being used, one potential pitfall of estimating G based on inbred lines and using it in a phylogenetic framework is the assumption that the structure of G based on laboratory animals is a good approximation for the structure of G in the ancestral species. While this is not an unreasonable assumption given that independent analyses indicate that marsupials share highly conserved covariance structures for skull traits (Porto et al., 2009; Shirai & Marroig, 2010), one should keep in mind that this assumption permeates the results presented here.

Test of neutral evolution using N_e

In order to differentiate between stabilizing and directional selection, we carried out more exact tests of neutrality by using divergence time estimates for all nodes of the phylogeny (Pavan et al., 2014; Pavan, S.E. unpublished data). More specifically, we used a Brownian motion model to test whether the amount of evolutionary change along a particular branch of the phylogeny is too large or too small to be compatible with drift (Lande, 1976; Turelli et al., 1988). The model is based on the probability of observing an absolute divergence of d = |μ(t) − μ(0)| under drift alone (Walsh & Lynch, n.d.):

$$Pr(\mid \mu (t)-\mu (0)\mid \le \mathrm{d})=Pr(\frac{\mid \mu (t)-\mu (0)\mid }{\sqrt{{\sigma }^2}}\le \frac{d}{\sqrt{{\sigma }^2}})=Pr(\mid U\mid \le \frac{d}{\sqrt{{\text{tV}}_{\mathrm{A}}/Ne}})$$ (7)

where U is a unit normal random variable, t is time in generations and V_A is the additive variance along the principal component in question. Based on this equation, one can estimate critical values for N_e that are consistent with morphological evolution occurring by drift. As our tests involve 30 PCs and 10 phylogenetic branches, we used Šidák’s correction (Šidák, 1967) to adjust our probability cutoff (p<0.0002) and have an overall significance of α =0.05.

Since Pr(|U| ≥ 3.71) = 0.0002, the critical maximum N̂_e for which drift can still explain the amount of morphological divergence is:

$${\widehat{N}}_{\mathrm{e}}(\text{fast})\le {(3.71)}^2{\text{tV}}_{\mathrm{A}}/{\mathrm{d}}^2$$ (8)

If our assumed N_e is larger than N̂_e (fast), then we can reject drift in favor of directional selection. Likewise, since Pr(|U| ≤ 0.0003) = 0.0002, the critical minimum N̂_e expected under drift is:

$${\widehat{N}}_{\mathrm{e}}(\text{slow})\ge {(0.0003)}^2{\text{tV}}_{\mathrm{A}}/{\mathrm{d}}^2$$ (9)

If our assumed N_e is smaller than N̂_e (slow), then we can reject drift in favor of stabilizing selection. Since we have no estimate for the N_e of Monodelphis, we assumed that it falls between the minimum effective population size for a population to be viable (10³) (Lynch & Lande, 1998) and the upper limit of effective population sizes reported for mammals (10⁵) (Bedford et al., 2008). Estimates reported for Thylamys opossums suggest that Monodelphis should fall near the lower limit of this distribution (Giarla, 2013). Similarly, since we have no estimate of V_A for each of the nodes of the phylogeny, we here used V_A as estimated for the strain data across the whole phylogeny, scaling it up or down following the identity:

$$\mathit{Var}(aX)=a^{\mathit{2}}\mathit{Var}(X)$$ (10)

where Var(aX) is the rescaled additive genetic variance at the node of interest, Var(X) is equal to V_A as estimated from the strain data and a is the ratio between the mean skull size at the node of interest and the mean skull size of the strain data. Note that the approach described above has the same theoretical foundation as the approaches implemented in several other papers (Lemos et al., 2001; Roseman & Weaver, 2007) and software (e.g. MIPoD) (Hohenlohe & Arnold, 2008).

For sake of comparison, we also applied the neutrality test to the brevicaudata group as a whole (i.e., maximum observed divergence). In all cases, uncertainty in our estimates of V_A were taken into account in this analysis, with the 1,000 posterior estimates of V_A being used to calculate confidence intervals for N̂_e(slow) and N̂_e(fast).

RESULTS

G-matrix

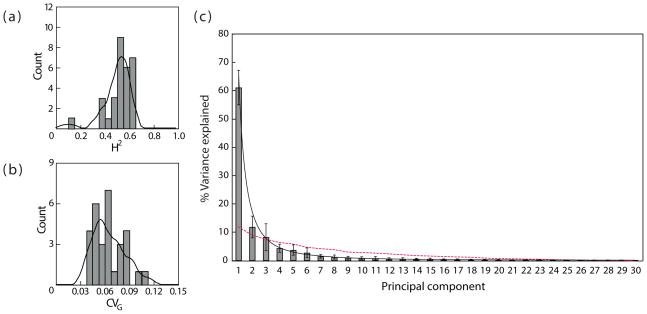
The BSFG model’s estimate of G indicates that genetic variation accounts for 52% of the total morphological variation in this system (Figure 2a). With the exception of BA-OPI, all traits present abundant genetic variation when analyzed individually (Mean CV_G~0.06; Figure 2b). The same cannot be said about trait combinations (PCs). The distribution of genetic variation in the morphospace fits almost perfectly a negative exponential distribution (r²=0.99; Figure 2c). Most of the genetic variation is concentrated in a few axes of the morphospace, with allometric size variation representing 61% of the between-strain variation and with the first six PCs accounting for more than 90% of the genetic variance (Figure 2c). This high percentage of variation along the first PC cannot be explained by sampling error, as shown by bootstrap resamples of Monodelphis P (Figure S3a) and by the standard deviation of this statistic in the posterior (Figure 2c). It also cannot be a consequence of overly constraining the model, since randomly assigning individuals to strains leads to a genetic matrix (G_noise) in which eigenvalues are much more homogeneously distributed (red dashed line; Figure 2c). Accordingly, theoretical predictions suggest that the percentage of variation along the PC1 of Monodelphis, given 15 data points, should only be inflated by a factor of around 10% (Figure S3b).

Figure 2.

(a) Frequency histogram of trait-specific broad-sense heritabilities calculated for each of the 30 cranial traits;(b) Frequency histogram of trait-specific genetic coefficients of variation calculated for each of the 30 cranial traits; (c) Percent variance explained by each principal component of the G-matrix. Solid line indicates the best-fit exponential curve. The dashed line indicates the eigenvalue distribution observed once the genetic signal was replaced by random signal (G_noise).

Consistently, the overall magnitude of genetic integration among traits is high and within the range reported for marsupial phenotypic traits (r_g²=0.29) (Porto et al., 2009). Bootstrap resamples suggest r_g² values are within the expected range given the r_p² of phenotypic traits and the number of independent data points (Figure S3c). It’s worth noting that this overall magnitude of genetic integration is more than 50% higher than observed for Saddle-back tamarins (r_g²=0.19), even though the latter was estimated with even fewer data points (Cheverud, 1996).

Rate of skull evolution

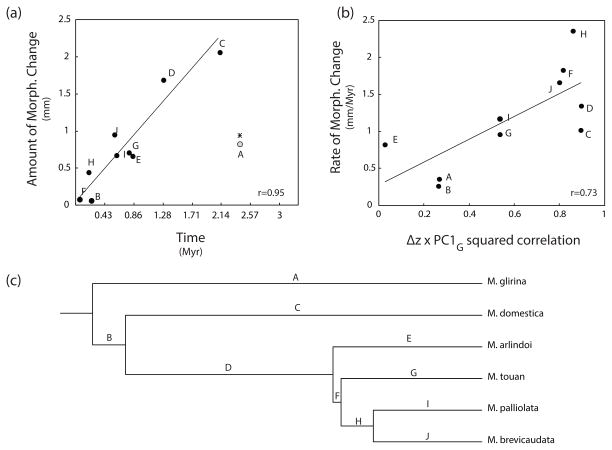
We found a strong association between the amount of morphological change occurring along the branches of the phylogeny and their corresponding branch lengths (r=0.95, t₇=7.769, p=8.5 10⁻⁵, Figure 3a). M. glirina’s morphological diversification from its ancestor represents the only exception to this pattern. Even though it’s the longest branch of the phylogeny (~2.4 Myr), very little morphological change has occurred along it. Morphological evolution along the other branches presented an almost clock-like behavior, with longer branches presenting higher amounts of morphological change than shorter ones.

Figure 3.

(a) Plot of the amount of morphological change on each branch of the brevicaudata group’s phylogeny against the corresponding branch length. Note that M. glirina (branch A) represents an exception to the clock-like behavior of other branches; (b) Plot of the rate of morphological change on each branch of the brevicaudata group’s phylogeny against the direction of evolutionary change. Direction of evolutionary change is measured in terms of its alignment with an allometric size vector (Δz x PC1_G squared correlation); (c) Most recently published phylogeny of the Monodelphis brevicaudata species group.

Similarly, the rate of morphological evolution along each branch of the phylogeny is strongly associated to whether morphological evolution occurred along the genetic LLR (r=0.73, t₈=3.028, p=0.017, Figure 3b). Whenever evolution occurred along the genetic LLR, evolution proceeded at a fast pace, and vice versa. As a consequence, morphological change occurring along the genetic LLR amounts to 83.5% of the total morphological diversification observed in the clade. Branch H (Figure 3c) is the branch with the highest rate of morphological evolution, and represents a period during which a large reduction in cranial size occurred. Branches A, B and E (Figure 3c) are the branches with slowest rate of evolution.

It’s important to note that our results are not a consequence of the method of ancestral state reconstruction, as simple parsimony results are qualitatively similar (Figure S4).

Evolutionary inference when dealing with a highly integrated skull

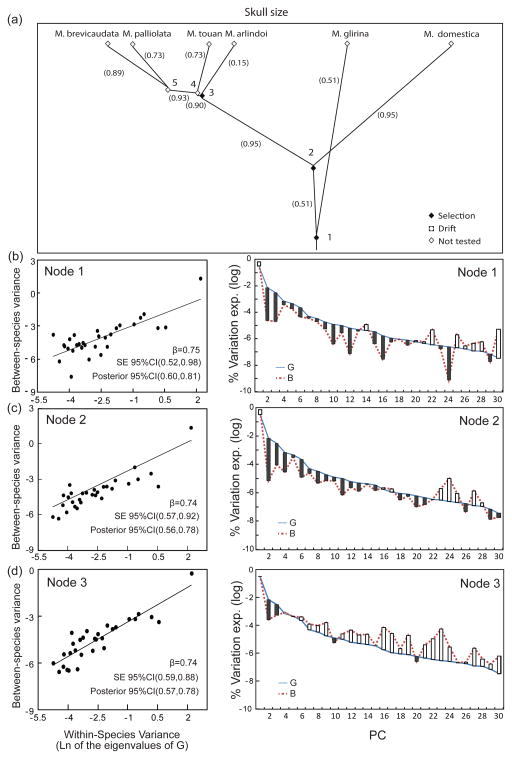
Tests of the null hypothesis of diversification by drift indicate that species differences were incompatible with drift in all three nodes presenting four or more taxa, when taking genetic covariances into account (Figure 4a,b,c,d, left panel). Specifically, the regression of the between-species matrix (B) eigenvalues on G’s eigenvalues indicates that βs are significantly lower than one and, therefore, that either: (a) the morphological diversification along the first PCs was relatively smaller than what would be expected under drift; or (b) that morphological diversification along the last PCs was relatively bigger than would be expected under drift. The first case would indicate the action of stabilizing selection and the second case would indicate the action of directional selection. Interestingly, PC2, PC3 and PC10 are the only PCs consistently underrepresented in the pattern of between-species divergence; and PC25, PC27 and PC28 are the only PCs consistently overrepresented in the pattern of between-species divergence (Figure 4b,c,d, right panel).

Figure 4.

(a) Size phylomorphospace of the Monodelphis brevicaudata group. Distances between species (X-axis) are proportional to their overall skull size differences. Numbers in parentheses indicate the overall correlation between the direction of divergence on each branch and PC1_G; (b,c,d) Tests of the null hypothesis that diversification in the Monodelphis brevicaudata species group occurred by drift, for each of the three nodes of the phylogeny presenting four or more taxa, while taking genetic covariances into account. The regression line, its equation and its confidence intervals are illustrated for all three nodes (left panel). Within-species variances are calculated as the natural logarithm of the eigenvalues of G, while between-species variances are calculated as the natural logarithm of the variance of the species’ mean PC scores, when projected in G’s space. The percent variance explained by each principal component of G and B is also shown (log scale; right panel). Bars represent the overall difference between the two matrices in terms of the percent variance explained by each PC.

When we assumed traits to evolve independently, estimated βs were not significantly different from 1, indicating that species differences were compatible with drift in all three nodes with four or more taxa (Figure 5).

Figure 5.

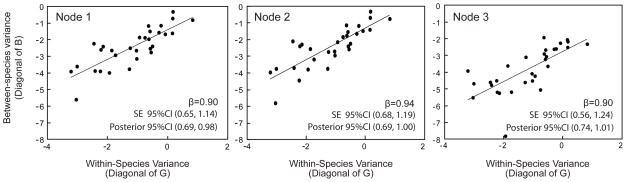
Tests of the null hypothesis that diversification in the Monodelphis brevicaudata species group occurred by drift, while assuming traits can evolve independently. The regression line, its equation and its confidence interval are illustrated for all three nodes.

Test of neutral evolution using N_e

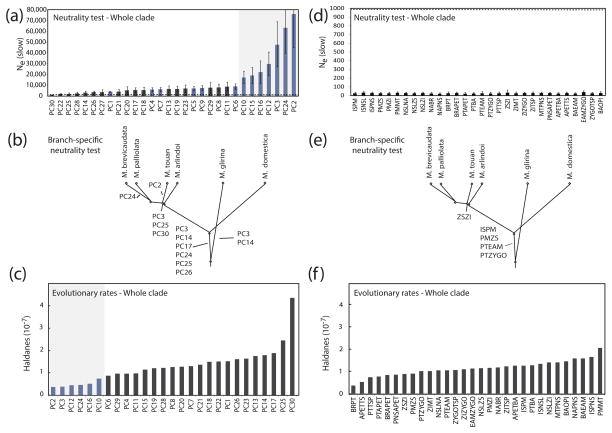
Tests of the null hypothesis of diversification by drift using N_e paint a similar picture regarding morphological diversification in the brevicaudata group. Strong evidence for stabilizing selection is found when incorporating information about genetic covariances (Figure 6a,b,c), but most of this signal is lost when setting covariances to zero (Figure 6d,e,f). For example, Figure 6a illustrates the critical effective population size (N̂_e(slow)) calculated for each principal component when looking at the diversification of the entire brevicaudata group from the most basal node of the phylogeny. In cases where N̂_e(slow) is significantly higher than our assumed N_e (N_e =1,000; dashed line), we rejected drift in favor of stabilizing selection.

Figure 6.

(a) Critical effective population size (N̂_e(slow)) calculated for each PC in the overall tests of neutrality (whole phylogeny). If N̂_e(slow)is significantly higher than our assumed N_e, then we reject drift in favor of stabilizing selection. PCs with values of N̂_e(slow) significantly higher than 10³ are highlighted in blue. Standard deviations for N̂_e(slow) are calculated based on the uncertainty in our estimates of V_A; (b) PCs under stabilizing selection on each branch of the brevicaudata group’s phylogeny, when using branch-specific tests of neutrality; (c) PC-specific rate of morphological evolution along the brevicaudata group’s phylogeny; (d) N̂_e(slow) calculated for each trait in the univariate tests of neutrality. (e) Traits under stabilizing selection on each branch of the brevicaudata group’s phylogeny, when using branch-specific univariate tests of neutrality; (f) Trait-specific rate of morphological evolution along the brevicaudata group’s phylogeny.

As can readily be seen, a total of 13 PCs can be considered under stabilizing selection (blue bars). For seven of these PCs (gray background), N̂_e(slow) values are exponentially larger than for the remaining ones, indicating these PCs are under particularly strong stabilizing selection. They are also the ones with lowest rate of evolution in the clade (Figure 6c, gray background). Among these, PC2 (nasal projection) and PC3 (skull shape) emerge as particularly important because these axes represent two major axes of genetic variation within populations and, at the same time, the two axes with the slowest rate of evolution. Moreover, when the same test is applied to each branch of the phylogeny (Figure 6b) instead of the whole clade, PC2 and PC3 emerge again as two PCs under stabilizing selection.

With covariances set to zero, all critical values of N̂_e(slow) fall well below a realistic range of N_e, when looking at the diversification of the whole clade (Figure 6d). Genetic drift cannot be rejected, therefore, as the source of morphological diversification of the clade. When the same test is applied to each branch of the phylogeny, only two instances of stabilizing selection are found (Figure 6e), and the correspondence between traits under stabilizing selection and rates of evolution is lost (Figure 6f).

For all tests, none of critical values of N̂_e(fast) fall within a realistic range of N_e for mammals (>10⁷, results not shown). In other words, no evidence of directional selection was detected by any of the exact tests.

DISCUSSION

When considered together, the results presented here highlight the importance of taking genetic integration into account in studies of morphological evolution. Especially in strongly integrated clades, like marsupials, genetic covariation among traits has the potential to influence the pattern of between-species divergence, favoring evolutionary change along genetic lines of least resistance (LLR). Failure to incorporate information on genetic integration can therefore lead to incorrect conclusions regarding the evolutionary processes that operated during species diversification in this group.

We support our argument with three main analyses. First, we show that genetic variation is concentrated in a few axes of the morphospace and that the strong phenotypic integration in marsupials reflects strong genetic integration among traits. Second, we illustrate the influence of this strong genetic integration over morphological evolution by showing that there is a strong relationship between the rate of morphological divergence and whether divergence occurred along the genetic LLR. Finally, we demonstrate that the conclusions of the test of the null hypothesis of diversification by drift are strongly influenced by whether genetic covariances are taken into account.

While many of these analyses are not new for marsupial mammals, this is the first work to directly link observed patterns of genetic integration among traits to macroevolutionary patterns of between-species morphological divergence in this clade. This link is particularly important given the recent proliferation of studies showing that occupation of morphospace by marsupials is more restricted than by eutherians, even when fossils are taken into account (e.g., (Sears, 2004; Cooper & Steppan, 2010; Kelly & Sears, 2011; Bennett & Goswami, 2013). In particular, our results suggest that the occupation of morphospace in Monodelphis is the result of a complex interplay between the limited dimensionality of available genetic variation in multivariate space and strong stabilizing selection on two major axes of genetic variation. While these results should not be automatically extrapolated to other marsupial clades, it’s noteworthy that Lemos et al. (2001) found the same pattern of strong stabilizing selection on skull shape when analyzing evolutionary rates in large-bodied opossums. Therefore, strong genetic integration plus stabilizing selection on skull shape provide us with a proximate cause (Mayr, 1963) for such constrained evolution in Monodelphis (and perhaps other marsupials). Ultimate causative explanations are far more controversial. Ultimate causation hypotheses are usually divided in two main branches: (a) those involving intrinsic factors, the main one being the developmental constraint hypothesis (Jason, 1975; Sears, 2004); and (b) those involving extrinsic factors, the main one being the biogeographic hypothesis (Sanchez-Villagra, 2012). The constraint hypothesis argues that the reproductive strategy of marsupials, involving highly altricial neonates and short gestation times, places functional requirements on early skeletal structures that limit the possibility of morphological diversification (Jason, 1975). The main source of support for this hypothesis comes from the observation that skeletal structures involved in the newborn’s crawl and attachment to the teat are more constrained than other skeletal structures. Examples span skeletal elements such as the scapulae (Sears, 2004), forelimbs (Kelly & Sears, 2011), and mandible/maxillae (Bennett & Goswami, 2013). Criticism regarding this hypothesis comes from the observation that developmental constraints have often been circumvented by species during their diversification (Sanchez-Villagra, 2012), such as human limb proportions (Young et al., 2010) and birth canal (Grabowski, 2012), and talpid moles’ digits (Mitgutsch et al., 2012).

The biogeographic hypothesis argues that the marsupial’s restricted occupation of the morphospace is a direct consequence of the metatherian distribution during major Mesozoic/Cenozoic events. In particular, Sanchez-Villagra (2012) recently pointed out that: (a) marsupial diversification has been largely restricted to the southern hemisphere, a place where eutherians have also diversified less than their counterparts of more global distribution;(b) and that marsupials emerged as a clade at least 20 Myr later than eutherians. It is important to note that these hypotheses are not mutually exclusive, and while our results shed no additional light on their relative roles, they highlight that the marsupial’s restricted occupation of the morphospace extends to how genetic variation is produced within laboratory populations, and, therefore, is not a simple consequence of lack of ecological opportunity. This becomes particularly evident when we compare Monodelphis to other mammal groups. In tamarin species (Primates), for example, overall magnitudes of genetic integration are much lower than what we observed for Monodelphis (Cheverud, 1996), indicating that genetic variation is more evenly distributed in the morphospace of the former. Finally, the evolutionary rates of skull shape evolution reported here fall outside the lower range of the distribution of evolutionary rates compiled by Pitchers et al.(2014), indicating that the restricted occupation of the morphospace is not a simple consequence of time since divergence.

Another important point is that the constraint hypothesis doesn’t necessarily imply lack of morphological diversification, even though it is often portrayed that way. Constraints can actually facilitate morphological evolution along certain dimensions, since they can create genetic lines of least resistance (LLR) (Schluter, 1996). A clear example of how evolutionary processes may interact with a LLR comes from a work with New World Monkeys (NWM). Marroig & Cheverud (2005) showed that a size-related LLR influenced the path, amount, and rate of morphological change in this group of primates. When selection was aligned with the LLR, evolution proceeded at a fast rate, creating the adaptive radiation pattern observed in the morphology of those organisms. Evolution also occurred away from the LLR in some taxa, but this occurred at a slower rate and resulted in a relatively small amount of morphological change.

The relationship between the genetic LLR and the rate morphological diversification in Monodelphis is even stronger than the one reported for NWM (Marroig & Cheverud, 2005). As argued above, this is partially due to the selective scenario underlying the diversification of these clades and partially due to the availability of genetic variation in the morphospace. In NWM, several instances of directional selection pushing species along smaller dimensions of the morphospace were detected (Marroig & Cheverud, 2010). Likewise, genetic variation was more homogeneously distributed across the dimensions (Cheverud, 1996). In Monodelphis, not only was stabilizing selection rampant along PC2 and PC3, the availability of additive genetic variation was also skewed towards the first principal component, fundamentally shaping the diversification of the group. Interestingly, most traits present abundant genetic variation within populations when analyzed based on trait-specific heritabilities. In our view, this is a strong argument in favor of multivariate approaches in evolutionary biology, as several authors have recently emphasized (e.g., Blows, 2007; Hansen & Houle, 2008; Walsh and Blows, 2009). When analyzing traits individually, one would invariably conclude that the brevicaudata species group diversified as a consequence of lineages freely drifting in a multidimensional morphospace. Instead, we have provided strong evidence for selection.

As a final point, it should be noted that our results do not imply that directional selection played no role in the diversification of the brevicaudata species group. Tests of the null hypothesis of diversification by drift using N_e are not capable of detecting episodes of directional selection occurring for few generations, as that change tends to get stretched out to the entire branch (Lemos et al. 2001). Rather, what our results emphasize is that, regardless of any localized episode of directional selection, stabilizing selection was a dominant force throughout the groups’ diversification.

In sum, we here provided evidence that strong genetic covariation among traits influenced the rate of morphological diversification of the brevicaudata group, with between-species divergence occurring fastest when occurring along the genetic line of least resistance. We also showed that accounting for this strong genetic covariation considerably increases our ability to detect the selective regimen underlying species diversification, leading to more informed evolutionary inferences and a better understanding of the groups’ evolutionary history.