Perspective: A Dynamics-Based Classification of Ventricular Arrhythmias

Abstract

Despite key advances in the clinical management of life-threatening ventricular arrhythmias, culminating with the development of implantable cardioverter-defibrillators and catheter ablation techniques, pharmacologic/biologic therapeutics have lagged behind. The fundamental issue is that biological targets are molecular factors. Diseases, however, represent emergent properties at the scale of the organism that result from dynamic interactions between multiple constantly changing molecular factors. For a pharmacologic/biologic therapy to be effective, it must target the dynamic processes that underlie the disease. Here we propose a classification of ventricular arrhythmias that is based on our current understanding of the dynamics occurring at the subcellular, cellular, tissue and organism scales, which cause arrhythmias by simultaneously generating arrhythmia triggers and exacerbating tissue vulnerability. The goal is to create a framework that systematically links these key dynamic factors together with fixed factors (structural and electrophysiological heterogeneity) synergistically promoting electrical dispersion and increased arrhythmia risk to molecular factors that can serve as biological targets. We classify ventricular arrhythmias into three primary dynamic categories related generally to unstable Ca cycling, reduced repolarization, and excess repolarization, respectively. The clinical syndromes, arrhythmia mechanisms, dynamic factors and what is known about their molecular counterparts are discussed. Based on this framework, we propose a computational-experimental strategy for exploring the links between molecular factors, fixed factors and dynamic factors that underlie life-threatening ventricular arrhythmias. The ultimate objective is to facilitate drug development by creating an in silico platform to evaluate and predict comprehensively how molecular interventions affect not only a single targeted arrhythmia, but all primary arrhythmia dynamics categories as well as normal cardiac excitation-contraction coupling.

1. Introduction

With the advent in the 1940’s and 1950’s of intracellular microelectrode recordings and the development in subsequent decades of sophisticated arrhythmia mapping and imaging techniques, followed by the blossoming of molecular ion channel biophysics and computational biology, a wealth of information about arrhythmia mechanisms at the molecular, cellular, organ and organism scales has come to light [1– 6]. Based on this research, major advances in arrhythmia treatment have occurred over the past century, culminating with the development of surgical and catheter ablation techniques and implantable cardioverter-defibrillators (ICDs). Pharmacologic/biologic approaches to treat arrhythmias, however, have lagged behind. Well-designed clinical trials, such as CAST [7] and SWORD [8], revealed that promising agents that were effective at suppressing one arrhythmia mechanism proved to be proarrhythmic by exacerbating other mechanisms. As a result, the enthusiasm of the pharmaceutical industry for antiarrhythmic drug development has been severely curtailed. Yet the need is clearly there. Ablation is curative for some arrhythmias, but others do not have discrete anatomical structures to target. Device therapy is also not ideal, since ICDs terminate arrhythmias effectively, but do not prevent them. Moreover, 80% of patients who will die suddenly each year do not meet clinical indications (i.e. low ejection fraction or prior documented arrhythmia history) for implanting an ICD [9]. Of the ones who do, only 1 of 5 ICDs implanted will actually deliver a life-saving shock due to the difficulty in predicting which patients are at the greatest risk [10].

Why has the development of effective antiarrhythmic drugs been so frustrating?

The generic challenge in controlling or curing any disease pharmacologically is that drugs target molecules, but diseases occur at the organism scale, and the relationship between the behavior of a molecule and the behavior of an organism is hardly straightforward. In the case of arrhythmias, electrophysiological properties that determine the likelihood of an arrhythmia at the tissue level are not directly controlled in a straightforward way by single molecules. Rather, very complex nonlinear interactions between many molecules first integrate to produce the electrophysiological properties at the level of the cell, including the action potential (AP), Ca cycling features, automaticity, early (EAD) and delayed (DAD) afterdepolarizations, excitability and refractoriness, etc. These cellular electrophysiological factors next integrate, again in complex nonlinear ways, to generate the tissue electrophysiological properties, including excitability characteristics, conduction properties, dispersion of refractoriness, electrical alternans and a variety of other factors impacting the initiation and maintenance of cardiac arrhythmias. Meanwhile, other organ systems in the body are constantly dynamically modulating these factors at the molecular, cellular and organ scales through autonomic tone, electrolyte balance, various endocrine functions, etc. Given the complexity of the system, predicting how modifying a single target molecule will impact the behavior of the overall system is a daunting task. Despite this complexity, however, successful precedents exist. For example, beta blockers targeting the beta adrenergic receptor, and drugs inhibiting angiotensin-converting enzyme (ACE) and antagonizing the hormone aldosterone have been proven to reduce the incidence of sudden cardiac death in large cohorts of patients with heart failure and ischemic heart disease [11]. Unfortunately, we have been much less successful with drugs targeting the ion channels that directly influence cardiac electrophysiological properties, possibly because available pre-clinical experimental and clinical arrhythmia induction paradigms incompletely recapitulate clinical arrhythmias.

Can this impasse be broken? In our view, to make substantive progress will require a comprehensive analysis linking the function of molecules, the material entities such as ion channels or receptors that can be targeted by drugs or biologics, to electrophysiological factors that determine arrhythmia risk at the organism scale. This is an inherently multiscale problem which requires linking molecular factors first to electrophysiological and structural factors at the subcellular scale (e.g. Ca cycling properties), then to factors at the cellular scale (e.g. action potential properties), next to factors at the tissue scale (e.g. conduction properties), and finally factors to the organism scale (e.g. autonomic and metabolic properties) [6]. An advantage of the arrhythmia field, compared to many other disease areas, is that we already have a fairly detailed understanding of the electrophysiological and structural factors at the subcellular, cellular, organ and organism levels that promote arrhythmias. What is lacking is an integrated framework for evaluating and predicting how the behaviors of proteins at the molecular scale are linked to the relevant electrophysiological and structural factors promoting arrhythmias at the subcellular/cellular/organ/organism scales. Too often antiarrhythmic drug development strategies have focused on one arrhythmia mechanism without considering, in any systematic way, how the drug may impact other arrhythmia mechanisms. For example, the CAST study [7] evaluating Na channel blockers was based on the premise that suppressing premature ventricular complexes (PVCs), the triggers that initiate reentry, should decrease the incidence of reentrant ventricular tachycardia (VT) and fibrillation (VF). This was a very reasonable hypothesis, but failed to take into account the effects of Na channel blockers on the tissue substrate. We know now that Na channel blockers increase the vulnerability of the tissue to initiation of reentry. Thus, if the PVC frequency is reduced by a factor of five, but vulnerability is concomitantly increased by a factor of ten, the net effect is to double the incidence of reentrant arrhythmias. Similarly, the SWORD trial [8] evaluating the K channel blocker d-sotalol was based on the premise that prolonging the refractory period would suppress reentrant arrhythmias by eliminating excitable gaps in reentry circuits, but failed to take into account the pro-arrhythmic effects of K channel blockers on a different mechanism, namely Torsades de Pointes (TdP).

The goal of this perspective is to take stock of our current understanding of the molecular, electrophysiological and structural factors that underlie various mechanisms of ventricular arrhythmias, and begin to organize this information into a conceptual framework that will link molecular behaviors to the subcellular/cellular/organ/organism scale behaviors underlying ventricular arrhythmias. The ultimate objective is to utilize this framework to evaluate systematically, through combined computational and experimental approaches, how potential molecular targets impact not just a single arrhythmia mechanism, but all major mechanisms that are clinically relevant to ventricular arrhythmias. Even if our understanding of arrhythmia dynamics is currently incomplete, the proposed framework will serve as a starting point that can be further developed to incorporate new information as it becomes available.

2. Rationale

The rationale for developing a dynamics-based classification of ventricular arrhythmias is to link molecular factors to the dynamic factors controlling arrhythmias at the supra-molecular scales. Molecular factors are the material biological entities, e.g. druggable or genetically-modifiable proteins like ion channels, transporters, receptors, transcription factors or their post-translational modification sites, as well as nucleotides, lipids or carbohydrates, etc., that can be directly targeted to modify behavior in a desired fashion. Arrhythmias, however, are not molecules, but behaviors of an integrated dynamical system, namely the excitable medium of cardiac tissue, whose behavior is governed by dynamic factors [12]. Dynamics refers to processes that change in time and/or space. Dynamic factors refer to the functional electrophysiological properties that are not actual material entities, like molecules, but represent the aggregate behavior of many interacting material entities. For example, the cardiac AP is a phenomenological descriptor of the change of voltage in a myocyte that arises from the aggregate behavior of a large number of interacting ion channels/transporters. A drug does not interact directly with the AP to modify its properties. A drug can only physically interact with another molecule, such as an ion channel/transporter or signaling protein, whose interaction with other molecules then influences the AP. Moreover, a given property of the AP, such as its refractory period, is not uniquely specified by a single combination of ion channel/transporter properties. There are literally billions of combinations of ion channel/transporter properties that can produce a nearly identical AP duration (APD) or refractory period [13, 14].

In addition to molecular and dynamic factors, a third category also plays a vital role in arrhythmogenesis, which we call fixed factors. Fixed factors include structural and electrophysiological tissue heterogeneities, such as fibrosis, scars and other anatomic obstacles, transmural and apex-to-base AP gradients and electrical ion channel remodeling (including gap junction remodeling). These pre-existing tissue heterogeneities create dispersion of refractoriness and excitability, which play critical roles in arrhythmogenesis. In our view, however, fixed factors do not directly cause ventricular arrhythmias – rather, they increase the probability that dynamic factors will initiate arrhythmias by generating triggers and exacerbating tissue heterogeneity. In other words, the fixed factors and dynamic factors interact synergistically to lower the threshold of dynamic instability required for arrhythmias to emerge.

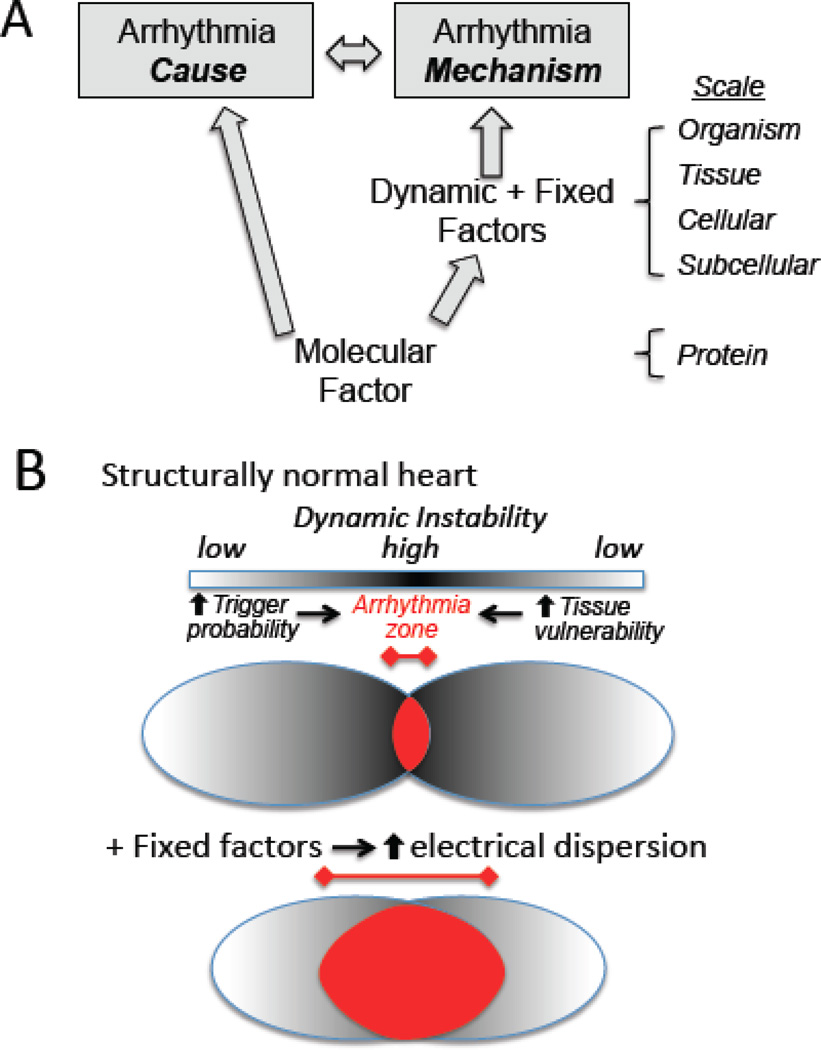
Fig. 1A summarizes schematically the relationship between molecular factors and the dynamic factors and fixed factors that promote arrhythmias, and also makes an important distinction – that it is possible to understand the cause of an arrhythmia without understanding the mechanism. For example, a genetic mutation in an ion channel protein (channelopathy) can cause, unequivocally, a long QT syndrome. However, identification of the abnormal protein does not, by itself, provide direct information about the mechanism (Fig. 1A). Rather, the mechanism is governed by dynamic factors and fixed factors that link the abnormal protein function at the molecular scale to the arrhythmia syndrome at the organism scale.

Fig. 1.

A. The cause versus the mechanism of an arrhythmia. A molecular factor, such as a genetic mutation that alters a protein’s function, can unequivocally be the cause of an arrhythmia, but does not directly define the mechanism. The mechanism of the arrhythmia is defined by the effects of the molecular factor on the dynamic factors and fixed factors at each increasingly integrated scale. B. Fixed factors which increase electrical dispersion decrease the threshold of dynamic instability at which arrhythmias occur. Dynamic factors creating dynamic instability (dark shading) jointly increase the probability of triggers (left oval) and tissue vulnerability (right oval), whose overlap defines the arrhythmia zone (red). Fixed factors that increase structural and electrophysiological heterogeneity act synergistically with dynamic factors to promote triggers and increase vulnerability, widening the arrhythmia zone.

3. Dynamics-based Classification of Arrhythmias

Traditionally, arrhythmias are often classified by mechanism: reentry, triggered activity or automaticity. In the ventricles, reentry can take several forms [6]: 1) anatomic reentry around an obstacle (such as a scar) manifesting as monomorphic VT ; 2) functional reentry due to a stable rotor (spiral/scroll wave reentry), also manifesting as monomorphic VT; 3) reentry due to a meandering rotor manifesting as polymorphic VT or TdP; 4) multiple wavelet VF due to rotor (spiral/scroll wave) breakup; 5) mother rotor VF due to a fast stable rotor with peripheral wavebreaks (fibrillatory conduction block) in surrounding tissue. Triggered activity is caused by EADs or DADs, and typically manifests as PVCs or monomorphic or polymorphic VT. Automaticity is due to spontaneous diastolic depolarization, which is generally slower and manifests as PVCs and idioventricular rhythms. Ventricular arrhythmias can be nonsustained or sustained, purely focal or purely reentrant or involve a mixture of focal and reentrant mechanisms. In addition, reentry which is inherently nonsustained can be constantly reinitiated by focal activations (mixed focal-reentrant VF). In this scenario, the rapid rates during reentry also promote additional triggers (via Ca overload), creating a positive feedback loop that sustains the arrhythmia [15].

The lessons from the CAST study [7] and SWORD trial [8] suggest that antiarrhythmic strategies focused solely on suppressing triggers (CAST) or preventing reentry (SWORD) are not likely to be successful. Both factors must be taken into account concomitantly. PVCs are generally benign if the tissue substrate is not in a state vulnerable to reentry, i.e. if electrical dispersion is low. Conversely, PVCs only become dangerous when electrical dispersion is high, enhancing the risk of reentry. The highest risk of arrhythmias arises when dynamic factors, interacting with fixed factors, simultaneously promote the emergence of triggers while enhancing electrical dispersion in the tissue (Fig. 1B)

Accordingly, the goal of a dynamics-based classification of ventricular arrhythmias is to place the primary focus on the trigger-tissue substrate interactions – that is, to base the classification on the conditions in which the underlying dynamics promote the emergence of triggers and electrical dispersion simultaneously. As illustrated in Fig. 1B, the basic premises are: 1) Arrhythmias arise acutely from interactions between a trigger and a vulnerable tissue substrate, made vulnerable by a combination of dynamic and fixed factors promoting electrical dispersion; 2) The interactions between triggers and substrate vulnerability are dynamic and interdependent, both acutely and chronically; 3) The episodic nature of arrhythmias indicates that fixed factors causing electrical dispersion, such as anatomical structures, scars, fibrosis, etc., do not directly cause arrhythmias, but rather sensitize the heart to arrhythmia episodes by lowering the threshold of dynamic instability required for arrhythmias to emerge.

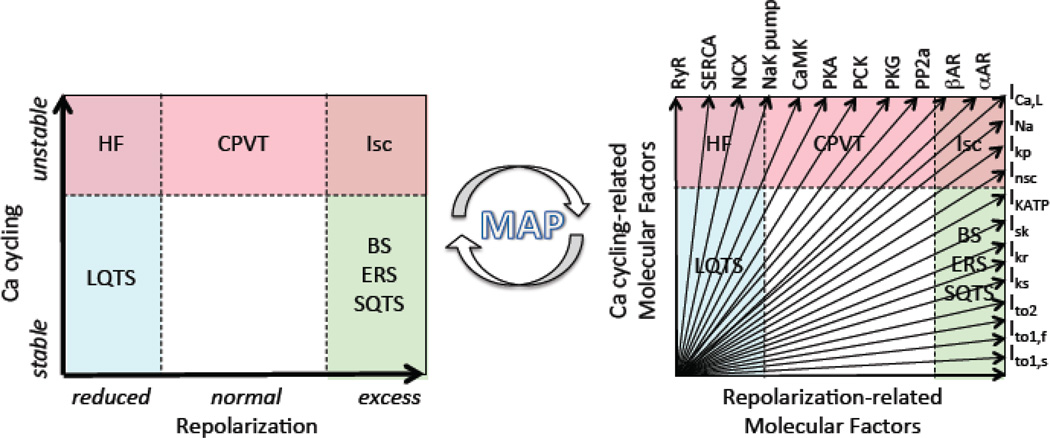
Based on these premises, Table 1 presents a proposed dynamics-based classification of ventricular arrhythmias summarizing how the dynamic factors at the cellular, tissue and organism scales relate to arrhythmia risk at the organ scale. In this classification, the major clinically relevant ventricular arrhythmias fall into three broad categories, in which the primary dynamic instability promoting arrhythmias is related to 1) unstable Ca cycling, 2) reduced repolarization, or 3) excess repolarization. Each category specifies the relevant rare and common clinical diseases, arrhythmia mechanisms, cellular and tissue dynamics and the key dynamic factors controlling them that can serve as targets to prevent arrhythmias. The final row in Table 1 suggests potential molecular factors, still largely speculative at this point, that might be targeted biologically to regulate the key dynamic factors/targets. Each category is discussed in detail below.

TABLE 1. Dynamics-based Classification of Cardiac Arrhythmias.

Clinical settings, arrhythmia mechanisms, the relevant dynamic instabilities, dynamic factors/targets and several molecular factors under exploration as potential biological targets are summarized for each category. Not shown here are fixed factors that also increase electrical dispersion synergistically with dynamic factors to promote arrhythmias.

Dynamics Category	Unstable Ca Cycling	Reduced Repolarization	Excess Repolarization
Clinical (rare) setting (common)	CPVT HF & Ischemia	LQTS HF	BS, ERS, SQTS Ischemia
Arrhythmia mechanisms	DAD-mediated VT Multiple wavelet VF Mother rotor VF	TdP & PVT Mixed focal-reentrant VF	Multiple wavelet VF Mother Rotor VF
Dynamic instability	SDA Ca waves/DADs	EADs Chaos synchronization Biexcitability	AP domes Chaos synchronization Phase 2 reentry
Dynamic factors/targets	Steep SR ca release-load relationship Steep APD restitution Broad CV restitution	Steep APD (EAD) restitution	Steep APD (AP dome) restitution
Molecular factors/Potential biological targets	RyR modification?	Late INa blockade? Late ICa,L blockade?	Ito blockade?

Abbreviations: AP, action potential; APD, action potential duration; BS, Brugada syndrome; CPVT, catecholaminergic polymorphic ventricular tachycardia; CV, conduction velocity; DAD, delayed afterdepolarization; EAD; early afterdepolarization; ERS, early repolarization syndrome; HF, heart failure; I_Ca,L, L-type Ca current; I_Na, Na current; I_to, transient outward K current; LQTS, long QT syndrome; PVT, polymorphic ventricular tachycardia; SDA, spatially discordant APD alternans; SQTS, short QT syndrome; TdP, Torsade de pointes

3.1 Arrhythmias Related to Unstable Ca Cycling

Clinical settings

The prototype in this arrhythmia dynamics category is CPVT [16, 17], in which mutations to the ryanodine receptor (RyR) and/or its associated sarcoplasmic reticulum (SR) proteins, such as calsequestrin, cause RyRs to become overly sensitive to Ca, especially when SR Ca stores are potentiated by catecholamine stimulation. Ca cycling instabilities are also an important component promoting arrhythmias in heart failure, in which RyR Ca sensitivity is increased by chronic adrenergic and Ca-calmodulin kinase II (CaMKII) activation, in addition to other changes [18, 19]. Acute ischemia also alters Ca cycling by direct and indirect effects of high energy phosphate depletion and metabolite accumulation on the function of ion channels/transporters in the sarcolemma and SR.

Arrhythmia mechanisms

The major triggers are DADs, which can induce focal ventricular tachycardia (monomorphic, polymorphic or bidirectional VT) due to DAD-mediated triggered activity [20, 21], or initiate reentry degenerating to multiple wavelet or mother rotor VF. Substrate vulnerability is also increased by spatially discordant APD and Ca alternans causing dispersion of refractoriness, and subthreshold DADs causing dispersion of excitability.

Dynamic mechanisms

Altered Ca cycling under these conditions makes ventricular myocytes susceptible to spontaneous SR Ca release from regions of the subcellular Ca release unit network, which propagates through the network regeneratively as a Ca wave. The resulting elevation in intracellular Ca is sensed by Ca-sensitive inward currents, primarily the Na-Ca exchange current (I_NCX). When Ca waves occur during diastole, the activation of depolarizing inward current causes DADs, which, if they reach the threshold for Na current (I_Na) activation, can elicit triggered activity from the myocyte. For DADs to elicit a PVC or triggered activity in tissue, however, a large number of myocytes (up to hundreds of thousands in well-coupled three-dimensional (3D) tissue [22]) must develop Ca waves synchronously to overcome the source-sink (loading) effect of adjacent myocytes without Ca waves. The mechanisms by which large numbers of myocytes synchronously develop Ca waves sufficient to induce a DAD in tissue is still under investigation [23, 24]. In one-dimensional (1D) tissue, however, the number of myocytes required falls dramatically, into double digits [22]. This may be one reason why Purkinje fibers, which are quasi-1D cables, are more susceptible to DADs than 3D ventricular tissue, although electrophysiological differences such as a lower density of inward rectifier K channels also contributes. Other factors affecting source-sink relationships in tissue can also markedly reduce the number of myocytes required for a DAD-mediated PVC to emerge. For example, fibrosis has the effect of electrically insulating strands of myocytes from one another, effectively converting 3D tissue into a network of interconnected 1D cables [25, 26]. When DADs do overcome the source-sink mismatch in tissue, PVCs and focal ventricular tachycardia (VT) can result. Bidirectional VT, a hallmark of CPVT [17] and Ca-overload induced by digitalis toxicity [27, 28], has been explained by reciprocating bigeminy in which DAD-triggered APs arising from different regions of the His-Purkinje system trigger each other in a ping-pong fashion [29].

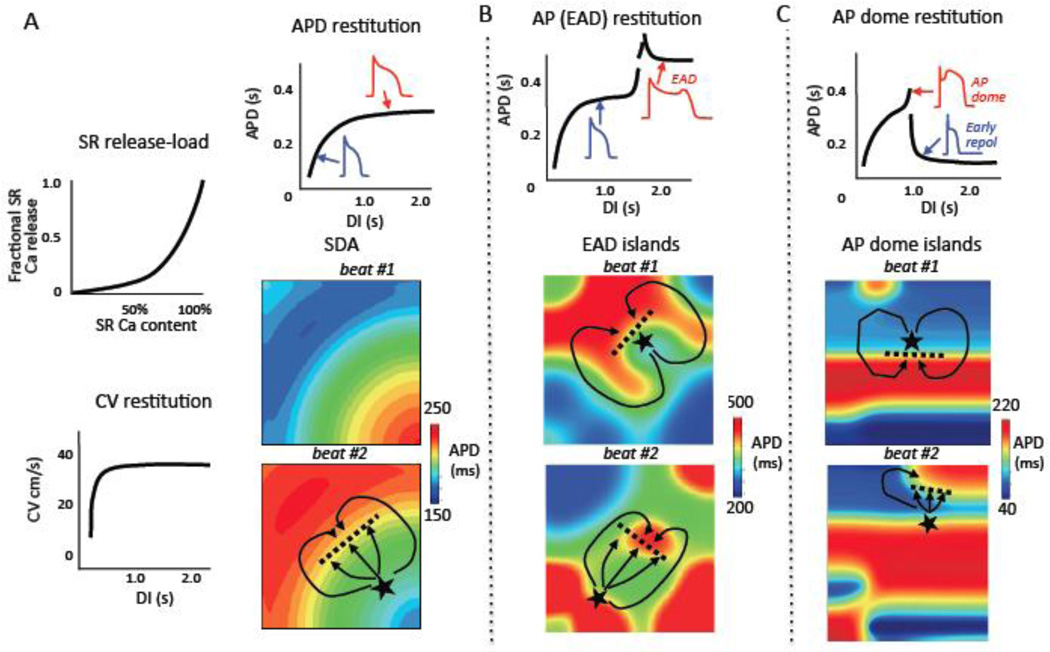
In addition to PVCs triggered by DADs, unstable Ca cycling can simultaneously dynamically increase substrate vulnerability by two mechanisms: promoting dispersion of excitability, and promoting dispersion of refractoriness. In the first case, regions of tissue in which DADs do not reach the threshold to trigger an AP can nevertheless depolarize the resting membrane voltage sufficiently to depress excitability by inactivating Na channels. This can lead to regional conduction block of impulses arising from adjacent regions with supra-threshold DADs, thereby initiating reentry [30, 31]. In the second case, the rapid rates during DAD-induced triggered activity can also promote Ca transient alternans (manifesting clinically as pulsus alternans in heart failure) which secondarily causes APD to alternate, equivalent to T wave or repolarization alternans (for review see [32]). APD alternans, when coupled to conduction velocity (CV) restitution, results in spatially discordant APD alternans [33, 34]. During spatially discordant APD alternans, APD alternates in a long-short pattern in some regions but a short-long pattern in adjacent regions, producing a steep APD gradient between the two regions (Fig. 2A). This makes the tissue highly vulnerable to initiation of reentry [35], since a DAD-mediated PVC arising from the region with short APD encounters a gradient of increasing refractoriness as it propagates into the region with long APD. If this APD gradient is too steep, the impulse will block and propagate around the long APD region until it regains excitability, and then reenter this region retrogradely to induce reentry, as illustrated in Fig. 2A (beat #2). Once reentry is induced, the arrhythmia can either self-terminate by colliding with a border, or degenerate into multiple wavelet or mother rotor VF.

Fig. 2. Trigger-substrate interactions initiating reentry.

A. Spatially discordant alternans: steep SR Ca release relationship and/or steep APD restitution coupled with conduction velocity (CV) restitution causes APD alternate on a short-long (blue-red) pattern in one region and long-short (red-blue) in another region, separated by a nodal line where APD does not alternate (white). The pattern in beat #1 reverses in beat #2. In beat #2, a DAD arising from the short APD region triggers a PVC (★) which blocks superiorly (dashed line) but conducts laterally (solid lines), initiating reentry. B. EAD chaos synchronization: steep EAD restitution causes EADs to occur chaotically from beat-to-beat. In tissue, electrotonic coupling causes regional chaos synchronization to generate EAD islands (red regions), separated by regions without EADs (blue), whose position and size vary from beat-to-beat. Beat #1 illustrates a scenario in which a triggered PVC (★) arising from an EAD island blocks superiorly (dashed line) but conducts inferiorly (solid line), subsequently reentering the blocked region to induce reentry. Beat #2 illustrates a scenario in which the triggered PVC arising from an EAD island encounters another EAD island, resulting in conduction block (dashed line) and reentry (solid lines). C. AP dome chaos synchronization: steep AP dome restitution causes AP domes to appear chaotically from beat-to-beat. In tissue, electrotonic coupling causes regional chaos synchronization to generate AP dome islands (red regions), separated by regions with very short APD due to all-or-none repolarization (blue regions), whose position and size vary from beat-to-beat. An AP dome (★) propagating into the short APD region induces phase 2 reentry. In tissue, electrotonic coupling causes regional chaos synchronization to generate AP dome islands (red regions), separated by regions with very short APD due to all-or-none repolarization (blue), whose position and size varies from beat-to-beat. Beat #1 illustrates a scenario in which an AP dome (★) propagating out of an island blocks inferiorly (dashed line) but conducts laterally (solid line), subsequently reentering the blocked region to induce phase 2 reentry. Beat #2 illustrates a scenario in which the propagating AP dome (*) encounters another AP dome region that is still refractory, resulting in conduction block (dashed line) and reentry (solid lines).

Spatially discordant APD alternans is also a mechanism by which extremely rapid pacing (>300 beats per min) induces VF in completely normal hearts [32, 35]. Normally, such fast heart rates are not physiologically achievable, so that VF arising directly from sinus tachycardia in normal hearts is extremely uncommon. However, VF is almost universally inducible by very rapid external pacing in normal hearts. In heart failure and acute ischemia, the threshold required to induce spatially discordant alternans decreases to much slower heart rates, as evidenced clinically by pulsus alternans and frank or microvolt T wave alternans, both of which portend an increased risk of sudden cardiac death [32, 36–38]

Dynamic factors/targets

The relationship between SR Ca release and SR Ca load (Fig. 2A) plays a key role in the genesis of both Ca waves causing DADs and Ca alternans leading to spatially discordant APD alternans (for review see [39]). The SR Ca release-load relationship in cardiac myocytes is normally very steep [40, 41], such that as the SR Ca load increases, the probability that spontaneous openings of RyRs in one region of a myocyte will trigger a regenerative Ca-induced Ca release wave that propagates throughout the myocyte to cause a DAD also increases. A steep SR Ca release-load relationship also promotes Ca alternans [42]. Dynamically, the SR Ca release-load relationship can be thought of as an input-output relationship with a high gain. If a large amount of SR Ca is released on one beat, the SR is depleted to a greater extent and may not be able to refill to the same level before the next beat arrives. The lower SR Ca then results in a smaller release, causing less SR depletion, which allows the SR to refill to a higher level before the next beat, causing a large release, and so forth, generating an alternating large-small-large-small release pattern. This mechanism of Ca alternans is called SR load-dependent Ca alternans. In addition, Ca alternans can result from an SR load-independent mechanism due to RyR refractoriness [43]. The consequence of Ca alternans is APD alternans, since the Ca transient amplitude affects Ca-sensitive currents regulating APD, including the L-type Ca current (I_Ca,L), the slow component of the delayed rectifier K current (I_Ks) and I_NCX. This relationship is referred to as Ca-voltage coupling [44], and can be either positive (a large Ca transient prolongs APD) or negative (a large Ca transient shortens APD), depending on whether the net effect on Ca-sensitive currents is inward or outward. Finally, Ca alternans in cardiac myocytes can become spatially discordant at the subcellular levels, such that one region of the myocyte exhibits a large-small pattern of Ca release, whereas another region exhibits a small-large pattern [45, 46]. This tends to attenuate APD alternans, since the whole cell Ca transient shows less beat-to-beat variation when regions are alternating out-of-phase with each other.

In addition to Ca alternans, APD alternans can be caused by steep APD restitution [32, 47]. APD restitution refers to the dependence of APD on the previous diastolic interval (DI). Normally, when heart rate increases, APD also shortens in order to preserve diastolic filling time and coronary blood flow. This relationship, plotted graphically in Fig. 2A, also represents an input-output relationship. At a constant heart rate, the cycle length equals the sum of the APD and DI, so that if the DI is short, then the subsequent APD will be short. That will prolong the DI before the next beat arrives, causing a long APD. This long APD means a shorter DI, so the next beat will have a shorter APD, and so forth, in an alternating long-short-long-short pattern. Dynamical analysis reveals that the slope of the APD restitution curve is a critical determinant of whether the APD alternans will gradually disappear (slope <1) or increase (slope >1) to cause persistent APD alternans (or block). In reality, the situation is somewhat more complex, because although the previous DI has a powerful influence of the subsequent APD, it is not the sole determinant. The other determinants are collectively referred to as memory effects, so that the onset of APD alternans often does not correlate precisely with APD restitution slope >1 [48]. Nevertheless, other factors being equal, flattening APD restitution slope will suppress APD alternans and vice versa.

A third dynamic factor that plays a critical role in whether APD alternans becomes spatially discordant is CV restitution [33, 34, 49]. CV restitution is the dependence of CV on the previous DI (Fig. 2A). At very short DI, incomplete recovery from inactivation of I_Na causes CV to slow. Dynamically, this acts once again as an input-output relationship for a wave propagating through tissue. At very short DI, the wavefront slows, increasing its DI with respect to the wave in front of it. As the DI becomes longer, however, the APD prolongs, which shortens the DI of the wave behind it, initiating a chain reaction that causes the APD (and CV) to oscillate as the wave moves through the tissue, resulting in spatially discordant APD alternans. In this situation, APD alternans drives oscillations in the waveback, whereas CV restitution drives oscillations in the wavefront, together creating head-tail interactions that, if unstable and self-amplifying, can lead to wavebreak. In promoting spatial discordance, the steepness of CV restitution is not as important as the range of DI over which the CV varies. Therefore we refer to “broad,” rather than “steep,” CV restitution as promoting spatially discordant alternans. Premature beats arising from a different location in the tissue can convert spatially concordant APD alternans to spatially discordant alternans [34]. Fixed factors, such as pre-existing APD gradients or tissue fibrosis, can markedly reduce the threshold of dynamic instability required for spatially discordant alternans to develop [50].

There are also mechanisms that generate APD alternans at normal or slow heart rates in the settings of reduced or excessive repolarization reserve [51], but these do not typically generate spatially discordant alternans because the rate is too slow to engage CV restitution. Other dynamic mechanisms promote electrical dispersion in these settings, as discussed later.

Molecular factors/biological targets

The strategy to identify molecular factors as biological targets to suppress DADs and spatially discordant APD alternans requires a multiscale analysis. First, how molecular factors relate to the dynamic factors and fixed factors promoting Ca waves and Ca alternans at the subcellular level must be defined. Next, how these subcellular behaviors relate to DADs and APD alternans at the cellular level must be defined. Finally, how these cellular behaviors relate to DAD-mediated PVCs and spatially discordant APD alternans at the tissue level must be defined. In addition, to qualify as biological targets, molecular factors must meet two equally important criteria – that they do not impair normal excitation-contraction (EC) coupling, and do not exacerbate the dynamic factors promoting arrhythmias in the other two major arrhythmia dynamics categories.

At the subcellular level, the task is to identify molecular factors regulating the dynamic factors promoting Ca waves and Ca alternans. The theoretical analysis of Ca cycling has revealed three key dynamic factors underlying the emergence of Ca waves and Ca alternans: random activation, refractoriness and recruitment of Ca release units in their subcellular network (the 3 R’s theory) [39, 52]. The regulation of the 3 R’s by molecular factors, however, is very complex, since Ca cycling proteins not only affect the 3 R’s directly, but also indirectly by altering SR Ca load. Nevertheless, the theory provides a comprehensive computational framework to systematically identify properties of Ca cycling proteins that can be targeted to suppress Ca waves and Ca alternans, for example by altering RyR properties or upregulating SERCA activity, without adversely impacting normal Ca cycling and excitation-contraction coupling.

At the cellular level, an important dynamic factor for DAD formation is the sensitivity of diastolic membrane voltage to spontaneous SR Ca release, referred to as the diastolic Ca-voltage coupling gain [53]. For example, when a Ca wave stimulates I_NCX to generate a DAD in a myocyte, the amplitude of the DAD depends on the resting K conductance, mainly determined by the inward rectifier K current I_K1, relative to the amplitude of I_NCX. When resting K conductance is low, the same I_NCX will generate a much larger DAD than when resting K conductance is high, facilitating DAD-mediated triggered activity. In heart failure, I_K1 is down-regulated by approximately 50% while I_NCX is typically doubled [54], important factors contributing to the increased incidence of DAD-mediated triggered activity in failing hearts. Therefore, I_K1 is an important molecular factor that directly regulates a dynamic factor (diastolic Ca-voltage coupling gain) that controls DAD amplitude. This could be a potential biological target, with the caveat that its effects on normal EC coupling and other dynamic factors in all three arrhythmia categories must be shown to be neutral or anti-arrhythmic.

Another key dynamic factor at the cellular level is APD restitution slope, which, if steep (>1), promotes APD alternans and spiral wave breakup initiating multiple wavelet VF [55]. A multitude of molecular factors affect APD restitution slope, but one of the most influential determinants is I_Ca,L, specifically its kinetics of recovery from inactivation. By reducing the influence of I_Ca,L on APD, Ca channel blockade flattens APD restitution slope, thereby suppressing voltage-driven APD alternans [56], and also inhibits DADs by reducing cellular Ca loading. However, the degree of Ca channel blockade required to produce these effects also significantly depresses EC coupling, making Ca channel blockade impractical as an antiarrhythmic strategy. Moreover, although Ca channel blockade suppresses voltage-driven APD alternans, it can promote Ca-driven APD alternans [52, 57], which is pro-arrhythmic. These adverse effects of Ca channel blockade arise largely from suppressing the early peak of I_Ca,L which is critical for normal EC coupling. However, modifying the kinetics of inactivation and recovery from inactivation of I_Ca,L alone, without suppressing the early peak current can flatten APD restitution slope without greatly impacting the whole cell Ca transient amplitude [58]. Thus, modification of I_Ca,L kinetics could be a potential molecular factor to target, assuming it does not adversely affect dynamic factors in the other arrhythmia categories.

At the tissue level, an important dynamic factor promoting spatially discordant APD alternans is broad CV restitution [33, 34]. The main molecular factor controlling CV restitution is recovery of inactivation of I_Na. Speeding I_Na recovery from inactivation reduces the range of DI over which CV varies, and is a potential molecular factor that could serve as a biological target. Conversely, slowing I_Na recovery from inactivation broadens CV restitution, which promotes spatially discordant APD alternans. Na channel blockers typically slow I_Na recovery from inactivation [59], and the increased propensity to develop spatially discordant APD alternans may have contributed to the excess mortality in patients treated with Na channel blockers in the CAST study [7], despite the >80% reduction in PVCs. Chronic and acute ischemia also slow I_Na recovery from inactivation [59–61], potentiating spatially discordant APD alternans.

Fixed factors causing electrical dispersion can also be biological targets. Fibrosis plays a key role in both promoting triggers and creating a vulnerable tissue substrate [26]. The source-sink relationship is much more favorable for DADs (and EADs) to emerge and cause triggered activity in moderately fibrotic tissue than in normal tissue [22]. Fibrosis also promotes spatially discordant APD alternans [50] and slow conduction, facilitating reentry. Molecular interventions that reverse fibrosis completely could have powerful antiarrhythmic actions. A caveat, however, is that if such agents only partially reverse fibrosis, such that regions of severe fibrosis were converted to moderate fibrosis, the net effect could be proarrhythmic. This is because impulses that cannot propagate into or out of severely fibrotic tissue may regain the ability to propagate slowly through moderately fibrotic regions, unmasking sources for triggers and creating new slow conduction pathways for reentry.

The above are only a few conceptual examples illustrating how molecular factors can be related to subcellular, cellular and organ scale dynamic and fixed factors promoting DADs and spatially discordant APD alternans. Their plausibility as biological targets, however, depends on systematically demonstrating that they do not interfere with normal EC coupling and do not exacerbate the dynamic factors controlling the other arrhythmia categories.

3.2. Arrhythmias Related to Reduced Repolarization

Clinical settings

The prototype clinical settings for this dynamical category of arrhythmias are the congenital and acquired LQT syndromes, in which repolarization reserve is reduced due to either decreased outward or increased inward currents during the AP plateau [62, 63]. Heart failure is also associated with reduced repolarization reserve as a result of electrical remodeling [19, 64], predisposing the failing heart to this category of arrhythmias in addition to arrhythmias in the unstable Ca cycling category discussed above in section 3.1.

Arrhythmia mechanisms

In this category, EAD-mediated PVCs and triggered activity are the major triggers which can initiate TdP, polymorphic VT, and/or mixed focal-reentrant VF.

Dynamical mechanisms

When repolarization reserve is reduced, myocytes become susceptible to EADs [65, 66]. At the cellular level, EADs often exhibit chaotic and bistable behaviors [15, 67]. At the tissue level, these factors lead to EAD-mediated arrhythmias arising from regional chaos synchronization and biexcitability. The relevant subcellular, cellular and tissue level mechanisms are discussed below.

At the subcellular level, spontaneous SR Ca release due to a mix of Ca waves and I_Ca,L-triggered Ca release before repolarization is complete can stimulate inward I_NCX, thereby slowing and/or transiently reversing repolarization [68–70]. However, as voltage depolarizes and/or the Ca elevation subsides, inward I_NCX decreases and cannot by itself trigger an AP at the cellular level. A regenerative current is required for the latter. This most commonly involves reactivation of I_Ca,L, although if the takeoff potential of the EAD is sufficiently low, as in a phase-3 EAD, I_Na reactivation can also be involved [71].

At the cellular level, the major factor promoting EADs of sufficient amplitude to trigger an AP is I_Ca,L [72]. The dynamics of the process is now reasonably well-understood (for review see [66]). APD prolongation by itself is not sufficient to induce EADs, since if the membrane voltage remains above 0 mV, there is no possibility of reactivating I_Ca,L. When the membrane voltage falls below 0 mV, however, the window region of I_Ca,L is engaged, such that L-type Ca channels are neither fully activated nor fully inactivated (Fig. 3B). Depending on the relative rates at which L-type Ca channels recover from inactivation and K channels deactivate as the AP repolarizes into this voltage window, the membrane voltage may begin to oscillate as a result of a Hopf bifurcation [73]. A Hopf bifurcation is a generic cause of oscillations in systems containing positive and negative feedback loops which are coupled with a time delay (other examples include the cell cycle and sinus node pacemaking). In the case of EADs, the positive feedback element is the reactivation of I_Ca,L, such that as voltage increases during the EAD upstroke, I_Ca,L is further activated, causing more rapid depolarization, and so forth. The negative feedback elements are the inactivation of I_Ca,L and the activation of I_Ks (or other outward currents) as the membrane depolarizes during the EAD upstroke, which causes the cell to repolarize. The time constants of inactivation/recovery from inactivation of I_Ca,L and activation/deactivation of I_Ks must be in a properly balanced range for oscillations to develop. A characteristic feature of Hopf bifurcation dynamics is that the oscillations grow in amplitude over time, eventually repolarizing the voltage to a negative enough level to allow full blown reactivation of I_Ca,L to elicit triggered activity. Eventually, the oscillations amplify to a level that engages another type of bifurcation, called a homoclinic bifurcation, which terminates the oscillations and triggered activity, leading to full repolarization [73]. This Hopf-homoclinic bifurcation scenario is similar to that underlying bursting behavior in neurons[74, 75]. In the case of EADs, the Hopf-homoclinic bifurcation dynamics do not result solely from the I_Ca,L-I_Ks interaction independently of other ionic currents. Rather, all of the ionic currents influencing repolarization must be balanced in a certain range for the EAD dynamics to emerge. The key requirement is for the rate of repolarization to be delayed as the plateau voltage falls below 0 mV. This is the reason why triangular-shaped APs are more susceptible to EADs than long square-shaped APs in which voltage remains above 0 mV [76]. It also explains why I_to, despite being an outward K current, can promote EADs by holding the early plateau voltage at a lower level, which delays the activation of I_Ks and thereby reduces repolarization reserve during the late phase of the plateau [77]. Fibroblast coupling to myocytes can have a similar effect [78]. Thus, repolarization reserve evolves dynamically during the AP plateau phase, and is impacted by all ionic currents during the plateau, even though the active dynamics underlying the oscillations are primarily mediated by the I_Ca,L-I_Ks interaction. An analogy can be drawn to pacemaking by ventricular myocytes – I_K1 normally stabilizes the resting voltage of myocytes, preventing automaticity from emerging. If I_K1 is suppressed, however, the myocyte develops spontaneous diastolic depolarization by allowing other conductances, such as I_f, to depolarize the resting potential to the activation threshold. Similar to I_K1, most of the ionic conductances during the AP are passively summating to determine whether or not the background is permissive for the active currents to generate the voltage oscillations. Therefore, repolarization reserve is not a static factor that is either high or low, but a key dynamic factor linking alterations of many different outward and inward ionic currents to EAD susceptibility. This accounts for the wide variety of genetic causes of LQT syndromes (currently LQT1-LQT13) as well as drugs inducing acquired LQT syndrome. Various signaling pathways (adrenergic, Ca-calmodulin kinase) and electrolyte disturbances (hypokalemia, hypomagnesemia) can also modify channel properties to make myocytes more vulnerable to EADs.

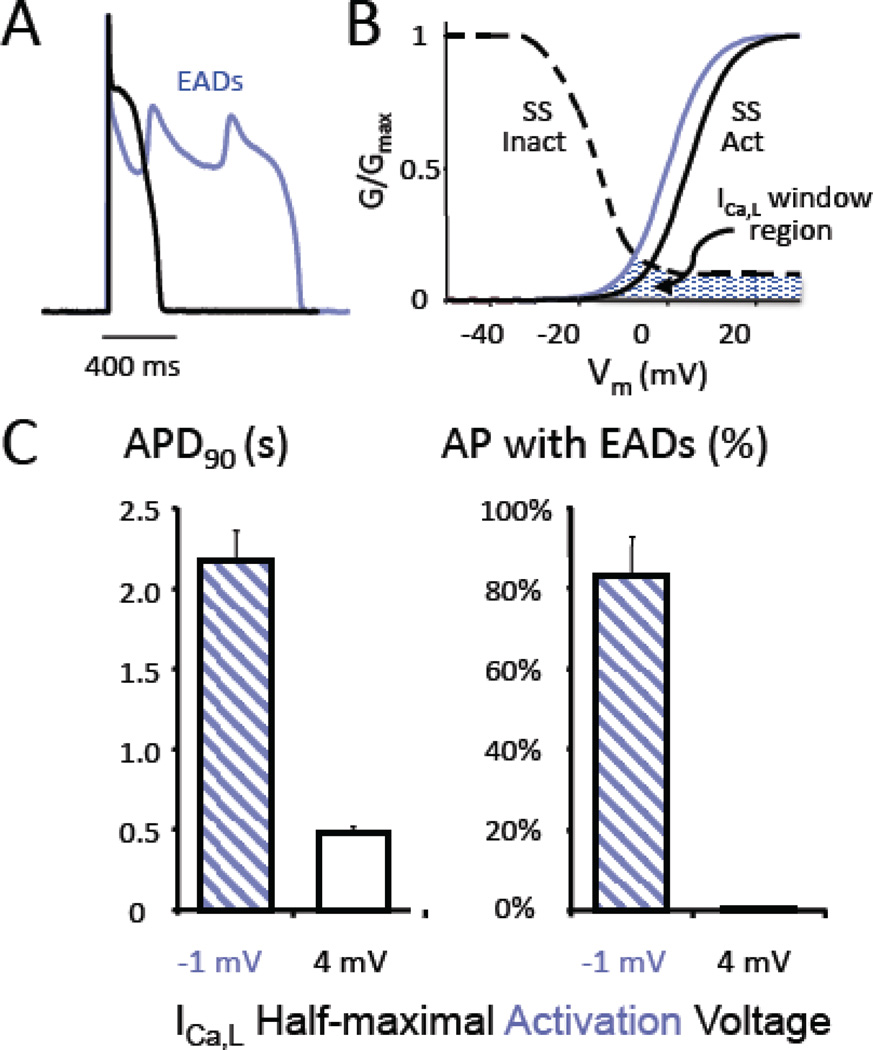
Fig. 3. The L-type Ca window current and EADs.

A. A rabbit ventricular myocyte was exposed to hypokalemia (2.7 mM) to induce EADs, after which the endogenous L-type Ca current (I_Ca,L) was pharmacologically blocked and replaced with a virtual I_Ca,L using the dynamic clamp technique, which reconstituted the EADs (blue trace). B. Shifting the I_Ca,L half-maximal activation voltage from −1 mV (blue curve) to +4 mV (black curve) to reduce the overlap between the steady state activation (SS Act) and inactivation (SS Inact) curves defining the I_Ca,L window current region (blue-hatched area) suppressed EADs and restored APD to normal (black trace in A). C. Summary results from 3 myocytes, showing that APD was restored from >2 s (with EADs present in 80% of action potentials) to < 0.5 s (with 0% EADs present). (Adapted from Madhvani et al [93], with permission).

Whereas the Hopf bifurcation initiates the voltage oscillations during the EAD, a homoclinic bifurcation terminates the oscillations and causes repolarization [73]. The homoclinic bifurcation mechanism is important because its dynamical signature is chaos. That is, the termination of voltage oscillations during the EAD is a chaotic process, such that at a constant heart rate, the pattern of EADs will vary unpredictably, with some beats exhibiting one or many EADs, while other beats repolarize without EADs. The chaotic behavior of EAD termination has important consequences at the tissue level, referred to as regional chaos synchronization [15]. The principle is straightforward. When two myocytes are coupled electrotonically via gap junctions, they cannot exhibit markedly different AP waveforms, since any voltage difference between the cells causes electrotonic current to flow through gap junctions (by Ohm’s law), which hyperpolarizes the more depolarized cell, and conversely depolarizes the more hyperpolarized cell. Thus, if one myocyte is set to have an EAD but its neighbor is not, one or the other will predominate, and either both myocytes will have an EAD or both will repolarize. When this situation is extended to cardiac tissue level, in which thousands of myocytes are electrotonically coupled to each other, democracy rules. In regions in which a large majority of myocytes are poised to have an EAD (EAD+ myocytes), they will force all of the myocytes in that region will exhibit an EAD. However, in regions in which less than the critical majority are poised to have an EAD (EAD− myocytes), all of the cells will repolarize. The chaotic behavior of EADs therefore can tip the balance in either direction, so that some regions fall below the critical threshold of EAD+ myocytes, while other regions are above the threshold. The result is the formation of islands of myocytes all exhibiting EADs, between which are interposed regions without EADs (Fig. 2B). The size of the EAD islands (referred to in dynamics as their characteristic length scale) depends on the violence of the chaos (tending to create voltage differences) relative to the strength of electronic coupling (tending to smooth voltage differences) [15, 66]. On each beat, the pattern changes unpredictably (compare beat #1 and beat #2, Fig. 2B). The result is marked dispersion of refractoriness whose pattern changes on each beat. Moreover, if one of the EAD islands reaches the threshold to trigger an AP which propagates unidirectionally (due to the irregular contour of the EAD island) into adjacent repolarized tissue, the impulse can potentially reenter the EAD region after it repolarizes and thereby induce reentry (illustrated in beat #1, Fig. 2B). Alternatively, the triggered AP can propagate out of the EAD island until it encounters an adjacent EAD island which has not yet repolarized. If the APD gradient is steep enough, wavebreak can result, initiating reentry (illustrated in beat #2 in Fig. 2B). The resulting arrhythmia involves a mixture of EAD-mediated triggered activity and reentry, manifesting as polymorphic VT which can quickly degenerate into mixed focal-reentrant VF.

Reentry induced by EAD-mediated arrhythmias also can exhibit an unusual property. It has been known for decades that under some conditions of reduced repolarization reserve (such as hypokalemia), myocytes can exhibit two stable resting membrane potentials, one near −80 mV and the second at a more depolarized voltage around −50 mV [79], a phenomenon known in dynamics as bistability. When the combination of EAD-mediated triggers and electrical dispersion created by EAD islands leads to initiation of reentry, the resulting rotors can arise from either resting potential [67, 80]. If the rotor arises from the more polarized resting potential, the rotor propagates primarily via I_Na (with I_Ca,L activated secondarily). However, if the rotor arises from the depolarized resting potential, at which I_Na is inactivated, I_Ca,L mediates propagation. We call this condition biexcitability, such that either I_Na- or I_Ca,L-mediated rotors, or mixtures of the two, can coexist in the same tissue. Whereas I_Na-mediated rotors have a very rapid rate, typically around 600 beats per min, I_Ca,L-mediated rotors are much slower, in the range of 150–300 beats per min. I_Ca,L-mediated rotors also tend to meander, causing the QRS morphology to vary. These features of I_Ca,L-mediated rotors match both the typical rates and varying QRS morphologies of TdP, in contrast to I_Na-mediated rotors which are much faster and produce the high frequency activation more characteristic of VF. We have proposed that as ischemia develops during TdP or polymorphic VT, the activation of ATP-sensitive K channels increases repolarization reserve and converts I_Ca,L-mediated rotors to I_Na-mediated rotors, causing degeneration of TdP and polymorphic VT into multiple wavelet or mother rotor VF [81].

It is important to note that the EAD-mediated arrhythmias described above can all originate purely from dynamic mechanisms, in the absence of any fixed factors, such as pre-existing structural or electrophysiological tissue heterogeneities [66]. This can be demonstrated in computer simulations performed in completely homogeneous isotropic cardiac tissue. Fixed factors creating electrical dispersion, however, generally lower the threshold of dynamic instability required to generate these behaviors. Thus, real cardiac tissue, which always contains pre-existing heterogeneities, is inherently more sensitive to the emergence of these dynamic instabilities, and becomes even more sensitive when disease processes exacerbate the degree of heterogeneity further as a result of electrical and structural remodeling. For example, phase 3 EADs caused by tissue heterogeneities have been shown to initiate reentrant arrhythmias [82].

Dynamic factors/targets

At the subcellular level, Ca cycling abnormalities that promote spontaneous SR Ca release and Ca waves during diastole can also generate spontaneous Ca release during systole, contributing to the formation of EADs by stimulating inward I_NCX. This may be an important factor in phase-3 EADs, since inward I_NCX amplitude is enhanced at negative voltages. Thus, dynamical targets designed to suppress spontaneous Ca release and DADs based on the 3R theory described in section 3.1 [39, 52] may potentially have efficacy against EAD-mediated arrhythmias.

At the cellular level, the main dynamic factor regulating EAD behaviors can be observed from the APD restitution curve (Fig. 2B), which exhibits a very steep region corresponding to the sudden APD prolongation when EADs appear (Fig. 2B) due to the Hopf-homoclinic bifurcation mechanism. As noted earlier, from a dynamics standpoint APD restitution is an input-output relationship, since the preceding DI determines the APD for the next beat, but the APD of the next beat determines the next DI, and so forth. The slope is the gain of this input-output function, so that steeply-sloped regions act as amplifiers of small differences, creating instability. In LQT syndromes, one manifestation of this instability is APD (and T wave) alternans [83], which can occur when heart rate is such that the DI falls in the steeply-sloped region of the APD restitution curve [51]. These DIs may correspond to slow or normal heart rates in LQT syndromes. Since CV restitution (which occurs at very short DI) is not typically engaged, APD alternans is not likely to become spatially discordant at the tissue level. Instead, electrical dispersion at the tissue level is generated when the EAD behavior becomes chaotic and the chaos synchronization mechanism comes into play, as described above [15, 66]. The chaotic EAD behavior is also predicted from the APD restitution curve, since not only does the region of the Hopf-homoclinic bifurcation have a very steep slope, but a portion of this region is negatively-sloped (Fig. 2B). The latter is a well-recognized generator of higher order periodicities and chaotic behavior, as can be readily demonstrated by a cobweb diagram [15]. Eliminating this steeply-sloped region in the APD restitution curve is predicted not only to prevent EADs and EAD chaos at the cellular level, but also to prevent EAD chaos synchronization at the tissue level. This is a powerful dynamic factor to target, since it simultaneously prevents EADs from generating PVCs as triggers and from creating marked dispersion of refractoriness by forming EAD islands.

Molecular factors/biological targets

Molecular factors, if appropriately identified, can be targeted to suppress subcellular, cellular, or tissue scale dynamic factors promoting the instability creating EADs. At the subcellular scale, Ca waves play a facilitatory role in EAD generation. Thus, molecular factors targeting the 3R’s as dynamic factors at the subcellular scale may potentially have favorable effects at suppressing EAD- and as well as DAD-mediated arrhythmias.

At the cellular scale, a promising dynamic target for EADs is the steep APD restitution curve, reflecting the underlying Hopf-homoclinic bifurcation sequence that generates chaotic behavior of EADs. This is a potent target since it generates not only EADs at the cellular scale, but is also allows chaos synchronization to generate both triggers and a vulnerable substrate at the tissue scale. What molecular factors control the Hopf-homoclinic bifurcations? There are many potential candidates, since, as noted above, all ionic currents during the AP plateau are involved in setting the conditions for the Hopf-homoclinic bifurcation to occur and generate chaotic EADs. Most of these currents play relatively passive background roles at reducing overall repolarization reserve, whereas the key active currents generating the oscillatory dynamics are I_Ca,L and I_Ks, and in some cases, I_Na [84]. Two examples, one from the passive group (late I_Na) and one from the active group (I_Ca,L), are discussed below.

Late I_Na

One of the common congenital LQT syndromes, LQT3, is caused by mutations that interfere with inactivation of I_Na, such that a small component of residual inward current, called late I_Na (typically only 1–2% of the peak current, remains active during the AP plateau [85]. This increase in inward current relative to the normal outward K currents during the AP plateau reduces repolarization reserve, setting the stage for EADs to occur. The importance of late I_Na, however, is not restricted to LQT3. Late I_Na is also induced by signaling pathways which modify Na channel function, notably CaMKII activation [86] and phosphoinositol 3 kinase (PI3K) inhibition [87]. CaMKII signaling is activated in heart failure by both Ca overload and oxidative stress [18]. Moreover, late I_Na poses an increased Na load on the heart, which contributes to the rise in intracellular [Na] during heart failure, secondarily potentiating Ca overload by inhibiting forward I_NCX [88]. The Ca overload causes further activation of CaMKII, initiating a positive feedback cycle. PI3K signaling has recently been shown to be inhibited by a variety of I_Kr blocking drugs known to cause acquired LQT syndrome, such as dofetilide [87]. These observations have stimulated considerable interest in drugs that selectively block late I_Na, without depressing the early peak I_Na, such as the antianginal agent ranolazine and newer derivatives. Unlike other Na channel blockers which block both peak and late I_Na, ranolazine does not appear to increase mortality in patients with coronary artery disease or heart failure [89], and in experimental studies has been shown to potently suppress EAD-mediated arrhythmias [90, 91]. The reason may be that drugs selectively blocking late I_Na do not simultaneously exacerbate arrhythmia risk by potentiating spatially discordant APD alternans (via broadening CV restitution) and conduction block like drugs blocking peak I_Na.

I_Ca,L

I_Ca,L is a molecular factor that plays a key dynamic role in EAD generation. I_Ca,L normally has a substantial late component, averaging 10–20% of peak I_Ca,L. Genetic mutations that interfere with voltage- or Ca-induced inactivation of I_Ca,L and thereby increase this late component of inward current during the AP plateau cause clinical LQT syndromes [92]. CaMKII activation and drugs such as BayK4688 which reduce repolarization reserve by increasing both peak and late I_Ca,L also are potent generators of EADs and EAD-mediated arrhythmias [18]. The major factor promoting the EAD upstroke is reactivation of I_Ca,L, which is determined by the properties of I_Ca,L in the window current range from approximately −40 to 0 mV [72]. In this voltage range, I_Ca,L is neither fully activated nor inactivated, and generates a sustained current that regeneratively increases from −40 to −20 mV, after which it peaks and then falls off to the late I_Ca,L pedestal component above 0 mV. Fig. 3B illustrates the quasi-steady state I_Ca,L window conductance, measured 300 ms after a voltage clamp to different membrane potentials. As the voltage during the AP plateau repolarizes into this voltage range, the I_Ca,L window current grows larger as channels recover from inactivation. The rate at which the current increases is governed by the time constant of recovery from inactivation. Since the rate of repolarization is normally too rapid for much recovery to occur, I_Ca,L remains too small to reverse repolarization. If the rate of repolarization has been slowed, because of reduced outward K currents like I_Kr or I_Ks or increased inward currents like late I_Na or late I_Ca,L, then the recovery of I_Ca,L may be adequate to reverse repolarization and initiate an EAD. The amplitude of the EAD depends on how much I_Ca,L is available to be reactivated, such that the lower the take-off potential of the EAD, the larger its amplitude. In this scenario, both the size and the kinetics of the I_Ca,L window region play major roles. EADs can be powerfully suppressed by manipulating the size of the I_Ca,L window current region in a manner that does not suppress the peak I_Ca,L critical for regulating Ca release and normal EC coupling. Fig. 3 illustrates the effects of a modest 5 mV depolarizing shift in the voltage dependence of the steady state activation to reduce the overlap between these curves and make the window current region smaller. This intervention had no major effect on the peak I_Ca,L, Ca transient amplitude or APD, but potently suppressed EADs induced by either oxidative stress (H₂O₂) or modest hypokalemia [93]. Hyperpolarizing the steady state inactivation curve by 5 mV to reduce the window current region had comparable effects, as did reducing the late I_Ca,L non-activating pedestal current. In contrast, altering other I_Ca,L parameters, such as time constants of activation, inactivation and recovery from inactivation or the slopes of steady state activation and inactivation curves had less reliable effects (Olcese R, unpublished observations). These studies demonstrate that it is possible, in principle, to modify the biophysical properties of I_Ca,L to suppress EADs, while preserving peak I_Ca,L and normal EC coupling. This raises the possibility that a drug that selectively blocks late I_Ca,L, analogous to the manner in which ranolazine selectively blocks late I_Na, could have powerful antiarrhythmic effects at suppressing EAD-mediated arrhythmias, either alone or in combination with a drug that blocks late I_Na. Identifying compounds that selectively block late I_Ca,L seems plausible, given the overall structural similarities between gating of Na and Ca channels and the fact that selective late I_Na blockers such as ranolazine already exist and are in clinical use. The biophysical properties of I_Ca,L could potentially also be modified by altering the subunit composition of L-type Ca channels. Cardiac L-type Ca channel complexes are comprised of pore-forming α subunit as well as accessory α –δ and β subunits. The β subunits have a large number of isoforms expressed differentially in various tissues. In heart, the predominant isoform is the β_2a subunit, which confers a relatively large non-inactivating pedestal component to I_Ca,L, but other β subunits have different effects on inactivation which may potentially reduce the size of the I_Ca,L window current region [94]. This raises the possibility of a gene therapy approach to replace the native β subunits with β₃.

At the tissue level, the dynamical factors that regulate the spatial scale at which EAD islands form during regional chaos synchronization also can be potentially targeted by molecular factors. As noted above, the characteristic length scale at which these islands form is determined by the violence of the chaos generating EADs relative to the smoothing effect of electrotonic coupling [15]. The latter is determined by gap junction coupling between adjacent myocytes. If gap junction coupling is very strong, the characteristic size of the EAD islands increases, and if the characteristic size exceeds the physical size of the ventricles, then multiple islands cannot form, reducing both the dispersion of refractoriness and frequency of EAD-triggered activity in the tissue. Thus, drugs that increase gap junction conductance could have antiarrhythmic properties. Similarly, molecular interventions that prevent gap junction remodeling or fibrosis (which effectively reduces myocyte-myocyte coupling by interposing fibrous strands between myocytes) in diseased hearts could have beneficial effects by this mechanism.

We have used the above examples to illustrate how molecular factors might be targeted to suppress the dynamical factors causing EAD-mediated arrhythmias, but these represent only a few of myriad possibilities. Many other potential interventions targeting various biophysical properties of different ion channels/transporters, their trafficking and regulation by various signaling pathways are also possible, once the proper framework for systematically evaluating their dynamical effects has been established. As with DAD-mediated arrhythmias, fixed factors can also be biological targets for EAD-mediated arrhythmias. Fibrosis again plays a key role in both promoting triggers and creating a vulnerable tissue substrate [26]. The source-sink relationship is much more favorable for EADs to emerge and cause triggered activity in moderately fibrotic tissue than in normal tissue [22, 95]. Fibrosis also promotes slow conduction and conduction block, facilitating initiation of reentry by EAD-mediated PVCs.

Even if pharmacologic or gene therapy-based approaches to prevent EAD-mediated arrhythmias can be identified, they must not interfere with normal EC coupling if they are to be clinically useful. For example, in animal models currently available Ca channel blockers which block both peak and late I_Ca,L are very effective at preventing EAD-mediated arrhythmias as well as arrhythmias related to Ca cycling instabilities. However, the doses required markedly impair EC coupling, which limits their usefulness clinically. Second, the intervention must not increase susceptibility to ventricular arrhythmias in the other dynamic categories. These issues have yet to be fully evaluated for the molecular factors, such as late I_Na blockers or the I_Ca,L- modifying interventions, discussed above.

3.3. Arrhythmias Related to Excess Repolarization

Clinical settings

The prototype clinical settings for this dynamical category of arrhythmias are Brugada Syndrome, Early Repolarization Syndrome, and Short QT Syndromes [96, 97]. In these cases, excessive repolarization reserve is classically caused by decreased inward current (Na or Ca channel loss-of-function mutations) or increased outward current (K current gain-of-function mutations) affecting the AP plateau. Acute myocardial ischemia is also associated with excessive repolarization reserve as a result of activation of the ATP-sensitive K current (I_KATP) and decreased I_Na and I_Ca,L, which, together with accompanying Ca cycling instabilities, to promote arrhythmias.

Arrhythmia mechanisms

Excessive repolarization reserve causes all-or-none repolarization which can promote phase 2 reentry [98], resulting in reentrant VT and/or multiple wavelet or mother rotor VF. Phase-3 EADs arising from a short APD can also occur in the settings of SQT syndromes and acute ischemia.

Dynamical mechanisms

At the cellular level, the main dynamic factor regulating arrhythmias in this category manifests itself in the APD restitution curve (Fig. 2C) [99], which exhibits a very steep region corresponding to the all-or-none early repolarization of the AP. All-or-none repolarization is a feature arising primarily in epicardial ventricular myocytes with a prominent early notch in the AP before the plateau fully develops, called a spike-and-dome morphology, as seen in the traces in Fig. 2C. The early repolarization phase (phase 1) is caused by I_to, which is largest in the right ventricle epicardium. In Fig. 2C, APD is relatively normal at short DI because I_to is small, having not yet recovered from inactivation. As the DI becomes longer, I_to has more time to recover and progressively increases. If I_to has a large enough density and increases sufficiently, inward Na and Ca currents are no longer able to sustain the AP plateau, and the AP suddenly repolarizes, causing all-or-none repolarization. Note that just before reaching the DI at which APD suddenly shortens, APD prolongs due to an accentuation of the AP dome. The upstroke of the accentuated AP dome in the setting of excessive repolarization reserve plays the same role as the upstroke of an EAD in the setting of reduced repolarization reserve. If the upstroke is rapid enough, the AP dome can propagate into adjacent regions of tissue with shorter APD that have already repolarized and recovered excitability. When I_to density is heterogeneous in different regions of the epicardium, a stimulated beat which propagates into a region with high I_to density can develop early repolarization and very short APD, whereas an adjacent regions with slightly less I_to density can develop an AP with a large dome that then propagates unidirectionally into the very short APD region, generating a closely-coupled PVC. The PVC can then propagate through the short APD region until the region with the AP dome repolarizes, and then reenter this region to induce phase 2 reentry (Fig. 2C). Alternatively, the PVC may encounter an adjacent region with longer APD, causing wavebreak and initiation of reentry (Fig 2C).

Heterogeneous I_to distribution, however, may not be required for phase 2 reentry. In the simulation shown in Fig. 2C, the tissue is completely homogeneous. This highlights the second consequence of the steeply-sloped region of APD restitution curve associated with all-or-none repolarization. As noted earlier, the APD restitution curve reflects an input-output relationship, in which the preceding DI determines the APD for the next beat, but the APD of the next beat determines the next DI, and so forth. When a pacing rate is such that the DI falls in the steeply-sloped region, very small changes in DI cause large changes in APD (i.e. AP’s with and without domes), which then feed back to cause large changes in DI. Thus, at a constant heart rate, some AP’s will have prominent AP domes while others will exhibit very short AP’s without domes. Depending on the range of DIs visited, this can produce APD alternans or higher order periodicities, similar to EAD-mediated APD behavior associated with the EAD restitution curve in Fig. 2B. The AP domes can also appear irregularly in a chaotic pattern at some heart rates. The dynamic mechanisms underlying the chaotic pattern of AP domes are still under investigation. However, because chaos is present, the same scenario of regional chaos synchronization described for EADs in the setting of reduced repolarization (section 3.2) also applies to AP domes in the setting of excessive repolarization. In regions in which a critical percentage of myocytes are poised to have an AP with a dome, all of the myocytes in that region will be forced by electrotonic coupling to exhibit an AP with a dome. However, in regions below that critical percentage, all of the myocytes will be forced to have a short AP without a dome. The chaotic behavior of the AP dome is critical, because some regions will fall below the percentage of myocytes required for an AP dome, while other regions fall above this threshold. The result is the formation of islands of myocytes all exhibiting AP domes, separated by regions with very short APD due to all-or-none repolarization (Fig. 2C). Similar to EAD islands, the size of the AP dome regions depends on the violence of the chaos (tending to create voltage differences) versus the strength of electronic coupling (tending to smooth voltage differences). On each beat, the pattern changes (Fig. 2C). The result is marked dynamically-generated dispersion of refractoriness.

When the AP dome within an island becomes large enough, the dome may propagate into adjacent repolarized tissue, decrementally at first, and then regeneratively for larger domes. When the AP dome propagates decrementally, the local electrogram will exhibit late potentials following the initial voltage deflection. In patients with BS, these late potentials have been interpreted by some investigators to represent slow conduction due to localized fibrosis in the right ventricular epicardium. This interpretation has led to an alternative “depolarization” hypothesis that slow conduction is the most important factor promoting initiation of reentry [100], rather than the “repolarization hypothesis” of phase 2 reentry [97]. Ablating these sites has been shown to prevent arrhythmias in some of these patients. Imaging techniques do not currently have sufficient resolution to detect regions of fibrosis, which may be microscopic rather than macroscopic, in these patients. Therefore, validation of this alternative hypothesis will require improvements in imaging techniques or histological analysis at autopsy. One possibility that might explain both observations is that areas which chronically repolarize early would also begin to relax shortly after excitation and then be stretched by the surrounding tissue with normal APD that is still contracting. The systolic stretching might activate signaling pathways involved in electrical and structural remodeling, promoting fibrosis and slow conduction in these areas, as has been documented for electrical remodeling at late-activated sites in pacing studies [101]. In this case, phase 2 reentry and slow conduction might interact synergistically to promote arrhythmias, explaining why ablation of these regions can be therapeutically effective in some patients with BS. At the present time, however, this scenario is purely speculative.

When the AP dome becomes large enough to propagate regeneratively, the consequence is a PVC with a short coupling interval that may initiate phase 2 reentry by the following scenario [97]. As the AP propagates unidirectionally into the adjacent repolarized tissue, it can reenter the AP dome region after it has repolarized to induce reentry (illustrated in beat #1, Fig. 2C). Alternatively, the triggered AP can propagate unidirectionally until it encounters an adjacent AP dome island which has not yet repolarized. If the APD gradient is steep enough, wavebreak can result, initiating reentry (illustrated in beat #2 in Fig. 2C). Because real cardiac tissue is heterogeneous, further experimental studies are required to determine whether the AP dome islands are primarily due to pre-existing heterogeneous I_to distribution in ventricular epicardium (in which case the islands should be stationary from one beat to the next) or due to chaos synchronization of AP domes (in which case the island should change location from beat to beat). This is currently an area of active investigation.

When wavebreak due to phase 2 reentry occurs and initiates a rotor, the wavefront propagates via I_Na and therefore is very rapid (in the 10 Hz range). The arrhythmia is likely to manifest as a closely-coupled PVC initiating brief polymorphic VT which then either spontaneously terminates (if the core of the rotor drifts to a tissue boundary and extinguishes), or degenerates into multiple wavelet or mother rotor VF depending on the tissue dynamics. This corresponds to the classic pattern of idiopathic VF initiated by a closely-coupled PVC observed clinically in BS and SQT syndromes as well as acute ischemia.

Thus, the same process of regional chaos synchronization that underlies EAD-mediated arrhythmias is likely to be important in the setting of excess repolarization. The main difference is that with reduced repolarization, the chaotic behavior of EADs creates islands with long APD (due to EADs) next to regions with normal APD (Fig. 2B), whereas with excess repolarization, the chaotic behavior of all-or-none repolarization creates islands with normal APD (due to AP domes) next to regions with short APD (Fig. 2C). Both scenarios result in marked dispersion of refractoriness.

Finally, excess repolarization can also result in late phase 3 EADs by a mechanism that does not necessarily involve I_to-induced all-or-none repolarization. Late phase 3 EADs have been observed when the duration of the Ca transient markedly outlasts the duration of the AP. The Ca transient duration is mostly determined by the rate of reuptake of cytoplasmic Ca back into the SR by the SERCA pump. If the AP is short enough to fully repolarize while cytoplasmic Ca remains elevated, inward I_NCX can delay full repolarization, allowing I_Na and/or I_Ca,L to recover from inactivation sufficiently to trigger another AP. This phenomenon was first observed in atrial pulmonary vein myocytes [102], but has been observed in ventricular tissue as well [103]. Whether these EADs exhibit chaotic behavior has not been determined, and therefore the role of chaos synchronization in promoting arrhythmias by this mechanism is uncertain and will require further experimental and modeling studies.

Dynamic factors/targets

Similar to EADs, the main dynamic factor regulating all-or-none repolarization at the cellular level is embodied in the steeply-sloped region of the APD restitution curve (Fig. 2C). This region corresponds to the DI at which I_to becomes large enough to overcome inward currents and induce all-or-none repolarization (Fig. 2C), causing the AP dome to appear irregularly [104, 105]. Unlike the reduced repolarization reserve case in which chaotic behavior can be directly predicted from a cobweb diagram of the APD restitution curve [15], however, the mechanism of chaotic all-or-none repolarization behavior is more complex and not yet fully understood. Several mechanisms appear to be at play, depending on the properties of the I_to current, which varies in different regions of the heart and in different species. The dynamic target, however, is the same – suppressing the steeply-sloped region in the APD restitution curve. In principle, this is predicted not only to prevent all-or-none repolarization at the cellular scale, but also to prevent chaos synchronization from forming islands with AP domes generating phase 2 reentry at the tissue scale.

Molecular factors/biological targets

All-or-none repolarization depends on lowering the voltage following the AP upstroke to a range which delays the activation of I_Ca,L sufficiently to prevent the formation of a normal AP plateau. Below this voltage threshold, inward current is insufficient to prevent full repolarization. Above this threshold, I_Ca,L grows slowly but regeneratively, forming the AP dome. This feature is observed in the APD restitution curve in Fig. 2C. At short DI, I_to has not had sufficient time to recover from inactivation, and the APD is normal. As the DI increases, however, I_to amplitude grows progressively due to its more complete recovery from inactivation. A key feature is that just before I_to grows large enough to induce sudden all-or-none repolarization, its effect at the lowering of voltage during the early plateau delays the activation of I_Ks, which causes the APD to prolong immediately prior to the onset of all-or-none repolarization [106, 107]. This accentuated APD prolongation is associated with a prolonged upstroke (+dV/dt phase) of the AP dome that propagates similar to an EAD and plays a critical role in inducing phase 2 reentry at the tissue level [108].

From these considerations, the molecular factor that offers the most direct biological target to prevent phase 2 reentry is I_to. Complete block of I_to should eliminate phase 2 reentry. A caveat, however, should be noted. If only partial block of I_to is achieved, this may be sufficient to prevent phase 2 reentry, but might increase the risk of EAD-mediated arrhythmias (see above). Also, phase 3 EADs that are independent of I_to would not be impacted by I_to blockade. Restoring I_to has been suggested as a therapeutic target in heart failure, in which I_to is down-regulated. However, the reduced repolarization in heart failure also involves down-regulation of I_K1 and I_Ks, upregulation of I_NCX and increased late I_Na [54]. Selective upregulation of I_to in this setting would only partially correct the defect in reduced repolarization, and could make the heart susceptible to phase 2 reentry, especially if acute ischemia is superimposed upon heart failure, as in ischemic cardiomyopathy.

Enhancing I_Na or I_Ca,L to suppress all-or-none repolarization would also require precise titration in order to avoid converting excess repolarization to reduced repolarization with increased risk of EAD-mediated arrhythmias. There is also the risk that in heterogeneous cardiac tissue, enhancing I_Na or I_Ca,L to improve slow conduction in some regions might convert previously non-conducting regions into slow conducting regions and unmask new circuits capable of sustaining reentry.

Other K currents also require further study to evaluate their potential as biological targets. The apamin-senstive small Ca-activated K current (I_SK) has been shown to be upregulated in heart failure, which may partially compensate for the alterations in various other currents that reduce overall repolarization reserve. However, both pro- and anti-arrhythmic effects of I_SK blockade have been reported in failing hearts [109].

Fixed factors can also be biological targets for arrhythmias in this category. For example, the heterogeneous distribution of I_to in the right ventricle promotes phase 2 reentry in BS [97], as does fibrosis by promoting slow conduction and conduction block [100].

4. Linking Molecular Factors to Dynamic and Fixed Factors

In Table 1, each primary arrhythmia dynamics category (Ca cycling instability, reduced repolarization reserve and excessive repolarization reserve) is exemplified by a class of genetic channelopathies (CPVT, LQT syndromes, and BS/ERS/SQT syndromes, respectively). Depending on the specific mutation involved, some congenital channelopathies may span more than one primary arrhythmia dynamics category. The common clinical diseases causing the majority of ventricular arrhythmias, such as heart failure and ischemia, also represent mixtures of the primary categories. To develop a successful antiarrhythmic strategy, biological targets that suppress arrhythmia dynamics in one category must not exacerbate arrhythmia dynamics in the other categories, or impair normal cardiac function. This is particularly important when the clinical condition predisposing to ventricular arrhythmias spans more than one primary category.

Another way to visualize the interaction between the three dynamics-based arrhythmia categories is illustrated by the graph in Fig. 4A, in which Ca cycling instability is plotted along the vertical axis and repolarization on the horizontal axis. This graph introduces the concept of parameter space, which is used in dynamics to segregate different behaviors into distinct regions of parameter combinations, where each relevant parameter is represented by a separate axis. Any combination of molecular factors which collectively produce a particular level (parameter value) of repolarization and a particular level (parameter value) of Ca cycling instability can be represented by a point (x,y) on this two-dimensional graph. Normal cardiac function falls in the central region in which both repolarization reserve and Ca cycling are in the physiologically normal ranges. Classic CPVT occupies the region in which Ca cycling is unstable, but repolarization is normal. Classic LQT syndromes fall in the region with stable Ca cycling but reduced repolarization. Classic BS/ERS/SQT syndromes fall in the region with stable Ca cycling but excess repolarization. Heart failure and acute ischemia exhibit features of both unstable Ca cycling and abnormal repolarization, and so occupy their own distinct regions in this parameter space (upper left and upper right, respectively). The hypothetical boundaries between these different parameter regions are indicated by dashed lines as a simplification, because the boundaries are more likely to be nonuniform gradients rather than distinct straight lines.

Fig. 4. Parameter space representation of arrhythmia dynamics.

A. Two-dimensional representation. The vertical axis represents the aggregate state of Ca cycling varying from stable to unstable, and the horizontal axis the aggregate state of repolarization from reduced to excessive. The white region represents the normal heart, and various combinations of Ca cycling instability and reduced or excess repolarization define the colored regions corresponding to CPVT, LQTS, BS/ERS/SQTS, HF and ischemia (Isc). The black line indicates the hypothetical daily trajectory in parameter space of a patient with heart failure which episodically leaves the normal region and enters high risk arrhythmia regions. The red trajectory shows the same patient after treatment with a beta blocker to confine the trajectory to the white region (i.e. lower arrhythmia risk) by blunting excessive sympathetic activation. The green trajectory shows the heart failure patient treated with a Class III antiarrhythmic drug (K channel blocker) that further reduces repolarization reserve, increasing arrhythmia risk. B. Three-dimensional representation of arrhythmia parameter space incorporated fixed factors which increase electrical dispersion. A third axis has been added, corresponding to the aggregate state of fixed factors (pre-existing heterogeneities related to electrical and structural remodeling, etc) which increase electrical dispersion and lower the threshold for unstable Ca cycling and abnormal repolarization required to cause ventricular arrhythmias. This has the effect of shrinking the low risk white region and expanding the high arrhythmia risk colored regions, such that the same daily trajectory (black line) now enters the high risk regions.

Graphically, the arrhythmia risk profile of a patient can be represented as a trajectory in this parameter space. Over a 24 hour period, levels of repolarization and Ca cycling instability vary continuously in response to the daily activities of living such as exercise, emotional stress, eating and sleeping, and changing environmental conditions such as temperature, electrolyte balance, drugs, etc. At a given point in time, each parameter combination can be represented by a point on the graph, defining a trajectory that wanders through this parameter space during the course of the day. The trajectory varies from day to day depending on the environmental factors encountered, but generally remains within a bounded region in this parameter space. Thus, in a healthy person, the trajectory stays within the normal region, whereas in a person with heart disease, the trajectory can wander into other regions in which the probability of a potentially lethal ventricular arrhythmia increases.

For example, in a heart failure patient in which electrical remodeling and post-translational signaling have reduced repolarization and destabilized Ca cycling, the trajectory may wander from the normal region to visit the upper right region in response to changing environmental conditions such as stress or exercise or hypokalemia, placing them at increased risk for a lethal ventricular arrhythmia (black trace). Treatment with a beta blocker confines the trajectory to a more restricted region by eliminating parameter combinations associated high levels of sympathetic activation, thereby reducing the time spent in dangerous parameter space regions, as illustrated in Fig. 4A (red trace). In contrast, treatment of the same patient with a Class III antiarrhythmic drug such as the I_Kr-blocker D-sotalol would further reduce repolarization, shift the trajectory to the left and increasing the time spent in dangerous regions (green trace). As another example, the trajectory of a patient with ischemia heart disease might visit the upper right region during an anginal episode, which could also be potentially avoided by effective antianginal therapy with a beta blocker.

The therapeutic goal of antiarrhythmic therapy, then, is to prevent a patient’s trajectory from crossing into these high risk regions of parameter space. Beta blockers accomplish this by reducing the dynamic responsiveness to sympathetic activation, whereas other drugs may accomplish this by altering different molecular factors that restore normal repolarization and/or Ca cycling stability. Pro-arrhythmic effects occur when an intervention that restricts entry into one dangerous region inadvertently facilitates entry into another dangerous region.

To incorporate fixed factors that increase electrical dispersion, such as pre-existing structural and electrophysiological heterogeneity, into the conceptual framework, we can add a third axis to reflect the aggregate level of structural and electrical heterogeneity throughout the tissue (Fig. 4B). In our view, fixed factors increasing electrical dispersion do not directly cause arrhythmias. Rather, they sensitize the heart to arrhythmias by reducing the level of dynamic instability required to initiate arrhythmias. For example, tissue fibrosis (structural remodeling) markedly alters the source-sink relationship to facilitate the emergence of triggers such as EADs and DADs, as well as promote slow conduction by reducing gap junction coupling (for review see [26]). However, the process that generates the trigger that initiates reentry in the region of slow conduction is a dynamic process. Thus, the general effect of fixed factors is to expand the arrhythmogenic regions in parameter space so that they encroach upon and shrink the normal region, as illustrated in Fig. 4B. In other words, fixed factors increasing electrical dispersion make the tissue more vulnerable to the emergence of triggers and initiation of reentry by dynamic factors. Thus, the daily trajectory through this parameter space in a patient with a structurally and electrically normally heart may never wander outside of the normal region, whereas the same daily trajectory in a patient with a structurally and electrically abnormal heart take them into high risk arrhythmogenic regions, as illustrated by the black traces in Fig. 4B.

Within this conceptual framework, there are three general strategies to reduce arrhythmia risk. The first is to expand the normal region so that the patient’s trajectory does not wander outside of the normal region during the course of the day. For example, in the case of a damaged heart in which fixed factors increasing electrical dispersion have lowered the threshold of dynamic instability required to induce arrhythmias, reversing pre-existing structural and electrical heterogeneities (i.e. moving back to the normal region along the third axis in Fig. 4B) will restore the low-risk region to its previously larger normal range. The same daily trajectory may then no longer enter the high risk arrhythmia regions. Interventions which reverse fibrosis would fall into this class. For example, the anti-fibrotic effects of ACE inhibitors might contribute to their protective effects against sudden cardiac death in heart failure by this mechanism.

The second general strategy is to restrict the patient’s daily trajectory in parameter space, so that the trajectory remains within the boundaries of the low risk region. For example, beta blockers and antianginal agents fall into this class, as illustrated by the red trajectory in Fig. 4A. The third strategy is to reposition the patient’s trajectory so that it is more centrally located in the low risk region. In this case, the same level of excursion of the trajectory may no longer cross into the high risk regions. For example, in a patient with LQT3 syndrome caused by defective I_Na inactivation, a late I_Na blocker would move their trajectory into the low risk region by increasing repolarization from the reduced into the normal range.

5. Developing an in silico drug-testing strategy

How does the dynamic state in parameter space illustrated in Fig. 4 relate to the actual molecular state of a patient? The molecular state of a patient can also be displayed on a graph, in which each molecular factor, such as the state of each ion channel and transporter, ion concentration, drug concentration, metabolic state, etc., is represented along a separate axis (Fig. 5). These molecular parameters also change continuously over the course of each day, tracing a trajectory through this very high dimensional parameter space with thousands of dimensions instead of just two. The challenge, then, is to create a map that links the high-dimensional parameter space to the low-dimensional parameter space – that is, to define which combinations of molecular parameter values correspond to which aggregate dynamic parameter combinations of repolarization state and Ca cycling instability. If this can be achieved, then in principle one can predict systematically how a molecular intervention will impact all of the relevant dynamic factors, in all three categories of arrhythmia dynamics. A molecular factor could be profiled to define its potential antiarrhythmic and proarrhythmic actions, as well as its effects on normal excitation-contraction coupling.

Fig. 5. Linking dynamic factors to molecular factors.

The aggregate dynamic parameters in the low dimensional parameter space defining arrhythmia risk (left) are ultimately determined by the interactions between molecular factors in a much higher dimensional parameter space (right) in which each molecular factor (e.g. properties of an ion channel) is represented by its own axis. The ultimate goal is to create a map that links the high dimensional space to the low dimensional space, allowing molecular factors to be evaluated as biological targets to lower arrhythmia risk.

Is this a wild fantasy, or a realistic possibility? Already, the U.S. Federal Drug Administration is exploring the modeling-based approaches for preclinical assessment of drug cardiotoxicity [110]. As computational power has increased and computational approaches to explore high dimensional parameter spaces have become more sophisticated [13, 14], in silico drug testing to link drug effects at the molecular level to arrhythmogenic cellular and tissue properties has become increasingly feasible [111, 112]. In addition, dimension reduction techniques have been developed to condense high dimensional information systems into more tractable low dimensional representations for a range of ‘big data’ applications [113]. One approach might be to create a panel of detailed multi-scale models that integrate behaviors at the subcellular, cellular and tissue levels to represent the different behaviors in each arrhythmia dynamics category. For example, a thousand or more detailed models with different molecular parameter settings could be generated to represent each of the six normal and arrhythmogenic parameter regions in Fig. 4A spanning a range of organism-scale physiological conditions (autonomic tone, electrolyte values, etc). To screen a molecular factor as a potential biological target in silico, the molecular intervention could be implemented in each of these models, and the effects on the dynamic factors regulating arrhythmias in each category assessed.

This approach has several conceptual advantages. First, it automatically provides a balanced evaluation of both anti- and pro-arrhythmic effects of a molecular intervention across the full spectrum of arrhythmia dynamics categories as well as normal cardiac function. Second, the effects of a molecular intervention are assessed on populations of models [13, 14], emulating the genetic and environmental diversity encountered in human populations, rather than on a single model in each arrhythmia dynamics category. Third, in addition to human cardiac electrophysiology, complementary populations of models can be generated for nonhuman species to facilitate direct comparison and validation of in silico predictions with experimental findings in nonhuman arrhythmia models.

How would this work in practice? The in silico approach could be used in two complementary ways. First, to facilitate drug design, the approach can be used to predict theoretically the ideal modifications to a molecular factor, such as the properties of an ion channel that will suppress arrhythmias. For example, there are many possible biophysical manipulations to reduce the I_Ca,L window current towards the goal of suppressing EAD-mediated arrhythmias. These include shifting the voltage dependence of activation or inactivation, altering kinetic parameters, and reducing the non-inactivating pedestal component. Implementing these altered parameters in the population of models can be used to identify ideal parameter combinations that are most effective at suppressing EAD-mediated arrhythmias without disturbing normal EC coupling, exacerbating Ca cycling instability to a level that promotes DADs and/or alternans, or altering repolarization reserve in a manner promoting all-or-none repolarization and phase 2 reentry. In a complementary fashion, the approach could be used to facilitate drug screening. Imagine that a small molecule drug screen identifies a compound with novel effects on the biophysical properties of an ion channel. For example, the compound might selectively block the late I_Ca,L without affecting the peak amplitude (analogous to ranolazine for late I_Na). The detailed biophysical properties could be implemented in the population of models to predict whether the altered I_Ca,L properties would be effective at suppressing EAD-mediated arrhythmias without creating the other adverse effects. Thus, as it is refined, the in silico approach could serve as a drug-development and screening platform both to predict ideal antiarrhythmic drug properties, and to evaluate drugs whose biophysical properties have already been experimentally characterized, prior to moving forward to costly animal models for further testing.

6. Application to Supraventricular Arrhythmias

Many supraventricular arrhythmias can now be effectively and permanently cured by catheter ablation techniques, including atrioventricular reentrant tachycardia, atrioventricular nodal reentrant tachycardia, atrial tachycardia and atrial flutter. The most challenging, however, remains atrial fibrillation (AF). AF mechanisms are still controversial, in part because of the greater structural and electrophysiological complexity of the atria and its associated structures including the sinus and atrioventricular nodes, venae cavae, pulmonary veins and valvular annuli. AF is also the most common sustained arrhythmia, affecting 5–10% of the population over the age of 70 [114] and accounting for a quarter of cerebrovascular accidents (strokes) in the elderly. Under the most favorable conditions (paroxysmal atrial fibrillation in structurally normal hearts), the current success rate of ablation is around 70%, and under 50% for long-standing persistent AF in patients with enlarged atria or heart failure [115]. Repeat ablations are often necessary, and each procedure carries a 5% risk of significant complications [116]. Thus, as with ventricular arrhythmias, development of effective pharmacologic/biologic therapy for AF is highly desirable.

Although the dynamics-based classification in Table 1 focuses on ventricular arrhythmias, the same approach can be adapted to supraventricular arrhythmias and AF, once the key dynamic mechanisms have been appropriately defined. There is no reason to believe that the dynamic mechanisms outlined in Table 1 are not also applicable to the atria. DADs, DAD-mediated trigger activity [117] and spatially discordant alternans [118] have been described in atrial tissue, as have EADs and EADmediated triggered activity [102]. In addition, evidence of both multiple wavelet and mother rotor fibrillation have been presented in atria (for review see [119]). Excessive repolarization reserve caused by gain-of-function K channel mutations has also been associated with familial AF [96]. Direct experimental evidence for chaos synchronization, biexcitability and phase-2 reentry in atrial tissue, however, has yet to be obtained. Is AF driven by fundamentally different mechanisms than VF? Unlike VF, which is lethal if not immediately defibrillated, atrial fibrillation is usually tolerated hemodynamically, so that its dynamical mechanisms may evolve over time as electrical and structural remodeling develop. For example, paroxysmal AF in normal sized atria may initially be related to triggers emanating from the pulmonary veins and/or other venous structures, caused by localized focal activity or microreentry which initiates nonsustained multiple wavelet or mother rotor fibrillation. This would account for the reasonably high success rate of ablation at this stage. However, as AF becomes persistent and long-lasting, the underlying electrical and structural remodeling may alter the tissue substrate sufficiently to allow multiple wavelet or mother rotor fibrillation to continue indefinitely [120], so that isolation of triggers is no longer effective. Enlarged atria due to valvular disease or diastolic ventricular dysfunction may also fall into the latter category due to electrical and structural remodeling induced by chronic hemodynamic stress.

7. Summary and Challenges

Our goal has been to illustrate how molecular factors interact with dynamic and fixed factors at the subcellular, cellular and tissue and organism scales to cause ventricular arrhythmias. Achieving a thorough understanding of these interactions is critical for developing novel effective pharmacologic/biologic therapies for cardiac arrhythmias. Pharmacologic/biologic targets are molecular factors, but arrhythmias are determined by dynamic factors at the subcellular, cellular, tissue and organism scales interacting with fixed factors increasing electrical dispersion at the tissue scale. The highest risk of arrhythmias arises when dynamic factors, interacting with fixed factors, simultaneously promote the emergence of triggers while enhancing electrical dispersion within the tissue. The proposed dynamics-based classification outlined in Table 1 represents an attempt to synthesize what is currently known about these relationships. Accordingly, we have classified ventricular arrhythmias into three major dynamic categories relating to unstable Ca cycling, reduced repolarization and excess repolarization. Each of these primary categories is represented by a group of inherited channelopathies (CPVT, LQT syndrome and BS/ERS/SQT syndrome, respectively). In addition, the more common causes of ventricular arrhythmias, heart failure and ischemia, represent mixtures of the primary categories. We have summarized the current state-of-knowledge about the dynamic factors operating at the subcellular, cellular, tissue and organism scales relevant to each arrhythmia dynamics category, and provided illustrative examples of how these dynamic factors can be related to molecular factors.

To illustrate conceptually how these arrhythmia dynamics might apply to a patient at increased risk of ventricular arrhythmias, we presented the parameter space concept (Fig. 4). We envision the patient as wandering through this parameter space during the course of their daily activities, defining a trajectory. The trajectory of a healthy person with a normal heart does not wander outside of the normal region, whereas the trajectory of a patient with congenital or acquired heart disease crosses into the abnormal regions, placing them at increased risk of a ventricular arrhythmia. In this representation, the goal of pharmacologic/biologic antiarrhythmic therapy is to prevent a patient’s trajectory from wandering outside of the normal region (Fig. 4A). In principle, this can be accomplished by one of three strategies: 1) expanding the normal region by reversing fixed factors that make the heart more sensitive to dynamic instability (e.g. reversing fibrosis in heart failure); 2) reducing the extent to which the trajectory wanders (e.g. beta blocker therapy in ischemia); or 3) re-centering the trajectory in the normal region (e.g. late I_Na blocker drugs to correct the defect in LQT3 syndrome). The great challenge will be to create an accurate map that links the low dimensional parameter space of dynamic factors to the high dimensional parameter space of molecular factors, using computational methods and dimensional reduction analytics (Fig. 5). If successful, this endeavor has the potential to provide a systematic approach to evaluate and predict in silico how molecular factors, such as altered biophysical properties of an ion channel, affect not only the targeted arrhythmia category, but all of the other relevant arrhythmia categories as well as normal cardiac EC coupling. Efficacy and safety will be addressed simultaneously. May the journey begin!

Highlights.

• We group ventricular arrhythmias into three categories based on their underlying dynamics

• The Ca cycling instability group includes CPVT, heart failure and ischemia

• The reduced repolarization group includes long QT syndromes and heart failure

• The excessive repolarization reserve group includes J wave syndromes and ischemia

• Strategies to link arrhythmogenic dynamic factors to molecular targets are proposed

Abbreviations

AP

action potential

APD

AP duration

BS

Brugada syndrome

CaMKII

Ca-calmodulin kinase II

CPVT

catecholaminergic polymorphic ventricular tachycardia

CV

conduction velocity

DAD

delayed afterdepolarization

EAD

early afterdepolarization

ERS

early repolarization syndrome

ICD

implantable cardioverter-defibrillator

I_{Ca, L}

L-type Ca current

I_Kr

rapid component of the delayed rectifier K current

I_Ks

slow component of the delayed rectifier K current

I_Na

Na current

I_to

transient outward K current

LQT

long QT

NCX

Na-Ca exchanger

PVC

premature ventricular complex

RyR

ryanodine receptor

SERCA

sarco-endoplasmic reticulum Ca ATPase

SQT

short QT

SR

sarcoplasmic reticulum

VF

ventricular fibrillation

VT

ventricular tachycardia