Spatial population expansion promotes the evolution of cooperation in an experimental Prisoner’s Dilemma

Summary

Cooperation is ubiquitous in nature, but explaining its existence remains a central interdisciplinary challenge [1–3]. Cooperation is most difficult to explain in the Prisoner’s Dilemma (PD) game, where cooperators always lose in direct competition with defectors despite increasing mean fitness [1, 4, 5]. Here we demonstrate how spatial population expansion, a widespread natural phenomenon [6–11], promotes the evolution of cooperation. We engineer an experimental PD game in the budding yeast Saccharomyces cerevisiae to show that, despite losing to defectors in non-expanding conditions, cooperators increase in frequency in spatially expanding populations. Fluorescently labeled colonies show genetic demixing [8] of cooperators and defectors followed by increase in cooperator frequency as cooperator sectors overtake neighboring defector sectors. Together with lattice-based spatial simulations, our results suggest that spatial population expansion drives the evolution of cooperation by 1) increasing positive genetic assortment at population frontiers and 2) selecting for phenotypes maximizing local deme productivity. Spatial expansion thus creates a selective force whereby cooperator-enriched demes overtake neighboring defector-enriched demes in a “survival of the fastest”. We conclude that colony growth alone can promote cooperation and prevent defection in microbes. Our results extend to other species with spatially restricted dispersal undergoing range expansion, including pathogens, invasive species and humans.

Cooperation forms the basis for numerous complex phenotypes, from cell-cell communication and biofilm formation in microbes to nest construction in multicellular species [12, 13]. Explaining how cooperation evolves despite the direct fitness advantage gained by free-riding remains a central challenge in biology and the social sciences [1–3]. This is particularly true in the Prisoner’s Dilemma game [1, 4, 5] where cooperators always lose in direct competition with defectors, leading to a “Tragedy of the Commons” [14]. Nearly half a century of research on social evolution has offered insight into this dilemma, with inclusive fitness theory focusing attention on the importance of high genetic relatedness [15], multilevel selection theory highlighting the role played by competition among social groups [16, 17], and spatial games showing the importance of population structure [18–21]. Here we bring these three frameworks together, demonstrating that spatial population expansion creates a setting where both relatedness and intergroup competition are amplified, promoting the evolution of cooperation.

Spatial population expansion occurs when a species spreads outward to fill vacant eco-space or to supplant resident species, resulting in increased geographic range. Human migration out of Africa [7] is one salient example, while more generic examples include ecological invasions, epidemics, growth of microbial colonies, and expansion due to habitat modification caused by environmental disturbance or climate change [8–11]. Spatially expanding populations form a propagating density wave called a “Fisher wave” with a constant speed proportional to the square root of the mean growth rate (i.e., Malthusian fitness) of subpopulations at the front [22]. Genetically heterogeneous populations may also form an “allele frequency” wave representing the spatial spread of alleles [22] (see Supplemental Information).

A small number of colonists initiate new subpopulations at the leading edge of the propagating Fisher wave, creating a repeated series of genetic bottlenecks or “founder effects” that cause stochastic loss of genetic diversity at frontiers [23, 24]. Because cooperation is favored under conditions of high genetic relatedness [15], range expansions could thus in principle favor the evolution of cooperation. However, there are at least three complicating factors. First, within-subpopulation selection favoring defection opposes genetic demixing, potentially preventing high cooperator relatedness from ever arising. Second, even with high relatedness it is not clear what selective force, if any, favors cooperation over defection in expanding populations. Finally, almost any genotype that stochastically fixes at the front can increase in frequency via “surfing” [6, 10, 24, 25]. Other genotypes that stochastically fall behind this front cannot typically catch up, even if they are more fit. This is because they expand outwards in a trailing allele frequency wave traveling at a speed determined by the difference in fitness between defector and cooperator genotypes, (W_D − W_C), which will often be much smaller than mean absolute fitness. For social traits, a genotype fixed at the frontier will outrun genotypes in the population interior and increase in global frequency provided that (1+b)/2 > c, where b is the social and c the direct fitness effect of the leading genotype (Supplemental Information). The social effect here refers to the fitness increment or decrement received by an individual from social partners (e.g. the benefit of the public good), while the direct effect is the fitness increment or decrement accrued to an individual for engaging in a social behavior (e.g. the cost of producing the public good). Note that this condition (1+b)/2 > c can be satisfied even when b < 0, and thus in principle surfing may promote cooperation’s opposites, selfishness and spite [26], including spite against relatives. Given these complications, it is not clear whether spatial expansion will in fact promote the evolution of cooperation.

To test the effect of spatial expansion on defector/cooperator dynamics, we engineered an experimental Prisoner’s Dilemma game using cooperative sucrose metabolism in haploid, vegetatively growing strains of the budding yeast, Saccharomyces cerevisiae [27]. Yeast secrete the exo-enzyme invertase in order to digest the disaccharide sucrose, which cannot easily be imported into the cell, forming monosacharides that are readily imported. In our strains, sucrose cannot be imported at all due to disruption of the genes mal12 and mal22 [28]. Because digestion occurs externally, invertase producers (“cooperators”) create a public good that is exploitable by non-producers (“defectors”), who gain a relative fitness advantage by not paying the fitness cost of production [27, 29]. We engineered a fluorescently marked defector strain by deleting the invertase gene SUC2.

We note that in minimal sucrose media (YNB + 2% sucrose), competitions between SUC2⁺ and suc2⁻ strains in shaken liquid culture were previously found to follow Snowdrift game dynamics [29]. In a Snowdrift game, the rare type (regardless of whether it is a cooperator or a cheater) has a fitness advantage, leading to stable maintenance of both cooperators and defectors [1, 30]. The maintenance of cooperation is therefore easily ensured, in contrast to the Prisoner’s Dilemma game where the maintenance of cooperation is much more difficult to explain [1, 30]. In addition, cooperators in a Snowdrift game have a colonization advantage over defectors since defectors cannot colonize habitat unoccupied by cooperators [28]. This conflates colonization ability and cooperation by linking both to a single genotype. Because spatial expansion is already known to select for colonization ability [31, 32], such linkage would prevent us from concluding that spatial expansion favors cooperation per se rather than superior colonization ability. By contrast, defectors in a Prisoner’s Dilemma game do not require the presence of cooperators to colonize new habitat, making it possible to disentangle selection for cooperation from colonization ability.

We therefore used two approaches to construct a Prisoner’s Dilemma from this system. First, we eliminated the rare advantage of cooperators that is necessary for Snowdrift dynamics by conducting competitions in media (YEP + 2% sucrose) in which our defector strains could grow in the absence of cooperators (most likely by consuming amino acids available in YEP, although growth is slower than for cooperators; Fig. 1A). This environment also eliminates the difference in colonization ability between cooperator and cheater strains, as cheaters no longer require the presence of cooperators to colonize the frontier (green line in Fig. 1A). Next, we engineered a defector strain that is resistant to cycloheximide, a translation-inhibiting drug that limits growth by binding to ribosomal subunit cyh2. This creates a system in which we can experimentally impose a tunable “cost of cooperation” by varying the level of cycloheximide in the growth media. Specifically, increasing the cycloheximide concentration slows the growth of cooperators but not the resistant defectors, leading to an increased “cost of cooperation.”

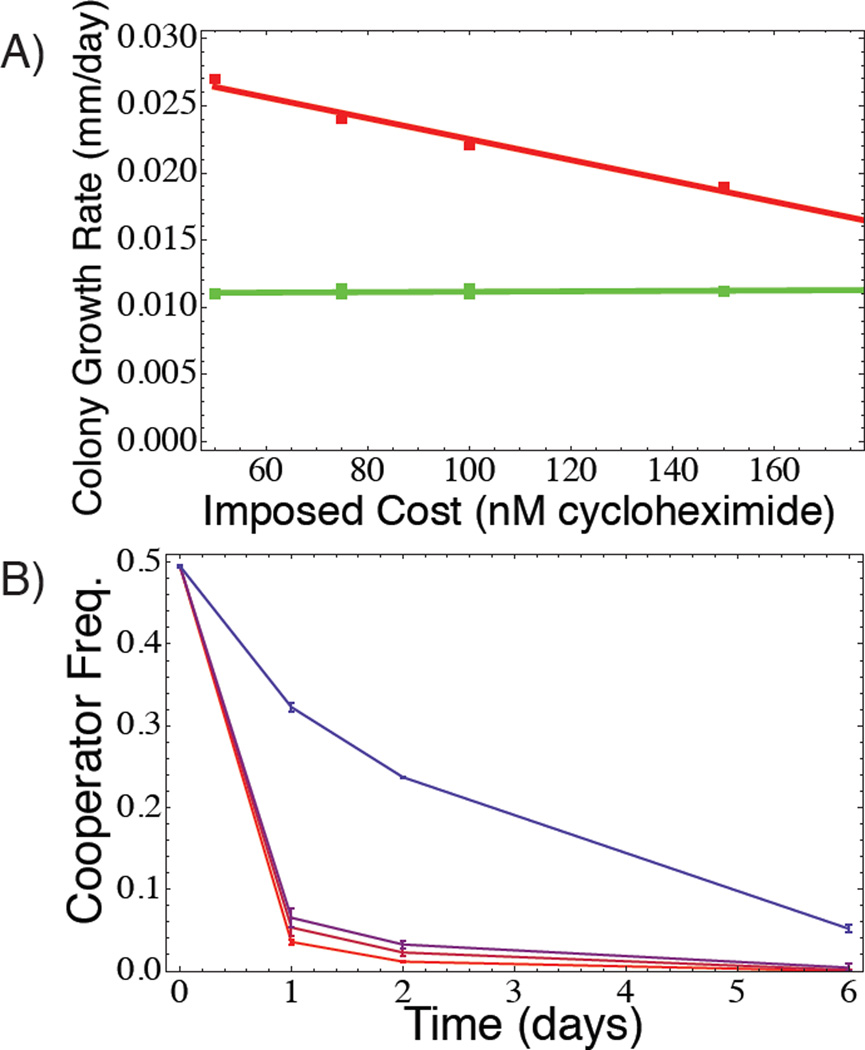
Figure 1. An experimental Prisoner’s Dilemma.

A) Populations composed of all cooperators (red) have a higher growth rate than pure defector populations (green), but B) cooperators lose to defectors within mixed populations. Growth rate in A) was assayed on agar plates by measuring colony radius over time, which is directly proportional to rate of cell division S. cerevisiae [8]. Lines in B) represent cooperator frequency trajectories, measured with FACS, in shaken liquid culture over the course of one week for four different levels of imposed cost (cycloheximide concentrations: 50, 75, 100, and 150nM, from top to bottom and blue to red).

When mixed with our defector strain in an unstructured environment (shaken liquid culture), our cooperator strain declines at all frequencies when a cost of cooperation is imposed, despite having a superior growth rate over defectors in pure culture (Figs. 1, S3). These results are consistent with Prisoner’s Dilemma evolutionary dynamics. Unlike in a Snowdrift game, any increase in frequency of cooperators in our experiments is not due to rare cooperator advantage.

To determine whether spatial expansion can promote cooperation in our experimental Prisoner’s Dilemma, we initiated spatial expansions by spotting a droplet of mixed cooperator/defector cultures onto solid media (YEP + 2% sucrose + 2% agar) for a range of imposed costs (see Experimental Procedures). Spatial diffusion of cells in S. cerevisiae is caused when cellular growth generates an outward force leading to radial spatial expansions of colonies [8]. Note that expansion is not caused by active cell motility in this system as yeast lack motility. Relative frequency measurements taken using flow cytometry show that cooperators initially declined in frequency at a rate consistent with that of well-mixed liquid competitions, but then increased in frequency as expansion proceeds (Fig. 2C). Likewise, image analysis of fluorescently labeled colonies shows low cooperator frequency near the initial site of inoculation (the “homeland”), but then increasing frequency with increasing distance from the homeland (Fig. 2E). Lattice-based spatial simulations of a Prisoner’s Dilemma show the same spatio-temporal dynamic of initial decline in cooperator frequency followed by increase as expansion proceeds (Fig. 2D). Cooperators invade when rare over a range of imposed costs (Fig. 3). Furthermore, when the benefit of cooperation is removed by competing strains on glucose media, the cooperator strain no longer increases in frequency upon spatial expansion (Fig. S4). These data clearly demonstrate that spatial expansion can promote the evolution of cooperation.

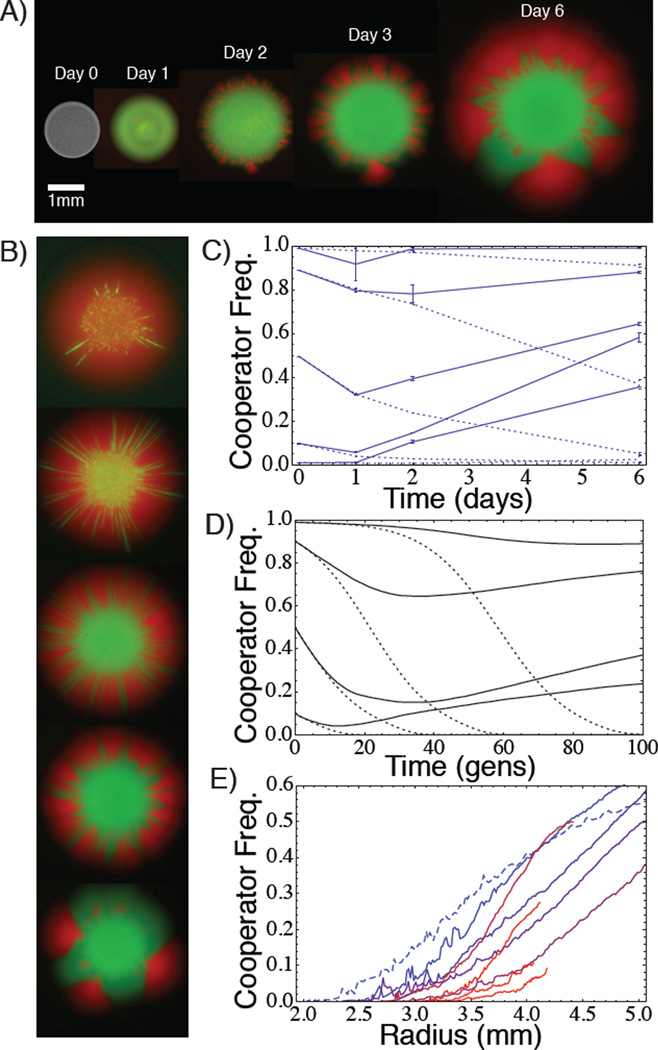
Figure 2. Spatial expansion promotes the evolution of cooperation in a Prisoner’s Dilemma.

A) Growth of fluorescently labeled colonies (cooperators in red, defectors green). B) Competitions inoculated with different initial cooperator frequencies (from top to bottom: 0.99, 0.90, 0.50, 0.10, and 0.01) after 7 days of growth (not to scale). Note visible expansion of cooperator (red) sectors at colony frontiers, and proliferation of defectors (green) in colony interior. C) Frequency trajectory of the cooperator strain in spatially expanding (solid lines) and stationary (non-expanding) (dotted lines) competitions as measured by flow cytometry (FACS) over the experiment. Dotted lines follow the same populations over the whole time-course, while spatial expansions required destructive sampling of colonies at each time point. Note that frequency is measured over whole colony, not just at frontier. D) Frequency dynamics from lattice-based spatial simulations of a PD game with non-overlapping generations in radially expanding (solid lines) and stationary (dotted lines) populations initiated from well-mixed (relatedness = 0) homelands of varying initial cooperator frequencies, with simulation parameters: W₀ = 1, K = 50, m = 0.2, b = 0.5, c = 0.1 (see Methods). E) Image analysis of experimental colonies after 7 days of growth. Cooperator frequency measured along the circumference of a circle of radius r centered at the colony center (importantly, this means that frequency is not cumulative). Each line denotes the average over 3 replicates for different imposed cost (cycloheximide concentrations 0nM [dashed blue line] to 200nM [solid red line] at 25nM increments) with initial cooperator frequency of 0.10. Imposed cost in A,B,C was 50nM cycloheximide.

Figure 3. Invasion of rare cooperators during colony expansion over a range of imposed costs.

Colonies imaged after 7 days of growth (not to scale). Competitions inoculated with cooperators at frequency 0.10 (top row) or 0.01 (bottom row), at different cycloheximide concentrations.

How does spatial expansion promote cooperation? Fluorescent colony images reveal the formation of discrete sectors of fixed genotypes (Figs. 2A,B, 3), which is the colony-level signature of genetic demixing [8]. Thus, spatial expansion can lead to high positive assortment of cooperators via genetic demixing, even though this assortment is opposed by selection favoring defectors within demes (Fig. 1B, Supplemental Information). Local fixation of cooperators at frontiers despite counterselection within demes is analogous to surfing by deleterious mutations [6, 10, 24, 25] and requires similar conditions to obtain. In other words, spatial expansion leads to the formation of uniform sectors of cooperators or defectors, increasing genetic relatedness of nearby individuals. This diminished local genetic diversity reduces the direct competition between cooperators and defectors (see also [33]), thereby mitigating the principle selective advantage of defection.

We note that genetic demixing (i.e. “sectoring”) is particularly clear in our experimental yeast system because yeast lack motility and “dispersal” of offspring is local. In other systems, movement of individuals and dispersal of offspring can in principle blur sector boundaries and oppose demixing at the frontier. In the extreme case where movement and dispersal are very long-range, the spatial sectoring we describe here will not occur, and our analysis or results will not generalize to this situation. However, in real populations movement and dispersal are usually spatially restricted: a migrant is more likely to disperse nearby than far away. In this case, genetic demixing will occur provided that outward range expansion is sufficiently rapid compared to the rate of dispersal between occupied demes across sector boundaries (i.e., perpendicular to the expansion direction) [24, 25, 34]. In nature, species as diverse as rabies virus [35] and humans [36] show genetic signatures of expansion-associated demixing and sectoring, suggesting that the phenomenon we describe here may apply more generally. To the extent that spatial expansion-associated genetic demixing is possible in a species, the mechanism we describe here promoting the evolution of cooperation will also be possible.

Once cooperator sectors establish, their overall productivity will be higher than that of defector sectors provided the fitness benefit of cooperation exceeds the cost of cooperation, b > c (Supplementary Information). When this is true, cooperator sectors will expand radially faster than neighboring defector sectors, leading to a corresponding expansion of the boundaries of the cooperator sectors at the expense of neighboring defector sectors as we see in our experiements (Figs 2BE, 3). This leads to an overall increase in cooperator frequency, and suggests that range expansion creates a force of natural selection favoring the “survival of the fastest.” This force acts to promote genotypes supporting maximal group productivity, since high productivity sectors expand at a faster rate, allowing them to overtake lower productivity sectors.

We turn to stochastic, lattice-based spatial simulations to further test the survival of the fastest hypothesis. To test whether survival of the fastest is indeed necessary for range expansion to promote cooperation, we eliminate this force by restricting expansion to one dimension in our spatial simulations. In one dimension, an expanding subpopulation has no neighboring subpopulations to compete with so that intergroup competition is absent. In this case, we find that the probability of cooperator establishment at the front is never greater than the neutral probability of establishment (which is equal to the initial frequency of the allele, p₀) and declines with increasing cost (Fig. 4). Put differently, cooperators can only outrun defectors in a one-dimensional Prisoner’s Dilemma if they randomly take over the frontier, an outcome uniformly opposed by selection (Supplemental Information).

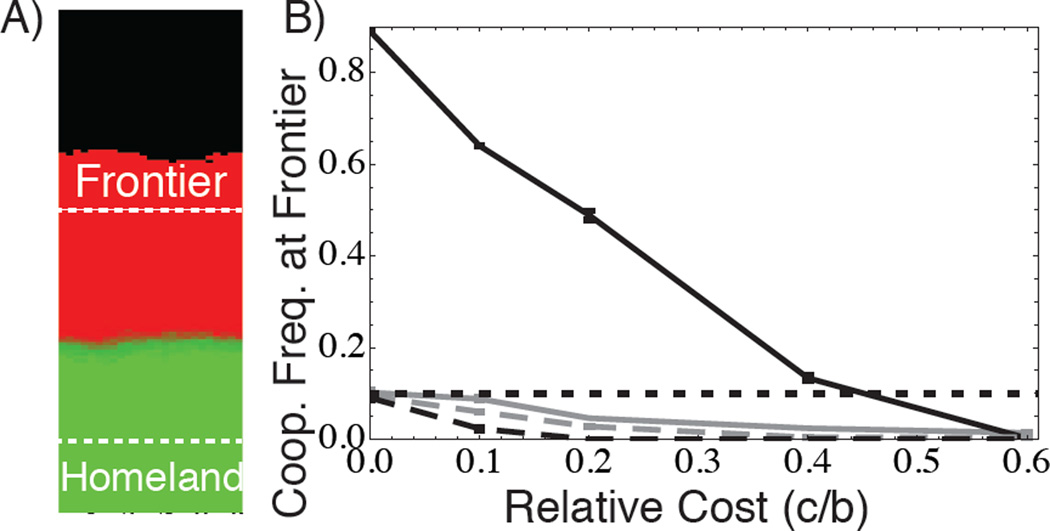
Figure 4. Selection for cooperation in spatially expanding populations requires competition among neighboring frontier subpopulations.

Results of lattice-based spatial simulations of a PD game in a population expanding in one direction (i.e., a linear front[8]). A) Example of the endpoint of a two-dimensional simulation (cooperators in red, defectors in green), while B) shows averages over 100–500 iterations, for two-dimensional (black) and one-dimensional (grey) simulations. Each lattice site is a subpopulation growing logistically to size K = 50 in a metapopulation of dimension 1×150 (one-dimensional) or 25×150 (two-dimensional) sites. The vertical axis in B) gives the frequency of cooperators at the population frontier (defined here as a 1×10 or 25×10 area at the furthest edge of the population) after 200 generations. Horizontal dotted line indicates neutral expectation of this value. Simulations initiated with cooperators at 0.10 frequency in a well-mixed (relatedness = 0) homeland of length 10 sites. Two-dimensional expansions (black) select for cooperation, but one-dimensional expansions (grey) cannot. b = 0.5 for solid lines, and dashed lines denote zero social effect (b = 0); note that the horizontal axis has been normalized by b = 0.5. Simulation parameters: W₀ = 1, K = 50, m = 0.2.

In contrast to the one-dimensional case, the probability of cooperators fixing at the frontier is substantially higher in two dimensions, where subpopulations compete with neighbors for occupancy of uncolonized habitat (Fig. 4). Two-dimensional expansions are also more efficient at purging deleterious alleles from frontiers, as seen in comparison of the black and gray dashed lines in Fig. 4. Our data support the conclusion that two-dimensional spatial expansions generates selection at the frontier for genotypes that maximize group productivity, as these genotypes lead to the greatest expansion velocity of the front, allowing cooperator enriched demes to overtake defector enriched demes. Spatial expansion generates both conditions necessary for natural selection: heritability (positive assortment of social strategies, making one’s social environment heritable) and differential success (survival of the “fastest”).

Microbes posses a multiplicity of cooperative phenotypes [12], and rapid cell division in conjunction with large colony sizes makes the repeated emergence of defector mutants inevitable in nature. We have demonstrated that colony growth itself creates a force that promotes cooperation and inhibits colony invasion by defector mutants. Range expansions may promote cooperation more generally and may allow already cooperative species to shed social parasites, so long as the pattern and rate of dispersal and reproduction allow for genetic demixing upon expansion. It is possible that reduced cheater load upon expansion may accelerate biological invasion by cooperative species, with potential implications for biological control. Stochastic demixing may also occur with culturally transmitted phenotypes, such that range expansion may have been important in the spread of cultural norms facilitating cooperation in humans. Yet this force persists only as long as expansion continues. Repeated cycles of expansion and contraction, possibly due to frequent disturbance, may be necessary to maintain persistent selection for cooperation by this mechanism.

Highlights.

• -Spatial population expansion selects for cooperation at population frontiers
• -Frontiers possess high genetic relatedness and create among-group competition favoring “survival of the fastest”
• -Spatial expansion favors genotypes promoting maximization of group productivity
• -Colony growth in microbes is a force promoting cooperation