The role of wall shear stress in the assessment of right ventricle hydraulic workload

Abstract Abstract

Pulmonary hypertension (PH) is a devastating disease affecting approximately 15–50 people per million, with a higher incidence in women. PH mortality is mostly attributed to right ventricle (RV) failure, which results from RV hypotrophy due to an overburdened hydraulic workload. The objective of this study is to correlate wall shear stress (WSS) with hemodynamic metrics that are generally accepted as clinical indicators of RV workload and are well correlated with disease outcome. Retrospective right heart catheterization data for 20 PH patients were analyzed to derive pulmonary vascular resistance (PVR), arterial compliance (C), and an index of wave reflections (Γ). Patient-specific contrast-enhanced computed tomography chest images were used to reconstruct the individual pulmonary arterial trees up to the seventh generation. Computational fluid dynamics analyses simulating blood flow at peak systole were conducted for each vascular model to calculate WSS distributions on the endothelial surface of the pulmonary arteries. WSS was found to be decreased proportionally with elevated PVR and reduced C. Spatially averaged WSS (SAWSS) was positively correlated with PVR (R² = 0.66), C (R² = 0.73), and Γ (R² = 0.5) and also showed promising preliminary correlations with RV geometric characteristics. Evaluating WSS at random cross sections in the proximal vasculature (main, right, and left pulmonary arteries), the type of data that can be acquired from phase-contrast magnetic resonance imaging, did not reveal the same correlations. In conclusion, we found that WSS has the potential to be a viable and clinically useful noninvasive metric of PH disease progression and RV health. Future work should be focused on evaluating whether SAWSS has prognostic value in the management of PH and whether it can be used as a rapid reactivity assessment tool, which would aid in selection of appropriate therapies.

Pulmonary hypertension (PH) is a degenerative disease that can arise as a result of a primary etiology (pulmonary arterial hypertension [PAH], i.e., World Health Organization [WHO] group I) or can be secondary to multiple causes, most notably left heart disease (WHO group II), interstitial lung disease (WHO group III), and chronic thromboembolic PH (WHO group IV).^1,2 Women are disproportionately affected by PH, which typically affects 15–50 persons per million.³ The medical and scientific communities have made significant advances in the diagnosis and treatment of this disorder in the past several decades.^4-6 However, the disease remains poorly understood and still requires an extensive workup, including invasive procedures for its diagnosis. Patients suspected of having PH currently undergo right heart catheterization (RHC) for acquisition of diagnostic hemodynamic data and contrast-enhanced chest computed tomography (CT) to assess the lung parenchyma and morphology as well as to evaluate for pulmonary embolism.⁷ If the cause of PH is deemed to be of primary etiology, then PAH-specific therapies, including endothelin-1 receptor antagonists, prostanoids, and phosphodiesterase-5 inhibitors, are generally used as either monotherapy or combination therapy, depending on the severity of symptoms, response to specific agents, and tolerability of medication side effects.

Physicians intimately involved in the management of this disorder are well aware that the definitive diagnosis is usually made in the symptomatic phase of the disease, since no validated screening tool currently exists to detect the disease in its presymptomatic, or subclinical, phase. This might partially explain the poor prognosis, especially in the case of PAH, since many patients would have already had significant remodeling of the pulmonary arteries and some measure of right ventricle (RV) dysfunction at diagnosis using conventional metrics.⁸ Even after successful diagnosis and implementation of therapy, the physician lacks a quality noninvasive tool to assess physiologic response to therapy that is not fraught with the inadequacies of assessing the RV by transthoracic echocardiography^9,10 or the limited availability of cardiac magnetic resonance imaging (MRI). Computational fluid dynamics (CFD) and the ability to estimate spatially averaged wall shear stress (SAWSS) of the pulmonary arteries together might prove to be an ideal screening tool for PAH. The possibility of using routinely acquired CT images of the chest to evaluate pulmonary artery (PA) geometry, noninvasively assess pulmonary hemodynamics by CFD, and validate the ensuing novel metrics to diagnose PH and clinically follow its progression would greatly enhance the physician’s armamentarium in combating this disease.

The cardiopulmonary system consists of 3 primary components: (1) the RV, (2) the proximal pulmonary vasculature, and (3) the distal pulmonary vasculature. In normal conditions, the RV ejects blood against a relatively low afterload by contractile motion in the circumferential and longitudinal directions.¹¹ Being highly afterload sensitive, changes in pulmonary hemodynamics can quickly initiate RV hypotrophy and RV dysfunction.¹¹ The initial remodeling response maintains normal RV function but turns counterproductive at the onset of dilation, which is believed to represent the maladaptive form of RV remodeling.¹² The medical community has long believed that PH was a disease that arises as a result of increased resistance in the distal pulmonary vasculature, the cause of which is likely related to a compromise in endothelial response. Endothelial cells lining the pulmonary arteries are known to be highly responsive to the local hemodynamics.¹³ They control the release of vasoconstrictors/dilators¹⁴ and are believed to play a critical role in initiating and perpetuating vascular remodeling via apocrine and paracrine mechanisms.¹⁵ This adverse remodeling ultimately affects the arteries’ mechanical properties.¹⁶ An elevated resistance in the distal arteries causes a pressure increase in the large proximal vasculature, leading to proximal arterial remodeling in the form of increased arterial stiffness and thickness. This compromises the proximal vasculature’s role as a hydraulic damper to the distal vessels,^17,18 causing distal endothelial cells to be exposed to nonphysiological pulse pressure and initiating a destructive cycle.

Proximal arterial stiffening is also believed to affect wave reflections and has been shown to contribute to cardiac workload in the systemic circulation.¹⁹ There is no current consensus on the role of wave reflections in the pulmonary circulation, but changes in wave dynamics have been linked to PH disease progression in hypoxic-animal models.²⁰ One possible reason for worsening disease progression is vascular-ventricular decoupling, resulting in a desynchronization of the RV and the proximal arterial dynamics (e.g., RV ejection and wave reflections). To this end, an index of wave reflections, Γ, is known to increase in PH²¹ and is governed by (1) the steady (zero-frequency) component of vascular impedance, i.e., pulmonary vascular resistance (PVR), and (2) the characteristic impedance, Z_c. The latter is the mean impedance modulus at the high-frequency harmonic plateau, which is intuitively understood as the impedance in the absence of wave reflections (e.g., an infinitely long compliant tube) and is documented to remain relatively constant in PH.²¹

Previous studies have utilized computational modeling to show that the pulmonary vasculature is exposed to varying wall shear stress (WSS) in resting and exercise conditions.²² Computational simulations of the pulmonary vasculature have been used to predict treatment reactivity^23,24 and for surgical planning,²⁴ in addition to generally suggesting that WSS could play an important role in PH disease progression.^23,25 Computational models²⁶ and direct processing of phase-contrast MRI (PC-MRI) velocity data^27,28 have revealed a WSS decrease in the general PH population but have stopped short of directly linking decreased WSS to disease outcome. Noteworthy is that there is a major distinction between the two methods, i.e., (1) CFD analysis in a reconstructed patient-specific geometry (up to the seventh generation) and (2) evaluating WSS at an arbitrary vessel cross section from PC-MRI velocity measurements. Assuming that the pulmonary vasculature can be adequately reconstructed from thoracic scans, a computational model resolves sufficient flow detail to integrate the WSS over the reconstructed pulmonary endothelium (e.g., SAWSS). This allows for the computation of a metric that takes into account flow conditions in the proximal and distal vasculature, which are strongly driven by vascular morphology. Calculating WSS from PC-MRI reveals velocity gradients normal to a plane, which can be used to calculate WSS at the wall where the plane intersects the endothelial surface. The location of the plane is chosen by the MRI technician, which can make the method subjective, considering that the WSS in the PA varies significantly among different cross sections.

The overall objective of this work is to identify correlations between metrics of WSS that have characteristics indicative of increased afterload and metrics indicative of a PH disease state that have been shown to be predictive of longitudinal outcome. To this end, we calculated WSS maps for the pulmonary arterial tree of 20 PH patients with varying disease severity, characterized by PVR and compliance (C), both considered established indicators of RV hydraulic workload and mortality risk.²⁹

Methods

Twenty PH patients were admitted to Allegheny General Hospital (Pittsburgh, PA) and underwent a standard-of-care RHC and an electrocardiogram-gated contrast-enhanced chest CT scan. This study involved retrospective processing of hemodynamic and imaging data for a patient population with varying PH causes and treatments. Upon diagnosis of PH, disease severity was assessed according to the WHO PAH function classification, and RV function was qualitatively assessed by a trained cardiologist on an echocardiogram. Catheterization data revealed elevated pulmonary arterial pressure and flow, which were used to compute two metrics commonly accepted as indicators of RV afterload,²¹ PVR (eq. [1]) and C (eq. [2]):

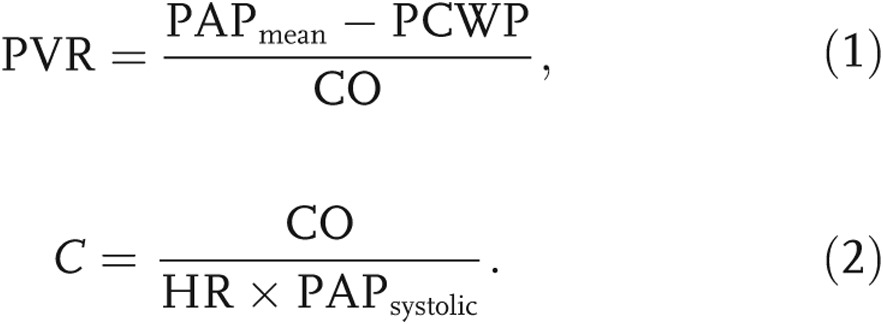Here, PAP is the pulmonary arterial pressure, PCWP is the pulmonary capillary wedge pressure—approximated as the pressure in the left atrium¹²—CO is the cardiac output, and HR is the heart rate.

Calculating the index of wave reflections

The index of wave reflections, Γ, is a function of the zero-frequency and characteristic impedances and reports on the relative region of wave reflections in the impedance spectrum, normalized by the patient’s total impedance. The arterial impedance can be used to describe the transient relationship between pressure and flow in an artery. Intuitively, the zero-frequency impedance can be considered the total PVR of the pulmonary vasculature, because it corresponds to the ratio of the mean pressure to the mean flow. As described above, the characteristic impedance is the impedance of the vasculature if it were hypothetically free of wave reflections, thereby allowing computation of the relative impact of wave reflections in the local pulmonary arterial system (Γ, computed in eq. [8]). Calculating the zero-frequency impedance from mean pressure and flow data is necessary to approximate the characteristic impedance needed to compute Γ for each PH patient in our data set. The characteristic impedance is generally calculated from a Fourier decomposition of the time-varying pressure and flow waveforms in the main PA (MPA), which were not available from the retrospectively acquired data. Alternatively, to estimate this critical metric, we take the ratio of proximal arterial stiffness to fluid inertia,²¹

where ρ is the blood density (1.06 g/mL), E is the proximal arterial elastic modulus, h is the arterial wall thickness, and R is the lumen radius. Because the characteristic impedance is a function of the arterial stiffness, it must be related to the pulse wave velocity. In fact, in light of the Moens-Korteweg equation (eq. [4]),³⁰ Z_c can be rewritten as a function of the pulse wave velocity, c, and further simplified to be a function of distensibility with the Braumwell-Hill equation (eq. [5]):³⁰

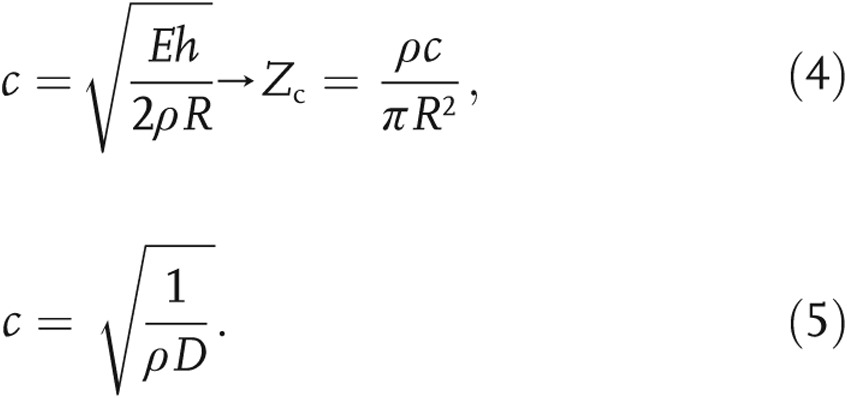Proximal arterial distensibility (D; eq. [6]) was estimated, for each PH patient, as a function of the RHC metrics³¹ with equation (7), which was solved with Newton’s method by iterating until the “offset” was less than 10⁻⁶:

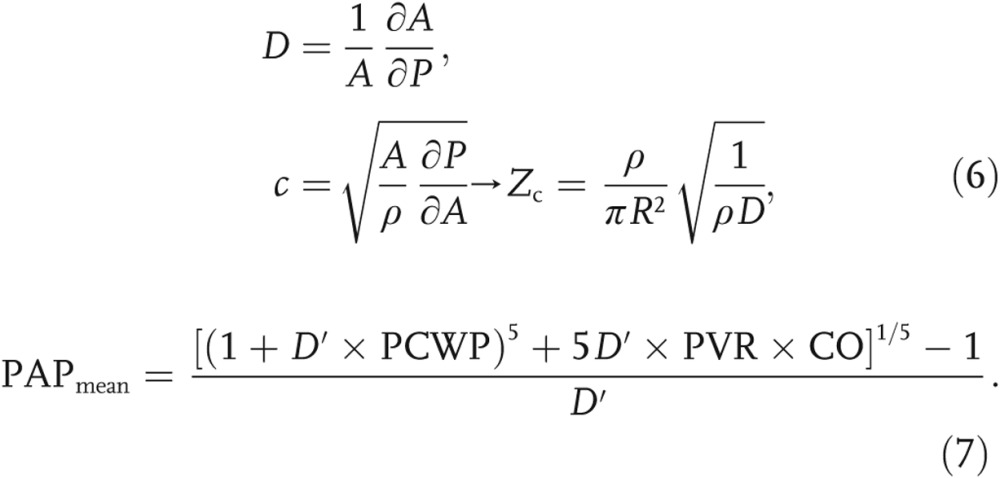Noteworthy is that equation (7) was slightly modified from its original derivation,³¹ as zero-pressure PVR was not a clinically available metric. Therefore, we assume that D′, approximated from PVR, would be slightly higher than the true distensibility, D. Finally, after calculation of the characteristic impedance and recognition that the zero-frequency harmonic is equal to PVR (Z₀ = PVR),³² each patient’s state of disease progression is characterized by Γ as

Calculating WSS in the pulmonary vasculature

In addition to RHC measurements, each patient underwent a contrast-enhanced chest CT scan of the pulmonary vasculature. The pulmonary arteries were reconstructed up to the seventh generation with Mimics 14.0 (Materialise, Leuven, Belgium), according to a protocol outlined in our previous work.⁷ CFD simulations based on solving the mass and momentum conservation equations (eqq. [9], [10]) for the velocity () and pressure (P) distribution within the vascular conduits were carried out under the following assumptions: (1) a constant flow rate at the entrance of the MPA, equivalent to the RHC-measured CO, and (2) a pure resistance approximation of the truncated distal pulmonary vasculature (i.e., beyond the seventh generation), which was approximated by a virtual tree (a “structured-tree outflow boundary condition”) at the physical outlets reconstructed from the clinical images.

An implicit finite-volume method (ANSYS Fluent, Canonsburg, PA), with a SIMPLE discretization scheme, was used to solve the governing flow equations:

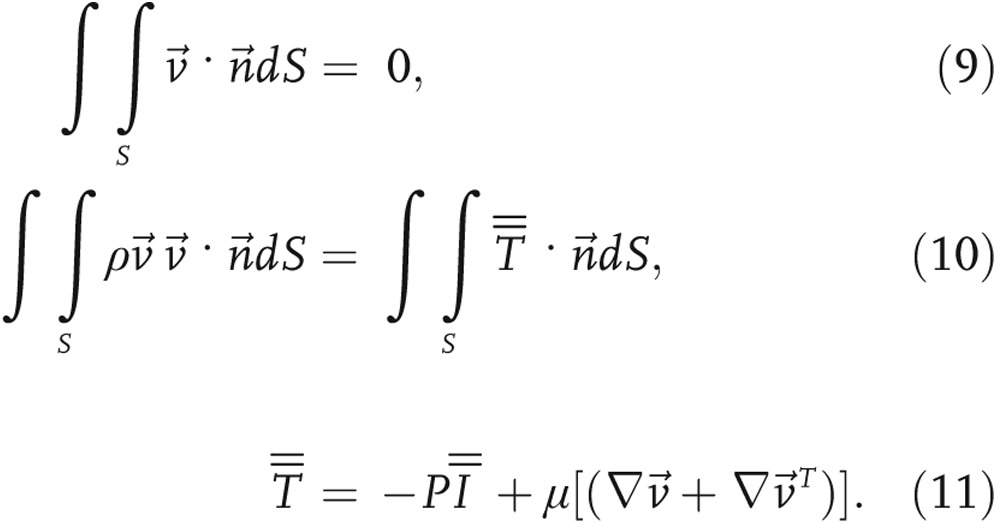In equations (9) and (10), 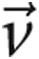is the velocity vector, S is the element surface area, 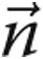is the unit vector orthogonal to S, ρ is the density (1.05 g/cm³), and 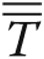is the stress tensor. In equation (11), P is the pressure, μ is the dynamic viscosity (0.035 poise), 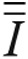is the unit tensor, and ∇ is the gradient operator.

The inflow condition was approximated as a fully developed Poiseuille velocity profile, which was applied to a noncircular inlet via Schwarz-Christoffel mapping.³³ A mesh sensitivity analysis was conducted according to the procedure outlined by Prakash and Ethier,³⁴ with independence achieved on the basis of spatial distributions of WSS. The structured-tree outflow boundary condition dictated the flow split by assigning a distal outlet resistance proportional to the outlet radius (see Fig. 1a). Briefly, a unique structured tree is developed for each patient, with dimensional metrics (α and β; see Fig. 1b) determined from a full vascular tree (starting with the MPA), equating to the individually measured PVR. The total resistance in the tree is calculated analogous to that in an electrical circuit, with the resistance in each branch calculated according to equation (12), where the radius of each branch, r, is determined from the tree morphology (α and β) and l is the vessel length, obtained from morphometric data³⁵ specific to the vessel’s generation,

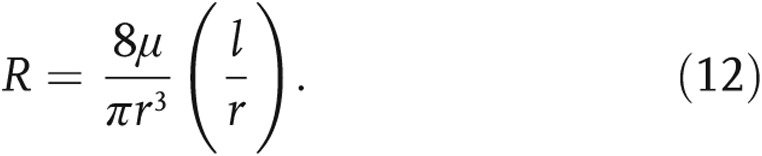Finally, each computational solution yielded a pressure and stress distribution, with MPA flow and pressure in agreement with the RHC-acquired data. This required some tuning of the outflow boundary condition, suggesting that the structured tree dictated the flow split at each distal vessel and not necessarily the total pulmonary resistance.

Figure 1.

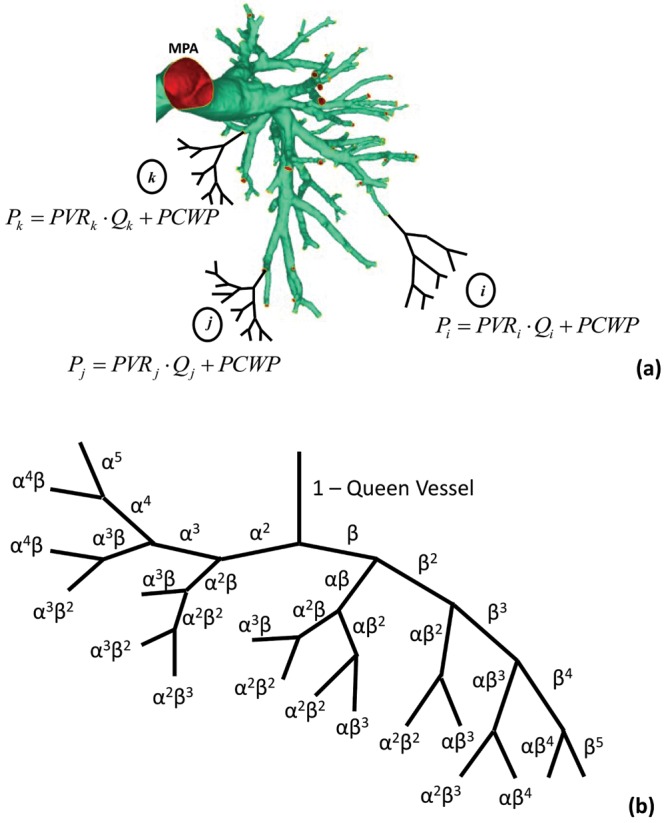
a, Reconstructed pulmonary vasculature with hypothetical structured tree extruding from 3 random outlets (i, j, and k), with calculations of pressure coupled to outlet flow rate (Q_i). MPA: main pulmonary artery; PCWP: pulmonary capillary wedge pressure. b, The patient-specific structured-tree distal resistance at a given outlet, PVR_i, is calculated according to the α and β specific for each patient.

Statistical analysis

The association between two variables is assessed by a Pearson correlation coefficient (r), with no prior hypothesis as to the sign of the correlation, which is confirmed with a 2-tailed probability (P). Nevertheless, regardless of the sample, the threshold for statistical significance is considered to be at P < 0.05. A 2-tailed t test was used to compare the difference in mean between two groups to assure that there is no difference in either direction.

Results

RHC data

With Institutional Review Board approval at Allegheny General Hospital and the University of Texas at San Antonio, the patient population in this study consisted of 11 women and 9 men, for whom demographic data and other clinical variables of interest are summarized in Table 1. When hemodynamic (PAP_mean, PCWP, PVR, and CO) and morphological (average MPA diameter) measurements were compared between the two groups, no statistically significant differences (P < 0.05) were observed after a 2-tailed t test.

Table 1.

Fundamental demographics and other clinical variables of interest for the human subjects data acquired for this study

	Female (n = 11)	Male (n = 9)
Age, years	60.9 ± 9.9	56.3 ± 8.9
Height, inches	62.2 ± 1.8	70.3 ± 2.1
Weight, pounds	215.7 ± 55.9	187.2 ± 41.0
Heart rate, bpm	74.7 ± 2.0	72.9 ± 6.1
Cardiac output, L/min	6.0 ± 1.2	5.0 ± 1.5
Mean pulmonary artery pressure, mmHg	35.3 ± 9.2	39.7 ± 14.5
Pulmonary capillary wedge pressure, mmHg	14.9 ± 6.6	13.8 ± 11.6

^NoteData are mean ± standard deviation.

Consistent with previous findings,²¹ PAP_mean revealed a weak correlation with PVR (R² = 0.30, P < 0.05). Nevertheless, a moderate linear regression correlation was found with C (R² = 0.70, P < 0.05) and an excellent power regression correlation with D′ (R² = 0.89, P < 0.05), where an increase in PAP_mean suggests a corresponding increase in stiffness. PVR (equated to the zero-frequency impedance) did not correlate with the estimated characteristic impedance but revealed a strong power regression correlation with Γ (R² = 0.75, P < 0.05). These results are not represented graphically in this article.

A trained cardiologist’s qualitative assessment of RV function, based on echocardiography, demonstrated that PVR is an indicator of RV function with modest consistency. For example, the 2 patients with the highest PVR also presented severely dilated RV morphology with significant dysfunction. Nevertheless, some patients with moderately high PVR revealed normal RV function, while other patients with lower PVR presented mild to moderate dysfunction. The patient population evaluated in this study suffered from PH as a result of left heart disease and idiopathic PH. Therefore, pressure measurements and direct RV morphological observations could depend on the epidemiology and might reveal inconsistencies. However, local hemodynamics is governed by the remodeled vascular geometry and pressure gradient (ΔP = PAP_mean − PCWP). To this end, WSS in the pulmonary vasculature is simply a reflection of local hemodynamics, driven by inflow/outflow conditions and geometry and independent of etiology. Therefore, hemodynamics could yield a better indicator of ultimate vascular remodeling because it reveals the flow conditions acting on the endothelium at the time of a patient’s follow-up visit.

CFD data

Figure 2 shows patient-specific WSS distributions superimposed on four reconstructed pulmonary models. The highest WSS is observed at the smaller vessels, with occasional local maxima in the proximal vessels. WSS is bound by 50 dyn/cm², because of regions of high stress concentrations that can arise in the CFD simulations from geometric anomalies in distal vessels reconstructed from poor image resolution.⁷

Figure 2.

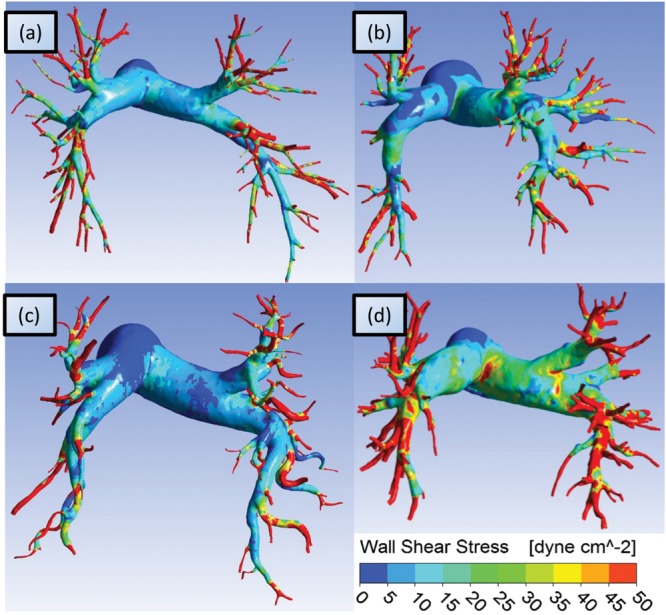
Computational fluid dynamics solutions of wall shear stress (WSS) superimposed on four exemplary pulmonary vasculatures. Generally, higher WSS is seen in the distal vessels, with occasional high stress concentrations at the left/right arterial bifurcations (see d).

WSS was evaluated in the form of the following metrics: (1) WSS integrated over the entire pulmonary geometry and normalized by the endothelial surface area, i.e., SAWSS (eq. [13]), and (2) WSS averaged along the perimeter of an arbitrary circumferential location (see Fig. 4a) at the MPA (WSS_MPA), the right PA (WSS_RPA), and the left PA (WSS_LPA),

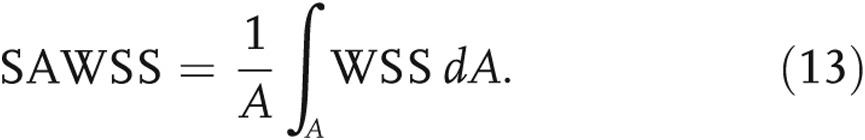The mean (± standard deviation) SAWSS in the study population is 13.2 ± 3.7 dyn/cm², with no statistically significant difference between men and women. Figure 3 shows SAWSS correlated against established metrics of PH disease progression and RV function, some of which have been directly correlated with mortality. Figure 3a shows a power regression correlation between SAWSS and PVR (R² = 0.66, P < 0.05), while Figure 3b shows a proportionally linear relationship between SAWSS and C (R² = 0.73, P < 0.05). Consistent with previous findings,²⁶ shear stress appears to decrease with PH disease severity (high PVR and low C). Figure 3c shows SAWSS as a function of Γ (R² = 0.50, P < 0.05), confirming previous findings that advanced PH, corresponding to a low WSS, results in a higher Γ. Figure 3d shows SAWSS correlated against a metric of RV geometry that has been linked to disease outcome. RV geometry data are available for only 5 patients in this study, but they suggest a likely strong correlation between SAWSS and the end-diastolic midcavitary RV diameter.

Figure 4.

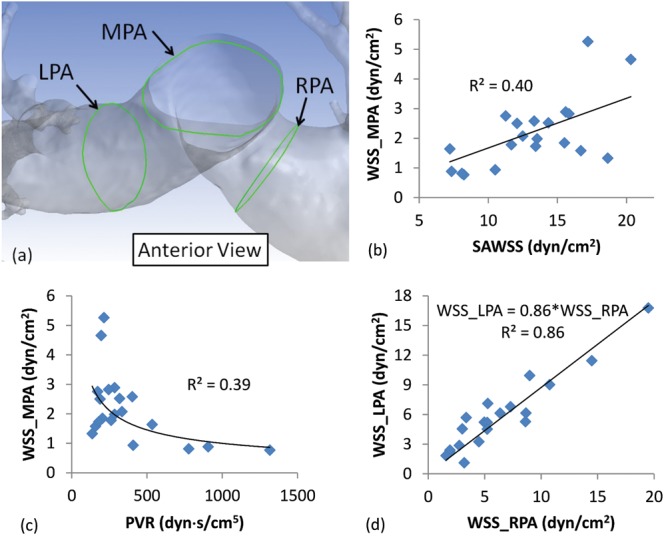
a, Schematic showing a sample reconstructed pulmonary vasculature, with lines along the endothelium found at the intersection of the main, right, and left pulmonary arteries (MPA, RPA, and LPA, respectively) and three arbitrary planes normal to the centerline of the lumen at these vessels, represented by the green lines. Average wall shear stress (WSS) was measured along these lines (WSS_MPA, WSS_RPA, and WSS_LPA), which is the typical WSS that can be calculated from phase-contrast magnetic resonance imaging (PC-MRI). b, A weak correlation between WSS_MPA (typically available from PC-MRI) and spatially averaged WSS (SAWSS, available from computational fluid dynamics simulations). This weak relationship could suggest that the inconsistency (between patients) in locating the plane of interest for PC-MRI could make the imaging technique unsatisfactory for approximating patient-specific pulmonary endothelium WSS distribution. c, A weak correlation between WSS_MPA and pulmonary vascular resistance (PVR) suggests that approximating WSS from PC-MRI might not be accurate for predicting right ventricular afterload. d, A strong correlation between WSS_LPA and WSS_RPA values suggests a consistent flow distribution in the vasculature and a relatively similar velocity profile downstream of the bifurcation. Note that all correlations satisfied the criterion for statistical significance, P < 0.05.

Figure 3.

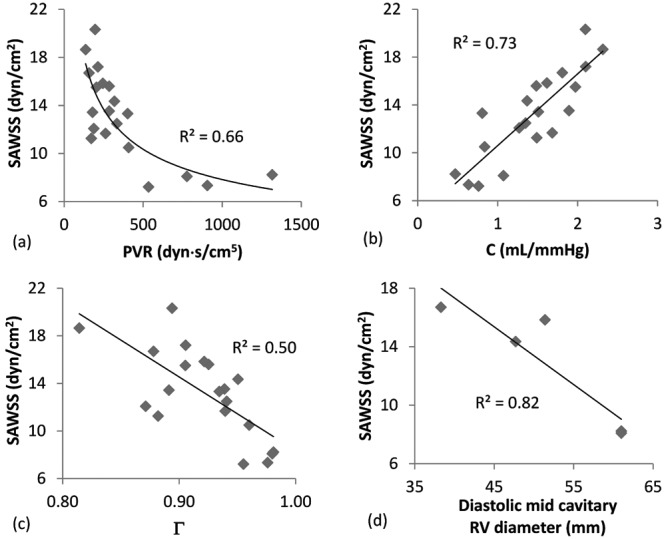
Correlations between spatially averaged wall shear stress (SAWSS) and pulmonary vascular resistance (PVR; a), between SAWSS and compliance (C; b), between SAWSS and the index of wave reflections (Γ; c), and between SAWSS and the diastolic midcavitary right ventricle (RV) diameter (d). Note that all correlations satisfied the criterion for statistical significance, P < 0.05.

Calculating WSS directly from phase-contrast imaging data (e.g., PC-MRI) has led others to conclude that WSS is low in patients suffering from PH. The plane phase velocity slices are normally taken at arbitrary locations orthogonal to the vessel’s longitudinal axis,²⁸ but it is unclear whether these recordings are truly indicative of the local hemodynamics. Therefore, we evaluated WSS_MPA, WSS_RPA, and WSS_LPA at the locations shown in Figure 4a. The means (± standard deviation) for WSS_MPA, WSS_RPA, and WSS_LPA were found to be 2.2 ± 1.2, 5.9 ± 3.7, and 6.4 ± 4.5 dyn/cm², respectively. When the hemodynamics in the 3 proximal arteries is considered, WSS increases with new generations of smaller vessels but might not be particularly reliable as an indicator of local hemodynamics, since isolated regions of a given artery can reveal “hot spots” of high stress. Figure 4b shows that WSS_MPA is poorly correlated against SAWSS and PVR. Interestingly, there is a strong correlation between WSS_RPA and WSS_LPA, (R² = 0.86, P < 0.05), with a slightly lower WSS in the left lung.

In the absence of an anatomical obstruction (e.g., stenosis, pneumothorax), experimental data suggest that relatively equal blood flow is distributed to both lungs. To investigate the impact of vascular reconstruction on CFD solution reliability, we compared hemodynamic data of the same patient segmented to a different generation. Figure 5a illustrates the WSS distribution for the same pulmonary geometry segmented to the seventh (left) and third (right) generations. Likewise, Figure 5b shows the flow split in percentages of flow originating from the MPA in both geometries. The WSS distribution appears to be similar between the two reconstructed models; however, the SAWSSs differ by 14%. The geometry reconstructed to the seventh generation leads to a more physiological flow split between the right and left lungs. To this end, the 20 chest CT scans in this study were all segmented to the highest vessel generation allowable by the CT image resolution. Figure 5c shows the physiological flow split for the patient population, indicating an average 51∶49 distribution between the right and left lungs, respectively.

Figure 5.

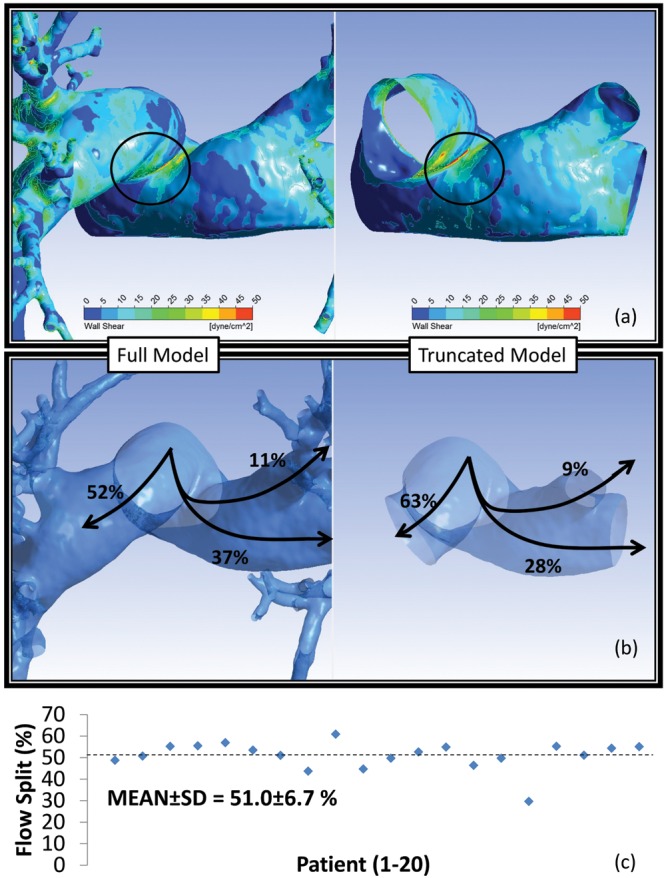
Impact of vascular reconstruction on the computational fluid dynamics solution. a, Wall shear stress (WSS) distribution on the same vasculature reconstructed to the third (right) and seventh (left) generations. Regions of stress concentrations in the proximal vasculature are common between the two models, but with a spatially averaged WSS difference of 14%. b, The full model calculates a more physiological flow split (52% to the right lung and 48% to the left lung), while the truncated model likely overestimates perfusion into the right lung (63% vs. 37% to the left lung). c, All patient-specific models in this study were reconstructed to the limit of image resolution (ca. seventh generation), leading to a 51.0% ± 6.7% (indicated by the horizontal dotted line) flow split between the two lungs. SD: standard deviation.

Discussion

The objective of this work was to evaluate whether WSS correlates positively with established clinical metrics of PH progression and RV function. Furthermore, we investigated the influence of measurement techniques on the ensuing WSS calculations and identified criteria for generating patient-specific computational models to calculate pulmonary hemodynamics. The comparison of PH hemodynamic metrics with a healthy control population was out of the scope of this study.

RHC data did not reveal a statistically significant difference in pulmonary arterial hemodynamics between the male and female PH subjects in this study. Therefore, all patients were grouped into the same population to compare hemodynamic and continuum metrics across known indicators of RV function. Intuitively, an increase in distal PVR would suggest an increase in upstream pressure, although no significant correlation was observed between the two metrics. This may have been due to the inclusion of patients with left heart disease. Interestingly, pressure correlated well with C (a volume metric) and even better with distensibility (a point metric), consistent with previous correlations between pulse pressure and relative area change.³⁶ The current finding would suggest that RHC mean pressure measurements could be used to approximate distensibility and, consequently, the pulse wave velocity and characteristic impedance without the need for processing time-varying data.

The most common cause of mortality in PH is maladaptive RV remodeling, which ultimately leads to a disruption in RV ejection and failure. Consistent with previous findings,²⁶ we found that the pulmonary vasculature of patients suffering from PH is exposed to a SAWSS that is reciprocal to disease severity (as assessed by PVR and C). This finding is generally nonintuitive, considering that, given the well known Hagen-Poiseuille flow equation, we would expect a local constriction of the vasculature to increase the WSS. Nevertheless, a decreased SAWSS could be a result of decreased CO or a change in the blood viscosity of a PH patient due to pharmacological treatment, which were not investigated in this study. We studied the isolated impact of CO to show that it did have a significant influence on our correlations (data not presented). Nevertheless, incorporating patient-specific PVR into the simulations improved those correlations. The strong relationship with PVR and the fact that experimental PC-MRI data reveal lower WSS in PH patients suggest that the increased resistance resulting from constriction of the distal vasculature will alter the local velocity profiles in the proximal vessels. This explains the overall decrease in SAWSS and agreement with previous findings based on PC-MRI measurements. PH disease severity and RV function have been closely linked to an increase in PVR, vascular stiffness, and wave reflections.²¹ SAWSS in our patient population changes proportionally to the three aforementioned variables, and our preliminary data suggest a relationship with end-diastolic RV geometry. Therefore, for the aforementioned reasons, a low SAWSS in subjects with high PVR is likely because of local hemodynamic changes resulting from a decrease in proximal luminal cross-sectional area, but it can also indicate a cycle of system breakdown. The evident coupling between local hemodynamics and endothelial cell response could lead one to infer that a low WSS might precede irreversible vascular and ventricular remodeling and could have significant prognostic and risk stratification value. Moreover, WSS can be calculated noninvasively and could be a plausible alternative to the invasive standard-of-care RHC procedure.

The index of wave reflections (Γ) is the ratio of the difference between zero-frequency impedance (PVR) and the characteristic impedance and their sum. Characteristic impedance is known to stay relatively constant over the course of PH;^20,21 this is believed to be due to a synchronized increase in stiffness and fluid inertia. Therefore, an increase in PVR would cause the numerator in the equation for Γ to increase disproportionally, compared to the denominator, increasing Γ and suggesting an early return of the reflected waves due to an increase in pulmonary stiffness (and thus pulse wave velocity).¹⁹ This desynchronization between normal cardiac rhythm and reflected waves possibly contributes to pressure increases inside the RV, leading to an increase in afterload. As the RV begins the process of adaptive remodeling by changing local cardiac dynamics and morphology, vascular-ventricular decoupling prevents any meaningful change to the system dynamics. This study confirms previous findings that Γ increases in PH but is the first to show that it is linearly correlated with SAWSS. This suggests that gauging therapeutic response on the basis of computationally calculated WSS could lead to vascular-ventricular coupling normalization and help predict long-term RV outcome. Measuring RV pressure-volume data simultaneously with computational hemodynamics could expose low WSS as the cause of vascular-ventricular decoupling and wave timing desynchronization.

In future work, we aim to consider larger patient populations in prospective studies that control treatment and stratify risk according to epidemiology. Animal studies should be pursued to investigate the cause and effect of WSS in the diseased cardiopulmonary circulation and the overall impact of RV wall stress. In addition, techniques for postprocessing phase-contrast imaging flow data to estimate WSS, as an alternative to computationally expensive CFD analysis, should be investigated further, although our study suggests that single-plane WSS calculations are not well correlated with disease prognosis metrics. To this end, we calculated WSS from CFD simulations at typical cross sections used previously for PC-MRI,²⁸ to investigate the impact of calculating WSS at a single plane, compared to integrating over a significantly larger portion of the endothelium, on the ensuing correlations with RV afterload. The results presented here do not take into account the accuracy of processing PC-MR images; rather, this study is focused exclusively on the patient-specific data obtained from evaluating WSS at arbitrary planes. While the WSS calculated at isolated locations in the pulmonary vasculature suggests a lower mean WSS for PH, no correlation was found with SAWSS or any metric of disease progression and RV function. Interestingly, a strong correlation was found between the WSSs calculated at planes in the left and right pulmonary arteries, which were generally independent of the WSS in the MPA. This may be due to nearly equal flow distribution to both lungs and represents a future opportunity to study the impact of local flow dynamics on endothelial response in partially occluded pulmonary arteries.

One limitation of this study is the steady-flow assumption used in the computational simulations. Pulsatile flow and pressure in the MPA were not measured for any of the subjects in the study, as this is not part of the standard of care for PH patients. Having such data available would have allowed for a more informative CFD analysis and a better approximation of the characteristic impedance. Nevertheless, we conducted a proof-of-concept study by executing a CFD pulsatile-flow simulation using an inlet velocity waveform measured at the MPA of a PH subject not included in this work. We compared the outcome of the pulsatile-flow simulation to that of a CFD simulation of the same pulmonary geometry with a constant inlet velocity equal to the time-averaged velocity in the pulsatile waveform. The result was a 3.6% difference between the time-averaged SAWSS in a cardiac cycle and the SAWSS of the constant-flow-rate simulation. This comparison indicates that steady-flow CFD simulations can adequately estimate WSS distributions with a small margin of error, compared to pulsatile-flow conditions.

Another important limitation of this work is the assumption of a rigid pulmonary arterial wall, which would not allow for application of a flow waveform measured simultaneously with a pressure waveform. This is because neglecting the reactive component of impedance would neglect the strong influence of hydraulic damping and keep the pressure in phase with the flow. Such unrealistic physics can be overcome with fluid-structure interaction simulations, which require assigning patient-specific mechanical properties to the pulmonary arteries, evidently a difficult task to accomplish. Nevertheless, it is worth noting that previous studies by our group have shown that the rigid-wall assumption overestimates WSS in the abdominal aorta,³⁷ which suggests that the effect of wall compliance should be evaluated in future pulmonary hemodynamics work.

Further processing of the data obtained in this work would involve correlation of the calculated parameters with direct metrics of RV function and morphology that are indicative of long-term outcome. PVR and C have been repeatedly linked to mortality but are, in fact, approximations of pump resistance commonly equated to RV afterload, which might be an oversimplification. Therapeutic changes to RV ejection fraction are better correlated with ultimate mortality than are changes to PVR.² The stress developed in the RV endocardium cannot be studied in isolation from RV geometry and wall motion dynamics. Therefore, the aforementioned metrics are more indicative of RV hydraulic work, which could be better approximated with time-varying pressure/flow data. Future studies should be focused on directly calculating RV hydraulic work and wall stress to confirm the suspected relationship between these metrics and the hemodynamics in the pulmonary vasculature. In addition, the experimental validation of the CFD analyses using a technique such as particle image velocimetry should be performed in a follow-up study that acknowledges the inherent limitations of such an experimental method.

Conclusion. We performed computational simulations of pulmonary hemodynamics in a PH patient population to assess correlations between SAWSS and metrics indicative of RV hydraulic workload. We found that integrating WSS, calculated with CFD from patient thoracic CT scans and hemodynamic data, on a large region of the endothelial surface was a promising indicator of RV function and PH disease progression. SAWSS correlated positively with characteristics indicative of vascular resistance and stiffness and may be related to wave propagation and changes in RV morphology. Nevertheless, approximating WSS in the proximal vessels did not reveal the same promising results. This discovery suggests the potential for a noninvasive strategy to arrive at a patient-specific metric that encompasses both the resistive and reactive components of RV afterload, making computational analysis a surrogate in scenarios where invasive RHC procedures are impractical. Additional work is needed to investigate whether SAWSS is sensitive to treatment reactivity or whether it offers an opportunity to predict vascular/ventricular remodeling.

Source of Support: NIH award 1P01HL103455–01, the University of Pittsburgh, the University of Texas at San Antonio’s Department of Biomedical Engineering, and the University of Texas System Board of Regents Science and Technology Acquisition and Retention (STARS) program. The use of ANSYS Fluent software was facilitated through an academic agreement with ANSYS.

Conflict of Interest: None declared.