Abstract
The isometric tetanic tension of skeletal muscle increases with temperature because attached crossbridge states bearing a relatively low force convert to those bearing a higher force. It was previously proposed that the tension-generating step(s) in the crossbridge cycle was highly endothermic and was therefore itself directly targeted by changes in temperature. However, this did not explain why a rapid rise in temperature (a temperature jump) caused a much slower rate of rise of tension than a rapid length step. This led to suggestions that the step targeted by a temperature rise is not the tension-generating step but is an extra step in the attached pathway of the crossbridge cycle, perhaps located on a parallel pathway. This enigma has been a major obstacle to a full understanding of the operation of the crossbridge cycle. We have now used a previously developed mechano-kinetic model of the crossbridge cycle in frog muscle to simulate the temperature dependence of isometric tension and shortening velocity. We allowed all five steps in the cycle to be temperature-sensitive. Models with different starting combinations of enthalpy changes and activation enthalpies for the five steps were refined by downhill simplex runs and scored by their ability to fit experimental data on the temperature dependence of isometric tension and the relationship between force and shortening velocity in frog muscle. We conclude that the first tension-generating step may be weakly endothermic and that the rise of tension with temperature is largely driven by the preceding two strongly endothermic steps of ATP hydrolysis and attachment of M.ADP.Pi to actin. The refined model gave a reasonable fit to the available experimental data and after a temperature jump the overall rate of tension rise was much slower than after a length step as observed experimentally. The findings aid our understanding of the crossbridge cycle by showing that it may not be necessary to include an additional temperature-sensitive step.
Key points
Muscle performance increases with temperature in a wide variety of animals but has been studied most fully in frogs and mammals.
While it has been previously proposed that the tension-generating step in the muscle crossbridge cycle is temperature-sensitive, this does not explain why tension increases after a rapid temperature rise much more slowly than after a length step.
We have developed a model of an unbranched crossbridge cycle that simulates the effects of temperature on the tension and force–velocity relationship of frog muscle and the tension rise after a rapid temperature rise.
We conclude that the increased tension produced by raising temperature is principally due to enhancement of the two steps before the tension-generating step.
By integrating the interpretation of several key physiological experiments, this simplifies our understanding of the crossbridge cycle and the effect of temperature on human muscle performance.
Introduction
Muscle performance improves with temperature in a wide range of animals (Rall & Woledge, 1990; James 2013). This has been investigated most fully in frogs and mammals where it is well established that isometric tetanic tension, unloaded shortening velocity and maximum power output of skeletal muscle increase with temperature (frogs: Hill, 1951; Ford et al. 1977; Edman, 1979, 1988; Rome, 1983; Renaud & Stevens, 1984; Piazzesi et al. 2003; Radzyukevich & Edman, 2004; Griffiths et al. 2002; mammals: Ranatunga, 1982, 1984, 1996; Bottinelli et al. 1996; Coupland et al. 2001; Coupland & Ranatunga, 2003; Kawai 2003). The temperature sensitivity of muscle performance tends to be high at low temperatures and to decrease closer to active body temperature but there is wide variation with endotherms exhibiting higher temperature sensitivity than ectotherms (James, 2013). In mammals the isometric tension–temperature relationship is sigmoidal with the tension reaching a plateau at physiological temperatures and the sensitivity to temperature greatest at half-maximum tension (Ranatunga, 1996; Davis, 1998; Coupland et al. 2001). As the fibre stiffness is little altered by temperature (Tsaturyan et al. 1999; Galler & Hilber, 1998; Piazzesi et al. 2003), the increase in tension with temperature is caused by the attached myosin heads (crossbridges) exerting more force, rather than by an increase in their number. It is widely accepted that the population of attached heads achieves this by a shift from a conformational state, or states, exerting low tension to a state, or states, bearing higher tension (Ranatunga, 1996; Coupland et al. 2001; Piazzesi et al. 2003; Decostre et al. 2005). What is less clear is how this comes about. There must be an endothermic step (or steps) in the crossbridge cycle that drives this change but its identity has not been unequivocally established. It has been proposed that the sigmoidal relationship could arise if the tension-generating step were itself strongly endothermic (Davis, 1998; Coupland et al. 2001; Piazzesi et al. 2003). Then raising the temperature would increase the equilibrium constant of this step favouring the state with a higher tension, while lowering the temperature would favour the precursor state with a lower tension.
Despite its attractive simplicity, there are difficulties with that suggestion. First, the tension-generating step is not the only step in the cycle that is temperature-sensitive. It is known that the hydrolysis step M.ATP = M.ADP is strongly endothermic in mammalian muscle (ΔH∼120 kJ mol−1) (Xu et al. 2003) and the attachment of M.ADP.Pi to actin is also highly temperature-sensitive (White & Taylor, 1976). As the entire cycle is exothermic (ΔH ∼ −48 kJ mol−1) (Woledge et al. 1985), at least one other step must be markedly exothermic. It seems likely that other steps would have a positive or negative enthalpy change so that changing temperature would alter the kinetics of several steps to varying degrees. Promoting endothermic steps before the tensing step or inhibiting exothermic steps after the tensing step would both tend to raise tension. [For brevity and to emphasise the distinction between tension generation and lever arm swing, we abbreviate tension-generating step to tensing step.]
A second issue is that the rate of early tension recovery after a length step, which is thought to reflect the operation of the tensing step, is only moderately sensitive to temperature with a Q10 of 1.85 corresponding to an activation enthalpy, ΔH‡, of only ∼42 kJ mol−1 (Ford et al. 1977).
A third and major problem is that in response to a temperature jump (T-jump), the tension rises to the value expected of the higher temperature but the overall rate of rise is more than an order of magnitude lower than the rate of rise of tension after a small length release (Goldman et al. 1987; Bershitsky & Tsaturyan, 1992, 2002; Davis & Harrington, 1993; Ranatunga, 1996, 1999; Coupland & Ranatunga, 2003; Davis & Epstein, 2003; Ferenczi et al. 2005). As a tensing step is necessarily strongly strain-sensitive, the application of Le Chatelier's principle indicates that it must be the primary target of a length release. It therefore seemed likely that a T-jump principally targets a different step in the attached pathway of the cycle but the identity and location of that step have been controversial (Huxley, 2000; Ferenczi et al. 2005; Woledge et al. 2009). Resolution of this puzzle is urgent if a broad consensus is to be achieved on the mechanism of the crossbridge cycle. Previous suggestions include the proposal that the attached pathway of the crossbridge cycle is branched and a T-jump targets a step in a parallel pathway from that in which the tensing step is located (Huxley, 2000; Woledge et al. 2009) or a step sequential to the tensing step in the attached pathway. These proposals, however, would add considerable complexity to the crossbridge cycle and it is desirable that simpler mechanisms are fully investigated.
Here we propose a simpler explanation that does not require a branched pathway or the introduction of a new step in the attached pathway. We suggest that the tensing step perturbed by a length step is only weakly endothermic and instead a T-jump primarily targets the two strongly endothermic steps that precede it: ATP hydrolysis and the subsequent attachment of M.ADP.Pi to actin. That would cause a rise in occupancy of the M.ADP.Pi and AM.ADP.Pi states, thus shifting the equilibrium of the tensing step towards the higher tension product by a mass action effect.
Huxley & Simmons (1971) and Huxley & Tideswell (1996) were able to explain the tension transients after rapid length steps with models having two tensing steps in the attached pathway of the crossbridge cycle. Following this precedent, we recently refined a model of the full crossbridge cycle having two tensing steps that was able to account for the force–velocity relationship as well as the tension response to length steps of frog (Rana temporaria) muscle at 2°C (Offer & Ranatunga, 2013). Remarkably, the stroke distances for the two tensing steps (5.6 and 4.6 nm) found for our model were identical to those reported by Huxley & Tideswell (1996). In this paper we have used our model to investigate the effect of temperature and T-jumps on tension and shortening velocity, thereby testing the plausibility of our alternative proposal.
Methods
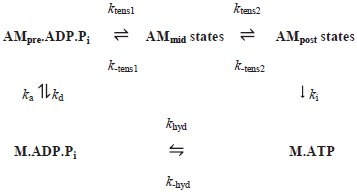
The model we developed for frog (Rana temporaria) anterior tibialis muscle has been fully described (Offer & Ranatunga, 2013). The crossbridge cycle in that model had five steps and tension was generated in two of them. We used the same rate constants for each step in the crossbridge cycle in solution as used in that paper. The exception was the forward rate constant khyd of the ATP hydrolysis step. Alterations in this parameter made little difference to fitting of the experimental data in our previous work but was likely to affect the temperature sensitivity of force and velocity; this parameter was therefore allowed to vary in the current modelling. The rate constants of the steps were then combined with the crossbridge and filament stiffness, the stroke distances for the two tensing steps and the strain dependencies of the steps to define the rate and equilibrium constants for each step in the crossbridge cycle in active muscle. For simplicity, we used the version of the previous model in which the filament compliance was Hookean.
The additional parameters we required in this paper to define the temperature dependence of muscle performance were the enthalpy change (ΔH) and activation enthalpy (ΔH‡) of the forward reaction of each of the five steps. The activation enthalpy of each reverse reaction is then given by their difference. We initially constrained the range of these parameters so that the activation enthalpies of both forward and reverse reactions, ΔH‡ and (ΔH‡–ΔH), were positive, but later allowed them to be negative. While the activation enthalpies of elementary chemical reactions are usually positive, the activation enthalpy for the folding of polypeptide chains is negative (Oliveberg et al. 1995) and this may also be the case for large-scale protein conformational changes where the exposure of hydrophobic groups to water alters. In addition, each of the five steps in our model may well be composite and involve more than one sub-step. If, for example, a step consisted of one sub-step that was a fast equilibrium (equilibrium constant K) followed by a slower sub-step with rate constant k then the overall rate constant would be given by Kk. If the first sub-step were substantially exothermic so that K diminished with a rise of temperature, the overall rate of the step could decrease with temperature. The rate constant kT at absolute temperature T for a step in the cycle for actomyosin in solution is related to the rate constant k275 at 2°C (275 K) by the van't Hoff relation
An important constraint is that the total enthalpy change round the cycle should simply be that for the hydrolysis of ATP to ADP + Pi, which is known to be exothermic (−48 kJ mol−1; Woledge et al. 1985).
Ford et al. (1977) found that the rate of tension rise after a length release had a Q10 of 1.85, corresponding to an activation enthalpy of 42 kJ mol−1. So assuming that this tension rise was caused principally by the first tensing step, we initially constrained the modelling so that the activation enthalpy of this step, 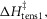 was constant at 42 kJ mol−1.
was constant at 42 kJ mol−1.
The assumptions made in the model were: (i) the enthalpy changes and activation enthalpies of all steps were constant and independent of temperature; (ii) all crossbridges are active at all temperatures; and (iii) temperature directly affects the kinetics of the steps of the crossbridge cycle in solution but not indirectly by affecting the strain dependence of the steps or the stroke distances, or the stiffness of crossbridges and filaments, or the pH, or the Pi and ADP concentrations, or the extent of chemical modification (e.g. phosphorylation) of the muscle proteins.
The initial values of the parameters for ten separate refinements were chosen to lie at random between limits shown in Table1. The constraints applied throughout the refinements were (i) that the total enthalpy change round the cycle should be close to the experimental value of −48 kJ mol−1 and (ii) the enthalpy change for the ATP hydrolysis step, 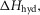 was fixed at 120 kJ mol−1, the value for mammalian myosin. In the first phase of refinement the constraints also included (iii) the total enthalpy change round the cycle should lie between −38 and −58 kJ mol−1, (iv) the activation enthalpy for the first tensing step,
was fixed at 120 kJ mol−1, the value for mammalian myosin. In the first phase of refinement the constraints also included (iii) the total enthalpy change round the cycle should lie between −38 and −58 kJ mol−1, (iv) the activation enthalpy for the first tensing step, 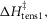 was fixed at 42 kJ mol−1, (v) the activation enthalpies for both forward and reverse steps should be positive and (vi) the rate constant of ATP hydrolysis was fixed at 100 s−1. Models were refined by repeated downhill simplex runs (Press et al. 1992). The starting simplex was created by incrementing or decrementing in turn each of the starting parameters by up to ±20 kJ mol−1, the magnitude being chosen to avoid violating the above constraints.
was fixed at 42 kJ mol−1, (v) the activation enthalpies for both forward and reverse steps should be positive and (vi) the rate constant of ATP hydrolysis was fixed at 100 s−1. Models were refined by repeated downhill simplex runs (Press et al. 1992). The starting simplex was created by incrementing or decrementing in turn each of the starting parameters by up to ±20 kJ mol−1, the magnitude being chosen to avoid violating the above constraints.
Table 1.
Upper and lower limits allowed for the parameters during the two phases of refinement
| Phase of refinement | Limits | khyd (s−1) |
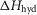 (kJ mol−1) (kJ mol−1) |
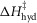 (kJ mol−1) (kJ mol−1) |
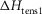 (kJ mol−1) (kJ mol−1) |
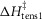 (kJ mol−1) (kJ mol−1) |
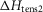 (kJ mol−1) (kJ mol−1) |
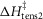 (kJ mol−1) (kJ mol−1) |
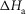 (kJ mol−1) (kJ mol−1) |
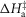 (kJ mol−1) (kJ mol−1) |
 (kJ mol−1) (kJ mol−1) |
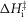 (kJ mol−1) (kJ mol−1) |
Total 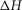 (kJ mol−1) (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lower | 100 | 120 | 110 | −80 | 42 | −150 | 5 | −150 | 5 | −150 | 5 | −58 |
| Upper | 100 | 120 | 180 | 30 | 42 | 150 | 150 | 150 | 150 | 150 | 150 | −38 | |
| 2 | Lower | 30 | 120 | −200 | −80 | 80 | −200 | −200 | −200 | 150 | −200 | −200 | −68 |
| Upper | 150 | 120 | 200 | 30 | 80 | 200 | 200 | 200 | 150 | 200 | 200 | −28 |
Each model was scored first by determining the isometric tension (normalised to that at 2°C) at 25 different temperatures. The temperatures chosen lay in the range −0.5 to 24°C as in experimental data from the anterior tibialis muscle of Rana temporaria (Ford et al. 1977; Edman, 1979, 1988; Radzyukevich & Edman, 2004; Griffiths et al. 2002). The P0 score for each model was defined as the root mean square deviation (r.m.s.) between the normalised isometric tensions of the model and the experimental values. Second, we determined the force–velocity (PV) relationship at 1.8 and 11°C for ten approximately equally spaced velocities chosen from the data which Edman (1988) had published. The procedure was as described by Offer & Ranatunga (2013). The PV score was defined as the r.m.s. deviation between the model and experimental tensions (again normalised to the isometric tension at 2°C). The total score was the sum of the P0 score and the PV score.
When this first phase of downhill simplex refinement was completed, the fit of the refined models to the experimental data of the temperature dependence of isometric tension and of the force–velocity relationship was only fair. In addition we found that the temperature dependence of the early tension recovery after length steps was only roughly half that experimentally found. Therefore, we continued the refinements in a second phase where now (vii) the activation enthalpies of the five forward steps were allowed to be negative as well as positive, (viii) the rate constant of the forward hydrolysis step was allowed to alter, (ix) the total enthalpy change round the cycle was allowed to lie between −28 and −68 kJ mol−1, (x) the activation enthalpy for the first tensing step, 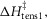 was fixed at 80 kJ mol−1 and (xi) the activation enthalpy for the attachment of M.ADP to actin was fixed at 150 kJ mol−1 (White & Taylor, 1976). (Note, however, that this reaction includes a Pi release step so this value of the activation enthalpy may be an upper limit.) The final lower and upper limits for each parameter in this second phase are also shown in Table1.
was fixed at 80 kJ mol−1 and (xi) the activation enthalpy for the attachment of M.ADP to actin was fixed at 150 kJ mol−1 (White & Taylor, 1976). (Note, however, that this reaction includes a Pi release step so this value of the activation enthalpy may be an upper limit.) The final lower and upper limits for each parameter in this second phase are also shown in Table1.
We also used the refined models to simulate the tension response of T-jumps from 2 to 7°C in 0.2 ms. The time course of the changes in tension were calculated by the procedures described in Offer & Rantunga (2013) with a time interval for the integration of the differential equations of 1 μs. To simulate the tension drop coincident with the T-jump due to thermal expansion of the filaments, we took the filaments to have a thermoelastic coefficient, α, of 4 × 10−5 per °C rise (Ranatunga, 1994).
We determined the contribution made by steps in the crossbridge cycle to the tension change after a T-jump in the following way. For a crossbridge stiffness κ, if the throughput at a particular time through a tensing step with stroke distance l were δotens, the tension contribution would be 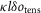 in the absence of filament compliance. If at this time the fraction of the sarcomere compliance due to crossbridges were ct, the tension contribution due to the tensing step would be reduced to
in the absence of filament compliance. If at this time the fraction of the sarcomere compliance due to crossbridges were ct, the tension contribution due to the tensing step would be reduced to 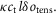 Similarly, if the throughput through an attachment step were δoatt and the average strain of those heads that participated in the throughput were
Similarly, if the throughput through an attachment step were δoatt and the average strain of those heads that participated in the throughput were 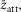 the tension contribution would be
the tension contribution would be 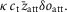 If the throughput through a detachment step were δodet and the average strain of those heads that participated in the throughput were
If the throughput through a detachment step were δodet and the average strain of those heads that participated in the throughput were 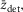 the tension contribution would be
the tension contribution would be 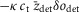 (the minus sign arising because detachment of heads with positive strain would diminish tension).
(the minus sign arising because detachment of heads with positive strain would diminish tension).
Programs were written in C and calculations made on the high performance BlueCrystal phase 3 computer at Bristol University using the OpenMP protocol for parallel programming. Fitting of exponential functions to model tension responses was made by simulated annealing followed by repeated downhill simplex runs to minimise the r.m.s. deviation between model and experimental data.
Results
Fitting the experimental tension–temperature relationship to a sigmoid plot
Figure 1 shows the temperature dependence of the experimental isometric tension for the anterior tibialis muscle of R. temporaria (Ford et al. 1977; Edman 1979, 1988; Griffiths et al. 2002; Radzyukevich & Edman, 2004). The tensions have been normalised to their value at 2°C. The experimental data are well fitted with a sigmoidal plot analogous to a logistic function. The equation used for the temperature dependence of isometric tension was that given by Coupland et al. (2001):
where P is the isometric tension at absolute temperature T, Pmax is that at high temperatures and the midpoint T0.5 is the absolute temperature at which P = Pmax/2. This equation is based on the hypothesis that in an isometric contraction a single tensing step is in equilibrium and is sensitive to temperature with an enthalpy change of ΔH. The best fit had a ΔH of 115 kJ mol−1 and a T0.5 of −1.8°C. This ΔH value is similar to that found for mammalian muscle (140 kJ mol−1; Coupland et al. 2001), although the midpoint for mammalian muscle is substantially higher at ∼10°C, consistent with the higher working temperature in mammalian muscle. The ΔH of 115 kJ mol−1 for R. temporaria is substantially higher than the ΔH value of 73 kJ mol−1 for Rana esculenta (Piazzesi et al. 2003).
Figure 1. Fitting of experimental data on the temperature dependence of isometric tension with a sigmoid plot.
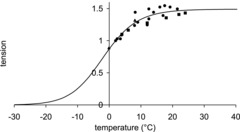
Experimental data of (▴) Ford et al. (1977), (•) Edman (1979, 1988) and Radzyukevich & Edman (2004) circles, and (▪) Griffiths et al. (2002). Continuous line: best fit to the data using the equation of Coupland et al. (2001) with ΔH = 115 kJ mol−1 and T0.5 = −1.8°C. Tensions are normalised to their value at 2ºC.
Studying the dependence of isometric tension on temperature for simple models
We made a preliminary study of the temperature dependence of isometric tension of the model by allowing only one step of the crossbridge cycle to have a non-zero enthalpy change and activation enthalpy. Making only the first tensing step endothermic (with ΔH of 120 kJ mol−1 and ΔH‡ of 140 kJ mol−1) did not give a sigmoidal tension–temperature relationship; instead the tension rose almost linearly with temperature (Fig. 2). This raises concerns about the previous explanation that the temperature dependence of isometric tension arises from a tensing step being uniquely targeted by temperature.
Figure 2. Temperature dependence of isometric tension for models with only one or two temperature-sensitive steps.
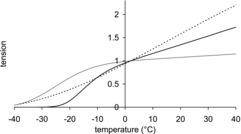
Dotted line: only the first tensing step is allowed to be temperature-sensitive. Grey line: only the hydrolysis step is allowed to be temperature-sensitive. Full line: both the hydrolysis step and the attachment of M.ADP.Pi to actin are allowed to be temperature-sensitive. In each case the temperature-sensitive steps had an enthalpy change of 120 kJ mol−1 and an activation enthalpy of 140 kJ mol−1. Tensions are normalised to their value at 2°C.
With only the hydrolysis step endothermic (with ΔH = 120 kJ mol−1 and ΔH‡ = 140 kJ mol−1) the tension–temperature plot was now sigmoidal but the mid-point of the sigmoid occurred at a much lower temperature (−20°C) than in the experimental plots (Fig. 2). Thus, a mechanism in which the ATP hydrolysis step was the only driver for the temperature-induced change also appeared unsatisfactory.
Finally we examined a model in which the hydrolysis step and the attachment step were both strongly endothermic (with ΔH = 120 kJ mol−1 and ΔH‡ = 140 kJ mol−1 for both steps), while all other steps had an enthalpy change and activation enthalpy of zero (Fig. 2). Now the plot was sigmoidal with a much higher inflection point. However, the sigmoid was not symmetrical in that the slope decreased much less rapidly at temperatures above the inflection point than at temperatures below the inflection point.
Refining the model against the experimental temperature dependence of isometric tension and force–velocity relationship
We now considered in depth models in which all the steps in the cycle could assume non-zero enthalpy changes refining by downhill simplex runs the ΔH and ΔH‡ parameters for all forward steps of the cycle. The exceptions were that the enthalpy change of the hydrolysis step and the activation enthalpy for the first tensing step were fixed. Each trial model was scored by its ability to fit the experimental tension–temperature data of Ford et al. (1977), Edman (1979, 1988), Radzyukevich & Edman (2004) and Griffiths et al. (2002) as well as the force–velocity relationship at two temperatures, 1.8 and 11°C (Edman, 1988) (see Methods).
Table1 gives the lower and upper limits allowed for the parameters in the first phase of the refinements. The enthalpy change for the attachment step (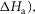 the second tensing step (
the second tensing step (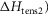 and the irreversible step (
and the irreversible step (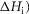 that follows were all given limits of ±150 kJ mol−1, subject to the constraint that the total ΔH around the cycle was close to −48 kJ mol−1 (Woledge et al. 1985); the range allowed was −38 to −58 kJ mol−1. The activation enthalpy for the first tensing step (
that follows were all given limits of ±150 kJ mol−1, subject to the constraint that the total ΔH around the cycle was close to −48 kJ mol−1 (Woledge et al. 1985); the range allowed was −38 to −58 kJ mol−1. The activation enthalpy for the first tensing step (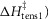 was fixed at 42 kJ mol−1. The activation enthalpy of the attachment step (
was fixed at 42 kJ mol−1. The activation enthalpy of the attachment step (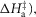 the second tensing step (
the second tensing step (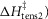 and the irreversible step (
and the irreversible step (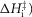 were all given a lower limit of 5 kJ mol−1 and an upper limit of 150 kJ mol−1, while the activation enthalpy of the hydrolysis step (
were all given a lower limit of 5 kJ mol−1 and an upper limit of 150 kJ mol−1, while the activation enthalpy of the hydrolysis step (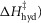 was given a lower limit of 110 kJ mol−1 and an upper limit of 180 kJ mol−1.
was given a lower limit of 110 kJ mol−1 and an upper limit of 180 kJ mol−1.
The parameters of the ten starting models were randomised within the ranges given in Table1, so a step could be endothermic in some starting models and exothermic in others. The score of a model was the sum of the r.m.s. deviation of the normalised isometric tension over a range of temperatures from the experimental data plus the r.m.s. deviation of the normalised tension for a set of velocities at two temperatures. Table2 gives the values of the parameters and scores for these ten models before (A) and after (B) this first phase of refinement. The refinement produced substantial improvements in the score. Despite the divergent character of the ten starting models, on refinement all but one of them converged to very similar models with similar scores. (The remaining model, number 2B in Table2, had a substantially poorer score.) For the models at this stage (B) of their refinement the attachment of M.ADP.Pi to actin was consistently substantially endothermic, the first tensing step was consistently weakly endothermic with a ΔH value at or close to the upper limit of its range, while the second tensing step and the irreversible step were consistently strongly exothermic with ΔH values at or near the lower end of their ranges.
Table 2.
Values of parameters and scores of the models (A) before and (B) after the first phase of refinement, and (C) after the second phase
| Model | Stage | khyd (s−1) |
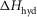 (kJ mol−1) (kJ mol−1) |
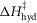 (kJ mol−1) (kJ mol−1) |
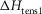 (kJ mol−1) (kJ mol−1) |
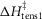 (kJ mol−1) (kJ mol−1) |
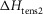 (kJ mol−1) (kJ mol−1) |
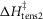 (kJ mol−1) (kJ mol−1) |
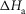 (kJ mol−1) (kJ mol−1) |
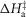 (kJ mol−1) (kJ mol−1) |
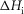 (kJ mol−1) (kJ mol−1) |
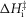 (kJ mol−1) (kJ mol−1) |
Total  (kJ mol−1) (kJ mol−1) |
P0 score | PV score | Total score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 100 | 120 | 134 | −2.0 | 42 | −19.1 | 50.1 | −56.5 | 69.1 | −90.6 | 89.0 | −48 | 0.35834 | 0.10663 | 0.46497 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 109 | 114 | −148 | 53.8 | −38 | 0.11400 | 0.06587 | 0.17987 | |
| C | 61.9 | 120 | 85.4 | 30.0 | 80 | −135 | −73.6 | 154 | 150 | −198 | 62.8 | −28 | 0.09511 | 0.05561 | 0.15072 | |
| 2 | A | 100 | 120 | 153 | −51.2 | 42 | −59.8 | 65.0 | −39.3 | 97.0 | −8.8 | 95.9 | −39 | 0.45282 | 0.13496 | 0.58778 |
| B | 100 | 120 | 168 | 23.7 | 42 | −150 | 57.8 | 80.6 | 85.6 | −132 | 49.7 | −57 | 0.14576 | 0.06950 | 0.21525 | |
| C | 62.8 | 120 | 54.6 | 30.0 | 80 | −134 | −25.4 | 155 | 150 | −199 | 56.6 | −28 | 0.09661 | 0.05310 | 0.14963 | |
| 3 | A | 100 | 120 | 142 | −22.0 | 42 | −48.6 | 89.2 | 11.7 | 106 | −103 | 96.5 | −42 | 0.33004 | 0.14005 | 0.47009 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.1 | 108 | 113 | −149 | 54.0 | −41 | 0.11489 | 0.06533 | 0.18022 | |
| C | 62.7 | 120 | 53.1 | 30.0 | 80 | −134 | −22.6 | 154 | 150 | −200 | 55.8 | −29 | 0.09673 | 0.05290 | 0.14963 | |
| 4 | A | 100 | 120 | 147 | −57.0 | 42 | −17.7 | 126 | −52.2 | 123 | −38.9 | 110 | −46 | 0.48617 | 0.17604 | 0.66220 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 110 | 115 | −149 | 54.1 | −39 | 0.11369 | 0.06608 | 0.17976 | |
| C | 62.4 | 120 | 48.6 | 29.8 | 80 | −135 | −8.1 | 156 | 150 | −200 | 53.9 | −28 | 0.09695 | 0.05251 | 0.14946 | |
| 5 | A | 100 | 120 | 138 | −50.7 | 42 | 14.4 | 33.9 | −31.4 | 73.9 | −99.5 | 117 | −47 | 0.45225 | 0.12948 | 0.58173 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 111 | 117 | −150 | 54.0 | −39 | 0.11272 | 0.06684 | 0.17956 | |
| C | 63.5 | 120 | 65.0 | 30.0 | 80 | −136 | −43.2 | 156 | 150 | −199 | 58.7 | −28 | 0.09612 | 0.05392 | 0.15004 | |
| 6 | A | 100 | 120 | 142 | 0.1 | 42 | −58.8 | 63.5 | 2.8 | 105 | −104 | 83.6 | −40 | 0.27687 | 0.12105 | 0.39792 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 110 | 115 | −150 | 54.0 | −40 | 0.11368 | 0.06607 | 0.17974 | |
| C | 63.9 | 120 | 54.1 | 30.0 | 80 | −136 | −27.5 | 157 | 150 | −199 | 56.8 | −28 | 0.09653 | 0.05322 | 0.14975 | |
| 7 | A | 100 | 120 | 148 | 6.7 | 42 | −88.0 | 6.1 | −9.6 | 15.7 | −74.6 | 101 | −46 | 0.29335 | 0.11507 | 0.40842 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 111 | 116 | −150 | 53.8 | −39 | 0.11294 | 0.06658 | 0.17952 | |
| C | 61.5 | 120 | 56.6 | 30.0 | 80 | −139 | −24.9 | 155 | 150 | −195 | 55.9 | −28 | 0.09648 | 0.05324 | 0.14972 | |
| 8 | A | 100 | 120 | 127 | −47.9 | 42 | −36.2 | 46.7 | −11.6 | 16.2 | −70.2 | 36.9 | −46 | 0.43102 | 0.13006 | 0.56108 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.1 | 111 | 116 | −149 | 53.7 | −38 | 0.11300 | 0.06653 | 0.17953 | |
| C | 64.8 | 120 | 49.9 | 30.0 | 80 | −132 | −20.3 | 156 | 150 | −200 | 55.9 | −28 | 0.09679 | 0.05285 | 0.14964 | |
| 9 | A | 100 | 120 | 147 | −31.0 | 42 | −31.8 | 54.8 | −17.9 | 105 | −86.7 | 123 | −47 | 0.38330 | 0.13773 | 0.52103 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.0 | 111 | 117 | −150 | 53.9 | −38 | 0.11269 | 0.06672 | 0.17941 | |
| C | 64.0 | 120 | 66.2 | 30.0 | 80 | −135 | −51.5 | 156 | 150 | −200 | 60.0 | −28 | 0.09590 | 0.05434 | 0.15024 | |
| 10 | A | 100 | 120 | 148 | 1.2 | 42 | −23.6 | 64.5 | −50.6 | 56.3 | −87.8 | 67.4 | −41 | 0.34588 | 0.08874 | 0.43462 |
| B | 100 | 120 | 125 | 30.0 | 42 | −150 | 5.1 | 104 | 109 | −148 | 54.1 | −44 | 0.11716 | 0.06401 | 0.18118 | |
| C | 63.0 | 120 | 56.6 | 30.0 | 80 | −136 | −28.9 | 156 | 150 | −198 | 57.1 | −28 | 0.09648 | 0.05332 | 0.14980 |
In the second phase of the refinement the range allowed for the total ΔH around the cycle was increased to −28 to −68 kJ mol−1, activation enthalpies were allowed to be negative, the rate constant for ATP hydrolysis was allowed to vary, the activation enthalpy of the first tensing step was now fixed at 80 kJ mol−1 and the activation enthalpy of the attachment of M.ADP.Pi to actin was fixed at 150 kJ mol−1. This second phase produced further improvement in the scores (stage C). Substantial convergence of all ten models was observed, the only significant variation being in the activation enthalpy for the second tensing step. The refined model 4C, which by a small margin had the lowest score, was used for further analysis; henceforth it will simply be called ‘the model’.
Effect of temperature on isometric tension of model
Figure 3 compares the tension–temperature relationship for this model with the experimental data. The plot for the model was sigmoidal but at high temperatures a plateau was not reached and the tension still increased slowly with temperature. In this respect it resembled a Gomperz sigmoid and contrasted with the symmetrical sigmoid plot predicted by the Coupland et al. (2001) equation. At ∼−3°C the tension for the model sigmoidal plot was half that at 24°C while the inflection point occurred at ∼−10°C. The model plot was straddled by the experimental data at the lower and higher temperatures but tended to give lower tensions than the experimental data at intermediate temperatures. The scatter in the experimental data makes it hard to determine whether there is a true plateau in the temperature range studied. It is noteworthy that the experimental data for the edible frog, R. esculenta, shows little sign of a plateau of tension being reached at temperatures up to 24°C (Piazzesi et al. 2003; Woledge et al. 2009).
Figure 3. Temperature dependence of isometric tension of model.
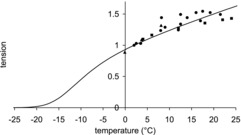
Continuous line: model tension. Experimental data of (▴) Ford et al. (1977), (•) Edman (1979, 1988) and Radzyukevich & Edman (2004), and (▪) Griffiths et al. (2002). Tensions are normalised to their value at 2°C.
Effect of temperature on occupancies
Figure 4A shows for the model how the occupancies of the attached states in an isometric contraction depend on temperature. Due to the strongly endothermic character of the hydrolysis step, as the temperature rises, the occupancy of M.ADP.Pi rises, while that of M.ATP falls. This rise in occupancy of M.ADP.Pi causes a small increase in the total occupancy of attached heads in our model; it rose from 0.525 to 0.650 as the temperature rises from 0 to 22°C. The occupancy of the mid-tensing state increased from 0.204 to 0.306 for this rise of temperature. The occupancy of the pre-tensing state also increased but to a much smaller extent, from 0.319 to 0.342. The occupancy of the post-tensing state remained very low, decreasing slightly from 0.0023 to 0.0021.
Figure 4. Temperature dependence of occupancies of attached states, their tension contributions and half-sarcomere stiffness.
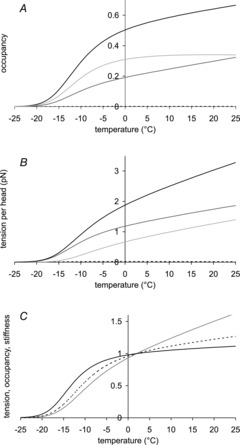
A, temperature dependence of occupancies of attached states. Occupancy of pre-tensing heads light grey, mid-tensing heads mid-grey, post-tensing heads dotted, total attached heads black. B, temperature dependence of tension contributions by attached states: pre-tensing heads light grey, mid-tensing heads mid-grey, post-tensing heads dotted, total tension of all attached heads black. C, temperature dependence of total tension (light grey), occupancy of attached heads (dotted) and half-sarcomere stiffness (black), all normalised to their values at 2°C.
For this rise in temperature the isometric tension increased from 2.02 to 3.13 pN per head. The pre- and mid-tensing states contributed about equally to this increase, 52.6% of this coming from the pre-tensing heads and 48.1% from the mid-tensing heads (Fig. 4B). The small tension contribution of the post-tensing heads fell at the higher temperature. It could be questioned why despite the substantial rise in the occupancy of the mid-tensing heads and the much smaller rise in the occupancy of the pre-tensing heads, both make similar contributions to the increase in tension. The reason is that while the average strain in the mid-tensing heads is relatively insensitive to temperature decreasing from 3.62 nm at 2°C to 3.44 nm at 22°C, the average strain in the pre-tensing heads rose substantially from 1.37 to 2.28 nm. This arises because the pre-tensing heads executing the tensing step tend to be those with the more negative strain.
The total occupancy of attached heads rises only slightly at temperatures greater than 0°C and falls relatively slightly at temperatures lower than 0°C down to −5°C. Using the value of c (the fraction of the half-sarcomere compliance due to crossbridges) at 2°C of 0.483, the effect of temperature on the half-sarcomere stiffness can be calculated for the model from 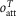 , the occupancy of attached heads at temperature T and
, the occupancy of attached heads at temperature T and 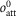 , the occupancy of attached heads at the reference temperature of 2°C:
, the occupancy of attached heads at the reference temperature of 2°C:
where 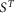 is the half-sarcomere stiffness at temperature T and S0 is that at 2°C. So as temperature is raised, the fractional increase in half-sarcomere stiffness is approximately half the fractional change in the occupancy of attached heads provided that this is small. Half-sarcomere stiffness of the model is therefore relatively insensitive to temperature compared with tension (Fig. 4C). For example, the stiffness of the model increases by only 6% for a rise in temperature from 2 to 12°C.
is the half-sarcomere stiffness at temperature T and S0 is that at 2°C. So as temperature is raised, the fractional increase in half-sarcomere stiffness is approximately half the fractional change in the occupancy of attached heads provided that this is small. Half-sarcomere stiffness of the model is therefore relatively insensitive to temperature compared with tension (Fig. 4C). For example, the stiffness of the model increases by only 6% for a rise in temperature from 2 to 12°C.
Effect of temperature on ATPase
Figure 5 compares the temperature dependences of the isometric tension and ATPase of the model both normalised to their values at 2°C. Importantly, the ATPase is much more sensitive to temperature than the tension. As found experimentally (White & Taylor, 1976; Rall & Woledge, 1990), the ATPase increased steeply with temperature with a Q10 for the range 2–12°C of 2.7.
Figure 5. Comparison of temperature dependence of isometric tension and ATPase for the model.
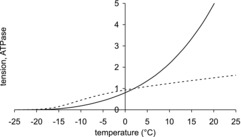
Isometric tension, dotted line; ATPase, continuous line. Both tension and ATPase are normalised to their value at 2°C.
Effect of temperature on the force–velocity relationship
Figure 6 compares the force–velocity relationship at two temperatures (1.8 and 11°C) of the model with the experimental data of Edman (1988) for the anterior tibialis muscle of R. temporaria. The unloaded shortening velocity vmax of the model was similar to the experimental value at both temperatures; raising the temperature from 1.8 to 11°C doubled the value of vmax for the model. This rise in temperature increased the isometric tension for the model by a factor of 1.27 compared with the experimental value of 1.20. The curvature of the plots for the model were, however, less than for the experimental data, particularly at the higher temperature as found in mammalian muscle experiments (Ranatunga, 1984).
Figure 6. Force–velocity relationship for the model at two temperatures.
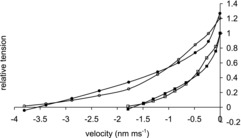
Force velocity relation of model at 1.8°C (▪) and at 11°C (•). Experimental force–velocity relationship of Edman (1988) at 1.8°C (□) and at 11°C (○). Tensions are normalised to the isometric tension at 2°C.
Modelling the time course of the rise of tension after a T-jump
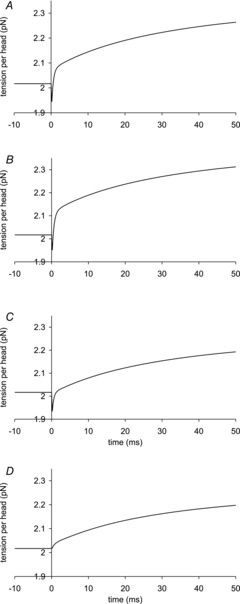
A crucial test for the model was whether it could explain the tension response of muscle to a T-jump. Figure 7A shows a simulation of the early time course of the tension transients of the model before and after a T-jump from 2 to 7°C; Fig. 8A shows the full time course after the T-jump. It is well established that the filaments behave thermoelastically and their rest length increases instantaneously as the temperature rises, causing the tension to drop (Goldman et al. 1987; Davis & Harrington, 1993). Assuming that the filaments have a thermoelastic coefficient, α, of 4 × 10−5 per °C rise (Ranatunga, 1994), this caused the tension in our simulation to fall by 2.1% concurrently with the T-jump (Fig. 7A). This tension fall was immediately followed by a very fast early tension rise with a rate of 2200 s−1; this resembles the τ1 component of the experimental tension response (Goldman et al. 1987; Davis & Harrington, 1993). This is explained by the thermoelastic expansion of the filaments causing the strain on the attached crossbridges to become more negative, thereby accelerating the first tensing step in a similar way to that in the tension response to a length release (Goldman et al. 1987).
Figure 7. Early time course of tension transients by the model responding to a T-jump.
The T-jumps from 2 to 7°C started at zero time and lasted 0.2 ms. A, unaltered model (α kept at 4 × 10−5 per °C rise and ΔHtens1 kept at 29.8 kJ mol−1); B, model with α kept at 4 × 10−5 per °C rise but ΔHtens1 raised to 50 kJ mol−1; C, model with α kept at 4 × 10−5 per °C rise but ΔHtens1 lowered to 0 kJ mol−1; D, for the model with α, ΔHtens1 and 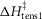 all lowered to zero.
all lowered to zero.
Figure 8. Fitting with three exponential functions of the time course of the tension transient by the model after the end of a T-jump.
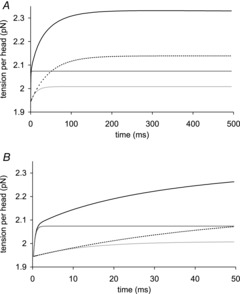
A, long time course over 500 ms; B, early time course over 50 ms. The T-jump from 2 to 7°C started at zero time and lasted 0.2 ms. The tension is shown only after the end of this T-jump. Model tension, black line; phase 1 tension, dark grey line; phase 2 tension, light grey line; phase 3 tension, dotted line. The fitted line with three exponentials coincides with the model tension at this resolution.
This very fast early recovery raised the tension to slightly above the starting tension at ∼1 ms, after which the tension rise slowed. The full tension recovery after the instantaneous tension fall was well fitted by three exponentials with rates of 2200, 68 and 21 s−1 with amplitudes of 0.13, 0.074 and 0.18 pN per head, respectively, or relative amplitudes of 0.34, 0.19 and 0.47 (Fig. 8). After 500–1000 ms the tension reached the steady state value appropriate for the higher temperature, as is found experimentally (Coupland & Ranatunga, 2003).
Figure 7B shows the early time course of a simulation where the ΔH value for the first tensing step was increased to 50 kJ mol−1 without any change in the other parameters. This resulted in the amplitude of the fast early tension rise increasing. Figure 7C shows the early time course if instead the ΔH value for the first tensing step was lowered to 0 kJ mol−1 so that a rise in temperature would not shift the equilibrium of the first tensing step. This reduction in ΔH of the first tensing step caused a reduction in the amplitude of the fast early tension recovery, which now finished when the tension had regained its starting value; this resembles the experimental observation. In Fig. 7D the thermoelastic constant α, ΔH and ΔH‡ of the first tensing step were all reduced to zero. This means that the rise in temperature causes no thermoelastic expansion and does not alter the forward and reverse rate constants of the first tensing step. Consequently, there was now no drop in tension concurrent with the T-jump and the amplitude of the fast early tension rise was significantly reduced although there was still no lag before the rise in tension. We conclude that the fast early tension rise caused by acceleration of the first tensing step arises from two effects: (a) increasing negative strain on the crossbridges arising from the thermoelastic effect and (b) a direct effect of the raised temperature increasing to a small extent the equilibrium constant and forward rate constant of the first tensing step.
Time course of throughputs through the steps in the crossbridge cycle after a T-jump
To understand the events produced by the T-jump, it was helpful to follow the time course of the number of myosin heads passing through each step in the crossbridge cycle. We define the throughput through a step at a particular time as the fraction of the total heads that have passed through that step in the forward direction since the start of the T-jump, minus the fraction that have passed in the reverse direction. The incremental throughput through a step is defined as the throughput in excess of the value that would have occurred over the same time without the T-jump. Figure 9A and B shows the long and early time courses of the incremental throughputs for steps for the model after a T-jump from 2 to 7°C. Corresponding to the initial rapid tension rise immediately following the T-jump, there is a rapid early burst of throughput thro-ugh the first tensing step lasting ∼1 ms continuing with a slower second burst; by ∼300 ms the incremental rate (the slope of the plot) nears the steady state value appropriate for the final temperature. The early burst through the first tensing step is followed successively by bursts in the incremental throughputs through the hydrolysis step and then the net attachment of pre-tensing heads. The incremental throughputs through the second tensing step and detachment of post-tensing heads which follow are nearly identical and show only a minimal burst. After ∼1000 ms the rates of all five steps become equal again as the new steady state at the higher temperature is gained.
Figure 9. Time course of incremental throughputs through steps and their contributions to tension in response to a T-jump.
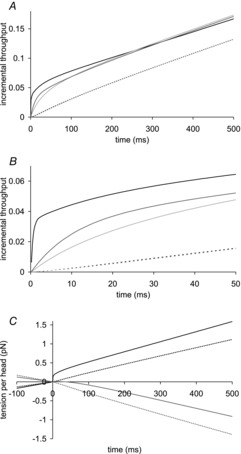
A, long time course of incremental throughputs through steps over 500 ms; B, early time course over 50 ms. Incremental throughput through first tensing step, black line; through hydrolysis step, dark grey line; through attachment of pre-tensing heads, light grey line; through second tensing step and detachment of post-tensing heads; dotted black and dotted light grey lines (these two time courses nearly coincide). C, long time course of tension contributions before and after the T-jump by: first tensing step, black line; by second tensing step, black dotted line; by attachment of pre-tensing heads, light grey line; by detachment of post-tensing heads, dotted light grey line.
The time courses of the incremental throughputs through each step were well fitted by the sum of two exponentials plus the linear incremental throughput when the new steady state had been reached. For the first tensing step, the rates of the two exponentials were 2100 and 46 s−1 with amplitudes (the fraction of all the heads that pass through the step) of 0.028 and 0.021, respectively. For the second tensing step, the rates of the two exponentials were 161 and 8 s−1 with amplitudes of −0.001 and 0.016, respectively. For the net attachment of pre-tensing heads the rates of the two exponentials were 65 and 13 s−1 with amplitudes of 0.021 and 0.034 heads, respectively. For the detachment of post-tensing heads the rates were 120 and 8 s−1 with amplitudes −0.002 and 0.017, respectively. For the hydrolysis step the rates of the two exponentials were 99 and 9 s−1 with amplitudes of 0.033 and 0.019, respectively. We conclude that in the very fast initial phase (τ1) of tension rise the only significantly increased throughput is that through the first tensing step. In the fast phase of tension rise (τ2), there is increased throughput through the hydrolysis step, the net attachment of pre-tensing heads and the first tensing step. And in the slow phase of tension rise (τ3) there is increased throughput through the hydrolysis step, the net attachment of pre-tensing heads and the second tensing step.
Time course of tension contributions to tension gains and losses after a T-jump
Figure 9C shows the time course of the contributions to tension change made by throughputs through the steps. Before the T-jump, when the muscle is in an isometric steady state, the tension is constant and so the contributions to changes in tension made by the steps other than the hydrolysis step must sum to zero. The sum of the rates of tension production by the two tensing steps must exactly equal the sum of the rates of tension loss by the net attachment of pre-tensing heads and the detachment of post-tensing heads. In the first ∼2 ms after the T-jump there is a rapid burst of tension production by the increased throughput through the first tensing step. The rate of tension production by the first tensing step then slows until at ∼100 ms it approaches its steady state level. In contrast, the rate of tension production by the second tensing step is only minimally changed; it increases slightly immediately after the T-jump and then only slightly decreases to reach its steady state level. The rate of tension loss by the detachment of post-tensing steps similarly shows only a minimal burst increasing immediately after the T-jump and then only slightly decreasing towards its steady state level. The tension production by the net attachment of pre-tensing heads shows a more complex time course; the loss of tension occurring before the T-jump is initially reversed so for the first 35 ms this step contributes slightly to positive tension production; afterwards the tension loss resumes, reaching the steady state rate at ∼120 ms. So the sum of the tension produced by the steps of the crossbridge cycle shows a rapid burst in the first ∼2 ms and then over the next ∼100 ms a slower rise of tension caused mainly by transients in the tension production of the first tensing step and the attachment/detachment of pre-tensing heads. After 500–1000 ms when all four steps approach their steady state level, the sum of the tension productions by the steps reaches a plateau, and the rate of tension production becomes zero again as is appropriate for an isometric state.
The time courses of the contributions made by each step to the change in tension were well fitted with two exponential functions plus a linear tension contribution appropriate for the final steady state at the higher temperature. For the first tensing step, the rates of the two exponentials were 2100 and 49 s−1 with amplitudes of 0.13 and 0.091 pN per head, respectively. For the second tensing step, the rates of the two exponentials were 200 and 8 s−1 with amplitudes of −0.003 and 0.057 pN per head, respectively. For the net attachment of pre-tensing heads the rates of the two exponentials were 32 and 15 s−1 with amplitudes of 0.051 and 0.10 pN per head, respectively. Finally, for the detachment of post-tensing heads the rates of the two exponentials were 120 and 8 s−1 with amplitudes of 0.007 and −0.081 pN per head, respectively.
Thus, for the model the only process producing the first (τ1) phase of the tension rise is the first tensing step. The processes producing the second (τ2) phase of tension rise are the first tensing step with a smaller contribution from the net attachment of pre-tensing heads, while the processes producing the third (τ3) phase of tension rise are the net attachment of pre-tensing heads with a smaller contribution from the second tensing step.
Simulation of tension transients after a length step at several temperatures
A final test of the model was whether it could account for the temperature dependence of the rate of the early tension recovery after length steps (Ford et al. 1977). To follow this dependence, Ford et al. (1977) plotted the time course of 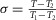 , where T1 is the tension at the end of the length step, T2 is the tension at the end of the early tension recovery and T is the tension at any intermediate time. From the context, it appears likely that they compared the times to reach a value of σ = 0.5 for the three tempe-ratures. They concluded that the rate of early tension recovery increased with a Q10 of 1.85 after the releases and with a slightly higher Q10 (2.0–2.5) after the stretches.
, where T1 is the tension at the end of the length step, T2 is the tension at the end of the early tension recovery and T is the tension at any intermediate time. From the context, it appears likely that they compared the times to reach a value of σ = 0.5 for the three tempe-ratures. They concluded that the rate of early tension recovery increased with a Q10 of 1.85 after the releases and with a slightly higher Q10 (2.0–2.5) after the stretches.
In Fig. 10A we show the time course of σ for our model after releases of 4.5 nm hs−1 at the three temperatures. The increase in rate of the early tension recovery at 8.1°C compared with the rate at −0.1°C has a small dependence on σ, being nearly constant for σ > 0.4 but declining at low σ. For σ = 0.5 the rate is 1.76 times faster at 8.1°C than at −0.1°C; for the experimental data (Ford et al. 1977) the factor was 1.89. Plots of the time course of σ for the model in response to stretches of 1.5 nm hs−1 at the three temperatures are shown in Fig. 10B. As with the releases, the rate of early tension recovery increases with temperature. The increase in rate is nearly constant for σ > 0.2 but declined at lower σ. For σ = 0.5 the increase in rate at 8.1°C compared with that at −0.1°C, 2.12, was higher than for the releases; the factor for the experimental data was 1.81.
Figure 10. Time courses of sigma for model after rapid length steps.
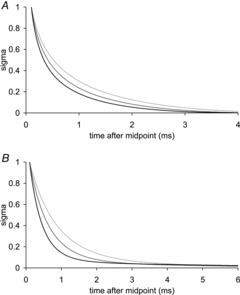
A, after a 4.5 nm hs−1 release; B, after a 1.5 nm hs−1 stretch at three temperatures: −0.1°C (light grey), 3.7°C (mid grey) and 8.1°C (black).
Discussion
We have shown that a model of the crossbridge cycle, in which the ATP hydrolysis step and the attachment of M.ADP.Pi to actin are both strongly endothermic while the first tensing step is only weakly endothermic, can account for the experimental data on the temperature dependence of isometric tension and shortening velocity in frog muscle. The implication is that a rise in temperature stimulates the first tensing step directly only to a small extent and primarily increases tension indirectly by accelerating the formation of AM.ADP.Pi and thus increasing the rate of the first tensing step by a mass action effect.
Tension response of model to a T-jump
A key test of the model was to explore whether it could explain why the tension rise in response to a T-jump in isometric muscle is much slower than after a length release. After the initial very fast fall in tension due to thermoelastic expansion of the filaments, our model showed a triexponential tension rise to its final level. The three exponential functions (τ1, τ2 and τ3) had rates of 2200, 78 and 22 s−1 and relative amplitudes of 0.33, 0.16 and 0.50, respectively. These values compare with experimental data from frog semitendinosus muscle at a final temperature of 3.5°C where the tension recovery was fitted with three exponentials with similar rates to these of 1840, 94 s−1 and 8.5 s−1 and with relative amplitudes of 0.19, 0.51 and 0.30, respectively (Davis & Harrington, 1993). At a final temperature of 13.5°C the rates of τ2 and τ3 were 302 and 9.7 s−1, respectively, with the amplitude of τ3 now greater than that of τ2. For rabbit muscle fast fibres at 12°C at a low Pi concentration the rates of τ2 and τ3 were 66 and 9 s−1, respectively, with the amplitude of τ3 again greater than that of τ2 (Ranatunga, 1996, 1999). The rate of the τ2 phase of tension rise in both frogs and rabbits is very sensitive to temperature and is increased by Pi while the τ3 phase is less sensitive to temperature and Pi (Davis & Harrington, 1993; Ranatunga, 1996, 1999).
The fastest component (τ1) of tension rise after a T-jump for our model had a rate similar to the experimental rate of early tension recovery after a rapid length release (Ford et al. 1977) while the other two components had substantially smaller rates. Thus, much of the model tension response to a T-jump had a rate more than an order of magnitude slower than the rate after a rapid length step. If T-jumps and length steps targeted only the first tensing step, we would expect the early tension responses to be similar. As previously argued, this indicates that T-jumps target steps other than, or in addition to, the first tensing step (Goldman et al. 1987; Bershitsky & Tsaturyan, 1992, 2002; Davis & Harrington, 1993; Ranatunga, 1996, 1999; Coupland & Ranatunga, 2003; Davis & Epstein, 2003). This seems very reasonable as the high strain-sensitivity of tensing steps would make them especially sensitive targets for a length step, but as most steps in the cycle are likely to be temperature-sensitive to some degree, a T-jump would be expected to be a much less specific type of perturbation.
Modelling of the incremental throughput through the steps in the cycle in response to a T-jump shows that after the very rapid (2100 s−1) burst through the first tensing step triggered by the thermoelastic expansion, there is successively a burst through the hydrolysis step (99 s−1) appropriate for the rate constants at 7°C, followed by the net attachment of pre-tensing heads (65 s−1) and then a slower second burst (46 s−1) through the first tensing step. This supports the view that the main response to a T-jump after the initial response to the thermoelastic expansion is due to a mass action effect caused by the rise in the occupancy of M.ADP.Pi, and the increased attachment of M.ADP.Pi to actin increasing the occupancy of AM.ADP.Pi and hence the rate through the first tensing step. These two steps thus dictate the slower second burst through the first tensing step and hence the second (τ2) phase of tension rise is substantially slower than after a length release.
With this explanation it might be supposed that the tension rise after a T-jump would occur only after a lag, but a lag is not observed experimentally (Ranatunga, 1996), and in the model simulations (Fig. 7) the lag in tension rise is minimal (about 0.1 ms, the same as the lag in the incremental throughput through the hydrolysis and attachment steps, and equal to the half-time of the T-jump). Even in the simulation in Fig. 7D where the thermoelastic coefficent had been reduced to zero, and the temperature dependencies of both forward and reverse rate constants of the first tensing step in solution had been made zero, we still observed no significant lag. The explanation is that the forward and reverse rate constants in the model simulating muscle, unlike actomyosin in solution, are strain-dependent and the equations defining them have a work term that is temperature-dependent (see Offer & Ranatunga, 2013). This causes the forward rate constant to increase with temperature and the reverse rate constant to decrease even when the first tensing step in solution is temperature-insensitive. While these effects are small, the first tensing step is nearly in equilibrium at the lower temperature and the net rate is the difference between nearly equal forward and reverse rates. So the net rate of the first tensing step increases during the T-jump to a maximum before falling again. Consequently, the tension rises right from the start of the T-jump. This enhancement of the first tensing step causes the occupancy of the pre-tensing heads to fall for the first 2 ms and only after this does the mass action effect of the enhanced hydrolysis and attachment steps start raising its occupancy. So while a lag time of the order of 2 ms might have been expected before the mass action effect of the enhanced attachment step and the hydrolysis step acted to increase the net rate of the first tensing step and raise tension, this is effectively masked by the temperature rise directly stimulating the first tensing step to a small extent right from the beginning of the T-jump.
Our modelling thus not only provides a simple answer to the long-standing problem of why the rate of tension rise after a T-jump is an order of magnitude slower than the rate of tension rise after a length release, but leads us to suggest that it may not be necessary to include an extra temperature-sensitive step in the attachment pathway of the crossbridge cycle either in sequence to the tensing step or in parallel to it, or to suppose that tension generation occurs by different mechanisms after these two types of perturbation (Huxley, 2000; Ferenczi et al. 2005; Woledge et al. 2009) (see below).
Compatability with X-ray diffraction studies on muscle subject to a T-jump
Although our model is primarily mechano-kinetic rather than structural in nature, the responses of our model to a T-jump are compatible with reported X-ray diffraction data and can be rationalised in structural terms. When permeabilised frog and rabbit fibres were subject to large T-jumps, the intensity of the first actin layer line (IA1) increased and that of the 1,0 equatorial reflection (I1,0) decreased with no change in stiffness (Bershitsky et al. 1997; Tsaturyan et al. 1999; Ferenczi et al. 2005). This was attributed to a transition of some heads that were non-stereospecifically attached to actin to become stereospecifically attached at a lower radius. Our model would be compatible with these X-ray changes if the first tensing step were accompanied by this transition.
In response to a T-jump, the intensity of the M3 meridional reflection (IM3), after an initial small fall, increased with a time course similar to that of the tension rise, the increase in IA1 and decrease in I1,0 (Ferenczi et al. 2005). In contrast, a (large) length release caused IM3 to fall. It was concluded that the tension rise after a T-jump involved a different process than after a length step (Bershitsky & Tsaturyan, 2002). In this paper we draw the opposite conclusion, namely that the process principally responsible for the second phase of the tension rise after a T-jump is the first tensing step, the same process giving the early tension rise after a small length release. Knupp et al. (2009) explained the changes in IM3 occurring after length steps on the basis that before the length step the attached heads were ∼2 nm nearer the Z-line than the detached heads. A small shortening of 2 nm hs−1 would then cause the attached and detached heads to become axially in register, so they would then contribute in phase to the M3 reflection and cause IM3 to increase to a maximum. Further shortening would cause them to become increasingly out of axial alignment and IM3 would decrease again, as is experimentally found. It is therefore important to stress that whether IM3 increases or decreases after a T-jump or a length step depends critically on the amount of filament sliding that occurs. The fact that IM3 rises after the mild perturbation of a T-jump but decreases after a (large) length release does not in itself show that the tension is generated by a different process. In our paper on the temperature response to a T-jump in shortening muscle (Ranatunga et al. 2010) we also criticised the conclusion that Bershitsky & Tsaturyan (2002) had made after studying the effect of a T-jump applied soon after a length step.
Knupp et al. (2009) also concluded that the changes in IM3 were not evidence for changes in the shape of the crossbridges (e.g. swinging of the lever arm), but merely reflected filament sliding. Our modelling indicates that in response to a T-jump from 2 to 7°C, even though the fibres are held at constant length, filament sliding occurs as changes in tension cause the filament backbones to change length, thereby altering the strain on the crossbridges. Accompanying the initial instantaneous thermoelastic expansion of the filaments, the strain on the crossbridges would decrease, and in our model the filaments slid 0.15 nm hs−1 in a shortening direction accompanying the drop in tension. This would result in the attached heads moving axially closer to the detached heads, increasing IM3. As tension thereafter increased, the filaments lengthen further and cause further sliding of the filaments in a shortening direction totalling 0.6 nm hs−1 and resulting in a further rise in IM3.
Effect of Pi and ADP on isometric tension
Although we have not explicitly modelled the Pi and ADP release steps, our model is broadly compatible with experimental observations of the effect of Pi and ADP on tension and shortening velocity. Coupland et al. (2001) showed that Pi causes minimal inhibition of isometric tension at 30°C, but substantial inhibition at lower temperatures causing the sigmoidal tension–reciprocal temperature relationship to shift to higher temperatures. Their explanation of this effect of Pi can be readily adapted to our new model by taking into account that the hydrolysis and attachment steps are strongly endothermic. So by the mass action effect a temperature rise causes an increase in the occupancy of AM.ADP.Pi, thus driving the equilibrium of the first tensing step to the right. Conversely, increasing [Pi] drives this equilibrium to the left. At high temperatures the equilibrium lies sufficiently to the right that even high concentrations of Pi cannot shift it appreciably to the left. Conversely, at lower temperatures the equilibrium is more poised and Pi can exert a greater effect.
Coupland et al. (2005) showed that addition of ADP enhanced isometric tension proportionately more at low temperatures than at high temperatures, i.e. the tension–reciprocal temperature curve was shifted by ADP to lower temperatures, the opposite of the effect of Pi. Increasing temperature substantially increased the unloaded shortening velocity but ADP decreased it at all temperatures. This was explained by a scheme in which the release of ADP occurred in a two-step mechanism, a moderately slow conformational change followed by a slower release step whose rate increased with temperature. The addition of ADP causes reversal of the ADP release step thereby increasing the occupancy of the AM.ADP state and hence tension, while decreasing the occupancy of the AM state and thus slowing the rate of detachment of crossbridges and hence the shortening velocity. The same features would apply in our model. The irreversible step leading to detachment of crossbridges has a substantially positive activation enthalpy so raising the temperature would increase the rate of the irreversible step, thereby enhancing shortening velocity. Addition of ADP could again reverse the ADP release step lowering the occupancy of the AM state and thus lowering the shortening velocity, while increasing the occupancy of the AM.ADP.Pi state and thus increasing tension.
Effect of temperature on muscle performance
Different aspects of muscle performance respond very differently to temperature (Rall & Woledge, 1990; Ranatunga, 1998). The Q10 for each of these aspects is larger at low temperature than at high temperature and increases in the order isometric tension, unloaded shortening velocity (vmax), the velocity at which power output is maximal, and the power output and rate of energy liberation. In the following sections we discuss how the different temperature sensitivities of the steps in our model can explain why these aspects differ in their sensitivity to temperature change.
Isometric tension
While the isometric tension of frog muscle increases with temperature, the increase is relatively small (about 1.4 for an increase from 2 to 24°C). The analysis in the Results indicates that the increased tension is due to two main factors: (a) an increase in the number of mid-tensing heads with little change in their strain and (b) an increased strain in the pre-tensing heads with little change in their number.
vmax
The unloaded shortening velocity vmax is much more sensitive to temperature than the isometric tension. In frog fibres Edman (1988) found that a rise in temperature from 1.8 to 11°C increased vmax by a factor of 2.09 while the isometric tension was increased by a factor of only 1.21. The shape of the force–velocity relationship was relatively unaffected, so the shortening velocity was accelerated by a similar factor over a wide range of loads, unlike in mammalian muscle (Roots & Ranatunga, 2008).
Huxley (1957) reasoned that the unloaded shortening velocity would be determined by the lifetime of attached crossbridges. Siemankowski et al. (1985), Weiss et al. (2001) and Nyitrai & Geeves (2004) extended that analysis by proposing that the unloaded shortening velocity is determined by the lifetime of the attached intermediate that precedes the rate-limiting step in the attached pathway. They provided evidence that the rate-limiting step was the release of ADP, which had activation energies of 64 and 76 kJ mol−1 for rat and rabbit cardiac actomyosin, respectively. In our modelling we found that the irreversible step converting post-tensing heads to M.ATP had a similar activation enthalpy (54 kJ mol−1), consistent with the irreversible step in our model being associated with ADP release, possibly with an isomerisation step immediately preceding ADP release (Nyitrai & Geeves, 2004).
Power output
The power output of a shortening muscle is the product of its tension and shortening velocity. Both quantities increase with temperature, so it is understandable that the power output has a higher Q10 than either of them alone (Ranatunga, 1998). As the curvature of the force–velocity relationship in frog muscle is not much affected by temperature (Edman, 1988), the Q10 for the maximum power output will be the product of the Q10 for isometric tension and the Q10 for vmax.
Turnover
As discussed by Siemankowski et al. (1985), the rate-limiting step of actomyosin ATPase in solution, and probably also that of the turnover of the crossbridge cycle during unloaded shortening, is likely to be the ATP hydrolysis step. They found that the actomyosin ATPase has a high activation enthalpy (122 and 105 kJ mol−1 for rabbit and rat cardiac actomyosin, respectively). Our model had an activation enthalpy for the hydrolysis step of 120 kJ mol−1 and hence, as found experimentally (Rall & Woledge, 1990), showed a very high temperature sensitivity of the turnover (ATPase) of the crossbridge cycle with a Q10 of 2.7 in the range 2–12°C.
Fibre stiffness
Raising the concentration of Pi in mammalian fibres causes reversal of the tensing step and lowers fibre stiffness (Caremani et al. 2008). If the first tensing step were appreciably endothermic, lowering the temperature should also decrease its equilibrium constant and cause detachment of some heads, thereby lowering fibre stiffness. For mammalian muscle a wide range of temperatures can be studied and there are indications that the stiffness does indeed decrease slightly at low temperatures (Galler & Hilber, 1998). But for frog muscle fibre stiffness appears to be insensitive to temperature (Piazzesi et al. 2003). In part this may be because it is not experimentally feasible to lower the temperature appreciably below 0°C so as to produce low tensions and in part because the first tensing step is only weakly endothermic. The existence of filament compliance causes changes in occupancy of attached heads to result in smaller changes in fibre stiffness.
Comparison with previous hypotheses
The hypothesis previously proposed in which temperature primarily targets the tensing step gives an excellent fit to the temperature dependence of isometric tension, particularly in mammalian muscle, so it is important to discuss its drawbacks in addition to those mentioned in the Introduction. That hypothesis assumed that:
The targeted tensing step was in equilibrium. Our previous modelling of frog muscle (Offer & Ranatunga, 2013) indicated that the first tensing step was sufficiently fast that it was nearly in equilibrium, so this assumption seems reasonable. However, the other assumptions made are questionable.
The state before the targeted tensing step carried no force. On the contrary, our previous modelling suggested that in an isometric contraction an appreciable fraction (34%) of the force is carried by pre-tensing heads.
The state formed in the targeted tensing step had a constant force independent of temperature. The force carried by an attached head depends on its strain. Heads in one conformational state have a distribution of strain and there is no reason to suppose that this distribution will be unaltered by temperature. Our finding that in our model about half of the increase in tension with a rise in temperature is due to the increased strain in the pre-tensing heads reinforces our belief that it is not appropriate to assume that each state bears a constant force.
Only the tensing step has an appreciable temperature sensitivity. As discussed in the Introduction, it is well established that the hydrolysis step and the attachment of M.ADP.Pi to actin are both strongly endothermic and that at least one step in the cycle is strongly exothermic. The effect of temperature on these steps will undoubtedly contribute to the kinetics.
In other proposals (Huxley, 2000; Woledge et al. 2009), the fact that a T-jump elicits a much slower tension response than a length step led to the suggestion that the attached pathway of the crossbridge cycle is branched and that a T-jump targeted a temperature-sensitive step in a pathway parallel to the pathway containing the tensing step. Woledge et al. (2009) focused on the fact that although in an isometric contraction filaments do not slide, ATP is nevertheless hydrolysed. They therefore concluded: ‘Consequently, there must be a branch (or branches) in the pathway represented by the model so that the two processes can occur somewhat independently. It is an open question where these branches are to be found but it is generally understood that branches are needed.’ It is common ground that these two processes can occur somewhat independently by heads detaching without undergoing a working stroke. We think the flaw in their argument that a branch is needed is their implicit supposition that conformational transitions producing tension (tensing steps) must necessarily cause lever arm swinging and therefore filament sliding. As we have pointed out previously (Offer & Ranatunga, 2011), if the compliant element of the crossbridge is located between the motor domain and lever arm, conformational changes can occur, generating tension by straining the compliant element and storing energy in it but without necessarily causing lever arm movement. In this scenario only if the filaments slide would the lever arm of an attached head swing. If that happens the energy stored in the compliant element might be used in a purely passive process to do work, but would be entirely wasted as heat if the filaments do not slide and the head detaches. In this concept the working stroke (the swinging of the lever arm) is not tightly coupled to the conformational transition and correspondingly a branched pathway is not needed to allow the ATP hydrolysis and sliding to occur somewhat independently. We emphasise that in our model ATP is split in an isometric contraction yet our model does not have a branched pathway.
Although advocating a branched pathway containing a temperature-sensitive step, Woledge et al. (2009) did not consider that this step was tension-generating. They argued that in the crossbridge cycle each biochemical state may not be uniquely associated with a mechanical state. They proposed that the biochemical steps involving a change in chemical composition (e.g. Pi release) lie on a pathway parallel to one containing tension-generating steps. Biochemical steps would be expected to involve a change in enthalpy and hence would be directly targeted by temperature change, while tension-generating steps would be strain-sensitive and hence directly targeted by a length step. Each biochemical state could therefore exist in more than one mechanical state (conformation), and conversely each mechanical state could exist in more than one biochemical state. So although the changes in the parallel pathways would not be tightly coupled, execution of a biochemical step targeted by a temperature rise could promote the execution of a tension-generating step whose rate would depend on the local rate constants. Using a simple model with a parallel pathway, Woledge et al. (2009) were able to explain the temperature dependence of isometric tension and the difference in tension response to T-jumps and length steps in R. esculenta muscle. However, they have not produced a full model of the crossbridge cycle to enable them to simulate the effect of temperature on the force–velocity relationship. If they had and included two detached states, as is customary, the full model would have had six states, one more than our model, and seven steps, two more than ours.
In another example of a branched pathway, Huxley (2000) proposed that there were two different types of tensing steps acting in parallel pathways to explain why a T-jump produced a much slower tension rise than a length release. The slower of these (rocking of the motor domain of the myosin head about the actin–myosin interface to produce a stereospecific attachment) was sensitive to temperature, the faster (tilting of the lever arm) was insensitive. But because they were both strain-sensitive, both responded to length changes. However, Huxley did not develop this concept into a full model that could be tested against experimental data. If he had done so, and employed two detached states, the crossbridge cycle would have had six states, one more than our model, and a total of seven steps, two more than ours.
Ferenczi et al. (2005) proposed the ‘roll and lock’ mechanism in which there were two distinct tension-generating processes, a step producing stereo-specific attachment followed by a step in which the lever arm tilted. Unlike the proposal of Huxley (2000), (a) the two steps were sequential rather than being on parallel paths and (b) the roll-and-lock step converting non-stereospecifically attached to stereospecifically attached heads produced tension by axial as well as azimuthal movement of the motor domains attached to actin.
The Ferenczi et al. kinetic scheme is shown above; the layout has been altered to place the pre-tensing heads on the left and detachment of heads after tension generation on the right. The scheme has eight states and nine steps. Hydrolysis of ATP on detached myosin heads is taken to occur in two stages, an open to closed conformational change (D1 to D2) followed by the hydrolysis step itself (D2 to D3). All detached heads (D1, D2 and D3) were taken to bind actin reversibly. Detached heads D2 and D3 bind to form the pre- and post-hydrolysis attached states (N2 and N3), which were taken to have the same closed conformation. Tension is produced by the roll-and-lock transition between N3 and S1 and by tilting of the lever arm between S1 and S2. The forward and backward rate constants for the roll-and-lock transition and for the lever arm tilt were assumed to have the same temperature dependence. The ATP hydrolysis steps on actomyosin and myosin were taken to be equally fast and to have identically high enthalpy changes. The roll-and-lock transition was taken to be three times faster than the lever arm tilt but both were assumed to have zero enthalpy change so that their equilibrium constants were unaffected by changing temperature. The irreversible step consisting of the detachment of products and the subsequent binding of ATP was taken to be slow.
The merit of the Ferenczi et al. model is that it was able to explain the time course of tension and changes in IA1 and IM3 after T-jumps. To explain the slow rise in tension and IA1 after a T-jump, it was proposed that a rate-limiting temperature-sensitive ATP hydrolysis step on actomyosin (N2 to N3) precedes the roll-and-lock transition and drives the rise in tension. In an isometric contraction at low temperature most of the heads are in the open state N1 that does not bear tension. Tension is borne by a small fraction of heads in the S1 state. After the T-jump, the temperature-sensitive D1 to D2 equilibrium is shifted in favour of D2 and the fraction of heads in the D2 and N2 states increase transiently. As hydrolysis is favoured at the higher temperature, after a delay D3, N3, S1 and S2 become more populated but the total number of attached heads is unchanged. This mechanism can be compared with our model where the rise in temperature targets the two steps that precede the first tensing step, the ATP hydrolysis step on detached myosin heads and the attachment of M.ADP.Pi to actin.
Ferenczi et al. did not attempt to simulate the tension transients after a length step but implicitly assumed that their model would account for them. In contrast to our model, for any particular temperature, the rate constant of each step in their model is a constant and unaffected by strain despite the expectation that the two tensing steps would be very strain-sensitive. This absence of strain sensitivity implies that the application of their model would be restricted to cases where filament sliding does not occur because if the strain on attached heads changed from the isometric state, the crossbridge cycle would be entirely unaltered. Their model, at least in its present form, cannot therefore account either for the force–velocity relationship or for the tension transients after length steps of different sizes. Even if their model took into account the increased negative strain produced by a length release and was therefore able to explain the fall in tension during phase 1, it would provide no mechanism for the tension recovery in phase 2 as the rate constants of the two tensing steps are unaltered by the change in strain. A second problem is that the model of Ferenczi et al. assumed that non-stereospecifically attached heads bear no tension, while stereospecifically attached heads bear a constant tension. This contrasts with our model where the pre-tensing heads bear a significant fraction of the isometric tension and almost all of the tension when active muscle is lengthened. The Ferenczi et al. model would therefore not be able to explain the near-doubling of tension in lengthening muscle. A third concern with the Ferenczi et al. model is that the rate constant of ATP hydrolysis on actomyosin was taken to be the same as on myosin. This is contrary to one of the main conclusions drawn by Lymn and Taylor (1971) that ATP hydrolysis occurs on detached myosin heads, not on actomyosin. Indeed, there is experimental evidence that for rabbit at 20°C the hydrolysis step on myosin is 25-fold faster than on actomyosin (White et al. 1997).
In summary, these proposals of Huxley (2000), Ferenczi et al. (2005) and Woledge et al. (2009) suggesting that an additional temperature-sensitive step should be included in the attached pathway, possibly in a parallel pathway, merit further consideration, but because they have many states they add considerable complexity to the crossbridge cycle. It is therefore highly desirable that experiments should be devised to discriminate between them and the simpler model we are proposing here.
Glossary
- PV
force–velocity
- r.m.s.
root mean square
- T-jump
temperature jump
- hs
half-sarcomere
Additional information
Competing interests
There are no competing interests.
Author contributions
Both authors contributed to the conception and design of this research. G.W.O. wrote the programs and carried out the calculations and refinement of models. Both authors contributed to the writing of the paper. Both authors approved the final version of the manuscript. All those who qualify for authorship are listed.
Funding
Neither author was in receipt of funding for this work.
References
- Bershitsky SY. Tsaturyan AK. Tension response to Joule temperature jump in skinned rabbit muscle fibres. J Physiol. 1992;447:425–448. doi: 10.1113/jphysiol.1992.sp019010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershitsky SY. Tsaturyan AK. The elementary force generation process probed by temperature and length perturbations in muscle fibres from the rabbit. J Physiol. 2002;540:971–988. doi: 10.1113/jphysiol.2001.013483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershitsky SY, Tsaturyan AK, Bershitskaya ON, Mashanov GI, Brown P, Burns R. Ferenczi MA. Muscle force is generated by myosin heads stereospecifically attached to actin. Nature. 1997;388:186–190. doi: 10.1038/40651. [DOI] [PubMed] [Google Scholar]
- Bottinelli R, Canepari M, Pelligrino MA. Reggiani C. Force–velocity properties of human skeletal muscle fibres: myosin heavy chain isoform and temperature dependence. J Physiol. 1996;495:573–586. doi: 10.1113/jphysiol.1996.sp021617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caremani M, Dantzig J, Goldman YE, Lombardi V. Linari M. Effect of inorganic phosphate on the force and number of myosin cross-bridges during the isometric contraction of permeabilized muscle fibers from rabbit psoas. Biophys J. 2008;95:5798–5808. doi: 10.1529/biophysj.108.130435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME, Puchert E. Ranatunga KW. Temperature dependence of active tension in mammalian (rabbit psoas) muscle fibres: effect of inorganic phosphate. J Physiol. 2001;536:879–891. doi: 10.1111/j.1469-7793.2001.00879.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME, Pinniger GJ. Ranatunga KW. Endothermic force generation, temperature-jump experiments and effects of increased [MgADP] in rabbit psoas fibres. J Physiol. 2005;567:471–492. doi: 10.1113/jphysiol.2005.090084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME. Ranatunga KW. Force generation induced by rapid temperature jumps in intact mammalian (rat) skeletal muscle fibres. J Physiol. 2003;548:439–449. doi: 10.1113/jphysiol.2002.037143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JS. Force generation simplified. Insights from laser temperature-jump experiments on contracting muscle fibers. Adv Exp Med Biol. 1998;453:343–351. [PubMed] [Google Scholar]
- Davis JS. Epstein ND. Kinetic effects of fibre type on the two subcomponents of the Huxley–Simmons phase 2 in muscle. Biophys J. 2003;85:390–401. doi: 10.1016/S0006-3495(03)74483-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JS. Harrington WF. A single order–disorder transition generates tension during the Huxley–Simmons phase 2 in muscle. Biophys J. 1993;65:1886–1898. doi: 10.1016/S0006-3495(93)81259-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JS. Rodgers ME. Indirect coupling of phosphate release to de novo tension generation during muscle contraction. Proc Natl Acad Sci U S A. 1995;92:10482–10486. doi: 10.1073/pnas.92.23.10482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decostre V, Bianco P, Lombardi V. Piazzesi G. Effect of temperature on the working stroke of muscle myosin. Proc Natl Acad Sci U S A. 2005;102:13927–13932. doi: 10.1073/pnas.0506795102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman KAP. The velocity of unloaded shortening and its relation to sarcomere length and isometric force in vertebrate muscle fibres. J Physiol. 1979;291:143–159. doi: 10.1113/jphysiol.1979.sp012804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman KAP. Double hyperbolic force–velocity relation in frog muscle fibres. J Physiol. 1988;404:301–324. doi: 10.1113/jphysiol.1988.sp017291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferenczi MA, Bershitsky SY, Koubassova N, Siththanandan V, Helsby WI, Panine P, Roessie M, Narayanan T. Tsaturyan AK. The “roll and lock” mechanism of force generation in muscle. Structure. 2005;13:131–141. doi: 10.1016/j.str.2004.11.007. [DOI] [PubMed] [Google Scholar]
- Ford LE, Huxley AF. Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galler S. Hilber K. Tension/stiffness ratio of skinned rat skeletal muscle fibre types at various temperatures. Acta Physiol Scand. 1998;162:119–126. doi: 10.1046/j.1365-201X.1998.0272f.x. [DOI] [PubMed] [Google Scholar]
- Goldman YE, McCray JA. Ranatunga KW. Transient tension changes initiated by laser temperature jumps in rabbit psoas muscle fibres. J Physiol. 1987;392:71–95. doi: 10.1113/jphysiol.1987.sp016770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths PJ, Bagni MA, Colombini B, Amenitsch H, Bernstoff S, Ashley CC. Cecchi G. Changes in myosin S1 orientation and force induced by a temperature increase. Proc Natl Acad Sci U S A. 2002;99:5384–5389. doi: 10.1073/pnas.082482599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill AV. The influence of temperature on the tension developed in an isometric twitch. J Physiol. 1951;138:349–356. [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys. 1957;7:255–318. [PubMed] [Google Scholar]
- Huxley AF. Mechanics and models of the myosin motor. Philos Trans R Soc Lond B Biol Sci. 2000;355:433–440. doi: 10.1098/rstb.2000.0584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley AF. Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Huxley AF. Tideswell S. Filament compliance and tension transients in muscle. J Muscle Res Cell Motil. 1996;17:507–511. doi: 10.1007/BF00123366. [DOI] [PubMed] [Google Scholar]
- James RS. A review of the thermal sensitivity of the mechanics of vertebrate skeletal muscle. J Comp Physiol B. 2013;183:723–733. doi: 10.1007/s00360-013-0748-1. [DOI] [PubMed] [Google Scholar]
- Kawai M. What do we learn by studying the temperature effect on isometric tension and tension transients in mammalian striated muscle fibres. J Muscle Res Cell Motil. 2003;24:127–138. doi: 10.1023/a:1026093212111. [DOI] [PubMed] [Google Scholar]
- Knupp C, Offer G, Ranatunga KW. Squire JM. Probing muscle myosin motor action: X-ray (M3 and M6) interference measurements report motor domain not lever arm movement. J Mol Biol. 2009;390:168–181. doi: 10.1016/j.jmb.2009.04.047. [DOI] [PubMed] [Google Scholar]
- Lymn RW. Taylor EW. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 1971;10:4617–4624. doi: 10.1021/bi00801a004. [DOI] [PubMed] [Google Scholar]
- Nyitrai M. Geeves MA. Adenosine diphosphate and strain sensitivity in myosin motors. Philos Trans R Soc Lond B Biol Sci. 2004;359:1867–1877. doi: 10.1098/rstb.2004.1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Offer G. Ranatunga KW. Crossbridge and filament compliance: implications for tension generation and lever arm swing. J Muscle Res Cell Motil. 2011;31:245–265. doi: 10.1007/s10974-010-9232-7. [DOI] [PubMed] [Google Scholar]
- Offer G. Ranatunga KW. A crossbridge cycle with two tension-generating steps simulates skeletal muscle mechanics. Biophys J. 2013;105:928–940. doi: 10.1016/j.bpj.2013.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveberg M, Tan Y-J. Fersht A. Negative activation enthalpies in the kinetics of protein folding. Proc Natl Acad Sci U S A. 1995;92:8926–8929. doi: 10.1073/pnas.92.19.8926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Koubassova N, Decostre V, Linari M, Lucii L. Lombardi V. Temperature dependence of the force-generating process in single fibres from frog skeletal muscle. J Physiol. 2003;549:93–106. doi: 10.1113/jphysiol.2002.038703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT. Flannery BP. Numerical Recipes in C. 2nd edn. Cambridge, UK: Cambridge University Press; 1992. [Google Scholar]
- Radzyukevich T. Edman KAP. Effects of intracellular acidification and varied temperature on force, stiffness and speed of shortening in frog muscle fibers. Am J Physiol Cell Physiol. 2004;287:C106–113. doi: 10.1152/ajpcell.00472.2003. [DOI] [PubMed] [Google Scholar]
- Rall JA. Woledge RC. Influence of temperature on mechanics and energetics of muscle contraction. Am J Physiol. 1990;259:R197–203. doi: 10.1152/ajpregu.1990.259.2.R197. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW. Temperature-dependence of shortening velocity and rate of isometric tension development in rat skeletal muscle. J Physiol. 1982;329:465–483. doi: 10.1113/jphysiol.1982.sp014314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. The force–velocity relation of rat fast- and slow-twitch muscles examined at different temperatures. J Physiol. 1984;351:517–529. doi: 10.1113/jphysiol.1984.sp015260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Thermal stress and Ca-independent contractile activation in mammalian skeletal muscle fibers at high temperatures. Biophys J. 1994;66:1531–1541. doi: 10.1016/S0006-3495(94)80944-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Endothermic force generation in fast and slow mammalian (rabbit) muscle fibers. Biophys J. 1996;71:1905–1913. doi: 10.1016/S0006-3495(96)79389-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Temperature dependence of mechanical power output in mammalian (rat) skeletal muscle. Exp Physiol. 1998;83:371–376. doi: 10.1113/expphysiol.1998.sp004120. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW. Effects of inorganic phosphate on endothermic force generation in muscle. Proc Biol Sci. 1999;266:1381–1385. doi: 10.1098/rspb.1999.0791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW, Roots H. Offer GW. Temperature-jump induced force generation in rabbit muscle fibres gets faster with shortening and shows a biphasic dependence on velocity. J Physiol. 2010;588:479–493. doi: 10.1113/jphysiol.2009.179200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud JM. Stevens ED. The extent of short-term and long-term compensation to temperature shown by frog and toad sartorius muscle. J Exp Biol. 1984;108:57–75. [Google Scholar]
- Rome LC. The effect of long-term exposure to different temperatures on the mechanical performance of frog muscle. Physiol Zool. 1983;56:33–40. [Google Scholar]
- Roots H. Ranatunga KW. An analysis of the temperature dependence of force during steady shortening at different velocities in mammalian fast muscle fibres. J Muscle Res Cell Motil. 2008;29:9–24. doi: 10.1007/s10974-008-9138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siemankowski RF, Wiseman MO. White HD. ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc Natl Acad Sci U S A. 1985;82:658–662. doi: 10.1073/pnas.82.3.658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsaturyan AK, Bershitsky SY, Burns R. Ferenczi MA. Structural changes in the actin–myosin cross-bridges associated with force generation induced by temperature jump in permeabilised frog muscle fibers. Biophys J. 1999;77:354–372. doi: 10.1016/S0006-3495(99)76895-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss S, Rossi R, Pelligrino MA, Bottinelli R. Geeves MA. Differing ADP release rates from myosin heavy chain isoforms define the shortening velocity of skeletal muscle fibers. J Biol Chem. 2001;276:45902–45908. doi: 10.1074/jbc.M107434200. [DOI] [PubMed] [Google Scholar]
- White HD, Belknap B. Webb MR. Kinetics of nucleoside triphosphate cleavage and phosphate release steps by associated rabbit skeletal actomyosin, measured using a novel fluorescent probe for phosphate. Biochemistry. 1997;36:11828–36. doi: 10.1021/bi970540h. [DOI] [PubMed] [Google Scholar]
- White HD. Taylor EW. Energetics and mechanism of actomyosin adenosine triphosphatase. Biochemistry. 1976;15:5818–5826. doi: 10.1021/bi00671a020. [DOI] [PubMed] [Google Scholar]
- Woledge RC, Barclay CJ. Curtin NA. Temperature change as a probe of muscle crossbridge kinetics: a review and discussion. Proc Biol Sci. 2009;276:2685–2695. doi: 10.1098/rspb.2009.0177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woledge RC, Curtin NA. Homsher E. Energetic Aspects of Muscle Contraction. New York: Academic Press; 1985. [PubMed] [Google Scholar]
- Xu S, Offer G, Gu J, White HD. Yu LC. Temperature and ligand dependence of conformation and helical order in myosin filaments. Biochemistry. 2003;42:390–401. doi: 10.1021/bi026085t. [DOI] [PubMed] [Google Scholar]


