Abstract
Neuromuscular fatigue increases the amplitude of fluctuations in torque output during isometric contractions, but the effect of fatigue on the temporal structure, or complexity, of these fluctuations is not known. We hypothesised that fatigue would result in a loss of temporal complexity and a change in fractal scaling of the torque signal during isometric knee extensor exercise. Eleven healthy participants performed a maximal test (5 min of intermittent maximal voluntary contractions, MVCs), and a submaximal test (contractions at a target of 40% MVC performed until task failure), each with a 60% duty factor (6 s contraction, 4 s rest). Torque and surface EMG signals were sampled continuously. Complexity and fractal scaling of torque were quantified by calculating approximate entropy (ApEn), sample entropy (SampEn) and the detrended fluctuation analysis (DFA) scaling exponent α. Fresh submaximal contractions were more complex than maximal contractions (mean ± SEM, submaximal vs. maximal: ApEn 0.65 ± 0.09 vs. 0.15 ± 0.02; SampEn 0.62 ± 0.09 vs. 0.14 ± 0.02; DFA α 1.35 ± 0.04 vs. 1.55 ± 0.03; all P < 0.005). Fatigue reduced the complexity of submaximal contractions (ApEn to 0.24 ± 0.05; SampEn to 0.22 ± 0.04; DFA α to 1.55 ± 0.03; all P < 0.005) and maximal contractions (ApEn to 0.10 ± 0.02; SampEn to 0.10 ± 0.02; DFA α to 1.63 ± 0.02; all P < 0.01). This loss of complexity and shift towards Brownian-like noise suggests that as well as reducing the capacity to produce torque, fatigue reduces the neuromuscular system's adaptability to external perturbations.
Key points
Healthy physiological systems generate time series possessing complex structures, as seen for example in heart rate variability, respiratory rate and gait.
A loss of complexity in physiological time series has been associated with system dysfunction, and this loss is a characteristic feature of torque output from the ageing neuromuscular system.
We sought to determine the effect of neuromuscular fatigue on the complexity of knee extensor torque output in healthy young humans performing repeated maximal and submaximal contractions.
Fatigue resulted in a substantial loss of knee extensor torque complexity, with the noise in the torque signal becoming increasingly Brownian in character.
Complexity has been associated with system adaptability, and the fatigue-induced loss of complexity, the physiological origin of which is obscure, may contribute to the inability to sustain physical exercise.
Introduction
It is well known that neuromuscular fatigue (an exercise-induced decline in maximal force-generating capacity; Taylor & Gandevia, 2008) has both central and peripheral components that can be identified by supramaximal motor nerve stimulation during and after a maximal voluntary contraction (for review see Gandevia, 2001). Neuromuscular fatigue also has functional effects on motor output during submaximal tasks. One of these effects is to increase the variability in motor output during isometric contractions (Furness et al. 1977; Galganski et al. 1993). Classically, increased variability is reflected in an increase in the standard deviation (SD) or the coefficient of variation (CV) of force or torque output (Galganski et al. 1993; Slifkin & Newell, 2000; Hunter & Enoka, 2003; Contessa et al. 2009). The increase in force variability as fatigue progresses has been suggested to be a consequence of alterations in motor unit recruitment and/or discharge timing as task failure approaches (Hunter & Enoka, 2003; Contessa et al. 2009). However, whilst the magnitude of fluctuations in force or torque output has been heavily investigated, the temporal structure or ‘complexity’ of these fluctuations has received less attention. In this context, complex time series produce irregular fluctuations resembling non-linear chaos, whereas less complex signals produce more regular/periodic fluctuations (Lipsitz & Goldberger, 1992).
Measures of complexity are derived from the field of non-linear dynamics, and include metrics related to information theory (such as approximate entropy, ApEn; Pincus, 1991; and sample entropy, SampEn; Richman and Moorman, 2000), which provide a measure of the apparent randomness or regularity of a system's output, and measures of fractal scaling (such as detrended fluctuation analysis, DFA; Peng et al. 1994, 1995). The latter can be used to differentiate signals that are random (white noise), statistically self-similar (pink or 1/f noise) or Brownian in character, as well as identify long-term correlations (Hausdorff et al. 1995; Goldberger et al. 2002a). It has been suggested that self-similarity is a salient feature of the spatial structure of a range of physiological systems, most notably the vascular and respiratory trees (Glenny, 2011). Moreover, these ‘fractal’ structures are also evident in physiological time series, as long-range correlations are observed in heart rate (Yamamoto & Hughson, 1994; Pikkujämsä et al. 1999), respiratory frequency (Peng et al. 2002; Schumann et al. 2010), and gait (Hausdorff et al. 1995, 2001). Thus, a variety of healthy physiological systems produce outputs containing DFA α values >0.5 (white noise), but <1.5 (Brownian noise). A change in these fractal structures (i.e. a shift from 1/f noise [α ∼1.0] towards white or Brownian noise) has been associated with system dysfunction and a variety of pathologies (see Goldberger et al. 2002a for review).
The neuromuscular system is composed of ensembles of interconnected components (e.g. motor cortical neurones, spinal motoneurons, muscle fibres, muscle afferents) whose interactions produce complex patterns of force output (Vaillancourt & Newell, 2003; Forrest et al. 2014). A reduction in complexity and a change in fractal scaling of force output (from pink towards Brownian noise) have been frequently observed in healthy ageing (Vaillancourt & Newell, 2003; Vaillancourt et al. 2003; Challis, 2006; Sosnoff & Newell, 2008). Reductions in complexity, especially when combined with an increase in the amplitude of force fluctuations (Hunter et al. 2005), imply a loss of system control (Lipsitz & Goldberger, 1992; Peng et al. 2009; Lipsitz, 2004; Manor & Lipsitz, 2013; Sejdić & Lipsitz, 2013) and a tendency for system components to operate in increasing isolation (Pincus, 1994). In addition, it has been demonstrated that the complexity of force output is dependent on the intensity of the contractions, with complexity (measured using ApEn) being highest at ∼30–50% MVC and declining as torque requirements are increased (Slifkin & Newell, 2000). The effect of neuromuscular fatigue on the complexity of joint torque during isometric contractions is, however, currently unknown.
Recently, Cashaback et al. (2013) observed a reduction in the complexity of biceps brachii surface electromyogram (EMG) in the final third of exhaustive submaximal isometric elbow flexion exercise, which may translate to reduced complexity of torque output through the process of excitation–contraction coupling. In addition, because neuromuscular fatigue, by definition, reduces MVC torque, a given submaximal target torque will require an increasing fraction of the MVC torque as fatigue develops. We would therefore predict that fatigue will result in a reduction in complexity and a move from pink (1/f) to Brownian noise during submaximal contractions of the knee extensors, reflecting a neuromuscular system that becomes less able to adapt to external perturbations (Lipsitz & Goldberger, 1992; Seely & Macklem, 2012). In the same vein, we would predict that during maximal contractions, complexity would initially be lower than during submaximal contractions, but that the rapid development of fatigue in this situation (e.g. Burnley, 2009) would reduce complexity still further. In order to quantify both the complexity of torque output during contractions and the development of central and peripheral fatigue, and provide sufficient data for complexity and fractal scaling analyses (Lipsitz & Goldberger, 1992), we used the intermittent isometric contraction regime of Bigland-Ritchie et al. (1986).
The aim of the present study, therefore, was to determine whether the complexity of knee extensor torque was perturbed by neuromuscular fatigue, and to test the following experimental hypotheses: (1) that for fresh muscle, the knee extensor torque would be more complex during submaximal contractions and would exhibit more fractal-like scaling (DFA α ∼1.0); (2) that, compared to the complexity of fresh contractions, neuromuscular fatigue would result in a reduction in the complexity of knee extensor torque during maximal and submaximal isometric contractions; and (3) that the reduction in the complexity of knee extensor torque would be accompanied by a change in fractal scaling from pink (DFA α ∼1.0) toward Brownian noise (DFA α = 1.5).
Methods
Ethical approval
Eleven healthy participants (10 male, 1 female; mean ± SD: age 25.0 ± 5.6 years; height 1.77 ± 0.05 m; body mass 78.6 ± 13.7 kg) provided written informed consent to participate in the study, which was approved by the ethics committee of the University of Kent, and which adhered to the Declaration of Helsinki. Participants were instructed to arrive at the laboratory rested (having performed no heavy exercise in the preceding 24 h) and not to have consumed any food or caffeinated beverages in the 3 h before arrival. Participants attended the laboratory at the same time of day (±2 h) during each visit.
Experimental design
Participants were required to visit the laboratory on three occasions over a 2 week period, with a minimum of 48 h between each visit. During their first visit, participants were familiarised with all testing equipment and procedures, and the settings for the dynamometer and stimulator were recorded. During their second and third visits, participants performed either a series of 30 intermittent maximal isometric contractions, accompanied by peripheral nerve stimulation (the ‘maximal test’; see below) or a series of intermittent submaximal isometric contractions until task failure, accompanied by peripheral nerve stimulation (the ‘submaximal test’; see below). The maximal and submaximal tests were presented in a randomised order.
Dynamometry
During all visits, participants were seated in the chair of a Cybex isokinetic dynamometer (HUMAC Norm; CSMi, Stoughton, MA, USA), initialised and calibrated according to the manufacturer's instructions. Their right leg was attached to the lever arm of the dynamometer, with the seating position adjusted to ensure that the lateral epicondyle of the right femur was in line with the axis of rotation of the lever arm. Participants sat with relative hip and knee angles of 85 deg and 90 deg, respectively, with full extension being 0 deg. The lower leg was securely attached to the lever arm above the malleoli with a padded Velcro strap, while straps secured firmly across both shoulders and the waist prevented any extraneous movement and the use of the hip extensors during the isometric contractions. The seating position was recorded during the first visit and replicated for each subsequent visit.
Peripheral nerve stimulation
An Ag/AgCl electrode (32 mm × 32 mm; Nessler Medizintechnik, Innsbruck, Austria) coated in conductive gel acted as the cathode, and was placed in the femoral triangle, over the femoral nerve. The anode, a carbon rubber electrode with adhesive gel (100 mm × 50 mm; Phoenix Healthcare Products Ltd, Nottingham, UK), was placed lateral to the ischial tuberosity, on the posterior aspect of the leg. A constant-current, variable voltage stimulator (Digitimer DS7AH, Welwyn Garden City, UK) was used to deliver single (200 μm pulses) and doublet stimuli (200 μm pulses, 10 ms interval) at 400 V. The precise location of the cathode was established using a motor point pen (Compex; DJO Global, Guildford, UK), and determined based on the location giving the largest twitch and greatest peak-to-peak amplitude of the compound muscle action potential (M-wave) following single stimulation at 100 mA.
Following establishment of the cathode location, single stimuli were initiated starting at 100 mA, and the stimulator current increased in steps of 20 mA until there was no further increase in the measured twitch torque or M-wave. Participants then produced an MVC, and then subsequently reproduced 50% MVC. A single pulse was delivered during the contraction at 50% MVC in order to test whether there was any further increase in the M-wave. If there was a decrease in the M-wave, the current was increased again until the M-wave plateaued. Once a plateau in the M-wave was obtained, the current was increased to 130% of the plateau current (range utilised 260–598 mA) to ensure supramaximality, and this intensity was used for stimulation during the subsequent tests.
Surface EMG
The EMG of the vastus lateralis was sampled using Ag/AgCl electrodes (32 mm × 32 mm; Nessler Medizintechnik, Innsbruck, Austria). Prior to attachment of the electrodes, the skin of the participants was shaved, abraded and then cleaned with an alcohol-soaked cotton pad, in order to reduce impedance. Positioning of the electrodes was preceded by palpation of the muscle during a manually resisted contraction, to outline its length and belly. The electrodes were placed in a direction parallel to the alignment of the muscle fibres over the belly of the muscle. A reference electrode was placed on prepared skin medial to the tibial tuberosity. The raw EMG signals were sampled at 1 kHz, amplified (gain 1000; Biopac MP150, Biopac Systems Inc., Goleta, CA, USA) and band-pass filtered (10–500 Hz; Biopac MP150, Biopac Systems Inc.).
Protocol
All visits followed a similar pattern of data acquisition, beginning with the instrumentation of the participants and the (re-)establishment of the correct dynamometer seating position and supramaximal stimulation response. Participants then performed a series of brief (3 s) MVCs to establish their maximum torque. The contractions were separated by 60 s rest, and continued until three consecutive peak torques were within 5% of each other. Participants were given a countdown, followed by very strong verbal encouragement to maximise torque. The first MVC was used to establish the fresh maximal EMG signal, against which the subsequent EMG signals were normalised (‘Data analysis’; see below). The second and third MVCs were performed with peripheral nerve stimulation; at 1.5 s into the contraction, during a plateau in torque, a doublet was delivered and a further doublet delivered at rest 2 s after the contraction. The pulses superimposed on the contraction tested the maximality of the contraction and provided the fresh voluntary activation, while the pulses after the contraction established the fresh potentiated doublet response (‘Data analysis’; see below). All subsequent contractions with peripheral nerve stimulation were conducted in this manner. Following the final MVC, participants rested for 10 min, after which they performed either the maximal or submaximal test.
Maximal test
A 5-minute all-out test, adapted from the test developed by Burnley (2009), was performed by all participants during their familiarisation visit and again during either their second or third visit to the laboratory. The test consisted of 30 intermittent MVCs, with a contraction regime of 6 s work and 4 s rest (Bigland-Ritchie et al. 1986). Participants were given feedback on their previous MVCs and were encouraged to equal or exceed these values during the first 2–3 contractions. Participants were also informed to expect their torque to decrease by more than 50% during the test, but to still produce a maximal effort during each contraction despite this occurrence. During the test the participants were very strongly encouraged to maximise and maintain their torque, but were not informed of the number of contractions remaining or the elapsed time. The test was ended after the 30th contraction was completed. During the test, peripheral nerve stimulation was delivered every sixth contraction (i.e. at the end of each minute).
Submaximal test
A test at 40% MVC was performed by all participants during either their second or third visit to the laboratory. The target torque at 40% MVC was determined from the MVCs measured at the start of the visit. Participants were instructed to match their instantaneous torque with a target bar superimposed on the display in front of them and were required to continue matching this torque for as much of the 6 s contraction as possible. The test was conducted until task failure, the point at which the participant failed to reach the target torque on three consecutive occasions, despite strong verbal encouragement. Participants were not informed of the elapsed time during the test, but were informed of each ‘missed’ contraction. During the test, participants were required to perform an MVC, accompanied by peripheral nerve stimulation, every sixth contraction (i.e. at the end of each minute). After the third missed contraction, participants were instructed to immediately produce an MVC, which was accompanied by peripheral nerve stimulation.
Data acquisition
Data were acquired from all peripheral devices through BNC cables connected to a Biopac MP150 (Biopac Systems Inc.) and CED Micro 1401-3 (Cambridge Electronic Design, Cambridge, UK) interfaced with a personal computer. All signals were sampled at 1 kHz. The data were collected in Spike2 (Version 7; Cambridge Electronic Design).
Data analysis
All data were analysed using code written in MATLAB R2013a (The MathWorks, Natick, MA, USA). The data analysis focused on three specific areas: (1) basic measures of torque and EMG; (2) measures of central and peripheral fatigue; and (3) the variability and complexity of the torque output.
Torque and EMG
The peak and mean torque for each contraction were determined for both the maximal and submaximal tests. The mean torque was calculated from the steadiest 5 s of each contraction, i.e. the 5 s with the least variation. To establish the point of task failure the mean torque recorded during the first five contractions (i.e. during the first minute of the test, before the MVC) was calculated. Task failure was deemed to have occurred when the mean torque recorded during three consecutive contractions was more than 5 N m below the mean torque of the first five contractions, with the first of these contractions being considered the point of task failure.
The EMG output from the vastus lateralis for each contraction was full-wave rectified. The average rectified EMG (arEMG) was then calculated and normalised by expressing the arEMG as a fraction of the arEMG obtained during an MVC from the fresh muscle preceding commencement of the maximal and submaximal tests.
Central and peripheral fatigue
The potentiated doublet torque, the decline of which was our measure of peripheral fatigue, was calculated as the peak torque attained following doublet stimuli at rest between contractions. The superimposed doublet torque was calculated as the increment in torque immediately following doublet stimuli during the contraction. Voluntary activation was determined using the twitch interpolation technique (Belanger & McComas, 1981; Behm et al. 1996), and was calculated as:
 |
1 |
where the superimposed doublet was that measured during the contraction of interest and the potentiated doublet was measured at rest 2 s after the contraction.
Variability and complexity
All measures of variability and complexity were calculated using the steadiest 5 s of each contraction. The amplitude of variability in the torque output of each contraction was measured using the SD and CV. The SD provides a measure of the absolute amount of variability in a time series, while the CV provides a measure of the amount of variability in a time series normalised to the mean of the time series. The temporal complexity of these fluctuations was examined using a cluster of time domain analyses as recommended by Goldberger et al. (2002b). ApEn and SampEn were used to estimate the complexity of torque output, while DFA was used to estimate the noise colour and temporal fractal scaling. The calculation of these statistics is briefly described below.
The ApEn statistic (Pincus, 1991) quantifies the negative natural logarithm of the conditional probability that a template of length m (set at 2) is repeated during the time series. Matching templates that remain arbitrarily similar (i.e. within the tolerance, r, set at 0.1SD; Pincus, 1991; Forrest et al. 2014) are then counted; the number of matches to the ith template of length m is designated Bi. Then the number of these matches that remain similar for the m + 1th point is counted; this number for the ith template is designated Ai. The conditional probability that the template including the m + 1th data point matches given that the template of length m is then calculated for each template match. The negative logarithm of the conditional probability is calculated for all templates and the results averaged (eqn 2). If the data are highly ordered then templates that are similar for m points are likely to also be similar for m + 1 points. For such data sets the conditional probability will therefore be close to 1, and the negative log and therefore the entropy will be close to zero. This will reflect low complexity and high predictability.
| 2 |
where N is the number of data points in the time series, m is the length of the template, Ai is the number of matches of the ith template of length m + 1 data points, and Bi is the number of matches of the ith template of length m data points.
To avoid the occurrence of ln(0) in the ApEn algorithm, a template is allowed to match itself. Therefore each template occurs at least once. A more recent algorithm, ‘sample entropy’ (SampEn, Richman & Moorman, 2000) avoids this by taking the logarithm after averaging (as shown in eqn 3). This method avoids the introduction of self-matching but moves away from entropy calculated in the information theoretic sense. The SampEn thus was calculated as:
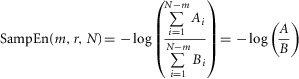 |
3 |
The fractal scaling of the torque time series was assessed using detrended fluctuation analysis (DFA). In this algorithm, the time series is first integrated and then the vertical characteristic scale of the integrated time series is measured. The integrated time series is divided into boxes of length n and a least-squares line is fitted, representing the trend in each box. The y coordinate of the straight line segment of length n in the kth box is denoted by yn(k), and the integrated time series is detrended by subtracting the local trend in each box. For a given box size n, the characteristic size of fluctuation for the integrated and detrended time series is given by:
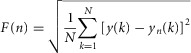 |
4 |
This computation is then repeated over all time scales or box sizes (57 box sizes in total ranging from 1250 to 4 data points) to provide a relationship between box size and F(n). The slope of the log–log plot of n and F(n) determines the scaling parameter α.
Statistics
One-way analysis of variance with repeated measures was used to analyse the temporal profiles of potentiated doublet torque and voluntary activation over the course of the tests. Contrasts between end-test values and all other time points were made using Bonferroni-adjusted 95% paired-samples confidence intervals. The variability and complexity of the torque and EMG outputs were analysed using averages from the first minute and final minute before task failure of each test using two-way ANOVAs with repeated measures (condition × time). Post hoc Bonferroni-adjusted 95% paired-samples confidence intervals were then used to identify specific differences. All data are presented as means ± SEM, and results were deemed statistically significant when P < 0.05.
Results
Preliminary measures
The peak instantaneous MVC torque recorded prior to the maximal test was 235.6 ± 15.5 N m and the voluntary activation achieved was 89.6 ± 2.0%; while the peak instantaneous MVC torque recorded prior to the submaximal test was 237.7 ± 14.8 N m and the voluntary activation achieved was 90.6 ± 1.8%. Neither of these values was significantly different (95% paired samples confidence intervals (CIs): peak MVC torque, –11.9, 16.2 N m; voluntary activation, –1.4, 3.0%).
Torque and EMG
The mean torque profiles during the maximal test are shown in Fig.1A. Torque declined from a peak of ∼96% MVC during the first contraction to an average of ∼44% during the last three contractions of the maximal test. The mean data for the arEMG of the vastus lateralis for each contraction of the maximal test are shown in Fig.1B. The arEMG, normalised to a fresh pre-test MVC, significantly decreased from 96.3 ± 2.5% (first contraction) to 73.8 ± 5.8% (last contraction; CIs –38.2, –9.7%).
Figure 1. Torque and muscle activity during maximal and submaximal contractions.
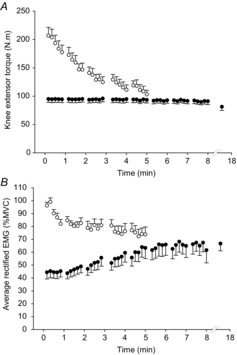
Knee extensor torque (A) and average rectified EMG amplitude (B) during the maximal test (open circles) and submaximal test (filled circles). The penultimate data point in the submaximal test represents the last common contraction, whereas the final data point represents task failure. Values are mean ± SEM.
The mean data for mean torque during each common contraction and that at task failure in all participants for the submaximal test are shown in Fig.1A. The target torque, as calculated from the pre-test MVCs, was 95.1 ± 5.9 N m, and task failure occurred when participants were not able to achieve this target torque, despite continued effort. The mean torque achieved during the MVC at task failure (87.4 ± 8.3 N m) was not significantly different from the test target torque (CIs –23.9, 8.4), indicating that participants required a maximal effort to achieve the target torque. The mean time to task failure was 17.3 ± 4.3 min, with a range of 8.2–58.0 min. The arEMGs of the vastus lateralis for each contraction of the submaximal test are shown in Fig.1B. The normalised arEMG significantly increased from 44.4 ± 5.2% (first contraction) to 68.5 ± 5.6% (last contraction; CIs 10.7, 37.5%; Table1).
Table 1.
Voluntary and stimulated torque, muscle activation and complexity during maximal and submaximal contractions
| Maximal test | Submaximal test | |||
|---|---|---|---|---|
| Fresh | Test end | Fresh | Task failure | |
| Variable | ||||
| Peak MVC torque (N m) | 235.6 ± 15.5 | 112.6 ± 10.9* | 237.7 ± 14.8 | 109.2 ± 9.7* |
| Potentiated doublet (N m) | 105.3 ± 7.1 | 62.4 ± 8.6* | 112.4 ± 7.9 | 70.3 ± 10.0* |
| Voluntary activation (%) | 89.8 ± 2.0 | 68.6 ± 5.6* | 90.6 ± 1.8 | 66.2 ± 4.7* |
| Electromyogram | ||||
| arEMG (%MVC) | 96.3 ± 2.5 | 73.8 ± 5.8* | 44.4 ± 5.2 | 68.5 ± 5.6* |
| Variability | ||||
| Standard deviation (N m) | 8.5 ± 1.3 | 10.2 ± 1.3 | 2.6 ± 0.2† | 7.1 ± 0.7* |
| Coefficient of variation (%) | 4.2 ± 0.5 | 8.2 ± 1.4* | 2.8 ± 0.8† | 8.1 ± 2.3* |
| Complexity statistics | ||||
| ApEn | 0.15 ± 0.02 | 0.10 ± 0.02* | 0.65 ± 0.09† | 0.24 ± 0.05* |
| SampEn | 0.14 ± 0.02 | 0.10 ± 0.02* | 0.62 ± 0.09† | 0.22 ± 0.04* |
| DFA α | 1.55 ± 0.03 | 1.63 ± 0.02* | 1.35 ± 0.04† | 1.55 ± 0.03* |
Values are mean ± SEM. *Significantly different from ‘Fresh’ in the same condition. † Significantly different from ‘Fresh’ in the maximal test (P < 0.05).
Global, peripheral and central fatigue
The potentiated doublet responses and voluntary activation decreased as both tests progressed, indicating the presence of peripheral and central fatigue, respectively. In the maximal test, the potentiated doublet response had decreased by ∼40% at the end of the test (F5,10 = 69.98, P < 0.001; Table1, Fig.2A); while voluntary activation had fallen by ∼24% by the end of the test (F5,10 = 3.74, P = 0.01; Table1; Fig.2B). During the submaximal test, the potentiated doublet response had decreased by ∼37% at task failure (F9,10 = 18.65, P < 0.001; Fig.2A), while voluntary activation had fallen by ∼27% at task failure (F9,10 = 11.91, P = 0.004; Table1, Fig.2B).
Figure 2. Central and peripheral fatigue during maximal and submaximal contractions.
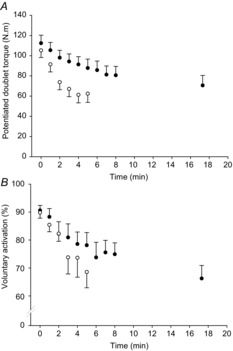
Peripheral fatigue measured from the potentiated doublet torque (A) and central fatigue measured from voluntary activation of the knee extensors (B) for the maximal and submaximal tests (open and filled symbols, respectively). Values are mean ± SEM.
Torque variability
The metrics associated with the variability in torque (SD and CV) are presented in Table1. The SD of torque fluctuations was higher in the maximal test than the submaximal test (F1,10 = 14.59, P = 0.003), and there was a main effect of time (F1,10 = 42.55, P < 0.001). The CV significantly increased over time in both tests (F1,10 = 95.7, P < 0.001). The SD was significantly higher at the start of the maximal test (8.4 ± 1.3 vs. 2.6 ± 0.3; CIs 2.6, 9.2 N m). During the maximal test the standard deviation did not increase (CIs –0.4, 3.8 N m), in contrast to the increased CV (CIs 2.4, 6.0%). During the submaximal test there were significant increases in both the SD (CIs 2.9, 6.1 N m) and CV (CIs 3.5, 7.2%; Table1).
Complexity
Maximal contractions were associated with smaller ApEn (F1,10 = 34.79, P < 0.001) and SampEn values (F1,10 = 33.50, P < 0.001) and a larger DFA α scaling exponent (F1,10 = 37.22, P < 0.001; Fig.3) than submaximal contractions. In the first minute of contractions, there was significantly lower complexity in the torque output during the maximal test compared to the submaximal test, as evidenced by lower ApEn (CIs –0.69, –0.30; Fig.3A) and SampEn (–0.68, –0.28; Fig.3B); and a significantly higher DFA α scaling exponent (0.13, 0.27; Fig.3C). These data are shown for comparison in Table1. The grand mean r2 values of the fits for the DFA were 0.98 ± 0.01 for the maximal test and 0.97 ± 0.01 for the submaximal test.
Figure 3. Complexity and fractal scaling analyses of knee extensor torque.
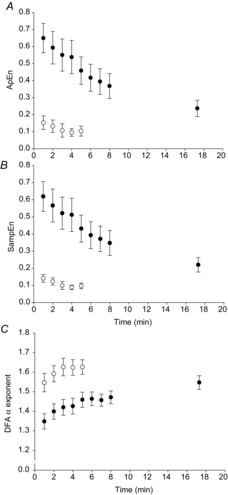
A, approximate entropy (ApEn). B, sample entropy (SampEn). C, detrended fluctuation analysis scaling exponent α (DFA α). The open symbols represent the maximal test, filled symbols represent the submaximal test.
There was a main effect of time for all three complexity statistics (ApEn: F1,10 = 73.86, P < 0.001; SampEn: F1,10 = 58.93, P < 0.001; DFA α F1,10 = 48.88, P < 0.001). In the maximal test, there was a decrease in ApEn from 0.15 ± 0.02 (first minute) to 0.10 ± 0.02 (last minute; CIs –0.08, –0.01; Fig.3A) and SampEn (from 0.14 ± 0.02 (first minute) to 0.10 ± 0.02 (last minute); CIs –0.08, –0.01; Fig.3B). The DFA α scaling exponent significantly increased from 1.55 ± 0.03 (first minute) to 1.63 ± 0.02 (last minute; CIs 0.04, 0.13; Fig.3C).
Over the course of the submaximal test, ApEn decreased (from 0.65 ± 0.09 (first minute) to 0.27 ± 0.04 (task failure); CIs –0.55, –0.28; Table1, Fig.3A), as did SampEn (from 0.62 ± 0.09 (first minute) to 0.22 ± 0.04 (task failure); CIs –0.54, –0.25; Fig.3B). The DFA α scaling exponent increased (from 1.35 ± 0.04 (first minute) to 1.55 ± 0.03 (task failure); CIs 0.12, 0.28; Fig.3C). Example contractions from the beginning and end of the submaximal test are shown in Fig.4.
Figure 4. Raw torque output from the submaximal test.
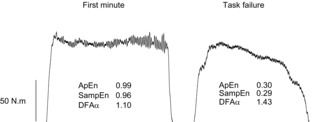
The data represent the second contraction performed (from 10 to 16 s – ‘First minute’) and the contraction at task failure (from 500 to 510 s – ‘Task failure’) at 40% MVC. The complexity metrics associated with each contraction are given, showing the reduced complexity (lower ApEn and SampEn values) and change of fractal scaling (DFA α increasing towards 1.5) at task failure.
Discussion
The major novel finding of the present study was that neuromuscular fatigue was associated with reduced complexity in motor output, whether the muscle was driven maximally or submaximally, during repeated isometric contractions. Our results also demonstrate that when the muscle is driven maximally in the absence of fatigue, the fluctuations present in knee extensor torque are substantially less complex than when the muscle is driven submaximally. As the complexity of torque fluctuations decreased during submaximal contractions performed to task failure, these fluctuations became increasingly Brownian in character (DFA α = 1.50). Finally, and in contrast to our hypothesis, we did not observe 1/f noise (DFA α = 1.00) during fresh submaximal contractions. Nevertheless, the torque signal possessed long-range correlations and this fractal-like scaling of torque changed as fatigue progressed.
Complexity during ‘fresh’ maximal and submaximal contractions
It has been suggested that an inverted U-shaped relationship exists between contraction intensity and the complexity of torque output, with complexity peaking at ∼40% MVC (Slifkin & Newell, 1999, 2000; Svendsen & Madeleine, 2010). In light of this, we predicted that for fresh muscle, torque output during submaximal contractions would be more complex than maximal contractions. Our data support this hypothesis: ApEn and SampEn were both significantly greater during the initial contractions of the submaximal test, indicating a more complex output at 40% MVC. Furthermore, the DFA α scaling exponent was significantly lower during the submaximal test. Slifkin & Newell (1999) reasoned that complexity peaked at ∼40% MVC in their experiments because, at least for muscles of the fingers, at this point force could be modulated by either motor unit recruitment or rate coding. Below 40% MVC increased force would typically occur primarily through increased motor unit recruitment; above that point increased discharge rates would be the dominant means of force increase. An intensity of 40% MVC thus represented the point of maximal system adaptability and information transfer (Slifkin & Newell, 1999). It is known, however, that limb muscles, such as m. quadriceps femoris, are able to modulate force output by motor unit recruitment over a considerably greater range of intensities than muscles of the hand (DeLuca et al. 1982). Thus, whether the same inverted U-shaped relationship between contractile intensity and torque complexity in the finger flexors holds for the knee extensors is unclear. Nevertheless, the present results confirm that submaximal contractions are associated with greater complexity than MVCs.
Submaximal contractions rarely achieve tetanic rates of discharge (Enoka & Fuglevand, 2001), meaning the force exerted by a muscle will exhibit fluctuations due to submaximal activation of motor units (Taylor et al. 2003). As contraction intensity increases, a higher discharge rate is required (Bigland & Lippold, 1954; Moritz et al. 2005). Such higher discharge rates are more likely to result in output approximating a fused tetanus (Buller & Lewis, 1965), which may result in a smoother, more periodic torque output with fewer fluctuations. The greater complexity during the submaximal test was in contrast to the amount of variability, which was significantly lower for submaximal contractions (Table1). This confirms that variability metrics assess different properties of the torque signal to complexity and fractal scaling statistics (the former characterises the amplitude of torque fluctuations whereas the latter quantifies their temporal structure; Lipsitz & Goldberger, 1992).
Fatigue-induced reduction in complexity during submaximal contractions
During submaximal contractions performed to task failure, central and peripheral fatigue developed progressively, and the arEMG gradually increased (Fig.1B, Fig.2, Table1). These responses are typical of exhaustive submaximal contractions, in which the neuromuscular system compensates for the loss of peripheral output by increasing central motor drive at the expense of a loss of maximal torque-generating capacity (Bigland-Ritchie et al. 1986; Hunter et al. 2009; Burnley et al. 2012). The results of the present study demonstrate that the complexity of submaximal torque output, measured using ApEn, SampEn and DFA, also systematically falls as fatigue progresses (Fig.3, Table1). Given that the compensatory adjustments made by the neuromuscular system would increase the number of activated motor units and their firing frequency (Adam & De Luca, 2003, 2005), the reduced complexity observed is at first sight surprising. Indeed, the fall in complexity was in contrast to the rise in variability in torque output (SD and CV, Table1) as exercise progressed. This increase in variability has been observed consistently in previous work and has been attributed to various properties of motor unit recruitment and firing frequency for both fresh and fatiguing muscle (Hunter & Enoka, 2003; Contessa et al. 2009; Missenard et al. 2009). However, complexity has been shown to decrease as the intensity of muscle contractions increases from ∼40% MVC to the maximum attainable torque (see above). Functionally, fatigue reduces the MVC torque and thus systematically increases the relative demand of a submaximal task, which might explain why complexity falls as an increasing proportion of the motor unit pool is engaged in the task.
The DFA demonstrated that reduced complexity during the submaximal test was also associated with a change in the fractal scaling of torque as fatigue developed. We hypothesised that fresh submaximal contractions at 40% MVC would produce pink (1/f) noise, and that this output would become Brownian as fatigue developed. This hypothesis was only partially supported, since the DFA α scaling exponent was ∼1.35 at the beginning of the contractions and rose to ∼1.55 at task failure. The latter value approximates Brownian noise (α = 1.50), whereas the former value, whilst representing output possessing long-term correlations, cannot be described as pink noise. Nevertheless, these results suggest that fatigue is associated with a change in fractal scaling in the torque signal (Brownian noise being inherently less complex than 1/f noise; Goldberger et al. 2002a). Such a change, and more generally the loss of complexity, has not been previously observed in the output of fatiguing muscle. Reduced complexity in torque output is, however, often observed in motor output in ageing (Vaillancourt & Newell, 2003; Vaillancourt et al. 2003; Challis, 2006; Sosnoff & Newell, 2008).
The ‘loss of complexity’ hypothesis in ageing first proposed by Lipsitz & Goldberger (1992), and much studied since (for review see Manor & Lipsitz, 2013), postulates that healthy physiological systems produce inherently complex temporal outputs. In this context, complex fluctuations in output allow a system to explore a variety of control solutions (that is, it is adaptable), whereas a loss of complexity reduces this exploratory freedom (Peng et al. 2009; Stergiou & Decker, 2011), with system components becoming increasingly isolated and less responsive to other inputs (Pincus, 1994). The present work extends the loss of complexity hypothesis to the neuromuscular fatigue process in otherwise healthy young humans. Yet the physiological origin of the loss of knee extensor torque complexity is not clear, since both central and peripheral fatigue was observed. Nevertheless, a loss of torque complexity must, by definition, be the result of mechanisms directly affecting the output of the motor unit pool. For example, the fall in the force output of fatiguing motor units, consequent to metabolite-mediated peripheral fatigue (Allen et al. 2008), may have contributed to the less complex torque profile as contractions progressed. Additionally, reduced responsiveness of repetitively activated motoneurones to increasing excitatory input (Johnson et al. 2004; Taylor & Gandevia, 2008) could result in either no change or diminished motor unit firing rate, further reducing the complexity of the torque signal. At the same time, recruitment of fresh higher-order motor units could increase targeting error and hence the coefficient of variation of torque output (Hunter & Enoka, 2003; Contessa et al. 2009). The net result would be a neuromuscular system that is unable to adjust torque output to match the required target as rapidly as in the absence of fatigue (Fig.4). Thus, task failure, which often occurs at apparently submaximal levels of muscle activity (Fig.1B; Dideriksen et al. 2011) and, for sustained contractions, with a significant torque ‘reserve’ (e.g. Hunter et al. 2004; Klass et al. 2008), may, in part, be a failure of the neuromuscular system to adapt to increasing task demands wrought by fatigue, rather than a failure of neuromuscular capacity.
Fatigue-induced reduction in complexity during maximal contractions
During the maximal test, central and peripheral fatigue developed rapidly, and torque fell systematically as the MVCs progressed (Figs1 and 2). Despite the relatively low complexity of these contractions in comparison to submaximal exercise, a reduction in complexity was still observed as ApEn and SampEn decreased and DFA α increased (Fig.3). This suggests that the torque signal became smoother as the contractions progressed, although, as with the submaximal contractions, torque variability (measured as the CV) increased during the maximal test. These apparently divergent results have been discussed above, but it is important to note that in this particular test there was no target torque – subjects simply produced the maximal attainable torque over each 6 s contraction. In this regard, measures of variability may be somewhat misleading as they quantify the inability to reach a stable plateau in torque during each contraction rather than the variance around a stable mean torque. Stated differently, the loss of complexity during the submaximal test appears to reflect a loss of motor control in achieving a required target, whereas the loss of complexity in the maximal test seems to be directly related to the loss of torque-generating capacity. Thus, peripheral fatigue (Fig.2A), as well as the reduced motoneurone firing frequency that accompanies fatiguing maximal contractions (Marsden et al. 1971; Bigland-Ritchie et al. 1983), may have resulted in an already relatively regular knee extensor torque time series becoming even more so as fatigue developed.
Conclusion
The performance of fatiguing maximal and submaximal isometric contractions of the knee extensors resulted in a progressive decrease in maximal voluntary torque that was accompanied by a significant reduction in the structural complexity of torque output. Fresh maximal contractions were associated with significantly lower complexity than submaximal contractions performed at 40% MVC. As the submaximal contractions progressed, neuromuscular fatigue reduced the complexity of motor output and resulted in a change in fractal scaling, leading to Brownian-like noise in the torque signal at task failure. The reduced complexity observed suggests that the impact of neuromuscular fatigue is not limited to a decrease in torque-generating capacity, but also affects the adaptability of the neuromuscular system to external perturbations.
Glossary
- ApEn
approximate entropy
- arEMG
average rectified electromyogram
- CI
confidence interval
- CV
coefficient of variation
- DFA
detrended fluctuation analysis
- MVC
maximal voluntary contraction
- SampEn
sample entropy
Additional information
Competing interests
The authors report no competing interests for this work.
Author contributions
This work was completed at the University of Kent. J.P., S.L.W. and M.B. were each involved in the conception and design of the study and contributed to the writing and critical revisions of the manuscript. J.P. and M.B. collected the data; S.L.W. wrote the MATLAB code to process the data. All authors were involved in the analysis and interpretation of the data. All authors approved the final version of the manuscript.
Funding
This work was supported by a University of Kent 50th Anniversary Scholarship. No external funding was rece-ived for this work.
References
- Adam A. De Luca CJ. Recruitment order of motor units in human vastus lateralis muscle is maintained during fatiguing contractions. J Neurophysiol. 2003;90:2919–2927. doi: 10.1152/jn.00179.2003. [DOI] [PubMed] [Google Scholar]
- Adam A. De Luca CJ. Firing rates of motor units in human vastus lateralis muscle during fatiguing isometric contractions. J Appl Physiol (1985) 2005;99:268–280. doi: 10.1152/japplphysiol.01344.2004. [DOI] [PubMed] [Google Scholar]
- Allen DG, Lamb GD. Westerblad H. Skeletal muscle fatigue: cellular mechanisms. Physiol Rev. 2008;88:287–332. doi: 10.1152/physrev.00015.2007. [DOI] [PubMed] [Google Scholar]
- Behm DG, St-Pierre DMM. Perez D. Muscle inactivation: assessment of interpolated twitch technique. J Appl Physiol (1985) 1996;81:2267–2273. doi: 10.1152/jappl.1996.81.5.2267. [DOI] [PubMed] [Google Scholar]
- Belanger AY. McComas AJ. Extent of motor unit activation during effort. J Appl Physiol Respir Environ Exerc Physiol. 1981;51:1131–1135. doi: 10.1152/jappl.1981.51.5.1131. [DOI] [PubMed] [Google Scholar]
- Bigland-Ritchie B, Furbush F. Woods JJ. Fatigue of intermittent submaximal voluntary contractions: central and peripheral factors. J Appl Physiol (1985) 1986;61:421–429. doi: 10.1152/jappl.1986.61.2.421. [DOI] [PubMed] [Google Scholar]
- Bigland-Ritchie B, Johansson R, Lippold OC, Smith S. Woods JJ. Changes in motoneurone firing rates during sustained maximal voluntary contractions. J Physiol. 1983;340:335–346. doi: 10.1113/jphysiol.1983.sp014765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigland B. Lippold OCJ. Motor unit activity in the voluntary contraction of human muscle. J Physiol. 1954;125:322–335. doi: 10.1113/jphysiol.1954.sp005161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buller AJ. Lewis DM. The rate of tension development in isometric tetanic contractions of mammalian fast and slow skeletal muscle. J Physiol. 1965;176:337–354. doi: 10.1113/jphysiol.1965.sp007554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnley M. Estimation of critical torque using intermittent isometric maximal voluntary contractions of the quadriceps in humans. J Appl Physiol (1985) 2009;106:975–983. doi: 10.1152/japplphysiol.91474.2008. [DOI] [PubMed] [Google Scholar]
- Burnley M, Vanhatalo A. Jones AM. Distinct profiles of neuromuscular fatigue during muscle contractions below and above the critical torque in humans. J Appl Physiol (1985) 2012;113:215–223. doi: 10.1152/japplphysiol.00022.2012. [DOI] [PubMed] [Google Scholar]
- Cashaback JGA, Cluff T. Potvin JR. Muscle fatigue and contraction intensity modulates the complexity of surface electromyography. J Electromyogr Kinesiol. 2013;23:78–83. doi: 10.1016/j.jelekin.2012.08.004. [DOI] [PubMed] [Google Scholar]
- Challis JH. Aging, regularity and variability in maximum isometric moments. J Biomech. 2006;39:1543–1546. doi: 10.1016/j.jbiomech.2005.04.008. [DOI] [PubMed] [Google Scholar]
- Contessa P, Adam A. De Luca CJ. Motor unit control and force fluctuation during fatigue. J Appl Physiol (1985) 2009;107:235–243. doi: 10.1152/japplphysiol.00035.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca CJ, Le Fever RS, McCue MP. Xenakis AP. Behaviour of human motor units in different muscles during linearly varying contractions. J Physiol. 1982;329:113–128. doi: 10.1113/jphysiol.1982.sp014293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dideriksen JL, Enoka RM. Farina D. Neuromuscular adjustments that constrain submaximal EMG amplitude at task failure of sustained isometric contractions. J Appl Physiol. 2011;111:485–494. doi: 10.1152/japplphysiol.00186.2011. [DOI] [PubMed] [Google Scholar]
- Enoka RM. Fuglevand AJ. Motor unit physiology: some unresolved issues. Muscle Nerve. 2001;24:4–17. doi: 10.1002/1097-4598(200101)24:1<4::aid-mus13>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- Forrest SM, Challis JH. Winter SL. The effect of signal acquisition and processing choices on ApEn values: towards a ‘gold standard’ for distinguishing effort levels from isometric force records. Med Eng Phys. 2014;36:676–683. doi: 10.1016/j.medengphy.2014.02.017. [DOI] [PubMed] [Google Scholar]
- Furness P, Jessop J. Lippold OCJ. Long-lasting increases in the tremor in human hand muscles following brief, strong effort. J Physiol. 1977;265:821–831. doi: 10.1113/jphysiol.1977.sp011746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galganski ME, Fuglevand AJ. Enoka RM. Reduced control of motor output in a human hand muscle of elderly participants during submaximal contractions. J Neurophysiol. 1993;69:2108–2115. doi: 10.1152/jn.1993.69.6.2108. [DOI] [PubMed] [Google Scholar]
- Gandevia SC. Spinal and supraspinal factors in human muscle fatigue. Physiol Rev. 2001;81:1725–1789. doi: 10.1152/physrev.2001.81.4.1725. [DOI] [PubMed] [Google Scholar]
- Glenny RW. Emergence of matched airway and vascular trees from fractal rules. J Appl Physiol (1985) 2011;110:1119–1129. doi: 10.1152/japplphysiol.01293.2010. [DOI] [PubMed] [Google Scholar]
- Goldberger AL, Amaral LAN, Hausdorff JM, Ivanov PC, Peng CK. Stanley HE. Fractal dynamics in physiology: Alterations with disease and aging. Proc Natl Acad Sci U S A. 2002a;99:2466–2472. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberger AL, Peng C-K. Lipsitz LA. What is physiological complexity and how does it change with aging and disease? Neurobiol Aging. 2002b;23:23–26. doi: 10.1016/s0197-4580(01)00266-4. [DOI] [PubMed] [Google Scholar]
- Hausdorff JM, Peng CK, Ladin Z, Wei JY. Goldberger AL. Is walking a random walk? Evidence for long-range correlations in the stride interval of human gait. J Appl Physiol (1985) 1995;78:349–358. doi: 10.1152/jappl.1995.78.1.349. [DOI] [PubMed] [Google Scholar]
- Hausdorff JM, Rios DA. Edelberg HK. Gait variability and fall risk in community-living older adults: a 1-year prospective study. Arch Phys Med Rehab. 2001;82:1050–1056. doi: 10.1053/apmr.2001.24893. [DOI] [PubMed] [Google Scholar]
- Hunter SK, Critchlow A. Enoka RM. Muscle endurance is greater for old men compared to strength-matched young men. J Appl Physiol (1985) 2005;99:890–897. doi: 10.1152/japplphysiol.00243.2005. [DOI] [PubMed] [Google Scholar]
- Hunter SK, Critchlow A, Shin IS. Enoka RM. Fatigability of the elbow flexor muscles for a sustained submaximal contraction is similar in men and women matched for strength. J Appl Physiol (1985) 2004;96:195–202. doi: 10.1152/japplphysiol.00893.2003. [DOI] [PubMed] [Google Scholar]
- Hunter SK. Enoka RM. Changes in muscle activa-tion can prolong the endurance time of a submaximal isometric contraction in humans. J Appl Physiol (1985) 2003;94:108–118. doi: 10.1152/japplphysiol.00635.2002. [DOI] [PubMed] [Google Scholar]
- Hunter SK, Griffith EE, Schlachter KM. Kufahl TD. Sex differences in time to task failure and blood flow for an intermittent isometric fatiguing contraction. Muscle Nerve. 2009;39:42–53. doi: 10.1002/mus.21203. [DOI] [PubMed] [Google Scholar]
- Johnson KVB, Edwards SC, Van Tongeran C. Bawa P. Properties of human motor units after prolonged activity at a constant firing rate. Exp Brain Res. 2004;154:479–487. doi: 10.1007/s00221-003-1678-z. [DOI] [PubMed] [Google Scholar]
- Klass M, Lévénez M, Enoka RM. Duchateau J. Spinal mechanics contribute to difference in time to failure of submaximal fatiguing contractions performed with different loads. J Neurophysiol. 2008;99:1096–1104. doi: 10.1152/jn.01252.2007. [DOI] [PubMed] [Google Scholar]
- Lipsitz LA. Physiological complexity, aging, and the path to frailty. Sci Aging Knowledge Environ. 2004;2004:pe16. doi: 10.1126/sageke.2004.16.pe16. [DOI] [PubMed] [Google Scholar]
- Lipsitz LA. Goldberger AL. Loss of ‘complexity’ and aging: Potential applications of fractals and chaos theory to senescence. JAMA. 1992;267:1806–1809. [PubMed] [Google Scholar]
- Manor B. Lipsitz LA. Physiologic complexity and aging: Implications for physical function and rehabilitation. Prog Neuropsychopharmacol Biol Psychiatry. 2013;45:287–293. doi: 10.1016/j.pnpbp.2012.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsden CD, Meadows JC. Merton PA. Isolated single motor units in human muscle and their rate of discharge during maximal voluntary effort. J Physiol. 1971;217:12–13P. [PubMed] [Google Scholar]
- Missenard O, Mottet D. Perrey S. Factors responsible for force steadiness impairment with fatigue. Muscle Nerve. 2009;40:1019–1032. doi: 10.1002/mus.21331. [DOI] [PubMed] [Google Scholar]
- Moritz CT, Barry BK, Pascoe MA. Enoka RM. Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. J Neurophysiol. 2005;93:2449–2459. doi: 10.1152/jn.01122.2004. [DOI] [PubMed] [Google Scholar]
- Peng C-K, Buldyrev SV, Havlin S, Simon M, Stanley HE. Goldberger AL. Mosaic organization of DNA nucleotides. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1994;49:1685–1689. doi: 10.1103/physreve.49.1685. [DOI] [PubMed] [Google Scholar]
- Peng C-K, Costa M. Goldberger AL. Adaptive data analysis of complexity fluctuations in physiologic time series. Adv Adapt Data Anal. 2009;1:61–70. doi: 10.1142/S1793536909000035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng C-K, Havlin S, Stanley HE. Goldberger AL. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos. 1995;5:82–87. doi: 10.1063/1.166141. [DOI] [PubMed] [Google Scholar]
- Peng C-K, Mietus JE, Liu Y, Lee C, Hausdorff JM, Stanley HE, Goldberger AL. Lipsitz LA. Quantifying fractal dynamics of human respiration: age and gender effects. Ann Biomed Eng. 2002;30:683–692. doi: 10.1114/1.1481053. [DOI] [PubMed] [Google Scholar]
- Pikkujämsä SM, Mäkikallio TH, Sourander LB, Raiha IJ, Puukka P, Skytta J, Peng C-K, Goldberger AL. Huikuri HV. Cardiac interbeat interval dynamics from childhood to senescence: comparison of conventional and new measures based on fractals and chaos theory. Circulation. 1999;100:393–399. doi: 10.1161/01.cir.100.4.393. [DOI] [PubMed] [Google Scholar]
- Pincus SM. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci U S A. 1991;88:2297–2301. doi: 10.1073/pnas.88.6.2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pincus SM. Greater signal regularity may indicate increased system isolation. Math Biosci. 1994;122:161–181. doi: 10.1016/0025-5564(94)90056-6. [DOI] [PubMed] [Google Scholar]
- Richman JS. Moorman JR. Physiological time-series analysis using approximate and sample entropy. Am J Physiol Heart Circ Physiol. 2000;278:H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- Schumann AY, Bartsch RP, Penzel T, Ivanov PC. Kantelhardt JW. Aging effects on cardiac and respiratory dynamics in healthy subjects across sleep stages. Sleep. 2010;33:943–955. doi: 10.1093/sleep/33.7.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seely AJE. Macklem P. Fractal variability: An emergent property of complex dissipative systems. Chaos. 2012;22:013108. doi: 10.1063/1.3675622. [DOI] [PubMed] [Google Scholar]
- Sejdić E. Lipsitz LA. Necessity of noise in physiology and medicine. Comput Methods Programs Biomed. 2013;111:459–470. doi: 10.1016/j.cmpb.2013.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slifkin AB. Newell KM. Noise, information transmission, and force variability. J Exp Psychol Hum Percept Perform. 1999;25:837–851. doi: 10.1037//0096-1523.25.3.837. [DOI] [PubMed] [Google Scholar]
- Slifkin AB. Newell KM. Variability and noise in continuous force production. J Mot Behav. 2000;32:141–150. doi: 10.1080/00222890009601366. [DOI] [PubMed] [Google Scholar]
- Sosnoff JJ. Newell KE. Age-related loss of adaptability to fast time scales in motor variability. J Gerontol. 2008;63:344–352. doi: 10.1093/geronb/63.6.p344. [DOI] [PubMed] [Google Scholar]
- Stergiou N. Decker LM. Human movement variability, nonlinear dynamics and pathology: Is there a connection. Hum Mov Sci. 2011;30:869–888. doi: 10.1016/j.humov.2011.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svendsen JH. Madeleine P. Amount and structure of force variability during short, ramp and sustained contractions in males and females. Hum Mov Sci. 2010;29:35–47. doi: 10.1016/j.humov.2009.09.001. [DOI] [PubMed] [Google Scholar]
- Taylor AM, Christou EA. Enoka RM. Multiple features of motor-unit activity influences force fluctuations during isometric contractions. J Neurophysiol. 2003;90:1350–1361. doi: 10.1152/jn.00056.2003. [DOI] [PubMed] [Google Scholar]
- Taylor JL. Gandevia SC. A comparison of central aspects of fatigue in submaximal and maximal voluntary contractions. J Appl Physiol (1985) 2008;104:542–550. doi: 10.1152/japplphysiol.01053.2007. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE, Larsson L. Newell KM. Effects of aging on force variability, single motor unit discharge patterns, and the structure of 10, 20 and 40 Hz EMG activity. Neurobiol Aging. 2003;24:25–35. doi: 10.1016/s0197-4580(02)00014-3. [DOI] [PubMed] [Google Scholar]
- Vaillancourt DE. Newell KM. Ageing and the time and frequency structure of force output variability. J Appl Physiol (1985) 2003;94:903–912. doi: 10.1152/japplphysiol.00166.2002. [DOI] [PubMed] [Google Scholar]
- Yamamoto Y. Hughson RL. On the fractal nature of heart rate variability in humans: effects of data length and beta-adrenergic blockade. Am J Physiol Regul Integr Comp Physiol. 1994;266:R40–R49. doi: 10.1152/ajpregu.1994.266.1.R40. [DOI] [PubMed] [Google Scholar]


