Non-invasive assessment of failure torque in rat bones with simulated lytic lesions using computed tomography based structural rigidity analysis

Abstract

This study applies CT-based structural rigidity analysis (CTRA) to assess failure torque of rat femurs with simulated lytic defects at different locations (proximal and distal femur) and diameters (25% and 50% of the cross-section at the site), and compared the results to those obtained from mechanical testing. Moreover, it aims to compare the correlation coefficients between CTRA-based failure torque and DXA-based aBMD versus actual failure torque.

Twenty rats were randomly assigned to four equal groups of different simulated lesions based on size and location. Femurs from each animal underwent micro-computed tomography to assess three-dimensional micro-structural data, torsional rigidity using structural rigidity analysis and dual energy X-ray absorptiometry to assess bone mineral density. Following imaging, all specimens were subjected to torsion.

Failure torque predicted from CT-derived structural rigidity measurements was better correlated with mechanically derived failure torque [R² = 0.85] than was aBMD from DXA [R² = 0.32].

In summary, the results of this study suggest that computed tomography based structural rigidity analysis can be used to accurately and quantitatively measure the mechanical failure torque of bones with osteolytic lesions in an experimental rat model. Structural rigidity analysis can provide more accurate predictions on maximal torque to mechanical failure than dual energy X-ray absorptiometry based on bone mineral density.

1. Introduction

Strength of bone is determined by its material composition and structural organization. Pathologic fractures occur when the structural and/or material properties of bone are compromised to the degree that the bone can no longer withstand a given load. Based on the assumption that fragility fractures are caused by low bone mass, the World Health Organization (WHO) has identified individuals at risk for these fractures based on their areal bone mineral density (aBMD, g cm⁻²) measured by dual energy X-ray absorptiometry (DXA). However, DXA does not measure volumetric bone mineral density (vBMD, g cm⁻³) and does not distinguish changes in bone mineral composition from changes in bone structure and geometry. This distinction is important when diagnosing and treating skeletal pathologies associated with altered bone properties. Additionally, it has been shown that aBMD based fracture predictions are neither sensitive nor specific (Riggs and Melton, 2002; Heaney, 2003) for metastatic lesions.

In contrast, quantitative computed tomography (CT) based structural rigidity analysis (CTRA), a 3D imaging modality, can provide information about specific changes in bone microstructure and tissue density for both cortical and trabecular bone. This technique can be used to non-invasively assess the axial, bending and torsional rigidities of bones from their trans-axial cross-sectional images (Whealan et al., 2000; Hong et al., 2004; Snyder et al., 2006, 2009). With this technique, modulus of elasticity is treated as a function of bone density, and bone geometry is represented by its cross-sectional area and moment of inertia (Martin, 1991; Turner, 2002). While CTRA has been used to assess fracture in studies of benign and metastatic musculoskeletal lesions in humans, the efficacy of this technique in assessing fracture risk in animal models of skeletal metastasis has not been characterized. Since osteolytic metastasis is associated with significant bone resorption and frequently leads to pathological fracture (Bunting, 1985), we decided to use a simulated lytic defects model for this study.

Given the ability of CTRA to detect structural and material changes within bone, we hypothesize that CTRA-based failure torque correlates well with actual failure torque in bones with simulated lytic defects, and that CTRA is significantly more accurate than DXA-based aBMD measures in predicting failure torque. To that end, we aim to use CT-based structural rigidity analysis to assess the failure torque of rat femurs with simulated lytic defects at different locations (proximal and distal femur) and diameters (25% and 50% of the cross-section at the site) and compare the results to those obtained from mechanical testing. Moreover, we aim to compare the correlation coefficients between CTRA-based failure torque and DXA-based aBMD versus actual failure torque.

2. Materials and methods

2.1. Specimen preparation

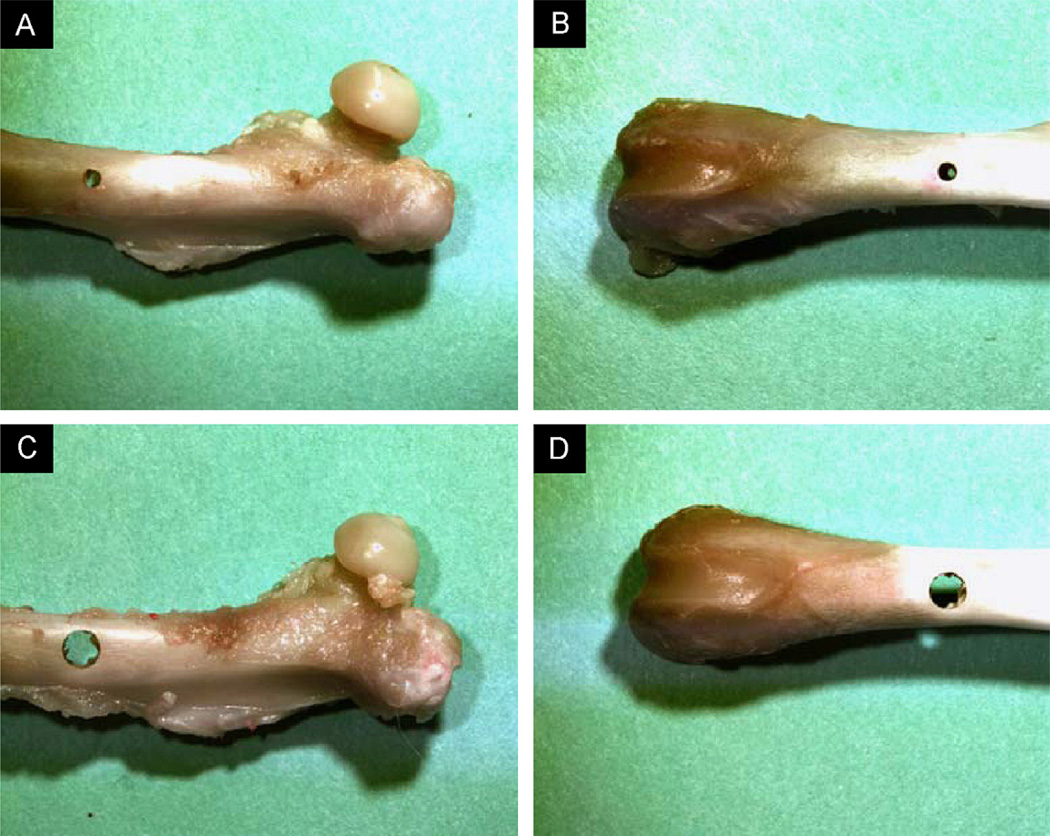
The study protocol was approved by Beth Israel Deaconess Medical Center’s Institutional Animal Care and Use Committee (IACUC). Twenty female Sprague Dawley rats (15 weeks old, mass = 250–275 g) were obtained from Charles River Laboratories (Charles River, Charlestown, MA, USA). One femur per animal, selected at random, was excised for the study. In order to simulate lytic defects, circular through holes were created in the sagittal plane using a carbide drill bit under copious irrigation, while securing the bone in place using a padded vise. The defect diameters were chosen based on previous work performed by the authors (Hong et al., 2004). Four equally sized groups (n = 5) were created based on different configurations of defect size and location: (1) Group A: proximal defect of 25% femoral diameter (Fig. 1A), (2) Group B: distal defect of 25% femoral diameter (Fig. 1B), (3) Group C: proximal defect of 50% femoral diameter (Fig. 1C) and (4) Group D: distal defect of 50% femoral diameter (Fig. 1D).

Fig. 1.

Representative specimens demonstrating the simulated lytic lesions in groups. (i) A: proximal femur at 25% diameter; (ii) B: distal femur at 25% diameter; (iii) C: proximal femur at 50% diameter and (iv) D: distal femur at 50% diameter.

2.2. Imaging and image analysis

Areal bone mineral density (aBMD, g cm⁻²) and bone mineral content (BMC, g) in the anterior–posterior direction were measured at the site of the defect using DXA (Lunar PIXImus2, General Electric, Waukesha, WI, USA). A uniformly sized region of interest (ROI), defined as a 38 pixel wide by 33 pixel long (1 pixel = 0.186 mm → ROI of 7.06 mm by 6.14 mm), was used to calculate aBMD and BMC for all specimens.

Sequential transaxial images through the entire non-embedded bone sections were obtained using micro-computed tomography (µCT40, Scanco Medical AG, Brüttisellen, Switzerland) at an isotropic voxel size of 20 µm, integration time of 250 ms and tube voltage and current of 55 kVp and 145 µA, respectively. Bone mineral density was calculated using a hydroxyapatite phantom (0, 100, 200, 400 and 800 mg HA cm⁻³), supplied by the manufacturer, to convert X-ray attenuation coefficient (µ) to an equivalent bone mineral density.

2.3. Structural rigidity analysis

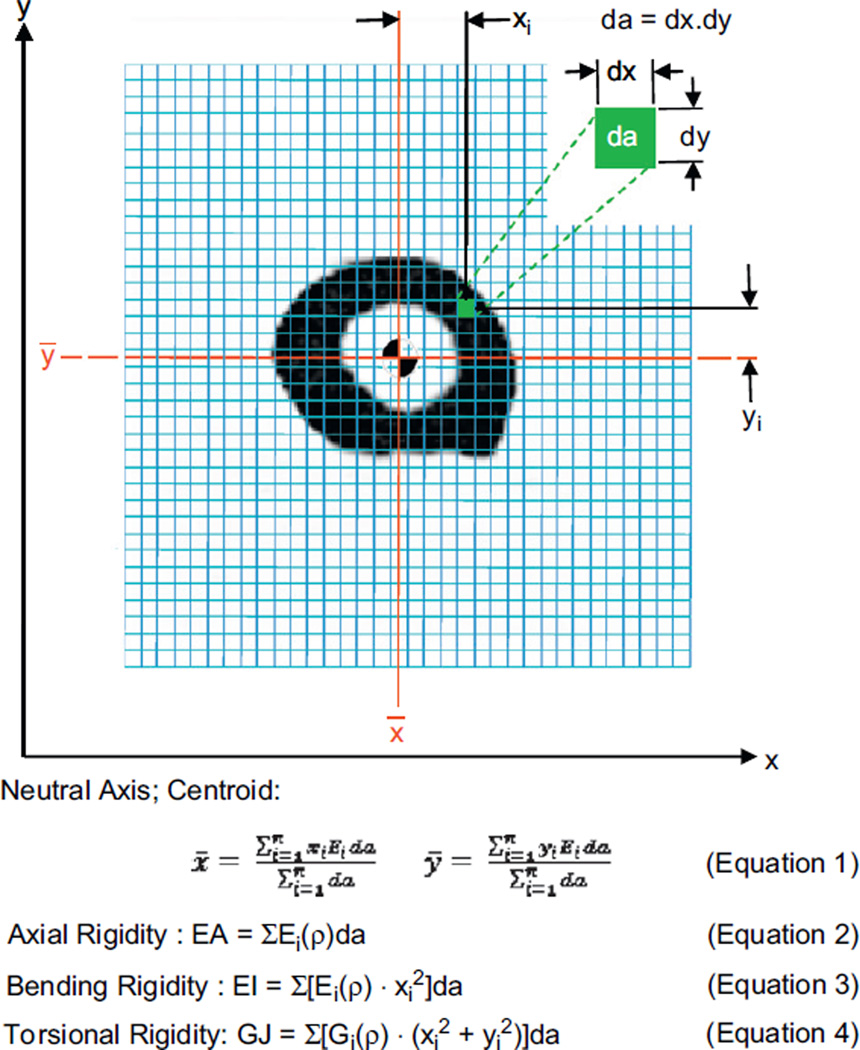
Torsional rigidity (GJ), the product of the bone tissue shear modulus of elasticity and bone cross-sectional geometry, describes the structural behavior of a bone and its resistance to deformation when subjected to torsional loading. Torsional relationships describing the mentioned mechanical properties of rat bone as a function of µCT generated density were used to convert the densities to their respective modulus values (Cory et al., 2009; Nazarian et al., 2009; Fig. 2). The failure torque was calculated based on previous work by the authors using the GJ obtained from CTRA imaging and other specimen-specific information (Nazarian et al., 2009):

$$G=\frac{4T(1+{\xi }^2)}{k{\xi }^2\alpha }$$ (1)

where T is torque, ξ the ratio of the minor axis to major axis (assessed from µCT imaging for each slice), α is a constant (0.06) representing twist per unit length, and k is the torsional constant, which is equivalent to J (polar moment of inertia) for a hollow elliptical cross-section such as rat femur.

Fig. 2.

Schematic diagram illustrating the pixel-based CTRA analysis technique to assess axial (EA), bending (EI) and torsional (GJ) rigidities presented here. Each grid element is intended to represent one pixel (exaggeration of the grid element size is solely for illustration purposes). The EA, EI and GJ equations have been presented here, where ρ represents bone density, x_i and y_i represent the distance of each pixel from the y- and x-axes respectively, da represents the area of each pixel, E_i represents Young’s modulus of elasticity (defined as the ratio of tensile strength to strain in the linear region) and G_i represents shear modulus (defined as the ratio of shear stress to shear strain in the linear region). Each pixel is filtered through a bone density threshold and converted to material modulus (E or G depending on the loading mode) and using empirically derived relationships for rat bone as a function of bone density. Relative distance between pixels is determined by calibration of imaging modality. Modulus weighted neutral axis and centroid (Eq. (1) in Fig. 2) are determined based on the coordinates of the ith pixel, its modulus (E_i), area (da) and total number of pixels in the bone cross-section (n). Axial rigidity (Eq. (2) in Fig. 2) is the sum of the products of each elastic modulus (E_i) and pixel area (da). Bending rigidity about the y-axis (Eq. 3 in Fig. 2) is the sum of the products of the elastic modulus (E_i), square of the ith pixel distance to the neutral axis (_y) and the pixel area (da). Torsional rigidity (Eq. (4) in Fig. 2) is the sum of the products of the density dependent shear modulus (G_i), square of the pixel distance to the centroid (x̄, ȳ) and the pixel area (da).

Reconfiguring Eq. (1), failure torque can be defined as

$$T=\frac{GJ{\xi }^2\alpha }{4(1+{\xi }^2)}$$ (2)

For a shape such as that of rat femur, Cowin elegantly demonstrated that St. Venant’s method of solution of the isotropic elastic torsion problem for a particular cross-section also solves the elastic torsion problem for a cylinder with shape intrinsic orthotropy of the same cross-section, given that the isotropic shear modulus G is replaced by the orthotropic shear modulus G_tz. Shape intrinsic orthotropy is defined as the general situation when the symmetry coordinate system for orthotropic symmetry of a cylinder is coincident with the long axis of the cylinder, with the local tangent and normal to a closed family of curves, one of which forms the lateral boundary of the cylinder (Cowin, 1987). Additionally, St. Venant observed that the stresses and strains in a cylinder with arbitrary cross-section could be closely approximated by those of a cylinder with elliptical cross-section (Cowin, 2001). Based on the observations by St. Venant that for most practical purposes the stresses and strains in any cylinder could be closely approximated by those of a cylinder with elliptical cross-section (Cowin, 2001) and the availability of micro-computed tomography to generate accurate geometric properties of long bones for every slice, the authors generate an equivalent ellipse for each cross-section of the bone and apply the torsion equations derived above to calculate effective torsional material properties of the cross-section. An equivalent ellipse is calculated using the k and A values obtained from µCT imaging and calculating the major axis and ξ for each cross-section. A similar approach can be undertaken for other bones to generate the appropriate values for these constants.

2.4. Mechanical testing

Following µCT imaging, a torsion system designed for a non-homogeneous orthotropic or non-axis-symmetric specimens that accommodates out of plane warping and bending was used for this study (Nazarian et al., 2008). Specimens underwent angular displacement controlled torsion to failure at a rate of 0.083 rad s⁻¹. Angular displacement (θ, rad) and torque (T, Nm) were recorded for the duration of each test. Angular failure displacement (θ_mech, rad) and failure torque (T_mech, Nm) were calculated at the point where the angular load–displacement curve ceased to be linear (yield point).

2.5. Statistical analysis

Simple linear regression analysis was applied to test whether failure torque as assessed by µCT based CTRA correlated with actual failure torque, and if so, the relationship between actual failure torque and CTRA-based failure torque differed from the identity line, y = x (which implies a slope of 1 and intercept of 0).

Multiple regression was used to assess the correlation between failure torque values obtained from mechanical testing and µCT based structural rigidity analysis with defect location and size as additional independent variables.

The coefficient of determination (R²) was used as the criterion to compare the different regression models. Our strategy was based on the Fisher R-to-Z transformation with a back-transformation of the bounds to produce a 95% confidence interval (CI) and Z test with a two-sided P value for the difference between the correlations being compared (CTRA-based failure torque versus DXA-based aBMD; Dunn and Clark, 1969; Meng et al., 1992). Slopes for the different regression models were compared using generalized estimating equations (GEEs) with the Wald test for comparing slopes between groups. In order to assess the accuracy of the CTRA technique, failure torque differences between mechanical testing and CTRA-based techniques were compared for each pair of data using analysis of variance (ANOVA) followed by a Bland–Altman analysis.

Statistical analysis was performed using the SPSS software package (version 18.0, SPSS Inc., Chicago, IL, USA). Two-tailed values of P < 0.05 were considered statistically significant.

3. Results

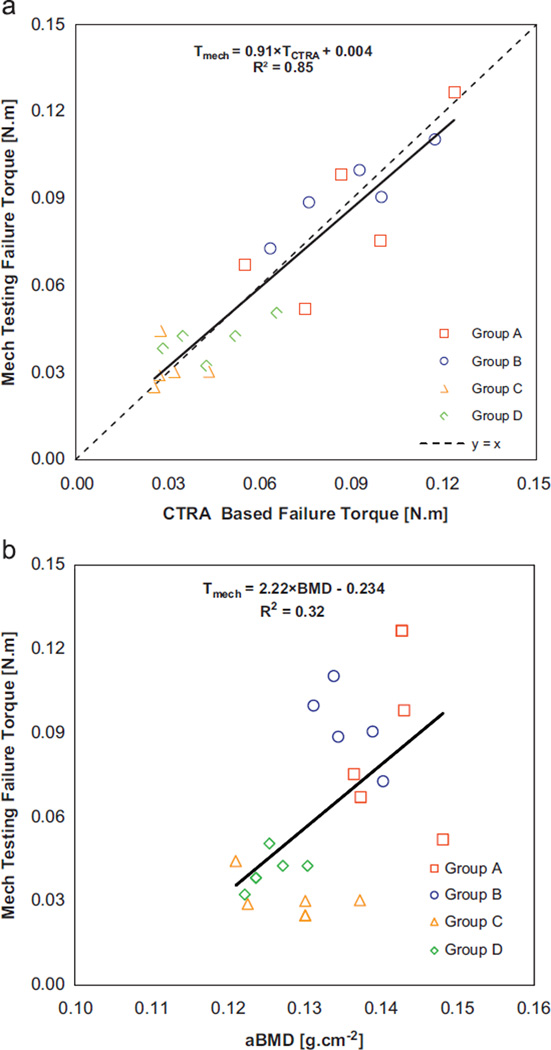
All specimens subjected to pure torsion fractured through the defect in a spiral line of fracture as shown in Fig. 3. CTRA-based failure torque was highly correlated with mechanical testing based failure torque results [T_mech = 0.91 T_CTRA + 0.004, R² = 0.85, P < 0.001, Fig. 4a]. Additionally, analysis results demonstrated that the slope and y-intercept of the failure torque regression line were not different from those of the line y = x (P = 0.46), suggesting that the correlation between the CTRA-based failure torque and actual failure torque, as assessed by mechanical testing, was not skewed. aBMD could describe only 32% of the variation in the actual failure torque [aBMD = 2.22T_mech–0.234, R² = 0.32, P = 0.054; Fig. 4b].

Fig. 3.

Images of 4 failed specimens following mechanical testing, where spiral fracture through the defect is observed.

Fig. 4.

(a): Linear regression of failure torque as assessed by CTRA versus mechanical testing and (b): linear regression of failure torque as assessed via mechanical testing versus DXA-based aBMD.

Multiple regression with defect size and location and actual failure torque as independent variables and CTRA-based failure torque as dependent variable indicated a strong correlation between the two failure torques (adjusted R² = 0.83, P < 0.001), where defect size (P = 0.43) and location (P = 0.95) had no effect on the correlation. Using Z-transformation test, coefficients of determination for the linear regressions where actual failure torque was the dependent variable and CTRA-based failure torque was the independent variable were significantly better than the linear regression where DXA-based aBMD was the independent variable (P < 0.001).

Failure torque differences between actual mechanical testing and CTRA methods were calculated for all pairs of data. There were no differences between the 4 groups (A–D) with respect to the average difference between actual mechanical and CTRA-based failure torques (p = 0.82). Overall, the mean torque difference was essentially zero, but the standard deviation of the difference was 0.012 Nm. Thus, a Bland–Altman method would indicate that the 95% confidence interval around the difference is ± 0.024 Nm as an estimate of the accuracy and error associated with predicting failure load.

4. Discussion

This study investigated the correlation of CTRA-based failure torque and DXA-based aBMD with actual mechanical testing in a simulated osteolytic rat model. We demonstrated that torsional rigidity measured non-invasively by CTRA can explain 85% of the variation in failure torque as obtained by mechanical testing, while DXA-based aBMD can explain only 32% of variation in failure torque. The correlation coefficient of CTRA-based failure torque versus actual failure torque was significantly higher than that of the DXA-based aBMD versus actual failure torque (P < 0.001). We also tested our hypothesis in different defect sizes (25% versus 50% of bone diameter) and locations (proximal versus distal) across a long bone, indicating that CTRA is location independent, since linear regressions from all sites correlate better with failure torque than aBMD. We did not observe any significant difference among different size holes, a finding also confirmed by Robertson et al. (2007), who also showed that lesion size did not correlate with bone strength.

Non-invasive prediction of failure torque in a simulated osteolytic rat model aims to answer a clinically relevant question, although these results should be interpreted with some considerations regarding this model. Naturally, bone metastasis starts by homing of tumor cells in the bone marrow sinusoids with initial involvement of trabecular bone and later extension to cortical areas (Phadke et al., 2006). We have simulated this phenomenon by creating a symmetric through hole in the bone. Additionally, our model is limited to two anatomical locations across a single bone, where bones are tested under torsional loading. We acknowledge that lytic lesions occur in a variety of locations across the skeleton and are subjected to complex mechanical loading conditions. Despite these limitations, we believe that this model provides useful insight into the ability of CTRA to predict failure torque in bones with osteolytic lesions.

The current gold standard for fracture risk assessment is DXA, which measures the average bone mineral content and density in a 2D projected area without the ability to differentiate changes in bone microstructure with those in bone tissue density. In contrast, computed tomography provides an accurate measurement of the changes in both bone tissue mineral density and microstructure in cancellous and cortical bone. Previous studies by Whealan et al. (2000) indicated that CT-derived metrics can accurately predict the biomechanics of vertebral fractures with lytic lesions. Snyder et al. (2009) have recently shown clinical application of CTRA with a cohort of 94 patients with spinal metastases. They showed that CTRA was significantly more specific (while maintaining high sensitivity) in predicting vertebral fractures than the current clinical guidelines. This technique is a computationally efficient approach that is relatively easy to implement using CT scan data to assess fracture risk.

The results of our study suggest a considerable potential for using CTRA in animal models to non-invasively assess failure torque in bones with lytic defects.