Integrative models of vascular remodeling during tumor growth

Abstract

Malignant solid tumors recruit the blood vessel network of the host tissue for nutrient supply, continuous growth, and gain of metastatic potential. Angiogenesis (the formation of new blood vessels), vessel cooption (the integration of existing blood vessels into the tumor vasculature), and vessel regression remodel the healthy vascular network into a tumor-specific vasculature that is in many respects different from the hierarchically organized arterio-venous blood vessel network of the host tissues. Integrative models based on detailed experimental data and physical laws implement in silico the complex interplay of molecular pathways, cell proliferation, migration, and death, tissue microenvironment, mechanical and hydrodynamic forces, and the fine structure of the host tissue vasculature. With the help of computer simulations high-precision information about blood flow patterns, interstitial fluid flow, drug distribution, oxygen and nutrient distribution can be obtained and a plethora of therapeutic protocols can be tested before clinical trials. In this review, we give an overview over the current status of integrative models describing tumor growth, vascular remodeling, blood and interstitial fluid flow, drug delivery, and concomitant transformations of the microenvironment. © 2015 The Authors. WIREs Systems Biology and Medicine published by Wiley Periodicals, Inc.

Introduction

Blood vessels supply every part of a living organism with oxygen and nutrients for which reason the establishment of a mature organized vascular network is fundamental for tissue homeostasis. Therefore angiogenesis, the creation of new blood vessels, is vital for successful embryogenesis and organ growth and plays a major role in wound healing and tissue repair. During these processes, angiogenesis is tightly controlled by manifold molecular and mechanical factors^1,2 resulting in tissue-specific, structured, hierarchically organized vascular networks optimized to meet the needs of the organ and of the body. Importantly, all living cells of the tissue are commonly located within 100–200 µm of perfused blood vessels, the diffusion limit for oxygen. Solid tumors are in many respects similar to a developing organ³ comprising also a functional vasculature.

Tumor vasculature, the blood vessel network supplying a growing tumor with nutrients such as oxygen or glucose, is in many respects different from the hierarchically organized arterio-venous blood vessel network in normal tissues. In order to grow beyond a size of approximately 1–2 mm³, the tumor has to switch to an angiogenic phenotype and to induce the development of new blood vessels mainly via sprouting angiogenesis, i.e., the formation of new vessels from pre-existing vasculature.^1,2 This process is regulated by a variety of pro- and antiangiogenic factors and as a consequence the anatomy of a solid, vascularized tumor grown within in a vascularized tissue displays a characteristic compartmentalization into essentially three regions^4–7: (1) the highly vascularized tumor perimeter with a microvascular density (MVD) that is substantially higher than the MVD of the surrounding normal tissue; (2) the well-vascularized tumor periphery with dilated blood vessels and a tortuous vessel network topology; and (3) a poorly vascularized tumor center with large necrotic regions threaded by only a few very thick vessels that are surrounded by a cuff of viable tumor cells.

Several microscopic phenomena on the cellular level have been identified to be involved in this remodeling process: (1) Angiogenic sprouting: Upregulation of proangiogenic factors in tumor-cells [such as vascular endothelial growth factor (VEGF) and other growth factors] can create additional vessels via sprouting angiogenesis in some regions of the tumor, most frequently in its perimeter.^1,2 (2) Vessel regression: The maintenance of incorporated mature microvessels depends on the survival of endothelial cells (ECs) and their survival is intimately tied to their local microenvironment and, in particular, to the presence of pericytes, survival promoting cytokines, and extracellular matrix (ECM) proteins. The major molecular players that control this process are angiopoietins and VEGF,^6,7 and in coopted blood vessels Ang-2 is upregulated, causing the destabilization of their capillary walls, i.e., the detachment of pericytes from the endothelial tube. Once ECs are separated from pericytes, they become particularly vulnerable resulting in the regression of destabilized vessels. (3) Vessel dilation: The vascularization program of the proangiogenic phenotype can be switched from sprouting angiogenesis to circumferential growth in the interior of the tumor. This switch is mediated by the guidance molecules EphB4 (and its ligand ephrinB2), both expressed by ECs of malignant brain tumors,⁸ which acts as a negative regulator of blood vessel branching and vascular network formation, and also reduces the permeability of the tumor vascular system via activation of the Ang-1/Tie-2 systems at the endothelium/pericyte interface.

Besides pro- and antiangiogenic molecular factors, physical determinants such as mechanical, hydrodynamical, and collective processes are involved in the transformation or remodeling of the original arterio-venous blood vessel network into a tumor-specific vasculature. As for the generation of vascular networks in organ development a complex interplay among chemical signals, guidance proteins, and mechanical forces determines the morphology and the function of the emerging tumor vasculature.

Theoretical modeling and computer simulations can help to understand and quantify the influence of the various factors determining this complex multiscale phenomenon (for recent reviews, see Refs ^9–10; and references therein). The ultimate clinical goal of computer-based models is the development of patient-specific predictive models to improve diagnosis, therapy planning, and treatment of a tumor. A particular problem in anticancer therapies is the delivery of blood borne drugs to the tumor cells,¹¹ which is intimately linked to the peculiarities of the tumor vasculature and the resulting characteristics of interstitial fluid pressure and flow within tumors.¹² Ideally, an integrative model of the dynamics of the tumor vasculature would be able to predict consequences of, e.g., antiangiogenic therapies¹³ or tumor vessel normalization,¹⁴ for a specific tumor in a specific tissue by performing computer simulations rather than an expensive clinical trial. The same holds for drug-induced alterations of tissue permeabilities^15,16 or other therapies targeting parameters defining the spatiotemporal distribution of blood and interstitial fluid flow. Realistic quantitative in silico models for tumor vasculature will also help to develop new diagnostic tools by providing detailed information about the characteristics of the distribution of oxygen, glucose, or blood-borne tracer particles within the tumor. Last, but not least, the tumor vasculature is besides the lymphatic network, the main entry point for circulating tumor cells leading to metastasis, responsible for most cancer deaths.¹⁷ In silico models of tumor vascularization will help to shed light on the complex interplay between antiangiogenic therapies and metastatic potential of the growing tumor.

Model Components

A vascularized solid tumor growing in healthy tissue is a complex system, similar to a developing organ.³ A first step in a systems biological approach is to identify several interacting subsystems and to find appropriate mathematical representations for each as well as for their biochemical and physical interactions between them. Consequently, mathematical models for vascular remodeling during tumor growth comprise several interacting components or modules, among which the following ones might represent a backbone: (1) a tumor growth module representing the expanding tumor mass within healthy tissue, involving the proliferation, movement, and death of tumor cells, which depend on available oxygen and nutrients, on available space, solid pressure, drug concentrations, and so on; (2) a vasculature module comprising a representation of a blood vessel network that includes intravascular blood flow and that changes dynamically due to the presence of pro- and antiangiogenic factors, solid pressure, and blood perfusion; (3) a module for intravascular transport of oxygen [via red blood cells (RBC)], extravasation and subsequent diffusion of oxygen; (4) a module for fluid extravasation and the emerging interstitial fluid flow; and (5) a module for blood-borne drug transport, extravasation of drugs, convective and diffusive drug transport through the interstitium, and adsorption of drug by tumor cells. In the following, we summarize the physiological characteristics of these subsystems and the commonly used modeling approaches for the individual modules.

Tumor Growth

Two basically distinct mathematical approaches toward avascular tumor growth can be taken: (1) particle-based models, in which each cell (or microscopic tissue volume) is represented by a particle that can move, divide, vanish, and interact with other particles, and (2) continuum models, in which the spatiotemporal evolution of the densities, pressure field, velocities fields, and so on of cells of different phenotypes are described by partial differential equation. Particle-based models follow the spirit of molecular dynamics or Monte Carlo simulations¹⁸ commonly used in physics and chemistry and allow for a microscopic description of tissues, whereas continuum models find their roots in the constitutive mesoscopic equations of hydrodynamics, phase mixtures, nonlinear elasticity, and so forth. In both cases, the additional challenge posed by growing tissues in general and tumors in particular is cell proliferation and death.

Particle-based Models

The minimal requirements for single-cell-based models involve cell–cell adhesion, volume exclusion, growth pressure, fluctuating random forces, expansion during maturation, division when mature, and apoptosis under certain circumstances. Cell division rate and apoptosis should depend on oxygen and/or glucose supply. Physically, a tissue surface tension should arise from the cell–cell interactions and force balance and momentum conservation should be fulfilled.

Single Particle Models in Continuous Space

The models of Drasdo,¹⁹ based on Langevin dynamics (thus following a stochastic approach), and Elgeti,²⁰ based on dissipative particle dynamics (following a deterministic approach), fulfill the aforementioned requirements and reproduce experimentally measured morphological properties of tumor spheroids growing in vitro²¹: a compartmentalization of the tumor into a proliferating rim, a shell of quiescent tumor cells in the interior, and a necrotic core emerging beyond a certain tumor radius. By varying adhesion parameters and confinement conditions, these models predict mechanically induced morphological instabilities such as buckling²² and fingering.²³

Integration of a particle-based tumor growth model into an integrative modeling framework is straightforward: The single-cell parameters determining the cells phenotype, comprising growth rate, division rate, motility, susceptibility to external clues, and so on are then made depend on the current local concentrations of oxygen, nutrients, growth factors, therapeutic drugs, and so forth as determined by other modules, as well as on mechanical solid pressure and shear forces. Conceptually, more difficult is the integration of a blood vessel network that is not represented by individual cells, but by, e.g., pipes. For low relative vessel volume, it is a good approximation to neglect the excluded volume of the individual pipes as well as the longitudinal deformation of blood vessels due to solid pressure. Nevertheless, the latter plays a role for transverse deformation of vessels (i.e., vessel constriction), eventually leading to vessel collapse (see below).

Stochastic Models on Discrete Lattices

An alternative particle-based approach is the Cellular Potts Model (CPM).^24,25 In contrast to the former single-cell-based models the CPM operates on a two- or three-dimensional (3D) grid or lattice and each cell (or microscopic piece of tissue) is represented by a certain number of connected lattice points, in arbitrary shapes. An energy function reminiscent of the Potts model in statistical physics (therefore the name) quantifies the interactions between cells, and Lagrangian parameters provide bounds for volume and surface fluctuations of the individual cells. The dynamics of this system is defined to be stochastic and the emerging stochastic process is computationally studied with Monte Carlo simulations. The transition probabilities are chosen to fulfill the detailed balance with respect to the Boltzmann weight for the model energy. Different interaction energies between cells of different times lead to differential adhesion and concomitantly to cell sorting and related phenomena. Introducing a nutrient concentration field in connection with a diffusion-limitation parameter, the model predicts fingering instabilities due to competition for nutrients.²⁶ The latter is a diffusional instability as in dendritic growth, but not a mechanical instability. This tumor growth model has also been combined with a vessel network model²⁷ (see below).

Caveats

Particle-based models are analyzed with the help of computer simulations and it is clear that the concept ‘one particle–one cell’ becomes computationally extremely demanding when studying macroscopic vascularized tumors of a size a several cm³, in which case one faces billions (10⁹) of tumor or tissue cells. The mere memory requirements would be enormous, in the range of tens to hundreds of Gigabytes depending on the number of variables describing the state of each individual cell (such as position, age, genetic state, etc.). Thus, particle-based models are currently restricted to rather modest system sizes (i.e., length scales of a few hundred micrometer). It is, however, conceivable to extend the particle concept to ‘one particle–one piece of tissue’, in which a single particle is equipped with the mechanical, chemical, and dynamical properties of hundreds of cells.

Continuum Models

Continuum models provide a coarse-grained description of tumor development via partial differential equations that have to be solved numerically by using, e.g., finite element methods implemented on a computer. The latter discretize the problem and one should bear in mind that modern computers can currently handle only of the order of 10⁶ discretization volumes or voxels. For a tumor volume of 1 cm³, this implies that one voxel has a volume of 100 µm³, which could contain thousands of tumor or tissue cells. Thus, in continuum models for macroscopic tumors all quantities, such as cell densities, concentration fields, velocity, pressure, force fields, and so on, always represent a spatial average.

A comprehensive review on continuum models for avascular tumor growth can be found in Ref 10. An integrated description of the developing tumor should comprise terms that quantify cell proliferation and death, cellular motility via chemo-, hapto-, and mechanotaxis, cell–cell adhesion, and possibly visco-elastic and compressibility properties. Cell proliferation and dead are represented by source terms in the constitutive equations for the temporal evolution of cell densities, which might depend on other concentration and in particular on pressure. Cellular motility is represented by convective terms that depend on gradients of other fields, and cell–cell adhesion can, e.g., be incorporated by introducing a surface tension for the tumor boundary.^28,29 Solid pressure can either be defined by a constitutive equation of state (a nonlinear relation between density and pressure) or results from additional equations modelling stress relaxation in tumors.³⁰ Mechanical effects involving solid pressure and stress play an important role, too, as has been demonstrated in Ref 31, where the diameter of growing cellular spheroids in gels of different rigidity have been measured. It was demonstrated that the tumor size depends on the normal load exerted by the surrounding gel on the multicellular spheroid. Thus, solid pressure eventually leads to growth arrest, and is also responsible for vessel collapse.³²

A number of growth instabilities may emerge depending on the details of the chosen growth model and the physical parameters: a diffusion-limited instability similar to dendritic growth in diffusion-limited aggregation³³ originating in preferential growth at tips of the tumor boundary that has better access to oxygen or nutrients, a fingering instability similar to the Saffmann-Taylor instability in Hele-Shaw cells³⁴ that occurs when one immiscible fluid of lower viscosity penetrates another fluid of higher viscosity, and buckling or wrinkling instabilities similar to elastic materials under an external load which occur when a growing tissue generates sufficient residual stress to destabilize its body.³⁵ In addition to morphological changes in which the tumor mass maintains its integrity, aggressive tumors in nutrient-poor environments can break up into small fragments that penetrate the surrounding tissue, as predicted by a model presented in Ref 36. These instabilities are universal and each has its own basic mathematical representation sometimes hidden within the complexity of a given tumor growth model. Which one is physiologically relevant and should be integrated into a continuum modeling framework depends on the tumor type, the (healthy) host tissue, and the microenvironment. It should be mentioned that the aforementioned instabilities also occur in appropriately designed particle-based models.

Vasculature and Blood Flow

Solid tumors grow in an originally healthy tissue, which already contains a normal vasculature, a hierarchically organized arterio-venous blood vessel network, and which is then dynamically modified by the growing tumor. An integrative modeling approach thus has to address two issues: first, it has to find an appropriate representation of the original vasculature of the host tissue; and second, the dynamics of the given blood vessel network has to be defined, which includes the insertion of new vessels via angiogenesis as well as the removal of existing vessels (old and new) via vessel regression, and the modification of existing vessels via dilation, constriction or occlusion. Moreover, the network carries a blood flow, which has to be represented, too.

In well-vascularized tissue, the average intercapillary distance is 50–100 µm, in highly vascularized tissue like brain even less (depending on the oxygen demand and the resulting diffusion length), implying the importance of the incorporation of the original vasculature into a model for tumor-induced angiogenesis. This vasculature is organized in a hierarchical way, in which an arterial and a venous tree are interdigitated by capillaries. Oxygen and other nutrients are distributed into the surrounding tissue by the lowest-level capillaries, the two trees representing their supply and drainage system. The microvascualr density (MVD), given by the average intercapillary distance, is homogeneous in one kind of tissue to provide a homogeneous oxygen and nutrient supply, but the two interdigitating hierarchical trees form a spatially very inhomogeneous blood vessel network. Consequently, the vascular remodeling process in a growing tumor will also be spatially inhomogeneous: Sprouting angiogenesis occurs mainly from capillaries and venules, higher-level arteries protected by a thick layer of pericytes are more stable and regress later or not at all, regression of higher level arteries has fatal consequences for the whole arterial subtree below it, and newly formed vessels between arteries and veins could act as shunts redirecting huge amount of blood. In more than one respect, the original vasculature determines the fate of the emerging tumor vasculature.

Original Vasculature

In mathematical modeling, blood vessel networks are commonly represented as pipe networks, and with modern computers the microvasculature of even macroscopic tissue samples of several cubic centimeter can be represented completely, i.e., vessel by vessel: With a characteristic intercapillary distance of 100 µm a tissue volume of 1 cm³ contains of the order of 10⁶ vessels, which is manageable. Also the blood flow computation on pipe networks of this size is manageable as the connectivity is low which allows for sparse matrix inversion methods to solve the underlying set of blood flow equations. Thus, in order to be physiologically or even clinically relevant a major modeling effort has to be made to represent the original vasculature of the tissue of interest.

Recent progress in enhanced image acquisition techniques such as confocal microscopy and microcomputer tomography (μCT) applied to the microvasculature in connection with improved image processing allowed to obtain 3D vessel network representations of the complete microvasculature of several different tissues: pieces of the human cerebral cortex,³⁷ the complete rat heart vasculature,³⁸ cortical gray matter of primate brain³⁹ (see Figure 1) and even breast tumor microvasculature.⁴⁰ For the reconstructed networks, the resulting blood flow and other hemodynamic parameters have been computed^39–42 using Poiseulle's law for ideal pipe flow and a radius-dependent effective viscosity taking into account the Faraeus-Lindqvist effect.^43,44 Care has to be taken as to choose appropriate boundary conditions for the tissue samples under consideration⁴⁵ because blood pressure or flow values in the vessels exiting or entering the sample are not know experimentally.

Figure 1.

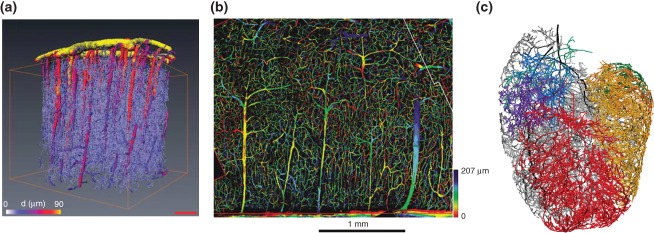
Vascular network reconstruction: (a) A section of a cortical blood vessel network after reconstruction based on micro-CT images. Vessels are color coded according to their radius. (Reprinted with permission from Ref 39. Copyright 2010 Nature Publishing Group). (b) Depth-coded image obtained from confocal laser microscopy. This shows a section of human brain tissue (Reprinted with permission from Ref 37. Copyright 2006 Wiley-Blackwell). (c) A coronary vascular network based on micro-CT images. Various subnetworks are distinguished by random colors (Reprinted with permission from Ref 38. Copyright 2007 Elsevier Science).

On the way to an integrative modeling framework for vascular tumor growth within a particular tissue type, first a representative microvascular network for this tissue should be reconstructed, as reviewed above, and then be used as the initial vasculature for an integrative model. This is a step that has still to be carried out, up to now researchers relied on computer-generated synthetic networks. Early modeling attempts represented the original vasculature as a capillary network in which capillaries are arranged in a 2D or 3D grid.^46–51 These grid networks can be adapted to a given MVD, average capillary radius and total pressure drop, but they lack a hierarchical organization, neither represent arteries nor veins, and produce artifacts due to a global flow bias in one direction imprinted by the boundary conditions. In Refs ^52–53, a synthetic arterio-venous vessel networks were generated that match the observed statistical distributions and satisfied given pressure drops and flow rates (see Figure 2(a)).

Figure 2.

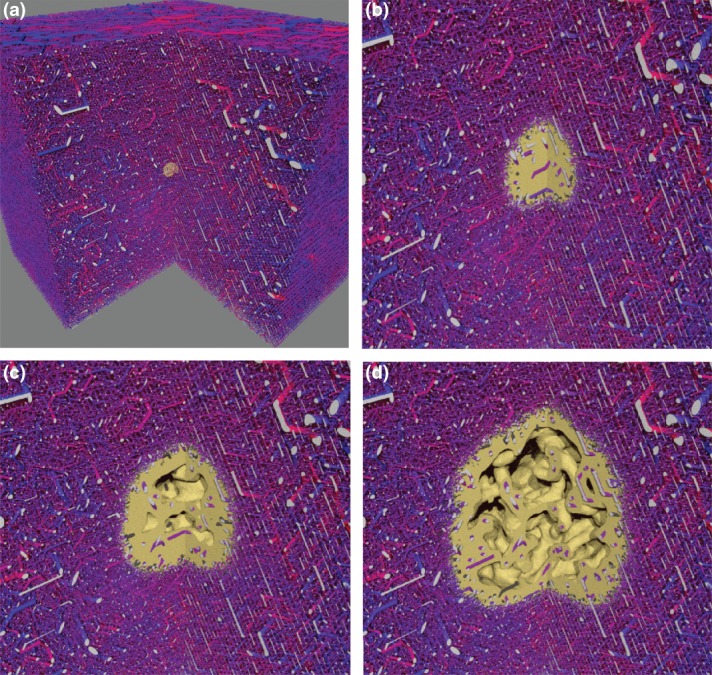
Tumor vascular network remodeling, based on simulations of the model described in Ref 54: An initial vascular network was synthetically generated. Then a simulation of tumor growth was performed using this network. The network edges are visualized as cylinders, color coded according to their associated blood pressure value. The viable tumor tissue is visualized as yellow mass. Hollow interior regions appear due to necrotic tissue which was once viable but has died from oxygen deprivation. The simulated area is a box of ca. 8 mm lateral size of which a quarter is cut away for display purposes. The cutting faces of vessels are colored light grey. (a) The initial state with a small tumor nucleus. (b) 200 h later angiogenesis has set in. Many tumor vessels have collapsed due to reduced blood flow. Surviving interior vessels are dilated due to switching from angiogenesis to circumferential growth. (c) After 400 h, the tumor network is thinned out sufficiently that tumor regions are located well outside the diffusion distance of oxygen, causing hypoxia and subsequent necrosis. (d) As the tumor continues to grow it pushes the region of angiogenic activity further into normal tissue and leaves a sparse network behind its rim. This state, as seen after 800 h simulated time, shows typical features of tumor vasculature: compartmentalization, highly vascularized rim, decreasing vascular density toward the center where the network is very sparse, vessel dilation, loss of hierarchical organization. The model parameter selection for this case was guided by experimental data for human melanoma.

Blood Flow and Hematocrit

Blood flow rates in all vessels are determined according to conservation of mass at vessel junctions and the Hagen-Poiseuilles law for ideal pipe flow, in which the blood flow rate is proportional to the pressure gradient along the vessel and the fourth power of the radius and inversely proportional to the blood viscosity. The blood pressures at inlets (veins) and outlets (arteries) are predetermined through boundary conditions. This leads to a system of linear equations the solution of which yields the pressure values at the vessel junctions. The boundary conditions are of Dirichlet type where the pressure at all root nodes is set to a fixed value p^(BC)(r) depending on the respective vessel radius.

Blood viscosity and oxygen content depend on hematocrit, which has therefore to be taken into account. Hematocrit is the fractional volume taken up by RBCs, which might vary from vessel to vessel. The viscosity dependence, which is known as Fahraeus-Lindqvist effect, is treated by decomposing the viscosity into the plasma viscosity and a correction due to the RBC content. For the latter, a phenomenological formula is commonly used.^43,44

Two well-known effects contribute to the uneven distribution of hematocrit.⁵⁵ First, the Fahraeus effect, where the hematocrit in a small perfused tube is lower than the hematocrit at the inlet. This is due to the formation of a RBC-free boundary layer, so that RBCs in a central RBC rich core travel faster than the average blood velocity. The second effect is the phase separation effect where RBCs at arterial bifurcations prefer to flow into either of the branches depending on blood flow rates and geometry. Again aphenomenological formula was constructed that describes the phase separation effect at a junction based on in vivo measurements.⁵⁵ It yields the downstream RBC flow in one downstream vessel at a bifurcation as a function of the upstream hematocrit and the radius and blood flow of downstream and upstream vessels. This relation holds for arterial bifurcations, at venous junctions the downstream hematocrit is determined by mass conservation alone as only the hematocrit in one downstream vessel is unknown. As blood flow depends on hematocrit and hematocrit distribution at bifurcations depends on blood flow one conveniently uses iteration schemes.⁵⁶

Vascular Remodeling

Blood vessel network remodeling during tumor growth transforms the hierarchically structured initial network of healthy tissue into a tumor-specific vasculature and involves several processes. The most important ones are angiogenesis, vessel dilation, vessel wall degeneration, and vessel collapse. Besides angiogenesis also vasculogenesis, vasculogenic mimicry, and intussusception can contribute to the formation of new blood vessels.² In addition to the latter, the tumor coopts the already existing vasculature and often destroys much of it, which has dramatic consequences for network morphology, blood and interstitial fluid flow patterns and drug delivery. Recent comprehensive reviews either on mathematical models for the formation and remodeling of vascular networks⁵⁷ or on a systems biology view on blood vessel growth and remodeling⁵⁸ summarizes the current state of knowledge. Here we sketch the most important processes that must be taken into account.

Sprout generation. VEGF stimulates ECs to proliferate and migrate. The initial event is the formation of a sprout made of one or two ECs of a specialized phenotype (tip cells) that starts to migrate into the ECM. A common modeling approach^54,59,60 is to substitute the effect of the complex biochemical pathway involving pro- and antiangiogenic factors leading to a sprouting event by a stochastic model in which sprouts emerge from existing vessels with a certain probability that depends on the local VEGF concentration, possibly also antiangiogenic factors, tumor environment, and lateral inhibition. The latter, delta-like 4 (Dll4)/notch-mediated process, prevents sprouts from being initiated where another one has already been created earlier in the neighborhood (for a modeling approach, see Ref 61). Within solid tumors, angiogenic sprouting is strongly inhibited, instead the presence of VEGF leads to circumferential growth⁸ (see below). Depending on the local VEGF gradient, the sprout is also initiated with a preferred migration direction.

Sprout migration. The tip cell of a sprout responds to VEGF stimulation by extending filopodia and migrating toward the signal, i.e., the VEGF source.⁶² Behind the tip cells, the so-called stalk cells maintain the contact with the original location of sprout formation. They divide in response to VEGF by which the sprout elongates. The tip cells are further stimulated and the process repeats. Frequently one stipulates that sprout migration is biased along a VEGF gradient, but regarding the fact that the average vessel to vessel distance in healthy tissue is less than 100 µm and that sprouts produce filopodia of 10–20 µm length in all directions a migrating sprout will hit nearby vessels with a high probability, irrespective of potential variations of the growth factor gradient, which are low anyway close to the tumor boundary, where most of the angiogenic activity takes place. Modeling has shown^54,59,60 that imprinting a growth direction at sprout initialization parallel to the local VEGF gradient is sufficient and that later directional correction due to VEGF gradient variations do not significantly improve target finding in dense vessel networks. In case a target vessel is not found within a certain distance (ca. 200 µm) found sprouts retreat and vanish. Finally, sprouts become normal vessels if the tip cells fuse with another vessel (anastomosis) such that blood can flow. Obviously, blood flow has to be recomputed after such an event. Sprout initiation can also start from sprouts that emulates tip splitting as observed in vivo and in vitro.

Wall degeneration. As has been reported in Ref 6–7 the tumor environment degrades vessel walls by detachment and disintegration of cell layers and membranes around the vessel lumen. It can be implemented, e.g., by a parameter for each vessel segment, that reflects the vessel wall thickness for normal vessels, and continuously decreases for tumor vessels (i.e., vessels in contact with tumor cells) with the a given rate until zero.

Vessel collapse. Vessels inside the tumor can collapse and disintegrate completely.^6,7 Obviously, blood flow is pinched off inside a collapsed vessel that necessitates again the recomputation of blood flow. It can be modeled as a stochastic process^54,59,60 where a vessel segment can be removed with a certain probability that depends on its wall degeneration parameter, blood flow shear stress, and local solid stress. As inside the tumor wall degeneration and solid stress do not vary strongly it is the shear force dependence of the collapse probability that appears to have the most important effect on the morphology of the tumor vasculature.⁴⁹

Vessel dilation. It has been shown⁸ that inside tumors VEGF-stimulated angiogenic activity switches from angiogenic sprouting to circumferential growth. During circumferential growth, the vessel radius increases continuously with a certain rate until maximum radius is reached or local conditions (such as solid stress or flow conditions) induce dilation arrest. It should be emphasized that this process is particular important for blood flow characteristics within the tumor as the blood flow varies with the fourth power of the radius and only modest vessel radius increase by a factor of 2 or 3 has lead to an extreme increase in blood flow.

Structural adaption. In response to tissue needs, microvascular networks are capable of inducing long-term changes of vessel diameters.⁶³ Based on experimental data from healthy tissues, a theoretical model of this structural adaption quantifies the change of vessel diameters in dependence of various stimuli such as endothelial wall shear stress, intravascular pressure, a flow-dependent metabolic stimulus, and a stimulus conducted from distal to proximal segments along vascular walls.⁶³ It is not clear in how far these radius adaption mechanisms work also for tumor vessels, but is straightforward to implement them.^46,47,50

The above processes can be incorporated into a modeling approach based on a representation of vessel segments by flow-carrying cylinders with variable radius and permeability, which neglects topological shape transformations of the endothelial layer. Intussusception, which is the transluminal pillar formation and remodeling through the interaction of blood flow induced shear force and endothelial sheets, and vascologenesis, the formation of capillary networks by self-assembly of ECs assemble via directed cell migration and cohesion need more sophisticated modeling approaches, which are restricted to small sample sizes. For a mathematical model for intussusception, see Refs ^64–65 and models for vasculaogenesis are reviewed in Ref 66.

Oxygen Concentration

The theory of oxygen transport to tissue started a century ago with Krogh⁶⁷ is now well developed.^68,69 To formulate an integrative modeling approach with which one can compute the spatiotemporal evolution of oxygen concentration in large volumes (e.g., 1 cm³) of inhomogeneously vascularized tissues one has to find a sufficiently coarse-grained description of oxygen transport, which we sketch here.

The main carrier of oxygen in blood are RBCs containing a large amount of the protein Hemoglobin (35% of the total weight), which has four oxygen binding sites resulting in an oxygen-binding capacity of 1.34 mL oxygen per gram of hemoglobin. Oxygen dissolved in the blood plasma contributes only a few percent to the total oxygen concentration in blood. Thus the hematocrit computation along the lines sketched in Section Blood Flow and Hematocrit serves also as a basis to calculate the oxygen concentration—first in the individual blood vessels, then within the surrounding tissue.

The fraction of occupied binding sites depends on the partial pressure PO2 of dissolved oxygen, and this dependence is conveniently described by a Hill equation.⁶⁸ Oxygen is extravasated from the blood stream through the vessel walls into the tissue the oxygen partial pressure of blood drops on its journey from main arteries through the vasculature into the veins. In principle, oxygen can flow in and out of the vessels depending on the difference between intravascular and interstitial oxygen partial pressure. The oxygen flux gives rise to a loss/gain in oxygen partial pressure and thus to the oxygen saturation, which has to be taken into account in the computation of the intravascular oxygen partial pressure.

Oxygen transport into the tissue is diffusive with boundary conditions determined by an oxygen current density across vessel walls. Radial oxygen transport is a complex problem by itself. More accurate models include the effects of boundary flow layers, and diffusion within RBC compartments.^70–73 These models achieve very good agreement with experiments but they require the solution of nonlinear convection–diffusion type partial differential equation in cylindrical geometry. For large blood vessel networks, such approaches are prohibitively expensive. Instead Secomb et al.⁷⁴ assumed the oxygen flux to be proportional to the difference between oxygen partial pressures at the inner and outer vessel walls (assumed to be constant along the whole circumference) with the proportionality constant being an oxygen permeability of the vessel walls. The complexities of radial transport are incorporated into a vessel radius dependence of the permeability K based on data presented in Ref 71.

Secomb et al.⁷⁴ also conceived a computational approach that uses Greens Functions to formulate the solution for a system of coupled equations describing diffusion in tissue and transvascular exchange. In general, a Green's function G(x, x) describes the response of a linear differential L operator at location x to a point-like unit source at location x′. In the case of pure diffusion, the Green's function falls off like 1/|x − x′|, which implies an interaction between all discretization points in the discretized equations for the numerical solutions. The solution and storage of such ‘dense’ systems are much more demanding in both time and memory than sparse systems with nearest neighbor interactions, i.e., as they arise from finite difference methods. In fact, the tissue sections analyzed in Ref 74 where quite small on the submillimeter scale, but an advantage of the method is a fast convergence and an elegant handling of transvascular coupling, alleviating the need for excessively fine tessellation for boundary conditions.

Goldman and Popel⁷⁵ coupled a small blood vessel network to interstitial space via boundary conditions that relate the radial oxygen flux out of the vessels at each point on the vessel walls with the PO2 gradient at the respective location in the interstitial space. While being accurate, the method of transvascular coupling requires a fine resolution of the numerical grid to resolve the PO2 gradients around the vascular walls. Indeed, in Ref 75 a tissue block with a length of 400 µm was considered which was discretized into 200 grid points, where a typical capillary has a radius of 3 µm. Several follow-up papers^76–80 applied this method to sections of muscle tissue and analyze various pathological conditions and networks with different characteristics. The limitation to relatively small systems has however remained.

In order to target larger tissue volumes, the same remarks as for continuum models of tumor growth hold: In order to handle volumes of the order of 1 cm³ with around 10⁶ discretization points one has to average oxygen extravasation (i.e., the oxygen source term in the diffusion equation) over volumes with a lateral size of 100 µm, possibly containing already 10–20 vessels, an approach that has yet to be tested for its efficiency and accuracy. As an example for the application of such a scheme the emerging oxygen distribution together with the haemoglobin saturation is shown in Figure 3.

Figure 3.

Tumor oxygen distribution, based on simulations of the model described in Ref 54, with a vascular network and tumor growth module as in Figure 2, augmented by an oxygen concentration field computation as outlined in Section Oxygen Concentration: The distribution of intravascular and tissue oxygen was computed for an artificially generated vascular network. Tumor vascular remodeling was simulated, where the tumor size increases from a small nucleus to ca. 4 mm diamter, which is about half of the lateral size of the simulation box. Parameter settings were guided by experimental data from breast tumors. The result is a typical chaotic compartmentalized tumor network which is connected to an arterio-venously structured vasculature of the host. This configuration was taken as input for a detailed computation of oxygen. Respective model couples advective oxygen transport by the blood stream via transvascular fluxes with diffusion within the tissue domain and seeks a self consistent solution. Advection in each vascular segment is approximated as one dimensional problem, neglecting radial concentration and velocity variations. These images depict slices through the simulation domain where the location of the tumor is indicated roughly by the circle. (a) depicts the vascular and tissue oxygen partial pressure (PO2). Vessels are shown as cylinders, but everything outside a central slab of 300 µm thickness has been cut away. The remaining vessels protrude up from the cutting plane showing the tissue oxygen distribution. (b) The vascular oxygen saturation where the slab thickness has been increased to 600 µm.

Chemical Concentration Fields

The basis for the description of dissolved chemicals is a diffusion convection reaction equation which determines the dynamical evolution of the concentration of a constituent, such as growth factors and nutrients.⁸¹ A prominent representative is VEGF which is overexpressed in under-oxygenated tumor cells. Its local production rate is coupled to the state of tumor cells, which again depends on local oxygen concentration. VEGF occurs in different Isoforms, soluble and matrix-bound, and binds to receptors on the EC membrane, i.e., vessel walls, and can degrade. Matrix-bound VEGF can be cleaved by Matrix Metalloprotease (MMP), which is released by migrating sprouts (see below) to dissolve the ECM.

If one neglects convective transport of VEGF by the interstitial fluid instead of solving a diffusion equation one conveniently uses a simpler and faster approximation based on a Green's function approach⁴⁸: every source site generates a linearly decaying contribution to the VEGF concentration with the cutoff or diffusion radius. Consequently, sprouting occurs within the cutoff radius of oxygen deprived tumor cells and a concentration gradient arises along which sprouts are oriented.

Interstitial Fluid Flow

Interstitial fluid is commonly modeled as a liquid within a porous medium, e.g., Refs ^{54, 82–85} constituted by the ECM and cells. Combining d'Arcys law, which relates the fluid velocity with the fluid pressure gradient via a proportionality constant that represents a tissue-dependent permeability for fluid flow, with the fluid conservation law yields an elliptic partial differential equation for interstitial fluid pressure with source terms. The latter is composed of contributions from the vessel network and lymphatic sinks. Both are determined by the flux across the channel walls, which enter quantitatively as channel surface area densities. For vessels, this flux is driven by the pressure difference and an osmotic contribution (Starlings equation).⁸⁶ For lymphatics one usually assumes an analogous relation but neglects osmosis due to the lack of data. Vessel wall and lymphatic wall permeabilities appear as additional physiological parameters.

As not many data are available for lymph networks, except it is drastically reduced, if not completely destroyed within solid tumors, one usually assumes a homogeneous density of lymphatic sinks in the different compartments (low in tumors and high in healthy tissue).

The standard approach for modeling exchange with vessels on a small-scale would again use boundary conditions at the vessel walls, while tessellating the surrounding space with a fine-grained mesh. However, this would make the large length scale one is interested in inaccessible due to the system size. Instead one can integrate the flux (approximately) over the vessel surfaces within each numerical grid cells and add it as source term.⁵⁴ An approximation inherent to this method is that the space covered by the vasculature is not excluded from the interstitial space. As an example for the application of such a scheme the emerging interstitial fluid pressure together with the fractional blood volume distribution is shown in Figure 4.

Figure 4.

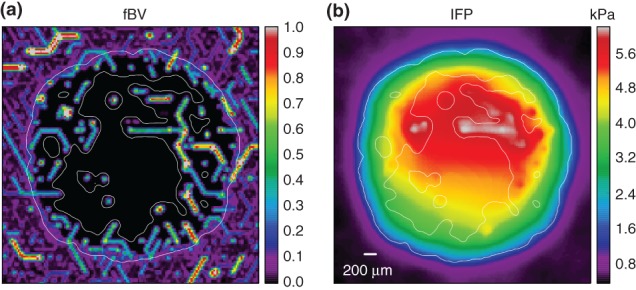
Interstitial fluid flow, based on simulations of the model described in Ref 54, with a vascular network and tumor growth module as in Figure 2: (IFF) and interstitial fluid pressure (IFP) were computed for an artificially generated vascular network, incorporating a tumor vascular network in its center as a result of simulated tumor growth and vascular remodeling. Parameter settings were guided by experimental data for melanoma. The resulting network was taken as input for the IFF model. It was assumed that IFF behaves like flow through a porous medium following Darcy's law where flow velocity is proportional to the hydrostatic pressure gradient. Vessels can be sources or sinks of interstitial fluid, depending on the blood − IF pressure difference. The IFP coupling to tumor vessels was assumed to be particularly strong due to increased leakiness (permeability). A homogeneous background of lymphatics absorbs most of the flow coming from the tumor. These two plots depict a slices although the center of the tissue domain, displaying the fractional vascular volume (percentage occupied by vessels) in (a) and the IFP in (b). The location of the tumor is best inferred by the sharp drop in fBF, but it is also indicated by a thin white line. The IFP profile exhibits the expected plateaus near the center of the tumor and a steep gradient near the tumor edge. The simulation moreover predicts heterogeneities due to the particular vessel arrangement. It also shows that tumor vessels can reabsorb a significant amount of fluid if their blood pressure is much lower than neighboring vessels.

In principle, the loss of blood plasma volume due to extravasation into the interstitial space should be take into account in the mass balance for blood flow through the vasculature. It turns out that this loss lies in the range of less than one percent⁵⁴ so that it can, as a first approximation, be neglected.

Drug Transport and Delivery

After injection of a drug into a main artery, it will be transported with the blood flow downstream and then extravasated through the vessel walls into the interstitial space, where it is then diffusively or convectively transported and delivered to the target cells. The starting point to compute blood-borne drug transport is a given configuration for the vasculature with precomputed variables for flow, flow velocity, vessel length, and radius. The computational scheme used in Refs ^{51, 60, 87–89} involves a mass parameter associated with each vessel describing the amount of drug in the blood volume contained in the vessel. The mass content is deterministically updated in successive steps as follows: First, the drug amount flowing out of vessels is determined and added to corresponding node mass variables. Under the assumption of perfect mixing, the nodal masses are then redistributed into further downstream vessel, by which mass conservation is strictly enforced. In order to simulate the application of drug over a certain time interval, various injection schemes (therapeutic protocols) into the main arteries can be applied.

Interstitial drug transport and uptake of drug are modeled as diffusion advection process in the interstitial fluid and sequestration into the cell constituent. One distinguishes between the concentrations in the interstitial fluid and the concentration within cells as average over the solvent volume. The constitutive equation is again a diffusion convection reaction equation with source/sink terms that involve extravasation from vessels, lymphatic uptake, and exchange between interstitial fluid and cells.^54,83,84

Current Implementations and Results

Early Modelling Attempts

Earlier work focusing on tumor-induced angiogenesis can roughly be divided into three categories: (1) continuum models without a proper representation of a blood vessel network and blood flow (see e.g., Refs ^90–92); (2) hybrid models with a fixed vessel network geometry and a dynamically evolving tumor (see, e.g., Refs ^{46–47, 93}), and (3) hybrid models with a fixed tumor (as a source of a diffusing growth factor) and a dynamically evolving tumor vasculature starting from a single parent vessel far away from the growth factor source (inspired by the original work of Anderson and Chaplain,⁹⁴ see e.g., Refs ^{83, 88–89, 95–97}). The latter models are also denoted as vessel-ingrowth models as the whole tumor vasculature grows from outside toward the tumor surface, a setup motivated by VEGF experiments in the rabbit eye cornea.⁹⁸

Models of category 1 contained just the tumor growth module (in Section Continuum Models) and chemical concentration fields (Section Chemical Concentration Fields), whereas models of category 2 comprised tumor growth (Section Tumor Growth), an original vasculature and blood flow (Section Vasculature and Blood Flow) with vascular adaption but no vascular remodeling (see, however, Ref 50 for an Ansatz with vessel pruning), with oxygen (Section Oxygen Concentration) in a rudimentary form and chemical concentration fields (Section Chemical Concentration Fields). Category 3 models as in Refs ^{88–89, 96} finally incorporated (in addition to chemical concentration fields) vascular remodeling only via sprouting angiogenesis, blood flow (Section Vasculature and Blood Flow) and drug delivery (Section Drug Transport and Delivery), some even interstitial fluid flow.^83,95,97 The caveat of blood (and interstitial fluid) flow and drug delivery studies within vessel ingrowth models (as reviewed in Ref 96 are unrealistic predictions for blood flow and vessel perfusion due to the lack of an initial vasculature. As tumor vessels are destined to be far away from a well-perfused parent vessel the emerging blood pressure gradients are shallow, flow velocities low, and perfusion impeded.

The process of sprouting angiogenesis from a single parent vessels with a static VEGF source representing the tumor was also the focus of recent detailed modeling attempts.^99,100 Subsequent work was still inspired by these vessel-in-growth models comprising the modules of category 3 plus elaborated tumor growth modules,^{52,53,101,102}: although in these studies the tumor evolved dynamically, focusing on a detailed analysis of the interactions between tumor and host tissue, all new vessels started to grow from one or more parent vessels in a nonphysiologically far distance from the tumor. The remodeling process that transforms the original arterio-venous vasculature of the host tissue into a tumor specific vessel network has not been addressed with this Ansatz.

Studies of Vascular Remodeling

The first studies of vascular remodeling during tumor growth that aimed at the incorporation of all modules described in Section Model Components assumed a simplified initial vasculature representing a capillary network arranged on a regular grid: Bartha and Rieger⁴⁸ introduced the concept of vessel cooption, regression, and dilation into models for vascularized tumor growth, which were extended from two space dimension, and studied the dynamical change of vessel network morphology in tumor growth in two space dimensions^48,51 and in three space dimensions.⁴⁹

As a robust model prediction emerged the characteristic compartmentalization of tumor vasculature into the highly vascularized tumor perimeter, a well-vascularized tumor periphery with dilated blood vessels and a tortuous vessel network topology and a poorly vascularized tumor center with large necrotic regions threaded by only a few very thick vessels that are surrounded by a cuff of viable tumor cells. Models with an arterio-venous initial vasculature showed an identical compartmentalization.^54,59,60 Wu et al.^84,103 later added interstitial fluid flow and drug delivery (see below) to a model with a grid-like geometry for the initial vasculature. Shirinfard et al.²⁷ used a particle (or cell)-based approach also starting with a small grid-like initial network. It was found that tumor cells proliferate preferentially along existing vessels.

The essential drawback of models assuming a grid-like initial vasculature is a global blood flow bias from one corner of the simulation box toward the opposite imprinted by the boundary conditions for the blood pressure. Such a bias is generally absent in large physiological blood vessel networks and leads, if shear force-determined vessel collapse is taken into account to a preferential direction of inner tumor vessels.^48,49,51 Moreover, due to the absence of strong pressure differences between nearby vessel (as they occur between arteries and veins in realistic tumor vessel networks¹⁰⁴), the formation of strongly perfused shunts is excluded., altering the expected blood and interstitial fluid flow characteristics in an unphysiological way.

These artifacts could only be avoided by using realistic arterio-venous initial networks, as was performed by Welter et al. in Refs ^59–60 with a model that incorporated a tumor growth module (Section Tumor Growth), a dynamical blood vessel network with an arterio-venous initial vasculature (Section Vasculature and Blood Flow), an oxygen module (Section Oxygen Concentration), VEGF concentration field (Section Chemical Concentration Fields), and blood borne drug transport (Section Drug Transport and Delivery). The authors augmented this modeling framework in Ref 54 by an interstitial fluid flow module (Section Interstitial Fluid Flow) and a drug delivery module (Section Drug Transport and Delivery), which completed the modeling framework described in Section Model Components.

The initial blood vessel network used^54,59,60 was synthetically generated and fulfilled certain physiological statistical constraints as homogeneous microvascular (capillary) density, vessel radius and branching number distribution, homogeneous oxygen distribution in the tissue, and so on. Indeed, the emerging tumor vasculature morphology and blood flow distribution displayed significant differences when compared quantitatively with tumor vasculature predicted by models using a grid like initial network. In Figure 2, we show a sequence of tumor-vessel-configurations obtained from a computer simulation of the model described in Ref 54. The strong influence of the initial vascular network on the tumors growth dynamics and its long-time composition was also reported by Perfahl et al.,¹⁰⁵ who used an small initial network that was derived from experimental data.

Predictions

A number of results have been obtained by the studies within the modeling framework described in the last subsection that appear to be robust against further model refinements. The characteristic compartmentalization of the tumor vasculature was already mentioned in the previous subsection. In Ref 49, it was pointed out that the formation of the global morphology of the tumor vasculature is dominated by vessel collapse inside the tumor rather than angiogenic sprouting, which is restricted to the outer rim of the growing tumor. Consequently, its (apparently) fractal nature is reminiscent of a flow correlated percolation process⁴⁹ rather than an invasion percolation as was hypothesized in Refs ^106–107.

The formation of hot-spots, i.e., regions of drastically increased blood density within the tumor was shown to be related to regions with strong blood pressure gradients in the initial arterio-venous vasculature.⁵⁹ For shear force-determined vessel collapse, such a scenario is plausible, as between vessels with strongly different blood pressure a shunt generated by angiogenic sprouting will carry a strong blood flow and therefore collapse with a correspondingly reduced probability. Blood-borne drug transport within the tumor is actually very efficient,⁶⁰ in contrast to what is predicted by vessel-in-growth models.^87,108 The reason is that badly perfused vessels collapse with increased probability which implies that predominantly well perfused tumor vessels will sustain.

Interstitial fluid pressure is generally increased in vascularized tumors but computer simulations of interstitial fluid flow in vascularized tumors within an arterio-venous initial network showed⁵⁴ that it cannot be a direct cause for impeded drug delivery, as was hypothesized in Refs ^{11–12, 109} The model predicts that an increase of the permeability of vessel walls or tumor tissue or lymphatic walls will always increase interstitial fluid pressure but also the interstitial fluid flow and thus improves drug delivery via convective transport. The physical explanation is simply that it is misleading to consider the pressure drop along the vessel wall alone as the driving force for IFF—in principle the complete network of hydraulic resistors has to be taken into account to obtain reliable predictions. Similar results were later obtained with a related model using a grid-like initial vasculature.¹⁰³

A consequence of the simulations performed in Ref 54 is that a tumor therapy aimed solely at reducing the vessel leakiness cannot be effective, implying that concepts like normalization of tumor vasculature¹⁴ have intrinsic problems if they target for a reduction of vessel wall permeability (or hydraulic conductivity) alone. Only cases in which the tumor vessel walls are so leaky that they extravasate such a substantial amount of blood plasma (including drug) that leads to a drastic reduction of the downstream flux rate and thus blood-borne drug concentration a decrease of wall permeability would improve tumor vessel perfusion and potentially drug delivery. This extreme case was studied in the highly simplified model presented in Ref 110, which uses a percolation network as a representation of the tumor vasculature. It should be noted that the drug delivery improvement reported there is not a consequence of reducing the putative interstitial fluid pressure barrier^11,12,109 but simply a consequence of improved vessel perfusion in the central part of the assumed percolation network. It is questionable that comparable effects can be obtained in realistic tumor vasculature derived from arterio-venous networks and displaying the characteristic compartmentalization mentioned above.

The simulation results of Ref 54 also demonstrated that increasing the permeability of tumor tissue itself has the potential to improve drug delivery, supporting experimental observations reviewed in Ref 15–16. We would like to stress that the point here is not whether experiments or simulations were first in revealing correctly the role of different permeabilities (hydraulic conductivities) in the complex tumor-vasculature-lymphatics system. The point is that in the end, ideally, they should reach identical conclusion—but simulations, or in silico models, are much faster and much cheaper than clinical trials.

Outlook

The current state of in silico models of the dynamical evolution of tumor vasculature is still in the beginning and still far from the ultimate goal to become a patient-specific predictive tool to improve diagnosis, therapy planning and treatment of a tumor. We have sketched the basic components that an integrative model must necessarily have and showed that the few serious implementations of model frameworks that comprise all the sketched modules already produce nontrivial predictions that are in agreement with recent experimental data.

The different modeling approaches of different groups now appear at least to converge in an agreement about which components an integrative model must necessarily have. Still, as long as different models are based on fundamentally different initial blood vessel networks (grid-like networks in some and synthetic arterio-venous networks in other models) a quantitative comparison between their predictions is not very meaningful. Some qualitative features (such as tumor compartmentalization and relations between interstitial fluid pressure and vessel wall permeabilities) appear to be robust against details of the initial vasculature, others are not (e.g., vessel radius distributions, blood, and interstitial fluid flow patterns). Future developments would certainly profit if simulation results between different models could be compared on a ‘test case’, either a precisely defined bench-mark model or against detailed quantitative experimental data.

To make further progress efforts have to be made that exceed even the Cardiac Physiome Project,¹¹¹ which deals with the vasculature of only one type of tissue, the heart, whereas tumors and tumor vasculature differs from tissue type to tissue type. Since, as we have tried to emphasize here, the original vasculature of the healthy tissue in which a tumor is growing, influences strongly the characteristics of the emerging tumor vasculature, one needs detailed, reliable and accessible data for them. A first step toward the realization of integrative models that can differentiate between different tissues or cancer types is to have a library of representations of the complete (micro-) vasculature of large (macroscopic) patches of different tissue types. Some of them are already available (see Section Original Vasculature), others have still to be collected. Ideally one has several samples for each type of vasculature in order to have a measure for statistical fluctuations and an equivalent to different patients. The vasculature representations have to be made accessible to other groups working on the implementation of the complete modeling framework. Although we did not mention it explicitly similar libraries for the (tissue) micro-environment as well as for different cancer cell types should be established.

Next, a unified frame for the implementations of the different model components should be set up, which allows for an easy exchange and integration of new modules and still has sufficient flexibility to incorporate features not discussed so far, like a model of cell metabolism, genetic variability, macro-environment etc. It is clear that such an endeavor is too large to be tackled by a single research group. The EU spends a billion Euro to build a brain simulator—there are not many chances to have a tumor simulator for less.