Assessing the Impact of Population Stratification on Association Studies of Rare Variation

Abstract

Aims

The study of rare variants, which can potentially explain a great proportion of heritability, has emerged as an important topic in human gene mapping of complex diseases. Although several statistical methods have been developed to increase the power to detect disease-related rare variants, none of these methods address an important issue that often arises in genetic studies: false positives due to population stratification. Using simulations, we investigated the impact of population stratification on false-positive rates of rare-variant association tests.

Methods

We simulated a series of case-control studies assuming various sample sizes and levels of population structure. Using such data, we examined the impact of population stratification on rare-variant collapsing and burden tests of rare variation. We further evaluated the ability of two existing methods (principal component analysis and genomic control) to correct for stratification in such rare-variant studies.

Results

We found that population stratification can have a significant influence on studies of rare variants especially when sample size is large and the population is severely stratified. Our results showed that principal component analysis performed quite well in most situations while genomic control often yielded conservative results.

Conclusions

Our results imply that researchers need to carefully match cases and controls on ancestry in order to avoid false positive caused by population structure in studies of rare variants, particularly if genome-wide data are not available.

Introduction

Genome wide association studies (GWAS) have successfully identified 7817 associations between common variants and 743 traits as of November of 2012 (http://www.genome.gov/gwastudies/). However, the majority of these common SNPs have very small effect sizes (odds ratio between 1.1-1.5) and no apparent causal effects on the disease or trait of interest [1]. As GWAS are primarily designed to detect associations with common variants, an intuitive explanation of the missing heritability is that many common diseases are actually caused by rare variants [2,3]. Published literatures show that the odds ratios of rare variants are often much larger than those of common variants [4]. Furthermore, rare variants are more likely to have causal effects than common variants in that they are expected to change amino acids and further influence interactions among proteins [4]. From an evolutionary point of view, rare variants are rare either because they are selected against or because they are new and have not been under selection for a long time [5]. The above arguments suggest a role for rare variants in common disease and, with developments in cost-effective sequencing technology (which can obtain thousands of sequences in parallel), widespread search for rare susceptibility variants is now feasible. Sequencing studies have already identified several rare variants associated with common diseases, including type 2 diabetes [6] and asthma [7].

Using the popular case-control design, many studies are attempting to identify rare causal variants that increase risk for complex diseases. However, such studies require robust and powerful statistical tools for rare variant analysis that are somewhat distinct from those used previously to analyze common variants. As power to detect association with an individual variant is lower for less frequent variants, existing analytic methods typically used for GWAS are not powerful when applied to studies of rare variants. To avoid this power loss, most rare variant methods collapse less frequent variants in a region together into a composite variable, and then test the association between the composite variable and the disease. For example, the “Combined Multivariate and Collapsing” (CMC) method of Li and Leal [8] collapses the rare variants in a region into a composite variable (according to predefined criteria) and then constructs a multi-marker test of association between disease status and multiple composite variables (each composite variable corresponding to a different region). Another commonly used method is the “burden test” [9], in which the composite variable is calculated as the number of rare variants in a region. Simulation studies show that the burden test has higher power compared to other methods [9].

Although simulations suggested that these novel methods successfully increased the power to detect rare variants compared to standard tools used for the analysis of common variants, none of the available methods address an important issue that often arises in genetic studies: the potential for false positives due to population stratification. Population stratification is a systematic difference in allele frequencies between cases and controls caused by different subpopulation structures. It is well established that stratification, if not properly modeled, can lead to an increased number of spurious associations and further can reduce the power to detect true associations [10]. Several methods have been developed to correct the inflated false positive rate caused by population stratification, among which genomic control [11] and principal component analysis [12] are two popular approaches. The genomic control method assumes that population stratification will inflate the test statistics Y² from the ${\chi }_1^2$ distribution expected under the null hypothesis into a $\lambda {\chi }_1^2$ distribution, where λ is estimated as the mean value of Y² or the median value of Y² divided by 0.4549 (the expected median of a variable from the ${\chi }_1^2$ distribution). The disadvantage of the genomic control method is that it assumes all genetic variants are influenced to the same degree by population stratification (i.e., λ is constant across different loci). In contrast, principal component analysis aims to infer differences in individuals' ancestry by summarizing genomic variation via the eigenvectors of the sample genotypic covariance matrix, and can in turn allow the influence of population stratification to differ across variants.

Although it is clear that population stratification is a severe problem in association studies of common variants, little is known about the effect of population stratification on case-control studies of rare variants [13,14]. Without correctly accounting for confounders such as population stratification, sequencing studies could potentially be plagued by false positive results. Here, we use simulated sequence data based on coalescent models to examine whether population stratification affects studies of rare variants and whether existing methods can adequately adjust for this stratification.

Materials and Methods

1. Study Design and Notation

We assume a case-control study where N participants are sequenced for a region comprised of M variants. We define N_d and N_c as the number of cases and number of controls respectively with N=N_d+N_c. Let D be an N × 1 column vector that denotes the disease status for N research subjects, where D_i=1 if subject i is a case while D_i=0 if the subject is a control (i=1,2,….N). Define G as a N×M matrix comprised of the genotypes for the N subjects, where the (i,j)^th element of the matrix, g_ij, denotes the genotype of the i^th subject on the j^th locus (j=1,…,M). We code g_ij to take the values 0, 1, or 2 representing the number of copies of the rare variant that the subject possesses at the locus. We define rare variants as those alleles with minor allele frequencies ≤1% within the population.

2. Associations between rare variants and disease

2.1 Collapsing Methods

Many statistical methods for rare-variant analysis collapse rare variants in a region together and analyze them as a group in order to improve the power to detect disease-associated alleles. In this paper, we consider two ways to form composite variables: the Combined Multivariate and Collapsing (CMC) method is based on the presence or absence of rare alleles in a region [8] while the burden test is based on the total number of rare alleles in a region [9]. Assuming A regions under study, we let C_ia denote the composite variable in region a (a=1,…,A) for the i^th subject. For Li and Leal's collapsing method [8], C_ia=1 if person i possesses rare variants in region a and C_ia=0 if there are no rare variants in the region. For the burden test [9], C_ia= total number of rare variants in region a (a=1,…,A).

2.2 Test of association

We used Pearson chi-square tests and logistic regression to test whether the composite variables are significantly associated with the disease. When collapsing based on presence or absence of the rare variants in the region, we can apply the Pearson chi-square test statistic. Assuming equal number of cases and controls, the Pearson chi-square statistics for the a^th region, $X_a^2$, is defined as follows,

$$X_a^2=N_d\{\frac{{[P_a^D(C_a=0)-P_a^C(C_a=0)]}^2}{P_a^D(C_a=0)+P_a^C(C_a=0)}+\frac{{[P_a^D(C_a=1)-P_a^C(C_a=1)]}^2}{P_a^D(C_a=1)+P_a^C(C_a=1)}\},$$

where $P_a^D(C_a=1)$ and $P_a^C(C_a=1)$ represent proportions of cases and controls with rare variants in the a^th region, while $P_a^D(C_a=0)$ and $P_a^C(C_a=0)$ represent proportions of cases and controls without rare variants in the a^th region. When performing a burden test that counts the number of rare variants in a region, we use the score test based on logistic regression. The logistic regression model is defined as follows,

$$\mathit{Logit}(E(D_i))={\beta }^T{C}_i,$$

where C_i =(C_i1, C_i2,…, C_iA)′ are the composite variables for the i^th subject. The logistic regression can accommodate non-binary independent variables but is equivalent to the Pearson chi-square test shown above when the independent variable is binary.

3. Correction method

We examined whether two methods that correct for population stratification in case-control studies of common variation (genomic control [11,15] and principal component analysis [12,16]) were as effective for rare-variant analyses using the collapsing and burden methods described earlier. We describe each method in more detail below.

3.1 Genomic Control

As discussed in Devlin and Roeder [11] and Marchini et al.[15], genomic control is a popular method to adjust for population stratification in GWAS, though it has not been widely applied to studies of rare variants. This method is typically used when testing for association with a chi-square test with 1 degree of freedom such as the Pearson chi square test described above or a Cochran-Armitage trend test. The Cochran-Armitage test statistic for tests of common variants is defined as follows,

$$Y^2=\frac{N{\{N(N_{dAa}+2N_{dAA})-N_d(N_{Aa}+2N_{AA})\}}^2}{N_d{N}_c\{N(N_{Aa}+4N_{AA})-{(N_{Aa}+2N_{AA})}^2\}}$$

where N_dAa and N_dAA are the number of SNPs in cases with one minor allele and two minor alleles respectively, and N_Aa and N_AA are the total number of subjects with one minor allele and two minor alleles respectively. Without stratification, under the null hypothesis, the test statistic follows a chi-square distribution with 1 degree of freedom. The genomic control method assumes that, in the presence of stratification, test statistics will be inflated by a constant inflation factor λ, so that $Y^2~\lambda {\chi }_1^2$. In a GWAS, the genomic control factor λ can be estimated as either the median of all observed chi-square statistics divided by 0.4549 (the median of the ${\chi }_1^2$ distribution) or as the mean value of all observed chi-square statistics. In our simulated rare variant analyses (described below) we estimate λ as the median test statistic from GWAS data on common variants divided by 0.4549. To apply genomic control to the CMC and burden tests, we calculate the inflation factor λ from the Cochran-Armitage trend tests and then divide the observed CMC/burden test statistic by λ. For λ≤1, no adjustment is needed. We then calculate the p-value of the adjusted CMC/burden test assuming that the genomic-control adjusted test follows a chi-square distribution with 1 degree of freedom.

3.2 Principal Component Analysis

Principal component analysis aims to summarize the variation in a dataset as a sequence of uncorrelated components, which are linear combinations of the variables in the original dataset. The p^th component can be summarized as follows:

$${\mathrm{P}}_p=B_p^{\prime }G=b_{p1}{g}_{\cdot 1}+b_{p2}{g}_{\cdot 2}+\dots ‥+b_{pM}{g}_{\cdot M}$$

where B_p = (b_p1,b_p2,…,b_pM)′ is a M×1 vector and g._j represents the j^th column of G. The principal components are ordered by their ability to summarize the data. As a result, the first component, P₁, accounts for as much of the variation in G as possible for a linear combination of the variables; the second component, P₂, accounts for as much as possible of the remaining variation of G, and so on. To calculate the principal-components coordinates for each subject, we first subtracted the empirical column mean μ_j, calculated as $\frac{1}{N}\sum _{i=1}^N{G}_{ij}$, from each column j of G. We then divided each entry by its empirical column standard deviation, SD_j. We use S to denote the standardized G matrix with S_ij=(G_ij-μ_j)/SD_j. As discussed in Price et al. [12], B_p is the coordinate of the p^th eigenvector of the variance-covariance matrix of S. We define V as the M×M variance matrix of S, where element V_jj, represents the covariance between locus j and locus j′. We used the singular value decomposition method to compute the eigenvector of V. The singular value decomposition method can decompose S into the product of three matrices: S=UΣW^T, where U is a matrix whose columns are eigenvectors of the matrix SS^T, Σ is a N × M diagonal matrix with the values on the diagonal be the singular values of S, and columns in W are eigenvectors of the matrix S^TS. As SS^T is equivalent to the variance-covariance matrix V, the p^th column of U contains the coordinates of the p^th principal component for the subjects in the sample. To use the principal component method to correct for population stratification in our simulations described below, we include the top principal components as additional covariates in the logistic regression model:

$$\mathit{Logit}(E(D_i))={\beta }^T{C}_i+{\gamma }^T{P}_i,$$

where D_i denotes the disease status for the i^th subject, C_i =(C_i1, C_i2,…, C_iA)′ are the composite variables for the i^th subject and P_i denotes the vector of the top principal components.

4 Simulations

4.1 Type-I Error

To test the performance of the methods described above, we simulated case-control resequencing datasets subjected to confounding due to population stratification. To generate realistic resequencing data, we used cosi [17] to generate 250 kb haplotypes for 20,000 European and 20,000 African individuals. As discussed in Schaffner et al. [17], cosi can simulate haplotypes with high resemblance to empirical data collected by the International HapMap Project [18]. We first used cosi to generate the haplotypes under the “best-fit model” as described in Schaffner et al. [17]. We also simulated haplotypes under an exponential growth model where we assume that from the 50^th to 1000^th generation, the European population increased in size from 8,000 to 100,000 people while the African population increased from 10,000 to 100,000 people, based on common assumptions about effective population size [19]. We used R to simulate case-control studies with population structure as follows: we set the number of European versus African individuals to be 1:1 in controls and held this constant for all studies. However, we allowed the proportion of European and African individuals to vary in cases. We simulated across cases in four different proportions: 1) 50% European vs. 50% African, 2) 40% European vs. 60% African, 3) 25% European vs. 75% African, 4) 10% European vs. 90% African. Three different sample sizes were used: 100 cases/100 controls, 500 cases/500 controls, or 1000 cases/1000 controls. For each scenario considered, we performed 500 simulations. For all analyses, we assumed a significance threshold of α=0.05.

4.2 Power

To evaluate power, we generated case-control datasets prospectively assuming the odds of disease is a function of ancestry (European/African) and rare causal variants:

$$E(D)=\frac{exp({\beta }_0+\theta \times I(\mathit{\text{African}})+\eta )}{1+exp({\beta }_0+\theta \times I(\mathit{\text{African}})+\eta )},$$

where β₀ is the prevalence of disease, θ is the odds ratio of disease risk between African and European subjects, I is an indicator function, and η is the odds ratio of causal rare variants. For each model considered, we performed 300 simulations. For all analyses, we assumed a significance threshold of α=0.05.

4.3 Generating Additional Markers for Stratification Adjustment

We next generated SNP data for use in stratification adjustment of the collapsing and burden tests in the presence of population stratification. Since genomic control and principal component analysis require far more SNPs for an accurate correction than those found in a 10 kb region, we instead generated genome-wide SNP data using HapMap markers found on the Affymetrix 6.0 array SNPs. We used such HapMap SNP data from the Yoruban (YRI) and CEPH (CEU) populations to represent African and European populations respectively. We performed LD-based pruning in PLINK [20] to filter out SNPs in strong linkage disequilibrium (R² ≥0.5). We used the minor allele frequencies of the remaining SNPs to generate genotype data under the assumption of Hardy-Weinberg Equilibrium. We used the minor allele frequencies from the HapMap CEU samples to generate genotypes for European subjects and used the minor allele frequencies from the HapMap YRI samples to generate genotypes for African subjects. We assumed that these SNPs follow Hardy-Weinberg Equilibrium and simulated the genotypes based on the binomial distribution.

We next used the SNP genotype data to correct for population structure in our case-control study. In each simulation, we randomly selected a simulated GWAS genotype for each subject in our simulated case-control study, selecting from the set of African or European genotypes depending on the ancestry of each subject. Using the simulated data, we analyzed the GWAS data to calculate the inflation factor λ and to construct principal components using the methods discussed above. As there are only two populations (African and European) in our simulation, we only included the first and the second principal components in our logistic regression models; as a result, P is an N × 2 matrix.

We then evaluated the type I error rates and power of the CMC method [8] and burden test [9] when adjusting for population stratification with genomic control or principal components.

Results

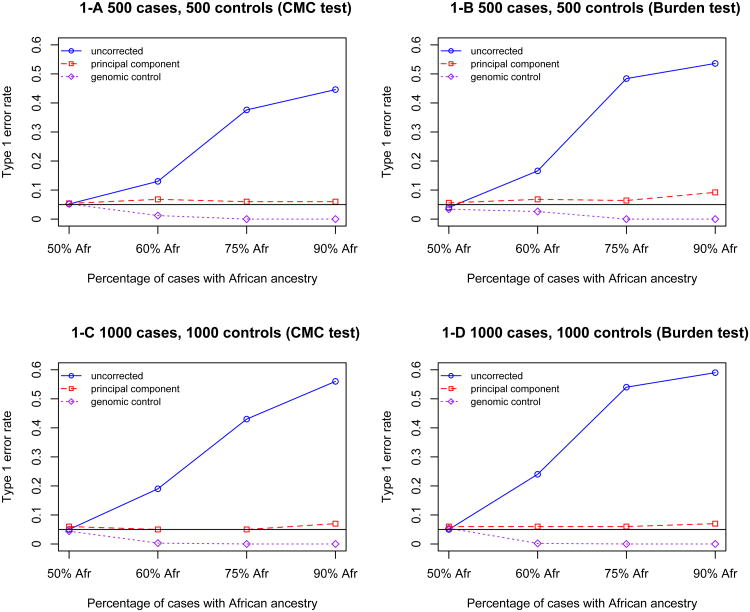
We first performed simulation studies under the null hypothesis of no association between rare variants and disease to assess whether population stratification can lead to spurious associations in resequencing studies. We simulated case-control studies subject to different stratification levels for various sample sizes (as described in Methods). We first used the “best fit model” of cosi [17] to simulate 20,000 European and 20,000 African haplotypes that have high resemblance to HapMap data. For each simulation, we randomly selected a 10kb region as the targeted region to study the association between genetic variants in the region and disease status. As described in Methods, we fitted logistic regression models using both the CMC method [8] and the burden method [9] in each of 500 simulations, and estimated the rate of type I error as the proportion of simulations with a significant association (P<.05). The type I error rates at different sample sizes and different stratification levels are shown in Figure 1. Type 1 error rate increases as stratification level increase. When there is no stratification (50% African vs. 50% European in both cases and controls), the type I error rate is around 0.05; however, when population stratification exists, the type I error rate is inflated up to 0.56 for the CMC method and 0.59 for the burden method. The inflation of type I error rate becomes larger as sample size increases. For large samples (1000 cases/1000 controls), even modest stratification (60% African vs. 40% European in cases) leads to an inflated type I error rate around 0.2. This is because the type I error rate under the null hypothesis is actually the power to detect any association with the disease, even a spurious association due to population stratification. As a result, the type I error rate goes up as the sample size goes up. The CMC method and the burden method have similar performance, although the burden test has systematically higher type 1 error rate compared to the CMC method.

Figure 1.

Type 1 error rate for the CMC and burden tests uncorrected or corrected by principal component and genomic control for a 10kb region. 1-A: 500 cases and 500 controls collapsed by the CMC method; 1-B: 500 cases and 500 controls collapsed by the burden test; 1-C: 1000 case and 1000 control collapsed by the CMC method; 1-D: 1000 cases and 1000 controls collapsed by the burden test. Note that in all simulations, 50% of controls have African ancestry and 50% have European ancestry, while the proportion of cases with African ancestry varies across simulations (X-axis).

To examine population stratification's effect on rare variation under different population-genetics models, we next simulated the European and the African haplotypes under the exponential growth model as described earlier. Overall, we observed no marked difference in the results generated under the exponential growth model compared to the results generated under the “best fit” model [17]. For the exponential growth model, when there are 900 African and 100 European in cases (500 African and 500 European in controls), the type 1 error rate is 0.55 for the CMC method and 0.57 for the burden method. These results are quite similar to the ‘best-fit’ results under the same stratification model. Thus, our results appear to be consistent under different population genetics models.

To examine how type 1 error rate is influenced by number of variants in a region, we also preformed simulations for 1kb and 50 kb regions. As the region size increased, we found that the behavior of the rare-variant tests depended on the collapsing method used. (Table 1). Interestingly, when stratification existed but was not adjusted for, we observed that the CMC method demonstrated less type-I error inflation for a 1kb region or a 50kb region compared to a 10 kb region. On the other hand, the burden test demonstrated greater type-I error inflation with increasing region size. While counterintuitive, we believe the reason the type-I error for CMC is the most inflated for a 10kb region is because the CMC method is based on presence/absence of the rare variants in a region. As the region size increases, more individuals will have at least 1 rare variant in a region even when stratification exists. Supplementary Table 1 demonstrates that in our simulations, the majority of individuals have 0 rare variants in a given 1kb region, while the majority of individuals have >0 rare variants in a given 50kb region. In contrast, the average number of individuals with 0 vs. >0 variants is roughly evenly distributed for regions of 10kb. Consequently, our ‘power’ to detect population stratification is greatest for the 10kb regions, while the effect of stratification is attenuated for the 1kb and 50kb regions. The burden test, on the other hand, is based on the total number of rare variants in a region and can take a larger range of values. Thus, we expect the type-I error inflation of this test to be exacerbated with increasing region size.

Table 1.

Type 1 error rate for the CMC and burden tests before and after correction by principal component (PCA) and genomic control (GC), based on 1,000 cases and 1,000 controls.

Cases that are of African Ancestry, %	Region size kb	Before correction		After correction (PCA)		After correction (GC)
		CMC	Burden	CMC	Burden	CMC	Burden
50%	1	0.064	0.068	0.064	0.058	0.064	0.068
	10	0.045	0.056	0.055	0.060	0.045	0.056
	50	0.064	0.075	0.058	0.062	0.064	0.075
90%	1	0.444	0.426	0.046	0.046	0	0
	10	0.580	0.610	0.060	0.060	0	0
	50	0.240	0.670	0.060	0.097	0	0

Simulations assume 50% of controls have African ancestry.

We next examined whether genomic control and principal components can correct for the confounding due to population stratification in the samples. For the genomic control method (Figure 1, purple line), the results are very conservative. When the stratification level is a bit more severe (75% African vs. 25% European), use of genomic control will lead to a type I error rate close to 0. This can seriously reduce the power in the presence of true association. However, the principal components method performed very well (Figure 1, red line): the type I error rates generally are distributed around 0.05 although there is a slight type-I error elevation under the extreme stratification model. We examined the same pattern for the 1kb region and the 50kb region (Table 1). In general, principal component correction works better for the CMC method compared to the burden method, especially when the region size is large (Figure 1, Table 1). As a comparison, we also applied these two correction methods to a simulated common variant of similar frequency. For each simulation, we calculated the average frequency of the composite variable after collapsing the rare variants in the region using the CMC method. In each simulation we then selected the common variant with allele frequency most similar to the composite variable, and computed type I error based on these common variants. In the presence of population stratification, the common variant has a much higher type I error rate than either the CMC or burden tests of rare variants (Table 2). Genomic control is also very conservative in the common variant simulations, although not as conservative as for rare variants. Principal component analysis, on the other hand, has much better performance.

Table 2.

Type 1 error rate for common variants, compared to rare variants collapsed by CMC or burden tests.

Cases that are of African Ancestry, %	Correction	Rare (CMC)	Rare (Burden)	Common
50%	Before	0.045	0.056	0.036
	PCA	0.055	0.060	0.032
	GC	0.045	0.056	0.036
90%	Before	0.58	0.61	0.87
	PCA	0.07	0.06	0.036
	GC	0	0	0.01

Rates are presented before and after correction by principal component (PCA correction) and genomic control (GC correction). Simulations are based on 10-kb regions in 1,000 cases and 1,000 controls. All simulations assumed 50% of controls have African Ancestry.

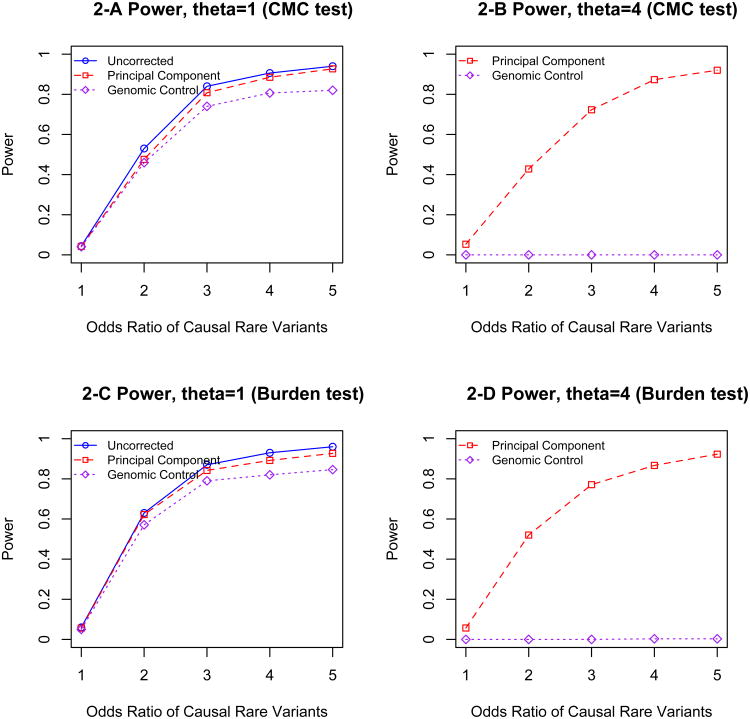
We next performed power calculations to examine the performance of these two correction methods in the presence of true association between rare variants and disease. Here we used the haplotypes generated by cosi to simulate case-control studies subjected to population stratification. For each simulation, we randomly selected a specified number of African and European haplotypes and randomly selected a 10kb region as the targeted region. We then generated case/control status prospectively such that the odds of having disease are a function of both rare causal variants and ancestry (European/African). For our simulations we assumed that the baseline prevalence of the disease is 0.05 and the probability that a rare variant is causal is 0.3. We allowed Africans to have a 4-fold increased odds of being a case compared to Europeans; as a comparison we also considered a separate simulation assuming equal disease odds for Africans and Europeans. We simulated such that the presence of the causal rare variants leads to a 1- to 5-fold increase in the risk of disease. The simulation results based on 300 simulations are summarized in Figure 2. This shows that it is necessary to adjust for population stratification to avoid spurious results due to an inflated false positive rate. Consistent with Figure 1, genomic control consistently leads to extremely conservative results while principal components analysis controls type I error at the target level. Although power increases with the odds ratio of causal rare variants, the power remains close to zero when using genomic control as a correction method and collapsing by CMC [8]. As in Figure 1, the burden method and CMC method have very similar performance.

Figure 2.

The power of rare variants sequencing studies subject to population stratification, 2-A: θ (the odds ratio of the disease risk between African and European subjects)=1, collapsed by the CMC method; 2-B: θ =4 collapsed by the CMC method; 2-C: θ =1, collapsed by the burden test; 2-D: θ =4 collapsed by the burden test.

Discussion

In this paper, we showed that population stratification can lead to an inflated type 1 error rate in rare-variant association studies. We examined two methods to correct for this stratification: principal component analysis and genomic control. Our simulations showed that principal component analysis could control the false positive rate at the desired level while maintaining power to identify true associations. Genomic control, on the other hand, leads to extremely conservative results in this setting. Using genomic control as a correction method in resequencing studies will lead to substantially lower power to detect association. Our analysis examined two methods of collapsing rare variants: the CMC method of Li and Leal [8] and the burden method of Morris and Zeggini [9]. Our simulation results suggested that the degree of inflation due to population stratification depended on the number of variants considered (i.e. region size) and the specific collapsing method used, and correction with principal components was more successful for the CMC method than for the burden method. A recent paper by Mathieson & McVean [21] also investigated the impact of confounding due to population stratification on rare-variant and common-variant tests but this work focused on spatially-structured, rather than discrete, populations.

Our results imply that researchers need to carefully match cases and controls on ancestry to avoid population stratification in studies of rare variants. Although principal component analysis can provide the desired correction, it effectively relies on genome wide data, which may not always be available, such as in targeted sequencing studies like the Dallas Heart Study. Consequently, the only way to ensure robustness of rare-variant association tests may be to use family-based studies and implement methods similar to the transmission disequilibrium test for analysis. We will explore such designs in a future manuscript.