Radiation Organ Doses Received in a Nationwide Cohort of U.S. Radiologic Technologists: Methods and Findings

Abstract

In this article, we describe recent methodological enhancements and findings from the dose reconstruction component of a study of health risks among U.S. radiologic technologists. An earlier version of the dosimetry published in 2006 used physical and statistical models, literature-reported exposure measurements for the years before 1960, and archival personnel monitoring badge data from cohort members through 1984. The data and models previously described were used to estimate annual occupational radiation doses for 90,000 radiological technologists, incorporating information about each individual's employment practices based on a baseline survey conducted in the mid-1980s. The dosimetry methods presented here, while using many of the same methods as before, now estimate 2.23 million annual badge doses (personal dose equivalent) for the years 1916–1997 for 110,374 technologists, but with numerous methodological improvements. Every technologist's annual dose is estimated as a probability density function to reflect uncertainty about the true dose. Multiple realizations of the entire cohort distribution were derived to account for shared uncertainties and possible biases in the input data and assumptions used. Major improvements in the dosimetry methods from the earlier version include: A substantial increase in the number of cohort member annual badge dose measurements; Additional information on individual apron usage obtained from surveys conducted in the mid-1990s and mid-2000s; Refined modeling to develop lognormal annual badge dose probability density functions using censored data regression models; Refinements of cohort-based annual badge probability density functions to reflect individual work patterns and practices reported on questionnaires and to more accurately assess minimum detection limits; and Extensive refinements in organ dose conversion coefficients to account for uncertainties in radiographic machine settings for the radiographic techniques employed. For organ dose estimation, we rely on well-researched assumptions about critical exposure-related variables and their changes over the decades, including the peak kilovoltage and filtration typically used in conducting radiographic examinations, and the usual body location for wearing radiation monitoring badges, the latter based on both literature and national recommendations. We have derived organ dose conversion coefficients based on air-kerma weighting of photon fluences from published X-ray spectra and derived energy-dependent transmission factors for protective lead aprons of different thicknesses. Findings are presented on estimated organ doses for 12 organs and tissues: red bone marrow, female breast, thyroid, brain, lung, heart, colon, ovary, testes, skin of trunk, skin of head and neck and arms, and lens of the eye.

INTRODUCTION

Much of our understanding about cancer associated with ionizing radiation exposures is based on epidemiological studies of the Japanese atomic bomb survivors who had a single exposure, and medically irradiated patients who received fractionated high-dose exposures over weeks. There are limited dose-response data from studies estimating cancer and other disease risks associated with protracted low-dose radiation exposures. These include studies of cancer and other disease risks in workers in the nuclear industry who have mostly received very low doses (1–3), and a few studies in medical radiation workers (4). None of the previous occupational studies of low-dose radiation have assessed potentially important confounders (smoking) or effect modifiers (sex, age at first exposure) nor have the studies of medical radiation workers with occupational radiation dose estimates examined risks in subsets of workers with exposures to newer, higher-dose (e.g., fluoroscopically-guided interventional procedures) or higher-energy procedures (e.g., administration of radionuclides in nuclear medicine).

To address these limitations, we launched a large-scale, long-term cohort follow-up study of 146,022 U.S. radiologic technologists (USRT) certified between the years 1926–1982 and followed up to the present (5). During this time, there have been notable changes in radiation protection measures as well as the introduction of many newer technologies and radiologic procedures, thus providing an opportunity to study a range of estimated cumulative occupational radiation doses. In three completed surveys of the USRT, detailed information has been collected about lifetime work history, procedures performed and protective measures utilized, as well as ascertainment of a broad range of covariates including potentially important confounders (e.g., smoking, alcohol use, body mass index, medical conditions and reproductive factors) and effect modifiers (e.g., sex, age at first exposure, personal medical diagnostic and therapeutic procedures involving exposure to ionizing radiation). The USRT also includes substantial subsets of technologists who have performed or assisted with the higher-dose and higher-energy procedures.

We have utilized the work history and covariate information in previous analyses in which we found significantly elevated incidence risks for breast cancer (6), melanoma (7), nonmelanoma skin cancer (8), combined leukemia types excluding chronic lymphocytic leukemia (9), and circulatory system diseases, particularly cerebrovascular disease (10) among those first working before 1940 or 1950 or working more than 5 years before 1950. There was little evidence of exposure-response for thyroid cancer (11) and lung cancer (12). The overall results, based on work history as a surrogate for occupational radiation exposure, suggested an exposure-response relation because risks were elevated among those employed in earlier years when radiation exposures were highest. The combination of the unique aspects of the USRT study characterized above along with the comprehensive occupational radiation dose reconstruction described in this article will enable assessment of dose-response risk estimates for cancer and other diseases that can contribute valuable data from the public health perspective about protracted low-dose radiation exposures.

In our earlier historical exposure reconstruction (13), we used: 1. Film badge measurements for three periods (before 1960, 1960–1977, 1977–1984); 2. Questionnaire-derived work history from a questionnaire administered in the mid-1980s; and 3. Measurements and other data from the literature to estimate annual occupational badge doses for 90,305 first questionnaire respondents years 1916–1984. We have combined these data with modeling and estimation techniques to reconstruct doses to 12 organs and tissues.

In our current dose reconstruction, estimates of annual badge doses and doses to 12 organs were made for 110,374 technologists who responded to either the first or second questionnaire. Significant methodological enhancements include expansion of badge dose estimates from 1916–1997, use of newly obtained badge dose and work history data, and improved information on protective apron usage and organ dose factor models. These improvements have allowed us to derive multiple estimates of annual personal dose equivalent (badge dose) to characterize uncertainty and radiation-absorbed doses to 12 organs and tissues. We describe the methods used to produce population realizations of individual annual dose estimates, which we will use to quantify the effects of occupational radiation exposure on cancer risks and to incorporate uncertainty in dose in the risk estimates.

METHODS

Objectives/Key Enhancements Since 2006

Our objectives were twofold: to derive a set of occupational organ-specific doses for all study participants using individual monitoring data, work history and the evolution of radiation protection policies over time; and to characterize uncertainty in individual dose estimates by creating multiple sets of organ-specific dose estimates for the entire cohort. In this schema, each set reflects multiple sources of uncertainty including possible biases and our interpretations of the uncertainties of data, and our assumptions. We refer to each set of doses derived for the entire group as a single “realization”.

To create the realizations of the cohort dose distribution, we developed a year-by-year probabilistic record of badge dose⁶ and organ-specific radiation absorbed doses for each participant that accounts for uncertainties shared among individuals or subgroups. Information about each technologist's annual badge dose can be represented by a sample from the probability density function (PDF) that was designed to capture the range and the likelihood of plausible values for the technologist's true annual badge dose given what is known about the population dose distribution and shielding practices in that year, together with individual information on work practices, type of facility where work was performed, and when available, film badge readings. Multiple values of individual annual doses were simulated from the PDFs using Monte Carlo simulation techniques that allowed for within-individual inter-year correlations. These individual annual badge dose values were used to generate estimates of annual organ doses that account for uncertainties in individual apron usage patterns, apron thickness and dose conversion factors. The realizations of cohort member doses derived in this study reflect both uncertainties in reconstructing individual doses and uncertainties that are shared between individuals.

Table 1 summarizes changes in the USRT dosimetry since the 2006 publication (13) and highlights important attributes of the current dosimetry system. These improvements include newly acquired film badge dose readings, and additional information on work history and practices collected in a 2003–2005 survey and methods and models that allow greater individualization of annual dose estimates. The updated badge dose data and work history information were used to estimate annual population badge dose distributions from 1916–1997. These distributions are dependent on the type of facility in which the technologist worked, e.g., a clinic or physician office and the nature of the employer (civilian or military). The badge dose and work history data were used to develop individual exposure scores, a metric that captures the dependence of the geometric mean (GM) of the annual population badge dose distribution on the frequency of performing specific types of radiologic procedures and the number of hours worked per week. Methods were developed to use exposure scores to individualize badge dose sampling densities for years in which a cohort member was believed to have worked but for which a badge dose reading was not available.

TABLE 1.

Comparison of Key Features of the 2006 Dose Reconstruction (13) and the Current Version

	2006 dose reconstruction (13) (90,305 respondents)	2013 dose reconstruction (110,374 respondents)
Input data	• 1977–1984 cohort badge doses (~350,000 annual readings).	• 1985–1997 cohort badge doses (581,423 annual readings).
	• 1960–1976 cohort badge doses (~500 annual readings).	• 1977–1984 cohort badge doses (324,039 annual readings).
	• Literature-based badge doses for pre-1940, 1940–1949 and 1950–1959 periods from 11 publications.	• 1967–1976 cohort badge doses (12,444 annual readings).
	• Work history from first survey.	• 1960–1966 badge doses (3,228 annual readings).
	• Doses estimated through 1984 for first survey respondents.	• Literature-based badge doses for pre-1940, 1940–1949 and 1950–1959 periods from 11 publications.
		• Work history from first, second and third surveys.
		• Doses estimated through 1997 for all survey respondents.
Population badge dose distributions	• Population badge dose lognormal probability density functions (PDFs) by facility type, summarized using geometric mean (GM) and geometric standard deviation (GSD) values.	• Annual population badge dose lognormal PDFs by facility type, summarized using GM and GSD values.
	• Literature doses for pre-1940, 1940–1949, and 1950–1959 weighted according to number of readings and relevance to the cohort.	• Literature-based dose distributions for pre-1940, 1940–1949, and 1950–1955 weighted on presumed relevance, with allowance for uncertainty in weights and for bias in the resulting badge dose GM estimates.
	• Actual badge dose readings for the 1960–1976 time period.	• 1966–1997 annual population badge dose GM and GSD values based on regression modeling of actual badge dose readings with work history effects used to define an exposure score function.
	• Actual badge dose readings for 1977–1984, or regression model using work history from first survey.	• Additional modeling to define upper and lower limits on population badge dose GM estimates that were used to allow for uncertainty in annual GMs.
		• 1956–1965 badge dose GM and GSD expected values and limits defined by interpolation between 1950–1955 values and 1966–1997 values.
		• Dose realizations based on conditional distribution when badge dose reading is below the minimal detectable limit.
Individualization of badge doses		• Population badge dose GMs adjusted for individual exposure score factors that reflect work patterns and practices (frequency performed specific procedures, shielding, holding patients) reported on third survey.
		• Actual badge dose readings adjusted using regression calibration assuming 20% measurement errors and individualized population badge dose GM and GSD.
		• Population badge dose GMs for years without an actual reading further adjusted for number of hours worked per week and whether the facility was military or civilian.
		• Autoregressive correlation structure used to allow for within worker correlations in annual doses.
		• Allow for possibility that some badge dose readings were for badges worn under the apron.
Generation of individual annual badge dose realizations	• Use actual badge dose reading if available and above the minimum detection limit (MDL).	• If actual badge dose reading is above the MDL badge dose reading then sample from measurement error distribution with 20% error.
	• Use 0.5 MDL if badge dose reading is below the MDL.	• If actual badge dose reading is below the MDL and badge is assumed to be worn above the apron, then sample from individualized annual population PDF is conditional on dose being less than the MDL.
	• Sample from population PDF if there is no actual badge dose reading.	• If actual badge dose reading is below MDL and the badge is assumed to be worn under the apron or if no badge dose reading then sample from the individual annual population PDF.
Apron usage and shielding	• Uses two variables: first year worked and probability of apron usage from first survey.	• Developed period specific apron usage distributions based on both a literature review and on responses to apron usage questions in the third survey.
	• Apron transmission factor assumed constant at 20%.	• Calibrated limited apron usage data from first two surveys using data from those who responded to the third survey to improve apron usage distributions for those who did not respond to the third survey
		• Allow for random year for transition from literature-based to questionnaire-based apron usage distributions
		• Apron transmission factors based on percentage transmitted air kerma for two typical thicknesses of lead and for 12 combinations of kV and X-ray filtration, reflecting uncertainty by time-period.
Protection/shielding	• Uses two variables: first year worked and probability of apron usage from first survey.	• Apron protection weighted by procedures performed as reported on third survey by decade.
	• Apron transmission factor assumed constant at 20%.	• Use of beta PDFs to calibrate first and second survey with third survey apron protection responses from categorical to numeric values, and to estimate third survey responses among those who responded to the first or second survey, but not the third.
		• Badge dose readings treated as measurements “outside the apron”.
		• Apron transmission factors based on percentage transmitted air kerma for two typical thicknesses of lead (0.25 and 0.50 mm) and for 12 combinations of kV and X-ray filtration reflecting uncertainty by time period.
Organ dose conversion coefficients	• Average x-ray energy assumed as 35 keV.	• Peak kV ranges from 70–90 with average X-ray energy from 32–47 keV.
	• Constant value for each organ dose conversion factor at 35 keV energy.	• Organ dose factors derived by air kerma weighting published mono-energetic values over X-ray energy spectra derived from literature by time period. Twelve spectra chosen reflecting uncertainty within time periods.
	• • Conversion coefficients for seven organs and tissues.	• Conversion coefficients derived for 12 organs and tissues.
		• Uncertainty of external dose conversion coefficients based on NCRP analysis.
Individualization of organ doses	• Doses for individuals correlated for successive years.	• Probabilistic apron usage.
	• Bias in geometric mean incorporated for individual realizations.	• Probabilistic apron transmission factors.
		• Probabilistic apron thickness.
		• Probabilistic kV values.
		• Body mass index-based dose factor for red bone marrow.
		• Simulations incorporate average length of time in a job by decade (used, e.g., in switching the probabilistic determination of apron thickness).
Treatment of uncertainty	• Dose uncertainty reflected numerous sources of uncertainty affecting individual dose reconstructions.	• Dose uncertainty reflects sources of uncertainty common to subgroups or common within time periods (i.e., shared errors) as well as conventional sources of uncertainty affecting individual dose reconstructions. Number of sources of uncertainty accounted for increased substantially (see article and Table 6).
Output of dose reconstruction	• PDFs of organ dosesa by cohort member reflecting individual uncertainty.	• Multiple realizations of entire cohort dose1 distribution for each organ or tissue reflecting both shared errors and uncertainty of each cohort member's reconstructed dose.
Dosimetry validation	• Dose-response of estimated bone marrow doses with chromosome translocation rate was not significant.	• Dose-response of estimated bone marrow doses with chromosome translocation rate was statistically significant.

^aOrgan doses can be either annual or cumulative.

Doses to specific organs are dependent on use of apron protection and shielding. Since publication of the original dosimetry system (13), we have developed methods that use a combination of literature-based and questionnaire-derived information on individual protection practices and use of shielding according to time period. Conversion from an estimated film badge dose to organ-specific doses utilizes newly developed energy- and period-specific dose conversion coefficients and apron transmission factors (TFs) (14).

Source of Exposure Data

The data used for dose reconstruction included annual badge dose measurements, literature-based period-specific estimates of the occupational dose distributions for workers like those in the USRT cohort, exposure and X-ray spectral measurements and survey-derived information on individual work patterns and protection practices.

1. Cohort badge dose data

We obtained 921,134 annual badge dose measurements for 79,959 cohort members from the years 1960– 1997 from Landauer, Inc., the largest commercial personnel dosimetry provider in the U.S. (N = 899,421 badge measurements for 1977–1997), three branches of the U.S. military (N = 14,825 badge measurements for 1960–1997) and several large civilian employers (N = 2,384 badge measurements for 1960–1976). We also obtained 194 anonymized annual badge doses received by technologists in the years 1949–1960 from a major medical facility, for workers not in the cohort but used for validation of our estimated doses for those years.

2. Data on work history and protection practices

Two questionnaires, the first sent to 133,298 U.S. radiologic technologists in 1984 (91% of total cohort) and returned by 90,305 (68%) and a second mailed to the 126,628 technologists known or presumed alive in 1995 and returned by 90,972 (72%) inquired about radiographic procedures performed and use of protective aprons by calendar period (<1980, 1980s, 1990+). A third survey carried out in 2004 provided additional information on the nature of the workplace (facility type), the frequency of performing specific radiologic procedures and apron and shield use associated with procedures for 72% of the surviving cohort members who had responded to at least one of the earlier surveys (73,567 respondents).

3. Other badge dose data

Using extensive data gathering resources of the National Institutes of Health libraries and records from the American College of Radiology, the U.S. Food and Drug Administration (FDA) and the American Society of Radiologic Technologists (ASRT), we conducted a comprehensive review of the literature on historical badge dose measurements, occupational radiation regulations, changes in protective measures and technical information on radiographic procedures.

Characterizing Population Badge Dose Distributions

We determined that the population distribution of badge doses in a given year could be described reasonably well by a lognormal distribution in which the annual GM depended upon facility type (hospital, physician office, combination) and whether the workplace was civilian or military. The geometric standard deviation (GSD) of badge doses for each year was assumed to be independent of facility type. When generating cohort realizations of annual doses, the system allows for uncertainty in the population distribution by varying the annual population badge dose GM and GSD values from realization to realization during time periods when there were few, if any, badge dose readings available.

As described in ref. (13), we used different methods to characterize the population badge dose distributions for different time periods. Until 1955, we relied on literature-based descriptions of the decade-specific population dose distributions. From the mid-1950s until the late 1970s, we interpolated between the literature-based estimates for the early years and the dose distributions developed from the cohort member badge readings for the later years, and for the late 1970s, we estimated population dose distributions using the archival badge dose readings available for cohort members. Annual film badge dose estimates were individualized using the technologist's actual badge dose reading, if available, or data on individual period-specific work patterns and practices obtained from the questionnaires.

1. Pre-1940 population badge dose distribution

As we previously described in ref. (13), we based the population badge dose distribution for fulltime hospital workers in the pre-1940 period on the only available publication (15) for those years. We defined the distribution to be lognormal with a GM of 71 mSv and a GSD of 2.4. To address uncertainty in the GM estimates for individual cohort members, we used a realization-specific multiplicative bias factor, sampled from a symmetric beta distribution scaled to range from 0.5–1.5 with an expected value of 1.0 to adjust the population GM.

2. 1940–1949 population badge dose distribution

Exposures for the 1940s were based on our analysis of data from four publications (13) using a regression method for censored normal data [Tobit regression, (16)] to estimate population badge dose GMs and GSDs for each of these articles. Based on our judgment, we assigned an expected weight and a weight range to the results from each publication. For each realization, we sampled a set of publication weights from a Dirichlet distribution (17) such that the expected value of a study's weight over all dose realizations was equal to the assigned average weight for that study. The realization-specific GM was then defined as the product of the weighted average of the publication-specific GMs and a random bias factor. The average literature-based badge dose GM for the 1940s (9 mSv) was almost an order of magnitude less than the pre-1940s estimate (72 mSv) and similar to the average GM for the 1950s (6 mSv). Hence, we decided to choose the realization-specific multiplicative bias factors for the 1940s badge dose GM from a symmetric beta-distribution PDF scaled to range from 1–5 with an arithmetic mean of 3.0.

Given the realization-specific population badge dose GM the population GSD was adjusted to preserve the 99th percentile of a lognormal distribution with the expected GM and GSD.

3. 1950–1955 population badge-dose distribution

We identified six publications (13) that provided information on badge dose distributions relevant to this period. Realization-specific GM and GSD estimates for this period were determined by using the same method that was used for the 1940s with realization-specific bias factors sampled from a symmetric beta distribution scaled to range from 0.5–1.5 with an expected value of 1.0.

4. 1956–1997 population badge-dose distribution

We obtained a total of 921,134 annual badge dose readings for 79,959 cohort members from 1960–1997. Readings from 1960–1976 were primarily obtained from military dosimetry registry records.

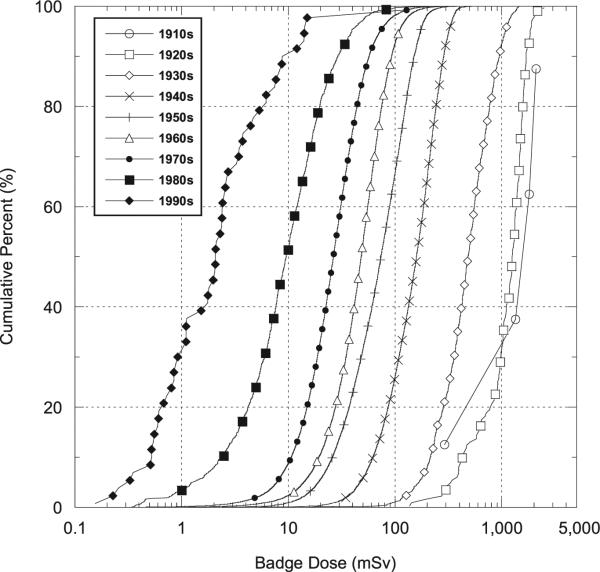
The archival badge dose readings were used to estimate population badge dose GMs and GSDs from 1966–1997. We did not use the badge dose readings for the 1960–1965 period, which were primarily for technologists who worked in military facilities, due to the relatively small numbers of badge doses and the potential lack of representativeness of the badge doses from technologists in the military to those in nonmilitary settings. The badge dose GM and GSD estimates were calculated by fitting a nonlinear regression model to the logarithm of the annual badge reading using methods for censored normal data. The censoring was based on the annual minimum detection limit (MDL), which was 4.8 mSv for 1960–1962, 2.4 mSv for 1964–1967 and 1.2 mSv for 1968–1997.⁷ The fitted annual population badge dose GM estimates for full-time civilian hospital workers are indicated by the filled circles in Fig. 1.

FIG. 1.

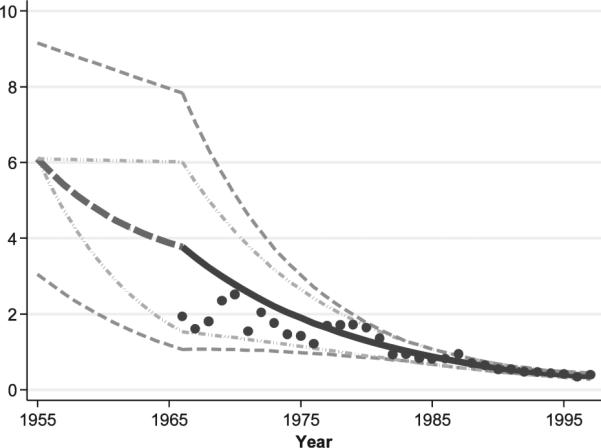
Temporal variation in annual estimates of the population GM badge doses for civilian full-time hospital workers incorporating within-year limiting values for the period from 1955–1997. Work-pattern adjusted annual badge dose GM estimates are based on data from workers with badge dose readings from 1966 onwards, indicated by the black dots. The light gray dash-dot curves represent the upper and lower badge dose GM limits developed from the badge dose data. The dark gray dashed curves represent the upper and lower limits for badge dose GMs after allowing for realization-specific random bias factors. The solid back line represents the expected badge dose GM values.

By the late 1960s, average annual doses were markedly lower than the average literature-based estimate of 6.1 mSv in the 1950s, and continued to decrease through 1997. This decline is presumed to be a result of improved technology and increased awareness of the importance of radiation protection. Since this decline likely began in the late 1950s, we interpolated annual population badge dose GM and GSD values in the period from 1956 (prior to which we used the literature-based estimates with uncertain bias factors) through 1982 (subsequent to our use of actual cohort member badge dose readings). The trend in the fitted badge dose GMs in Fig. 1 suggests that GM estimates for 1977–1980 are somewhat higher than one might expect based on the estimates for the periods before and afterwards.

We used this apparent difference to develop upper and lower uncertainty limits on the annual badge dose GMs. In particular, we modeled the temporal trend in the population GMs from 1960–1997 as a quadratic spline with binary period effects for either 1977–1980 (for the lower limits) or 1960–1976 (for the upper limits). To allow for uncertainty, we defined the upper and lower limits to be 10% beyond the fitted values. The lower limits for 1956–1966 were obtained by log-linear extrapolation from the value for 1950–1955 (6.1 mSv) to the estimated lower limit for 1966 (1.5 mSv). The upper limit for the period from 1960–1966 was taken as equal to the expected GM for 1950–1955. The smoothed curves defining these upper and lower limits are indicated by the gray lines with the dash-dot pattern in Fig. 1. The thick curves in Fig. 1 indicate the temporal pattern in the expected value of the badge dose GM for full-time civilian hospital technologists. The dashed curve represents the interpolated estimates for 1956–1966; the solid curve represents the film-badge-dose-model-based estimates for 1967–1997. The range of bias-adjusted badge dose GMs is indicated by the outer dashed curves in Fig. 1.

Individualization of Badge Dose Parameters

The data obtained from the three surveys together with individual badge dose readings, when available, were used to individualize the badge dose distributions that were used to generate realizations of individual annual badge doses. We used the data from the questionnaires to determine the number of years worked in a given decade, to assign workers to one of three facility types (hospital, physician office or combination/other) and to classify the facilities as either civilian or military. The third survey also provided information that could be used to provide decade-specific summaries of the type and frequency (number of times per week) of radiologic procedures performed, work practices such as shielding use and how often patients were held during X-ray examinations and the hours worked in a typical week during 1950–1997. This information was used together with the badge dose reading data for the years 1966–1997 to develop a nonlinear dose prediction model [Eq. (1)];

$$d_{iy}={\mu }_y{\varphi }_{iy,f}{\theta }_{iy,m}[1+ES(W_{iy},\beta )$$ (1)

in which d_iy is the badge dose reading for the individual i in year y; μ_y is the badge dose GM for the year, the ϕ_iy,f are facility-type adjustment parameters (defined as 1 for hospitals), and θ_iy,m are civilian/military facility adjustment parameters (defined as 1 for civilian facilities). Work history effects in the population badge dose GM are represented by the term [1 + ES(W_iy, β)] where ES( ) is an “exposure score” function that involves individual work history information (W_iy). The exposure score function has the form

$${\beta }_{0}I\left(hasesinfo\right)+{\beta }_1{N}_{fl}+{\beta }_2{N}_{dr}+{\beta }_3{N}_{itr}+{\beta }_4{N}_{dxnhsh}+{\beta }_5{N}_{dxnhus}+{\beta }_6{N}_{dxh}+{\eta }_{1}I(hpw<37)+{\eta }_{2}I(37\le hpw\le 44)+{\eta }_{3}I(hpw>44)$$ (2)

The variables used in the exposure score include an indicator [I(hasesinfo)] of whether the technologist provided procedure frequency data for the year (defined as 1 if there is performance frequency data for the year and 0 if not), counts of average weekly frequencies performed for fluoroscopic exams (N_fl), diagnostic radioisotope procedures (N_dr) and internal therapeutic radiation procedures (N_itr). Diagnostic X-ray examination frequencies were classified by whether the technologist was inside the X-ray room but shielded (N_dxnhsh), was inside the X-ray room and unshielded (N_dxnhus) or held the patient (N_dxh) during the X-ray examination. The model also includes hours-per-week (hpw) category indicators. The definitions and estimates of the exposure score parameters and the facility type adjustment factors, including civilian and military adjustments, are shown in Table 2. This nonlinear model was fit to the archival badge dose data using maximum likelihood methods for censored lognormal data, which are generalizations of Tobit regression methods (18). Badge dose readings below the MDL were treated as left-censored at the MDL in that time period. The data used for the modeling included all badge dose readings for 1966–1997, technologists who were believed to have worked for a full year (796,384 records). The annual population badge dose GM and GSD estimates from this modeling are shown in Table 3.

TABLE 2.

Exposure Score and Adjustment Factor Parameter Definitions and Estimates among U.S. Radiologic Technologists Who Worked Between 1916–1997

Effect	Variable name	Parameter estimate
Performance frequency effects*
Procedures performed frequencies available	I(hasesinfo)	–38.10%**
Diagnostic X rays per week: shielded inside room	Ndxnhsh	–0.18%**
Diagnostic X rays per week: unshielded inside room not holding the patient	Ndxnhus	0.14%**
Diagnostic X rays per week: holding patients	Ndxh	1.63%**
Fluoroscopies per week	Nfl	0.93%**
Diagnostic radioisotope procedures per week	Ndr	2.22%**
Internal therapeutic radioisotope procedures per week	Nitr	2.21%**
Hours worked category effects
Less than 37 h per week	I(hpw < 37)	–21.88%**
37–14 h per week	I(37 ≤ hpw ≤ 44)	–1.58%**
45+ h per week	I(hpw ≥ 45)	9.23%**
Unknown hours per week		0%
Facility adjustment factors†
Hospital		1
Combination facility/other		0.68**
Physician office		0.55**
Military adjustment factor†
Military		0.43**
Civilian		1

^*The exposure score (ES) model parameterization was chosen so that the ES is 1 for technologists without performance frequency or hours worked data. The performance frequency effects describe the percentage change in the GM per unit change in procedure frequency. The procedures-performed-frequencies-available effects describe the percentage difference between someone who reported performing no procedures in a week and someone who provided no performance frequency information.

^**P < 0.005.

^†The adjustment factor estimates are given here as the proportional change in the population GM for facility type and civilian/military status.

TABLE 3.

Person-Years and Badge Dose Data with Population GM and GSD Values for U.S. Radiologic Technologists Who Worked Between 1916–1997

		Badge readings			GM limits (mSv)*		GM (mSv)
Year	Person-years	Number	Detection limit (%)	Military (%)	Lower	Upper	Fitted†	Expected‡	Expected GSD
1916–1939	6,538	0			33.19	149.71		70.62	2.40
1940–1949	32,877	0			0.29	31.50		13.45	3.10
1950–1955	57,436	0			3.05	9.15		6.10	3.28
1956	13,519	0			2.79	9.03		5.74	3.32
1957	15,040	0			2.54	8.91		5.41	3.37
1958	16,924	0			2.31	8.79		5.13	3.42
1959	18,738	0			2.11	8.67		4.88	3.47
1960	21,018	171	91	84	1.92	8.55		4.66	3.53
1961	22,877	213	91	85	1.74	8.43		4.46	3.61
1962	24,932	243	93	85	1.58	8.31		4.29	3.71
1963	27,088	440	85	90	1.43	8.19		4.13	3.81
1964	29,455	582	79	89	1.30	8.07		4.00	3.92
1965	32,147	688	72	85	1.18	7.95		3.88	4.05
1966	35,122	891	79	75	1.06	7.84	1.91	3.77	3.46
1967	38,280	1,034	81	72	1.07	7.05	1.48	3.49	4.12
1968	41,948	1,133	64	70	1.07	6.34	1.80	3.23	3.68
1969	45,591	1,193	65	72	1.06	5.72	1.90	2.99	3.30
1970	49,858	1,334	59	70	1.06	5.15	2.04	2.78	3.20
1971	54,056	1,265	69	78	1.04	4.62	1.54	2.57	3.79
1972	58,523	1,285	68	76	1.04	4.16	1.55	2.38	3.55
1973	63,013	1,351	72	79	1.02	3.73	1.31	2.20	3.82
1974	67,812	1,313	73	76	1.00	3.36	1.16	2.04	3.94
1975	72,722	1,234	74	76	0.98	3.03	1.19	1.90	3.58
1976	77,680	1,302	74	74	0.96	2.71	1.10	1.75	3.98
1977	85,758	32,765	56	3	0.94	2.44	1.38	1.63	3.48
1978	88,833	35,527	57	2	0.91	2.20	1.34	1.51	3.52
1979	89,070	37,405	56	1	0.88	1.98	1.37	1.40	3.47
1980	88,043	43,462	58	1	0.85	1.77	1.40	1.29	3.32
1981	86,842	44,092	64	1	0.83	1.59	1.13	1.20	3.48
1982	85,260	37,049	72	1	0.79	1.43	0.77	1.11	3.76
1983	83,994	46,972	72	1	0.76	1.28	0.77	1.02	3.73
1984	81,707	46,767	76	1	0.71	1.18	0.70	0.94	3.87
1985	79,245	43,927	77	1	0.67	1.07	0.66	0.87	3.71
1986	77,384	45,319	77	1	0.63	0.98	0.69	0.81	3.62
1987	74,876	41,850	75	1	0.58	0.90	0.81	0.74	3.31
1988	72,894	41,262	80	1	0.55	0.82	0.59	0.68	3.58
1989	72,142	44,930	82	0	0.51	0.74	0.56	0.63	3.49
1990	69,971	44,960	84	0	0.47	0.68	0.46	0.58	3.66
1991	68,726	44,428	84	0	0.44	0.62	0.45	0.53	3.65
1992	67,404	46,744	85	0	0.41	0.59	0.41	0.50	3.91
1993	66,136	45,601	85	0	0.38	0.54	0.40	0.46	3.87
1994	64,749	45,137	87	0	0.35	0.50	0.37	0.43	3.96
1995	62,054	44,380	87	0	0.33	0.48	0.35	0.40	4.04
1996	59,945	45,720	89	0	0.30	0.46	0.29	0.38	4.22
1997	58,449	47,165	88	0	0.28	0.44	0.33	0.36	4.08
Total	2,506,676	921,134	76	2

^*Lower and upper bounds for annual population badge dose geometric means (GMs) and geometric standard deviations (GSDs). Before 1955 these values were determined from the in the pre-1940, 1940–1949 and 1950–1959 periods with additional bias factors. For the 1956–1997 period the limits determined from the 1966–1997 badge dose data with extrapolation back to the values for 1955 (i.e., the literature-based values for the 1950–55) period. Details are given in the Characterizing Population Badge Dose Distributions section of the text.

^†Fitted value of population badge dose GM based on the intercept in a categorical regression model for observed badge dose model with hours-worked and work-practice effects. This model is described in the Individualization of Badge Dose Parameters section of the text.

^‡Expected values based on the distribution of realization-specific random bias factors for the pre-1940 and 1950–1955 periods. These are based on the random weights applied to literature-based estimates. From 1956–1997 they were based on the expected value of 0.5 for weights given to the upper and lower GM limits.

1. Exposure-Score Adjusted Badge Dose Distributions

The badge dose estimation model was used to develop exposure score-adjusted GM and GSD estimates of dose for each technologist for each year worked. In developing these estimates, it was assumed that, given estimates of the annual population badge dose GM and GSD for civilian hospital workers, the facility adjustment factor and exposure score parameter estimates based on the 1966–1997 badge dose readings could be applied to earlier years. The facility adjustments were made using the parameters from the badge dose estimation model [Eq. (1)] while the exposure-score adjustments were based on exposure-score categories defined using the fitted badge dose estimation model [Eq. (2)]. The exposure-score adjusted GM and GSD for badge dose estimates were defined as

$$G{M}_y(f,m,escat)={\mu }_y{\varphi }_f{\theta }_m{\omega }_{escat}$$ (3)

$$GS{D}_y=\exp \left({\sigma }_y\right){\psi }_{escat}$$ (4)

The exposure-score category (escat) adjustment factors were defined relative to the badge dose GM and GSD values for cohort members who worked in the year but did not have procedure-frequency data or hours-per-week data for that year. Since there was no information on procedure-frequency or hours-per-week before 1950, only the facility adjustment was applied for those years.

The exposure categories used in computing these adjustments were defined by dividing the empirical distribution of exposure score estimates among all cohort members in each year from 1950–1970 into 20 groups of roughly equal size. The category-specific badge dose GM-adjustment factors were defined as 1 + average ES value in each group. Since there is no such direct method to compute the badge dose GSD adjustment factors, we estimated values for these factors by fitting a Tobit regression model to the badge readings with ES category effects on both the badge dose GM and the GSD.

For each cohort member who worked in a given year and did not have an actual badge dose reading available, the individualized annual population badge dose GM was defined as the product of the population GM for that year, the facility adjustment factors and the fraction-of-year worked. The annual individual badge dose GSD was taken as the population GSD for that year. For the years before 1950, these were the only individualization factors. From 1950 onward, it was possible to use the procedure-frequency and hours-worked-per-week data to compute an individual exposure score and determine the ES category for the year. When this information was available, the individualized badge dose GM and GSD were computed as the population badge dose GM and GSD estimates times the respective category-specific exposure-score adjustment factors.

2. Badge dose GM and GSD individualization when real badge dose readings were available

There were 921,134 annual badge dose readings available for the more than 110,000 radiologic technologists until the end of 1997. Among the 110,374 technologists for whom dose estimates were made, 79,959 had at least one badge dose reading. Since badge dose readings above the MDL are often associated with measurement errors of approximately 20% (19), we assume here that individual measurement errors can be represented by a lognormal distribution with a GSD of 1.2. When the badge dose reading was above the MDL, we used regression calibration (20) to determine the expected film badge dose given the measured value and the population badge dose GM and GSD values for the year. In this case, the population GM was defined as the annual population badge dose GM times the facility adjustment factor with no adjustment for fraction of year worked or exposure score (since these effects are directly reflected in the badge dose measurement). Since we assume that both the measurement error and the population badge dose distribution are lognormally distributed, the logarithm of the adjusted badge dose (d_adj) for an individual with measured dose d_meas can be computed as

$$\log \left(d_{adj}\right)=w\log \left(d_{meas}\right)+(1-w)\log \left(G{M}_{pop}\right)$$ (5)

where GM_pop is the population badge dose GM and w is a weight that depends on the measurement error GSD (assumed to be 1.2) and the population GSD (GSD_pop). The weight is computed as

$$w=\frac{\log {\left(GS{D}_{pop}\right)}^2}{\log {\left(GS{D}_{pop}\right)}^2+\log {\left(1.2\right)}^2}$$ (6)

Since the population badge dose GSDs for 1960–1996 range from about 3.25–4.25, the weight assigned to log(d_meas) is close to 0.98.

Computation of Individual Annual Badge Dose Realizations

1. Accounting for badge position with respect to protective aprons

When the badge dose reading is less than the MDL, the derived individual badge dose distribution depends on whether we assumed that the badge was worn outside the apron. If the badge was assumed to have been worn outside the apron, then the true badge dose is assumed to be distributed as a sample from a normal distribution with mean log(GM_pop) and standard deviation log(GSD_pop) conditional on log(d_true) being less than log(MDL). However, if the badge was assumed to have been worn under the apron, then the badge reading is uninformative about the air kerma (i.e., the exposure outside the apron). In this case, we assume a hypothetical measurement outside the apron, distributed as a sample from a lognormal distribution with badge dose GM = GM_pop and variance GSD = GSD_pop, which can be combined with the apron usage probability and the transmission factor.

Our assumption that most badge measurements were outside aprons follows from federal radiation protection regulations and instructional materials, although we do know that occasionally some institutions instructed medical personnel to wear badges under aprons. Support of the notion that most badge measurements were outside of aprons comes from radiation protection guidelines (21), which specified: “. . .the assigned deep-dose equivalent must be for the part of the body receiving the highest exposure”. Literature has shown that, particularly for medical personnel participating in fluoroscopic examinations, the front collar area receives the highest exposure (22, 23). These findings have led numerous experts (22, 24–26), as well instructional textbooks (27), to recommend wearing personal monitoring badges outside the apron and mostly at collar level.

As noted earlier, information on badge location was only obtained in our third survey. Analysis of the responses to the badge location question from technologists with badge readings above the MDL suggested that there was some misunderstanding of the question and that the answers were not reliable. If badges were worn under the apron, then the badge reading should always be below the MDL. However, in fact the proportion of technologists who reported that their badge was worn inside the apron and who also had readings above the MDL was only slightly less than for those who reported that the badge was worn outside the apron. We used the data to estimate the proportion of technologists in the reported-inside but lower-than-the-MDL group who actually wore the badge under the apron for each year when badge doses were available. These proportions varied from year to year but were about 35% for those who reported wearing the badge inside the apron and about 10% for those who did not respond to the question. In generating annual dose realizations for technologists with under-the-MDL badge readings, we randomly assigned the badge reading to be inside or outside the apron according to the above probabilities.

2. Correlation of a technologist's annual doses over time

Radiologic technologists tend to perform similar activities from one year to the next and thus, one can expect that even as mean annual doses decrease over time for all technologists, the badge doses for an individual technologist will exhibit some correlation over contiguous years. The Landauer badge dose data for 1977–1997 were used to estimate the autocorrelation structure of the logarithms of the individual annual doses. Our analysis indicated correlations of about 0.5, 0.4 and 0.3 for lags of one, two and three years, respectively.

For each technologist, the dosimetry system uses Monte Carlo simulation methods to generate multiple realizations of individual annual badge doses. To accomplish this, we used standard statistical methods to generate a sequence of doses in each realization with the correlation structure based on Cholesky decomposition (28) of the desired autocorrelation matrix.

3. Implementation of badge dose estimation methods

The USRT dosimetry system uses simulation to provide multiple values of annual badge dose for each study participant taking into account individual dosimetric uncertainties as well as sources of shared errors. The goal in designing the system was to provide annual badge dose realizations that represent a sample from the actual (true) badge dose distribution given what is known about the uncertainties in the time-dependent population dose distribution, the individual's work patterns and practices and individual badge dose measurements (when available). The previous sections have described various components of the dosimetry calculations. Below, we present an outline of steps involved in producing a single realization of annual badge dose estimates, i.e., one badge dose for every member of the cohort for each work-year. The process is repeated for a desired number of iterations, e.g., 1,000.

1. Generate realization-specific population annual badge dose GM and GSD estimates:

   • Generate a multiplicative badge dose GM bias factor to be applied to the pre-1940 GM;
   • Generate a population badge dose GM and GSD estimate to be used for the 1940–1949 period using study-specific weights applied to literature-based GM and GSD estimates for this period. Apply a random realization-specific multiplicative bias factor to the expected badge dose GM;
   • Generate a population badge dose GM and GSD estimate to be used for the 1950–1955 period using study-specific weights applied to literature-based GM and GSD estimates for this period. Apply a random realization-specific multiplicative bias factor to the expected badge dose GM;
   • Generate a random weight that is used to compute the weighted average of the badge dose GM limits for the years after 1955 and multiply this value by the scaled 1950–1955 bias factor;
   • Adjust the annual population badge dose GSD estimates to reflect the scaling of the population badge dose GM values and the negative correlation between the GM and GSD values that is seen in the badge dose data;
2. Individualize the population badge dose GM and GSD estimates:

   • Make no changes to the adjusted realization-specific population GM and GSD estimates computed in step 1 above for years before 1950;
   • Apply the appropriate individual ES adjustment factors to the realization-specific population GM and GSD values from years 1950 through 1997;
3. Compute the individual badge dose realization values:

   • For technologists in years without an actual badge dose reading, generate a random annual badge dose sample from the individualized distributions developed in step 2 above. To allow for the between-year correlations, compute the random value used to generate the dose as a weighted sum (w) of a value sampled from a N(0,1) distribution and the values used for the last two years for this person. The realized dose (d_r) is computed as d_r = GM exp[wlog(GSD)];
   • For years with an actual badge dose reading above the MDL, use regression calibration based on the individualized realization-specific population badge dose GM and GSD values (from step 1 above) to compute the calibrated expected value of the badge dose reading given the assumed 20% measurement error and the individualized badge dose GM and GSD values. The realized badge dose is sampled from a lognormal distribution with the badge dose GM equal to the calibrated expected badge dose and a GSD of 1.2;
   • For years with an actual badge dose reading below the MDL, randomly assign the badge location as inside or outside the apron;
   • If the badge is assigned as in an outside-the-apron reading, generate a random sample from the individualized population distribution for the year given that the dose is less than the individual's MDL for the year. This random value is taken as the realized dose; and
   • If the badge is assigned as in an inside-the-apron reading, generate a random sample from the individualized population distribution for the year. This random value is taken as the realized dose.

Accounting for Individual Usage of Protective Aprons

The first questionnaire from the mid-1980s provided only limited information on apron usage from responses to two questions: “usually wore an apron when first worked? (Y/N)” and “usually wear an apron now? (Y/N)”, i.e., at the time the self-administered mailed questionnaire was completed. Our third self-administered questionnaire, which was sent to subjects in 2003–2005, elicited information on the percentage of time an apron was worn when performing four types of procedures (diagnostic X ray, fluoroscopy, administration of diagnostic radioisotope and administration of internal therapeutic radioisotope) in four time periods (1950–1959, 1960–1969, 1970– 1979 and 1980). A special telephone survey of cohort members who began working before 1950 was used to elicit information on apron usage before 1950. Of the 110,374 cohort members for whom doses were estimated, 72,620 responded to the third survey.

Third survey participants were asked to indicate the percentage of time an apron was worn when performing each procedure: 0%, <25%, 25–74% and ≥75%. For each question, we fit a beta PDF to the categorical responses and used these distributions to determine the expected percentage apron usage for each category. The expected values were then averaged over the four procedure types by time period for those workers first employed as radiologic technologists in the 1950s or later and by year for those first employed before 1950 to obtain a single summary value (S) for the apron usage percentage for each year in which the person worked.

The uncertainty in individual period-specific apron protection usage for the third survey respondents was described using PDFs, in the form of beta distributions, defined for each respondent in each year worked. For each survey respondent, the parameters of the individualized apron usage PDF were defined so that the mean was equal to the individual's average value of S while the variance was 1.5 times the variance of a triangular-shaped PDF with a mode at S and a range defined by individual upper and lower limiting values. The lower limiting values for S were defined as 0 for years 1940–1957 and as the largest value among 0, 0.02, 0.25 or 0.75 that was smaller than S for years 1958–1997. The upper limiting values were taken as the smallest value among 0.02, 0.25, 0.75 and 1 that was greater than S. It was assumed, based on literature, that aprons were not used by technologists before 1940.

We compared our summary distributions of apron usage with information we derived from historical publications, e.g., the journal of the AART/ASRT⁸ (reviewed from its inception in 1929 through the year 2000) and other historical compendia, e.g. (29), and found that questionnaire responses were likely to be overstating apron usage in the early years of the profession. To correct this problem, we defined a set of more conservative, literature-based apron usage PDFs for six contiguous time periods, pre-1940, 1940–1947, 1948–1949, 1950–1957, 1958–1959, 1960–1969 and 1970+, for use as an alternative to the questionnaire-based PDFs described above. Before 1953, these PDFs were defined so that the apron usage was rare while there was a slight increase in usage in the 1953–1957 period. From 1958 forward, the PDFs were defined in a manner similar to the questionnaire-based PDFs but the lower limiting value was always taken to be zero. The questionnaire-based estimates of protective apron usage are considerably greater than the literature-based estimates from 1950 onward.

The individualized literature- and questionnaire-based PDF's described above could only be developed for cohort members who responded to the third survey. However, there are 36,720 cohort members who responded to either the first or second survey but did not respond to the third survey. To develop apron usage PDFs for those cohort members, the group was divided into two subgroups: 1. Technologists (28,677) who responded to the first survey and 2. Technologists (8,083) who only responded to the second survey. The PDFs for members of those subgroups were based on the apron usage patterns of third-survey respondents with the corresponding pattern of responses to the first and second surveys.

Data from the third survey respondents in seven time periods (1940–1947, 1948–1952, 1953–1957, 1958–1969, 1970–1979, 1980– 1989 and 1990–1997) were used to identify work history patterns characterized by relatively homogenous apron usage. These work history patterns were:

1. Any fluoroscopy in any facility-type;

2. Diagnostic X rays without fluoroscopy in hospitals;

3. Diagnostic X rays without fluoroscopy in physician offices or other facility types;

4. Diagnostic or therapeutic radioisotopes or external beam procedures without fluoroscopy or diagnostic X rays in any facility before 1970;

5. Diagnostic or therapeutic radioisotopes or external beam procedures without fluoroscopy or diagnostic X rays in hospitals from 1970 onward;

6. Diagnostic or therapeutic radioisotopes or external beam procedures without fluoroscopy or diagnostic X rays in physician offices or other facility types from 1970 onward; and

7. No reported procedures in any facility type.

Since some of the patterns are defined only for a subset of the periods, there are only 39 possible time-period/work history pattern groups. For each of these groups, both literature- and questionnaire-based PDFs were created for cohort members who responded to the first survey and for cohort members who responded to the second survey, but not the first. For each of these 156 groups (i.e., 39 work patterns × 2 methods × 2 response groups), empirical PDFs were defined by averaging the relevant subset of individual apron usage PDFs (e.g., first-survey respondents who carried out diagnostic X rays in a hospital between 1953–1957). The annual literature-based and questionnaire-based apron usage PDFs for a subject who did not respond to the third survey, but for whom doses were estimated, were chosen from among these empirical distributions based on their work-history pattern in the year of interest.

Individual realization-specific apron usage probabilities were generated using a two-step process. The first step involved the identification of a year for that individual for the transition from the conservative literature-based apron usage PDF to the questionnaire-based PDF. The second step involved sampling from the individualized apron usage PDF for each year in which the person worked. For the first step, it was assumed that there was no apron usage prior to 1940 and that after 1979, apron usage probabilities were determined solely by the questionnaire-based apron usage PDFs. The distribution of years for the transition from the literature-based to the questionnaire-based apron usage PDF in a given realization was assumed to follow a beta distribution scaled to range from 1940–1979, in which the two parameters of the PDF were chosen as independent random values between 8 and 16. This choice lead to distributions in which the mean transition year over all realizations is about 1960 with less than 5% of the realizations having mean transition years before 1950 or after 1970. Given the realization-specific transition year PDF, individual transition years were determined by independent (over individuals) sampling from this distribution.

Once an individual's transition year was determined for a realization, their apron usage probability was determined by a sample from the appropriate individual apron usage PDF. For third survey participants, these are the PDFs defined by their survey responses. For those who did not respond to the third survey, the sampling involved using the value of a uniform (0, 1) random variable to define their apron usage percentile and then using a linear interpolation in tables that define the relevant cumulative apron usage PDF function.

Organ Dose Estimation Methods

Depending on the year of exposure, organ doses can be reconstructed from badge doses that were based on calibrations as either: (1) personal dose equivalent H_p(d) (30, 31), presently reported in the U.S. in mrem, or (2) exposure X, measured in Roentgen (R) including backscatter, common through 1984. In the simplest case, where no protective apron is used and badge doses are reported as “personal dose equivalent”, organ dose can be estimated as the product of the badge dose (mSv) and a dose factor (mGy/Sv) where the dose factor includes a conversion from badge dose to air kerma and from air kerma to organ dose.

$$D_T=H_p\left(d\right)\cdot D{F}_{noapron}$$ (7)

where, D_T = tissue or organ dose (Gy or rad); H_p(d) badge dose when calibrated as personal dose equivalent (Sv or rem); and DF_{no apron} = dose factor for tissues not covered by a lead apron.

Dose factors for this study were derived (14) from data published by the International Commission on Radiological Protection (32) by airkerma weighting over typical X-ray spectra. When H_p(d) is reported in mrem, then D_T is estimated in mrad. To convert to mGy to conform to the International System of Units, division by 100 is necessary.

When exposures are reported in Roentgen, H_p(d) can be estimated as shown in Eq. (8) and then used in Eq. (7).

$$H_p\left(d\right)=X\left(\frac{K_a}{X}\right)\mid \left(\frac{K_a}{H^p\left(d\right)}\right)$$ (8)

where, H_p(d) = badge dose when calibrated as personal dose equivalent (Sv or rem); K_a = air kerma (Gy or rad); X = measurement of exposure in Roentgen (R); and K_a/X = 0.0087 Gy per R (4).

For this study, we derived 348 dose factors for: 1. Twelve tissues and organs (red bone marrow, ovary, colon, brain, lung, heart, female breast, skin of trunk, skin of head and neck and arms, testes, thyroid and lens of the eye); 2. The relevant combinations of kilovoltage (kV) and filtration, which were assumed to vary by time period (14); and 3. Combinations of apron usage including no protective apron, a 0.25 mm thick Pb apron and a 0.5 mm thick Pb apron.

In the case where a lead protective apron is worn, the badge may be either outside or inside the apron. To properly calculate the organ dose, proper choice of the two components of the dose factor (organ dose per air kerma and personal dose equivalent per air kerma) are necessary, as well as the apron transmission factor. The data and procedures to calculate organ doses are provided in ref. (14). Apron thickness was also an important determinant of organ dose. Based on information from a dedicated literature review, we assumed the equal likelihood of 0.25 and 0.5 mm thick Pb aprons before 1970. In later years, we assumed the probabilities of apron thickness for 0.25 and 0.5 mm Pb aprons to be 10 and 90%, respectively.

There are several assumptions inherent in the use of the chosen dose coefficients: 1. Radiation is received almost exclusively on the anterior surface of the body because the technologist usually faces the patient as well as the source of radiation; 2. The scattered X-ray energy distributions are not significantly different from the emitted X-ray energy distributions (33); and 3. The scattered radiation field is the main radiation field to which technologists are exposed and is relatively uniform from, at least, the top of the pelvic bone to the head (34).

Individual Adjustments to Red Bone Marrow Dose to Account for Body Size

We developed a strategy to individualize values of the D_T/K_a component of the dose factor for red bone marrow (RBM) based on each individual's body mass index (BMI) using weight and height values reported in their baseline questionnaire responses. Using this adjustment, the dose to RBM could be adjusted to be as much as +40% greater (for very thin individuals) to −20% (for heavy individuals). Further details can be found in ref. (14).

Implementation of Organ Dose Estimation Methods

This version of the USRT dosimetry provides multiple cohort realizations (sets of doses for the entire cohort) to each of 12 organs or tissues. The calculation of a cohort realization for an organ dose proceeds as follows:

1. Generate realization-specific annual apron usage probabilities:

   • Define period-specific literature and third-questionnaire-based apron usage distributions;
   • Define the parameters of the distribution of transition years from the literature-based to the questionnaire-based apron usage PDFs;
   • Generate (independent) transition years for each person; and
   • enerate the annual individual apron usage probabilities based on the transition year, work history and survey response patterns.
2. Retrieve dose factors (badge dose to air kerma and air kerma to organ dose):

   • Select peak kV for each year from among 70, 80 and 90 kV using equal probabilities as described in ref. (14);
   • Use the selected kV value for each year to choose the expected value of dose equivalent-to-air kerma conversion coefficient (14);
   • Define apron transmission factors (14) for each year based on time period, selected apron thickness and kV values;
   • Apply truncated random lognormal error (GM = 1, GSD = 1.15, with truncation at the 2.5 and 97.5 percentiles) to the dose equivalent-to-air kerma conversion factor value to generate a realization-specific factor;
   • Compute individual annual air kerma;
   • Determine the expected air kerma-to-tissue-dose conversion factors for each organ based on the selected kV without apron protection;
   • For organs with the potential for apron protection, determine the expected organ-specific conversion factors based on the selected kV and apron thickness parameters;
   • Adjust expected marrow dose conversion factors using BMI and kV data;
   • Apply truncated random lognormal error (GM = 1, GSD = 1.15, with truncation at the 2.5 and 97.5 percentiles) to the air kermato-tissue dose conversion factor values; and
   • Define the weighted dose factor for each organ as the sum of the product of the probability of not wearing an apron and unprotected dose factor and the product of the apron usage probability, the protected dose factor and the apron transmission factor, TF.

3. Compute the realized organ doses as the product of the badge dose and various organ-specific weighted dose factors.

Using the data described and the basic dose equations for individuals [Eqs. (7) and (8)], organ doses can be estimated for the cohort in each realization by using Eqs. (9–11). In the simplest case, the organ-absorbed dose can be estimated for organs that are not protected by protective lead aprons:

$$D_{o,r,i,y}=B{D}_{r,i,y}\times DF{\left(noapron\right)}_{o,r,i,y}$$ (9)

where, D_o,r,i,y is absorbed dose (mGy) and is a function of organ (o), realization (r), individual (i) and year (y); BD_r,i,y is badge dose (mSv) and is a function of realization (r), individual (i) and year (y); and DF(no apron)_o,r,i,y is dose factor (mGy per mSv), assuming no lead apron usage, and is a function of organ (o), realization (r), individual (i) and year (y).

The organ-absorbed dose to organs other than RBM, which may be protected by lead aprons some, or all, of the time:

$$D_{o,r,i,y}=[(1-AU{P}_{r,i,y})\times B{D}_{r,i,y}\times DF{\left(noapron\right)}_{o,r,i,y}]+[AU{P}_{r,i,y}\times B{D}_{r,i,y}\times T{F}_{r,i,y}\times DF{\left(apron\right)}_{o,r,i,y}]$$ (10)

where, AUP_r,i,y is apron usage probability, a function of realization (r), individual (i) and year (y); DF(apron)_o,r,i,y is the dose factor (mGy per mSv), assuming a lead apron is used, and is a function of organ (o), realization (r), individual (i) and year (y); and TF_r,i,y is the apron transmission factor (proportion of air kerma transmitted through apron) and is a function of realization (r), individual (i) and year (y).

Finally, the absorbed dose to bone marrow that is partially protected by protective lead aprons (some, or all, of the time) is estimated as:

$$D_{o,r,i,y}=\left\{(1-AU{P}_{r,i,y})\times B{D}_{r,i,y}\times DF{\left(noapron\right)}_{o,r,i,y}\right\}+\left\{AU{P}_{r,i,y}\times B{D}_{r,i,y}\times [FRBM{U}_y\times DF{\left(apron\right)}_{o,r,i,y}+FRBM{P}_y+T{F}_{r,i,y}\times DF{\left(apron\right)}_{o,r,i,y}]\right\}$$ (11)

where, FRBMP is the fraction of red bone marrow protected in a given year (y), equal to 0.8 before 1960 and 0.83 for the years 1960 and after (14); FRBMU_y is the fraction of red bone marrow unprotected in a given year (y) = 1 − FRBMP.

FINDINGS AND DISCUSSION

This section summarizes our estimated badge and organ doses and uncertainties. As noted earlier, the term “badge dose” refers to measurements or estimates of personnel monitoring devices during 1916–1997. All organ doses are reported in mGy.

Dose Estimates

1. Badge doses

The estimated badge dose GMs declined rapidly from the 1960s until the early 1990s after which they remained relatively constant (Fig. 1). The data also suggest a discontinuity in the mean pre- and post-1977 trends, with pre-1977 doses being systematically lower than what might be expected based on the later data. In part, this reflects the fact that a much higher percentage of cohort-member badge doses in the early period were for military technologists, and military doses were substantially lower than civilian doses.

Efforts were made to formally estimate bias corrections by modeling the temporal trend in the population geometric mean (median) badge dose as a smooth linear-quadratic spline in time and allowing for a multiplicative bias correction for the pre-1940, 1940–1949 and 1950–1955 periods.

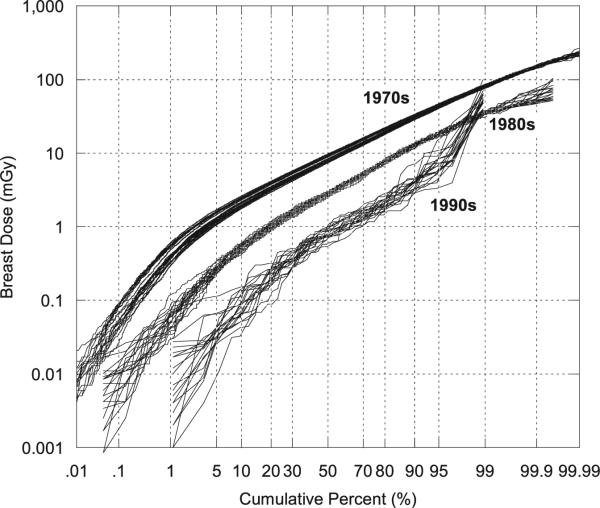
Between the mid-1960s and the 1990s the arithmetic mean population badge dose decreased about 92% (Table 4). A notable finding is that the coefficient of variation (%) of badge doses increased over the same time interval from about 56% to about 280%. The larger coefficient of variation in recent years may be due to greater job specialization of technologists, leading some technologists to receive very small doses, e.g., those involved in external beam radiotherapy, while others receive substantially higher doses, e.g., those involved in interventional fluoroscopy and nuclear medicine. As explained earlier the GM (or GSD) of the adjustment factor for the exposure score is the ratio of the GM (or GSD) for technologists in a given exposure score category to the population GM (or GSD). As one would expect, individualized exposure score GMs increase with higher exposure scores (i.e., for those who conducted more higher-dose procedures) while the exposure score GSD adjustment factors tend to be less than 1 since they are based on relatively homogeneous subpopulations while the population exposure score GSD is based on technologists with a broad range of work practices. Temporal variation in the distributions of mean badge doses is shown in Fig. 2, which presents the empirical cumulative distribution functions (CDFs) of arithmetic mean badge doses by the decade in which the technologist was first employed. Figure 2 shows, as does Table 4, the shift in the mean badge dose to progressively smaller values in later decades, with somewhat greater variations in more recent periods, presumably owing to increased job specialization.

TABLE 4.

Temporal Pattern and Summary Statistics for Estimated Cumulative Mean Badge Doses (mSv) and Female Breast Doses from 1,000 Dose Realizations Grouped by Decade First Worked for U.S. Radiologic Technologists Who Worked between 1916–1997

	1910s	1920s	1930s	1940s	1950s	1960s	1970s	1980s	1990s
	Badge dose (mSv)
Number of radiologic technologists	4	157	1,070	5,102	15,196	32,768	53,475	1,463	65
Minimum	350	180	23	2.9	1.5	0.37	0.19	0.41	0.20
Maximum	2,500	3,000	1,900	900	530	450	790	200	120
Meana	1,700	1,500	710	270	110	69	36	15	5.5
Median	1,900	1,600	670	260	100	62	31	11	2.6
Standard deviation	940	590	350	130	68	39	25	15	15
Standard error	470	47	11	1.9	0.55	0.21	0.11	0.39	1.9
Coefficient of variation (%)	56	40	49	49	59	56	69	99	280
	Female breast dose (mGy)
Number of female technologists	3	128	816	3,348	11,337	25,686	40,428	1,111	46
Minimum	290	150	19	1.70	0.71	0.085	0.058	0.082	0.089
Maximum	1,800	2,500	1,500	660	380	210	180	57	61
Meana	1,200	1,200	560	180	54	27	14	6.2	2.8
Median	1,400	1,200	510	160	46	22	11	4.2	1.2
Standard deviation	770	490	280	92	36	20	12	6.6	8.9
Standard error	450	43	10	1.6	0.34	0.12	0.060	0.20	1.3
Coefficient of variation (%)	66	42	51	51	67	74	86	110	320

Note. All doses are rounded to two significant digits.

^aArithmetic mean of the mean cumulative doses from 1,000 dose realizations for each radiologic technologist.

FIG. 2.

Cumulative percentage of arithmetic mean badge doses (mSv) by decade first worked (see Table 4).

2. Organ doses

There were 109,300 technologists that had non-zero doses⁹ (Table 5). On average, the RBM had the lowest mean cumulative occupational dose (8.7 mGy), followed (in order of increasing population mean dose) by ovary (11 mGy), brain (12 mGy), colon (16 mGy), lung (17 mGy), heart (22 mGy), female breast (37 mGy), testis (57 mGy), skin on anterior side of trunk (57 mGy), thyroid (64 mGy), lens of eye (77 m Gy) and skin on the anterior of the head and neck (91 mGy). Table 5 shows wide ranges of cumulative occupational doses even to the same organ. Much of the variation was due to the number of years each technologist worked, the number of procedures performed in each year and individual use of protective aprons.

TABLE 5.

Summary Statistics for Estimated Mean Cumulative Badge (mSv) and Mean Cumulative Organ (mGy) Doses from 1,000 Dose Realizations among U.S. Radiologic Technologists Who Worked between 1916–1997

	Badge	RBM	Ovary	Brain	Colon	Lung	Heart	Female breast	Testis	Skin of trunk (anterior)	Thyroid	Eye lens	Skin of head and neck (anterior)
Number of radiologic technologists	109,300	109,300	82,903	109,300	109,300	109,300	109,300	82,903	26,397	109,300	109,300	109,300	109,300
Minimum	0.19	0.021	0.021	0.032	0.028	0.028	0.037	0.058	0.078	0.075	0.16	0.18	0.21
Maximum	3,000	430	530	310	750	810	1,000	2,500	2,300	3,900	2,300	3,500	4,000
Meana	76	8.7	11	12	16	17	22	37	57	57	64	77	91
Median	47	4.8	6.0	8.1	8.4	8.6	11	17	26	24	40	45	53
Standard deviation	120	15	20	14	30	32	40	88	113	140	91	130	150
Standard error	0.35	0.045	0.070	0.043	0.090	0.10	0.12	0.31	0.69	0.43	0.28	0.40	0.46
Coefficient of variation (%)	150	170	180	120	180	190	180	240	197	250	140	170	170

Note. Organs are ordered left to right by increasing population mean cumulative organ dose (all doses are rounded to two significant digits).

^aArithmetic mean of the mean cumulative doses from 1,000 dose realizations for each radiologic technologist.

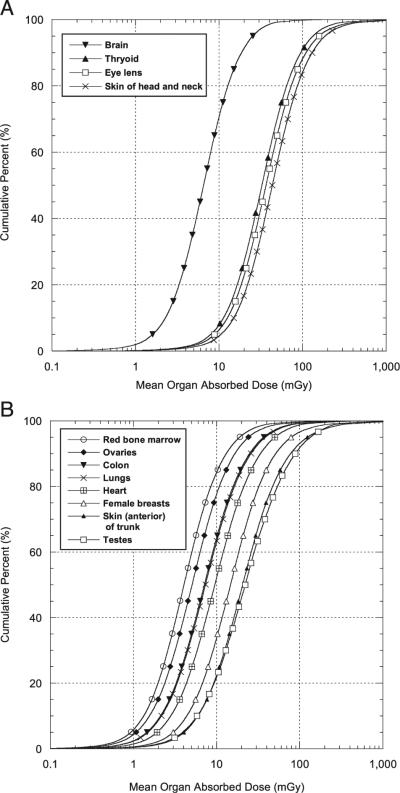
Empirical CDFs of arithmetic mean organ dose (mGy) are shown in Fig. 3A for four organs/tissues that are never covered by protective aprons [brain, eye lens and front skin of face and head (see Table 5)] and thyroid, which was not typically protected in the years of this study. Similarly, empirical CDFs of arithmetic mean organ dose (mGy) for eight tissues/organs that are sometimes protected by protective aprons are shown in Fig. 3B. These include breast, RBM, ovary, lung, testes, heart, colon and frontal skin of the trunk. Because the doses in Fig. 3A and B represent a combination of exposures with and without aprons, the range of doses is much greater than for tissues never protected by aprons. For example, for the tissues in Fig. 3A the 95th percentile is about 10 times greater than the 5th percentile while in Fig. 3B the 95th percentile for most tissues is about 20–40 times the 5th percentile.

FIG. 3.

Cumulative percentage of estimated cumulative occupational arithmetic mean doses (mGy) to four organs/tissues not covered by protective lead aprons (panel A) and eight organs potentially covered by protective lead aprons (panel B) (see Table 5). Doses are for technologists who ever worked from 1916–1997.

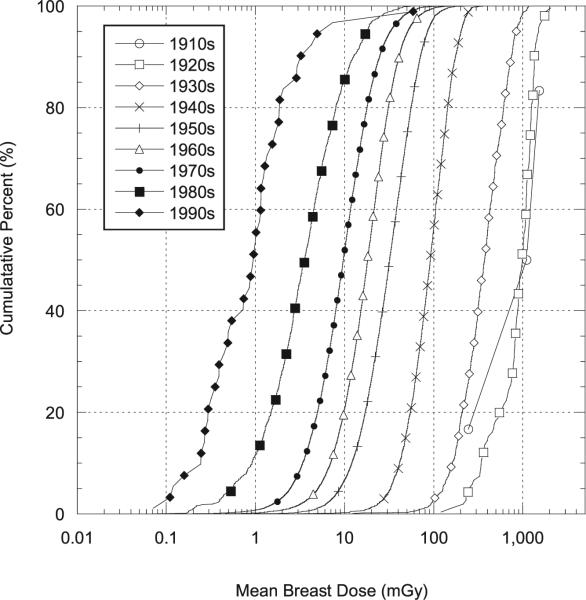
The population mean cumulative occupational female breast dose (mGy) decreased 40-fold from about 560 mGy in the 1930s to about 14 mGy beginning in the 1970s, and decreased another fivefold by the 1990s to an annual mean of 2.8 mGy (Table 4). Cumulative distributions for arithmetic mean doses to the female breast as a function of decade first worked are shown in Fig. 4 (see Table 4). Figure 4 in particular demonstrates the change in the mean dose to the breast by decade first worked, which diminished from a mean of about 1,200 mGy in the 1920s to about 14 mGy in the 1970s and to about 3 mGy 1990s (Table 4). Despite the clear decrease in the mean values, the distributions in all decades were wide and overlapped.

FIG. 4.

Cumulative percentage of estimated arithmetic mean doses (mGy) to the female breast as a function of decade first worked (see Table 4). Doses are for technologists who ever worked from 1916–1997.

Uncertainty

The USRT dosimetry system is designed to produce multiple realizations of the cohort dose distribution with each realization representing one possible true distribution. The variations of the realized sets represent the uncertainty about the true but unknown dose distribution. To simulate the uncertainty of cohort realizations, the state-of-knowledge about numerous factors important to estimating individual doses must be assessed. Table 6 lists the important components of uncertainty in the USRT dosimetry system and specifies the uncertain components as either shared or unshared assignment errors. Shared errors arise from parameters that are assigned the same value, within a single realization, to all subjects in the cohort or in a subgroup. Unshared errors refer to uncertain values that vary independently from person-to-person within a realization of cohort doses. The term “assignment error” refers to errors that arise when a quantity of interest is assigned a representative value, the expected value of which is believed to be equal to the true value of the quantity. The latter is a form of Berkson error (35).

TABLE 6.

Classification of Uncertain Parameters in the Dosimetry System

Time period	Parameters being estimated	Uncertain component	Type of uncertainty	Description of uncertainty	Uncertainty distribution parameters
Badge dose estimation
Pre-1940	Population badge dose GM/GSD estimates.	Realization-specific random bias factor.	Shared† assignment error*.	Beta (2,2) scaled to range from 0.5–1.5.	GM: mean = 72; σ = 16; GSD: mean = 2.85.
1940–1949	Population badge dose GM/GSD estimates.	Realization specific random weights for literature reports.	Shared assignment error.	Random sample of weights chosen using a Dirichlet distribution.	GM: mean = 18; σ = 4.3; GSD: mean = 4.3; σ = 0.10.
		Realization-specific random bias factor.	Shared assignment error.	Beta (2,2) scaled to range from 1 to 5.
1950–1955	Population badge dose GM/GSD estimates.	Realization specific random weights for literature reports.	Shared assignment error.	Random sample of weights chosen using a Dirichlet distribution.	GM: mean = 6.1; σ = 0.41; GSD: mean = 2.3; σ = 0.07.
		Realization-specific random bias factor.	Shared assignment error.	Beta (2,2) scaled to range from 0.5–1.5.
1956–1997	Population badge dose GM/GSD estimates.	Realization-specific weight for interpolation between GM limits.	Shared assignment error.	Uniform (0, 1).	Interpolation weight: mean = 0.5; σ = 0.29.
		Realization-specific weight for random bias factor (dependent on 1950–1955 bias factor, interpolation weight and year).	Shared assignment error.	Linear interpolation of bias factor between 1950–1955 value in 1955 and 1 for the 1983–1997 period.	Annual value determined by year, random bias factor and random interpolation weight.
All	Individual annual badge dose GM/GSD estimates.	Individual exposure-score-category-based adjustment of population badge dose GM and GSD.	Unshared† assignment error.	GM scaled by individual, period specific exposure score scaling factor, GSD scaled to preserve 99th percentile standard population distribution.	If has exposure score (ES), GM adjustment mean = 0.96; σ = 0.51; GSD adjustment mean = 0.93; σ = 0.06; if no ES, then GM and GSD adjustment factors are both 1.
All	Film badge dose generation (given individualized badge dose GM and GSD) with no film badge reading.	Random dose from individualized lognormal population distribution.	Unshared assignment error.	Multivariate lognormal (GMiry, GSDiry) and autoregressive correlation structure.	**
		Adjustment for between-year dose correlations.	Unshared assignment error.
All	Film badge dose generation (given individualized badge dose GM and GSD) with film badge reading above MDL.	Regression calibration adjustment using individualized population badge dose GM/GSD estimates assuming 20% measurement error.	Unshared classical measurement error.	Calibration assumes multiplicative lognormal measurement error and an individualized lognormal population dose distribution with the GM and GSD individualized for person and year within realization.	Measurement error with GM = 1, GSD = 1.2; population GM/GSD by year within realization.
		Random badge dose with calibration-adjusted badge dose as GM and a GSD representing 20% measurement error.	Unshared assignment error.	Lognormal measurement error.	Measurement error: GM = 1; GSD = 1.2 with individualized annual population GMiry; and GSDiry.
All	Film badge dose generation (given individualized badge dose GM and GSD) with film badge reading below MDL.	Random assignment as inside or outside apron reading	Unshared assignment error.	Location is treated as binomial with year-dependent probabilities determined from questionnaire data.	**
		Inside apron (generate dose from individualized unconditional population distribution)
		Outside apron (generate dose from individualized population distribution conditional on dose being less than the MDL).
Organ dose estimation
Pre-1940	Apron usage probability.	Assumption that apron was never worn.	Shared, assignment error.	Assume never wore apron.	None.
1940–1979	Apron usage probability.	Parameters of the probability distribution for the year of transition from use of “literature-based” apron usage to “questionnaire-based” usage.	Shared, assignment error.	Realization-specific beta distribution for year of transition from literature- to questionnaire-based usage probability distribution with parameters chosen as independent uniform (8, 16) variables.	Mean transition year 1959, standard deviation 4.8 years.
		Individual literature-based to questionnaire-based apron usage PDF transition year.	Unshared assignment error.	Sampled from beta density defined above.
		Individual apron-usage probability (from individual work-history and period specific apron usage PDFs).	Unshared assignment error.	Sampled from literature- or questionnaire-based empirical work-history-dependent apron-usage densities.	**
1980–1997	Apron usage probability.	Individual apron usage probability (from questionnaire-based individual work-history and period specific apron usage PDFs).	Unshared assignment error.	Sampled from questionnaire-based empirical work-history-dependent apron-usage densities.	**
All	Apron thickness (0.25 or 0.5 mm Pb equivalent).	Period-specific probability of 0.5mm Pb equivalent apron.	Shared assignment error.	0.5 mm Pb apron probability = 0.5 before 1970 and = 0.9 after 1969.	Before 1970: mean = 0.375 mm; σ = 0.125; 1970–1997: mean = 0.475 mm; σ = 0.076 mm.
		Individual annual apron thickness.	Unshared assignment error.	Binomial using period-specific probabilities with transitions allowed only once every j years where j is the period-specific average job length.	**
All	Hp(10) to air kerma ratio (i.e., Hp(10)/Ka).	Period-specific ratio GM for realization.	Shared assignment error.	Select individual kV (70, 80 or 90) with equal probability. Assign, period- and kV-dependent GM.	1916–1949: mean = 0.83; σ = 0.13; 1950–1954: mean = 1.14; σ = 0.17; 1955–1968: mean = 1.28; σ = 0.18; 1968+ mean = 1.34; σ = 0.19.
		Individual ratio.	Individual assignment error.	Lognormal with selected GM and GSD=1.15 with range restricted to 0.135 to 7.39.
All	Tissue dose to air kerma ratio (i.e., DT/Ka), without apron shielding and with shielding by 0.5 or 0.25 mm thick Pb aprons.	Period-specific ratio GMs for realization.	Shared assignment error.	Assign organ-, period- and kV-dependent GM.	**
		Individual ratios.	Unshared assignment error.	Lognormal with selected GM and GSD = 1.15 with range restricted to 0.75–1.32.
All	BMI-adjusted marrow dose: tissue dose to air kerma ratio (i.e., DT/Ka).	Period-specific, body mass index (BMI)-group slope and intercept for GM.	Shared assignment error.	Use period- and kV-dependent functions of BMI to compute GM.	**
		Individual ratio.	Unshared assignment error.	Lognormal with selected GM and GSD = 1.15 with range restricted to 0.75–1.32.
All	Organ dose realization.	Individual organ doses computed as apron-usage probability-weighted average of organ dose with and without apron usage.	Unshared assignment error.	Apron-usage probability-weighted average of organ dose with and without apron usage.	**

^†“Shared errors” refer to uncertain values for which the same values are used for all cohort member doses in a specific realization of cohort member doses. Unshared errors refer to uncertain values that vary independently from person-to-person within a realization of cohort doses.

^*“Assignment error” refers to errors that arise when a quantity of interest is assigned a representative value, the expected value of which is believed to be equal to the true value of the quantity. This is a form of Berkson error.

^**Complex function of year and individual parameters that is not amenable to a useful, simple summary description.

The variation of the mean, variance and shape of cohort organ dose distributions is clearly influenced by the degree of shared error and the total organ dose uncertainty for each individual. The uncertainty of doses to each individual can be evaluated by assessing the variation of organ dose to the individual across the 1,000 cohort realizations. For example, the geometric standard deviation (GSD) of breast dose for each female in the cohort was derived from the 1,000 realized cohort dose data sets. Figure 5 illustrates the individual breast dose GSD values as a function of the individual GM breast doses. While there were a few cases of relatively small absorbed doses (<1 mGy) with large uncertainty (GSDs >4), most of the uncertainties for individual cumulative occupational female breast doses were less with GSDs between 1.5–3.0 (Fig. 5). The minimum breast dose GSD (~1.2) was for those subjects with actual badges dose readings who were exposed only in a single year, and for whom there was no uncertainty regarding apron usage. High breast dose uncertainty (i.e., GSD >3) was found for subjects with complex job histories, who did not have measured badge doses in some years and lacked definitive information about critical exposure variables such as apron usage.

FIG. 5.

Empirical relationship between estimated GSDs of individual cumulative female breast doses (mGy) and estimated individual GM dose (mGy) to the female breasts. Doses are for technologists who ever worked from 1916–1997.

The variation in 20 randomly selected cohort realizations of female breast dose from among the 1,000 total realizations is shown in Fig. 6 for women who began working in the 1970s (n = 40,428), 1980s (n = 1,111) and 1990s (n = 46). While the global mean breast doses for these subgroups were 14 mGy, 6.2 mGy and 2.8 mGy, respectively (see Table 4), the variation in the shape of the CDFs shows the uncertainty about the true but unknown dose distribution.

FIG. 6.

Cumulative percentage of 20 randomly chosen cohort realizations of cumulative occupational absorbed dose (mGy) to the breast of female technologists who began working in three decades: 1970s (n = 40,428), 1980s (n = 1,111) and 1990s (n = 46) (see Table 4).

Generation of multiple realizations of cohort distributions is becoming more commonplace in dose reconstruction and epidemiology, although there is still considerable discussion and research underway concerning methods for assessing risks with complex uncertainty. The Monte Carlo realizations of dose, in theory, can be directly used to estimate risks that take into account the dose uncertainties by full likelihood methods (36, 37). Regression calibration (20), using the mean of the dose realizations in the regression, can also be used if the degree of shared error is minimal. The preferred methods for analyzing risks for the USRT cohort are currently under investigation.

Biodosimetry and Other Validation Exercises

Badge dose

We compared our estimated badge doses for the 1949–1960 period with 194 annual doses to non-cohort members abstracted from radiation log books at a major U.S. hospital and a publication by Bushong (38) that reported badge doses for 1960–1976 from four Houston-area hospitals. The agreement between the population PDFs derived from our dosimetry system and those derived from the two external sources was very high, with the annual median values differing by only 0.1–0.3 mSv (data not shown).

RBM dose

. We previously assessed chromosome trans-location frequencies using fluorescent in situ hybridization (FISH) in separate groups of 79 and 150 radiologic technologists and evaluated the relationships between chromosome translocation rates and estimated occupational radiation doses, finding borderline statistical significance (39, 40). We reevaluated (41) the chromosome translocation dose-response relationship in the 229 biodosimetry study participants using the RBM doses reported here. About 95% of the RBM doses in the combined groups ranged from 0.2– 100 mGy. With our new doses, we found a statistically significant association (P = 0.0188) with 5.7 (95% CI 0.2, 11.3) translocations per 100 cell equivalents per Gy, after adjusting for personal diagnostic medical radiation exposure (41) (Table 7). A significant excess translocation rate was observed even when the analysis was restricted to technologists receiving less than 100 mGy to RBM (41).

TABLE 7.

Comparison of Dose-Response Findings from Studies of Chromosome Translocation Rates in Relation to Current and Previous Estimates of Occupational Radiation Dose to Red Bone Marrow in Two Groups of U.S. Radiologic Technologists

Chromosome translocation group	Number of technologists	Source of radiation exposure	Year of dosimetry version	Dose range (Gy)	Ref.	Number of chromosome translocations per 100 CEa/Gy (95% C.I.)
Group 1 and 2 combined	238	Occupational	2013	0–0.14	(41)	5.7 (0.2, 11.3)b
Group 1 and 2 combined	238	Occupational + personal medical exposure	2013	0–0.36	(41)	4.4 (2.5, 6.5)c
Group 1	79	Occupational	2008	0.00–0.03	(40)	30 (–7, 70)d
Group 2	150	Occupational	2007	0.00–0.07	(39)	9 (–1, 20)e

^aChromosome translocations were assessed using a process of fluorescent in situ hybridization that painted 6 chromosomes in circulating lymphocyte cells (39). Whole chromosome equivalents (CE) represent the normalized translocation frequency per 100 cells assuming full-genome painting of the nuclear DNA.

^bAdjustment for age, study group (1 vs. 2), sex × study group and personal diagnostic medical exposure.

^cAdjustment for age, study group (1 vs. 2), sex × study group with the coefficients for occupational exposure and personal diagnostic medical exposure constrained to be equal.

^dAdjustment for age at blood draw, prior radiotherapy and history of prior radioisotope therapy.

^eAdjustment for age at blood draw, personal diagnostic red bone marrow dose and gender.

Our finding of a statistically significant excess translocation rate with cumulative RBM dose is important to our effort to obtain independent support of our dose estimation system. Moreover, our determined translocation rate of 5.7 translocations per 100 cell equivalents per Gy is close to the average of 5.4 from translocation studies in atomic bomb survivors of Hiroshima and Nagasaki [see Table 6, ref. (41)]. Because doses to other organs, in the absence of differences in use of protective aprons, differ primarily by constant values related to the dose factors for each organ, support of the RBM doses lends support to the dose estimates for all other organs.

CONCLUSIONS

We have developed and implemented significant improvements in our system to estimate annual and cumulative occupationally received radiation doses to individual organs of medical radiologic technologists. Support for this dosimetry system is provided by new, statistically significant findings on the relationship between dose to bone marrow and chromosome translocation rate assayed in a subset of cohort subjects.

A number of common suppositions about exposures of medical personnel over time are supported by this dosimetry reconstruction, including a decline in the population average dose equivalent to technologists. Less well known, however, was that badge doses during the early 1960s appeared nearly constant (Table 4), similar to the situation in the United Kingdom (42), although soon after, badge doses declined dramatically, dropping 50% around 1980 with another 50% decline in the 1990s.

Our dosimetry estimations also indicate substantial differences in organ doses that would not, otherwise, be obvious from film-badge measurements alone. Superficial organs and tissues, e.g., thyroid, testes, female breast, and skin of the head and neck region, were estimated to have received, on average, similar cumulative doses, and were among the highest doses of all organs assessed. The exception to this generalization was for technologists who used protective lead aprons that could reduce breast dose by as much as 99%. More deeply-seated organs, such as the ovary, lung and, even more so, red bone marrow, received cumulative doses that were 15% (or less) than doses received by the more superficial organs.

In addition to significant improvements in dose estimation, we also developed and implemented a strategy for assessing uncertainty for each cohort subject and a strategy to produce multiple realizations of doses for the entire study population for the purposes of estimating cancer and other health risks. To do this, we considered numerous sources of potential error and uncertainty that are specified as either shared or unshared among groups or individuals. While a single set of mean annual and cumulative doses per subject can be produced from multiple realizations and truncated relative to disease onset for use in regression calibration and conventional risk analyses, the availability of multiple realizations of the cohort dose distribution will allow exploration of more sophisticated risk analysis methods, such as weighted likelihood profile averaging and Bayesian methods.

The models and reconstructed doses presented herein represent, to our knowledge, the most comprehensive dose reconstructions undertaken to date for a cohort of medical radiation workers.