Abstract
Phenotypic heterogeneity of depression has been cited as one of causes of the limited success to detect genetic variants in genome-wide studies. The 7-item Hospital Anxiety and Depression Scale (HADS-D) was developed to detect depression in individuals with physical health problems. An initial psychometric analysis showed that a short version (“HADS-4”) is less heterogeneous and hence more reliable than the full scale, and correlates equally strong with a DSM-oriented depression scale. We compared the HADS-D and the HADS-4 to assess the benefits of using less heterogeneous phenotype measures in genetic analyses. We compared HADS-D and HADS-4 in three separate analyses: (1) twin- and family-based heritability estimation, (2) SNP-based heritability estimation using the software GCTA, and (3) a genome-wide association study (GWAS). The twin study resulted in heritability estimates between 18 and 25%, with additive genetic variance being the largest component. There was also evidence for assortative mating and a dominance component of genetic variance, with HADS-4 having slightly lower estimates of assortment. Importantly, when estimating heritability from SNPs, the HADS-D did not show a significant genetic variance component, while for the HADS-4, a statistically significant amount of heritability was estimated. Moreover, the HADS-4 had substantially more SNPs with small p-values in the GWAS analysis than did the HADS-D. Our results underline the benefits of using more homogeneous phenotypes in psychiatric genetic analyses. Homogeneity can be increased by focusing on core symptoms of disorders, thus reducing the noise in aggregate phenotypes caused by substantially different symptom profiles.
Keywords: reliability, heterogeneity, depression, HADS, GCTA, GWAS
Introduction
Major Depressive Disorder (MDD) and its symptoms are both widespread and heritable [Flint and Kendler 2014]. Since the mid-20th century, dozens of studies have found that genetic variation explains between 30% and 40% of the variance in depression [Sullivan, et al. 2000]. The explosive growth of genotyping technology has made it possible to search for the specific genetic variants that underlie this heritability. To date, variants that reliably predict depression have been largely elusive [Hek, et al. 2013]. The most likely explanations include lack of statistical power to detect the small effects of individual variants and the heterogeneity of depression [Levinson, et al. 2014]. To achieve sufficient power to detect the weak associations of individual variants, research groups have formed consortia to reach the required extremely large sample sizes [Pedersen, et al. 2013; Psaty, et al. 2009; Ripke, et al. 2012]. However, heterogeneity of the phenotype counteracts these efforts as it reduces power [Levinson, et al. 2014; Lubke, et al. 2014]. Heterogeneity of depression refers to the presence of different subgroups that are characterized by different depression profiles on the symptoms [Lamers, et al. 2013]. It can also refer to the fact that when depression scales are factor-analyzed often multiple factors emerge, showing that these scales are multidimensional rather than unidimensional [Jang, et al. 2004; Straat, et al. 2013], and individuals can have different profiles on these factors. In this study we focus on the second type of heterogeneity. Genetic analyses of depression most commonly use aggregate scores of a depression scale (i.e., sum scores, total scores). In principle, aggregate scores that are computed from a unidimensional scale (i.e., scales that have a single underlying factor) are more reliable than when computed from a multidimensional scale that also measures additional factors. More reliable aggregate scores lead to more consistent results when applied under similar conditions [Jöreskog 1971; Mellenbergh 1996]. This is due to the fact that the additional factors can introduce heterogeneity because of differences in profiles on these additional factors. Stated more simply, there are many different possible combinations of the factors that lead to the same sum score on a multidimensional scale, and this introduces noise in statistical analyses. In our study we show that using a more reliable unidimensional version of a depression scale can contribute to improving statistical power in genetic analyses.
GWA studies have increasingly been supplemented with heritability estimation using the software Genome-wide Complex Trait Analysis [Lango-Allen, et al. 2010; Lubke, et al. 2012; Pedersen, et al. 2013]. In this approach to heritability estimation, a genetic relationship matrix calculated from single nucleotide polymorphism (SNP) data is used to estimate how much of the variance of the phenotype is due to SNPs [Speed, et al. 2012]. However, standard errors of the variance estimates in these studies are often large, leading to wide confidence intervals [Lubke, et al. 2012]. As shown by Lubke et al. for Borderline Personality Disorder, this lack of power can at least partially be due to using aggregate phenotype measures that are heterogeneous [Lubke, et al. 2014]. The effects of reliable versus unreliable phenotype measures have been the subject of much research in psychometrics. An important result is that unreliably measured phenotypes lead to decreased power in statistical analyses [Kaplan 1990].
The present study focuses on the benefits of a reliable measure of depression in: 1) twin and family-based heritability estimation; 2) SNP-based heritability estimation; and 3) a genome-wide association study (GWAS). In all three parts, the Hospital Anxiety and Depression Scale (HADS-D, [Zigmond and Snaith 1983]), is compared to more reliable short version of this scale that we selected in this study.
The HADS-D was developed to identify non-somatic depressive symptoms in patients undergoing general medical care, and therefore only assesses part of the DSM depression symptoms. Factor-analytic studies of depression scales commonly discriminate between somatic and non-somatic factors [Jang, et al. 2004; Lux and Kendler 2010]. Still, although focusing exclusively on non-somatic depressive symptoms, the HADS-D has been shown in psychometric analyses to be multi-dimensional, featuring several correlated factors [Mykletun, et al. 2001; Straat, et al. 2013]. These results imply a decreased utility of the HADS-D total score in genetic analyses because of phenotypic heterogeneity [Bollen and Lennox 1991]. In other words, the HADS-D score is as a less reliable measure of depression because it sums correlated but different dimensions. In order to increase reliability in measuring depression, we constructed a total score derived from a unidimensional subset of HADS-D items. We compared the performance of this subscale score (“HADS-4”) to that of the HADS-D total score in three separate genetic analyses.
Our study consisted of: 1) an investigation of the psychometric properties of the HADS-D using item factor analysis, resulting in the construction and validation of a unidimensional, more reliable short version, the HADS-4; 2) heritability estimation based on nuclear families of twins (twin pairs, their siblings, and parents); 3) heritability estimation based on SNPs collected on essentially unrelated individuals using the software GCTA, an increasingly common approach in psychiatric genetics to test if twin-based heritability estimates can be recovered with SNP data; and 4) a GWAS. In parts (2)-(4), we compared the performance of the HADS-D and HADS-4. For all analyses we used data collected in the Netherlands Twin Register (NTR) [Willemsen, et al. 2013]. Note that based on the sample size with available HADS-D and SNP data in the NTR (N=5777) we did not expect significant results in the GWAS. This part was included to assess the difference in statistical power between the two versions of the HADS in a GWAS.
Materials and Methods
Subjects & Materials
Individuals who participated in the eighth wave of data collection by the NTR supplied data on depression from multiple instruments. The NTR is a longitudinal twin-family study of mental and somatic health. A detailed description of the data collection and methods used, including IRB approval, measurements taken, genotyping procedures, and quality control is provided in [Willemsen, et al. 2013].
We analyzed phenotypic data from a sample of 15,997 individuals in 7,078 families. The depression phenotype data consisted of responses to Dutch translations of the HADS-D and the ASEBA Adult Self Report Depressive Problems Scale (ASR) [Reef, et al. 2009; Spinhoven, et al. 1997]. The ASR is an instrument for which a scoring algorithm based on DSM symptomology was developed, and which also records somatic symptoms that are omitted from the HADS-D [Achenbach, et al. 2005]. We used ASR scores as a criterion to validate that the HADS-4 performs similarly to the full HADS-D as a measures of depression. We used maximum-likelihood estimation with the EM algorithm, which enabled us to use individuals missing a small number of responses. Individuals missing more than 30% of responses to HADS-D, HADS-4, or ASR items were excluded in order to ensure convergence.
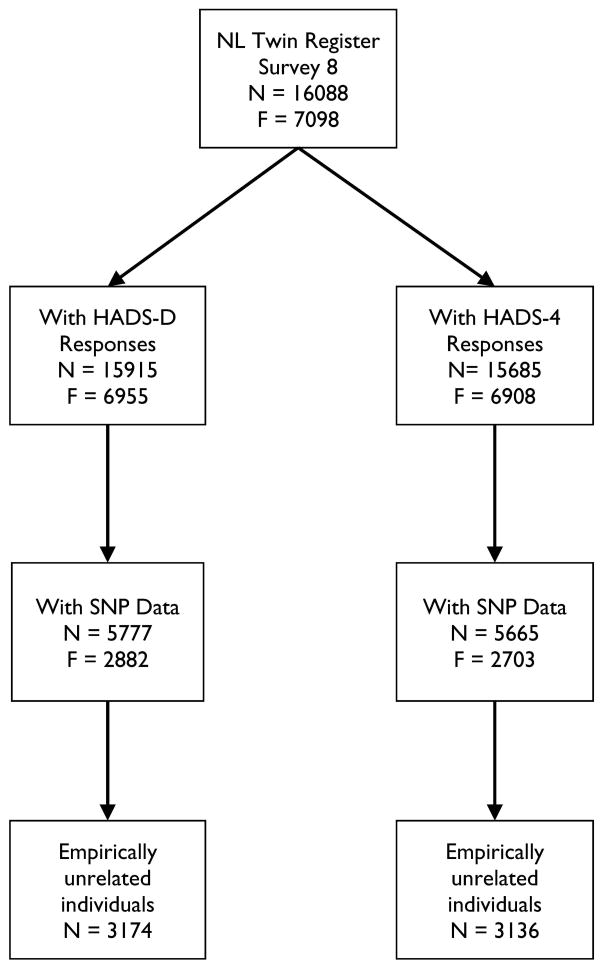
Figure 1 provides a flowchart showing the available data on the different scales, as well as which parts of the data were used for which part of the analyses. For the psychometric analyses, all individuals of each family were included, and analyses were carried out with statistical corrections for relatedness [Savalei 2014]. In the twin and family analyses, within-family covariance matrices were based on the data of two twins, their parents, and two siblings. Many families did not have data from the complete set of six individuals; due to this incomplete data, the EM algorithm was used to estimate the covariance matrix [Jamshidian and Jennrich 1997]. Table S1 in the Supporting Information gives percentages of families by structure; for example 44.6% of families had maternal data and 29.8% had paternal data, and 21.7% had data from both parents. The lower percentage of subjects with parent data reflects the presence of older subjects in the data. SNP-data were available for N=5777 with HADS-D, and for N=5665 with HADS-4. The difference in N was due to missing two of the HADS-4 items, which exceeded the 30% missingness criterion for the HADS-4 but not the HADS-D. The sample sizes for essentially unrelated individuals were N=3174 (HADS-D), and N=3136 (HADS-4). All individuals with SNP data were included in the GWAS whereas the GCTA analysis was based on essentially unrelated individuals. For individuals who had been genotyped, four additional covariates were defined: three principal component (PC) scores representing geographic origin in the Netherlands and a fourth representing genotyping platform [Boomsma, et al. 2014]. These PCs were used in the GCTA analysis as well as the GWAS.
Figure 1.
Flowchart of study participants with non-missing genotypic and phenotypic data.
In the next four sections, we outline the methods for (1) analyzing the measurement properties of the HADS-D and for choosing the first four items as the most reliable, homogeneous subset, (2) the twin-based heritability analyses, (3) the SNP-based heritability analyses with GCTA, and (4) the GWAS which was done in Plink [Purcell, et al. 2007].
Analysis 1: HADS-D and its Psychometric Properties
The HADS-D is a 7-item scale. Each HADS-D item has ordered responses that are coded from 0 to 3, with the total score ranging from 0 to 21. The individual items and their responses are listed in Table S2 of the Supporting Information.
We analyzed the dimensionality of the HADS-D and the reliability of its items using factor analysis. To avoid unnecessary capitalizing on chance, we split the data into a smaller set for the exploratory factor models (data from 2,986 families, 2,418 males and 4,342 females), and a larger set for the confirmatory factor models (data from the remaining 4,092 families, 3,338 males and 5,899 females). Model fitting was done using Mplus 7 [Muthén and Muthén 1998–2012]. Since we included related individuals in the factor analyses, we used maximum likelihood estimation with robust standard errors [Savalei 2014]. The EFA showed that the first four HADS-D items loaded on a single factor, whereas the remaining items also loaded on additional factors, thus replicating previous findings [Mykletun, et al. 2001; Straat, et al. 2013]. We therefore performed item selection in the confirmatory sample, creating a short version of the HADS-D consisting of the first 4 items (abbreviated as “HADS-4”). Details concerning item selection and the derivation of the reliability of the HADS-D and HADS-4 scores are provided in the Supporting Information. The derivation shows that large item-specific variances can lead to a total score that is less reliable than a score based on only a few items [Bollen and Lennox 1991].
In addition to reliability, our initial psychometric analyses also evaluated the convergent validity of the HADS-D and HADS-4 items. This was done by regressing the ASR total score on the HADS-D and HADS-4, respectively, The resulting R2’s were used as a validity coefficient [Lord, et al. 1968]. The validity coefficient for the HADS-4 indicates its ability to measure the same non-somatic aspects of depression that are targeted by the full HADS-D. In our sample, N = 15,018 individuals with HADS-D scores also had ASR scores. As in all analyses, age, sex, and their interaction were used as covariates, and sandwich-type covariance estimates were used to correct standard errors for familial clustering.
Analysis 2: Heritability Estimates based on Twins and Relatives
In this approach to estimating heritability, the expected genetic relatedness between family members is used to decompose the phenotypic variance into genetic and environmental effects [Martin, et al. 1997]. Different models of inheritance allow for the estimation of additive and non-additive genetic effects as well as shared environment or cultural transmission [Posthuma, et al. 2003]. We used Mplus 7 to fit different models of inheritance to HADS-D and HADS-4 data from twins and their families. Details are provided in the online Supporting Information. We used goodness-of-fit-statistics to compare models that included additive genetic, non-additive genetic, family environment, gene-environment covariance, familial transmission, and assortative mating effects on phenotypic variance. We fit these models in the nuclear families of 6955 twin pairs (2364 MZ/4591 DZ) in which the twin(s) and family members had HADS-D data and in the 6908 (2356 MZ/4552 DZ) twin families with HADS-4 data.
Analysis 3: Heritability Estimates based on SNPs
The GCTA software (http://www.complextraitgenomics.com/software/gcta/) was used to estimate the proportion of phenotypic variance that is due to SNPs [Davis, et al. 2013; Lubke, et al. 2012; Plomin and Simpson 2013]. First, a genetic relatedness matrix is calculated from the individuals’ genotypes at all available SNPs. Next, the genetic relationship matrix is used as a predictor in a constrained linear mixed model to estimate the genetic variance component. Previous research using the approach has shown that considerable sample sizes are needed to obtain heritability estimates with small confidence intervals [Visscher, et al. 2014].
We used GCTA software to estimate the heritability of depression in 3,174 individuals with HADS-D data and 3,136 individuals with HADS-4 data. These sample sizes are relatively small for two reasons: 1) fewer than half of the individuals in the sample used for the twin analyses had been genotyped, and 2) relatedness of participants. A pair of individuals was considered essentially unrelated if they had estimated relatedness coefficients under 0.025, the default cutoff in applications of GCTA [Yang, et al. 2011]. GCTA estimates of relatedness tend to underestimate true relatedness [Powell, et al. 2010]. As a result, the relatedness cutoff excludes pairs that have a most recent common ancestor approximately four generations distant, assuming no inbreeding [Lynch and Walsh 1998]. Genetically unrelated but socially related individuals (spouses, adoptive children, etc.) were not excluded from our analysis.
Relatedness calculations were based on the genotyped SNPs in our sample that passed quality control requirements: MAF > 0.01, missingness on fewer than 1% of individuals, and a non-significant test of Hardy-Weinberg Equilibrium (p > 1e-06).
Analysis 4: GWAS
GWAS differs from the heritability estimating approaches because it aims at detecting specific SNPs that are associated with the phenotype. The association is tested between each SNP and the HADS-D and the HADS-4, respectively. The power to detect a significant association is affected by the reliability of the phenotype. In consequence, we expected that using the HADS-4 would lead to more powerful tests of association than using the HADS-D.
We performed a GWAS on 5,777 individuals with HADS-D data and a separate GWAS on 5,665 individuals with HADS-4 data. As before, the difference in sample sizes occurred because some individuals with less than 30% missing HADS-D items had more than 30% missing responses on the HADS-4 items. All individuals from each family were included in the analysis in order to optimize power [Minica, et al. 2014]. Therefore association tests were based on robust standard errors.
Quality control was carried out using standard protocol, as described in detail in [de Zeeuw, et al. 2014]. Thresholds for allele frequency (>.01), call rate (>.99), and tests of Hardy-Weinberg Equilibrium (p > 1e-06) were applied. After QC, 7,957,814 SNPs remained in the sample.
Results
Analysis 1: Psychometric Investigation of HADS-D
1. Factor analyses
Correlations between individual items and the total score were relatively large (as shown in Table I) and were generally stronger in females than in males. Inter-item correlations were moderate and also tended to be stronger in females. Items 7 (can enjoy mass media) and 5 (indifferent to appearance) had the weakest inter-item correlations overall.
Table I.
Correlation matrix of HADS-D items for males (lower triangle) and females (upper)
| Item | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.61 | 0.52 | 0.44 | 0.3 | 0.48 | 0.27 | 0.83 |
| 2 | 0.56 | 1 | 0.64 | 0.53 | 0.35 | 0.52 | 0.3 | 0.91 |
| 3 | 0.46 | 0.52 | 1 | 0.57 | 0.35 | 0.4 | 0.31 | 0.91 |
| 4 | 0.38 | 0.47 | 0.42 | 1 | 0.34 | 0.34 | 0.21 | 0.74 |
| 5 | 0.26 | 0.28 | 0.29 | 0.32 | 1 | 0.32 | 0.25 | 0.75 |
| 6 | 0.48 | 0.51 | 0.35 | 0.38 | 0.34 | 1 | 0.34 | 0.77 |
| 7 | 0.26 | 0.27 | 0.24 | 0.22 | 0.15 | 0.31 | 1 | 0.63 |
| Total | 0.78 | 0.86 | 0.8 | 0.71 | 0.69 | 0.79 | 0.59 | 1 |
Note: Item-total score correlations are in the bottom row and the right-most column. All other entries are correlations between items.
In both males and females, the eigenvalues of the correlation matrices suggested that the first factor accounts for about 45% of the variance. These are presented in Table S3 in the Supporting Information. We fit EFA models with one to three factors using Mplus 7 [Muthén and Muthén 1998–2012]. Although the three-factor model had significantly better fit than the two factor and single-factor models, the observed eigenvalues, the modest decreases in residual variances when adding more than one factor, and large correlations between factors all pointed to a single-factor model. Patterns of factor loadings from the EFA are presented in Tables S4 and S5 of the Supporting Information. Further justification for the single-factor model is also given in the ‘Item Factor Analysis and Item Selection’ subsection of the Supporting Information. The confirmatory factor analysis showed that when fitting a single factor model, the first four items of the HADS-D were the most reliable indicators as quantified by squared correlations with the factor (R2>.4). The factor loadings in the confirmatory model are presented in Table S6 of the Supporting Information.
2. Validity
The ASR was used as a criterion to assess the potential loss of information when using the HADS-4 compared to the full HADS-D. Note that this does not imply that the ASR has to be a golden standard. The correlation between HADS-D scores and DSM-oriented ASR scores was .54 (SE =.008, p < .001), whereas the HADS-4 total score had r=.59 (SE =.007, p < .001). This result demonstrates the validity of the HADS-4. Further support for our choice of the first 4 HADS-D items as a reliable measure of depression comes from regressing the ASR on the individual HADS-D items. The HADS-4 items had the largest partial correlations with depression as measured with the ASR. In the multiple regression predicting ASR, the HADS-4 items alone had multiple R2 of .354. Conditioning on the covariates age, gender, and their interaction increased this to R2 = .395. Adding the remaining HADS items to the analysis yielded R2=.401 . Given the first 4 HADS items and covariates, the remaining HADS items contribute little to the validity of the HADS-D.
Analysis 2: Heritability Estimates based on Twins and Relatives
Families consisted of twin pairs, their parents, and up to two siblings of the twins. Patterns of missingness in families are given in Supporting Information Table S1. Note that although fewer than 30% of families had sibling or paternal data, there were still 1,530 siblings and 2,073 fathers providing data to these analyses. Table II shows familial correlations for HADS-D scores; HADS-4 scores are similar, and are shown in the online Supporting Information (Table S7). In all models, the sibling-sibling and DZ twin-pair correlations were constrained to be equal. See the Supplementary Methods section of the Supporting Information for more specific information concerning the fitted twin models.
Table II.
Observed correlations of HADS-D scores of twins and their families
| DZ Fams
| |||||||
|---|---|---|---|---|---|---|---|
| T1 | T2 | Sib1 | Sib2 | Father | Mother | ||
| MZ Fams | T1 | . | .136* | .001 | .261* | .068 | .161* |
| T2 | .312* | . | .081 | .152 | .098* | .138* | |
| S1 | .026 | .021 | . | −.120 | .155* | .179* | |
| S2 | .179 | .146 | −.086 | . | −.002 | .221* | |
| F | .153* | .060 | .063 | .067 | . | .270* | |
| M | .137* | .075 | .046 | −.153 | .23* | . | |
Note: MZ families are below the diagonal; a
indicates a correlation that is more than 2 standard errors from 0. About 90% of families lack sibling data and 80% lack paternal data, resulting in standard errors being large for correlations not involving twins or their mothers.
We fitted models that estimated additive and dominant genetic variance components (denoted ‘A’ and ‘D’), the effects of shared environment (denoted ‘C’), assortative mating (‘μ’), and cultural transmission, which induces gene-environment covariance (‘W’). The variance due to non-shared environment and measurement error cannot be distinguished, and their joint variance was denoted ‘E’. The models that were compared are listed according to the parameters estimated in them: for example, the ‘ACE’ model contains estimates of additive genetic, shared environment, and non-shared environmental variance components. Model fit comparisons were based on the sample-size adjusted Bayesian Information Criterion [Sclove 1987].
The two HADS phenotypes showed very similar patterns of results across the twin and family models (see Supporting Information, Tables S8, S9). Importantly, for both phenotypes, estimates of the additive heritability tended to be lower than previous twin studies that used depression scales including somatic symptoms [Sullivan, et al. 2000]. However, our results are in line with heritability estimates of non-somatic depression factors [Jang, et al. 2004].
The best-fitting models, both for HADS-D and HADS-4, included significant effects of assortative mating. Model fit comparisons made ADEμ (i.e., ADE with assortative mating) the model of choice.
A comparison of HADS-D and HADS-4 showed that the HADS-4 had slightly smaller estimates of non-shared environmental/error variance, confirming that this phenotype is more reliable. In addition, phenotypic assortment was slightly lower in the HADS-4 than the HADS-D. This suggests that the excluded HADS-D items may measure features that contribute to assortative mating.
Analysis 3: Heritability Estimates based on SNPs
The narrow-sense heritability estimate that was calculated using GCTA in essentially unrelated individuals was significant for the HADS-4 phenotype but not for the HADS-D. The heritability estimates were .13 for the HADS-D and .21 for the HADS-4 (Table III). This result shows that the HADS-D is indeed a more heterogeneous phenotype measure that is associated with less variance explained by genetic similarity between participants. Note that again, the estimates were somewhat lower than previously published SNP-based heritability estimates of other, alternative depression measures. For instance, for an MDD case/control phenotype estimates were .32, [Lubke, et al. 2012] and .21 [Lee, et al. 2013], for antidepressant response this was .42 [Tansey, et al. 2013]; and for age at depression onset 0.51 [Power, et al. 2012]. As noted before, the HADS differs from other depression measures in that it does not take into account somatic symptoms, which are likely contributing to estimates of heritability [Mykletun, et al. 2001; Zigmond and Snaith 1983]. However, the additive genetic variance estimate of 21% using the HADS-4 as phenotype agrees with previous twin-based heritability estimates of non-somatic depression factors [Jang, et al. 2004], and also with our twin-based estimate of additive variance in the ADEμ model. The standard errors of the estimates were still relatively large even for the HADS-4 (i.e., 0.10), due to the small sample size of N=3136 in the GCTA analyses.
Table III.
SNP-based heritability of depression as measured by HADS-D and HADS-4
| Phenotype | A(SE) | logLik | -value |
|---|---|---|---|
| HADS-D | 0.13(0.10) | 2.06 | 0.15 |
| HADS-4 | 0.21(0.10) | 4.98 | 0.026 |
Note: “A” denotes the estimated additive variance, “SE” denotes standard error, and logLik is twice the difference in log likelihood between the models with and without the additive variance component.
Analysis 4: GWAS
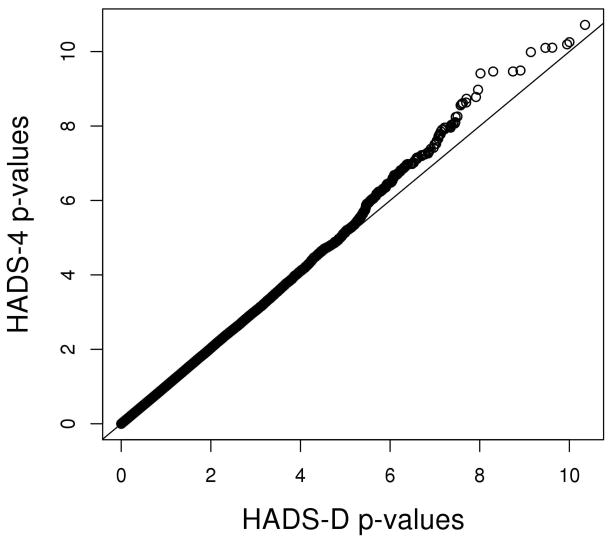
The HADS-4 showed a larger number of strong GWAS associations than did the HADS-D. This is illustrated in Figure 2, which shows the heavier right tail of the distribution of negative, log-transformed HADS-4 p–values. This result shows that on average, the HADS-4 had more powerful tests than did the HADS-D.
Figure 2.
A quantile-quantile plot of -values from the HADS-D and the HADS-4 shows a trend toward more significant associations for the HADS-4 (p-values are log-transformed)
Note that this result does not imply that for any given SNP, the HADS-4 phenotype provided a more powerful test. To illustrate, we ranked SNPs by their p-values under both phenotypes and correlated the rankings. The top-ranked HADS-D SNPs did not have the same p-value rankings under the HADS-4 phenotype, and vice-versa. For instance, the p-values of the top 1000 SNPs using the HADS-D correlated only 0.352 with the p-values resulting from using the HADS-4. The low correlations might be due to noisier GWAS results of the HADS-D, which would again suggest that the HADS-4 is a preferable measure in a GWAS.
Finding genetic markers associated with depression is challenging since depression is highly polygenic—caused by many mutations of small effects [Gratten, et al. 2014]. Furthermore, depression is characterized by a diverse set of symptoms. As a consequence, a sum score of all symptom endorsements can be due to quite different symptom profiles. Our result that the HADS-4 had a larger number of strong associations compared to the HADS-D shows that power can be gained by focusing on core symptoms, and that more homogeneous depression measures should be preferred in association analyses.
Discussion
Our analyses showed that the sum of responses to the first four HADS-D items (“HADS-4”) provides a more homogeneous measure of non-somatic depression, and that HADS-4 performed as well as or better than the full HADS-D scale. Generally, the HADS-4 yielded more powerful tests in different genetic analyses. The GCTA and GWAS analyses confirmed that the increased homogeneity of the HADS-4 led to increased statistical power. The twin and family analyses were consistent with these results as the estimate of non-shared environment/error variance was smaller for the HADS-4 than for the HADS-D.
More specifically, our twin analyses suggested that additive genetic variance is responsible for approximately 20% of the variability in HADS-D and HADS-4 scores. This is lower than has been observed for depression in general, and is likely due to the content of the HADS. The HADS was designed to measure the non-somatic symptoms of depression in the hospital setting, where unrelated medical complaints could easily confound self-reports of somatic depression symptoms (e.g., lethargy, changed appetite, sleep problems, etc.). Our estimate is consistent with estimates of twin-based heritability of non-somatic depression factors [Jang, et al. 2004]. Our finding that shared environment was not a significant contributor to depression is consistent with previous results [Flint and Kendler 2014]. Further research might focus on investigating the heritability of the somatic symptoms. For instance, Trzaskowski et al. [2013], observed low SNP-based heritability estimates both for somatic and non-somatic depressive symptoms in children, which they attributed to non-additive inheritance. We observed some evidence that non-additive effects are associated with HADS scores in our twin-and-family analyses.
Both our SNP-based heritability analyses and the GWAS supported our claim that genetic analyses benefit from using homogeneous phenotype measures. Specifically, the HADS-4 provides a more homogenous depression phenotype that should be preferred by consortia researching depression using the HADS [Bjerkeset, et al. 2008; Deary, et al. 2013; Zammit, et al. 2012]. To illustrate, if the true heritabilities of the HADS phenotypes were equal to our SNP-based estimates, then a replication study testing heritability of the HADS-4 would have statistical power of .76, while one using the HADS-D would have power of .37 [Visscher, et al. 2014, http://spark.rstudio.com/ctgg/gctaPower/]. This comparison is based on strong assumptions, but if our results are representative, using the HADS-4 is nevertheless likely to yield considerably more powerful tests. In the GWAS analyses, the HADS-4 phenotype had a larger number of strong associations than did the HADS-D. The HADS-D and HADS-4 samples were nearly identical, which implies that using the HADS-4 results in more powerful tests of association on average, making it more desirable as a depression phenotype. The relationship between SNP association coefficients and polygenic risk scores implies that using HADS-4 are also likely to yield increases in power in polygenic risk score analyses of depression [Dudbridge 2013].
Increases in power as well as consistency of results across different cohorts should be expected more generally in genetic analyses when phenotypic heterogeneity is reduced. Homogeneity can be increased by focusing on core symptoms, thus reducing the noise in the aggregate scores that is due to substantially different symptom profiles.
The main limitation of our study is that all analyses were conducted in a single data set, and with a specific depression measure. The next step is to conduct similar analyses with different phenotype measures and with simulated data in order to generalize the results and conclusions. We expect that using homogeneous phenotypes in genetic studies will generally be beneficial, but also that there will be a lower limit to the number of items that need to be included when summing a scale. As shown in Lubke et al., using individual items is clearly not optimal as they contain too much error [2014]. The challenge in deriving homogeneous phenotype measures is therefore to select individual scale items that measure the characteristic symptoms of a unidimensional trait.
Supplementary Material
Acknowledgments
CL was supported by a Presidential Fellowship from The University of Notre Dame, GL was supported by NIDA-DA018673. The computational work was carried out on the clusters of the Center of Research Computing at Notre Dame which is partially funded by NSF-MRI grant BCS-1229450 of which GL is one of the PIs. All data came from the Netherlands Twin Registry (NTR), which is funded by multiple grants: the Netherlands Organization for Scientific Research (NWO) and MagW/ZonMW grants 904-61-090, 985-10-002, 904-61-193,480-04-004, 400-05-717, Addiction-31160008, Middelgroot-911-09-032, Spinozapremie 56-464-14192, Center for Medical Systems Biology (CSMB, NWO Genomics), NBIC/BioAssist/RK(2008.024), Biobanking and Biomolecular Resources Research Infrastructure (BBMRI–NL, 184.021.007). VU University’s Institute for Health and Care Research (EMGO+ ) and Neuroscience Campus Amsterdam (NCA); the European Science Foundation (ESF, EU/QLRT-2001-01254), the European Research Council (ERC Advanced, 230374), Rutgers University Cell and DNA Repository (NIMH U24 MH068457-06), the Avera Institute, Sioux Falls, South Dakota (USA) and the National Institutes of Health (NIH R01 HD042157-01A1, MH081802, Grand Opportunity grants 1RC2 MH089951. Part of the genotyping were funded by the Genetic Association Information Network (GAIN) of the Foundation for the National Institutes of Health.
Footnotes
The authors declare no conflict of interest.
References
- Achenbach TM, Bernstein A, Dumenci L. DSM-oriented scales and statistically based syndromes for ages 18 to 59: Linking taxonomic paradigms to facilitate multitaxonomic approaches. Journal of Personality Assessment. 2005;84(1):49–63. doi: 10.1207/s15327752jpa8401_10. [DOI] [PubMed] [Google Scholar]
- Bjerkeset O, Romundstad P, Evans J, Gunnell D. Association of Adult Body Mass Index and Height with Anxiety, Depression, and Suicide in the General Population: The HUNT Study. American Journal of Epidemiology. 2008;167(2):193–202. doi: 10.1093/aje/kwm280. [DOI] [PubMed] [Google Scholar]
- Bollen K, Lennox R. Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin. 1991;110(2):305–314. [Google Scholar]
- Boomsma DI, Wijmenga C, Slagboom EP, Swertz MA, Karssen LC, Abdellaoui A, Ye K, Guryev V, Vermaat M, van Dijk F, et al. The Genome of the Netherlands: design, and project goals. European Journal of Human Genetics. 2014;22(2):221–227. doi: 10.1038/ejhg.2013.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis LK, Yu DM, Keenan CL, Gamazon ER, Konkashbaev AI, Derks EM, Neale BM, Yang J, Lee SH, Evans P, et al. Partitioning the Heritability of Tourette Syndrome and Obsessive Compulsive Disorder Reveals Differences in Genetic Architecture. Plos Genetics. 2013;9(10):14. doi: 10.1371/journal.pgen.1003864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Zeeuw EL, van Beijsterveldt CEM, Glasner TJ, Bartels M, Ehli EA, Davies GE, Hudziak JJ, Rietveld CA, Groen-Blokhuis MM, et al. Social Science Genetic Association C. Polygenic scores associated with educational attainment in adults predict educational achievement and ADHD symptoms in children. American Journal of Medical Genetics Part B: Neuropsychiatric Genetics. 2014;165(6):510–520. doi: 10.1002/ajmg.b.32254. [DOI] [PubMed] [Google Scholar]
- Deary IJ, Pattie A, Starr JM. The Stability of Intelligence From Age 11 to Age 90 Years: The Lothian Birth Cohort of 1921. Psychological Science. 2013;24(12):2361–2368. doi: 10.1177/0956797613486487. [DOI] [PubMed] [Google Scholar]
- Dudbridge F. Power and Predictive Accuracy of Polygenic Risk Scores. Plos Genetics. 2013;9(3):17. doi: 10.1371/journal.pgen.1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint J, Kendler Kenneth S. The Genetics of Major Depression. Neuron. 2014;81(3):484–503. doi: 10.1016/j.neuron.2014.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratten J, Wray NR, Keller MC, Visscher PM. Large-scale genomics unveils the genetic architecture of psychiatric disorders. Nature Neuroscience. 2014;17(6):782–790. doi: 10.1038/nn.3708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hek K, Demirkan A, Lahti J, Terracciano A, Teumer A, Cornelis MC, Amin N, Bakshis E, Baumert J, Ding J, et al. A Genome-Wide Association Study of Depressive Symptoms. Biological Psychiatry. 2013;73(7):667–678. doi: 10.1016/j.biopsych.2012.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamshidian M, Jennrich RI. Acceleration of the EM algorithm by using quasi-Newton methods. Journal of the Royal Statistical Society Series B-Methodological. 1997;59(3):569–587. [Google Scholar]
- Jang KL, Livesley WJ, Taylor S, Stein MB, Moon EC. Heritability of individual depressive symptoms. Journal of Affective Disorders. 2004;80(2–3):125–133. doi: 10.1016/S0165-0327(03)00108-3. [DOI] [PubMed] [Google Scholar]
- Jöreskog KG. Statistical analysis of sets of congeneric tests. Psychometrika. 1971;36(2):109–133. [Google Scholar]
- Kaplan D. Evaluating and modifying covariance structure models: A review and recommendation. Multivariate Behavioral Research. 1990;25(2):137–155. doi: 10.1207/s15327906mbr2502_1. [DOI] [PubMed] [Google Scholar]
- Lamers F, Vogelzangs N, Merikangas KR, de Jonge P, Beekman ATF, Penninx B. Evidence for a differential role of HPA-axis function, inflammation and metabolic syndrome in melancholic versus atypical depression. Molecular Psychiatry. 2013;18(6):692–699. doi: 10.1038/mp.2012.144. [DOI] [PubMed] [Google Scholar]
- Lango-Allen H, Estrada K, Lettre G, Berndt SI, Weedon MN, Rivadeneira F, Willer CJ, Jackson AU, Vedantam S, Raychaudhuri S. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467(7317):832–838. doi: 10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Ripke S, Neale BM, Faraone SV, Purcell SM, Perlis RH, Mowry BJ, Thapar A, Goddard ME, Witte JS, et al. Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs. Nature Genetics. 2013;45(9):984. doi: 10.1038/ng.2711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinson DF, Mostafavi S, Milaneschi Y, Rivera M, Ripke S, Wray NR, Sullivan PF. Genetic Studies of Major Depressive Disorder: Why Are There No Genome-wide Association Study Findings and What Can We Do About It? Biological psychiatry. 2014;76(7):510–2. doi: 10.1016/j.biopsych.2014.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lord FM, Novick MR, Birnbaum A. Statistical theories of mental test scores. Oxford: Addison-Wesley; 1968. [Google Scholar]
- Lubke GH, Hottenga JJ, Walters R, Laurin C, De Geus EJ, Willemsen G, Smit JH, Middeldorp CM, Penninx BW, Vink JM. Estimating the genetic variance of major depressive disorder due to all single nucleotide polymorphisms. Biological psychiatry. 2012;72(8):707–709. doi: 10.1016/j.biopsych.2012.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubke GH, Laurin C, Amin N, Hottenga JJ, Willemsen G, van Grootheest G, Abdellaoui A, Karssen LC, Oostra B, van Duijn CM, et al. Genome-wide analyses of borderline personality features. Molecular Psychiatry. 2014;19(8):923–929. doi: 10.1038/mp.2013.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lux V, Kendler KS. Deconstructing major depression: a validation study of the DSM-IV symptomatic criteria. Psychological Medicine. 2010;40(10):1679–1690. doi: 10.1017/S0033291709992157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. Genetics and analysis of quantitative traits 1998 [Google Scholar]
- Martin N, Boomsma D, Machin G. A twin-pronged attack on complex traits. Nature Genetics. 1997;17(4):387–392. doi: 10.1038/ng1297-387. [DOI] [PubMed] [Google Scholar]
- Mellenbergh GJ. Measurement precision in test score and item response models. Psychological Methods. 1996;1(3):293–299. [Google Scholar]
- Minica CC, Boomsma DI, Vink JM, Dolan CV. MZ twin pairs or MZ singletons in population family-based GWAS? More power in pairs. Molecular Psychiatry. 2014;19(11):1154–1155. doi: 10.1038/mp.2014.121. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 7. Los Angeles, CA: Muthén & Muthén; 1998–2012. [Google Scholar]
- Mykletun A, Stordal E, Dahl AA. Hospital Anxiety and Depression (HAD) scale: factor structure, item analyses and internal consistency in a large population. British Journal of Psychiatry. 2001;179(6):540–544. doi: 10.1192/bjp.179.6.540. [DOI] [PubMed] [Google Scholar]
- Pedersen NL, Christensen K, Dahl AK, Finkel D, Franz CE, Gatz M, Horwitz BN, Johansson B, Johnson W, Kremen WS. IGEMS: The consortium on interplay of genes and environment across multiple studies. Twin Research and Human Genetics. 2013;16(01):481–489. doi: 10.1017/thg.2012.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plomin R, Simpson MA. The future of genomics for developmentalists. Development and Psychopathology. 2013;25(4):1263–1278. doi: 10.1017/S0954579413000606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posthuma D, Beem AL, de Geus EJC, van Baal GCM, von Hjelmborg JB, Lachine I, Boomsma DI. Theory and practice in quantitative genetics. Twin Research. 2003;6(5):361–376. doi: 10.1375/136905203770326367. [DOI] [PubMed] [Google Scholar]
- Powell JE, Visscher PM, Goddard ME. Reconciling the analysis of IBD and IBS in complex trait studies. Nature Reviews Genetics. 2010;11(11):800–805. doi: 10.1038/nrg2865. [DOI] [PubMed] [Google Scholar]
- Power RA, Keers R, Ng MY, Butler AW, Uher R, Cohen-Woods S, Ising M, Craddock N, Owen MJ, Korszun A, et al. Dissecting the Genetic Heterogeneity of Depression Through Age at Onset. American Journal of Medical Genetics Part B-Neuropsychiatric Genetics. 2012;159B(7):859–868. doi: 10.1002/ajmg.b.32093. [DOI] [PubMed] [Google Scholar]
- Psaty BM, O’Donnell CJ, Gudnason V, Lunetta KL, Folsom AR, Rotter JI, Uitterlinden AG, Harris TB, Witteman JC, Boerwinkle E. Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) Consortium Design of Prospective Meta-Analyses of Genome-Wide Association Studies From 5 Cohorts. Circulation: Cardiovascular Genetics. 2009;2(1):73–80. doi: 10.1161/CIRCGENETICS.108.829747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reef J, Diamantopoulou S, van Meurs I, Verhulst F, van der Ende J. Child to adult continuities of psychopathology: a 24-year follow-up. Acta Psychiatrica Scandinavica. 2009;120(3):230–238. doi: 10.1111/j.1600-0447.2009.01422.x. [DOI] [PubMed] [Google Scholar]
- Ripke S, Wray NR, Lewis CM, Hamilton SP, Weissman MM, Breen G, Byrne EM, Blackwood DH, Boomsma DI, Cichon S. A mega-analysis of genome-wide association studies for major depressive disorder. Molecular psychiatry. 2012;18(4):497–511. doi: 10.1038/mp.2012.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savalei V. Understanding Robust Corrections in Structural Equation Modeling. Structural Equation Modeling-a Multidisciplinary Journal. 2014;21(1):149–160. [Google Scholar]
- Sclove SL. APPLICATION OF MODEL-SELECTION CRITERIA TO SOME PROBLEMS IN MULTIVARIATE-ANALYSIS. Psychometrika. 1987;52(3):333–343. [Google Scholar]
- Speed D, Hemani G, Johnson MR, Balding DJ. Improved heritability estimation from genome-wide SNPs. American Journal of Human Genetics. 2012;91(6):1011–1021. doi: 10.1016/j.ajhg.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spinhoven P, Ormel J, Sloekers PPA, Kempen G, Speckens AEM, VanHemert AM. A validation study of the Hospital Anxiety and Depression Scale (HADS) in different groups of Dutch subjects. Psychological Medicine. 1997;27(2):363–370. doi: 10.1017/s0033291796004382. [DOI] [PubMed] [Google Scholar]
- Straat JH, van der Ark LA, Sijtsma K. Methodological artifacts in dimensionality assessment of the Hospital Anxiety and Depression Scale (HADS) Journal of Psychosomatic Research. 2013;74(2):116–121. doi: 10.1016/j.jpsychores.2012.11.012. [DOI] [PubMed] [Google Scholar]
- Sullivan PF, Neale MC, Kendler KS. Genetic epidemiology of major depression: review and meta-analysis. American Journal of Psychiatry. 2000;157(10):1552–1562. doi: 10.1176/appi.ajp.157.10.1552. [DOI] [PubMed] [Google Scholar]
- Tansey KE, Guipponi M, Hu XL, Domenici E, Lewis G, Malafosse A, Wendland JR, Lewis CM, McGuffin P, Uher R. Contribution of Common Genetic Variants to Antidepressant Response. Biological Psychiatry. 2013;73(7):679–682. doi: 10.1016/j.biopsych.2012.10.030. [DOI] [PubMed] [Google Scholar]
- Trzaskowski M, Dale PS, Plomin R. No Genetic Influence for Childhood Behavior Problems From DNA Analysis. Journal of the American Academy of Child and Adolescent Psychiatry. 2013;52(10):1048–1056. doi: 10.1016/j.jaac.2013.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Hemani G, Vinkhuyzen AAE, Chen GB, Lee SH, Wray NR, Goddard ME, Yang J. Statistical Power to Detect Genetic (Co)Variance of Complex Traits Using SNP Data in Unrelated Samples. Plos Genetics. 2014;10(4):10. doi: 10.1371/journal.pgen.1004269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willemsen G, Vink JM, Abdellaoui A, den Braber A, van Beek J, Draisma HHM, van Dongen J, van’t Ent D, Geels LM, van Lien R, et al. The Adult Netherlands Twin Register: Twenty-Five Years of Survey and Biological Data Collection. Twin Research and Human Genetics. 2013;16(1):271–281. doi: 10.1017/thg.2012.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. American Journal of Human Genetics. 2011;88(1):76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zammit AR, Starr JM, Johnson W, Deary IJ. Profiles of physical, emotional and psychosocial wellbeing in the Lothian birth cohort 1936. Bmc Geriatrics. 2012;12:11. doi: 10.1186/1471-2318-12-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigmond AS, Snaith RP. The Hospital Anxiety and Depression Scale. Acta Psychiatrica Scandinavica. 1983;67(6):361–370. doi: 10.1111/j.1600-0447.1983.tb09716.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.