Abstract
To confirm associations with a large number of single nucleotide polymorphisms (SNPs), each with only a small effect sizes, as hypothesized in the polygenic theory for schizophrenia, the International Schizophrenia Consortium (2009, Nature 460:748-752) proposed a polygenic risk score (PRS) test and demonstrated its effectiveness when applied to psychiatric disorders. The basic idea of the PRS test is to use a half of the sample to select and up-weight those more likely to be associated SNPs, and then use the other half of the sample to test for aggregated effects of the selected SNPs. Intrigued by the novelty and increasing use of the PRS test, we aimed to evaluate and improve its performance for GWAS data. First, by an analysis of the PRS test, we point out its connection with the Sum test [Chapman and Whittaker, 2008, Genet Epidemiol, 32:560-566; Pan, 2009, Genet Epidemiol, 33:497-507]; given the known advantages and disadvantages of the Sum test, this connection motivated the development of several other polygenic tests, some of which may be more powerful than the PRS test under certain situations. Second, more importantly, to overcome the low statistical efficiency of the data-splitting strategy as adopted in the PRS test, we reformulate and thus modify the PRS test, obtaining several adaptive tests, which are closely related to the adaptive sum of powered score (SPU) test studied in the context of rare variant analysis [Pan et al., 2014, Genetics 197:1081-1095]. We use both simulated data and a real GWAS dataset of alcohol dependence to show dramatically improved power of the new tests over the PRS test; due to its superior performance and simplicity, we recommend the whole sample-based adaptive SPU test for polygenic testing. We hope to raise the awareness of the limitations of the PRS test and potential power gain of the adaptive SPU test.
Keywords: aSPU test, GWAS, Logistic regression, Polygenic variation, SSU test, SSUw test, SPU tests, Sum test
Introduction
Genome-wide association studies (GWASs) have been successful in identifying genetic variants, mostly single nucleotide polymorphisms (SNPs), associated with complex diseases and other traits (Hindorff et al 2010). The most popular statistical method is univariate testing on each individual SNP separately. Univariate testing is powerful in detecting few associations with large effect sizes. However, if there are a large number of associations, each with only a small effect size, univariate testing will not be powerful, as to be confirmed later. This latter case arises as predicted by Fisher’s (1918) polygenic theory, which in particular is adopted to account for unexplained genetic variations contributing to the risk of psychiatric disorders [Gottesman and Shields, 1967] and other complex diseases. When failing to identify any or a sufficient number of associated SNPs based on univariate testing, one would question whether it is due to polygenic effects, which may shed light on the underlying genetic architecture, such as the common variants-common disease hypothesis stating that common diseases are caused by many common genetic variants. The International Schizophrenia Consortium (ISC) (2009) proposed a polygenic risk score (PRS) test to detect the possible existence of small individual effects from a large number of SNPs. When applied to a GWAS dataset with trait schizophrenia, univariate testing only identified several strongly associated loci that could not explain a substantial genetic component; however, the PRS test did find strong evidence of associations of many SNPs with schizophrenia, presumably each with only a small effect that cannot be detected by univariate testing on each individual SNP. Interestingly, when applied to the WTCCC samples [The Welcome Trust Case Control Consortium, 2007] with a large number of SNPs selected and their effect sizes estimated based on the ISC schizophrenia sample, the PRS test also detected statistically significant polygenic effects on bipolar disorder (BD), but not on six other non-psychiatric diseases. On the other hand, for traits such as breast cancer and prostate cancer [Machiela et al., 2011] and the Framingham Coronary Heart Disease Risk Score [Simonson et al., 2011], the PRS test either did not identify significant polygenic effects or only detected marginally significant polygenic effects.
In a motivating example we were interested in the possible polygenic effects of alcohol dependence, a mental disorder characterized by tolerance, withdrawal, uncontrollable drive to drink, and repeated use of alcohol despite serious psychological or physiological problems [Bierut et al., 2010]. Alcohol dependence is the third leading cause of preventable death in the United States [Mokdad et al., 2004]. Both genetic and environmental factors contribute to the liability to alcohol dependence. Previous twin and family-based studies estimated that 50% to 60% of the individual differences in liability to alcohol dependence can be explained by genetic factors [Gelernter and Kranzle, 2009]. However, few susceptibility SNPs for alcohol dependence have been identified by GWAS in spite of its relatively high heritability and the success of GWAS for other diseases. For example, in the “Study of Addiction: Genetics and Environment”(SAGE), one of the first large-scale case-control GWAS of alcohol dependence with 2,544 European American and 1,104 African American individuals, did not identify any genome-wide significant SNP by the conventional single SNP analysis [Bierut et al., 2010]. We, however, hypothesized that there might be polygenic effects of alcohol dependence captured by the genome-wide SNPs, and therefore applied the PRS test as well as some new and more powerful tests to be introduced later to analyze the SAGE GWAS data.
In light of the novelty and importance of the PRS test, it is desirable to learn more of its properties, such as: why/when it works (or does not work)? how is it related to other existing tests? Through some simple algebra, we establish a strong connection between the PRS test and the Sum test [Chapman and Whittaker, 2008; Pan, 2009]. Naturally one can also construct a polygenic version of the Sum test, called Poly-Sum, which is shown to be essentially the same as the PRS test. More importantly, since it is known that the Sum test may not perform well in the presence of many non-associated SNPs [Basu and Pan, 2011], which is expected to be the norm in any polygenic analysis with thousands or more of SNPs, this connection motivates modifications to the PRS test, leading to other versions of the polygenic testing, such as Poly-SSU based on a more robust and often more powerful sum of squared score (SSU) test [Pan, 2009]. This analysis also sheds light on why the PRS test is powerful in the presence of differing association directions of SNPs, deviating from the common problem of the usual Sum test [Pan, 2009].
Among others, our analysis also suggests a severe shortcoming of the PRS test: its data-splitting strategy. The PRS test uses a half of the original sample to select and over-weight more promising (i.e. more likely to be associated) SNPs, and then uses the other half of the sample to test their aggregated association with the trait/disease. As to be shown in more details later, although selection and weighting of SNPs are desirable, the main reason of data-splitting is for the applicability of the usual statistical theory for the final test; it is straightforward to use the whole sample to select and weight SNPs, which however complicates the derivation of the null distribution of the resulting test. As discussed in other contexts, e.g. in the two-stage design of GWAS [Skol et al., 2006], in spite of its simplicity and wide applications (e.g. Wu et al., 2010), data-splitting is generally less efficient than its counterpart based on the whole sample. Hence, our new formulation of the PRS test naturally suggests its modifications with the use of the whole sample to select and weight SNPs, leading to two adaptive tests, called adaptive thresholded variance-weighted sum of squared score (atSSUw) test and adaptive thresholded sum of squared score (atSSU) test, which are variants of the adaptive SSUw and adaptive SSU tests studied in the context of rare variant (RV) analysis [Pan and Shen, 2011]. These two tests are in turn closely related to some special cases of the adaptive sum of powered score (aSPU) test and its weighted version aSPUw test originally proposed for analysis of small sets of RVs [Pan et al., 2014]. With both simulated and real GWAS data, we demonstrate that the two new atSSUw and atSSU tests performed similarly, both much more powerful than the PRS test; most importantly, it turns out that the aSPU test was most powerful across a wide range of scenarios and thus is recommended.
Besides the issue of sample splitting, our results also support the importance of adaptive weighting in practice. In contrast to a fixed set of weights as used in PRS, the powerful aSPU test is built on the idea of assigning multiple sets of weights to SNPs, from which the most effective set of weights is selected and adopted. The idea of adaptive weighting can be broadly applicable, not only to association testing as focused here. For example, we envision that adaptive weighting on SNPs might be able to improve the performance for risk prediction based on one’s genome-wide genotypes, as to be elaborated in the final section. Another issue we touch on is SNP selection versus SNP weighting. Our conclusion is the same as those in other applications [Newton et al., 2007] and the theory of model selection versus model averaging [Yuan and Yang, 2005; Shen and Huang, 2006]: in the presence of many weak signals, such as weak associations of many SNPs, accurate selection will be too difficult to outperform weighting, as demonstrated by relative performance of SNP selection (via p-value thresholding as adopted in a thresholded SSU test) and SNP weighting (as used in the aSPU test) to be shown later. In summary, we feel that our results obtained here may prove useful to not only genetic association testing but also other problems in practice.
Methods
Data and some existing tests
We consider the case-control study design, though the methods may be easily extended to other study designs, e.g. with a quantitative or survival trait. Suppose that for subject i, i = 1,…,n, Yi = 0 or 1 is a binary trait, e.g. an indicator of disease, and Xi = (Xi1, …, Xik)′ is the genotype score at k SNP loci. We use additive coding for each SNP; that is, Xij is the count of the minor allele at SNP j for subject i. It is straightforward to include covariates, but for simplicity of presentation we ignore them. We consider a logistic regression model:
| (1) |
We’d like to test the null hypothesis H0 : β = (β1, …, βk)′ = 0; that is, there is no association between any SNPs and the trait under H0.
The score vector U = (U1, …, Uk)′ for β in model (1) and V = Cov(U) are simply
where Y¯ and X¯ are the sample means of Yi’s and Xi’s respectively. Five global multilocus tests [Pan, 2009] can be constructed as
where Vjj = Var(Uj) is the jth diagonal element of V. The score test is classical, while the SSU test ignores the covariance matrix of the score vector U. As discussed in Pan (2009, 2011), the SSU test is closely related to an empirical Bayes test for high-dimensional data [Goeman et al., 2006] and a variance-component score test in kernel machine regression [Wu et al., 2010]; the SSUw test is a weighted version of the SSU test that accounts for varying variances of the score components. The UminP test is a representative univariate test based on minimum p-value of all the SNPs. The Sum test can be interpreted as the score test under the working (and in general incorrect) assumption β1 = β2 = … = βk, under which the general logistic regression model (1) reduces to , which regresses the trait (Yi) on the sum of the genotype scores .
In the current context, even after selecting some nearly independent SNPs (without using trait Yi’s), we have a large k (and a large n); both k and n are typically larger than thousands. If we apply the standard score test (or its asymptotically equivalent Wald or likelihood ratio test), the power will be low. In fact, as shown theoretically in Fan (1996) and to be shown empirically later, as the dimension k increases, the power of the score test gradually diminishes, tending to the Type I error rate α. Similarly, if we have many small |βj | /= 0, the most popular single SNP-based UminP test in GWAS is also low-powered. As a response, the PRS test was recently proposed by the ISC.
Next we review the PRS test, then reformulate it in two ways to illuminate its connections with some existing tests, motivating the development of several other tests. A summary of the two sets of results is presented in Tables 1 and 2 respectively so that one may choose to skip technical details in the remaining sections.
Table 1.
A summary of the PRS test and its modifications based on sample splitting.
|
| |
| Data | D ={(Yi, Xi)|i = 1, …, n} = D1 υ D2 split to two parts D1 and D2. |
|
| |
| Model | Logit [Pr(Yi = 1)] = βM,0 + XijβM,j, i ∈ D1. |
|
| |
| Output | , |
| . | |
|
| |
| Model | . |
|
| |
| Output | , |
| . | |
|
| |
| Tests | . |
| . | |
| . | |
| . | |
|
| |
Table 2.
A summary of the PRS test and its modifications without sample splitting. T is for a test statistic and P is for its p-value.
|
| |
| Data | D ={(Yi, Xi)|i = 1, …, n} = D1 υ D2 split to two parts D1 and D2. |
|
| |
| Model | Logit [Pr(Yi = 1)] = βM,0 + XijβM,j, i ∈ D1. |
|
| |
| Output | P-values pj(D1)’s for H0: βm,j = 0. |
|
| |
| Model | , |
|
| |
| Output | , |
| . | |
|
| |
| Tests | . |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
|
| |
The PRS test and its connection with other tests
Recognizing that many SNPs may have only small effects on the trait while many others (called null SNPs) are not at all associated with the trait, the PRS test aims to look at the overall or collective effects of those non-null SNPs without singling out their identities. Since it is unknown which SNPs are null, and considering null SNPs simply adds noise into the resulting test and thus may reduce its statistical power, the PRS test selects and over-weights those more promising (i.e. more likely non-null) SNPs. To avoid adjusting for complicated effects of SNP selection, the PRS test takes a two-step procedure with data splitting. The original sample D = {(Yi, Xi) : i = 1, …, n}, possibly conditional on some covariates (e.g. gender), is randomly split into two (almost) equal parts, called the discovery sample D1 and target sample D2 respectively. Without loss of generality, suppose that the first n1 = |D1 | ≈ n/2 observations are in the discovery sample, while the remaining ones are in the target sampleof size n2 = |D2 |. First, the discovery sample D1 is used to fit a univariate logistic regression model for each SNP j:
| (2) |
with i = 1, …, n1, to obtain a maximum likelihood estimate (MLE) and its p-value pj = pj (D1), for j = 1, …, k. Note that, i) we use βM ,j to distinguish it in the marginal model (2) from βj in the joint model (1); ii) if necessary, we use, e.g. , to show the explicit dependence of an estimate on the data being used. Second, using weights for a given threshold PT based on the discovery sample, one constructs a new “score” for each subject in the target sample: . Note that only those SNPs with their p-values pj < PT will have non-zero weights and thus be used. Then one would test whether there is any difference in the mean scores (i.e. E(si)) between the cases and controls by a t-test. The numerator of the t-statistic is
where n2,1 and n2,0 are the numbers of the cases and controls in the target sample D2 respectively. As shown by Clayton et al (2004),
is the score function for βj in the joint model (1) or for βM ,j in the marginal model (2) with the target sample D2. Accordingly, it is easy to verify that the numerator of the t-statistic is the same as the score statistic in the logistic regression model:
corresponding to the Sum test for H′ : α1 = 0 with the new genotype scores wj Xij. In other words, the ISC polygenic test uses a half of the sample (i.e. discovery sample) to construct weights for the SNPs, then uses the remaining half of the sample (i.e. target sample) to conduct a Sum test with the weighted genotype scores. Since under some situations, the Sum test may not perform better than some other tests, especially than the UminP and SSU tests in the context with a small k [Chapman and Whittaker, 2008; Pan, 2009], it may be better to use some other tests. In particular, Basu and Pan (2011) found that the performance of the Sum test deteriorated quickly as more nonassociated SNPs were added in, which is expected to be the case in the current context with more than thousands of the SNPs to be tested. Hence, if we apply the SSU, SSUw and UminP tests [Pan, 2009] to the target sample with the weighted genotype scores (i.e. replacing Xij by wj Xij), we obtain the polygenic versions of these tests, called Poly-SSU, Poly-SSUw and Poly-UminP respectively. It is noted that both the SSUw and UminP tests are invariant to non-zero weighting on genotype scores, but do depend on SNP selection through thresholding, hence the two tests and their polygenic versions will operate differently. In our simulations, we did find improved performance of these tests over the PRS test under some situations; however, since these tests were still lower powered than other adaptive tests to be presented next, we will only briefly discuss their performance in simulations.
Although the weighting is expected to be effective in boosting the power of the polygenic tests while the sample splitting allows treating the weights as fixed and thus applying the usual statistical theory (e.g. for the t-test here), the practice of sample splitting can be too costly as shown in other contexts [Faraway, 1992; Skol et al., 2006] and in our later simulations. Hence, we would pursue strategies without sample splitting while mimicking the PRS test, motivating the development of other tests.
Another formulation of the PRS test and two adaptive tests
To yield a test that is data-adaptive while maintaining the advantages of weighting SNPs and avoiding data splitting, we first have a careful look at the weights in the PRS test. As shown in Pan (2009),
where U = (U1, U2, …, Uk)′ is the score vector, IM ,d = diag(IM) is a diagonal matrix with diagonal elements of IM, and IM = −∂U/∂βM |βM =0 is the (observed) Fisher information matrix based on the marginal logistic regression model (2). It is easy to verify that in the current case, the jth diagonal element of is . Hence, we have
Accordingly, the PRS test statistic is
where v1 is the (estimated) variance of the numerator of TPRS(PT).
We propose modifying the above reformulated PRS test such that all the quantities are obtained from the whole sample without data splitting, leading to
which is exactly the variance-weighted sum of squared score (SSUw) test [Pan, 2009] being applied only to the set of the SNPs with their p-values less than the threshold PT ; we call it a thresholded SSUw (tSSUw) test. Of course, due to SNP selection, we cannot use the usual statistical theory for the SSUw test (e.g. its null distribution as a mixture of chi-squared distributions with degrees of freedom 1). We propose using the permutation [Churchill and Doerge, 1994], or the parametric bootstrap [Buzkova et al., 2011] in the presence of covariates, to obtain its p-value, say PtS S U w(PT) ; more details are to be given later. Since the result of the tSSUw(PT) test depends on the choice of the threshold PT, it is natural to try a few possible values of PT before combining their results. Hence, we propose an adaptive tSSUw (atSSUw) test
where Ω is a set of possible threshold values. The atSSUw test is a variant of the adaptive SSUw test as studied in Pan and Shen (2011). Differing from the adaptive SSUw test therein, rather than using all possible threshold values, the current test only uses those specified in Ω, largely reducing the computing demand.
Analogous to using the SSUw test to define the atSSUw test, we can similarly define an adaptive test based on the sum of squared score (SSU) test. In some situations, the SSU test was found to perform better than the SSUw test (as shown in our later simulations). Furthermore, as discussed in Pan (2009, 2011), the SSU test is closely related to an empirical Bayes test for high-dimensional data [Goeman et al., 2006], a variance component test in kernel machine regression (KMR) [Tzeng and Zhang, 2007; Kwee et al., 2008; Wu et al., 2010], and a pseudo-F test in genomic distance-based regression (GDBR) [Wessel and Schork, 2006]; see Schaid (2010a, 2010b) for more reviews and discussions. Specifically, a new adaptive thresholded SSU (atSSU) test is defined as
where PtSSU(PT) is the p-value of the thresholded SSU (tSSU) test
We recourse to the permutation [Churchill and Doerge, 1994], or the parametric bootstrap [Buzkova et al., 2011] in the presence of covariates, to calculate the p-value of either atSSUw or atSSU test. It may appear that a double permutation or bootstrap procedure is needed, but indeed not necessary. Specifically, for example, for the atSSU test, the procedure is as following. First, by permutation (or bootstrapping) we generate B independent copies of Y (b) under H0, b = 1, 2, …, B. Second, based on each copy of Y (b) and genotypes X, we calculate the corresponding tSSU statistic for each threshold , and its p-value . Third, we have , and the final p-value of the atSSU test .
Instead of using the more time-consuming Wald test to calculate the p-value pj for each SNP j, we propose using its asymptotically equivalent and much faster score test, under H0.
Further generalizations and connections
For analysis of relatively small sets of RVs, Pan et al (2014) proposed a class of sum of powered score (SPU) tests:
| (3) |
indexed by a parameter γ ≥ 1. Note that TSPU is based on the whole sample D (without data-splitting). The SPU tests cover the Sum and SSU tests as two special cases with a corresponding γ = 1 and γ = 2 respectively. Importantly, as γ → ∞ (and as an even integer), then the SPU test would approach the UminP test if the variances of the score components are a constant (or if their varying variances are ignored, which may be advantageous in certain cases as to be shown); the reason is simple:
As compared to the use of weight wj ≈ Uj (D1)I(pj (D1) < PT)/Var(Uj (D1)) in the PRS test and weight wj = Uj (D)I(pj (D) < PT) in the tSSU or tSSUw test, the SPU(γ) test uses weight wj = Uj (D)γ −1 . Aside from using the whole sample versus a half of the sample, the SPU tests differ from other tests in the following key aspect: rather than using a fixed set of weights, the parameter γ in the SPU tests indexes varying sets of weights, allowing more flexibility and adaptivity to the unknown truth. For example, as to be shown, in the presence of many non-associated SNPs, a larger value of γ would perform better than a smaller γ of the SPU test; that is, either PRS or tSSU might not be sufficiently adaptive to the situation with a huge number of non-associated SNPs, and thus would suffer from loss of power. Note that there is no thresholding or SNP selection in the SPU tests; one may argue that among a large number of candidate SNPs, it will always be too difficult to correctly select out those causal SNPs with only weak effects. As to be shown later, depending on the unknown underlying genetic architecture, we may need use different values of γ and associated weights Uj(D)γ−1 to yield high power. For example, if most SNPs are almost equally associated with a trait, then a γ ≈ 1 may be optimal; on the other hand, if only few SNPs are associated with large effect sizes, then a larger γ would give higher power.
For a given dataset, to adaptively choose the value of γ for the SPU tests, an adaptive SPU (aSPU) test was proposed to combine the results of multiple SPU tests. Suppose that we have some candidate values of γ in Γ, e.g. Γ = {1, 2, 4, 8, 16, 32, ∞} if the SNPs are believed to have different association directions, or more generally, Γ = {1, 2, …, 8, ∞} as used in our later experiments, and suppose that the p-value of the SPU (γ) test is PSPU(γ), then the aSPU test combines the multiple SPU tests as
Borrowing the idea of SNP selection with p-values, we can further generalize a SPU test to a thresholded SPU (tSPU) test:
and thus define an adaptive thresholded SPU (atSPU) test:
where PtSPU(γ,PT) is the p-value of the tSPU (γ, PT) test. We can similarly define the tSPUw and atSPUw tests.
Again we use the permutation or parametric bootstrap procedure as for the tSSUw and atSSUw tests to obtain the p-value for the above tests. As to be shown in simulations, it turns out that thresholding for SNP selection has minimal effects on performance in the atSPU test, presumably because the aSPU test has effectively incorporated SNP weighting.
Results
Simulation set-ups
We conducted extensive simulation studies to evaluate and compare the performance of various tests. The simulated data were generated as in Wang and Elston (2008). First, we generated a latent vector Z = (Z1, …, Zk)′ from a multivariate Normal distribution with a first-order auto-regressive (AR1) covariance structure: Corr(Zi, Zj) = ρ|i−j| between any latent components i and j; we used ρ = 0 and ρ = 0.2 to generate (neighboring) SNPs in linkage equilibrium and in (weak) linkage disequilibrium (LD) respectively. Second, the latent vector was dichotomized to yield a haplotype with MAFs each randomly selected uniformly between 0.05 and 0.5. Third, we combined two independent haplotypes and obtained genotype data: Xi = (Xi1, …, Xik)′ for subject i. Fourth, for a non-null case we randomly chose k1 causal SNPs with their corresponding βj /= 0 (specifically, ORj = exp(βj) ~ U (1, a) or U (1/a, a) with a > 1), while all other βj = 0; for a null case, all βj = 0. Fifth, the disease status Yi of subject i was generated from the logistic regression model (1). We used β0 = − log(0.05/0.95) for a 5% background disease probability; that is, Pr(Yi = 1|Xi = 0) = 0.05. Sixth, as in a case-control study, we sampled n/2 cases and n/2 controls in each dataset.
We considered several set-ups with various values of ρ = 0 or 0.2, k1 = 20, 50 or 100, k from 1000 to 20000, and n = 2000 with 1000 cases and 1000 controls.
Throughout the simulations, we fixed the test significance level at α = 0.05. The results were based on 1000 independent replicates for each set-up. For the tSSU and tSSUw tests, we used two sets of the thresholds for PT ∈ Ω = {0.05, 0.1, 0.2, 0.3, 0.4, 0.6} or Ω = {0.005, 0.01, 0.05, 0.1, 0.2, …, 0.9, 1}; for the γ in the SPU and aSPU tests, we used Γ = {1, 2, 4, 6, 8, 16, 32, ∞} for k = 1000 and Γ = {1, 2, 3, …, 8, ∞} for others; for the atSPU and atSPUw tests, we used Ω = {0.005, 0.01, 0.05, 0.1, 0.2, …, 0.9, 1} and Γ = {1, 2, 3, 4, 6, 8, 16, 32}.
Simulation results
We fixed the sample size n = 2000. We first investigated the cases with k = 1000 independent SNPs; we gradually increased the number of causal SNPs from k1 = 20 to 100. Since the results were similar, while in the current context it is more of interest to investigate a denser set of associated SNPs with weak effects, we focused on k1 = 100.
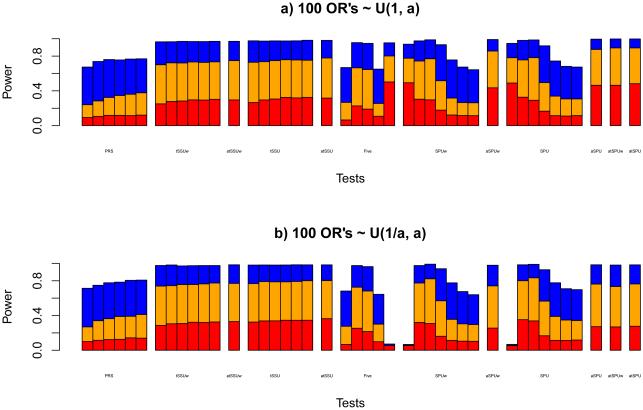
All the tests could control the Type I error rates satisfactorily (not shown). For power comparison (Figure 1), it is noteworthy that, as expected from our earlier analysis, the PRS test was much less powerful than the tSSUw and tSSU tests, whereas the latter two performed similarly. Hence, in the sequel we will only discuss the tSSU and atSSU tests. It is noted that the atSSU test could maintain the high power of the tSSU tests while avoiding the difficult choice of a single threshold PT and the multiple testing problem with the use of several values of PT .
Figure 1.
As shown in Figure 1, the asymptotics-based Score, SSU and SSUw tests could be conservative, due to the relatively small ratio of n/k. It is interesting to see that the Sum test was or nearly was the most powerful if the non-zero associations were in the same direction. Comparing the SPUw and SPU tests, they gave similar results if the same γ was used, hence we will skip the SPUw and aSPUw tests. Among the SPU tests, it seems that the SPU(4) test was most powerful, though the SPU(2), i.e. SSU, test also performed similarly. It is noteworthy that the aSPU test maintained high power across all the situations, as a useful summary on all the SPU tests. We also note that the tSPU tests’ applying thresholding on the SPU tests barely gained; the atSPU and atSPUw tests were almost equally powerful as the aSPU test. Hence, for simplicity, we would not need to apply thresholding, and will focus on the aSPU test. Overall, we claim that the aSPU test was the winner; in particular, the aSPU test was much more powerful than the PRS test.
We note that, although the SPU(1) and SPU(2) test statistics are equal to that of the Sum and SSU tests respectively, due to different methods used in calculating their p-values (i.e. permutation-based versus asymptotic approximations to the null distributions of the test statistics), their results were close but not exactly the same. For a larger number of SNPs with k > 1000, we will no longer consider the asymptotics-based tests due to their questionable application of asymptotics.
If the SNPs were weakly correlated (in LD) (with ρ = 0.2), we obtained similar results (not shown).
Now we gradually increased the number of SNPs from k = 1000 to 2000, 5000, 10000 and finally 20000, while fixing other parameters (Tables 3 and 4). The previous conclusions held. Here we emphasize a few major points. First, again we see that the aSPU test was the overall winner; in particular, the power difference between the PRS and aSPU test could be dramatic. Second, as k increased, we do see the advantage of the PRS test over the global Sum, i.e. SPU(1), test, and that of the tSSU over the SSU, i.e. SPU(2), test, e.g. for k = 20000. It confirms the intuition of applying p-value thresholding to select SNPs to gain power for a large k. Nevertheless, as compared to the aSPU test, thresholding in the PRS and tSSU tests, and the weighting scheme in PRS, were still much less effective than using the weighted score vector in the SPU tests as summarized by the aSPU test. Third, as k increased, an SPU(γ) test with a larger, but not the largest, γ would be most powerful. For example, for a = 1.25 and k = 20000, the power of Sum=SPU(1), SSU=SPU(2) and SPU(∞) tests was 0.148, 0.418 and 0.533 respectively, much lower than 0.819 of the SPU(6) test; as a comparison, the aSPU test was most powerful at 0.822. This confirms the adaptivity and thus its power advantage of the aSPU test. At the same time, it also demonstrates the severe limitation of using any test with a fixed set of weights, e.g. the Sum or SSU test. In particular, due to the close connection between the SSU test and KMR and GDBR, we expect that the KMR and GDBR would share the same drawback as the SSU test.
Table 3.
Empirical Type I error rate (for a = 1) and power (for a > 1) for various tests. There are k1 = 100 causal SNPs with ORj ~ U(1, a) and all other k – k1 SNPs with ORj = 1. The highest power is in boldface.
| k = 2000 SNPs | k = 5000 SNPs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| Test | PT | a = 1 | 1.1 | 1.15 | 1.2 | 1 | 1.1 | 1.15 | 1.2 |
| PRS | .01 | 0.052 | 0.064 | 0.114 | 0.369 | 0.038 | 0.060 | 0.078 | 0.209 |
| .05/.025 | 0.049 | 0.063 | 0.155 | 0.449 | 0.045 | 0.050 | 0.092 | 0.240 | |
| .1/.05 | 0.048 | 0.066 | 0.146 | 0.502 | 0.038 | 0.060 | 0.090 | 0.240 | |
| .2/.1 | 0.050 | 0.088 | 0.191 | 0.511 | 0.056 | 0.062 | 0.103 | 0.261 | |
| .3/.15 | 0.052 | 0.091 | 0.202 | 0.533 | 0.050 | 0.069 | 0.100 | 0.259 | |
|
| |||||||||
| tSSU | .01/.005 | 0.042 | 0.159 | 0.455 | 0.875 | 0.038 | 0.097 | 0.268 | 0.653 |
| .05/.01 | 0.055 | 0.201 | 0.487 | 0.883 | 0.052 | 0.109 | 0.276 | 0.623 | |
| .1/.05 | 0.048 | 0.199 | 0.501 | 0.867 | 0.054 | 0.125 | 0.310 | 0.597 | |
| .2/.1 | 0.054 | 0.189 | 0.492 | 0.858 | 0.052 | 0.127 | 0.313 | 0.586 | |
| .3/.2 | 0.051 | 0.193 | 0.501 | 0.854 | 0.056 | 0.132 | 0.307 | 0.586 | |
|
| |||||||||
| atSSU | 0.054 | 0.213 | 0.550 | 0.920 | 0.061 | 0.131 | 0.349 | 0.686 | |
|
| |||||||||
| SPU(1) | 0.050 | 0.277 | 0.503 | 0.716 | 0.047 | 0.128 | 0.236 | 0.365 | |
| SPU(2) | 0.048 | 0.200 | 0.524 | 0.876 | 0.052 | 0.136 | 0.321 | 0.597 | |
| SPU(3) | 0.048 | 0.285 | 0.647 | 0.936 | 0.050 | 0.137 | 0.340 | 0.709 | |
| SPU(4) | 0.051 | 0.218 | 0.594 | 0.942 | 0.056 | 0.145 | 0.378 | 0.756 | |
| SPU(5) | 0.052 | 0.214 | 0.565 | 0.934 | 0.042 | 0.108 | 0.348 | 0.750 | |
| SPU(6) | 0.046 | 0.171 | 0.512 | 0.896 | 0.044 | 0.117 | 0.344 | 0.733 | |
| SPU(∞) | 0.048 | 0.098 | 0.227 | 0.514 | 0.044 | 0.087 | 0.181 | 0.370 | |
|
| |||||||||
| aSPU | 0.059 | 0.287 | 0.674 | 0.969 | 0.045 | 0.152 | 0.435 | 0.795 | |
Table 4.
Empirical Type I error rate (for a = 1) and power (for a > 1) for various tests. There are k1 = 100 causal SNPs with ORj ~ U(1, a) and all other k – k1 SNPs with ORj = 1. The highest power is in boldface.
| k = 10000 SNPs | k = 20000 SNPs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| Test | PT | a = 1 | 1.15 | 1.2 | 1.25 | 1 | 1.2 | 1.25 | 1.3 |
| PRS | .001 | 0.038 | 0.068 | 0.135 | 0.315 | 0.057 | 0.083 | 0.196 | 0.532 |
| .005 | 0.058 | 0.057 | 0.140 | 0.328 | 0.046 | 0.073 | 0.206 | 0.538 | |
| .01 | 0.055 | 0.058 | 0.127 | 0.352 | 0.053 | 0.097 | 0.203 | 0.497 | |
| .025 | 0.055 | 0.070 | 0.160 | 0.337 | 0.055 | 0.089 | 0.193 | 0.453 | |
| .05 | 0.051 | 0.075 | 0.149 | 0.338 | 0.050 | 0.099 | 0.186 | 0.434 | |
| .1 | 0.060 | 0.079 | 0.154 | 0.304 | 0.055 | 0.105 | 0.182 | 0.396 | |
|
| |||||||||
| tSSU | .001 | 0.063 | 0.154 | 0.436 | 0.841 | 0.057 | 0.288 | 0.685 | 0.958 |
| .005 | 0.057 | 0.170 | 0.439 | 0.831 | 0.050 | 0.289 | 0.636 | 0.883 | |
| .01 | 0.052 | 0.181 | 0.442 | 0.781 | 0.046 | 0.292 | 0.569 | 0.833 | |
| .025 | 0.053 | 0.188 | 0.436 | 0.716 | 0.055 | 0.246 | 0.497 | 0.763 | |
| .05 | 0.059 | 0.189 | 0.409 | 0.670 | 0.063 | 0.241 | 0.465 | 0.690 | |
| .1 | 0.055 | 0.194 | 0.382 | 0.629 | 0.059 | 0.223 | 0.434 | 0.637 | |
|
| |||||||||
| atSSU | 0.065 | 0.229 | 0.515 | 0.880 | 0.061 | 0.334 | 0.686 | 0.940 | |
|
| |||||||||
| SPU(1) | 0.059 | 0.159 | 0.190 | 0.278 | 0.047 | 0.129 | 0.148 | 0.215 | |
| SPU(2) | 0.049 | 0.181 | 0.377 | 0.637 | 0.053 | 0.240 | 0.418 | 0.626 | |
| SPU(3) | 0.051 | 0.189 | 0.432 | 0.756 | 0.055 | 0.245 | 0.500 | 0.774 | |
| SPU(4) | 0.059 | 0.245 | 0.581 | 0.880 | 0.058 | 0.361 | 0.714 | 0.939 | |
| SPU(5) | 0.055 | 0.213 | 0.555 | 0.893 | 0.035 | 0.358 | 0.746 | 0.954 | |
| SPU(6) | 0.054 | 0.244 | 0.600 | 0.911 | 0.047 | 0.417 | 0.819 | 0.980 | |
| SPU(oo) | 0.053 | 0.122 | 0.305 | 0.628 | 0.063 | 0.234 | 0.533 | 0.853 | |
|
| |||||||||
| aSPU | 0.056 | 0.268 | 0.609 | 0.926 | 0.062 | 0.423 | 0.822 | 0.979 | |
While we fixed the number of causal variants in Figure 1 and Tables 3-4, we also investigated the performance of various tests as the number of causal SNPs increased for a fixed total number of SNPs. Table 5 shows the results for k = 1000 independent SNPs with the number of causal SNPs, k1, increasing from 20 to 100. For easy comparison, we also include some previous results for k1 = 100 (e.g. in Figure 1 for PRS). First of all, it is clear that the aSPU test (without sample splitting) was substantially more powerful than the various polygenic tests (with sample splitting), including the PRS test. Among the SPU(γ) tests, it is clear that as the number of causal SNPs, k1, increased, a smaller γ would give higher power, demonstrating again the importance of adaptive weighting. Second, it was confirmed that the PRS and Poly-Sum tests were essentially the same. Third, among the polygenic tests, when the number of causal SNPs was relatively small to medium with k1 = 20 or 50, Poly-SSU test was much more powerful than the PRS (or Poly-Sum) test, while they performed similarly when there was a high proportion of causal SNPs with k1 = 100. This phenomenon can be explained by the relative performance of the SSU(1) and SSU(2) tests (due to their equivalence to the Sum and SSU tests respectively). Fourth, although less powerful than Poly-SSU, both Poly-SSUw and Poly-UminP might or might not outperform the PRS test, again depending on the number of causal SNPs.
Table 5.
Empirical Type I error rate (for OR = 1) and power (for a > 1) for polygenic tests (with sample splitting) and SPU/aSPU tests (without sample splitting) for 1000 independent SNPs, including k1 causal SNPs with ORj’s ~ U(1, a). The highest power is in boldface.
| Null | k1 = 20 | k1 = 50 | k1 = 100 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||||
| Test | P T | a = 1 | a = 1.2 | 1.3 | 1.4 | 1.1 | 1.2 | 1.3 | 1.1 | 1.15 | 1.2 |
| PRS | 0.05 | .044 | .109 | .344 | .728 | .056 | .298 | .769 | .093 | .240 | .674 |
| 0.1 | .053 | .115 | .299 | .676 | .057 | .311 | .767 | .106 | .284 | .738 | |
| 0.5 | .041 | .101 | .258 | .488 | .078 | .298 | .731 | .121 | .377 | .769 | |
|
| |||||||||||
| Poly-Sum | 0.05 | .044 | .111 | .344 | .730 | .056 | .299 | .769 | .093 | .240 | .674 |
| 0.1 | .053 | .114 | .299 | .676 | .057 | .311 | .768 | .106 | .284 | .738 | |
| 0.5 | .042 | .103 | .258 | .489 | .078 | .299 | .731 | .121 | .377 | .768 | |
|
| |||||||||||
| Poly-SSU | 0.05 | .046 | .163 | .610 | .925 | .066 | .350 | .887 | .086 | .228 | .645 |
| 0.1 | .041 | .143 | .593 | .917 | .072 | .379 | .896 | .094 | .253 | .693 | |
| 0.5 | .030 | .124 | .584 | .907 | .062 | .363 | .906 | .093 | .284 | .760 | |
|
| |||||||||||
| Poly-SSUw | 0.05 | .043 | .144 | .494 | .845 | .065 | .306 | .838 | .074 | .220 | .595 |
| 0.1 | .038 | .113 | .418 | .781 | .060 | .319 | .827 | .078 | .233 | .631 | |
| 0.5 | .023 | .053 | .198 | .398 | .041 | .179 | .553 | .091 | .184 | .525 | |
|
| |||||||||||
| Poly-UminP | 0.05 | .050 | .134 | .458 | .787 | .072 | .191 | .642 | .066 | .131 | .364 |
| 0.1 | .039 | .123 | .415 | .751 | .063 | .202 | .592 | .064 | .136 | .326 | |
| 0.5 | .039 | .097 | .287 | .590 | .063 | .166 | .442 | .066 | .111 | .241 | |
|
| |||||||||||
| SPU(1) | .053 | .139 | .182 | .296 | .162 | .439 | .733 | .490 | .781 | .946 | |
| SPU(2) | .062 | .234 | .565 | .819 | .158 | .657 | .966 | .327 | .756 | .981 | |
| SPU(4) | .058 | .364 | .817 | .984 | .159 | .763 | .994 | .292 | .782 | .986 | |
| SPU(8) | .049 | .348 | .830 | .982 | .122 | .630 | .978 | .166 | .495 | .918 | |
| SPU(16) | .056 | .308 | .769 | .961 | .105 | .465 | .924 | .114 | .339 | .744 | |
| SPU(32) | .056 | .293 | .741 | .950 | .103 | .413 | .903 | .110 | .307 | .682 | |
| SPU(∞) | .058 | .297 | .737 | .949 | .109 | .408 | .887 | .115 | .307 | .674 | |
|
| |||||||||||
| aSPU | .055 | .348 | .806 | .971 | .203 | .747 | .992 | .464 | .877 | .995 | |
Application to an alcohol dependence GWAS dataset
We applied the PRS test as well as our proposed aSPU test to analyze the aforementioned GWAS of alcohol dependence. We obtained the “Study of Addiction: Genetics and Environment”(SAGE) GWAS data from the database of Genotypes and Phenotypes (dbGaP) through accession number phs000092.v1.p1. Case subjects were identified as having a lifetime history of alcohol dependence using DSM-IV (Diagnostic and Statistical Manual of Mental Disorders, edition 4) criteria; control subjects were individuals who reported a history of drinking, but did not meet the DSM-IV criteria. Genotyping was performed using Illumina Human1Mv1 CBeadChips on 2,544 European American individuals (1,165 cases and 1,379 controls). A total of 948,658 SNPs were available from dbGaP. We followed the same quality control procedure as in the original SAGE GWAS paper (Bierut et al 2010). We selected autosomal SNPs with a sample MAF of 2% or greater, Hardy-Weinberg equilibrium (HWE) test p-value > 1 × 10−4, and genotyping rate of at least 99%. The final genotype data after quality control consisted of 607,033 SNPs. As a further quality control step, we performed conventional single SNP-based association analyses and found no genome-wide significant SNPs, consistent with that reported in the original SAGE GWAS. In addition, the genomic control factor λ was 1.05, suggesting no noticeable population stratification [Devlin and Roeder, 1999].
To obtain a set of SNPs in approximate linkage equilibrium as done in the ISC paper [The International Schizophrenia Consortium 2009], we applied PLINK [Purcell et al., 2007] to prune the SNPs with a sliding window of 200 SNPs (with a moving step of 20 SNPs) and a criterion of LD r2 ≤ 0.1, leading to 62,801 SNPs remaining.
Due to the consistently good performance of the aSPU test in simulations, here we focus on contrasting the results from the PRS and aSPU tests. When the PRS test was applied to the SAGE samples, it yielded highly significant p-values of 5.04 × 10−5 and 1.23 × 10−6 with the threshold PT = 0.1 and PT = 0.5 respectively (Table 6). Taking into account the multiple testing issue entailed by the multiple thresholds, the Bonferroni-adjusted overall p-value for the PRS test was 1.23 × 10−6 × 7 = 8.64 × 10−6.
Table 6.
P-values of various tests on the GWAS of alcohol dependence in 2544 European American samples (1165 cases and 1379 controls). PT : the p-value threshold used in the PRS test.
| Test | PT | p-value |
|---|---|---|
| PRS | 0.01 | 0.0042 |
| 0.05 | 7.29 × 10−5 | |
| 0.10 | 5.04 × 10−5 | |
| 0.20 | 1.61 × 10−5 | |
| 0.30 | 5.85 × 10−6 | |
| 0.40 | 1.37 × 10−6 | |
| 0.50 | 1.23 × 10−6 | |
|
| ||
| Bonferroni-adjusted p-value | 8.64 × 10−6 | |
|
| ||
| SPU(1) | 5.12 × 10−4 | |
| SPU(2) | < 1 × 10−7 | |
| SPU(3) | 0.0433 | |
| SPU(4) | < 1 × 10−7 | |
| SPU(5) | 0.1925 | |
| SPU(6) | 6.54 × 10−5 | |
| SPU(7) | 0.3111 | |
| SPU(8) | 0.0235 | |
| SPU(oo) | 0.3383 | |
|
| ||
| aSPU | 9.00 × 10−7 | |
Although a p-value < 0.05 is sufficient to reject the null hypothesis of no polygenic effects, we performed 10 million permutations for the aSPU test to demonstrate possible power differences between the aSPU and PRS tests. The aSPU p-value was 9 × 10−7, more significant than the PRS test. As shown in Table 6, none of the test statistics for SPU(2) and SPU(4) in the 10 million permutated datasets was larger than those observed in the real dataset, leading to both p-values less than 1 × 10−7 . A larger number of permutations might result in a even smaller p-value for the aSPU test. Although both tests strongly suggested polygenic effects of alcohol dependence, the aSPU test appeared to be more powerful than the PRS test, consistent with the conclusions from our extensive simulation studies. A closer look at the individual SPU tests revealed some interesting insights. First, SPU(1), i.e., the Sum test, had a small p-value of 5.12 × 10−4, suggesting that most of the polygenic effects were likely in the same direction (either protective or increasing risk). Second, SPU of higher odd powers, i.e., SPU(3), SPU(5) and SPU(7), led to larger p-values; so did SPU(6) and SPU(8) compared with SPU(2) and SPU(4). The relative performance within the SPU test family in the real data appeared to be more consistent with simulations in Table 3 than those in Table 4, i.e., a larger proportion of causal SNPs, each with smaller effect size (a = 1.1). Finally, SPU(∞), i.e., the UminP test, had an insignificant p-value of 0.3383, in agreement with the single SNP-based association analysis result. In summary, the polygenic effects of alcohol dependence as identified by both of the aSPU and PRS tests suggested that increasing the sample size of the GWAS for alcohol dependence in future studies might lead to the identification of genome-wide significant individual SNPs. In fact, a more recent GWAS of alcohol dependence with much larger sample size (16,087 subjects in the combined discovery and replication samples of both European American and African American individuals), including the SAGE samples as a subset, identified a number of genome-wide significant SNPs [Gelernter et al., 2014], which in turn supported the polygenic effects of alcohol dependence we identified here.
For the permutation-based SPU and aSPU tests, we used B = 108 permutations. We split the job into 10 runs on a Texas Advanced Computing Center (TACC) HPC cluster, each run with B = 107 permutations requested on 30 nodes (and three cores on each node); it took about 21 hours to finish. Then it took less than an hour to assemble the results across the 10 runs. The total time was close to (but less than) one day.
We also analyzed 1104 African American samples (625 cases and 476 controls) in the SAGE GWAS; however, neither the PRS nor the aSPU test identified significant polygenic effects (all p-values > 0.1) based on 119,494 SNPs in approximate linkage equilibrium. Given the polygenic effects of alcohol dependence in the African American population suggested by the more recent GWAS [Gelernter et al., 2014], the insignificant results of both the PRS and aSPU tests were likely due to the smaller sample size than that of the European American samples and thus insufficient power, motivating the development of perhaps even more powerful tests in the future.
Conclusions and Discussion
We have carefully analyzed and reformulated the PGS test proposed by the ISC, pointing out its many connections with existing tests, serving to both highlight its limitations and motivate the development of new tests. In particular, we have stressed the low efficiency of the sample-splitting strategy adopted in the PRS test, which was also pointed out by other authors [Dudbridge, 2013]; without sample splitting, however, the usual asymptotics and some theoretical results of Dudbridge (2013) may no longer be used.
Nevertheless, modifying the PRS test with the use of the whole sample leads to a thresholded version of the existing SSUw test. We further generalize the thresholded SSUw test to the thresholded SPU and SPUw tests. Although our numerical studies confirmed the higher power of some adaptive tests over the PRS test, we found that thresholding with the univariate analysis p-values had minimal effects on the performance of the atSPU test as compared to the aSPU test. Application to the SAGE GWAS of alcohol dependence demonstrated the higher power of the aSPU test. Due to its consistently superior performance and simplicity, we recommend the use of the whole sample-based aSPU test.
It is noted that the PRS test can be used to test for shared polygenic effects between different diseases, where sample splitting is not needed. For example, the training sample is a GWAS dataset for schizophrenia while the test sample is another GWAS dataset for bipolar disorder [ISC, 2009]. Although not pursued here, our results may prove useful in this new context. First, as shown in Table 5, depending on the genetic architecture of the disease, including the proportion of the causal SNPs, other versions of the polygenic tests, such as Poly-SSU, could be more powerful than the PRS (or Poly-Sum) test, and thus can be used. Second, based on our important observation of the necessity and effectiveness of adaptive weighting, rather than using the fixed weight wj ∝ Uj for each SNP j, we may apply the adaptive weight wj (γ) ∝ U γ −1 with a suitably chosen γ ≥ 1 to obtain the polygenic scores before applying a global test, which does not have to be the Sum test as in PRS, and could be a more powerful and robust test like SSU or aSPU.
While we have here focused on testing polygenic effects of complex disease, the polygenic score in the PRS test has also been used to predict disease risk, which, however, needs much larger sample size than that for testing polygenic effects [Dudbridge, 2013; Chatterjee et al., 2013]. Specifically, a training sample, say D1, is used to obtain weight for each SNP j. Then for any subject i ∈ D2 in a new test sample, its polygenic risk score is used for outcome prediction. One of our main results on the necessity and effectiveness of adaptive weighting on SNPs for association testing may be borrowed for risk prediction. As for the aSPU test, rather than using the weight wj ∝ Uj (D1), we may use adaptive weight wj (γ) = Uj (D1)γ −1 (with or without thresholding), where γ ≥ 1 is a tuning parameter to be determined (e.g. by cross-validation or another model selection criterion), and thus construct an adaptive risk score for each subject i as ),j wj (γ)Xij . Further studies are needed to evaluate this approach.
Finally, we point out that polygenic testing may be conducted on just a subset of the genome, which is related to but still differs from the usual gene- or SNP-set analysis, in which the number of the SNPs to be tested is often much smaller. In light of its robust power in the presence of thousands of neutral SNPs, the aSPU test might be promising in gene-set association analysis of GWAS data [Wang et al., 2007; Torkamani et al., 2008; Schaid et al., 2012; Wei et al., 2012], where hundreds to thousands of SNPs grouped by biological functions are tested simultaneously. However, some modifications may be needed to account for special features in pathway analysis, such as different gene sizes (i.e. with different numbers of SNPs), overlapping SNPs in multiple genes, and how to assign SNPs in inter-genic regions to genes. This could be a direction of future investigation.
R code will be posted at http://www.biostat.umn.edu/~weip/prog.html
Acknowledgment
We thank the two reviewers for many helpful and constructive comments. This research was supported by NIH grant R01HL116720; WP was also supported by NIH grants R01GM081535, R01GM113250 and R01HL105397, YMC by R25DA026120, and PW by R01CA169122 and R21HL126032. The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper. Funding support for the SAGE study was provided through the NIH Genes, Environment and Health Initiative [GEI] (U01HG004422). The datasets used for the analyses described in this manuscript were obtained from dbGaP through accession number phs000092.v1.p.
References
- Basu S, Pan W. Comparison of Statistical Tests for Association with Rare Variants. Genetic Epidemiology. 2011;35:606–619. doi: 10.1002/gepi.20609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzkova P, Lumley T, Rice K. Permutation and Parametric Bootstrap Tests for Gene-Gene and Gene-Environment Interactions. Ann Human Genetics. 2011;75:36–45. doi: 10.1111/j.1469-1809.2010.00572.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bierut LJ, Agrawal A, Bucholz KK, Doheny KF, Laurie C, Pugh E, et al. Gene, environment association studies consortium: a genome-wide association study of alcohol dependence. Proc Natl Acad Sci USA. 2010;107:5082–5087. doi: 10.1073/pnas.0911109107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman JM, Whittaker J. Analysis of multiple SNPs in a candidate gene or region. Genetic Epidemiology. 2008;32:560–566. doi: 10.1002/gepi.20330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee N, Wheeler B, Sampson J, Hartge P, Chanock SJ, Park JH. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nature Genetics. 2013;45:400–405. doi: 10.1038/ng.2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton D, Chapman J, Cooper J. Use of unphased multilocus genotype data in indirect association studies. Genet Epidemiol. 2004;27:415–428. doi: 10.1002/gepi.20032. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- Dudbridge F. Power and Predictive Accuracy of Polygenic Risk Scores. PLoS Genet. 2013;9(3):e1003348. doi: 10.1371/journal.pgen.1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J. Test of significance based on wavelet thresholding and Neyman’s truncation. JASA. 1996;91:674–688. [Google Scholar]
- Faraway JJ. On the cost of data analysis. J. Comp. Grap. Stat. 1992;1:213–229. [Google Scholar]
- Figueiredo TC, de Oliveira JR. Reconsidering the association between the major histocompatibility complex and bipolar disorder. J Mol Neurosci. 2012;47:26–30. doi: 10.1007/s12031-011-9656-6. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Philos Trans R Soc Edinb. 1918;52:399–433. [Google Scholar]
- Gelernter J, Kranzler HR. Genetics of alcohol dependence. Hum Genet. 2009;126:91–99. doi: 10.1007/s00439-009-0701-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelernter J, Kranzler HR, Sherva R, Almasy L, Koesterer R, Smith AH, et al. Genome-wide association study of alcohol dependence: significant findings in African- and European-Americans including novel risk loci. Mol Psychiatry. 2014;19:41–49. doi: 10.1038/mp.2013.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goeman JJ, van de Geer S, van Houwelingen HC. Testing against a high dimensional alternative. J R Stat Soc B. 2006;68:477–493. [Google Scholar]
- Gottesman II, Shields J. A polygenic theory of schizophrenia. Proc Natl Acad Sci USA. 1967;58:199–205. doi: 10.1073/pnas.58.1.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindorff LA, Junkins HA, Hall PN, Mehta JP, Manolio TA. A Catalog of Published Genome-Wide Association Studies. 2010 Available at: www.genome.gov/gwastudies. Accessed October 31, 2010. [Google Scholar]
- Kwee LC, Liu D, Lin X, Ghosh D, Epstein MP. A powerful and flexible multilocus association test for quantitative traits. Am. J. Hum. Genet. 2008;82:386–397. doi: 10.1016/j.ajhg.2007.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machiela MJ, Chen CY, Chen C, Chanock SJ, Hunter DJ, et al. Evaluation of polygenic risk scores for predicting breast and prostate cancer risk. Genet Epidemiol. 2011;35:506–514. doi: 10.1002/gepi.20600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mokdad AH, Marks JS, Stroup DF, Gerberding JL. Actual causes of death in the United States, 2000. JAMA. 2004;291:1238–1245. doi: 10.1001/jama.291.10.1238. [DOI] [PubMed] [Google Scholar]
- Newton MA, Quintana FA, den Boon JA, Sengupta S, Ahlquist P. Randomset methods identify distinct aspects of the enrichment signal in gene-set analysis. Annals of Applied Statistics. 2007;1:85–106. [Google Scholar]
- Pan W. Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genetic Epidemiology. 2009;33:497–507. doi: 10.1002/gepi.20402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. Relationship between Genomic Distance-Based Regression and Kernel Machine Regression for Multi-marker Association Testing. Genetic Epidemiology. 2011;35:211–216. doi: 10.1002/gepi.20567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W, Shen X. Adaptive tests for association analysis of rare variants. Genetic Epidemiology. 2011;35:381–388. doi: 10.1002/gepi.20586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W, Kim J, Zhang Y, Shen X, Wei P. A powerful and adaptive association test for rare variants. Genetics. 2014;197(4):1081–1095. doi: 10.1534/genetics.114.165035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira M, Bender D, Maller J, Sklar P, De Bakker P, Daly M, Sham P. Plink: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ. Genomic Similarity and Kernel Methods I: Advancements by Building on Mathematical and Statistical Foundations. Hum Hered. 2010a;70(2):109–131. doi: 10.1159/000312641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ. Genomic Similarity and Kernel Methods II: Methods for Genomic Information. Hum Hered. 2010b;70(2):132–140. doi: 10.1159/000312643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, Sinnwell JP, Jenkins GD, McDonnell SK, Ingle JN, Kubo M, Goss PE, Costantino JP, Wickerham DL, Weinshilboum RM. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genet Epi. 2012;36:3–16. doi: 10.1002/gepi.20632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Huang H-C. Optimal model assessment, selection and combination. JASA. 2006;101:554–568. [Google Scholar]
- Simonson MA, Wills AG, Keller MC, McQueen MB. Recent methods for polygenic analysis of genome-wide data implicate an important effect of common variants on cardiovascular disease risk. BMC Med Genet. 2011;12:146. doi: 10.1186/1471-2350-12-146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skol AD, Scott LJ, Abecasis GR, Boehnke M. Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nat Genet. 2006;38:209–213. doi: 10.1038/ng1706. [DOI] [PubMed] [Google Scholar]
- The International Schizophrenia Consortium Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Welcome Trust Case Control Consortium Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torkamani A, Topo EJl, Schork NJ. Pathway analysis of seven common diseases assessed by genome-wide association. Genomics. 2008;92:265–272. doi: 10.1016/j.ygeno.2008.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng JY, Zhang D. Haplotype-based association analysis via variance-components score test. Am J Hum Genet. 2007;81:927–938. doi: 10.1086/521558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T, Elston RC. Improved power by use of a weighted score test for linkage disequilibrium mapping. Am J Hum Genet. 2007;80:353–360. doi: 10.1086/511312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Abbott D. A principal components regression approach to multilocus genetic association studies. Genetic Epidemiology. 2007;32:108–118. doi: 10.1002/gepi.20266. [DOI] [PubMed] [Google Scholar]
- Wei P, Tang H, Li D. Insights into Pancreatic Cancer Etiology from Pathway Analysis of Genome-Wide Association Study Data. PLoS ONE. 2012;7(10):e46887. doi: 10.1371/journal.pone.0046887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessel J, Schork NJ. Generalized genomic distance-based regression methodology for multilocus association analysis. Am J Hum Genet. 2006;79:792–806. doi: 10.1086/508346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Devlin B, Ringquist S, Trucco M, Roeder K. Screen and clean: a tool for identifying interactions in genome-wide association studies. Genetic Epidemiology. 2010;34:275–285. doi: 10.1002/gepi.20459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Kraft P, Epstein MP, Taylor DM, Chanock SJ, Hunter DJ, Lin X. Powerful SNP-Set Analysis for Case-Control Genome-wide Association Studies. Am J Hum Genet. 2010;86:929–942. doi: 10.1016/j.ajhg.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Z, Yang Y. Combining linear regression models: when and how? JASA. 2005;100:1202–1214. [Google Scholar]