Mechanism for Anaphase B: Evaluation of “Slide-and-Cluster” versus “Slide-and-Flux-or-Elongate” Models

Abstract

Elongation of the mitotic spindle during anaphase B contributes to chromosome segregation in many cells. Here, we quantitatively test the ability of two models for spindle length control to describe the dynamics of anaphase B spindle elongation using experimental data from Drosophila embryos. In the slide-and-flux-or-elongate (SAFE) model, kinesin-5 motors persistently slide apart antiparallel interpolar microtubules (ipMTs). During pre-anaphase B, this outward sliding of ipMTs is balanced by depolymerization of their minus ends at the poles, producing poleward flux, while the spindle maintains a constant length. Following cyclin B degradation, ipMT depolymerization ceases so the sliding ipMTs can push the poles apart. The competing slide-and-cluster (SAC) model proposes that MTs nucleated at the equator are slid outward by the cooperative actions of the bipolar kinesin-5 and a minus-end-directed motor, which then pulls the sliding MTs inward and clusters them at the poles. In assessing both models, we assume that kinesin-5 preferentially cross-links and slides apart antiparallel MTs while the MT plus ends exhibit dynamic instability. However, in the SAC model, minus-end-directed motors bind the minus ends of MTs as cargo and transport them poleward along adjacent, parallel MT tracks, whereas in the SAFE model, all MT minus ends that reach the pole are depolymerized by kinesin-13. Remarkably, the results show that within a narrow range of MT dynamic instability parameters, both models can reproduce the steady-state length and dynamics of pre-anaphase B spindles and the rate of anaphase B spindle elongation. However, only the SAFE model reproduces the change in MT dynamics observed experimentally at anaphase B onset. Thus, although both models explain many features of anaphase B in this system, our quantitative evaluation of experimental data regarding several different aspects of spindle dynamics suggests that the SAFE model provides a better fit.

Introduction

The propagation of all cellular life depends on mitosis, during which piconewton-scale forces generated by dynamic polymer ratchets and mitotic motors are used to accurately separate copies of the replicated genome packaged into chromosomes (1,2). During mitosis, chromosomes are separated by a combination of anaphase A, in which chromosomes move from the spindle equator toward opposite poles, and anaphase B, in which the spindle poles move apart, pulling the chromosomes along with them (1,3,4). Anaphase B requires a precise control of mitotic spindle length (4,5) because the spindle is maintained at a constant length during pre-anaphase B (i.e., metaphase and/or anaphase A) and then elongates at a characteristic rate to a characteristic extent. Two models have been proposed to account for the control of mitotic spindle length in two different systems, namely, the slide-and-cluster (SAC) model (6) and the slide-and-flux-or-elongate (SAFE) model (7). These two models are based on a sliding-filament mechanism driven by kinesin-5 motors, but, as discussed below, otherwise differ (8–17). We reasoned that a comparison of the ability of the SAFE and SAC models to account for the control of spindle length changes associated with anaphase B might help to identify common and distinct principles underlying aspects of mitosis in different systems.

The SAFE model was initially proposed to describe anaphase B in Drosophila embryo mitotic spindles (7). These spindles assemble by a centrosome-directed mechanism that can be augmented by chromatin- and augmin-directed MT assembly (18), and then segregate chromosomes using both anaphase A and B (19,20). Whereas anaphase A depends on a combined kinesin-13-dependent pacman-flux mechanism (21), we propose that anaphase B depends on a persistent kinesin-5-generated interpolar microtubule (ipMT) sliding-filament mechanism that engages to push apart the spindle poles when poleward flux is turned off (22). Thus, in pre-anaphase B spindles, the outward sliding of ipMTs is balanced by the kinesin-13 (KLP10A)-catalyzed depolymerization of their minus ends at the poles, producing poleward flux (21), and the spindle maintains a steady length. After cyclin B degradation occurs, however, the MT minus-end capping protein patronin (23) counteracts KLP10A activity at spindle poles to turn off ipMT minus-end depolymerization so that poleward flux ceases and the outwardly sliding ipMTs can now elongate the spindle (24).

The SAC model was initially proposed to account for control of the constant, steady-state length of metaphase spindles in Xenopus egg extracts (6). These spindles assemble by a chromatin-directed pathway (25) and can be induced to separate chromosomes by a flux-based mechanism (26). In the SAC model, MT nucleation occurs around the chromosomes and then kinesin-5 slides the nucleated antiparallel MTs outward (25,27–29). Around the spindle equator, a minus-end-directed motor (e.g., kinesin-14 or dynein) accumulates at the minus ends of MTs and helps slide them along neighboring MTs toward the minus end of these MTs, thus assisting kinesin-5 around the spindle equator, but opposing it and clustering MTs near the poles (6,27). In this model, the spindle length is determined by the lifetime of the poleward sliding MTs (which in turn is based on MT dynamic instability parameters solely at the plus ends) and the rate of poleward transport of the MTs.

Xenopus extract spindles are thought to have a different architecture compared with Drosophila embryo mitotic spindles (4,30), so it is perhaps not surprising that the SAC and SAFE models differ. Also, because the SAC model was proposed to explain the control of metaphase spindle length in Xenopus, we were initially skeptical of the idea that the SAC model could be adapted to anaphase B in fly embryos. On the other hand, recent work has uncovered unexpected features in common between these two types of spindle, such as the existence of chromatin- and augmin-directed MT nucleation mechanisms in Drosophila (18), suggesting that the two models might be more broadly applicable than we initially thought. Specifically, we wondered whether both the SAFE and SAC models might be able to account for the spindle length changes associated with pre-anaphase B and anaphase B in Drosophila embryo spindles.

Here, we explored this possibility by using quantitative, computational models to compare the ability of the SAC and SAFE models to reproduce all the experimental data on changes in spindle length and MT dynamics observed using live-cell imaging, fluorescence recovery after photobleaching (FRAP), and fluorescence speckle microscopy (FSM) experiments in the Drosophila embryo mitotic spindle as it transitioned from its steady-state pre-anaphase B length to anaphase B spindle elongation. Both models, as well as a hybrid SAC-SAFE model, displayed remarkably good agreement with the experiments, although only the SAFE model fit all of the data.

Materials and Methods

Here, we outline the basic features of the two published models together with the new hybrid model, and compare the models for their ability to explain spindle length control associated with anaphase B in Drosophila embryo mitosis. They are described in more detail in the Supporting Material (see Fig. 1). First, we list the similarities and differences between the SAFE and SAC models.

Figure 1.

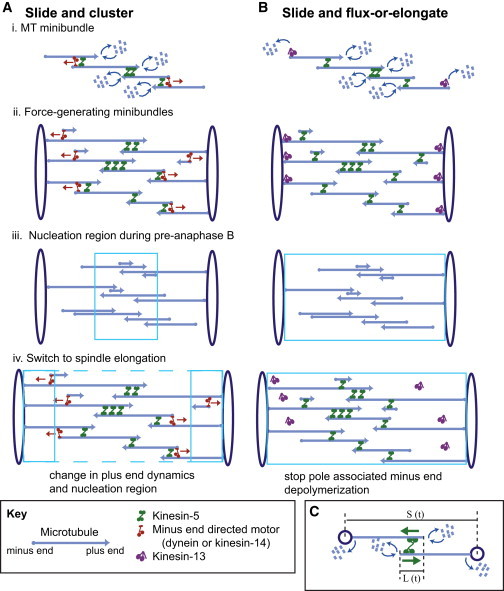
(A and B) SAC (A) and SAFE (B) models. To compare the two models, we set up spindles of 50–200 minibundles, each consisting of four MTs, overlapping antiparallel in the spindle equator. (i) In both models, kinesin-5 cross-links and slides ipMTs apart. In the SAC model (left), a minus-end-directed motor (kinesin-14 or dynein) accumulates at the minus ends of MTs and walks toward the minus end of neighboring MTs; thus, it helps kinesin-5 in the spindle equator but opposes it near the poles (6). In the SAFE model, kinesin-13 at the poles depolymerizes MT minus ends during pre-anaphase B, thus maintaining the spindle at a steady-state length. (ii) Only minibundles spanning the spindle from pole to pole can generate force on the poles. (iii) In the SAC model, nucleation is higher around the chromosomes and thus around the equator during pre-anaphase B. In the SAFE model, nucleation is even along the spindle length. (iv) Anaphase spindle elongation is initiated by a change in parameters. For the SAC model, the dynamic instability of MT plus ends is changed, so the MTs are longer. In addition, nucleation is either uniform along the spindle length or higher around the poles. In the SAFE model, minus-end depolymerization at the poles is turned off, allowing kinesin-5 to push the poles apart. (C) Simplified spindle to illustrate the FB equations used in the SAFE model.

Major similar features

• 1.Mitotic spindles are made up of bundles of 50–200 minibundles of four MTs each (Fig. 1 i).
• 2.The MT-MT plus-end-directed sliding motor is kinesin-5, characterized by its free sliding velocity (V_m) and maximal force (F_m). Kinesin-5 cross-links both parallel (p) and antiparallel (ap) MTs into bundles, displaying a 3-fold preference for the antiparallel polarity pattern (11,15). When it bundles MTs in the antiparallel orientation, it can slide them apart. When it bundles MTs in the parallel orientation, it cannot generate force between them, but it can synchronize the sliding rate of parallel MTs.
• 3.Only bundles of MTs that span the entire pole-pole distance with antiparallel overlapping MTs, either directly or through interactions with parallel MTs, can exert force on the poles (Fig. 1 ii).
• 4.MTs exhibit dynamic instability at their plus ends as described by the four standard parameters, i.e., the growth and shrinkage velocities, v_g and v_s, which are both fixed parameters based on experimental data and a parameter scan, respectively, and the rescue and catastrophe frequencies, f_r and f_c, which are variable parameters (31,32).
• 5.When an MT completely depolymerizes, its assembly is renucleated in the same half spindle to maintain a constant number of MTs throughout.

Major differences

• 1.The assembly of MTs is nucleated throughout the entire spindle in the SAFE model during both pre-anaphase B and anaphase B. In the SAC model, during pre-anaphase B MTs are nucleated predominantly around chromatin at the equator. Anaphase B begins after chromosomes have moved to the poles of Drosophila embryo mitotic spindles (20), so chromatin nucleated-MT assembly can no longer occur exclusively around the spindle equator. Therefore, during anaphase B, we tested MT nucleation predominantly around the poles or throughout the entire spindle (Fig. 1 iii).
• 2.In the SAFE model, the minus ends of poleward sliding MTs are depolymerized at the poles during pre-anaphase-B by a kinesin-13-like minus-end MT depolymerase that depolymerizes every MT minus end that reaches the pole and whose rate of depolymerization (v_depoly) is a fixed parameter (Fig. 1 i). This depolymerization is turned off at anaphase B onset (Fig. 1 iv). In the SAC model, after anaphase B onset, the dynamic instability parameters of MT plus ends change so that the MTs become longer (Fig. 1 iv).
• 3.In the SAC model, when the nonmotor MT-binding tail of a minus-end-directed motor (e.g., kinesin-14 or dynein) reaches the minus end of one MT (its cargo), it can bind by its motor domains to a second parallel MT track and slide the first MT, minus end leading, away from the spindle equator, as in the original model (6). These motors cooperate with kinesin-5 motors to enhance poleward MT transport around the equator, but act antagonistically to kinesin-5 around the poles (6).

Model outline and core equations

All models considered in this study are based on a force-balance (FB) approach in which the rate of movement of MTs or the spindle poles is equal to the net force acting on them divided by their drag coefficient (7). In all descriptions of the modeling strategy and the model framework outlined below and further detailed in the Supporting Material, forces and velocities are positive in the poleward direction. For simplicity, we will refer to the minus-end-directed motor in all equations as Ncd, and to the bipolar kinesin as kinesin-5.

The realistic spindle consists of minibundles of four potentially overlapping MTs with two MTs facing in opposite directions (Fig. 1 i), each of which is referred to as a four-MT minibundle. Such a four-MT minibundle can generate force on the spindle poles when it spans the pole-pole distance with an overlapping antiparallel pair, and the antiparallel pair can span the pole-pole distance either directly or through interactions with parallel MTs (Fig. 1 ii). Forces on the MTs are generated by plus- and/or minus-end-directed motors. An average number of motors per unit overlap length or per minus end are active and generate force on the MTs’ parallel and antiparallel overlaps. Because the binding and dissociation of motors to and from the MTs occur on a millisecond timescale (much faster than the movement rate of the MTs and spindle poles), these kinetics are not explicitly included. The number of motors changes instantly with changes in the overlap length due to sliding and/or MT plus-/minus-end dynamics.

SAFE model

The equations for the SAFE model were previously derived in Brust-Mascher et al. (7). Essentially, the model consists of a system of coupled differential equations based on the following set of three core equations that describe an idealized and simplified spindle formed by a single pair of antiparallel overlapping MTs, as shown in Fig. 1 C. Both MTs polymerize/depolymerize at exactly the same rate, with kinesin-5 motors generating outward forces on the MT antiparallel overlaps, and the MTs’ plus and minus ends undergoing dynamic instability and depolymerization, respectively:

$$\begin{array}{l}{v}_{pole}=V_{sliding}\left(t\right)\text{-}{v}_{depoly}\hfill \\ \frac{dL}{dt}=2\left(V_{poly/depoly}\left(t\right)\text{-}{V}_{sliding}\left(t\right)\right)\hfill \\ {\mu }_{pole}{v}_{pole}=F_{total}=k_{ap}L\left(t\right)F_m\left(1\text{-}\frac{V_{sliding}\left(t\right)}{V_{kinesin5}^{max}}\right)\hfill \end{array},$$ (1)

where v_pole is the velocity of the pole, V_sliding is the sliding rate of the left- and right-pole-associated overlapping MTs, L(t) is the antiparallel MT overlap at time t, μ_pole is the drag coefficient of the pole, k_ap is the number of kinesin-5 motors per unit antiparallel MT overlap, and v_depoly and V_poly/depoly are the MT minus-end depolymerization and the MT plus-end growth or shrinkage rate resulting from MT dynamic instability, respectively. The above set of equations is adequate for an oversimplified, highly ordered spindle (Fig. 1 C). A realistic spindle consists of many four-MT minibundles spanning the region between the spindle poles. Each such bundle can potentially generate force on the poles according to its set of parallel and antiparallel overlaps, whereas each MT plus end can undergo dynamic instability independently of the others. This yields different sliding rates of MTs due to differences in the overlap lengths and thus the number of motors and the load per motor, and results in rapid and asynchronous changes in each overlap. We describe the FB equations in such a spindle by a large set of coupled equations that describe the forces generated on each parallel and antiparallel MT overlap at each time step, based on the current spindle architecture. Thus, the force on each parallel and antiparallel MT overlap is described based on the number of active bound motors (proportional to the overlap size), assuming that the motor-generated forces are additive (i.e., with equal load sharing). Kinesin-5 motors stepping on the i^th pair of overlapping MTs moving with velocity $V_2^i$ and $V_3^i$ generate a force of magnitude $f_{anti-parallel}^i=k_{ap}{L}_{ap}^i\left(t\right)F_{kinesin5}^{stall}\left(1-\left(\left(V_2^i+V_3^i\right)/2V_{kinesin5}^{max}\right)\right)$ on antiparallel overlaps, and a force of magnitude $f_{parallel}^i=k_p{L}_p^i\left(t\right)F_{kinesin5}^{stall}\left(\left(V_2^i-V_1^i\right)/2V_{kinesin5}^{max}\right)$ on MTs moving with velocity $V_1^i$ and $V_2^i$ on parallel overlaps, where k_p is the number of kinesin-5 motors per unit parallel MT overlap. The total force on the spindle poles is the sum of all forces on all overlapping arrays of MTs, $F_{total}=\sum f$. Since the spindle poles and MTs are coupled through the FB equation acting on the spindle poles, this results in a large set of coupled equations that describe the force across each MT array spanning the distance between the poles together with the kinematic and FB equations acting on the poles, depending on the parallel and antiparallel overlap lengths of MTs at any given time. The solution to these equations yields the sliding velocities of each spindle MT that contributes to force generation and the velocities of the spindle poles, based on forces generated by motors working on parallel and antiparallel MT overlaps at that time point.

It is important to note that in this model there is no minus-end-directed motor, but MT minus ends contacting a pole are subject to depolymerization according to the activity level of the kinesin-13 MT depolymerase located around the spindle pole. This depolymerase is active during pre-anaphase B and inactive during anaphase B (Fig. 1 B).

SAC model

In adapting the SAC model to Drosophila embryo mitosis, we modified the original model by introducing MT dynamic instability into the simulations. The general framework of the FB equations for a four-MT minibundle contacting both the left and right poles (and therefore generating forces on the poles) is shown in Fig. 1 Ai and described as follows:

FB on the top MT of the four-MT minibundle shown in Fig. 1 Ai (MT 1), overlapping in parallel with MT 2:

$$F_{parallel}^1=f_{kinesin5}^{parallel}-f_{Ncd}=L_1\left(t\right)k_p{F}_{kinesin5}^{stall}\left(\frac{V_2-V_1}{V_{kinesin5}^{max}}\right)-n{F}_{Ncd}^{stall}\left(1-\frac{V_2-V_1}{V_{Ncd}^{max}}\right).$$ (2)

FB on MT 2 of the four-MT minibundle shown in Fig. 1 Ai, overlapping parallel with MT 1 and antiparallel with MT 3:

$$\begin{array}{l}{F}_{drag}=-f_{kinesin5}^{parallel}+f_{Ncd}+f_{kinesin5}^{anti-parallel}\hfill \\ {\eta }_{MT}{v}_2=-L_1\left(t\right)k_p{F}_{kinesin5}^{stall}\left(\frac{V_2-V_1}{V_{kinesin5}^{max}}\right)+n{F}_{Ncd}^{stall}\left(1-\frac{V_2-V_1}{V_{Ncd}^{max}}\right)+L_2\left(t\right)k_{ap}{F}_{kinesin5}^{stall}\left(1-\frac{V_2+V_3}{V_{kinesin5}^{max}}\right)\hfill \end{array},$$ (3)

where n is the number of Ncd motors per MT minus end and η_MT is the drag coefficient of an MT.

The FB equations for MTs 3 and 4 are derived similarly.

For each minibundle, these FB equations are complemented with two kinematic equations:

$$V_L=V_1\text{and}{V}_R=V_4.$$ (4)

We further assume that all forces are additive at the poles, yielding

$$\sum _i{F}_{parallel,i}^1={\mu }_{pole}{V}_L+{\eta }_{MT}\sum _i{V}_1^i\text{and}\sum _i{F}_{parallel,i}^4={\mu }_{pole}{V}_R+{\eta }_{MT}\sum _i{V}_4^i.$$ (5)

The FB equations for bundles with an antiparallel overlap with one or no parallel overlaps spanning the pole-pole distance (Fig. 1 Aii, upper and middle bundles) are derived similarly, and the kinematic equations and the cumulative force exerted on the spindle poles by the MT mini bundles are described as in Eq. 4, with the appropriate modifications.

Combined model

The combined model (SAC-SAFE) has both the minus-end-directed motor and a depolymerase at the spindle poles. The FB equations are the same as in the SAC model, but the kinematic equations are complemented with the MT minus-end depolymerization rates, as in the SAFE model:

$$V_L=V_1-v_{depoly}\text{and}{V}_R=V_4-v_{depoly}.$$ (6)

In all three models, MT minibundles that do not span the pole-pole distance do not contribute to the forces exerted on the poles. The FB equations for the MTs are derived as above (Eqs. 1 and 2), i.e., forces generated between parallel and/or antiparallel overlaps are balanced by the drag forces on the MTs. MTs that do not overlap with their immediate neighbors are assumed to slide freely at the average rate of sliding of other overlapping MTs in the quarter of the spindle in which they reside (see Numerical Solutions section in the Supporting Material for details). In the SAFE and SAC-SAFE models, MT minus ends that contact the spindle poles are depolymerized according to the level of activity of the MT depolymerase located around the spindle poles.

The FB and kinematic equations form a large system of coupled ODEs, which are solved numerically as described in the Supporting Material, to recover the time-dependent velocities of the MTs and the spindle poles.

Generation of virtual kymographs

Once a numerical simulation of the dynamics of the spindle pole has been completed, the positions of the spindle MTs’ plus and minus ends, and the position of the spindle poles for each time step are stored. To generate virtual kymographs, a segment centered at the spindle equator is defined and divided into 120-nm-long subregions. The amount of tubulin or the number of speckles or MT plus/minus ends is determined for each subregion at each time point and plotted using the built in imagesc function in MATLAB (The MathWorks, Natick, MA).

To generate tubulin kymographs, the number of MTs in each subregion and at each time point is determined as that which corresponds to the number of MTs with segments within the boundary of the subregion. To generate speckled tubulin kymographs, a number of fiduciary marks proportional to the rounded length of each MT are selected at random locations along the lattice of each MT at the initial time step. At each subsequent time step, the position of each one of these marks is updated using the instantaneous velocity and position of the MT on which it is located. If an MT shortens or its minus end is depolymerized beyond a mark, the mark is eliminated. If an MT grows beyond a certain length, a new mark is added at a random position between the mark closest to its plus end, and its plus end. Newly nucleated MTs acquire new marks as they grow. To generate the FSM kymograph, the total number of fiduciary marks within the boundaries of each subregion at each time point is determined. Virtual MT plus- or minus-end kymographs are generated using the time-dependent positions of the MT plus or minus ends, respectively.

Generation of virtual FRAP curves

Virtual FRAP curves were generated as described previously (7). To outline, we assume that the fluorescence intensity is proportional to the total length of polymerized tubulin in a given region. We calculate the total length of MTs within a predetermined bleach region, typically a 2-μm-wide region, at successive iteration time points before a predetermined bleach time. At the time of the bleach, the total length of MTs in the bleach region and the locations of the ends of the bleached MT portions are stored, and the total fluorescence intensity is set to zero, portraying a full and complete loss of fluorescence in the bleach region. During the time steps after the bleach time, the total length of the nascent fluorescent portions of MTs in the bleach zone is calculated as the total fluorescence intensity. These values are plotted over time and fit by a single exponential curve to calculate the half time and percent recovery.

Results

Typical experimental data on the dynamics of the Drosophila embryo spindle are displayed in Fig. 2 and Table 1 (see Supporting Material for experimental details). The spindle maintains a steady-state length of ∼10–11 μm during pre-anaphase B (0–100 s) and then elongates to ∼15 μm during anaphase B (100–150 s) (after which the separated nuclear envelopes reassemble around decondensing chromatin, compressing the spindles and causing the observed slight decrease in spindle length; Fig. 2 A). Tubulin turnover, as monitored by FRAP of fluorescent tubulin, is rapid and complete throughout the pre-anaphase B spindle and at the anaphase B spindle equator, but during anaphase B, the extent of recovery around the poles is decreased (Fig. 2 B; Table 1). Kymographs of tubulin, tubulin speckles, EB1, and patronin throughout pre-anaphase B and anaphase B reveal the distribution and dynamic behavior of MTs, growing MT plus ends, and MT minus ends (Fig. 2 C). During the pre-anaphase B steady state, MTs lying between the spindle poles undergo persistent poleward flux, but at anaphase B onset, poleward flux ceases and MTs slide outward at the same rate as the spindle poles as growing MT plus ends redistribute to the spindle equator. Our aim was to compare the ability of the SAFE and SAC models to account for these experimental data.

Figure 2.

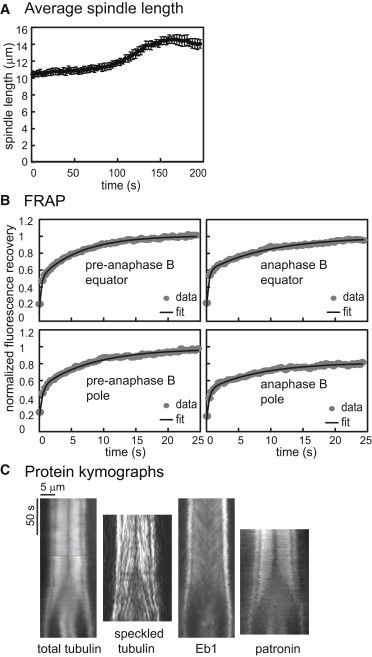
Experimental data for Drosophila syncytial embryo mitosis. (A) Average spindle length as a function of time during cycle 12 (time 0 corresponds to the start of the pre-anaphase B steady state). (B) Examples of FRAP recovery. Left: FRAP during pre-anaphase B is rapid and complete both at the equator and near the poles. Right: at the poles, fluorescence recovery decreases at anaphase B. Note that the initial very fast increase is due to diffusion of free tubulin and is not included in the model simulations (see Table 1 for averages). (C) Kymographs of tubulin, Eb1, which marks growing plus ends, and patronin, which binds to minus ends.

Table 1.

FRAP parameters for both models (average of 20 runs) versus experimental data

		Equator		Pole
		Half time (s)	Percent recovery	Half time (s)	Percent recovery
Experimental dataa	pre-anaphase B	5.3 ± 2.0	99 ± 7	8.9 ± 2.9	96 ± 10
		N = 56		N = 103
	anaphase B	5.0 ± 2.8	100 ± 11	7.0 ± 2.8	86 ± 11
		N = 31		N = 41
Model
SAFE	pre-anaphase B	6.9 ± 1.2	102 ± 6	9.7 ± 2.6	95 ± 6
	anaphase B	5.9 ± 1.4	102 ± 8.8	8.7 ± 1.9	84 ± 10
SAC (higher anaphase B pole nucleation)	pre-anaphase B	4.8 ± 0.7	99 ± 4	9.1 ± 3	99 ± 19
	anaphase B	5.8 ± 1	64 ± 4	8.3 ± 2.9	92 ± 9
SAC (even anaphase B nucleation)	pre-anaphase B	4.8 ± 0.7	99 ± 4	9.1 ± 3	99 ± 19
	anaphase B	6.9 ± 1.2	81 ± 4	14.2 ± 2.9	136 ± 20

^aTubulin FRAP data are biphasic with a fast initial recovery due to diffusion of free tubulin and a second slower phase (see Fig. 2). The models do not consider free tubulin; therefore, we are comparing the model results with the slower phase of experimental FRAP.

For this purpose, we solved each model for a steady-state, pre-anaphase B Drosophila embryo virtual mitotic spindle that was induced to undergo anaphase B-like spindle elongation by turning off MT minus-end depolymerization around the poles in the SAFE model or by changing the MT plus-end dynamic instability parameters in the SAC model (6,7). We solved the model equations repeatedly using the model parameters listed in Table 2. First, we explored the parameter space to find parameters that produced a stable steady-state pre-anaphase B spindle with rapid tubulin dynamics consistent with the experimental FRAP data (Fig. 2 B). The equation solutions are most sensitive to the dynamic instability parameters, and therefore we thoroughly explored these parameters (Fig. 3).

Table 2.

Model parameters

Parameter	Value or range tested	Reference	SAC model (Fig. 4)	SAFE model (Fig. 5)
Time step (s)	0.5		0.5	0.5
Number of ipMTs per bundle	10–30	(14)	30	30
Number of bundles	5–10	(14)	5	5
Drag coefficients (pN × s/μm)
MT (ηMT)	0.5	(34)	0.5	0.5
Pole (μpole)	1000	(35)	1000	1000
Dynamic instability parameters
Vgrowth (μm/s)	0.27	(33)	0.27	0.27
Vshrinkage (μm/s)	0.1–0.4		0.3	0.3
frescue (1/s)	0.02–0.3	(36,37)	See Fig. 2 and Table 3
fcatastrophe (1/s)	0.02–0.5	(36–38)
Sliding motor
Fm (pN)	1–10	(39)	5	5
Vm (μm/s)	0.01–0.1		0.06	0.06
Number of motors per μm of ap overlap, kap	3–300	(14,15)	30	30
Number of motors per μm of p overlap, kp	1–100	(14,15)	10	10
Minus-end motor
Fm (pN)	1–10	(40)	1	N/A
Vm (μm/s)	0.1–1	(40)	0.1	N/A
Number of motors per MT minus end, n	1–300		15	N/A
Minus-end depolymerase at pole
vdepmax (μm/s) preanaphase B	0.01–0.1	(7)	N/A	0.06
vdepmax (μm/s) anaphase B	0		N/A	0

Figure 3.

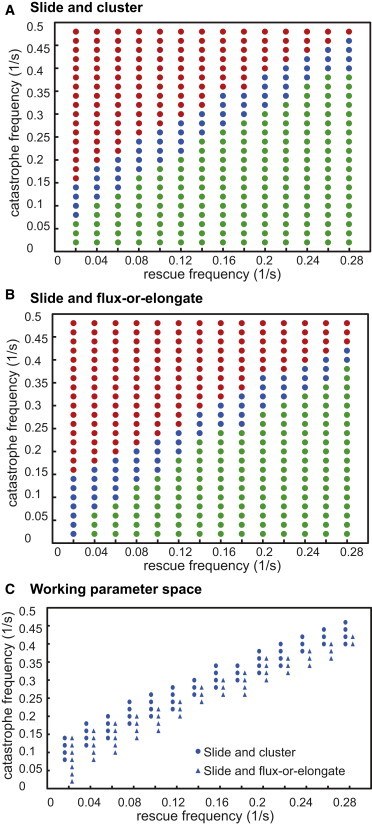
Steady state in SAC versus SAFE models. (A and B) We explored the dynamic instability parameter space for the SAC (A) and SAFE (B) models, looking for parameters that maintain a steady spindle length and exhibit rapid FRAP recovery both near the poles and at the equator (v_g = 0.27 μm/s, v_s = 0.3 μm/s, f_r varied from 0.02 to 0.3 /s, and f_c varied from 0.02 to 0.5/s). (C) In both models, the parameters have to be fine-tuned to maintain a stable spindle with rapid dynamics. If catastrophe is too high, the spindles collapse (red); in a narrow region the spindles are stable and exhibit rapid dynamics (blue); and if rescue is too high, spindles grow in the SAC model (A) or exhibit slow dynamics in the SAFE model (B) (green).

The steady-state pre-anaphase B spindle

Solutions to both models with appropriate dynamic instability parameters yielded virtual spindles capable of maintaining the experimentally observed pre-anaphase B steady-state length (20,24). The parameter space that yielded a good fit was found to be similar for both models. The MT growth rate, v_g, was set at 0.27 μm/s based on the rate of poleward flux plus the observed velocity of EB1 speckles, which mark growing MT plus ends in Drosophila embryo mitotic spindles (33). Then the rate of MT shrinkage, v_s, was set at 0.3 μm/s, a value that yielded the largest range of catastrophe (f_c) and rescue (f_r) frequency parameter space to explore for testing the two models. Having set these two parameters, we sought values of f_c and f_r capable of maintaining a constant spindle length and displaying rapid FRAP recovery for the two models, varying these parameters within the ranges shown (Fig. 3, A and B). We find that the dynamic instability parameters used in solving both models have to be fine-tuned (Fig. 3 C); otherwise, the spindle collapses, grows, or displays unrealistic dynamic behavior. Note that for the same rescue frequency, the range of catastrophe frequencies that give an acceptable fit is slightly lower for the SAFE model (Fig. 3 C). This is because excess MT growth is opposed by MT minus-end depolymerization, which stabilizes the spindle length. However, the range is not larger because although spindle length is stable for all lower catastrophe frequencies, FRAP recovery is too slow to account for observations of real spindles. The significance of the narrow dynamic instability parameter space is discussed below (see Discussion).

Anaphase B spindle elongation

A key difference between the SAC and SAFE models is the nature of the change in MT polymer dynamics that produces a change in spindle length, being confined to MT plus ends facing the spindle equator in the former case and to the minus ends around the poles in the latter model (6,7).

To determine whether solutions to the SAC model could account for anaphase B spindle dynamics in Drosophila embryo spindles, we elongated the virtual pre-anaphase B spindles by changing MT plus-end dynamic instability parameters by increasing the rescue frequency (f_r), lowering the catastrophe frequency (f_c), or using a combination of both. Because anaphase B spindle elongation was not addressed in the original model (6) (and indeed is not a consistent feature of Xenopus extract spindles (26)), we solved the model under conditions in which MT nucleation occurs throughout the spindle during anaphase B, consistent with Drosophila embryo spindles. The results obtained show that spindle elongation at the observed experimental rate is possible (Fig. 4 A, i and ii), although in repeated runs there was variability in the timing of the initiation of spindle elongation, a feature that was not shared with real spindles in this system.

Figure 4.

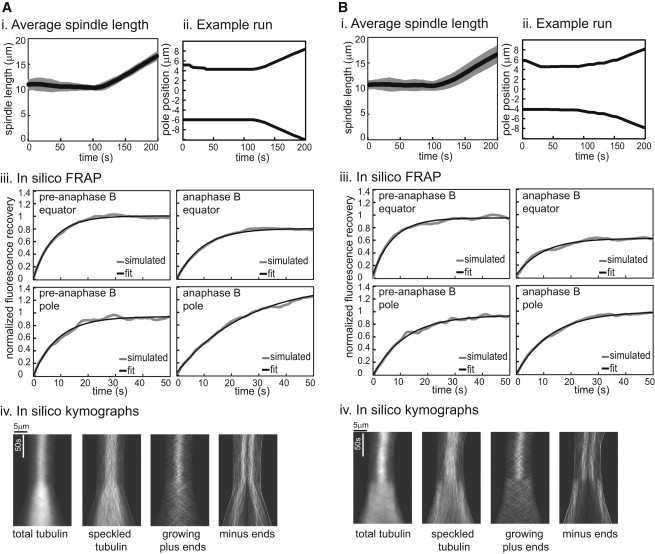
The SAC model explains the observed spindle-length data and FRAP during pre-anaphase B, but not the change in MT dynamics during anaphase B. (A and B) We tested two assumptions at anaphase B onset: even nucleation throughout the spindle (A) and higher nucleation around the poles (B). (i) Average spindle length for 20 runs. Spindle length is maintained at a steady length and a change in plus-end dynamics leads to spindle elongation. (ii) Poles move apart when the plus-end dynamics change. (iii) Left: FRAP during pre-anaphase B is rapid and complete both at the equator and near the poles. Right: during anaphase B, FRAP recovery at the equator is lower and recovery near the poles is higher than observed experimentally (see Fig. 2 and Table 1). (iv) Kymographs.

Because the SAC model assumes MT nucleation around chromatin, and chromosomes have mostly moved to the poles by anaphase B onset, we also tested higher nucleation at the poles during anaphase B (Fig. 4 B). Coupled with a change in plus-end dynamics, this also leads to spindle elongation at the observed rate, again with a delay in the initiation of elongation after the parameter change.

In both cases, the spindle elongation extends beyond that observed experimentally and therefore yields a larger spindle length. In exploring the parameters, we found that changing the dynamic instability parameters affected both the rate and extent of spindle elongation (Fig. S1). For further study, we chose parameters that gave the observed elongation rate, even if the extent of elongation was larger than that observed in vivo.

To elongate virtual spindles in the SAFE model framework, we inhibited MT minus-end depolymerization at the spindle poles and again observed that realistic anaphase B-like spindle elongation could be produced (Fig. 5, i and ii). In this case, in repeated runs, the initiation of spindle elongation was very reproducible. To match the extent of spindle elongation, we also introduced a small additional change in dynamics at the MT plus ends so that the overlap length was maintained, but this was not necessary for initial spindle elongation at the observed rate (Fig. S2). In the case of the SAC model, we did not find parameters that yielded anaphase B spindle elongation that matched both the rate and extent observed experimentally. Only one or the other condition was satisfied, which may reflect a deficiency of the SAC model relative to the SAFE model.

Figure 5.

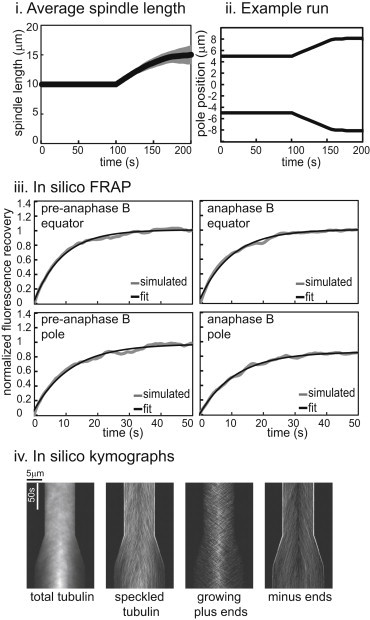
The SAFE model explains all of the data. (i) Average spindle length for 20 runs. Spindle length is maintained at a steady length and spindle elongation starts once depolymerization at the poles stops. (ii) Poles move apart when MT minus-end depolymerization at the poles stops. (iii) Left: FRAP during pre-anaphase B is rapid and complete both at the equator and near the poles. Right: at the poles, fluorescence recovery decreases at anaphase B, as observed experimentally (see Fig. 2 and Table 1). (iv) Kymographs.

In addition to comparing spindle length versus time plots, we generated virtual FRAP and kymographs displaying the dynamic behavior of total tubulin, fluorescent tubulin speckles, growing MT plus ends, and minus ends from solutions to both models. The spindle length and kymographs correspond quite well to those obtained from real spindles (compare Figs. 4 and 5 with Fig. 2). However, in the SAC model, the pre-anaphase B spindle length exhibits more fluctuations and the total tubulin distribution is uneven, with a higher concentration of tubulin at the sites of MT nucleation around the equator, in contrast to experimental observations.

FRAP analysis of spindle dynamics

The two models differed mainly in their ability to account for Drosophila embryo mitotic spindle dynamics as monitored by FRAP throughout pre-anaphase B and anaphase B (Table 1). In experiments, we observed that FRAP recovery was fast and complete both around the equator and near the spindle poles during pre-anaphase B; however, during anaphase B, recovery was incomplete near the spindle poles (Fig. 2 B) (33). Within the range of parameters tested, we were unable to find conditions that satisfied this requirement in solutions of the SAC model both with pole-centered nucleation and even nucleation (Fig. 4 iii; Table 1). In contrast, the SAFE model satisfied this condition when we applied an inverse Gaussian catastrophe frequency, with catastrophe (f_c) being higher near the poles than near the equator (Fig. 5 iii; Table 1) (33). Strikingly, this solution also reproduced the experimentally observed EB1/growing MT plus-end relocalization to the spindle midzone (Fig. 5 iv). A gradient of this same form also yielded the best (albeit unsatisfactory) results within the SAC model framework under the even nucleation assumption (Table 3). We also tried other forms of catastrophe gradient as well as rescue gradients, all of which yielded an even poorer fit to the experimental FRAP data. Interestingly, under the pole-centered nucleation assumption, we obtained better FRAP results without the addition of a gradient.

Table 3.

Rescue and catastrophe frequencies for best results

Parameter	SAC model (Fig. 4)		SAFE model (Fig. 5)
Pre-anaphase B
frescue (1/s)	0.08		0.13
fcatastrophe (1/s)	0.21		0.24
Anaphase B
frescue (1/s)	0.1	0.1	0.15
fcatastrophe (1/s)	pole nucleation 0.15	even nucleation 0.08 at equator∗ 0.19 at poles	0.15 at equator∗ 0.38 at pole

^∗During anaphase B, the best results were obtained with an inverted Gaussian gradient for the catastrophe frequency for the SAFE model and the SAC model with even nucleation.

Effect of parameter variations

We tested the effect of parameter changes using variations around the best parameter set, i.e., starting from the best set, we systematically varied each parameter within the range shown in Table 2. We found that the models display the highest sensitivity to variations in the dynamic instability parameters, as noted above, and are also sensitive to changes in the unloaded sliding velocity of kinesin-5, but they are relatively insensitive to variations in all other parameters that were tested (see Figs. S3 and S4). For example, since both models are relatively insensitive to changes in the number of motors, increasing or decreasing the number of motors by a factor of 10 has no effect on the behavior of the pre-anaphase B spindle and causes changes in the anaphase B spindle elongation rate of up to 25% upward or downward, respectively. In the SAC model, the anaphase B spindle elongation rate decreases with a decrease in the number of bipolar motors (Fig. S3, top left) or an increase in the number of minus-end-directed Ncd motors (Fig. S4, top). Both models are sensitive to a decrease or increase in the maximal velocity of kinesin-5 (Fig. S3, middle), with a slower motor yielding a shorter pre-anaphase B spindle and a slower anaphase B spindle elongation rate. In the SAC model, increasing the maximal velocity of kinesin-5 leads to a longer pre-anaphase B spindle, with no change in the anaphase B spindle elongation rate, but in the SAFE model a higher maximal velocity leads to a premature spindle elongation during pre-anaphase B (the depolymerization rate was not increased). Decreasing or increasing the maximal stall force of kinesin-5 has no effect on the dynamics of the pre-anaphase B spindle and only a small effect on anaphase B spindle elongation in both models. Finally, in the SAC model, changes in the maximal velocity or force of the minus-end-directed MT motor have no effect on the pre-anaphase B spindle, but increasing either parameter leads to a small decrease in the rate of anaphase B spindle elongation (Fig. S4).

Combination SAC-SAFE model

To test the possibility that the two models are compatible with each other, we tested a hybrid SAC-SAFE model in which a minus-end-directed motor is present and anaphase B spindle elongation is associated with the inhibition of MT minus-end depolymerization at spindle poles, a change in MT plus-end dynamics, and a change in the site of MT nucleation. The results show that 1) the addition of a minus-end motor to the SAFE model does not significantly change the results and 2) restricting the nucleation of MT assembly to the spindle equator during pre-anaphase B in the SAFE model or permitting nucleation throughout the spindle in the SAC model yields FRAP recovery data that are inconsistent with experimental observations. Overall, the results show that even in this combined model framework, the best fit to data from Drosophila embryo mitotic spindles is obtained under conditions that resemble the SAFE model.

Discussion

To summarize, the SAC, SAFE, and hybrid SAC-SAFE models all yield a very reasonable agreement with experimental data on the dynamics of the Drosophila embryo mitotic spindle during pre-anaphase B and anaphase B, but only the SAFE model fits all of the available data (41). The SAC model can account for spindle length changes throughout pre-anaphase B and anaphase B, but only the pre-anaphase B and not the anaphase B FRAP data. Also, the SAFE model yields virtual spindles that display a more stable steady-state pre-anaphase B length than the SAC model. This is because MT depolymerization maintains the spindle at a constant length, primed for elongation as soon as this depolymerization ceases. This also explains why the timing of the initiation of anaphase B is highly predictable in the SAFE model and displays more variability due to stochasticity in the SAC model. The model reveals the strong influence of the site of MT nucleation on spindle dynamics and underscores the importance of acquiring as much data as possible, using multiple techniques to discriminate between different models for mitosis.

An examination of the range of parameters that yields such a reasonable fit between the experimental data and all three of the SAC, SAFE, and hybrid SAC-SAFE models suggests that the mitotic spindle is sensitive to changes in MT minus- and plus-end dynamics as well as the bipolar kinesin-5 motor sliding rate, but is extremely robust to changes in almost all other parameters, including the maximal kinesin-5 stall force, number of motors, and MTs. In particular, the dynamic instability parameter space is especially narrow. However, it is important to emphasize that when DI parameter values lying outside this narrow range are used, we do not necessarily encounter mitotic failure; instead, we observe spindles that are a bit smaller or larger than normal, or have slower dynamics, but can still function to mediate normal chromosome segregation. This may also shed light on why perturbations of MT plus-end and minus-end regulatory molecules such as CLASP, kinesin-8, and kinesin-13 have profound effects on spindle length and mitotic progression in almost all studied organisms, because they may normally be used to keep the dynamic instability parameters fine-tuned within the narrow range required for optimal performance (4). One assumption of the models is equal load sharing by multiple kinesin-5 motors; however, recent experimental and theoretical evidence indicates a negative cooperativity between some kinesin motors undergoing collective motility, leading to a lower effective number of bound motors relative to multiple motors acting independently (42–44). However, we observed no significant effect of large increases or decreases in the number of bound, active motors on the model simulations.

Our study helps to define both common and distinct principles underlying the mechanism of mitosis in distinct systems. Specifically, it suggests that both the SAC and SAFE models for spindle length control can account for many aspects of Drosophila embryo mitosis throughout the pre-anaphase B (i.e., metaphase-anaphase A) steady-state and anaphase B spindle elongation, as revealed by measurement of changes in pole-pole separation, fluorescent tubulin speckle behavior, and FRAP analysis. This is perhaps not surprising in the case of the SAFE model, which was developed to account for the switch between pre-anaphase B and anaphase B in this system (7). However, it is quite surprising that the SAC model also provides a very reasonable fit, given that this model was developed initially to account for control of the metaphase steady-state spindle length in Xenopus egg extracts, where spindle architecture appears to be very different (6) and anaphase B is not observed in a consistent way (26). We note that the broad applicability of the two models is also supported by recent reports that a model similar to the SAFE model can account for spindle assembly and length control in Xenopus extracts (45), whereas the SAC model is supported by experiments performed in other vertebrate systems, including human cells (46).

As we noted in a recent commentary, these findings raise the possibility that both the SAC and SAFE models could operate synergistically but to different extents in different spindles (47), as in the combined SAC-SAFE model. It is plausible to think that mitotic spindles are constructed in a combinatorial manner from a set of conserved biochemical modules, such as 1) MT nucleation around centrosomes versus chromatin versus the Augmin-decorated walls of preexisting MTS; 2) spindle-length changes mediated by changes in MT dynamic instability parameters at their plus ends versus their minus ends; and 3) spindle elongation mediated by cortical pulling forces versus outward kinesin-5-driven ipMT sliding. In this view, various combinations of these modules could be deployed to a varying extent in different systems as needed, producing the observed diversity of spindle design observed among different cell types. For example, Xenopus extract spindles assemble predominantly by the chromatin-directed MT nucleation pathway, and Drosophila embryo spindles assemble by a centrosome-directed pathway. However, under the appropriate circumstances, Xenopus extracts can utilize centrosome-directed spindle assembly (48), and Drosophila embryo spindles are also capable of utilizing the augmin- and chromatin-directed assembly pathways if the contribution of the centrosomal pathway is compromised (18). Indeed, to date, the only functional module proposed in the SAC model that has not been found to be deployed in Drosophila embryo mitotic spindles is the minus-end-directed sliding and clustering motor (6). Drosophila embryo spindles contain a minus-end-directed MT-based motor, the kinesin-14 Ncd, which cooperates with kinesin-5 and spindle membranes to maintain the prometaphase spindle (49). To determine whether this motor could function as the proposed minus-end-directed MT clustering motor, we used FSM to investigate the dynamic behavior of fluorescently tagged GFP-Ncd in living, transgenic embryo spindles (50). However, we observed that Ncd speckles moved both poleward and antipoleward at much higher velocities than would be expected for Ncd-driven transport velocities. We note that if Ncd is acting as the minus-end-directed motor proposed in the SAC model in small numbers, these speckles may not be detected in our measurements.

In spite of our view that features of both the SAC and SAFE models are deployed to varying extents in different spindles, we found it possible to discriminate which one dominates in a particular system by testing models against all of the experimental data available on Drosophila embryo spindles (the converse approach was not possible because of the lack of, e.g., FRAP data during anaphase B in Xenopus extract spindles). When we do this, we find that the SAC model is capable of reproducing the steady-state spindle length during pre-anaphase B and also the observed rate of anaphase B spindle elongation, but it does not fit the experimental FRAP data or EB1 relocalization or the extent of elongation. Moreover, although both models yield a steady-state virtual spindle when the appropriate parameters are used, the SAFE model spindle is more stable overall and contains generally more stable MTs characterized by a higher rescue frequency (f_r) or a lower catastrophe frequency (f_c), or both. This means that the system is primed and ready to go, and anaphase B onset begins immediately when MT depolymerization is switched off at the spindle poles. In contrast, in the SAC model, the timing of the initiation of spindle elongation is not as reproducible and there is a variable delay from the point at which the relevant change in the MT plus-end dynamic instability parameter is applied until the time at which the spindle starts to elongate. In parallel experimental work, we observed that the minus-end MT capping protein patronin (23) can turn off MT depolymerization at the spindle poles, turn off poleward flux, and induce anaphase B spindle elongation (24), again supporting the operation of a mechanism more consistent with the SAFE model in this system. Overall, therefore, this work suggests that the SAFE model provides a realistic description of the underlying molecular mechanism of anaphase B spindle elongation during mitosis in Drosophila embryos.

Author Contributions

I.B.-M. performed the experiments, implemented the model code, analyzed the results, and produced the figures. G.C.-S. wrote the model code and worked with I.B.-M. to improve the models. J.M.S. conceived the project, wrote the article, and was the PI for the laboratory and grant. All three authors discussed the project regularly and edited the manuscript.

Editor: Fazoil Ataullakhanov.

Supporting Citations

References (51–53) appear in the Supporting Material.