The Mechanical Properties of Early Drosophila Embryos Measured by High-Speed Video Microrheology

Abstract

In early development, Drosophila melanogaster embryos form a syncytium, i.e., multiplying nuclei are not yet separated by cell membranes, but are interconnected by cytoskeletal polymer networks consisting of actin and microtubules. Between division cycles 9 and 13, nuclei and cytoskeleton form a two-dimensional cortical layer. To probe the mechanical properties and dynamics of this self-organizing pre-tissue, we measured shear moduli in the embryo by high-speed video microrheology. We recorded position fluctuations of injected micron-sized fluorescent beads with kHz sampling frequencies and characterized the viscoelasticity of the embryo in different locations. Thermal fluctuations dominated over nonequilibrium activity for frequencies between 0.3 and 1000 Hz. Between the nuclear layer and the yolk, the cytoplasm was homogeneous and viscously dominated, with a viscosity three orders of magnitude higher than that of water. Within the nuclear layer we found an increase of the elastic and viscous moduli consistent with an increased microtubule density. Drug-interference experiments showed that microtubules contribute to the measured viscoelasticity inside the embryo whereas actin only plays a minor role in the regions outside of the actin caps that are closely associated with the nuclei. Measurements at different stages of the nuclear division cycle showed little variation.

Introduction

A developing embryo presents a striking example of complex biological self-organization and dynamic formation of patterns and structure. Drosophila melanogaster is a well-established model system to study embryonal development (1,2). Drosophila melanogaster embryos develop as a syncytium in their early developmental stages, i.e., nuclear division happens without cytokinesis inside a common cytoplasm. After the 9th nuclear division cycle, most of the nuclei migrate from the interior of the embryo to the cortex and form a two-dimensional layer that shows hexagonal order (3). The center of the embryo consists of an ellipsoidal kernel of yolk, containing yolk granules and vitellophages. The syncytial stage persists for another four nuclear divisions. Then cellularization separates the nuclei into individual cells (4).

The cortical layer of nuclei forms a pre-tissue, rapidly growing while confined to a plane and to the constant area of the tough egg shell. Nuclei interact via an embedding cytoskeleton consisting largely of microtubules and actin. There are no intermediate filaments in Drosophila. Actin forms a cortical layer and actin caps that are located between the nuclei and the egg membrane (Fig. 1 A). Microtubules, originating from the centrosomes, form basket-like structures that enclose the nuclei. Astral microtubules point from the centrosomes toward the cortex and overlap with astral microtubules of neighboring nuclei (5–10). The nuclear layer shows large-scale collective dynamics, for example, density waves traveling through the layer during synchronized mitosis (11). Mechanical forces between the nuclei generated by molecular motors are necessary to drive the dynamics. Microtubules and actin play a key role in maintaining an ordered pattern and in driving motion (12). Possible force generators during interphase are Kinesin-5 motors between overlapping microtubules, direct active interactions of astral microtubules with nuclei, or active interaction of microtubules with the actin caps via dynein-dynactin complexes (13,14).

Figure 1.

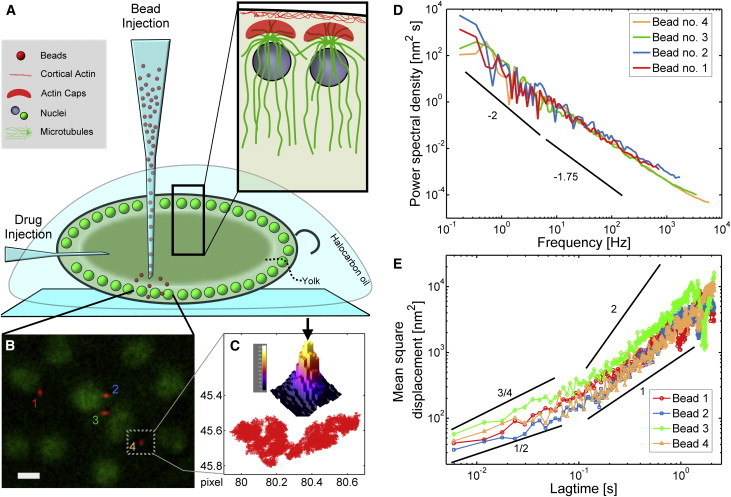
Schematic of the embryo and particle fluctuation data. (A) Schematic drawing of the syncytial blastoderm and the injection geometries we used. Inset: detailed cortical organization of nuclei, microtubules, and F-actin. (B) Fluorescence image of beads (red) dispersed within the nuclear layer (green). Scale bar = 5 μm. (C) Intensity map of bead 4 with its center of mass indicated by an arrow. The red trajectory shows the bead movement determined with subpixel resolution at a rate of 16,000 frames/s over ∼93,000 frames (pixel size: 331 nm). (D) Position power spectral densities in x direction of all four beads shown in the fluorescence image. (E) Mean squared displacements in x direction of all four beads shown in the image. Power-law slopes are drawn for comparison. To see this figure in color, go online.

To quantitatively understand the developing embryo as an active material, one needs to determine both the mechanical properties of the embryo’s interior and the driving forces. Since it turned out that nonequilibrium dynamics are very slow, in this study we used video-based microrheology to measure local shear moduli inside the embryo, relating position fluctuations of embedded micron-sized particles to the viscoelastic response function of the surrounding medium (15–23). We characterized mechanical response below, inside, and above the nuclear layer and probed different stages during the nuclear division cycle.

Materials and Methods

Drosophila embryos

Genetics

The following fly strains were used: nuclei in control and injected embryos were labeled by expression of a Histone 2Av-GFP construct (24). Microtubules were labeled by expression of cherry-tubulin driven by the Histone2Av promoter (kind gift from C. Lehner, University of Zurich, Zurich, Switzerland). Utrophin-GFP served as a live marker for F-actin (25). Fly stocks were obtained from the Bloomington stock center (Indiana University, Bloomington, IN).

Immunostaining of fixed embryos

For immunostaining, embryos were treated as previously described (12). Embryos were dechorionated with 50% (v/v) bleach, fixed with 37% (v/v) formaldehyde, manually devitellinized, and finally rinsed with phosphate-buffered saline (PBS) containing 0.1% (v/v) Tween20. Then they were sequentially incubated in 0.5% (v/v) TritonX-100, in a 5% (w/v) bovine serum albumin solution, in a solution of primary antibody against α-tubulin and in PBS. Embryos were stained with an Alexa568-labeled secondary antibody against a tubulin primary antibody, by an Alexa488-labeled phalloidin solution and finally with a DAPI solution with several PBS washing steps in between. Fixed embryos were mounted in Aquapolymount and imaged with a confocal microscope (SP5, Leica Microsystems, Wetzlar, Germany).

Preparation and injection of living embryos

Developing embryos were dechorionated (Danklorix, CP GABA, Hamburg, Germany), glued to a cover slip, desiccated for 10 min, and then covered with halocarbon oil (Voltalef 10S oil, Lehmann & Voss, Hamburg, Germany) to prevent further desiccation while providing oxygen for proper development. Carboxylated, crimson fluorescent beads (1 μm diameter, FluoSpheres F-8816, Molecular Probes, Eugene, OR) were pressure-injected with a standard micro-injector (Femtojet Express, Eppendorf, Hamburg, Germany) using custom-pulled borosilicate capillaries. Before injection, the aqueous bead solution (0.067% (v/v) solids) was ultrasonicated for 3 min. Beads were injected into the embryo before the formation of the cortical nuclear layer under an angle of 90° to the long axis of the embryo, straight down toward the substrate with the pipette tip 3 to 6 μm above the surface of the cover slip. The temperature was controlled at 22.5°C. Imaging was performed after the 9th nuclear division when the nuclear layer had formed. Optionally, chemical agents were injected at the posterior end of the syncytial embryo. The concentrations of injected colcemid (EMD Chemicals, San Diego, CA), latrunculin A (Cayman Chemical Company, Ann Arbor, MI), and rho kinase inhibitor Y-27632 (Sigma Aldrich, St. Louis, MO) were 0.1 mg/ml, 1 mM, and 10 mM, respectively. As a control, the same tracer particles, but in a different color (FluoSpheres F-8823, Molecular Probes), were passivated with polyethylene glycol (PEG) after the protocol described previously (26). Then a mixture of passivated and untreated probes was injected as described above and imaged simultaneously.

Setup and imaging

Embryos were imaged with a custom-built microscope (Fig. S1 in the Supporting Material): excitation sources were a 561 nm diode-pumped solid state laser (500 mW, Cobolt Jive, Cobolt, Solna, Sweden), a 532 nm diode-pumped solid state laser (Compass 215M 50 mW, Coherent Inc., Santa Clara, CA), and a 489 nm diode-pumped solid state laser (Obis 50 mW, Coherent Inc.). Epi-fluorescence images were taken with a high-NA objective (CFI Plan-Apo IR, 60x, NA = 1.27 water, Nikon, Tokyo, Japan). A tube lens (MXA20696, Nikon) focused the light into the input plane of an image splitter (Optosplit III, Cairn Research, Kent, UK) that projected two images (red and green channel) onto different regions of a low-noise EM-CCD camera (iXon+ DU-888, Andor Technology, Belfast, UK). A dichroic mirror could be placed between the tube lens and the image splitter to alternatively direct the red fluorescence light onto a high-speed CMOS camera (SA1.1, Photron, Bucks, UK). The sample stage was either moved manually or by a three-axis piezo-controlled positioner (NanoCube P611.3S; Physik Instrumente, Karlsruhe, Germany).

With this setup, we could simultaneously observe beads and nuclei at slow video rates (200 ms exposure and frame time) to identify spots of interest inside the embryo, to determine and document the developmental stage of the embryo by observing the nuclei, and to measure lateral distances between the beads and nuclei. We measured normal distances (to the cortex) between the nuclear layer and the beads by means of the feedback-controlled piezo stage. Fluctuating beads were then recorded with the high-speed camera, optionally followed by a recording with the low-speed camera. A region of 128 × 160 pixel was recorded at frame rates of 8, 16, or 20 kHz over 2 to 6 s for high-speed recording. For these short periods, the sample was exposed to the 561 nm laser with peak power densities of 6 kW/cm² = 60 mW/μm². The camera cooling fan was switched off to reduce noise. After each recording, the camera had to cool down for 5 min, which limited the possible number of recordings during a division cycle. Bead tracking at low speed was performed at a frame rate of 20 Hz by choosing a region of interest of 256 × 256 pixel and performing 2 × 2 pixel binning. We recorded image series of typically 1000 to 3000 frames. The sample was illuminated with the 489 nm laser and the 532 nm laser for imaging at normal video rates. Peak power densities were 25 W/cm² at 532 nm, and 62 W/cm² at 489 nm in the sample plane.

Microrheology analysis

Imaging in the Drosophila embryo had to be done in epi-illumination because the yolk in the center of the embryo strongly scatters light. For the same reason, we could not use a standard optical tweezers-based microrheology approach with interferometric displacement detection through the sample (27). This means that it is impossible to perform active microrheology, optically driving the probe (28,29). Even in a nonequilibrium system it is nevertheless possible to measure mechanical properties from particle fluctuations as long as those fluctuations are predominantly thermally driven. This typically occurs at high-enough frequencies. A disadvantage of standard video microrheology, however, is the limited bandwidth, with frame rates of 50/60 Hz when using standard cameras. We therefore extended the bandwidth to kHz, using a high-speed camera.

We determined positions and trajectories of the fluorescent beads by a feature-finding and tracking algorithm kindly provided by Maria Kilfoil (30), based on the work of Crocker and Grier (31). Position trajectories were further processed by custom-written MATLAB (The MathWorks, Natick, MA) routines, following standard 1-particle (1PMR) and 2-particle (2PMR) microrheology routines based on Fourier analysis (27,32): the Fourier transform of the position cross-correlation $C_{AB}\left(\mathit{\omega }\right)={\int }_{-\infty }^{\infty }\langle x_A\left(0\right)x_B\left(t\right)e^{i\mathit{\omega t}}\rangle dt$ was directly calculated by multiplying Fast Fourier Transforms (FFT) of the time traces $x_i\left(t\right)$ projected on the line connecting the two particles for 2PMR. For 1PMR, $A=B$, and $C\left(\omega \right)$ is the power spectral density (PSD) of the particle motion. In an equilibrium system, the fluctuation-dissipation theorem relates the PSD to the imaginary part of the response function (33) $C\left(\mathit{\omega }\right)=2k_{B}T/\mathit{\omega }\mathrm{\cdot }{A}^{”}\left(\mathit{\omega }\right)$ (and equivalently for 2PMR). The real part of $A\left(\omega \right)$ was obtained by means of a Kramers-Kronig relation $A^{\text{'}}\left(\mathit{\omega }\right)=2\pi P{\int }_0^{\infty }\mathit{\upsilon }\mathrm{\cdot }{\mathit{{\rm A}}}^{”}\left(\mathit{\upsilon }\right)/\left({\mathit{\upsilon }}^{\mathrm{2}}-{\mathit{\omega }}^{\mathrm{2}}\right)d\mathit{\upsilon }$, where P denotes a principal-value integral. Finally, the complex shear modulus G(ω) was calculated via the Generalized Stokes-Einstein relation $G\left(\mathit{\omega }\right)={\left(6\pi \mathrm{\cdot }\mathit{R}\mathrm{\cdot }\mathit{A}\left(\mathit{\omega }\right)\right)}^{-1}$, where R is the bead radius. The compressional modulus is assumed to be negligible because of the incompressibility of water, as usual (16). 1PMR can both under- and overestimate shear moduli in the presence of semiflexible filaments because of depletion and local nonaffinity effects (34). 2PMR avoids such problems (21,22,35,36), but because it involves extensive ensemble- and time averaging, the approach is not feasible in the rather inhomogenous interior of the rapidly developing embryos. Since we found a rather viscous response in the embryos, we do not expect a major error because of 1PMR artifacts. When imaging and tracking beads at high frame rates, shot noise eventually became dominant. PSD curves were truncated where the signal vanished in this noise floor. PSD curves typically had to be further modified by locally cutting out distinct sharp noise peaks (Fig. S2). For display, marginal regions of the shear moduli curves that were affected by cut-off effects in the Kramers-Kronig integral (27) were truncated.

Results

Probe bead fluctuations

The first problem to solve was the micro-injection of fluorescent beads into the embryo. The tip of an injection capillary is likely to interfere with or at least temporarily strongly perturb the cytoplasm near the path of insertion. To minimally perturb the regions of the embryo that we planned to probe and to target the sites of interest as precisely as possible, we settled on an injection geometry perpendicular to the cover slip (Fig. 1 A). We furthermore injected early in embryonal development, before nuclear migration, to allow the system to heal.

Fig. 1 B shows a typical fluorescence image of four beads within the nuclear layer. Bead positions of the probe particles were determined with subpixel resolution (Fig. S3) by the centroid estimator and, in a second step, linked into motion trajectories (Fig. 1 C). PSD curves (Fig. 1 D) calculated from probe bead position fluctuations exhibit a frequency dependence that follows a power law with a logarithmic slope of ∼-2 for low frequencies and a slope of ∼-1.75 for high frequencies. For comparison, the mean squared displacement $\langle \mathrm{\Delta }{x}^2\left(\tau \right)\rangle =\langle {\left[x\left(t+\tau \right)\mathrm{-}x\left(t\right)\right]}^2\rangle$ is shown for the four beads in Fig. 1 E. The four beads tracked in the nuclear layer of the embryo imaged in Fig. 1 B gave very consistent results with variations below the noise level. In general, we found the nuclear layer to be relatively homogeneous. Fluctuations varied little within this layer compared with the difference to other sections of the embryo (Fig. S4). In particular, we did not resolve a dependence of the fluctuation amplitudes on the distance of the beads to nuclei as one might have expected.

Tests for nonequilibrium activity

Using the combination of high-speed and conventional camera, we measured the shear moduli over five decades of frequency up into the kHz range. Active force-generating processes in biological systems typically dominate over thermal agitations on timescales above ∼100 ms (37), that are longer than our fast frame times. Hence, although we used a passive method and recorded fluctuations, it is likely that we recorded predominantly thermal fluctuations on timescales faster than ∼100 ms. To further control if active dynamics contributed measurably to the probe fluctuations, especially at low frequencies, we looked for anticorrelations in the fluctuations of pairs of probe beads, which are a telltale indicator for nonequilibrium fluctuations driven by embedded force dipoles such as cytoplasmic myosins (37). We calculated the FFT of the position cross-correlation signal for different interparticle distances. When the cross-correlation signal showed predominantly (threshold: 70%) positive values in the frequency range of 0.1 to 300 Hz, the motion was taken to be correlated, if negative, anticorrelated, and uncorrelated otherwise (Fig. S12). This analysis did not produce any evidence for nonequilibrium activity (Fig. 2 A): as expected from hydrodynamic interaction, we found a fraction of positively correlated bead-pair trajectories for short interparticle distances. This fraction decreased with increasing distance. The remainder were uncorrelated signals.

Figure 2.

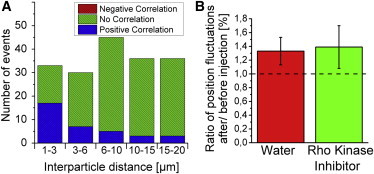
Test for nonequilibrium activity. (A) Distribution of positively and uncorrelated motion of bead pairs at different interparticle distances. No anticorrelated motion appeared. (B) Ratio of position fluctuations (obtained by PSD integration) after and before injection of rho kinase inhibitor and water. N_RKI = 15 embryos. Particles were widely spread inside the embryo (z_RKI = -9 ... 32 μm). To see this figure in color, go online.

To further test for nonequilibrium contributions to the measured fluctuations, we inhibited motor activity pharmacologically. Since Drosophila myosin is insensitive to the commonly used drug blebbistatin, we injected the rho kinase inhibitor Y-27632 to inactivate nonmuscle myosin II motor proteins (8). We integrated the power spectral density of particle motions in the range of 0.3 to 300 Hz to quantify the effect of the drug injection. We did not find a significant difference between the drug-treated embryos compared with the control embryos into which only water was injected (Figs. 2 B and S13).

We conclude from these controls that the bead motions we observed were predominantly thermally driven at all frequencies above 0.3 Hz. Active force generation in the embryo appears thus to be restricted to long timescales, and fluctuation-based microrheology can be safely used to measure viscoelastic properties.

Shear moduli in different layers of the embryo

The cytoplasm of the Drosophila embryo is a dense macromolecular solution (38), but the concentration of structural cytoskeletal components strongly varies within the embryo. F-actin and microtubules are more concentrated in between and near the nuclei. We measured the viscoelastic moduli in different layers of the embryo. With the embryo oriented with its long axis parallel to the substrate, we define the parameter z as the distance along the optical axis of the microscope between the probe particle and the nuclear layer, with positive z pointing toward the yolk of the embryo (Fig. 3 A).

Figure 3.

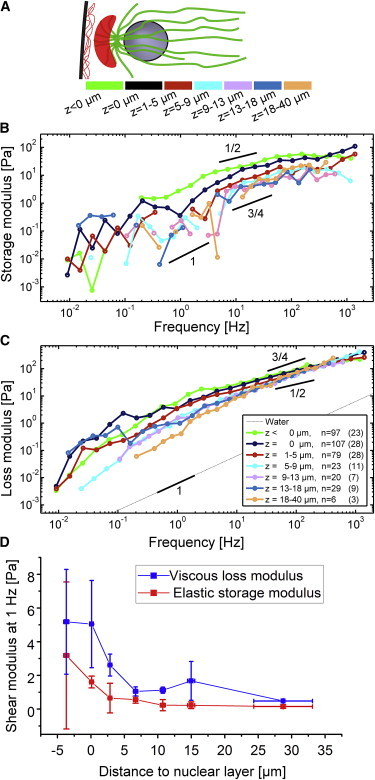
Shear moduli in different sections of the embryo. (A) Sketch of a nuclear compartment with layers along the z axis indicated by color code (not drawn to scale). (B) Frequency-dependent elastic modulus measured at different distances z to the nuclear layer (color codes as in A). Slopes are drawn for comparison. (C) Viscous modulus measured in the same layers. Curves are ensemble averaged over several experiments (Fig. S10). Given are the total numbers of tracked beads (N) and the number of embryos (in parentheses). (D) Elastic and viscous moduli at 1 Hz for different distances z (determined after interpolating the curves in (B) and (C) with a second-order polynomial). Error bars: x-error: mean ± SE, y-error: mean ± SE (embryo-to-embryo variance).

Our probe particles did not appear to enter the dense actin caps or the actin cortex. This phenomenon is a general problem for microrheology inside cells or organisms. The probe particles have to be larger than the mesh size of a network to report its mesoscopic mechanics, but in that case they cannot enter an existing network unless it turns over rapidly in such a way that particles are ingested. We therefore measured viscoelasticity only in regions outside the caps.

In general, the loss modulus G”(f) dominated over the elastic modulus G'(f) (see Fig. 3, B and C). The latter was more noisy, both because of its lower amplitude and the way it needs to be calculated via a Kramers-Kronig integral (27). G'(f) showed approximate power-law dependency on frequency at frequencies above ∼5 Hz. Power-law slopes were clearly smaller than unity indicative of a viscoelastic material and consistent with the measured G'(f) of similar amplitude. For comparison, slopes of 1/2 and 3/4 are drawn in Fig. 2, B and C: 1/2 being the expected exponent for Rouse dynamics of flexible polymers, e.g., DNA (20,39); and 3/4 expected for networks of semi-flexible filaments, e.g., entangled F-actin networks (16,22,27,40,41). At lower frequencies, curves bend toward slopes closer to 1, reflecting more viscous fluid-like response. The elastic modulus G'(f) shows a power-law slope between 1 and 3/4 in the relatively noisy low-frequency range and appears to approach an elastic plateau at high frequencies between 100 and 1000 Hz. This behavior distinctly differs from what is seen in differentiated cells (42) or in strongly entangled or cross-linked in-vitro F-actin networks (22,34) and is more comparable with the response of dilute weakly entangled polymer solutions such as filamentous virus (43) where internal filament dynamics become visible at short times, below a characteristic disentanglement time. We therefore conclude that the parts of the embryo we could access with our 1 μm probe beads contain at most loosely entangled cytoskeletal networks.

Although the response was predominantly viscous in all the layers of the embryos that we probed, we did measure a gradient of the moduli from the yolk toward the cortex. Fig. 3 D shows absolute values of G' and G” at different distances from the nuclear layer averaged around 1 Hz. G' and G” increased when approaching the cortex from the interior of the embryo. We found the distance between cortex and nuclear layer to be ∼8 to 11 μm. Thus, all measurements were taken far enough away from the cortex to exclude any hydrodynamic near-field boundary effects. Note that G' and G” were almost constant in the range of z = 5 - 40 μm and only started to increase when further approaching the embryo’s external shell. The mean values for the storage and loss moduli at intermediate distances (5 to 40 μm) to the nuclear layer are G'(1 Hz) = 0.29 ± 0.14 Pa and G” (1 Hz) = 1.08 ± 0.04 Pa (mean ± SE). This makes the interior of the embryo three orders of magnitudes more viscous than water that is comparable with what was found in the cytoplasm of embryos of Caenorhabditis elegans (44) and in oocytes of Astropecten aranciacus starfishes (45), but about 50 times more viscous than weakly diluted Xenopus egg cytoplasmic extracts (46).

To ensure that surface interactions between probe particles and the embryonal cytoplasm did not influence our results, we performed control experiments with passivated beads (Fig. S5). Beads were passivated by covalently attaching a monolayer of PEG. Passivated beads were coinjected with untreated particles for direct comparison in the same embryo in the same locations. We imaged beads in layers z = -2.3…27.4 μm and quantified fluctuations by integrating the PSDs in the range of 25 to 300 Hz. We found only a marginal difference between the fluctuations of the two kind of probes of 18 ± 11%.

Constancy of shear moduli over the nuclear division cycle

Up to now we have assumed that the probe bead fluctuations we measured were predominantly thermally driven. This assumption is likely valid because forces act slowly and because the lack of a connected elastic cytoskeleton also means that motors cannot generate and transmit forces very efficiently. However, obvious motions occur in the nuclear cortex during nuclear division cycles. To probe for nonequilibrium fluctuations in these phases, we tracked fluctuations through division cycles. During the coordinated and synchronized nuclear division periods, the cytoskeletal structures in the nuclear layer change quite dramatically, with the microtubule networks rearranging to form the mitotic spindles and actin caps extending further down into the embryo separating neighboring nuclei (5). We calculated apparent shear moduli from probe fluctuations recorded over a nuclear division cycle, still assuming predominantly thermal driving forces throughout. Fig. 4 A displays a representative series of fluorescence images taken over a period of 16 min.

Figure 4.

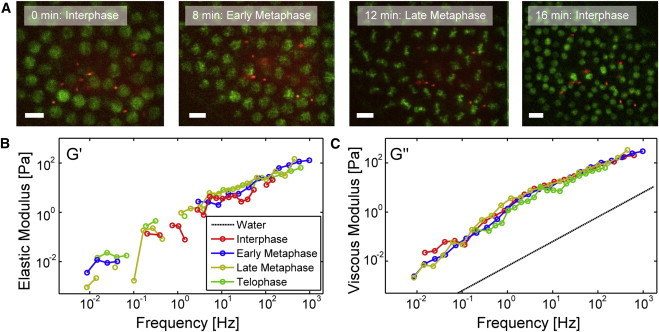
Change of viscoelastic moduli during nuclear division. (A) Sequence of fluorescence images of the nuclear layer with dispersed beads at different stages of the nuclear division cycle. Scale bar = 10 μm. (B) Elastic storage moduli for the different nuclear division stages shown in (A). Curves are ensemble averages over six beads. Negative values are not shown in the double logarithmic scale. (C) Viscous loss moduli over frequency in the different division stages.

Beads remained embedded in the nuclear layer from interphase, early metaphase, late metaphase, and then telophase/early interphase again. Within the accuracy of the measurements, G'(f) and G”(f) showed no obvious variation (Fig. 4, B and C). This result makes it very likely that fluctuations in the frequency range evaluated were indeed still mostly thermally driven, despite obvious slow active motions in the nuclear layer during nuclear divisions. The explanation of this observation is likely that the active processes happen on a timescale of minutes, which would affect at most the very low end of our frequency range, where measurement noise may have masked subtle changes. We also typically observed that the probe beads were pushed out or possibly diffused out of the nuclear layer after mitosis so that measurements over more than one division cycle could not be taken with the same beads. Similar time series measurements for probe beads located above and below the nuclear layer showed a comparable behavior, i.e., only little variation of G' and G” through the nuclear division cycle (Figs. S7 and S8).

We did, however, find some preliminary evidence for slow nonequilibrium motion in recordings taken during and right after anaphase, where some probe trajectories showed directed segments. In those cases, the PSDs show deviations from the normally observed functional form (Fig. S6).

Drug interference experiments

To test the contribution of actin and microtubules to the measured shear moduli, we performed drug interference experiments. We injected latrunculin A and colcemid to disrupt actin filaments and microtubules, respectively. Embryos that expressed fluorescently labeled tubulin and utrophin, an F-actin-binding protein, served as controls to confirm successful depolymerization. Fig. 5 A shows images of actin caps (green) and microtubules around the centrosomes (red) before and after drug injection.

Figure 5.

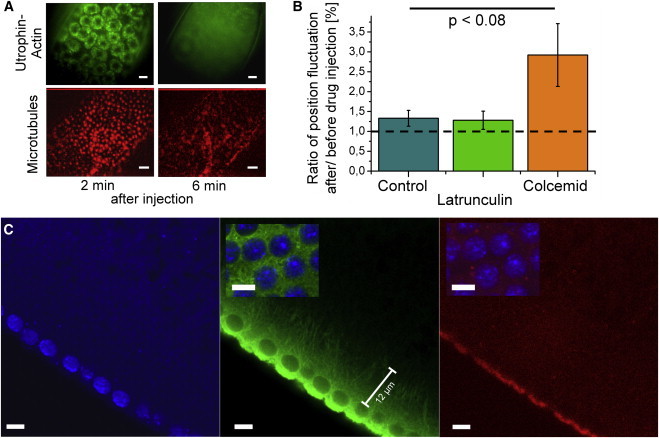
Drug interference and cytoskeletal filament distribution. (A) Fluorescence images of actin caps (green) and microtubules (red) ∼2 and 6 min after drug injection. The 2 min images were indistinguishable from images of untreated embryos. (B) Ratio of position fluctuations (obtained by PSD integration from 5 to 300 Hz) after and before drug injection with latrunculin, colcemid, and control injection with water. N_latrunculin = 18 embryos; N_Colcemid = 11 embryos, N_Water = 15 embryos. Particles were widely spread inside the embryos (z_colcemid = 0 ... 15 μm; z_latrunculin = -8 ... 40 μm, z_Water = -2.3…27.4 μm). The drug injection often moved the beads out of their former positions. In some cases the same beads (identified by their position pattern) could be recorded before and after injection. Otherwise, beads found closest to the original positions were recorded. (C) Confocal fluorescence images of fixed embryos showing a side view of the nuclear layer with nuclei (blue), microtubules (green), and actin (red). Insets: nuclei and microtubules (left) and nuclei and actin (right) both within the nuclear layer. Scale bars = 5 μm.

Distinct cytoskeletal structures disappeared over a time period of ∼270 s for actin and ∼250 s for microtubules after drug injection. Microrheology measurements were performed before and ∼5 min after injection. Probe beads were located across different layers. In about one-half of the colcemid-treated embryos, we saw increased probe fluctuations. The generally relatively small effects are consistent with the fact that the response was dominantly viscous to begin with, corresponding to, at best, a loose cytoskeletal filament network in the regions of the embryo we could access with the probe beads. To quantify the effect of the drugs, the variance of bead position was calculated by integrating the PSDs over a frequency window from 5 to 300 Hz (Fig. S9). The mean ratios of bead-position variance after and before drug injection averaged over all measured beads are shown in Fig. 5 B. Treatment with colcemid increased position variance in the selected frequency band ∼threefold, whereas the addition of latrunculin did not produce a significant effect. These findings are in good agreement with the distribution of cytoskeletal filaments in the embryo. In control experiments with fixed embryos we analyzed the filament distribution in interphase (Fig. 5 C). The confocal images show a dense cloud of microtubules around the nuclear layer, which thins out rapidly toward the interior of the embryo, such that individual filaments or bundles can be optically resolved. F-actin was solely concentrated close to the cortex and inside the actin caps but could not be seen in the interior of the embryo or inside the nuclear layer.

Since the micron-sized probe beads we used did not readily enter the dense network of the actin caps or the cortical actin, our results are valid for the parts of the embryo between the shell and the yolk, but outside of the actin caps. PSDs of beads below the nuclear layer generally varied broadly in fluctuation amplitude, and in some cases elastic plateaus could be seen (Figs. S10 and S11). Some of these beads might have entered the actin caps, but these results were not reproducible enough to draw conclusions. A further exploration of the actin caps needs to await specifically targeted probes.

Discussion

Several approaches have been used to measure the mechanical properties of cells. Probing the response of adherent cells from the outside (17,47) typically results in elastic moduli in the kPa range, reflecting the elastic behavior of the dense actin network of the cortex (48,49). Some experiments have addressed the elastic response of suspended rounded cells to external forces (50,51), showing relatively low stiffness, likely to still be dominated by the actin cortex. Some studies have directly addressed the mesoscale viscoelasticity of intracellular networks and the cytosol (23,29,42,44,52–54). Depending on cell geometry, nonequilibrium fluctuations can greatly complicate the interpretation, and can, for example, make probe particles move as if they were diffusing in a viscous medium (55–57).

Oocytes and early embryos are likely to not be comparable with cells in later stages of development, because of their typically large size and differing internal structure. Cytoskeletal structures are typically concentrated in small subregions and are diluted in the rest of the organism. It is consistent with such dilution, that motor activity is also largely reduced. Reported measurements of the viscoelastic properties of the cytoplasm of cells in early C. elegans embryos found mean viscosity values of 1.03 ± 0.08 Pa (mean ± SE) similar to the ones we measured in Drosophila, whereas intracellular elasticity was found to be negligible (44). Interestingly, diffusion constants measured for small molecules in syncytial Drosophila embryos (58) led to an estimate of microscopic viscosity of ∼4 mPa·s much lower than our measurements of mesoscopic viscosity, arguing again for a dilute macromolecular solution. In this study, we show that microtubules rather than actin filaments contribute to the viscoelastic response of the embryonal cytoplasm in the Drosophila embryos, more strongly near the cortex where the microtubule concentration can be seen to steeply increase.

Conclusions

Our broadband microrheology experiments in living Drosophila embryos have shown that the embryo’s interior is a primarily highly viscous medium. In a region of ∼35 μm thickness, between the cortical nuclear layer and the central yolk, mechanical properties are homogeneous and the viscosity is ∼1000 times higher than that of water. Toward the cortex, shear moduli increase as expected from the higher density of cytoskeletal filaments, predominantly microtubules. Even though nuclei divide and kinesin and dynein motors drive movement on longer timescales, fluctuations faster than ∼1 Hz remain thermally dominated. Further work will have to address the slow movements of larger structures, such as centrosomes, in the nuclear layer with enough accuracy to analyze the nonequilibrium dynamics in the embryo that lead to the observed fascinating large-scale dynamics during embryonal development.

Supporting Citations

Reference (59) appears in the Supporting Material.