RedMDStream: Parameterization and Simulation Toolbox for Coarse-Grained Molecular Dynamics Models

Abstract

Coarse-grained (CG) models in molecular dynamics (MD) are powerful tools to simulate the dynamics of large biomolecular systems on micro- to millisecond timescales. However, the CG model, potential energy terms, and parameters are typically not transferable between different molecules and problems. So parameterizing CG force fields, which is both tedious and time-consuming, is often necessary. We present RedMDStream, a software for developing, testing, and simulating biomolecules with CG MD models. Development includes an automatic procedure for the optimization of potential energy parameters based on metaheuristic methods. As an example we describe the parameterization of a simple CG MD model of an RNA hairpin.

Main Text

Molecular dynamics (MD) (1) is a technique to study biomolecular motions with a molecular mechanics model and numerical solution of Newton’s equations of motions. The first few picosecond-long full-atomic MD of a trypsin inhibitor in a vacuum was carried out in 1977 (2). Recently the dynamics of the same protein was simulated on a millisecond timescale (3). Despite huge progress in increasing MD efficiency and computer power, there is still a large gap between the MD capability and timescales of biological processes. For example, protein translation and folding require up to seconds and involve much larger systems than a trypsin inhibitor.

A possible methodological remedy is to develop reduced MD models, also termed coarse-grained (CG) (4–6) models. In CG models, a biomolecule is represented as a set of interaction centers (beads) that group together multiple atoms. This approach leads to the extension of spatial and temporal scales; the number of degrees of freedom is reduced; and because the simplified interactions usually correspond to the highest-frequency ones, the MD time step can be enlarged. With CG MD models, millisecond timescale simulations for systems much larger than a trypsin inhibitor can be performed on desktop computers. CG MD models have been successfully applied to processes such as nucleic acid thermal denaturation (7), protein folding (8–10), and conformational changes (11), as well as equilibrium dynamics of ribosome (12) or nucleosome (13). However, the common use of CG MD simulations is hindered by the huge effort associated with developing such models.

For full-atomistic MD, there are well-established protocols on how to derive a potential energy function and parameters from quantum chemistry (14). Although there exist methods for systematic parameterization of CG MD models, such as iterative Boltzmann inversion (15) or renormalization group (16), they are not standardized for systems of biophysical interest. Moreover, the emphasis is on the results of the author-selected problem, and not on the thorough description of the model preparation process (reviewed in (6)). This process, typically only briefly described in publications, is hard to repeat. Although most CG MD models work well, they are limited to a particular problem or molecule class, even though in most cases they could be easily adapted to similar problems or related biomolecules. CG MD models’ range of applications can be only extended if protocols for their development are improved and systematized. The obstacle has been the fragmentation of CG MD tools and benchmarks.

A CG MD model itself is not enough to run a simulation; tools to prepare starting files, a CG MD simulation engine, and tools to analyze results are necessary. For full-atomistic MD models, well-tested software packages, such as NAMD/VMD (17,18) or Amber/AmberTools (19), are available. However, in CG modeling, the user often has to combine tools from different sources. Some CG MD models are available only as in-house toolboxes; others are published only as a set of equations without the simulation tools. Another issue has been the benchmarking of these models. For example, comparison of radial distribution functions (or their subsets corresponding to a particular set of bead pairs) is widely used to assess models, although there is no well established method to describe this difference in numerical terms. So providing tools to make the CG MD models more universal has been essential.

We present RedMDStream—an application to develop CG MD force field parameters using a user-specified protocol and perform CG MD simulations. RedMDStream is suitable for the development and simulations of low-resolution (one to three beads per residue) and off-lattice CG MD models. It is a standalone application written in C and C++ languages, working on Linux machines, parallelized with MPI and OpenMP (see the Supporting Material for the scalability benchmarks), and freely available under GNU public license from http://bionano.cent.uw.edu.pl/Software/RedMD.

RedMDStream architecture

To develop a CG MD model with RedMDStream, one has to perform the following steps (see Fig. 1).

• 1.
  Design CG topology. State the rules to transform an atomistic structure into a CG representation. These rules describe the bead type, placement, mass, and charge, as well as the connectivity network and potential energy terms.

  • a.
    Beads can be placed in the positions of particular atoms or residues' centers of masses. See Fig. 2 b for an example.
  • b.
    The connectivity network, including pseudo-bonds, angles, and dihedrals, is set according to user-defined criteria: the sequence (neighbor interactions), distance (distance cut-off in a reference structure), or secondary/tertiary structure (complementary pairing in nucleic acids, salt, or disulphide bridges in proteins). See Fig. 2, c–d.
  • c.
    Interactions are assigned for the connectivity network by providing potential energy terms. Users choose between the predefined terms, such as harmonic and Morse potential, or provide their own equation. This equation along with its derivative is tabularized by RedMDStream for better performance. Parameters of the predefined and custom potential terms depend on the properties of a particular interacting pair (triple, quadruple), e.g., beads closer in the reference structure will have stronger bonding, as in elastic network models (12,13). See Table S1 for an example.

Figure 1.

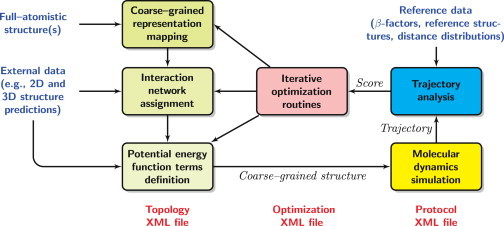
RedMDStream workflow. Frames list the tasks performed by RedMDStream. Information read from the input files is in blue font. The control files are in red font. Italic font refers to data produced by RedMDStream that can be stored in the output file or memory. To see this figure in color, go online.

Figure 2.

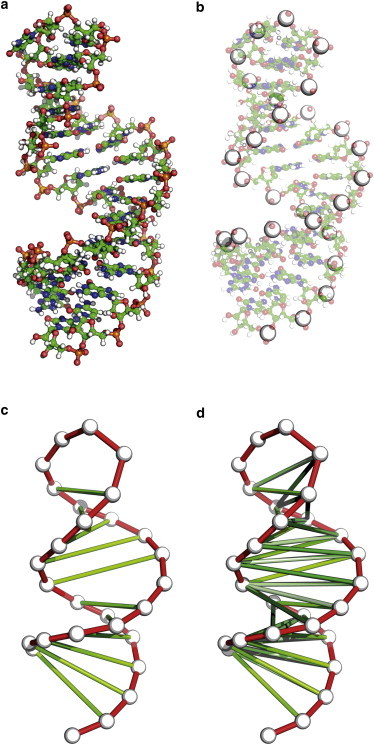
(a) A full-atomistic structure of the microROSE element (21) (PDB ID: 2GIO (21), NMR resolved structure). (b) Bead placement (large white spheres) on the phosphorus atom in the CG MD model. (c) Pseudo-bonds in variant 1 of the force field model. (d) Pseudo-bonds in variants 2 and 3. To see this figure in color, go online.

All these rules are written in an XML (20) file allowing us to share the developed model with others (see Fig. S2).

• 2.
  Provide a simulation protocol. The user describes the implementation of the force field: the files to load, MD simulation method and length, and steps to analyze the trajectory.

  • a.
    Molecules can be provided in PDB (21), PDBML (22), and PQR (23) formats. In addition to a coordinate file, one may include structural information from RNAView (24), in a dot-bracket notation for nucleic acids or plain text format. Protein secondary structure annotations are read from PDB and PDBML files. PDBML also includes base pairing annotations (25) for nucleic acids.
  • b.
    For MD simulation NVE and NVT (with the Berendsen thermostat), ensembles are available, as well as Langevin and Brownian MD regimes (1). MD is performed using the fully integrated RedMD engine (26).
  • c.
    MD trajectory is saved in the DCD binary format and analyzed for pseudo-atoms’ root mean square deviation (RMSD), root mean square fluctuations (RMSF), and distance distributions. To efficiently test many CG model modifications, RedMDStream can refrain from saving the trajectory on the disk and use the analyzed measures as a sole outcome of the MD simulation.
• 3.Perform parameter optimization. The optimal topology parameters of the CG model can be determined using a built-in optimization routine. The criteria of the quality of the CG model are selected by the user and the score comes from CG MD simulation(s) outcome. The criteria can be based on comparing the RMSD, RMSF, and distance distributions with a user-selected reference. RedMDStream incorporates metaheuristic optimization methods: evolutionary algorithm, particle swarm optimization, and simplex algorithm. To efficiently find the optimum of the function, the methods follow strategies inspired by nature instead of strict mathematical rules (27). The parameters selected for the optimization can be the same as defined in the potential energy function or some parameters can be either excluded or fixed. Also, one can provide a mathematical expression between a parameter used in the optimization and one or many parameters defining the energy function of the CG MD model.

RNA one-bead force field

As an example, we optimized a one-bead-per-nucleotide CG MD model (28) for an RNA hairpin, a fragment of the repression of heat shock gene expression element, called microROSE (29) (Fig. 2 a). As a reference, a 100 ns MD simulation with a full-atomistic force field was performed, see Supporting Material for details.

Three variants of the CG model were tested (Fig. 2, c–d, Table S1, and Fig. S3), differing in the interactions of complementary pairs: variant 1 had a single pseudo-bond per one complementary pair; variant 2 had three bonds per one complementary pair; and variant 3 had the same as in variant 2 but one of the bonds was sequence specific. We wanted to verify if one bond per complementary pair is sufficient, and if adding the base pair type specificity improves the model. To find the best parameters for each variant, we optimized the model (with particle swarm optimization and evolutionary algorithm) based on 5 ns CG MD simulations of microROSE (for the protocol, see Supporting Material). Optimization was scored by comparing RMSD, RMSF, and distance distributions with the full-atomic trajectory. For the scoring criteria, see Table S2. Input files necessary to repeat this optimization are in the file microrose.RedMDStream.zip in the Supporting Material.

The best optimization scores are shown in Table 1. The results depend on the Langevin dumping constant used in CG MD simulations whose increase drops the best score by 10% to 20%. This constant affects mostly RMSF (Fig. S4), but the low dumping constant gives high unstable RMSD in the simulation of variant 1 (Fig. S5).

Table 1.

Best score for each of the force field variants, depending on the Langevin dumping constant

	γ = 5 ps−1	γ = 20 ps−1
Variant 1	0.27	0.21
Variant 2	0.27	0.23
Variant 3	0.24	0.22

Scores are normalized to 0.0 to 1.0 scale. Lower values correspond to better models. Scoring criteria are described in Table S2.

Further, we verified the performance of the CG models optimized based on 5 ns CG MDs in longer 100 ns simulations. The simple model (variant 1) became unstable in the first few ns with RMSD up to 15 Å (see Fig. S6). However, the additional bonds per complementary pair in variants 2 and 3 provided stable 100 ns simulations. The distance distributions (Figs. S7–S10) suggest that instability and low score on short timescales are connected. Additional complementary bonds provide extra-stabilization, but for the cost of too narrow distributions (see Figs. S9 and S10). No extra bonds ensure better flexibility, which better resembles the distributions from an all-atom MD but leads to the unnatural unfolding of the structure. On the other hand, the effect of adding the base pair specificity to the potential is minor; it neither improves the score nor distributions. As shown in Fig. S8 (variant 3, γ = 5.0 ps⁻¹) this addition has even an adverse effect on the distributions, resulting in a split of the single P–P i:j peak for different base pairs (A–U, C–G, and wobble). This effect does not appear in a model optimized with a higher Langevin dumping constant. This is consistent with the distributions from the full-atomistic model that share the same maximum for all the base types. Overall, variant 2 seems optimal, as it provides the best score without introducing too many parameters.

Besides analyzing the best model, we looked for a general relationship between the parameter value and score (Fig. S11). Overall, the three CG model variants give similar preferable bonding parameters for neighboring beads (both the force constant and equilibrium distance). However, variant 1 requires stronger angle and dihedral force constants to compensate for the lack of extra pseudo-bonds. In variants 2 and 3, the loop region could be even unrestricted in terms of angle and dihedral (force constant approaching to zero). Finally, variant 3 correctly predicted that CG pairs are stronger (higher force constant) and closer than AU pairs. For details of the methodology, such as the choice of evolutionary algorithm parameters and examples of CG models, please refer to (28).

Conclusions

In a single software package RedMDStream allows defining a CG model (mapping and force field), its further optimization and simulation, as well as its analysis. Combining all the tools provides a consistent environment for a CG MD model developer. Using the software may replace hours of manual trial-and-error tests, as well as provide an overview of CG MD model properties.

Although RedMDStream aids in the CG force field design and optimization process, it does not operate as a blackbox. Especially, the optimization results should be visually inspected to verify if the scoring function was well defined and does not accept unphysical models. This effect can be minimized by using physically reasonable parameter ranges, e.g., based on the Boltzmann inversion. Tests on longer timescales should be also performed. Note, that the outcome depends on the used structure set. If a CG force field aims to describe a whole class of molecules, it would be better to include many representative molecules in the optimization protocol (28), see Supporting Material for the discussion on the optimization procedure.

RedMDStream uses the XML format to define the CG topology. This topology definition could work as interoperable format to store CG MD models, so authors could share their XML files with others. Future releases will extend the trajectory quality measures with force matching (30) and include LAMMPS (31) support.

Author Contributions

F.L. and J.T. designed the research; F.L. wrote the software, performed the simulations, and analyzed the data; J.T. supervised the research; F.L. and J.T. wrote the article.

Supporting Citations

References (32–34) appear in the Supporting Material.