Calcium-Voltage Coupling in the Genesis of Early and Delayed Afterdepolarizations in Cardiac Myocytes

Abstract

Early afterdepolarizations (EADs) and delayed afterdepolarizations (DADs) are voltage oscillations known to cause cardiac arrhythmias. EADs are mainly driven by voltage oscillations in the repolarizing phase of the action potential (AP), while DADs are driven by spontaneous calcium (Ca) release during diastole. Because voltage and Ca are bidirectionally coupled, they modulate each other’s behaviors, and new AP and Ca cycling dynamics can emerge from this coupling. In this study, we performed computer simulations using an AP model with detailed spatiotemporal Ca cycling incorporating stochastic openings of Ca channels and ryanodine receptors to investigate the effects of Ca-voltage coupling on EAD and DAD dynamics. Simulations were complemented by experiments in mouse ventricular myocytes. We show that: 1) alteration of the Ca transient due to increased ryanodine receptor leakiness and/or sarco/endoplasmic reticulum Ca ATPase activity can either promote or suppress EADs due to the complex effects of Ca on ionic current properties; 2) spontaneous Ca waves also exhibit complex effects on EADs, but cannot induce EADs of significant amplitude without the participation of I_Ca,L; 3) lengthening AP duration and the occurrence of EADs promote DADs by increasing intracellular Ca loading, and two mechanisms of DADs are identified, i.e., Ca-wave-dependent and Ca-wave-independent; and 4) Ca-voltage coupling promotes complex EAD patterns such as EAD alternans that are not observed for solely voltage-driven EADs. In conclusion, Ca-voltage coupling combined with the nonlinear dynamical behaviors of voltage and Ca cycling play a key role in generating complex EAD and DAD dynamics observed experimentally in cardiac myocytes, whose mechanisms are complex but analyzable.

Introduction

Early afterdepolarizations (EADs) and delayed afterdepolarizations (DADs) are known to cause arrhythmias in a variety of cardiac diseases, including long QT syndromes (1–3), catecholaminergic polymorphic ventricular tachycardia (CPVT) (4,5), and heart failure (6,7). EADs are voltage oscillations that occur during the repolarizing phases of the action potential (AP). By prolonging the AP duration (APD) regionally, EADs can increase dispersion of refractoriness, forming a tissue substrate vulnerable to reentry. Furthermore, if EADs reach the threshold to propagate out this region as premature ventricular contractions, they can serve as triggers to induce reentry. DADs, on the other hand, are voltage oscillations during diastole. By depolarizing the resting membrane potential regionally, DADs can cause conduction block (8), and, if they reach the threshold for sodium (Na) channel activation, can generate triggered activity (TA) manifesting as premature ventricular contractions that induce reentry.

EADs occur in the setting of reduced repolarization reserve, such as long QT syndromes, and have classically been attributed to voltage-driven oscillations in the repolarizing phase of the AP, although spontaneous sarcoplasmic reticulum (SR) calcium (Ca) release has also been proposed as an important mechanism. DADs, on the other hand, are promoted by Ca cycling disorders, such as CPVT and digitalis toxicity, which promote Ca-driven oscillations. Heart failure represents a combination of reduced repolarization reserve and abnormal Ca cycling resulting from electrical and excitation-contraction coupling remodeling processes driven by both genetic transcriptional and posttranslational signaling components. In all of these settings, it is common for EADs and DADs to coexist and influence each other. This is because membrane voltage is strongly affected by Ca-sensitive ionic currents, and, conversely, cellular Ca loading is strongly influenced by voltage-dependent ionic currents, referred to as bidirectional Ca-voltage coupling. Ca-voltage coupling can promote complex AP dynamics in the heart (9). Analyzing the interactions between EADs and DADs (and voltage and Ca-cycling coupling dynamics in general), however, has been challenging, because the Ca cycling dynamics (e.g., Ca waves and oscillations) result from a spatially distributed heterogeneous network of Ca release units (CRUs) in the cell. The Ca waves emanating from various subcellular regions integrate to depolarize diastolic membrane voltage by activating Ca-sensitive inward currents including the Na-Ca exchange (NCX) current (I_NCX) and Ca-activated nonselective cation channels (I_ns(Ca)), generating DADs. Similarly, spontaneous SR Ca release during the AP plateau can potentially trigger EADs (10–13), in concert with voltage-dependent mechanisms generating voltage oscillations. Therefore, to analyze EAD and DAD dynamics realistically requires a detailed cardiac AP model incorporating spatiotemporal Ca cycling that can simulate Ca waves, such as the ones developed recently (14–16), rather than single pool models of Ca cycling.

In this study, we used our AP model incorporating detailed spatiotemporal Ca cycling in a network of diffusively-coupled CRUs to investigate systematically how bidirectional voltage-Ca coupling affects EAD and DAD dynamics. We show the following: 1) Alteration of the Ca transient can either promote or suppress EADs due to its complex effects on Ca-sensitive ionic currents. 2) Spontaneous Ca oscillations have complex effects on the occurrence and behavior of EADs, but cannot generate EADs of significant amplitude without the participation of I_Ca,L; the timing of a rise in intracellular Ca relative to membrane depolarization is not sufficient criteria to indicate that an EAD is caused by spontaneous SR Ca release. 3) Two different DAD mechanisms are identified (Ca-wave-independent and Ca-wave-dependent), and lengthening of APD promotes DADs by increasing intracellular Ca loading. The presence of EADs further enhances Ca loading to promote DADs due to more L-type Ca channel (LCC) openings during EADs. 4) Complex EAD patterns occur due to Ca-voltage coupling and are promoted under Ca overload conditions in both computer simulation and experiments of mouse ventricular myocytes. The mechanisms underlying these different EAD and DAD dynamics are analyzed and discussed.

Materials and Methods

Computer model

The myocyte model contains a three-dimensional network of 19,305 (65 × 27 × 11) CRUs, modified from Restrepo et al. (14). Each CRU contains five subvolumes: network SR, junctional SR, dyadic space, submembrane space, and cytosolic space. Each CRU has a cluster of 100 ryanodine receptor (RyR) channels associated with a cluster of 12 LCCs, both simulated using random Markov transitions. The governing equation for voltage is

$$\frac{dV}{dt}=-\left(I_{Na}+\sum _{\mathit{k}=\mathrm{1}}^{N\mathrm{\times }\mathit{m}}{\mathit{i}}_{\text{LCC}}\left(k\right)+I_{Ks}+I_{Kr}+\sum _{k=1}^N{i}_{\text{NCX}}\left(k\right)+I_{\text{NaK}}+I_{K1}+I_{to,f}+I_{to,s}\right)/C_m,$$ (1)

where i_LCC is the current of a single LCC, i_NCX is the NCX current of a single CRU, N is the total number of CRUs in the cell, and m is the total number of LCCs in a CRU. Because the I_Ca,L window current is extremely important in the genesis of EADs (17–21), we reformulated the Markov LCC model to allow the window current to be directly manipulated. This was necessary because the Markov LCC formulation in the AP model by Restrepo et al. (14) has many linked states, and it is not straightforward to alter the window current without affecting other properties of the current. Therefore, we adopted a Hodgkin-Huxley type of formulation modified from the model of Luo and Rudy (22), in which the window current can be directly altered by shifting the steady-state activation and inactivation curves. In addition, the Hodgkin-Huxley-type model can be directly modified based on whole-cell measurements of the channel kinetics. A full description of the computer model and the numerical methods used are presented in the Supporting Materials and Methods.

Myocyte experiments

Patch-clamp recordings and optical imaging of Ca in isolated mouse ventricular myocytes were carried out. Details of the experimental methods are described in the Supporting Materials and Methods. All procedures comply with UCLA Animal Research Committee policies.

Results

EAD and DAD generation in the computer model

A straightforward method of inducing EADs in the model was to shift the voltage activation curve of I_Ca,L to more negative voltages to increase the I_Ca,L window current (17), mimicking the effects of Ca channel mutations that cause long QT syndrome, such as Timothy syndrome (23) and other disease conditions such as hypertrophy (18). This shift had very small effects on I_Ca,L and the Ca transient under AP clamp conditions (Fig. S4 in the Supporting Material). Under free-running conditions in which the AP was not clamped, however, this small shift in the activation curve lengthened APD and resulted in EADs, which then had much larger effects on I_Ca,L and the Ca transient. Conversely, a straightforward method of inducing DADs in the model was to raise [Na]_i, such as might occur in chronic heart failure (24); this increased intracellular Ca loading via NCX sufficiently to cause spontaneous SR Ca release during diastole. Elevating [Na]_i increased the Ca transient that augmented Ca-dependent currents, such as I_NCX and I_Ks, but also increased outward I_NaK (Fig. S4).

To study the interactions between EADs and DADs, we varied both parameters simultaneously. Fig. 1 summarizes the spectrum of AP behaviors observed for different hyperpolarizing left-shifts in the I_Ca,L activation curve (0–9 mV) coupled with different levels of [Na]_i (5–15 mM) during pacing at PCL = 2, 1, and 0.5 s, respectively. Six typical AP behaviors were observed at all PCLs, illustrated in the sample traces shown in Fig. 1 D: 1) normal AP, 2) EADs only, 3) repolarization failure, 4) DADs only, 5) a mixture of EADs and DADs, and 6) repolarization failure with voltage oscillations. More complex EAD and DAD behaviors, including TA, also occurred under specific conditions, which are discussed in detail later. In general, Fig. 1, A–C, shows that shifting the I_Ca,L activation curve to more negative voltages promoted EADs and repolarization failure without inducing DADs. On the other hand, increasing [Na]_i caused DADs by elevating [Ca]_i and enhancing spontaneous SR Ca waves, but tended to suppress EADs and repolarization failure by increasing outward I_NaK and reducing inward (forward mode) NCX current. When both I_Ca,L activation was shifted and [Na]_i was elevated, EADs and DADs commonly occurred together.

Figure 1.

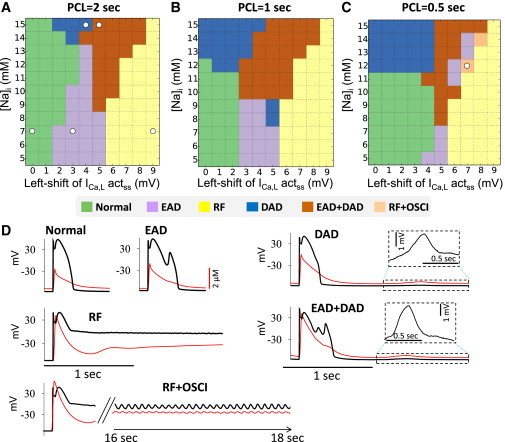
AP behaviors induced by shift in I_Ca,L steady-state activation curve and [Na]_i. (A–C) Phase diagrams showing different AP behaviors by changing [Na]_i and left-shifting the steady-state activation curve of I_Ca,L at PCL = 2 s (A), 1 s (B), and 0.5 s (C). (D) Example traces of voltage and Ca for different AP behaviors taken from the parameter settings marked in (A) (RF+OSCI was from C). RF, repolarization failure without oscillations; RF+OSCI, repolarization failure with oscillations. To induce EADs, the open probability of the LCCs was increased by increasing α_d′ from 0.3 to 1.5 ms⁻¹ from the normal control case. Except for repolarization failure, we used 20 pacing beats for each parameter set to determine the AP behaviors. To see this figure in color, go online.

The size of the regions exhibiting DADs or EADs varied with PCL. A faster heart rate (PCL = 0.5 s) expanded the DAD region, induced TA, and shrank the EAD region, whereas a slower heart rate (PCL = 2 s) had the converse effects. The results are consistent with experimental observations that EADs are often promoted by bradycardia, which reduces repolarization reserve, whereas DADs and TAs are often promoted by tachycardia, which exacerbates intracellular Ca loading. The combined EAD+DAD region was largest at the intermediate heart rate (PCL = 1 s). PCL had only minor effects on the normal AP and AP repolarization failure regions.

Modulation of EAD dynamics by Ca cycling

As shown in Fig. 1, A–C, when I_Ca,L activation was left-shifted to induce EADs, elevating [Na]_i promoted DADs but tended to suppress EADs, so that EADs were either replaced by DADs, or coexisted with DADs as [Na]_i increased. The suppression of EADs occurred because elevating [Na]_i enhanced outward I_NaK and inhibited inward I_NCX.

Because altered sarco/endoplasmic reticulum Ca ATPase (SERCA) activity and RyR leakiness are important features that impact Ca cycling in CPVT and heart failure, we also investigated the effects of these factors on EADs. At PCL = 2 s, doubling SERCA activity strongly promoted DADs but had only small and mixed effects on EADs, as can be seen by comparing the DAD and EAD regions in Fig. 2, A and B. Increasing RyR leakiness also strongly promoted DADs with only a small effect on suppressing EADs (compare Fig. 2, A and C). Combining both alterations enhanced these effects (Fig. 2 D). In this case, the amplitude of DADs also greatly increased, which caused DAD-mediated TA in both the pure DAD and mixed EAD+DAD regions. Because the TA occurred at a shorter cycle length than the PCL (Fig. 3 D), this also contributed to the suppression of EADs.

Figure 2.

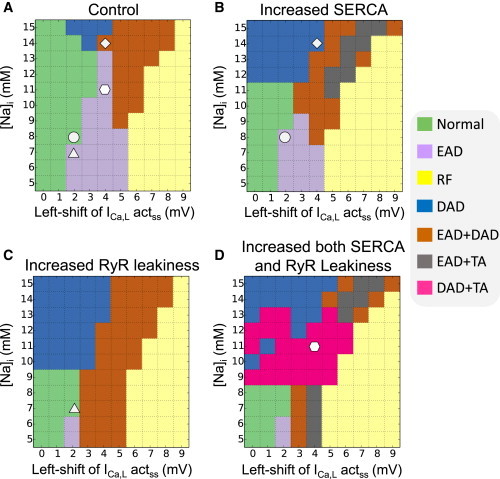
Phase diagrams showing modulation of EAD-DAD dynamics by Ca cycling properties at PCL 2 s. (A) Control (same as Fig. 1A). (B) SERCA activity doubled. (C) RyR leakiness was increased by setting the transition rate from close to open to be threefold of the control value. (D) Combined increased SERCA activity and RyR leakiness. (Marked symbols are the parameter sets for the traces shown in Fig. 3.) To see this figure in color, go online.

Figure 3.

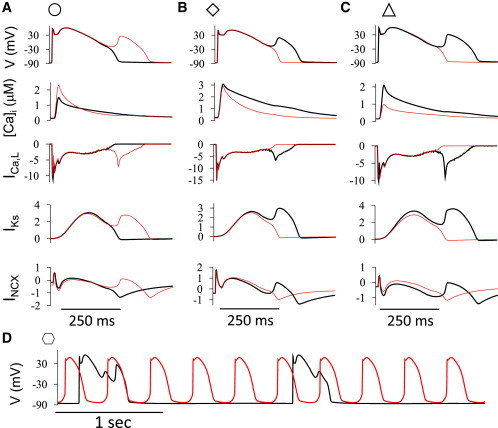
Comparison of APs and ionic currents before (black traces) and after (red traces) a change in Ca cycling. Indicating symbols for each case are parameter sets marked in Fig. 2. (A) Doubling SERCA activity with low [Na]_i (8 mM) promoted EADs. (B) Doubled SERCA activity with high [Na]_i (14 mM) suppressed EADs. (C) Increased RyR leakiness suppressed EADs. (D) Increased SERCA activity and RyR leakiness promoted DAD-driven TA and suppressed EADs. The unit of the currents is pA/pF. To see this figure in color, go online.

To illustrate the mechanisms by which SERCA activity and RyR leakiness affected EADs, representative AP and Ca-dependent ionic current traces are presented in Fig. 3. In Fig. 3 A, with [Na]_i = 8 mM, increasing SERCA activity promoted EADs. The peak of the Ca transient increased due to the greater SR Ca content, but the decay was accelerated due to more rapid SR Ca reuptake. These changes in the Ca transient caused: 1) a reduced peak I_Ca,L due to stronger Ca-dependent inactivation, but almost no difference during the plateau phase until the EAD occurred; 2) a small decrease in I_Ks in the late plateau phase due to the lower [Ca]_i (note that the K_d for Ca-dependent activation of I_Ks was set at 0.5 μM); and 3) increased I_NCX in the early phase but reduced I_NCX in the later phase of the plateau. The voltages were almost identical in the two cases until just before the EAD occurred, but the reduction in I_Ks predominated over the reduction in I_NCX to promote the EAD. The converse outcome is illustrated in Fig. 3 B when [Na]_i was raised to 14 mM. In this case, increasing SERCA did not increase the peak of the Ca transient, but still sped up its decay. This change had almost no effect on I_Ca,L but reduced both I_Ks and I_NCX. In this case, reduction in I_NCX predominated over the reduction of I_Ks, and the EAD was suppressed. Fig. 3 C illustrates an example in which increasing RyR leakiness suppressed EADs. In this case, the Ca transient was smaller, which had a small effect on peak I_Ca,L but reduced I_Ks and I_NCX. Similar to Fig. 3 B, the reduction of I_NCX predominated, suppressing the EAD. Finally, Fig. 3 D shows an example of the combined effects of increasing RyR leakiness and SERCA activity together. In this case, EADs were suppressed and sustained DAD-mediated TA occurred at cycle length < 0.5 s, shorter than the PCL of 2 s.

The results shown above demonstrate that the effects of Ca-voltage coupling are complex and nonintuitive, affecting multiple ionic currents in subtle ways to suppress or potentiate EADs and DADs. For example, in our model, increasing RyR leakiness suppressed EADs due to a smaller Ca transient. This finding generally agrees with previous experimental observations (25,26) that a larger Ca transient under Ca overload conditions tended to promote EADs via increased I_NCX. On the other hand, a recent study by Terentyev et al. (27) demonstrated that increased RyR leakiness caused a smaller Ca transient but nevertheless promoted EADs in long QT rabbit ventricular myocytes, illustrating the complexity of the interactions.

Spontaneous Ca oscillations and EADs

Spontaneous Ca oscillations associated with EADs have been observed in many experimental studies (10,11,13,28,29), and have been interpreted to be the cause of EADs when an intracellular Ca rise precedes the EAD upstroke (28). Supporting this conjecture, other experiments have shown that Ca oscillations associated with EADs can persist after voltage is clamped (13). However, the validity of these criteria for concluding that EADs can be caused by spontaneous Ca release events has not been quantitatively validated. In our computer simulations, we also observed these phenomena, as illustrated in Fig. 4 A. Following a long AP with multiple EADs, a subsequent DAD triggered a second AP (marked by an asterisk) with a single EAD (marked by arrow). Differing from other cases shown earlier (Figs. 1 and 3), the Ca transient during the EAD was much larger and started to rise (∼10 ms) before voltage. In particular, the Ca concentration in dyadic space (DS) ([Ca]_p) rose much earlier than the EAD upstroke (arrow in Fig. 4 B). The line scan of [Ca]_i was also dysynchronous, consistent with multiple spontaneous SR Ca release sites rather than a voltage-driven SR Ca release. These features agree with the above-mentioned experimental observations of spontaneous Ca release-induced EADs. To investigate the validity of this interpretation, we carried out additional simulations in which we either clamped voltage (Fig. 4 B) or clamped intracellular Ca (Fig. 4 C) at the EAD onset.

Figure 4.

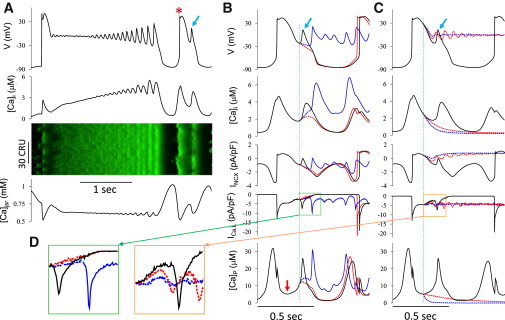
EADs elicited by spontaneous Ca release. (A) Voltage, [Ca]_i, [Ca]_jSR versus time, and line scan of [Ca]_i showing an EAD elicited by spontaneous Ca release (arrow) after an AP with multiple EADs. (Asterisk) AP triggered by a DAD. (B) Voltage, [Ca]_i, I_NCX, I_Ca,L, and Ca concentration in DS ([Ca]_p) versus time from the second AP in (A) (black trace). (Superimposed red and blue traces) Effects of voltage-clamping the model with a steeply (red) or slowly (blue) repolarizing voltage-clamp at the onset of the EAD (vertical dashed line). (Arrow in the [Ca]_p trace) Time of spontaneous rise of Ca, which occurred much earlier than the onset of the EAD. (C) Same as (B), but [Ca]_p was clamped with a slow (red) and a fast (blue) decay, and the clamp began when spontaneous [Ca]_p rise started (vertical dashed line). (D) Enlarged views of I_Ca,L from the clamping period (see boxes in B, left panel, and C, right panel). The parameters are the same as in Fig. 2B (SERCA activity doubled, [Na]_i = 15 mM and 7 mV left-shift in act_ss of I_Ca,L). Note: for Ca concentrations in this study, the line graphs are for whole-cell concentrations averaged over space while line scans show local concentrations in space. To see this figure in color, go online.

In the voltage-clamp case, voltage was clamped at the onset of the EAD period (marked by the vertical dashed line in Fig. 4 B) with a linear decay at different rates. When the voltage decay had a steeper slope (red trace), [Ca]_i still rose during the clamped period as in the free-running case, although not as rapidly. This indicates that the initial [Ca]_i rise was not triggered by the EAD, but was due to spontaneous (i.e., non-voltage-driven) Ca release. After the clamp was terminated, voltage repolarized to the resting potential, after which another spontaneous Ca release occurred several hundred milliseconds later, triggering a DAD-induced AP. In contrast, when the voltage decay had a shallower slope (blue trace), [Ca]_i rose faster than in the steeper case, and after the voltage-clamp was released, both voltage and [Ca]_i rose sharply due to reactivation of the LCCs (Fig. 4 D). Moreover, instead of repolarizing back to the resting potential, the voltage remained at the plateau level due to continuous opening of LCCs. Multiple EADs occurred with a frequency very different from that of the spontaneous Ca release. This is because after the first large release, most CRUs were refractory and could not respond to the first several EADs. Additional simulations at intermediate voltage decay slopes (not shown) defined a critical voltage at the end of the clamped period, below which no reactivation of LCCs occurred, and the cell repolarized to the resting potential. Above this value, reactivation of LCCs occurred, resulting in EADs. These findings indicate that the upstroke of the EAD requires the reactivation of LCCs and cannot be supported solely by I_NCX or other nonregenerative Ca-sensitive currents.

The consequences of clamping intracellular Ca, instead of voltage, during the EAD period are shown in Fig. 4 C. Because Ca concentrations varied at different locations in the cell, we clamped the Ca concentration in the DS at their existing values in all 19,305 CRUs, starting at the time when the mean Ca in the DS started to rise (marked by the vertical dashed line in Fig. 4 C). We then let Ca in the DS decay linearly at either a fast (blue traces) or slow (red traces) rate. In both cases, despite Ca in the DS being clamped, the voltage remained in the plateau range and oscillated with decrementing amplitude, eventually culminating in repolarization failure. It is interested to note that a faster Ca decay (blue trace) resulted in smaller EADs and a more stable plateau voltage. This is because when the clamp ended at a lower intracellular Ca, I_NCX was smaller but I_Ca,L became larger (see Fig. 4 D) due to less Ca-depended inactivation. This increased window I_Ca,L, resulting in EADs and repolarization failure after intracellular Ca was clamped. The converse effect occurred in the free-running case, in which the progressive rise in Ca in the DS caused more I_Ca,L inactivation, which suppressed the window I_Ca,L. This resulted in a lower take-off voltage for the EAD, which allowed a stronger voltage-dependent activation of LCCs to give rise to a larger depolarization. From this observation, we conclude although the amplitude of the EAD in the free-running case was potentiated by the increase in Ca preceding the EAD upstroke, the EAD was driven primarily by the LCC reactivation-mediated voltage oscillation, and not underlying Ca oscillations.

These voltage- and Ca-clamp simulations demonstrate the following important mechanistic points. 1) A spontaneous Ca release event preceding the upstroke of an EAD does not necessarily imply that the spontaneous Ca release event is the cause of the EAD; rather, it participates, together with LCC reactivation, in the initiation of the EAD upstroke. 2) The role of spontaneous Ca release is complex—it can suppress EAD amplitude by facilitating Ca-dependent inactivation of LCCs, or enhance EAD amplitude for the same reason depending on the voltage range and balance of other contributing factors.

Modulation of DAD dynamics by voltage

To study the effects of voltage on DADs, we first studied conditions producing a small DAD shown in Fig. 5 A. In an experimental study in canine hearts by Burashnikov and Antzelevitch (30), blocking I_Ks prolonged APD, which increased Ca loading sufficiently to induce DADs. Here, we also reduced I_Ks to study how APD affects DADs. As I_Ks was gradually reduced, APD was prolonged and EADs were induced (Fig. 5 B). The additional Ca loading by the EAD caused the DAD to occur earlier with a larger amplitude (Fig. 5 B). Fig. 5, C–F, plots DAD amplitude versus APD (C), DAD coupling interval versus APD (D), DAD amplitude versus SR load (E), and DAD amplitude versus the diastolic [Ca]_i preceding the DAD (F), respectively. The DAD amplitude increased almost linearly with APD in either the absence (circles) or the presence (triangles) of EADs. The DAD coupling interval deceased as APD increased. In the absence of EADs, the SR load increased with APD, which in turn increased DAD amplitude.

Figure 5.

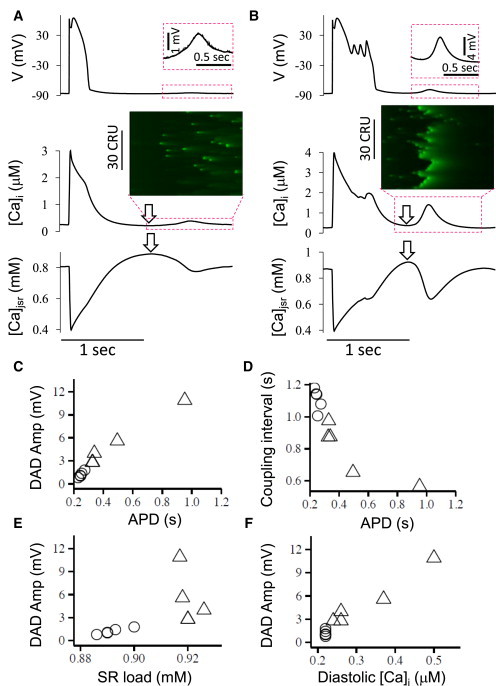
Modulation of DADs by APD. (A) Voltage, [Ca]_i, and [Ca]_jSR versus time showing a regular AP followed by a small DAD. (B) Same as (A) but for a long AP with EADs followed by large DAD. (Insets) Line scans of [Ca]_i during the DAD periods. (C–F) Plots of DAD amplitude versus APD (C), SR load (E), diastolic [Ca]_i (F), and coupling interval versus APD (D) for DADs after APs of varying duration without (circles) or with (triangles) EADs. The definitions of SR load and diastolic [Ca]_i (arrows) are indicated in (A) and (B). The coupling interval was defined as the interval from the end of the AP to the peak of the DAD. The parameters are the same as in Fig. 1A, but under Ca overload ([Ca]_o = 5 mM) with [Na]_i = 10 mM and 1 mV left-shift in act_ss of I_Ca,L. The control I_Ks was used in (B) but was increased by a factor of 1.6 to shorten APD in (A). To see this figure in color, go online.

Note, however, that diastolic [Ca]_i preceding the DAD did not increase significantly. In the presence of EADs, the SR load was near maximal and did not increase further as multiple EADs further prolonged APD. But despite the constant SR load, DAD amplitude continued to increase as APD was prolonged by EADs. The increase in DAD amplitude now tracked the progressive rise in diastolic [Ca]_i preceding the DAD. As shown in the line scans (insets), in the case without EADs, Ca elevation was caused by random CRU firings, while in the case with EADs, Ca elevation was caused by more coordinated CRU firings (due to CRU recruitment). These results indicate: 1) regardless of whether EADs are present, lengthening APD increases Ca loading that promotes DADs and shortens the coupling interval; and 2) two mechanisms of DADs exist: the first depends only on the SR load, and the second depends on both the SR load and the diastolic [Ca]_i level. Note that although APs with or without EADs were used to distinguish between the first and second behaviors in Fig. 5, EADs are not specifically required for the second DAD mechanism to occur. When EADs occur, however, the APD is much longer, enhancing Ca loading. Moreover, more LCCs open during EADs, which further enhances Ca load to potentiate the second mechanism.

Complex EAD dynamics in experiments

Some examples of complex EAD-DAD dynamics observed experimentally are illustrated in Fig. 6, obtained from mouse ventricular myocytes loaded with Fluo-4-AM to record [Ca]_i fluorescence. Myocytes were exposed to elevated [Ca]_o (2.7 mM) to induce Ca overload. Fig. 6 A shows simultaneous membrane voltage, [Ca]_i fluorescence, and a line scan of [Ca]_i during an electrically stimulated AP in a patch-clamped myocyte (current clamp mode). Early in the plateau phase of the AP, both [Ca]_i and voltage fluctuated with small amplitudes. Later, both [Ca]_i and voltage began to oscillate with increasing amplitude until full repolarization occurred. The line scan of [Ca]_i shows that Ca release exhibited random spatiotemporal dynamics in the early plateau phase, which then transitioned into synchronized oscillations in the late plateau phase.

Figure 6.

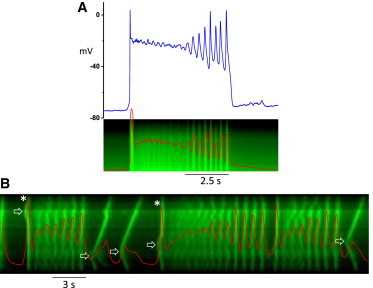
Complex EAD dynamics recorded from Fluo-4-AM-loaded mouse ventricular myocytes. (A) Voltage and [Ca]_i fluorescence versus time, and line scan of [Ca]_i measured from a patch-clamped mouse ventricular myocyte after a stimulus. (B) [Ca]_i versus time, and line scan of [Ca]_i recorded from a different isolated mouse ventricular myocyte that was not patch-clamped. No stimulus was given and the activity was spontaneous. (Red traces in the line scans) Integrated whole-cell Ca transients. (Open arrows) Initiation sites of the Ca waves that caused DADs or (asterisk) triggered APs. To see this figure in color, go online.

Similar complex behaviors were observed in Fluo-4-AM loaded myocytes that were deliberately not patch-clamped so as to leave the intracellular milieu minimally perturbed. Fig. 6 B shows [Ca]_i fluorescence and a line scan from such a myocyte, taken during a long recording in which all activity was spontaneous (see Fig. S6 for the entire recording). Although voltage was not directly recorded, AP upstrokes, DADs, EADs, and full repolarization can be generally inferred from the patterns of Ca release observed in the line scan, because voltage-gated Ca release is reflected by vertical lines and Ca waves by chevrons. In this tracing, a Ca wave in the upper portion of the line scan (arrow) initiated a triggered AP, in which multiple secondary Ca oscillations began immediately and grew in amplitude (reflecting EADs) before full repolarization. Repolarization was followed by two diastolic Ca waves (chevrons) that failed to trigger APs, after which a third Ca wave originating from the lower half of the line scan (arrow) triggered a second AP upstroke. Unlike the first AP, Ca oscillations during the second AP did not develop immediately, and the Ca release pattern was initially disordered, as evident from the line scan. The dysynchronous Ca release then gradually organized into synchronous oscillations with complex variations in amplitude. The largest release after the brief pause may reflect a late phase-3 EAD, because it did not appear to be triggered by a preceding Ca wave. After this event, the Ca oscillations became much smaller but quickly grew in amplitude, culminating in full repolarization, followed by a diastolic Ca wave (chevron) that failed to trigger an AP.

Several features are notable in both of these experimental recordings. When an AP was preceded by a relatively long diastolic interval (as in Fig. 6 A and the second AP in Fig. 6 B), the initial Ca transient during the AP upstroke was followed by dysynchronous Ca release with only small fluctuations in the plateau voltage and whole cell Ca. With time, however, these fluctuations self-organized into synchronous oscillations that subsequently grew progressively in amplitude, eventually culminating in full repolarization. In contrast, after a short diastolic interval (Fig. 6 B, first and third APs), the early phase of dysynchronous Ca releases did not occur, and synchronous Ca oscillations began immediately and grew rapidly, shortening the time to full repolarization. The features of the EADs generally agree with observations in previous experiments (e.g., long plateau, complex EAD pattern, and EAD-DAD interactions), as illustrated in Figs. S2 and S3.

Complex EAD dynamics in computer simulations

To analyze the mechanisms underlying complex EAD dynamics, we systematically scanned the parameters of the AP model with detailed Ca cycling to identify parameter regimes resembling the complex EAD (and DAD) dynamics, which were observed experimentally in the mouse myocytes in Fig. 6 and other species reported in the literature. Fig. 7 (also Fig. 4) illustrates a case similar to Fig. 6 A, in which the AP exhibited a very long plateau phase during which the voltage initially exhibited no or very small oscillations as the voltage slowly declined. This was followed by gradually increasing voltage oscillations generating progressively larger EADs culminating in full repolarization. This behavior has also been observed in many previously published experiments (examples are shown in Fig. S2) (31–37). In the model, [Ca]_i increased gradually during the plateau phase with no significant Ca oscillations until after voltage oscillations developed. Both I_NCX and I_Ks slowly increased in concert with [Ca]_i. I_Ca,L remained almost constant until EADs occurred. The relatively stable SR Ca content indicates that the increase in [Ca]_i resulted primarily from maintained Ca entry via I_Ca,L. As shown in the line scan, before the onset of frank EADs, Ca release exhibited a random spatiotemporal pattern—one that gradually became more synchronous as EADs developed. When the EADs reached a large enough amplitude, I_Ks activation became sufficient to induce full repolarization. A second paced AP was then elicited after a short diastolic interval. Similar to the second AP in Fig. 6 B, the long plateau disappeared and EADs and Ca oscillations began immediately as the voltage decayed into the LCC window voltage range.

Figure 7.

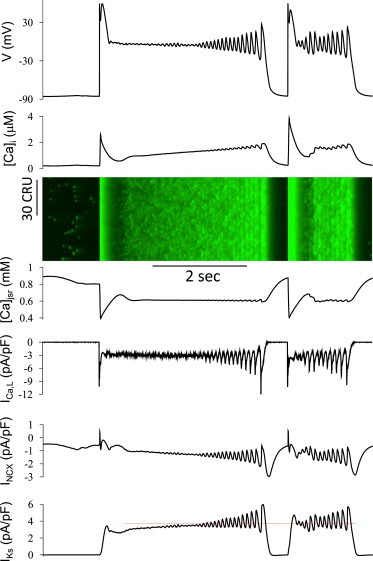
EAD onset after a long quasi-stable plateau phase. Shown are voltage, [Ca]_i, [Ca]_jSR, I_Ca,L, I_NCX, and I_Ks versus time, and a line scan of [Ca]_i. The parameters are the same as in Fig. 2A with [Na]_i = 7 mM and a 5-mV left-shift in act_ss of I_Ca,L. To see this figure in color, go online.

Because the experiments in Fig. 6 were done in mouse ventricular myocytes exposed to elevated extracellular [Ca], we also carried out computer simulations using a mouse ventricular myocyte model with the ionic currents from the model by Morotti et al. (38) (see the Supporting Materials and Methods). Similar complex EAD behaviors and spontaneous APs were obtained (see Fig. S6), indicating that the behaviors are not model-specific.

EADs and Ca oscillations with alternating or more complex patterns are shown in Fig. 8. In this example, both the take-off potential and amplitude of the EADs exhibited a period-3-like pattern most of the time. Moreover, switching between EADs and DAD-mediated-triggered APs (asterisks in Fig. 8) occurred. These behaviors are similar to Fig. 6 as well as previous experiments (sample voltage traces are shown in Fig. S3) (3,31,37). Note that in Fig. 8, the first AP was elicited by a stimulus and the following three APs were triggered by DADs. As shown in Fig. 5, lengthening of APD by EADs causes excessive Ca loading of the cell, promoting spontaneous Ca release after full repolarization, resulting in DADs. Thus, the long APs with many EADs enhanced Ca overload and thus promoted DADs, illustrating a case of complex EAD and DAD interactions. The underlying mechanisms are addressed in the Discussion.

Figure 8.

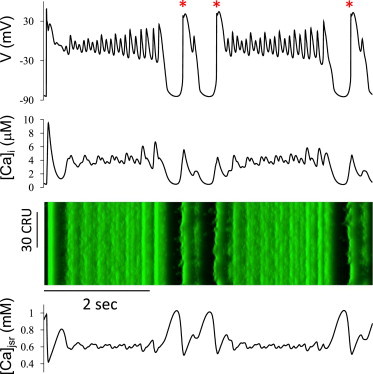
Complex EAD dynamics due to bidirectional voltage-Ca coupling. Voltage, [Ca]_i, and [Ca]_jSR versus time, and a line scan of [Ca]_i. The parameters are the same as in Fig. 2B (SERCA activity doubled with [Na]_i = 14 mM and a 7 mV left-shift in act_ss of I_Ca,L). (Asterisks) Spontaneous Ca-release-induced APs. To see this figure in color, go online.

Discussion

EADs and DADs were first described more than a half century ago (39,40), and many EAD and DAD behaviors, from simple to very complex, have been observed in experiments. However, due to the complex interactions between voltage and Ca, it has been difficult to pinpoint experimentally the exact underlying mechanisms for different behaviors. Computer modeling and simulations are a complementary means to reveal the underlying ionic mechanisms. Many computer modeling studies (41–46) have been carried out to investigate the mechanisms of EADs, but for the most part these have focused on EADs caused by voltage-driven oscillations, because the AP models lacked detailed spatiotemporal Ca cycling required to simulate Ca waves and oscillations. In this study, we investigated the effects of bidirectional Ca-voltage coupling on the genesis of EADs and DADs in ventricular myocytes, using an AP model with a detailed spatiotemporal Ca cycling regulation incorporating stochastic LCC and RyR openings and experiments of mouse ventricular myocytes. Mechanistic insights we consider novel have been revealed, and these are discussed below.

Modulations of EADs by Ca cycling dynamics

It is well known that LCC window current is a key component for EADs (17–21), but all other currents during the plateau also contribute to the formation of the EADs (21,41). Using bifurcation analysis (21,44), we have previously identified the bifurcations that initiate and terminate the voltage oscillations, and characterized the contribution of each ionic current in generating these bifurcations. The Ca transient modulates EAD dynamics via its effects on multiple Ca-dependent ionic currents. Because the [Ca]_i dependences of these inward and outward currents are different, the net effect of changing [Ca]_i on the bifurcations and the time course of voltage oscillations is complex and often nonintuitive. Changing [Ca]_i can either promote or suppress EADs, depending on the balance of factors under a given set of conditions (Figs. 2 and 3).

Spontaneous Ca oscillations have been proposed to cause EADs in a number of experimental studies (10,11,13,28,29), primarily based on evidence such as a rise in [Ca]_i preceding the EAD upstroke (28), or continuation of spontaneous Ca oscillations when voltage oscillations were prevented by imposing an AP clamp (13). A fresh mechanistic insight arising from our analysis is that the interpretation of these experimental findings may be overly simplistic. Intuitively, because voltage and Ca are coupled, if Ca oscillates in the repolarizing phase of the AP, voltage will also oscillate. However, based on our present simulations (Fig. 4), the role of spontaneous Ca oscillations as a pure mechanism for generating EADs is far from straightforward. First, I_NCX is not a regenerative current like I_Ca,L. That is, as voltage depolarizes during the EAD upstroke, I_NCX becomes weaker, not stronger. Because I_NCX is small and decreases as voltage rises, reactivation of I_Ca,L is required for EADs to become large enough to generate TA and propagate in tissue. Thus, a spontaneous Ca release event can potentially initiate an EAD upstroke by activating I_NCX, but cannot generate significant EAD amplitude or TA without the participation of I_Ca,L reactivation. This situation is further complicated by the interactions between intracellular Ca and I_Ca,L inactivation, which inevitably affect the I_Ca,L window current, the key driver for voltage-dependent EADs. As shown in Fig. 4, high intracellular Ca due to spontaneous Ca release just preceding the EAD strongly enhanced Ca-dependent inactivation of I_Ca,L, which offset its effect at increasing I_NCX. The consequence was a lower take-off potential of the EAD, which then resulted in a large-amplitude EAD due to greater I_Ca,L reactivation. However, additional EADs were suppressed due to a stronger Ca-induced inactivation of I_Ca,L. This scenario may be relevant to isoproterenol-induced EADs, which typically exhibit only one EAD in each AP, with two or more EADs per AP being rare (10,11,13). In summary, the modeling results show that the effect of spontaneous Ca release events on EAD genesis is extremely complex, and intuitive interpretations, like assuming that the timing of the intracellular Ca rise relative to the EAD upstroke implies causality, are overly simplistic.

Mechanisms of DADs

It is widely accepted that DADs are mediated by Ca waves (47–50), in which spontaneous SR Ca release from a group of adjacent CRUs recruits neighboring CRUs to initiate a propagating wave (51,52). On the other hand, the simulations in Fig. 5 A demonstrate, to our knowledge, a novel mechanism of small DADs with long coupling intervals in the absence of Ca waves, purely by synchronous resetting of the recovery period of CRUs by an AP, without recruitment. In this case, after an AP with normal Ca release, the SR Ca rose to a level higher than its equilibrium load. This occurred because the SERCA pump is fast relative to NCX, causing the SR to refill to a higher level. After the CRUs had recovered from the preceding normal AP, spontaneous CRU firings occurred due to high SR Ca load, which summed to produce a small whole-cell [Ca]_i increase eliciting a small DAD. As seen in the line scans in Fig. 5 A, the release events were random individual CRU firings that did not propagate to neighboring CRUs. In contrast, in Fig. 5 B, the EADs during the AP greatly enhanced the cellular Ca load, elevating diastolic [Ca]_i. In this case, when CRUs fired during the subsequent diastole, they propagated as mini-waves, facilitated by both the high SR Ca content and the elevated diastolic [Ca]_i level. Therefore, in the non-Ca-wave-mediated mechanism of DADs in Fig. 5 A, the high SR Ca load due to fast SERCA pump activity after an AP synchronizes the subsequent diastolic spontaneous Ca release by independently firing CRUs. However, diastolic [Ca]_i is not sufficiently elevated for these Ca sparks to trigger propagating Ca waves. For this reason, only a single DAD occurs after the AP. On the other hand, in the Ca-wave-mediated mechanism, diastolic [Ca]_i as well as SR Ca load both become important by facilitating CRU recruitment to form Ca waves, and multiple DADs can be seen after an AP. Finally, although not addressed in this study, DAD amplitude is determined not only by the synchronicity of spontaneous Ca release, but also by the Ca-voltage coupling gain (53,54), i.e., the amplitude of the Ca-sensitive currents such as I_NCX and I_ns(Ca) activated by the spontaneous Ca transient in relation to the outward currents opposing depolarization, principally I_K1 in ventricular tissue.

Mechanisms of complex EAD patterns

As shown in Figs. 6, 7, 8, and S1–S3, EADs can exhibit very complex patterns and behaviors. From this study and the nonlinear dynamics analysis (21,44), we can provide a unified theory for these complex EAD patterns based on the interactions of Ca dynamics with the Hopf-homoclinic bifurcation mechanism of voltage-driven EADs. Fig. 9 shows a schematic diagram illustrating the bifurcations leading to and terminating EADs. By 100–200 ms after the AP upstroke, most currents have reached quasi-steady states except for slow currents, including slowly activating I_Ks, slowly inactivating late I_Na, slow accumulation of [Na]_i causing slowly changing I_NaK, etc. The inward currents and the outward currents are roughly equal during the AP plateau, forming a quasi-equilibrium state. As time continues, slowly increasing outward currents progressively activate, destabilizing the quasi-equilibrium state and initiating oscillations via a Hopf bifurcation. As the net outward current at the trough of the EADs becomes progressively larger during the voltage oscillations, the system approaches another bifurcation point, called a homoclinic bifurcation, at which the oscillation terminates because the inward current is no longer strong enough to prevent the voltage from repolarizing, leading to full repolarization in the resting potential. Depending on the stability of the quasi-equilibrium state, the decay rate of voltage, and the activation speed of the slowly increasing net outward current, as well as Ca-voltage coupling, different EAD patterns can occur. Based on the bifurcation theory and results in previous simulations (21,44,55–57) and the observations in this study, we summarize below the mechanisms underlying six characteristic patterns of EAD behaviors:

Figure 9.

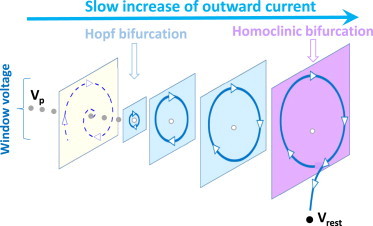
Schematic diagrams for the mechanisms of EADs. Schematic diagram showing the bifurcations for EADs. The value V_p is the quasi-equilibrium steady-state voltage in the plateau, and V_rest is the resting potential. To see this figure in color, go online.

EADs with growing amplitude

This is the most widely seen EAD pattern in experiments (Fig. S1 A) and computer simulations. As shown in Fig. 9, after the Hopf bifurcation point, the oscillation amplitude grows as the slowly increasing outward current makes the trough of the EAD more and more negative, reaching a maximum at the homoclinic bifurcation point. If voltage decays into the window voltage range at roughly the same time as the slowly increasing outward current increases to the level sufficient to initiate the Hopf bifurcation, then the EAD amplitude will grow from very small oscillations to the maximum oscillation at the homoclinic bifurcation point before full repolarization.

EADs with decreasing amplitude (Fig. S1 B)

Although the quasi-equilibrium state is stable before the Hopf bifurcation point, the voltage entering into the window range may spiral toward the quasi-equilibrium (see the spiral curve in Fig. 9), resulting in a transiently decreasing oscillation amplitude. If the Hopf-homoclinic bifurcation does not exist, then the oscillation gradually dampens out until repolarization to the resting potential occurs, resulting in EADs with decreasing amplitude. This scenario was analyzed in detail using bifurcation theory by Xie et al. (56).

EADs with decreasing and then increasing amplitude (Fig. S2 A)

If voltage decays into the window range earlier than the Hopf bifurcation, then the voltage may oscillate transiently with decreasing amplitude (see the spiral curve in Fig. 9). As the slowly increasing outward current increases to the critical value initiating the Hopf bifurcation, oscillation resumes with a growing amplitude, reaching its maximum at the homoclinic bifurcation point.

EADs after a long plateau (Figs. 6, 7, and S2, A and B)

If voltage decays to the plateau level much earlier than the Hopf bifurcation, it will remain at the plateau voltage until the slow outward current increases sufficiently to induce the Hopf bifurcation for oscillations. Therefore, the duration of the plateau depends on the speed of the slowly growing outward current (or slowly decreasing inward current). In the simulation in Fig. 7 using our AP model based on rabbit ventricle, I_Ks is the slowly increasing current, such that the onset of oscillations is very sensitive to I_Ks (Fig. 7): the plateau is shorter when I_Ks starts at a larger value (referenced by the dashed horizontal line in the I_Ks trace in Fig. 7), e.g., after a short diastolic interval.

A key question is why the intracellular Ca, despite being quite high, does not oscillate during the long plateau phase until EADs are present. To reveal the underlying mechanisms, we did a series of simulations under different voltage-clamp conditions (see Figs. S7 and S8 and description). We showed that random LCC openings trigger spatiotemporally random CRU firings, which prevent the CRUs from recovering synchronously as required for spontaneous Ca oscillations. After the Hopf bifurcation, however, the voltage oscillations cause LCC openings to synchronize, which synchronizes the CRU openings, so that voltage and Ca oscillate together.

Although I_Ks played the major role as the slowly increasing outward current in our AP model based on rabbit ventricle, other slowly changing currents can also play the equivalent role, and may be more important in other species. For example, [Na]_i accumulates very slowly, causing a very slow increase in I_NaK, which can also initiate the Hopf-homoclinic bifurcation, as shown in our previous simulations (57). Late I_Na is another candidate because it may slowly inactivate (58). Finally, the gradual rise in [Ca]_i may also activate other outward currents, such as the Ca-activated Cl current (I_Cl(Ca)) (59) or small conductance Ca-activated K current (60). Because I_Ks has a very low density in mouse ventricular myocytes, one or more of these currents may be responsible for the slow process that is causing the long plateau shown in the experimental recordings in Fig. 6.

EAD bursts (Fig. S2 C)

If voltage quickly decays into window voltage for oscillations and then outward current increases very slowly through the Hopf-homoclinic bifurcation window, a very long EAD burst can result. As demonstrated in our previous simulations (57), the slow accumulation of [Na]_i causing a very slow increase of I_NaK can be a candidate for finally terminating the long-lasting EAD burst.

EAD alternans and more complex EAD patterns (Figs. 6, 8, and S3)

To our knowledge, a key novel finding of this study is that the Hopf-Homoclinic bifurcation dynamics alone do not explain alternating and more complex EAD patterns. As shown by the simulations in Figs. S7 and S8, EAD alternans arises as a result of Ca-voltage coupling when voltage oscillations during EADs encounter CRU refractoriness, generating Ca transient alternans or more complex patterns. The Ca transient behaviors then feed-back to affect the amplitude of the EADs via Ca-sensitive currents, or via frequency competition of voltage oscillation and spontaneous Ca oscillations. Therefore, EAD alternans and more complex EAD patterns directly result from bidirectional Ca-voltage coupling.

Limitations

Several limitations should be noted. The AP and spatiotemporal Ca cycling model in this study simulates a three-dimensional network of CRUs representing a ventricular myocyte, but it is still much simpler than a real myocyte (61,62). Heterogeneous ion channel densities and CRU properties may potentially introduce novel dynamics not captured in a homogeneous model. However, the homogeneous model appears to capture most of the experimentally observed behaviors, and in addition provides a key framework for future exploration of the role of heterogeneity. The RyR model developed by Restrepo et al. (14) incorporated calsequestrin-mediated SR luminal Ca regulation, whereas recent experiments have demonstrated a luminal Ca-sensing site in the RyR mediating this effect (63). Moreover, the refractoriness of Ca release is controversial, with a wide range of experimentally measured values (64–69) and different proposed causes. Different refractory period choices may impact the Ca cycling dynamics, as well as the voltage dynamics caused by Ca-voltage coupling. In our model, the effects of Ca on EADs are mediated through direct effects on ionic currents. It is well known that Ca-dependent signaling pathways, such as CaMKII signaling, can affect many ionic currents as well as Ca cycling properties (70), which can have much more complex effects on EADs and DADs. Our AP model does not include some of the Ca-dependent ionic currents, such as I_ns(Ca) (71,72) and the small conductance Ca-activated K channel (60), which may play important roles in bidirectional Ca-voltage coupling and Ca-dependent EAD genesis. In addition, we have clamped [Na]_i in this study. It has been shown that elevation of [Ca]_i causing activation of CaMKII enhances late I_Na, which further elevates [Na]_i, causing further elevation of [Ca]_i (38). Therefore, a dynamic [Na]_i may have additional effects on EADs and DADs.

Another limitation is that the specific ionic mechanisms of EADs may vary among different species. For example, in the rabbit model, slow activation of I_Ks plays a key role in the EAD dynamics, whereas I_Ks is a very small current in mouse ventricular myocytes. As discussed earlier, however, I_Ks is not the only slow component that can play this role in the dynamics. Other candidates include slow Na accumulation activating outward I_NaK, the progressive Ca accumulation activating I_Cl(Ca), and/or slow inactivation of late I_Na, all of which can in principle replace the role of I_Ks in initiating and terminating EADs via the Hopf-homoclinic bifurcation scenario. In the mouse ventricular cell model in which I_Ks is insignificant, the slow inactivation of late I_Na substitutes for the role of I_Ks in the rabbit ventricular cell model (see Supporting Materials and Methods and Fig. S6). Because the complex EAD behaviors have been widely observed in many different types of cardiac cells and species exposed to varying pathophysiological stresses (e.g., Figs. 6 and S1–S3), we believe that different species and cell types share a common general dynamical mechanism, i.e., the Hopf-homoclinic bifurcation scenario depicted in Fig. 9. Our study focused mainly on phase-2 EADs and DADs, and did not address phase-3 EADs, which may involve additional or different mechanisms.

Finally, although our simulation results of complex EAD behaviors agree well with our own experimental observations and those from the literature, some of the theoretical predictions of our study need to be validated by future experiments. These would include the complex effects of the amplitude and morphology of Ca transient on modulating EADs, the effects of spontaneous Ca release on generating and suppressing EADs, and the non-Ca-wave-mediated DADs.

Author Contributions

Z.Q. designed the overall research and supervised the simulations; Z.S. contributed to the overall research design and performed the simulations; J.N.W. contributed to the overall research design and supervised the biological experiments; C.Y.K. contributed to the overall research design and performed the biological experiments; M.N. contributed to the overall design; Z.S., C.Y.K., J.N.W., and Z.Q. analyzed data; and Z.S., C.Y.K., J.N.W., and Z.Q. wrote the article.