Abstract
In this study, we evaluated the hypothesis that the constituent fibers follow an affine deformation kinematic model for planar collagenous tissues. Results from two experimental datasets were utilized, taken at two scales (nanometer and micrometer), using mitral valve anterior leaflet (MVAL) tissues as the representative tissue. We simulated MVAL collagen fiber network as an ensemble of undulated fibers under a generalized two-dimensional deformation state, by representing the collagen fibrils based on a planar sinusoidally shaped geometric model. The proposed approach accounted for collagen fibril amplitude, crimp period, and rotation with applied macroscopic tissue-level deformation. When compared to the small angle x-ray scattering measurements, the model fit the data well, with an r2 = 0.976. This important finding suggests that, at the homogenized tissue-level scale of ∼1 mm, the collagen fiber network in the MVAL deforms according to an affine kinematics model. Moreover, with respect to understanding its function, affine kinematics suggests that the constituent fibers are largely noninteracting and deform in accordance with the bulk tissue. It also suggests that the collagen fibrils are tightly bounded and deform as a single fiber-level unit. This greatly simplifies the modeling efforts at the tissue and organ levels, because affine kinematics allows a straightforward connection between the macroscopic and local fiber strains. It also suggests that the collagen and elastin fiber networks act independently of each other, with the collagen and elastin forming long fiber networks that allow for free rotations. Such freedom of rotation can greatly facilitate the observed high degree of mechanical anisotropy in the MVAL and other heart valves, which is essential to heart valve function. These apparently novel findings support modeling efforts directed toward improving our fundamental understanding of tissue biomechanics in healthy and diseased conditions.
Introduction
The mitral valve (MV) is one of the four heart valves. It is located in between the left atrium and the left ventricle, and it regulates the unidirectional blood flow and normal functioning of the heart during cardiac cycles. During systole of the cardiac cycle, the MV leaflets close to prevent blood backflow from the left ventricle, accompanied by shrinkage of the MV annulus, ventricular contraction of the papillary muscles, and tightening of the MV chordae tendineae. As in many physiological systems, mechanical stimuli occur and have biological impacts at the organ, tissue, and cellular levels. It is thus axiomatic that a complete understanding of the MV function in healthy and diseased conditions must be built on the biomechanics of the constituent tissues and cellular populations.
Structurally, MV leaflet tissues are composed of four layers: the atrialis (A) layer facing the atrium, the ventricularis (V) layer on the ventricular side, and the inner spongiosa (S) and fibrosa (F) layers. The fibrosa is the thickest layer, consisting mainly of a dense network of type I collagen fibers, and is the primary load-bearing layer. The ventricularis and atrialis layers are composed of a dense network of collagen fibers and radially aligned elastin fibers, which provide sufficient resistance to large radial strains when the MV is fully open. The spongiosa layer contains a high concentration of hydrated glycosaminoglycans and proteoglycans as the lubricant of shear deformation between the fibrosa and ventricularis layers. Each of these four layers has its distinct microstructure and mechanical properties, leading to the highly nonlinear and anisotropic tissue-level mechanical behaviors of the mitral valve.
MV leaflets can be classified as a subclass of planar soft connective tissues composed of collagen, elastin, and muscle fibers, which include such structures as skin, vasculature, and membranes (e.g. pericardium). The mechanics of planar tissues is complex, involving both the straightening of highly crimped collagen fibers and the rotation of all fibers toward the stretch axis (1). An understanding of how these structures work together to produce tissue-level responses remains an active research area. One group of approaches is to develop constitutive models based on tissue structural features. Such modeling approaches attempt to link tissue-level deformation at the macroscopic scale to the microscopic (fiber) scale, and they can be deemed statistical multiscale approaches (2). The idea of taking tissue structure into mechanical models of soft tissues goes back to the work on leather mechanics by Mitton (3) in 1945. In part of the first available planar biaxial data for soft tissues, Lanir (4) developed the first comprehensive formulation of a multidimensional structural constitutive model. More recent studies have directly incorporated measures such as fiber crimp and orientation (5–8). Structural constitutive modeling approaches have been extended to computational simulations of soft tissue function (9–13).
A critical aspect of understanding the underlying structure-function relation in soft tissues is to clarify how the constituent fibers rotate and stretch as the tissue is loaded. Existing structural constitutive models typically assume that the local deformation of the fibers follows the macroscopic tissue deformation—the so-called “affine” deformation assumption. An attractive feature of this simplifying approach is the easy computation of the local fiber stretch from the tissue-level deformation gradient tensor. However, this intrinsically assumes that the local deformation is homogenous and we can potentially ignore more complex local interactions as well as microscopic kinematics. The first study known to the authors that explored this assumption was performed on pericardium and aortic valve leaflet tissues (14,15). In these studies, it was observed that the predicted responses were not in good agreement with the experimental results under strip biaxial stretch. Recently, a correction to the original data analysis was performed, which suggested that affine kinematics for collagenous tissues is a reasonable assumption at the macro level (9).
Other studies of the affine behavior in soft tissues using various loading scenarios, such as tension and compression (16–18), have revealed mixed findings. For example, Huyghe and Jongeneelen (18) reported the three-dimensional finite strain of extracellular matrix samples of bovine annulus fibrous tissue under physiological osmotic prestress. The results indicate that the changes in external prestress induce strongly nonaffine deformation of the tissue, and that the macroscopic strains were generally not a good evaluation of microscopic strains around clefts and cells. Yet, the results were based on a small sample number and the authors stated that no definite conclusions could be drawn. A study of the inhomogeneous, anisotropic, and nonlinear properties of human supraspinatus tendon by Cortes et al. (16) suggested that affine deformation is more evident for tendon regions of higher alignment, and that nonaffine fiber behavior is dependent on specific tissue. Hepworth et al. (19) studied the through-thickness reorientation of collagen fibers in skin for testing a simple geometrical affine deformation model. While the measured reorientation of collagen fibers was found to be quite variable, the average reorientation was consistent with the predictions by the affine deformation model, and the systematic deviation of the model predictions from the measurements can be explained by a nonaffine relationship between the collagen fibers and the ground substance at the microscopic scale. Collectively, these studies suggest that the deformation of fibrous proteins under applied loading is still not completely understood.
A well-known technique to study collagen fibril structure and deformation under loading is small angle x-ray scattering (SAXS), which has been applied to soft collagenous tissues under uniaxial stretch (20–24). To our knowledge, we have carried out the first study of the kinematics of collagen fibrils under controlled biaxial stretch (25). As expected, the collagen fibril kinematics under biaxial stretch was found to be more complex than that under uniaxial deformation. Moreover, the magnitude of the D-period strain of the collagen fibrils was observed to be substantially less than that of the tissue strain and with a delayed onset, while the alignment and orientation of the collagen fibrils undergoes substantial changes in response to the applied biaxial loading (26). We have also utilized this approach in conjunction with simultaneous force measurements to study kinematics and mechanical properties of collagen fibrils in the MV anterior leaflet (MVAL) tissues (27). In that study, collagen fibril straining did not initiate until the end of the nonlinear region of the tissue-level stress-strain curve under equibiaxial tension. At higher tissue tension levels, the collagen D-spacing strain increased linearly with increasing tension, with changes in the orientation distribution of the collagen fibrils mainly having occurred in the tissue toe region. The tangent modulus of collagen fibers was estimated to be 95.5 ± 25.5 MPa, which was ∼27 times higher than the tissue tensile tangent modulus of 3.58 ± 1.83 MPa. The relation to time-dependent properties was also investigated, suggesting that the collagen fibrils in the MVAL tissue do not exhibit intrinsic viscoelastic behavior.
In this study, we utilized this unique dataset to evaluate the key assumption of the structural models for planar tissues—that the constituent fiber deformations follow an affine deformation kinematic model. It should be noted that the SAXS measurements are restricted to collagen fibrils only, and are not affected by the presence of the elastin fibers and other tissue components. Thus, believed-novel optical-level studies using MVAL tissues under similar controlled biaxial stretch conditions were conducted additionally to explore simultaneous collagen and elastin fiber-level kinematics and to clarify the role of the measurement scale. We then developed a geometric model, based on affine kinematics for straight and planar sinusoidally shaped fibers, to simulate the changes in the fibril and fiber orientation distribution functions with applied deformations. The proposed approach accounted for collagen fibril amplitude, crimp period, and rotation in response to applied macroscopic deformation, and was used to evaluate the assumption of an affine kinematics model.
Materials and Methods
Experimental
Synchrotron small angle x-ray scattering measurements—collagen fibril kinematics
Details of the experimental techniques and system have been previously presented in Liao et al. (27). Briefly, a device was developed and utilized to perform simultaneous measurements of tissue-level forces and deformations under planar biaxial loading. Fresh porcine MVs were acquired from a local USDA-approved abattoir. MVALs were cut into 15 × 15 mm squared specimens (n = 5) with sides parallel to the circumferential and radial directions of the leaflet, and the specimen was immersed in PBS (phosphate-buffered saline) at room temperature for the SAXS measurements. From the measured forces and initial specimen dimensions, Lagrangian membrane tension T (in N/m) was computed. Collagen fibrillar orientation distributions were measured under an equibiaxial tension path to a peak tension of 98 N/m.
Optical and histological measurements
Fresh ovine hearts were acquired from 40-kg sheep at a local abattoir, and a 10 × 10 mm sample was taken from the anterior leaflet just below the annulus to just above the first chordae tendineae attachment site (Fig. 1 A). The overall approach and methods were utilized in our previous work on the native pulmonary artery (28). In brief, samples were loaded into a miniature biaxial testing system in conjunction with a model No. FV1000 multiphoton microscopy (MPM) imaging device (Olympus, Center Valley, PA) for measurements of both tissue-level deformations and the microstructure of collagen and elastin fiber networks. Here, the specimen’s circumferential and radial directions were aligned with the device axes and submerged in a bath of PBS at room temperature. Four graphite fiducial markers were placed in the center region of the specimen and their positions were tracked optically with a Sony XCD-SX910 camera (Sony, Tokyo, Japan) for computation of the macroscopic tissue-level deformation gradient tensor F (29,30). The MVAL tissue specimens were then divided into the following two groups (Fig. 1 B): 1) real-time deformation and en face imaging, and 2) fixation and subsequent imaging.
Figure 1.
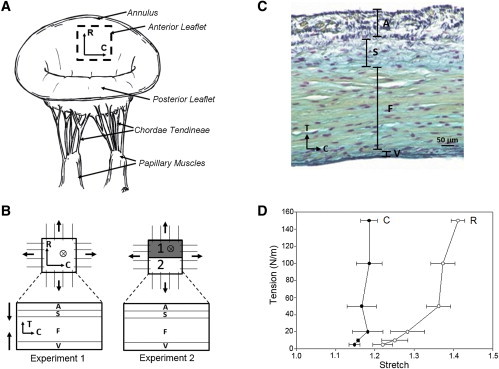
(A) An illustrative diagram of the native mitral valve, showing key anatomical components and the central belly region. (B) Schematic of the experimental setup: two samples were loaded at seven tension levels (0, 5, 10, 20, 50, 100, and 150 N/m) and imaged with two-photon microscopy (TPM) in real time for visualizing the collagen and elastin fiber networks in four different layers in the first experiment; three samples were loaded and fixed for 2 h in 2% PFA. Half of each sample was scanned with SALS and the other half of sample was imaged with TPM. (C) Stained histologic image showing four-layered structure of the MV leaflet tissue (black, elastin fibers; blue, proteoglycans and glycosaminoglycans; yellow, collagen fibers; and magenta, MV interstitial cells). (D) Typical tension-stretch profile of the anisotropic mechanic behavior of the MVAL tissue under equibiaxial loading. (Legend: A, atrialis; S, spongiosa, F, fibrosa; V, ventricularis; C, circumferential direction; R, radial direction; T, transmural direction.) To see this figure in color, go online.
Experiment 1: multiphoton imaging and analysis of fiber kinematics. The first experimental group was facilitated to quantitatively characterize collagen and elastin fiber networks as a function of controlled physiological loading. The MPM imaging was performed with a field of view of 500 μm and an excitation wavelength of 800 nm at a 7% laser intensity transmissivity via two-photon exited fluorescence: one channel was set at 400 ± 100 nm for second-harmonic generation (SHG) signal of collagen fiber network and the other one was set at 525 ± 50 nm for elastin autofluorescence (31). The sampling speed was set at 2 μs/pixel with a Kalman filter and at an incremental z-step of 2 μm. The sample was first imaged en face to a maximum penetration depth of 100 μm from the atrialis surface, and then the process was repeated from the ventricularis surface. En face imaging from the atrialis and ventricularis surfaces encompassed the spongiosa and fibrosa layers, respectively (Fig. 1 C). Each MVAL tissue specimen was loaded under equibiaxial tension up to a peak tension of 150 N/m (32), which corresponds to the in vivo transvalvular pressure during systole, and macroscopic deformation and MPM images of the collagen fiber network in the atrialis and fibrosa layers and the elastin fiber network in the atrialis and ventricularis layers (n = 2) were acquired for the following analysis.
Image stacks were compiled into a maximum intensity z-projection (Fig. 2, A and B) using an in-house MATLAB program (The MathWorks, Natick, MA). The superimposed image stack was first separated into the collagen and elastin contents based on color channels. An algorithm developed by Chaudhuri et al. (33), Karlon et al. (34), and Courtney et al. (35) was used to obtain the pixel intensity gradient for determination of the preferred fiber direction for each subregion (Fig. 2 C). The analyzed preferred fiber direction was then placed into a histogram to quantify the fiber orientation distribution function (ODF) of the layer-specific collagen and elastin fiber networks.
Figure 2.
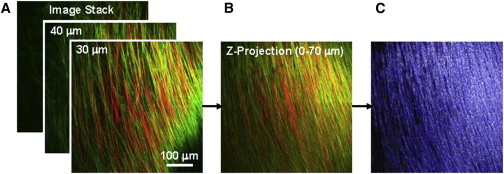
Image analysis of the fiber networks: (A) image stack from TPM visualizing collagen (red) and elastin (green) fibers from SHG and autofluorescence, respectively; (B) image stack compiled into a single image via maximum intensity z projection; and (C) Karlon’s algorithm applied to track both collagen and elastin fibers based on color-separated images. To see this figure in color, go online.
Experiment 2: SALS technique for fiber straightening and alignment. The second experimental group was designed to quantitatively determine the collagen fiber straightening and alignment under controlled physiological loading. MVAL tissue samples (n = 3) were loaded and fixed at 0 and 150 N/m. Each tissue specimen was fixed for 2 h in 2% PFA (paraformaldehyde) in the loaded configuration, and each sample was split into two sections (Fig. 1 B). The first section was used to measure the extracellular matrix fiber alignment over the entire area of the specimen using the SALS technique (36). Briefly, the specimen was glycerol-dehydrated in graded solutions of glycerol and saline for 1 h. The fiber ODFs were recorded and then fitted by a dual Gaussian distribution function. The resultant preferred fiber direction as well as the fiber splay was determined from the fitted local minimum. The second section was paraffin-embedded and cryosectioned on the circumferential-transmural plane. The sample slides were deparaffinized and permeabilized with Triton-X for 20 min. Each sample slide was then taken for MPM imaging at an excitation wavelength of 830 nm with an incremental z-step of 1 μm. Representative slices of the image stack were imported into the software IMAGEJ (National Institutes of Health, Bethesda, MD) for the analysis of collagen fiber structure. Percent observable collagen fiber crimp was determined with a threshold function for the fibrosa layer. Fiber crimp was characterized by manually measuring 10 different crimp periods per sample.
Simulations
Affine fiber kinematic model for sinusoidally shaped fiber populations
A deformation is affine if it can be composed of a linear transformation and a rigid body translation. In geometry, an affine transformation, affine map, or an affinity (from the Latin, affinis, which means “connected with”) is a function between affine spaces that preserves points, straight lines, and planes. An affine transformation does not necessarily preserve angles between lines or distances between points, although it does preserve ratios of distances between points lying on a straight line. Affine deformations, also called homogeneous deformations, have the general form of
| (1) |
where x and X are the position vectors of a point in the deformed and reference configurations, respectively; t is time; F is the deformation gradient tensor; and c is the rigid-body translation.
In this work, we consider large populations of planar fibers characterized by an ODF that changes in some fashion with the applied macroscopic deformation. We thus drop any dependence on c because we are focusing on material deformation phenomena only. Note that this approach can be extended to three dimensions, but there are many applications in which planar organization is either an actual organization or a good approximation of the local structure. The method for accounting for the changes in an ODF with applied strain has been previously presented in Fan and Sacks (9). Briefly, we start with an infinitesimal element dΩ0 of tissue, and let a fiber direction in the reference (undeformed) configuration Ω0 be denoted by with an orientation angle θ. Each individual fiber is assumed to reorient and stretch independently but in accordance with the macroscopic tissue-level deformation. Based on affine kinematics, the unit vector n(β) associated with the fiber direction in the loaded (deformed) configuration Ωt can be determined by (37)
| (2) |
where F is the macroscopic deformation gradient tensor, and the orientation angle in the loaded configuration . Affine fiber kinematics states that the total number of fibers contained within an infinitesimal angular element is preserved under deformation, i.e., By adopting Nanson’s relation in finite strain theory (Fung (38)), the fiber ODF Γt(β) in the deformed configuration can be determined by (9)
| (3) |
where λN = ||FN|| denotes the stretch ratio along the fiber direction N, and J2D is the determinant of the in-plane components of the deformation gradient tensor. Equation 3 renders a means to predict the fiber ODF at the deformed state based on the orientation angle at the reference state and the given macroscopic tissue-level deformation.
Simulations of SAXS measurements. To simulate the collagen fibril angular orientations as measured by SAXS, we assumed that the undulated fibers can be idealized by planar sinusoids (Fig. 3 A)
| (4) |
where x and y are the coordinates associated with the sinusoidal undulated fiber along the x- and y axes, respectively, and a and p are the fiber amplitude and crimp period, respectively. Under the assumption that as fibers are extended up to the point of just being fully straightened they undergo no stretch, the fiber amplitude at the deformed state given the fiber stretch λN can be determined by solving the nonlinear equation
| (5) |
where a0 and p0 are the fiber amplitude and fiber crimp period at the unreformed state, respectively; and is the arc length of the undulated fiber at the undeformed state, pt = min(L0, λN∗p0) is the fiber crimp period at the deformed state, and Lt is the arc length of the fiber at the deformed state.
Figure 3.
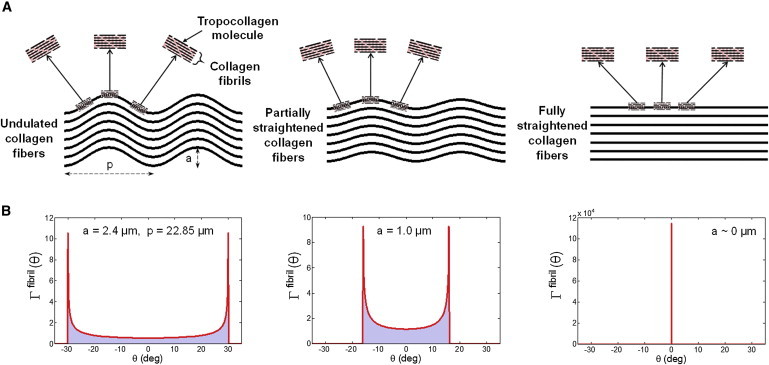
(A) A schematic diagram of the hierarchical structure of the collagen fiber network, from undulated collagen fibers idealized by a sinusoidal geometry, to collagen fibrils composed of tropocollagen molecules under stretch, and (B) the corresponding probability density functions of a single fiber at different stretching states. To see this figure in color, go online.
Utilizing the SHG measurements of the collagen fiber crimp, we determined the mean values for a and p. As noted above, the effects of fiber undulation depend only on the a/p ratio, so we kept p fixed and represented the variance in fiber geometry via a Gaussian distribution with the mean amean and standard deviation asd for the fiber amplitude. Because the SAXS technique is a transmitted electromagnetic energy technique, it includes combined effects of all fiber undulations and orientations (Fig. 3 A), and, therefore reflects what is actually measured is the composite ODF.
To account for both effects, we develop an expression for the composite probability density function as follows. The fibrillar orientation angle at location x is obtained by which is a function of the random variable x ∈ [−p/2, p/2] with a uniform probability density function, i.e., x ∼ Uniform(1/p). Using the theory of the function of a random variable (39),
| (6) |
and
| (7) |
We then obtain a single sinusoidal fibrillar angular orientation distribution function
| (8) |
In the unloaded state, Eq. 8 will produce a dual peaked distribution that will collapse to a Dirac delta function δ(θ = 0) for a fully straightened fiber (Fig. 3).
To scale to the tissue level, we first note that the SAXS-measured ODF represents the sum of the overall collagen fibril orientation, including the effects of the sinusoidal geometry of each individual fibril and the fibrillar angular probability density function. Therefore, as the MV leaflet tissue is stretched, the ODF will change due to the rotation of the fibers in response to the anisotropic stretching patterns (Fig. 1 D) as well as the straightening of the constituent collagen fibrils. To derive the total expression, it was first noted that the collagen fibers were completely straightened at the peak equibiaxial tensions of ∼100 N/m in the SHG measurements. We thus assumed that all the collagen fibrils are straight with no crimp at this loading level. Following Fata et al. (7) and Fan and Sacks (9), we model the ODF at the reference state Γ0(θ) by a β-distribution function with a mean μsplay and a standard deviation σsplay. Based on affine kinematics (Eqs. 2 and 3) and the measured deformation gradient tensor F, the fibrillar ODF at the fully loaded state Γt(β) can be computed, and the fiber splay parameters μsplay and σsplay were determined by nonlinear least-squares fit of the ODF at the fully loaded state Γt(β) between the model predictions and the SAXS measurements (Fig. 4 A), using
| (9) |
where nSAXS is the number of the orientation angle data points of the SAXS data.
Figure 4.
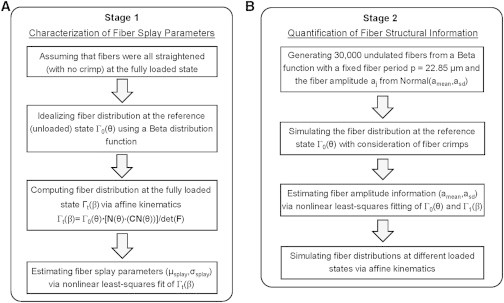
(A) Flowchart of the characterization of fiber splay parameters based on affine kinematics by assuming a β-function for the ODF at the reference state Γ0(θ) and all straightened fibers at the fully loaded state, and (B) flowchart of the quantification of the structural information about the collagen fiber network considering 30,000 undulated collagen fibers with fiber crimp effect and the subsequent simulations of the ODFs in different loading states Γt(β).
Next, we simulated the collagen fiber network of the MVAL tissue by considering 30,000 collagen fibers, which represents the approximate number contained in a transmural section of the tissue. This number was estimated based on the collagen fiber diameter of 3.75 μm, collagen fiber volume fraction of 0.51, and the tissue thickness of 0.578 mm. This number was also sufficiently large for accurate representation of the histogram of the fibrillar ODF.
In our simulation, the amplitude associated with each undulated fiber aj at the unloaded state was generated from a Gaussian distribution with a mean amean and a standard deviation asd. It is noted again from our SHG analysis that the fiber crimp period p was kept constant and the ODF only depends on the a/p ratio in our calculation. These two parameters (amean, asd) associated with the fiber structural information were estimated by nonlinear least-squares fit of the fiber ODFs between the simulated results and the SAXS data (Fig. 4 B):
| (10) |
Herein, we used the ODFs at the reference state Γ0(θ) and the first loaded state Γ1(β) at the fitting procedure, and this yielded predictions at all other loaded states in better agreement with the SAXS measurements. The overall fiber orientation distributions at the subsequent loading states Γt(β) were obtained using
| (11) |
where is the summation of the contributions of all 30,000 simulated fibers at the deformed state, and is the model predicted ODF renormalized to unit area.
Simulations of MPM measurements. To investigate fiber reorientation of the collagen and elastin fiber networks in different layers of the MVAL tissue under physiological loading, we adopted the aforementioned two-step algorithm to simulate the collagen fiber networks in MVAL layers (Fig. 4, A and B). This was done by considering affine kinematics and fiber crimp, in which layer-specific collagen fiber splay parameters μsplay and σsplay, as well as the fiber microstructural information (amean and asd), were quantitatively estimated via the nonlinear least-squares fit of the collagen fiber ODFs at the reference and fully loaded states between the MPM measurement and the simulation results. On the other hand, we noted in our SHG measurements that the elastin fibers are all approximately straight in all loading states, and, therefore, only the first stage of the proposed algorithm (Fig. 4 A) was used to characterize layer-specific elastin fiber splay parameters in the atrial and ventricularis layers without consideration for the fiber crimp effect. It should be noted that the alignments of the collagen and elastin fiber networks in the atrialis layer were orthogonal to those fiber networks in the fibrosa and ventricularis layers based on our observations with SALS. Also, reliable elastin fiber measurements for only the ventricularis layer could be obtained.
Summary of experimentations and usage of acquired data sets for the proposed affine kinematic model
We summarized in Table 1 the experimentations described previously, what data were acquired, and how each of the data sets was used for the subsequent analyses and in the parameter estimation of the proposed affine kinematic model. Briefly, for real-time measurements of collagen fibril kinematics, SAXS data were used to validate the assumption of affine collagen fibril kinematics as well as for the parameter estimation of the proposed model for a collagen fiber network at the fibrillar level. In addition, we used the MPM SHG data, which provided layer-specific information about both collagen and elastin fiber networks, to evaluate the proposed affine kinematic model for both collagen and elastin fiber networks at the fiber level. Next, we used the SALS data only, to present the transmural composite fiber architecture in specimens fixed at the zero-stress state. Finally, we used the MPM imaging on transmural sections from these same fixed specimens to quantify layer-specific collagen fiber crimp amplitude and crimp period in the unloaded state.
Table 1.
Summary of experimental techniques and the use of each acquired data set
| Modality | Acronym | Source | Data Acquired | Structure | Usage |
|---|---|---|---|---|---|
| Small angle x-ray scattering (real-time) | SAXS | x-ray (λ = 12.4 nm, beam size = 0.4 mm) | angular orientation distribution derived from SAXS patterns | collagen fibrils | quantifying fibril ODF (steps 1 and 2 in Fig. 4) |
| Multiphoton microscopy (second harmonic generation, real-time) | MPM (SHG) | optical fluorescence at 400 ± 100 nm | angular orientation distribution based on image analysis | collagen fiber network | quantifying layer-specific collagen fiber ODF (steps 1 and 2 in Fig. 4) |
| Multiphoton microscopy (autofluorescence, real-time) | MPM (AF) | optical fluorescence at 525 ± 50 nm | angular orientation distribution based on image analysis | elastin fiber network | quantifying layer-specific elastin fiber ODF (step 1 in Fig. 4) |
| Small angle light scattering (fixation) | SALS | optical He-Ne laser (λ = 632.8 nm, beam size = 0.254 mm) | angular orientation distribution based on SALS patterns | effective fiber network | total tissue ODF in unloaded state |
| Multiphoton microscopy (fixation) | MPM | optical fluorescence (λ = 830 nm) | images of collagen fiber structure | collagen fiber network | quantifying layer-specific collagen fiber crimp |
ODF, orientation distribution function.
Results
General observations
Consistent with previously published results in Grashow et al. (40) and May-Newman and Yin (41), the biaxial response of the MV was nonlinear, anisotropic with peak circumferential and radial strains of 20 and 40% (Fig. 1 D), respectively. The strain levels reached were similar to the previously reported in vivo analysis, suggesting that the designed equibiaxial tension protocol accurately approximated the strain field of the MV during systolic closure. Histologically, the collagen-rich fibrosa layer, proteoglycan-rich spongiosa layer, and the elastin-rich atrialis and ventricularis layers were evident (Fig. 1 C). The elastin-rich atrialis also contained collagen fibers, whereas the ventricularis layer was effectively only a thin surface layer of elastin fibers that quickly transitioned to the collagen-rich fibrosa layer. From the circumferential-transverse sections, the collagen and elastin fibers in the atrialis were more punctate, indicating an out-of-plane orientation in the radial direction, while the collagen fibers in the fibrosa layer and elastin fibers in the ventricularis layer were oriented along the circumferential direction that is perpendicular to the fiber direction in the atrialis layer (Figs. 1 C and 5, A and B).
Figure 5.
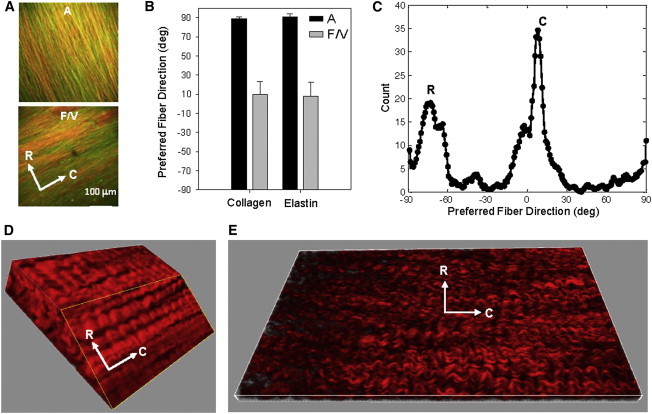
(A) SHG images superimposed with the autofluorescence from TPM of the MVAL tissue at the fully loaded state (150 N/m), showing that the collagen and elastin fibers in the atrialis layer were aligned in the radial direction whereas the fiber networks oriented along the circumferential direction in the fibrosa and ventricularis layers (red, collagen fiber; green, elastin fiber). (B) The mean preferred fiber directions of the collagen and elastin fiber networks. (C) Histogram of the collagen fiber orientation at the fully loaded state quantified by SALS, clearly indicating the aforementioned two fiber populations of the MVAL tissue. (D and E) Representative three-dimensional rendering of the collagen fiber network in the fibrosa and atrialis layers. To see this figure in color, go online.
Moreover, we found that the collagen and elastin fibers in the atrialis layer were closely packed (Fig. 5 A). Confirmation of the orientation of these two fiber networks at a larger scale (∼250-μm-diameter region) was performed with SALS. This corresponded with the collagen and elastin fiber networks oriented radially in the atrialis layer, and the collagen and elastin fibers oriented circumferentially in the fibrosa and ventricularis layers (Fig. 5 C). It was also found that, in the fibrosa layer, although the fibers were largely oriented along the circumferential direction, there was a distinct weaving pattern (Fig. 5, D and E).
In the unloaded state, the collagen fibers were crimped with an identifiable period (Fig. 6 A). With the application of tension loading, the majority of the collagen fibers lost their crimp as mechanically engaged, although some residual crimp remained (Fig. 6 B). Collagen fiber crimp was quantified for the collagen fibers of the atrialis and fibrosa layers as summarized in Table 2.
Figure 6.
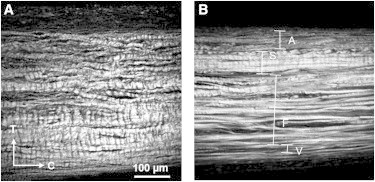
Collagen fibers visualized with SHG from TPM for transverse cryosections at equibiaxial tension of (A) 0 N/m and (B) 150 N/m, showing substantial reduction in collagen fiber crimp amplitude in the loaded state. To see this figure in color, go online.
Table 2.
Quantified microstructural information of the collagen fiber network in the fibrosa and atrialis layers at the unloaded (reference) state using the MPM imaging technique (n = 3 MVAL samples)
| Description | Amplitude a (μm) | Crimp Period p (μm) | Mean a/p Ratio |
|---|---|---|---|
| Fibrosa layer | 2.4 ± 0.4 | 22.85 ± 2.7 | 0.105 |
| Atrialis layer | 5.92 ± 1.4 | 19.96 ± 5.0 | 0.297 |
Note that the atrialis layer exhibited larger crimp amplitudes but similar crimp periods so that its a/p ratio was nearly three times that of the fibrosa layer.
Predictions of fibril-level kinematic results
We first fitted one typical measured collagen fibril angular distribution at the fully loaded state by applying affine kinematics, resulting in a fit of the β-parameters μsplay = −6.53° and σsplay = 17.22°, with an r2 = 0.985 (Fig. 7 A). Next, we utilized these values and the measured fiber crimp period (p = 22.85 μm) to simulate Γ0(θ) by summing up the contributions of all 30,000 undulated fibers. The model fit the SAXS measured data quite well (Fig. 7 B), with an r2 = 0.903, whereas the prediction of the collagen fibril ODF Γ0(θ) at the reference state without fiber crimp was very poor, with an r2 = 0.252 (Fig. 7 C). This demonstrated the essential need of incorporating the proposed sinusoidal geometry to account for the fiber crimp effect in modeling the collagen fiber/fibril micromechanisms. Moreover, the collagen fiber amplitude was estimated as follows: amean = 2.42 μm, asd = 0.92 μm, which agrees with our SHG observation for the collagen fiber network in the fibrosa layer (aSHG = 2.4 ± 0.4 μm). The estimated fiber splay parameters, and collagen fiber structural data of the five MVAL tissue specimens, were summarized in Table 3.
Figure 7.
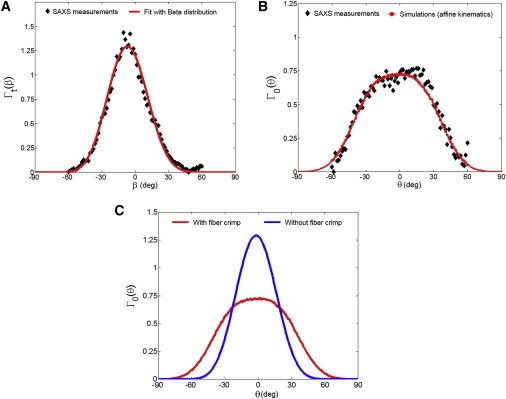
Comparisons of the typical collagen fibril ODFs between the SAXS measurements and the model predictions: (A) at the fully loaded state considering all straight fibers, and (B) at the reference state considering 30,000 undulated fibers with fiber crimp effect. (C) Predicted ODFs at the unloaded state with and without the consideration of the fiber crimp effect. To see this figure in color, go online.
Table 3.
SAXS and SHG fitted collagen fibril, collagen fiber, and elastin fiber fitted structural parameters
| Description | Fibrosa Layer (SAXS) | Fibrosa Layer (SHG) | Atrialis Layer (SHG) |
|---|---|---|---|
| Collagen fiber network | |||
| amean (μm) | 1.98 ± 0.54 | 2.58 | 4.94 |
| asd (μm) | 0.73 ± 0.35 | 0.36 | 0.96 |
| μsplay (deg) | −11.49 ± 6.75 | 19.65 | −70.85 |
| σsplay (deg) | 17.31 ± 0.22 | 11.75 | 14.78 |
| Elastin fiber network | |||
| μsplay (deg) | N/A | 26.62 | −62.75 |
| σsplay (deg) | N/A | 10.21 | 11.68 |
The SAXS results are reported as mean ± SE (n = 5). Note here that the SAXS mean crimp amplitude agreed well with measured SHG, because both were taken from the fibrosa layer. Moreover, the SHG data suggest that the collagen and elastin fibers have very similar fiber splay and preferred directions.
We further investigated model predictions of the collagen fibril ODFs at different loading states by applying the measured deformation gradient F at each state and considering the corresponding rotation and straightening of the undulated fibers. As observed, the overall model predictions are in very good agreement with the ODFs Γt(β) measured in SAXS (Figs. 8 and 9). These remarkable results suggest that the collagen fiber network in the MVAL deforms very closely to the affine fiber kinematic model (Eq. 3) at the homogenized tissue-level scale of ∼1 mm. Moreover, we estimated the effective fiber splay’s standard deviation by the direct fit of the collagen fibril ODF at each loading state. Both the SAXS measured and numerically predicted fiber splay properties indicate that the straightening of the constituent collagen fibers dominates the SAXS measured pattern (Fig. 8, A–C) in the low-strain regime (<∼25 N/m) during equibiaxial stretch, leading to the reduction of the effective fiber splay’s standard deviation from ∼30° to ∼20°, whereas the fiber splay tends to remain constant beyond the above-tension level (Fig. 9).
Figure 8.
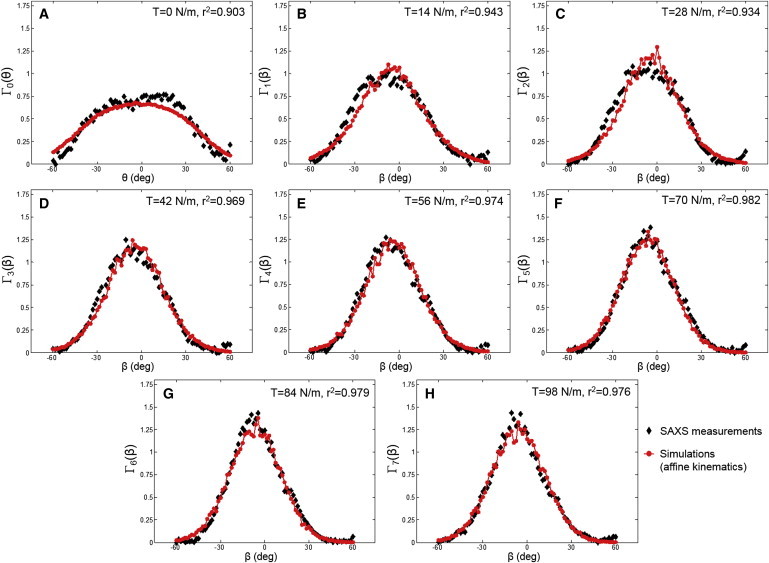
(A–H) Comparisons of the collagen fibril ODFs at the reference state Γ0(θ) and at different loading states Γt(β) between the typical SAXS measurements and the model predictions. To see this figure in color, go online.
Figure 9.
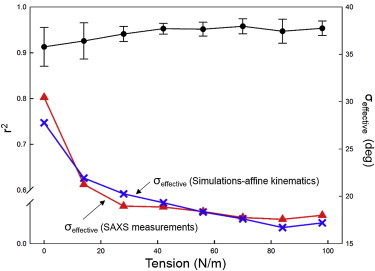
Fitting error metric r2 versus the applied tension level, and the comparison of the effective fiber splay at different loading states between the SAXS measurements and the simulation results via affine kinematics. Note that σeffective was determined by fitting the collagen fibril ODF data with a β-distribution. To see this figure in color, go online.
Predictions of fiber-level kinematic results
It should be reemphasized that the SAXS measurements analyzed in the previous section are restricted to collagen fibrils only, and are not directly influenced by the presence of the elastin fibers and other components. On the other hand, the MPM imaging technique offers a means to explore both the collagen and elastin fiber networks in different layers of the MV tissue under physiological loading. For collagen fibers, the predictions of the fiber ODFs at the reference and fully loaded states via the affine fiber kinematic model in conjunction with a sinusoidal fiber geometry (Table 3) were in fairly good agreement with the MPM measurements for both the atrialis and fibrosa layers (Fig. 10). For elastin fibers, only affine kinematics was used and the model predictions (Table 3) agreed well with the MPM measurements for both the atrialis and fibrosa layers (Fig. 10). These results indicate that the elastin fiber network behaves as a group of straight fibers, in accordance with our observations in the MPM images. Results of both collagen and elastin fiber networks serve as another validation of the affine kinematics assumption at the fiber level.
Figure 10.
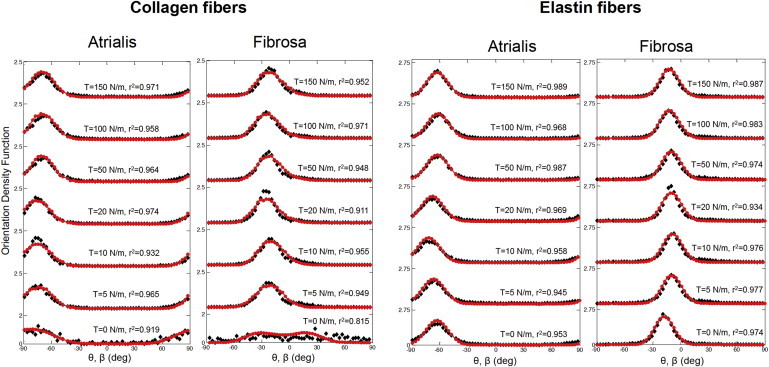
Comparisons of the collagen and elastin fiber ODFs at different loading states between the simulated results and the SHG measurements for the atrialis and fibrosa layers (solid diamond, SHG measurements; solid circle with line, simulations). In all cases the model agreed very well with the measured data, suggesting that the both the affine kinematic and fiber crimp (for collagen) model was appropriate for MVAL tissues. To see this figure in color, go online.
Discussion
Overall findings
In this work, we attempted to address the question of how the constituent fibers in dense planar tissues respond kinematically to loading, using the MVAL as a representative tissue. By simulating MV networks of fibrils or fibers, changes in orientation and stretch were determined based on affine fiber kinematics and the predictions were in good agreement with the experimental observations at both fibrillar and fiber levels. When compared to the SAXS measurements (Figs. 8 and 9), the model fit the data quite well, with an r2 = 0.976. Similar agreement was obtained from the optical-level measurements, for both undulated collagen fibers and straight elastin fibers (Fig. 10). To our knowledge, this is the first known fully generalized kinematic study conducted for soft collagenous tissues. These straightforward yet remarkable results suggest that the collagen and elastin fiber networks in the MVAL tissue deform according to an affine kinematic model at the homogenized tissue-level scale of ∼1 mm. The implications of this finding are many. They include both fundamental and applied subjects, such as improving our understanding of native heart valve design, providing a means to model valvular function, and helping in development of therapies for treating MV diseases. Moreover, with respect to understanding its function, affine kinematics suggests that the constituent fibers within the MV leaflet tissues are largely noninteracting and deform with the bulk tissue. This greatly simplifies the modeling efforts at the tissue- and organ levels, because affine kinematics allows a straightforward connection between the macroscopic tissue and local fiber strains. It also suggests that the collagen and elastin fiber networks act independently of each other. Why is this? Most likely, it suggests that the collagen and elastin form long fiber networks that allow free rotations. Such freedom of rotation can greatly facilitate the observed high degree of mechanical anisotropy (42), which is essential to heart valve function. It also suggests that the collagen fibrils are tightly bounded and deform as a single fiber-level unit.
On a larger scale, we also found substantial layer differences in the collagen and elastin fiber planar organizations. We identified two opposing collagen and elastin networks on the opposite sides of the mitral valve leaflet—a structure not observed in the semilunar valves. For semilunar valves (aortic and pulmonary), the bulk collagen fibers were in the fibrosa layer, which orient in the circumferential direction, resulting in minimal strain along this direction. So, why does the MV have two separate opposing networks? The MV is under the highest transvalvular pressure gradient and may need a secondary fiber network in the atrialis layer to provide further support during the cardiac cycle. This could be achieved simply with an increase in thickness or a single randomly oriented network, but instead, there exists two fiber networks on the opposite sides of the mitral valve that are perpendicular to each other. The radially oriented collagen fibers in the MV atrialis layer may serve to decrease compliance along the radial direction. Moreover, the radially oriented elastin fibers in the atrialis layer may further aid in restoration of the valve to its initial/unloaded configuration, as seen in the ventricularis layer for the aortic valve (43,44). The distribution of these two separate networks may also allow for greater controllability over the two axes of flexure to further optimize the gross three-dimensional leaflet deformations during the closure of the valve. Although exploration of such possibilities is beyond the scope of this study, the quantitative architectural data set derived from this work will provide the necessary parameters to answer the aforementioned hypotheses with a computation-modeling-based approach.
Relation to short fiber systems
The affine deformations found in this study occur commonly in long fiber systems. However, in the case of short fiber systems, particularly with fiber-fiber interconnections, local nonaffine behaviors can manifest themselves (45–48). The additional local degrees of freedom allow for local nonaffinity, whereas long, relatively free fiber networks do not have such interconnections and can follow the strain fields at the larger scale. However, it should be noted that they still reproduce many of the salient features of affine-deformed networks because the fiber systems can be locally nonaffine. We have demonstrated this in our recent studies of electrospun fibrous systems (49,50).
Relation to cellular deformation and strain-induced tissue failure
Within each of the four layers of the MV leaflet tissues there resides a heterogeneous population of interstitial cells that maintain the structural integrity of the MV tissue via protein biosynthesis and enzymatic degradation (51–54). Among all valve interstitial cells (VICs), mitral valve interstitial cells (MVICs) have the characteristics of both fibroblasts and smooth muscle cells. Studies of VICs in both human and porcine valve tissues have revealed that the cells are present throughout the valve leaflet tissues (55,56). Recent long-term studies have indicated that the recurrence of significant mitral regurgitation after surgical repair may be much higher than previously believed, particularly in patients with ischemic mitral regurgitation (57–59). Surgery-induced excessive tissue stress and the resulting tissue failure have been viewed as potential etiological factors (57). These repair-induced stress alterations lead to changes in MVIC metabolism and collagen biosynthesis, and are essential in understanding the biomechanical responses at the organ, tissue, and cellular levels. Moreover, tissue stress-induced MVIC deformation can have deleterious effects on the biosynthetic states of MVICs that are related to the reduction of tissue maintenance as well as the organ-level failure.
Therefore, to better understand the interrelationships between tissue-level loading and cellular responses, we developed an integrated experimental-computational approach in a parallel study (60) to quantify the in situ layer-specific MVIC deformations under controlled biaxial tension loading, and to explore the interrelationship between the MVIC stiffness and deformation to layer-specific tissue mechanical and structural properties. We found that MVIC deformation is primarily controlled by each tissue layer’s respective structure and mechanical behavior rather than the intrinsic MVIC stiffness. To our knowledge, this novel finding further suggests that while the MVICs may be phenotypically and biomechanically similar throughout the leaflet, they experience layer-specific mechanical stimulatory inputs due to distinct extracellular matrix architecture and mechanical behaviors of the four MVAL tissue layers. These results underscore the need for layer-specific biomechanical information, such as the fiber kinematic presented herein, in our understanding of valve functioning mechanisms and in motivating the development of reliable computational modeling approaches.
Relation to structurally driven constitutive models
One could use this sinusoidal model, based on elastica solutions, to simulate effects of the exogenous cross-linking that occurs when collagenous tissues are chemically modified. Such cross-linking can dramatically increase the fiber flexural stiffness, so that measurable forces can be generated by the simple straightening of the fibers. However, the primary goal of this work is the verification of the affine deformation assumption for planar collagenous tissues. This allows one to determine the local fiber strain Ef in the fiber direction N(θ) from the macroscopic tissue-level Green-Lagrange strain tensor using
| (12) |
where
| (13) |
Next, we idealized the elastic behavior of soft tissues as pseudo-hyperelastic composite materials (61). The total strain energy function Ψ of soft tissue at a representative volume element can then be defined using
| (14) |
where Ψf and Ψm are the strain energy density functions for the collagenous fiber and nonfibrous matrix phases, respectively; ϕf and ϕm are the volume fractions of the fiber phase and matrix phase, respectively, with ϕf + ϕm = 1, ; and p is the Lagrange multiplier to enforce the incompressibility due to soft tissue’s high water content. Subsequent development of Ψ will depend on the information available, the issues of the biological problem to be addressed, and the preferences of the investigator. It is important that, regardless of the particular strain energy function form chosen, affine deformation of the fibers allows this structural constitutive modeling approach to be employed, which greatly simplifies the computational effort for modeling the mechanical behavior of collagenous soft tissues.
Study limitations
In this study, we utilized an equibiaxial tension state to simulate physiological loading scenarios. Based on our understanding of the MV in vivo deformations (29), the resulting strains (Fig. 1) appeared as reasonably good approximations. We also utilized a quasi-static loading scenario due to experimental limitations. Yet, we know that the MVAL undergoes very high strain rates during normal operation (29,62). However, it has been observed that valvular tissues are largely strain-rate insensitive (63), so that the responses measured here are likely to represent the in vivo response.
The SHG imaging systems has been successfully utilized previously in several studies (7,64,65), although it does have resolution limitations and the results presented herein are necessarily limited by the technique’s ability to distinguish fiber structures. Overall, our fiber-level results are a good approximation of the ensemble fiber responses, but we cannot rule out local (i.e., submicron scale) nonaffine deformations of individual fibers. And while there are undoubtedly similarities in tissue architectures, details of the findings in this study should be understood only for MVAL tissues. Continued studies will be needed to evaluate the findings for specific tissues that have very different physiological features and functions.
Conclusions
In this study, we utilized two experimental datasets at two scales (nanometer and micrometer) of the MVAL tissues to evaluate the key assumption of the structural models for planar collagenous tissues—the collagen fibrillar deformation follows an affine deformation kinematic model. We simulated the MV collagen fiber network by representing the collagen fibrils via a sinusoidal geometric model for an ensemble of undulated fibers under a generalized two-dimensional deformation state. The proposed approach accounted for collagen fibril amplitude, crimp period, and rotation with applied macroscopic deformation. When compared to the SAXS measurements, the model fit the data quite well, with an r2 = 0.976. This basic result suggests that the collagen fiber network in the mitral valve anterior leaflet deforms according to the affine model at the homogenized tissue-level scale of ∼1 mm. Moreover, with respect to understanding its function, affine kinematics suggests that the constituent fibers within the MV are largely noninteracting and deform with the bulk tissue. It also suggests that the collagen fibrils are tightly bounded and deform as a single fiber-level unit. This greatly simplifies the modeling efforts at the tissue and organ levels, because affine kinematics allows a straightforward connection between the macroscopic tissue and local fiber strains. It also suggests that the collagen and elastin fiber networks act independently of each other, and, most likely, the collagen and elastin form long fiber networks that allow free rotations. Such freedom of rotation can greatly facilitate the observed high degree of mechanical anisotropy (42), which is essential to heart valve function.
Author Contributions
C.-H.L. performed all computations and wrote most of the article. W.Z. and J.I.S. assisted with all preliminary data analysis of the SAXS and SHG data and helped in developing the computational approach. J.L. assisted with providing and interpreting the SAXS data, and C.A.C. performed the SHG experiments.
Acknowledgments
The assistance from Dr. Simon C. Watkins and Greg Gibson for the multiphoton microscope and Bryan Good for design and development of the mini-biaxial device is greatly appreciated.
This work was funded by National Institutes for Health grants No. R01 HL119297 and No. HL63954. C.-H.L. was supported in part by an American Heart Association Postdoctoral Fellowship grant No. 14POST18160013. C.A.C. was partially supported by National Institutes for Health grant No. 5T32EB003392 and a National Science Foundation Graduate Research Fellowship.
References
- 1.Millington P., Gibson T., Barbenel J. Structural and mechanical aspects of connective tissue. Adv. Biomed. Eng. 1971;1:189–248. [Google Scholar]
- 2.Qin Z., Buehler M.J., Kreplak L. A multi-scale approach to understand the mechanobiology of intermediate filaments. J. Biomech. 2010;43:15–22. doi: 10.1016/j.jbiomech.2009.09.004. [DOI] [PubMed] [Google Scholar]
- 3.Mitton R. Mechanical properties of leather fibers. J. Soc. Leather Trades’ Chem. 1945;29:169–194. [Google Scholar]
- 4.Lanir Y. A structural theory for the homogeneous biaxial stress-strain relationships in flat collagenous tissues. J. Biomech. 1979;12:423–436. doi: 10.1016/0021-9290(79)90027-7. [DOI] [PubMed] [Google Scholar]
- 5.Hollander Y., Durban D., Lanir Y. Constitutive modeling of coronary arterial media—comparison of three model classes. J. Biomech. Eng. 2011;133:061008. doi: 10.1115/1.4004249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hollander Y., Durban D., Lanir Y. Experimentally validated microstructural 3D constitutive model of coronary arterial media. J. Biomech. Eng. 2011;133:031007. doi: 10.1115/1.4003324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fata B., Carruthers C.A., Sacks M.S. Regional structural and biomechanical alterations of the ovine main pulmonary artery during postnatal growth. J. Biomech. Eng. 2013;135:021022. doi: 10.1115/1.4023389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fata B., Zhang W., Sacks M.S. Insights into regional adaptations in the growing pulmonary artery using a meso-scale structural model: effects of ascending aorta impingement. J. Biomech. Eng. 2014;136:021009. doi: 10.1115/1.4026457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fan R., Sacks M.S. Simulation of planar soft tissues using a structural constitutive model: finite element implementation and validation. J. Biomech. 2014;47:2043–2054. doi: 10.1016/j.jbiomech.2014.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee C.-H., Oomen P.A., Sacks M. A high-fidelity and micro-anatomically accurate 3D finite element model for simulations of functional mitral valve. In: Ourselin S., Rueckert D., Smith N., editors. Functional Imaging and Modeling of the Heart. Springer; Berlin, Germany: 2013. pp. 416–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee C.H., Amini R., Sacks M.S. An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment. J. Biomech. 2014;47:2055–2063. doi: 10.1016/j.jbiomech.2013.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee C.H., Amini R., Sacks M.S. Mitral valves: a computational framework. In: Suvranu D., Kuhl E., Hwang W., editors. Multiscale Modeling in Biomechanics and Mechanobiology. Springer; London, UK: 2015. [Google Scholar]
- 13.Jor J.W., Nash M.P., Hunter P.J. Estimating material parameters of a structurally based constitutive relation for skin mechanics. Biomech. Model. Mechanobiol. 2011;10:767–778. doi: 10.1007/s10237-010-0272-0. [DOI] [PubMed] [Google Scholar]
- 14.Billiar K.L., Sacks M.S. A method to quantify the fiber kinematics of planar tissues under biaxial stretch. J. Biomech. 1997;30:753–756. doi: 10.1016/s0021-9290(97)00019-5. [DOI] [PubMed] [Google Scholar]
- 15.Billiar K., Sacks M. Annual Fall Meeting. Blackwell Science; San Diego, CA: 1997. A micro-structural constitutive model for the aortic valve cusp; p. S20. [Google Scholar]
- 16.Cortes D.H., Lake S.P., Elliott D.M. Characterizing the mechanical contribution of fiber angular distribution in connective tissue: comparison of two modeling approaches. Biomech. Model. Mechanobiol. 2010;9:651–658. doi: 10.1007/s10237-010-0194-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lake S.P., Barocas V.H. Mechanics and kinematics of soft tissue under indentation are determined by the degree of initial collagen fiber alignment. J. Mech. Behav. Biomed. Mater. 2012;13:25–35. doi: 10.1016/j.jmbbm.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huyghe J.M., Jongeneelen C.J. 3D non-affine finite strains measured in isolated bovine annulus fibrosus tissue samples. Biomech. Model. Mechanobiol. 2012;11:161–170. doi: 10.1007/s10237-011-0300-8. [DOI] [PubMed] [Google Scholar]
- 19.Hepworth D.G., Steven-Fountain A., Vincent J.F. Affine versus non-affine deformation in soft biological tissues, measured by the reorientation and stretching of collagen fibers through the thickness of compressed porcine skin. J. Biomech. 2001;34:341–346. doi: 10.1016/s0021-9290(00)00183-4. [DOI] [PubMed] [Google Scholar]
- 20.Folkard W., Geercken W., Koch M.H. Structural dynamic of native tendon collagen. J. Mol. Biol. 1987;193:405–407. doi: 10.1016/0022-2836(87)90228-2. [DOI] [PubMed] [Google Scholar]
- 21.Fratzl P., Misof K., Bernstorff S. Fibrillar structure and mechanical properties of collagen. J. Struct. Biol. 1998;122:119–122. doi: 10.1006/jsbi.1998.3966. [DOI] [PubMed] [Google Scholar]
- 22.Purslow P.P., Wess T.J., Hukins D.W. Collagen orientation and molecular spacing during creep and stress-relaxation in soft connective tissues. J. Exp. Biol. 1998;201:135–142. doi: 10.1242/jeb.201.1.135. [DOI] [PubMed] [Google Scholar]
- 23.Sasaki N., Odajima S. Elongation mechanism of collagen fibrils and force-strain relations of tendon at each level of structural hierarchy. J. Biomech. 1996;29:1131–1136. doi: 10.1016/0021-9290(96)00024-3. [DOI] [PubMed] [Google Scholar]
- 24.Sasaki N., Shukunami N., Izumi Y. Time-resolved x-ray diffraction from tendon collagen during creep using synchrotron radiation. J. Biomech. 1999;32:285–292. doi: 10.1016/s0021-9290(98)00174-2. [DOI] [PubMed] [Google Scholar]
- 25.Liao J., Yang L., Sacks M.S. Molecular orientation of collagen in intact planar connective tissues under biaxial stretch. Acta Biomater. 2005;1:45–54. doi: 10.1016/j.actbio.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 26.Liao, J., L. Yang, …, M. S. Sacks. 2005. Collagen fibril kinematics in mitral valve leaflet under biaxial elongation, creep, and stress relaxation. Proc. Society for Heart Valve Disease Third Biennial Meeting, Vancouver, BC, Canada. Abstract #85, 154.
- 27.Liao J., Yang L., Sacks M.S. The relation between collagen fibril kinematics and mechanical properties in the mitral valve anterior leaflet. J. Biomech. Eng. 2007;129:78–87. doi: 10.1115/1.2401186. [DOI] [PubMed] [Google Scholar]
- 28.Fata B., Gottlieb D., Sacks M.S. Estimated in vivo postnatal surface growth patterns of the ovine main pulmonary artery and ascending aorta. J. Biomech. Eng. 2013;135:71010–71012. doi: 10.1115/1.4024619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sacks M.S., Enomoto Y., Gorman J.H., 3rd In-vivo dynamic deformation of the mitral valve anterior leaflet. Ann. Thorac. Surg. 2006;82:1369–1377. doi: 10.1016/j.athoracsur.2006.03.117. [DOI] [PubMed] [Google Scholar]
- 30.Sacks M. Biaxial mechanical evaluation of planar biological materials. J. Elast. 2000;61:199–246. [Google Scholar]
- 31.Watkins S. Current Protocols in Cytometry. John Wiley; New York: 2001. Immunohistochemistry. [Google Scholar]
- 32.Huang H.Y., Liao J., Sacks M.S. In-situ deformation of the aortic valve interstitial cell nucleus under diastolic loading. J. Biomech. Eng. 2007;129:880–889. doi: 10.1115/1.2801670. [DOI] [PubMed] [Google Scholar]
- 33.Chaudhuri B.B., Kundu P., Sarkar N. Detection and gradation of oriented texture. Pattern Recognit. Lett. 1993;14:147–153. [Google Scholar]
- 34.Karlon W.J., Covell J.W., Omens J.H. Automated measurement of myofiber disarray in transgenic mice with ventricular expression of Ras. Anat. Rec. 1998;252:612–625. doi: 10.1002/(SICI)1097-0185(199812)252:4<612::AID-AR12>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 35.Courtney T., Sacks M.S., Wagner W.R. Design and analysis of tissue engineering scaffolds that mimic soft tissue mechanical anisotropy. Biomaterials. 2006;27:3631–3638. doi: 10.1016/j.biomaterials.2006.02.024. [DOI] [PubMed] [Google Scholar]
- 36.Sacks M.S., Smith D.B., Hiester E.D. A small angle light scattering device for planar connective tissue microstructural analysis. Ann. Biomed. Eng. 1997;25:678–689. doi: 10.1007/BF02684845. [DOI] [PubMed] [Google Scholar]
- 37.Dafalias Y.F. Orientation distribution function in non-affine rotations. J. Mech. Phys. Solids. 2001;49:2493–2516. [Google Scholar]
- 38.Fung Y.C. Prentice-Hall; Englewood Cliffs, NJ: 1965. Foundations of Solid Mechanics. [Google Scholar]
- 39.Papoulis A. WCB McGraw-Hill; Boston, MA: 1991. Probability, Random Variables, and Stochastic Processes. [Google Scholar]
- 40.Grashow J.S., Sacks M.S., Yoganathan A.P. Planar biaxial creep and stress relaxation of the mitral valve anterior leaflet. Ann. Biomed. Eng. 2006;34:1509–1518. doi: 10.1007/s10439-006-9183-8. [DOI] [PubMed] [Google Scholar]
- 41.May-Newman K., Yin F.C. A constitutive law for mitral valve tissue. J. Biomech. Eng. 1998;120:38–47. doi: 10.1115/1.2834305. [DOI] [PubMed] [Google Scholar]
- 42.Billiar K.L., Sacks M.S. Biaxial mechanical properties of the natural and glutaraldehyde treated aortic valve cusp—part I: experimental results. J. Biomech. Eng. 2000;122:23–30. doi: 10.1115/1.429624. [DOI] [PubMed] [Google Scholar]
- 43.Scott M., Vesely I. Aortic valve cusp microstructure: the role of elastin. Ann. Thorac. Surg. 1995;60(Suppl.):S391–S394. doi: 10.1016/0003-4975(95)00263-k. [DOI] [PubMed] [Google Scholar]
- 44.Vesely I. The role of elastin in aortic valve mechanics. J. Biomech. 1998;31:115–123. doi: 10.1016/s0021-9290(97)00122-x. [DOI] [PubMed] [Google Scholar]
- 45.Aghvami M., Barocas V.H., Sander E.A. Multiscale mechanical simulations of cell compacted collagen gels. J. Biomech. Eng. 2013;135:71004. doi: 10.1115/1.4024460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Stylianopoulos T., Barocas V. Volume-averaging theory for the study of the mechanics of collagen networks. Comput. Method Appl. Mech. Eng. 2007;196:2981–2990. [Google Scholar]
- 47.Chandran P.L., Barocas V.H. Deterministic material-based averaging theory model of collagen gel micromechanics. J. Biomech. Eng. 2007;129:137–147. doi: 10.1115/1.2472369. [DOI] [PubMed] [Google Scholar]
- 48.Pence T.J., Monroe R.J., Wright N.T. On the computation of stress in affine versus nonaffine fibril kinematics within planar collagen network models. J. Biomech. Eng. 2008;130:041009. doi: 10.1115/1.2917432. [DOI] [PubMed] [Google Scholar]
- 49.D’Amore A., Amoroso N., Sacks M.S. From single fiber to macro-level mechanics: a structural finite-element model for elastomeric fibrous biomaterials. J. Mech. Behav. Biomed. Mater. 2014;39:146–161. doi: 10.1016/j.jmbbm.2014.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Carleton J.B., D’Amore A., Sacks M.S. Geometric characterization and simulation of planar layered elastomeric fibrous biomaterials. Acta Biomater. 2014;12:93–101. doi: 10.1016/j.actbio.2014.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Messier R.H., Jr., Bass B.L., Hopkins R.A. Dual structural and functional phenotypes of the porcine aortic valve interstitial population: characteristics of the leaflet myofibroblast. J. Surg. Res. 1994;57:1–21. doi: 10.1006/jsre.1994.1102. [DOI] [PubMed] [Google Scholar]
- 52.Taylor P.M., Batten P., Yacoub M.H. The cardiac valve interstitial cell. Int. J. Biochem. Cell Biol. 2003;35:113–118. doi: 10.1016/s1357-2725(02)00100-0. [DOI] [PubMed] [Google Scholar]
- 53.Filip D.A., Radu A., Simionescu M. Interstitial cells of the heart valves possess characteristics similar to smooth muscle cells. Circ. Res. 1986;59:310–320. doi: 10.1161/01.res.59.3.310. [DOI] [PubMed] [Google Scholar]
- 54.Mulholland D.L., Gotlieb A.I. Cell biology of valvular interstitial cells. Can. J. Cardiol. 1996;12:231–236. [PubMed] [Google Scholar]
- 55.Bairati A., DeBiasi S. Presence of a smooth muscle system in aortic valve leaflets. Anat. Embryol. (Berlin) 1981;161:329–340. doi: 10.1007/BF00301830. [DOI] [PubMed] [Google Scholar]
- 56.Merryman W.D., Youn I., Sacks M.S. Correlation between heart valve interstitial cell stiffness and transvalvular pressure: implications for collagen biosynthesis. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H224–H231. doi: 10.1152/ajpheart.00521.2005. [DOI] [PubMed] [Google Scholar]
- 57.Braunberger E., Deloche A., Carpentier A. Very long-term results (more than 20 years) of valve repair with Carpentier’s techniques in nonrheumatic mitral valve insufficiency. Circulation. 2001;104(Suppl. 1):I8–I11. [PubMed] [Google Scholar]
- 58.Flameng W., Herijgers P., Bogaerts K. Recurrence of mitral valve regurgitation after mitral valve repair in degenerative valve disease. Circulation. 2003;107:1609–1613. doi: 10.1161/01.CIR.0000058703.26715.9D. [DOI] [PubMed] [Google Scholar]
- 59.Flameng W., Meuris B., Herregods M.-C. Durability of mitral valve repair in Barlow disease versus fibroelastic deficiency. J. Thorac. Cardiovasc. Surg. 2008;135:274–282. doi: 10.1016/j.jtcvs.2007.06.040. [DOI] [PubMed] [Google Scholar]
- 60.Lee C.H., Carruthers C.A., Sacks M.S. Quantification and simulation of layer-specific deformations under physiological loading. J. Theor. Biol. 2015 doi: 10.1016/j.jtbi.2015.03.004. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Fung Y.C. Springer; New York: 1993. Biomechanics: Mechanical Properties of Living Tissues. [Google Scholar]
- 62.Amini R., Eckert C.E., Sacks M.S. On the in vivo deformation of the mitral valve anterior leaflet: effects of annular geometry and referential configuration. Ann. Biomed. Eng. 2012;40:1455–1467. doi: 10.1007/s10439-012-0524-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sacks M.S., David Merryman W., Schmidt D.E. On the biomechanics of heart valve function. J. Biomech. 2009;42:1804–1824. doi: 10.1016/j.jbiomech.2009.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Dye W.W., Gleason R.L., Humphrey J.D. Altered biomechanical properties of carotid arteries in two mouse models of muscular dystrophy. J. Appl. Physiol. 2007;103:664–672. doi: 10.1152/japplphysiol.00118.2007. [DOI] [PubMed] [Google Scholar]
- 65.Chen H., Liu Y., Kassab G.S. The layered structure of coronary adventitia under mechanical load. Biophys. J. 2011;101:2555–2562. doi: 10.1016/j.bpj.2011.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]


