Isoforms Confer Characteristic Force Generation and Mechanosensation by Myosin II Filaments

Abstract

Myosin II isoforms with varying mechanochemistry and filament size interact with filamentous actin (F-actin) arrays to generate contractile forces in muscle and nonmuscle cells. How myosin II force production is shaped by isoform-specific motor properties and environmental stiffness remains poorly understood. Here, we used computer simulations to analyze force production by an ensemble of myosin motors against an elastically tethered actin filament. We found that force output depends on two timescales: the duration of F-actin attachment, which varies sharply with the ensemble size, motor duty ratio, and external load; and the time to build force, which scales with the ensemble stall force, gliding speed, and environmental stiffness. Although force-dependent kinetics were not required to sense changes in stiffness, the myosin catch bond produced positive feedback between the attachment time and force to trigger switch-like transitions from transient attachments, generating small forces, to high-force-generating runs. Using parameters representative of skeletal muscle myosin, nonmuscle myosin IIB, and nonmuscle myosin IIA revealed three distinct regimes of behavior, respectively: 1) large assemblies of fast, low-duty ratio motors rapidly build stable forces over a large range of environmental stiffness; 2) ensembles of slow, high-duty ratio motors serve as high-affinity cross-links with force buildup times that exceed physiological timescales; and 3) small assemblies of low-duty ratio motors operating at intermediate speeds are poised to respond sharply to changes in mechanical context—at low force or stiffness, they serve as low-affinity cross-links, but they can transition to force production via the positive-feedback mechanism described above. Together, these results reveal how myosin isoform properties may be tuned to produce force and respond to mechanical cues in their environment.

Introduction

Actomyosin contractility involves interactions of myosin II motors with actin filament (F-actin) arrays and powers a wide range of physiological processes, including muscle contraction (1,2), cell migration (3,4), cell division (5,6), and tissue morphogenesis (7,8). These diverse contractile functions are mediated by functionally distinct myosin II isoforms operating within actin arrays that range from highly ordered muscle sarcomeres to highly disordered networks. Contractile forces generated by myosin II are sensitive to mechanical context. This mechanosensitivity has been best studied in muscle, but may also allow nonmuscle cells to sense and respond to mechanical signals such as external force and stiffness (9–11). However, we still lack a quantitative understanding of how myosin force generation depends on the interplay of motor properties and cellular mechanics.

All myosin II motors operate within larger bipolar ensembles known as myosin filaments, which vary in size from a few dozen heads for mini-filaments of nonmuscle myosin II to hundreds of heads for the thick filaments of skeletal muscle myosin (12–16). Likewise, all myosin motors share a conserved mechanochemical cycle in which the energy of ATP hydrolysis is coupled to motor filament binding and a force-generating powerstroke. However, the rates of individual steps in this cycle vary widely across isoforms (17–23), leading to large differences in the duty ratio (20–22,24) and unloaded F-actin gliding speed (24–26). Finally, a key feature believed to be shared by all myosin II isoforms is that the lifetimes of the actin-bound state, and thus the duty ratio, increase with opposing loads and decrease with assisting loads (27–29). Previous models of force production by skeletal and smooth muscle myosin suggested that force-dependent release can enhance both tension and the maximum shortening speed during contraction (30,31). How force-dependent release affects the rate and magnitude of tension buildup by other myosin II isoforms in other cellular contexts remains poorly understood. A general challenge is to understand how isoform-specific properties shape the rate, magnitude, and mechanosensitivity of force production by ensembles of myosin II motors against dynamic and compliant actin arrays in living cells.

The swinging cross-bridge model for myosin II has played a key role in connecting the molecular properties of single motors to the macroscopic dynamics of contractile force production (32). The cross-bridge model has been used mainly in the context of skeletal muscle contraction, where the large number of motors and sarcomeric organization make it possible to relate microscopic dynamics to tissue-scale responses in a straightforward way (30,33–39). More recently, cross-bridge models have been used to study the dynamics of force production and filament translocation in nonsarcomeric contexts (31,40–42). However, these models have yet to be used in a more systematic analysis of how force production varies with isoform-specific motor properties, filament size, and substrate (i.e., F-actin network) compliance.

Here, we used computer simulations based on a simple form of the swinging cross-bridge model to explore how motor properties and environmental stiffness shape the magnitude, stability, and mechanosensitivity of force generation by myosin II filaments. We found that force generation is regulated by two competing timescales: one associated with force buildup via motor activity and the other with the duration of actomyosin attachment. Using parameters consistent with different myosin II isoforms, we identified three characteristic regimes. First, skeletal muscle myosin filaments can produce large forces with relatively small buildup times over a large range of stiffness values. Second, filaments of nonmuscle myosin IIB serve as stable cross-linkers, but are poor force generators due to their exceedingly slow cross-bridge cycle. Third, filaments of nonmuscle myosin IIA behave as low-affinity cross-linkers at low forces or stiffness, but can undergo switch-like transitions to a productive force-generating state with small changes in motor parameters or mechanical context. The basis for these switch-like transitions is positive feedback between force buildup and attachment mediated by the force-dependent detachment (catch-bond behavior) of individual myosin motors. Our results clarify how isoform variations in microscopic motor properties and the local mechanical environment can lead to regulation of cellular contractility by myosin II motors.

Materials and Methods

Model description

The main goal of this study was to characterize how force production by myosin II filaments depends on the interplay of network compliance and basic motor properties. To this end, we used a simple version of the cross-bridge model that captured the essential phenomenology of motor-filament interactions with a minimal number of parameters. These parameters could be tuned to capture variations in motor properties, filament size, and network compliance. Below, we describe the design and implementation of this model and a set of benchmarking tests that validate its use for the purposes of our analysis.

We started with the basic mechanochemical cycle shared by all myosin II motors (Fig. 1 A), in which 1) hydrolysis of ATP puts the ATP-bound motor (Myo.ATP) into a primed (Myo.ADP.Pi) state that binds weakly to F-actin; 2) Pi release, transition to a strongly bound state, and an internal conformation change (the powerstroke) convert the stored energy of ATP hydrolysis into force applied to the actin filament; and 3) ADP release followed by 4) ATP rebinding and filament unbinding complete the cycle. We simplified this as follows. First, we assumed that the weak-to-strong binding transition (step 2) could be represented by a first-order rate constant with no force dependence, as previously described (31). This ignored the possibility that the free-energy cost of the powerstroke transition could become limiting under external loads (30,40–42). Second, we assumed that the weak-to-strong transition is rate limiting relative to ATP hydrolysis (20,21) and combined Myo.ATP and Myo.ADP.Pi into a single unbound state, neglecting the small reverse rate of ATP hydrolysis. Third, consistent with in vitro studies, we assumed that ATP is sufficiently abundant for force-dependent ADP release to be rate limiting for motor detachment (17,18,20,21). With these assumptions, the mechanochemical cycle simplifies to a two-state cross-bridge model with a first-order binding rate constant k_on and a force-dependent detachment rate k_off (Fig. 1 A).

Figure 1.

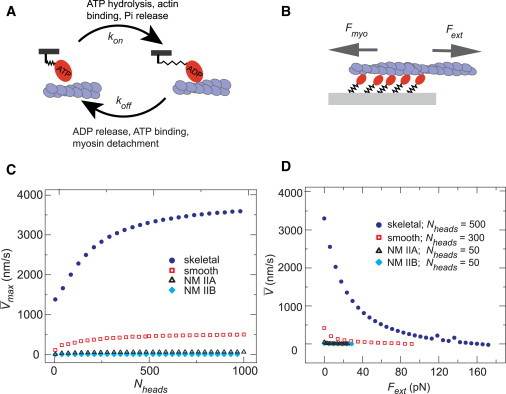
A two-state cross-bridge model reproduced expected gliding velocity and force-velocity curve of motor clusters. (A) Description of the mechanochemical cycle: myosins strongly attached actin filaments at a rate k_on and detached at a rate k_off. (B) Simulation setup: motor heads were attached to a fixed surface. The heads pulled with a force F_myo against an external force F_ext. (C) Mean gliding velocity of an unloaded actin filament ($\overline{\text{V}}$_max) as a function of N_heads for parameters consistent with different myosin isoforms, described in Table 1. Only the velocity while at least one myosin head was attached was considered. (D) Mean gliding velocity with varying F_ext. Each data point is the average of 10⁷ samples over 100 s of simulation time. The standard error of the velocity was smaller than the size of the data points. A full description of the velocity distribution is included in Fig. S9. To see this figure in color, go online.

We represented the cross-bridge as an elastic element tethered at position X₀ to a rigid substratum representing the backbone of the myosin filament or the surface of a glass coverslip (Fig. 1 B). We assumed that the cross-bridge bound actin in a prestrained (post-powerstroke) state at X = X₀ + d_step and exerted a force F(X) = k_x-bridge(X − X₀) before unbinding.

All myosin II isoforms studied thus far exhibit catch-bond behavior in which forces that oppose the motor (resisting loads) reduce the rate of motor detachment from F-actin, while assisting loads increase motor detachment (27–29). Above a critical force, the bond behaves like a traditional slip bond (28). To represent this behavior, we used the force-dependent form of k_off determined experimentally for skeletal muscle myosin II in Guo and Guilford (28):

$$k_{off}\left(F\right)=k_{off}\left(0\right)\left[{\alpha }_{catch}exp\left(-\raisebox{1ex}{$F{x}_{catch}$}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.\right)+{\alpha }_{slip}exp\left(\raisebox{1ex}{$F{x}_{slip}$}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.\right)\right],$$ (1)

where the force F is positive for a resisting load, k_B is Boltzmann’s constant, T is temperature, x_catch and x_slip are characteristic bond lengths, and α_catch and α_slip are prefactors that control the weights of the catch and slip components, respectively (Table 1). The unloaded detachment rate k_off(0) can be tuned to model variation in detachment rates and duty ratios across different isoforms (see below).

Table 1.

Parameter values

Name	Description	Value	Reference
Nheads	number of heads	variable; 2–1000	see Table 2
kon	binding rate	variable; 0.2–10 s−1	see Table 2
koff(0)	unloaded unbinding rate	variable; 0.35–500 s−1	see Table 2
αcatch	see Eq. 1	0.92	(28)
αslip	see Eq. 1	0.08	(28)
xcatch	see Eq. 1	2.5 nm	(28)
xslip	see Eq. 1	0.4 nm	(28)
koff(F)	force-dependent unbinding rate	see Eq. 1	(28)
dstep	step size	5.5 nm	(27)
Kx-bridge	cross-bridge stiffness	0.7 pN/nm	(27)

Simulations

We considered a linear ensemble of myosin crossbridges attached at 5 nm intervals to a rigid substrate (Fig. 1 B) that bound and exerted force upon an actin filament. The actin filament was subjected to a constant external load (Fig. 1 B) and/or attached to a linear spring that represented stiffness of the surrounding network (see Fig. 3 A). Binding sites for myosin II were arrayed at 2.7 nm intervals and motors bound only to the closest site. The spacing of the motors and binding sites we used differed from experimentally measured values (24,43). However, we verified that these differences had modest effects on the outcomes of our simulations and that these effects were negligible given the main goal of this work, which was to study the effects of varying motor properties and network stiffness on force production (see Fig. S1 in the Supporting Material).

Figure 3.

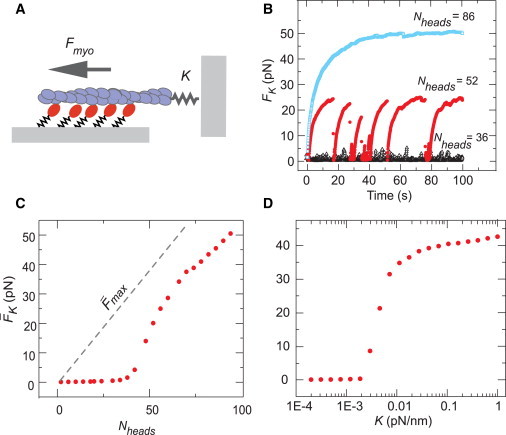
Myosin filament size and actin stiffness determined the magnitude and stability of force generation. (A) Simulations were arranged with fixed myosin heads building force on F-actin anchored to a spring with constant K. (B) Increasing the size of the myosin filament produced a transition from transient force buildup and release to stable force maintenance. Each curve is from a single simulation. (C) Average force on the spring for different values of N_heads. (D) A sharp increase in the average force was also observed with increasing ρ_d(0) and K. Parameter values: (B and C) ρ_d(0) = 0.05 (k_on = 10 s⁻¹, k_off(0) = 191) K = 0.02 pN/nm; (D) ρ_d(0) = 0.05 (k_on = 10 s⁻¹, k_off(0) = 191), N_heads = 74. Each point in C and D is the average of 10000 values from 10 independent simulations of 100 s. The standard error of the forces was smaller than the data points. The full distribution of forces is described in Fig. S10. To see this figure in color, go online.

We sampled binding and unbinding rates stochastically to determine transitions between bound and unbound states (44). Between transitions, we computed the instantaneous F-actin velocity by numerically solving the following equation of motion for F-actin:

$$0=-\gamma \dot{x}-F_{myo}+F_{ext},$$ (2)

where F_myo is the total force exerted by the myosin crossbridges, F_ext is the external force on the filament, and γ is a drag coefficient of 4 × 10⁻⁴ pN ⋅ s/nm. This method is inefficient relative to approaches that assume instantaneous mechanical relaxation between binding/unbinding events (31,40,41). We chose to use it here because it extends naturally to simulations of larger motor/filament ensembles and because computational time was not rate limiting for our analysis.

Simulations began with all motors in an unbound state. However, the distribution of filament velocities converged rapidly relative to the timescale of typical simulations (Fig. S2), and thus the results we report are independent of initial conditions. For most results, we report the mean values obtained by averaging over the duration of at least one simulation (see figure legends for details). For a given quantity X, we use $\overline{X}$ to denote the mean value and σ to represent its standard deviation. In a few cases (see data in Figs. 6 and S8), we indicate values obtained by curve fitting using Wolfram Mathematica with the superscript fit.

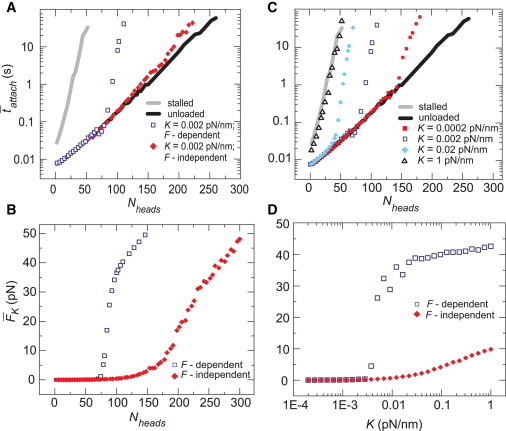
Figure 6.

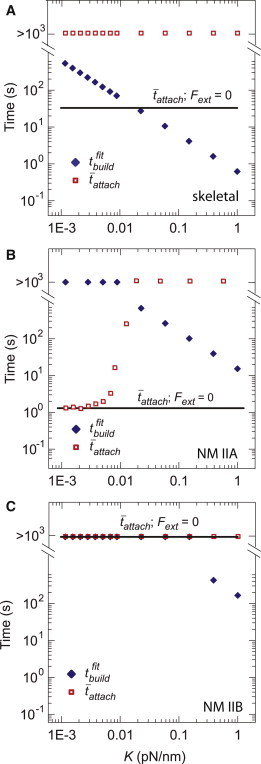
Myosin isoforms are predicted to display varying types of behavior on elastic substrates due to differences in t_attach and t_build. (A) For motor parameters that correspond to skeletal muscle myosin, the unloaded $\overline{\text{t}}$_attach (solid line) was comparable to or larger than ${\text{t}}_{\text{build}}^{\text{fit}}$ (diamonds), producing values of $\overline{\text{t}}$_attach on spring-loaded filaments (open squares) longer than the simulation time of 1000 s for all values of K. (B) For parameters representative of nonmuscle myosin IIA, $\overline{\text{t}}$_attach transitions from values much less than ${\text{t}}_{\text{build}}^{\text{fit}}$ to values much greater than ${\text{t}}_{\text{build}}^{\text{fit}}$ at a threshold value of K, leading to a sharp increase in effective force production. (C) For parameters representative of a nonmuscle myosin IIB type motor, both $\overline{\text{t}}$_attach and ${\text{t}}_{\text{build}}^{\text{fit}}$ are large for all values of K. For all panels, the default parameters in Table 1 and isoform-specific parameters from Table 2 were used. Values of N_heads: (A) 500, (B) 50, and (C) 50. Data points for $\overline{\text{t}}$_attach are average values over 15 simulations of 1000 s, and ${\text{t}}_{\text{build}}^{\text{fit}}$ was calculated using a fit to the scaling relationship in Fig. 4. To see this figure in color, go online.

Benchmarking tests: a simple two-state model captures variation in motor performance for myosin II isoforms

We first tested the ability of the model to capture variation in myosin II isoform performance as measured in gliding assays and force-velocity curves. We assigned isoform-specific values for the attachment rate k_on and the unloaded detachment rate k_off(0) based on in vitro studies (see Table 2). For each set of parameters, we measured the average unloaded gliding velocity, ${\overline{V}}_{\mathit{max}}$, as a function of the number of myosin heads (N_heads). In all four cases, ${\overline{V}}_{\mathit{max}}$ increased monotonically with N_heads and saturated at high values (Fig. 1 C). The maximal gliding velocities agreed reasonably well with those observed experimentally for these four isoforms (24–26). The saturation of ${\overline{V}}_{\mathit{max}}$ with increasing N_heads was consistent with experimental gliding filament assays (24,45) and previous models (31,40,45), and reflected the transition to a detachment-limited regime in which newly attached motors face increasing opposition from previously attached cross-bridges that become negatively strained before detachment (Fig. S3). Notably, the isoform-specific curves collapsed when we scaled the velocity by the maximum (saturated) value, and the x axis by the unloaded duty ratio ρ_d(0) = k_on/(k_on + k_off(0)) (Fig. S4 A).

Table 2.

Tunable parameter values used to represent myosin isoforms in Fig. 1

Parameter	Isoform	Value	Reference
koff(0)	skeletal	500 s−1	(19)
	smooth	22 s−1	(17,18)
	nonmuscle IIA	1.71 s−1	(20)
	nonmuscle IIB	0.35 s−1	(21)
kon	skeletal	10 s−1	(23)
	smooth	1 s−1	(17)
	nonmuscle IIA	0.2 s−1	(20)
	nonmuscle IIB	0.2 s−1	(21)
Nheads	skeletal	500	(14)
	smooth	300	(15,16)
	nonmuscle IIA	50	(12)
	nonmuscle IIB	50	(12)

We further verified that our simulations reproduced the concave force-velocity relationship observed experimentally (46,47) and in previous models (30,33–39) (Fig. 1 D). Again, we found that isoform-specific data collapsed onto a single curve when the force and velocity were scaled by ${\overline{V}}_{\mathit{max}}$ and the average ensemble stall force ${\overline{F}}_{\mathit{max}}$, respectively (Fig. S4 B). In all cases, the average ensemble stall force ${\overline{F}}_{\mathit{max}}$ matched the expected value given by

$${\overline{F}}_{max}=F_{sm}{N}_{heads}{\rho }_d\left(F_{sm}\right),$$ (3)

where F_sm = K_x-bridged_step is the stall force for a single motor, and ρ_d (F_sm) = k_on[k_on + k_off(F_sm)]⁻¹ is the duty ratio of a single motor at stall.

These data confirm that our simple two-state model captures the expected qualitative dependencies of velocity on force and gliding speed on motor density. By varying just two parameters (k_on and k_off), we can approximate the observed variation in unloaded duty ratios and gliding speeds for different myosin II isoforms. Additional mechanochemical steps would be required to explain more detailed behavior, such as oscillations or pauses observed in actin gliding (30,42), or the effects of limiting ATP binding (31) or hydrolysis rates. Isoform-specific differences in other parameters (e.g., x_catch (27,28)) will also affect motor performance. This variation would affect the data collapse shown in Fig. S4, A and B. Nevertheless, this simple model is adequate to assess how variation in binding rates and the presence of load-dependent release impact force buildup in different mechanical contexts.

Results

The number of myosin heads, motor duty ratio, and external force determine myosin filament processivity

We began by assessing the dependence of motor filament processivity on motor properties. Because individual myosin II motors are nonprocessive (20,21,24), assembly of multiple motors into filaments is essential for stable engagement. Consistent with this, increasing either N_heads or ρ_d(0) drove a transition from cycles of rapid attachment/detachment to stable, processive translocation (Figs. 2 A and S5 A). Consistent with a previous model (40), the mean attached time ($\overline{t}$_attach) increased exponentially with both N_heads (Fig. 2 B, black curve) and ρ_d(0) (Fig. S5 C, black curve).

Figure 2.

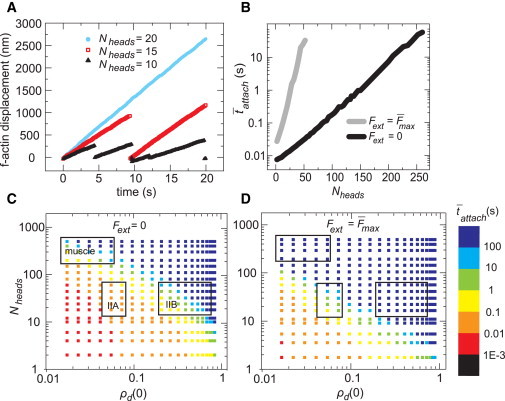
Myosin filament processivity depends on motor properties and external force. (A) Simulated F-actin trajectories for different values of N_heads. The actin filament was assumed to return to its original position upon release by the myosin. Each curve represents a single simulation. (B) The mean attached time as a function of N_heads showed a shift under stalled compared with unloaded conditions. (C) Mean attached time on an unloaded F-actin for a range of N_heads and ρ_d(0). The boxes indicate published values for muscle myosins, nonmuscle myosin IIB, and nonmuscle myosin IIA (see main text for references) starting at the top left and going clockwise. (D) Increased mean attached time for a stalled F-actin over the same range as in (C). Parameter values: (A) ρ_d(0) = 0.34 (k_on = 10s⁻¹, k_off(0) = 19.1 s⁻¹), F_ext = 4 pN; (B) ρ_d(0) = 0.05 (k_on = 10 s⁻¹ and k_off(0) = 191 s⁻¹); (C and D) k_on = 10 s⁻¹. Averages in (B)–(D) were taken over 1000 s of simulation time. The standard error in B was smaller than the data points. The distribution of t_attach is described in Fig. S9. To see this figure in color, go online.

Strikingly, the dependence of attachment time on N_heads and ρ_d(0) was sharply affected by the presence of an external load. As expected from the force-dependent release kinetics of myosin II (27–29), increasing an external load from 0 to 10 pN for fixed values of N_heads and ρ_d(0) both reduced the filament gliding speed and dramatically increased the attachment time (Fig. S5 B). Slip dominated at forces greater than the stall force of the myosin cluster, resulting in negative F-actin displacements (Fig. S5 B, diamonds). In addition, the exponential rise in $\overline{t}$_attach with N_heads (Fig. 2 B) or ρ_d(0) (Fig. S5 C) was significantly steeper for filaments subjected to a stall force (F_ext = $\overline{F}$_max given by Eq. 3) than for unloaded filaments. Thus, external loads steepen the response of $\overline{t}$_attach to motor properties.

To quantify the potential magnitude of this effect for different myosin II isoforms, we constructed phase plots of $\overline{t}$_attach versus filament size and duty ratio for unloaded (Fig. 2 C) and stalled (Fig. 2 D) filaments. We then identified regions in these phase plots corresponding to experimentally measured ranges of filament size and motor duty ratio for skeletal or smooth muscle (14–16,24), nonmuscle IIA (12,13,20), and nonmuscle IIB isoforms (12,13,21,22). A comparison of each matched region across Fig. 2, A and B, suggests that attachment times could vary up to several orders of magnitude between the unloaded and stalled conditions. Thus, changes in myosin filament processivity due to forces from the surrounding environment could be significant for myosin II filaments in vivo.

Motor properties and external stiffness shape the magnitude and stability of force generation

We then examined how changes in filament processivity affect force production. We considered a simple force-generating system consisting of an ensemble of N_heads motors building force on a single actin filament anchored by its barbed end to an elastic spring with a stiffness K that represented compliance of the surrounding network (Fig. 3 A). We varied N_heads or ρ_d(0) to tune filaments through the transition from weak attachment to processive engagement and monitored force buildup. As expected, highly processive ensembles built force steadily to the maximum stall force, F_max (Figs. 3 B and S6 A, blue squares). At intermediate processivities, the initial rate of force buildup was similar, but the filaments detached before reaching F_max (Figs. 3 B and S6 A, red circles). At the smallest values of N_heads or ρ_d(0), no force was built (Figs. 3 B and S6 A, open black triangles).

Plotting the average force generated by myosin filaments, $\overline{F}$_K, revealed a surprisingly sharp dependence on N_heads (Fig. 3 C) and ρ_d(0) (Fig. S6 C). In both cases, the average force remained ∼0 up to a threshold value and then increased rapidly with N_heads or ρ_d(0) to approach the average myosin filament stall force, $\overline{F}$_max, given by Eq. 3.

We observed a similarly sharp dependence of force buildup on network stiffness K. Increasing K produced a transition from no force to intermittent force buildup and release, and finally to stable force generation (Fig. S6 B). Plotting $\overline{F}$ _K versus stiffness revealed a sharp transition from ∼0 to maximal force for a ∼4-fold change in K (Fig. 3 D). The value of K at which this transition occurred depended on both N_heads and ρ_d(0).

The sharp dependence of average force on motor properties or network stiffness reflects a competition between timescales of myosin attachment and force buildup. Intuitively, a sharp increase in force output should occur when the attachment time exceeds the time to build the maximum (i.e., stall) force. Thus, in addition to their affects on attachment time, we must understand how motor properties and network stiffness control the rate of force buildup.

Determinants of characteristic timescale of force buildup

To this end, we varied k_on, k_off, and N_heads and measured the time required to build 70% of the maximum force (t_build) as a function of ${\overline{F}}_{\text{max}}$, ${\overline{V}}_{\mathit{max}}$, and K. As expected, faster motors built force more rapidly, such that t_build scaled linearly with $1/{\overline{V}}_{\mathit{max}}$ (Fig. 4 A). For a constant motor speed, t_build should also increase in proportion to the number of steps required to reach the stall force. Consistent with this, t_build was directly proportional to ${\overline{F}}_{\mathit{max}}$ (Fig. 4 A) and inversely proportional to K (Fig. 4 B). Combining these, we observed a single scaling relationship for t_build as a function of all three parameters (Fig. 4 C)

$$t_{build}\sim \frac{{\overline{F}}_{max}}{K{\overline{V}}_{max}}.$$ (4)

Interestingly, we observed a similar scaling when we removed the force dependence of myosin release, albeit with a lower slope (Fig. 4 C, dark blue diamonds). Thus, myosin motors build force more quickly on stiffer substrates regardless of the exact mechanochemistry. This suggests that force-dependent kinetics may not be required for experimentally observed increases in the rate of force generation with external stiffness of contractile cells as previously assumed (11,48,49).

Figure 4.

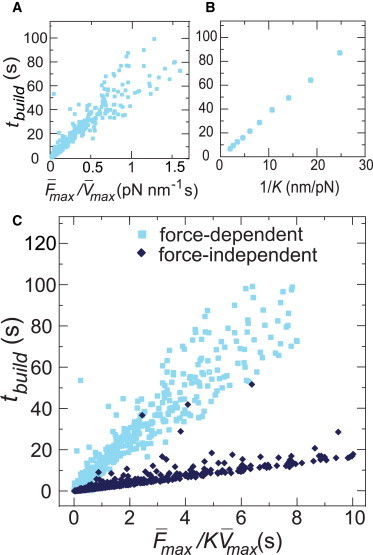
Characteristic time required for processive motors to build to stall, t_build, scaled as $\overline{\text{F}}$_max$\overline{\text{V}}$ max⁻¹K⁻¹. (A) A linear increase of t_build was observed with $\overline{\text{F}}$_max / $\overline{\text{V}}$_max, with K = 0.01 pN/nm. The values of k_off(0), k_on, and N_heads were varied from 10 s⁻¹ to 191 s⁻¹, 1 s⁻¹ to 10 s⁻¹, and 6 to 600, respectively. (B) t_build also increased linearly with 1/K. Parameter values: N_heads = 50, ρ_d(0) = 0.05 (k_on = 10 s⁻¹ and k_off(0) =191 s⁻¹). (C) Final scaling relationship for both force-dependent and force-independent motors. The same ranges of k_off(0), k_on, and N_heads as in A were used, with K ranging from 0.001 to 1 pN/nm. Each data point is from a single simulation of 200 s. To see this figure in color, go online.

Force-dependent myosin kinetics produced a switch-like transition from nonprocessive to processive force generation

The above analysis shows that motor properties and network stiffness control force output by controlling the balance of t_attach and t_build. In addition, given the force-dependent release kinetics, t_attach should increase during force buildup, and this increase could sharpen the response of the force output to varying N_heads, duty ratio, or external stiffness. For myosin filaments building force against an elastic load, the mean attachment time ($\overline{t}$_attach) should fall between the two extreme values measured under unloaded or stalled conditions (Fig. 2 B). Indeed, for relatively small myosin filaments (Fig. 5 A, open squares), the values of $\overline{t}$_attach resembled those of unloaded motors (Fig. 5 A, black line). Increasing N_heads produced a sharp, faster-than-exponential increase in $\overline{t}$_attach (Fig. 5 A, open squares) that coincided with a sharp increase in average force (Fig. 5 B, open squares). Absent force-dependent kinetics, both the faster-than-exponential increase in $\overline{t}$_attach and the sharp increase in force were completely abolished, and the dependence of mean attachment times on N_heads was very similar to that of unloaded motor ensembles (compare red diamonds and dark blue open squares in Fig. 5, A and B). Thus, the number of motors required to generate a given level of force was significantly higher for motors lacking force-dependent kinetics, and the rate of force increase with N_heads at a threshold value was lower.

Figure 5.

Force-dependent myosin kinetics produced a switch-like transition into a processive state. (A) The average attached interval, $\overline{\text{t}}$_attach, increased with N_heads for unloaded, stalled, and spring-loaded actin filaments. For the spring-loaded case, curves in which the force dependence of k_off was either included or neglected are shown. (B) Average force output in the spring-loaded cases from (A). (C) The steep increase of $\overline{\text{t}}$_attach for spring-loaded actin filaments was shifted with varying K. (D) Force production at a single value of N_heads was sharply dependent on stiffness when k_off was force dependent. Force-independent motors showed a weaker dependence on K. N_heads = 50. In all panels, ρ_d(0) = 0.05 (k_on = 10 s⁻¹ and k_off(0) = 191). Each data point represents an average over 15 200 s simulations. The standard error was smaller than the size of the data points. To see this figure in color, go online.

These data reveal how force-dependent kinetics mediate a positive feedback in which force buildup promotes increased attachment and further force buildup. This feedback sharpens the effect of an increasing duty ratio or filament size such that small increases in either quantity above threshold values cause a rapid transition from a state in which transient attachments produce little force to one in which force is built and maintained over long timescales. As a consequence of this feedback, large force fluctuations (depicted by the red circles in Figs. 3 B and S6, A and B) occur only within narrow ranges of N_heads or the motor duty ratio.

Mechanical cues regulate the switch to processive force generation

The same positive feedback could also explain the increased sensitivity of force production to environmental stiffness, as shown in Fig. 3 D, because motor filaments will build force faster on stiffer substrates and thus engage positive feedback more readily. Consistent with this, the sharp increase in average force with increasing network stiffness was completely abolished in motor filaments lacking force-dependent kinetics (red versus dark blue traces in Fig. 5 D).

Moreover, we found that different levels of external stiffness shifted the threshold filament size (Fig. 5 C) or duty ratio (not shown) required to engage positive feedback. In very stiff environments (i.e., when K exceeded the myosin cross-bridge stiffness of 0.7 pN/nm), $\overline{t}$_attach was similar to that expected from stalled motors (Fig. 5 C, gray line) because the motors reached stall very quickly (Fig. 5 C, open triangles). In softer environments, the threshold filament size required to engage positive feedback increased with decreasing K from N_heads ∼1 for K = 1 pN/nm to N_heads ∼40 for K = 0.02 pN/nm, and to N_heads ∼150 for K = 0.0002 pN/nm (Fig. 5 C).

Finally, we found that the same positive feedback could also render force production sensitive to an externally applied force, as could be seen by holding K constant and applying a small constant load (F_ext) to the actin filament (Fig. S7 A). As shown in Fig. S7 B, increasing F_ext from 0% to 7% of the myosin filament stall force, F_max, reduced the threshold filament size required to transition from nonprocessive to processive engagement from N_heads ∼100 to N_heads ∼60. Alternatively, increasing the externally applied force for fixed motor parameters and filament size produced a very sharp increase in average force over a narrow range of F_ext. For the motor parameters used in Fig. S7 C, an increase in F_ext from 0 to 1 pN (∼5% of the stall force) produced an increase in the average force from ∼0 to F_max. Thus, the myosin catch bond renders force production on an elastic substrate highly responsive to relatively small variations in applied force.

Myosin II isoform performance in elastic networks

To assess the potential consequences of the behaviors described in Figs. 2, 3, 4, and 5 on different myosin II isoforms, we utilized parameters that reflected N_heads and enzymatic rates of skeletal muscle myosin, nonmuscle myosin IIA, and nonmuscle myosin IIB, and considered the timescales of attachment and force buildup as the environmental stiffness K was varied.

For parameters consistent with skeletal muscle myosin filaments (Table 2; Fig. 1), the unloaded $\overline{t}$_attach was ∼70 s. As K varied from 0.001 to 1 pN/nm, $t_{build}^{fit}$ obtained from the scaling relationship of Fig. 4 decreased from ≈400 s to 0.5 s, while $\overline{t}$_attach rapidly increased to values exceeding our simulation time of 1000 s (Fig. 6 A). Thus, the combination of the large filament size and high speed of skeletal muscle myosin II allowed for a rapid and stable buildup of force over a wide range of stiffness.

Using motor parameters and filament size appropriate for nonmuscle myosin, IIB yielded stable attachment ($\overline{t}$_attach > 1000 s) in unloaded conditions for all values of K (Fig. 6 C). However, $t_{build}^{fit}$ also was >1000 s for K < 0.1 pN/nm, decreasing to ∼100 s only for K > 1 pN/nm. These data suggest that myosin IIB is well tuned to function as a high-affinity cross-linker over a wide range of environmental stiffness and force, as speculated previously (20,21). However, the exceedingly slow force buildup time suggests that myosin IIB would be very ineffective at generating force against actin networks that turn over on timescales relevant for rapid morphogenic change (1–100 s; see Discussion).

Intriguingly, when we chose parameters appropriate for nonmuscle myosin IIA filaments, our simulations predicted qualitatively distinct behaviors at low and high K (Fig. 6 B). When K is large, myosin IIA filaments are predicted to bind processively at stall. However, for K < 0.01 pN/nm, the time required to build force was too long to engage positive feedback and switch to stable attachment, so the attachment time remained quite short ($\overline{t}$_attach < 1 s). Around 0.01 pN/nm, a sharp transition to processive force buildup occurred as $t_{build}^{fit}$ decreased from 500 to 1 s with a concomitant increase in $\overline{t}$_attach. These results suggest that myosin IIA may be poised to serve as a low-affinity cross-linker at low stiffness, but as a processive force generator at high stiffness.

Finally, we assessed the functional consequences of mixing myosin II isoforms within individual filaments (50), focusing on mixtures of nonmuscle myosin IIA and IIB, and holding filament size constant. Not surprisingly, the model predicted values for filament processivity, stall force, and filament gliding speeds intermediate between those of pure IIA and IIB filaments (the latter reflects a competition between the slower IIB and faster IIA motors that is mitigated by force-dependent release kinetics) (Fig. S8, A–E). Both $t_{build}^{fit}$ and $\overline{t}$_attach are predicted to increase with an increasing fraction of IIB motors. At low K, where $t_{build}^{fit}$ is already prohibitively high for force buildup, the simulations predict a sharp increase in $\overline{t}$_attach, implying a sharp increase in cross-linking affinity (Fig. S8 F). At higher K, where the filament processivity is high (i.e., above the force buildup transition in Fig. 6 B), we observed a modest increase in $t_{build}^{fit}$ with increasing fractions of IIB (Fig. S8 G). Thus, small to moderate amounts of IIB in a composite filament could yield large increases in affinity at low K, with relatively minor increases of force buildup time for the same filament at higher K. These mixed filaments would still allow for faster force buildup than filaments composed entirely of myosin IIB.

Discussion

Cross-bridge models have been used extensively to model force generation by skeletal muscle contracting against a constant load (30,33–38). Here, we used this approach to examine how the production and maintenance of force is influenced by the filament size, motor duty ratio, and actin gliding velocity, which vary among myosin II isoforms, as well as the force dependence of the motor duty cycle, which all isoforms possess. We found that the amount of force generated against loads of varying stiffness is regulated by the relative timescales of force buildup and force relaxation due to myosin filament detachment, and characterized the parameters that control these two quantities.

Our results provide insight into how cellular contractility may be regulated by internal or external mechanics, or the presence of myosin isoforms with varying properties. For example, the mechanical stiffness, K, affects the time to build force through t_build ∼ ${\overline{F}}_{\mathit{max}}/K\ast {\overline{V}}_{\mathit{max}}$. At small K, this timescale may limit the amount of force that is built before force relaxation (due to myosin filament detachment or other mechanisms) occurs. However, if this timescale is sufficiently small compared with the relaxation times, myosin filaments will generate their stall force and further increases in K will not affect the force output. In dynamic cellular networks, other processes, such as actin cross-linker unbinding (51,52) and F-actin turnover (53), may help to set the timescale of force relaxation.

Therefore, the mechanosensitivity of force generation does not require catch-bond kinetics as has been assumed in previous models (11,48,49). However, the catch bond allows the timescale of myosin attachment, t_attach, to depend on external force or stiffness. In our simulations, this created a positive feedback between generated force and myosin filament attachment. As a result, myosin filaments could transition from a low-force-generating state (t_build ≫t_attach) to a more processive state, and the dependence of force output on K was sharper when the catch bond was included. A similarly sharp transition also occurred with small changes in the myosin filament parameters. We expect that there are many ways in which cells could tune myosin filaments into a regime where small forces engage this feedback and effectively turn on contractility. The size and density of myosin filaments, affinity of myosin for different actin network geometries, and actin network viscoelasticity may all vary significantly and be regulated spatiotemporally. For example, the nonlinear elasticity of actin networks is highly dependent on internal or external prestress and network connectivity (54). Relaxation due to crosslinker unbinding (51,52) or actin turnover (53) may occur on the order of 1–100 s.

We predict that parameter values spanned by different isoforms of myosin II could produce distinct patterns of force generation in environments with varying stiffness due to these effects of relative timescales. Motor clusters representative of skeletal muscle myosin processively built force over the entire range of stiffness we explored. In contrast, we expect the nonmuscle myosin isoforms to show greater selectivity for stiffness or other mechanical signals. In the case of a nonmuscle IIA-like filament, the attachment time and average force showed a steep increase with increasing stiffness, consistent with the positive feedback described above. For myosin IIB, the attachment time even for an unloaded filament was over 1000 s. However, force generation on soft substrates is likely limited due to the long timescale of force buildup, and in this regime the filaments may function primarily as actin cross-linkers. Although it has been proposed that the nonmuscle myosin IIA and nonmuscle myosin IIB duty cycles are better tuned for tension generation and tension maintenance, respectively (20,21), this is the first study, to our knowledge, to demonstrate this behavior with experimentally measured parameters and reveal its dependence on stiffness. Recent work has shown copolymerization of nonmuscle myosin isoforms in vivo (50), which may serve as an additional regulatory mechanism to construct myosin filaments with varying biophysical properties (Fig. S8).

Finally, our results have implications for coarse-graining of myosin activity in simulations and analytical work. For example, alternative representations of myosin activity as either time-independent force dipoles (55) or force dipoles that transiently pull and release (56) within a continuum elastic or fluid medium have been used to predict the strain field from interacting dipoles and the mechanical properties of active networks. Our results suggest that the appropriate representation will depend on the myosin isoform and the mechanical context in which the motor operates. More detailed representations that allow the dipole kicking rate to depend on force may be essential to capture the force-dependent dynamics that underlie large-scale deformations of an actomyosin network (57). How motor properties influence an actomyosin network’s ability to produce force or change its shape, and how they may modulate such activity if the network is subjected to external force or tethering to an external substrate are interesting questions for future study.