Registered and Antiregistered Phase Separation of Mixed Amphiphilic Bilayers

Abstract

We derive a mean-field free energy for the phase behavior of coupled bilayer leaflets, which is implicated in cellular processes and important to the design of artificial membranes. Our model accounts for amphiphile-level structural features, particularly hydrophobic mismatch, which promotes antiregistration, in competition with the direct transmidplane coupling usually studied, which promotes registration. We show that the phase diagram of coupled leaflets allows multiple metastable coexistences, and we illustrate the kinetic implications of this with a detailed study of a bilayer of equimolar overall composition. For approximate parameters estimated to apply to phospholipids, equilibrium coexistence is typically registered, but metastable antiregistered phases can be kinetically favored by hydrophobic mismatch. Thus, a bilayer in the spinodal region can require nucleation to equilibrate, in a novel manifestation of Ostwald’s rule of stages. Our results provide a framework for understanding disparate existing observations in the literature, elucidating a subtle competition of couplings and a key role for phase-transition kinetics in bilayer phase behavior.

Introduction

Phase separation in amphiphilic bilayers is of great interest, both because of cellular roles of lipid rafts (1,2) and as a means of designing function into artificial membranes. A full understanding of their rich phase behavior requires consideration of the separate, yet coupled, leaflets of the bilayer (3–9). Such interleaflet coupling is especially important in, for example, mechanisms of protein localization via lipid demixing (2).

Experiment and simulation yield disparate results. Observations of registered domains (10–12) (Fig. 1 a) imply a mismatch free energy per area favoring registration (R), which we call direct coupling. However, R domains of different phases typically differ in hydrophobic thickness, arising from different preferred lengths of the mixed species due to differences in the molecular length and degree of ordering of their tails. In model phospholipid bilayers, typical measured thickness differences are between ∼0.2 and ∼1.6 nm for liquid-ordered versus liquid-disordered (L_o-L_d) lipid phases (13), and slightly more for liquid-gel coexistence (14). Such hydrophobic mismatch can be alleviated by antiregistration (AR) (Fig. 1 b); thus, an indirect coupling favoring AR competes with the direct coupling. AR has been inferred experimentally on the single-amphiphile level (15,16), whereas AR domains have appeared in L_o-L_d (17) and liquid-gel (18,19) simulations, and atomic force microscopy (AFM) on solid-supported bilayers has shown R gel domains decaying into AR (14).

Figure 1.

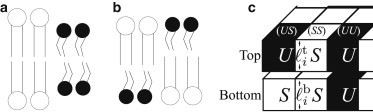
(a) Registration (R), satisfying the direct coupling but with thickness mismatch penalized by the indirect coupling. (b) Antiregistration (AR), without thickness variation but with a mismatch penalty from the direct coupling. (c) Lattice model for coupled bilayer leaflets.

Despite its wide practical importance, there is still no full theoretical picture of this complex behavior. Existing theories (3,7,8) treat the bilayer as two phenomenologically coupled phase-separating leaflets, with an order parameter to describe the demixing transition. The phenomenological free energies and parameters in these models do not relate directly to molecular or structural features of bilayers. Hydrophobic mismatch is often not explicitly included in coarse-grained modeling (3,5,7–9,20), so that the competition between direct and indirect interleaflet couplings described above cannot be captured. (Hydrophobic mismatch appears naturally in more complex molecular models (21), and it was included in coarse-grained modeling in Wallace et al. (22), but without resolving the individual leaflets.)

We approach the problem by deriving the bilayer’s local free-energy density from a lattice model of the coupled leaflets, in which simplified molecular interactions and bilayer structural features, including hydrophobic mismatch, appear explicitly. We show how competing interactions (favoring Fig. 1, a and b) lead to phase diagrams with multiple, competing coexistences. This implies competing modes of phase separation, and helps reconcile observations of R and AR in the literature (10–12,14,17,18).

As a test case, we study how AR competes against R for a bilayer containing an overall equimolar mixture of species in both leaflets. AR can become equilibrium, which arises from treating hydrophobic mismatch among individual molecules in the bulk (not only at domain boundaries), although most expected parameters yield equilibrium R. However, metastable AR states are still kinetically favored by hydrophobic mismatch. Hence, a bilayer in the conventional spinodal region can, paradoxically, require nucleation to reach equilibrium. Thus, metastable phases can interfere with bilayer domain registration and even prevent equilibration.

Materials and Methods

Lattice bilayer model

To obtain the local free energy, we begin with a lattice model (Fig. 1 c) for the two leaflets and their competing direct and indirect couplings. A local patch of the bilayer is modeled as a square lattice of L² = N sites, where each site contains a top (t) and a bottom (b) leaflet amphiphile. The lattice spacing is the lateral distance between amphiphiles, a ∼ 0.8 nm for phospholipids. Each amphiphile has a hydrophobic length ${\ell }_i^{\text{t}\left(\text{b}\right)}$. We define the bilayer thickness as $d_i\equiv {\ell }_i^{\text{t}}+{\ell }_i^{\text{b}}$, and the difference between the two layer thicknesses as ${\text{Δ}}_i\equiv {\ell }_i^{\text{t}}-{\ell }_i^{\text{b}}$. Extension of the tails also entails greater tail ordering, which we implicitly map onto the length variables ${\ell }_i^{\text{t}\left(\text{b}\right)}$ (23). We define ${\hat{\varphi }}_i^{\text{t}\left(\text{b}\right)}=1\text{or }0$ if the top (bottom) of site i contains an S- or U-species amphiphile. These labels are chosen to suggest saturated and unsaturated lipids, where S prefers a longer, more ordered tail structure; however, they can represent any two species, or two of the lipid phases (L_o, L_d, or gel) available to a ternary (S + U + cholesterol) bilayer (20,24–26). (We use “phase” to refer to a bilayer phase, i.e., a given combination of the order parameters in each leaflet (7); lipid phase refers to particular ordering types (L_o, L_d, gel, etc.) which, in our model, are abstracted onto the binary S and U species (20,24,25).) Each lattice site may be pairwise R ($SS$ or $UU$), or AR ($SU$ or $US$). The species-dependent ideal hydrophobic lengths are ${\ell }_{S0},{\ell }_{U0}$. We define ${\text{Δ}}_0\equiv {\ell }_{S\text{0}}-{\ell }_{U\text{0}}$, $d_0\equiv {\ell }_{S\text{0}}+{\ell }_{U\text{0}}$. We choose ${\ell }_{S\text{0}}>{\ell }_{U\text{0}}$, although this choice is arbitrary.

The exact lattice Hamiltonian considered is

$$H=\sum _{\langle i,j\rangle }\left(V_{{\hat{\varphi }}_i^{\text{t}}{\hat{\varphi }}_j^{\text{t}}}+V_{{\hat{\varphi }}_i^{\text{b}}{\hat{\varphi }}_j^{\text{b}}}\right)+\sum _{\langle i,j\rangle }\frac{1}{2}\tilde{J}{\left(d_i-d_j\right)}^2+\sum _i\frac{1}{2}B{\left({\text{Δ}}_i\right)}^2+\sum _i\frac{1}{2}\kappa \left({\left({\ell }_i^{\text{t}}-{\ell }_0^{\text{t}i}\right)}^2+{\left({\ell }_i^{\text{b}}-{\ell }_0^{\text{b}i}\right)}^2\right),$$ (1)

where ${\ell }_0^{\text{t}\left(\text{b}\right)i}={\ell }_{S\text{0}}$ or ${\ell }_{U0}$ for an S or a U amphiphile, respectively, at the top (bottom) of site i.

The first two terms of Eq. 1 are nearest-neighbor interactions. An Ising interaction V_uv occurs among S and U amphiphiles within each leaflet separately, representing interactions independent of amphiphile length, such as those between headgroups. The hydrophobic penalty $\tilde{J}$ acts on the total bilayer thickness, indirectly coupling the top and bottom amphiphiles of a given site via the surrounding thickness, and favors AR to minimize thickness variation (Fig. 1 b). The final two terms are on-site terms; B is a direct coupling that favors R, similar to the conventional mismatch free-energy density γ (3,4,26–28) by penalizing differences in length (thus tail ordering) between the top and bottom amphiphiles of a site. κ penalizes length stretching relative to the ideal lengths of the species.

Local free energy

Our goal is the free energy per lattice site f as a function of the coarse-grained local compositions ${\varphi }^{\text{t}\left(\text{b}\right)}\equiv N_S^{\text{t}\left(\text{b}\right)}\text{/}N$, bilayer thickness $\overline{d}\equiv \sum d_i\text{/}N$, and thickness difference $\overline{\text{Δ}}\equiv \sum {\text{Δ}}_i\text{/}N$. We calculate this within a mean-field approximation (Appendix A) in which the neighbor terms of Eq. 1, which involve V and $\tilde{J}$, are approximated by on-site terms. The coarse-grained local variables impose the constraints

$$\sum _{\alpha }{N}_{\alpha }{d}_{\alpha }=N\overline{d},$$ (2a)

$$\sum _{\alpha }{N}_{\alpha }{\text{Δ}}_{\alpha }=N\overline{\text{Δ}},$$ (2b)

$$N_{SU}-N_{US}=\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)N,$$ (2c)

$$N_{SS}+N_{SU}={\varphi }^{\text{t}}N,$$ (2d)

$$N_{UU}+N_{US}=\left(1-{\varphi }^{\text{t}}\right)N,$$ (2e)

where $N_{\alpha }$ are the occupancies of the four possible site types $\alpha \in \left\{SS,UU,SU,US\right\}$ with thickness variables $d_{\alpha },{\text{Δ}}_{\alpha }$. After some work, we find (see Eq. A19) that the desired local free energy per site $f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)$ is given by minimizing

$$f^{\text{′}}N=\sum _{\alpha }\left(N_{\alpha }{H}_{\alpha }+k_{\text{B}}T{N}_{\alpha }\text{ln}{N}_{\alpha }\right)-2VN{\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}^2-2VN{\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)}^2,$$ (3)

subject to Eqs. 2a–2e, where $H_{\alpha }$ contains the thickness-dependent, mean-field interactions for each site type (cf. Eq. A15),

$$H_{\alpha }=\frac{1}{2}J{\left(d_{\alpha }-\overline{d}\right)}^2+\frac{1}{2}B{\left({\text{Δ}}_{\alpha }\right)}^2+\frac{1}{2}\kappa \left({\left({\ell }_{\alpha }^{\text{t}}-{\ell }_0^{\text{t}\alpha }\right)}^2+{\left({\ell }_{\alpha }^{\text{b}}-{\ell }_0^{\text{b}\alpha }\right)}^2\right),$$ (4)

in which ${\ell }_0^{\text{t}\alpha }={\ell }_{A0}$, ${\ell }_0^{\text{b}\alpha }={\ell }_{B0}$ for $\alpha =AB$, and $J\equiv 4\tilde{J}$. $V\equiv V_{10}-\left(1/2\right)\left(V_{11}+V_{00}\right)$ sets the strength of the length-independent interaction.

f may be minimized over thickness variables $\overline{d}$ and $\overline{\text{Δ}}$ to yield annealed values (equilibrated at given local composition) ${\overline{d}}^{\left[\text{ann}.\right]}={\text{Δ}}_0\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)+d_0$ and ${\overline{\text{Δ}}}^{\left[\text{ann}.\right]}=\kappa {\text{Δ}}_0\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)/\left(2B+\kappa \right)$. This gives the local free energy as a function of the local compositions of the top and bottom leaflets,

$$f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)\equiv f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},{\overline{d}}^{\left[\text{ann}.\right]},{\overline{\text{Δ}}}^{\left[\text{ann}.\right]}\right).$$ (5)

Explicit expressions are given in Eqs. A24 and A26. Symmetry under exchange of labels S and U implies symmetry under ${\varphi }^{\text{t}}\to 1-{\varphi }^{\text{t}},{\varphi }^{\text{b}}\to 1-{\varphi }^{\text{b}}$. Differing molecular area (for example) would break this symmetry but not affect the qualitative conclusions (in such a case, equimolar should be read as equal area fractions). Identical material parameters within each leaflet imply symmetry under ${\varphi }^{\text{t}}\to {\varphi }^{\text{b}},{\varphi }^{\text{b}}\to {\varphi }^{\text{t}}$; the qualitative effect of breaking this assumption is demonstrated in (7).

We emphasize that f describes the bulk free energy of a local patch of bilayer. Hence, within f, neighbor interactions V and J penalize composition or thickness mismatch at the microscale, i.e., among individual amphiphiles in the local patch. f does not include the contribution of boundaries between domains, which are irrelevant for large domains and so do not affect phase equilibria. Their important effect on kinetics is examined in the section Growth rates of competing modes.

Results

We now study the implications of the free energy derived from our model. We show how a particular local free-energy landscape relates to the phase diagram of the system, and then study how model parameters affect the coexistences and instabilities governing an example bilayer in which the overall composition of each leaflet is an equimolar mixture of S and U.

Parameters

First, we discuss the estimated values/ranges and physical content of our model interaction parameters V, J, B, and κ. Full details can be found in Appendix C. The length-independent Ising interaction strength V controls whether the leaflets would phase-separate in the absence of coupling ($J=B=0$, such that each leaflet acts as an independent Ising lattice). In the mean-field approximation, the Ising model requires $V>V_0\equiv 0.5k_{\text{B}}T$ for phase separation, so we test values of V above and below this threshold.

The indirect coupling $\tilde{J}$ quantifies the penalty for mismatched total hydrophobic thickness. We take a fiducial value $\tilde{J}\approx 0.8k_{\text{B}}T{\text{nm}}^{-2}$, as estimated in Wallace et al. (22) as a surface tension for hydrocarbon tails in contact with the watery headgroups of phospholipids. This gives $\tilde{J}\approx 0.5a^{-2}{k}_{\text{B}}T$, thus $J\approx 2a^{-2}{k}_{\text{B}}T$, and varying J corresponds to varying the strength of hydrophobic mismatch/hydrophobicity.

The direct coupling parameter B plays a similar role to the interleaflet mismatch energy γ, for which widely varying estimates have been made (3,4,27,28). The mechanism responsible is unclear. One proposal is tail interdigitation entropy (3), whereas Garbès Putzel et al. (4) consider an interplay of entropic and enthalpic effects (such as tail orientation interactions and gauche bond energy) calculated from a molecular mean-field theory. Our specific choice of coupling B to leaflet thickness, hence tail ordering, captures the idea that tail structural features underlie the direct coupling (3,4), but it does not qualitatively affect the results; it can simply be thought of as leading to an effective γ (see Fig. 5 and Eqs. C6–C8).

Figure 5.

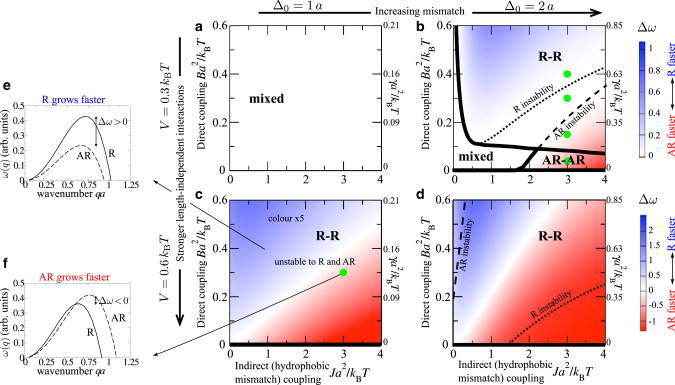
(a–d) Stability diagrams for $\left(0.5,0.5\right)$ overall composition, for varying indirect and direct couplings J and B and values of the length-independent interaction strength V and mismatch ${\text{Δ}}_0$. Thick lines and bold labels indicate where the equilibrium state is R-R, AR-AR, or mixed. Thin lines denote where the bilayer is unstable to R/AR modes and are labeled on the side of the line to which they refer. The secondary (right) axis indicates approximate values of the interleaflet mismatch free energy per area γ (Eq. C6). Colors indicate growth rates from linear stability analysis of the initial homogeneous state, $\text{Δ}\omega >0$ (R mode faster (blue)) and $\text{Δ}\omega <0$ (AR faster (red)). Different color scales are used for visibility, since comparison of growth rates between different panes of the figure has little meaning. In (c), the color range is reduced five times from that indicated on (d). The green dots in (b) correspond to Fig. 4, and that in (c) corresponds to Fig. 2. (e and f) Illustrative q-dependent growth rates. To see this figure in color, go online.

The stretching modulus κ can be related to the area stretching modulus ${\kappa }_A$ —we use $\kappa =3a^{-2}{k}_{\text{B}}T$, corresponding to ${\kappa }_A\approx 60k_{\text{B}}T{\text{nm}}^{-2}$, in the range for lipid bilayers at 300 K (29–31). Details of this mapping, as well as that from B to γ, appear in Appendix C.

Due to the simplicity of our model, precisely assigning the meaning and values of parameters is impossible; for example, amphiphiles could respond to length mismatch by exploring tilt and splay as well as the stretching modeled by our κ. Instead, our aim is to succinctly capture important structural features of the bilayer and study their effects over a range of reasonable estimates for the parameters involved.

Given a quench into a phase-separating region, we broadly expect increased direct coupling B to penalize the existence of pairwise AR sites $SU$ and $US$, whereas increased hydrophobic penalty J will penalize the mixing of sites with different ideal thickness ($SS$, $UU$, and SU/US). Varying stiffness κ affects the characteristic energy scale of the interleaflet couplings; $\kappa \to 0$ would represent infinitely floppy amphiphiles that can adjust their length and structuring so as to experience no indirect or direct coupling energy.

Phase diagram

Our $f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)$ plays the same role as the local free energies postulated in Garbès Putzel and Schick (7) and Wagner et al. (8), except that we have derived it explicitly from the lattice model. In a similar way, it can be used to find a phase diagram (7,8), which we now perform for the particular local free-energy landscape shown in Fig. 2. Hereafter, we assume no flip-flop or solvent exchange, so the overall composition (total proportion of S and U) within each leaflet is conserved. The total free energy F is found by integrating f laterally over the entire bilayer (8). The equilibrium state—which coexisting phases are present at equilibrium—is then determined by minimizing F subject to constraints specifying the overall leaflet compositions

$$\begin{array}{c}\sum ^{\text{phases}}{\theta }_n=1,\\ \sum ^{\text{phases}}{\theta }_n{\varphi }_n^{\text{t}}={\text{Φ}}^{\text{t}},\\ \sum ^{\text{phases}}{\theta }_n{\varphi }_n^{\text{b}}={\text{Φ}}^{\text{b}},\end{array}$$ (6)

where ${\theta }_n$ label the coexisting phases’ area fractions. The overall (conserved) leaflet compositions in Eq. 6 are labeled ${\text{Φ}}^{\text{t},\text{b}}$, but by convention it is unnecessary to introduce a new symbol, as the distinction between local and overall compositions is clear from context (8).

Figure 2.

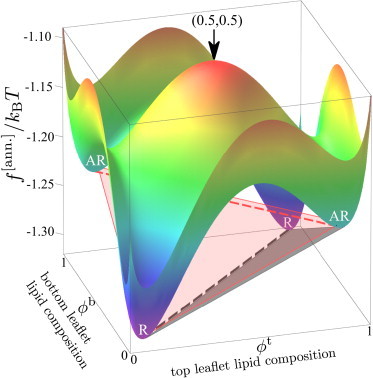
Local free-energy landscape for the parameter point indicated by the green dot in Fig. 5c. The AR-AR and R-R central tie-lines (dashed lines) of Fig. 3 are superimposed, along with two illustrative tangent planes corresponding to three-phase triangles (equilibrium R-R-AR (black shading) and metastable AR-AR-R (red shading)). To see this figure in color, go online.

To stably (or metastably) coexist, phases must have 1) equal chemical potential ${\mu }^{\text{t}}\equiv \partial f/\partial {\varphi }^{\text{t}}$ in the top leaflet; 2) equal chemical potential ${\mu }^{\text{b}}\equiv \partial f/\partial {\varphi }^{\text{b}}$ in the bottom leaflet; and 3) equal surface tension $f-{\mu }^{\text{t}}{\varphi }^{\text{t}}-{\mu }^{\text{b}}{\varphi }^{\text{b}}$ (7). This is equivalent to drawing common tangent planes touching the surface $f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)$ at two or three points, which define two-phase tie-lines or triangles of three-phase coexistence. This concept is illustrated on Fig. 2.

The phase diagram derived from Fig. 2 is shown in Fig. 3. Equilibrium coexistences are qualitatively identical to those in Garbès Putzel and Schick (7) and Wagner et al., (8). Spinodal lines around each free-energy minimum indicate the region of local stability (8). The R central tie-line runs along ${\varphi }_{\text{R}}^{\text{b}}\left({\varphi }^{\text{t}}\right)={\varphi }^{\text{t}}$ through $\left(0.5,0.5\right)$, linking the R minima of Fig. 2. (Hereafter, we use $\left(0.5,0.5\right)$ as shorthand for ${\varphi }^{\text{b}}={\varphi }^{\text{t}}=0.5$.) It sits within a region of two-phase R-R equilibrium. This is surrounded by triangles of three-phase R-R-AR equilibrium, where two R phases coexist with one AR phase. These connect to two-phase arms of R-AR coexistence.

Figure 3.

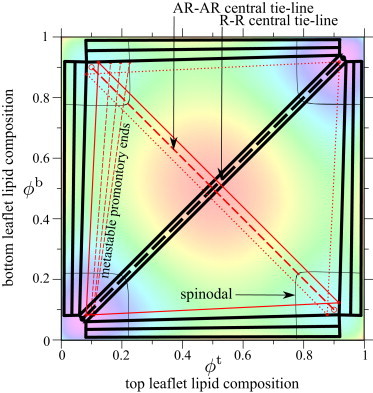
Phase diagram calculated from the local free-energy landscape in Fig. 2. Thick black tie-lines or triangles show equilibrium two- or three-phase coexistence. Thin red lines or triangles mark metastable two- or three-phase coexistence. One of the overlapping AR-AR-R triangles is dotted for clarity. A two-phase promontory is shown; other metastable two-phase regions are omitted. Thin black lines mark the spinodals. To see this figure in color, go online.

We also show some metastable coexistences, which satisfy the common tangent condition but do not fully minimize F. Metastable AR-AR-R triangles overlap one another, and a central AR-AR tie-line runs along ${\varphi }_{\text{AR}}^{\text{b}}\left({\varphi }^{\text{t}}\right)=1-{\varphi }^{\text{t}}$. Each pair of free-energy minima is associated with a metastable promontory that encroaches on an equilibrium three-phase region. This is illustrated for one promontory on the figure; a similar idea applies to each pair of minima. Because tie-line endpoints must not be unstable, the spinodals determine where these promontories end. A careful inspection of Fig. 3 reveals two three-phase (R-R-AR) and five two-phase (four R-AR plus one R-R) equilibrium regions. The metastable regions are: two three-phase (AR-AR-R); six two-phase (four R-AR, one AR-AR and one R-R). Metastable states, unlike equilibria, are not uniquely defined for each point on the phase diagram. For example, a state point near an AR minimum could lie within both metastable three-phase triangles, and three distinct two-phase promontories.

Metastable coexistences are not restricted to the free energy derived here, but apply to any landscape containing both R and AR minima. Such free energies have been used to explain existing observations (7,11), suggesting that bilayer free energies may generically permit the metastable coexistences identified here. The free energy and phase diagram are symmetric under inversion through $\left(0.5,0.5\right)$ for the reasons outlined above (see Local free energy). (For a general free-energy landscape without these symmetries, coexisting phases need not be minima so long as points of inflection exist. In our symmetric case, R-R-AR could occur without AR minima, but coexistence of two AR phases requires AR minima.) Breaking the up-down leaflet symmetry (e.g., one leaflet containing different species $S^{\prime }$ and $U^{\prime }$) could be treated by modifying the Hamiltonian. The qualitative effects would resemble the case in Garbès Putzel and Schick (7), where a different intraleaflet parameter is used for each leaflet.

Kinetics for ϕ^b = ϕ^t = 0.5

The importance of metastable states in determining the kinetics of realized phase behavior has long been known in the fields of metallurgy and colloid science (32–34) but until now has not been examined for bilayer leaflets. We show these kinetic implications by studying an example bilayer whose leaflets each contain an equimolar mixture of S and U. Immediately after a quench from high temperature, its local composition will everywhere be homogeneous at $\left(0.5,0.5\right)$. Varying model parameters (hence the free-energy landscape) we consider the following questions. 1) What is its equilibrium state? 2) To which instabilities is the initial homogeneous state subject and, if more than one, which will dominate at the start of phase separation?

For $\left(0.5,0.5\right)$ overall composition, the equilibrium state must, if phase-separated, be two-phase, since any three-phase tangent plane would pass through $\left(0.5,0.5\right)$ at a higher free energy than a plane linking the two absolute minima of f. For the initial homogeneous state, we compare the R phase separation mode (in which the bilayer splits in the direction of the R-R central tie-line) to the AR mode (splitting along the perpendicular AR-AR tie-line), ignoring the metastable three-phase triangles in which $\left(0.5,0.5\right)$ also falls. Restricting attention to the two perpendicular modes simplifies the kinetic analysis. Simulations to be presented in upcoming work suggest that, for $\left(0.5,0.5\right)$ overall composition, metastable three-phase separation is either kinetically disfavored or occurs only in small transient fluctuations about an overall AR-AR state.

R and AR modes

Fig. 4 shows slices through $f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)$ in the R/AR modes for different parameter points (marked in Fig. 5 b) of varying direct coupling B. For the lowest B, the AR minima are lower than R, so AR-AR phase separation is the equilibrium state of our $\left(0.5,0.5\right)$ bilayer. This arises because in a R domain of $SS$ (say), the entropic gain of inserting minority sites $SU$, $US$, or $UU$ is offset by a prohibitive hydrophobic cost from J. In contrast, an AR $SU$ domain can gain entropy from minority $US$, which are of the same thickness and so experience no hydrophobic penalty. Thus, if J is large, the bulk free energy for AR-AR coexistence can be lower than that for R-R, despite a finite direct coupling B.

Figure 4.

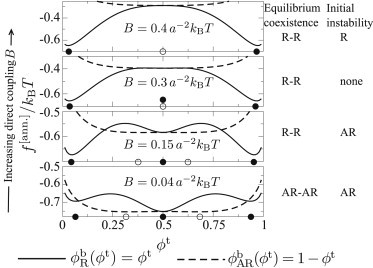
R and AR slices through $f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)$ for the sequence of parameter points indicated by the green dots in Fig. 5b. Solid and open circles mark minima in the R and AR directions, respectively. We label, for a bilayer of overall composition $\left(0.5,0.5\right)$, whether equilibrium coexistence is R-R or AR-AR, and which modes (R or AR) the initially uniform homogeneous state is unstable to.

Upon increasing B (penalizing AR), R-R phase separation becomes equilibrium, but the homogeneous state $\left(0.5,0.5\right)$ is a local minimum of f along ${\varphi }_{\text{R}}^{\text{b}}\left({\varphi }^{\text{t}}\right)={\varphi }^{\text{t}}$, so it is metastable against the R mode. At $B=0.3a^{-2}{k}_{\text{B}}T$, the minima in the AR mode have disappeared and the homogeneous state is not unstable to either mode. For the largest B, the homogeneous state becomes unstable to R-R phase separation, the local minimum having disappeared. Note that unlike any of the parameter points in Fig. 4, the free-energy landscape in Fig. 2 is unstable at $\left(0.5,0.5\right)$ to both R and AR modes of phase separation, being concave down along both ${\varphi }_{\text{R}}^{\text{b}}\left({\varphi }^{\text{t}}\right)={\varphi }^{\text{t}}$ and ${\varphi }_{\text{AR}}^{\text{b}}\left({\varphi }^{\text{t}}\right)=1-{\varphi }^{\text{t}}$ directions.

Instability criteria

Instability to phase separation requires negative curvature of $f^{\left[\text{ann}.\right]}$. We define $f^{\text{m}\left[\text{ann}.\right]}\left({\varphi }^{\text{t}}\right)\equiv f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }_{\text{m}}^{\text{b}}\left({\varphi }^{\text{t}}\right)\right)$, where m = R, AR labels the phase separation mode. Hence, instability of the equimolar homogeneous state to mode m requires ${\left(d^2/d{\varphi }^{\text{t}2}\right)f^{\text{m}[\text{ann}.]}|}_{{\varphi }^{\text{t}}=0.5}<0$. We find that

$$\frac{d^2}{d{\varphi }^{\text{t}2}}{f}^{\text{R}\left[\text{ann}.\right]}{|}_{0.5}=\frac{4}{\beta }\left(1+e^{-\beta \sigma }\right)-16\left(V+\frac{{\text{Δ}}_0^{2}J\kappa }{4\left(2J+\kappa \right)}\right),$$ (7a)

$$\frac{d^2}{d{\varphi }^{\text{t}2}}{f}^{\text{AR}\left[\text{ann}.\right]}{|}_{0.5}=\frac{4}{\beta }\left(1+e^{\beta \sigma }\right)-16V,$$ (7b)

with ${\beta }^{-1}\equiv k_{\text{B}}T$, where

$$\sigma \equiv \frac{1}{2}\left(H_{SU}+H_{US}-H_{SS}-H_{UU}\right)$$ (8a)

$$=-\frac{{\text{Δ}}_0^2{\kappa }^2\left(J-B\right)}{2\left(2J+\kappa \right)\left(2B+\kappa \right)}$$ (8b)

is the (mean-field) energy per site for converting two sites from R to AR $\left(SS+UU\to SU+US\right)$. The curvatures contain a positive entropy-like part that inhibits instability and a negative enthalpic part that promotes it. The more negative is $\left(d^2/d{\varphi }^{\text{t}2}\right)f^{\text{m}\left[\text{ann}.\right]}$, the stronger is the bulk driving force for instability to mode m.

σ controls the excess proportion, $x_{\text{reg}}^{\text{mixed}}$, of pairwise R amphiphile pairs present in the homogeneous state. (While it is laterally mixed, the bilayer can contain more or fewer pairwise R versus AR sites. At ${\varphi }^{\text{b}}={\varphi }^{\text{t}}=0.5$, in particular, anything from full pairwise R to AR is possible.) Evaluating the $N_{\alpha }$ at $\left(0.5,0.5\right)$ gives

$$x_{\text{reg}}^{\text{mixed}}\equiv \frac{N_{SS}+N_{UU}-N_{SU}-N_{US}}{N}=\text{tanh}\frac{\beta \sigma }{2}.$$ (9)

For $J>B$, as expected in most cases, $\sigma <0$ which implies that $x_{\text{reg}}^{\text{mixed}}<0$. This implies that most pairs in the homogeneous state are AR, i.e., amphiphiles predominantly align with the opposite species (as measured in Zhang et al. (15,16)). The Boltzmann factors $e^{\pm \beta \sigma }$ in Eqs. 7a and 7b control the loss of configurational entropy, relative to the homogeneous state, for creating excess pairwise R (AR) sites required by the R (AR) phase separation mode. Increasing J (decreasing σ) promotes pairwise AR (i.e., SU and US) by penalizing the mixing of pairwise R (SS and UU) sites in the homogeneous state. To access the R phase separation mode, the bilayer must thus overcome a free-energy barrier to create the required pairwise R sites. This can lead to a local minimum at $\left(0.5,0.5\right)$ in the R slice through f (see Fig. 4), implying that the homogeneous state is metastable against the R mode. (The homogeneous state may become metastable against the AR mode if $B\gg J$, but for phospholipids, the literature suggests that $J\mathrm{\gtrsim }B$ or $J\gg B$ (see Appendix C). Further, the complementary matching measured in Zhang et al. (15,16) requires, within our model, $J>B$ (via Eq. 9).) Hence, hydrophobicity J, unlike the Ising interaction V, does not trivially increase instability to the R mode. This complex interplay with bilayer microstructure cannot be captured in theories that a priori assume purely inter- and intraleaflet couplings (3,7).

Growth rates of competing modes

If the initial homogeneous state is unstable to both R and AR modes, initial phase separation will be determined by the competition between them. The bulk free energy f drives separation into domains, whereas gradient terms arising from the nearest-neighbor interactions V and J penalize the resulting inhomogeneities in composition and thickness. Although they do not affect the phase diagram, these gradient terms do affect the growth rates of the competing modes. We employ linear stability analysis of a Ginzburg-Landau (G-L) free energy (35), $F_{\text{G}-\text{L}}=\int d^{2}r\left(\left(f/a^2\right)+f_{\text{grad}}\right)$, with gradient terms given by

$$f_{\text{grad}}=\frac{1}{2}\tilde{J}{\left(\nabla \overline{d}\right)}^2+V{\left(\nabla {\varphi }^{\text{t}}\right)}^2+V{\left(\nabla {\varphi }^{\text{b}}\right)}^2.$$ (10)

We obtain wavenumber-dependent growth rates ${\omega }^{\text{m}}\left(q\right)$, whose maxima over q yield ${\omega }_{\text{max}}^{\text{m}}$. The difference $\text{Δ}\omega \equiv {\omega }_{\text{max}}^{\text{R}}-{\omega }_{\text{max}}^{\text{AR}}$ determines which mode is faster and dominates the initial phase separation after a quench. Hydrophobic mismatch penalizes the thickness gradients of the R mode without necessarily providing a compensating boost to instability (see Instability criteria), so it can render the AR mode fastest. The detailed calculations are given in Appendix B.

Stability diagrams

Fig. 5 summarizes the equilibria and kinetics of a $\left(0.5,0.5\right)$ bilayer, showing whether the equilibrium state is R-R, AR-AR, or mixed (no phase separation at all). We also show where the initial homogeneous state of the bilayer is unstable to R and AR modes, as well as the relative growth rates of the modes.

Weak mismatch (${\text{Δ}}_0=1a$). For $V=0.3k_{\text{B}}T$ and weak thickness mismatch, no phase separation takes place, since $V<V_0$ (Fig. 5 a), whereas $V=0.6k_{\text{B}}T$ (Fig. 5 c) induces phase separation as for the mean-field Ising model. The equilibrium coexistence is R-R, but the bilayer is unstable to both R and AR modes. For strong enough hydrophobic mismatch, the AR mode is faster (Fig. 5 c, red). Hence, for the parameter point marked in Fig. 5 c (green dot), the bilayer will initially undergo spinodal decomposition in the AR mode, accessing metastable AR-AR coexistence, and subsequently requiring nucleation to reach equilibrium R-R coexistence.

Strong mismatch (${\text{Δ}}_0=2a$). Increasing ${\text{Δ}}_0$ strengthens both the indirect and direct couplings (physically, this could arise from increasing the length mismatch and the difference in unsaturation of the species tails). In contrast to the weak mismatch case, for $V=0.3k_{\text{B}}T$ (Fig. 5 b) the interleaflet couplings induce phase separation, although (since $V<V_0$) neither leaflet would separate without interleaflet coupling (3,7,8). A large hydrophobic penalty J promotes pairwise AR. Due to the doubled effective Ising interaction between $SU$ and $US$ pairs ($2V>V_0$), AR minima appear in the free-energy landscape and AR-AR phase separation is possible. There is a region where AR-AR coexistence is the equilibrium state. (A small region of AR-AR equilibrium also exists in Fig. 5, c and d, for $B{a}^2/k_{\text{B}}T\mathrm{\lesssim }0.005$.) Increasing the direct coupling B favors R-R phase separation, which is enhanced by hydrophobic thickness mismatch between $SS$ and $UU$ sites, yet large J renders the homogeneous state metastable, not unstable, against the R mode (within the R-R region but outside the R instability line). For $V=0.6k_{\text{B}}T$ (Fig. 5 d), phase separation always takes place, since $V>V_0$. Compared to $V=0.3k_{\text{B}}T$, the R instability and AR instability lines move past each other; increased V promotes instability (Eq. 7), so larger B/smaller J is required to inhibit AR instability, and larger J/smaller B is required to inhibit R instability.

Discussion

We have modeled the coupled leaflets of a bilayer in which hydrophobic mismatch causes an indirect coupling J, promoting antiregistration (AR). This competes with a direct coupling B, arising from tail-structure mismatch, which promotes transmidplane registration (R) of like species. Both interleaflet couplings interplay with the stiffness κ: small κ allows amphiphiles to adapt to the couplings, decreasing the energy scale and washing out interleaflet coupling effects, whereas large κ (as in a gel, for instance) strengthens them.

The free-energy landscapes derived from our model permit multiple metastable coexistences in the phase diagram. Such coexistences are possible for any free-energy landscape with R and AR minima (7,11), but their consequences for bilayers have not previously been investigated. Moreover, by explicitly incorporating structural features, our theory demonstrates how hydrophobic mismatch kinetically favors metastable AR phase coexistence (or can even lead to equilibrium AR), thus providing a novel link between bilayer microstructure and phase transition kinetics.

We demonstrated the kinetic effects of metastability in a $\left(0.5,0.5\right)$ bilayer (each leaflet containing an overall equimolar mixture), by studying competing R and AR phase separation modes corresponding to perpendicular tie-lines passing through $\left(0.5,0.5\right)$ (see Fig. 3). For plausible phospholipid parameters ($J\sim 2a^{-2}{k}_{\text{B}}T$) with a significant lipid-length mismatch ${\text{Δ}}_0\sim 0.8\text{nm}$ ($\sim 1a$), Fig. 5 c may apply. Taking $\gamma \approx 0.15k_{\text{B}}T{\text{nm}}^{-2}\approx 0.1a^{-2}{k}_{\text{B}}T$ (3,27,28) (so $B\approx 0.23a^{-2}{k}_{\text{B}}T$) in that figure implies comparable R/AR growth rates. However, Garbès Putzel et al. (4) argue for $\gamma \sim 0.01a^{-2}{k}_{\text{B}}T$ ($B\approx 0.02a^{-2}{k}_{\text{B}}T$), in which case, the bilayer would first access AR-AR coexistence and require nucleation to reach equilibrium R-R coexistence (a manifestation of Ostwald’s heuristic rule of stages (32)).

A general experimental signature of such kinetics would be the total amounts of R and AR phases changing through time, as the bilayer converts AR to R or vice versa (14). This could be discerned via AFM, with growing $SS$ and $UU$ nuclei exhibiting different thickness to one another as well as to the surrounding AR background. This signature applies also to overall compositions away from $\left(0.5,0.5\right)$, where metastable states can compete with equilibrium three- or two-phase coexistence. AR-AR coexistence may not be detected by standard height-mode AFM or fluorescence microscopy, because $SU$ and $US$ domains would be of similar height and fluorescence. Hence, three-phase coexistence involving two AR phases can masquerade as two-phase coexistence.

Observations of L_o-L_d phase coexistence (10,11) suggest that the equilibrium state typically comprises R domains, in agreement with our results. In contrast, AFM experiments (14) have shown R gel domains converting to AR. This could indicate decay of subcritical R nuclei into a metastable AR state, although the interpretation of experiments with a solid support is complicated by substrate effects (36), which could break the bilayer symmetry. Domain AR observed upon increasing hydrophobic mismatch in simulation (17,18) can be understood as a kinetically favored metastable state, and thus reconciled with R as the equilibrium state (10–12). The intriguing complementary matching (i.e., pairwise AR) measured in Zhang et al. (15,16) can be related to Eq. 9, which implies (for $J>B$) predominant pairwise AR in a laterally homogeneous bilayer.

To study these effects in experiment and molecular simulation, ideal systems would have strong hydrophobic mismatch due to different tail lengths. Differing headgroups may ensure that the length-independent interaction V is sufficient for AR free-energy minima to exist (so $SU$ and $US$ form distinct domains). Although metastability is possible over wide regions of the phase diagram, a mixture of near-equal area fractions (near $\left(0.5,0.5\right)$) could minimize bias toward R phases and allow pure AR-AR coexistence (cf. Perlmutter and Sachs (17)). Amphiphiles with relatively stiff tails (corresponding to a large area compressibility modulus) would maximize the energy scale of interleaflet couplings. The behavior within the individual leaflets should be carefully monitored (11,36), ideally in the early kinetics after a quench, where one might witness the bilayer passing through metastable states. Note, however, that some existing simulation (17,18) and experimental results imply long-lived AR. These could provide useful starting points for investigations, e.g., molecular simulations aimed explicitly at determining whether AR domains in the Perlmutter and Sachs study (17) are stable and how they may transition to R domains.

Notwithstanding quantitative effects on the parameters, our theory applies equally to L_o-L_d or liquid-gel systems; gels entail slower kinetics but still evolve through time (14) in a manner governed by a free-energy landscape. In our idealized treatment, it is hard to precisely assign parameters or predict timescales. Rather, we have shown that bilayer structural features lead—over a wide range of reasonable model parameters—to uniquely rich free energies that can reconcile apparently contradictory R/AR observations in the literature. Future work will flesh out the kinetics beyond the linear regime studied here by direct simulation of the lattice model and will examine the nucleation energetics for reaching equilibrium.

We have implicitly considered a flat membrane. Membrane curvature can drive domain formation (37) and has been proposed as a factor in domain interleaflet coupling (26), whereas AR may cause nonzero spontaneous curvature and lead to an undulating membrane (5). In principle, our theory could be supplemented with curvature terms (5), though it is not obvious whether these could be derived from microscopic considerations or would be phenomenological. We focused here on approximate phospholipid parameters, but the phenomenology also applies to, e.g., polymeric bilayers (38,39), whose properties, and hence predicted phase behavior, may be quite different. Hybrid lipids, where one tail varies in saturation/length relative to the other, may act as linactants (40–42). Further work is required to establish their effects on the physics studied here, but we speculate that such linactants could favor R by diminishing the energy cost for the thickness mismatch at R domain boundaries.

Author Contributions

J.J.W. and P.D.O. designed the model and wrote the article. P.D.O. supervised the research and J.J.W. performed the research.

Appendix A. Derivation of Mean-Field Free Energy

The underlying lattice model is a $L^2=N$ square lattice of sites with top (t) and bottom (b) leaflet amphiphiles, whose Hamiltonian is given by Eq. 1. The exact partition function is

$$Z=\underset{\left\{{\hat{\varphi }}_i^{\text{t}},{\hat{\varphi }}_i^{\text{b}}\right\}}{\sum ^{\text{constrained}}}\int \mathcal{D}\text{Δ}\mathcal{D}d\text{exp}\left(-\beta H\right),$$ (A1)

where the sum is constrained by the average leaflet compositions ${\varphi }^{\text{t}\left(\text{b}\right)}\equiv N_S^{\text{t}\left(\text{b}\right)}/N$, and we have defined $\mathcal{D}\text{Δ}\equiv \prod _{i}d{\text{Δ}}_i$ and $\mathcal{D}d\equiv \prod _{i}d{d}_i$. Recall that ${\hat{\varphi }}_i^{\text{t}\left(\text{b}\right)}=1$ or 0 if the top (bottom) of site i contains an S or U amphiphile. The free energy is related to the partition function by

$$fN=-k_{\text{B}}T\text{ln}Z,$$ (A2)

and our aim is to find a mean-field approximation to the free energy per site f that depends only on local coarse-grained variables for the leaflet compositions ${\varphi }^{\text{t}\left(\text{b}\right)}$, bilayer thickness $\overline{d}\equiv \sum d_i/N$, and thickness difference $\overline{\text{Δ}}\equiv \sum {\text{Δ}}_i/N$.

Mean-field (on-site) approximation

We use a mean-field approximation, ignoring correlations between neighboring sites. This requires approximating the neighbor interaction terms of H (those involving V and $\tilde{J}$) with on-site terms. For the $\tilde{J}$ term, we employ the local mean-field bilayer thickness $\overline{d}$ and write

$$\begin{array}{l}\sum _{\langle i,j\rangle }{\left(d_i-d_j\right)}^2=\sum _{\langle i,j\rangle }{\left(\left[d_i-\overline{d}\right]-\left[d_j-\overline{d}\right]\right)}^2\\ =\sum _{<i,j>}\left({\left[d_i-\overline{d}\right]}^2+{\left[d_j-\overline{d}\right]}^2-2\left[d_i-\overline{d}\right]\left[d_j-\overline{d}\right]\right)\\ \approx \sum _{i}4{\left(d_i-\overline{d}\right)}^2.\end{array}$$ (A3)

The mean-field approximation consists of assuming that the cross term $\left[d_i-\overline{d}\right]\left[d_j-\overline{d}\right]$ sums to zero, i.e., that $d_i$ and $d_j$ are uncorrelated.

For the Ising-like term in (say) the top leaflet, the interaction matrix V_uv permits a mapping to the Ising model. Define the exchange parameter, $J^{\text{Ising}}$ (unrelated to the J in our model), and the spin variable, $s_i^{\text{t}}\equiv 2{\hat{\varphi }}_i^{\text{t}}-1$, which takes the value 1 or −1, and consider the Ising model in which the interaction energy between spins i and j is $E_{ij}=-J^{\text{Ising}}{s}_i^{\text{t}}{s}_j^{\text{t}}$. In the mean-field approximation, the total energy of this Ising model is $E\approx -2J^{\text{Ising}}{\left({\overline{s}}^{\text{t}}\right)}^{2}N$, where ${\overline{s}}^{\text{t}}$ is the mean value of the spin. This can be written as

$$E=\sum _{\langle i,j\rangle }-J^{\text{Ising}}{s}_i^{\text{t}}{s}_j^{\text{t}}\approx \sum _i-2J^{\text{Ising}}{s}_i^{\text{t}}{\overline{s}}^{\text{t}}.$$ (A4)

The excess interaction energy for unlike versus like neighbors in the Ising model is $E_{ij}{|}_{s_i^{\text{t}}=-s_j^{\text{t}}}-E_{ij}{|}_{s_i^{\text{t}}=s_j^{\text{t}}}=2J^{\text{Ising}}$. For V_uv this difference is $V\equiv V_{10}-\left(1/2\right)\left(V_{00}+V_{11}\right)$. Hence, equivalence with the Ising model is established by setting $V=2J^{\text{Ising}}$. Therefore, in the mean-field approximation of our lattice Hamiltonian, we can write

$$\sum _{\langle i,j\rangle }{V}_{{\hat{\varphi }}_i^{\text{t}}{\hat{\varphi }}_j^{\text{t}}}\approx \sum _i-V{s}_i^{\text{t}}{\overline{s}}^{\text{t}}=\sum _i-V{s}_i^{\text{t}}\left(2{\varphi }^{\text{t}}-1\right),$$ (A5)

and a similar expression for the bottom leaflet. The mean-field (i.e., on-site) approximation to the Hamiltonian is thus given by

$$H\approx H_{\text{MF}}=\sum _i{H}_i,$$ (A6)

where

$$H_i=-V{s}_i^{\text{t}}\left(2{\varphi }^{\text{t}}-1\right)-V{s}_i^{\text{b}}\left(2{\varphi }^{\text{b}}-1\right)+\frac{1}{2}J{\left(d_i-\overline{d}\right)}^2+\frac{1}{2}B{\left({\text{Δ}}_i\right)}^2+\frac{1}{2}\kappa \left({\left({\ell }_i^{\text{t}}-{\ell }_0^{\text{t}i}\right)}^2+{\left({\ell }_i^{\text{b}}-{\ell }_0^{\text{b}i}\right)}^2\right),$$ (A7)

and $J\equiv 4\tilde{J}$.

Site types

We now note that, given a mixture of S and U species in each leaflet, there are four possible site types, $\alpha \in \left\{SS,UU,SU,US\right\}$, where an $AB$ site contains species A on the top and B on the bottom. $SS$ and $UU$ sites are pairwise R, whereas $SU$ and $US$ sites are pairwise AR. All sites of type α share the same values of the species-dependent constants $s_i^{\text{t}}$, $s_i^{\text{b}}$, ${\ell }_0^{\text{t}i}$, and ${\ell }_0^{\text{b}i}$ in their $H_i$. We can therefore express the total mean-field Hamiltonian H_MF as a sum over the noninteracting site-level Hamiltonians,

$$H_{\text{MF}}=\sum _{\alpha }\stackrel{N_{\alpha }}{\sum _{j_{\alpha }}}{H}_{j_{\alpha }},$$ (A8)

where $j_{\alpha }$ labels the jth out of $N_{\alpha }$ sites of type α, and

$$H_{j_{\alpha }}=\pm V\left(2{\varphi }^{\text{t}}-1\right)\pm V\left(2{\varphi }^{\text{b}}-1\right)+\frac{1}{2}J{\left(d_{j_{\alpha }}-\overline{d}\right)}^2+\frac{1}{2}B{\left({\text{Δ}}_{j_{\alpha }}\right)}^2+\frac{1}{2}\kappa \left({\left({\ell }_{j_{\alpha }}^{\text{t}}-{\ell }_0^{\text{t}\alpha }\right)}^2+{\left({\ell }_{j_{\alpha }}^{\text{b}}-{\ell }_0^{\text{b}\alpha }\right)}^2\right).$$ (A9)

Here, ${\ell }_0^{\text{t}\alpha }={\ell }_{A0}$ and ${\ell }_0^{\text{b}\alpha }={\ell }_{B0}$ for $\alpha =AB$, and the signs are −− for $\alpha =SS$, ++ for $UU$, −+ for $SU$, and +− for $US$.

The sum over the top and bottom leaflet configurations can be rewritten as a sum over the occupancies of the set of site types, i.e.,

$$\underset{\left\{{\hat{\varphi }}_i^{\text{t}},{\hat{\varphi }}_i^{\text{b}}\right\}}{\sum ^{\text{constr}.}}=\underset{\left\{N_{\alpha }\right\}}{\sum ^{\text{constr}.}}\frac{1}{{\prod }_{\alpha }{N}_{\alpha }!},$$ (A10)

where the factorials avoid overcounting indistinguishable configurations and the sum is constrained by Eqs. 2c–2e.

Defining $\mathcal{D}{\text{Δ}}_{\alpha }\equiv \prod _{j\alpha }d{\text{Δ}}_{j\alpha }$ and $\mathcal{D}{d}_{\alpha }\equiv \prod _{j\alpha }d{d}_{j\alpha }$, the mean-field partition function $Z_{\text{MF}}$ is

$$Z_{\text{MF}}=\underset{\left\{N_{\alpha }\right\}}{\sum ^{\text{constr}.}}\frac{1}{{\prod }_{\alpha }{N}_{\alpha }!}\prod _{\alpha }\int \mathcal{D}{\text{Δ}}_{\alpha }\mathcal{D}{d}_{\alpha }\text{exp}\left(-\beta \stackrel{N_{\alpha }}{\sum _{j_{\alpha }}}{H}_{j_{\alpha }}\right).$$ (A11)

Since all sites are now independent of one another, the integral may be rewritten in terms of the partition function for a single site of type α. In addition, the constraints of Eqs. 2c–2e allow the Ising interaction, V, to be factored out. We thus have

$$Z_{\text{MF}}=\underset{\left\{N_{\alpha }\right\}}{\sum ^{\text{constr}.}}\text{exp}\left(-\beta N{V}^{\text{∗}}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)\right)\frac{{\prod }_{\alpha }{Z}_{\alpha }^{N_{\alpha }}}{{\prod }_{\alpha }{N}_{\alpha }!},$$ (A12)

where we have defined

$$V^{\text{∗}}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)\equiv -2V{\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}^2-2V{\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)}^2.$$ (A13)

The single-site thickness partition function is given by

$$Z_{\alpha }=\int d{\text{Δ}}_{\alpha }d{d}_{\alpha }\text{exp}\left(-\beta H_{\alpha }\right),$$ (A14)

in which

$$H_{\alpha }=\frac{1}{2}J{\left(d_{\alpha }-\overline{d}\right)}^2+\frac{1}{2}B{\left({\text{Δ}}_{\alpha }\right)}^2+\frac{1}{2}\kappa \left({\left({\ell }_{\alpha }^{\text{t}}-{\ell }_0^{\text{t}\alpha }\right)}^2+{\left({\ell }_{\alpha }^{\text{b}}-{\ell }_0^{\text{b}\alpha }\right)}^2\right),$$ (A15)

now contains only the thickness-dependent interactions.

Self-consistency, free energy

For self-consistency of the locally averaged bilayer thickness $\overline{d}$ and difference $\overline{\text{Δ}}$ we require the integrations over $d_{\alpha },{\text{Δ}}_{\alpha }$ to be performed subject to Eqs. 2a and 2b. Since these integrals are Gaussian, and the constraints of Eqs. 2a and 2b are linear, the integrations can be performed exactly to yield

$$\prod _{\alpha }{Z}_{\alpha }^{N_{\alpha }}=\text{exp}\left(-\beta \sum _{\alpha }{N}_{\alpha }{H}_{\alpha }\{d_{\alpha }^{\text{∗}},{\text{Δ}}_{\alpha }^{\text{∗}}\}\right),$$ (A16)

where $\left\{d_{\alpha }^{\text{∗}},{\text{Δ}}_{\alpha }^{\text{∗}}\right\}$ values minimize $\sum _{\alpha }{N}_{\alpha }{H}_{\alpha }$ subject to Lagrange multipliers enforcing Eqs. 2a and 2b.

Now the mean-field partition function can be written as

$$\begin{array}{l}{Z}_{\text{MF}}=\underset{\left\{N_{\alpha }\right\}}{\sum ^{\text{constr}.}}\text{exp}\left(-\beta \left[N{V}^{\text{∗}}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)+\sum _{\alpha }{N}_{\alpha }\left(H_{\alpha }\left\{d_{\alpha }^{\text{∗}},{\text{Δ}}_{\alpha }^{\text{∗}}\right\}+k_{\text{B}}T\text{ln}{N}_{\alpha }\right)\right]\right)\\ \equiv \underset{\left\{N_{\alpha }\right\}}{\sum ^{\text{constr}.}}\text{exp}\left(-\beta N\tilde{f}\right),\end{array}$$ (A17)

where Stirling’s approximation ($\text{ln}{N}_{\alpha }!\approx N_{\alpha }\text{ln}{N}_{\alpha }-N_{\alpha }$) has been used, contributing an irrelevant constant.

The three constraints of Eqs. 2c–2e leave only one $N_{\alpha }$ over which to sum. For this, we perform a saddle-point approximation, which is equivalent to removing the sum and setting $\left\{N_{\alpha }\right\}$ to their values that minimize $\tilde{f}$ subject to Eqs. 2c–2e. This yields

$$Z_{\text{MF}}\approx \text{exp}\left(-\beta N{\tilde{f}}^{\text{∗}}\right),$$ (A18)

where ${\tilde{f}}^{\text{∗}}$ is the minimized value of $\tilde{f}$. Then, by Eq. A2, our desired free energy per site $f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)$ is given by ${\tilde{f}}^{\text{∗}}$.

The steps described above can be summarized compactly by stating that the free energy $f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)$ per site is given by minimizing

$$f^{\text{′}}N=\sum _{\alpha }{N}_{\alpha }\left(H_{\alpha }+k_{\text{B}}T\text{ln}{N}_{\alpha }\right)-2VN{\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}^2-2VN{\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)}^2$$ (A19)

over $\{d_{\alpha },{\text{Δ}}_{\alpha },N_{\alpha }$} subject to Lagrange multipliers enforcing Eqs. 2a–2e, as written in Eq. 3. The variables fixed in the minimization procedure are

$$d_{SS}=\overline{d}+\frac{\kappa {\text{Δ}}_0}{2J+\kappa }\left(2-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right),$$ (A20a)

$$d_{UU}=\overline{d}-\frac{\kappa {\text{Δ}}_0}{2J+\kappa }\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}\right),$$ (A20b)

$$d_{SU}=d_{US}=\overline{d}-\frac{\kappa {\text{Δ}}_0}{2J+\kappa }\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right),$$ (A20c)

$${\text{Δ}}_{SS}={\text{Δ}}_{UU}=\overline{\text{Δ}}-\frac{\kappa {\text{Δ}}_0}{2B+\kappa }\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right),$$ (A20d)

$${\text{Δ}}_{SU}=\overline{\text{Δ}}-\frac{\kappa {\text{Δ}}_0}{2B+\kappa }\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}-1\right),$$ (A20e)

$${\text{Δ}}_{US}=\overline{\text{Δ}}-\frac{\kappa {\text{Δ}}_0}{2B+\kappa }\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}+1\right),$$ (A20f)

$$N_{SS}/N=A\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right),$$ (A20g)

$$N_{UU}/N=A\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)+1-{\varphi }^{\text{t }}-{\varphi }^{\text{b}},$$ (A20h)

$$N_{SU}/N=-A\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)+{\varphi }^{\text{t}},$$ (A20i)

$$N_{US}/N=-A\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)+{\varphi }^{\text{b}}.$$ (A20j)

We have defined

$$A\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)\equiv \frac{2{\varphi }^{\text{t}}{\varphi }^{\text{b}}}{{\varphi }^{\text{∗}}+\sqrt{{\varphi }^{\text{∗}2}+4{\varphi }^{\text{t}}{\varphi }^{\text{b}}\left(e^{-2\beta \sigma }-1\right)}},$$ (A21)

where

$${\varphi }^{\text{∗}}\equiv {\varphi }^{\text{t}}+{\varphi }^{\text{b}}+e^{-2\beta \sigma }\left(1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right),$$ (A22)

and

$$\begin{array}{l}\sigma \equiv \frac{1}{2}\left(H_{SU}+H_{US}-H_{SS}-H_{UU}\right)\\ =-\frac{{\text{Δ}}_0^2{\kappa }^2\left(J-B\right)}{2\left(2J+\kappa \right)\left(2B+\kappa \right)}\end{array}$$ (A23)

is the energy change per site for converting two R sites into two AR sites. The expected self-consistency requirements are fulfilled; for example, ${\varphi }^{\text{b}}={\varphi }^{\text{t}}\to 1$ (forcing all sites to be of $SS$ type) leads to $d_{SS}\to \overline{d}$.

To construct the local free energy $f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)$ we insert Eqs. A20–A23 into Eq. A19. We find

$$f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)=k_{\text{B}}T\left[A\text{ln}A+\left(A+1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)\text{ln}\left(A+1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)+\left({\varphi }^{\text{t}}-A\right)\text{ln}\left({\varphi }^{\text{t}}-A\right)+\left({\varphi }^{\text{b}}-A\right)\text{ln}\left({\varphi }^{\text{b}}-A\right)\right]+\frac{1}{2}\kappa [\frac{1}{2}{\left(\overline{d}-d_0\right)}^2+{\text{Δ}}_0\left(\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)\left(d_0-\overline{d}\right)-\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)\overline{\text{Δ}}+\frac{1}{2}{\text{Δ}}_0\right)]+\frac{1}{4}{\overline{\text{Δ}}}^2\left(2B+\kappa \right)+\frac{{\kappa }^2{\text{Δ}}_0^2}{2\left(2B+\kappa \right)\left(2J+\kappa \right)}\left[\left(2A-2{\varphi }^{\text{t}}{\varphi }^{\text{b}}\right)\left(J-B\right)-\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-{\varphi }^{\text{t}2}-{\varphi }^{\text{b}2}\right)\left(J+B+\kappa \right)\right]-2V{\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}^2-2V{\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)}^2,$$ (A24)

where ${\text{Δ}}_0\equiv {\ell }_{S0}-{\ell }_{U0}$, $d_0\equiv {\ell }_{S0}+{\ell }_{U0}$.

Upon further minimizing f over the mean-field thickness variables $\overline{d}$ and $\overline{\text{Δ}}$, we obtain $f^{\left[\text{ann}.\right]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)$, which determines the minima in the local free-energy landscape (see, e.g., Figs. 2 and 4). The annealed thickness variables are

$${\overline{d}}^{\left[\text{ann}.\right]}={\text{Δ}}_0\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)+d_0,$$ (A25a)

$${\overline{\text{Δ}}}^{\left[\text{ann}.\right]}=\frac{\kappa {\text{Δ}}_0\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}{2B+\kappa },$$ (A25b)

giving

$$f^{[\text{ann}.]}\left({\varphi }^{\text{t}},{\varphi }^{\text{b}}\right)=k_{\text{B}}T\left[A\text{ln}A+\left(A+1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)\text{ln}\left(A+1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)+\left({\varphi }^{\text{t}}-A\right)\text{ln}\left({\varphi }^{\text{t}}-A\right)+\left({\varphi }^{\text{b}}-A\right)\text{ln}\left({\varphi }^{\text{b}}-A\right)\right]+\frac{1}{2}\frac{B\kappa {\text{Δ}}_0^2\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}\right)}{2B+\kappa }\left(2-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)-\sigma \left(2A+[{\varphi }^{\text{t}}+{\varphi }^{\text{b}}][1-{\varphi }^{\text{t}}-{\varphi }^{\text{b}}]\right)-2V{\left({\varphi }^{\text{t}}-{\varphi }^{\text{b}}\right)}^2-2V{\left({\varphi }^{\text{t}}+{\varphi }^{\text{b}}-1\right)}^2.$$ (A26)

Appendix B. Ginzburg-Landau Analysis

$f\left({\varphi }^{\text{t}},{\varphi }^{\text{b}},\overline{d},\overline{\text{Δ}}\right)$ is the coarse-grained free energy per site. This can serve as the Landau part of a Ginzburg-Landau-type free energy, $F_{\text{G}-\text{L}}$, to study kinetics:

$$F_{\text{G}-\text{L}}=\int d^{2}r\left(\frac{f}{a^2}+f_{\text{grad}}\right),$$ (B1)

where

$$f_{\text{grad}}=\frac{\tilde{J}}{2}{\left(\nabla \overline{d}\right)}^2+V{\left(\nabla {\varphi }^{\text{t}}\right)}^2+V{\left(\nabla {\varphi }^{\text{b}}\right)}^2.$$ (B2)

This gradient contribution depends on the terms of the Hamiltonian by which laterally neighboring sites interact. The composition gradient term in each leaflet involving V is simply that for the mean-field Ising model (43), and the thickness gradient term involving $\tilde{J}$ is the corresponding term of Eq. 1 in the limit of small lattice spacing.

We study the instabilities about a reference homogeneous state defined by ${\varphi }^{\text{b}}={\varphi }^{\text{t}}=0.5$, $\overline{\text{Δ}}=0$, $\overline{d}=d_0$, applying small perturbations to this state and determining the resultant change in $F_{\text{G}-\text{L}}$. The thermodynamic driving force for instability to demixing, determined by f, competes with the gradient terms f_grad which penalize the resultant inhomogeneity. Combining these with evolution equations for composition and thickness, we find preferred lengthscales for initial demixing, and associated rates that can be compared between the R and AR modes.

A perturbation is described by $\delta {\varphi }^{\text{t}},\delta {\varphi }^{\text{b}},\delta {\overline{\ell }}^{\text{t}},\delta {\overline{\ell }}^{\text{b}}$. Considering separately the R mode (in which ${\varphi }_{\text{R}}^{\text{b}}\left({\varphi }^{\text{t}}\right)={\varphi }^{\text{t}}$, $\overline{\text{Δ}}=0$ and $\delta {\overline{\ell }}^{\text{b}}=\delta {\overline{\ell }}^{\text{t}}$) and the AR mode (in which ${\varphi }_{\text{AR}}^{\text{b}}\left({\varphi }^{\text{t}}\right)=1-{\varphi }^{\text{t}}$, $\overline{d}=d_0$ and $\delta {\overline{\ell }}^{\text{b}}=-\delta {\overline{\ell }}^{\text{t}}$), we now apply linear stability analysis to perturbations governed by Eq. B1 to determine which mode initially grows fastest.

Evolution of perturbations

The free-energy change due to a perturbation in mode m is

$$\delta F_{\text{G}-\text{L}}^{\text{m}}=\frac{1}{2}\int d^{2}r\left(\left(\begin{array}{c}\delta {\varphi }^{\text{t}}\\ \delta {\overline{\ell }}^{\text{t}}\end{array}\right)·{\underset{¯}{\underset{¯}{C}}}^{\text{m}}·\left(\begin{array}{c}\delta {\varphi }^{\text{t}}\\ \delta {\overline{\ell }}^{\text{t}}\end{array}\right)+{\nabla }_{\mu }\left(\begin{array}{c}\delta {\varphi }^{\text{t}}\\ \delta {\overline{\ell }}^{\text{t}}\end{array}\right)·{\underset{¯}{\underset{¯}{P}}}^{\text{m}}·{\nabla }_{\mu }\left(\begin{array}{c}\delta {\varphi }^{\text{t}}\\ \delta {\overline{\ell }}^{\text{t}}\end{array}\right)\right),$$ (B3)

where the Einstein convention has been used, $\text{m}=\text{R},\text{AR}$ and the matrices ${\underset{¯}{\underset{¯}{C}}}^{\text{m}}$ and ${\underset{¯}{\underset{¯}{P}}}^{\text{m}}$ contain the bulk and gradient free energy terms, respectively:

$$a^2{\underset{¯}{\underset{¯}{C}}}^{\text{R}}=\left[\begin{array}{cc}{f}_{{\varphi }^{\text{t}}{\varphi }^{\text{t}}}^{\text{R}}& 2f_{\overline{d}{\varphi }^{\text{t}}}^{\text{R}}\\ 2f_{\overline{d}{\varphi }^{\text{t}}}^{\text{R}}& 4f_{\overline{d}\overline{d}}^{\text{R}}\end{array}\right]=2\left[\begin{array}{cc}\left(2k_{\text{B}}T[e^{-\beta \sigma }+1]+\frac{{\kappa }^2{\text{Δ}}_0^2}{2J+\kappa }-8V\right)& -\kappa {\text{Δ}}_0\\ -\kappa {\text{Δ}}_0& \kappa \end{array}\right],$$ (B4a)

$$a^2{\underset{¯}{\underset{¯}{C}}}^{\text{AR}}=\left[\begin{array}{cc}{f}_{{\varphi }^{\text{t}}{\varphi }^{\text{t}}}^{\text{AR}}& 2f_{\overline{\text{Δ}}{\varphi }^{\text{t}}}^{\text{AR}}\\ 2f_{\overline{\text{Δ}}{\varphi }^{\text{t}}}^{\text{AR}}& 4f_{\overline{\text{Δ}}\overline{\text{Δ}}}^{\text{AR}}\end{array}\right]=2\left[\begin{array}{cc}\left(2k_{\text{B}}T[e^{\beta \sigma }+1]+\frac{{\kappa }^2{\text{Δ}}_0^2}{2B+\kappa }-8V\right)& -\kappa {\text{Δ}}_0\\ -\kappa {\text{Δ}}_0& 2B+\kappa \end{array}\right],$$ (B4b)

$${\underset{¯}{\underset{¯}{P}}}^{\text{R}}=\left[\begin{array}{cc}4V& 0\\ 0& 4\tilde{J}\end{array}\right],{\underset{¯}{\underset{¯}{P}}}^{\text{AR}}=\left[\begin{array}{cc}4V& 0\\ 0& 0\end{array}\right].$$ (B4c)

$f^{\text{R}}\left({\varphi }^{\text{t}},\overline{d}\right)$ represents f evaluated for ${\varphi }_{\text{R}}^{\text{b}}\left({\varphi }^{\text{t}}\right)={\varphi }^{\text{t}}$, $\overline{\text{Δ}}=0$, and $f^{\text{AR}}\left({\varphi }^{\text{t}},\overline{\text{Δ}}\right)$ represents f evaluated for ${\varphi }_{\text{AR}}^{\text{b}}\left({\varphi }^{\text{t}}\right)=1-{\varphi }^{\text{t}}$, $\overline{d}=d_0$. Subscripts indicate derivatives evaluated at the homogeneous state, i.e., ${\varphi }^{\text{t}}=0.5$, $\overline{d}=d_0$, $\overline{\text{Δ}}=0$.

Since composition is conserved, it evolves (29) via

$$\frac{\partial \delta {\varphi }^{\text{t m}}}{\partial t}=M{\nabla }^2\left(C_{11}^{\text{m}}\delta {\varphi }^{\text{t}}+C_{12}^{\text{m}}\delta {\overline{\ell }}^{\text{t}}-P_{11}^{\text{m}}{\nabla }^2\delta {\varphi }^{\text{t}}-P_{12}^{\text{m}}{\nabla }^2\delta {\overline{\ell }}^{\text{t}}\right),$$ (B5)

where the mobility M sets the timescale.

We assume thickness to behave in a nonconserved fashion so that it evolves relaxationally (29) via

$$\frac{\partial \delta {\overline{\ell }}^{\text{t m}}}{\partial t}=-\eta \left(C_{21}^{\text{m}}\delta {\varphi }^{\text{t}}+C_{22}^{\text{m}}\delta {\overline{\ell }}^{\text{t}}-P_{21}^{\text{m}}{\nabla }^2\delta {\varphi }^{\text{t}}-P_{22}^{\text{m}}{\nabla }^2\delta {\overline{\ell }}^{\text{t}}\right),$$ (B6)

where the mobility η incorporates frictional forces involved in length stretching and compression of amphiphiles (in principle it can acquire wavenumber dependence via coupling to the conserved solvent flow).

In Fourier space, the coupled evolution equations are

$$\begin{array}{l}\frac{\partial }{\partial t}\left(\begin{array}{c}\delta {\varphi }_q^{\text{t m}}\\ \delta {\overline{\ell }}_q^{\text{t m}}\end{array}\right)=-\underset{¯}{\underset{¯}{M}}\left(q\right)·\left({\underset{¯}{\underset{¯}{C}}}^{\text{m}}+q^2{\underset{¯}{\underset{¯}{P}}}^{\text{m}}\right)·\left(\begin{array}{c}\delta {\varphi }_q^{\text{t}}\\ \delta {\overline{\ell }}_q^{\text{t}}\end{array}\right)\\ \equiv -{\underset{¯}{\underset{¯}{L}}}^{\text{m}}\left(q\right)·\left(\begin{array}{c}\delta {\varphi }_q^{\text{t}}\\ \delta {\overline{\ell }}_q^{\text{t}}\end{array}\right),\end{array}$$ (B7)

where

$$\underset{¯}{\underset{¯}{M}}\left(q\right)\equiv \left(\begin{array}{cc}M{q}^2& 0\\ 0& M\xi \end{array}\right).$$ (B8)

The dimensionless parameter $\xi \equiv \eta /M$ controls how fast the thickness relaxation is relative to diffusion. Instabilities of the R or AR mode correspond to a negative eigenvalue of their ${\underset{¯}{\underset{¯}{L}}}^{\text{m}}$. Their wavenumber-dependent growth rates are given by ${\omega }^{\text{m}}\left(q\right)=-{\lambda }^{\text{m}}$, where ${\lambda }^{\text{m}}$ is the eigenvalue for the eigenmode of ${\underset{¯}{\underset{¯}{L}}}^{\text{m}}$. Maximizing ${\omega }^{\text{m}}\left(q\right)$ over q yields ${\omega }_{\text{max}}^{\text{m}}$, the peak growth rate of the given mode (R or AR).

The blue and red colors in Fig. 5 are obtained by first calculating ${\omega }_{\text{max}}^{\text{m}}$ for the R and AR modes. Then, the difference $\text{Δ}\omega \equiv {\omega }_{\text{max}}^{\text{R}}-{\omega }_{\text{max}}^{\text{AR}}$ is plotted as the background of Fig. 5. If a given mode m has a negative peak growth rate (i.e., is not unstable), then its ${\omega }_{\text{max}}^{\text{m}}$ is set to zero. Thus, $\text{Δ}\omega =0$ (white) is ambiguous; either 1) both modes are stable or 2) both are unstable but with equal peak growth rates. This ambiguity is easily resolved by referring to the instability lines when interpreting the plot, since if the peak growth rate of mode m is zero, then we must be outside the instability region of mode m. Note that the ranges of the color scales in Fig. 5 are asymmetric.

To model the physically likely scenario, we used ξ = 100, since any frictional drag involved in stretching should be far less than that for lateral diffusion (22,29). This value is close to saturation, i.e., the composition relaxation is the limiting timescale and significant further increases in ξ have only marginal quantitative effects on ${\omega }^{\text{m}}\left(q\right)$. Therefore, the conclusions drawn from the colors in Fig. 5 are independent of ξ in the expected physical regime. Even if the opposite regime is assumed ($\xi =0.1$), the values of ${\omega }^{\text{m}}\left(q\right)$ change, but the key feature of the $\text{Δ}\omega$ landscape—which mode is fastest—is not strongly affected (Fig. 6).

Figure 6.

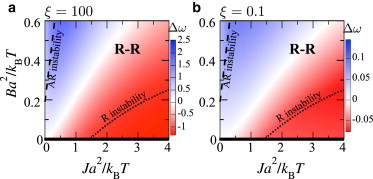
Lines and colors are defined as in Fig. 5d. (a) $\xi =100$, as in Fig. 5d. (b) $\xi =0.1$. To see this figure in color, go online.

Appendix C. Physical Meaning of Parameters

For comparison with phospholipids, we set the lattice spacing at $a\sim 0.8\text{nm}$, corresponding to an area per lipid of $0.64{\text{nm}}^2$ (44).

Stretching modulus

The stretching and compression of a bilayer of amphiphiles is measured experimentally via the area stretching modulus ${\kappa }_A$, with a free energy given by

$$G_{{\kappa }_A}^{\text{bilayer}}=\int d^{2}r\frac{{\kappa }_A}{2}{\left(\frac{\delta A}{A_0}\right)}^2,$$ (C1)

where $\delta A$ represents an area difference relative to the equilibrium area $A_0$. In the continuum representation of the lattice model here, the stretching free energy for an individual leaflet of the bilayer is given by

$$G_{\kappa }^{\text{leaflet}}=\int \frac{d^{2}r}{a^2}\frac{\kappa }{2}{\left(\delta \ell \right)}^2,$$ (C2)

where $a^2$ is the lattice site area and $\delta \ell$ is a tail-length difference relative to an equilibrium length ${\ell }_0$. Assuming that the volume $v=A\ell$ remains constant upon stretching/compression, $A\delta \ell =-\ell \delta A$, we have

$$G_{\kappa }^{\text{leaflet}}=\int d^{2}r\frac{{\ell }_0^2}{a^2}\frac{\kappa }{2}{\left(\frac{\delta A}{A_0}\right)}^2.$$ (C3)

Noting that Eq. C1 describes the area stretching energy for the whole bilayer, and assuming the energy to be distributed evenly between the two leaflets, we can write

$$G_{\kappa }^{\text{leaflet}}=\frac{1}{2}{G}_{{\kappa }_A}^{\text{bilayer}}.$$ (C4)

Identifying the lattice-site area a² as the equilibrium area per amphiphile A₀ gives the correspondence

$$\kappa =\frac{A_0}{2{\ell }_0^2}{\kappa }_A,$$ (C5)

where ${\ell }_0$ is a representative value for the equilibrium length of a real amphiphile. For typical values ${\ell }_0=2\text{nm}$ and $A_0=0.64{\text{nm}}^2$ for phospholipid leaflets, the value $\kappa =3a^{-2}{k}_{\text{B}}T$ used in this work corresponds to ${\kappa }_A\approx 40a^{-2}{k}_{\text{B}}T\approx 60k_{\text{B}}T{\text{nm}}^{-2}$, in the range for lipid bilayers at 300 K (29–31).

Indirect coupling

The indirect coupling parameter, $\tilde{J}$, quantifies the penalty for mismatch in the total hydrophobic thickness between neighboring lattice sites, arising from hydrophobic surface tension. We take a fiducial value $\tilde{J}\approx 0.8k_{\text{B}}T{\text{nm}}^{-2}$, approximately that estimated in Wallace et al. (22) as a surface tension for hydrocarbon tails in contact with the watery headgroup region of phospholipids. This gives $\tilde{J}\approx 0.5a^{-2}{k}_{\text{B}}T$ for the lattice model, so for the mean-field parameter, $J\approx 2a^{-2}{k}_{\text{B}}T$. Increasing J (Fig. 5) can be thought of as increasing hydrophobic mismatch/hydrophobicity. Our model cannot capture all the intricacies of hydrophobic mismatch between molecules. Instead, through J and its interplay with κ, we mean to capture the fact that such mismatch is disfavored at the molecular scale (15–18), and to estimate a reasonable scale for the energy penalty involved.

Direct coupling

The direct coupling parameter B plays a similar role to the interleaflet mismatch free energy per area γ estimated in the literature. We can define an effective γ (that shown in Fig. 5) by considering an isolated AR site and minimizing its energy arising from stretching (κ) and direct coupling (B) energies over the top and bottom amphiphile lengths, where the reference state is an isolated R site that experiences zero direct coupling energy. This microscopic energy per AR site is

$$\gamma a^2=\frac{{\text{Δ}}_0^2\kappa B}{2\left(\kappa +2B\right)},$$ (C6)

in terms of which

$$B=\frac{2\gamma a^2\kappa }{\kappa {\text{Δ}}_0^2-4\gamma a^2}.$$ (C7)

For example, the value $\gamma \approx 0.15k_{\text{B}}T{\text{nm}}^{-2}$ estimated in Risselada and Marrink (27,28) is, in model units, $\gamma \approx 0.1a^{-2}{k}_{\text{B}}T$. Assuming ${\text{Δ}}_0=1a$ and $\kappa =3a^{-2}{k}_{\text{B}}T$, this gives $B\approx 0.23a^{-2}{k}_{\text{B}}T$. However, even compared to the other parameters of our idealized model, γ is poorly understood. Garbès Putzel et al. (4) estimate an order of magnitude lower ($\gamma \sim 0.01a^{-2}{k}_{\text{B}}T$, so that $B\sim 0.02a^{-2}{k}_{\text{B}}T$), and find that the method used to extract γ in simulation (27,28) is inaccurate, since it assumes larger characteristic fluctuations than were measured. On the other hand, Pantano et al. (26) find that the effective γ measured while artificially pulling domains out of registration depends strongly on mismatch area, and proposes a role for membrane curvature, which we have not studied.

Interpretation of γ

There are subtleties in defining the mismatch free energy per area γ. We have defined it microscopically in Eq. C6 as the direct coupling energy density for an AR site. It is possible instead to construct a macroscopic definition by comparing the free energies of AR and R domains:

$${\gamma }_{\text{macro}}\equiv \underset{A\to \infty }{\text{lim}}\frac{1}{A}\left(G^{\text{antireg}}\left(A\right)-G^{\text{reg}}\left(A\right)\right),$$ (C8)

where $G^{\left(\text{anti}\right)\text{reg}}\left(A\right)$ is the free energy of an AR/R domain of area A. The limit $A\to \infty$ emphasizes that boundary contributions to the free energies are typically ignored (3,4). For example, in the study by Garbès Putzel et al. (4), ${\gamma }_{\text{macro}}$ is computed theoretically by comparing the free energies of AR and R arrangements of domains within a molecular mean-field theory, the domains being assumed large enough that contributions from their boundaries can be neglected. It is important to note that any effects of hydrophobic mismatch energy at the edges of R domains (incorporated in our Ginzburg-Landau analysis via the $\tilde{J}$ term of $f_{\text{grad}}$) cannot be properly captured by γ or ${\gamma }_{\text{macro}}$, since these describe only energies that scale as the domain area.

In the well-segregated limit such that an AR/R domain contains purely pairwise AR/R sites, the definition of Eq. C8 becomes equivalent to Eq. C6. Near this limit, within our model, ${\gamma }_{\text{macro}}\approx \gamma$, because the dominant contribution to the free-energy difference in Eq. C8 will be from the direct coupling energy experienced by AR sites (Eq. C6), whereas contributions associated with the remnant fraction of pairwise R sites in the AR demixed phase (and vice versa) will be small. Thus, for example, the free energy difference between the R and AR minima of $f^{\left[\text{ann}.\right]}$ (Fig. 2) is similar to the value of γ quoted for that parameter point on Fig. 5 e, calculated using Eq. C6.

In general, however, Eq. C8 requires specification of the compositions of the R and AR phases whose free energies are to be compared, and Fig. 4 shows us that the leaflet compositions in the AR phases generally differ from those in the R phases. Therefore, the assumption (4) that the relevant AR configuration for comparison is that obtained by rearranging the domains from the R configuration, without altering their compositions, is incorrect. It may be suitable for describing small fluctuations into AR at the boundary of a large R domain (as was the purpose in Garbès Putzel et al. (4)), but only if one assumes that spatial fluctuations of the domain boundaries out of R are not also accompanied by compositional fluctuations of the domains in each leaflet.

In some situations, the relationship between γ and ${\gamma }_{\text{macro}}$ is complicated by ambiguity in implementing the macroscopic definition. Given registered domain coexistence, one might assume that we should take a metastable AR rearrangement of the domains for comparison. However, in Fig. 4 (top), no AR minima exist in the free energy, so moving R-R coexisting domains into antiregistration (4) would not yield a metastable state. A single AR phase could still exist as part of R-R-AR equilibrium, depending on the free energy’s detailed shape, but the intuitive “R-R to AR-AR” rearrangement used in (4) becomes difficult to interpret. In another case, in a small region of Fig. 5 b, the AR minima are lower in free energy, so AR-AR or AR-AR-R state becomes equilibrium. Under Eq. C8, this would imply a negative value of ${\gamma }_{\text{macro}}$, although the per-site γ defined by Eq. C6 is positive.

Hence, it is clear that describing interleaflet coupling is complex, both in terms of specifying the relevant bulk free energy and in terms of the domain-size-dependent competition of edge and area energies. This latter aspect in particular, and its role in nucleation kinetics of domain registration, will be further studied in future work. In relation to this discussion, it is unclear precisely which coupling or combination of couplings is being measured in molecular simulation studies of interleaflet coupling (27,28), where the probability of fluctuations into AR is monitored and fit to a Boltzmann distribution. These fluctuations may be subject to effects related to hydrophobic mismatch and composition dependence, as discussed above, so that even if the approach of measuring fluctuations is essentially correct (challenged in Garbès Putzel et al. (4)), it is likely that energies additional to that described by γ are at work. In summary, much further work is required in defining, measuring, and studying the implications of the competing forms of interleaflet coupling.