The energy and work of a ligand-gated ion channel

Abstract

Ligand-gated ion channels are allosteric membrane proteins that isomerize between C(losed) and O(pen) conformations. A difference in affinity for ligands in the two shapes influences the C↔O ‘gating’ equilibrium constant. The energies associated with adult-type mouse neuromuscular nicotinic acetylcholine receptor-channel (AChR) gating have been measured by using single-channel electrophysiology. Without ligands the free energy, enthalpy and entropy of gating are ΔG₀=+8.4, ΔH₀=+10.9 and ΔS₀=+2.4 kcal/mol (−100 mV, 23 °C). Many mutations throughout the protein change ΔG₀, including natural ones that cause disease. Agonists and most mutations change approximately independently the ground state energy difference, so it is possible to forecast and engineer AChR responses simply by combining perturbations. The free energy of the low↔high affinity change for the neurotransmitter at each of two functionally-equivalent binding sites is ΔG_B^ACh=−5.1 kcal/mol. ΔG_B^ACh is set mainly by interactions of ACh with just three binding site aromatic groups. For a series of structurally-related agonists there is a correlation between the energies of low- and high-affinity binding, which implies that gating commences with the formation of the low affinity complex. Brief, intermediate states in binding and gating have been detected. Several proposals for the nature of the gating transition state energy landscape and the isomerization mechanism are discussed.

Allosteric proteins are molecular switches that regulate the flow of material and information through metabolic and signaling pathways. These macromolecular systems isomerize between alternative conformational ensembles that have different functional outputs. The probability adopting each conformation is influenced by chemical, electrical, mechanical or thermal energy deposited from the environment at discrete ‘sensor’ sites in the protein. Different amounts of energy are deposited in the different shapes, so a change in the environmental energy forces a new conformational equilibrium to be established. The sensors and the site(s) that regulate functional output are separated and communicate only by a global rearrangement of the system.

Here I discuss the thermodynamics of the allosteric process in adult mouse neuromuscular acetylcholine receptors (AChRs), five-subunit ligand-gated ion channels that mediate ion flux across cell membranes (Fig. 1a) (for reviews see ). This AChR is a model for understanding the molecular operation of a large superfamily of related receptor-channels that are present in many cell types, from prokaryotes to those in the human brain. Members of this group are modulated by a variety of ligands and are targets for toxins and drugs, both therapeutic and of-abuse.

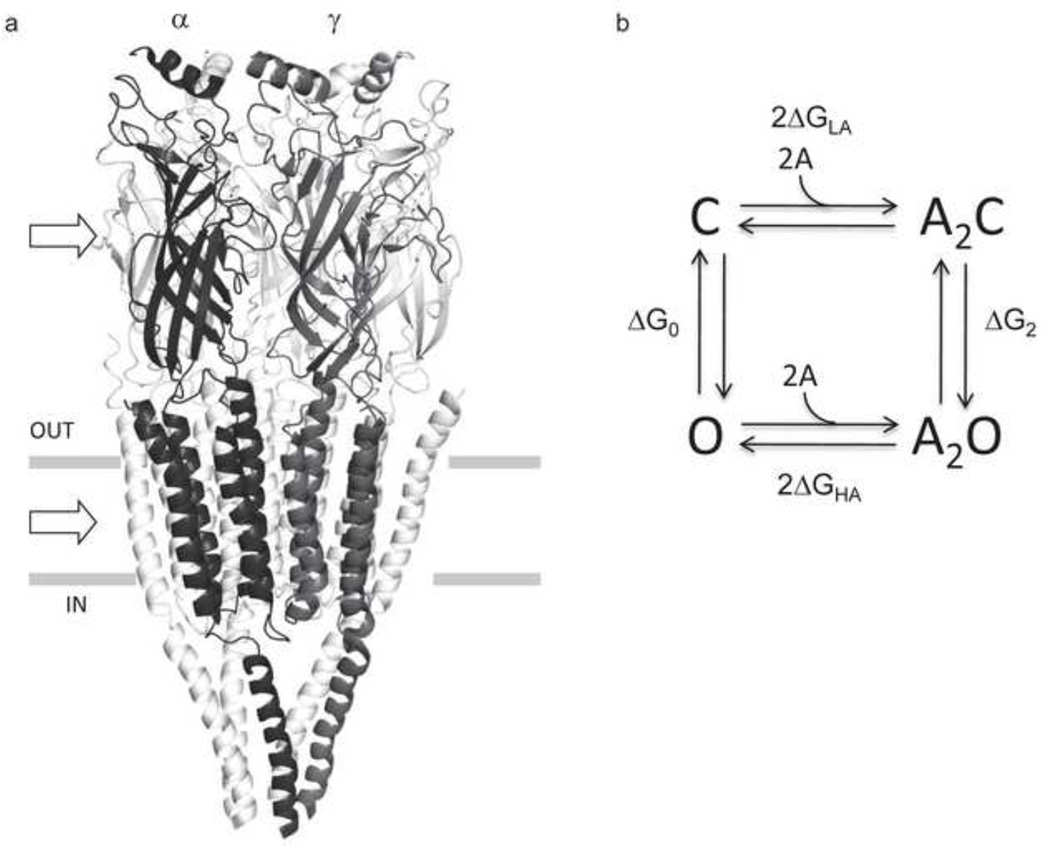
Figure 1. AChR structure and function.

a. The Torpedo marmorata AChR (subunit stoichiometry α₂βδγ; pdb accession number 2bg9 ⁸³). In adult mouse AChRs an ε subunit replaces γ. The upper and lower arrows mark the levels of a transmitter binding site (at the subunit interface) and the gate region of the pore. b. Thermodynamic cycle for AChR activation. Horizontal arrows, binding to two equivalent binding sites (A, the agonist); vertical arrows, the gating conformational change (C and O, the closed- and open-channel ensembles of the system). ΔG_O and ΔG₂, the O vs. C energy difference without and with two agonist molecules bound; ΔG_LA and ΔG_HA, the free energy of binding, low and high affinity. From detailed balance, 2ΔG_B=ΔG₂-ΔG₀, where ΔG_B=ΔG_HA-ΔG_LA. ΔG_B is the energy from the affinity change for one agonist that serves to increase the open-channel probability.

AChRs can adopt more than two global shapes, but I will focus on the rapid (<ms) ‘gating’ conformational change in which the alternative ensembles have a closed (C) or an open (O) ion-conducting pathway. The neuromuscular AChR has two transmitter binding sites that receive energy from the extracellular solution in the form of a ligand concentration. Certain ligands (‘agonists’) bind with a higher affinity to O compared to C and, hence, reduce (make more negative) the relative free energy of the ion-conducting conformation. As a consequence, when agonists are present at the binding sites the probability of being open increases.

Below, I first discuss the thermodynamic cycle for ligand binding and channel gating. I then consider the relative ground state energies that determine the gating equilibrium constant, either without or with ligands at the binding sites. Third, I outline several hypotheses that have been proposed for the mechanics of the isomerization itself. This perspective is based on the groundbreaking theoretical framework developed first for hemoglobin ⁴ and later applied to AChRs ⁵, and follows the pioneering single-channel experiments of Jackson .

II. The Cycle

The above definition of allostery describes a thermodynamic cycle (Fig. 1b). The letters represent the reaction ground states (energy wells) and the arrows represent the transition states (energy barriers), for which crossing involves movements or changes in the dynamics of structural elements. The core assumption of the model is that same, essential C↔O conformational change occurs either without or with agonists (A) at the transmitter binding sites.

The free energy differences between the ground states of the isomerization are ΔG₀ (G_O-G_C; unliganded gating) and ΔG₂ (G_A2O-G_A2C; diliganded gating). The horizontal arrows represent the exchange of ligand binding energy at two sensor sites that for ACh and the adult mouse AChR happen to be approximately functionally-equivalent. The free energy for binding to the lower-affinity, C shape is ΔG_LA and that for the higher-affinity, O shape is ΔG_HA. From detailed balance, 2ΔG_LA+ΔG₂=ΔG₀+2ΔG_HA. Rearranging, and defining ΔG_B as the net binding free energy from each ligand (ΔG_HA-ΔG_LA),

$$\Delta {\mathrm{G}}_2=\Delta {\mathrm{G}}_0+2\Delta {\mathrm{G}}_{\mathrm{B}}$$ Eqn. 1

ΔG_B is the average amount of free energy generated by the affinity change for the agonist at each transmitter binding site that ultimately contributes to the increased relative stability of A₂O vs. A₂C.

Although the cycle provides a satisfactory, first-order description of AChR gating ⁸, experiments have shown that the scheme is incomplete. There is evidence that the C ↔O and A₂C↔A₂O transitions occur through one or more intermediate steps that are not fully-resolved in the single-channel current record. In channel-opening, intermediate structures are adopted, briefly, that are no longer C but not quite yet O. Given the AChR’s size (~300 kD), there undoubtedly are many small wells populating the isomerization energy landscape. The patch clamp instrument has a limited bandwidth and sojourns in states having lifetimes <~30 μs are typically not resolved as discrete events.

The ΔG₂ values that we measure are the energy differences between the end states of the isomerization and, hence, their magnitudes are not dependent of the number or character of the intermediates. For example, the simplest extended kinetic scheme for diliganded gating is A₂C↔A₂F↔A₂O, where F represents a single intermediate state. In this scheme the apparent ΔG₂ is simply the sum of the energy changes for each of the two steps.

There are also intermediate states within the binding arrows of the cycle. There is evidence that the LA association of some agonists is not by diffusion alone but also requires a conformational change of the protein that may involve an inward displacement (‘capping’) of loop C at the transmitter binding site (see Fig. 5)⁹. The cycle only specifies two affinity states, but the binding site apparently can adopt three different conformations (apo, LA and HA) that are connected by two structural rearrangements called ‘catch’ (apo↔LA) and ‘hold’ (LA↔HA). In the cycle, the LA ‘catch’ rearrangement lies within the binding arrows and the HA ‘hold’ rearrangement lies within the gating arrows.

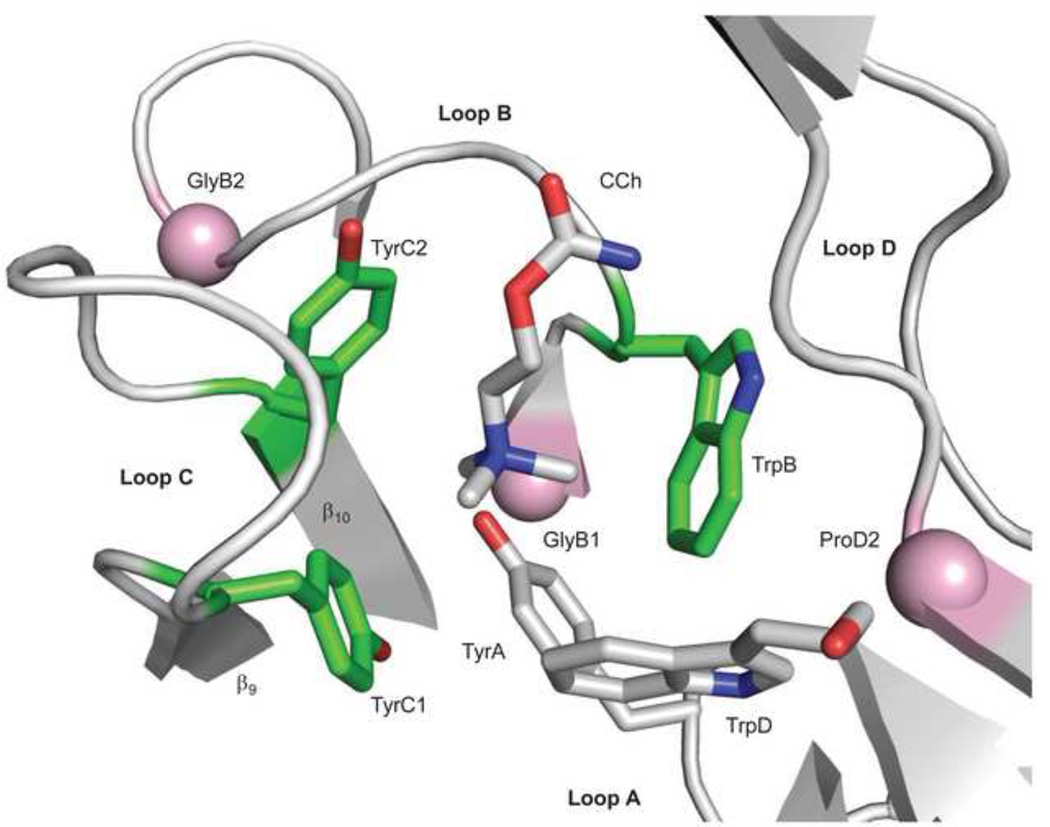
Figure 5. Sources of ΔG_B.

The ligand binding site of AChBP with carbamylcholine (CCh)(pdb accession number 1uv6; ⁸⁵). The view is from extracellular solution of a subunit interface. Left, the ‘principal’ subunit that corresponds to α in AChRs (loops A, B and C) and right, the ‘complimentary’ subunit that corresponds to ε/γ or δ in AChRs (loop D). An ‘aromatic triad’ (green) provides most of the ΔG_B^ACh energy (~2 kcal/mol each, from the indole and benzene rings of TrpB, TyrC1 and TyrC2). The pink spheres are the Cα atoms of the residues that correspond to GlyB1, GlyB2 and ProD2 in AChRs. Mouse numbering: TyrA=αY93; GlyB1=αG147; TrpB=αW149; GlyB2=αG153; TyrC1=αY190; TyrC2=αY198; TrpD=εW55 or δW57; ProD2=εP121 or δP123.

An important observation is that for some structurally-related ligands ΔG_LA and ΔG_HA are correlated, to an extent that the diliganded gating equilibrium constant can be predicted only from knowledge of the agonist’s low-affinity association rate constant. For this agonist series at least, the apo↔LA energy (structure) change and the LA↔HA change appear to be two stages of a single, integrated process called ‘catch-and-hold’. This correlation in energies joins the horizontal and vertical arrows of the cycle and blurs the distinction between binding and gating that is implicit in the model.

If ‘catch-and-hold’ is an integrated structural rearrangement of the binding site, then gating can be considered to start with the formation of the LA complex, which occurs within the binding arrows of the model. The ‘catch’ conformation change appears to be sufficient (but not necessary) to modify the channel-opening rate constant, either by lowering the gating transition state barrier, modifying the rate constant prefactor or both. The evidence suggests that the subsequent LA→HA transition serves only to stabilize the O conformation rather to initiate the isomerization. As discussed below, the ‘hold’ rearrangement may occur at any point within the global A₂C↔A₂O reaction.

II. Ground State Energies

Measurements

It is possible to measure experimentally ΔG₂ and ΔG₀ by using single-channel electrophysiology, and with high precision (~±0.2 kcal/mol) (Fig. 2). When the concentration of the agonist ([A]) is sufficiently high, channel openings occur in clusters that reflect the activity of a single AChR. In addition to C↔O gating, AChRs can take on ‘desensitized’ conformations that are non-conducting (like C) but have a high affinity for agonist (like O). In neuromuscular AChRs the rate constants for desensitization and recovery are much slower than those for binding and gating and, hence, serve to isolate periods of activity arising from individual AChRs. This isolation, and the fact that AChRs are ion channels, offer a huge advantage for studying the allosteric process because it provides a long-lasting signal from single molecules at a ~30 μs time resolution.

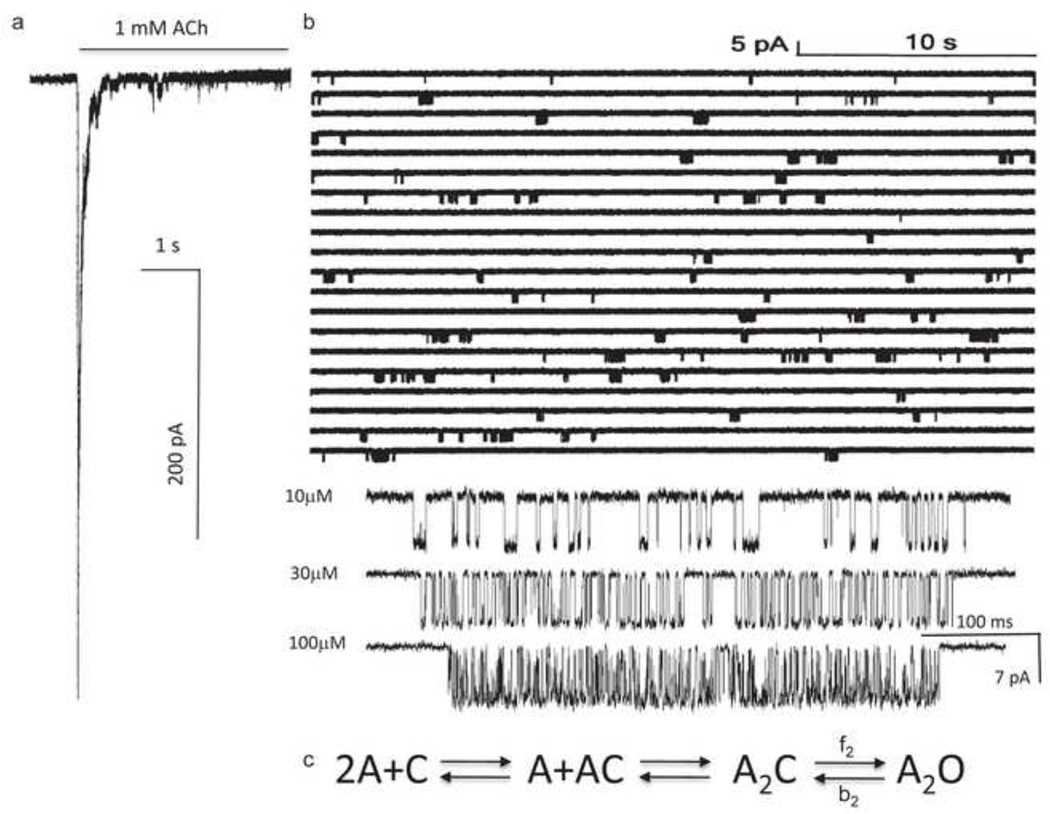
Figure 2. Measuring ΔG₂.

a. Outside-out patch current following a step to high [ACh] (opening downward). The rising phase is binding plus gating and the falling phase is desensitization. b. Single-channel currents in a cell-attached patch exposed continuously to 1 mM ACh. Each cluster is the binding and gating activity of a single AChR. The silent periods between clusters of openings are periods when all AChRs in the patch are desensitized. Below, higher resolution views of clusters at different [ACh]. The shut times reflect binding and opening, and the open times reflect closing. c. Sequential scheme for estimating rate and equilibrium constants with activation by agonists. ΔG₂=−0.59ln(f₂/b₂), where f₂ and b₂ are the diliganded opening and closing rate constants.

When [A] is much greater than the LA equilibrium dissociation constant (K_d), most of the fully-resolved current intervals within clusters reflect A₂C↔A₂O gating. The rate constants are estimated from the intra-cluster shut and open interval durations, and their ratio gives the diliganded gating equilibrium constant, E₂. ΔG₂ is proportional to the natural logarithm of this equilibrium constant (ΔG₂ in kcal/mol=−0.59lnE₂). For mouse adult-type neuromuscular AChRs at a membrane potential of −100 mV and at 23 °C, E₂^ACh=25 and ΔG₂^ACh=−1.9 kcal/mol.

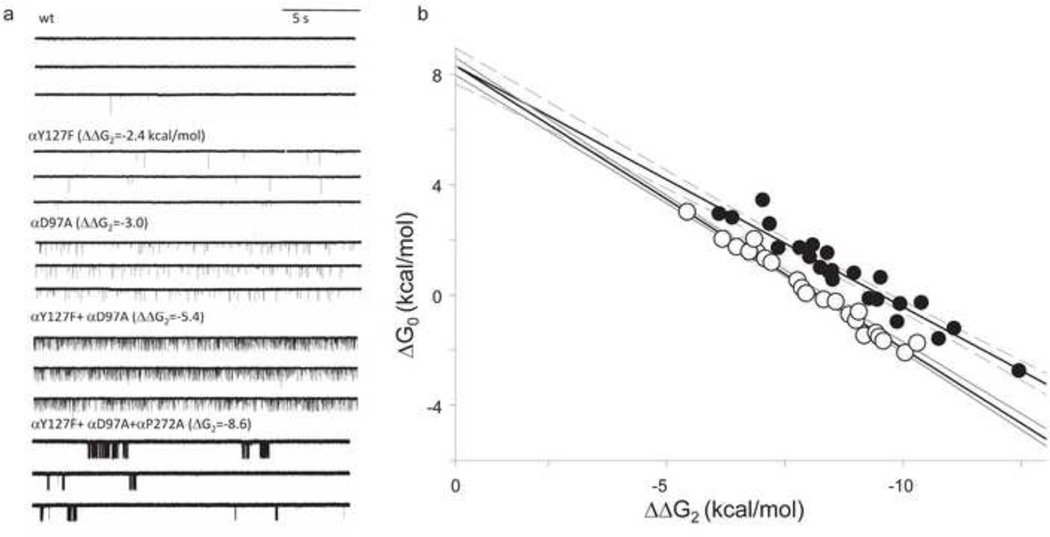
It is a bit more difficult to estimate ΔG₀ because the unliganded C↔O gating equilibrium constant of wt AChRs is small and openings are not clustered. However, many background mutations increase this equilibrium constant sufficiently to generate clusters (Fig. 3a) ¹². Desensitization proceeds mainly from the O state and with a rate constant that is approximately the same regardless of whether or not ligands occupy the binding sites. By assuming that each mutation only changes ΔG₀ (and not ΔG_B) and does so independently of others, it is possible to extrapolate the apparent unliganded gating equilibrium constant to the wild-type condition (Fig. 3b). The slope of the line for one set of mutant combinations (filled circles) is exactly that predicted if the change in ΔG₂ was equivalent that in ΔG₀, indicating that both assumptions were valid. For another mutant set (open circles) the slope was slightly smaller than predicted, probably because of some energy coupling between the mutations. From these experiments, based only on brief unliganded openings, ΔG₀=+8.3 kcal/mol (−100 mV, 23 °C) ¹³.

Figure 3. Measuring ΔG₀.

a. Continuous traces of currents obtained in the absence of agonists. Mutations that make ΔG₂ more negative to known extents (in parentheses) increase constitutive activity. Bottom, with a sufficient decrease in ΔG₂ the unliganded currents are clustered, indicating that desensitization occurs in the absence of agonists. b. The observed ΔG₀ of clusters is correlated linearly with the change in ΔG₂ caused by the background mutations (units are kcal/mol). Open and filled circles are different sets of mutation combinations. The intrinsic ΔG₀ of wt AChRs (at −100 mV) is estimated by extrapolating to the condition where ΔΔG₂=0 (+8.4 kcal/mol).

There is another way to estimate ΔG₀. With ACh, each of the two adult-type AChR transmitter binding sites provides the same amount of ‘hold’ energy, hence, ΔG₂-ΔG₁=ΔG₁-ΔG₀. Because we know ΔG₂, all that is necessary in order to calculate ΔG₀ is to measure ΔG₁. The binding site mutation αW149M greatly reduces ΔG_B^ACh but has almost no effect on ΔG₀ ¹⁴. By examining clusters of currents (−100 mV) from AChRs having this mutation at just one binding site it was estimated that ΔG₁^ACh=+3.3 kcal/mol, or that ΔG₀=+8.4 kcal/mol ¹⁵. The same result for ΔG₀ was obtained using the partial agonist choline. That the extrapolation method and the monoliganded method give the same quantitative result for ΔG₀ demonstrates that brief unliganded openings and longer mono- and diliganded openings are generated by the same essential, global isomerization. This observation confirms the core assumption of the cyclic scheme.

A negative membrane voltage stabilizes the O conformation. By measuring ΔG₀ at different membrane potentials it was found that the intrinsic chemical energy of gating (at 0 mV) is +9.4 kcal/mol. This energy reflects gating of AChRs with only water at the transmitter binding sites, because the removal of monovalent cations from the extracellular solution has no effect on ΔG₀ ¹³.

From Eqn. 1, 2ΔG_B^ACh=−10.2 kcal/mol (this value is not voltage-dependent). Because equal energies are provided by each ACh molecule, ΔG_B^ACh=−5.1 kcal/mol.

The intrinsic gating free energy, ΔG₀

The effect of mutations on gating has been measured from single-channel currents for >1000 mutations of >100 residues in many different regions of the AChR (see ⁸). Two essential features of the mutational energy changes emerge from these studies ¹¹.

First, mutations away from the binding sites change ΔG₂ and, hence, dose-response curves by an approximately-equivalent change in ΔG₀. To a good approximation, ΔG_B and K_d are not altered by non-binding-site mutations. The energy from the agonist affinity change appears to be determined by a small, select group of amino acids immediately at the binding sites. In AChRs, most changes in cellular responses consequent to side-chain substitutions can be attributed to a change in the relative stability of unliganded C vs. unliganded O.

Second, the ΔG₀ energy changes are mostly independent. In mutant cycle analysis the combined effect of two mutations is compared to the sum of the energy changes for each mutation separately. More than 50 such pair-wise combinations have been tested, and in most cases the net and sum energies are similar. Also, the effects of most background mutations are independent of the agonist and, hence, of ΔG_B. There are, however, some exceptions. There is a small-but-measureable amount (~0.5 kcal/mol) of long-distance energy coupling between side chains apparent across the protein that is a bit larger than the resolution limit of the analysis. This low-level, background coupling may be a clue for understanding how the binding sites and the gate are linked energetically (see below). Also, some closely-apposed side chains at the extracellular-membrane domain (EM) interface interact more strongly, by ~1–2 kcal/mol. In some cases, however, the reported degree of interaction here may have been overestimated because ΔG₂^ACh values for the single mutants αP272A and αE45A were underestimated. Also, one residue pair in the extracellular domain (αA96 and αY127) has been found to interact by ≥6 kcal/mol, suggesting that these two side chains act effectively a single structural unit in the gating isomerization ²⁰.

These two essential qualities of mutational effects suggest that i) most mutations change ΔG₀ simply because the substituted side chain is relatively more (or less) stable in O vs. C compared to the wt side chain, and ii) the structural changes (in bonds, water and dynamics) associated with mutational gating free energy changes occur close to the site of the mutation. The simplest explanation for independence is that the energy changes are local because multiple, long range energy transfers would be expected to interact. The energy of the gating transition state is linked to those of the C and O ground states, so a perturbation(s) that changes ΔG₀ will also change the forward and backward rate constants of the isomerization and the kinetics of the cellular response. To a first approximation, in AChRs mutations and agonists alter functional responses by changing the relative energies of the gating ground states, mainly by local interactions.

There are likely to be rigid body motions of domains and secondary structures within the AChR isomerization, for example a rotation of the extracellular β-sandwich and tilting movements of the pore-lining M2 transmembrane helices. However, the essential independence of the effects of mutations on these domains suggests that the side chain substitutions do not affect generally these motions, insofar as each amino acid changes energy independently of others on the rigid structure. Because of the independent nature of side chain energy changes, it appears to be possible to make of map of gating energy changes, residue-by residue, that can be superimposed approximately on the map of electron densities.

That most side chain substitutions change only ΔG₀ and do so nearly independently has implications with regard to engineering AChR function. First, natural selection of AChRs appears to be mainly about setting the intrinsic C vs. O ground state energy difference. Most mutations decrease ΔG₀, so survival apparently is enhanced when constitutive activity is low. Some myasthenic syndromes ²⁴ and epilepsies ²⁵ are caused by AChR mutations that make ΔG₀ less positive ²⁶. As a consequence, ions leak into cells, synaptic currents are prolonged and choline, a natural breakdown product of ACh, becomes a stronger, perhaps-inappropriate signal ²⁷. The fact that the effects of side chain substitutions on ΔG₀ are nearly independent makes the process of natural selection stable. If a mutation to one residue had an effect on ΔG₀ that depended on the side chain at another position, then assessing its selective advantage would be more problematic. It appears that survival is optimized, stepwise, by random mutations that alter ΔG₀ nearly independently.

Second, it is easy to design and control AChR properties in the laboratory ¹¹. The effect of a combination of mutations of ΔG₀ and the liganded gating rate equilibrium constants can be forecast simply by adding each separate energetic effect. Because mutations away from the binding site typically do not change ΔG_B (or K_d) regardless of the agonist, the ligand energy, too, can be added to this sum to predict ΔG₂ and the cellular response (Eq. 1). This engineering capability means that it is possible to quantify rate constants that are either too fast or too slow to be measured accurately in wt AChRs simply by adjusting the ΔG₀ of the background construct.

The map of ΔΔG₀

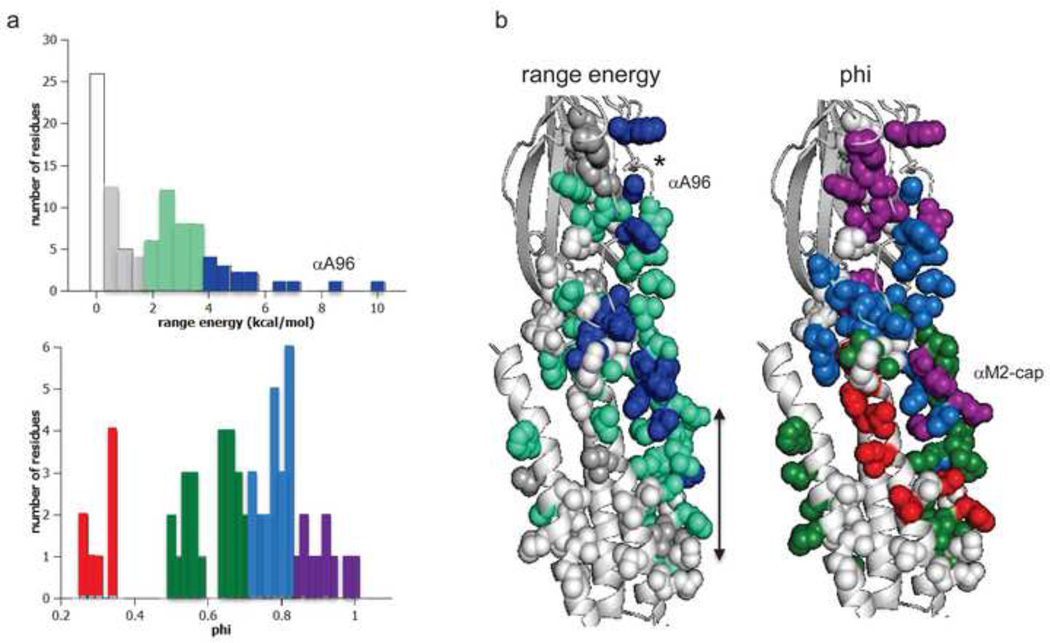
Of the many mutational changes in ΔG₀ that have been measured so far, only ~15% have little or no effect (<0.5 kcal/mol) and most of the rest make ΔG₀ less positive (Fig. 4a, top). Mutations in many different regions of the protein change ΔG₀ but the spatial distribution is not random (Fig. 4b, left). Larger effects are apparent for amino acids located between the binding site and the gate. The range in ΔG₀ for a series of mutations of one residue is one way to quantify the sensitivity of a position in the gating isomerization. In this active zone mutations of amino acids in all secondary structures of the α subunits can generate substantial range-energies (>2 kcal/mol).

Figure 4. ΔG₀ and phi in the α subunit.

a. Distributions. Top, range–energy is the difference between the smallest and largest ΔG₀ for a series of mutations of one amino acid. ~15% of residues are iso-energetic between C and O (white). Bottom, phi is the slope of a log-log plot of the forward rate vs. gating equilibrium constant and gives the relative timing of energy change, early (purple) to late (red). There are ~4 phi populations. b. Maps (view is from the γ subunit interface). *, binding site; arrow marks the narrow region of the pore, alongside the M2 helix. Large range-energy residues are mainly along the subunit interface between the binding site and the gate, with some having ≥4 kcal/mol range (blue). There is approximately a decreasing, coarse-grained, longitudinal gradient in phi values. αA96 has the largest range-energy of any residue measured so far and a phi value that is lower than its neighbors. There is an isolated, large-range and high-phi patch of residues near the C-terminus of the M2 helix (the αM2-cap).

In the extracellular domain, a column of residues located at the α-ε and α-δ subunit interfaces show the largest range-energies changes in the C↔O isomerization (≥4 kcal/mol) ²⁰. This is consistent with the idea that this region of the protein experiences large, local energy changes between C and O. The largest range measured so far is for an alanine in loop A (αA96; 8.1 kcal/mol), where a histidine substitution (in both α subunits) increases the unliganded gating equilibrium constant by a factor of ~100,000 ²⁸. A nearby tyrosine also has an extraordinarily large range-energy. It so happens that these are the exceptional, tightly-coupled amino acid pair ²⁸. The large range-energies of αA96 and αY127 mutations indicate that these two positions experience a large C vs. O energy change in their local environment. These amino acids also have similar phi-values, which indicates that the energy changes of the elements of this structural unit occur synchronously (see below). αA96 and αY127 are close to a hydrophilic pocket in the interior of the α-subunit extracellular domain, but the large range-energies likely reflect only the ground state energy difference and do not shed light on the hypothesis that this region confers structural flexibility for the gating isomerization itself ²⁹.

Some residues buried within the core of the extracellular domain do not show a significant effect on ΔG₀, so this compact region may remain iso-energetic between C and O ³¹. There are large changes in ΔG₀ apparent with mutations of some residues at the EM interface, mainly in the α subunit. In the membrane domain, near the C-terminus (extracellular limit) of the M2 helix, there is a cluster of amino acids that have large range-energies, but apparently only in the α subunit ³⁸. At the M2 gate region, near middle of the pore (positions 9’, 12’ and 13’), residues in all subunits show substantial ΔG₀ changes, in all subunits. A large energy change implies a significant change in the local side chain environment between C and O, perhaps from water entry here. Range-energies of 1–3 kcal/mol have been observed for amino acids in the M3 and M4 helices of the α-subunit. The effects of mutations of residues in the M1 helix ⁴⁶ and the intracellular domain (not shown in Fig. 4) of the α subunit, and the extracellular and other domains of the non-α subunits, have not been studied in detail with regard to ΔG₀.

Free energy from the ligand, ΔG_B

ΔG_B is the energy of stabilization to the O ground state provided by the LA→HA ‘hold’ conformational change at the binding site. The LA ‘catch’ rearrangement effectively adds a new, side-chain-sized structural element (the agonist) to the binding site that is more stable in O compared to C. In this sense, agonist ΔG_B values are similar to mutational ΔG₀ changes: they are consequences of structural rearrangements that change the relative stability of O vs. C mainly by local interactions. Eq. 1 could be rewritten as ΔG₂=ΔG₀^wt+∑ΔΔG^p, where ∑ΔΔG^p is sum of the free energy changes to the ground states caused by all perturbations, including voltage, side chain substitutions and newly-added ligands.

The binding energies for some ‘physiological’ ligands of AChRs have been measured. At the neuromuscular synapse the neurotransmitter (ΔG_B^ACh=−5.1 kcal/mol) is hydrolyzed to choline (ΔG_B^choline=−3.3 kcal/mol), which can be oxidized to betaine (ΔG_B^betaine=−1.9 kcal/mol). Nicotine is the predominant tobacco alkaloid (ΔG_B^nicotine=−4.1 kcal/mol). ΔG_B values for some agonists are given in Table 1.

Table 1.

Net binding energy (ΔG_B) from different agonists

Agonist	ΔGB (kcal/mol)
Acetylcholine11	−5.1
Anabasine87	−5.1
Nornicotine87	−4.7
Carbamylcholine11	−4.7
TMA11	−4.5
BTMA88	−4.5
DMThM11	−4.2
Nicotine87	−4.1
4OH-BTMA88	−4.1
DMT11	−4.0
DMP11	−3.9
ETMA88	−3.8
PTMA88	−3.8
Chlorocholine88	−3.7
3OH-PTMA88	−3.6
Choline11	−3.3
Cholamine (pH 9.0)88	−3.2
2OH-PTMA88	−3.0
Cholamine (pH 6.1)88	−2.1
Betaine88	−0.8

Energies calculated assuming equal contributions from two binding sites. TMA, tetramethylammonium; BTMA, butyltrimethylammonium; DMthM, 4,4-dimethylthiomorpholinium; 4OH-BTMA, 4-hydroxybutyltrimethylammonium; DMT, 1,1-dimethylthiazolidinium; DMP, 1,1-dimethylpyrrolidnium; ETMA, ethlytrimenthyammonium; PTMA, propyltrimenthyammonium; 3OH-PTMA, 3-hydroxypropyltrimethylammonium; 2OH-PTMA, 2-hydroxypropyltrimethylammonium

Although most mutations change only ΔG₀, a handful of residues at the transmitter binding sites are important in setting ΔG_B. Each binding site is a discrete apparatus that has evolved to derive binding energy from ligands to enforce the gating conformational change. So far the operation of this ‘engine’ has been investigated by estimating ΔG_B^ACh in AChRs having mutations of eight binding site residues (Fig. 5).

There are five conserved aromatic amino acids at each binding site. Just three of these, an α-subunit ‘aromatic triad’ comprised of TrpB, TyrC1 and TyrC2, contribute significantly to ΔG_B^{ACh 49}. The indole or benzene groups of these side chains each contribute ~-2 kcal/mol to ΔG_B^{ACh 49} by cation-π interactions. In adult-type AChRs, the two other aromatic groups (TrpD and TyrA) make little or no contribution to ΔG_B^ACh.

The removal of the hydroxyl groups from TyrC2 and TyrA have almost no effect on ΔG_B^ACh, but a Y-to-F substitution at TyrC1 makes this energy more positive by ~2 kcal/mol. It is likely that this reduction in binding energy is not directly from losing an interaction with the quaternary ammonium group of ACh, but rather from one with a nearby lysine ⁵².

Two glycines in loop B bracket TrpB. All mutations of GlyB1 reduce activation (by making ΔG₀ and ΔG_B more positive and by increasing K_d) whereas all those of GlyB2 increase activation (by making ΔG₀ less positive and by reducing K_d, with little effect on ΔG_B). Given its location in AChBP structures, the ΔG_B energy arising from GlyB1 is probably not from a direct interaction with the ligand. The fact that GlyB2 mutations alter K_d but not ΔG_B indicates that these substitutions increase the low and high affinities of the binding site to nearly equivalent extents. Some substitutions of ProD2 (on the complimentary face of the pocket) make ΔG_B^ACh more positive by >2 kcal/mol, with the larger effects apparent at the α-ε vs. α-δ binding site (unpublished observations).

This list of structural elements that contribute to ΔG_B^ACh is probably not complete and may be different at the two binding sites, for different agonists and for different AChR subtypes. Energetic interactions between groups that influence ΔG_B have not been examined in detail, nor have the sources and magnitudes of binding energy for agonists other than ACh. Our understanding of the AChR binding sites is in its infancy.

Temperature

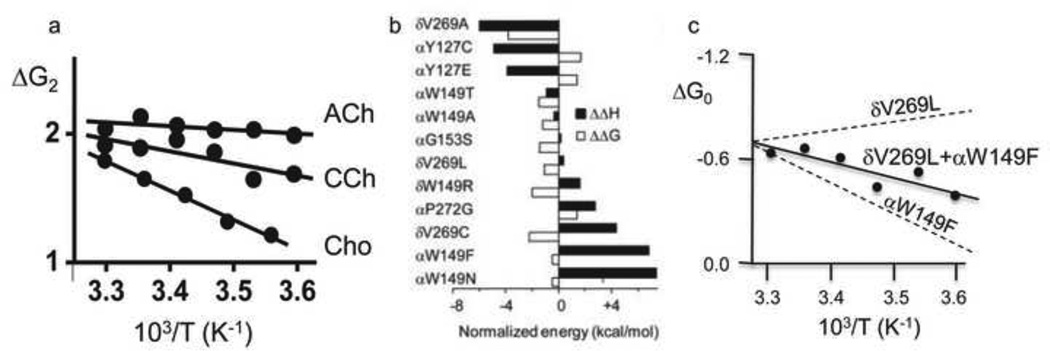
It is possible to dissect free energy into enthalpy and entropy components by measuring AChR binding and gating equilibrium constants at different temperatures ⁵⁶. The temperature dependence of the diliganded gating equilibrium constant depends on the agonist (Fig. 6a). For ACh, carbamylcholine and choline, the gating enthalpy differences are approximately the same as the ΔG_B free energy differences. This suggests that ΔG_B is essentially all enthalpy and that little heat is generated by the low-to-high affinity change.

Figure 6. Temperature dependence of AChR gating.

a. The slope of the van’T Hoff plot (ΔG₂ vs. 1/T) is agonist-dependent ⁸⁶. b. The enthalpy change (black bars) associated with most mutations is larger than the free energy change (white bars) because of a compensating entropy change. c. An example where enthaply changes of mutations are approximately additive.

With this information, the intrinsic enthalpy change of the unliganded gating isomerization (ΔH₀) has been estimated. From Eq. 1, the enthalpy change for diliganded gating (ΔH₂) is the sum of those for the affinity change (2ΔH_B) and ΔH₀. The measured value is ΔH₂^ACh =+0.7 kcal/mol (at −100 mV). Because 2ΔH_B≈2ΔG_B=−10.2 kcal/mol, we calculate ΔH₀≈+10.9 kcal/mol, which is equivalent to breaking just a few hydrogen bonds. From the relationship ΔG₀=ΔH₀-TΔS₀ (where T is the absolute temperature and S is the entropy) and the value ΔG₀=+8.4 kcal/mol, we estimate that ΔS₀=+8.5 cal/mol-K (+2.4 kcal/mol at 23 °C). At room temperature, ~20% of the total energy of unliganded gating is heat (=TΔS₀).

There are other good reasons to separate free energy into enthalpy and entropy components. When we compare structural models of a protein in C vs O we focus our attention on the changes in atomic positions and bonds. These differences relate more closely to enthalpy than to free energy because the entropy changes (from dynamics or solvent) are mostly invisible in the structures. Also, enthalpy changes are typically larger than free energy changes because of compensating changes in entropy (Fig. 6b). For example, for the mutation αW149N, ΔΔH₀ is +7.4 kcal/mol while ΔΔG₀ is only =−0.5 kcal/mol ⁵⁷. A map of ΔH₀ will provide a larger signal regarding changes in bonding than that of ΔG₀. An enthalpy mutant-cycle analysis shows that the enthalpy changes caused by mutations of different residues can be approximately independent (Fig. 6c), so this map could show the spatial distribution of heat exchange in the conformational transition.

With ACh as the agonist, the gating equilibrium constant has very little temperature dependence. However, temperature has a large ‘catalytic’ effect and substantially influences both the forward and backward isomerization rate constants. This indicates that there is a large (~20 kcal/mol) enthalpy component to the gating transition state barrier. The free energy of this barrier for diliganded gating has been estimated to be ~5 kcal/mol so large, compensating entropy changes likely prevail within the isomerization. The AChR appears to be partially ‘unfolded’ in the gating transition state ensemble.

The independence of mutational effects on ΔG₀ also applies to the transition state. By combining mutations that, for example, increase both the forward and backward gating rate constants it is possible to engineer the kinetics of the AChR response, including at different temperatures.

III. Gating Transition State

Intermediate gating states

A thermodynamic cycle is useful for estimating the relative ground state potential energies but provides little information about the energy transfer between the binding sites and the gate. This energy transfer defines the mechanical work and transition state ensemble (TS) of the isomerization itself. Presumably, the system is at all times in thermal equilibrium and there are no large-scale, ballistic gating motions. The assumption is that within the isomerization the moving parts are displaced in straight lines and with constant velocities only for short times (<ns) before collisions slow them and randomize their directions.

Mutations, ligands and voltage change the relative ground state free energies to force the global isomerization and establish a new equilibrium, but the process by which one protein shape converts to another is not revealed by measurements of these potential energies. It is therefore important to separate ‘coupling’ as defined by the thermodynamic linkage between ligand/voltage and ground state potential energies given by the cycle, and ‘coupling’ as defined by the actual mechanical work of the isomerization. To understand the details of the reversible energy flow between the binding sites and the gate (and elsewhere) we must go within the arrows of the cycle and examine the nature of gating TS.

One way to approach this problem is by investigating the short-lived states that exist between the C and O ground states. There are several lines of evidence indicate that such intermediate states can be detected in single-channel currents. The standard sequential model for activation by agonists is A↔AC↔A₂C↔A₂O. This scheme is just a section of the full cycle that ignores sojourns in O and AO that are rare under physiological conditions. Kinetic modeling studies indicate that an extra, brief AC’ state interposed between AC and A₂C improves the statistical fit of the interval durations. One interpretation is that ligand energy from each binding site is transferred independently towards the gate, with rapid opening happening only after both transfers have taken place ⁶². Accordingly, AC’ could be a gating intermediate in which only one of the two transfers has occurred.

Other direct evidence for gating intermediates has come from analyses of open-channel currents. The open current has excess, high-frequency noise (compared to the baseline) that does not arise from instrumentation or shot sources but from rapid interruptions in the channel current ⁶³. Advanced analysis methods have been used to extract directly a ~5 μs closing event (‘flip’) from this signal ⁶⁴. Neither the amplitude nor lifetime distribution of this gap is fully-resolved, nor can its placement within a state model for activation be established unambiguously. However, if it is assumed that ‘flip’ is a full closure that occurs between A₂C and A₂O, then it is a non-conducting intermediate state. If it is further assumed that its lifetime is distributed as a single exponential, then it reflects just one such state. The detection of ‘flip’ is significant because it offers the possibility that states between C and O can be probed directly by using discrete Markov models, and that ΔG₀ can be separated into its addends.

Another way to investigate intermediate gating states is by rate-equilibrium analysis. Although each gating rate constant is estimated independently (as a free parameter), in many chemical reactions, including AChR gating, the forward and backward rate constants for series of mutations of one amino acid are correlated inversely ⁶⁵. For example, AChR mutations that decrease ΔG₀ do so by increasing the forward and decreasing the backward gating rate constants, to varying extents. This correlation can be quantified by plotting (on a log-log scale) the forward rate constants vs. the equilibrium constants for a series of mutations of one amino acid.

The slope of this relationship is called phi. In AChRs the values of the rate constants can vary by orders of magnitude, but the correlation remains constant. The interpretation of phi is complex and not founded in a definitive theory. It could reflect the height of the transition state barrier relative to that of the product state, the rate constant prefactor (specifically, the transmission coefficient) ⁶⁸ or, perhaps, both. However, there is some agreement that it provides information about the relative timing of the energy (structure) changes of the perturbed site within the channel-opening reaction, on a scale from 1 (earlier) to 0 (later).

Gating phi values have been measured for mutations of many AChR residues, and, remarkably, there is a spatial organization (Fig. 4b, right). Phi values of residues near the transmitter binding sites are high (earlier), those near the gate are low (later), and those in between are intermediate. As shown in Fig. 4b, in opening the sequence of energy changes is purple-blue-green-red, and in closing this order is reversed.

Another feature of the map is that residues having similar phi values are clustered into contiguous groups. There appears to be 4 such clusters, which suggests that there are at least three intermediate states interposed between A₂C and A₂O ²⁸. The approximately longitudinal, decreasing gradient of phi values suggests that in opening the clusters move in sequence, starting with the binding site and ending with the gate (but see below). This led to the proposal that the AChR isomerization is a diffusional process. The suggestion is that if we could look inside the protein with ~ns time resolution, the domain movements would appear as a Brownian conformational ‘wave’ between the sensors and the gate ⁶⁹.

There are two curious characteristics of the phi map. First, there is an isolated patch of residues at the C-terminus of the M2 helix in the α subunit (the αM2 cap) that has among the largest range energies (blue) and highest phi-values (purple) in the protein (Fig. 4b) ³⁸. The phi values for some amino acids in this region appear to be even higher than those for residues at the transmitter binding sites. This raises the possibility that the first domain to move in channel opening is not the binding site, but, rather, the αM2-cap. It may be relevant that a recent crystal structure of the AChR homolog GLIC shows a protein mostly in the O conformation but with this portion of the M2 helix locally in the C position ⁷⁰. Although this observation is consistent with the idea that phi-clusters move as discrete structural units, it is unclear if the locally-closed GLIC structure represents a gating intermediate state or, perhaps, a desensitized conformation.

The second notable feature of the map is that phi values of binding site elements appear to be mutable. The phi values of all binding site residues measured so far are higher in diliganded vs. unliganded gating. For the eight residues shown in Fig. 5, the average diliganded phi is 0.93 (range, 0.88–1.0) and the average unliganded phi is 0.76 (range, 0.68–0.89). Residues away from the binding sites apparently do not show such mutability ¹², which suggests that the phi-shift may be caused by events local to the binding sites rather than by a shift in the position of the overall TS barrier. It is possible that the position of the LA↔HA ‘hold’ conformational change within the global isomerization can be influenced by experimental conditions.

Phi analysis is silent with regard to the conductance status of the intermediates. However, ‘flip’ as an intermediate gating state has a high affinity for the agonist and a non-conducting pore. This description applies to desensitized states as well. It is possible that the slow rate constant for desensitization could reflect a much faster process proceeding from a brief, non-conducting gating intermediate state ⁶⁹.

Flip and phi are in good agreement, with the main incongruence being with regard to the number of brief intermediate states (one vs. several). One possibility is that flip underestimates the number of TS energy wells. The distribution of flip lifetimes is not fully-resolved, so it may be that these events reflect the tail of a multi-exponential distribution that appears in experiments as a partially-resolved, single exponential because of the limited time resolution of the patch clamp. Another possibility is that phi overestimates the number of intermediates. Phi quantifies side chain energy changes, and there is no reason to assume that an amino acid is perturbed only once during the isomerization. For example, assuming that there is only one intermediate state (C↔F↔O), phi could reflect a weighted average of the energy changes occurring in the C↔F entry step vs. the F↔O exit step ⁴⁰. In this case the purple residues in Fig. 4b would change energy mainly in the entry step, the blue and green residues in both exit and entry (to different extents) and the red residues mainly in the exit step. The number and conductance(s) of the gating intermediates is an open question.

Site-gate energy transfer

Electrophysiology experiments indicate that there are one or a few metastable intermediate states between C and O. What are their structural correlates, and what are the forces that motivate energy flow between the binding sites and the gate? Mutational changes in ΔG_B and ΔG₀ and phi values provide information regarding which structural elements change energy (move) in gating and in what order, but they do not illuminate the forces that underlie these energy changes. There have been several proposals for the isomerization mechanism, but as yet no consensus has emerged.

With ACh molecules bound to wt AChRs in low-affinity complexes at both binding sites, the opening isomerization rate constant is ~10 million times faster than when only water is present. The event that triggers this dramatic change in the gating TS appears to be the ‘catch’ rearrangement, which probably involves partial loop C capping. In this regard, the AChR gating isomerization commences with the low-affinity binding of agonists.

What happens next? It is important to emphasize that there is no a priori reason to assume that the subsequent gating rearrangements begin at any particular place in the protein. Because everything is in thermal equilibrium, neither the agonists at the binding site nor the ions in the pore have any significant momentum. The energy from the LA→HA affinity change may occur at any point in the isomerization: the onset, middle or end, and either before or after the low→high conductance rearrangement of the pore. (If ‘flip’ is a gating intermediate, then it suggests that ‘hold’ precedes the conductance change). The LA→HA switch serves only to stabilize the O ground state, mainly by local interactions with the aromatic triad. The mechanical work of gating could begin anywhere and proceed in any sequence.

The ‘priming’ hypothesis for work is related to the AC’ intermediate state inferred from kinetic modeling. In this scheme, agonist HA binding causes an inward displacement of loop C at each transmitter binding site that transfers energy independently to the EM interface via a motions of secondary structures, most likely β-strands 9–10 ¹⁷. This perturbs a proline ⁷³ and, perhaps, a salt bridge ¹⁷ at this interface and, eventually, the pore-lining M2 helix, to initiate ion conduction.

There is evidence, however, that many of the experimental results presented in support of this hypothesis reflect perturbations of the ground state energies rather than of the energy transfer process. For instance, brief unliganded openings, purportedly generated by ‘singly-primed’ AChRs (in which energy from only one binding site has been transferred to the gate region), are in fact from AChRs that have had the same amount of energy transferred to the gate as with two ligands present. We know this because ΔG₀^wt estimated only from these brief unliganded gating events, and ΔG₀^wt estimated from di- and monliganded gating events, are the same. Also, the deletion of loop C, the proposed structure that triggers the ‘priming’ energy transfer, debilitates agonist binding but has almost no effect on unliganded gating (unpublished observations). LA capping appears to be sufficient to increase the opening rate constant, but not necessary. The effect of loop C cross-linking and the evidence for a specific energy transfer pathway can be explained by alterations in the C vs. O ground state energies rather than to alterations in the transfer process. Mutations of the key proline and salt bridge residues at the EM interface do not cripple gating. Further, phi values suggest that in channel opening the αM2 cap moves (changes energy) before rather than after the interface. The hypothesis that the AChR gating isomerization occurs by a specific pathway involving top-down, sequential motions of secondary structures and select residues at the EM interface is appealing from the perspective of structure, but this idea is not supported by experiments.

In the ‘Brownian wave’ model for gating it is proposed that the isomerization of each phi-cluster triggers that of its neighbor ⁶⁹. In this mechanism the motions of the backbone and side chains in each group transfers energy to the adjacent one, and so on through the protein. In support of this hypothesis, the phi-clusters coincide roughly with structural domains that adopt alternative positions in C vs. O in the prokaryote homologues of the AChR, ELIC and GLIC. However, mutations of key residues at cluster boundaries do not change the map of phi, and, importantly, the longitudinal gradient in phi is neither absolute nor fixed. Specifically, the phi values of residues in the i) αM2-cap appear to be the highest in the protein, ii) membrane domain are not organized longitudinally, ii) presumably-rigid αM2 helix are inhomogeneous, and iv) binding sites are mutable ⁷⁶.

The ‘wave’ hypothesis for site-gate communication is appealing because it rationalizes much of the phi map. However, this map may be an effect, rather than a cause, of the mechanical work of gating. It is likely that the amino acids change energy in the sequence given by their phi values, but the forces that generate this sequence may be independent of side chain and domain energy changes that may serve only to set the relative stability of C vs. O.

Another hypothesis, called the ‘quaternary twist’, has been proposed based on elastic network model (ENM) analyses of the whole protein backbone ⁷⁷. Using a homology model of the α7 AChR, movement along the softest mode widens and narrows the pore, as expected for a gating transition. However, the pore-widening mode was not apparent in the simulations using prokaryote receptor structures. Interestingly, interpolated ENMs, using ELIC (presumably closed) and GLIC (presumably open), predict a spatial distribution of phi values that is, to some extent, consistent with the experimental map ⁷⁸. It is possible that motions of the backbone generate the forces that result in a ‘Brownian wave’ of side chain energy changes, like branch movements shaking the leaves of a tree.

It may be relevant is that there is small-but-measurable amount of background ΔG₀ energy coupling (~0.5 kcal) between widely-separated side chains. For example, mutant-cycle analysis indicates that the ProD2 residues at the two binding sites are coupled by ~0.7 kcal/mol, which is slightly larger than the experimental resolution (unpublished observations). These low-level coupling energies could reflect a long-range transfer of energy, for instance by the backbone breathing motions. In the ‘quaternary twist’ mechanism the binding site and the gate communicate via the collective motion of all of the backbone atoms. It may be that there not a discrete communication pathway between the binding sites and the gate.

Final Thoughts

Cellular responses emerge from complex combinations of rate and equilibrium constants. The constants for agonist binding, channel gating and desensitization together determine steady-state dose-response profiles, the time course of individual synaptic currents and even the change in response amplitude within a synaptic train. The equilibrium constants in turn are determined by the relative free energies of the reaction ground states and, because the transition state energies are linked to those of the ground states, so too are the rate constants. In AChRs the path between DNA sequence and survival of the organism seems clear. Sequence determines the side chain, which determines ΔG_B^ACh and ΔG₀, which determine the gating rate and equilibrium constants, which determine the character of the physiological response. The mechanism of the actual work of the gating isomerization is less-well understood and may less-dependent on side chain composition. Here, it could be the overall fold of the protein that is the basis for energy transfer between the transmitter binding sites and gate. In this view, members of the AChR superfamily, which are functional as chimeras, could gate by the same essential mechanism even though they have a very low sequence homology.

1. Allostery in the AChR can be studied in single molecules with electrophysiology

2. The intrinsic energy changes of the ‘gating’ without ligands are known

3. Most mutations change the intrinsic energy, not that from the ligand

4. The effects of most mutations are additive

5. The ligand energy is from interactions with just three amino acids