Less Is More: An Adaptive Branch-Site Random Effects Model for Efficient Detection of Episodic Diversifying Selection

Abstract

Over the past two decades, comparative sequence analysis using codon-substitution models has been honed into a powerful and popular approach for detecting signatures of natural selection from molecular data. A substantial body of work has focused on developing a class of “branch-site” models which permit selective pressures on sequences, quantified by the ω ratio, to vary among both codon sites and individual branches in the phylogeny. We develop and present a method in this class, adaptive branch-site random effects likelihood (aBSREL), whose key innovation is variable parametric complexity chosen with an information theoretic criterion. By applying models of different complexity to different branches in the phylogeny, aBSREL delivers statistical performance matching or exceeding best-in-class existing approaches, while running an order of magnitude faster. Based on simulated data analysis, we offer guidelines for what extent and strength of diversifying positive selection can be detected reliably and suggest that there is a natural limit on the optimal parametric complexity for “branch-site” models. An aBSREL analysis of 8,893 Euteleostomes gene alignments demonstrates that over 80% of branches in typical gene phylogenies can be adequately modeled with a single ω ratio model, that is, current models are unnecessarily complicated. However, there are a relatively small number of key branches, whose identities are derived from the data using a model selection procedure, for which it is essential to accurately model evolutionary complexity.

Introduction

Modern biologists take a keen interest in deciphering how the action of various evolutionary processes generated the patterns of variation in extant or fossil genetic sequences (Kosiol and Anisimova 2012). Because of the foundational importance of natural selection, a mature and diverse library of computational approaches has been developed to infer its targets and mechanisms at the molecular level (Delport et al. 2009; Anisimova and Kosiol 2009). Methods that quantify the strength and type of natural selection by estimating the ratio of nonsynonymous to synonymous substitution (ω) using phylogenetic codon-substitution models, pioneered by Muse and Gaut (1994) and Goldman and Yang (1994), have proven particularly popular and useful. In the context of infectious diseases (see Aguileta et al. 2009 for a review), these models have been used successfully to study transmission (Jonges et al. 2011), zoonosis (Demogines et al. 2012), the evolution of drug resistance (Stanhope et al. 2008; Hill et al. 2009; Murrell, De Oliveira, et al. 2012), escape from host immune response (Frost et al. 2005; Cento et al. 2013), the development of pathogenicity and virulence (Brault et al. 2007), emergence of new strains (Schuh et al. 2014), and evolutionary arms-races between viruses and host antiviral defenses (Duggal et al. 2011; Daugherty et al. 2014).

A key feature of natural selection is its variability. The strength and direction of selective effects differ from site to site and change over time, and an ideal model should produce reliable results in the presence of such variation. The original Muse and Gaut (1994) model (MG94) estimated nonsynonymous and synonymous substitution rates independently for each branch b, allowing the average strength of natural selection (quantified by branch-specific ω_b ratios) to vary through time but not across sites. Conversely, Nielsen and Yang (1998) introduced a model in which ω varied from site to site, but was constant among branches. Combining the two ideas, Yang and Nielsen (2002) published the first tractable “branch-site” model which incorporated limited variation in ω both among sites and among branches and could be used for detecting episodic positive selection. Considering that this model and its refinements (Zhang et al. 2005; Anisimova and Yang 2007) have been cited over 2,000 times in peer-reviewed literature, it is clear that many researchers are using branch-site models to study the history of natural selection in their systems. However, these models have two key limitations. First, they explicitly disallow positive selection on a subset of “background” lineages. Second, they only permit four configurations of branch-specific rate parameters: 1) $\omega ={\omega }_0<1$ everywhere on the tree, 2) $\omega ={\omega }_1=1$ everywhere on the tree, 3) $\omega ={\omega }_0<1$ on background branches with $\omega ={\omega }_2\ge 1$ on foreground branches, and 4) $\omega ={\omega }_1=1$ on background branches with $\omega ={\omega }_2\ge 1$ on foreground branches. We have previously shown that these limitations can cause uncontrolled false positive rates and loss of power when model assumptions are violated (i.e., when there are sites that do not conform to one of the above four configurations, for instance, due to rate variation among the background lineages) and simultaneously proposed a method, branch-site random effects likelihood (BSREL), that allowed all possible configurations of branch-specific rate parameters (Kosakovsky Pond et al. 2011).

The essential idea of the BSREL method is to endow each branch with three ω parameters and to allow each site to evolve under any of the three ω values. For a tree with B branches, the resulting model considers $3^B$ configurations of ω values at a given site (instead of only four configurations in the original branch-site models), but remains tractable thanks to an efficient algorithm for marginalizing the phylogenetic likelihood function over all possible assignments of rates to sites and branches, which requires the assumption that ω values are independent among branches.

By using a more complex model, BSREL avoids the uncontrolled false positive results that are obtained by previous branch-site models in the presence of rate variation in background lineages, while achieving substantial improvements in power. Although BSREL is no slower than previous models, it is relevant to ask how complex should a model be for optimal statistical performance?

In general, both the overall complexity and the specific structure of the best model choice will depend on the particular data set. Consider only a single branch in the tree. If the branch is very short, the number of substitutions observed will not be very different at different sites, and it will not be possible to accurately infer multiple rate categories. For longer branches, site-to-site rate variation will become more evident (Scheffler and Seoighe 2005), allowing a larger number of rate categories to be inferred. At the other extreme, if the branch is long enough for saturation to occur, the observed substitution rate will again become less informative so that fewer rate categories can be inferred. The adaptive BSREL (aBSREL) model developed and presented here exploits this phenomenon by adapting its complexity to the data set, inferring the optimal number of rate categories to be used for each branch through the small-sample Akaike Information Criterion (AICc; Sugiura 1978). This approach was originally motivated by our analyses of rapidly evolving viral pathogens (Wertheim and Kosakovsky Pond 2011; Wertheim et al. 2013), whose phylogenetic trees often exhibit characteristic patterns with many short branches connecting recent isolates from a viral species or a local epidemic, and several long branches which relate different epidemics or different viral species, for example, see figure 4 in Wertheim and Kosakovsky Pond (2011).

Fig. 4.

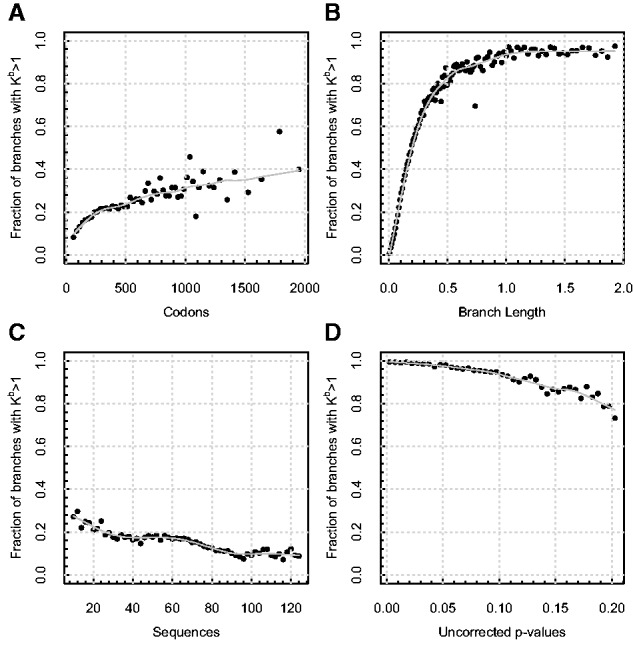
Correlates of signal for evolutionary process complexity in the selectome data sets. Each panel depicts the fraction of all alignments reported by aBSREL as having more than one ω rate class selected by the step-up procedure (K^b), as a function of (A) the length of the alignment (codons), censored at 2,000 due to sparse sampling afterwards (binned in increments of 50 codons); (B) branch length (expected substitutions per site [binned in increments of 0.01]); (C) the number of sequences (binned in increments of 2 sequences); (D) uncorrected P value for episodic positive selection (binned in increments of 0.005). Each point represents an average over at least 100 individual branches. Lowess smoothing polynomials (smoothing span 0.25) are shown in solid light gray.

We evaluate the aBSREL method using comprehensive simulated and large-scale empirical data collections, encompassing six carefully chosen examples, and a set of 8,893 Euteleostomes gene alignments, included in version 06 of the Selectome database (Moretti et al. 2014) previously analyzed for evidence of episodic selection. Finally, we compare the computational performance of aBSREL, BSREL, with that of a highly tuned and algorithmically sophisticated implementation of the Nielsen–Yang class of branch-site models (Valle et al. 2014).

New Approaches

Evolutionary Model

At the heart of efficient episodic selection detection is adaptive model complexity, implemented in aBSREL as a branch-wise model selection procedure. Branch-wise adaptation to the complexity supported by the data set removes the assumption that all branches, even of different lengths and spanning various evolutionary events such as speciation, contain evidence of the same degree of substitution rate heterogeneity. Instead, we infer an appropriate number of substitution rate classes for each branch and use the method originally described in Kosakovsky Pond et al. (2011) to mix these rate classes according to the proportion of sites they are inferred to describe. For this and other models of codon substitution (Anisimova and Kosiol 2009; Delport et al. 2009) the rate of instantaneous substitution from a sense codon x to a sense codon y is described by the (x, y) entry in the generator matrix $\left(Q=\left\{q_{xy}\right\}\right)$ of the time-homogeneous, stationary, continuous-time, and time-reversible discrete state Markov process, using the Muse–Gaut equilibrium frequency parameterization (Kosakovsky Pond, Delport, et al. 2010),

$$q_{xy}^{bs}=\{\begin{array}{cc}{r}^{bs}(x,y){\theta }_{ij}{\pi }_j^p,& x\text{\hspace{0.5em}and\hspace{0.5em}}y\text{\hspace{0.5em}differ\hspace{0.5em}by\hspace{0.5em}one\hspace{0.5em}nucleotide},\\ 0,& x\text{\hspace{0.5em}and\hspace{0.5em}}y\text{\hspace{0.5em}differ\hspace{0.5em}by\hspace{0.5em}}>1\text{\hspace{0.5em}nucleotide},\\ -{\displaystyle \sum _{z\ne x}{q}_{xz}^{bs}},& x=y.\end{array}$$

We make use of several common modeling assumptions (see table 1 for notation and parameter definitions). Only single nucleotide substitutions (from nucleotide $i\in \{A,C,G,T\}$ in codon x to nucleotide j in codon y) have nonzero instantaneous rates (see Kosiol et al. 2007 for an example of models relaxing this assumption). We use the general time-reversible model for nucleotide substitution rates, parameterized by five rate multipliers θ_ij (the sixth parameter is confounded with time) and nine position-specific nucleotide equilibrium frequency parameters ${\pi }_j^p$ (for codon positions $p\in \{1,2,3\}$) derived from observed proportions in the data using a bias-corrected CF3 × 4 estimator (Kosakovsky Pond, Delport, et al. 2010). It can also be shown that the equilibrium frequency of a particular codon is the product of position-specific ${\pi }_j^p$ for the three constituent nucleotides, normalized for the absence of stop codons in the model; see Kosakovsky Pond, Delport, et al. (2010) for an extensive discussion on the subject.

Table 1.

aBSREL Model Parameters.

Parameter	Notation	Domain	Estimation
Number of ω classes per branch	Kb	Positive integers	Greedy step-up (AICc)
Branch-specific ω rates	${\omega }_k^b$	[0,1] for $k<K^b$	MLE
		$[0,\infty )$ for $k=K^b$
Branch-specific ω proportions	$f_k^b$	$[0,1],{\displaystyle \sum _k{f}_k^b}=1$	MLE
Branch lengths	tb	$[0,\infty )$	MLE
Nucleotide substitution rate multipliers	θij	$[0,\infty )$	MLE
Nucleotide frequency parameters	${\pi }_j^p$	$[0,1],{\displaystyle \sum _{j\in \{A,C,G,T\}}{\pi }_j^p}=1\forall p$	Transformed counts

Note.—MLE, maximum-likelihood estimation. b indexes branches in the phylogenetic tree. i, j enumerate nucleotides. p is the position of a given nucleotide in a codon (1, 2, 3). k enumerates K^b

Both BSREL and aBSREL focus their attention on estimation of codon-level rates, denoted by $r^{bs}(x,y)$, with superscript bs used to make explicit the dependence of model parameters on a specific branch in the phylogeny (b) and a specific site in the alignment (s). In implementing these methods, we made two further common simplifying assumptions: Only synonymous and nonsynonymous codon substitution rates are distinguished (i.e., for fixed values of b and s and $x\ne y,r^{bs}(x,y)$ will depend only on whether or not x and y encode the same amino acid), and synonymous substitution rates do not vary from site to site or from branch to branch. Both of these assumptions can be readily relaxed without altering the core of the model (Pond and Muse 2005; Delport et al. 2010), but doing so would complicate comparison with existing models.

In accordance with these assumptions, we set

$$r^{bs}(x,y)=\{\begin{array}{cc}{\Omega }_b(s),& x\text{\hspace{0.5em}and\hspace{0.5em}}y\text{\hspace{0.5em}encode\hspace{0.5em}different\hspace{0.5em}amino\hspace{0.5em}acids},\\ 1,& x\text{\hspace{0.5em}and\hspace{0.5em}}y\text{\hspace{0.5em}encode\hspace{0.5em}the\hspace{0.5em}same\hspace{0.5em}amino\hspace{0.5em}acid}.\end{array}$$

The rate ${\Omega }_b(s)$ is drawn from a branch-specific discrete distribution of ω values: ${\Omega }_b(s)\in \{{\omega }_1^b,\dots ,{\omega }_{K^b}^b\}$, with the probability weights of ${\omega }_k^b$ denoted as $f_k^b$ $({\displaystyle {\sum }_{k=1}^{K^b}{f}_k^b}=1)$. The parameters ${\omega }_k^b$ and $f_k^b$ are estimated from the data.

In BSREL, this distribution was modeled as having three rate categories ($K^b=3$) at each branch. The key difference in aBSREL is that K^b is now allowed to vary from branch to branch and is estimated from the data using a step-up procedure. The result of this procedure (described in detail below) is a single branch-site REL model, in which each branch b has been assigned a model complexity K^b ranging from 1 to a predefined limit (10 in our implementation). Using such a data-informed model is conceptually similar to performing a maximum-likelihood tree search for an alignment and then using this fixed, but data-dependent, tree for downstream inference.

Likelihood Calculation

To compute the likelihood of single alignment site D_s under a branch-site REL model, M, it is necessary to marginalize over all possible assignments of ω values to individual branches.

$$\begin{array}{c}P\left(D_s|M,\text{\hspace{0.5em}model\hspace{0.5em}parameters}\right)\\ ={\displaystyle \sum _{\vec{\omega }}P}\left(D_s|M,\text{\hspace{0.5em}model\hspace{0.5em}parameters\hspace{0.5em}},\vec{\omega }\right)P\left(\vec{\omega }|M\right).\end{array}$$

The sum is taken over all possible vectors $\vec{\omega }$ assigning ${\omega }_k^b$ values to individual branches. Because there are generally combinatorially many ($K={\displaystyle {\prod }_b{K}^b}$) such assignments, the sum cannot be computed by brute force. For a particular assignment, the likelihood $P\left(D_s|M,\text{\hspace{0.5em}model\hspace{0.5em}parameters\hspace{0.5em}},\vec{\omega }\right)$ is computed efficiently with the canonical dynamic programming pruning algorithm (Felsenstein 1981). Kosakovsky Pond et al. (2011) showed that if $P\left(\vec{\omega }|M\right)$ is assumed to be the product of individual $f_k^b$ terms—that is, ω vary independently from branch to branch—then marginalizing over $\vec{\omega }$ is possible in a single pass of the pruning algorithm. To do so, one defines the transition probability matrix, P^b (for each branch b) as the convex mixture of K^b transition matrices where in calculating individual rate matrix entries $q_{xy}^{bs}\in Q_k^b$, the distribution ${\Omega }_b(s)$ is replaced by individual ${\omega }_k^b$ parameters:

$$P^b(t)={\displaystyle \sum _{k=1}^{K^b}{f}_k^b}\exp \left[t{Q}_k^b({\omega }_k^b)\right].$$

Finally, assuming independence among sites, the likelihood of the entire alignment is obtained as the product of individual site likelihoods.

To control the number of differentially constrained parameters during branch-wise testing for positive selection, only a single rate class per branch is permitted to represent positive selection. The range of possible parameter values for ${\omega }_{k<K^b}^b$ is constrained to $[0,1]$, whereas ${\omega }_{k=K^b}^b$ can take on any value in $[0,\infty )$. Changing the model to enforce the absence of positive selection requires changing only the constraint on one parameter, ${\omega }_{k=K^b}^b$, to [0,1].

Determining Model Complexity

Unlike BSREL, where $K^b=3$ for all branches, aBSREL begins by fitting the baseline model with $K^b=1$ for all b. This is conceptually equivalent to the original MG94 (Muse and Gaut 1994) model extended to handle different nucleotide substitution rates, and the free ratio model of Yang (1998). To improve computational performance and convergence, we fix θ_ij parameters at their values estimated from the baseline model for the duration of the model selection process, and use ${\omega }_1^b$ and t^b estimates as initial values for subsequent optimizations. The heuristic step-up procedure for aBSREL follows these steps:

1. Sort all the branches by their length under the baseline model in descending order and iterate over sorted branches, that is, start with the longest branch.

2. Fix all current parameter estimates at their current estimated values, except for those affecting the branch currently considered (b), namely ${\omega }_k^b,f_k^b$, and t^b.

3. Increment K^b by 1, introducing two new parameters ${\omega }_{K_b}^b$ and $f_{K_b}^b$. Determine the best initial values for the newly introduced parameters by a rapid search over a fixed grid of values. Our implementation uses a grid of 10 × 6 pairs for ${\omega }_{K_b}^b\times f_{K_b}^b$.

4. Fully optimize all branch-level parameters (${\omega }_k^b,f_k^b$ and t^b, $2K^b$ in total) and compute the AICc score.

5. If AICc is improved by adding the new class, accept the new class and go to step 2 to test an additional class for the same branch, otherwise reset K^b to the value with the best AICc and move to step 2 for the next branch in the sorted list.

This algorithm describes a standard stepwise variable addition procedure in that it uses a greedy search to maximize the AICc score in a setting where the complete search over all combinations of K^b is combinatorially complex. Step 2 is essential for ensuring that aBSREL is computationally tractable; otherwise we would be performing O(B) complete codon-based optimizations, where B is the number of branches in the tree. Because we restrict the optimization to the set of parameters that affect a single branch in the tree, and because the evolutionary model is time-reversible, the phylogenetic likelihood calculations for the entire tree in step 4 are reduced to those of a tree with three branches (see Kosakovsky Pond et al. 2009 for details). This modification means that steps 3 and 4 run at speeds which are essentially independent of the number of sequences in the full alignment, and that the entire model selection algorithm runs in time comparable to the time that would be needed for a single reoptimization of all parameters on all branches.

Our greedy procedure will be sensitive to the order in which parameters are considered. We consider longest branches first because parameters added early on in the selection process affect all downstream inference; short branches are assumed to have relatively little impact on the model likelihood and on inference at other branches.

Fitting the Full Model

Estimates obtained during the model complexity determination are used as a starting point to fully reoptimize all continuous aBSREL parameters (table 1). Because of known convergence issues for complex mixture models, having a good starting point is essential for reducing run-times and avoiding convergence to suboptimal values (Anisimova and Yang 2007; Kosakovsky Pond, Scheffler, et al. 2010; Yang and dos Reis 2011). The final optimized model becomes the universal alternative hypothesis for tests of positive selection (see below) and is the basis for branch length calculations. Branch lengths for mixture aBSREL models are defined as

$$L(b)={\displaystyle \sum _{k=1}^{K^b}{f}_k^b}L\left(b|\omega ={\omega }_k^b\right),$$

and the branch length for a particular value of ω is computed using the standard expression:

$$L(b|\omega ={\omega }_k^b)=-{\displaystyle \sum _i{\pi }_i}{t}^b{q}_{ii}^b.$$

Testing for Episodic Positive Selection at Individual Branches

We test for significant positive diversifying selection on each branch by defining a null model in which no positive selection rate class is allowed on that branch, and using the LRT to determine whether the null model can be rejected in favor of the universal alternative, defined by the full model.

Because the aBSREL hypothesis tests are performed under a model whose complexity is inferred from the data, standard theoretical results on the asymptotic distribution of the LRT statistic are not applicable. For example, assume that the true model at a branch has one ω component. Ignoring the effect of other branches for the time being, consider two distinct cases: The aBSREL complexity analysis could infer $K^b=1$ (the correct model), or $K^b>1$ (an overfitted model). The distribution of the LRT statistic is then dependent on the outcome of model selection:

$$\text{LRT}\sim \{\begin{array}{cc}0.5({\chi }_0^2+{\chi }_1^2),& K^b=1,\\ {\displaystyle \sum _{i=0}^{2K^b-1}{c}_i}{\chi }_i^2,& K^b>1.\end{array}$$

Both cases follow from Self and Liang (1987), except that the mixing coefficients can be inferred analytically in the first case but not in the second. The number of ${\chi }^2$ mixture components corresponds to the maximum numbers of degrees of freedom that can be lost in a K^b-component mixture model, which can occur when all estimates of ${\omega }_k^b$ are the same so that only one parameter is identifiable. A further complication is that incorrectly inferred model complexity on other branches will have some biasing effects.

A practical solution is to infer an empirical distribution of the LRT under the worst case null, namely a single ω = 1 at a branch, under a range of other model parameters (described below) and fit a ${\chi }^2$ mixture to it, as we have previously done in the context of site-wise mixture models (Murrell, Wertheim, et al. 2012). We limit the consideration to a three-component mixture, because in all of our simulations the worst case of overfitting was by a single rate class (two extra degrees of freedom; supplementary table S1, Supplementary Material online). The mixture which allocates 50% to ${\chi }_0^2$, 20% to ${\chi }_1^2$, and 30% to ${\chi }_2^2$ is in excellent agreement with the tail of the empirical LRT distribution based on 50,000 samples (10,000 replicates of five-branch trees) simulated under a strict null (supplementary fig. S1A, Supplementary Material online, see Simulated Data) and controls false positive rates in all simulated scenarios considered here. We stress that it is very unlikely that biological sequences other than pseudogenes ever evolve under the strict null (ω = 1 everywhere) model; hence, the test is likely conservative in the vast majority of practical scenarios.

This test statistic is more conservative than the 50:50 mixture of ${\chi }_0^2$ and ${\chi }_1^2$ used in the original BSREL paper (Kosakovsky Pond et al. 2011). Applying the same fitting procedure to the distribution of LRT under the null using three-rate BSREL (supplementary fig. S1B, Supplementary Material online), we find that a mixture which allocates 50% to ${\chi }_0^2$, 5% to ${\chi }_1^2$, and 45% to ${\chi }_2^2$ controls false positive rates, and we have updated publicly available versions of BSREL to use this distribution.

Note that if none of the ${\omega }_k^b$ estimates under the alternative model exceeds 1, then the alternative and the null models coincide for branch b, and we fail to reject the null with P = 0.5. If more than one branch is being tested, the Holm–Bonferroni sequential rejection procedure is used to control the family-wise error rate. Other, less restrictive procedures could be used to bound the false discovery rate; these corrections are straightforward to obtain from raw P values for individual tests.

Results

Simulated Data

The following properties of aBSREL were demonstrated by an analysis of 10,000 simulated alignments with 500 codons each:

1. The false positive rate for detecting episodic positive selection, when all branches in the tree are tested, was well controlled at less than 5% using a nominal test size of 0.05. This rate applied to the worst case scenario of strict neutrality on all branches and did not depend on the length of the branch being tested (supplementary fig. S2, Supplementary Material online). The empirical test mixture statistic derived from null simulations on the four-taxon tree also controlled false positive rates (3.9% at $P\le 0.05$) on independently generated replicates with 32-taxon trees. Note that our null hypothesis is not strict neutrality, but rather neutral evolution or negative selection, that is, all ${\omega }_k^b\le 1$ at a branch. As expected, the rate of false detection was significantly below 5% for branches where the largest ${\omega }_k^b$ was much less than 1, and it approached 5% for branches with largest ${\omega }_k^b$ close to 1 (results not shown).

2. The power of aBSREL to identify branches subject to episodic diversifying selection has a clear dependence on the amount of evidence present in the branch, dictated usually by three parameters: the strength of selection (${\omega }_k^b>1$), the extent of selection ($f_k^b$), and the branch length (proportional to the t^b parameter). This dependence is well known and applies to all ω-based methods (Scheffler and Seoighe 2005; Yang and dos Reis 2011; Murrell, Wertheim, et al. 2012). Episodic selection was found for 80–90% of the branches unless they were simulated under weak positive selection (${\omega }_k^b<2.5$), with a small proportion of sites subject to positive selection ($f_k^b<0.1$) or along short (<0.15 substitutions per site) branches (fig. 1).

3. The model selection procedure is not prone to overestimating model complexity. For example, only 2% of branches simulated under a single rate class were inferred to have more than one rate class (supplementary table S1, Supplementary Material online). For branches simulated with more than one rate class, 47% of rate classes beyond the first were recovered by aBSREL. This includes scenarios where recovery was potentially confounded by rate classes with very low proportions, very small differences between ω values, or by very short branches with very few total substitutions.

Fig. 1.

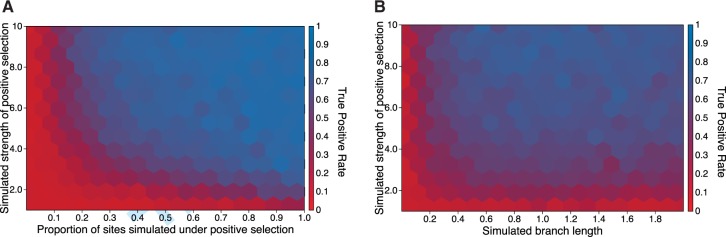
The power of aBSREL to correctly detect branches with diversifying positive selection from the simulated alignments as a function of selection strength (ω) and proportion of sites subject to selection (A), or selection strength and the length of the simulated branch (B).

Empirical Data Sets

Model Performance

As expected, the step-up procedure successfully optimized AICc, yielding the best scoring result among the three models compared (table 2). In all cases, the three-rate BSREL appears to be vastly overparametrized. We also applied the “training” and “hold-out” cross-validation sets technique from machine learning to explore the generalizability of the model. We trained the aBSREL model on randomly chosen 50% of alignment sites (the training set), and then fitted that (now fixed) model to the remaining 50% of the sites (validation). This generally yielded a simpler model than that inferred from the entire alignment, but for sufficiently large data sets (Ebola virus [EBOV], measles virus [MeV], avian influenza virus [AIV]), this model which no longer depended on the data had the best AICc (see the 50% AICc column in table 2), implying that the model selection procedure captures generalizable complexity patterns.

Table 2.

Comparative Model Performance on Empirical Data Sets.

Data Set	N	L	Model	$\log L$	df	AICc	50% AICca	T	$K^b>1$, %	# pos.sel.b	Tc
CD2	10	187	MG94d	−3,450.4	46	6,995.1	3,549.7	1.74	0.0	—	—
			aBSRELe	−3,415.0	60	6,954.0	3,552.7	2.30	44.0	3 (6)	00:02:35
			BSREL	−3,410.2	110	7,054.2	3,642.6	2.51	100	3 (6)	00:07:05 ($2.7\times$)
BRCA	10	1,162	MG94d	−13,270.5	48	26,637.4	13,227.2	0.66	0.0	—	—
			aBSRELe	−13,260.2	52	26,624.9	13,230.1	0.74	11.8	0 (1)	00:01:59
			BSREL	−13,255.0	116	26,744.3	13,348.9	0.74	100	0 (1)	00:15:48 ($7.9\times$)
Lysozyme	19	130	MG94d,e	−1,012.6	80	2,190.6	1,168.3	0.23	0.0	—	—
			aBSRELd,e	−1,012.6	80	2,190.6	1,168.3	0.23	0.0	0 (0)	00:00:59
			BSREL	−1,009.2	212	2,483.8	1,513.7	0.25	100	0 (0)	00:02:25 ($2.8\times$)
MeV	122	525	MG94	−12,044.3	496	25,088.3	12,727.8	4.47	0.0	—	—
			aBSRELd,e	−11,914.5	518	24,882.5	12,689.5	5.22	4.6	1 (6)	00:39:32
			BSREL	−11,909.3	1,460	26,806.8	14,698.7	5.33	100	0 (6)	03:05:16 ($4.7\times$)
EBOV	32	463	MG94	−6,660.9	136	13,596.3	7,150.7	4.47	0.0	—	—
			aBSRELd,e	−6,604.4	150	13,512.0	7,131.3	$1,{623.05}^{\text{f}}$	11.0	0 (1)	00:12:47
			BSREL	−6,603.2	380	13,986.4	7,601.9	5.34	100	0 (1)	00:19:58 ($1.6\times$)
AIV	267	419	MG94	−44,366.15	1,076	90,905.21	45,094.7	$9,{921.99}^{\text{f}}$	0.0	—	—
			aBSRELd,e	−43,568.56	1,140	89,440.61	44,515.8	${301.74}^{\text{f}}$	6.0	1 (7)	09:33:38
			BSREL	−43,531.1	3,200	93,650.7	48,859.5	$3,{647}^{\text{f}}$	100	0 (8)	36:08:50 (3.8×)

^aModel AICc on the validation subset of the alignment (see text).

^bThe numbers in parentheses show the counts based on uncorrected P < 0.05.

^cTime to run the complete analysis and test all branches for selection (HH:MM:SS format).

^dFor each data set, the model with the best AICc on the validation subset of the alignment (see text).

^eFor each data set, the model with the best AICc.

^fAt least one branch in the tree was saturated, that is, had an estimated length equivalent to numerical infinity (Wertheim and Kosakovsky Pond 2011).

Mammalian Cluster of Differentiation 2

This alignment includes sequences from ten mammalian species coding for the extracellular domain of the cluster of differentiation 2 (CD2) receptor found in the T-helper and natural killer cells. It is known to play an important role in the innate and adaptive immune responses (Davis et al. 2003). This alignment was originally analyzed by Lynn et al. (2005) and used as a test case in Anisimova and Yang (2007) and Kosakovsky Pond et al. (2011). In all previous analyses, several branches were identified as targets of episodic diversifying selection. The aBSREL model selection procedure identifies 7/16 (44%) branches with $K^b=2$, and 9/16 which were adequately described by the baseline MG94 model ($K^b=1$). With only 14 additional parameters relative to the baseline model with no site-to-site rate variation, aBSREL captured most of the likelihood improvement seen with the full BSREL model, which utilized 64 additional parameters (table 2). The reduction in model complexity also resulted in a dramatic improvement in run times, with aBSREL testing all branches for evidence of positive selection $2.7\times$ faster than BSREL. Both methods found the same three branches to be under positive selection (fig. 2) at $P\le 0.05$, suggesting that despite a much simpler model structure, aBSREL does not miss important patterns of evolutionary rate variation. In all cases, it is clear that branches in the phylogeny assumed to have $K^b=3$ under the BSREL model do not support this level complexity. For example, the short (0.002 substitutions/site) branch leading to “baboon” (fig. 2) was inferred to have a single $\omega =0.0$ under aBSREL (no nonsynonymous substitutions). A more complex model is likely to overfit the data, and an examination of the parameter estimates for the three-rate distribution under BSREL supports this expectation as the distribution collapses to a point mass at 0. Other branches may have partially resolved BSREL-deduced distributions, for example, for “pig”: ${\omega }_1=0.00(f_1=0.19),{\omega }_2=0.00(f_2=0.26),{\omega }_3=2.82(f_3=0.55)$, which comprises two distinct rate classes, but there is no statistically significant (based on AICc) evidence for more than one rate class, leading aBSREL to assign a single $\omega =1.27$ to this branch. Even on long branches inferred to be under selection, for example, “cat,” aBSREL was able to collapse two of the rate classes inferred by BSREL, from ${\omega }_1=0.00(f_1=0.31),{\omega }_2=1.00(f_2=0.31),{\omega }_3=6.59(f_3=0.38)$ to ${\omega }_1=0.33(f_1=0.57),{\omega }_2=5.94(f_2=0.43)$. Finally, we note that the inclusion of variable selection pressures in the model increases the estimated total path length of the tree to 2.3 expected substitutions per site, compared with 1.74 under the baseline model.

Fig. 2.

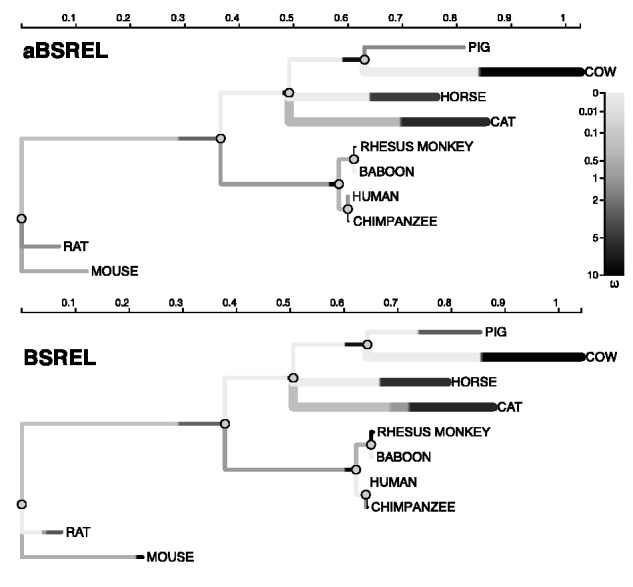
Selection analyses of the extracellular domain of the mammalian CD2 receptor with the standard BSREL and the aBSREL models. Each branch b is annotated according to the inferred ω^b distribution; the total length of the branch is partitioned according to the proportion of sites in a particular class ($f_k^b$), and the color of the segment depicts the magnitude of the corresponding ${\omega }_k^b$. Branches which are thicker than others are those which have P < 0.05 (corrected for multiple testing) for rejecting the null hypothesis of all ${\omega }_k^b\le 1$ on that branch, that is, identified as having experienced diversifying positive selection.

Breast Cancer 1, Early Onset

We reanalyzed the alignment of ten mammalian (including eight primate) BRCA1 (Breast Cancer 1, Early Onset) sequences of exon 11 of the gene, previously examined with Nielsen–Yang branch-site models by Yang and Nielsen (2002) and Zhang et al. (2005). A more recent analysis that considered the full gene sequence and studied over 40 sequences reported extensive adaptive evolution at this locus among primates, using the same class of models and population genetic tests (Lou et al. 2014). In an even more dramatic example of model reduction than CD2, aBSREL found only 2/17 branches with evidence of more than one (two each) ω classes and yielded the best AICc score among the three models compared (table 2) using 64 fewer parameters than BSREL, performing the tests on all branches $7.9\times$ faster. Neither aBSREL nor BSREL identified any branches as subject to episodic diversifying selection, although the branch leading to the Primate clade (fig. 3) had an uncorrected P < 0.01 for both models. Support for the original hypothesis of Huttley et al. (2000), that the human and chimpanzee lineages may be under positive selection, was not supported by this aBSREL analysis; as none of the branches in this group had uncorrected P values of 0.05 or below for rejecting the null hypothesis of neutral or negative selection only.

Fig. 3.

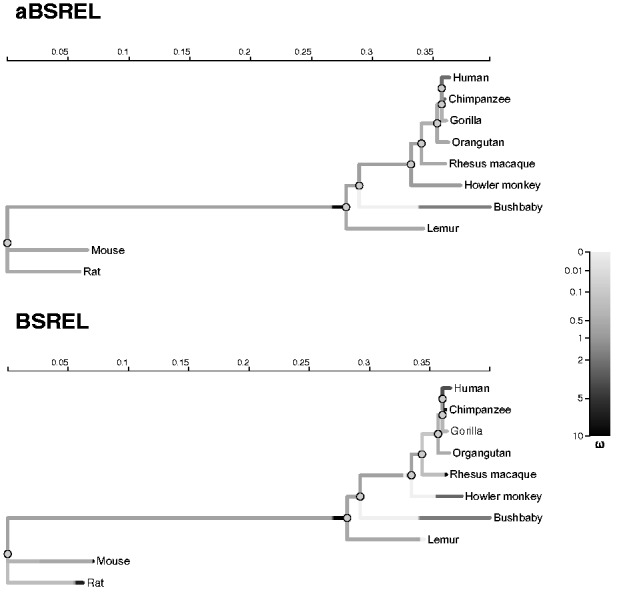
Selection analyses of exon 11 of the BRCA1 gene with BSREL and the aBSREL models. Annotation is the same as in figure 2.

Primate Lysozyme c

This canonical data set (Messier and Stewart 1997) was used by Yang (1998) to illustrate the power of models allowing ω to vary from branch to branch. The initial analysis showed elevated ω on a subset of branches relative to the rest of the tree, but when it was later reanalyzed by Zhang et al. (2005) using branch-site models, no evidence of positive selection had been found. Because of the short gene length and the relatively low levels of sequence divergence (table 2), aBSREL deduces the most extensive model simplification possible—none of the branches is assigned more than a single ω class, that is, 132 parameters are eliminated. aBSREL tested all 33 branches $2.3\times$ faster than BSREL, and similarly found no branches under selection.

Rapidly Evolving Viral Pathogens

aBSREL performed as expected on gene alignments of AIV, MeV, and EBOV previously analyzed in Wertheim and Kosakovsky Pond (2011). In all three cases, only a small proportion of branches (5–11%) supported models with multiple ω rate classes; invariably, these branches include long internal branches (supplementary fig. S2, Supplementary Material online), which span long evolutionary time periods and whose lengths are underestimated by selection-agnostic models (Wertheim and Kosakovsky Pond 2011). aBSREL is always preferred to BSREL by AICc and yields a $1.6-4.7\times$ speedup; because of the large number of tests, branches with significant uncorrected $P\le 0.05$ rarely survive multiple testing corrections. In the cases of MeV and AIV, a single branch remains significant for aBSREL, whereas none do for BSREL (using the more appropriate mixture statistic defined in this article).

A Large-Scale Analysis of Mammalian Genes

An aBSREL analysis of 8,893 Euteleostomi coding alignments from the Selectome database (Moretti et al. 2014) revealed that a substantial majority of individual branches (84.5%) can be adequately modeled with a single ω rate class ($K^b=1$, see table 3). On average, across 493,172 analyzed branches, K^b was 1.16 (compared with $K^b=3$ for BSREL), implying greatly reduced model complexity and improved run times. Branches with three rate classes were exceedingly rare (about 1 in 3,600 tested), and there was not a single branch with $K^b>3$, implying that inference based on a single branch is necessarily limited in site-level resolution (Murrell, Wertheim, et al. 2012).

Table 3.

Branch-Level Statistics for the aBSREL Analysis of the 8,893 Selectome Coding Alignments (493,172 total branches), Stratified by the Inferred Number of ω Classes (K^b).

Kb	% of Total	Median (interquartile range)			% with $P\le 0.05$
		Branch Length	Sequence Length, Codons	Branch Count	Corrected	Uncorrected
1	84.51	0.02 (0.005–0.05)	145 (89–226)	67 (55–77)	0.0043	0.054
2	15.46	0.16 (0.08–0.42)	190 (124–293)	63 (51–73)	3.5	26.6
3	0.028	0.46 (0.07–5.3)	232.5 (139–412.5)	67 (55–77)	9.6	78.6

Branches inferred to have multiple ω rate classes tended to come from longer alignments (fig. 4A, P < 0.001 analysis of variance [ANOVA]), as expected because sites are modeled as independent and identically distributed samples from an underlying distribution, and increasing sequence length increases sample size and power (e.g., Scheffler et al. 2014), although pushing model complexity past $K^b=3$ may require sequence lengths far exceeding a typical gene length. There was also a pronounced trend to choose $K^b>1$ more frequently for longer branches (fig. 4B, p < 0.001 ANOVA), which confirmed both our prior intuition and well-known simulation-based results which require some minimum divergence level (branch lengths) for codon-based methods to gain power (e.g., Anisimova et al. 2001; Murrell, Wertheim, et al. 2012; Scheffler et al. 2014). We also noticed a drop in the proportion of branches with more than one ω as the number of sequences was increased (fig. 4C, P < 0.001 ANOVA). One possible explanation of this behavior is that increasing the density of taxonomic sampling, that is, shortening the average branch length by adding more sequences, dilutes the power to detect $K^b>1$. The confounding effect of this behavior depends on the data set at hand: For instance in many viral applications deep internal branches segregating viral species or subtypes are going to be unaffected by additional sampling of recent isolates (Wertheim and Kosakovsky Pond 2011), whereas the effect of adding new taxa to a fixed clade (Selectome) is more complex, and should be considered before undertaking exploratory selection analyses. Finally, figure 4D confirms the trend that nearly all significant results for episodic positive selection arise on branches with $K^b>1$.

Examining the results from the standpoint of individual alignments, aBSREL evinced episodic selection along at least one branch in 2,079 alignments or 23.4% of the total. This number increases to 7,109 (80.0%) if no multiple testing correction is carried out. Previous analyses with Nielsen–Yang branch-site analyses using uncorrected P values found at least one branch under selection in 3,747 of these alignments at $P\le 0.05$, suggesting that episodic positive selection is far more prevalent than previously reported and that aBSREL has far higher sensitivity. According to aBSREL there was evidence of episodic selection along a mean of 0.3 branches (2.3 branches without multiple testing correction) per alignment. Comparing the results of aBSREL with those reported by the Selectome pipeline (both using uncorrected P values), we found that the methods agreed on 17.7% of the alignments with no evidence of episodic selection, and 39.8% with evidence of selection along at least one branch. aBSREL reported a positive finding of positive diversifying selection (vs. a negative finding by selectome) for 39.8% of the alignments, whereas the reverse was true only for 2.3% of the alignments. Restricting aBSREL inferences by requiring that P values pass multiple testing correction, something not done by the Selectome pipeline, we still found that 8.9% of the data sets are reported as selected by aBSREL but not Selectome (the reverse was now true for 27.6% of the data sets).

Computational Performance Comparison with Nielsen–Yang Branch-Site Models

Recently, Valle et al. (2014) developed a highly tuned implementation of the Nielsen–Yang branch-site models for detecting diversifying episodic selection. We benchmarked our implementation of aBSREL versus fastCODEML 1.1 on the six empirical data sets discussed previously. We measured the time it took to test all internal branches in the tree one at a time (as fastCODEML iterates only over internal tree branches when no specific foreground is specified), as well as peak resident memory usage. Because the statistical methods implemented in the two programs differ in a variety of key features (evolutionary models, hypothesis testing implementation, optimization, and parallelization algorithms), our comparison is not that of algorithmic or implementation efficiency, but rather of methodological efficiency for typical practical applications. It is clear that aBSREL runs dramatically faster (up to three orders of magnitude) on the same hardware, using comparable or smaller memory footprints, with increasing benefits for larger data sets (table 4).

Table 4.

Comparative Performance of aBSREL versus an Efficient Implementation of Nielsen–Yang (NY) Branch-Site Models by Valle et al. (2014) in Testing for Selection on all Internal Branches of the Tree.

Data Set	Number of Tests	Run Time			Peak Memory Use, MB
		aBSREL	NY	×	aBSREL	NY	×
CD2	6	113 s	225 s	2	23.6	15.1	0.64
BRCA1	7	2 min	15 min	7.5	27.6	49.3	1.79
Lysozyme	14	1 min	30 min	30	26.1	16.2	0.62
EBOV	29	7 min	9 h	$\approx 77$	51.4	81.2	1.58
MeV	119	0.5 h	$\approx 2\text{\hspace{0.5em}weeks}$a	$\approx 670$	190.8	331.0	1.73
AIV	264	6.5 h	$\approx 1.5\text{\hspace{0.5em}years}$b	$\approx 2,000$	195.3	596.4	3.05

Note.—× factors are relative to the aBSREL baseline, that is, larger factors mean that NY was slower or used more memory.

^aRun times were extrapolated from testing ten branches, because of long run times of the NY method.

^bRun times were extrapolated from testing three branches, because of long run times of the NY method.

Discussion

The aBSREL method presented here is the first branch-site approach to allow the complexity of the model to be inferred from the data together with continuous model parameters. By reducing the total number of parameters relative to existing models, applications of aBSREL benefit from improved computational tractability and numerical stability, while producing the same or better inferences. The ability to accurately and efficiently detect positive selection with aBSREL in substantially less time than other complex branch-site codon models makes possible more detailed analyses with longer and more sequences than before.

Using comprehensive simulation data, we establish that aBSREL is statistically well behaved, and that it matches or exceeds the statistical performance of the original (fixed complexity) branch-site REL method (Kosakovsky Pond et al. 2011), while using 20–60% fewer parameters. We exploit several optimization techniques to accelerate the model selection problem, so that it performs selection tests several times faster than BSREL, and up to 3 orders of magnitude faster than highly tuned and algorithmically sophisticated implementations of the Nielsen–Yang class of branch-site models (Valle et al. 2014), reducing an estimated run time from an intractable 1.5 years on a medium size Avian influenza virus data set to a much more manageable 6.5 h.

Unlike previous work by us and others (Anisimova and Yang 2007; Kosakovsky Pond et al. 2011; Yang and dos Reis 2011; Lu and Guindon 2014), where a small number of “representative” scenarios are considered in simulations, we have explored the statistical performance of the test by sampling from the parametric space in a systematic manner. This permitted us to discover “edge” cases and revealed that the asymptotic distribution for the likelihood ratio statistic is more complex than we had previously thought, because multicomponent mixture models, such as aBSREL or the original BSREL (Kosakovsky Pond et al. 2011), possess null likelihood ratio test (LRT) distributions which are best described by multicomponent ${\chi }^2$ mixtures. In particular, we realized that the test statistic in the BSREL method (Kosakovsky Pond et al. 2011) could lead to anticonservative behavior in worst-case scenarios (strict neutrality along the entire sequence), which, while highly unlikely in biological data, must still be accounted for in the design of the test statistic. We estimated a more conservative null LRT distribution using an empirically determined mixture of ${\chi }^2$ components, which controls the worst case false positive rate, but lowers the power of the BSREL test somewhat. In practical applications, this change means that some results previously close to the significance level (e.g., P = 0.03) are no longer significant (P > 0.05). The new implementation referenced here uses this new test statistic, and this finding also highlights that simulations used to validate new tests must be systematic, and not only limited to a few preselected sets of parameter values.

As is often the case in evolutionary analyses, the model used to perform tests on the evolutionary process is a “nuisance” parameter. Our procedure infers the aBSREL model from the data and uses the inferred model for further testing on the same data. This shortcut could introduce potential statistical artifacts, but is very common in the literature: For example, the popular approach of using ModelTest to select the best-fitting model of sequence evolution (Posada and Crandall 1998) and then using this model for further tree inference or other analyses commits the same statistical transgression. More robust approaches including model-averaging in information theoretic (Posada 2008; Delport et al. 2010) or Bayesian (Li and Drummond 2012) frameworks are not practical in the context of codon-substitution branch-site models because of the computational complexity of fitting even a single model. Although we cannot exclude the possibility of scenarios in which errors in model inference affect the identification of branches under selection, such pathological scenarios are biologically unrealistic. A further encouraging point is the congruence between the inferences of aBSREL and the BSREL model of fixed complexity on biological data.

aBSREL appears markedly more sensitive in detecting episodic selection than Nielsen–Yang branch-site methods, and, in line with our prior expectations, longer branches in phylogenies and longer sequences tend to support more complex models of variation. aBSREL analyses also draw attention to previously underappreciated points. First, the majority of branches (70–90%) are adequately handled by simple models, but for the few branches where more complex selection patterns can be inferred, the complexity should be captured. Not doing so may decrease power to detect positive selection and reduce the accuracy of branch length inferences. Second, there appears to be an upper bound to practical model complexity on any single branch—we have not found a single instance when the inclusion of four or more ω_b values on a single branch was justified. Both of these points indicate that adaptive model complexity is essential for studying episodic diversifying selection. This also makes aBSREL an attractive alternative to other strategies that have been developed to capture selection rate heterogeneity, including the covarion models of Guindon et al. (2004) and the full Bayesian treatment of Rodrigue et al. (2010), because these models are computationally costly and often parameter rich.

Selective pressure acting on functional sequences can be expected to vary from site to site on any given branch, and the importance of recognizing this variation by incorporating site-to-site variation of nonsynonymous rates into codon-based models has long been recognized (Nielsen and Yang 1998). However, when we also want to incorporate rate variation over time, we can no longer aggregate information over the whole phylogeny; the information available for inferring site-to-site rate variation at a single branch is limited. As a consequence, aBSREL tends to infer only a small number of rate categories (usually one or two, and never more than three) for any given branch. When aBSREL infers only a single rate category it may be the case that there is little site-to-site rate heterogeneity on that branch (e.g., the strength of selection is similar at almost all sites), but a single rate category can also be inferred even when there is substantial site-to-site heterogeneity. For multiple rate categories to be inferred, there must be evidence that different sites have experienced different numbers of substitutions, and this will not be the case for branches that are too short (all sites having close to zero substitutions) or too long (the number of substitutions appearing to be similar at all sites due to saturation). With aBSREL we are able to identify and assign complex models to those branches that are informative for site-specific selection inference. These branches will be neither too short nor too long, and display sufficient site-to-site rate heterogeneity; it is only these branches for which it is advantageous to infer complex rate distributions and where sufficient evidence for inferring positive and/or purifying selection is likely to be available.

There are several features that may add additional sensitivity or specificity to applications of aBSREL, such as synonymous substitution rate heterogeneity or nonuniform amino acid substitution rates. It has frequently been shown that substitution rate heterogeneity exists not just between nonsynonymous classes of sites but also synonymous sites which are frequently assumed to be selectively neutral and serve as the basis for most positive selection inference methods. Selective forces such as mRNA secondary structure (Tuplin et al. 2002) or overlapping genes (Miyata and Yasunaga 1980) can affect inferences of positive selection, especially for viral sequences. Similarly, different organisms are going to have different amino acid substitution rates much like nucleotide substitution rates. Incorporating these features into aBSREL could return increased power from greater biological realism, at the expense of additional computation complexity.

Materials and Methods

Simulated Data

We investigated the statistical performance of aBSREL on simulated data; in the case of step-up variable selection, it is particularly important to ensure that we do not overfit the data or consistently misindentify the model because of the greedy nature of the method. To investigate false positive rates in the worst case, we simulated 10,000 alignments with 1,000 codons each using a balanced four-taxon tree assuming ω = 1 along every branch in the tree, and 400 alignments with 1,000 codons each using a balanced 32-taxon tree (see below for the distribution of branch lengths). Despite its simplicity, we previously used the same four-taxon setup to demonstrate undesirable statistical behaviors of the Yang and Nielsen (2002) class of models when model assumptions had been violated. The model parameters (table 1) under which these sequences were simulated were randomly drawn from probability distributions selected to approximate empirical data sets.

To systematically explore model parameter space, we implemented a rejection sampling method to ensure a minimum level of uniformity in sampling the space of parameter value combinations. This procedure involved binning all potential combinations by strength of positive selection, proportion of sites under positive selection, and branch length into a three-dimensional histogram with 18, 18, and 14 bins, respectively. Rejecting branches that fall within a bin already occupied by 50 other branches drove sampling of other, more extreme combinations of parameter values. The three-dimensional histogram was collapsed by one dimension for each of the power heatmaps in supplementary figure S3, Supplementary Material online, resulting in at least 50 branches per hexagon. The distributions from which parameter values were drawn largely reflected the necessary uniform sampling. Branch lengths were drawn from a uniform distribution between 0 and 2 and rate class proportions were drawn from a Dirichlet distribution. All ω values were limited to $[0,10]$, and all but one rate class for each branch was further limited to between 0 and 1. Positive selection strengths for branches with a single rate class and fewer than ten rejections were drawn from an exponential distribution with a rate parameter of 2, whereas parameter values for branches with more than one rate class or with one rate class and more than ten rejections were drawn from a uniform distribution. The number of rate classes was drawn from a Poisson distribution (λ = 2) truncated to take values in {1, 2, 3}. After 500 rejections, the number of rate classes for a branch was automatically increased to 3 to add additional uniformity in proportion sampling.

We tabulated false positive error rates and power to detect selection from analyzing these alignments as functions of model parameters.

Empirical Data Sets

To demonstrate the performance of aBSREL on biological data and compare it with other models, we selected the three empirical data sets we had used in the BSREL manuscript (Kosakovsky Pond et al. 2011), and the three alignments of viral genes where we had previously demonstrated the importance of modeling temporally variable selection in the context of molecular dating (Wertheim and Kosakovsky Pond 2011).

To test whether or not the findings from the six empirical data sets are generalizable, we also ran aBSREL on 8,893 of the coding sequence alignments from Euteleostomi included in version 06 of the Selectome database (Moretti et al. 2014).

Computational Performance Comparison

One of the expected advantages of performing model selection prior to testing for selection is the significant reduction in run times of the method. To test this expectation, we compared the run times of aBSREL with those of BSREL on the six empirical data sets of varying sizes. For comparison purposes, we modified BSREL to take advantage of the same procedure for finding a good starting point for full model optimization as aBSREL except that $K^b=3$ for all branches (as in the original method). We did not count the time needed to find the starting point in BSREL runtime metrics, thereby biasing the comparison against aBSREL. Additionally we evaluated how aBSREL compares with highly tuned parallelized implementation of the Nielsen–Yang class of branch-site models, in package fastCodeML v 1.1 (Valle et al. 2014) on the same six data sets.

Implementation and Availability

aBSREL is implemented in the HyPhy software package (Kosakovsky Pond et al. 2005) and the Datamonkey.org webserver http://www.datamonkey.org/absrel (Kosakovsky Pond and Frost 2005). As part of HyPhy, it uses OpenMP, pthreads, MPI, SIMD intrinsics, and other technologies to parallelize individual likelihood calculations and independent optimization tasks. A simple aBSREL tutorial (with links to components and documentation) can be found at http://bit.ly/hyphy-tutorial-aBSREL, last accessed February 25, 2015.

All speed comparisons were performed on a Mac Pro (2013) with a six-core Intel Xeon E5 processor clocked at 3.5 GHz, 16 GB of DDR3 ECC RAM, running Mac OS X version 10.9.4, and gcc-4.8.3 to compile both HyPhy and fastCodeML.

Supplementary Material

Supplementary table S1 and figures S1–S3 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).