Gene-Wide Identification of Episodic Selection

Abstract

We present BUSTED, a new approach to identifying gene-wide evidence of episodic positive selection, where the non-synonymous substitution rate is transiently greater than the synonymous rate. BUSTED can be used either on an entire phylogeny (without requiring an a priori hypothesis regarding which branches are under positive selection) or on a pre-specified subset of foreground lineages (if a suitable a priori hypothesis is available). Selection is modeled as varying stochastically over branches and sites, and we propose a computationally inexpensive evidence metric for identifying sites subject to episodic positive selection on any foreground branches. We compare BUSTED with existing models on simulated and empirical data. An implementation is available on www.datamonkey.org/busted, with a widget allowing the interactive specification of foreground branches.

There is not yet an uncontroversial way to answer the question: “Has a particular gene evolved under positive selection?” Even if one restricts attention to approaches that estimate the dN/dS or ω ratios from multiple sequence alignments—which are commonly used to distinguish between purifying selection ($\omega <1$), neutrality (ω = 1), and diversifying positive selection ($\omega >1$)—there are many different models based on varying biological assumptions, each addressing different versions of the above question (Anisimova and Kosiol 2009; Delport et al. 2009). In this letter, we consider the detection of positive selection in a whole gene, while accounting for the variation of selection patterns from site to site and over time. Methods that do this include the branch-site (Yang and Nielsen 2002; Zhang et al. 2005; Anisimova and Yang 2007; Yang and dos Reis 2011; Kosakovsky Pond et al. 2011; Murrell, Wertheim, et al. 2012) and covarion (Guindon et al. 2004) models of codon evolution.

Even when positive selection is undetectable on any one codon site or branch in isolation, using the random effects framework to pool evidence for positive selection across multiple sites and branches can make their cumulative effect apparent. Recently, Lu and Guindon (2014) presented a comprehensive study of covarion models (Guindon et al. 2004) in the context of detecting gene-wide evidence of positive selection, and argued that these models are preferable to random effects branch-site models. Regrettably, they chose to use a method designed to detect selection at the level of individual sites (MEME; Murrell, Wertheim, et al. 2012) to infer selection on the entire gene—an approach that we cannot recommend. Combining a set of results from individual sites to draw conclusions about a whole gene while controlling the false discovery rate leads to an unavoidable drop in power to detect gene-wide selection, especially when the number of taxa (which drive signal at individual sites) is limited.

Here, we present a branch-site unrestricted statistical test for episodic diversification (BUSTED) that is capable of detecting positive selection that has acted on a subset of branches in a phylogeny at a subset of sites within the gene. The clear advantage of such a “stochastic selection” test over those which average ω over branches (Nielsen and Yang 1998; Yang et al. 2000; Murrell et al. 2013), codon sites (Muse and Gaut 1994; Yang 1998), or both (Goldman and Yang 1994) is greater statistical power to detect transient or localized selective events (Murrell, Wertheim, et al. 2012). BUSTED is based on the unrestricted branch-site random effects (BS-REL) model (Kosakovsky Pond et al. 2011), which allows ω to vary from branch to branch by efficiently marginalizing over a combinatorially large number of assignments of ω to individual branches. We compare BUSTED with existing branch-site and covarion models in terms of statistical properties, and discuss a simple exploratory procedure to suggest which codon sites were likely targets of episodic diversifying selection.

New Approaches

Gene-Wide Test of Positive Selection

We model the evolutionary process using a BS-REL framework (Kosakovsky Pond et al. 2011) with three rate categories. The (i, j) entry of the instantaneous rate matrix Q_c describes the rate for category $c\in \{1,2,3\}$ at which codon i is replaced with codon j for a branch-site combination, and is given by the standard codon-substitution model structure:

$$q_{ij}(c,\theta ,\Pi )=\{\begin{array}{cc}{\theta }_{ij}{\pi }_j,& \delta (i,j)=1,AA(i)=AA(j),\\ {\omega }_c{\theta }_{ij}{\pi }_j,& \delta (i,j)=1,AA(i)\ne AA(j),\\ 0,& \delta (i,j)>1,\\ -{\displaystyle \sum _{l\ne i}{q}_{il}},& i=j.\end{array}$$

Here, $\delta (i,j)$ counts the number of nucleotide differences between codons i and j; AA(x) is the amino acid encoded by codon x; θ represents the underlying nucleotide substitution rate parameters (assumed to follow the general time-reversible form); Π are the equilibrium codon frequencies, obtained using the CF3x4 corrected empirical estimator (Kosakovsky Pond et al. 2010) with nine parameters; and ω_c is the nonsynonymous/synonymous rate ratio value associated with category c.

We allow branches to be split into two partitions: Foreground and background. Within each partition, parameters for the three categories are shared across all branches and sites, respectively, subject to ${\omega }_1\le {\omega }_2\le 1\le {\omega }_3$. Each category has an associated weight parameter p_c $\left({\displaystyle \sum }_{c=1}^3{p}_c=1\right)$. ω distributions are estimated separately between foreground and background branch sets. When no foreground branch set is specified, BUSTED assumes that all branches are in the foreground.

Using this model, we introduce a gene-wide test for positive selection, asking whether at least one site is under positive selection in at least one foreground branch. Positive selection may or may not also be present in the remaining (background) branches, and ω may vary over sites and time in both foreground and background branches. The alternative model is as described above, and we construct a null model with ${\omega }_3=1$ over the foreground branches. If the null model is rejected, it indicates that at least one site is under positive selection at least some of the time on the foreground branches. The actual asymptotic distribution of the likelihood ratio statistic is an analytically intractable mixture of ${\chi }_0^2,{\chi }_1^2$, and ${\chi }_2^2$ (Self and Liang 1987; Murrell, Wertheim, et al. 2012). The ${\chi }_2^2$ component arises in situations where the null model has two or more rate classes with ω = 1; in this case, the alternative model reduces to the null with the loss of two degrees of freedom (e.g., ${\omega }_3=1$, making p₃ unidentifiable or $p_3=0$, making ω₃ unidentifiable). We err conservatively with ${\chi }_2^2$, but note that the power could be improved by determining the null distribution using parametric bootstrap, at substantial computational expense.

Evidence of Selection at Individual Sites

When the primary question of interest concerns selection at individual sites rather than in the gene as a whole, we recommend using MEME (Murrell, Wertheim, et al. 2012). However, the gene-wide model can also be used to look for evidence of selection at an individual site s by comparing the site-specific likelihood under the alternative model (M) with that obtained under model (M_s) which differs only in that ${\omega }_3=1$ for foreground branches at s. We interpret the likelihood ratio $l_s=P(D_s|M)/P(D_s|M_s)$ for the data D_s at site s as measuring support for positive selection at s. By reusing the parameter values from the alternative model without a reoptimization step, we obtain this measure at no additional computational cost. We provide this measure of evidence with the caveat that we cannot expect it to obey asymptotic sampling properties, and, as such, report the evidence ratios (ER_s) scaled as the likelihood ratio statistic: $E{R}_s=2\times \text{log}(l_s)$.

Implementation and Availability

BUSTED is implemented in the HyPhy batch language (Kosakovsky Pond et al. 2005), which performs all likelihood calculations and parameter optimizations. The test is available as a part of the HyPhy distribution (http://github.com/veg/hyphy, http://bit.ly/BUSTED_tutorial, last accessed March 12, 2015). We provide a web-application implementation as well (www.datamonkey.org/busted, last accessed March 12, 2015); it includes an interactive browser-based widget (built using D3, d3js.org) for visually designating foreground branches (fig. 1). To improve convergence, we estimate initial branch lengths using the GTR (general time reversible) nucleotide model, optimize the likelihood under the unconstrained alternative model, and then under the null model with ${\omega }_3=1$.

Fig. 1.

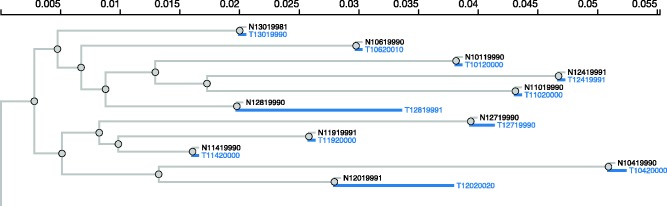
Depiction of our online widget used to interactively specify foreground branches, where such a priori information is available. This example is from a subset of the HIV-1 RT data set (Murrell, de Oliveira, et al. 2012), where terminal branches leading to samples taken after antiretroviral therapy are selected as foreground. Results for this analysis can be seen in table 2. The widget facilitates the annotation of large trees like this one (only a small subtree is shown for legibility), for example, by labeling all branches using a text pattern (e.g., here all branches of interest start with a “T”), and allowing automatic labeling of internal branches (e.g., using parsimony labeling).

Results

Simulated Data

We reanalyzed a subset of simulated data from Lu and Guindon (2014) (kindly provided by the authors), including scenarios designed to measure both false positives and power, simulated under varied patterns of site-wise and branch-wise variation—sufficiently complex to represent challenging model violations for all models considered here. We also applied BUSTED to sequences simulated both under the strict null (all sites and branches have ω = 1) used to evaluate the MEME method (Murrell, Wertheim, et al. 2012) (we refer the reader to the original manuscripts for details) as well as data simulated under BUSTED.

False Positive Rates Are Well Controlled

Due to the conservative test statistic, BUSTED empirical Type I error rates were consistently lower than the nominal test levels, (table 1 and supplementary table S1, Supplementary Material online).

Table 1.

BUSTED Results on Simulated Data from Lu and Guindon (2014).

Simulation Set	N	ps	pb	Detection Rate, by Method
				NYbs	LGc	BUSTED	BUSTEDFG
Tree 1 α XX	16	0	0	0.020	0.026	0.016	0.020
16 XX	16	0	0	N/A	0.028	0.006	N/A
32 XX	32	0	0	N/A	0.052	0.008	N/A
64 XX	64	0	0	N/A	0.150	0.012	N/A
Tree 1 α XV	16	0.20	0.03	0.102	0.028	0.008	0.259
Tree 2 $\delta \gamma$ XV	10	0.20	0.12	0.368	0.036	0.043	0.058
16 B XU	16	0.20	0.25	0.785	0.122	0.290	0.850
16 B XW	16	0.40	0.25	—	0.498	0.372	0.952
32 B XU	32	0.20	0.10	0.754	0.020	0.540	0.930
32 C XW	32	0.40	0.25	—	0.986	0.660	0.990
64 D XW	64	0.40	0.25	—	1.000	0.656	0.996

Note.—Simulation notation is adopted from the same manuscript; all alignments contained 300 codons, and each simulation scenario generated 500 replicates. N, number of sequences; p_s, proportion of sites in the alignment which were simulated with $\omega >1$ along some of the branches; p_b, proportion of branches in the alignment which were simulated with $\omega >1$ along some of the sites; NYbs, the current version of the Nielsen–Yang branch site models; LGc, the covarion model test of Lu and Guindon (2014); BUSTED, our method testing all branches at once; BUSTED^FG, our method testing the branches designated as foreground during the simulations. For NYbs and BUSTED^FG, the correct foreground branches were selected, whereas for the other two methods, the test is done across all branches. Rates for NYbs and LGc methods are taken from Lu and Guindon (2014), “—” indicates that the test was not performed there, and “N/A” indicates that no foreground branches were specified in the simulation. Note that, for the first four rows where $p_s=p_b=0$, the detection rate corresponds to a false positive rate from a simulation without positive selection; the other rows report true positive rates from a power simulation.

Power Increases with Simulated ω₃

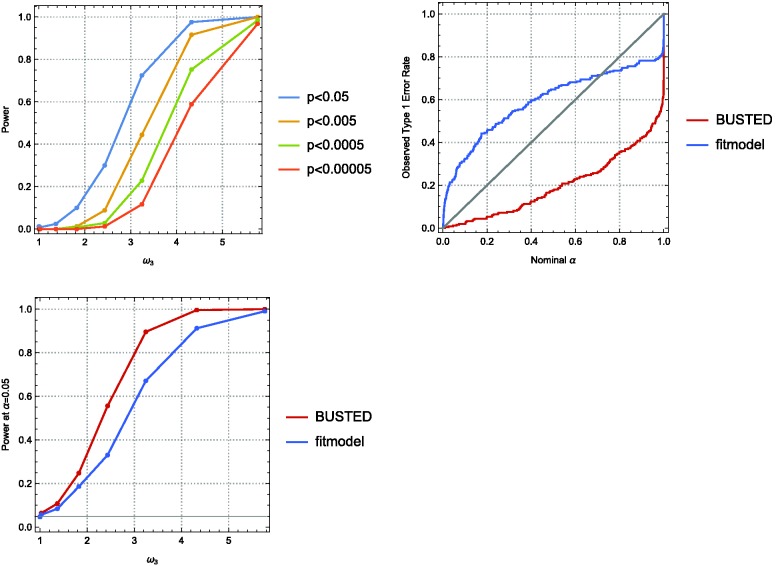
We simulated under our alternative model, fit to the sperm lysin data (Messier and Stewart 1997), using the maximum-likelihood estimates of the phylogeny and all continuous parameters under BUSTED’s alternative model (${\omega }_1=0,{\omega }_2=1$ with proportions of 57% and 33%, respectively, leaving 10% for ω₃), for a range of ${\omega }_3\ge 1$. As expected, BUSTED was conservative on the null simulations, and power increased rapidly with ω₃. Figure 2A depicts BUSTED’s power for various test cutoffs. Under these simulation conditions, the covarion model (as implemented by the fitmodel package; Lu and Guindon 2014) was anticonservative. For example, its false positive rate was 13% at $P\le 0.01$, and 23% at $P\le 0.05$ (fig. 2B). For a fair power comparison, we calibrate the likelihood ratio cutoff to achieve the nominal rate on false positive simulations, and compared the power of BUSTED and fitmodel in figure 2C, where, under these conditions, BUSTED is more powerful.

Fig. 2.

Statistical performance of BUSTED and fitmodel. (A) Power of BUSTED as a function of ω₃, for various nominal significance levels. The weight assigned to ω₃ by the model was 0.1. See text for other simulation parameters. (B) Type 1 error rate as a function of the nominal significance level (null data), showing that BUSTED is conservative and fitmodel is anticonservative. (C) Power of BUSTED and fitmodel as a function of simulated selective strength (ω₃), using test significance levels set to achieve 0.05 Type I error rate on null simulations (fitmodel was anticonservative).

Comparison with Existing Methods

On an array of simulations from Lu and Guindon (2014), using a discrete partition of branches each with fixed ω values, we compare BUSTED, fitmodel, and the Nielsen–Yang branch-site approach (table 1):

1. When the correct foreground partition is specified, BUSTED outperforms the Nielsen–Yang model, unless the alignment is small and there are only one or two branches in the partition. With a known foreground, BUSTED outperforms fitmodel which cannot make use of the foreground information.

2. When the entire tree is designated as foreground, BUSTED outperform fitmodel when a moderate (20%) as opposed to large (40%) proportion of sites are under positive selection on some branches, unless that proportion of branches is too low to be detectable by either method. Given the anticonservative behavior of fitmodel in some cases (e.g., see simulation 64XX), it is not clear how to fairly compare the power of fitmodel and BUSTED.

Empirical Data

HIV Drug Resistance

The ability to detect drug resistance-associated mutations in HIV-1 reverse transcriptase (RT) has been examined previously (Murrell, de Oliveira, et al. 2012), using FEEDS, MEDS, and EDEPS. MEDS and EDEPS were designed to focus on phenotype-altering substitutions occurring only on a known (a priori) subset of branches, with the “wild-type” residue being replaced by a single escape residue, which is then maintained by purifying selection.

Here, we examine the utility of BUSTED’s approximate site-wise evidence ratios on these sequences, using the same branch partition as in Murrell, de Oliveira, et al. (2012). Although these evidence ratios do not constitute a valid likelihood ratio test, we can nevertheless use a threshold informed by a ${\chi }_1^2$ distribution and P < 0.01. Table 2 shows the full list of all sites identified in this way, as well as all sites identified by other methods from Murrell, de Oliveira, et al. (2012).

Table 2.

Sites Identified by BUSTED, FEEDS, MEDS, and EDEPS in HIV-1 RT.

Site	BUSTED Evidence Ratio	MEDS P Value	FEEDS P Value	EDEPS Bayes Factor	Resistance
41	—a	0.00259	—	—	NRTIb
62	—	—	—	313	NRTI accessory
64	11.9612	0.00244	0.0067	—	NRTI accessory
65	7.36119	—	—	—	NRTI
69	9.70622	—	—	—	NRTI accessory
75	11.7751	—	—	—	NRTI accessory
77	—	—	—	211	NRTI
98	—	0.00488	—	—	—c
100	—	$<0.0001$	—	$>{10}^5$	NNRTId
102	—	—	0.0025	—
103	74.6745	<0.0001	<0.0001	$>{10}^5$	NNRTI
104	—	0.00244	—	—
115	—	—	—	3,110	NRTI
116	—	0.00319	—	—	NRTI accessory
151	24.1913	<0.0001	—	$>{10}^5$	NRTI
162	—	—	—	1,772
165	—	<0.0001	—	2,245
174	—	—	—	105
181	34.5139	<0.0001	—	$>{10}^5$	NNRTI
184	40.6307	<0.0001	—	$>{10}^5$	NRTI
188	29.4723	<0.0001	0.0002	$>{10}^5$	NNRTI
190	15.8163	<0.0001	—	$>{10}^5$	NNRTI
200	10.8219	—	<0.0001	—
215	14.8404	0.00035	—	2,727	NRTI
219	7.32553	—	—	—	NRTI
228	13.38	0.00029	—	1,401	NRTI accessory
230	—	0.00297	—	$>{10}^5$	NNRTI
245	17.9176	—	0.0006	—
286	—	0.00085	—	—

Note.—All methods employ the same foreground partition. FEEDS uses a site-wise fixed effects likelihood ratio test with distinct ω values estimated along FG and BG branches for each site, but admitting no stochastic branch-to-branch variation. MEDS and EDEPS are specifically designed with HIV-1 drug resistance in mind, powered to detect elevated substitution rates toward specific target residues at individual sites, using either a fixed effects codon approach (MEDS) or a site-wise random effects amino acid model (EDEPS). It is remarkable that introducing stochastic variation among branches (i.e., BUSTED) achieves similar power to explicitly directional methods on a genuinely directional system, even when directionality is not explicitly modeled.

^aNot significant.

^bNucleoside reverse-transcriptase inhibitor.

^cMEDS identifies 98S, but only 98G is a resistance mutation.

^dNonnucleoside reverse-transcriptase inhibitor.

The most appropriate benchmark comparison to BUSTED is FEEDS, which performs a site-wise test under a model with one ω per site on the foreground branches (and a nuisance ω on the background ones). FEEDS had little power in this case, presumably because averaging ω over all foreground branches at a site obscures $\omega >1$ on a subset of foreground lineages. BUSTED makes no such homogeneity assumption, and, surprisingly, performs comparably to the purpose-built episodic directional models, but without the loss of generality incurred by an explicit reliance on multiple convergent substitutions. True Positives/All Positives for all methods (using hivdb.stanford.edu as the gold standard) are BUSTED—13/15, MEDS—13/17, FEEDS—3/6, and EDEPS—13/16.

Large Scale Screens for Selection

We ran BUSTED on 10,779 Euteleostomes gene alignments, included in version 06 of the Selectome database (Moretti et al. 2014), to evaluate the rate at which BUSTED detects episodic diversifying selection and which features of the data set correlate with a positive result.

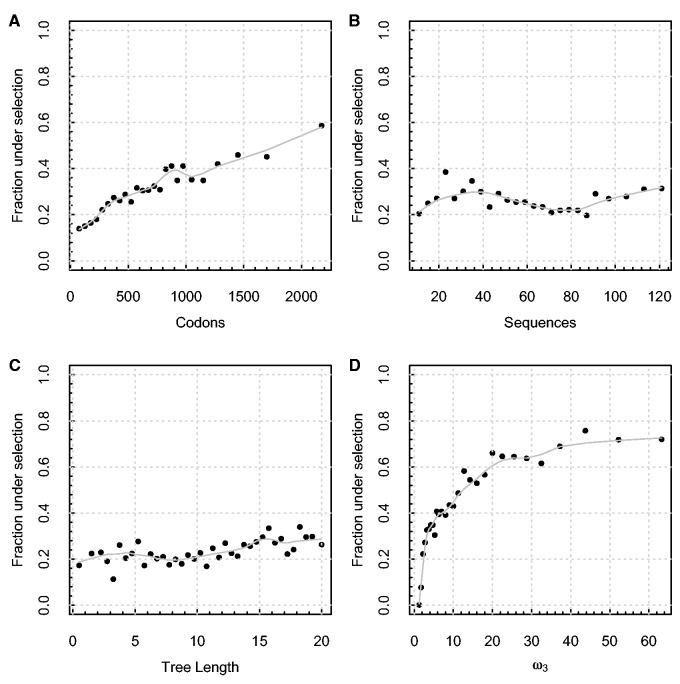
At $P\le 0.05$, 2,681 (24.87%) of the alignments contained evidence of episodic diversifying selection. Longer alignments generated a higher proportion of positive results (fig. 3A)—likely a consequence of the fact that the number of sites is the best proxy for sample size for independent sites methods (including BUSTED). The number of sequences in the alignment was largely uninformative with respect to detection rate (the proportion of alignments identified as evolving under positive selection—fig. 3B). Encouragingly, for a biologically realistic range of tree lengths, there is no evidence of loss of power due to codon substitution saturation (fig. 3C). Finally, as a check of the internal consistency of the method, the maximum-likelihood point estimate of ω₃ was positively correlated with the rate of detection (fig. 3D). The flattening of the trend curve around ${\omega }_3=40$ is explained by the practical upper bound on estimable ω₃ values: Increasing the value further does not alter the likelihood score very much (i.e., in this application $\approx 40$ is the empirical infinity).

Fig. 3.

Correlates of signal for episodic selection in the selectome data sets. Each panel depicts the fraction of all alignments reported by BUSTED as positively selected (at $P\le 0.05$), as a function of (A) the length of the alignment (codons), censored at 2000 due to sparse sampling afterwards, (B) the number of sequences, (C) the total tree length (expected number of substitutions per codon site), (D) the maximum-likelihood estimate of the ω₃ parameter, used as a proxy for the “strength” of selection. Plot points were chosen through an adaptive binning scheme, with each point representing at least 100 data sets. Lowess smoothing polynomials (smoothing span 0.25) are shown in solid light gray.

Discussion

The seminal Nielsen–Yang branch-site models allow sites to experience different patterns of selection in foreground and background branches, but fail to take account of variation among the foreground or among the background branches (Yang and Nielsen 2002; Zhang et al. 2005; Anisimova and Yang 2007; Yang and dos Reis 2011). We have previously demonstrated that our more recent models improve on this by allowing branch-to-branch variation across the entire phylogeny (Kosakovsky Pond et al. 2011; Murrell, Wertheim, et al. 2012). Our results, along with the those of Lu and Guindon (2014), underscore that models allowing selection to vary stochastically over branches should be adopted henceforth.

This approach shares limitations with most existing codon models: Using a fixed multiple sequence alignment, treating all amino acids as equally exchangeable, allowing only single nucleotide substitutions to occur instantaneously, not accounting for selection at the RNA or DNA level that could bias inference, and not explicitly modeling recombination. In the future, as important substitution process features are elucidated, we will expand the BUSTED modeling framework to include such features, for example, the ability to modulate residue exchangeabilities (Delport et al. 2010; Murrell et al. 2011; De Maio et al. 2013), site-to-site synonymous rate variation as a proxy for selection on DNA/RNA levels (Pond and Muse 2005), including substitution models with nonzero rates for multiple nucleotide substitutions (Kosiol et al. 2007), and the partitioning approach for mitigating the confounding effect of recombination (Scheffler et al. 2006).

The rates and selective patterns governing evolutionary processes surely change over time, although the nature of these changes will itself vary from one evolving system to another. Our random effects approach to branch-site models assumes that selective patterns change rapidly, so that the process governing evolution along a branch is independent of the processes on neighboring branches. In contrast, covarion models accommodate autocorrelation between nearby time points. The covarion model proposed by Guindon et al. (2004) models such autocorrelation in a statistically efficient manner, using a single switching rate parameter. However, assuming the switching rate is constant across sites is itself a homogeneity assumption that might be strongly violated, with unexplored consequences. It is also unclear why fitmodel is anticonservative when data are generated with independent branch-to-branch ω variation, but with no positive selection.

By incorporating the specification of a priori foreground lineages into a stochastic branch-site model, BUSTED gains the ability to test more focused hypotheses, permitting the identification of selection that occurred on the branches of interest, in the context of a model of flexible selection in the rest of the tree. The latter is essential lest the test be confounded by unmodeled positive selection on “background” branches (Kosakovsky Pond et al. 2011). There is also the corresponding increase in power (first demonstrated with the Nielsen–Yang branch site model) that comes from not having to share parameters across different regions of the phylogeny that we know a priori to be subject to distinct selective pressures.

We thus encourage the further exploration of branch-site models that allow the selection parameters to vary stochastically from one branch to another, but we caution against the inappropriate use of existing methods to test hypotheses at an incorrect level (e.g., using MEME to detect gene-wide evidence for selection).

Supplementary Material

Supplementary table S1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).