Structural fidelity and NMR relaxation analysis in a prototype RNA hairpin

Abstract

RNA hairpins are widespread and very stable motifs that contribute decisively to RNA folding and biological function. The GTP1G2C3A4C5U6U7C8G9G10U11G12C13C14 construct (with a central UUCG tetraloop) has been extensively studied by solution NMR, and offers and excellent opportunity to evaluate the structure and dynamical description afforded by molecular dynamics (MD) simulations. Here, we compare average structural parameters and NMR relaxation rates estimated from a series of multiple independent explicit solvent MD simulations using the two most recent RNA AMBER force fields (ff99 and ff10). Predicted overall tumbling times are ∼20% faster than those inferred from analysis of NMR data and follow the same trend when temperature and ionic strength is varied. The Watson–Crick stem and the “canonical” UUCG loop structure are maintained in most simulations including the characteristic syn conformation along the glycosidic bond of G9, although some key hydrogen bonds in the loop are partially disrupted. Our analysis pinpoints G9–G10 backbone conformations as a locus of discrepancies between experiment and simulation. In general the results for the more recent force-field parameters (ff10) are closer to experiment than those for the older ones (ff99). This work provides a comprehensive and detailed comparison of state of the art MD simulations against a wide variety of solution NMR measurements.

INTRODUCTION

Hairpins are the most common RNA motif and have a major impact on RNA function, being involved in protecting messenger RNA from degradation, RNA interference, or serving as important recognition elements between RNA and proteins (Leontis and Westhof 2003; Hendrix et al. 2005; Leontis et al. 2006). Structurally, hairpins consist of a base-paired stem and a loop that allows a single stranded RNA to fold back on itself, reversing the directionality of the fold (Bevilacqua and Blose 2008). Some RNA hairpins, especially those possessing loops made of 3 or 4 nt, are known to be very stable thermodynamically due to the presence of characteristic stacking interactions and hydrogen bonds (Varani et al. 1991; Varani 1995; Shu and Bevilacqua 1999; Blose et al. 2009; Tubbs et al. 2013). Both X-ray and NMR show that the formation of hairpin fold leads the adoption of noncanonical backbone conformations and base-pairings. For these reasons, certain RNA hairpins have received recently considerable attention in both molecular dynamics (MD) studies (Banas et al. 2010; Deng and Cieplak 2010; DePaul et al. 2010; Zuo et al. 2010; Chen and Garcia 2013; Henriksen et al. 2013; Kührová et al. 2013) that drove AMBER and CHARMM force-field modifications (Cheatham and Case 2013) as well as in RNA three dimensional structure prediction studies (Das 2011).

The UUCG tetraloop RNA hairpin considered here is unusually stable (Cheong et al. 1990; Antao et al. 1991), has been extensively studied by solution NMR (Akke et al. 1997; Fürtig et al. 2004; Duchardt and Schwalbe 2005; Vallurupalli and Kay; 2005, Rinnenthal et al. 2009; Nozinovic et al. 2010a) and offers an excellent opportunity to evaluate the structure and dynamical description afforded by MD simulations. NMR is a major source of structural and dynamical information on nucleic acids in solution (Latham et al. 2005; Fürtig et al. 2007; Shajani and Varani 2007; Cruz and Westhof 2009; Rinnenthal et al. 2011; Bardaro and Varani 2012; Salmon et al. 2014), and is broadly supported by other forms of spectroscopy (Abdelkafi et al. 1998; Leulliot et al. 1999; Schiemann et al. 2003; Qin and Dieckmann 2004; Bokinsky and Zhuang 2005; Zhuang 2005; Solomatin et al. 2010). NMR-derived time averaged quantities such as dipolar couplings, chemical shifts, J-couplings, or NOEs can be translated into geometric restraints to refine RNA structures or conformational ensembles. In addition, time-dependent NMR measurements such as NMR relaxation (Lipari and Szabo 1981; Boisbouvier et al. 2003; Fürtig et al. 2007; Shajani and Varani 2007) can be used to derive time-scales and amplitudes for internal motions and overall rigid-body tumbling (Kowalewski and Maler 2006). Such properties depend not only on the internal macromolecular dynamics but most importantly on the hydrodynamic and long range electrostatic interactions with the surrounding ion atmosphere (Kowalewski and Maler 2006; Bagchi 2012), providing a probe for the collective motion of the entire solvated macromolecule.

In this paper, we use multiple independent MD trajectories of the well-studied UUCG RNA hairpin to predict NMR auto- and cross-correlated relaxation rates and structural parameters that can be related to existing NOE or RDC measurements. To that end, we replicated closely experimental temperature and ionic strength conditions and RNA sequence to facilitate direct comparison with experiment. We find that the predicted overall tumbling times follow the same trend with those derived from experiments when temperature and ionic strength were varied. The absolute values of the overall tumbling times are, however, underestimated by 20%. Both Lipari–Szabo order parameters and cross-correlated relaxation rates pinpoint the G9–G10 step as the locus of the largest discrepancies between experiment and simulation that result from spurious torsional states of the sugar–phosphate backbone. Overall, the wealth of NMR measurements available for the UUCG tetraloop and MD simulations that closely mimic the experimental conditions allow one to carry out extensive diagnostics for RNA force fields.

RESULTS AND DISCUSSION

Overview of the simulations

In this paper, we present a set of explicit solvent molecular dynamics simulations that were utilized to test the ability of AMBER nucleic acid force fields to reproduce a wide series of NMR data obtained for a prototype UUCG RNA hairpin tetraloop. A detailed description of the simulation set up is given in Materials and Methods. Figure 1B shows a section through a typical system used in current simulations containing the RNA hairpin, water, and salt. We used both an older, ff99 (Wang et al. 2000), and more recent, ff10, Amber force fields. The ff10 force field builds upon ff99 by modifying the potential describing the α and γ torsion angles (Pérez et al. 2007) and the χ glycosidic torsion angle (Banas et al. 2010; Zgarbova et al. 2011). For simplicity, except where noted, results are reported for simulations using the ff10 force field. ff10 has been shown to be clear improvement over ff99; the latter's pitfalls have been documented extensively elsewhere (Pérez et al. 2007; Banas et al. 2010; Yildirim et al. 2010; Zgarbova et al. 2011; Yildirim et al. 2012; Chen and Garcia 2013), and can also been seen in the results in the Supporting information. For the purpose of careful comparison with experimental data, especially NMR relaxation, few simulation parameters had to be calibrated. We replicated two types of temperature and ionic strength conditions (labeled EC1 and EC2, see Table 1) used in most reported NMR experiments involving the UUCG hairpin. This is desired since both RNA tumbling and internal dynamics can depend on experimental conditions and as such can directly affect predicted NMR observables.

FIGURE 1.

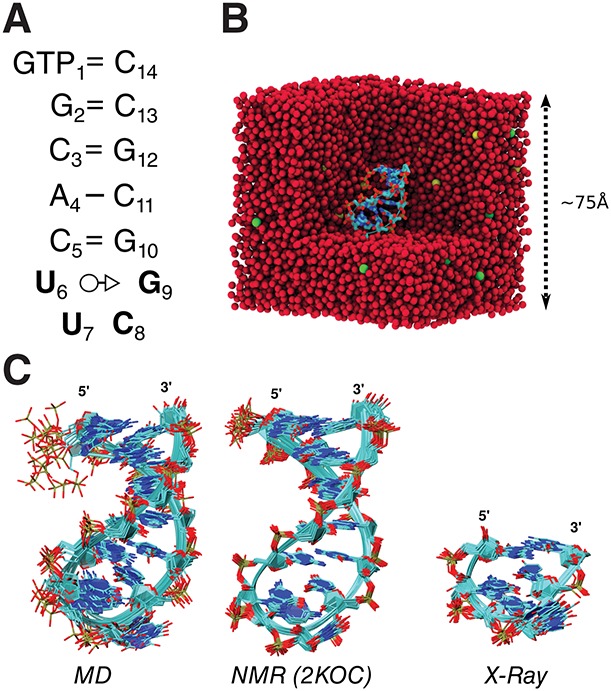
(A) Secondary structure. The RNA hairpin studied here consists of a base-paired stem and a loop, shown in bold. Most of the sequences used in NMR experiments with which comparison is drawn have a triphosphate at the 5′ end. (B) Section through the periodic boundary simulation box. RNA is shown as sticks, water oxygen as red spheres, K⁺ as yellow spheres, and Cl⁻ as green spheres. The cubic simulation box has a side of 75 Å, ensuring a buffer between the solute and the edges of the box of at least 22 Å. (C) The extent of structural fluctuations predicted by MD simulations and comparison with existing NMR and X-ray structures. Representative structures from molecular dynamics simulations (left), NMR refined structures PDB: 2KOC (middle), and all the CUUCGG sequences included in X-ray structures with resolution <3.0 Å.

TABLE 1.

Summary of simulations

Additionally, since one of the factors that affects overall macromolecular tumbling is solvent viscosity we have chosen to use the TIP4P-Ew water model that was reported to give good results in this respect (Horn et al. 2004). Finally, to diminish statistical uncertainties in time correlation functions, each simulations was extended to at least 100 times the overall tumbling time of the RNA hairpin. Overall, we run four sets of simulations corresponding to combinations of each experimental condition (EC1, EC2) and force field (ff99,ff10). Each set was comprised of three independent simulations (Table 1), resulting in a total of 12 independent simulations, sampling an aggregate of 2.4 msec.

Overall structure and dynamics

Samples from the conformational ensemble obtained from simulation are shown in Figure 1C together with structures obtained from NMR refinement (PDB ID: 2KOC) or CUUCGG tetraloop motifs occurring high resolution in X-ray structures (see Supplemental Table S2 for the list of crystal structures considered for analysis). A closer view of the the canonical structure of the UUCG tetraloop is shown in Figure 2A. The UUCG tetraloop is closed with a canonical WC base pair (C5 = G10) and contains a trans-Watson–Crick/sugar edge base pair (G9 $°\text{}-\text{}⊳$ U6), a hydrogen bond between the exocyclic amino group of the second residue (U7:N2) with the a nonbridging phosphate oxygen of the third (C8:O1P), a hydrogen bond between U7:O2′ and G9:N7 and through stacking interactions between the G9 $°\text{}-\text{}⊳$ U6 base pair and U7. Additionally, the furanose rings of U7 and U8 adopt C2′-endo pucker in contrast to all other nucleotides that adopt a C3′-endo pucker. The last nucleotide in the tetraloop, G9, assumes a syn orientation around the glycosidic bond as opposed to all other nucleotides that assume an anti orientation. This is a unique feature of all the tetraloops of the UNCG type (where N stands for any nucleotide) (Bevilacqua and Blose 2008).

FIGURE 2.

Overall structure and dynamics from simulation. (A) Survival rates of intramolecular hydrogen bonds occurring in the tetraloop region. For simplicity only the distances between the heavy atoms are shown, but hydrogen bonds have been identified using both distance and angular criteria. Distances labeled in red are not predicted by NMR measurements. (B) Interproton distances violating the nonambiguous NOE restraints used for NMR refinement. Out of a total of 133 distance restraints between the atoms of the tetraloop here we show only those spending >20% of simulation time out of the constraining bounds. (B, inset) Matrix of fractions (of intra- and interresidue) NOE distance violations involving residues of the tetraloop. The denominator corresponds to the total number of distance restraints for the residue pair and the numerator corresponds to the number of violations. (C) Distribution of the all heavy atom root mean square deviation (RMSD) with respect to the initial NMR model from simulation run at 310 K and 82 mM KCl (labeled EC1, left) and at 298 K and 32 mM KCl (labeled EC2, right). Data for each of the three independent simulations carried out at each temperature are shown with different colors. (D) Comparison between experimental and simulation-derived residual dipolar couplings obtained using the ff10 force field. Ensemble averaged RDCs were calculated using PALES (Zweckstetter 2008) using a single alignment tensor as described in the main text. Vertical error bars correspond to the standard deviation of averages obtained from simulation; the horizontal error bars correspond to the reported experimental errors. Red circles correspond to RDC's of dipolar vectors located on the tetraloop including the closing base pair; black circles correspond to RDC's measured on rest of the stem. Ensemble averaged RDCs derived from simulations using the ff99 force field are shown in the Supplemental Material (Supplemental Table S1; Supplemental Fig. S3).

All the sampled structures from simulation are very close to the initial NMR structure, with an average all heavy atoms RMSD of 1.5–1.7 Å (Fig. 2C). The shoulder of the RMSD distribution of one of the EC2 simulations (shown in black in Fig. 2C, right) is caused by an conformational intermediate occurring once and surviving for 2 nsec. Simulations using the ff99 force field showed similar values for the average RMSD with the exception when irreversible unfolding of the tetraloop was observed resulting in the excision of U7 toward to the solvent (see Supplemental Fig. S1 for RMSD time).

The hydrogen bonding pattern predicted by NMR is maintained for the entire WC base-paired stem as well as for the noncanonical interactions in the tetraloop. Most of the hydrogen bond involving atoms in the tetraloop region occur >60% of time period with the exception of the ones between U6:O2P and C8:N4 (42%) and U7:O2′ and G9:N7 (11%) due to formation of other intra- or intermolecular hydrogens. The distribution of the χ torsion angle of G9 show that the syn conformation along the glycosiddic bond of G9 is maintained in all simulations(see Supplemental Fig. S2) with averages from ff10 simulations being closer to those found in the NMR refined ensemble (PDB ID: 2KOC).

Nuclear Overhauser Effect (NOE) and residual dipolar couplings (RDCs) measurements are available for the UUCG hairpin studied here and provide further diagnostics for the final structural ensemble derived from simulation. NOE intensities are commonly used to derive bounds for specific interatomic distances. A summary of NOE unambiguous interproton distance violations is presented in Figure 2B. Out of a total of 133 distances involving at least one atom in the tetraloop region only 18 spend >20% of the simulation time outside of the constrained bounds. The largest number of distance violations involve at least one atom located on the G9–G10 step. The largest violations correspond to intraresidue distances involving atoms on the closing WC base pair, C5 and G10.

For the UUCG tetraloop studied here, RDCs are available for several types of bond vectors located on the nucleobases (C6H6, C8H8, and N1H1) and on the furanose rings (C1′H1′) (Nozinovic et al. 2010a). RDCs result from the incomplete averaging out of dipolar interactions in partially aligned samples and can provide information on the average orientation of dipolar bond vectors with respect to an alignment frame (Prestegard et al. 2000; Bax et al. 2001; de Alba and Tjandra 2002; Salmon et al. 2014). Estimating the ensemble averaged RDCs from simulation is conditioned by the determination of the five independent components of the alignment tensor (Prestegard et al. 2000; Bax et al. 2001; de Alba and Tjandra 2002). The alignment tensor parameters were obtained by fitting RDCs to the initial NMR structure followed by superimposing individual conformations obtained from simulation to this initial NMR structure and using the five-elements of the alignment tensor to calculate the ensemble averaged RDCsenglish. Overall, our calculations show that RDC rms deviation from experiment for simulations using the ff10 force field are 3.4 Hz which is larger than than the rms error of 2.5 Hz calculated for the NMR refined structural ensemble or the reported error of 1.5 Hz. A comparison between the experimentally measured RDCs and ensemble averages from simulation is presented in Figure 2D. With the exception of the terminal residues, all the calculated RDCs for the WC base-paired stem (shown in black) are very close to the experimental values. For vectors located on the tetraloop region (shown in red), most of the RDCs of bond vectors located C5, U6, U7 are close to experimental values, whereas those located on C8, G9, and G10 deviate from experiment with up to 7 Hz.

There is a concern as to whether using the entire structure to fit RDCs might lead to problems in the case of flexible RNA molecules. One way to circumvent this is to use only the rigid parts of an RNA molecule for determining the alignment tensor (Salmon et al. 2014). To address this concern we have estimated the ensemble averaged RDCs by fitting only the RDCs measured for dipolar vectors located on the Watson–Crick base-paired stem of the hairpin followed by superimposing the conformations obtained from simulation on the reference structure using the same helical region. The complete results are shown in the Supplemental Material (Supplemental Table S1; Supplemental Fig. S3). We find that the rms error with respect to the available experimentally measured RDCs is marginally increased to 3.7 Hz, while the overall trends remain similar. These observations can be explained by the overall rigidity of the UUCG hairpin structure and the lack of interdomain motion between the helical and tetraloop domains.

Overall, we found that typical measures of structural integrity such as RMSD or hydrogen bond network analysis suggest a strong similarity between the simulated ensemble and the NMR-derived structures. However, comparing against RDCs or NOE restraints reveals global deviations as well as localized deviations from experiment located mainly the second half of the tetraloop.

Backbone torsional substates

Nucleic acids backbone is rotameric (Murray et al. 2003) and analysis of populations of adopted torsional states is often used for discovering force-field flaws or identify structural motifs (Leontis et al. 2006). Here we identify torsional substates by assigning each torsion to one of three conformations specific to rotation around a single bond: gauche +, −, or trans. For simplicity, our analysis includes only the α, β, γ, δ, ε, δ backbone torsions as the other types torsions do not populate more than one rotamer. The advantage this approach resides in the fact that the states of each torsion are well defined and one is not confronted with choosing a predefined and often arbitrary number of clusters.

In Table 2, we summarize the torsional conformational substates and corresponding populations adopted by the backbone of the tetraloop region including the closing canonical base pair. It can easily be noted that it is only the backbone conformations of the G9–G10 linkage that are able to differentiate between the entire set of substates, as the C5, U6, U7, and C8 remain in the same conformation. Two substates are majority, labeled s1 and s2, each being populated >28% of the simulation time. The s2 substate is also adopted by all NMR structures (PDB ID: 2KOC) and by one of the UUCG tetraloops resolved in the crystal structure of a 57-nt long fragment of the 16s rRNA (PDB ID: 1F7Y) that is often used as reference for RNA structure prediction or folding (Das 2011; Chen and Garcia 2013). The lifetimes of the torsional states identified here are of the order of up 0.1 nsec and transitions between states take place multiple times.

TABLE 2.

Conformational substates adopted by the UUCG tetraloop during MD simulations

Carrying out the same type of analysis on a set of CUUCGG structures found in crystallized RNA's with a resolution of <3.0 Å (Supplemental Table S3) reveals that the backbone of all nucleobases belonging to the tetraloop region can adopt several conformations. Most importantly the central nucleobases of the tetraloop (U7, C8) are able to adopt the largest variety of backbone conformations, which can be attributed to tertiary interactions caused by the packed crystal environment. Overall, this suggests that the backbone conformational states adopted by crystallized UUCG motifs differ significantly from those observed in simulation.

NMR relaxation from simulation

A wide variety of NMR relaxation studies have been carried out using the RNA UUCG hairpin analyzed here (Duchardt and Schwalbe 2005; Vallurupalli and Kay 2005; Rinnenthal et al. 2007; Ferner et al. 2008; Rinnenthal et al. 2009; Nozinovic et al. 2010b). This offers an unique opportunity to test the ability of current force fields to reproduce such data. NMR relaxation is potentially affected by internal macromolecular dynamics, hydrodynamic interactions with the solvent and, due to the highly charged nature of nucleic acids, by long range electrostatic interactions with the surrounding ion atmosphere (Kowalewski and Maler 2006; Bagchi 2012). As such, the analysis of predicted NMR relaxation parameters presented below should bring new information to complement the comparisons against structural parameters found in the previous sections.

The connection between NMR relaxation measurements and molecular dynamics is established using time correlation functions of the type:

$$C_{12}(\tau )=\langle Y_{20}[{\Omega }_1^{\text{LF}}(0)]Y_{20}^{\ast }[{\Omega }_2^{\text{LF}}(\tau )]\rangle$$ (1)

where 1 and 2 indexes correspond to vectorial interaction such as those shown in Figure 4A below, Y₂₀ is a spherical harmonic of rank 2, Ω^LF is the solid angle of the vectorial interaction with respect to the laboratory frame (LF), τ is a time lag and the angled brackets signify ensemble average. Time correlation functions can be readily obtained from molecular dynamics simulations that are propagated deterministically. Statistical errors increase with the time lag, τ, and for this reason it is usually recommended to extend molecular dynamics trajectories to durations that are at least 100 times the overall tumbling time (Wong and Case 2008).

FIGURE 4.

(A) Localization of the dipolar vectors and chemical shift tensors involved in NMR (cross-) relaxation analysis. Interacting groups are indexed only when residing on different residues. (B) Comparison between cross-correlated rates from simulation and predictions based on isotropic tumbling with internal motion (see below) for the pair of vectors C1′H1′ and C8H8 located on G9. (C) Comparison between cross-correlated relaxation rates from simulation versus experiment. Larger symbols correspond to rates between tensorial interactions located on the tetraloop region. The rates are calculated using Equation 4 using the experimentally derived overall tumbling time of 2.3 nsec to be able to asses the impact of internal motion on estimates. (D) Examining the impact of conformational averaging on ${\Gamma }_{{({\text{C4}}^{\prime }{\text{H4}}^{\prime })}_9,P_{10}}^{\text{DD},\text{CSA}},$ whose value estimated from simulation (enclosed in a square in C) has one of the highest deviations from the experimental value. The distribution of projection cosines of the C4′H4′ vector on the plane made by the first two principal axises of CSA tensor is shown in a surface representation. To simplify notation, $\text{cos}({\theta }_{ii})$ corresponds to $v\cdot {\delta }_{ii}$ in Equation 4. The rate calculated from Equation 4 is shown using iso-value lines. Projection cosines from the NMR ensemble (2KOC) are shown as black dots.

The time correlation function in Equation 1 can be broken into a product of an internal [C^int(τ)] and an overall rigid-body rotation [C^rigid(τ)] part (Kowalewski and Maler 2006; Cavanagh et al. 2012) under the assumption that the tumbling and internal motions are independent or that the tumbling is isotropic or axially symmetric with a high degree of symmetry (Canet et al. 2003). This is a valid approximation for the current system since the large majority of the bond vectors or tensors analyzed here relax on the 0–50 psec scale, whereas the overall tumbling times are on the nanosecond scale. Only few vectors relax on the nanosecond scale in the molecular frame, but as a result of local fluctuations.

Analysis of C^int(τ) for the case of auto-correlated relaxation (using the well known Lipari–Szabo model-free approach [Lipari and Szabo 1982]) provides information on the time scales and amplitudes of macromolecular internal motion with respect to the molecular frame. In the case of cross-correlated relaxation, C^int(τ) reports on the average relative orientation of dipolar vectors or chemical shift tensors and can be related to local torsional dynamics. The overall rigid-body rotation correlation function C^rigid(τ) is used to derive the macromolecular diffusion tensor from where the overall tumbling time or anisotropy can be obtained. The separation of internal and overall tumbling motions can be exploited to diagnose separately different force-field components since overall tumbling is mainly affected by the interactions between the nucleic acid and ion atmosphere, whereas internal motion is affected mainly by changes of internal coordinates.

Rotational diffusion and overall rigid-body tumbling

NMR relaxation analysis can provide information about overall rotational Brownian motion. This is an essential prelude to a robust extraction of information about internal motions, and offers a additional point of comparison with MD simulations, that is influenced by the water molecules and the strength of nucleic acid interactions with its surrounding solvent and ion atmosphere (Wong and Case 2008). For the RNA hairpin considered here, NMR relaxation measurements have been carried out at both EC1 and EC2 experimental conditions for several nuclei. We summarize these data in Table 3 together with estimates from simulation and the hydroNMR program that is often used to estimate diffusion tensors from structure (Garcia De La Torre et al. 2000). Recently, some of the NMR relaxation rates used here as reference for EC2 case (Duchardt and Schwalbe 2005; Ferner et al. 2008) have been refitted simultaneously to yield similar overall tumbling times, but significantly larger anisotropies (Berlin et al. 2013) and no information on the order parameters.

TABLE 3.

Comparison between rotational diffusion parameters obtained from simulation and experiment

Overall tumbling times, τ_ov estimates follow the same trend with those from experiment, decreasing with increasing temperature. The ratio of τ_ov at the 298 and 310 K is the same for values obtained from experiment and simulation. Additionally, the ratio of τ_ov is very close to the value estimated from a Stokes–Einstein–Debye hydrodynamic rotational diffusion model (0.7) using experimental water viscosities (Bird et al. 2007) at the corresponding temperatures.

τ_ov obtained from simulations using the ff10 force field are underestimated with 20% at both temperatures. To test the origin of this trend we have repeated the same simulations using the ff99 force field, known to have less restrictions on the sampled torsional substates and consequently more internal flexibility. In this case the estimates for τ_ov are very close to those from ff10 for both EC1 and EC2 sets of simulations and slightly larger anisotropies. For the case of EC1 simulations, both simulation sets overestimate the anisotropy. For EC2 set of simulations, anisotropies (1.46 for ff10 and 1.78 for ff99) are less than the consensus values of 2.3, but larger than earlier estimates (Table 3).

Internal motion from auto-correlated NMR relaxation

Typical internal time correlation functions, C^int(τ), are shown in Figure 3B. The most popular way to analyze such functions is using the well known Lipari–Szabo model-free approach where $C^{\text{int}}(t)=S^2+(1-S^2)e^{-t/{\tau }_s}$, where S² is an order parameter and τ_s corresponds to an internal correlation time (Lipari and Szabo 1982). The S² order parameters measure the amplitude of the fluctuations of the corresponding vector with respect to the molecular frame. S² depends on the spatial restriction of the associated vector and ranges from 0.0, corresponding to total random motion, to 1.0, corresponding to rigid orientation with respect to the molecular frame.

FIGURE 3.

(A) Comparison between Lipari–Szabo model-free parameters obtained from simulation and experiment. The comparisons between experiment and simulation-derived order parameters are made to match the corresponding experimental conditions (see Materials and Methods and Results). Order parameters obtained from simulation are shown in red, in green results obtained from ²H quadrupolar relaxation (Vallurupalli and Kay 2005) (EC2), in blue results from ¹³C CSA and dipolar relaxation (Duchardt and Schwalbe 2005; Ferner et al. 2008) (EC2), and in orange results from ³¹P CSA relaxation (Rinnenthal et al. 2009) (EC1). (B) Comparison between internal auto-correlation functions obtained from simulation for several C5′H5′ vectors located on C8, G9, and G10. Experiment suggests very similar values of the order parameters of these 3 nt (0.7–0.9) and internal relaxation times of the order of tens of psec and hence similar profiles for auto-correlation functions. As shown here, the C5′H5′ vector located on G10 has a larger correlation time on the order of the overall tumbling as well as a lower value for the order parameter, S² (see also A). This behavior can be correlated with multiple torsional states spanned by the backbone. (C) Comparison between internal cross-correlation functions for several dipolar and chemical shift anisotropy tensors. (D) Overlay of representative structures taken from the highest occupied torsional clusters summarized in Table 2. All the structures shown have been rms-fitted with respect to the tetraloop region of the starting NMR structure. The G9–G10 backbone (marked with a square) is the locus of highest conformational variability of the tetraloop.

Order parameters available from analysis of various NMR experiments as well as corresponding values derived from current simulations are shown in Figure 3A. In general, NMR-derived order parameters reveal a rigid WC base-paired stem and a relatively more flexible tetraloop. As it will be pointed out below, this trend is followed by estimates from MD simulations, with few significant exceptions.

Both experiment and molecular dynamics simulations show that the terminal base pair (G1 = C14) has order parameters lower than the other canonical base pairs. For example, in the case of relaxation of C2′H2′ vectors, simulations are able to capture very well the big drop in S² values from residue 13 to residue 14. For vector types located on the nucleobases (C5H5,C6H6,C8H8) the variation patterns and their corresponding values are very similar to those derived from experiment. Indeed, simulation is able to capture the increased mobility of U7, C8 nucleobases captured in two independent NMR experiments. A similar trend is observed for vectors located on the sugar (C1′H1′,C2′H2′,C4′H4′) with a single exception for G9:C2′H2′ vector.

C5′H5′ and C5′H5″ order parameters show larger deviations from experiment, the largest being located on G10 with deviations up to 0.5. In Figure 3B we compare the aspect of internal auto-correlation functions for few C5′H5″ type vectors where it can be observed that not only the G10:C5′H5″ vector has a low order parameter, but it decays with a correlation time of 1.5 nsec, on the same order as that of the rotational tumbling. Overall, these observations indicate a higher mobility than expected for the G10:C5′H5″ vector that can be correlated with a large set torsional states of the sugar phosphate backbone between G9 and G10 (see Table 2; Fig. 3D), as well as with large deviation of cross-correlated relaxation rates (see next section, “Internal motion from cross-correlated NMR relaxation”).

While it is known that the magnitude as well as the orientation of the ³¹P CSA tensor are dependent on the backbone conformations, we will follow the original analysis of experimental data and consider that CSA tensor is axially symmetric and aligned along the P–O3′ bond (Rinnenthal et al. 2009). The order parameters corresponding to ³¹P relaxation are shown in Figure 3. Order parameters from simulations are overestimated uniformly along the sequence, suggesting that the sugar–phosphate backbone dynamics is too restricted with current force fields. Overall, this suggests that the overall sugar–phosphate backbone dynamics can be globally misrepresented with current force fields.

Internal motion from cross-correlated NMR relaxation

NMR cross-correlated relaxation rates can be used to extract average orientations between tensorial interactions, such as chemical shift anisotropy tensors or dipolar interactions that can be further related to dynamics along torsional degrees of freedom (Schwalbe et al. 2001). The models for cross-correlated relaxation are more complex than those for auto-correlation due to their dependence on the orientation of two tensorial interactions. For this reason, experimentally measured cross-correlated relaxation rates are analyzed usually assuming a isotropic overall tumbling (neglecting the diffusion tensor anisotropy, ▵) with fast internal motion model. In this case, the total time correlation function from Equation 1 is assumed to have the form (Frueh 2002; Canet et al. 2003):

$$C_{12}(\tau )=\langle P_2[v_1\cdot v_2]\rangle (S^2+(1-S^2)e^{-{\tau }_s/\tau })e^{-{\tau }_c/\tau },$$ (2)

where the first two terms correspond to the internal correlation function plotted in Figure 3C (see Materials and Methods). To test the validity of this approximation in the case of the simulations presented here, in Figure 4B we show an overlay between the overall cross-correlated correlation functions of two dipolar vectors as derived from simulation and the corresponding approximations derived using Equation 2. It can be observed that the overlap between the model and the actual cross-correlation function is very good at both temperatures at which the present simulations were run. This adds support to the approximation in Equation 2. To reveal the effects of just the internal motion on the predicted cross-correlated relaxation rates from simulation we can replace in Equation 2 the overall tumbling time predicted by simulation, known to underestimate the experimental values, with that from experiment. (For a discussion on the deviations of the predicted and experimentally derived overall tumbling times, see previous section.)

Two types of cross-correlated relaxation rates will be analyzed here. The first type involves dipolar–dipolar interactions(Г^DD,DD) between C1′H1′ and C6H6/C8H8 vectors located on the furanose ring and the nucleobase, respectively. These rates are affected by conformations, along the χ torsion that spans the glycosidic bond (Rinnenthal et al. 2007). The second type (Г^DD,CSA) involves dipolar and CSA interactions and has been measured between C3′H3′, C4′H4′, C5′H5′, and C5′H5″ dipolar vectors on one side and the CSA tensor of the backbone phosphate on the other. These Г^DD,CSA are related to conformations of the sugar—phosphate backbone controlled by α, ζ torsions that cross the phosphodiester backbone (Nozinovic et al. 2010b). See Figure 4A to localize the dipolar vectors and tensors on typical dinucleotide step.

A comparison between experimental rates and estimates from simulation is presented in Figure 4C for both DD,DD and DD,CSA types of cross-correlated relaxation. Values involving at least one tensorial interaction located on the tetraloop are shown as large circles while the others are shown using small circles. In general, cross-relaxation rates estimated for tensorial interactions located on the helical stem show a reduced dependence on the sequence as opposed to experiment. This is caused by the fact that the average orientation between vectors is practically identical and independent on the position on the stem.

On the other hand, estimates for cross-correlated relaxation rates for groups located on the tetraloop have a wider spread due to the larger conformational diversity improving the overall correlation with experiment. Most of the values of ${\Gamma }_{{\text{C1}}^{\prime }{\text{H1}}^{\prime },\text{C6/8H6/8}}^{\text{DD},\text{DD}}$ rates are accumulated between −5 and 5 Hz due to very small values of the $\langle P_2[v_1\cdot v_2]\rangle$ terms in Equation 2 caused by the predominant anti conformations along the χ torsion. The only exception is G9, whose χ torsion angle is in syn conformation.

Values of the Г^DD,CSA rates span a larger interval, between −20 and 20 Hz. The largest deviation from experiment is observed for ${\Gamma }_{{({\text{C44}}^{\prime }{\text{H4}}^{\prime })}_9,P_{10}}^{\text{DD},\text{CSA}}$, marked with a square in Figure 4C, which is located on the G9–G10 linkage which was identified to adopt a multiple series of backbone torsional substates. In Figure 4D we show the distributions of the projection cosines of the G9:C4′H4′ vector on the two main axis of the CSA tensor of the G10:P from simulation and from the conformational ensemble resulting from NMR structure refinement. The two distributions overlap partially, but structures obtained from simulation spend more time outside of the overlapping area and as such leading to a high deviation in ${\Gamma }_{{({\text{C44}}^{\prime }{\text{H4}}^{\prime })}_9,P_{10}}^{\text{DD},\text{CSA}}$. Consequently, the large conformational space spanned by the two projection cosines is directly related to the large number of torsional states observed in a previous section for the backbone torsions spanning the G9–G10 linkage.

CONCLUSIONS

This work presents a comprehensive analysis of the extent to which current MD simulations of a prototype RNA hairpin are consistent with a wide variety of solution NMR experiments. We used multiple independent explicit solvent molecular dynamics simulations using the most recent Amber RNA force fields and replicated the exact sequence, temperature and ionic strength conditions used in a wide variety of NMR experiments. The results presented here indicate that the experimentally observed NMR structure and fluctuations are closely reproduced by the simulations using the most current force field, suggesting that experimental ensemble is well-represented by the free energy basin sampled in the simulations. This need not imply that we have found the global minimum for these force fields, and more global studies of tetraloop structures (Banas et al. 2010; Cheatham and Case 2013; Bergonzo et al. 2014), including some with a UUCG tetraloop similar to that studied here (TE Cheatham and N Henriksen, pers. comm.) suggest that the Amber ff10 force field may preferentially stabilize some alternate loop conformations.

Although there is a considerable overlap between the conformational ensembles obtained from simulations and NMR refinement, it is only through direct comparison to available NMR measurements (i.e., the primary experimental data as opposed to the interpreted data) that one can identify possible structural and dynamical failures in the molecular simulation force fields. We found that the overall rigid-body tumbling times follow the same trends as those estimated from experiment when varying temperature and ionic strength, but the absolute values of tumbling times are underestimated. Large localized deviations from ²H relaxation–derived order parameters are observed at the G9–G10 linkage, which can be directly correlated to multiple backbone torsional states exchanging on a sub-nanosecond time-scale. The conformational mobility at the G9-G10 linkage also induces large localized deviation of cross-correlated relaxation rates and RDCs from experiment. Order parameters derived from ³¹P relaxation suggest that the amplitude of motions of the backbone are somewhat more restricted than those suggested by experiment. The comparisons between experiment and simulation outlined here can be used as a benchmark as newer force fields become available.

MATERIALS AND METHODS

Rotational diffusion from simulation

The method used here to determine the diffusion tensor has been presented in detail by (Wong and Case 2008). In short, the rigid-body tumbling motion of a molecule is described by a time series of rotation matrices obtained from rms fitting each molecular dynamics trajectory frame to a reference structure. A set of local tumbling times, $t_i^{\text{loc}}$ is obtained from numerically integrating the correlation functions generated for a random set of uniformly distributed unit vectors whose time evolution is calculated using the previously determined rotation matrices. Finally, the diffusion tensor $\overleftrightarrow{D}$ is obtained from a χ² fit of the form:

$$\underset{\overleftrightarrow{D}}{\text{min}}{\displaystyle \sum _i{(t_i^{\text{loc}}(\overleftrightarrow{D})-t_i^{\text{loc}})}^2,}$$

where $t_i^{\text{loc}}(\overleftrightarrow{D})$ are local diffusion times derived for an asymmetric top rigid-body model. The diffusion tensor is 3 × 3 matrix with eigenvalues D_z > D_y > D_x. The overall diffusion tumbling time ${\tau }_c^{\text{av}}$ and anisotropy ▵ are computed using:

$$\begin{array}{c}{\tau }_c^{\text{av}}=\frac{1}{2(D_x+D_y+D_z)},\\ \Delta =\frac{2D_z}{D_x+D_y}.\end{array}$$

Internal correlation functions

Calculation of time correlation function from simulation has been reviewed many times (see for example Bruschweiler and Case 1994; Case 2002). Internal correlation functions were computed using:

$$C^{\text{int}}(\tau )=\langle P_2[v_1(0)\cdot v_2(\tau )]\rangle ,$$ (3)

where v₁ and v₂ are vectors describing the orientation of dipolar vectors or tensor components in the molecular frame at instances in time separated by a lag, τ; P₂ = (3x² − 1)/2 is the second order Legendre polynomial. In the case of auto-correlated relaxation v₁ and v₂ correspond to orientations of the same vector at different times along the trajectory.

Auto-correlated relaxation in the molecular frame

For the case of auto-correlated relaxation, C^int has been modeled using the single and double exponential versions of the Lipari–Szabo (LS) model-free approach: $C^{\text{int}}(t)=S^2+(1-S^2)e^{-t/{\tau }_s}$, $C^{\text{int}}(t)=S^2+(1-S_f^2)e^{-t/{\tau }_f}+(S_f^2-S^2)e^{-t/{\tau }_s}$ (Clore et al. 1990). We used the latter in case fitting the first model was not satisfactory. One has to keep in mind that fitting multiexponentials is an ill-defined problem especially for noisy data, and usually the best strategy for getting meaningful results is to resort to the simpler models first.

Cross-correlated relaxation rates from simulation

Within the isotropic rotation approximation (see Equation 2), cross-correlated relaxation rates between dipolar couplings or chemical shift anisotropy tensors are usually modeled using (Schwalbe et al. 2001):

$$\begin{array}{c}{\Gamma }_{v_1,v_2}^{\text{DD},\text{DD}}=C_{v_1,v_2}^{\text{DD},\text{DD}}{r}_{v_1}^{-3}{r}_{v_2}^{-3}{P}_2[v_1\cdot v_2]{\tau }_{\text{av}}^c{S}^2,\\ {\Gamma }_{v,\overleftrightarrow{\sigma }}^{\text{DD},\text{CSA}}=C_{v,\overleftrightarrow{\sigma }}^{\text{DD},\text{CSA}}{r}_v^{-3}\{({\sigma }_{11}-{\sigma }_{33})P_2[v\cdot {\delta }_{11}]\\ +({\sigma }_{22}-{\sigma }_{33})P_2[v\cdot {\delta }_{22}]\}{\tau }_{\text{av}}^c{S}^2,\end{array}$$ (4)

where v_i are dipolar vectors oriented in this case along C–H bonds, r_v are their corresponding bond lengths; $\overleftrightarrow{\sigma }$ are chemical shift tensors, σ_iiσ_ii are the corresponding eigenvalues and δ_ii eigenvectors. $C_{v,\overleftrightarrow{\sigma }}^{\text{DD},\text{CSA}}$ and $C_{v_1,v_2}^{\text{DD},\text{DD}}$ depend on universal constants and the strength of the magnetic field. In Equation 4, the overall tumbling time is estimated from analysis of auto-correlated relaxation rates; the $P_2[v_1\cdot v_2]S^2$ can be obtained from an internal time correlation function of Equation 3, using the following model (see Equation 2; Frueh 2002; Canet et al. 2003): $C^{\text{int}}(\tau )=\langle P_2[v_1\cdot v_2]\rangle (S^2+(1-S^2)e^{-{\tau }^{\text{int}}\text{/}\tau })$.

General system setup and molecular dynamics simulation protocol

Simulations were performed with the CPU and GPU versions of PMEMD MD engine from the AMBER simulation suite of programs (versions 10, 11, and 12) (Pearlman et al. 1995; Case et al. 2005, 2012). The initial RNA structure was taken from the NMR structure deposited in PDB (ID: 2KOC) (Nozinovic et al. 2010a). The 5′ terminal residue was capped with an additional triphosphate group to mimic the sequence used in most experiments used here as reference. We replicated two types of temperature and ionic strength conditions (labeled EC1 and EC2, see Table 1) that were used in the NMR experiments used here as reference. This is desired for the purpose of comparison against experimental data as both overall tumbling and internal dynamics can be affected by changes in temperature and ionic strength. For simplicity, we used KCl to mimic the experimental ionic strength arising from the monovalent salt (KCl) and phosphate buffer.

RNA initial structures were immersed into the corresponding water box containing the the neutralizing counterions (K⁺) and as well as the coions (K⁺ and Cl⁻). The number of coions added to approximate the desired salt concentration was chosen so that the ratio of the number coions and water molecules in the simulation box was equal that of aqueous salt solution at the desired concentration. The size of the simulation box was chosen so that all solute atoms were at least 25 Å away from the margins of the box. Coions positions were initially randomized. In the first equilibration stage the overall density of the system as well as the distribution of ions were converged with the RNA restrained, keeping the system at the desired temperature (see Table 1) and a pressure of 1 atm in the isothermal-isobaric ensemble (NPT). In the second equilibration stage, the restraints on the RNA were removed, allowing the entire system to relax. This stage was carried out at constant volume and temperature in the canonical ensemble (NVT). Temperature was regulated using the Langevin thermostat with a collision frequency of 5 psec⁻¹. Pressure was controlled using the Beredensen barrostat using a relaxation time of 5 psec. The equilibration was carried for a total of 35 nsec. Note that the motions and relaxation of solvent and counter- and coions are notoriously slow to converge in nucleic acid simulations (Ponomarev et al. 2004), and careful equilibration is critical. The production was carried out in the microcanonical ensemble (NVE) using a 1 fsec integration step that ensures a very good energy conservation, allowing the dynamics of the system to be propagated deterministically. The temperature of the system drifted with a positive of rate of 10⁻² degree/ns.

A detailed description of the composition of the simulated systems and the force fields used is given in Table 1. As described in the text, both ff10 (Pérez et al. 2007; Banas et al. 2010; Zgarbova et al. 2011) and ff99 (Wang et al. 2000) Amber force fields were used. TIP4P-Ew (Horn et al. 2004) water model was preferred as it has better diffusive properties then the TIP3P (Jorgensen et al. 1983) model: At a temperature of 298 K the self-diffusion coefficient of TIP4P-Ew water model is 2.3 × 10⁻⁹ m² sec⁻¹ (Horn et al. 2004), whereas for TIP3P is 5.5 × 10⁻⁹ m² sec⁻¹ (Mark and Nilsson 2001). The experimental diffusion coefficient estimate for water at a temperature of 298 K is 2.2 × 10⁻⁹ m² sec⁻¹ (Mark and Nilsson 2001). Ion force-field parameters were taken from Joung and Cheatham (2008).

All simulations were run using cubic periodic boundary conditions. Long range electrostatic interactions were calculated using the smooth particle mesh Ewald (PME) method (Essmann et al. 1995; Sagui and Darden 1999) with a B-spline interpolation order of 6 and a direct-space cutoff of 9.0 Å. The FFT grid points used for the lattice directions were chosen using ∼1.0 Å spacing. Numerical integration was performed using the leap-frog Verlet algorithm with 1-fsec time steps (Allen and Tildesley 1987). Covalent bond lengths involving hydrogen atoms were constrained using the SHAKE algorithm with a tolerance of 10⁻⁶.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.