Localization of dense intracranial electrode arrays using magnetic resonance imaging

Abstract

Intracranial electrode arrays are routinely used in the pre-surgical evaluation of patients with medically refractory epilepsy, and recordings from these electrodes have been increasingly employed in human cognitive neurophysiology due to their high spatial and temporal resolution. For both researchers and clinicians, it is critical to localize electrode positions relative to the subject-specific neuroanatomy. In many centers, a post-implantation MRI is utilized for electrode detection because of its higher sensitivity for surgical complications and the absence of radiation. However, magnetic susceptibility artifacts surrounding each electrode prohibit unambiguous detection of individual electrodes, especially those that are embedded within dense grid arrays. Here, we present an efficient method to accurately localize intracranial electrode arrays based on pre- and post-implantation MR images that incorporates array geometry and the individual's cortical surface. Electrodes are directly visualized relative to the underlying gyral anatomy of the reconstructed cortical surface of individual patients. Validation of this approach shows high spatial accuracy of the localized electrode positions (mean of 0.96 mm±0.81 mm for 271 electrodes across 8 patients). Minimal user input, short processing time, and utilization of radiation-free imaging are strong incentives to incorporate quantitatively accurate localization of intracranial electrode arrays with MRI for research and clinical purposes. Co-registration to a standard brain atlas further allows inter-subject comparisons and relation of intracranial EEG findings to the larger body of neuroimaging literature.

Introduction

Resective surgery on patients with medically intractable epilepsy often requires invasive evaluation with intracranial EEG (iEEG) (Behrens et al., 1994; Engel, 1996; Rosenbaum et al., 1986; Spencer et al., 1990; van Veelen et al., 1990). Electrode arrays in the form of rectangular grids and strips implanted beneath the dura on the cortical surface, in addition to depth electrodes that are stereotactically guided to subcortical structures, are utilized for inpatient monitoring of ictal and interictal events. The information from these intracranial electrode arrays is used to localize regions of cortical hyperexcitability and ictal onset zones, which are then the targets of surgical resection. Further, functional mapping of eloquent cortex by electrical stimulation via these electrodes can tailor the resection to prevent post-resection functional deficits. Optimal resection is associated with favorable outcomes regarding seizure control and avoidance of unacceptable neurological deficits. Accurate localization of the electrodes with respect to structural and functional brain anatomy is, therefore, an important part of surgical planning that has great potential to affect outcome. Here, we present a method to localize intracranial electrodes that uses pre- and post-implant MR images by circumventing the problem of magnetic susceptibility artifacts induced by the electrodes.

Owing to its superior spatiotemporal resolution, iEEG has also been increasingly utilized to investigate human cognition and cortical neurophysiology (Cash et al., 2009; Lachaux et al., 2003). It has also been demonstrated to be an effective platform for brain–computer interfaces, with potential to improve communication, movement, or perception for patients in whom these functions are compromised (Felton et al., 2007; Leuthardt et al., 2006; Schalk et al., 2008). Finally, quantitatively accurate localization of the electrodes relative to cortical structures is necessary to relate findings to the larger body of neuroimaging literature and to conduct inter-subject comparisons of the iEEG signals.

Traditional localization methods involve qualitative estimates of electrode locations based on visual assessment upon reopening of the craniotomy for resection, in addition to notes, sketches, and photographs acquired intra-operatively during the implantation. These estimates are further limited by the fact that electrodes implanted via a burr hole or those placed under the edges of the craniotomy, the size of which is minimized by the neurosurgeon, cannot be visually assessed. Accurate quantitative localization of electrode positions has the potential to improve surgical outcomes by better accounting for potential shifts in the position of the electrodes during inpatient monitoring, in addition to obviating the need for man-made landmarks to mark electrode positions during resective surgery (Darcey and Roberts, 2010; Immonen et al., 2003; Kamida et al., 2010; Murphy et al., 2004).

Several methods have been developed to localize the implanted electrodes in relation to cortical surface structures, including those based on digital photography (Mahvash et al., 2007; Wellmer et al., 2002), X-ray radiographs (Miller et al., 2007, 2010), computerized tomography (CT) (Dykstra et al., 2011; Grzeszczuk et al., 1992; Hermes et al., 2010; Hunter et al., 2005; LaViolette et al., 2011a; Morris et al., 2004; Sebastiano et al., 2006; Tao et al., 2009; Wang et al., 2005; Winkler et al., 2000), magnetic resonance imaging (MRI) (Bootsveld et al., 1994; Kovalev et al., 2005; Morris et al., 2004; Schulze-Bonhage et al., 2002), and multiple image sets (Dalal et al., 2008).

Radiographs are low-cost and easily available at the bedside. However, their two-dimensional nature makes co-registration to the three-dimensional space of the brain problematic. CT produces three-dimensional images with relatively clear visibility of the electrodes. However, because of high levels of ionizing radiation, CT images cannot be obtained exclusively for research purposes and are only available if clinically indicated. Even if available, CT suffers from poor soft-tissue contrast, and is often not sufficient to elucidate electrode positions with respect to cortical surface structures. Published methods overcome this by cross-modal registration of the pre-implant MR and the post-implant CT images, which in itself can be a source of error in the electrode localization.

MRI is often used for post-implant imaging in the clinical setting because it is radiation-free and yields higher sensitivity in detecting post-implant complications, such as small subdural fluid collections, infections, ischemia, and undue mass effect. However, magnetic susceptibility artifacts caused by the implanted electrodes can obscure both the position of electrodes and the morphology of the underlying cortical surface. These artifacts manifest mainly as “black holes” that extend beyond the radius of the individual electrodes. Overlapping artifacts can create a large black area at the center of dense grid arrays (inter-electrode distances <10 mm), with only a few peripheral electrodes visually distinguishable from one another (Fig. 1D; sagittal plane). Previous methods based on post-implant MR images visualized individual electrodes indirectly via their susceptibility artifacts (Bootsveld et al., 1994; Kovalev et al., 2005; Morris et al., 2004; Schulze-Bonhage et al., 2002), making it difficult or impossible to determine the precise location of most electrodes with respect to the gyral anatomy.

Fig. 1.

Complete procedure for localization of grids from pre- and post-implant MR images. Post-implant MR image (B) is co-registered to the pre-implant MR image (A) using a rigid-body transformation. Widespread artifacts referred to as “black holes” surround each electrode of the dense grid, prohibiting unambiguous identification of all electrodes. Therefore, the co-registered image (D) is used to manually determine the xyz coordinates of two electrodes that are easily identifiable (yellow lines guide this procedure on simultaneous sagittal, axial, and coronal sections). These coordinates are in the same space as the smoothed pial surface reconstruction (C). The remaining electrodes are interpolated on a flat surface traversing the pial surface, referred to as the map plane (E). The two manually-localized electrodes on diagonal corners (blue) are on the cortical surface while the remaining electrodes (black) are either above or below the surface. Note that the entire lateral surface of the cortical hemisphere is shown here for illustrative purposes. The coordinates of the remaining electrodes are calculated using the inverse of the gnomonic projection to “fold” the grid onto the smoothed pial surface. Visualization is made on the subject-specific gyral surface (F).

Here, we present and validate a method that circumvents the problem of magnetic susceptibility artifacts on MRI by using the known geometry of the implanted grid and the curvature of the individual patient's cortical surface in order to derive accurate spatial positions of the electrodes relative to individual cortical anatomy. This novel method is characterized by high spatial accuracy, minimal user input, short processing time, and reliance on a radiation-free imaging modality. The MATLAB (The Mathworks Inc., Natick, MA, USA) code and user-end instructions can be downloaded at www.med.nyu.edu/thesenlab/software.

Materials and methods

Patients and electrode arrays

MRI scans were acquired from patients undergoing inpatient monitoring at the New York University Comprehensive Epilepsy Center for treatment of medically intractable epilepsy. This study was approved by the Institutional Review Board at the New York University School of Medicine and informed consent was obtained from each participant in accordance with the ethical standards promulgated in the Declaration of Helsinki. Three kinds of silastic-embedded stainless-steel electrode arrays were used: 20- or 64-contact grids (4×5 and 8×8, respectively), 4- to 12-contact linear strips, and 8-contact linear depth electrodes (AdTech, Racine, WI, USA). Artifacts on MRI from stainless-steel electrodes are larger than those from platinum electrodes, and hence the methods in this study can be applied to the latter as well. The center-to-center spacing between adjacent grid and strip electrodes is 10 mm. Each electrode is 4 mm in diameter with the exposed portion having a diameter of 2.3 mm. The inter-electrode spacing for depth electrodes is 5 mm, with cylindrical electrodes of 1.0 mm in diameter and 2.4 mm in length.

MRI data acquisition

T1-weighted MR images were acquired prior to (Fig. 1A) and within 24 h after electrode implantation (Fig. 1B). Scanner type and scanning sequence were based on clinical indications and availability only, and thus varied between patients, including 1.5T and 3T field strengths.

MRI of implanted patients has been shown to be safe, with respect to possible movement and heating of electrodes, in a retrospective study of clinical observations (Davis et al., 1999) and a systematic experimental study (Carmichael et al., 2008). There have been no reports of adverse outcomes in over a thousand patients at our center implanted with stainless-steel subdural electrodes as a result of MRI.

Electrode localization technique

Pial surface reconstruction

Subject-specific pial surfaces were reconstructed based on the pre-implant MR image using the Freesurfer image analysis suite (http://surfer.nmr.mgh.harvard.edu). The reconstruction procedure is automated, and involves (1) segmentation of the white matter (Fischl et al., 2002, 2004), (2) tessellation of the gray/white matter boundary (Fischl et al., 2001), (3) inflation of the folded surface tessellation (Fischl et al., 1999), and (4) automatic correction of topological defects (Segonne et al., 2007). The resulting output is a set of coordinates comprising the triangulated pial surface of the subject. A smoothed surface that tightly wraps around the reconstructed pial surface (Fig. 1C) is also created (Schaer et al., 2008). Because grids and strips traverse the sulci, the smoothed pial surface devoid of any sulcal deflections was subsequently used for the automatic localization of the electrode arrays placed on cortical surface, while the anatomically correct pial surface was used in the final visualization (Dykstra et al., 2011; Hermes et al., 2010).

Co-registration of pre- and post-implant MR images

The post-implant MR image was co-registered with the pre-implant MR image using FLIRT (Jenkinson and Smith, 2001), as implemented in FSL (Smith et al., 2004; http://fsl.fmrib.ox.ac.uk/fsl/). This implementation uses the multi-start, multi-resolution global optimization process to find the six parameters of a rigid body transform using the correlation ratio (Roche et al., 1998) as the cost function.

Manual localization of a subset of electrodes

For each array, a subset of electrodes were localized manually using FSLView (Smith et al., 2004), in which users are presented with visuals on synchronized axial, coronal, and sagittal slices of the co-registered MR image (Fig. 1D).

For each grid, three electrodes must be manually localized as initial conditions for the automated localization of the remaining grid electrodes presented in the following section. It is most expedient to select three of the corner electrodes for manual localization, as they are least obscured by artifact. Alternatively, the user can manually localize just two corner grid electrodes diagonally opposing each other (Fig. 1E; blue dots). In this case, the coordinates of the third electrode are automatically approximated such that the three electrodes form a right triangle in a plane approximately tangent to the cortical surface. In our experience, manual localization of all three electrodes leads to a negligible difference in the algorithmically defined positions of the remaining electrode for grids placed on the lateral convexities of either hemisphere.

For strips and depth electrodes, which can be bent from their original linear trajectories, each electrode must be manually localized. Visual localization of individual electrodes on these single-row arrays is feasible because the artifacts, which occur in one dimension only, are minimally overlapping.

“Folding” of grids on the cortical surface

Our electrode-localization method is essentially the inverse of the gnomonic projection. Historically utilized by cartographers to create maps of the Earth, the gnomonic projection requires selection of a map plane and a center of projection, usually a tangent plane and the center of the spherical object, respectively. To project a point on the surface of the spherical object onto the map plane, a line is drawn through this point and the center of projection to find where it intersects the map plane.

Here the inverse is done, where grid electrodes on some map plane are back-projected onto the cortical surface with respect to some center of projection. In our case, the map plane is uniquely determined by the three grid electrodes localized as in Manual localization of a subset of electrodes, and is roughly tangent to the cortical surface. The remaining grid electrodes are interpolated on this plane using the known inter-electrode distance (Fig. 1E; black dots). The set of all such planar electrode coordinates is denoted G={g_i≡(g_x,i, g_y,i, g_z,i)}.

The center of projection cannot simply be the “center” of the cortex, as the cortical surface does not resemble a sphere. Locally, however, the cortical surface can in fact resemble a sphere, especially on the lateral convexities of either hemisphere. We therefore isolate a patch of the cortical surface directly underlying G, denoted B={b_i≡(b_x,i, b_y,i, b_z,i)}. An approximation is then made of its center of curvature c≡(c_x, c_y, c_z), which can be thought of as the center of the sphere from which B can be sliced. This approximate center of curvature is taken as the starting point of an iterative optimization process, the goal of which is to find the optimal center of projection that would allow back-projection of points in G with minimal deformation to the grid geometry. The termination criteria of the optimization, as shown later, must therefore be defined in terms of the coordinates of the grid electrodes back-projected onto the cortical surface, denoted I={i_i≡(i_x,i, i_y,i, i_z,i)}.

The starting point of the optimization process is found as follows. The abovementioned cortical surface patch B can be more precisely defined as the smallest subset of adjacent vertices comprising the triangulated, smoothed pial surface (see Pial surface reconstruction) whose two-dimensional projection onto the x–y plane covers the full rostral–caudal (y-axis) and superior–inferior (z-axis) extent of G. Its center of curvature c is the point equidistant to all of the surface vertices (b_x,1, b_y,1, b_z,1), ..., (b_x,n, b_y,n, b_z,n) comprising B. This relation ship can be expressed with the following system of n-1 equations:

$$\begin{array}{cc}\hfill & {\left(b_{x,1}-c_x\right)}^2+{\left(b_{y,1}-c_y\right)}^2+{\left(b_{z,1}-c_z\right)}^2\hfill \\ \hfill & ={\left(b_{x,2}-c_x\right)}^2+{\left(b_{y,2}-c_y\right)}^2+{\left(b_{z,2}-c_z\right)}^2\hfill \\ \hfill & {\left(b_{x,2}-c_x\right)}^2+{\left(b_{y,2}-c_y\right)}^2+{\left(b_{z,2}-c_z\right)}^2\hfill \\ \hfill & ={\left(b_{x,3}-c_x\right)}^2+{\left(b_{y,3}-c_y\right)}^2+{\left(b_{z,3}-c_z\right)}^2\hfill \\ \hfill & {\left(b_{x,n-1}-c_x\right)}^2+{\left(b_{y,n-1}-c_y\right)}^2+{\left(b_{z,n-1}-c_z\right)}^2\hfill \\ \hfill & ={\left(b_{x,n}-c_x\right)}^2+{\left(b_{y,n}-c_y\right)}^2+{\left(b_{z,n}-c_z\right)}^2...\hfill \end{array}$$

An exact solution c does not exist as B is not exactly a spherical patch. The above system is therefore converted into its equivalent matrix form, and the least squares solution c is found using QR decomposition:

$$2\left[\begin{array}{ccc}\hfill b_{x,1}-b_{x,2}\hfill & \hfill b_{y,1}-b_{y,2}\hfill & \hfill b_{z,1}-b_{z,2}\hfill \\ \hfill b_{x,2}-b_{x,3}\hfill & \hfill b_{y,2}-b_{y,3}\hfill & \hfill b_{z,2}-b_{z,3}\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill b_{x,n-1}-b_{x,n}\hfill & \hfill b_{y,n-1}-b_{y,n}\hfill & \hfill b_{z,n-1}-b_{z,n}\hfill \end{array}\right]\left[\begin{array}{c}\hfill c_x\hfill \\ \hfill c_y\hfill \\ \hfill c_z\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \left(b_{x,1}^2-b_{x,2}^2\right)+\left(b_{y,1}^2-b_{y,2}^2\right)+\left(b_{z,1}^2-b_{z,2}^2\right)\hfill \\ \hfill \left(b_{x,2}^2-b_{x,3}^2\right)+\left(b_{y,2}^2-b_{y,3}^2\right)+\left(b_{z,2}^2-b_{z,3}^2\right)\hfill \\ \hfill \cdots \hfill \\ \hfill \left(b_{x,n-1}^2-x_{x,n}^2\right)+\left(b_{y,n-1}^2-b_{y,n}^2\right)+\left(b_{z,n-1}^2-b_{z,n}^2\right)\hfill \end{array}\right]$$

In the neighborhood of the starting point c, there are an infinite number of points in 3D space that can serve as a center of projection. In other words, the search space of our optimization process is infinite, and must therefore be constrained in some manner. Based on empirical considerations, we chose to constrain the search space to points along the c–m axis, where m is the center of mass of G. Note that the c–m axis is roughly orthogonal to the map plane, on which G lies, and the cortical patch B.

Starting at c, the center of projection is iteratively shifted back and forth along the c–m axis. At each iteration, I is found by drawing lines connecting the current center of projection with each point g_i, and finding the corresponding point b_i closest to where this line intersects the cortical patch B (Fig. 1E; black-red rays). At each iteration, we also find a corresponding set of scalars {d}, which is the set of inter-electrode distances between unique pairs of nearest-neighbor electrodes in I. The geodesic distances between electrode pairs on the triangulated, smoothed cortical patch B is calculated using the fast marching algorithm (Bronstein et al., 2010; Kimmel and Sethian, 1998).

The iterative optimization is terminated when {d} satisfies the following termination criteria. They are expressed in terms of the two quantities we seek to minimize, namely the mean absolute difference of {d} and the known inter-electrode distance d̂, in addition to the standard deviation of {d}:

$$\begin{array}{cc}\hfill 1)& \overline{\mid \left\{d\right\}-\widehat{d}\mid }<{\mathrm{t}}_{\mathrm{mean}}\hfill \\ \hfill 2)& \sigma \left(\left\{d\right\}\right)<{\mathrm{t}}_{\mathrm{std}}\hfill \end{array}$$

The constants t_mean and t_std reflect the accuracy level set by the user depending on image quality and other factors that may vary between image sets. The set of points I at the final iteration represents the final coordinates of the grid electrodes on the cortical surface.

To summarize, our final set of points I is the result of the inverse gnomonic projection of all points in G onto the cortical surface with respect to an optimized center of projection that minimizes distortions to the grid's spatial configuration. The above method is referred to as “folding” of the grid over the cortical surface.

Co-registration to a standard template brain

The spatial coordinates of each electrode are transformed from the individual patient space into the standard space of the Montreal Neurologic Institute (MNI) template brain using the DARTEL algorithm (Ashburner, 2007), as implemented in SPM8 (Wellcome Department of Imaging Neuroscience, London, United Kingdom). The resulting electrode coordinates in standard space can be reported and visualized across patients on the MNI template brain to allow comparisons across imaging modalities.

Validation

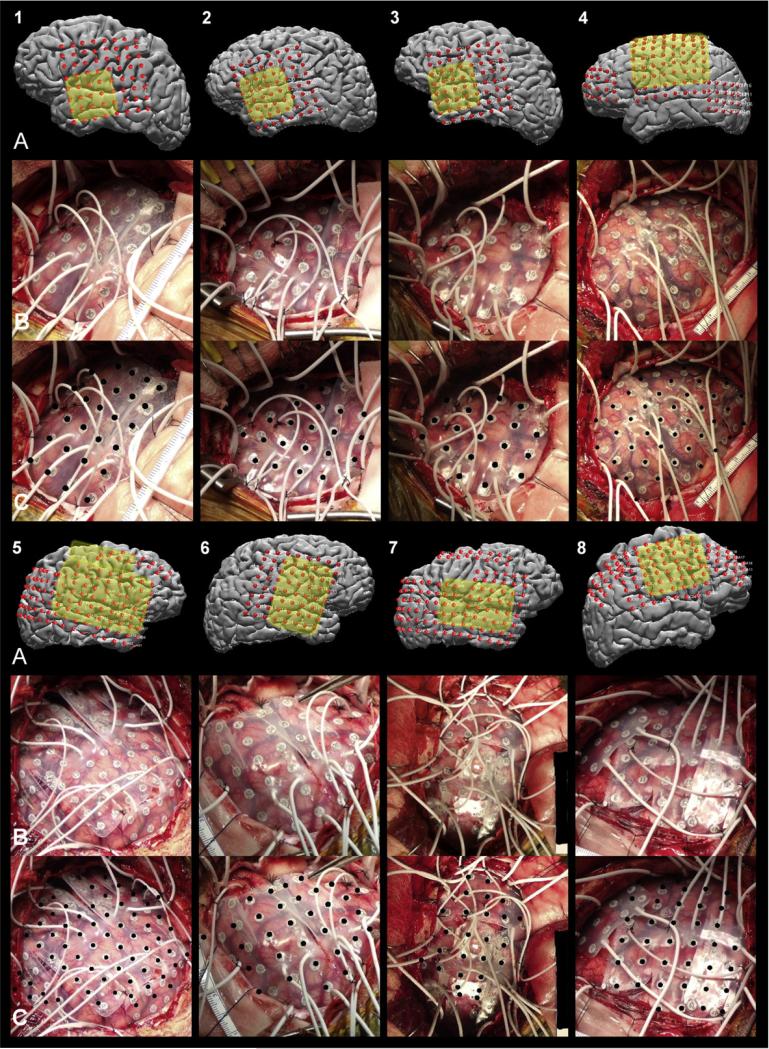
Digital photographs of the craniotomy, both before and after grid implantation, were taken using a consumer-grade camera placed 0.5 m from the exposed pial surface and oriented approximately orthogonal to it (Fig. 4B). These photographs were acquired from eight subjects, and were used as the presumptive “ground truth” to validate the presented localization algorithm for grid electrodes (Dalal et al., 2008; Dykstra et al., 2011; Hermes et al., 2010; Sebastiano et al., 2006; Tao et al., 2009). Individual electrode contacts that were not in their final positions at the time the photograph was acquired were not included in the validation. This includes one electrode in patient 2, one in patient 4, and two in patient 7 that were not yet adherent to the cortical surface. Also, eight of the electrodes visible in the photograph acquired from patient 8 were excluded because the most posteriorly-placed 4×5 grid had not yet been placed under the calvarium into its final position.

Fig. 4.

Localized grids in the 3D MRI space with the craniotomy regions highlighted in yellow (row A), raw intra-operative photographs (row B), and the same photographs with the localized grid electrodes, projected onto the photographs using the camera projection, shown as black dots (row C) for patients 1 through 8. Note that 8×8 grids were cut into 2x8 and 6×8 grids in patients 5 and 7.

Note that the set of coordinates I, algorithmically-localized as in “Folding” of grids on the cortical surface, are points within a 3D MR image space, whereas the coordinates of the “ground truth” electrodes, denoted N={n_i≡(n_x,i, n_y,i)}, are points within a 2D intra-operative photograph space. Ideally, either I or N should be transformed into the coordinate space of the other by some objective means to allow a direct comparison between I and N in the same coordinate space. With the exception of Hermes et al. (2010), previous studies have either not attempted such a transformation (Sebastiano et al., 2006; Tao et al., 2009), or manually transferred the 2D “ground truth” coordinates to the 3D MR image space using commonly-visible sulci and gyri as reference (Dalal et al., 2008; Dykstra et al., 2011).

In this study, each point in I is mapped to corresponding points in R={r_i≡(r_x,i, r_y,i)} in the photograph space using the camera projection. The camera projection is a general method of mapping a set of “world coordinates” in 3D space to the corresponding set of “image coordinates” in 2D space (Hartley and Zisserman, 2004), and is based on a simple linear model of a camera. It requires calculation of a 3×4 matrix P, referred to as the camera matrix, using all or a subset of corresponding coordinates in I and N as control points, a detailed explanation of which can be found in Dalal et al. (2008). Application of the camera matrix P to each coordinate in set I yields the set of projected coordinates R as follows:

$$P_{3\times 4}\left[\begin{array}{c}\hfill i_{x,i}\hfill \\ \hfill i_{y,i}\hfill \\ \hfill i_{z,i}\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill k{r}_{x,i}\hfill \\ \hfill k{r}_{y,i}\hfill \\ \hfill k\hfill \end{array}\right]$$

where the elements kr_x,i and kr_y,i of the output vector is divided by the third element, a constant k, to yield the projected coordinate r_i (Fig. 4C; black dots). This last step effectively removes perspective distortion associated with a finite camera.

If the presented localization technique is accurate, then each projected coordinate r_i should closely coincide with the corresponding coordinate n_i. The accuracy of the localization method can therefore be represented by the mean Euclidean distance between corresponding coordinates r_i and n_i within the 2D photograph space.

Electrode localization for validation purposes was performed with a common set of values for algorithm parameters d̂, t_mean, and t_std of 10, 0.1, and 1 mm, respectively. For each intra-operative photograph, the camera matrix P was found using all visible electrodes as control points. In order to assess accuracy for electrodes that are not used as control points, P was also calculated using only the ten electrodes at the center of the craniotomy as control points. In either case, the accuracy of the presented localization technique is then evaluated for all electrodes visible in the intra-operative photographs.

Results

Localization method output

Co-registration of the pre- and post-implant MR images can be performed in less than 10 min. Manual localization of a subset of the electrodes takes about 1 min for each electrode. In general, patients with several strips will have electrodes closely juxtaposed (≤10 mm) in an irregular manner, prolonging the time required for manual localization. Finally, automated localization of the remaining grid electrodes can be completed within tens of seconds. In total, localization of a grid for a given patient can be completed within 15 min after Freesurfer reconstruction of the brain surface. It is worth noting that Freesurfer reconstructions can take between 12 and 48 h with modern desktop computers. However, since the pre-implant MR image is used for the cortical reconstruction, this computational step is usually completed before the post-implant MR image is even available. Illustrations of the resulting localizations are shown for strips and grids in Fig. 2, and for depth electrodes in Fig. 3.

Fig. 2.

Localized electrodes in a patient with bilateral grids and multiple strips implanted. Accurate localization of all electrodes is possible even in cases with overlap in the coverage of the grids and strips.

Fig. 3.

Localized depth electrodes visualized in synchronized coronal, saggital, and axial planes, in addition to in 3D with the subject-specific pial surface rendered partially transparent.

Spatial accuracy

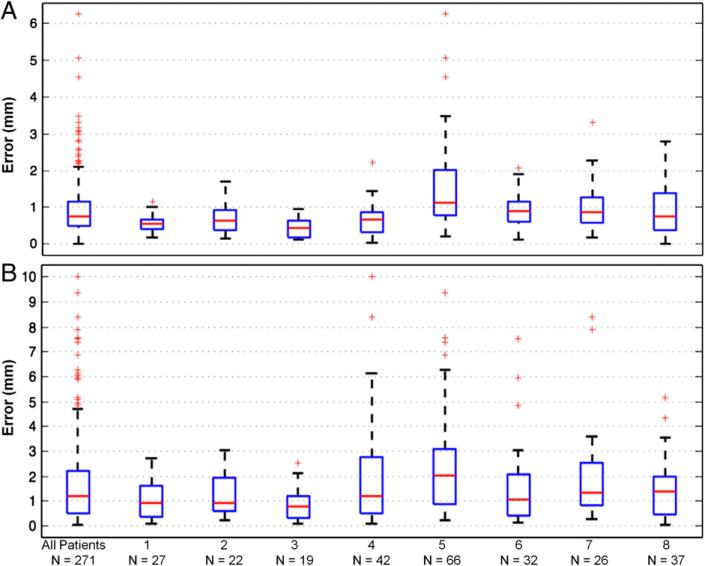
The spatial accuracy of the proposed method was validated using intra-operative photographs. When all visible electrodes were used as control points, the error for 271 electrodes across 8 patients was 0.96 mm±0.81 mm (mean±S.D.). Fig. 5A shows that the median error was 0.74 mm, 75% of the electrodes had an error <1.1 mm, and all electrodes had an error <2.1 mm. When only a subset of electrodes (n=10) roughly at the center of the craniotomy was used as control points, the resulting error for all 271 electrodes was 1.8 mm± 1.8 mm. Fig. 5B shows the median error was 1.2 mm, 75% had an error <2.2 mm, and all electrodes <4.7 mm. The median error in either case is less than the electrode diameter that is exposed to the brain surface (2.3 mm).

Fig. 5.

Validation results. Box plots are shown of the Euclidean distances between localized grid electrodes, projected onto the intra-operative photographs using the camera projection, and the corresponding “ground truth” electrodes visible in the photographs. These measures are shown for all electrodes (n=271) across eight patients, and separately for electrodes implanted in each patient. Validation was performed using either all visible electrodes (A) or a subset of electrodes (n=10) at the center of the craniotomy (B) as control points in the camera projection. Red lines indicate median distance, boxes 50% of the distribution, and dotted lines maximum and minimum distances. Outliers are indicated by red crosses, and are defined by points outside q₃±1.5 (q₃–q₁), where q₁ and q₃ are the 25th and 75th percentiles, respectively.

Discussion

This study describes a novel method to localize intracranial electrodes from pre- and post-implant MR images in spite of the magnetic susceptibility artifacts that surround and obscure the exact positions of the implanted electrodes. The procedure requires manual selection of two or three visually-discriminable electrodes on each grid. The remaining grid electrodes are automatically localized by back-projection onto the reconstructed brain surface of the individual patient while minimizing distortions to the grid geometry. Direct visualization of the localized electrodes with respect to the underlying gyral and sulcal anatomy is possible. The error in the positions of the localized electrodes was estimated to be 0.96 mm±0.81 mm. To the best of our knowledge, this value is lesser than or comparable to the reported error in previous studies (Table 1). The validation was performed on a total of 271 electrodes from sixteen grids implanted over eight patients, suggesting that the method presented in this study is robust with respect to diverse grid configurations on the cortical surfaces of several individuals.

Table 1.

Accuracy of published localization methods. Error reported in mean (mm) ± S.D. (mm) unless otherwise noted.

	Post-implant image set	Error	Validation technique
Morris et al. (2004)	CT	3.4	Stereotactic Navigational
	MRI	2.5	System
Hunter et al. (2005)	CT	0.91 ±0.41	CT
Sebastiano et al. (2006)	CT	2 ±0.12	Photograph
Dalal et al. (2008)	Photograph, X-ray, MRI	1.5±0.5	Photograph
Tao et al. (2009)	CT	3.1±1.3	Photograph
Hermes et al. (2010)	CT	2.6 (median)	Photograph
Dykstra et al. (2011)	CT	2.52, 3	Photograph

Many prior localization methods have used CT for post-implant imaging of the intracranial electrodes. Because CT has poor soft-tissue contrast and neuroanatomical structures can be difficult to discern, these localization methods necessitate co-registration of the post-implant CT image to a pre-implant MR image (Dykstra et al., 2011; Hermes et al., 2010; Morris et al., 2004; Sebastiano et al., 2006; Tao et al., 2009). CT-MRI co-registration, however, is known to be error prone (Maes et al., 1999; Thevenaz and Unser, 2000), most likely due to the intrinsic differences in the signal represented by each modality and the poor soft tissue contrast of CT.

In the context of electrode localization methods, the error introduced by CT-MRI co-registration is perhaps increased by the so-called “brain shift,” in which the craniotomy and implantation of electrodes/cables of non-zero volume induce soft tissue swelling, air invasion, leakage of CSF, and epi- or subdural hematomas, leading the brain to move away from the skull and assume an unpredictable shape (Miyagi et al., 2007; Roberts et al., 1998). This imposes a more stringent requirement on the quality of the image in areas that are not directly affected by the implanted arrays. This may account for the fact that CT-MRI co-registration is one significant source of error in the localized electrode positions (Dalal et al., 2008). The most recent methods based on post-implant CT have attempted to correct for the “brain shift” by projection of electrodes to the pre-implant surface (Dykstra et al., 2011; Hermes et al., 2010).

Use of post-implant MR images not only eliminates possible issues arising from inter-modal co-registration, but also benefits from the high soft tissue contrast of MRI. Mutual information (Viola and Wells, 1997), as a cost function for co-registration, has been widely used in localization methods based on post-implant CT because it does not require any assumptions about the nature of the signals involved, justifying inter-modal co-registration. However, any co-registration based on intensity-based cost functions such as mutual information will likely have error associated with the poor tissue contrast in CT as indistinguishable tissue in the CT image is mapped to highly-distinguishable tissue in the MR image. These considerations suggest that the slightly higher accuracy of the localization method presented in this study is in part due to the higher accuracy of the co-registration step. Morris et al. (2004) utilized either a post-implant CT or MR image in their localization method, and also found the accuracy to be improved using MR images, which the authors partly attributed to the co-registration step.

Intra-operative photographs used in the present validation represent the gold standard of electrode positions (Dalal et al., 2008; Dykstra et al., 2011; Hermes et al., 2010; Sebastiano et al., 2006; Tao et al., 2009). Due to the aforementioned “brain shift,” it is possible that the implanted electrodes were displaced between when the intra-operative photograph is acquired and when the post-implant MRI is completed. It is known that within 24 h of closure of the dura, the induced displacement of electrodes is limited primarily to compression, whose radial extent depends on inflation of the brain from reconstitution of the CSF and air absorption (Darcey and Roberts, 2010; Winkler et al., 2000). Such displacement does not pose a problem, however, as the relationship of the electrodes with the underlying gyri and sulci is preserved. Laviolette et al. (2011b) showed that clinically significant electrode movement with respect to the brain surface can occur throughout the remainder of the inpatient monitoring period, from factors such as violent seizures and reopening of the craniotomy. However, in this study the post-implant MRI was acquired within 24 h of closure of the dura, and hence any potential displacement between these two time points is likely not associated with changes in the electrode positions with respect to the underlying neuroanatomy.

The presented validation results are not definitive evidence that the accuracy of the current method is superior to that of other published methods. The surgical technique employed by the neurosurgeon, for example, alters the degree of “brain shift” following implantation, which influences the accuracy of the co-registration. At our institution, for instance, craniotomy size is limited by use of grids with perpendicular tail designs, CSF loss is minimized by closing the dura in a water-tight fashion after CSF loss is compensated for with physiologic solution, and dural grafts are routinely used to prevent decrease in the intracranial space due to dural shrinking, all of which are factors that can vary between institutions.

The method presented here is implemented entirely in MATLAB, and used in combination with the freely available software packages Freesurfer, SPM, and FSL. Normalization of the individual patient's brain to the MNI standard brain after localization allows comparisons across subjects and functional imaging modalities.

One limitation of the current method involves localization of grid electrodes when the geometry of the grid is altered. Grids can be bent or partially cut to achieve the desired coverage of areas that are not flat, such as the occipital lobe or the inter-hemispheric fissure. In these cases, prior knowledge of any such alterations of the grid geometry must be individually incorporated into the localization process. Grids that are completely bent between two adjacent rows can be considered as two smaller grids, and “folded” onto the cortical surface individually. For grids that are partially cut, the electrodes that are directly involved must be manually localized, while the unaffected portion of the grid can be treated as smaller grids and likewise “folded” onto the cortical surface. This is made possible by allowing the user to specify grid size prior to the “folding” step. Fig. 4 shows localization results for two patients in which 8×8 grids were completely cut into a 2×8 and a 6×8 grid.

An automated approach for the localization of strip and depth electrodes was not developed. This is because strips are often placed with some curvature, either deliberately to generate the desired coverage of the brain surface or inadvertently as a result of being pushed under the edge of the craniotomy. Depth electrode arrays may likewise incur bending during their stereotactic placement. However, as these are one-dimensional arrays, individual electrodes can be visually distinguished in spite of the susceptibility artifacts, and manual localization can easily be done. In fact, only strip electrodes that are connected to or in very close proximity to grid electrodes pose some difficulty.

In conclusion, we present a novel and validated method to accurately localize and visualize intracranial electrodes in relation to subject-specific gyral anatomy on MR images. This is the first method utilizing pre- and post-implant MRI to directly visualize electrodes, unobscured by susceptibility artifacts. This allows localization of each individual electrode on dense grids, even those with an inter-electrode spacing smaller than 10 mm. This study further validates the application of high-density iEEG recordings to answer questions in cognitive neuroscience and cortical neurophysiology. The presented method requires minimal user-end input, can be completed within a short period of time, and utilizes a radiation-free imaging modality, providing a strong incentive to incorporate quantitatively accurate electrode localization into clinical practice and research protocols.