Sources of dynamic variability in NF-κB signal transduction: A mechanistic model

Abstract

The transcription factor NF-κB (p65/p50) plays a central role in the coordination of cellular responses by activating the transcription of numerous target genes. The precise role of the dynamics of NF-κB signalling in regulating gene expression is still an open question. Here, we show that besides external stimulation intracellular parameters can influence the dynamics of NF-κB. By applying mathematical modelling and bifurcation analyses, we show that NF-κB is capable of exhibiting different types of dynamics in response to the same stimulus. We identified the total NF-κB concentration and the IκBα transcription rate constant as two critical parameters that modulate the dynamics and the fold change of NF-κB. Both parameters might vary as a result of cell-to-cell variability. The regulation of the IκBα transcription rate constant, e.g. by co-factors, provides the possibility of regulating the NF-κB dynamics by crosstalk.

Introduction

NF-κB signalling is involved in inflammatory responses, innate and adaptive immunity, cell proliferation and cell death. An aberrant activation is associated with a number of disease states, such as chronic inflammation, neurodegenerative diseases and cancer [1–5]. The NF-κB pathway is a complex signalling network consisting of two interconnected branches, the canonical (classical) branch and the non-canonical (alternative) branch [6–12]. Here, we study the dynamics of the canonical branch.

In mammalian cells, the NF-κB transcription factor family consists of five proteins: RelA (p65), RelB, cRel, p105/p50 (NF-κB1) and p100/p52 (NF-κB2). They can form different homo- and heterodimers that are able to induce or repress gene expression of specific target genes. One of the most abundant dimers is the p65/p50 heterodimer whose activity is tightly regulated by the canonical NF-κB branch [10]. In the absence of extracellular signals, p65/p50 is inactive in the cytoplasm, where it is sequestered by inhibitory κB (IκB) proteins including IκBα, IκBβ and IκBε [13]. Upon stimulation, e.g. by tumour necrosis factor α (TNFα), IκB kinases (IKKs) are activated [11], enabling the IKKs to phosphorylate IκB proteins. This modification leads to the subsequent degradation of the IκBs. Unbound p65/p50 translocates into the nucleus. This unbound, nuclear p65/p50 (referred to as active NF-κB), regulates target gene expression, including genes encoding IκB proteins [13,14]. IκBs bind NF-κB in the nucleus, leading to an export of the IκB/NF-κB-complexes to the cytoplasm, hence inhibiting the NF-κB signal establishing negative feedback loops [2,13–15]. In addition to the regulation via the feedbacks established by the IκB proteins, the activity of the canonical NF-κB pathway can be downregulated by the deubiquitinase A20 whose expression is also regulated by active NF-κB constituting another feedback mechanism [15,16].

The dynamical behaviour of NF-κB has been extensively investigated, experimentally [17–21] and via mathematical modelling [22,23], in the last decade. Tracing the DNA-binding activity of NF-κB by electrophoretic mobility shift assays (EMSA) in mouse embryonic fibroblast (MEF) cells revealed damped oscillations of active NF-κB on a cell population level upon TNFα stimulation [17,20,21]. To investigate the NF-κB dynamics in single cells, time-lapse fluorescence imaging was used to trace the translocation of NF-κB between nucleus and cytoplasm upon stimulation with TNFα [18,19,24–26]. Cells were transfected with vectors encoding the NF-κB subunit p65 tagged to a fluorescence protein (e.g. GFP, dsRed) to visualise the translocation of NF-κB [18]. These approaches revealed a cellular heterogeneity on the single cell level. Around 70% of the transfected cells were reported to show sustained oscillations in the ratio of nuclear to cytoplasmic NF-κB, while the rest showed a monotone increase or damped oscillations [18]. In a more refined setting, NF-κB dynamics was observed in single cells expressing fluorescence-labelled p65 which had been knocked into the native p65 locus [24]. Again, the majority of the cells (∼80%) was reported to show sustained oscillations, while around 20% of the cells showed a transient increase or damped oscillations.

It raises the question about the source of the observed variability in the dynamics of NF-κB in single cells. This is of particular interest since in the past few years several studies have indicated that cells are able to decode as well as encode cellular information by controlling the dynamics of signalling molecules [27–29]. In the case of the canonical NF-κB pathway, experiments have shown that different profiles and types of stimuli, e.g. TNFα or LPS stimulation, generate distinct NF-κB dynamics which then regulate gene expression differentially [19,30]. This indicates that the NF-κB dynamics may encode information. However, the underlying mechanisms remain unknown. In a recent publication [26], it was investigated which characteristic of the NF-κB time course correlates best with the downstream target gene expression. For this purpose, the translocation of fluorescent p65 in single cells after stimulation with TNFα was traced for 60 min and single molecule fluorescent in situ hybridization (smFISH) was performed in the same cells to measure the amount of specific NF-κB-dependent transcripts. The expression of these genes was reported to positively correlate with the fold change of fluorescent p65.

Here, we ask which intracellular components or processes of the pathway can contribute to the different dynamics of NF-κB upon stimulation and if those intracellular components or processes may also influence the fold change of NF-κB. This is done using a mathematical modelling approach. For the canonical NF-κB pathway a number of detailed models have been published that include the main biological processes [7,17,19–23,31–33]. The models are based on experimental data showing either damped or sustained oscillation upon pathway activation by TNFα. Generally, the possible dynamics of a model depend on its structure as well as on the chosen parameters. Here, we seek to determine the possible dynamics of a NF-κB model by varying all parameters individually. However, the detailed models of the NF-κB pathway that have been extensively validated by experimental data [7,17,19–21,31] are far too complex for such an analysis. Therefore, in a first step we derive a core model of the NF-κB pathway that preserves the dynamics of a detailed model. In a second step the core model is investigated by a bifurcation analysis enabling the determination of possible changes in the dynamics depending on individual parameters. In this way, certain conditions in the NF-κB system can be identified that cause the dynamical changes from monotone increase and damped oscillations to sustained oscillations and vice versa. We validate our findings with a second model to ensure that our findings are not a specific property of a certain model structure and parameter set, but a general feature of the signalling network. In a third step, we investigate whether and how the identified parameters affect the fold change of active NF-κB. Finally, we analyse the influence of input stimuli of different strength or duration on the dynamical behaviour of NF-κB.

Core model of the canonical NF-κB pathway

The starting point of the model reduction is the model published by Kearns et al. [20], hereafter referred to as the Kearns model. We aimed to derive a core model of that model, which maintains the dynamics of active NF-κB. Therefore, we first characterised the dynamics of the original model by three measures: its concentration in the (i) unstimulated and (ii) stimulated case as well as (iii) the characteristic time [34]. The first two measures (i, ii) characterise the steady states of the system, while the third measure (iii) characterises its dynamics. To investigate how the individual model parameters affect the three measures, the sensitivity coefficients were calculated for all three characterisations (Supplementary Figs. S1, S2 and S3) [35,36]. These characterise how strongly a measure changes given a change in an individual parameter. Subsequently, we eliminated all processes that have only a minor influence on the three measures (details are given in the Supplement).

The derived core model describes the dynamics of NF-κB, IκBα, IKK and their complexes in the cytoplasm and nucleus (scheme shown in Fig. 1A). It includes only the negative feedback via IκBα, which is known to be a main regulator in the canonical NF-κB pathway [17]. As in the Kearns model the stimulus is implemented by an increase in the total IKK concentration, which is then kept constant. The increase in IKK induces the degradation of IκBα by binding to the IκBα/NF-κB-complex. The release of NF-κB from its inhibitor IκBα results in the translocation of NF-κB to the nucleus, where it regulates the transcription of IκBα. IκBα can bind to NF-κB in the nucleus, inhibiting the transcription via the export of the complex to the cytoplasm. As in the original Kearns model, NF-κB is neither produced nor degraded.

Figure 1.

Core model. A: Scheme of the core model of NF-κB signalling derived from Kearns et al. [20] with 8 independent variables and 18 parameters including the total concentrations of NF-κB and IKK. The nucleus and cytoplasm are represented by a grey and white background, respectively. Single-headed arrows denote reactions taking place in the indicated direction. Double-headed arrows represent reversible reactions. Dashed lines depict activation reactions where no mass-flow occurs (transcription, translation). Components in the complex are separated by a slash. The stimulus is implemented by increasing the IKK concentration as a step-like function at t = 0 h. The total concentrations of NF-κB and IKK remain constant over time after stimulation. B: Comparisons of the dynamics of active NF-κB in the original model [20] (solid lines) and in the core model (dotted lines) with the original initial concentrations (black) as well as perturbations of the initial concentration of −20% (green) and +20% (blue) are shown. There are minor deviations in the early phase. The steady state concentrations differ less than 3%. C: Sensitivity coefficients of the core model for the stimulated steady state concentration of active NF-κB. For a detailed description of the parameters see Supplementary Table S1.

The parameters of the core model are taken from the Kearns model, for which they were partly determined experimentally and partly taken from the literature. We compared the temporal behaviour of active NF-κB upon stimulation of the core model with those of the Kearns model (Fig. 1B). The damped oscillations obtained by simulation of the core model are similar to the damped oscillations obtained by simulations of the Kearns model, not only for the originally published initial concentrations but also for perturbations of the initial concentrations by ±20%. For all three simulated conditions, there are minor deviations in the early phase. The steady state concentrations differ less than 3%. Taken together the core model reproduces the active NF-κB dynamics of the Kearns model very well, despite the fact that it includes less than one third of the parameters and less than half of the variables of the original Kearns model.

We next use the derived core model to study the most sensitive parameters with respect to the stimulated steady state of active NF-κB. The sensitivity analysis shows that the critical parameters are those that are directly involved in the synthesis and degradation of IκBα mRNA and protein (Fig. 1C). Additionally, small changes in the total NF-κB concentration strongly influence the stimulated steady state, while the total IKK concentration has only a minor influence. This can be explained by the different concentrations. The total NF-κB concentration is low and can therefore be a limiting factor for the signalling processes, while the total IKK concentration is high and the majority of IKK is freely available, hence making it insensitive to small perturbations.

Overall, we developed a medium-sized model that closely follows the dynamics of the detailed Kearns model [20]. For the derived model, the concentration of active NF-κB is strongly sensitive to small changes in the total NF-κB concentration and parameters associated with the IκBα feedback and degradation.

NF-κB dynamics is influenced by intracellular parameters

Having investigated the impact of the individual model parameters on the stimulated steady state concentration of NF-κB, we are now interested in their impact on the dynamical behaviour of the system. To systematically analyse the influence of individual parameters, we use the concept of bifurcation analyses. Here, we determine the transition between modes of dynamical behaviour, in particular, from stable steady states to sustained oscillations (stable limit cycle oscillations) for each parameter of the core model. A dynamical behaviour is stable if the system exhibits the same dynamical behaviour after perturbing one or more variables. It either always reaches the same steady state, or, in case of stable limit cycle oscillations, the period and amplitude remain the same after perturbation.

We performed a bifurcation analysis for every parameter, and determined the parameter ranges for which the core model shows stable limit cycle oscillations instead of a stable steady state. We varied every parameter separately and determined Hopf bifurcation points. At a Hopf bifurcation point the stable steady state becomes unstable, and limit cycle oscillations occur. The parameters for the rate constants were varied in a wide range from 0–500 min⁻¹ or min⁻¹ μM⁻¹. The parameters for the total NF-κB and IKK concentration were varied between 0–500 μM covering the published ranges for experimentally determined p65 abundances [37,38]. We found Hopf bifurcations for three parameter variations: (1) the total NF-κB concentration, (2) the NF-κB-dependent transcription rate constant of IκBα (tr4a) and (3) the association rate constant of IκBα with IKK (a1).

We first analysed the change in the total NF-κB concentration. Figure 2A shows the corresponding bifurcation diagram. With increasing concentrations of total NF-κB (Fig. 2A, from right to left), the dynamics of active NF-κB change from a monotone increase and damped oscillations to sustained oscillations at the Hopf bifurcation point (Fig. 2A, HB 1). For high concentrations of total NF-κB, active NF-κB shows sustained oscillations (Fig. 2A, B - I). Intermediate concentrations of total NF-κB lead to damped oscillations of active NF-κB resulting in a stable steady state (Fig. 2A, B - II). A monotone increase evolving in a stable steady state of active NF-κB can be observed for low concentrations of total NF-κB (Fig. 2A, B - III). The transition in the dynamics of active NF-κB upon variation of the total NF-κB concentration is shown in Fig. 2C. For low concentrations of total NF-κB, active NF-κB shows almost no response upon TNFα stimulation. For higher concentrations of total NF-κB, the dynamics of active NF-κB show sustained oscillations.

Figure 2.

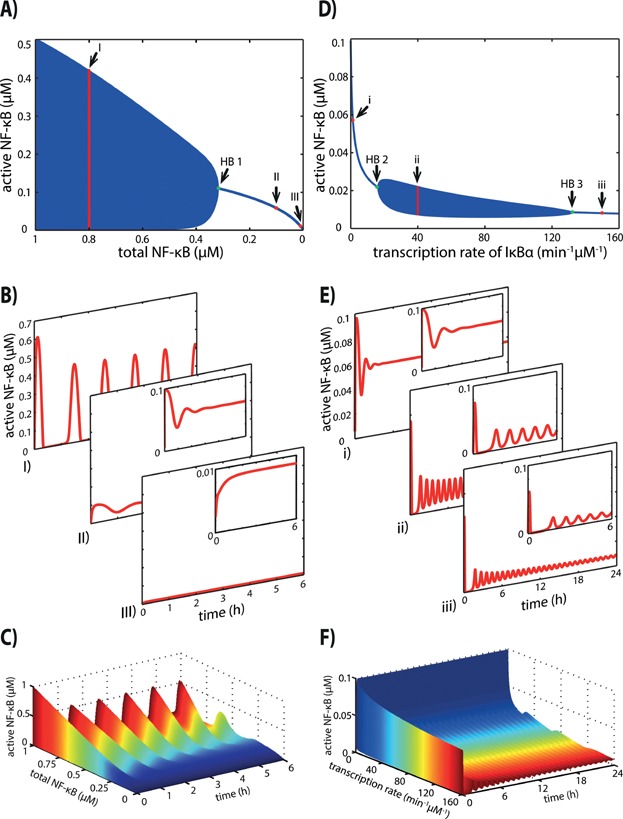
Bifurcation analysis of the core model. A: The bifurcation diagram shows the dynamical changes of active NF-κB upon variation of the total NF-κB concentration. For total NF-κB ranging from 0 to 0.3 μM each dot of the blue line represents the steady state concentration of active NF-κB for the corresponding parameter value. For each total NF-κB concentration above 0.3 μM, a vertical blue line represents the amplitude of the sustained oscillations of active NF-κB. The Hopf bifurcation point (green) is indicated as HB 1. I, II, III indicate the three examples of total NF-κB concentration at 0.8, 0.1 and 0.01 μM, respectively, for which the dynamical behaviour of active NF-κB is shown in Fig. 2B. B: I) Dynamical behaviour of active NF-κB with a total NF-κB concentration of 0.8 μM showing sustained oscillations. II) Dynamical behaviour of active NF-κB with a total NF-κB concentration of 0.1 μM showing damped oscillations and reaching stable steady state. III) Dynamical behaviour of active NF-κB with a total NF-κB concentration of 0.01 μM showing no oscillations, but increases monotonously reaching stable steady state. In each case the stimulus is given at t = 0 h. C: Change of dynamical behaviour of active NF-κB upon changing total NF-κB concentrations. For low concentrations of total NF-κB active NF-κB shows almost no response upon TNFα stimulation. With higher concentrations of total NF-κB, the concentration of active NF-κB reaches the maximal concentration with the first peak, followed by sustained oscillations. D: The bifurcation diagram shows the dynamical changes of active NF-κB upon variation of the transcription rate constant of IκBα. For very low and very high transcription rate constants of IκBα, active NF-κB reaches stable steady states, which are represented by blue dots for the corresponding parameter values forming a blue line. For intermediate transcription rate constants of IκBα (between 23.3 min⁻¹ μM⁻¹ and 86.7 min⁻¹ μM⁻¹) sustained oscillations of active NF-κB can be observed. The amplitudes of these oscillations are represented by the vertical blue lines. The Hopf bifurcation points (green) are indicated as HB 2 and HB 3. i, ii, iii indicate the three examples of the transcription rate constant at 1.386, 40 and 150 min⁻¹ μM⁻¹, respectively, for which the dynamical behaviour of active NF-κB is shown in Fig. 2E. E: i) Dynamics of active NF-κB with the published transcription rate constant of 1.386 min⁻¹ μM⁻¹ [20], showing damped oscillations reaching a stable steady state subsequently. ii) Dynamical behaviour of active NF-κB with an intermediate transcription rate constant of 40 min⁻¹μM⁻¹ showing sustained oscillations. iii) Dynamical behaviour of active NF-κB with a high transcription rate constant of 150 min⁻¹μM⁻¹ showing damped oscillations reaching a stable steady state subsequently. In each case the stimulus is applied at t = 0 h. F: Change of dynamical behaviour of active NF-κB upon changing the transcription rate constant of IκBα. For a low transcription rate constant active NF-κB simply increases in response to TNFα stimulation. For intermediate transcription rate constants, active NF-κB shows sustained oscillations. For high transcription rate constants active NF-κB shows damped oscillations.

The variation of the NF-κB-dependent transcription rate constant (tr4a) of IκBα leads to two Hopf bifurcations (Fig. 2D). When the transcription rate constant is low, the system shows damped oscillations (Fig. 2D, E - i). For median transcription rate constants, the system exhibits sustained oscillations (Fig. 2D, E - ii), and for high transcriptions rate constants it again shows damped oscillation evolving to a stable steady state (Fig. 2D, E - iii). The transition in the dynamics of active NF-κB upon variation of the NF-κB-dependent transcription rate constant of IκBα is shown in Fig. 2F. Note that the damping effect on the oscillations of active NF-κB is very weak for high transcription rate constants. Hence, the steady state is reached after a very long time. However, the canonical NF-κB pathway acts on a shorter timescale. On this timescale, the weakly damped oscillations observed for high transcription rate constants of IκBα may not be experimentally distinguishable from sustained oscillations. Therefore, there might only be a biologically relevant difference in the NF-κB dynamics between low and medium/high transcription rate constants of IκBα.

The association rate constant (a1) needs to be increased strongly (more than 30-fold) to lead to changes in the dynamics of active NF-κB. Since the biological variability in an association rate constant is likely much smaller, variations in this parameter have presumably no effect on the mode of dynamical behaviour of active NF-κB. Therefore, we will not investigate changes in this parameter further on.

Taken together, the modelling approach demonstrated that different modes of active NF-κB dynamics occur depending on the total NF-κB concentration and the NF-κB-dependent transcription rate constant of IκBα. In particular, monotone increase and damped oscillations or sustained oscillations are possible.

Verification of the model's insights

The analysed core model is derived from a model that exhibits damped oscillations for the published parameter set. We aimed to verify whether in an alternative model, parameters comparable to those identified in the core model would affect the NF-κB dynamics in a similar manner. For this investigation we chose the model published by Ashall et al. [19], hereafter referred to as the Ashall model. It was designed and parameterised to reproduce sustained oscillations. The structure of the Ashall model differs from that of the Kearns model. In particular, the activation of IKK is described in more detail and an additional transcriptional feedback mediated by A20 is included.

Interestingly, similar to the core model, simulations of the Ashall model also show changes in the dynamical behaviour of active NF-κB when varying either the total NF-κB concentration (Fig. 3A) or the NF-κB-dependent transcription rate constant of IκBα (Fig. 3B). The system already exhibits limit cycle oscillations when the originally published parameters are used. A decrease in the total NF-κB concentration leads to a damping of the oscillations, and the system reaches a stable steady state (Fig. 3A). Similar to the total NF-κB concentration, a decrease in the transcription rate constant of IκBα leads to a damping of the oscillations of active NF-κB (Fig. 3B). Additionally to the dynamical changes upon decreasing the transcription rate constant, the bifurcation analysis of the core model revealed that high transcription rate constants of IκBα result in a damping of the oscillations of active NF-κB. This effect also occurs for simulations of the Ashall model (simulations not shown).

Figure 3.

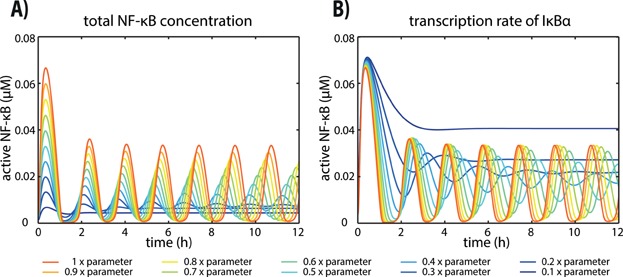
Simulations of the model published by Ashall et al. [19] A: Dynamical behaviour of active NF-κB with different total concentrations of NF-κB. The dynamics for the original parameter values show sustained oscillations (red). With decreasing total NF-κB concentrations damped, instead of sustained, oscillations occur (blue). B: Dynamical behaviour of active NF-κB with different transcription rate constants of IκBα⋅ The dynamics for the original parameter values show sustained oscillations (red). If the transcriptional rate constant of IκBα is decreased, damped, instead of sustained, oscillations occur (blue).

In the Ashall model, IKK does not bind to IκBα, but induces the phosphorylation of IκBα. Hence, there are no parameters in the Ashall model corresponding to the association rate constant in the core model (a1, Supplementary Table S1), for which a Hopf bifurcation point was determined.

Taken together, we verified our findings with an additional NF-κB model, which differs in structure and parameters from the core model. This indicates that our results are not restricted to the derived core model.

The total NF-κB concentration and the IκBα transcription rate constant affect the fold change of active NF-κB

So far, our investigations concentrate on the effects of parameter variation on the mode of dynamical behaviour of active NF-κB. Besides analyses that connect the dynamics of NF-κB with gene expression [19,24,30], it was reported that the gene expression correlates with the fold change, that is the maximal concentration of nuclear p65 (F_max) normalised by the initial concentration of nuclear p65 (F_i) [26]. Hence, we asked whether and how the total NF-κB concentration and the transcription rate constant of IκBα affect the fold change of active NF-κB.

Figure 4A illustrates the dependence of the fold change of active NF-κB on the two parameters. The fold change increases with an increase in either the total concentration of NF-κB or the transcription rate constant of IκBα or both. In addition, we trace the transition in the dynamical behaviour of active NF-κB with respect to both parameters (Fig. 4B). The Hopf bifurcation (blue line) divides the parameter space into areas with monotone increase or damped oscillations evolving to a steady state (white area) and sustained oscillations (blue area). It reveals that for very low and high total NF-κB concentrations the dynamical mode of active NF-κB does not depend on the transcription rate constant of IκBα. However, for intermediate concentrations of total NF-κB the dynamical mode of active NF-κB depends also on the transcription rate constant of IκBα and therefore transcriptional regulation may result in a change of the dynamics.

Figure 4.

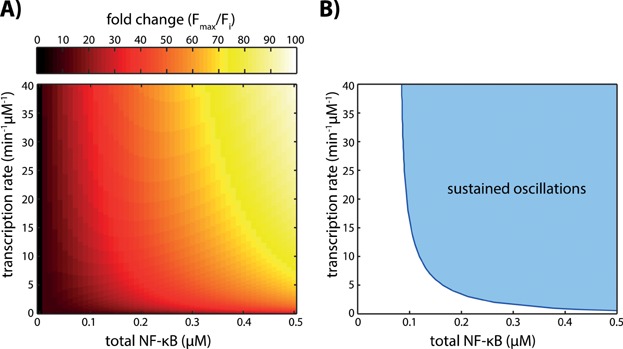
Influence of the total NF-κB concentration and the IκBα transcription rate constant on the fold change and the dynamical behaviour of active NF-κB in the core model. A: The fold change of active NF-κB defined in Lee et al. [26] increases with an increase in either one or both parameters. B: In the 2-parameter bifurcation diagram the curve traces the Hopf bifurcation points depending on the total NF-κB concentration and the transcription rate constant of IκBα. The curve divides the parameter space into two regions: sustained oscillations (light blue area) and monotone increase or damped oscillations evolving to a steady state (white area). For low concentration of total NF-κB the dynamics of active NF-κB always evolve to a stable steady state independent of the transcription rate constant of IκBα.

It therefore appears that variations in the two parameters, total NF-κB concentration or the transcription rate constant of IκBα, do not only lead to changes in the dynamical behaviour but also influence the fold change of active NF-κB (compare Fig. 4A and B). Please note that variations in the fold change can, but do not necessarily lead to changes in the dynamics of NF-κB.

The influence of intracellular parameters under different external stimuli

Our analyses emphasise the impact of the intracellular parameters, the total NF-κB concentration and the transcription rate constant of IκBα, on the NF-κB dynamics. So far we restricted the analysis to the application of a constant stimulus with a specific strength. Here, we aimed to analyse the impact of the two identified parameters on active NF-κB under different stimulation scenarios. For this purpose, we investigated the effects of different stimulation strengths as well as the effects of transient stimulations on the NF-κB dynamics.

In the core model, the strength of the stimulus is represented by the total IKK concentration. So far, all stimulations were performed by increasing the total IKK concentration from 0.00075 μM to 0.80075 μM at the time point of stimulation (see Supplementary Table S1). The increase in the total IKK level is now varied and we calculated a 2-parameter bifurcation diagram depending on the total IKK and either total NF-κB concentration (Fig. 5A) or the transcription rate constant of IκBα (Fig. 5B). The blue line traces the transition in the dynamics of active NF-κB and separates the dynamical response in a monotone increase or damped oscillations evolving to a steady state (white area) and sustained oscillations (blue area). For intermediate and high concentrations of total IKK the occurrence of damped or sustained oscillations depends on the total NF-κB level (Fig. 5A) or the transcription rate constant of IκBα (Fig. 5B). For small stimulation strengths (total IKK < 0.02 μM) no sustained oscillations exist (Fig. 5A, B).

Figure 5.

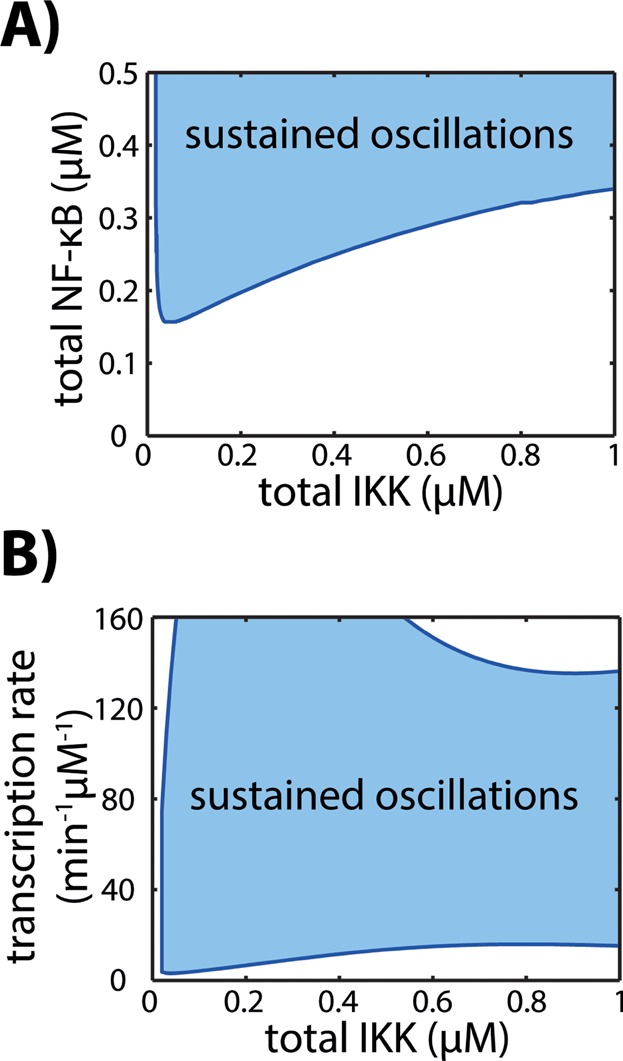
Impact of the stimulation strength on the NF-κB dynamics. The blue curves trace the Hopf bifurcation points depending on the total IKK concentration and either the total NF-κB concentration (A) or the transcription rate constant of IκBα (B). The curves divide the parameter space into regions, where the model dynamics comprises sustained oscillations (blue area) and monotone increase or damped oscillations evolving to a steady state (white area). For very small stimulation strengths (total IKK < 0.02 μM) only damped oscillations exist (A, B), while for higher concentrations of total IKK the occurrence of damped or sustained oscillations depends on the total NF-κB level (A) and on the transcription rate constant of IκBα (B).

In experiments not only the strength of the stimulation has been subject to variations but also the duration of the stimulation. To analyse the signal transduction of the system and its response to transient stimulation, we modified the model so that the total IKK concentration is not constant anymore but varies over time (for the model description see Supplement). To compare the results of the modified model with those of the core model we first analysed the response to a continuous stimulus (Fig. 6 left column). Similar to the core model (compare Fig. 2B), the modified model shows the different dynamics upon different concentrations of total NF-κB. For a transient stimulation of 60 min, the system shows generally a first peak independent of the total NF-κB concentration (Fig. 6 middle column). Only the deactivation time, that is the time required to reach the unstimulated steady state again, varies for different total concentrations of NF-κB. A transient stimulation of 80 min leads to differences in the dynamical response of active NF-κB (Fig. 6 right column). For low concentrations of total NF-κB a transient increase can be observed. For medium and high concentrations of NF-κB, the dynamics of active NF-κB show two peaks. Similar observations also hold for the transcription rate constant of IκBα (see Supplementary Fig. S5).

Figure 6.

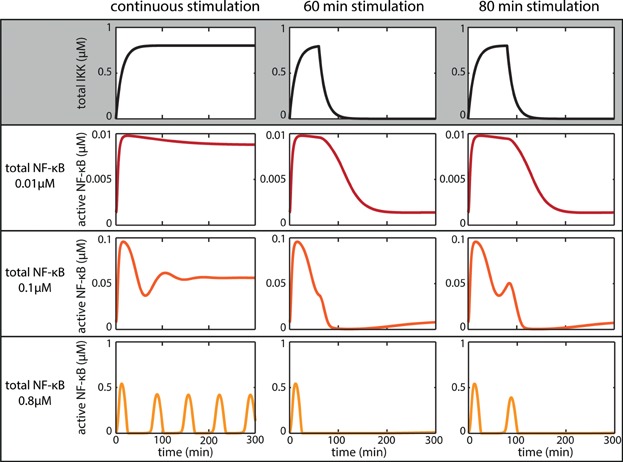
Response to transient external stimulation for various total NF-κB concentrations. The core model was modified to allow for a variable total IKK concentration (for model description see Supplement). The left column shows the dynamics of active NF-κB upon continuous stimulation for low (dark red), medium (red) and high (orange) total NF-κB concentrations. With increasing concentration of total NF-κB, the dynamics of active NF-κB change from a monotone increase and damped oscillations to sustained oscillations. The middle and right column show the dynamics of active NF-κB upon 60 and 80 min of stimulation for the different concentrations of total NF-κB, respectively.

For different stimulation strengths or durations, the response of active NF-κB is therefore dependent on the intracellular parameters, the total NF-κB concentration and the transcription rate constant of IκBα.

Dependence of the NF-κB dynamics on intracellular parameters and possible implications for gene expression

Here, we developed a core model that is in good accordance with the Kearns model (Fig. 1B) but contains only a small amount of variables and parameters. This core model can easily be used for further theoretical analyses and as a building block to investigate the interaction with other signalling pathways. While the core model comprises only the feedback via IκBα (Fig. 1A), the Kearns model includes the feedbacks via IκBα, IκBβ and IκBε [20]. It was reported that upon long-term stimulation, IκBε has a dampening effect on the NF-κB oscillation [20]. This raises the question whether sustained oscillations can also be observed in the detailed Kearns model or whether they would be dampened due to the inclusion of IκBε. Simulations of the Kearns model reveal that also in the detailed model the modes of the NF-κB dynamics change depending on the total concentration of NF-κB and the IκBα transcription rate constant (Supplementary Fig. S4). Besides, we validated the influence of these two parameters on the dynamical behaviour with an additional model, the Ashall model [19] revealing similar results (Fig. 3). Hence, our findings are not a specific property of a certain model structure and parameter set, but appear to be a more general feature of the signalling network.

One may ask if the two parameters, the total NF-κB concentration and the transcription rate constant of IκBα, are susceptible to variations, e.g. by cell-to-cell variability. Indeed, different levels of total p65 have been observed experimentally in HeLa cells [26] and in human A549 cells [39] stably expressing p65-GFP. The variability in the total NF-κB (p65) abundance might explain the detected difference in the NF-κB dynamics in single cells, where 70–80% of the cultured cells show sustained oscillation and 20–30% of the cells show a transient increase or damped oscillations upon stimulation with TNFα [18,24]. Furthermore, the total p65 abundance differs between different cell types. Published values range from 35,000 molecules per cell for murine fibroblasts [37] to 250,000 molecules per cell in murine macrophages [38]. The different levels of total NF-κB may therefore not only explain the differences in the NF-κB dynamics between cells within a population but also between different cell types. Variations could also be due to regulation by other signalling pathways. The NF-κB-dependent transcription rate constant of IκBα could be modulated by transcriptional co-factors of NF-κB. There are several co-factors that are able to either activate or repress NF-κB-driven transcription of IκBα, the best-known are SRC-1/2/3 or HDAC-1/2/3, respectively [40]. Taken together, this opens the possibility to regulate the NF-κB dynamics through crosstalk with other signalling pathways.

In general, the dynamics of transcription factors and key regulators of signalling pathways seem to play an important role in the encoding of signals. It has been analysed for a number of pathways [27–29], including the Msn2-mediated stress-response in yeast, the DNA damage induced p53 response and the growth factor driven MAPK signalling. The dynamics of the yeast transcription factor Msn2 can vary in amplitude, duration and/or pulse intervals in response to different stimuli. Those different dynamics have been shown to alter the downstream target gene expression [41]. The tumour suppressor p53 shows a single prolonged activation or repeated pulses, depending on the nature of DNA damage of either single or double strand breaks [42–45]. As a consequence different gene expression patterns are induced [46]. They either result in cell cycle arrest in the case of attenuated p53 pulses [47] or in apoptosis or induce senescence for prolonged activation of p53 [27,46]. The growth factor driven MAPK activation is one of the classical examples that show how the dynamics of a transcription factor activation regulate cell fate. While treatment with an NGF stimulus leads to a persistent ERK response and to differentiation in PC12 cells, pathway activation by an EGF stimulus leads to a transient ERK response and proliferation [48]. Under both stimulations, different target gene profiles have been found [49].

For the canonical NF-κB pathway various attempts have been made to externally perturb the dynamics of active NF-κB, with the objective of detecting changes in the gene expression. Application of different ligands resulting in distinct NF-κB dynamics was used to investigate the different gene expression profiles [30]. Cells treated with TNFα or LPS show mainly sustained oscillations or a single prolonged wave of active NF-κB, respectively. Those two stimuli result in different gene expression. This could result from the different signal transduction upstream of NF-κB or from different NF-κB dynamics. By varying pulses of TNFα stimulation, the frequency and amplitude of peaks of active NF-κB were varied, and differential gene expression was observed [19]. Such repeated peaks of active NF-κB are driven externally by the pulse frequency of TNFα stimulation, and might not be directly comparable with endogenous sustained oscillations of active NF-κB upon physiological TNFα stimulation. These examples show that the cellular response differs depending on the external stimulus.

We are only beginning to understand which signalling characteristics encode the target gene expression. Depending on the pathway, different features are discussed [27–29]. In the last years, the fold change was associated with the expression of specific target genes in MAPK and Wnt/β-catenin signalling [50,51]. For the canonical NF-κB branch, experimental findings indicate that the fold change of NF-κB (p65) correlates with the expression of the target genes encoding for IκBα, A20 and IL-8 [26]. Here we showed that the fold change of active NF-κB is influenced by the total NF-κB concentration and the transcription rate constant of IκBα (Fig. 4A), which are also the parameters affecting the dynamical mode of NF-κB (Fig. 4B).

Conclusion

In this study, we developed a core model of the canonical NF-κB pathway, which (i) reproduces the dynamics of the detailed Kearns model [20] and (ii) can be used to study the dynamical properties by a bifurcation analysis. We found two parameters that mainly determine the type of NF-κB dynamics: the total NF-κB concentration and the NF-κB-dependent transcription rate constant of IκBα.

High concentrations of total NF-κB cause sustained oscillations of active NF-κB upon stimulation with TNFα, while lower concentrations of total NF-κB result in a monotone increase or damped oscillations. Similar changes in the dynamical behaviour of active NF-κB can be observed by varying the NF-κB-dependent transcription rate constant of IκBα. For intermediate transcriptional rate constants, sustained oscillations of active NF-κB occur, whereas they do not occur for low and high transcription rate constants of IκBα.

The differences of active NF-κB dynamics in response to TNFα stimulation caused by different total NF-κB concentrations or NF-κB-dependent transcription rate constant of IκBα could be a result of cell-to-cell variability. In addition, the influence of the transcription rate constant of IκBα provides the possibility to regulate the NF-κB dynamics and gene expression profiles by crosstalk to other signalling pathways.

With our theoretical approach we determined important cellular parameters in the NF-κB signalling pathway that can modulate the dynamics of active NF-κB. We hypothesise that even though biological variations were reported especially for total cellular NF-κB [26,39], these two parameters are interesting targets for further analysis to study their influence on the NF-κB dynamics, its fold change and the regulation of its target gene expression.

Supporting Information

Additional supporting information may be found in the online version of this article at the publisher's web-site.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.