A probabilistic air segmentation and sparse regression method was developed for PET attenuation correction with a mean whole-brain PET error of 2.42% ± 1.0 by estimating continuous pseudo CT images from T1-weighted MR and atlas CT images.
Abstract
Purpose
To develop a positron emission tomography (PET) attenuation correction method for brain PET/magnetic resonance (MR) imaging by estimating pseudo computed tomographic (CT) images from T1-weighted MR and atlas CT images.
Materials and Methods
In this institutional review board–approved and HIPAA-compliant study, PET/MR/CT images were acquired in 20 subjects after obtaining written consent. A probabilistic air segmentation and sparse regression (PASSR) method was developed for pseudo CT estimation. Air segmentation was performed with assistance from a probabilistic air map. For nonair regions, the pseudo CT numbers were estimated via sparse regression by using atlas MR patches. The mean absolute percentage error (MAPE) on PET images was computed as the normalized mean absolute difference in PET signal intensity between a method and the reference standard continuous CT attenuation correction method. Friedman analysis of variance and Wilcoxon matched-pairs tests were performed for statistical comparison of MAPE between the PASSR method and Dixon segmentation, CT segmentation, and population averaged CT atlas (mean atlas) methods.
Results
The PASSR method yielded a mean MAPE ± standard deviation of 2.42% ± 1.0, 3.28% ± 0.93, and 2.16% ± 1.75, respectively, in the whole brain, gray matter, and white matter, which were significantly lower than the Dixon, CT segmentation, and mean atlas values (P < .01). Moreover, 68.0% ± 16.5, 85.8% ± 12.9, and 96.0% ± 2.5 of whole-brain volume had within ±2%, ±5%, and ±10% percentage error by using PASSR, respectively, which was significantly higher than other methods (P < .01).
Conclusion
PASSR outperformed the Dixon, CT segmentation, and mean atlas methods by reducing PET error owing to attenuation correction.
© RSNA, 2014
Introduction
An integrated positron emission tomography (PET)/magnetic resonance (MR) system that allows simultaneous acquisition of both MR and PET images offers a unique opportunity to study various diseases by taking advantage of the functional capabilities of PET and the anatomic imaging capabilities of MR imaging. MR imaging does not involve ionizing radiation and can be used safely in pediatric studies or for repeated longitudinal follow-up, while computed tomography (CT) increases the radiation dose delivered to patients. In addition, a simultaneous acquisition allows better spatial and temporal correlations of MR/PET measurements, which is invaluable for dynamic studies (1).
By using PET/CT systems, a piecewise bilinear rescaling of CT numbers (in Hounsfield units) of low-dose CT to PET of 511 keV yields an accurate attenuation map for PET imaging (2,3). This method, referred to as scaled CT, is considered the current standard of reference for PET attenuation correction (4,5). Unlike PET/CT, attenuation correction is challenging for PET/MR. A particular problem is differentiating bone from air; both have similar MR signal intensity but very different attenuation effects. Substituting the bone attenuation coefficient with that of air or soft tissue results in up to 20% underestimation of PET activity in the head (5–7).
A variety of MR-based attenuation correction approaches have been proposed by using either segmentation-based (5,7–12) or continuous CT prediction methods (13–15). Thus far, direct quantitative validations against the reference standard scaled CT attenuation correction have not yet been performed in a large number of subjects. In this study, we sought to develop a probabilistic air segmentation and sparse regression (PASSR) method for continuous pseudo CT estimation from T1-weighted MR images to improve air and bone separation and representation of local structure. The purpose of our study was to develop a PET attenuation correction method for brain PET/MR imaging by estimating pseudo CT images from T1-weighted MR and atlas CT images.
Materials and Methods
Avid Radiopharmaceuticals (a wholly owned subsidiary of Eli Lilly) provided the Florbetapir (Amyvid; Avid Radiopharmaceuticals, Philadelphia, Pa) tracers, and Siemens Medical Solutions provided financial support for this study. The authors had full control of the data and the information submitted for publication.
Image Acquisition
In this institutional review board–approved and Health Insurance Portability and Accountability Act–compliant study, PET/MR/CT images were acquired in 20 normal subjects (median age, 67.5 years; interquartile range, 63–70 years; 14 women) after obtaining written consent. This study started in May 2012 and ended in October 2013. The enrollment inclusion criteria included healthy adults (18 years and older) with no other injections of PET radiotracers within 24 hours. The exclusion criteria included contraindications to PET/MR or PET/CT (eg, electronic medical devices), known claustrophobia, pregnancy, or breastfeeding. Twenty subjects who underwent imaging by using both MR/PET and PET/CT were selected from a total of 115 enrolled subjects in this proof-of-concept study. This selection did not depend on the characteristics of the subject and was performed prior to any image analyses. None of the 20 subjects was excluded from analysis. Fluorine 18 (18F) florbetapir PET images and three-dimensional magnetization-prepared rapid gradient-echo T1-weighted MR images were acquired by using a hybrid MR/PET system (Biograph mMR; Siemens, Erlangen, Germany). Subjects were injected with 370 MBq of 18F florbetapir. The acquisition was started either 50 minutes after or immediately after tracer injection.
Structural T1-weighted images were acquired by using a magnetization-prepared rapid gradient-echo sequence (16) with the following imaging parameters: repetition time (msec)/echo time (msec)/inversion time (msec), 2300/2.95/900; flip angle, 9°; number of partitions, 176; field of view, 256 mm2; and voxel size of 1 × 1 × 1.2 mm3.
CT images were acquired by using a PET/CT system (Biograph 40 PET/CT; Siemens). CT images of the head were acquired by using 120 keV, 25 effective mAs with a voxel size of 0.59 × 0.59 × 3.0 mm3, and a matrix size of 512 × 512 × 74.
Head CT and MR/PET images were acquired within a mean ± standard deviation of 10.5 days ± 4 of each other, with no surgical procedures in between. All images were deidentified before image analysis.
Pseudo CT Derivation and Linear Attenuation Coefficient Maps
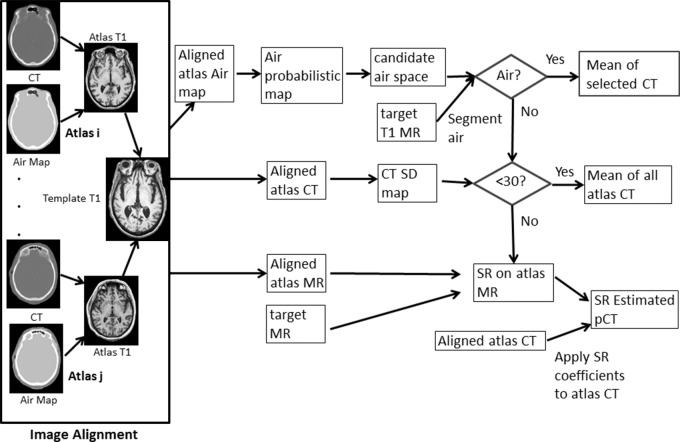
The major processing steps to derive pseudo CT by using the PASSR method include image registration, probabilistic air map–assisted air segmentation, and sparse regression (by Y.C., with 17 years of experience in image processing; a subject is outlined in Fig 1). We refer to the subject whose pseudo CT is to be estimated as the “template” and the remaining subjects as “atlases.” Twenty subjects were randomly divided into 10 pairs for tenfold cross-validation.
Figure 1:
Flowchart shows the PASSR pseudo CT estimation method. During image alignment, the atlas MR, CT, and air maps were all registered to target T1-weighted images. Candidate air space maps were then generated from the air probabilistic map. Air segmentation was performed by using target T1-weighted MR imaging within the candidate air space. For an air voxel, its pseudo CT number was the mean of the CT number (in Hounsfield units) of the selected atlas CT images in which this voxel was also labeled as air. For a nonair voxel, if the standard deviation of all atlas CT numbers was less than 30 HU, the mean of all atlas CT numbers was used as the estimated pseudo CT. Otherwise, a sparse regression for atlas MR was derived to represent the target MR images. For sparse regression, there were 7 × 7 × 7 × 18 = 6174 candidate patches included with a search window of 7 voxels in each dimension. A ”target” refers to a subject whose pseudo CT is to be estimated; “atlas” refers to other subjects.
CT images from each subject were classified (by Y.C.) into air, tissue, and bone with a k-means clustering algorithm. CT and air maps were rigidly aligned to the same subject’s T1-weighted MR images by using the linear registration toolkit in FSL (the FMRIB [Functional Magnetic Resonance Imaging of the Brain] Software Library of the University of Oxford; www.fmrib.ox.ac.uk/) (17). A nonlinear symmetric diffeomorphic registration algorithm was used (by Y.C.) for aligning atlas T1-weighted MR, CT, and air images to the template (18,19).
Separating air and bone on MR images is challenging because of the low MR signal intensity on T1-weighted images (Fig 2a). The air space in the frontal bone, sinuses, and petrous bone and part of the occipital bone all appeared dark (Fig 2b). Since air is only located within specific anatomic locations (marked air regions on Fig 2c), the probabilistic air maps were computed as the percentage of aligned CT atlases that labeled a voxel as air (Fig 2d). Regions with an air probability higher than 20% were considered the candidate air space, within which an air/tissue two-class segmentation was performed to identify the final air space by using a hidden Markov random field segmentation on T1-weighted MR images (20). For an air voxel, its pseudo CT number was the mean of the CT number (in Hounsfield units) of the selected atlas CT images on which this voxel was labeled as air.
Figure 2:
Representative images obtained in a 71-year-old man at two axial section locations (separated into upper and lower rows): A, T1-weighted anatomic MR image, B, rescaled T1-weighted MR image, C, aligned CT image, D, probabilistic air map, E, candidate air space, and, F, CT standard deviation maps. The color bar represents an air probability range of 20%–100% for D and a CT number standard deviation range of 30–300 HU for F.
For a voxel on the template MR images, a small neighborhood (eg, 5 × 5 × 5) centered around this voxel was referred to as the template patch (Pt in the following equation). In an aligned MR atlas, a same size neighborhood was referred to as an atlas MR patch (PMR). PMR values were selected from a vicinity (eg, 7 × 7 × 7) centered at the anatomically corresponding voxel in an atlas referred to as the “search window.” Sparse regression can be used to select the most relevant PMR value among all the atlas patches within the search window. We adopted an elastic net method to obtain a representation of local patch through the following minimizing equation (21,22):
where  is the vector representing the weighting coefficients used to combine all the atlas PMR values to approximate the template Pt, and λ1 and λ2 are the weights for sparse and ridge regression terms, respectively. In this study, the patch size, search window, and λ2 and λ1 were empirically chosen as 5 × 5 × 5, 7 × 7× 7, 0.01, and 0.0001, respectively. The obtained sparse coefficients were then applied for CT estimation via the following equation:
is the vector representing the weighting coefficients used to combine all the atlas PMR values to approximate the template Pt, and λ1 and λ2 are the weights for sparse and ridge regression terms, respectively. In this study, the patch size, search window, and λ2 and λ1 were empirically chosen as 5 × 5 × 5, 7 × 7× 7, 0.01, and 0.0001, respectively. The obtained sparse coefficients were then applied for CT estimation via the following equation:
where Pc is the estimated pseudo CT patch at the template location, while PCT represents all the CT patches from the atlas with the same size and location as the PMR patch. More details can be found in Figure 1.
Pseudo CT images were converted (by M.J., with 2 years of experience with MR and PET) into linear attenuation coefficient μ-maps by using the well-established bilinear model in the study of Bai et al (2) on a continuous scale. We compared the attenuation correction performance of PASSR with the Dixon method (vendor provided), CT segmentation, and a mean atlas method by using scaled CT as the standard of reference. With the Dixon method, three classes (air, fat, and soft tissue) were segmented, and linear attenuation coefficient values of 0, 0.085 cm−1, and 0.100 cm−1 were assigned, respectively. In the CT segmentation, a linear attenuation coefficient value of 0, 0.096 cm−1, and 0.151 cm−1 was given to air (CT number ≤ −200 HU), soft tissue (−200 HU ≤ CT number < 300 HU), and bone (300 HU ≤ CT number < 2000 HU), respectively (2,3,5). In the mean atlas, the mean of all the aligned atlas CT images were used as the pseudo CT template.
After uniformly dividing the whole computational domain into 16 regions, sparse regression was solved in parallel (by Y.C.) by using 16 2.8-GHz central processing units and 128-GB random access memory with one central processing unit for each domain. The total computational times for the mean atlas and PASSR methods were 2.5 hours and 10.5 hours, respectively.
PET Image Reconstruction and Accuracy Evaluation
The acquired PET list-mode raw data and the linear attenuation coefficient μ-maps generated with several different methods were reconstructed (by H.A., with 17 years of experience with MR and PET imaging) by using vendor-provided software (Siemens Medical Solutions). The ordered-subsets expectation maximization algorithm with three iterations and 21 subsets was used. The reconstructed images have a matrix size of 344 × 344 × 127 and a voxel size of 2.09 × 2.09 × 2.04 mm3. In addition to attenuation correction, random and scattered coincidences were also corrected by using this software.
A mean absolute relative percentage error (MAPE) was computed (by M.J.) for the reconstructed PET images with each attenuation correction method (PETtested in the following equation) versus the reference standard (PETCTscl, where “CTscl” represents “scaled CT”) as the absolute value of (PETtested − PETCTscl)/PETCTscl × 100 within whole brain, gray matter, and white matter. In addition, the percentage of voxels within 2%, 5%, and 10% MAPE and the 99th percentile MAPE were computed (by M.J.) to evaluate the error distribution. Friedman analysis of variance and Wilcoxon matched-pairs tests were performed for statistical comparisons (by H.A.) by using GraphPad Prism 5 (GraphPad Software, La Jolla, Calif).
Results
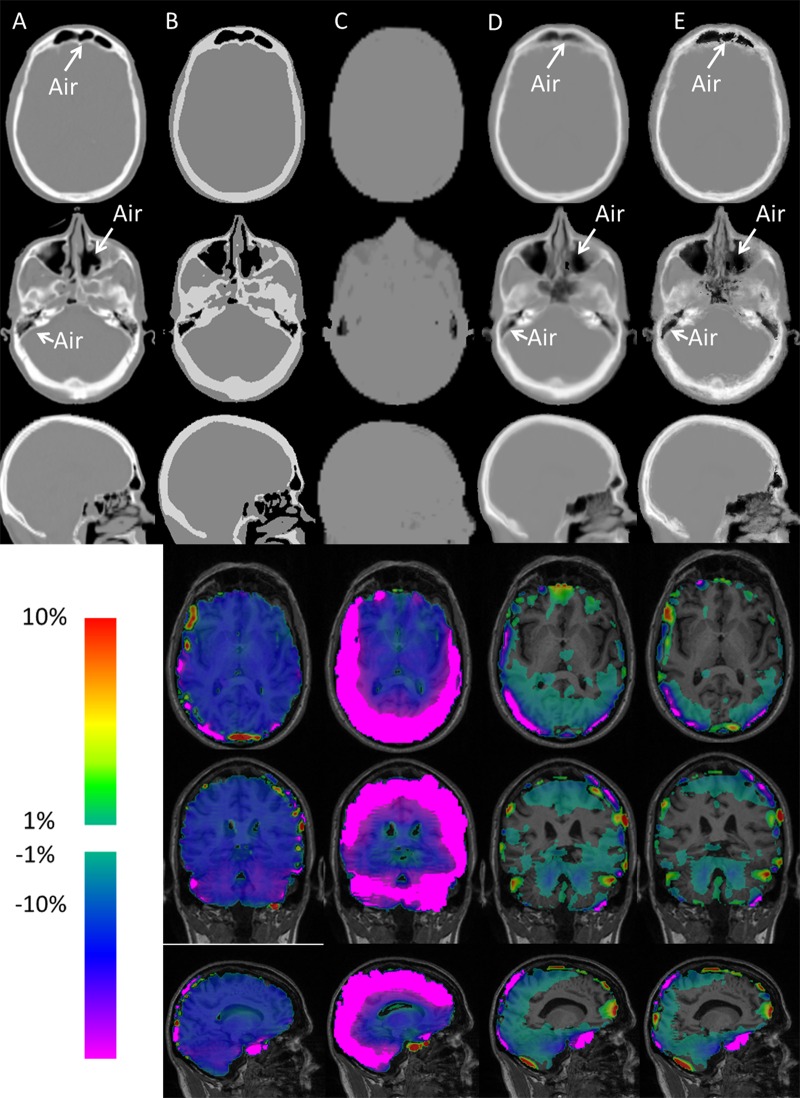
The segmented air space is demonstrated in Figure 2e. Attenuation maps with two axial locations and one midsagittal section location are demonstrated in Figure 3. The scaled CT (Fig 3a), mean atlas (Fig 3d), and PASSR (Fig 3e) methods provided attenuation maps on a continuous scale. The interface between air and bone appeared blurred with the mean atlas method, while PASSR provided a better delineation between air and bone even in the sinuses and petrous bone, as marked by arrows on Figure 3.
Figure 3:
Representative linear attenuation coefficient μ-maps obtained in the same 71-year-old man as in Figure 2 at the same two axial section locations (upper row and second row, respectively) and one midsagittal location (third row) by using, A, scaled CT, B, CT segmentation, C, Dixon method, D, mean atlas method, and, E, PASSR. Whole-brain percentage error maps were obtained at three orthogonal views (fourth, fifth, and sixth rows) by using μ-maps from, B, CT segmentation, C, Dixon method, D, mean atlas method, and, E, PASSR. Absolute percentage errors below 1% are not shown in color within the brain.
Representative percentage error maps within the brain are overlaid onto T1-weighted images in three orthogonal views (Fig 3). Owing to different proximities to skull and air, spatially varying attenuation correction errors were found across the brain. In general, the cortex region has larger attenuation correction errors than the deep brain (P < .0001).
Friedman analysis of variance was used to compare these four methods. Significant differences in MAPE were identified (Friedman analysis of variance, P < .0001) with PASSR, resulting in a significantly lower MAPE in the whole brain, gray matter, and white matter (Table 1). The percentage of voxels within ±2%, ±5%, and ±10% attenuation correction errors was also significantly different among these four methods (Friedman analysis of variance, P < .0001), with PASSR demonstrating significantly more voxels within each error range (Table 2). Moreover, the 99th percentile percentage error of PASSR (16.8% ± 4.5) was smaller than that of the Dixon method (50% ± 6.3, P < .0001), CT segmentation method (18.2% ± 4.2, P = .11), and mean atlas method (17.9% ± 4.5, P = .022).
Table 1.
Results of Wilcoxon Matched-Pairs Tests between PASSR and Dixon Method, CT Segmentation, or Mean Atlas Method regarding MAPE within the Whole Brain and Gray and White Matter

Note.—Unless indicated otherwise, data are means ± standard deviations.
Table 2.
Results of Wilcoxon Matched-Pairs Tests between PASSR and Dixon Method, CT Segmentation, or Mean Atlas Method regarding Percentage of Voxels within ±2%, ±5%, and ±10% Percentage Error

Note.—Unless indicated otherwise, data are means ± standard deviations.
Discussion
A probabilistic air segmentation and sparse regression method was developed for PET attenuation correction, with a mean whole-brain PET error of 2.42% ± 1.0 by estimating continuous pseudo CT images from T1-weighted MR and atlas CT images. The PASSR outperforms the Dixon, CT segmentation, and mean atlas methods by reducing MAPE and the spatial extent of attenuation correction errors. The accuracy improvement is more pronounced in the cortical gray matter regions (Fig 3, Table 1). The percentage error computed in this study is a measure of the percentage error in standardized uptake value (SUV) caused by attenuation correction. Of note, SUV is a PET semiquantitative measurement for normalized radioactivity in patients. It has been demonstrated that elevated carbon 11 Pittsburgh compound B and reduced 18F fluorodeoxyglucose SUV in brain cortical regions were found 15 and 10 years, respectively, before the estimated onset of Alzheimer disease (23). An accurate PET attenuation correction, particularly in the cortical region, is essential for early detection of the subtle relative SUV change in patients with Alzheimer disease. Moreover, a threshold of fluorodeoxyglucose SUV has often been used to define tumor on the pretreatment images, and 15%–20% change from pretreatment fluorodeoxyglucose SUV may indicate a treatment response (24). A PET attenuation correction method that provides low spatially varying errors will facilitate tumor staging and treatment response assessment.
In practical MR/PET imaging, only MR images are available for attenuation correction. CT segmentation provides the best possible outcome among all segmentation-based attenuation correction methods. When compared with scaled CT, CT segmentation has errors from an underrepresentation of a large range of CT number values (in Hounsfield units) by using a limited set of coefficients. Similar to a previous study (15), the performance of CT segmentation was inferior to that of the mean atlas and PASSR methods, suggesting PET attenuation correction benefits from a continuous-valued attenuation map.
On the basis of T1-weighted MR images alone, the PASSR method achieves PET attenuation correction accuracy on a par with reported methods by using multispectral MR data (8,15). Because T1-weighted MR images are acquired routinely in clinical imaging, PASSR does not necessitate the lengthening of total acquisition time by performing additional imaging for attenuation correction (25).
PASSR is distinctly different from two other pseudo CT–based methods published by Johansson et al (14) and Navalpakkam et al (15). PASSR emphasizes local information, while the two approaches are global methods that derive the whole-brain joint MR/CT distribution. We have demonstrated that sparse regression allows the selection of more closely correlated samples (22,26).
Major limitations of PASSR include the lengthy computation and challenges with abnormal anatomy. Use of more central processing units or a graphics processing unit for parallel computation and the inclusion of abnormal anatomy in the training samples may alleviate these problems.
In conclusion, we have developed a method for continuous pseudo CT estimation from probabilistic air map–assisted segmentation and sparse regression, which outperforms the Dixon, CT segmentation, and mean atlas methods in PET attenuation correction.
Advance in Knowledge
■ A probabilistic air segmentation and sparse regression (PASSR) method was developed for PET attenuation correction; by using the PASSR method, the mean ± standard deviation absolute percentage error on PET images for the whole brain, gray matter, and white matter were 2.42% ± 1.0, 3.28% ± 0.93, and 2.16% ± 1.75, respectively, which were significantly lower (P < .01) than their counterparts by using Dixon, CT segmentation, and mean atlas methods.
Implications for Patient Care
■ The proposed PASSR method provides PET attenuation correction without the need to acquire CT images, which simplifies imaging and reduces radiation exposure.
■ The PET accuracy achieved with this method allows for quantitative brain PET imaging by using PET/MR.
Received April 8, 2014; revision requested May 27; revision received August 7; accepted September 3; final version accepted October 17.
Supported by Siemens Medical Solutions, the Charles F. and Joanne Knight Alzheimer’s Research Initiative, and the Fred Simmons and Olga Mohan Barnes Jewish Hospital Foundation.
Funding: This research was supported by the National Institutes of Health (grants NIH 1R01 NS082561, NIH/NIA P50 AG05681, NIH/NIA P01AG026276, NIH/NIA P01AG003991, NIH 5P30NS048056, and NIH 2UL1TR000448).
Abbreviations:
- MAPE
- mean absolute percentage error
- PASSR
- probabilistic air segmentation and sparse regression
- SUV
- standardized uptake value
Disclosures of Conflicts of Interest: Y.C. disclosed no relevant relationships. M.J. Activities related to the present article: author received a grant from Siemens for salary support. Activities not related to the present article: disclosed no relevant relationships. Other relationships: disclosed no relevant relationships. Y.S. disclosed no relevant relationships. T.B. Activities related to the present article: author received a grant from Avid Radiopharmaceuticals, which provided the florbetapir doses and partially funded the scanning. Activities not related to the present article: author received a grant from the DIAN Therapeutic Unit and participated in a multicenter clinical trial with Avid Radiopharmaceuticals. Other relationships: disclosed no relevant relationships. B.G.R. disclosed no relevant relationships. Y.Z.L. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: author received a grant from Carestream. Other relationships: disclosed no relevant relationships. W.L. disclosed no relevant relationships. D.S. disclosed no relevant relationships. D.L. Activities related to the present article: author received a grant from Siemens Healthcare. Activities not related to the present article: disclosed no relevant relationships. Other relationships: disclosed no relevant relationships. H.A. Activities related to the present article: author received a grant from Siemens for trainee support and funding the costs of computation. Activities not related to the present article: disclosed no relevant relationships. Other relationships: disclosed no relevant relationships.
References
- 1.Catana C, Drzezga A, Heiss WD, Rosen BR. PET/MRI for neurologic applications. J Nucl Med 2012;53(12):1916–1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bai C, Shao L, Da Silva AJ, Zhao Z. A generalized model for the conversion from CT numbers to linear attenuation coefficients. IEEE Trans Nucl Sci 2003;50(5):1500–1515. [Google Scholar]
- 3.Kinahan PE, Hasegawa BH, Beyer T. X-ray–based attenuation correction for positron emission tomography/computed tomography scanners. Semin Nucl Med 2003;33(3):166–179. [DOI] [PubMed] [Google Scholar]
- 4.Kinahan PE, Townsend DW, Beyer T, Sashin D. Attenuation correction for a combined 3D PET/CT scanner. Med Phys 1998;25(10):2046–2053. [DOI] [PubMed] [Google Scholar]
- 5.Catana C, van der Kouwe A, Benner T, et al. Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. J Nucl Med 2010;51(9):1431–1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Samarin A, Burger C, Wollenweber SD, et al. PET/MR imaging of bone lesions—implications for PET quantification from imperfect attenuation correction. Eur J Nucl Med Mol Imaging 2012;39(7):1154–1160. [DOI] [PubMed] [Google Scholar]
- 7.Martinez-Möller A, Souvatzoglou M, Delso G, et al. Tissue classification as a potential approach for attenuation correction in whole-body PET/MRI: evaluation with PET/CT data. J Nucl Med 2009;50(4):520–526. [DOI] [PubMed] [Google Scholar]
- 8.Keereman V, Fierens Y, Broux T, De Deene Y, Lonneux M, Vandenberghe S. MRI-based attenuation correction for PET/MRI using ultrashort echo time sequences. J Nucl Med 2010;51(5):812–818. [DOI] [PubMed] [Google Scholar]
- 9.Fei B, Yang X, Nye JA, et al. MR∕PET quantification tools: registration, segmentation, classification, and MR-based attenuation correction. Med Phys 2012;39(10):6443–6454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Berker Y, Franke J, Salomon A, et al. MRI-based attenuation correction for hybrid PET/MRI systems: a 4-class tissue segmentation technique using a combined ultrashort-echo-time/Dixon MRI sequence. J Nucl Med 2012;53(5):796–804. [DOI] [PubMed] [Google Scholar]
- 11.Zaidi H, Montandon ML, Slosman DO. Magnetic resonance imaging–guided attenuation and scatter corrections in three-dimensional brain positron emission tomography. Med Phys 2003;30(5):937–948. [DOI] [PubMed] [Google Scholar]
- 12.Delso G, Carl M, Wiesinger F, et al. Anatomic evaluation of 3-dimensional ultrashort-echo-time bone maps for PET/MR attenuation correction. J Nucl Med 2014;55(5):780–785. [DOI] [PubMed] [Google Scholar]
- 13.Hofmann M, Steinke F, Scheel V, et al. MRI-based attenuation correction for PET/MRI: a novel approach combining pattern recognition and atlas registration. J Nucl Med 2008;49(11):1875–1883. [DOI] [PubMed] [Google Scholar]
- 14.Johansson A, Karlsson M, Nyholm T. CT substitute derived from MRI sequences with ultrashort echo time. Med Phys 2011;38(5):2708–2714. [DOI] [PubMed] [Google Scholar]
- 15.Navalpakkam BK, Braun H, Kuwert T, Quick HH. Magnetic resonance–based attenuation correction for PET/MR hybrid imaging using continuous valued attenuation maps. Invest Radiol 2013;48(5):323–332. [DOI] [PubMed] [Google Scholar]
- 16.Brant-Zawadzki M, Gillan GD, Nitz WRMP. MP RAGE: a three-dimensional, T1-weighted, gradient-echo sequence—initial experience in the brain. Radiology 1992;182(3):769–775. [DOI] [PubMed] [Google Scholar]
- 17.Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal 2001;5(2):143–156. [DOI] [PubMed] [Google Scholar]
- 18.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal 2008;12(1):26–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Klein A, Andersson J, Ardekani BA, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage 2009;46(3):786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging 2001;20(1):45–57. [DOI] [PubMed] [Google Scholar]
- 21.Tibshirani R. Regression shrinkage and selection via the lasso: a retrospective. J R Stat Soc Series B Stat Methodol 1996;73(3):273–282. [Google Scholar]
- 22.Zou H, Hastie T. Addendum: regularization and variable selection via the elastic net. J R Stat Soc Series B Stat Methodol 2005;67(5):768. [Google Scholar]
- 23.Benzinger TL, Blazey T, Jack CR, Jr, et al. Regional variability of imaging biomarkers in autosomal dominant Alzheimer’s disease. Proc Natl Acad Sci U S A 2013;110(47):E4502–E4509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Young H, Baum R, Cremerius U, et al. Measurement of clinical and subclinical tumour response using [18F]-fluorodeoxyglucose and positron emission tomography: review and 1999 EORTC recommendations. European Organization for Research and Treatment of Cancer (EORTC) PET Study Group. Eur J Cancer 1999;35(13):1773–1782. [DOI] [PubMed] [Google Scholar]
- 25.Zaidi H. Is MR-guided attenuation correction a viable option for dual-modality PET/MR imaging? Radiology 2007;244(3):639–642. [DOI] [PubMed] [Google Scholar]
- 26.Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y. Robust face recognition via sparse representation. IEEE Trans Pattern Anal Mach Intell 2009;31(2):210–227. [DOI] [PubMed] [Google Scholar]