Droplet confinement and leakage: Causes, underlying effects, and amelioration strategies

Abstract

The applicability of droplet-based microfluidic systems to many research fields stems from the fact that droplets are generally considered individual and self-contained reaction vessels. This study demonstrates that, more often than not, the integrity of droplets is not complete, and depends on a range of factors including surfactant type and concentration, the micro-channel surface, droplet storage conditions, and the flow rates used to form and process droplets. Herein, a model microfluidic device is used for droplet generation and storage to allow the comparative study of forty-four different oil/surfactant conditions. Assessment of droplet stability under these conditions suggests a diversity of different droplet failure modes. These failure modes have been classified into families depending on the underlying effect, with both numerical and qualitative models being used to describe the causative effect and to provide practical solutions for droplet failure amelioration in microfluidic systems.

I. INTRODUCTION

Droplet-based microfluidic technologies have wide-reaching applications in many fields including drug discovery,¹ high-throughput diagnostics,^2,3 single cell biology,⁴ and chemical synthesis.⁵ A major reason for such utility is due to the fact that droplets are considered to be miniaturised reaction vessels that can be addressed, manipulated, and interrogated individually and in high-throughput. The physical and engineering aspects of droplet control have been extensively studied,⁶ but phenomena that cause droplets to be “less than ideal” are commonly ignored with the self-contained nature of droplets being taken at face value. Nevertheless, if fouling or leakage does occur in droplet-based systems they undoubtedly have a disproportionally large effect on the integrity of the results generated due to the high surface-area-to-volume ratios characteristic of this scale.⁵

In most droplet-based microfluidic systems, surfactants are used to adjust interfacial tensions to allow stable and monodisperse droplet formation.⁷ Surfactants in such environments are normally long-chain molecules that contain hydrophilic and oleophilic regions and hence assemble at the water/oil interface, with the potential to stabilise droplets against aggregation and wetting.⁸ The most common surfactant used in microfluidic research (with fluorous continuous phases) is a polyethylene glycol-perfluoropolyether (PEG-PFPE) block copolymer⁹ known as “EA surfactant” or “RainDance.”^9,10 Considering the unarguable importance of surfactants in droplet-based microfluidic systems, there has been surprisingly little previous work assessing the choice of surfactant for a given application. Indeed, operating surfactant concentrations are generally based on qualitative or even historical reasoning. Similarly, polydimethylsiloxane (PDMS) based elastomers, typically Sylgard 184, are almost exclusively used as substrate materials for microfluidic devices,¹¹ despite the fact that PDMS possesses variable bulk and surface properties, which are strongly operator dependent. Even under ideal conditions, the surface properties of PDMS devices are less than perfectly suited for fluorous phases,¹² and hence often require surface derivatization.

The surface modification (or derivatization) of PDMS is normally achieved through the physical modification of the PDMS surface via plasma treatment or etching^13–15 or via the chemical derivatization of the surface with or without prior activation. Chemical modification relies on three primary methodologies for attaching a patent layer of alterant to the device surface: covalent attachment,^16–18 polymer grafting,^19–22 or matrix infiltration/chemisorption.²³ In each case, the longevity of the surface treatment is highly variable and depends strongly upon the usage conditions (see Sec. II E). Both physical modification and chemical derivatization of PDMS surfaces are complicated by a property of PDMS termed hydrophobic recovery.²⁴ During hydrophobic recovery, non-crosslinked silicone monomers perfuse from the interior of the material and permeate the elastomer surface.²⁵ This means that physical modification is ideally performed on a PDMS device that has had this residual monomer removed or at least depleted.²⁶ Significantly, the surfactant used in droplet-based microfluidic systems, as well as stabilising the droplet surface, also plays a role in the surface derivatization of the micro-channels. Anecdotally, it is well recognised that most PDMS microfluidic devices work better after being conditioned with the continuous phase (containing the surfactant) for a period of time. This is because surfactant molecules form lamellar structures, the simplest being monolayers, at phase boundaries²⁷ and these monolayers derivatise the PDMS surface. It is therefore unlikely that the continuous phase contacts the device wall at all in systems where surfactants are in use.

Given the dependence of droplet integrity on surfactant- and surface-related phenomena, the current work provides a systematic study of multiple oil/surfactant combinations, the droplet failure modes they cause, why such modes occur and what can be done to mitigate them. In this respect, a model PDMS microfluidic device was designed within which droplets could be subjected to common microfluidic operations (Figure S1 in supplementary material²⁸). These include formation at a T-junction,²⁹ mixing in a channel motif designed to induce chaotic advection,³⁰ droplet release into a larger chamber²⁹ (to assess the effect of close proximity and reduced flow rates), droplet exit from the chamber³¹ (to assess the effect of increased flow rates and compression), and storage in a large chamber containing a pillar network³² (to assess the effect of “open” versus “confined” storage conditions). Experiments were performed with a range of oils and surfactants that are commonly used in microfluidic systems, including FC-40, FC-770, mineral oil, silicone oil, decane, hexadecane, and soybean oil, and EA surfactant, Span 80 and ABIL EM 90, amongst others. For brevity, we have included the detailed experimental methodology in the supplementary material.²⁸ Using this system, twenty phenomena that may cause microfluidic droplets to behave differently to the spherical and self-contained reaction vessels described in literature^33,34 were observed. These failure modes are classified into families depending on the underlying effect (surface-, surfactant-, shear-, or phase-based) and both detailed descriptions and a numerical qualitative model are provided to explain the cause of each failure mode. These models are based on experimental data gathered from 44 combinations of commonly used oil/surfactant systems and their effect on droplet formation and droplet stability. Finally, possible amelioration strategies for experimental systems are discussed.

II. RESULTS AND DISCUSSION

Surfactants, as previously noted, play a significant role within droplet systems. As well as assembling at the liquid/solid boundary they also localise at the droplet/continuous phase interface.⁹ In both cases, although the actual structures formed may be more complex, they can be treated as self-assembled monolayers for simplicity since only the outer monolayer will be in contact with the oil phase. As such, for moderate surfactant concentrations, the surfactant monolayers in the system are populated according to Langmuir isotherm kinetics.³⁵ The ubiquity of surfactants within droplet microfluidic systems and the enormous effect they have on droplet behaviour means that almost any aberrant droplet behaviours must be considered in terms of surfactant distribution rather than solely in terms of physical characteristics such as shear flow.

Based on the experimental observations presented in Table S1 in the supplementary material,²⁸ we have built a model to help explain the theoretical basis of the droplet failure modes. Within the current work, the surfactant lamellar surface is treated as the determinant for surface properties, using a simple mathematical treatment throughout. Although surface modifications to make PDMS surfaces more fluorophilic will affect device performance, it is expected that they contribute far less to the stability of emulsions and the longevity of devices than the surfactant conditions do. This assumption also explains why it is standard practice to flow oil and surfactant through a device for several minutes before adding the water phase, as this allows the establishment of a patent surfactant adsorption layer which minimises wetting. Accordingly, only the surface modification of PDMS by surfactant molecules is assessed in our model.

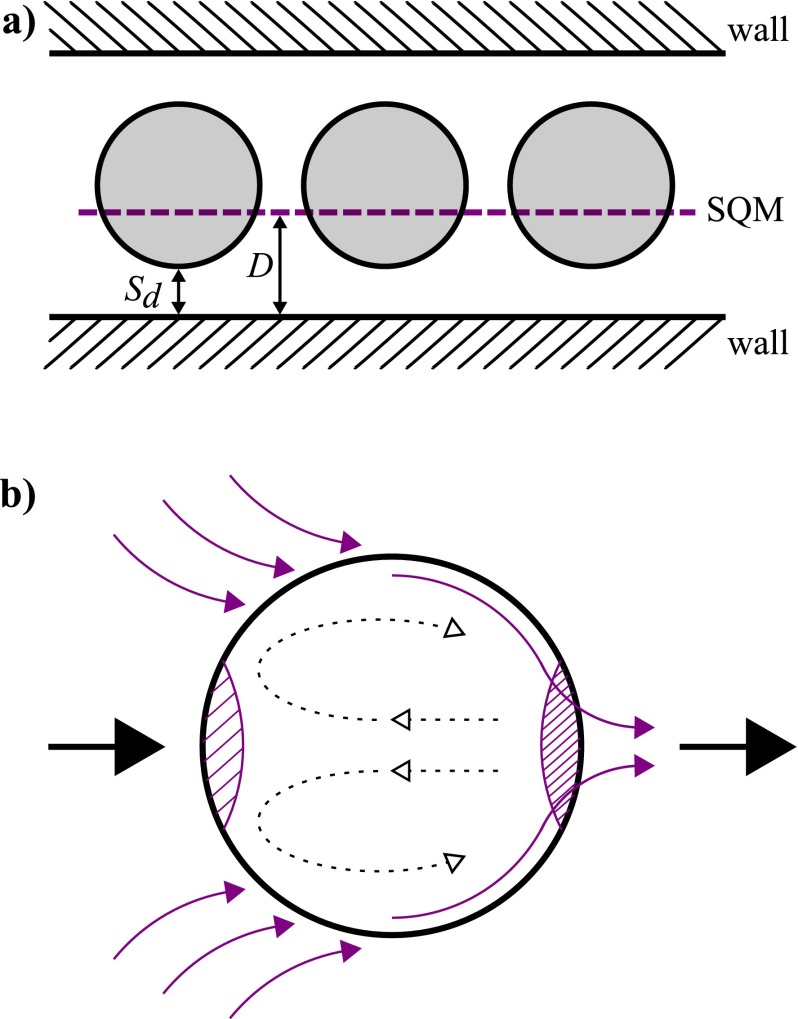
The Langmuir adsorption model³⁶ treats available surface sites as concentrations and is used in microfluidic systems, where surface-area-to-volume-ratios are appreciable.³⁷ To create the model, a typical microfluidic droplet system, where surfactant is delivered in the oil phase, is defined as an equilibrium between three parts: the wall surface, the oil, and a synthetic quorum membrane surface, SQM (Figure 1(a)). The synthetic quorum membrane is a notional single surface that corrects for the fact that the droplets represent a fluctuating surface of differing surface area. Instead of treating the droplets as such, they are simply treated as a planar surface at a set average distance from the wall surface. For many calculations based on our model this distance is irrelevant, but it must be assumed that the distance is not large enough to prevent diffusive equilibrium between the SQM and the wall surface. As such, the area and separation values of this layer depend on the droplet size and frequency, and on the inter-droplet spacing. Therefore, if the microfluidic system consists of small droplets that are far apart, they will have less impact on the surfactant concentration and hence the membrane will be smaller. Experimentally, this means that the droplets have less effect on the surfactant coverage of the wall and therefore the device will have a longer usable lifetime.

FIG. 1.

(a) Graphical representation of the synthetic quorum membrane (SQM, purple dotted line). Aqueous droplets (shaded grey) in a channel move past immobile walls (hashed sections) and their surface area and separation varies as a function of time. To simplify this system, droplets are treated as a membrane, in the same way as the wall. This membrane has an area A_d and is at a mean distance from the wall, D, which depends on the separation of the droplet from the wall, S_d, through the equation $D=\sqrt{\Sigma S_d^2}$. The geometric mean is used to calculate D due to the sinusoidal input associated with droplets moving past the wall surface. D must be a value such that the Fourier number is higher than 2 to allow equilibrium. (b) Surfactant effects seen in droplets due to diffusion and advection (in purple), with hashed sections showing areas of low and high surfactant concentration at the front and back of the droplet respectively (this can also be seen experimentally in analogous systems where there is an increased product concentration at the back of droplets⁶⁴). The relative movement of the oil past the droplet is shown by the big black arrows (from left to right) and internal droplet flow recirculation effects are shown by dashed arrows.

Mathematically, the surfactant distribution in the device can be described by defining the total surfactant burden of the system, N_tot, as a sum of the wall monolayer burden, N_w, the droplet monolayer burden, N_d, and the oil burden, N_o. This sum must be equal to the amount of surfactant that enters the system, which is the product of the initial concentration of surfactant in the oil, C, and the oil fraction of developed flow, $\theta$, multiplied by the total device volume, V (Eq. (1)). The adjustment for oil fraction is necessary because, even assuming that no surfactant molecules adsorb on the surface of aqueous droplets, since the surfactant is delivered in the oil phase, the presence of droplets lowers the surfactant content of the device

$$N_{\mathit{t}\mathit{o}\mathit{t}}=N_w+N_d+N_o=C\theta V.$$ (1)

We then apply the Langmuir model (Eq. (2)), where K is the distribution coefficient for the system and C₁ is the equilibrium concentration of surfactant in the oil phase, and describe the maximum space available for surfactant packing on the surface in question (for a particular surfactant-device material pairing) using Eq. (3), where k is the surface-adjusted distribution coefficient and A is the surface area. Assuming the oil phase is at equilibrium, the overall model (Eq. (4)) shows that the surfactant is distributed between the device surface and the droplet according to the ratio of distribution coefficients, K_d/K_w (subscript w throughout indicates wall and d indicates droplet), and that the amount of surfactant coverage of the device wall varies strongly according to the oil fraction and the ratio of the distribution constants

$$N=N_{\mathit{m}\mathit{a}\mathit{x}}\frac{K{C}_1}{1+K{C}_1},$$ (2)

$$N_{\mathit{m}\mathit{a}\mathit{x}}=kA,$$ (3)

$$C\theta V=\frac{k_w{A}_w{K}_w{C}_1}{1+K_w{C}_1}+\frac{k_d{A}_d{K}_d{C}_1}{1+K_d{C}_1}+C_1\theta V.$$ (4)

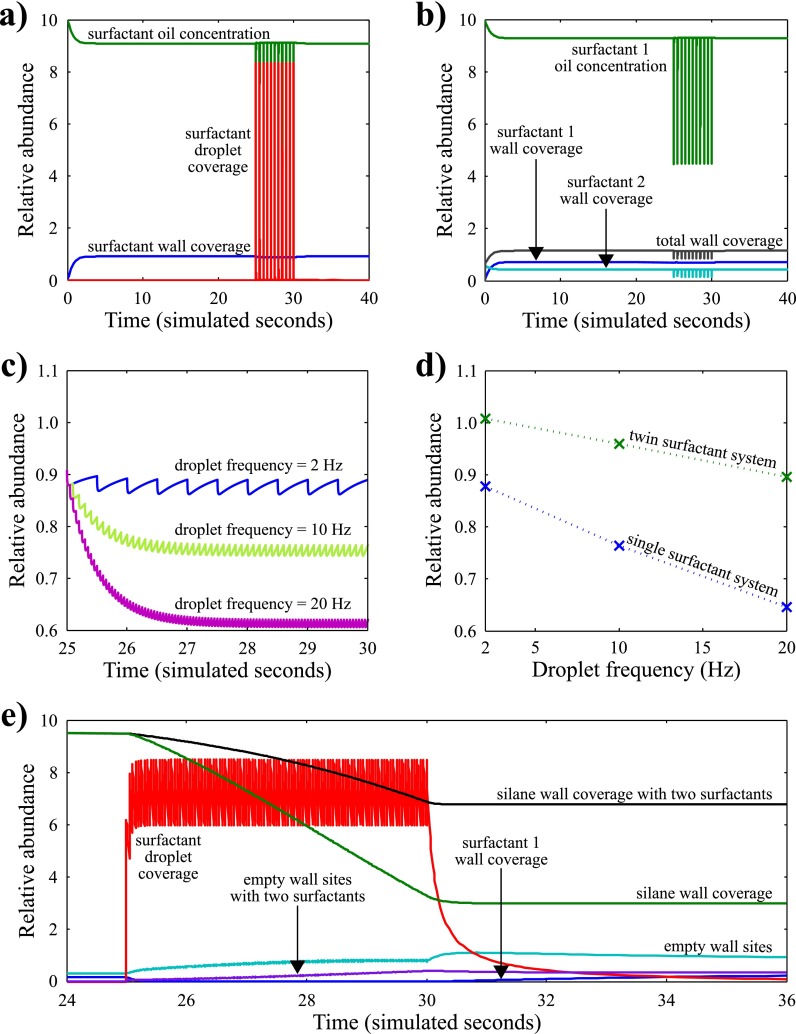
Based on the above, MATLAB SimBiology (MathWorks, version R2011a) was used to develop a model of the surfactant distribution within a microfluidic device assuming a Langmuir isotherm kinetic model for the coverage of available wall sites with surfactant. The surfactant, which is assumed to be insoluble in water, is given a distribution coefficient value for its equilibrium between the wall surface and the oil phase (K_w), and another for the equilibrium between the droplet surface and the oil phase (K_d). Droplets were simulated by consecutive dosing of water into the system against a pre-determined constant water drain to simulate bulk flow for systems with both one and two surfactants. The ratio of K_d to K_w for the surfactant was set at 1000 to mimic the known preference for EA surfactant to stabilise droplets.³⁸ This model is applicable to any system where K_d is larger that K_w. A second surfactant was also introduced into the model at 10% abundance compared to the first surfactant, with a distribution coefficient ratio of 0.01. This was used to show the effect of introducing a surfactant specifically to coat the walls of the device.

The effect that droplets have on surfactant abundance in the microfluidic system can be seen in Figure 2(a). At zero time, the surfactant concentration at the wall is zero because it is all in the oil phase. This quickly equilibrates so that there is a surfactant layer on the wall surface. At time equals 25 s, droplets are inserted into the system, draining the surfactant from the oil and, to a lesser extent, from the wall. Figure 2(b) shows how adding a second surfactant with a higher affinity to the wall creates a more stable system upon droplet insertion. Figure 2(c) shows how the wall surfactant coverage varies with the frequency of the inserted droplets. This clearly demonstrates that using lower droplet frequencies causes better wall coverage, as predicted by our Langmuir model. This graph also provides numerical evidence that the SQM is a valid approximation for the droplets within our system, because at each frequency the relative abundance settles at a mean value that corresponds to the value of the SQM. Further validation for the model was obtained experimentally by making droplets in a PDMS microfluidic device and running the device until a failure mode (in this case dripping mode, see Sec. II C) was observed. Briefly, the dripping failure mode occurs when, instead of droplet formation occurring due to shear forces at the droplet formation geometry, the incoming water phase wets the channel and droplets are formed at the end of the wetted section. The failure mode was quantified by measuring the extent of the wetted surface downstream of the T-junction and was plotted against the water fraction as calculated by the ratio of the droplet length to the length of oil. These data show that, as predicted by our model, at higher water fractions, more wetting occurs (see the supplementary material²⁸ for further details). Figure 2(d) shows that the mean values for wall surfactant coverage are markedly higher when using two-surfactant systems, suggesting that this is a valid method for protecting wall surfactant coverage. In summary, this simulation clearly shows that each droplet in a microfluidic channel results in a loss of surfactant wall coverage on its advent, followed by a recovery of the oil surfactant concentration on its departure and then by recovery of wall surfactant coverage. The numerical model also shows that different droplet frequencies result in different levels of surfactant depletion. This periodic fluctuation is complex, but stabilises at a consistent mean value after a short induction time, strongly suggesting that the SQM approach is justified numerically.

FIG. 2.

Graphs showing the effect that droplets have on the surfactant abundance on the wall, in the oil, and on the droplet with (a) one surfactant and (b) two surfactants, where the second surfactant specifically coats the device wall. (c) Effect of droplet frequency on the relative wall surfactant coverage. (d) Statistical mean of surfactant wall coverage at different droplet frequencies for systems with one and two surfactants. (e) Effect of adding a silane to functionalise the device wall surface. Droplets, at a frequency of 10 Hz, are added to the system at t = 25 s. Prior to this, the silane coverage of the wall is 95%. The addition of droplets causes the silane wall coverage to decrease to approximately 30%. Adding a second surfactant with an affinity for the wall ameliorates this effect to a certain extent. Relative abundance is the ratio of surfactant present on the wall surface compared to the theoretical maximum surface sites available for surfactant packing. Relative abundance is the equivalent of concentration.

Our and other studies of surfactant distribution^39,40 show that the kinetics of surfactant equilibrium on a surface dictate three distinct temporal regimes for the droplet interface. In the primary, or denuded, regime, such as when the droplet is first formed, the droplet surface is largely bare of surfactant. In the secondary or transitionary regime, the droplet surface is in the process of establishing an equilibrial surfactant concentration and therefore coverage varies strongly over time but is overall too low to form a monolayer. In the tertiary, or equilibrial, regime, the droplet surface is ornamented with an equilibrial coverage of surfactant, which is approximately a monolayer. Most of our discussion is predicated on the droplets being in the tertiary regime. This assumption is validated by tensiometric and other data³⁹ suggesting that droplet stabilisation occurs at or below the timescale of typical droplet formation. It should be noted that the SQM approach used in our model is time averaged and therefore its predictions can be disturbed by rapid morphological changes. Any rapid deformation that induces a change in droplet surface area also has the potential to produce local instabilities on the droplet surface resulting from insufficient surfactant coverage. The relaxation time for surfactant coverage recovery has been estimated as between 1 and 50 ms.³⁹ Therefore, it is reasonable that any droplet interaction occurring below 50 ms has the potential to destabilise the droplets in a way not predicted by the SQM, whereas interactions that take over 50 ms to occur are predicted by our model. Experimentally, this means that droplet formation and processing rates between 10 and 300 Hz fall within a regime where stabilisation at droplet formation occurs rapidly and droplet interactions fall outside the stabilisation time scale (tertiary/equilibrial regime).

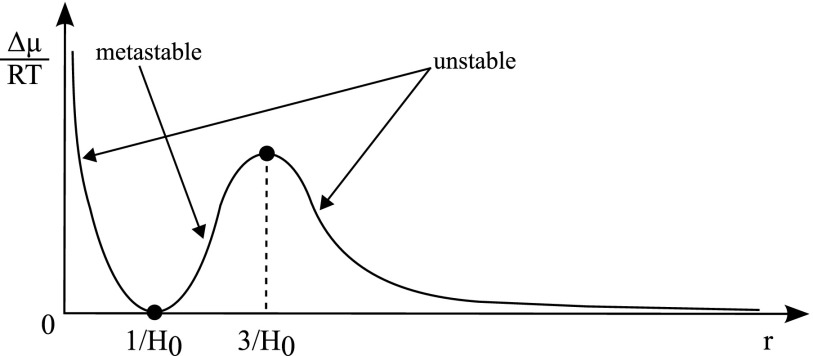
In 2001, Kabalnov studied the effect of droplet radius on chemical potential.⁴¹ His work is shown in Figure 3, which describes how the excess chemical potential of an internal component (water) versus the chemical potential of this internal component in an oil phase varies with respect to droplet radius. The model assumes that there are only two phases, though at some point it is thermodynamically favourable to form a third phase with a lower chemical potential than the bulk oil phase. Since the chemical potential is the partial molar derivative of the Gibbs free energy, it is a measure of the direction of spontaneous change in a real world system, taking into account, for example, impurities and changes in local concentrations and homogeneity. Figure 3 defines the thermodynamic stability of droplet systems and shows that droplet radius has a significant effect on droplet stability. Spontaneous change in droplet systems takes place from high to low chemical potential, and any non-zero point on the chemical potential graph shows a certain extent of thermodynamic instability where droplet contents will therefore leak out at a specific, though undefined, rate. In the regions marked unstable, droplets are both thermodynamically and kinetically unstable. In regions marked metastable, droplets are thermodynamically unstable but kinetically stable, and the rate at which water leaves the droplets is low due to a high activation energy. Therefore droplets, although stable initially, break down over time as shown in the droplet failure modes detailed herein. Data collected in our laboratory suggest that $1/H_0$ equals 300 ± 50 nm diameter for droplet systems using FC-40 with EA surfactant (the presence of droplets was measured through fluorescence and size was determined by filtration, where fluorescence was not detected after filtration through a 200 nm filter but was detected after filtration through a 400 nm filter). Comparable studies using dynamic light scattering (DLS) measurements suggest a size for EA surfactant stable inflated micelles of approximately 120 nm.⁴⁰ In the absence of other supporting data, it is clear that there is a broad agreement on length scales but that further work needs to be done to resolve the variability in these measurements. This graph of chemical potential explains the droplet shrinkage, micelle formation and, to some extent, budding failure modes described subsequently.

FIG. 3.

Graph of chemical potential versus droplet radius, showing unstable, metastable, and stable droplet regimes. H₀ is the spontaneous droplet curvature. Reproduced with permission from A. Kabalnov, J. Dispersion Sci. Technol. 22, 1 (2001).⁴¹ Copyright 2001 Taylor & Francis Ltd.⁶⁵

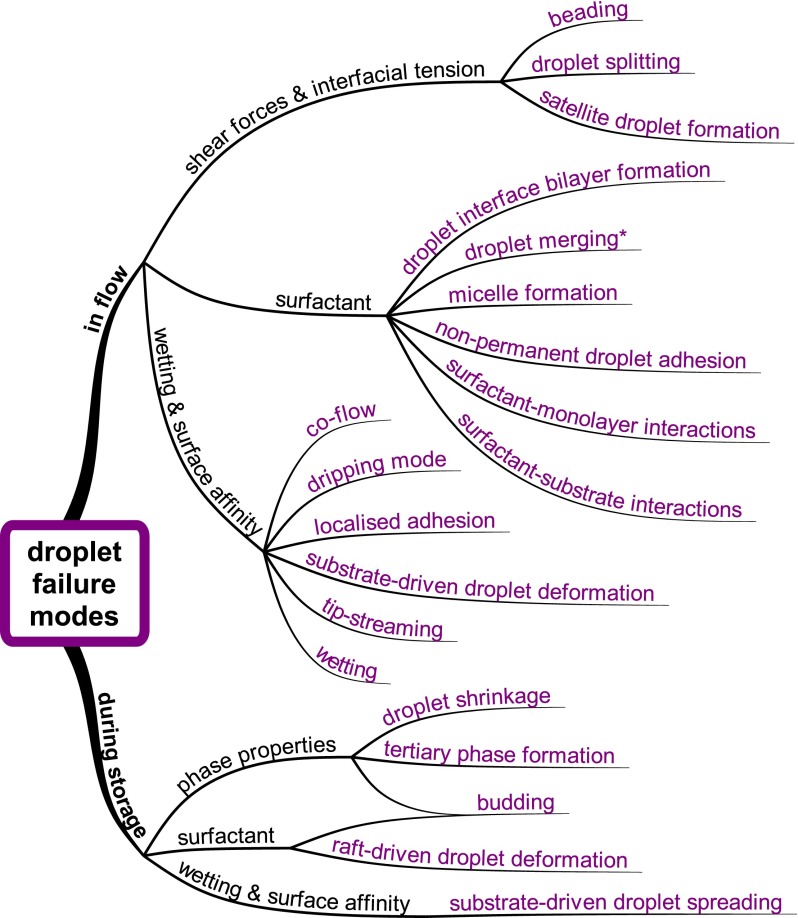
Twenty manifestations of droplet failure modes were identified during the course of these experiments and classified according to four underlying phenomena: wetting and surface affinity, shear forces and interfacial tension, surfactant properties, and phase properties (Figure 4). A video showing each failure mode and the experimental conditions under which each was taken are provided in the supplementary material.²⁸

FIG. 4.

Twenty droplet failure modes, in purple, observed during droplet flow or during storage of droplets on a PDMS microfluidic device. The failure modes are classified by underlying phenomena, as shown in black. An asterisk denotes failure modes that occur both in flow and during storage.

A. Shear forces and interfacial tension

Modes within this family are dominated by effects arising from shear forces and interfacial tension (Figures 5(a)–5(c)). The linking factor between these failure modes is that they arise either due to an interplay between bulk fluid forces which deform droplets due to differences in bulk shear, or due to differences in internal pressure and viscosity. Shear effects not only affect droplet morphology, and therefore droplet surface area, but also radically affect the surfactant distribution across the droplet surface.³⁹ The model for surfactant distribution derived previously takes into account the movement of droplets through the microfluidic channel via the synthetic quorum membrane. In a static model, the surfactant is evenly distributed over each surface in the device, however, in reality the surfactant has a higher affinity for the water phase and hence preferentially concentrates at droplet surfaces. This means that the droplet surface itself is not uniform. Because droplets in a channel are moving, the flow causes the surfactant to move away from the front of the droplet to the back, causing a surfactant coverage at the back of the droplet that is well above the predicted Langmuir coverage (Figure 1(b)). This is not a stable scenario and it is one of the factors that causes tip-streaming, satellite droplet formation, and micelle formation, each of which relies on high localised surfactant concentrations, which is one of the effects caused by the shear-induced surfactant redistribution (high surfactant concentration at the rear of the droplets, Figure 1(b)).³⁹

FIG. 5.

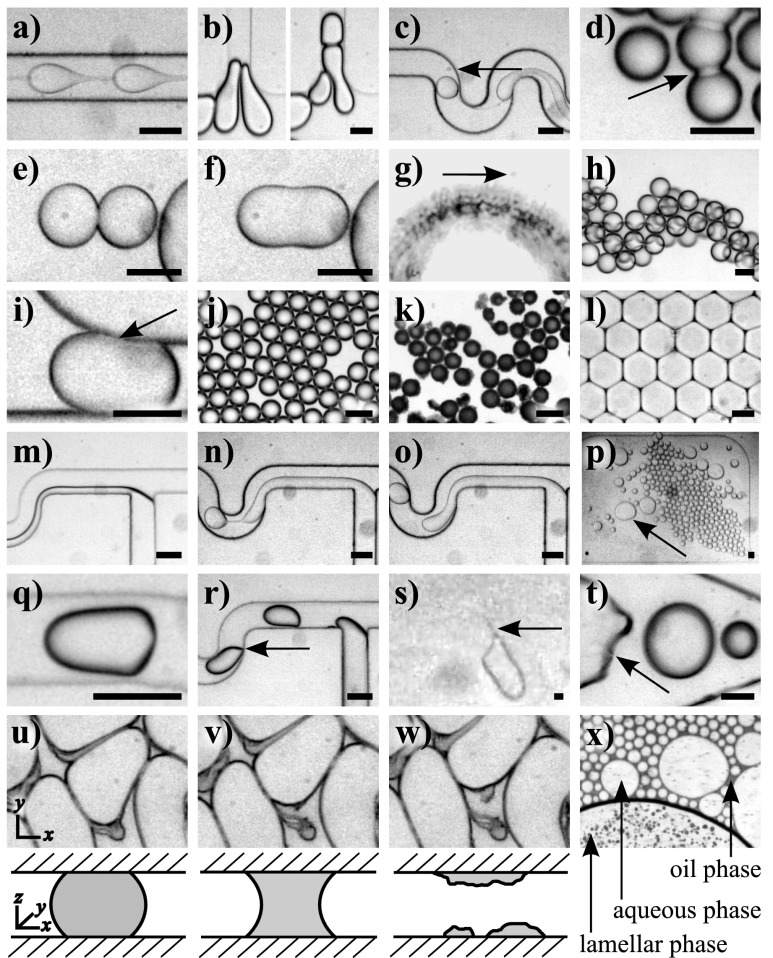
Images of droplet failure modes. Failure modes caused by shear forces and interfacial tension: (a) beading, (b) droplet splitting, and (c) satellite droplet formation. Failure modes that occur due to surfactant effects in flow: (d) DIB formation, (e) and (f) droplet merging, (g) micelle formation, (h) non-permanent droplet adhesion, and (i) surfactant-monolayer interactions. Failure modes that occur due to surfactant effects during storage: (j) and (k) budding and (l) raft-driven droplet deformation. Droplet failure modes caused by wetting and surface affinity in flow: (m) co-flow, (n) and (o) dripping mode, (p) localised adhesion, (q) generalised substrate-driven droplet deformation, (r) localised substrate-driven droplet deformation, (s) tip-streaming, and (t) wetting. Droplet failure modes caused by wetting and surface affinity during storage: (u)–(w) substrate-driven droplet spreading (sequential images were taken over the course of approximately 30 min), with a schematic representation of the cross-sectional view through the channel below. (x) Tertiary phase formation occurs due to the phase properties of the droplet system during droplet storage. Arrows highlight the failure modes and scale bars are approximately 50 μm. For experimental details and videos, see the supplementary material.²⁸

Beading (Video S1 in the supplementary material,²⁸ Figure 5(a)): In the beading failure mode, the dispersed phase is elongated as a thread through the continuous phase, and the thread shows moving spherical instabilities as bulges throughout the stream. These instabilities have the appearance of droplets linked together by a thread and may lead to droplet formation at the end of the thread. Beading, also called jetting, occurs at high capillary numbers (Ca = 0.2)⁴² and depends on the respective flow rates of the oil and water phases⁴³ and on the interfacial tension. At the droplet formation geometry, the dispersed phase is extended by shear flow into an extensional capillary. Instabilities form in the extensional capillary leading to differences in width, and these instabilities will then relax into a spherical shape in order to minimise surface energy. This spherical relaxation withdraws fluid from the extensional capillary. If the rate at which fluid flows into the extensional capillary is less than rate at which it is pulled out by the spherical relaxation of the droplet instability, droplets are formed. It is when the rates are balanced that pure beading occurs.

Droplet splitting (Videos S2a and S2b in the supplementary material,²⁸ Figure 5(b)): Another well-known droplet failure mode, splitting⁴⁴ can occur when droplets enter a constriction or encounter a structure in their path causing the droplets to be squeezed. At this point, the interplay between droplet anisotropy and surface tension versus spherical relaxation to give energetically favourable smaller droplets causes a droplet to split.

Satellite droplet formation (Video S3 in the supplementary material,²⁸ Figure 5(c)): Satellite droplet formation is a well-known phenomenon in microfluidic devices. As with the beading failure mode, upon droplet formation, a capillary (or thread) forms between the aqueous inlet stream and the emergent droplet. When the spherical relaxation of the large droplet withdraws fluid from the extensional capillary, and causes it to break, the remaining thread is itself unstable, and fluidic inertia means that it is incapable of relaxing elastically to the bulk of the aqueous phase. It therefore undergoes spherical relaxation of its own to form a smaller, satellite, droplet. Hence, satellite droplets are formed due to a combination of capillary relaxation and the speed of breakdown of this capillary.⁴⁵

B. Surfactant properties

Modes within this family are dominated by effects arising from the interactions between surfactant molecules and surfaces, and with the self-ordering of surfactant molecules (Figures 5(d)–5(l)). This is distinct from the role that surfactant molecules play in the wetting or philicity of surfaces and is based on other modes of surfactant behaviour such as micelle formation, self-assembly, interfacial tension modification, and molecular interactions. Modes within this family should be understood with the added proviso that surfactant molecules are not passive; they are subject to interactions with each other and with oil and water molecules. Additionally, the highly ordered monolayers they form mean that these interactions can become locally strong.

The model for surfactant distribution described previously (Eq. (4)) assumes that surface treatment on the device is ineffective and that the device surface is covered in surfactant molecules. It is therefore important that the integrity of this monolayer is maintained. Since maximising the first term in Eq. (4) will lead to a longer device lifetime, experimentally this translates to lowering the water fraction or maximising the initial surfactant concentration. However, high surfactant concentrations can lead to undesirable effects such as micelle formation and tip-streaming.⁴⁶ Another route to maximising device lifetime is to select a surfactant with a more balanced K_d/K_w ratio. Additionally, our model assumes that the system is in equilibrium, which is potentially misleading because this relies on the microfluidic device operating at high Fourier numbers which ensure equilibration between the surfactant molecules in the oil and on the wall. However, this effect is likely to be mitigated by the advective passage of droplets through the system, the net mixing effect of which should allow the model to achieve good results.

Droplet interface bilayer (DIB) formation (Video S4 in the supplementary material,²⁸ Figure 5(d)): DIB formation occurs when there is a higher affinity between surfactant tail groups in the droplet monolayer than between the tail groups and the oil,⁴⁷ and can be determined by the characteristic shadow pattern formed between the droplets.⁴⁸ When the attraction between the surfactant monolayers covering droplet surfaces becomes sufficiently pronounced, it largely excludes oil molecules from the shared interface and forms a DIB. Hence, the attraction becomes stronger and more permanent when compared to the non-permanent droplet adhesion failure mode described below, since the droplets are joined by a true bilayer. This failure mode has been observed previously in microfluidic devices with lipid surfactants⁴⁸ and can cause both droplet merging when the DIB is stretched or compressed, and droplet leakage of molecules that are soluble in the bilayer.⁴⁸

Droplet merging (Video S5 in the supplementary material,²⁸ Figures 5(e) and 5(f)): Droplet merging may occur either when droplets are in flow or during storage. Droplets created in a microfluidic channel are not necessarily stable when they come into contact with each other, even when a surfactant is present. When droplets come together during flow, the oil between the surfactant monolayers at the droplet surfaces is depleted^49,50 in an analogous manner to DIB formation. When the lead droplet moves away, it causes localised destabilisation between the droplets which, in turn, can initiate merging.⁴⁹ During storage, droplet merging occurs via two primary mechanisms: due to poor surfactant coverage⁵¹ or due to shock caused by moving the device, which causes droplet contact with increased force. Merging of droplets during storage is discussed in more detail in Sec. II E.

Micelle formation (Video S6 in the supplementary material,²⁸ Figure 5(g)): The spontaneous formation of droplets at a bulk droplet interface has been shown previously,⁵² with Kabalnov⁴¹ suggesting a mechanism for micelle formation based on the energetics of droplet stability in terms of chemical potential. Kabalnov also shows that the radius of curvature of the droplet is equivalent to the bulk radius of curvature and hence micelle formation is energetically favourable for certain droplet sizes. In Video S6 in the supplementary material,²⁸ the formation of an inflated micelle⁵³ at the surface of a Span 80 covered water droplet can be observed. This inflated micelle “evaporates” over time (see the supplementary material²⁸ for an explanation of this phenomenon and simulation data). The spontaneous disappearance of inflated micelles below a critical size has been observed previously.⁵⁴ This could be due to Ostwald Ripening,⁸ but this explanation would infer that another micelle is growing, which is not observed in this system. Since there is a non-equilibrium concentration of water in the carrier oil, we suggest that the contents of the inflated micelle will partition into the oil and hence the micelle gives the impression of evaporating. This is supported by the fact that Span 80 is present above the critical micelle concentration (0.025% w/v⁵⁵) and hence other mechanisms of micelle evaporation, such as micellar collapse through surfactant re-dispersion in the oil phase, are unlikely.

Non-permanent droplet adhesion (Video S7 in the supplementary material,²⁸ Figure 5(h)): When this failure mode is present, droplets come together and aggregate in three-dimensional structures in regions of decreased flow (e.g., in a large chamber). This non-permanent stacking behaviour is caused by similar attractive forces as described above for DIB formation, though in this case, the attractive forces are weaker and hence there is no full bilayer formation between the droplets.

Surfactant-monolayer interactions (Video S8 in the supplementary material,²⁸ Figure 5(i)): This failure mode manifests as a noticeable transient adhesion of droplets on the device surface without surface wetting of the droplet contents. The shadow pattern characteristic of DIB formation can also be seen in this failure mode, but at the droplet/wall interface instead of the droplet/droplet interface, indicating the presence of bilayer interactions at this surface. Surfactants self-assemble to form mono- or multi-lamellar layers on any surface where either a head or tail group is preferentially adsorbed,⁵⁶ and tail-tail or head-head interactions cause attractive forces between these ordered surfactant monolayers. Therefore, two nearby monolayers will attract once they are close enough for the interactions to overcome the competing interactions with oil molecules, causing bilayer formation to occur between the surfactant molecules covering the droplet and wall surfaces. This interaction occurs, interestingly, when using EA surfactant and FC-40 in a device treated with trichloro(1H,1H,2H,2H-perfluorooctyl)silane (PFOS).

Surfactant-substrate interactions: In this failure mode, droplet formation in a microfluidic device takes a long time to stabilise. This is caused by surfactants whose tail groups have a higher than desirable affinity for the device surface. The system equilibrates because eventually fluorous phase interactions with the surfactant tail group will dominate, allowing the surfactant to assemble on the device surface with the tail group in the oil phase.

Budding (Figures 5(j) and 5(k)): This failure mode occurs during droplet storage and is characterised by the formation of a black layer on droplet surfaces. Although not normally visible due to shadowing and diffraction effects at the droplet interfaces, droplets created in oil/water/surfactant systems are normally coated in inflated micelles.⁵⁴ These inflated micelles are attracted to the surface of the mother (bulk) droplet due to lamellar interactions rather than tail-tail or electrostatic interactions⁵⁷ and grow due to Ostwald Ripening or partitioning of water into the micelle from the adjacent droplet. Since lamellar interactions play an important role in this droplet failure mode, this mode is also classified under “Phase Properties.” As the micelles inflate they are expelled from the surface of the mother droplet and are replaced by other inflated micelles, causing the droplets to leak. Over time, this leads to a saturation of inflated micelles that causes the droplet system to be coated in a “black layer.” This hypothesis can be tested by creating droplets with a radius corresponding to the peak in Figure 3, i.e., where the system is at metastable equilibrium and there will be no micelle formation and hence no budding. This effect is not related to the substrate because it also occurs in oil-soaked devices. The micelle formation (and consequent evaporation) and budding droplet failure modes differ due to the equilibrial conditions at the droplet surface. In the micelle formation failure mode, there are no lamellae at the droplet surface, so the local conditions are non equilibrial. In the budding failure mode, there is more complex lamellar formation which causes localised equilibrial concentrations. An image of droplet budding can be found in the supplementary material.²⁸

Raft-driven droplet deformation (Figure 5(l)): This droplet failure mode is characterised by droplets losing their spherical shape and becoming rectilinear over time; in our experiments, this manifests as hexagonal droplets due to close packing, but it should be noted that this is distinct from simple pressure deformation of droplets. When droplets are stored in close-packing conformations, the oil between droplets can deplete to such an extent that it creates a lack of distributional equilibrium between surfactant molecules on the droplet surface, inhibiting their normal movement, and leading to an increase in rigidity of the droplet surface. Rigid organisational structures at droplet surfaces have been reported previously in the literature.⁵⁸

C. Wetting and surface affinity

Modes within this family are dominated by effects relating to wetting and surface affinity phenomena (Figures 5(m)–5(w)). These droplet failure modes occur both during flow and during storage, with flow effects classified as “active” (co-flow, dripping mode, substrate-driven droplet deformation, tip-streaming, and wetting) or “static” (localised adhesion and substrate-driven droplet spreading) depending on whether the failing droplet is moving or not. The wetting and surface affinity of droplets are determined by the differential affinity of surfaces within the device. Although it is often assumed that device surfaces have a uniform affinity, this is in fact rarely the case as slight differences in local conditions of monomer concentration, silane treatment, and most importantly, surfactant coverage will lead to differences in surface fluorophilicity (and hydrophobicity). Even within the same microfluidic channel, the local coverage of surfactant will be uneven as soon as the channel is operated under flow. This is due to a conflict between the kinetics of surfactant physisorption to the surface and the shear forces caused by flow of surfactant across the surface.⁵⁹ Since these two processes form a dynamic equilibrium, flow rates will affect wetting and hydrophilicity will increase at high flow rates, at the end of microfluidic channels or with long device usage. Experimentally, wetting can be caused by faulty surface treatment that has either worn off over time or was flawed when fabricated or due to device usage before hydrophobic recovery has taken place, leading to uncontrolled surface characteristics. Within the context of differences in surface affinities within a microfluidic device, several different manifestations of droplet irregularity or breakdown are discernible.

Co-flow (Video S9 in the supplementary material,²⁸ Figure 5(m)): Instead of droplet formation due to shear stress at the T-junction, two adjacent streams are formed and each stream contacts a channel wall. This occurs since it is energetically favourable for them to stabilise at the wall due to surface affinity and the minimisation of contact surfaces with the immiscible stream. In some cases, co-flow is flow-rate dependent because increased shear stress due to increased flow may overcome the local surface affinity that causes co-flow.

Dripping mode (Video S10 in the supplementary material,²⁸ Figures 5(n) and 5(o)): Droplet formation does not occur due to shear forces at the T-junction, as is normally the case. Instead, the water stream wets the device surface and causes co-flow in a limited spatial region with droplet formation occurring from “drips” formed at the end of the thread.⁶⁰ This mode is complicated as it has dependencies on differential viscosities and capillary numbers, as well as surface wetting. However, surface wetting plays a role in this as in all co-flow scenarios. Although this failure mode bears a resemblance to beading, it can be differentiated by the fact that instabilities only occur at the end of the thread.

Localised adhesion (Video S11 in the supplementary material,²⁸ Figure 5(p)): Microfluidic devices have non-homogenous surfaces where certain regions have a different impact on the flow speed and direction of droplets. This mode is different to conventional wetting in that droplets are still spherical and they lack the characteristic “streakiness” seen at the droplet boundary when aqueous droplets wet a hydrophilic surface. Droplets are, however, seen to deflect from strict compliance with flow streams or to reversibly adhere to the same spots within the channel network.

Substrate-driven droplet deformation (Videos S12a and S12b in the supplementary material,²⁸ Figures 5(q) and 5(r)): This failure mode has two manifestations, generalised substrate-driven droplet deformation and localised substrate-driven droplet deformation. Droplets affected by the generalised substrate-driven droplet deformation failure mode have a characteristic bullet shape. This is due to wetting occurring not at the channel walls (since there is a visible oil layer between the wall and the droplet) but on the bottom of the device. As is true in many microfluidic experiments, the bottom layer of the device used herein is made from a thin (approximately 15 μm) layer of PDMS elastomer spin-coated on a glass microscope slide, and droplets are hence in contact with two subtly different surfaces: the walls, which are 6–7 mm thick, and the bottom of the device, which is a lot thinner and is hence capable of less hydrophobic recovery. The bottom of the device also has less capacity for the absorption of water and hence reaches saturation faster than the walls, causing wetting to occur on this surface preferentially.⁶¹ Generalised substrate-driven droplet deformation tends to occur in regions of high shear stress, i.e., in channels rather than chambers and in the centre of channels rather than at their edges. This suggests that either the surface treatment at this differential surface is worse in channels or it erodes faster in channels due to higher flow rates. Unlike during generalised substrate-driven droplet deformation, droplets that undergo localised substrate-driven droplet deformation do not deform symmetrically. Instead, one side of the droplet drags close to the side or top walls of the channel in specific places. This indicates that the surface of the device is faulty in specific places, generally regions of high shear forces.

Tip-streaming (Video S13 in the supplementary material,²⁸ Figure 5(s)): As the droplet moves through the channel, tiny droplets stream off its end causing droplet leakage. A good indication that tip-streaming is occurring is that the channels become black and “muddy” away from the droplet creation point. Surfactant concentration alone can lead to tip-streaming. Figure 1(b) shows how surfactant advection effects on the droplet surface create regions of higher surfactant concentration at the tail end of droplets, which causes the expulsion of tiny droplets. However, in our experiments, significant wall interaction was necessary in order to initiate tip-streaming, suggesting that wall shear forces also play a role in this droplet failure mode.⁴⁶

Wetting (Video S14 in the supplementary material,²⁸ Figure 5(t)): Here, the device surface interacts significantly with the water phase, in the same way that raindrops wet windows. The localised deformation of droplets shows a major departure from the conventional spherical droplet shape, and the droplet no longer adopts a free surface energy minimised structure.

Substrate-driven droplet spreading (Video S15 in the supplementary material,²⁸ Figures 5(u)–5(w)): During storage, droplets lose their spherical shape because the affinity of the droplet for the device surface is greater than the surface tension of the droplet. Hence, droplets spread over the device surface until they detach in the z-dimension, i.e., droplets cease to contact both device surfaces simultaneously. This mode is driven by pure surface wetting rather than by differences in affinity and has been observed previously in mineral oil/ABIL storage systems.³²

D. Phase properties

Modes within this family are dominated by phase properties. The effects are chemical potential driven and rely on partition, diffusion, and the formation of thermodynamically stable phase systems.

Droplet shrinkage: During storage of the droplet volume falls (droplet contents leak) over time but the droplets remain spherical. This is caused either by Ostwald Ripening⁸ of the droplet population or by the partitioning of water from the droplets into the PDMS device (see supplementary material²⁸ for further information).⁶¹ Information on variables that affect droplet shrinkage are discussed as amelioration strategies in Sec. II E. When droplet shrinkage occurs due to partitioning of water into the PDMS device, it is analogous in mechanism to the substrate-driven droplet spreading failure mode, where the wetting of the droplet on the device surface is followed by partitioning of the aqueous droplet contents into the PDMS elastomer, causing fission of the droplet in the z-axis.

Tertiary phase formation (Figure 5(x)): During droplet storage, it is sometimes possible to distinguish three-phase systems comprised of the regular oil and water phases and an additional emulsion phase. We hypothesise that this phase is analogous to the lyotropic lamellar phase seen in liquid crystal systems at high surfactant concentrations.⁶² This mode occurs due to favourable phase transition thermodynamic conditions.

E. Amelioration of droplet failure modes

The fundamental function of droplet microfluidic platforms is the creation of droplets that are stable and able to be stored long-term. Of all of the oil/surfactant combinations tested in this study, the system that was most reliable in producing this type of droplets was FC-40 with EA surfactant, followed by FC-770 with EA surfactant, then mineral oil with ABIL EM 90 and finally mineral oil with Span 80. However, none of the combinations tested in this study were free of failure modes. These failure modes depend majorly on the surfactant characteristics and on the device surface characteristics. To a certain extent, the surfactant-based failure modes can be mitigated. For example, the numerical model provided in Figure 2 suggests that the addition of a second surfactant to coat the wall is highly beneficial at specific droplet frequencies. Additionally, to avoid micelle formation one can vary the surfactant to suit the droplet size, as suggested in Figure 3. However, the key conclusion of the current study is that a one-size-fits-all approach to surfactant use in microfluidic systems is flawed and that designer surfactant mixtures for microfluidic systems must be developed.

It may be considered that silanization of the PDMS surface would address many of the failure modes discussed above. However, silanization rarely, if ever, provides complete surface coverage.⁶³ Furthermore, the sites of imperfect coverage on the PDMS surface act as nucleation sites to accelerate the decay of the silane monolayer. This can be modelled using simple mass action kinetics and we used this to modify the model developed above. Figure 2(e) shows that silanization only acts to retard wetting effects, though this is very short term. Addition of a second surfactant with a higher affinity for the wall delays this decay. However, in both cases silanization is a temporary measure at best.

Long-term storage experiments performed in this study show that droplets stored in PDMS microfluidic devices exhibit differences in population characteristics over time since droplets are not stable (data provided in the supplementary material²⁸). In both cases, the device was soaked in water before the experiment, and in the non-control experiment, the device was additionally stored in water during droplet storage. Droplet populations change quickly (within the first hour) in conventional PDMS devices, but slowly when storing the device in water. Additionally, over time a population of small droplets is formed due to micelle formation or budding, and large droplets are formed due to droplet merging, as explained above. Hence, storing PDMS devices in water will ameliorate and delay droplet decay, but only to a certain extent. Conversely, the loss of droplet content due to shrinkage in unsaturated PDMS devices can be leveraged to allow control of the droplet volume.⁶¹

However, when using non-fluorinated oils for droplet creation, the device can instead be stored in mineral oil or silicone oil, though the later is hard to remove from the PDMS surface to enable visualisation. As can be seen in Table S1 in the supplementary material,²⁸ storage of droplets in mineral oil-soaked devices, for example, removes significant droplet failure modes when compared to systems where droplets were stored in water-soaked devices, such as localised substrate-driven droplet deformation, satellite droplet formation, and substrate-driven droplet spreading. This is hence a novel technique for optimising long-term droplet storage in PDMS devices.

To conclude, based on the experimental observations and the simulation data provided, we propose the following device- or surfactant-based amelioration strategies for droplet failure modes (a downloadable poster showing all failure modes, their underlying effect and proposed amelioration strategies is provided in the supplementary material²⁸). It is important to note that remedying one droplet failure mode may cause another, and hence we suggest that amelioration strategies for the major effect in the system are used predominantly. For example, our data show that surfactants must be used at low enough concentrations to avoid failure modes such as tip-streaming, budding, and micelle formation, but at high enough concentrations to avoid failures in the surfactant covering of either the droplet or the device surface.

In this list of amelioration strategies, device recovery means stopping the aqueous flow in the device and priming the device surface with a flow of oil and surfactant to attempt recovery to equilibrial surfactant surface coverage. Preliminary results presented in the supplementary material²⁸ show that a device recovery step can reduce the dripping failure mode, although further experiments are needed to refine this strategy. It should be noted that, as predicted by the model presented in this study, the recovery step only ameliorates the droplet failure modes transiently. This is a consequence of the surfactant surface coverage relaxing to its equilibrial value. For example, if a device operating at a droplet frequency of 20 Hz (Figure 2(c)) starts wetting at a relative abundance of 0.7 then, although a device recovery step resets the relative abundance to the starting value (in this case 0.9), upon renewed device usage at a droplet frequency of 20 Hz the surfactant surface coverage will follow the decay curve as previously and wet again at a relative abundance of 0.7.

• Beading and dripping mode: vary flow rates, adjust differential viscosities, and attempt device recovery.

• Droplet splitting: use lower flow rates, use smaller droplets, or vary the device geometry.

• Satellite droplet formation, micelle formation, tip-streaming, and budding: reduce surfactant concentration.

• Droplet interface bilayer formation, non-permanent droplet adhesion, and raft-driven droplet deformation: increase the oil fraction and decrease surfactant concentration.

• Droplet merging: increase the oil fraction, avoid expansions or contractions in the device geometry, and ensure that any shear stresses induced in the droplets are symmetrical.

• Surfactant-monolayer interactions: add a different surfactant with a higher affinity for the channel surface.

• Surfactant-substrate interactions: attempt device recovery.

• Co-flow, substrate-driven droplet deformation, localised adhesion, wetting, and substrate-driven droplet spreading: attempt device recovery and consider re-silanization.

• Droplet shrinkage and tertiary phase formation: store the device in oil or water, and consider altering the osmolarity of the dispersed phase.

III. CONCLUSIONS

The droplet failure modes observed herein range from those commonly reported in literature (such as tip-streaming and satellite droplet formation) to the entirely novel (such as substrate- or raft-driven droplet deformation). We present data showing that these failure modes affect all oil/surfactant systems tested, even such commonly used systems as FC-40 and EA surfactant. These failure modes detrimentally affect the integrity of droplets both during formation and during storage, and may have a potentially significant effect on the chemical or biological application of the droplet system. For example, surface wetting could lead to biofilm formation, and droplet leakage could affect metabolite-based assays via mechanisms such as micelle formation or DIB formation. We provide a list of amelioration strategies, such as a device recovery step, for each droplet failure mode and suggestions on the treatment of PDMS for long-term droplet storage experiments.

Finally, we suggest two crucial areas for microfluidic research in future: first, the synthesis of designer surfactants with structures that match the oil and device material, and second, the use of a device material with more uniform and reliable surface characteristics than PDMS, which is hence more amenable to long-term surface treatments.