Abstract
Objective
Dosimetry of singlet oxygen (1O2) is of particular interest because it is the major cytotoxic agent causing biological effects for type-II photosensitizers during photodynamic therapy (PDT). An in-vivo model to determine the singlet oxygen threshold dose, [1O2]rx,sh, for PDT was developed.
Material and methods
An in-vivo radiation-induced fibrosarcoma (RIF) tumor mouse model was used to correlate the radius of necrosis to the calculation based on explicit PDT dosimetry of light fluence distribution, tissue optical properties, and photosensitizer concentrations. Inputs to the model include five photosensitizer-specific photochemical parameters along with [1O2]rx,sh. Photosensitizer-specific model parameters were determined for benzoporphyrin derivative monoacid ring A (BPD) and compared with two other type-II photosensitizers, Photofrin® and m-tetrahydroxyphenylchlorin (mTHPC) from the literature.
Results
The mean values (standard deviation) of the in-vivo [1O2]rx,sh are approximately 0.56 (0.26) and 0.72 (0.21) mM (or 3.6×107 and 4.6×107 singlet oxygen per cell to reduce the cell survival to 1/e) for Photofrin® and BPD, respectively, assuming that the fraction of generated singlet oxygen that interacts with the cell is 1. While the values for the photochemical parameters (ξ, σ, g, β) used for BPD were preliminary and may need further refinement, there is reasonable confidence for the values of the singlet oxygen threshold doses.
Discussion
In comparison, the [1O2]rx,sh value derived from in-vivo mouse study was reported to be 0.4 mM for mTHPC-PDT. However, the singlet oxygen required per cell is reported to be 9×108 per cell per 1/e fractional kill in an in-vitro mTHPC-PDT study on a rat prostate cancer cell line (MLL cells) and is reported to be 7.9 mM for a multicell in-vitro EMT6/Ro spheroid model for mTHPC-PDT. A theoretical analysis is provided to relate the number of in-vitro singlet oxygen required per cell to reach cell killing of 1/e to in-vivo singlet oxygen threshold dose (in mM). The sensitivity of threshold singlet oxygen dose for our experiment is examined. The possible influence of vascular vs. apoptotic cell killing mechanisms on the singlet oxygen threshold dose is discussed by comparing [1O2]rx,sh for BPD with 3 hr and 15 min drug-light-intervals, with the later being known to have a dominantly vascular effect.
Conclusions
The experimental results of threshold singlet oxygen concentration in an in-vivo RIF tumor model for Photofrin®, BPD, and mTHPC are about 20 times smaller than those observed in vitro. These results are consistent with knowledge that factors other than singlet oxygen-mediated tumor cell killing can contribute to PDT damage in-vivo.
Keywords: photodynamic therapy, singlet oxygen production, oxygen dependence of singlet oxygen quantum yield
1 Introduction
Photodynamic therapy (PDT) is an anti-cancer treatment modality based on the interaction of light, a photosensitizing drug, and oxygen [1]. PDT has been approved by the US Food and Drug Administration for the treatment of microinvasive lung cancer, obstructing lung cancer, and obstructing esophageal cancer and Barrett’s esophagus with high-grade dysplasia, as well as for age-related macular degeneration and actinic keratosis [2].
PDT is inherently a complex process in which the photosensitizer (PS), light and oxygen vary dynamically and interdependently on timescales specific to an individual treatment condition. Thus, the distribution of light is determined by the light source characteristics and the effective tissue optical absorption and scattering at the treatment wavelength. The effective absorption is affected by the local concentration of PS and the concentration and oxygenation status of the blood. The oxygen distribution is altered by photodynamic consumption and any PDT-induced changes in blood flow [3]. The effective PS concentration and distribution may change due to photobleaching. These effects make accurate PDT dosimetry extremely challenging, but this is critical to achieve optimal efficacy and safety, particularly when there is curative intent, as is the case of PDT of multiple types of malignancies [4, 5].
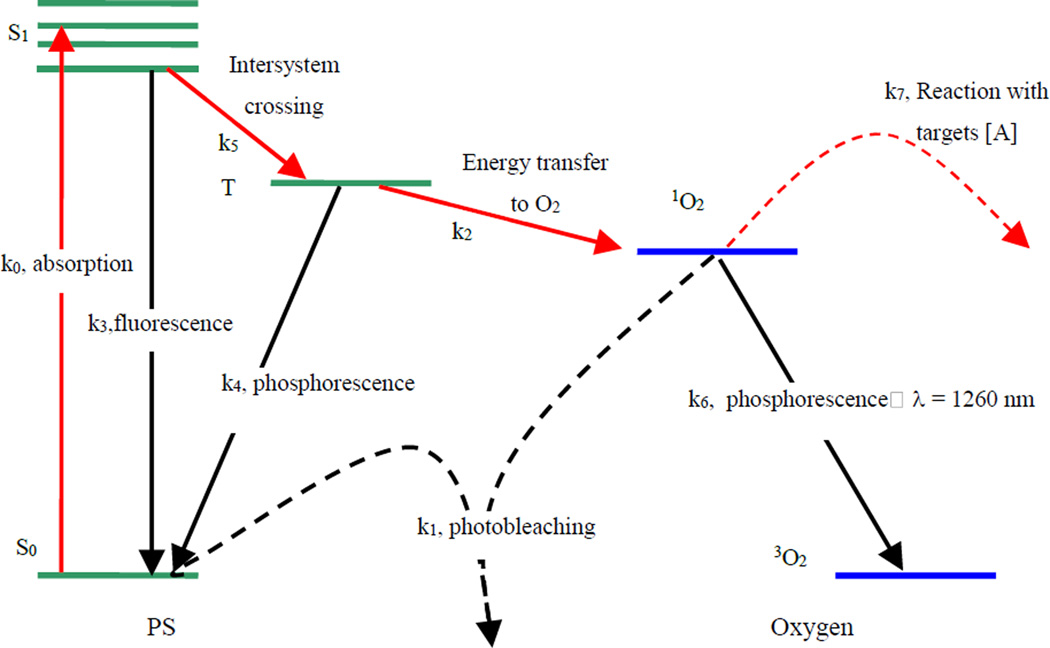
Most PSs available for PDT utilize type-II photodynamic processes, i.e., the photodynamic effect is achieved through the production of singlet oxygen [6, 7]. The energy level diagram shown in Figure 1 summarizes the underlying physical processes involved in type-II PDT with reaction rates (ki) defined in Table 1. The process begins with the absorption of a photon (k0) by PS in its ground state (S0), promoting it to an excited state (S1). The PS molecule can return to its ground state by emission of a fluorescence photon (k3), which can be used for fluorescence detection. Alternatively, the molecule may convert to a triplet state, a process known as intersystem crossing (k5). A high intersystem-crossing yield is an essential feature of a good type-II PS. Once in its triplet state, the molecule may undergo a collisional energy transfer with ground-state molecular oxygen (type II, k2) or with the substrate (type I) [6]. In type-II interaction, the PS returns to its ground state, and oxygen is promoted from its ground state (a triplet state) to its excited (singlet) state. Since the PS is not consumed in this process, the same PS molecule may create many singlet oxygen molecules. The PS triplet state can also return to the ground state spontaneously without interacting with oxygen by emitting a phosphorescence photon instead (k4). Once the singlet oxygen is created, it reacts almost immediately with cellular targets in its immediate vicinity. The majority of these reactions are irreversible, and leads to consumption of oxygen. This consumption of oxygen is efficient enough to cause measurable decreases in tissue oxygenation when the incident light intensity is high enough. In addition to its reactions with cellular targets (k7), singlet oxygen may react with the PS itself (k1). This leads to its irreversible destruction (photobleaching). Photobleaching can decrease the effectiveness of PDT by reducing the PS concentration; however it can also be useful for dosimetry, so-called singlet oxygen implicit dosimetry (SOID) [8]. Because of its high reactivity, singlet oxygen has a very short lifetime (τΔ) in tissue. However, a small fraction of the singlet oxygen produced may return to its ground state via emission of a phosphorescence photon (k6, λ = 1270 nm), which can be detected optically, so-called singlet oxygen luminescence dosimetry (SOLD) [9, 10].
Figure 1.
Jablonksi diagram of photosensitized singlet oxygen formation by type-II photosensitizer. The rate constants for monomolecular transition (solid lines) and bimolecular energy transfer (dashed lines) are indicated.
Table 1.
Parameters used in the macroscopic kinetics equations for photosensitizers
| Symbol (unit) | Definition [13] |
|---|---|
| k0 (1/s) | Photon absorption rate of photosensitizer per photosensitizer concentration, k0 = εϕ/hν, ϕ is the light fluence rate |
| k1 (1/s/µM) | Bimolecular rate for 1O2 reaction with ground-state photosensitizer |
| k2 (1/s/µM) | Bimolecular rate of triplet photosensitizer quenching by 3O2 |
| k3 (1/s) | Decay rate of first excited singlet state photosensitizer to ground state photosensitizer |
| k4 (1/s) | Rate of monomolecular decay of the photosensitizer triplet state |
| k5 (1/s) | Decay rate of first excited state photosensitizer to triplet state photosensitizer |
| k6 (1/s) | 1O2 to 3O2 decay rate |
| k7 (1/s/µM) | Bimolecular rate of reaction of 1O2 with biological substrate [A] |
For type-II PSs, excited-state singlet oxygen (1O2), the major cytotoxic species causing biological effects, is generated upon the absorption of light by the PS in the presence of ground-state molecular oxygen (3O2). Thus, direct measurement of 1O2 constitutes the ultimate PDT dosimetry method to correlate with PDT outcome. One method of determining the singlet oxygen is through in-vivo measurements of light and PS concentration, followed by calculation of the generation of singlet oxygen via a dynamic model, so called singlet oxygen explicit dosimetry (SOED). Compared to SOID and SOLD, SOED has the advantages that it is a more quantitative indication of the singlet oxygen concentration that is directly interacting with tissue and it is a natural extension of the existing in-vivo PDT dosimetry of light and PS concentration. However, SOED requires knowledge of photochemical parameters and the singlet oxygen threshold dose [1O2]rx,sh. The purpose of this study is to use SOED to estimate the magnitude of the reacted singlet oxygen threshold concentration where tissue necrosis occurs in an in-vivo model.
2 Materials and methods
In this study, ki (i = 0, 1, …, 7) are used to designate the reaction rate. The definitions associated with the reaction rates are summarized in Table 1.
2.1 Macroscopic kinetics rate equations
A rate equation approach first proposed by Foster et al. [11] and later refined by Hu et al. [12] was adopted to describe the PDT kinetics processes. The complete set of rate equations is published elsewhere [13, 14]. The lifetime of the singlet and triplet states of PS ([S1] and [T]) and the singlet oxygen 1O2 are very short (ns – µs time scale) since they either decay or react with cellular targets immediately after they are created. Thus, it is reasonable to set the time dependences, d[S1]/dt, d[T]/dt, and d[1O2]/dt to be zero. The simplified rate equations can be expressed as [13, 14]:
| (1) |
| (2) |
| (3) |
| (4) |
Notice that a macroscopic oxygen perfusion rate, g(1-[3O2]/[3O2](t=0)), is used to replace the microscopic diffusion and metabolic consumption of oxygen in tissue in a uniform vascular structures in the macroscopic model [13, 14], where g is the oxygen maximum perfusion rate. The specific oxygen consumption rate, , is the PDT oxygen consumption rate per fluence rate per PS concentration. The specific photobleaching ratio, σ = k1/(k7[A]), is the ratio of photobleaching rate by singlet oxygen between PS and all other acceptors [A] per PS concentration. The oxygen quenching threshold concentration, β = k4/k2, is the value of oxygen concentration where the quantum efficiency of singlet oxygen generation is reduced by half, following the oxygen dependence as [3O2]/([3O2]+β). Here the reacted singlet oxygen concentration is defined as , where f is the fraction of singlet oxygen interacting with target [A], and k7[A] = 1/τΔ is the inverse of the singlet oxygen lifetime in tissue. In this paper f = 1 is used.
The corresponding expressions for the instantaneous concentrations of singlet oxygen, as well as singlet, and triplet states of PS are:
| (5) |
| (6) |
| (7) |
The rate equations are implemented in the MATLAB code. The calculation time is in seconds for the rate equation alone (Eq. (2) – (7)) and minutes for the time and spatially coupled differential equation (Eq. (1)). All these quantities are a function of space (x,y,z) and time (t).
2.2 Necrosis experiment and SOED
Through in-vivo studies of a murine radiation-induced fibrosarcoma (RIF) tumor model, the extent of necrosis that is generated by PDT with benzoporphyrin derivative monoacid ring A (BPD) was measured to determine singlet oxygen threshold doses. Two drug-light intervals (DLI), 15 min and 3 hr, were used. The treatment laser wavelength was 690 nm. Table 2 summarizes the conditions that were evaluated for in-vivo PDT.
Table 2.
Parameters for the PDT experiments in murine RIF tumor model.
| Photosensitizers | BPD | BPD | Photofrin® |
|---|---|---|---|
| Incubation time | 15 min | 3 hr | 24 hr |
| Drug concentration (mg/kg) | 1 | 1 | 5 |
| Light wavelength (nm) | 690 | 690 | 630 |
RIF, radiation-induced fibrosarcoma; BPD, benzoporphyrin derivative monoacid ring A
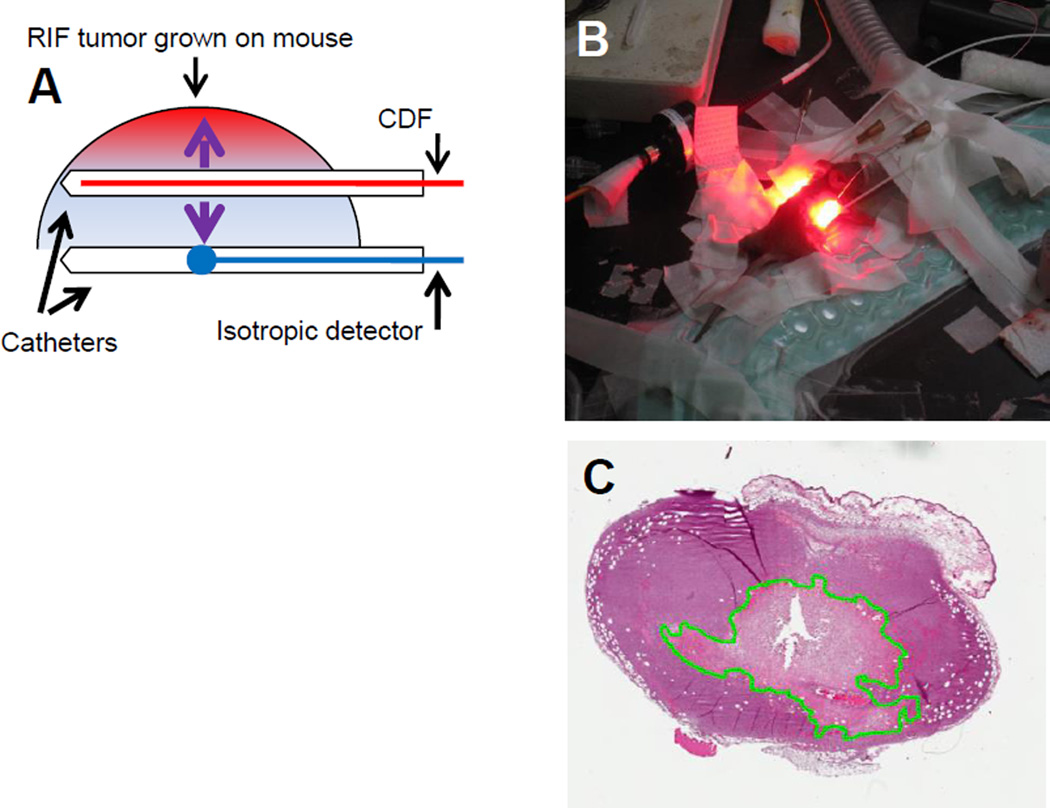
RIF tumors were grown by the intradermal injection of 3×105 cells on the right shoulders of mice and studies were initiated approximately 10 days later when tumors were 8–12 mm in diameter. Animal husbandry was provided by the University of Pennsylvania Laboratory Animal Resources in Association for Assessment and Accreditation of Laboratory Animal Care (AALAC)-accredited facilities according to protocols approved by the University of Pennsylvania Institutional Animal Care and Use Committee. PDT was performed using a 1-cm long cylindrical diffusing fiber (CDF) to deliver light at various fluence rates and total treatment times [14]. The mice were sacrificed at 24 hr after PDT and the tumor resected perpendicular to the CDF. Experimental set-up and an example of hematoxylin and eosin (H&E) staining of a RIF tumor section are shown in Figure 2. Slides were then digitally scanned to determine the area of necrosis. The radius of necrosis was found by calculating
| (8) |
Figure 2.
The mouse necrosis experiment. (A) Schematics of treatment catheter and isotropic detector used to measure the light fluence rate, tissue optical properties, and photosensitizer drug concentrations. (B) A picture of two mice undergoing PDT using 1-cm cylindrical diffusing fibers (CDFs). (C) The resulting tumor hematoxylin-eosin staining slides with the necrosis edge delineated.
The tumor shrinkage factors were determined by measuring the tumors immediately post-excision and just prior to sectioning for each mouse. From these data an average shrinkage factor of 30% was incorporated into the determination of the necrotic area. The standard deviation of the radius of necrosis was found by
| (9) |
For areas of necrosis that were very ellipsoidal in shape, multiple radii were measured from the location of the light source (indicated by the hole left behind by the catheter in the tumor section) to the edge of necrosis. Standard deviations were added to the standard deviations for the radius of necrosis for each group of mice that were treated with the same conditions. For the set of experiments performed with individual mice, a set standard deviation of 0.5 mm was applied. The necrotic radius due to insertion of the 1-cm CDF alone was measured as 0.5 or 1.0 mm in 9 unilluminated control mice. The radius in these controls was observed to be a function of whether a plastic catheter was used to house the 1-cm CDF during its insertion (note that a catheter was not used for CDF placement in most PDT-treated animals except for the ones used for optical properties measurement also). These uncertainties were included in the data analysis of the measured necrosis radius.
The optical properties (absorption and reduced scattering coefficients) of the tumor environment were determined using a two-catheter method [15]. A 2-mm point source and an isotropic detector were inserted into the tumor using two parallel catheters (Figure 2A). Light fluence data was scanned along the point source by moving the isotropic detector at various source positions. The data was then fitted with the diffusion approximation:
| (10) |
where S is the source strength of the point source (in mW), ϕ(r) is the fluence rate at position r, and [15, 16]. The light fluence rate (data not presented) at the second catheter per mouse was also measured and compared with the calculated light fluence rate using the measured optical properties as a second consistent check of the optical properties values. The light fluence rate at the radius of necrosis was calculated for each mouse along the radial axis with respect to the center of the CDF:
| (11) |
where r is the distance to the point of interest along the radial axis given the center of the CDF as origin, l is the length of the CDF, and s is the source strength of the CDF (mW/cm).
PS concentration in the tumor was determined using fluorescence spectra. A polished side-firing fiber was inserted into the source position catheter to excite the PS with 405 nm light and collect the fluorescence signal through a dichroic beam splitter to be collected by a multi-channel spectrometer. Spectra were analyzed by using singular value decomposition methods with known phantom fluorescence spectra [17]. Optical properties correction of fluorescence signal reduction due to tissue absorption and scattering was made using an empirical correction method [18].
2.3 Optimization algorithm to determine in-vivo singlet oxygen threshold dose
The optimization routine was performed by calculating the time series solution for reacted singlet oxygen, [1O2]rx. The PDT equations were solved by inputting initial estimates for the modeling parameters g, ξ, σ, along with the experimental light fluence rate, the initial oxygen concentration, and the initial PS concentration. Two parameters, β and δ, were held at fixed values based on the literature [19, 20], while g, ξ, σ, and the threshold singlet oxygen dose were free parameters. The initial oxygen concentration was assumed to be 83 µM, with 100% of the oxygen concentration present in the treatment environment reacting with the PS. The effect of initial oxygen concentration is beyond the scope of the current study. The effect of initial oxygen concentration is beyond the scope of the current study. After calculating the time series solution for [1O2]rx, this value at the radius of necrosis with the given input parameters is compared to the calculated singlet oxygen threshold dose, [1O2]rx,sh, by minimizing a standard deviation according to Eqn. (12):
| (12) |
where N was the total number of groups (or individual mouse for an earlier experiment) and ri is the measured radius of necrosis for group (mouse) i. In our most recent experiments, each group consisted of 3 mice with the same treatment conditions for which the radii of necrosiss and other measured parameters were averaged. In an earlier experiment (see Table 3B) individual mice were used. Multi-variable optimization uses the functional minimization function ‘fminsearch’ from MATLAB and is implemented in the same way as described elsewhere [14]. The quality of the fitted results was evaluated by examining the deviation of reacted singlet oxygen for the total number of mice around the threshold singlet oxygen dose fitted with our algorithm. Multiple fitting runs were performed with a range of initial parameter estimates in a physiologically reasonable range based on literature values. The specific oxygen consumption rate, ξ, was set to initially range between 20× 10−3 and 100 × 10−3 cm2mW−1s−1. The oxygen maximum perfusion rate, g, was initially varied from 0.5 to 2.5 µM/s. The specific photobleaching ratio, σ, was estimated to initially be between 0.5 × 10−5 and 2.5 × 10−5 µM−1. Finally, we also varied the initial threshold singlet oxygen dose, [1O2]rx,sh, from 0.5 to 1.5 mM. For the multiple runs, the maximum relative deviation of reacted singlet oxygen, defined as
| (13) |
were compared. By evaluating Eq. (13) for varying the initial estimate of parameters to be fit, the standard deviations of the fitted parameters were found. The sensitivity of the parameter determination depends also on the variation of necrosis for the light fluence rate and total fluence used. For a DLI of 15 min, the necrosis radii are all near 4.5 mm without substantial variability. The parameter set determined for BPD with a DLI of 15 min was considered to be “preliminary” due to the narrow range of experimental conditions that were performed. Additional experiments should be added to the study with DLI 15 min to improve the accuracy of the resulting parameters (ξ, σ, g, β) but it is not expected to change the conclusion that [1O2]rx,sh for the BPD DLI 15 min study is much lower than that of the BPD DLI 3 hr study.
Table 3.
Treatment conditions for BPD-mediated PDT (drug-light interval of 3 hr) experiments of the RIF tumor model.
| Group # | PS concentration (µM) |
LS source strength (mW/cm2) |
TX time (s) |
μa (cm−1) | μs' (cm−1) | Fluence rate at radius of necrosis (mW/cm2) |
Necrosis radius (mm) |
|---|---|---|---|---|---|---|---|
| (A) Experiment 1, each group contains 3 mice | |||||||
| 1 | 0.79±0.15 | 12 | 3000 | 0.67±0.16 | 9.44±2.1 | 16.5±3.4 | 2.62±0.86 |
| 2 | 0.70±0.10 | 150 | 420 | 0.82±0.18 | 9.93±2.6 | 144.0±44 | 2.94±1.11 |
| 3 | 0.51±0.21 | 20 | 1600 | 0.60±0.14 | 8.00±1.5 | 41.5±2.3 | 1.97±1.03 |
| 4 | 0.70±0.16 | 12 | 2000 | 0.79±0.16 | 8.02±0.5 | 12.7±3.5 | 2.78±1.12 |
| 5 | 0.82±0.14 | 30 | 1020 | 0.80±0.05 | 6.93±1.6 | 30.5±1.7 | 2.76±0.71 |
| 6 | 0.59±0.25 | 75 | 660 | 0.83±0.22 | 10.25±2.1 | 93.0±32 | 2.56±0.50 |
| (B) Experiment 2 from 2013 [21], individual ungrouped mice were used. The necrosis s.d. was taken as 0.5 mm for all cases. | |||||||
| 7 | 0.41 | 75 | 1800 | 0.66 | 10.44 | 147.0 | 2.14 |
| 8 | 0.35 | 30 | 1980 | 0.55 | 10.78 | 73.9 | 1.99 |
| 9 | 0.29 | 30 | 4500 | 0.53 | 14.28 | 131.0 | 1.40 |
| 10 | 0.33 | 12 | 4000 | 0.23 | 6.54 | 26.3 | 2.45 |
| 11 | 0.27 | 20 | 4000 | 0.14 | 15.15 | 70.1 | 2.98 |
| 12 | 0.14 | 150 | 660 | 0.79 | 9.43 | 273.0 | 2.03 |
| 13 | 0.18 | 75 | 660 | 0.35 | 9.01 | 175.8 | 2.33 |
PS, photosensitizer; LS, linear source; TX, treatment; μa, absorption; μs', reduced scattering.
3 Results and discussion
3.1 Macroscopic modeling of singlet oxygen threshold dose
The treatment conditions for BPD are listed in Tables 3 and 4 for a DLI of 3 hr and 15 min, respectively.
Table 4.
Treatment conditions for BPD-mediated PDT (drug-light interval of 15 min) experiments of the RIF tumor model. Each group contains 3 mice.
| Group # | PS concentration (µM) |
LS source strength (mW/cm2) |
TX time (s) |
μa (cm−1) | μs' (cm−1) | Fluence rate at radius of necrosis (mW/cm2) |
Necrosis radius (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 0.10±0.06 | 12 | 2000 | 0.64±0.08 | 12.31±1.54 | 5.6±2.0 | 4.46±2.03 |
| 2 | 0.17±0.07 | 12 | 3000 | 0.72±0.07 | 11.27±1.27 | 3.8±1.3 | 4.87±1.14 |
| 3 | 0.28±0.05 | 12 | 6000 | 0.96±0.18 | 7.30±1.40 | 2.9±1.6 | 4.91±0.80 |
| 4 | 0.15±0.12 | 20 | 2000 | 0.75±0.12 | 6.83±3.10 | 11.9±1.1 | 3.79±1.05 |
| 5 | 0.14±0.06 | 30 | 1300 | 0.94±0.28 | 9.13±4.04 | 11.4±8.8 | 4.14±1.24 |
| 6 | 0.17±0.05 | 75 | 1800 | 0.80±0.13 | 9.95±2.70 | 18.9±12.0 | 5.08±1.42 |
| 7 | 0.18±0.05 | 150 | 180 | 0.83±0.03 | 9.53±4.01 | 47.6±13.0 | 4.65±1.60 |
PS, photosensitizer; LS, linear source; TX, treatment; μa, absorption; μs', reduced scattering.
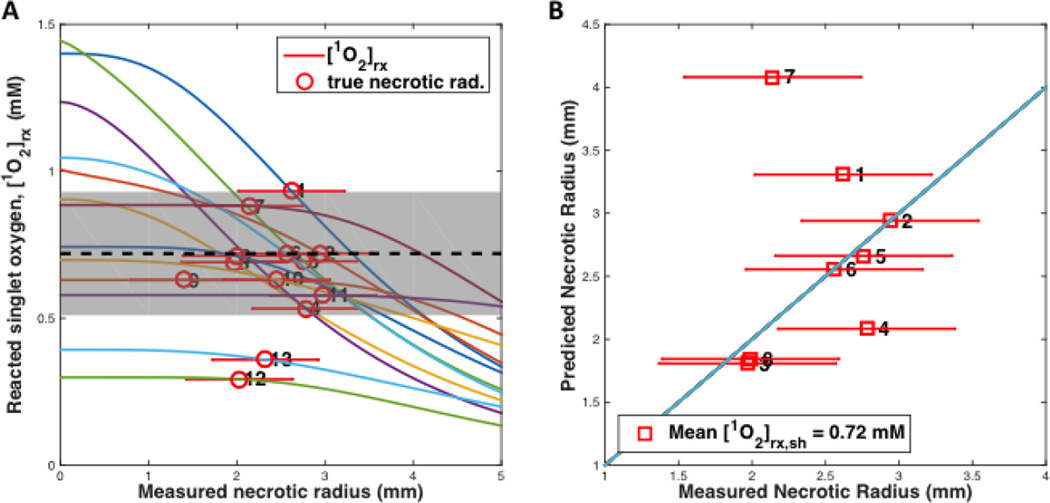
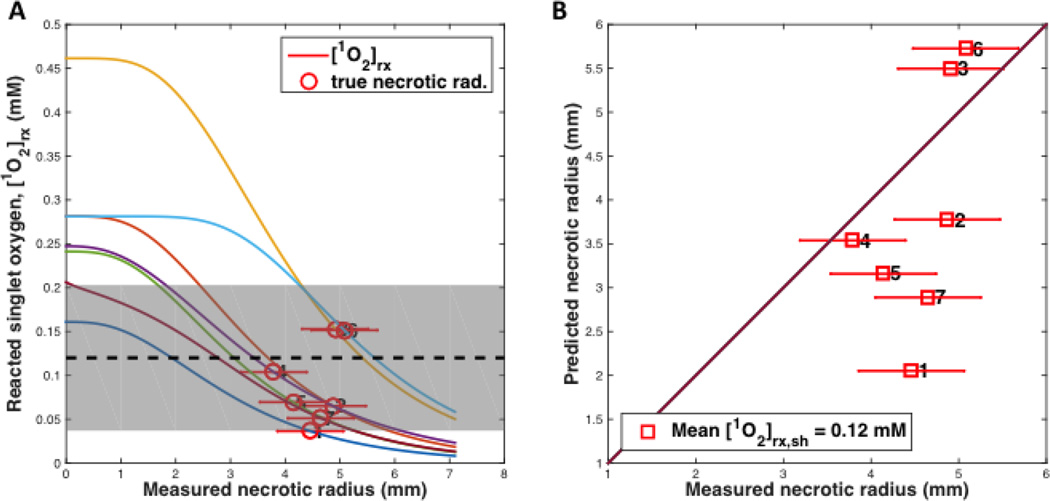
Figures 3 and 4 show the fitting results of (A) the reacted singlet oxygen concentration [1O2]rx versus radius of necrosis and (B) the comparison of predicted and measured radius of necrosis for BPD for a DLI of 3 hr and 15 min, respectively. Recovered photochemical parameters for the rate equations are listed in Table 5 for BPD and several other photosensitizers from the literature.
Figure 3.
(A) [1O2]rx profiles for 25 mice (6×3=18, 6 groups, in experiment 1 and 7 in experiment 2) using the model parameters (ξ, σ, β, g) in Table 5 for benzoporphyrin derivative monoacid ring A (BPD) with a drug-light interval of 3 hr. The corresponding initial photosensitizer (PS) concentration, linear source (LS) source strength (mW/cm), treatment (TX) time (s), μa, μs’, and fluence rate at radius of necrosis (mW/cm2). The symbol with error bar indicates the PDT-induced necrotic radius r with standard deviation for each mouse. (B) PDT-induced necrotic radius predicted versus measured for mice shown in figure (A). (The first 18 mice from experiment 1 were numbered 1 … 6, each is an average of 3 mice; The remaining 7 mice from expt. 2 is numbered: 7 … 13.)
Figure 4.
(A) [1O2]rx profiles for 21 mice (7×3=21, 7 groups) using the model parameters (ξ, σ, β, g) in Table 5 for benzoporphyrin derivative monoacid ring A (BPD) with a drug-light interval of 15 min (a preliminary study). The corresponding initial photosensitizer (PS) concentration, linear source (LS) source strength (mW/cm), treatment (TX) time (s), μa, μs’, and fluence rate at radius of necrosis (mW/cm2) for each group of 3 mice are shown in Table 4. The symbol with error bar indicates the PDT-induced necrotic radius r with standard deviation for each mouse. (B) PDT-induced necrotic radius predicted vs. measured for mice shown in figure (A). (The 21 mice were numbered 1 … 7, each is an average of 3 mice)
Table 5.
Parameters used in the macroscopic kinetics equations for photosensitizers.
| Symbol | Definition | Value | Ref. |
|---|---|---|---|
| SΔ(k5/(k5+k3)) | Singlet oxygen quantum yield | Photofrin®, ALA-PpIX: 0.56 | [22] |
| mTHPC: 0.65 | |||
| BPD: 0.76 | |||
| δ (µM) | Low concentration correction | Photofrin®, ALA-PpIX: 33 | [19] |
| mTHPC: 33 | |||
| BPD: 33 | |||
| ε (cm−1/µM) | Extinction coefficient of photosensitizer | Photofrin®, ALA-PpIX (630 nm): 0.0035 | [22] |
| mTHPC (650 nm): 0.048 | [23] | ||
| BPD (690 nm): 0.0783 | [24]a | ||
| ξ (cm2mW−1s−1) | Specific oxygen consumption rated |
Photofrin®: 3.7×10−3 | [20, 25] |
| Photofrin®: (2.9±0.8) × 10−3 | [26] | ||
| mTHPC: 30×10−3 | [25] | ||
| ALA-PpIX: 3.7×10−3 | b | ||
| BPD3 hr (51 ± 13) × 10−3 | fitted value | ||
| BPD15 min (49 ± 29) × 10−3 | fitted value | ||
| σ (µM−1) | Specific photobleaching ratiod k1/k7[A] | Photofrin®: 7.6 × 10−5 | [20] |
| Photofrin®: (8.4±0.8) × 10−5 | [26] | ||
| mTHPC: 2.97 × 10−5 | [25] | ||
| ALA-PpIX: 9 × 10−5 | [27] | ||
| BPD3 hr (1.7±0.3) × 10−5 | fitted value | ||
| BPD15 min (1.8±0.31) × 10−5 | fitted value | ||
| g (µM/s) | Macroscopic oxygen maximum perfusion rated | Photofrin®: 0.76 | [14] |
| Photofrin®: 0.71±0.06 | [26] | ||
| BPD3 hr 2.4±0.7 | fitted value | ||
| BPD15 min 0.96±0.56 | fitted value | ||
| β (µM) | Oxygen quenching threshold concentrationd k4/k2 | Photofrin®, ALA-PpIX: 11.9 | [20] |
| mTHPC: 8.7 | [25] | ||
| BPD3 hr 11.9 | c | ||
| BPD15 min 11.9 | c |
The literature value 0.034 cm−1/µM [24] is based on log10. Therefore this value was converted to that based on loge by multiplying by 2.303 to be consistent with the base-e definition for extinction coefficient used here.
The parameter ξ are obtained using the study of Georgakoudi et al. [20], and Mitra and Foster [25] from tumor spheroid studies, where ξ equals to βPDT/[S0]. βPDT is a proportional constant between photochemical oxygen consumption rate and the fluence rate [25]. ξ is either calculated according to the βPDT value from the literature [20, 25, 28] or based on the current mouse studies (fitted value).
These photochemical parameters are currently not available in the literature. Consequently, the value of Photofrin® was taken.
Specific oxygen consumption rate, ξ is the photochemical PDT oxygen consumption rate per fluence rate per PS concentration; Specific photobleaching ratio, σ, is the ratio of photobeaching rate by singlet oxygen between PS and all the acceptors per PS concentration; Oxygen quenching threshold concentration, β is the value of the oxygen concentration where the quantum efficiency of singlet oxygen generation is reduced by half, following the equation [3O2]/([3O2]+β).
Each data point was evaluated for their quality after the fitting runs was performed. Mice with lower than expected physiological concentrations of the PS were eliminated from the data analysis. In addition, light fluence rates were calculated for the distance of the detector away from the treatment linear source using the source strength and the measured optical properties. If the calculated fluence rates deviated more than 50% of the measured fluence rate during treatment, then the data point was not considered for analysis. Table 6 summarizes the singlet oxygen threshold dose calculated from the fits for BPD and other photosensitizers based either on similar data analysis of the existing in-vivo data or on the data analysis of in-vitro spheroid data in the literature. For comparison, singlet oxygen threshold dose for PDT from other studies are included. Clearly, there is a difference in singlet oxygen threshold dose between in-vivo results measured in mice (0.4–0.7 mM) and from spheroid measurements (8–12 mM). (The value for BPD DLI 15 min is ignored since it is completely vascular in nature.) The current study is consistent with other in-vivo mouse studies in mTHPC where threshold dose of 0.4 mM in-vivo was obtained. [29] However, the in-vivo results are at least 20 times smaller than those observed in spheroids, indicating that factors other than singlet oxygen-mediated tumor cell kill may contribute to PDT damage for these treatment conditions [29]. The singlet oxygen threshold dose obtained for BPD with a DLI of 15 min (BPD 1 mg/kg, 690 nm) were also included, where a vascular effect is predominant [31]. The lower singlet oxygen threshold dose of 0.12 mM that is associated with these conditions is to be expected, given the BPD concentration (~0.15 µM) in tissue after a DLI of 15 min is much lower than that (~0.6 µM) after administration of BPD with a DLI of 3 hr (which is associated with less of a vascular effect). The fact of the matter is that for BPD with a DLI of 15 min, most of the BPD remains in the vasculature and has not yet diffused into the surrounding tissue. As a result, damage of the vasculature is the dominant mechanism of PDT effect after a DLI of 15 min and the measured BPD concentration in tissue is only used as a surrogate to quantify the corresponding BPD concentration in the vasculature. For this reason, the singlet oxygen threshold dose obtained for BPD with a DLI of 15 min will be excluded in our final analysis of in-vivo singlet oxygen threshold dose for direct tissue damage due to singlet oxygen.
Table 6.
Summary of singlet oxygen threshold dose (in mM). The drug-light interval (DLI) is given for in-vivo mouse experiments only.
| PS, DLI (in vivo) | Media | Singlet oxygen threshold dose, [1O2]rx,sh (mM) |
Ref. | |
|---|---|---|---|---|
| 1 | Photofrin®, 24 hr | Mice RIF | 0.56±0.26 | [26] |
| 2 | mTHPC, 24 hr | Mice H-Meso1 | 0.4 | [29] |
| 3 | BPD, 3 hr | Mice RIF | 0.72±0.21 | This study |
| 4 | BPD, 15 min | Mice RIF | 0.12±0.08 | This study |
| 5 | Photofrin® | EMT6/Ro spheroid | 12.1±1.2 | [20] |
| 6 | mTHPC | EMT6/Ro spheroid | 7.9 ±2.2 | [30] |
3.2 Uncertainty in singlet oxygen threshold dose determination
The mean values and standard deviations of singlet oxygen threshold dose were determined to be 0.72 ± 0.21 mM and 0.12 ± 0.08 mM for BPD with DLI 3hr and 15 min, respectively. They were shown as dashed lines in Figs. 3 and 4, respectively. Similarly one found the value to be 0.56 ± 0.26 mM for Photofrin with DLI 24 hr [26]. The standard deviation for the fitted [1O2]rx,sh was found by evaluating the quality of each data point obtained. In figure 3, the mean [1O2]rx,sh is indicated with the black dashed line, and the standard deviation is indicated by the shaded grey region. The points numbered 12 and 13 were disregarded for the analysis due to their lower than physiologically sound PS concentrations compared to other data for similar fluence rate and fluence conditions (represented in data points 2 and 5). In figure 4, the data set appears to show two distinct model trends, further illustrating the need for a more detailed study. Most of the data points had exceedingly large areas of necrosis (with irregular shapes exceeding the boundary of the tumor). The standard deviation of singlet oxygen threshold dose (gray area) is very large and requires further study to improve it. However, it is clear that singlet oxygen threshold dose for DLI 15 min is substantially lower than that for DLI 3 hr.
To examine the error in the experiments to determine the singlet oxygen threshold dose, all the individual measurements between the reacted singlet oxygen and necrosis radius were plotted. Figure 5 shows all the necrosis results for BPD for a DLI of 3 hr (Figure 5A) and a DLI of 15 min (Figure 5B). From this, it can be concluded that the maximum spread in singlet oxygen threshold dose is 0.07–1.60 mM for BPD with a 3-hr DLI and 0.01–0.2 mM for BPD with a 15-min DLI. The upper limit of singlet oxygen threshold dose in vivo is 1.6 mM and 0.2 mM for BPD with a DLI of 3 hr and 15 min, respectively, from our studies (Figure 5A and B).
Figure 5.
[1O2]rx profiles for all mice using the model parameters (ξ, σ, β, g) in Tables 5 for benzoporphyrin derivative monoacid ring A (BPD) with a drug-light interval of (A) 3 hr and (B) 15 min, respectively.
3.3 Theoretical consideration of singlet oxygen threshold dose between in vivo and in vitro
Microscopically, one can write down the relationship between the reacted singlet oxygen concentration [1O2]rx and individual cell survival probability in vitro as [19]:
| (14) |
where [1O2]rx0 is the reacted singlet oxygen concentration when the cell survival is dropped to 1/e, SF is the cell survival fraction of each individual cell (SF=1 means all cell survive, and SF=0.1 means 1-in-10-cells survival). Suppose one needs to kill k cells to produce an observable necrosis in vivo, then the chance of all k cells not surviving is expressed as:
| (15) |
Inserting Eqn. (14) into Eqn. (15), one can determine the relationship between P and [1O2]rx. Figure 6A shows that P exhibits a threshold dose behavior, i.e., there is a very rapid increase in P when [1O2]rx is above a threshold dose. This value of threshold dose [1O2]rx,sh, defined as P=0.5, is proportional to [1O2]rx0 and the proportional constant, m, is a function of ln(k) (see Figure 6B, linear fit of data):
| (16) |
Figure 6.
(A) Relationship [Eqn. (15)] between the probability of kill for all k cells vs. normalized cumulative singlet oxygen concentration ([1O2]rx/[1O2]rx0), where [1O2]rx0 is the cumulative singlet oxygen to produce 1/e cell kill [Eqn. (14)]. The number of cells k varies between 106 and 1014. (B) [1O2]rx,sh/[1O2]rx0 vs. k based on P=0.5 [Eqn. (16)].
For k=108 cells, m=18.78; m varies between 13.8–32.2 for k varying between 106 and 1014, with the former corresponding to the number of cells in 2 mg of tissue and the later corresponding to the number of cells in 200 kg of tissue (a heavy human body weight), respectively. Using the direct measurement of the number of RIF tumor cells in vivo, 5×108 cm−3, the singlet oxygen threshold dose [1O2]rx0 for 1/e cell kill can be converted between mM and the number of singlet oxygen molecules per cell:
| (17) |
Equations 16 and 17 can be used to obtain singlet oxygen threshold dose from in-vivo tissue necrosis to 1/e cell killing for BPD from 0.72 mM for tissue necrosis to 4.6×107 (0.72 * 1.20×109/m, where m=18.78 is used assuming k=108) or equivalently 0.064 mM (0.72/m) for 1/e cell killing. In comparison, in-vitro measurement in MAT-LyLu (MLL) cells using m-tetrahydroxyphenylchlorin (mTHPC) gives this value as 9×108 molecules of singlet oxygen per cell [19], while in-vitro measurement for MLL cells using BPD gave 1.3 mM [32] to reduce the surviving fraction by 1/e. The in-vivo singlet oxygen threshold dose for necrosis (4.6×107/cell) is about 20 times smaller than that determined in vitro for 1/e cell killing (9×108/cell).
In conclusion, the singlet oxygen threshold dose measured in vivo is approximately 0.56 mM ((0.56+0.72+0.4)/3) to produce necrosis or 3.6×107 molecules of singlet oxygen per cell to reduce the surviving fraction by 1/e in studies of the RIF tumor model. This value is 20 times smaller than that determined from the spheroid model (~7.9 mM) [30] to produce necrosis or an in-vitro model of MLL cells [19] in which 9×108 molecules of singlet oxygen per cell were needed to reduce the surviving fraction by 1/e using mTHPC.
4 Conclusions
It was shown that using a set of rate equations and fitting the data to the necrosis radius in a RIF mouse model, the singlet oxygen threshold dose in vivo can be determined. Preliminary studies have identified that the singlet oxygen threshold dose is in the range of 0.56–0.72 mM for two photosensitizers studied: Photofrin® and BPD (Table 6). This value is about 20 times smaller than that determined in vitro. It is concluded that PDT is more potent in vivo than that in vitro, as pointed out by Wang et al. [29] as well.
Acknowledgments
We thank the technical supports from Dr. Baochang Liu for helps in BPD mice measurements and data analysis. We also thank Ken K.-H. Wang for his help in developing the optimization algorithm for determining the photochemical parameters.
Funding: National Institute of Health (NIH) (Grant/Award Number: ‘R01 CA154562-03, ‘R01 CA085831’, and ‘P01 CA87971’).
Contributor Information
Michele M. Kim, Department of Radiation Oncology, University of Pennsylvania, TRC 4W, 3400 Civic Center Blvd, Philadelphia, Pennsylvania 19104, United States
Xing Liang, Department of Radiation Oncology, University of Pennsylvania, TRC 4W, 3400 Civic Center Blvd, Philadelphia, Pennsylvania 19104, United States.
Jarod C. Finlay, Department of Radiation Oncology, University of Pennsylvania, TRC 4W, 3400 Civic Center Blvd, Philadelphia, Pennsylvania 19104, United States
Theresa M. Busch, Department of Radiation Oncology, University of Pennsylvania, TRC 4W, 3400 Civic Center Blvd, Philadelphia, Pennsylvania 19104, United States
References
- 1.Dougherty TJ, Gomer CJ, Henderson BW, Jori G, Kessel D, Korbelik M, Moan J, Peng Q. Photodynamic therapy. J Natl Cancer Inst. 1998;90(12):889–905. doi: 10.1093/jnci/90.12.889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhu TC, Finlay JC. Prostate PDT dosimetry. Photodiagnosis Photodyn Ther. 2006;3(4):234–246. doi: 10.1016/j.pdpdt.2006.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yu G, Durduran T, Zhou C, Wang HW, Putt ME, Saunders HM, Sehgal CM, Glatstein E, Yodh AG, Busch TM. Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy. Clin Cancer Res. 2005;11(9):3543–3552. doi: 10.1158/1078-0432.CCR-04-2582. [DOI] [PubMed] [Google Scholar]
- 4.Wilson BC, Patterson MS. The physics, biophysics and technology of photodynamic therapy. Phys Med Biol. 2008;53(9):R61–R109. doi: 10.1088/0031-9155/53/9/R01. [DOI] [PubMed] [Google Scholar]
- 5.Zhu TC, Finlay JC. The role of photodynamic therapy (PDT) physics. Med Phys. 2008;35(7):3127–3136. doi: 10.1118/1.2937440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Foote CS. Photosensitized oxidations and the role of singlet oxygen. Accounts Chem Res. 1967;1:104–110. [Google Scholar]
- 7.Ochsner M. Photophysical and photobiological processes in the photodynamic therapy of tumours. J Photochem Photobiol B. 1997;39(1):1–18. doi: 10.1016/s1011-1344(96)07428-3. [DOI] [PubMed] [Google Scholar]
- 8.Wilson BC, Patterson MS, Lilge L. Implicit and explicit dosimetry in photodynamic therapy: A new paradigm. Lasers Med Sci. 1997;12(3):182–199. doi: 10.1007/BF02765099. [DOI] [PubMed] [Google Scholar]
- 9.Niedre MJ, Patterson MS, Giles A, Wilson BC. Imaging of photodynamically generated singlet oxygen luminescence in vivo. Photochem Photobiol. 2005;81(4):941–943. doi: 10.1562/2005-03-15-TSN-462. [DOI] [PubMed] [Google Scholar]
- 10.Niedre M, Patterson MS, Wilson BC. Direct near-infrared luminescence detection of singlet oxygen generated by photodynamic therapy in cells in vitro and tissues in vivo. Photochem Photobiol. 2002;75(4):382–391. doi: 10.1562/0031-8655(2002)075<0382:DNILDO>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 11.Foster TH, Murant RS, Bryant RG, Knox RS, Gibson SL, Hilf R. Oxygen consumption and diffusion effects in photodynamic therapy. Radiat Res. 1991;126(3):296–303. doi: 10.2307/3577919. [DOI] [PubMed] [Google Scholar]
- 12.Hu XH, Feng Y, Lu JQ, Allison RR, Cuenca RE, Downie GH, Sibata CH. Modeling of a type II photofrin-mediated photodynamic therapy process in a heterogeneous tissue phantom. Photochem Photobiol. 2005;81(6):1460–1468. doi: 10.1562/2005-05-04-RA-513. [DOI] [PubMed] [Google Scholar]
- 13.Zhu TC, Finlay JC, Zhou X, Li J. Macroscopic modeling of the singlet oxygen production during PDT. Proc SPIE. 2007;6427:642708. doi: 10.1117/12.701387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang KK, Finlay JC, Busch TM, Hahn SM, Zhu TC. Explicit dosimetry for photodynamic therapy: macroscopic singlet oxygen modeling. J Biophotonics. 2010;3(5–6):304–318. doi: 10.1002/jbio.200900101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dimofte A, Finlay JC, Liang X, Zhu TC. Determination of optical properties in heterogeneous turbid media using a cylindrical diffusing fiber. Phys Med Biol. 57(19):6025–6046. doi: 10.1088/0031-9155/57/19/6025. 20127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhu TC, Dimofte A, Finlay JC, Stripp D, Busch T, Miles J, Whittington R, Malkowicz SB, Tochner Z, Glatstein E, Hahn SM. Optical properties of human prostate at 732 nm measured in mediated photodynamic therapy. Photochem Photobiol. 2005;81(1):96–105. doi: 10.1562/2004-06-25-RA-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Finlay JC, Conover DL, Hull EL, Foster TH. Porphyrin bleaching and PDT-induced spectral changes are irradiance dependent in ALA-sensitized normal rat skin in vivo. Photochem Photobiol. 2001;73(1):54–63. doi: 10.1562/0031-8655(2001)073<0054:pbapis>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 18.Finlay JC, Zhu TC, Dimofte A, Stripp D, Malkowicz SB, Busch TM, Hahn SM. Interstitial fluorescence spectroscopy in the human prostate during motexafin lutetium-mediated photodynamic therapy. Photochem Photobiol. 2006;82(5):1270–1278. doi: 10.1562/2005-10-04-RA-711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dysart JS, Singh G, Patterson MS. Calculation of singlet oxygen dose from photosensitizer fluorescence and photobleaching during mTHPC photodynamic therapy of MLL cells. Photochem Photobiol. 2005;81(1):196–205. doi: 10.1562/2004-07-23-RA-244. [DOI] [PubMed] [Google Scholar]
- 20.Georgakoudi I, Nichols MG, Foster TH. The mechanism of Photofrin photobleaching and its consequences for photodynamic dosimetry. Photochem Photobiol. 1997;65(1):135–144. doi: 10.1111/j.1751-1097.1997.tb01889.x. [DOI] [PubMed] [Google Scholar]
- 21.McMillan DD, Chen D, Kim MM, Liang X, Zhu TC. Parameter determination for singlet oxygen modeling of BPD-mediated PDT. Proc SPIE. 2013;8568:856810. doi: 10.1117/12.2003277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lovell JF, Liu TW, Chen J, Zheng G. Activatable photosensitizers for imaging and therapy. Chem Rev. 2010;110(5):2839–2857. doi: 10.1021/cr900236h. [DOI] [PubMed] [Google Scholar]
- 23.Johansson A, Svensson J, Andersson-Engels S, Bendsoe N, Svanberg K, Bigio I, Alexandratou E, Kyriazi M, Yova D, Gräfe S, Trebst T. mTHPC pharmacokinetics following topical administration. [[Accessed on October 31, 2014]];Proc SPIE. 2006 6094:60940C. http://luplubluse/luur/download?func=downloadFile&recordOId=617213&fileOId=2370306. [Google Scholar]
- 24.Aveline B, Hasan T, Redmond RW. Photophysical and photosensitizing properties of benzoporphyrin derivative monoacid ring A (BPD-MA) Photochem Photobiol. 1994;59(3):328–335. doi: 10.1111/j.1751-1097.1994.tb05042.x. [DOI] [PubMed] [Google Scholar]
- 25.Mitra S, Foster TH. Photophysical parameters, photosensitizer retention and tissue optical properties completely account for the higher photodynamic efficacy of meso-tetra-hydroxyphenyl-chlorin vs Photofrin. Photochem Photobiol. 2005;81(4):849–859. doi: 10.1562/2005-02-22-RA-447. [DOI] [PubMed] [Google Scholar]
- 26.Zhu TC, Liu B, Kim MM, McMillan D, Liang X, Finlay JC, Busch TM. Comparison of singlet oxygen threshold dose for PDT. Proc SPIE. 2014;8931:89310I. doi: 10.1117/12.2039719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Georgakoudi I, Foster TH. Singlet oxygen- versus nonsinglet oxygen-mediated mechanisms of PS photobleaching and their effects on photodynamic dosimetry. Photochem Photobiol. 1998;67(6):612–625. [PubMed] [Google Scholar]
- 28.Nichols MG, Foster TH. Oxygen diffusion and reaction kinetics in the photodynamic therapy of multicell tumour spheroids. Phys Med Biol. 1994;39(12):2161–2181. doi: 10.1088/0031-9155/39/12/003. [DOI] [PubMed] [Google Scholar]
- 29.Wang KK, Mitra S, Foster TH. Photodynamic dose does not correlate with long-term tumor response to mTHPC-PDT performed at several drug-light intervals. Med Phys. 2008;35(8):3518–3526. doi: 10.1118/1.2952360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Coutier S, Mitra S, Bezdetnaya LN, Parache RM, Georgakoudi I, Foster TH, Guillemin F. Effects of fluence rate on cell survival and photobleaching in meta-tetra-(hydroxyphenyl)chlorin-photosensitized Colo 26 multicell tumor spheroids. Photochem Photobiol. 2001;73(3):297–303. doi: 10.1562/0031-8655(2001)073<0297:EOFROC>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 31.Chen B, Pogue BW, Luna JM, Hardman RL, Hoopes PJ, Hasan T. Tumor vascular permeabilization by vascular-targeting photosensitization: effects, mechanism, and therapeutic implications. Clin Cancer Res. 2006;12(3 Pt 1):917–923. doi: 10.1158/1078-0432.CCR-05-1673. [DOI] [PubMed] [Google Scholar]
- 32.Weston MA, Patterson MS. Calculation of Singlet Oxygen Dose Using Explicit and Implicit Dose Metrics During Benzoporphyrin Derivative Monoacid Ring A (BPD-MA)-PDT in Vitro and Correlation with MLL Cell Survival. Photochem. Photobiol. 2011;87:1129–1137. doi: 10.1111/j.1751-1097.2011.00942.x. [DOI] [PubMed] [Google Scholar]