Modified screening and ranking algorithm for copy number variation detection

Abstract

Motivation: Copy number variation (CNV) is a type of structural variation, usually defined as genomic segments that are 1 kb or larger, which present variable copy numbers when compared with a reference genome. The screening and ranking algorithm (SaRa) was recently proposed as an efficient approach for multiple change-points detection, which can be applied to CNV detection. However, some practical issues arise from application of SaRa to single nucleotide polymorphism data.

Results: In this study, we propose a modified SaRa on CNV detection to address these issues. First, we use the quantile normalization on the original intensities to guarantee that the normal mean model-based SaRa is a robust method. Second, a novel normal mixture model coupled with a modified Bayesian information criterion is proposed for candidate change-point selection and further clustering the potential CNV segments to copy number states. Simulations revealed that the modified SaRa became a robust method for identifying change-points and achieved better performance than the circular binary segmentation (CBS) method. By applying the modified SaRa to real data from the HapMap project, we illustrated its performance on detecting CNV segments. In conclusion, our modified SaRa method improves SaRa theoretically and numerically, for identifying CNVs with high-throughput genotyping data.

Availability and Implementation: The modSaRa package is implemented in R program and freely available at http://c2s2.yale.edu/software/modSaRa.

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Single nucleotide polymorphisms (SNPs), structural variations (such as deletion, duplication or insertion of a chromosome segment) and epigenetic reasons account for the tremendous variability of human genomics. Copy number variation (CNV) is a type of structural variation, which is usually defined as genomic segments that are 1 kb or larger, presenting variable copy numbers when compared with a reference genome (Freeman et al., 2006). Duplication or deletion on any of the two copies of genomic segments results in variation of this region in human populations. CNVs are generated by recombination-based or replication-based mechanisms, which can be inherited; their formation also occurs when de novo locus-specific mutation happens (Zhang et al., 2009). With the new technologies developed in recent years, smaller copy number variants that are even in SNP level are detectable (Conrad et al., 2010).

Increasing evidence suggests that CNVs commonly exist and have strong impact on disease risks. Through CNV mapping of human genome from 270 individuals, researchers found that 12% of human genome is subject to CNVs (Redon et al., 2006). Meanwhile, other research revealed that the average number of CNVs per individual in the 112 HapMap individuals was 27 (Wang et al., 2007). Moreover, a large-scale CNV detection study in human genome demonstrated that a large amount of the identified CNVs overlapped with protein coding region (Sebat et al., 2004).

Changes of copy number influence the expression levels of genes included in the corresponding DNA segments, which makes transcription levels higher or lower than those that can be achieved by control of transcripts of a single copy per haploid genome (Hastings et al., 2009). Given this information, CNVs in human genome may significantly affect risks of not only Mendelian diseases but also many common diseases. Great effort is being made to uncover a causal role of CNVs in pathogenesis of human common disorders, such as pancreatic adenocarcinoma, autism, growth retardation and HIV progression (Fanale et al., 2013; Poultney et al., 2013; Shostakovich-Koretskaya et al., 2009; Zahnleiter et al., 2013). Precisely identifying CNVs and studying their genetic functions will greatly benefit the functional analysis of human genomics and complement current GWASs, which measure genome-wide genotype variations (Wang and Bucan, 2008).

Various techniques have been proposed for detecting DNA CNVs in humans and mammalians. The advent of whole-genome SNP genotyping array and the next generation sequencing which assays hundreds of thousands of points in parallel permits kilobase-resolution detection of CNVs. With the development of these high-resolution techniques, many population-based statistical algorithms have been developed for CNV studies including QuantiSNP (Colella et al., 2007), CNVCALL(Cardin et al., 2011), CNVDetector (Chen et al., 2008), CGHCall (van de Wiel et al., 2007), CNV-seq (Xie and Tammi, 2009), CNVtools (Barnes et al., 2008), BirdSuite (Korn et al., 2008) and CNVassoc (Subirana et al., 2011). PennCNV (Wang and Bucan, 2008) is probably the most popular software for CNV analysis, which implements hidden Markov model incorporating the Log R Ratio (LRR) values, B allele frequency (BAF) values and also the distances between neighbouring SNPs.

Meanwhile, many change-point-based approaches have also been developed and extensively applied to the detection of CNVs. Existing change-point-based approaches use exhaustive searching, such as binary segmentation method (Sen and Srivastava, 1975), circular binary segmentation (CBS; Olshen et al., 2004) and penalized regression (Huang et al., 2005). These global searching approaches present high computational complexity, given that the data points are repeatedly used in the process of determining change-points along the same sequence. As a result, finding multiple change-points in massive SNP genotyping array data accurately and efficiently is challenging.

The screening and ranking algorithm (SaRa) was recently proposed as an alternative approach for multiple change-points detection (Niu and Zhang, 2012). This algorithm hypothesizes that determining whether a position at the DNA sequence is a change-point or not does not depend on the information far away from this position. The SaRa algorithm searches along the sequence in a series of windows, and it finds the local maximizers for the scan statistic as the most probable change-points locally. These local maximizers are then ranked and chosen by a backward subset selection strategy based on Bayesian information criterion (BIC), which yields final change-points.

As discussed by Niu and Zhang (2012), it takes only $O(n)$ operations to perform the screening and ranking steps. Therefore, SaRa ensures low computational complexity down to $O(n)$, which makes it more efficient than the existing iterative searching algorithms with complexity at least $O(n^2)$. This statistical property makes SaRa more suitable for high throughput datasets.

However, some practical issues arise from the application of SaRa to SNP data for identifying CNVs. First, the distribution of intensities in high-throughput Affymetrix SNP array, for example, always presents heavy tails when compared with normal distributions, which violates the assumption of SaRa. Second, the change-points identified by SaRa are not clustered to make final calling of copy number states. In this article, to address the above two issues, we propose several strategies to implement SaRa on CNV detection. First, we use the quantile normalization (QN) on the original intensities to alleviate the requirement of normality. Second, we propose to use a novel normal mixture model and apply the BIC criterion for candidate change-point selection and further cluster the potential CNV segments to copy number states. After our modification, the SaRa algorithm is robust to the violations of the normal assumption and yields high sensitivity and specificity for identifying change-points. Through intensive simulation studies, we evaluated the validity of the modified SaRa on identifying change-points for CNVs. Our simulation results demonstrated that the modified SaRa achieved higher power than CBS (Venkatraman and Olshen, 2007). By applying it to real data from the HapMap project, we illustrated the performance of the modified SaRa on detecting CNV segments.

2 Methods

2.1 SaRa algorithm

First, we start with a brief review of the SaRa method. Let $\mathbf{Y}={(Y_1,Y_2,\mathrm{\dots },Y_n)}^T$ be a long linear sequence of random variables, for example, LRR values of an individual at one chromosome from genotyping array. $n$ is the length of the sequence presented by number of SNP and CNV markers. In SaRa, a high dimensional normal mean model is applied as follows,

$\mathbf{\mu }={({\mu }_1,{\mu }_2,\mathrm{\dots },{\mu }_n)}^T$ is the piecewise constant vector denoting the unknown underlying mean of each point. ${\epsilon }_i$’s are the independent and identically distributed errors with normal distribution. We then define a change-point vector $\mathbf{\tau }={({\tau }_1,{\tau }_2,\mathrm{\dots },{\tau }_J)}^T$ where ${\tau }_j(j=1,\mathrm{\dots },J)$ are the change-points in the model satisfying ${\mu }_{{\tau }_j}\ne {\mu }_{{\tau }_j+1}$. The total number of change-points $J$ is assumed to be much smaller than the total length $n$. As mentioned in the introduction section, on average, approximately 50 change-points corresponding to either end of the CNV regions, are sparsely dispersed among the hundreds of thousands of SNP array points for each individual. The major task becomes searching for the number of change-points $J$ and finding the exact locations of $\tau$’s.

First, a window with bandwidth $h$ is used to scan the long linear sequence which we call the screening step. At each point of interest $x$ ($1\le x\le n-1$), a simple diagnostic function $D_h(x)$ defined below is used to reflect the probability of this position being a change-point.

$$D_h(x)=\frac{\left({\displaystyle \sum _{t=1}^h{Y}_{x+t}}-{\displaystyle \sum _{t=1}^h{Y}_{x+1-t}}\right)}{h}.$$

This is the average difference between the right-hand side and the left-hand side local observations of the point of interest. Therefore, the larger deviation from zero that $D_h(x)$ presents, the more likely that $x$ is a change-point. A positive value of $D_h(x)$ means an increased mean, and a negative $D_h(x)$ is related to a decreased mean. Local maximizers of $\left|D_h(x)\right|$ are selected as the most probable candidates of change-points. For these local maximizers, the P-values corresponding to the test statistics are obtained by simulation from a sequence with no change-point. Then, by choosing a significance level, the local maximizers with the smallest P-values are selected to obtain a list for further selection, which has a much smaller size than the total length $n$. After these screening and ranking procedures, we find a pool of candidates that are most likely to be at or near the change-points. The next step is to remove the possible false-positive ones, which we will discuss in the following section.

Based on the basic idea of the SaRa algorithm described above, we illustrate the following strategies to optimize the performance of SaRa on detecting CNVs accurately and precisely.

2.2 QN of the original intensities

To alleviate the influence of the violation of normal assumption on the SaRa algorithm, we propose to perform QN on the original intensities in the preprocessing step. First, we rank the intensities of the whole dataset. Then we simulate a sample of the same size as the original datasets from the standard normal distribution $N(0,1)$. At last, we replace the original intensities by the simulated sample from $N(0,1)$ according to their ranks.

2.3 Multiple bandwidths in identifying local maximizers to optimize sensitivity

In the SaRa procedure, the bandwidth $h$ is an important parameter for accurately identifying the change-points. Choosing the optimal one is challenging and tricky. If a small bandwidth value $h$ is used, the CNVs with relatively small span sizes can be covered. However, the output will be noisy with an inflated number of false positives. Oppositely, if a relatively large bandwidth is used, the power will be low since small copy number segments will be missed. Obviously, the single bandwidth strategy is not satisfactory given the variable span size of CNVs in human population.

We attempt to increase the power or sensitivity of SaRa using multiple bandwidths as suggested in Niu and Zhang (2012). We select $k$ bandwidths $h_1,h_2,\mathrm{\dots },h_k$, and perform the screening and ranking steps with each bandwidth respectively. A total of $k$ sets of local maximizers will be obtained and combined to form a candidate pool of change-points. By default, three bandwidths are used for identifying CNVs in the current modSaRa package. Note that the estimation by different bandwidths will provide different sets of local maximizers, thus the combination of the $k$ sets of local maximizers allows better power than single bandwidth strategy. This was confirmed by our pilot study in simulated datasets (results not shown).

Although the power is increased by adopting multiple bandwidths, there are many redundant change-points since multiple candidates may be found in the close neighbourhoods. To find CNVs, we need to remove the seemingly repeated as well as the false-positive change-points effectively. In the next section, we will discuss the strategy of combining the previously published method and our new implementation.

2.4 Normal mixture model-based clustering and BIC criterion subset selection

Eliminating false positive or redundant points from the candidate change-points is a challenging and critical step for the SaRa algorithm. As suggested in Niu and Zhang (2012), a classic model selection approach, modified BIC, can be applied to the pooled maximizers for backward stepwise deletion. First, all the candidates are incorporated and the BIC score is calculated. Then, each candidate is evaluated one by one by checking the BIC values with and without this maximizer. The one candidate whose removal would lead to the largest BIC decrease will be removed. The same procedure is carried out recursively on the remaining candidates until the BIC score does not decrease. This approach is effective in deleting the redundant candidate change-points identified by different bandwidths according to our pilot study. However, according to simulations in our pilot study, we found that this BIC step was not satisfactory in eliminating the false positives. We noticed that these false positives were usually located in short segments with slight deviations from the normal copy number state. In this situation, SaRa seems to be over sensitive and detects a slight change, which may be an advantage in other applications but not ideal when only a limited number of states are of interest in the identification of CNVs.

To resolve this problem, we apply a mixture model-based clustering approach following the subset selection with BIC criterion to further delete the false positives in the candidate change-points. The basic idea is to assign the potential CNV segments between two neighbour candidate change-points to different copy number states according to the average intensity in the segment interval. In our study, we use three clusters including duplication, normal and deletion states. Each cluster is presented by a Gaussian distribution with unknown mean and variance. We then applied Expectation–Maximization algorithm for the mixture of Gaussians to assign each segment to the most probable cluster/state (details described in Supplementary Text). After this clustering procedure, if two physically linked candidate CNV segments are assigned to the same group, we treat them as one unique CNV segment.

Using this method, the segments obtained from SaRa are clustered and the neighbouring change-points with close jump sizes are grouped together. One advantage is that the short and false-positive segments with minor change can be removed. Additionally, the copy number state for each segment can be straightforwardly obtained.

2.5 modSaRa software

The modSaRa software has been implemented in R and is available online at http://c2s2.yale.edu/software/modSaRa. The general flowchart of the modified SaRa algorithm is shown in Figure 1. For a sequence of intensity values, the modified SaRa will process them by QN, search for local maximizers, eliminate unlikely change-points, and then output the potential CNV segments by presenting the start point and end point by SNP or CNV marker. The lengths of the copy number aberrant are also in the output. Users can change the significance level in the programming commands.

Fig. 1.

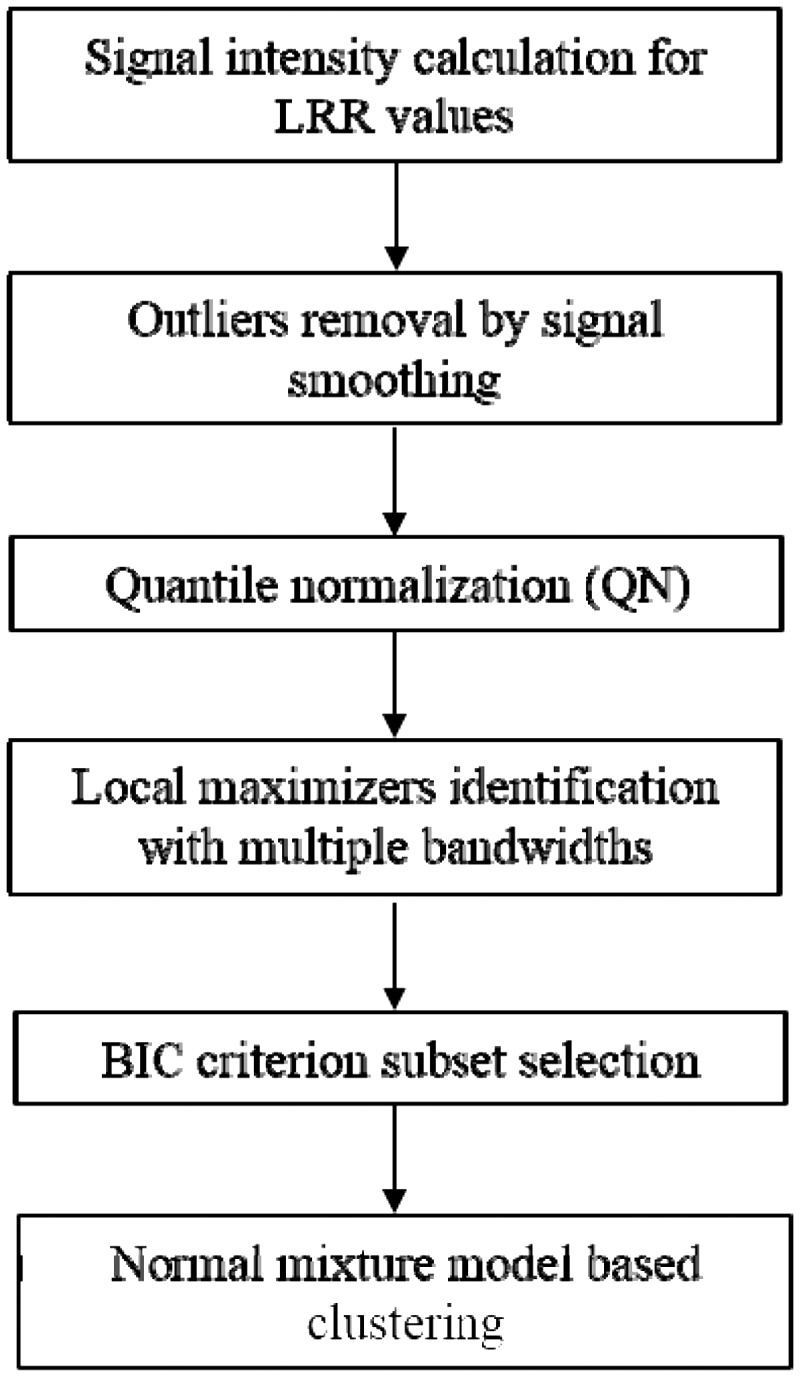
A general flowchart for CNV calling algorithm by the modified SaRa

2.6 Simulation studies

We performed simulation studies to investigate the performance of the modified SaRa method for CNV detection and comparing it to CBS. First, to provide evidence of the necessity of the QN strategy in our modification, we evaluated the performance of the original SaRa method in non-Gaussian errors with and without QN strategy. We then simulated intensities mimicking real datasets and examined the performance of the modified SaRa on change-point detection.

2.6.1 Simulation with noise from t distributions

As stated above, SaRa was proposed based on a normal distribution assumption. Thus, it might present poor performance if the intensity data violate this assumption. Therefore, we first evaluated the robustness of SaRa method on detecting change-points when the noise was from non-Gaussian distributions, for example, $t$-distributions.

Two independent scenarios were considered in which the errors were simulated from t-distributions with degrees of freedom as one and two, respectively. In each scenario, 100 sequences of length 10,000 were simulated. Ten change segments were inserted to each sequence with jump sizes (2.56, −3.47, 3.02, 3.26, −3.92, −3.12, 1.74, 3.05, −3.09, −2.69). The lengths of the segments were 35, 18, 79, 62, 51, 27, 84, 32, 26, 19. We then applied the SaRa diagnostic statistic with bandwidth $h=15$ to identify the local maximizers. The modified BIC criterion was applied for backward deletion of redundant points.

In parallel, we also applied SaRa after QN of the simulated datasets. The performance of SaRa on identifying the change-points with application of QN was compared with that without QN by evaluating the sensitivity and specificity.

2.6.2 Simulation studies of the modified SaRa

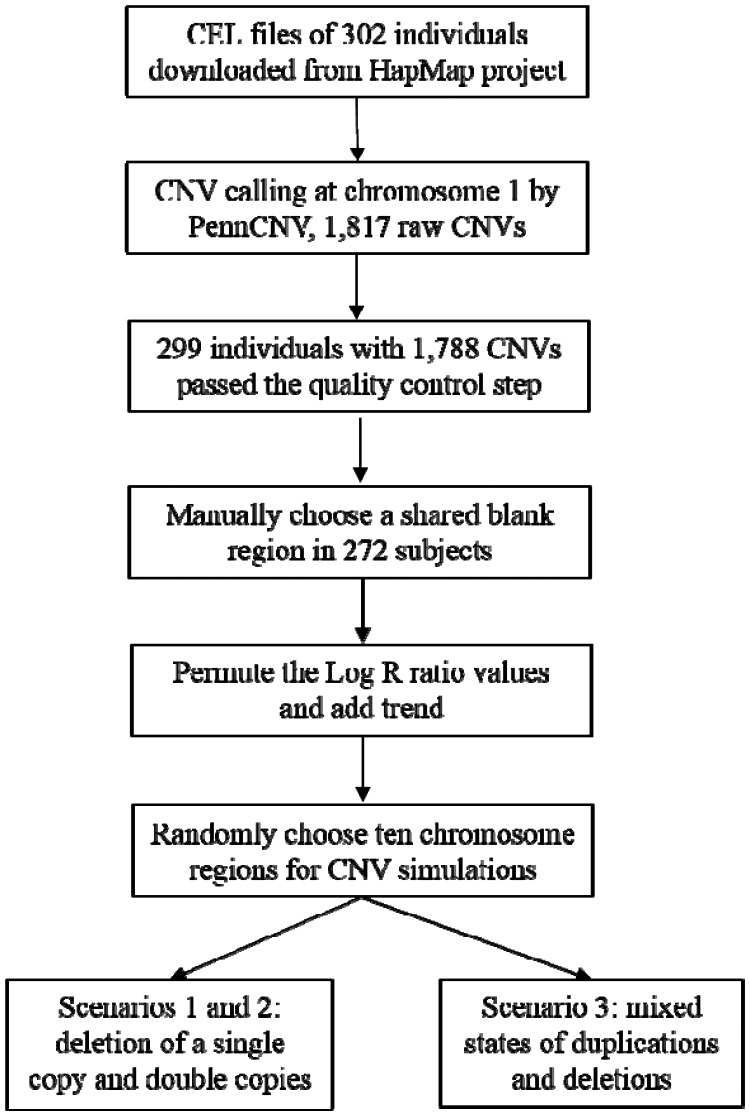
In this section, we propose a novel simulation approach to generate LRR values along DNA sequences mimicking real Affymetrix array data. Rather than generating from an artificial distribution, we used the LRR values from non-CNV SNPs in a “blank” region shared by multiple individuals. Simulations were based on the blank region to evaluate the performance of the modified SaRa versus existing methods. The general flowchart for simulating LRR sequences is shown in Figure 2.

Step 1: Generating DNA sequences mimicking real data

Fig. 2.

A flowchart for our proposed simulation procedure by mimicking a real dataset from the HapMap project

To mimic the real high-throughput genotyping array dataset, we searched for a relatively long blank (i.e., no CNV detected) sequence in real data according to the CNV identification results from PennCNV software. The details of the procedure for finding the blank region are illustrated in Supplementary Methods Section 1. We used 302 individuals from the international HapMap Phase 3 dataset (The International HapMap Consortium, 2003). Two hundred and seventy-two subjects sharing a blank region were then used for the following simulation (Fig. 2).

Step 2: Generating CNV regions

Based on the LRR values in the blank regions obtained from Step 1, we simulated CNV regions in three scenarios representing deletion of one copy, deletion of double copies and a mixture of copy number states, respectively. In each scenario, the LRR change level was simulated according to the distributions and proportions of the corresponding copy number states in the HapMap dataset (Tables 1 and 2). According to the results from PennCNV at chromosome 1, the average length of CNVs was larger in duplications compared with those from deletions (Table 1). The most frequent CNV was deletion of a single copy (cn = 1) and the least frequent one was duplication of double copies (cn = 4). Deletions occurred more often than duplications. The length of CNVs for changes of a single copy (either deletions or duplications) was obviously larger than those for double copies (Supplementary Fig. S1). Most CNV segments with changes of double copies (cn = 0 or cn = 4) were approximately 10–50 kb. Moreover, 94.97% of the CNVs spanned less than 100 markers (Supplementary Fig. S2). The details of the simulation can be found in Supplementary Methods Section 2.

Table 1.

Summary of identified CNVs by PennCNV software on chromosome 1 for the 302 normal subjects from HapMap

State	Mean of CNV lengths (kb)	Median of CNV lengths (kb)	Total number of CNVs (%)	LRR mean	LRR variance
cn = 0	24.16	30.35	409(23)	−1.28	0.65
cn = 1	56.22	28.60	820(46)	−0.51	0.18
cn = 3	167.26	63.45	378(21)	0.31	0.08
cn = 4	35.42	31.07	181(10)	0.58	0.11
cn = 2	–	–	–	−0.004	0.05

cn = 0: deletion of double copies; cn = 1: deletion of a single copy; cn = 3: duplication of a single copy; cn = 4: duplication of double copies; cn = 2: normal state. LRR mean: the average value of LRR across all samples; LRR variance: the variance of the LRR across all samples

Table 2.

Summary of the CNVs simulation in Scenarios 1 and 2

Simulation	State	$\mu$	${\sigma }^2$	Mean of CNV lengths	Median of CNV lengths
Scenario 1	cn = 1	− 0.51	0.18	31	30
Scenario 2	cn = 0	−1.28	0.65	32	32

To make the simulation mimic the real data, the mean and variance of the LRR shifted values ($\mu$ and ${\text{σ}}^2$) were computed in the original dataset according to the results from PennCNV. The LRR change values of each CNV were generated from N($\mu$, ${\text{σ}}^2$). The mean and median of CNV lengths were measured by the number of markers

We used the modified SaRa on the simulated datasets as in the flowchart in Figure 1. Its performance was compared with CBS algorithm implemented in R package DNAcopy (version 1.38.1). To make the comparison fair, we also performed QN on CBS.

We examined the sensitivity and specificity of the detection results from the modified SaRa algorithm and CBS. Since the local maximizers were identified in a window with length $2h_m\left(m=1,\mathrm{\dots },k\right)$, a change-point identified by SaRa was considered a true positive if it was within the $2h_m$ neighbourhood of a true change-point, whereas this acceptance range was set as 10 for CBS.

2.7 Real data analyses

Two hundred and ninety-nine individuals from HapMap project were used to test the modified SaRa algorithm. To reduce the effect from outliers, we first preprocessed the LRR sequence by smoothing them (Chen et al., 2013). For position $i$ in the sequence $\mathbf{Y}={(Y_1,Y_2,\mathrm{\dots },Y_n)}^T$, the smoothing region was defined as $\{i-R,\mathrm{\dots },i,\mathrm{\dots },i+R\}$, where we set the $R$ value as 10. If the intervals were out of region, we chose the start or end point of the sequence as boundaries. Let ${\widehat{\alpha }}_i$ be the mean and ${\widehat{\beta }}_i$ be the standard deviation of the samples in the smoothing region. We replaced $Y_i$ with the median of that region if $Y_i>{\widehat{\alpha }}_i+t*{\widehat{\beta }}_i$ or $Y_i<{\widehat{\alpha }}_i-t*{\widehat{\beta }}_i$, where the $t$ value was set as 2. After smoothing the signal data, we applied the SaRa software to the dataset to identify change-points. For fast CBS, the original dataset was also smoothed by its built-in command.

3 Results

3.1 Robustness of SaRa after QN

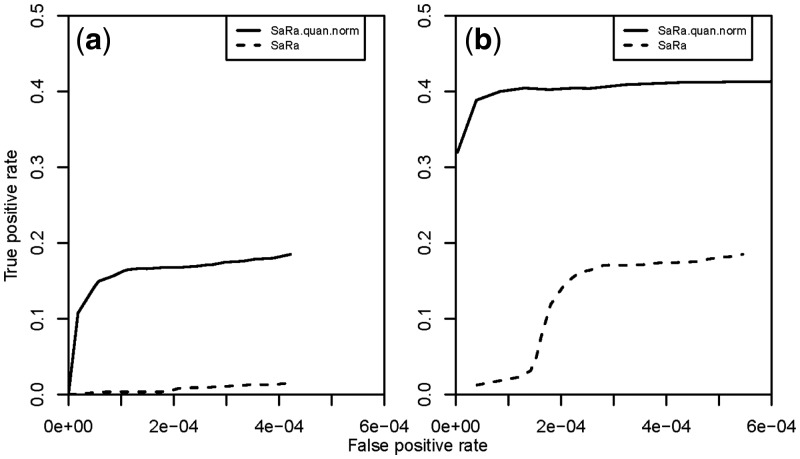
SaRa was developed based on normal assumption for error. In our simulation, we evaluated the robustness of the original version of SaRa in identifying change-points if the normal distribution assumption was violated. It was obvious that SaRa presented very poor power for change-points detection when the noises had t-distributions, especially when the degree of freedom was one (Fig. 3). After applying QN in the preprocessing step, SaRa presented greatly increased power when compared with that without QN in both simulation scenarios. Therefore, with the extra QN step, SaRa presented robustness to the normal assumption. This simulation underscored the necessity of QN strategy of SaRa on change-points detection with SNP genotyping array.

Fig. 3.

Performance of SaRa on simulated datasets with noise intensities following t-distributions. We simulated 100 signal sequences with length 10 000. Ten change regions were chosen at each sample sequence. The jump sizes for the change regions were (2.56, −3.47, 3.02, 3.26, −3.92, −3.12, 1.74, 3.05, −3.09, −2.69). The change segment lengths were (35, 18, 79, 62, 51, 27, 84, 32, 26, 19). The true positive rate was the ratio of the number of observed change-points to the total number of true change-points. The false-positive rate was the ratio of the observed false change-points to the total number of points. The dashed lines denote the performance of SaRa method on the simulated dataset. The solid lines denote the performance of the SaRa method after QN of the dataset. The simulated noise sequences were distributed as (a) t(1); and (b) t(2)

3.2 Simulation studies of the modified SaRa

To study the performance of the modified SaRa in more realistic settings, we conducted simulations mimicking real SNP genotyping data. Three scenarios were considered including: (1) CNV regions with deletion of one copy; (2) CNV regions with deletion of double copies and (3) CNV regions with a mixture of copy number states.

Figure 4 displays the histogram of the simulated data for Scenario 1. Obviously, the original data were far from normal distribution before QN. Though the assumption of the normal errors for each state was still not guaranteed after QN, it was mostly satisfied since a majority of the intensities were from the normal state with two copies.

Fig. 4.

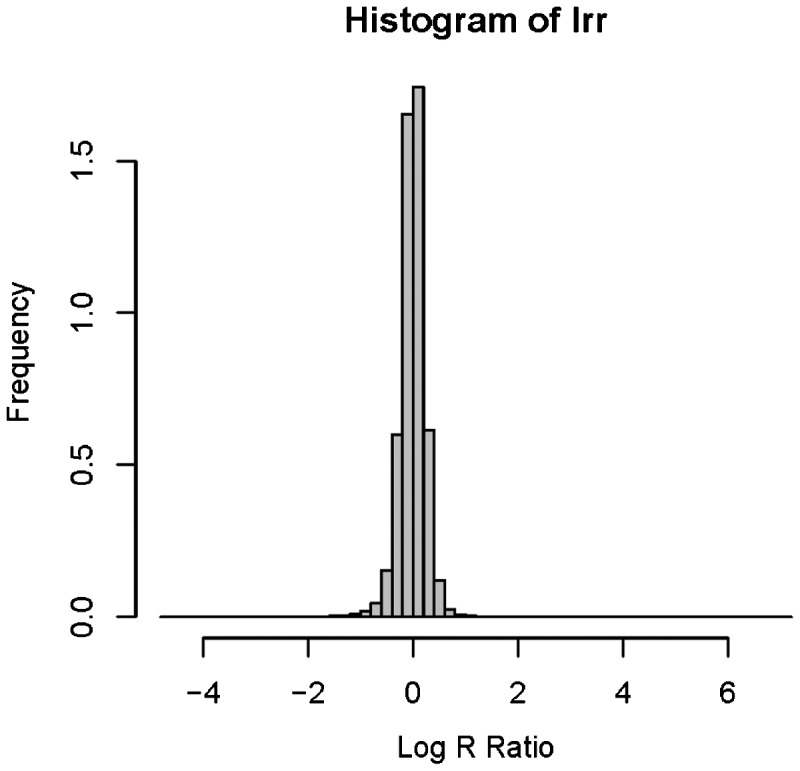
Histogram of the simulated data with CNV segments (deletions)

We compared the performance of the modified SaRa with that of CBS on the simulated datasets. For Scenario 1 with deletion of a single copy, the modified SaRa performed much better than CBS although CBS was overall improved with QN (Table 3). The modified SaRa usually identified much fewer false-positive change-points than CBS under the similar true positive rates no matter if QN is applied or not. For Scenario 2 with deletion of double copies (Table 4), similarly, the modified SaRa significantly outperformed CBS no matter if QN was applied or not. In conclusion, the modified SaRa achieved high sensitivity with much better filtering of the false positives than CBS. The overall performance of the modified SaRa was obviously better than CBS in detection of change-points of deletions.

Table 3.

Performance of the modified SaRa and CBS on detecting change-points in the simulated datasets in Scenario 1 with deletion of a single copy

modSaRa			CBS_QN			CBS
TP	FP	TPR	TP	FP	TPR	TP	FP	TPR
4658	285	0.856	4816	30613	0.885	4624	10328	0.850
4839	324	0.890	4887	31405	0.898	4839	16603	0.890
4919	384	0.904	4925	32268	0.905	4909	21463	0.902
4986	438	0.917	4994	33593	0.918	4960	26598	0.912
5042	492	0.927	5021	34343	0.923	5023	40295	0.923
5074	563	0.933	5097	37114	0.937	5075	60575	0.933
5097	1059	0.937	5127	38404	0.943	5115	74956	0.940
5099	1410	0.937	5174	41476	0.951	5191	145771	0.954

CBS_QN: CBS performed after QN of the intensities; TP: number of detected true positives; FP: number of detected false positives; TPR: true positive rate.

Table 4.

Performance of the modified SaRa and CBS on detecting change-points in the simulated datasets in Scenario 2 with deletion of double copies

modSaRa			CBS_QN			CBS
TP	FP	TPR	TP	FP	TPR	TP	FP	TPR
5401	49	0.993	5391	23042	0.991	5424	10977	0.997
5417	62	0.996	5415	32489	0.995	5432	12150	0.999
5423	68	0.997	5423	35505	0.997	5434	12709	0.999
5432	88	0.999	5432	60148	0.999	5435	13423	0.999
5436	99	0.999	5436	106448	0.999	5436	14565	0.999
5438	90	1	5437	208646	0.999	5438	16760	1

CBS_QN: CBS performed after QN of the intensities; TP: number of detected true positives; FP: number of detected false positives; TPR: true positive rate.

Scenario 3 considered a mixture of four states of CNVs in each subject. Although CBS reached high true positive rates when the number of false positives was very high, the modified SaRa was more powerful than CBS when the number of false positive was at a very low level (Supplementary Table 1). The modified SaRa still outperformed CBS regardless if QN was or was not applied to CBS. In summary, the modified SaRa was preferable to CBS.

3.3 Real data analyses

To demonstrate the performance of the modified SaRa in real data, we applied the modified SaRa to the 299 individuals from HapMap project. Before applying the change-point identification methods, we smoothed the intensities to remove outliers (Supplementary Fig. S3). By setting the significance level at 0.01, SaRa identified 11 254 change-points in total.

To evaluate the identified change-points, we checked the distribution of lengths of segments between adjacent change-points across all subjects. Ideally, approximately 50% of the segments were CNV segments and the remaining were inter-CNV segments if the change-points were detected perfectly. Most of the soundly identified CNV segments are fewer than 100 markers as indicated in Section 2.6.2 and Supplementary Figure S2, whereas the inter-CNV segments are usually much longer. As a consequence, ideally we would observe around 50% short segments. On the contrary, both false positives and false negatives would decrease this percentage. Therefore, a percentage of short segments closer to 50% implies better performance in detecting change-points. To this aspect, we found that the proportions of the segments identified by the modified SaRa which spanned less than 60 and 100 markers were 39.82 and 43.24%, respectively (Fig. 5), which were close to the expectation but suggested that there still existed a certain number of false positive change-points.

Fig. 5.

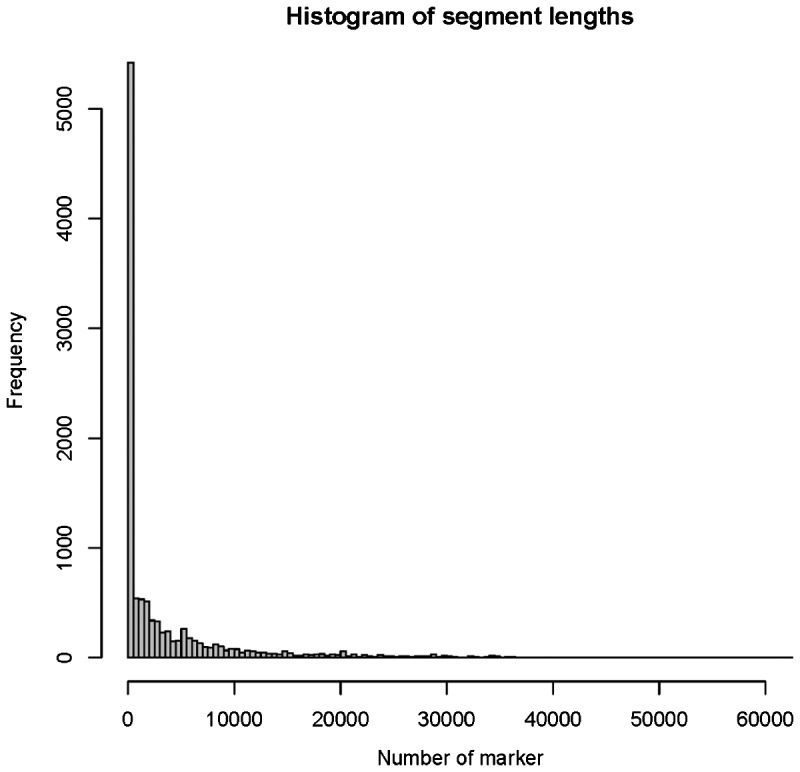
The distribution of number of markers between two adjacent change-points identified by the modified SaRa. The significance level was set as 0.01

Fast CBS identified 16 002 change-points in total similar to the output of modified SaRa. The proportions of the segments which spanned less than 60 or 100 markers were 30.23 and 34.53%, which were less than the modified SaRa. The fact that the modified SaRa identified more segments with sound CNV lengths indicated its better specificity in CNV detection to some extent.

Moreover, we also evaluated the overlapping proportion of the change-points identified by PennCNV and the modified SaRa on chromosome 1. Of the change-points identified by PennCNV, 78.41% were also identified by the modified SaRa when the acceptance range was set as 10. Only 37.64 and 31.18% of the change-points identified by PennCNV were discovered by CBS with and without QN, respectively. Admittedly, this comparison was not ideal since the results from PennCNV could not be considered as truth, but the fact that the modified SaRa presented large overlapping proportions with PennCNV implied its high sensitivity in CNV detection.

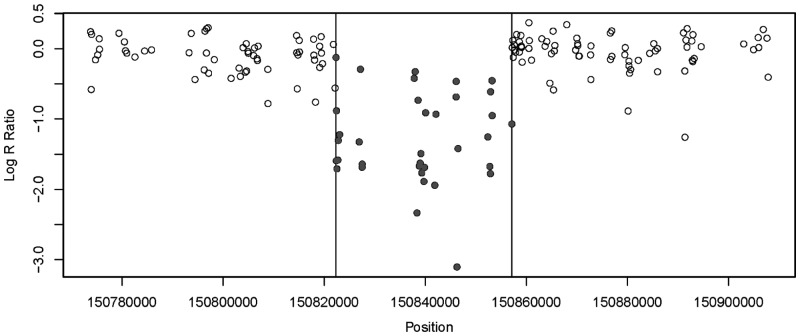
Figure 6 presents the change-points identified by the modified SaRa for individual A01_183598 from CEU population on chromosome 1 between markers CN_452249 and CN_453517. Noticeably the LRR values of the segment between 150.82 and 150.86 kb were significantly less than 0.

Fig. 6.

One identified CNV segment on chromosome 1 of individual A01_183598 from CEU population. Each dot denotes a marker

4 Discussion

In this article, we proposed a modified SaRa method to improve the power of SaRa by QN when the intensity is not normally distributed, and to reduce the false-positive errors by a clustering strategy. To evaluate the performance of our proposed method versus existing ones, we developed a novel method to generate DNA sequences that mimic real data for the purpose of evaluating CNV detection.

Our simulations with noises from t-distributions highlight the necessity of preprocessing by QN on SaRa which renders its robustness to the normal assumption (Fig. 3). Moreover, we propose to use multiple bandwidths in identifying change-point candidates to optimize the sensitivity, then a normal mixture model-based clustering strategy following BIC criterion in deletion of false positives to optimize its specificity. By applying the modified SaRa on a simulated dataset mimicking a real dataset from the HapMap project, we illustrated the great performance of the modified SaRa on detecting change-points with SNP genotyping arrays. In all the scenarios we simulated, the modified SaRa achieved better performance than CBS (Tables 3, 4 and Supplementary Table S1). QN also affected the performance of CBS to some extent. In addition, real data analyses indicated that the modified SaRa outperformed CBS in both sensitivity and specificity although they identified similar number of change-points. Our improvements emphasize the preference to use the modified SaRa in identification of CNVs. In conclusion, we propose a modified SaRa method by optimizing its performance in both theoretical and applicable aspects for identifying CNVs with high-throughput genotyping arrays.

The better performance of the modified SaRa on change-points detection compared with CBS highlights the necessity and contribution of our modification. The combination of multiple bandwidths and normal mixture model strategies allows optimized sensitivity and specificity. On the one hand, using multiple bandwidths, the modified SaRa achieves better power of the detection of change-points. While, on the other hand, the implementation of the normal mixture model-based clustering overcomes the over-sensitivity of the original SaRa to small mean changes, which is undesirable for CNV detection. Thus, the modified SaRa has more precise identification of the change-points corresponding to true CNVs. Such advantages are exhibited in the real data analysis results, in which the modified SaRa identified more realistic CNV segments than CBS. One concern of our modification is that larger CNV segments may be produced than the original version of SaRa. This is because we cluster two adjacent CNV segments together at the clustering step, when both have the same direction of change and similar jump sizes. However, as noted in the real data analysis, the proportion of short segments identified by SaRa was larger than CBS, which demonstrated that our modification did not mistakenly group adjacent change-points. We provide a reliable solution for the over-sensitivity issue of the original SaRa method in this study.

To effectively filter false-positive change-points, our suggestion is to apply normal mixture model-based clustering following subset selection based on modified BIC. Other combinations of these two strategies were also explored in the simulation studies: (i) selection with modified BIC criterion only; (ii) normal mixture model-based clustering only and (iii) selection with modified BIC criterion following normal mixture model-based clustering were all applied to the simulated datasets. However, our proposed combination exhibited the best performance on subset selection of the candidate pool. The underlying mechanism is of interest and will be further investigated in our future study.

Investigating the association of CNVs with common quantitative traits and human complex diseases is a challenging task in current genetic community. Our implementation in the SaRa method by optimizing its performance is of great value for CNV identification, which ensures more accurate and valid CNV calls for future association study. Compared with the originally developed SaRa, the improvements are reflected in three aspects. First, multiple bandwidths strategy assures better power. Second, the backward deletion strategy incorporating BIC criterion and normal mixture model allows better filtering of false positives and better calling of CNV segments. Last, QN strategy in the preprocess step makes the modified SaRa more robust for analyses of different data types.

As we stated above, one of the disadvantages of the modified SaRa is that it may incorrectly combine two neighbouring CNVs, which have minor differences in jump sizes in reality. For example, one segment presenting a large increase which may implicate duplication of double copies, and an adjacent one that has a smaller jump which may indicate duplication of a single copy, may be grouped to a single segment by our algorithm. This issue arises since we only use three copy number states in the clustering step. One possible solution is to introduce more states or clusters (e.g. five) in the clustering step using a normal mixture model, but more issues may arise such as the choices of initial parameters. Another solution is to incorporate the BAF values, which will further clarify the copy number states according to the distributions of BAF. This approach warrants future research.

In this study, we focus mainly on the optimal segment identification by local searching. Indeed, our proposed QN preprocessing procedure was initially motivated by evaluating the robustness of SaRa to non-Gaussian distributions. Most change-point-based methods assume normality for the noise intensities. In reality, the noise data of the SNP array sequences are usually not normally distributed, which makes the assumption of normal distribution invalid. In addition to the CNV detection methods developed for SNP arrays, the QN strategy can be extended to next generation sequencing data whose intensities may present heavy tailed noises (Cheung et al., 2011). Therefore, our study provides new insight on the CNV detection for next generation sequencing data. Moreover, it will be of great interest to develop a population based approach using data from multiple sequences or subjects for CNV identification, which will potentially improve the power of CNV detection.

Funding

This work was supported by National Institutes of Health grant, R01DA016750-10.

Conflict of Interest: none declared.