The role of inhibition in oscillatory wave dynamics in cortex

Abstract

Cortical oscillations arise during behavioral and mental tasks, and all temporal oscillations have particular spatial patterns. Studying the mechanisms that generate and modulate the spatiotemporal characteristics of oscillations is important for understanding neural information processing and the signs and symptoms of dynamical diseases of the brain. Nevertheless, it remains unclear how GABAergic inhibition modulates these oscillation dynamics. Using voltage sensitive dye imaging, pharmacological methods, and tangentially cut occipital neocortical brain slices (including layers 3–5) of Sprague-Dawley rat, we found that GABAa disinhibition with bicuculline can progressively simplify oscillation dynamics in the presence of carbachol in a concentration-dependent way. Additionally, GABAb disinhibition can further simplify oscillation dynamics after GABAa receptors are blocked. Both GABAa and GABAb disinhibition increase the synchronization of the neural network. By using a combination of GABAa and GABAb antagonists alone, theta frequency (5–15Hz) oscillations are reliably generated. These theta oscillations have basic spatiotemporal patterns similar to those generated by carbachol/bicuculline. These results are illustrative of how GABAergic inhibition increases the complexity of patterns of activity and contributes to the regulation of cortex.

Introduction

Brain oscillations are widely observed including the olfactory system (Lepousez et al., 2010), visual (Edden et al., 2009; Sun & Dan, 2009), sensorimotor (Reimer & Hatsopoulos, 2010), auditory (Luo & Poeppel, 2007) and hippocampus (Buzsaki, 2002; Geisler et al., 2010). In neocortex, oscillations occur at rest (Arieli et al., 1996; Mak & Wolpaw, 2009), and during spatial learning and working memory (Raghavachari et al., 2001; Rizzuto et al., 2003). Oscillations are important in spreading depression (Koroleva et al., 2009), migraine (Coppola et al., 2005), seizures (Worrell et al., 2004), and Parkinson`s disease (Schiff, 2010).

Oscillations are organized into spatiotemporal patterns, and patterns may propagate as traveling waves. Oscillatory traveling waves have been observed in olfactory bulb (Lam et al., 2000), motor cortex (Rubino et al., 2006), visual cortex (Xu et al., 2007), and spiral waves during sleep (Huang et al., 2010). In epilepsy, propagating waves of activity occur (Telfeian & Connors, 1998). The physiological role of traveling spatiotemporal oscillatory waves remains speculative (Ermentrout & Kleinfeld, 2001).

In vitro brain slices are useful for studying the mechanisms of oscillatory waves. Slice oscillations occur spontaneously in normal artificial cerebrospinal fluid (ACSF) (Wu et al., 2001). Theta frequency oscillations (4–15Hz in rodents) can be generated in slices by cholinergic activation using carbachol with GABAergic disinhibition (Bao & Wu, 2003; Cappaert et al., 2009; Lukatch & MacIver, 1997) or without (Fisahn et al., 1998; Palhalmi et al., 2004), and also employing 4-aminopyridine (Tancredi et al., 2000), high potassium (Towers et al., 2002) or low magnesium (Flint et al., 1997; Ziburkus et al., 2006).

Active inhibition limits the spread of epileptiform activity (Richter et al., 2010; Treiman, 2001). Oscillations in disinhibited tissues are associated with increased firing rates (Sanchez-Vives & McCormick, 2000), and true spiral waves are seen (Huang et al., 2004). The role of GABAb inhibition remains unclear (Buzsaki, 2002; de la Prida et al., 2006). We are aware of no systematic titration of the strength of inhibition with respect to spatiotemporal dynamic characteristics of oscillatory cortical waves.

The dynamics of neuron populations can be observed with voltage-sensitive dye (VSD) imaging in vitro (Bai et al., 2006; Carlson & Coulter, 2008; Yuste et al., 1997) and in vivo (Huang et al., 2010; Palagina et al., 2009; Prechtl et al., 1997; Xu et al., 2007). Unidirectional propagating waves (4–15Hz theta) in coronal cortical slices have a quasi 1-dimension character (Bao & Wu, 2003; Wu et al., 2001). However, in tangential slices, oscillations can propagate as complex two-dimensional waves (Huang et al., 2004). Four basic types of patterns in tangential slices are observed (Huang et al., 2004): irregular, plane, ring and spiral. Tangential slices preserve more of the natural dynamics of oscillations than coronal where oscillatory dynamics are more constrained.

Here we examine the effects of inhibition and excitation on 2-dimensional cortical wave dynamics with VSD imaging. We find increased complexity as inhibition increases, and demonstrate that a combination of pure disinhibitory GABAa and GABAb blockade permits robust oscillatory traveling wave formation without muscarinic activation.

Materials and methods

Tangential cortical slice preparation

All experiments were performed with approval from the Institutional Animal Care and Use Committee of Penn State University. Neocortical slices were obtained from 27 male Sprague-Dawley rats from P21 to P35. The animals were deeply anesthetized with diethyl-ether and decapitated. The whole brain was quickly removed and chilled in cold (4°C) artificial cerebrospinal fluid (ACSF) for 60s containing the following (in mM): 132 NaCl, 3 KCl, 2 CaCl₂, 2 MgSO₄, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 dextrose. ACSF was saturated with 95% O₂ and 5% CO₂ at room temperature for 1 hr before the experiment. Tangential slices were cut according to Huang et al. (2004), with a vibratome on the rostrocaudal and mediolateral coordinates of bregma −2 to −8 mm and lateral 1 to 6 mm, respectively. The first cut was made 300µm deep from the pial surface, and the tissue was discarded. The second cut was made 500µm deeper to obtain a 500µm-thick slice of middle cortical layers (including layers 3–5, Huang et al., 2004). The 500µm-thick slice was transferred into a holding chamber containing ACSF and incubated at 26 °C for at least 1 hr before staining. After 2 hr staining and 0.5 hr recovering in ACSF, the slice was transferred to a submersion chamber. The slice was perfused with ACSF at a rate of > 20ml/min for 30min (30–31°C) in the chamber before recording. Because of the curvature of the cortex, the size of the tangential slices was limited to about 5×6 mm². The anatomical regions included in these slices included primary and secondary visual cortex within the field of view imaged, with portions of the primary somatosensory and parietal association cortices lying outside of the field of view. Layer 5 was facing up in all the experiments and the slices in all the figures were oriented in the same way. The location of the stimulation electrode was kept consistent for the same slice in different experiments. The stimulus amplitude was chosen to be 1mA above the threshold amplitude for oscillation generation and kept consistent for the same slice for different drug conditions.

Voltage sensitive dye imaging

The imaging apparatus and methods are described in detail in Jin et al. (2002). Briefly, slices were stained for 2 h with 5 µg/ml of an absorbance oxonol dye, NK3630 (Nippon Kankoh-Shikiso Kenkyusho, Okayama, Japan). The dye was dissolved in ACSF (26 °C) on the day of use. Voltage-sensitive dye images were taken by a 464-element photodiode array (WuTech instruments) with 1.6 KHz sampling rate. An objective of 4× (0.10 NA, dry lens, Zeiss) was used to project the image of the tissue to the diode array and each photo detector received light from an area of 0.41×0.41 mm² of the tissue. The preparation was trans-illuminated by 705±20 nm light and was only exposed to the illumination light during optical recording trials for about 10s/trial. The typical voltage sensitive signal was 10⁻³ – 10⁻⁵ of the resting light intensity.

Pharmacological agents

Carbamylcholine chloride (carbachol), (−)-Bicuculline methiodide (Biomol®), picrotoxin, 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), 2,3-Dioxo-6-nitro-1,2,3,4-tetrahydrobenzo[f]quinoxaline-7-sulfonamide (NBQX), D-(−)-2-Amino-5-phosphonopentanoic acid (D-APV), DMSO and 3-[(3,4-Dichlorophenyl)methyl] aminopropyl (diethoxymethyl) phosphinic acid (CGP 52432), were used in combinations to evoke or suppress oscillations. Carbachol, bicuculline, CGP52432 and D-APV were made into high concentration stock solutions with deionized water (18MΩ resistance). Picrotoxin, CNQX and NBQX were dissolved in dimethyl sulfoxide (DMSO). The final concentration of DMSO was 0.05% (volume/volume) when picrotoxin was added into solution, and 0.1% (volume/volume) when CNQX or NBQX was added. As reported in Fink et al. (2000), these final concentrations of DMSO did not appear to affect our experiments. Carbachol, picrotoxin and DMSO were purchased from Sigma-Aldrich (St Louis, MO, USA). CNQX, NBQX, D-APV and CGP 52432 were purchased from Tocris (Ellisville, MO,USA).

Data analysis

Data visualization and dynamics analysis

The optical data were acquired using NeuroPlex software (RedShirtImaging, Fairfeild, CT). Oscillations from each slice were evoked by a 0.5ms 5–7mA square wave pulse, and further analyzed using MATLAB programs (Mathworks, Natick, MA). In brief, raw data acquired at 1.6KHz were resampled to 1000Hz. There is a 0.5–1.0 second latent period following brief stimulation when inducing such wave patterns which has not yet been characterized to our knowledge. To remove the initial stimulus artifact and coupled neuronal activation, as well as the latent period, the first 2 seconds of resampled data were discarded. (We illustrate examples of the initial stimulation and latent period in supplementary figures S1, S2, and S3). The remaining data were normalized by the maximum value from each photodiode signal; the normalized data were low-pass filtered under 30Hz for spectral coherency analysis (described below). Based on the results from spectral coherency analysis, the normalized data were further band-pass filtered between 5–30 Hz for synchrony and dynamics analysis to focus on results as free of artifact as possible. In supplementary figures S1, S2, and S3, we included frequencies 0–5 Hz in both optical and electrical signals, and the correlated low frequencies in optical tracings can clearly be seen in contrast with the electrical signal. At 705 nm, one can see intrinsic optical signal related to cell swelling in the optical measurements, but at this light frequency the intrinsic signal will not mask the neuronal voltage signal (Bai et al., 2006). Furthermore, intrinsic optical signal tends to correlated with and lag behind neuronal activity, features not clearly represented in our low frequency traces. We therefore attribute most of our optically only correlated optical signal to movement artifact, which is corroborated by the spectra in the supplementary figures demonstrating no difference in frequencies below 5 Hz in the different experimental conditions that affect the neuronal activity of these slices. Spectral analysis was performed using a multitaper method (Mitra & Pesaran, 1999). Since the presence of shot-noise in the optical signal makes direct visualization of the space-time data difficult, filtered data were further spatiotemporally denoised using singular value decomposition (Mitra & Pesaran, 1999; Schiff et al., 2007).

Activity patterns of denoised data were obtained by visualizing the full sequence of images displayed as pseudocolor images. In the pseudocolor images, data from each optical detector were normalized to their own maximum, and then each normalized data point was assigned a color according to a linear color scale. Therefore, the smallest normalized data point was assigned zero on the color scale and showed deep blue in the image; the maximum normalized data point was assigned 1 on the color scale and showed deep red. Displayed figures were further smoothed with a 3×3 spatial filter. The complexity of wave dynamics was quantified by a modal dimension analysis (Schiff et al., 2007). A 1-tailed t-test was used to determine the significance level of differences between 2 groups. One-way ANOVA and Tukey post hoc testing were used to determine the significance level of differences between more than 2 groups. P<0.05 was regarded as significant.

Bootstrap method

In the present study, bootstrapping was based on resampling time series multiple times by exchanging segments of a time series at a different random location (see detailed description in Schiff et al., 2005). The resultant surrogate data sets are measured in the same way as the original data to generate an ensemble of measurements. For the surrogate data sets, the local correlations are largely destroyed. Only the values above the 95^th percentile of the ensemble of measurements obtained from the surrogate data sets will be considered meaningful.

Spectral coherency analysis

In VSD measurements from brain slices, there are artifacts caused by vibrations and fluid waves in the light path. Motion artifacts in the VSD signal should have no relationship with the membrane potential changes of interest. In order to study neural activity without the contamination of vibration artifacts, the signal frequency range of interest for analysis was determined through a comparative coherency analysis.

We consider that signals coherent in frequency (or significantly correlated in the time domain) in both local field potential (LFP) and optical signals are electrical signals that are caused by membrane potential changes. If the signal in some frequency band is only coherent between optical detectors but not coherent in LFP at the same time, this signal is likely to be an artifact. It is also possible that the optical signals are correlated by slow intrinsic optical signals (Bai et al., 2006), which would not be relevant to the present study. In brief, LFP and signals from four optical detectors (labeled optical 1, optical 2, optical 3 and optical 4), which were spatially close to the tip of the LFP recording electrode, were chosen for each trial to do the coherency analysis. The LFP and optical signals were resampled to 1000Hz and low-pass filtered at 30Hz before calculating the multi-taper normalized cross-spectrum for each pair of filtered data from two optical detectors (data pairs include: optical 1-optical 2, optical 1-optical 3, optical 1-optical 4, optical 2-optical 3, optical 2-optical 4, optical 3-optical 4) or from the data pair of LFP and one optical detector (data pairs include: LFP-optical 1, LFP-optical 2, LFP-optical 3, LFP-optical 4). These 10 data pairs were analyzed for each trial. The bootstrap method was used to set the statistical reference for the confidence level. For each data (LFP or optical), the time series within each six-second window was resampled 1000 times by bootstrapping. The surrogate data pairs were subjected to the same multi-taper coherency analysis and the same 95^th percentile confidence level was used as with the original data pair. To be very conservative, only coherency levels of original data pair greater than the bootstrapped 95^th percentile were considered likely to be significant.

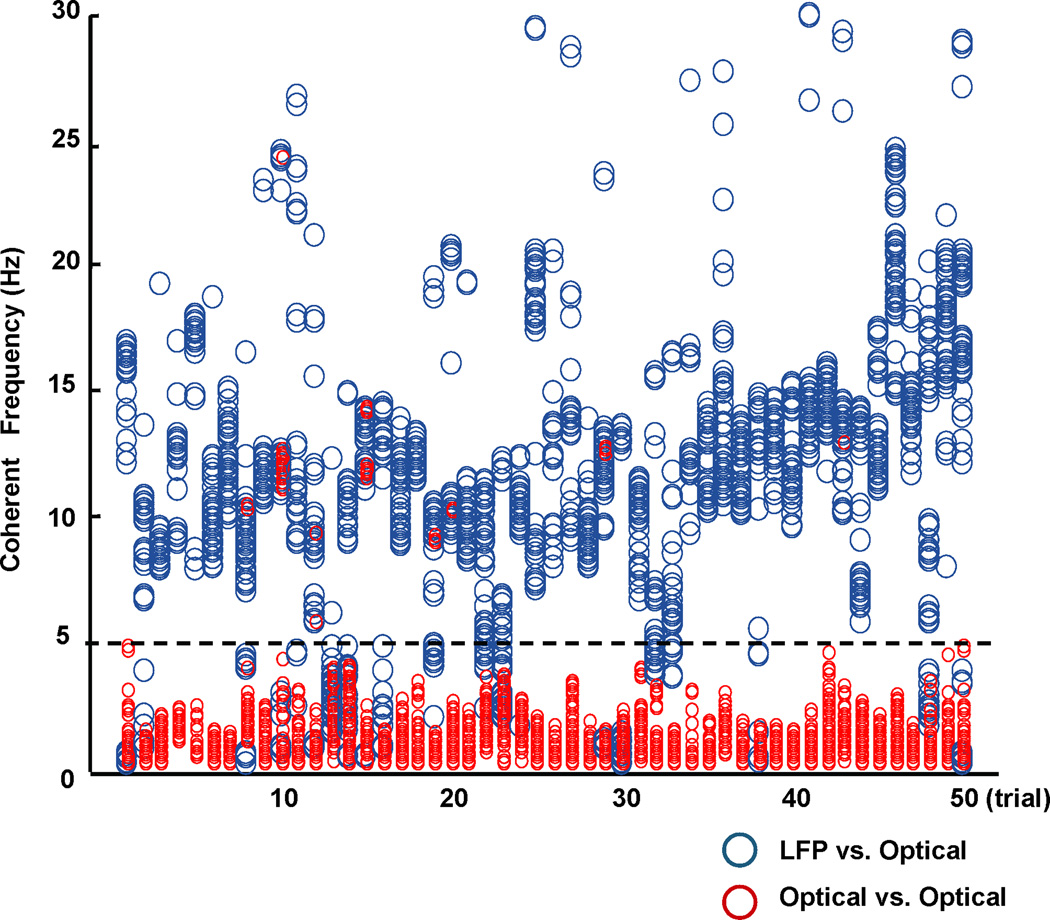
In Figure 1, most of the coherent frequencies between the LFP and optical signals (shown as blue circles) were within the range of 5–30Hz, while most of the coherent frequencies between optical signals alone (shown as red circles) were within the 0–5Hz range. When optical-optical signals were coherent within the 5–30Hz range, they all closely overlapped with coherent frequencies between LFP and optical signals. Therefore, coherent frequencies within the 5–30Hz band appear largely artifact free and reflect membrane potential changes. The situation below 5Hz is considerably more complex. As shown in Figure 1, there are examples where optical-optical coherency is confirmed by optical-LFP coherency, and many examples where the optical-optical and LFP-optical coherencies are separate. To be conservative, we will eliminate from study in this report all of the coherent results within this lower frequency range, recognizing that in this process we will eliminate some very real low frequency correlations that are present in our measurements. Based on these screening coherencies, we therefore band-pass filtered all data between 5–30 Hz to focus on describing results as free of artifact as possible.

FIG. 1.

Spectral coherency analysis. Each column of markers represents the coherency analysis of a 6-second oscillation episode in each of 50 trials from different slices. The oscillations were generated using six pharmacological combinations with the trigger of a 0.5ms 5–7mA single square wave electrical pulse. The pool of the coherent (or significantly correlated) frequencies derived from 4 pairs of LFP-optical data for one trial are shown in one column using gray circles; the black circles shown in the same column represent the coherent frequencies derived from 6 pairs of optical-optical data for the same trial. Note that gray and black circles above 5Hz overlap within narrow frequency ranges.

Synchrony analysis

Synchrony analysis was performed according to methods described in Schiff et al. (2005; a code archive is available with this citation). For computational efficiency, signals from 31 optical detectors were selected, so that the picked detectors were distributed in the imaging field as evenly as possible. The sampled detectors were the same for each experiment. Crosscorrelation at both zero lag and arbitrary lags, and phase variance for all data pairs, were calculated for each non-overlapping one-second window of 5–30Hz filtered data. For phase variance, phase was assigned from Hilbert transformation of each 6-second time series from each optical detector using Bendat and Piersol`s method (Bendat & Piersol, 1986). For each time point of the 6-second trial the sum of the cosine and the sum of the sine of the phases over all the 31 optical detectors were taken, and the average phase angle was calculated for each time point. The sequential average angle was unwrapped before calculating the difference between adjacent average angles. The variance of the differences between sequential average angles was calculated for each 1-second time window to generate the phase variance.

Bootstrapping was used to get the statistical confidence level of crosscorrelation at zero and arbitrary lags as well as the phase variance. Data were resampled 100 times within each non-overlapping 1-second window. The crosscorrelation at zero lag for each second was considered significant when its value was above the 95^th percentile of the ensemble of crosscorrelation obtained from the surrogate data sets. Mean value and standard deviation of the ensemble of crosscorrelation value can be calculated and mean ± twice the standard deviation was taken as the confidence interval; only the crosscorrelation values at arbitrary lag beyond the confidence interval were considered significant and their absolute value summed. The phase variance for each second was considered significant when the value was smaller than the 5^th percentile of the ensemble of bootstrapped phase variance. The sum of crosscorrelation at zero lag for the whole 6-second duration window for all data pairs was also calculated by summing the significant crosscorrelation at zero lag from each second of data. The sum of crosscorrelation at arbitrary lags for the whole 6-second window for all data pairs was calculated by summing the significant crosscorrelation at arbitrary lags from each second of data. The sum of phase variance for the whole 6-second duration window was calculated by summing the significant phase variance from 6 one-second windows. The sum of crosscorrelation at both zero lag and arbitrary lags and sum of phase variance were normalized before they were compared using 1-tailed t-test or ANOVA.

Results

Effects of GABAa receptor, GABAb receptor, NMDA receptor and AMPA receptor blockade on oscillation waveforms

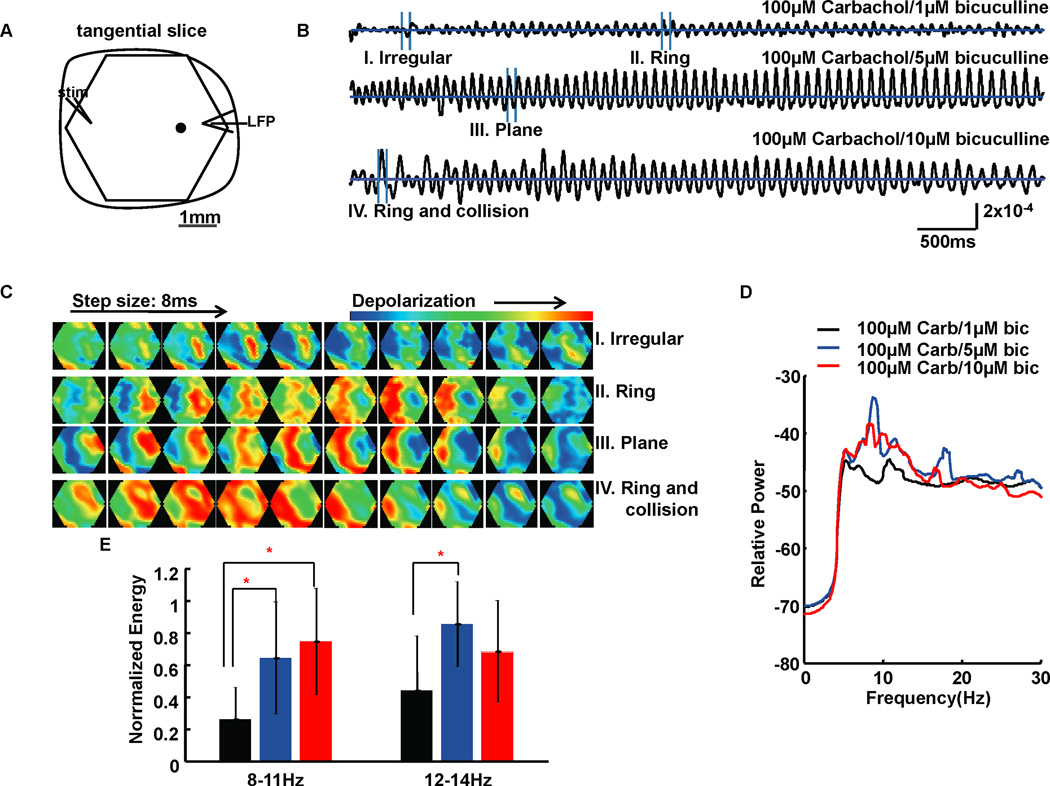
In the following GABAa titration experiments, 100µM carbachol was used in the perfusate to activate the slices (after Huang et al., 2004). Bicuculline concentration was increased gradually from 1µM to 10µM. Although in disinhibited transverse cortical slices oscillatory episodes will occur spontaneously, we typically have used small electrical stimuli to trigger such events in order to reduce exposure to phototoxic effects with VSD imaging (Huang et al., 2004). Without bicuculline in the perfusate, propagating oscillations could not be evoked by a single electrical pulse stimulus. With 1µM bicuculline, low amplitude propagating theta frequency oscillations were evoked (Fig. 2B). The beginning second or so of the trace in Figure 2B shows an irregular waveform, followed by more regular oscillations as the episode evolves (a more complete discussion of such event evolution can be found in Schiff et al. 2007). When bicuculline was increased to 5µM or 10µM, propagating theta frequency oscillations showed higher amplitudes and more regular waveforms (Fig. 2B). Power spectrum analysis was performed on the oscillations generated by different bicuculline concentrations and the energy of frequency components was compared between groups. When bicuculline was increased from 1µM to 5µM, the dominant frequency peak in the average power spectrum of 10 slices shifted towards lower frequency, from 10Hz to 8Hz; when bicuculline increased to 10µM, the frequency peak continued its drift towards lower frequency (Fig. 2D). Statistical analyses (1-way ANOVA and Tukey post-hoc testing) confirmed that when bicuculline was increased from 1µM to 5µM, the energy of 8–11Hz and 12–14Hz frequency components of 10 slices were significantly increased (df=29, F=6.25, P=0.0059; and df=29, F=4.52, P=0.0203; respectively) (Fig. 2E), and the energy of 8–11Hz (df=29, F=6.25, P=0.0059) frequency components were significantly increased by 10µM bicuculline compared with 1µM bicuculline (Fig. 2E).

FIG. 2.

Results for bicuculline titration experiments. (A) Schematic drawing of imaging field (hexagonal) with a 4× objective overlying a 500µm thick tangential occipital cortical slice. The slice included layers 3–5. A 0.5ms 6mA single square wave electrical pulse was given at the edge of the slice as a stimulus (stim) to evoke oscillations. LFP at the edge of the slice was recorded simultaneously with the optical recordings. One example optical detector is indicated as a black filled circle within the imaging field. Data from optical detectors that are spatially close to the LFP recording electrode tip are needed to get filter criteria by coherency analysis before further analyses, while traces from optical detectors used to accompany the gray scale images are not required to be close to the LFP recording electrode tip. Signals measured at the picked detector are shown as six-second traces in (B). The horizontal lines in traces of B are zero baselines. Vertical scale: 2×10⁻⁴ of resting light intensity. (C) Four sections from the temporal data (I–IV) in B are displayed as a sequence of gray scale images. These gray scale images are displayed at 8 ms intervals between frames. (D) Power spectrum (logarithmic scale) for optical signals during a 6-second episode averaged across all detectors of 10 slice experiments. Carb: carbachol; bic: bicuculline. (E) Bar plot shows the average normalized energy in two frequency ranges corresponding to three bicuculline concentrations. Error bars represent ± standard deviation. Light gray, gray and black bars represent 1µM, 5µM and 10µM bicuculline, respectively. The 10µM bicuculline group had significantly higher energy at 8–11Hz than 1µM bicuculline group, while the 5µM bicuculline group had significantly higher energy at 8–11Hz and 12–14Hz than 1µM bicuculline group. The significant differences between groups in E are marked by asterisks (*).

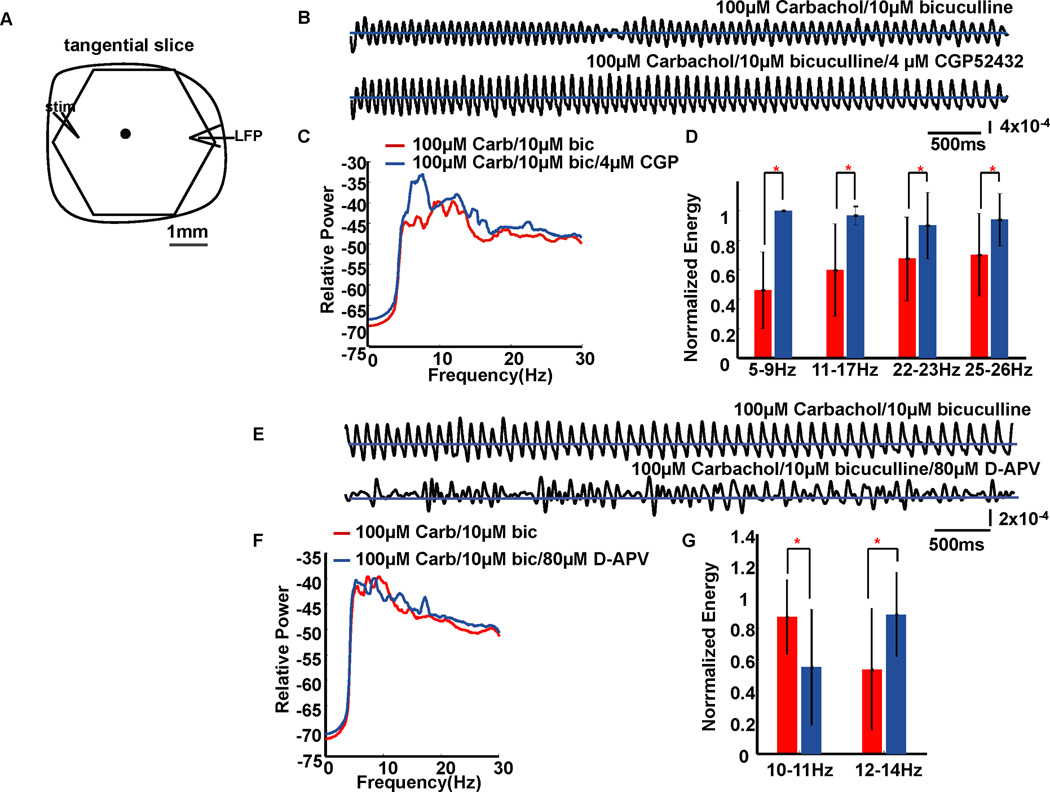
To examine the influence of GABAb on theta frequency oscillation, the GABAb antagonist CGP52432 was applied. Compared with those evoked without CGP52432, oscillation waveform became more regular with 100µM carbachol/10µM bicuculline/4µM CGP52432 (compare traces in Fig. 3B). These results are consistent with the increased oscillation amplitude shown for a similar drug combination in Lukatch & MacIver (1997), although they did not discuss these displayed findings. The dominant frequency peak in the average power spectrum of 9 slices shifted from 12Hz to 7Hz when compared with the group without CGP52432 (Fig. 3C). The energy of 5–9Hz (1-tailed t-test, df=16, P=6.74×10⁻⁶), 11–17Hz (df=16, P=0.0015), 22–23Hz (df=16, P=0.0396) and 25–26Hz (df=16, P=0.0235) frequency components were significantly increased by CGP52432 (Fig. 3D).

FIG. 3.

The effects of GABAb disinhibition and NMDA receptor blockade on theta oscillation waveforms. (A) Recording arrangement. Signals from one example optical detector (marked as a black filled circle in A) with and without GABAb inhibition are shown as 6-second traces in (B). Traces in (E) are signals from the same example optical detector with and without NMDA receptors activation. The horizontal lines in traces of B and E are zero baselines. In B, vertical scale: 4×10⁻⁴ of resting light intensity; in E, vertical scale: 2×10⁻⁴ of resting light intensity. (C) Power spectrum (logarithmic scale) for the optical signals during a 6-second episode, averaged across all detectors from 9 slice experiments. Carb: carbachol; bic: bicuculline; CGP: CGP52432. The average peak frequencies with 100µM carbachol/10µM bicuculline were about 10Hz and 12Hz. When CGP52432 was in the solution, the peak was about 7Hz with a more minor peak at about 12Hz. (D) Bar plot shows the average normalized energy in four frequency ranges corresponding to conditions with and without GABAb inhibition. Error bars represent ± standard deviation. Black and gray bars represent the 100µM carbachol/10µM bicuculline group and the 100µM carbachol/10µM bicuculline/4µM CGP52432 group, respectively. CGP52432 significantly elevated energy at 5–9Hz, 11–17Hz, 22–23Hz and 25–26Hz when compared to the group without CGP52432. (F) Power spectrum for conditions with and without NMDA receptor activation, averaged across all detectors from 8 slice experiments. (G) Energy analysis. Black and gray bars represent the 100µM carbachol/10µM bicuculline group and the 100µM carbachol/10µM bicuculline/80µM D-APV group, respectively. D-APV significantly decreased energy at 10–11Hz while significantly increasing energy at 12–14Hz when compared with the no D-APV group. The significant differences between groups in D and G are marked by asterisks (*).

Consistent with coronal neocortical slices (Lukatch & Maciver, 1997), blocking NMDA receptors using 80µM D-APV generated the appearance of large amplitude irregular waves in place of more rhythmic ones (compare traces in Fig. 3E). D-APV altered the frequency content of the oscillations (Fig. 3F), with energy of 10–11Hz components of eight slices significantly (1-tailed t-test, df=14, P=0.0289) decreased by D-APV, while the energy of 12–14Hz components were significantly (df=14, P=0.0276) increased (Fig. 3G).

Also similar with coronal neocortical slice results (Lukatch & Maciver, 1997), propagating oscillations in tangential occipital neocortical slices required AMPA receptor-mediated synaptic transmission. When AMPA receptors were blocked with 30µM CNQX (NBQX, which was also used in the present study, had very similar effects on these oscillations as CNQX), propagating oscillations were eliminated (supplementary Figure S4.).

Effects of GABAa, GABAb disinhibition and NMDA blockade on oscillation dynamics

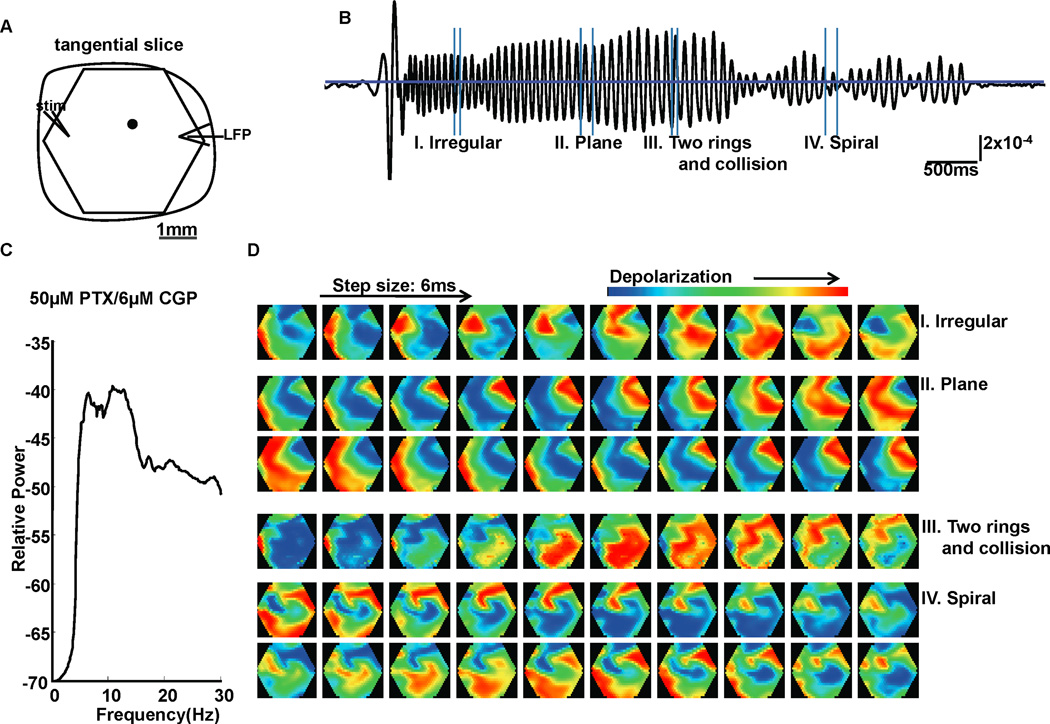
Each temporal oscillation cycle was associated with one spatial propagating wave (consistent with Bao & Wu, 2003). The spatiotemporal pattern of one propagating wave can be observed by visually inspecting sequential pseudocolor images. In general, the wave patterns can be classified as regular waves and irregular waves. Regular waves are defined as the waves that repeatedly appear in a certain pattern for several cycles of an oscillation episode. Simple regular waves include three basic patterns: ring waves (such as image in Figs. 2C. II, and supplemental movie file M1), plane waves (such as images in Fig. 2C. III, and supplemental movie file M2) and spiral waves (such as images in Fig. 6D. IV, and supplemental movie file M3). Besides simple basic patterns, regular waves in the present study also included complex patterns which were the combination of one or more basic wave patterns, such as ring with collision (Fig. 2C. IV, and supplemental movie file M4), multiple rings (Fig. 6D. III), etc. Irregular waves change pattern from cycle to cycle and are not periodic.

FIG. 6.

Oscillations evoked by combination of PTX and CGP52432. (A) Recording arrangement. Signal from one example optical detector (marked as a black filled circle in A) is shown in (B). Vertical scale: 2×10⁻⁴ of resting light intensity. (C) Power spectrum (logarithmic scale) for optical signals averaged from 7 slice experiments. The average peak frequencies were at about 6Hz and 11Hz. (D) Pattern examples of a 6-second oscillatory episode evoked with 50µM PTX/6µM CGP52432 in B. These gray scale images are displayed at 6 ms intervals between frames. In section III, responses that emerged at 2 locations in the imaging field developed into 2 connected rings and collided as the rings propagated.

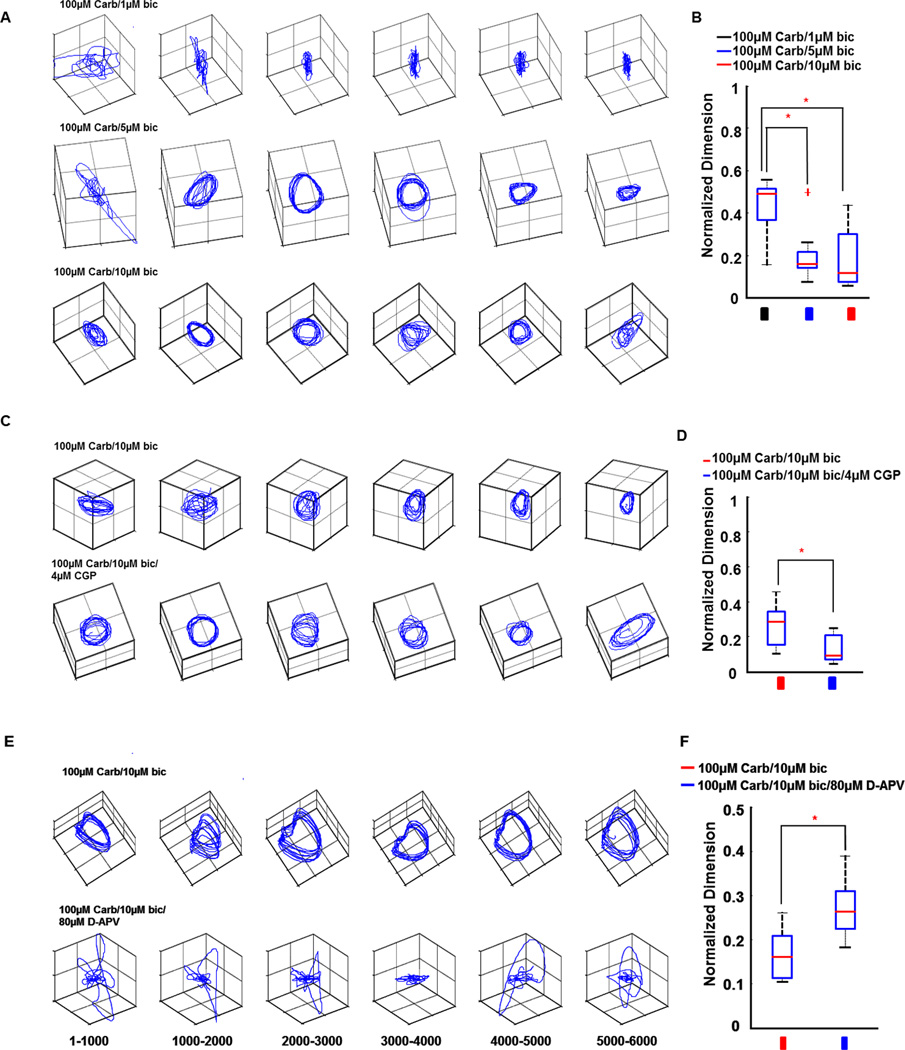
The changes in complexity of oscillation dynamics can be visualized by the use of trajectory plots of modal amplitudes (Schiff et al., 2007). These modal amplitudes are the amplitudes of the spatial modes calculated from a singular value decomposition, and these trajectory plots have been employed as a means of visualizing wave data from both whole brain (Senseman & Robbins, 1999) and slice data (Schiff et al., 2007). Simple periodic dynamics tend to show closed loops or limit-cycles when plotted in this manner. When the spatiotemporal dynamics are complex (substantially greater than 3-dimension), and aperiodic, the trajectory plots tend to show a lack of organized structure. Trajectory plots revealed that oscillations evoked with 5µM and 10µM bicuculline had much simpler dynamics than those evoked with 1µM bicuculline (compare three rows of trajectory plots in Fig. 4A). Analysis for 10 slices showed that oscillations evoked with 5µM and 10µM bicuculline had significantly lower dimension in spatial frequency (df=29, F=12.07, P=0.0002) and spatial amplitude (df=29, F=11.17, P=0.0003) modes than those evoked with 1µM bicuculline (Fig. 4B). The dynamics of oscillations evoked by 100µM carbachol/10µM bicuculline was further simplified by 4µM CGP52432 (Fig. 4C). Dimension analysis for 9 slices confirmed that CGP52432 significantly decreased dimension of oscillations in both spatial frequency (1-tailed t-test, df=16, P=0.0083) and spatial amplitude modes (df=16, P=0.0152) when compared with the group without CGP52432 (Fig. 4D). However, NMDA blockade by 80µM D-APV complicated the dynamics of oscillations evoked by 100µM carbachol/10µM bicuculline (Fig. 4E). Dimension analysis for 8 slices confirmed that D-APV significantly increased dimension of oscillations in both spatial frequency (df=14, P=0.0022) and spatial amplitude (df=14, P=0.0447) modes (Fig. 4F).

FIG. 4.

Dynamical complexity analyses for different conditions. (A) Dynamics from 6-second oscillatory episodes for three bicuculline concentrations are represented by three rows of trajectory plots in A. The trajectory plots are formed by plotting the time series of the amplitude of the first 3 spatial modes (called temporal modes) as the coordinates of the trajectory. Each trajectory plot is derived from a 1 s epoch. Note the simplification of trajectories when 5µM and 10µM bicuculline was added with 100µM carbachol when compared with 1µM bicuculline. (B) Box plot for dynamical complexity analysis. Light gray, gray and black bars in B represent 1µM, 5µM and 10µM bicuculline, respectively. Each box bounds the 25% and 75% percentiles (this defines the inter quartile range, IQR). The gray bar inside each box represents the median. Bars above and below the box represent 1.5 times the IQR. Plus sign (+) stands for outlier (defined as outside 1.5 times IQR). One-way ANOVA and Tukey post hoc analysis are used to check the significance level in dynamical complexity analysis in B. 5µM bicuculline and 10µM bicuculline groups had significantly lower dimension in spatial frequency mode than the 1µM bicuculline group. (C) Trajectory plots for groups with and without GABAb inhibition. (D) Dynamical complexity analysis for the effect of GABAb disinhibition. Black and gray bars in D represent groups without and with CGP52432, respectively. CGP52432 significantly decreased dimension in spatial frequency mode when compared to the group without CGP52432. (E) Trajectory plots for groups without and with NMDA receptor blockade. (F) The effect of NMDA receptor blockade on dynamical complexity. Black and gray bars in F represent groups without and with D-APV, respectively. D-APV significantly increased dimension in spatial frequency mode. Asterisks (*) in B, D and F indicate significant difference between groups. Carb: carbachol, bic: bicuculline, CGP: CGP52432.

In summary, in the presence of carbachol, GABAa, and GABAb disinhibition, there is a significant decrease in the dynamical complexity of oscillations, while NMDA blockade significantly increased the dynamical complexity.

Modulation of neural response synchronization by GABAa, GABAb disinhibition and NMDA blockade

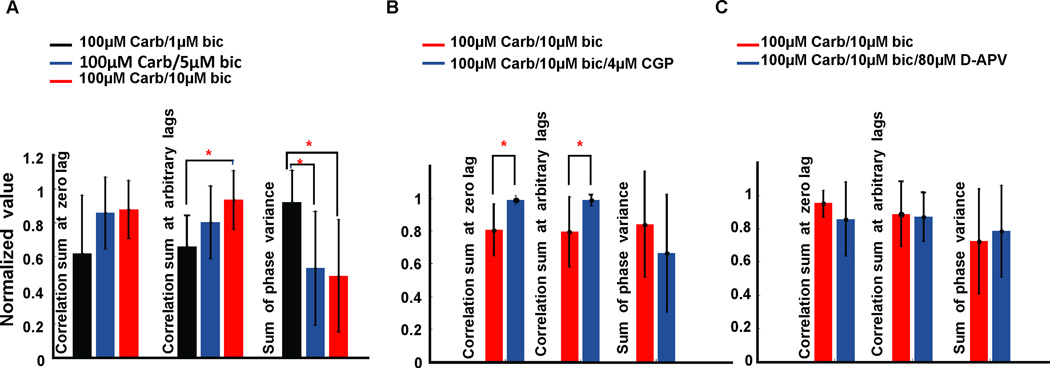
Synchronization of neural responses was measured by three parameters: crosscorrelation sum at zero lag, crosscorrelation sum at arbitrary lags, and sum of phase variance. The average results of 10 slices for the modulation of synchrony by GABAa disinhibition were shown in Figure 5A. There was no significant change in crosscorrelation sum at zero lag. However, 10µM bicuculline significantly increased the crosscorrelation sum at arbitrary lags when compared with 1µM bicuculline (ANOVA and Tukey post hoc analysis, df=29, F=5.23, P=0.012); 5µM and 10µM bicuculline also significantly decreased the sum of phase variance reflecting increased synchronization (df=29, F=4.07, P=0.0285) when compared with 1µM bicuculline. Phase can be a useful metric of synchronization in nonlinear systems when linear crosscorrelation may be insensitive (Pikovsky et al., 2000). But this issue is complex (Netoff et al., 2004) and we present both types of measurement here to more fully capture the characteristics of the interactions of these neuronal networks.

FIG. 5.

Synchrony analyses for different conditions. (A) Bar plots show the average normalized values of three parameters for synchrony corresponding to three bicuculline concentrations. Error bars stand for ± standard deviation. Light gray, gray and black bars in A represent 1µM, 5µM and 10µM bicuculline group, respectively. One-way ANOVA and Tukey post hoc analysis are used to check the significance level in A. 10µM bicuculline group had significantly higher crosscorrelation sum calculated at arbitrary lags than the 1µM bicuculline group; 5µM bicuculline and 10µM bicuculline groups had significantly lower sum of phase variance than the 1µM bicuculline group. However, there was no significant difference within groups in the correlation sum calculated at zero lag. (B) Synchrony analysis for the effect of GABAb disinhibition. Black and gray bars in B represent 100µM carbachol/10µM bicuculline group and the 100µM carbachol/10µM bicuculline/4µM CGP52432 group, respectively. CGP52432 significantly elevated the crosscorrelation sum at both zero lag and at arbitrary lags; however, it did not affect the sum of phase variance when CGP52432 was added. (C) Synchrony analysis for the effect of NMDA receptor blockade. Black and gray bars in C represent 100µM carbachol/10µM bicuculline group and the 100µM carbachol/10µM bicuculline/80µM D-APV group, respectively. There was no significant difference in crosscorrelation sum at any lag between groups nor in the sum of phase variance. Asterisks (*) in A and B indicate significant difference between groups. In A, B and C, Carb: carbachol, bic: bicuculline, CGP: CGP52432.

The average results of 9 slices for the modulation of synchrony by GABAb disinhibition are shown in Figure 5B. Crosscorrelation sum at both zero lag and arbitrary lags were significantly higher (1-tailed t-test, df=16, P=0.0018 and df=16, P=0.0081, respectively) with 100µM carbachol/10µM bicuculline/4µM CGP52432 than that without CGP52432. However, the sum of phase variance was not significantly changed when CGP52432 was added into the perfusate. There was no significant change in synchronization in the presence of NMDA receptor blockade (Fig. 5C).

In summary, there appeared to be an increase in both crosscorrelation and phase synchronization with GABAa disinhibition, and a further increase in crosscorrelation with GABAb disinhibition.

Oscillations and spatiotemporal patterns evoked by PTX/CGP52432

Might GABA modulation alone be sufficient to generate propagating oscillations? We found that bicuculline alone was insufficient to produce wave oscillations (data not shown). To focus on GABA modulation, we note that bicuculline not only competitively blocks GABAa receptors, but also blocks the apamin-sensitive small-conductance Ca-activated K⁺ (SK) channel (Kleiman-Weiner et al., 2009). Picrotoxin (PTX), which has no known action on the SK channel (Debarbieux et al., 1998), was therefore introduced as a more selective GABAa blocker without the confounding effects of SK channel blockade. It was found that 6µM CGP52432 and PTX (50µM, equally effective as 10µM bicuculline in blocking GABAa receptor-mediated inhibition (Pisani et al., 2002)) reliably evoked theta oscillations in 7 out of 7 slices (Fig. 6B). The dominant peak frequencies of the average power spectrum were 6Hz and 11Hz (Fig. 6C). All the basic wave patterns (spiral, plane, ring, irregular waves) generated by carbachol/bicuculline could be observed in experiments with 50µM PTX/6µM CGP52432 (Fig. 6D).

Discussion

The present study found that propagating theta oscillations in tangential occipital neocortical slices were based on AMPA receptor-mediated synaptic transmission. GABAergic inhibition affected both the dynamical complexity of oscillations and synchronization. Blockade of GABAergic inhibition significantly simplified oscillatory dynamics. The blockade of NMDA receptors significantly complicated oscillation dynamics. Both GABAa and GABAb disinhibition altered the synchronization of the spatial patterns in different ways. Blockade of GABAa and GABAb with PTX/CGP52432 reliably generated propagating theta oscillations that shared many of the characteristics of waves generated with carbachol/bicuculline.

Comparison with other studies

Oscillations in the brain can be evoked in many ways. In human neocortical, rat hippocampal, and rat coronal neocortical slices, oscillations evoked by bicuculline, carbachol, or their combination depend primarily on non-NMDA excitatory amino acids (Lukatch & Maciver, 1997; Macvicar & Tse, 1989; McCormick, 1989; Williams & Kauer, 1997). The present study confirmed that oscillations evoked by carbachol/bicuculline in rat tangential occipital neocortical slices were eliminated by AMPA receptor antagonists but could not be eliminated by either NMDA antagonists or GABA antagonists.

While it has been reported that GABAa receptor-mediated inhibition has no clear effect on carbachol-evoked theta oscillation in rat hippocampal slices (MacVicar & Tse, 1989), the titration of bicuculline in the present study slowed the peak frequency and increased the amplitude of oscillations. This result appears consistent with the shortening of up states and lengthening of down states of slow oscillations caused by bicuculline in coronal slices from ferret occipital cortex (Sanchez-Vives et al., 2010). Two spatiotemporal effects were found when GABAa receptor-mediated inhibition was decreased. First, the temporal profile of oscillations became more regular. Second, the dimension of the patterns of oscillations in both the spatial amplitude and spatial frequency domains significantly decreased, which means that the activity pattern of oscillations became simpler and the number of frequency components of the oscillations decreased.

Although the role of GABAa disinhibition has been extensively explored, the role of GABAb receptor-mediated inhibition in theta oscillation remains more elusive (Buzsaki, 2002; de la Prida et al., 2006; Scanziani, 2000). It has been reported that the blockade of GABAb receptors modulates the amplitude and duration of GABAa disinhibition-evoked epileptiform bursts in human cerebral cortex (McCormick, 1989), and helps generate oscillations with bicuculline in mouse primary motor cortex (Castro-Alamancos & Rigas, 2002). However, it has been difficult to characterize the effects of GABAb receptor blockade on oscillations evoked by carbachol/bicuculline in coronal neocortical slices (Lukatch & Maciver, 1997) and carbachol-evoked oscillations in hippocampal slices (Macvicar & Tse, 1989). We note that in Lukatch & MacIver (1997), adding GABAb blockade to carbachol and bicuculline induced oscillations produced an increase in amplitude and apparent regularization of the oscillations, although they did not comment on these changes. We found that GABAb disinhibition reliably increased the power of 5–9Hz, 11–17Hz, 22–23Hz and 25–26Hz components while shifting the dominant frequency peak toward lower frequencies when compared with carbachol/bicuculline without CGP52432. Combining the effect of bicuculline and CGP52432, more complete GABAergic disinhibition simplifies cortical dynamics.

It has been reported that in mouse coronal slices, the blockade of NMDA receptors reduces the power of the 10–15Hz frequency component of oscillations evoked by bicuculline/CGP35348, but increases the power of the 15–25Hz frequency component (Castro-Alamancos & Rigas, 2002). In coronal cortical slice of rat, the oscillations evoked by carbachol/bicuculline/D-APV intermingle with bursting activity (Lukatch & Maciver, 1997). Our findings of the effects of NMDA blockade are consistent with these prior reports.

At what point are large amplitude oscillations in cortex pathological? Our study in the largely deafferented slice cannot say. But our conjecture is that ‘normal’ likely lies somewhere between the most complex irregular, and the most simple of the large amplitude oscillations analyzed in this report. In a sense, one might view GABAa and GABAb receptor-mediated inhibition as helping to maintain the complexity of cortical dynamics. Recent work from Huang et al. (2010), suggests that long range connections to cortex may serve to break up organized oscillatory waves as we have here studied. Indeed, in prior work of Yuste et al. (1997), GABAa disinhibition served to remove modular architectural boundaries to wave propagation in tangential slices.

The types of coherent and persistent wave formation we have studied are likely pathological, and the normal connectivity of the cortex may serve to break up such wave dynamics (Huang et al., 2010). Spiral waves in excitable media, biological or chemical (Winfree, 2001), tend to be stable, and mammalian cortices may have sufficient inhibitory connections present to render the lifetime of such rotational waves brief. Whether these periodic dynamics share similarities with epileptic seizure dynamics remains an open question at present, since inhibition appears to play an important role in many types of seizure patterns (see, e.g., Ziburkus et al. 2006, and references within).

Comparison of paroxysmal discharges in tangential versus coronal slices

It has been reported that weakening inhibition in interconnected inhibitory networks of the hippocampus may disrupt population rhythmicity (Whittington et al., 1998). In contrast, the present study showed that weakening inhibition of interconnected excitatory networks of tangential occipital neocortical slice increased the synchronization of activity. The dynamics of brain slices, and their response to pharmacological manipulation, is dependent upon the topology of the slice cut and residual network anatomy.

In mouse barrel cortex, paroxysmal discharges evoked by bicuculline in tangential layer IV slices are different in characteristics from those evoked in coronal slices (Fleidervish et al., 1998). The paroxysmal discharges evoked in tangential layer IV slices are completely blocked by an NMDA receptor blocker and are unaffected by the AMPA receptor blocker CNQX, whereas events in coronal slices can only be generated if AMPA receptor-mediated transmission is intact (Golomb & Amitai, 1997). In contrast to barrel cortex, oscillations evoked by carbachol/bicuculline in rat tangential occipital neocortical slices share many similarities in mechanism with the ones evoked in coronal neocortical slices. The activation of AMPA receptors is necessary for the generation of propagating oscillations in both coronal neocortical slices (Lukatch & Maciver, 1997) and tangential occipital neocortical slices (the present study), while the activation of NMDA receptors both modulates oscillation expression in coronal (Lukatch & Maciver, 1997) and tangential occipital cortical slices.

The mechanism underlying the oscillation dynamics

Slice geometry is critical to the dynamics observed. In hippocampus, orthogonal networks of dendritic versus somatic innervating inhibitory neurons renders the dynamics and rhythmicity of transverse versus longitudinal slices very different (Glovelli et al., 2005). In our experiments, the tangential slice from middle cortical layers (3–5) is far more isotropic than a coronal slice, and permits the symmetries necessary for coherent traveling wave formation to occur. Another contrast between our findings and that of the oscillations in coronal slices is that our waves propagate readily even at relatively low levels of inhibitory blockade. In layer-by-layer study of propagation in coronal slices, layer 5 has been shown to be the layer that best supports propagating traveling waves (Telfeian & Connors, 1998). Although the superficial cortical layers (1–3) were important in the generation of stationary oscillations in coronal slices (Lukatch & MacIver, 1997), the middle cortical layers alone can support oscillations when slices are tangentially cut.

Spectral coherency analysis

Membrane voltage changes detected by VSD detectors near the tip of LFP recording electrodes should be most coherent with the LFP. However, there are many sources of noise in VSD signals ranging from photon shot noise to movement artifacts (Grinvald et al., 1988). In order to analyze data without artifact contamination, spectral coherency analysis was used in the present study to identify a heavily contaminated from a non-contaminated frequency band. We make the assumption that movement artifact in such optical imaging is independent of any movement induced neuronal activity, and is additive to the optical signal. We set a conservative criterion to identify a frequency cutoff that separated coherencies between optical channels that could be confirmed by electrical LFP recordings. Below 5 Hz, there were complex results that included many examples of coherencies between optical channels alone without LFP confirmation. We excluded all of these low frequency results in order to protect against analyzing coherent artifacts. Artifacts in VSD imaging of wave dynamics in brain are common and we offer our strategy as a general approach for artifact reduction in such scenarios. Our suspicion is that the frequency ranges exhibiting substantial movement artifact will differ from one experimental setup to another, subject to vibration-absorbing table characteristics, building vibration, room air circulation movements, etc. We found little evidence for coherency artifacts above 5 Hz in our experiments.

Characterizing cortical spatiotemporal dynamics

There is no general strategy to characterize the complexity and similarities of spatiotemporal patterns of brain activity. We have used multivariate metrics of synchronization (Schiff et al., 2005) and mode decompositions (Schiff et al., 2007) to help classify and characterize such dynamics. In the present study, in addition to standard Fourier frequency decomposition, we used metrics of synchronization and dynamical complexity to characterize the properties of oscillatory waves in neocortex. We were able to characterize consistent changes (for instance, with adding GABAb blockade to GABAa blockade) where other analyses have had some difficulty in observing such effects (Lukatch & Maciver, 1997). How complex the characterization of oscillatory wave patterns in cortex needs to be remains an open question. But the dynamics of cortex is complex, and our findings suggest that introducing metrics of complexity and synchronization are useful in our efforts to better define the dynamics and pharmacology of cortical wave dynamics. Whether this characterization of network activity, in combination with cellular level electrophysiology, would be an effective way to characterize the effects of aging, genetic variability or transgenic brain networks remains interesting to consider for future work.

Towards control of cortical oscillations

Although empirical data-driven control strategies can be effective in neuronal systems (Gluckman et al., 2001), we are interested in developing model-based observation and control of neuronal circuitry (Schiff & Sauer, 2008; Schiff, 2010, 2012). Such control systems may be useful for dynamical diseases such as epilepsy and Parkinson’s disease, and perhaps might affect the initiation of migraines by modulating spreading depression waves. A voltage sensitive dye experiment in a tangential cortical slice has many advantages for early control experiments. The simultaneous measurement of many different points across the photodiode array permits a multiple input measurement that can increase the observability of any spatiotemporal physical system (Aguirre & Letellier, 2005). The computational overhead for such control systems will be greatly decreased using a purely excitatory neuronal network with GABAa and GABAb blockade as shown in these present results, and as demonstrated numerically in (Schiff & Sauer, 2008). A more difficult challenge for future work will be to develop the technologies to handle multilayered excitatory and inhibitory networks in real-time for model-based control. The results of this present study will help enable the early attempts at this next generation of neuronal controllers.

Supplementary Material

Supp Fig S1. FIG. S1.

Traces without low frequency filtering and including initial stimulation and latent period. (A) Recording arrangement. Signals from two optical detectors (marked as 1 and 2 filled circles) and local field potentials (LFPs), under 3 drug conditions are shown in (C). The dashed lines in traces of C are zero baselines. Vertical scale: 2×10⁻³ of resting light intensity. Horizontal scale: 1second. The solid vertical lines in C mark the stimulus delivery time points. (B) Power spectrum (logarithmic scale) for optical signals during a 6-second episode averaged across all detectors of 10 slice experiments without low frequency filtering. Note that there was no substantial difference in spectra between 0–5 Hz between these different pharmacological conditions. There is substantial low frequency component in the raw traces in C that are not affected by the different drug applications. We attribute these low frequencies to likely movement artifact, but some intrinsic signal components may be present as well (not reflecting electrical activity). Note the latent period from stimulus to oscillation of about 1s clearly shown in the LFP traces in C. Carb: carbachol; bic: bicuculline; stim: stimulus.

Supp Fig S2. FIG. S2.

Traces without low frequency filtering with and without CGP52432. (A) Signals from two example optical detectors (marked as 1 and 2 in figure S1), along with LFPs, under 2 drug conditions. Vertical scale: 2×10⁻³ of resting light intensity. Horizontal scale: 1second. The solid vertical lines mark out the stimulus time points. (B) Traces of optical detectors 1 and 2 in A were filtered between 5–30Hz and denoised. Vertical scale: 2×10⁻⁴ of resting light intensity. (C) Power spectrum (logarithmic scale) for optical signals during a 6-second episode averaged across all detectors of 9 slice experiments without low frequency filtering. The dashed lines in traces of A and B are zero baselines. Carb: carbachol; bic: bicuculline; CGP: CGP52432.

Supp Fig S3. FIG. S3.

Traces without low frequency filtering with and without D-APV. (A) Signals from two example optical detectors (marked as 1 and 2 in figure S1), along with LFPs, under 2 drug conditions. Vertical scale: 2×10⁻³ of resting light intensity. Horizontal scale: 1 second. The vertical solid lines mark out the stimulus time points. (B) Traces of optical detectors 1 and 2 in A were filtered between 5–30Hz and denoised. Vertical scale: 2×10⁻⁴ of resting light intensity. (C) Power spectrum (logarithmic scale) for optical signals during a 6-second episode averaged across all detectors of 8 slice experiments without low pass filtering below 5 Hz. The dashed lines in traces of A and B are zero baselines. Carb: carbachol; bic: bicuculline.

Supp Fig S4. FIG. S4.

Theta oscillations were eliminated by CNQX. (A) Recording arrangement. Signals from one example optical detector (marked as a black filled circle in A) with and without CNQX are shown as 6-second traces in (B). The horizontal lines are zero baselines. Vertical scale: 2×10⁻⁴ of resting light intensity. (C) Two sections from the temporal data (I and II) in B are displayed as a sequence of gray scale images. Note there were no propagating waves during the recording period after CNQX was added.

Supp Movie S1. Movie M1.

Ring waves evoked by 1µM bicuculline/100µM carbachol. (AVI)

Supp Movie S2. Movie M2.

Plane waves evoked by 5µM bicuculline/100µM carbachol. (AVI)

Supp Movie S3. Movie M3.

Spiral waves. (AVI)

Supp Movie S4. Movie M4.

Ring waves and collisions evoked by 10µM bicuculline/100µM carbachol. (AVI)

Abbreviations

ACSF

artificial cerebrospinal fluid

CGP 52432

3-[(3,4-Dichlorophenyl)methyl] aminopropyl (diethoxymethyl) phosphinic acid

CNQX

6-cyano-7-nitroquinoxaline-2,3-dione

D-APV

D-(−)-2-Amino-5-phosphonopentanoic acid

DMSO

dimethyl sulfoxide

LFP

local field potential

NBQX

2,3-Dioxo-6-nitro-1,2,3,4-tetrahydrobenzo[f]quinoxaline-7-sulfonamide

PTX

picrotoxin

VSD

voltage-sensitive dye