Electronic and Structural Elements That Regulate the Excited-State Dynamics in Purine Nucleobase Derivatives

Abstract

The excited-state dynamics of the purine free base and 9-methylpurine are investigated using experimental and theoretical methods. Femtosecond broadband transient absorption experiments reveal that excitation of these purine derivatives in aqueous solution at 266 nm results primarily in ultrafast conversion of the S₂(ππ*) state to the vibrationally excited ¹nπ* state. Following vibrational and conformational relaxation, the ¹nπ* state acts as a doorway state in the efficient population of the triplet manifold with an intersystem crossing lifetime of hundreds of picoseconds. Experiments show an almost 2-fold increase in the intersystem crossing rate on going from polar aprotic to nonpolar solvents, suggesting that a solvent-dependent energy barrier must be surmounted to access the singlet-to-triplet crossing region. Ab initio static and surface-hopping dynamics simulations lend strong support to the proposed relaxation mechanism. Collectively, the experimental and computational results demonstrate that the accessibility of the nπ* states and the topology of the potential energy surfaces in the vicinity of conical intersections are key elements in controlling the excited-state dynamics of the purine derivatives. From a structural perspective, it is shown that the purine chromophore is not responsible for the ultrafast internal conversion in the adenine and guanine monomers. Instead, C6 functionalization plays an important role in regulating the rates of radiative and nonradiative relaxation. C6 functionalization inhibits access to the ¹nπ* state while simultaneously facilitating access to the ¹ππ*(L_a)/S₀ conical intersection, such that population of the ¹nπ* state cannot compete with the relaxation pathways to the ground state involving ring puckering at the C2 position.

Introduction

Interest in understanding the excited-state dynamics of the nucleic acid bases and their derivatives continues to grow. A large motivation for this pursuit is the detrimental effects that ultraviolet radiation has on the chemical integrity of DNA and RNA nucleic acid monomers and polymers.^1,2 More recently, the emphasis has shifted toward understanding the key structural and electronic elements that regulate the photostability of DNA,³⁻⁹ where investigations using the nucleic acid monomers and their derivatives have taken center stage.⁹⁻¹² Experimental and computational works have shown that in the nucleic acid derivatives relaxation of excess electronic energy to the ground state occurs primarily via ultrafast internal conversion pathways,³⁻⁹ which are mediated by the accessibility of conical intersections in the potential energy surfaces.

Kohler and co-workers¹³⁻¹⁵ have revealed that, in addition to the primary ultrafast internal conversion pathway to the ground state, direct excitation of the pyrimidine monomers results in the population of long-lived singlet and triplet states in solution. The relative yields of these long-lived states depend sensitively on the pyrimidine base and solvent used. It is thought that the initial excited-state population decays by two nonradiative pathways. The first channel is ultrafast internal conversion to the ground state,^16,17 while the secondary channel involves the population of a dark electronic state.^14,18−23 The mechanistic details regarding the secondary deactivation pathway have been the subject of intense debate. Specifically, two questions have been largely discussed: (1) the nature of the long-lived dark species that are being detected experimentally (¹nπ* or ³ππ*) and (2) the actual relaxation pathway that leads to the population of these states. Two population schemes have been proposed based on quantum-chemical studies. These schemes can be summarized as (1) S₂(ππ*) → S₁(nπ*) → triplet and (2) S₂(ππ*) → triplet,²⁴⁻²⁸ with the latter pathway possibly involving more than one triplet state.²⁴ Recent gas-phase molecular dynamics simulations including nonadiabatic and spin–orbit couplings point toward the first pathway, ¹ππ* → ¹nπ* → triplet, as the most probable deactivation mechanism in cytosine and uracil,²⁹⁻³¹ in agreement with the experimental observations by Kohler and co-workers in solution.¹³⁻¹⁵

For the guanine³²⁻³⁹ and adenine⁴⁰⁻⁴⁶ monomers, gas-phase quantum-chemical calculations hint at a relaxation coordinate in the S₁(ππ*) potential energy surface that involves a puckering deformation of the C2 atom in the six-membered ring as the mechanism responsible for internal conversion to the ground state on ultrafast time scales. Importantly, the explicit consideration of water molecules in the calculation modifies the topology of the potential energy surface, reducing its slope and leading to a planar region that slows the wavepacket before it reaches the S₁(ππ*)/S₀ conical intersection region.^7,39,46 However, Barbatti, Thiel, and their co-workers have recently concluded that, although calculations suggest that the C2 puckering is the primary internal conversion pathway in the S₁(ππ*) state decay to the ground state, substantial participation of the C6 puckering pathway is also expected in adenine and guanine.^38,47−49 On the other hand, using hypoxanthine and inosine as model compounds (Scheme 1), the groups of Temps and of Peón and Matsika have recently concluded that, although the exocyclic amino group at the C2 position of the guanine chromophore is not essential for the ultrafast internal conversion to the ground state,^10,11 C2 puckering is the main deactivation pathway, which is accelerated in hypoxanthine and inosine as a result of the absence of the amino group. Subsequently, Chen and Kohler¹² have proposed that methylxanthine derivatives seem to decay through a pathway that involves the out-of-plane deformation of the five-membered imidazole ring, as originally predicted by Yamazaki et al.,⁵⁰ because an ethylenic torsion at the C2 position is not possible in these compounds due to the absence of the C2=N3 double bond. Evidently, further experimental and computational work is needed to quantify and understand in detail how different functional groups attached to the purine chromophore affect the accessibility of key conical intersections and competition between radiative and nonradiative relaxation pathways.

Scheme 1. Proposed Correlation between the Substituents at the C2 and C6 Positions and the Primary Decay Lifetime to the Ground State in the Purine Derivatives in Aqueous Buffer Solution.

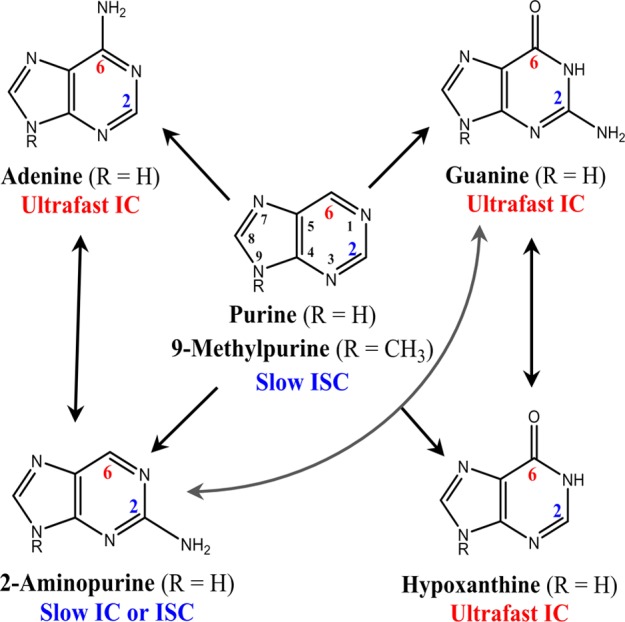
See main text for details. IC and ISC stand for internal conversion and intersystem crossing, respectively. The common ring numbering is also shown.

The purine free base is a logical model compound to investigate which structural elements influence the radiative and nonradiative decay pathways in the purine bases and their derivatives. Purine is a heterocyclic compound containing fused pyrimidine and imidazole rings (Scheme 1). This is the parent chromophore of the 2-aminopurine, adenine, guanine, and hypoxanthine nucleobases. 2-Aminopurine and adenine (6-aminopurine) are formed from purine by the exocyclic incorporation of an amino group at the C2 or C6 position, respectively, whereas guanine (2-amino-6-oxypurine) and hypoxanthine (6-oxypurine) are formed from purine by the exocyclic incorporation of an oxo group at position C6, in addition to an amino group at position C2 in the case of guanine. Strikingly, however, the excited-state dynamics of the purine free base have not received much attention, with only a handful of experimental^51,52 or theoretical^53,54 works investigating its photophysical and excited-state properties. This paucity of dynamical information is perhaps due to the fact that the purine free base exists as a mixture of the N7H and N9H tautomers in solution,⁵⁵⁻⁶⁰ which can significantly complicate the interpretation of the experimental results. This difficulty can be overcome by methylation of the purine free base at the N9 position forming 9-methylpurine, which has been shown to be present as a single tautomer in solution.⁵⁵

In this contribution, direct spectroscopic and computational evidence is obtained on the efficient population of long-lived ¹nπ* and ³ππ* excited states for both 9-methylpurine and the purine free base. This is in contrast to the adenine and guanine monomers,³⁻⁹ which decay by ultrafast internal conversion to the ground state. The synergistic comparison of the deactivation dynamics and transient absorption spectra obtained from both experiment and theory allows a detailed mapping of the molecular relaxation mechanism of the heterocyclic skeleton common to all purine derivatives, particularly to the canonical adenine and guanine monomers. It is shown that population of the ¹nπ* state is the primary internal conversion pathway of the initially populated ¹ππ* state. The ¹nπ* state leads to the population of the triplet state in near-unity yield. These results are important because it is thought that these long-lived excited states play a preponderant role as precursors to various DNA photoproducts.^1,2 Deactivation pathways through the ¹nπ* and the triplet states have been largely overlooked in the literature because they are commonly populated in low yields,^3,4,8,9 making 9-methylpurine and the purine free base excellent systems to scrutinize and to benchmark state-of-the-art static and dynamical methods with regard to their ability to accurately model the excited-state dynamics of the nucleic acid bases, as well as those of other biomolecules in general.

Experimental Results

Absorption and Emission Spectra of 9-Methylpurine and the Purine Free Base

Figure 1 shows the absorption and emission spectra of purine and 9-methylpurine in polar protic (aqueous buffer), polar aprotic (acetonitrile), and nonpolar (cyclohexane) solvents. The absorption and emission spectra of the purine free base in cyclohexane are not reported because the purine free base is insoluble in this solvent. The absorption maxima of the purine free base and 9-methylpurine are centered at 263 and 264 nm, respectively, and do not change appreciably with solvent. The flank sides of this absorption band blue shift in going from aqueous buffer solution to acetonitrile to cyclohexane. In addition, an absorption tail around 295 nm is observed in acetonitrile and cyclohexane, which vanishes in aqueous solution for both bases. A high-energy absorption band above 220 nm is also observed, which red shifts upon methylation and in going from acetonitrile to aqueous buffer solution to cyclohexane in 9-methylpurine.

Figure 1.

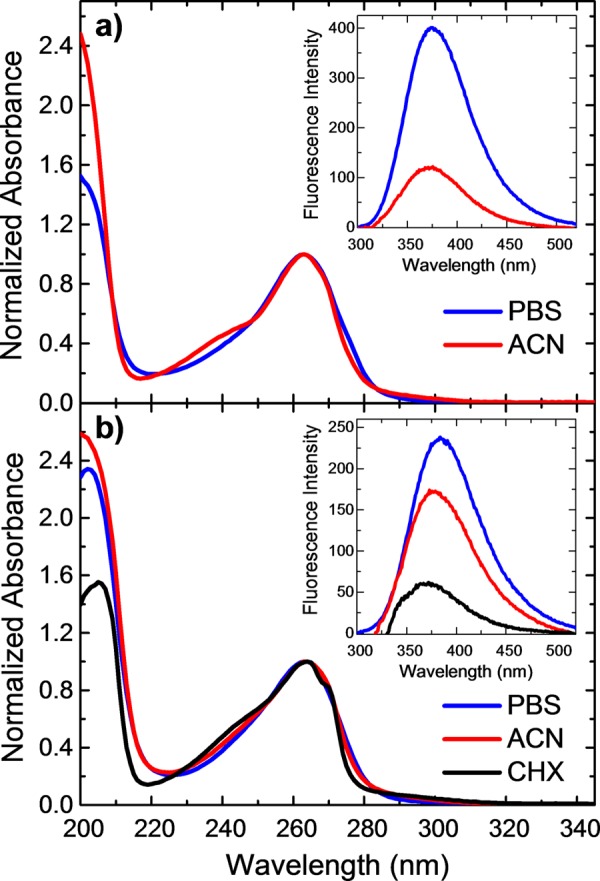
Normalized absorption spectra for the purine free base (a) and 9-methylpurine (b) in aqueous buffer solution (phosphate-buffered saline, PBS), acetonitrile (ACN), and cyclohexane (CHX). The relative emission spectra are inset and were recorded using the same absorbance at the excitation wavelength (267 nm).

The emission spectra of 9-methylpurine and the purine free base are inset in Figure 1. The fluorescence quantum yields were determined from these spectra as described in the Supporting Information (SI, Figure S1). The excitation spectra confirm that the emission originates from the purine chromophore (not shown). The E_0,0 energies were estimated by using the normalized emission and absorption spectra and are also reported in the SI (Figure S2). Interestingly, the purine free base is slightly more fluorescent (ϕ_F = (4.4 ± 0.3) × 10^–3) than 9-methylpurine (ϕ_F = (4.0 ± 0.3) × 10^–3) in aqueous solution, whereas the opposite is true in acetonitrile, with fluorescence yields of (2.0 ± 0.2) × 10^–3 and (2.4 ± 0.2) × 10^–3, respectively. We also estimated the fluorescence yield of 9-methylpurine in cyclohexane to be (1.2 ± 0.2) × 10^–3. The emission maximum does not shift appreciably in going from aqueous solution to acetonitrile for the purine free base, whereas a systematic blue shift from ∼387 to ∼372 nm is observed in going from aqueous solution to acetonitrile to cyclohexane for 9-methylpurine.

Broadband Transient Absorption Experiments

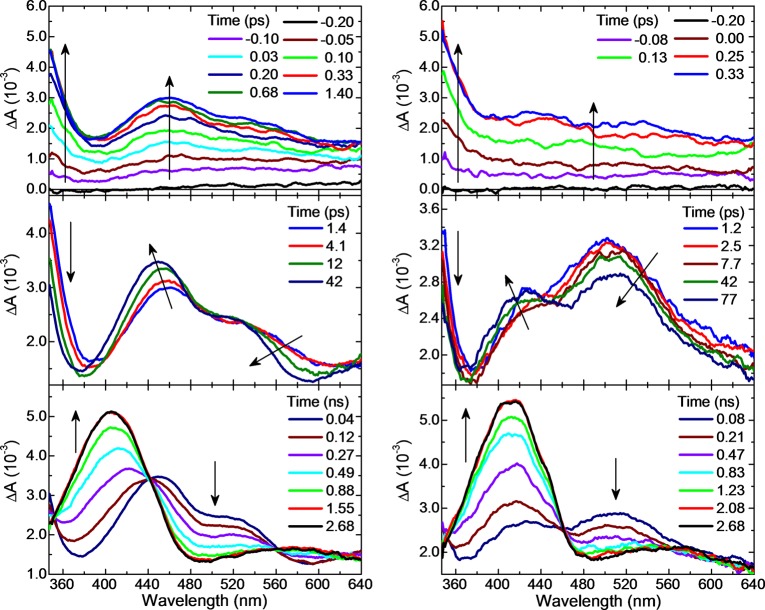
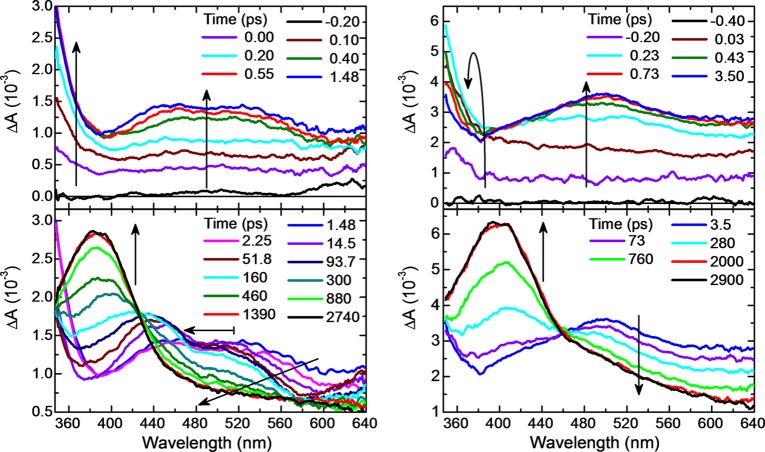
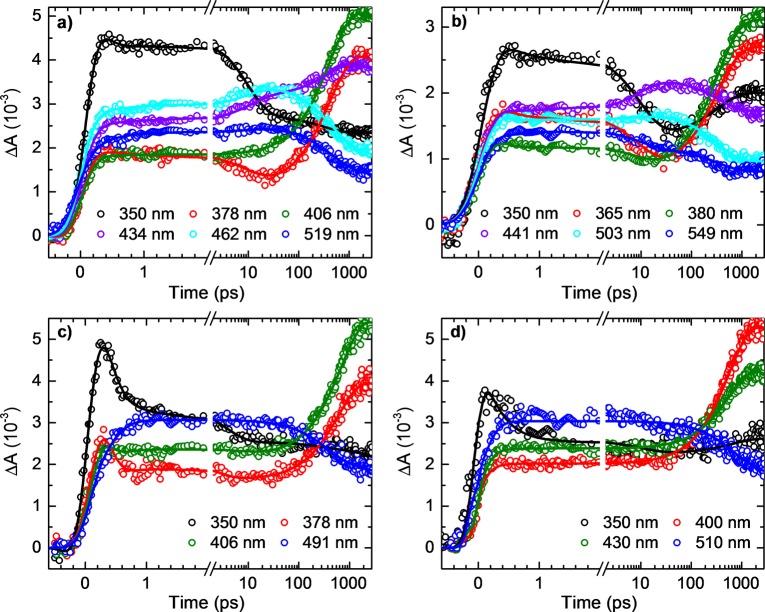
Time-resolved absorption spectra were recorded to probe the excited-state dynamics in the 9-methylpurine and purine bases and to reveal the decay pathways leading to the population of the long-lived triplet state. Figures 2 and 3 show the transient absorption spectra for 9-methylpurine and the purine free base in aqueous buffer solution and in acetonitrile after excitation at 266 nm. The corresponding contour plots of the multidimensional transient absorption data are shown in SI Figure S3. In addition, the decay-associated spectra for 9-methylpurine in aqueous buffer solution, acetonitrile, chloroform, and cyclohexane are shown in Figure 4, whereas representative decay signals for 9-methylpurine and the purine free base in acetonitrile and aqueous buffer solution are shown in Figure 5. The globally fitted lifetimes are presented in Table 1.

Figure 2.

Transient absorption spectra of 9-methylpurine in acetonitrile (left) and in aqueous buffer solution (right) after 266 nm excitation.

Figure 3.

Transient absorption spectra of the purine free base in acetonitrile (left) and in aqueous buffer solution (right) after 266 nm excitation.

Figure 4.

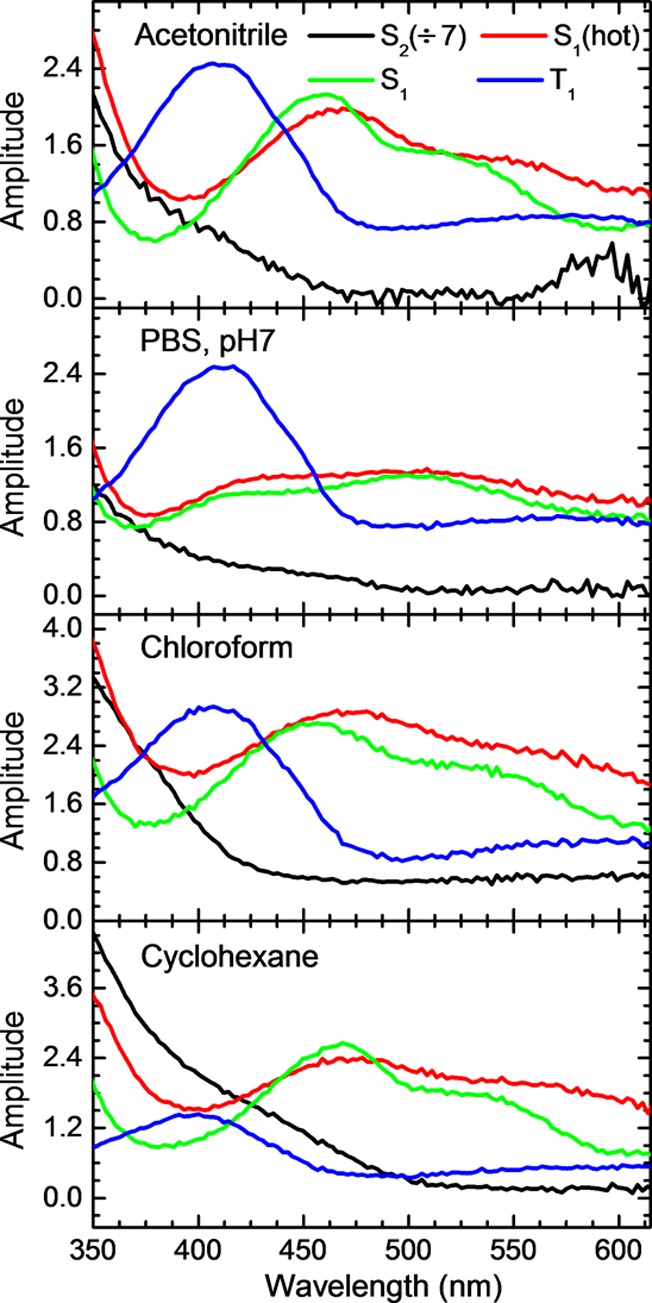
Decay-associated spectra of the multidimensional transient absorption data of 9-methylpurine in different solvents obtained using the target analysis method, where the lifetimes were obtained from a global analysis (see Table 1). The sequential model rate law used was composed of three exponential components plus a time-independent component (representing the long-lived T₁ state), convoluted with an instrument response function. The amplitude of the first decay-associated spectrum in each panel has been divided by a constant, as shown in the legend of the figure.

Figure 5.

Representative decay traces for 9-methylpurine (a,c) and for the purine free base (b,d) in acetonitrile (a,b) and aqueous buffer solution pH 7 (c,d) at the specified probe wavelengths.

Table 1. Globally Fitted Lifetimes for 9-Methylpurine and Purine Obtained from a Target Analysis of the Transient Absorption Data Using a Sequential Kinetic Model.

solvent	τ1 (ps)	τ2a (ps)	τ3 (ps)
9-methylpurine
water (PBS, pH 7)	0.25 ± 0.05	15 ± 5	600 ± 10
acetonitrile	0.15 ± 0.05	10 ± 1	350 ± 10
chloroform	0.15 ± 0.05	6 ± 1	380 ± 20
cyclohexane	0.30 ± 0.05	8 ± 2	195 ± 10
purine free base
water (PBS, pH 7)	0.20 ± 0.05	8 ± 3	645 ± 10
acetonitrile	0.19 ± 0.05	10 ± 3	360 ± 20

^aAverage lifetime from a global fit analysis; its actual value increases in going from the UV to the visible probe wavelengths.

Similar transient absorption spectra are observed in aqueous and acetonitrile solutions for the 9-methylpurine and the purine free base and for 9-methylpurine in polar protic, polar aprotic, and nonpolar solvents, although the time evolution and relative intensities of the transient absorption bands vary with solvent. Following excitation, an absorption band with a maximum below 350 nm grows within the cross-correlation of the pump and probe pulses independent of the solvent used, as can be observed in Figures 2 and 3. This absorption band decays, resulting in the population of a species with a transient absorption above ∼400 nm (τ₁ in Table 1). The absorption spectrum of this transient species blue shifts and becomes more structured over a few tens of picoseconds (see middle-left panel in Figure 2 and Figures 3, 4, and S4). It then decays in hundreds of picoseconds to populate a long-lived transient species that has a maximum at 412 and 400 nm for 9-methylpurine and the purine free base in aqueous buffer solution, respectively. The maximum of this long-lived transient species shifts to 406 and 385 nm for 9-methylpurine and the purine free base in acetonitrile, respectively.

Computational Results

Computed Absorption Spectra

Two different approaches have been considered in order to rationalize the experimental ground-state absorption spectra. Table 2 reports gas-phase vertical excitation energies for the lowest-lying excited states of 9-methylpurine and the two purine tautomers N7H and N9H, computed at the MS-CASPT2//SA10-CASSCF(16,12)/ANO-L level of theory (multistate complete active space perturbation theory of second order//complete active space self-consistent field; see SI for details) using the equilibrium geometry of the corresponding ground-state minima. Below 5.0 eV, the N9H purine spectrum is composed of three different absorptions. The most intense absorption, at 4.68 eV, is ascribed to a ππ* excitation. This transition is flanked by two additional nπ* absorptions, showing oscillator strengths 10 times weaker compared to the central band. Within the same energy window, the N7H purine shows a similar absorption pattern, consisting of a strong transition peaking at 4.58 eV. However, the N7H purine spectrum has a stronger absorption transition at 4.85 eV, 4 times more intense than the main band at 4.58 eV. This electronic transition appears in the absorption spectrum of N9H purine at 5.02 eV. Methyl substitution at position N9 leads to identical transition ordering and energies compared to the N7H purine, the only significant difference being the S₃(ππ*) state has half the oscillator strength of the S₂(ππ*) state.

Table 2. Vertical Excitation Energies in eV (nm), Oscillator Strengths (f), and Static Dipole Moments (μ) in Debye (D) for the Low-Lying Singlet Excited States of the Purine Tautomers and 9-Methylpurine at the MS-CASPT2//SA10-CASSCF(16,12)/ANO-L Level of Theory.

state	ΔE, eV (nm)	f	μ (D)
N9H purine
S1 nπ*	4.05 (306)	0.0038	3.31
S2 ππ*	4.68 (265)	0.0724	3.00
S3 nπ*	4.94 (250)	0.0027	1.88
S4 ππ*	5.02 (247)	0.0306	7.40
N7H purine
S1 nπ*	4.00 (309)	0.0006	5.03
S2 ππ*	4.58 (270)	0.0440	3.57
S3 ππ*	4.85 (255)	0.1504	8.84
S4 nπ*	4.97 (249)	0.0000	4.25
9-methylpurine
S1 nπ*	4.05 (306)	0.0036	3.93
S2 ππ*	4.69 (265)	0.0609	3.62
S3 ππ*	4.85 (255)	0.0384	8.33
S4 nπ*	4.96 (249)	0.0018	2.43

The absorption spectrum of purine was also computed by means of the line broadening method (see ref (61) and SI). This semiclassical spectrum, shown in Figure 6, has been red-shifted by 1 eV to match the experimental spectrum.⁶² In the energy range between 4 and 8 eV, the theoretical spectrum shows two bands, with maxima centered at 4.75 and 6 eV. Three different singlet electronic states, S₁–S₃, were found to be responsible for the first band at 4.75 eV (261 nm), while the S₄ state contributes to the second band of the spectrum. The second, much more intense band of the experimental spectrum is not fully described by the calculations because only four excited states were included in the computation of the absorption spectrum. As the focus of this study is concentrated on the excited-state dynamics after excitation to the first absorption band, dynamical calculations are performed only from the S₁–S₃ singlet excited states.

Figure 6.

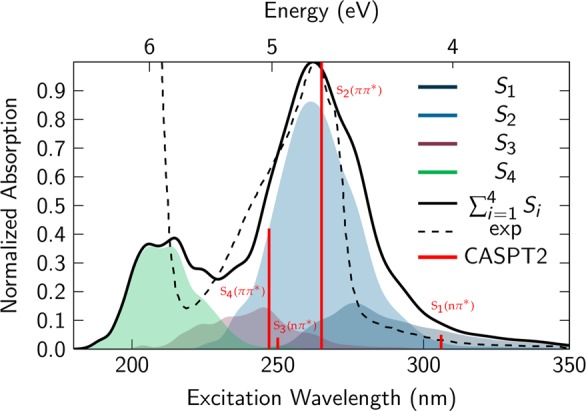
Simulated (gas phase) and experimental (in ACN) absorption spectra of the N9H tautomer of the purine free base. The individual bands corresponding to the S₁ to S₄ excitations, as well as the total sum, are obtained from CASSCF(12,9) calculations. The obtained spectrum is red-shifted by 1 eV to match the experimental one and the CASPT2 results (red bars).

The solvent effects on the vertical excitation energies of the first two lowest singlet excited states of the 9-methylpurine were studied. Time-dependent density functional theory (TD-DFT) calculations with a polarizable continuum model were performed (IEF-PCM; see SI for details), using water, chloroform, cyclohexane, and acetonitrile as solvents. In addition, the effect of three explicit water molecules on the vertical excitation energies, including and excluding the bulk water dielectric field, was investigated. Regardless of the solvent dielectric modeled, or whether the inclusion of three explicit water molecules was considered, the same trend is observed for the shifts of the ¹nπ* and ¹ππ* transitions. The ¹nπ* transitions experience a blue shift of up to 0.3 eV relative to the gas phase in going from cyclohexane to water, whereas only a minor blue shift is observed in the excitation energy of the ¹ππ* states in going from gas phase to water. These results are consistent with solvent effects observed on the absorption maximum of 9-methylpurine (Figure 1b).

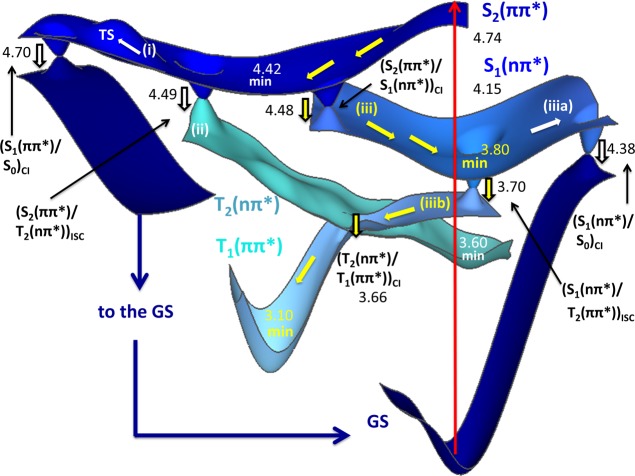
Static View of the Deactivation Mechanism of 9-Methylpurine and Purine Free Base: Minimum Energy Path Calculations from the S₂(ππ*) State

A deactivation mechanism scheme for the N9H tautomer of the purine free base and for 9-methylpurine obtained from minimum energy path calculations is shown in Figure 7. After vertical excitation to the S₂(ππ*) state (4.74 eV), the steepest descent path leads to a minimum close to a conical intersection, denoted as (S₂(ππ*)/S₁(nπ*))_CI. This conical intersection, placed 4.48 eV adiabatically over the ground-state minimum, shows stretched C–C and C–N bond distances, especially in the pyrimidine ring, as compared to the Franck–Condon initial geometry. Additionally, at the region of the ¹ππ* minimum, the triplet T₂(nπ*) state is nearly degenerate with the S₁(nπ*) and S₂(ππ*) states and is coupled to them with a spin–orbit coupling that amounts to 14 cm^–1. This region close to the ¹ππ* minimum, where the S₁(nπ*), S₂(ππ*), and T₂(nπ*) are nearly degenerate, is a crossroads for three different reaction pathways: (i) the first pathway returns population to the ground state via the internal conversion funnel, (S₁(ππ*)/S₀)_CI, and it is described by an upward profile showing a transition state (TS in Figure 7). This (S₁(ππ*)/S₀)_CI conical intersection is characterized by a pyrimidine ring puckered in the C2 position (dihedral C6–N1–C2–N3 = −82.5°) and a further stretching of the C2–N3 and C6–C5 bond distances. (ii) The second path directly transfers population into the ³nπ* minimum through the crossing (S₂(ππ*)/T₂(nπ*))_ISC. (iii) The third path results in the direct population of the ¹nπ* minimum, located 3.80 eV above the ground state. This minimum is characterized by a shortening of the heterocycle bond distances and a slight increase (0.01 Å) of the bonds adjacent to the one shared between the pyrimidine and imidazole heterocycles.

Figure 7.

MS-CASPT2/SA3-CASSCF(16,12) singlet and triplet deactivation mechanism of N9H purine free base and 9-methylpurine, as obtained from minimum energy paths. Energies are given relative to the ground-state minima in eV. Subscripts are used to describe the energetic ordering of the singlet and triplet states at a precise nuclear arrangement, whereas color is used to describe the character of a given state. Note also that the small discrepancies relative to the vertical energies in Table 2 are due to the different number of roots considered in the calculations.

Two additional deactivation pathways were obtained from the ¹nπ* minimum. One (iiia in Figure 7) involves the deactivation to the ground state via the (S₁(nπ*)/S₀)_CI funnel characterized by C6 puckering and out-of-plane displacement of the hydrogen at the same position. This geometrical distortion involves an energy increase of ∼0.6 eV relative to the ¹nπ* state minimum. In the second one (iiib in Figure 7), the system can undergo intersystem crossing via the crossing point (S₁(nπ*)/T₂(ππ*))_ISC, located in the vicinity of the minimum, where the spin–orbit coupling was estimated to amount to 18 cm^–1. Once in the triplet manifold, the system can populate either the ³nπ* minimum or the lower-energy ³ππ* minimum through the (T₂(nπ*)/T₁(ππ*))_CI conical intersection.

The minimum energy path from the most stable triplet minimum at 3.10 eV, T₁(ππ*), reveals that the decay to the ground state requires a significant out-of-plane deformation of the purine skeleton, especially affecting the positions C6 and N9, similar to what was found within the singlet manifold. The (T₁(ππ*)/S₀)_ISC crossing point was calculated at ≈2.2 eV above the T₁(ππ*) minimum (not shown in Figure 7).

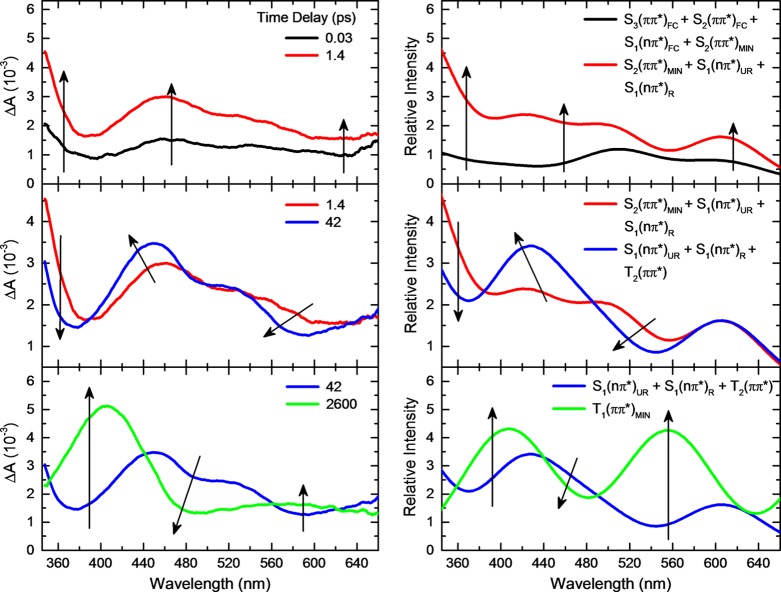
To assist in the interpretation of the experimental transient absorption data, the absorption spectra of the transient species at specific nuclear coordinates in these potential energy surfaces were calculated at the CASPT2 level of theory. These absorption spectra were only calculated at the nuclear coordinates predicted to be most relevant by the static and dynamics simulations. Specifically, the transient absorption spectra were calculated at six different points in the potential energy surfaces: (1) at the Franck–Condon region, S₃(ππ*)_FC, S₂(ππ*)_FC, and S₁(nπ*)_FC states; (2) at the S₂(ππ*) minimum, S₂(ππ*)_MIN, close to the (S₂(ππ*)/T₂(nπ*))_ISC and (S₂(ππ*)/S₁(nπ*))_CI; (3) at the (S₂(ππ*)/S₁(nπ*))_CI, unrelaxed S₁(nπ*)_UR state; (4) at the relaxed S₁(nπ*) minimum, S₁(nπ*)_R; (5) at the (S₁(nπ*)/T₂(ππ*))_ISC, T₂(ππ*) state; (6) and at the T₁(ππ*) minimum, T₁(ππ*)_MIN state. These spectra are shown in SI Figure S9. Linear combinations of the absorption spectra that are predicted to be contributing to the experimental transient absorption spectra at specific time delays were then computed (see Figure 8) in order to support the assignment of the transient data shown in Figures 2 and 3.

Figure 8.

Comparison of the experimental and simulated transient absorption spectra for 9-methylpurine at the specified time delays. Transient absorption spectra were simulated through a linear combination of the excited-state spectra at key points along the potential energy surfaces (see SI for full details). The intensity of each excited-state absorption spectrum was scaled based on its relative contribution to the dynamics at the specified time delay. The following linear combinations are shown in the right panel: 0.25 × (S₃(ππ*)_FC + S₂(ππ*)_FC + S₁(nπ*)_FC + S₂(ππ*)_MIN) at 0.03 ps; 0.42 × S₂(ππ*)_MIN + 0.15 × S₁(nπ*)_UR + 0.43 × S₁(nπ*)_R at 1.4 ps; 0.36 × S₁(nπ*)_UR + 0.52 × S₁(nπ*)_R + 0.12 × T₂(ππ*) at 42 ps; and 1.00 × T₁(ππ*)_MIN at 2600 ps.

Dynamical View of the Deactivation of Purine Free Base: Ab Initio Surface-Hopping Simulations

Ab initio molecular dynamics simulations using the SHARC method⁶³ for the N9H tautomer of the purine free base show two main deactivation pathways within 1 ps. After excitation, the excited-state population either relaxes to the ground state or shows intersystem crossing followed by triplet conformational relaxation that ultimately leads to the T₁(ππ*) state. A fraction of the population is still trapped in the precursor S₁(nπ*) state after 1 ps. The time evolution of the state populations and the reaction mechanism derived from the dynamics calculations are shown in SI Figure S18.

According to the simulated absorption spectrum of the N9H tautomer of the purine free base (Figure 6), absorption of 266 nm radiation excites 13% of the trajectories to the S₁(nπ*) state, 80% to the S₂(ππ*) state, and 7% to the S₃(ππ*) state. The trajectories starting in the S₃ state evolve adiabatically from ππ* to nπ* and then decay very fast to the S₂(ππ*) state through an (S₃(nπ*)/S₂(ππ*))_CI crossing point. This conical intersection shows a slight distortion of the pyrimidine ring (dihedral C6–N1–C2–N3 = 3.8°; SI Figure S19). The S₂ state also changes adiabatically from ππ* to nπ* in different dynamically accessible regions of the coordinate space. A total of 66% of the entire population initially excited from the ground state evolves further through the (S₂(ππ*)/S₁(nπ*))_CI, which is identical to the conical intersection found in the static calculations (vide supra). The remaining population in the S₂ state (21%; see SI Figure S18) goes through an (S₂(nπ*)/S₁(nπ*))_CI, which is not identified by the static calculations from the spectroscopic state, shown in Figure 7. At this point, it should be noted that these two S₂/S₁ conical intersections are distinct minima on the high-dimensional S₂/S₁ crossing seam, explaining why the state character of the S₂ state is different at these two intersections. The S₂(nπ*)/S₁(nπ*) conical intersection shows twisting in the pyrimidine ring (dihedral C6–N1–C2–N3 = 43.5°; SI Figure S19).

Once all the population reaches the S₁ state (i.e., the initial 13% in the S₁(nπ*) state plus the residual 87% from the S₂ and S₃ states in SI Figure S18), the dynamics disclose two possible reaction pathways: (1) relaxation to the S₀ state via an (S₁(nπ*)/S₀)_CI or (2) intersystem crossing via an (S₁(nπ*)/T₂(ππ*))_ISC singlet/triplet crossing. Although these two identified crossing points are identical to the ones obtained by static calculations above, the ratio of the population distributed between these two pathways predicted by the dynamics simulations is different from what is expected from quantum chemistry alone. According to Figure 7, the deactivation of the S₁(nπ*) state to the ground state is hindered because it requires overcoming a potential barrier of 0.6 eV, as predicted by CASPT2 calculations. However, CASSCF—the level of theory at which the dynamical calculations are done—does not predict any barrier, thereby favoring deactivation to the S₀ state to a larger extent than it should. Despite the different expected and predicted relative quantum yield, which is due to the lack of dynamical electron–electron correlation of the CASSCF method, the general picture provided by the dynamics simulations is correct.

After passing through a singlet–triplet crossing, (S₁(nπ*)/T₂(ππ*))_ISC, the trajectories decay to the T₁(ππ*) state via a T₂(nπ*)/T₁(ππ*) conical intersection, where the ππ* crosses with the nπ* potential energy surface. The involved T₂(nπ*)/T₁(ππ*) conical intersection shows a twisting of the pyrimidine ring, as well as a pyramidalization of H11 (SI Figure S19), and corresponds to the T₂(nπ*)/T₁(ππ*) conical intersection shown in Figure 7. After 1 ps of simulation time, all the population in the T₁ state has ππ* character, while hot population in the S₁ state is still present. Triplets higher than the T₂ state do not play a significant role in the relaxation dynamics.

A global fit analysis of the excited-state populations from the dynamics simulations revealed three time constants (see Figure S18). The initial relaxation from the S₂(ππ*) to the S₁(nπ*) state can be satisfactorily modeled with a 25 fs lifetime, while a 1.2 ps lifetime is required for ground-state relaxation from the S₁(nπ*) state. According to this global fit analysis, intersystem crossing to the triplet manifold occurs on a 5 ps time scale. Caution should be taken not to overinterpret the latter two lifetimes because the CASSCF method provides only a qualitative picture of the S₁(nπ*)/S₀ region of the potential energy surface. Furthermore, a time window of only 1 ps was used in the simulation, and the fraction of the initial trajectories that actually sampled the intersystem crossing pathway was small. It is also noticed that relaxation within the triplet manifold is apparently ultrafast because no appreciable T₂ state population was observed in the simulations (SI Figure S18).

Discussion

The primary goal of this work is two-fold: (1) to present a detailed description of the photophysics and the excited-state dynamics in 9-methylpurine and the purine free base using a combined experimental and computational approach and (2) to provide new, relevant insights about the primary electronic and structural elements that regulate the radiative and nonradiative decay pathways in several relevant purine derivatives including adenine and guanine. This information has been lacking in the scientific literature and is essential for a firm understanding of the factors that influence the photostability and the photochemistry of the nucleic acid bases.

The discussion begins with an overview on the assignment of the steady-state absorption and emission spectra of 9-methylpurine and the purine free base in polar protic, polar aprotic, and nonpolar solvents. This is followed by assignment of the transient absorption bands with the support of stationary quantum-chemical calculations and semiclassical dynamics simulations. A detailed kinetic mechanism that satisfactorily explains the excited-state dynamics in 9-methylpurine and the purine free base is then presented. Finally, the electronic mechanism revealed in this work for the purine chromophore is compared to those previously reported for the purine derivatives shown in Scheme 1, before summarizing the central results.

Assignment of Steady-State Absorption and Emission Spectra

The focus of this section is on the assignment of the electronic transitions that contribute to the lowest-energy absorption band and to the emission spectra of both 9-methylpurine and the purine free base shown in Figure 1, which are of direct relevance to understanding the excited-state dynamics reported in this work. A more thorough discussion of the steady-state spectra, the solvatochromic effects, and an in-depth comparison with previous experimental and computational results is presented in the SI.^{52−60,64−74}

As in the adenine and guanine monomers,^3,4 the lowest-energy absorption band in both 9-methylpurine and the purine free base is assigned to several ¹ππ* electronic transitions that overlap strongly in the spectral region around 260 nm. In particular, two pairs of ¹ππ* electronic transitions from both the N7H (S₂ and S₃) and N9H (S₂ and S₄) tautomers contribute to this absorption band to different extents in the purine free base (Table 2).⁵⁴ This band is perturbed insignificantly by the solvent used, mainly showing an increase in vibronic resolution when 9-methylpurine is dissolved in cyclohexane (Figure 1b).^64,70

A low intensity absorption tail is observed to the red side of the main 260 nm absorption band that shifts further to the red in going from acetonitrile to cyclohexane. This tail is not as prominent in aqueous buffer solution, suggesting that the electronic transition associated with it shifts to slightly higher energies in this polar protic solvent. In fact, this electronic transition is lower in energy than the stronger absorption band around 260 nm but hidden under its red side. These observations are consistent with an electronic transition that is less polar than the ground state and has smaller oscillator strength. Thus, this absorption tail is assigned to an nπ* electronic transition that is lower in energy than the lowest two ππ* electronic transitions in both the purine free base and 9-methylpurine.^{53,54,64,65,67−69}

The results presented in this work show that 9-methylpurine and the purine free base exhibit very small fluorescence yields of ≈10^–3. For 9-methylpurine, the emission maximum blue shifts and the fluorescence yield decreases approximately 4-fold in going from water to cyclohexane. In contrast, the emission maximum of the purine free base does not change appreciably, while its fluorescence yield exhibits approximately a 2-fold decrease upon going from water to acetonitrile. The comparison of the emission results for 9-methylpurine, and the purine free base indicates that both the N7H and N9H purine tautomers contribute to the observed fluorescence. Moreover, based on the theoretical calculations, it is proposed that the observed fluorescence emission originates from the ¹nπ* state of both the N7H and N9H purine tautomers and also from the ¹nπ* state of 9-methylpurine. This is consistent with the ultrafast decay of the ¹ππ* state and the hundreds of picoseconds intersystem crossing of the ¹nπ* state to the triplet manifold. In fact, the experimental fluorescence maximum for 9-methylpurine of ∼370 nm in cyclohexane, as well as the experimental E_0,0 energy reported in Table S1 of the SI, are in good agreement with the calculated ¹nπ* vertical (375 nm) and adiabatic (326 nm) emission energies.

Assignment of the Transient Absorption Spectra of 9-Methylpurine

As previously reported for adenine, guanine, and other purine derivatives,^{3,8,9,39,75−80} excitation at 266 nm takes the ground-state population primarily to the lowest-energy ππ* state (S₂), whereas a small fraction also populates higher-energy singlet states directly, both in the purine free base and 9-methylpurine (Table 2 and Figure 6). Assignment of the transient absorption bands for the purine free base is further complicated by the presence of both N7H and N9H purine tautomers in solution, as summarized in the previous section and discussed in more detail in the SI. Hence, the focus of this section is on the assignment of the broadband transient absorption spectra of 9-methylpurine, whereas the assignment of the transient absorption spectra of the purine free base is discussed in the next section.

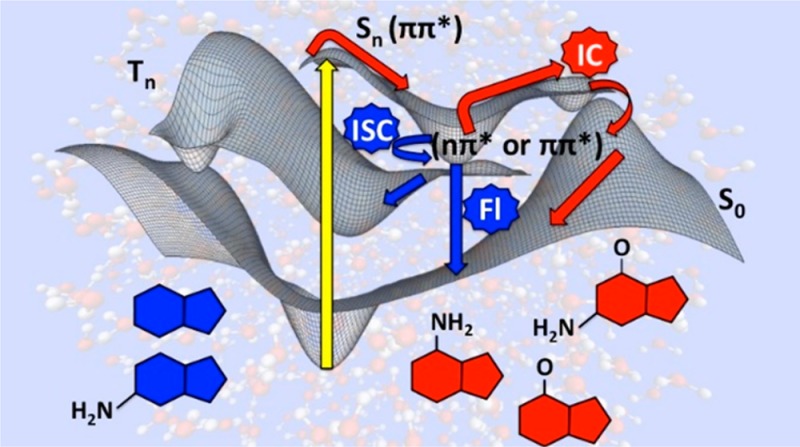
The time-resolved experiments depicted in Figure 2 show at least three primary relaxation processes taking place from the femtosecond to the nanosecond time scale for 9-methylpurine, which are schematically summarized in Figure 9. The initial growth in transient absorption spectra from about −0.10 to ∼0.20 ps (Figure 2, top panel) is assigned to absorption from a superposition of the optically excited singlet S₃, S₂, and S₁ states, weighted by the ground-state absorption cross sections at 266 nm. This is in agreement with the simulated ground-state absorption spectrum in Figure 6. This initial growth (i.e., within the cross-correlation of the pump−probe beams) is manifested as a broad, featureless transient absorption band that has an absorption maximum below 350 nm and an almost flat absorption between ∼460 and 650 nm. As shown in Figure 8, linear combinations of the calculated absorption spectra at specific and relevant nuclear coordinates in the potential energy surfaces can be used satisfactorily to simulate the transient spectra. These calculated excited-state absorption spectra, shown in Figure S9 (see discussion in the SI for further details), reveal several absorptions with considerable oscillator strengths in the region between 440 and 650 nm for the S₃(ππ*)_FC, S₂(ππ*)_FC, and S₁(nπ*)_FC states. The band below 350 nm is ascribed to excited-state absorption of molecules primarily in the S₃(ππ*)_FC and the S₂(ππ*)_MIN because the population of molecules in the S₂(ππ*)_FC and S₁(nπ*)_FC states does not show significant absorption in this spectral region.

Figure 9.

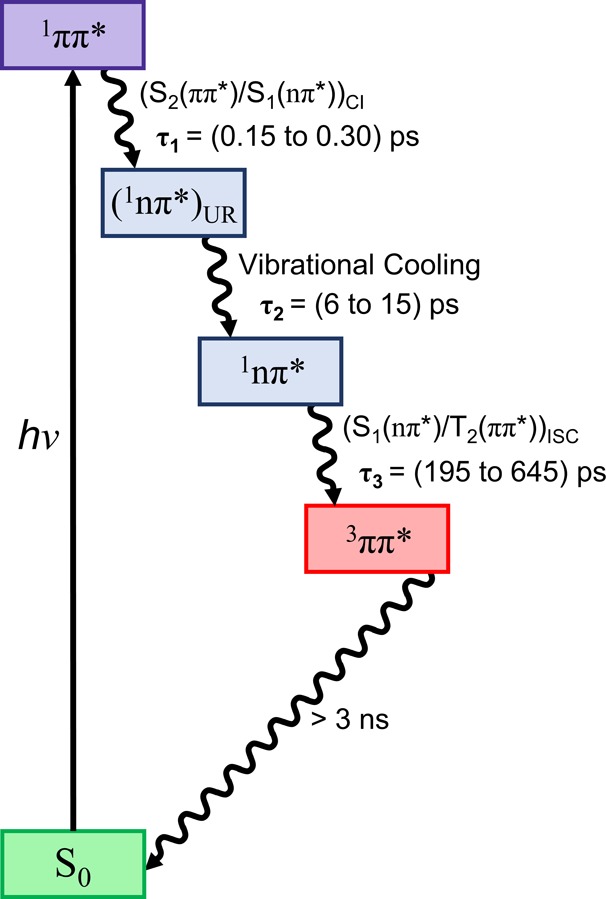
Proposed generic decay mechanism for 9-methylpurine and the purine free base based on the experimental and computational results. Characteristic lifetimes are shown in parentheses.

The most prominent relaxation pathway observed in the transient absorption spectra occurring at these early time delays (i.e., from about −0.10 to ∼0.20 ps) is proposed to be internal conversion from the S₂(ππ*) state to the S₁(nπ*) state (Figure 9). This is supported by the semiclassical dynamics simulations, which show that internal conversion from the S₂(ππ*) to the S₁(nπ*) state occurs on a sub-100 fs time scale—actually faster than the time resolution available in the experimental setup (IRF = 200 ± 50 fs). Further, the simulated transient absorption spectra shown in Figure 8 (top panel) lend support to the idea that a superposition of the S₃(ππ*)_FC, S₂(ππ*)_FC, S₁(nπ*)_FC, and the S₂(ππ*)_MIN absorption spectra is needed to reproduce the transient absorption spectra at a time delay of about 0.03 ps. Meanwhile, the absorption bands below 350 nm, around 465 nm, and above ≈560 nm continue to grow. As a result, the transient absorption spectra observed at time delays between 0.20 and 1.4 ps are assigned to a superposition of absorption spectra from the S₂(ππ*) state minimum and the unrelaxed S₁(nπ*) state, S₁(nπ*)_UR. This assignment is consistent with the plateau-like shape of the potential energy surface around the (S₂(ππ*)/S₁(nπ*))_CI (Figure 7), which allows for the coexistence of both ¹ππ* and ¹nπ* states at this geometry and for the existence of absorption maxima for both states in this region. According to the calculated absorption spectra at the (S₂(ππ*)/S₁(nπ*))_CI geometry, the absorption from the S₂(ππ*)_MIN and the unrelaxed S₁(nπ*) state at 504 and 466 nm, respectively, should be responsible for the experimentally observed band at 465 nm. Similarly, the strong absorption band experimentally observed below 350 nm is assigned to the transitions predicted theoretically at 330 nm from the S₂(ππ*)_MIN and at 315 nm from the unrelaxed S₁(nπ*) state. These transient species also contribute to the flat absorption above 560 nm (Figure 8, top panel). Experimentally, the lifetime associated with this relaxation process, τ₁ = 0.15 ± 0.05 ps in acetonitrile, is assigned to internal conversion from the S₂(ππ*) state to the unrelaxed S₁(nπ*) state (Figure 9; see Table 1 for τ₁ in other solvents). Importantly, this seems to be the first direct experimental observation of the excited-state absorption spectrum of the S₁(nπ*) state and of its participation in the excited-state dynamics of a purine base derivative in solution.

At the time delays between 1 and 42 ps (SI Figure S4 and Figures 2 and 8, middle panels), the absorption band at 465 nm blue shifts and narrows to a maximum of about 440 nm in acetonitrile, with a simultaneous decrease in intensity of the absorption band below 350 nm. In particular, the transient absorption spectrum with maxima at 465 and 528 nm at a time delay of ∼1 ps develops into an absorption spectrum with maxima at 440 and ∼520 nm at a time delay of ∼40 ps (Figures 2 and 4). These spectral changes are attributed to the full decay of the S₂(ππ*) state into the unrelaxed S₁(nπ*) state and the subsequent deactivation of S₁(nπ*)_UR into the relaxed ¹nπ* state, S₁(nπ*)_R (Figure 8). In particular, the 465 → 440 nm blue shift (Figure 2, left-middle panel) is ascribed to the vibrational relaxation of the S₁(nπ*) state population. The S1(nπ*) state absorbs at 420 and 438 nm at the position of the state minimum (recall that the absorption maximum of the unrelaxed S₁(nπ*) state is centered at 465 nm; SI Figure S9). This decay pathway is characterized by a solvent-dependent lifetime ranging from 6 to 15 ps (τ₂ in Table 1). This process is assigned to the vibrational relaxation of the S₁(nπ*) state. As shown in Figure 8 (middle panel), a linear combination of the calculated absorption spectra suggests that most of the excited-state population (∼90%) is in the unrelaxed and relaxed S₁(nπ*) state at about 40 ps. Vibrational relaxation in the lowest-energy S₁(nπ*) state of the pyrimidine monomers has been reported previously by the Kohler group,¹³⁻¹⁵ but this seems to be the first report to reveal this nonradiative decay pathway in the S₁(nπ*) state of the purine bases.

The simulation of the transient absorption spectrum at a time delay of about 40 ps shown in Figure 8 (middle panel) also suggests that a very small fraction of the population (∼10%) has reached the T₂(ππ*) potential energy surface at this time delay (see Figure S9 in the SI). This is fully consistent with the hundreds of picosecond intersystem crossing lifetime discussed in the next paragraph. In addition, this agrees with the static and dynamics calculations, which predict that the initial population in the ³ππ* potential energy surface, labeled T₂(ππ*) state in Figure 7, conformationally relaxes on an ultrafast time scale to populate the region of the ³ππ* potential energy surface minimum, which is labeled the T₁(ππ*) state in Figure 7 (i.e., pathway (iii) highlighted with yellow arrows).

The ³ππ* state (i.e., the T₁(ππ*) in Figures 7 and 9) is populated with a lifetime that varies from 600 to 195 ps in going from polar protic to polar aprotic to nonpolar solvents (τ₃ in Table 1). The ³ππ* state exhibits an absorption maximum at 406 nm with a broad, low-intensity absorption band centered at about 580 nm in acetonitrile (Figures 2 and 4). In aqueous buffer solution, the ³ππ* state exhibits an absorption maximum at 412 nm with a shoulder at about 575 nm. This is consistent with the calculated absorption maxima of 407 nm (f = 0.007) and 556 nm (f = 0.005) for the transient in the T₁(ππ*)_MIN shown in Figure 8 (bottom panel). The triplet state does not decay within the 3 ns time window of the instrument used in this work, as might be expected. The assignment of this long-lived species to the ³ππ* state of 9-methylpurine is further supported by previous nanosecond transient absorption experiments for the purine free base.⁵¹ The strong dependence of the τ₃ lifetime on the solvent is consistent with the decrease in the Franck–Condon energy gap between the S₁(nπ*) and T₁(ππ*) states in going from polar protic to polar aprotic to nonpolar solvents at the TD-DFT level of theory (SI Table S2). The decrease in the intersystem crossing lifetime in going from polar protic to polar aprotic solvents is also consistent with recent results for the 2-aminopurine nucleoside,⁸¹ suggesting that a solvent-dependent energy barrier must be surmounted to access the intersystem crossing region.

Figure 9 summarizes a generic kinetic mechanism proposed for 9-methylpurine. Excitation at 266 nm populates primarily the ππ* singlet states in the Franck–Condon region. The excited-state population then decays on an ultrafast time scale (τ₁) to populate the vibrationally excited ¹nπ* state, which cools in a few picoseconds (τ₂) to populate the relaxed ¹nπ* state. Intersystem crossing to the ³ππ* state occurs in hundreds of picoseconds (τ₃). Finally, the ³ππ* state can intersystem cross back to the ground state at longer time scales (>3 ns). This sequential mechanism is completely supported by the experimental and computational results reported in this work.

Assignment of the Transient Absorption Bands in the Purine Free Base

As mentioned above for 9-methylpurine, excitation of the purine free base at 266 nm is expected to result primarily in the simultaneous population of ¹ππ* excited states (Table 2), weighted by the ground-state absorption cross sections at 266 nm. However, the spectroscopy is more complex in the purine free base because of the ground-state prototropic equilibrium between the N7H and N9H purine tautomers in aqueous buffer solution and in acetonitrile. The N7H tautomer has been reported to be in slightly higher concentration than the N9H tautomer in aqueous solution,^55−58,60 whereas the N9H tautomer should dominate in aprotic solvents like acetonitrile.^54−56,70 This is in agreement with the analysis of the steady-state absorption spectra presented in this work (see also the discussion in the SI). Thus, excitation of the purine free base at 266 nm should populate the ππ* singlet states of both the N7H and N9H purine tautomers simultaneously, weighted by the N7H/N9H molar concentrations and by the absorption coefficients of the singlet excited states at 266 nm. Based on the calculations presented in this work, and those by others,⁵⁴ the two lowest-excited singlet states with ππ* character should be simultaneously populated upon 266 nm excitation, with most of the ground-state population arriving at the lowest ππ* state (S₂) for both the N7H and N9H purine tautomers.

Interestingly, a global fitting analysis based on the multidimensional transient absorption data for the purine free base in aqueous buffer solution and acetonitrile revealed excited-state dynamics very similar to those found for the 9-methylpurine in these two solvents (Table 1 and Figures 3 and 5). This observation suggests that the excited-state lifetimes of the N7H tautomer are similar to that of the N9H purine tautomer (or that the N7H decays on significantly faster time scales), in such a way that we are unable to disentangle its dynamics from those of the N9H tautomer. A similar conclusion has been reached recently in the case of other purine derivatives.¹⁰⁻¹² According to the kinetic analysis presented in this work, at least a three-step reaction sequence is needed to model the excited-state dynamics of the purine free base in acetonitrile and aqueous buffer solution (Figure 9), similar to 9-methylpurine. In analogy to the 9-methylpurine analysis, the sub-picosecond decay pathway is assigned to ultrafast internal conversion from the optically populated excited singlet states to the unrelaxed S₁(nπ*) state. As the unrelaxed S₁(nπ*) state cools in tens of picoseconds (τ₂ in Table 1), intersystem crossing and conformational relaxation from the T₂(ππ*) to the T₁(ππ*) of the potential energy surface take place in hundreds of picoseconds (τ₃ in Table 1 and pathways (iii) and (iiib) in Figure 7).

A similar transient absorption spectrum was reported by Quiñones and Arce for the lowest-energy ³ππ* state of the purine free base in aqueous solution at pH 5.9.⁵¹ According to these authors, the ³ππ* state decays back to ground state in 1.7 μs under N₂-saturated conditions.⁵¹ In addition, a triplet yield of 0.88 ± 0.03 has been reported for the purine free base in acetonitrile,⁸² lending further support to the assignment of the long-lived transient absorption spectrum observed in the experiments presented herein to the ³ππ* state (i.e., T_n ← T₁ transitions).

Finally, a closer inspection of the broadband transient absorption data reported in Figure 3 suggests the presence of one or more excited-state species originating from the N7H tautomer. These species seem to be decaying on similar time scales to those of the N9H tautomer, as proposed above from the kinetic analysis of the decay traces. Specifically, the transient absorption spectra show the presence of additional bands in the femtosecond to hundreds of picoseconds time window when compared with the transient absorption spectra of 9-methylpurine in aqueous buffer solution or acetonitrile (Figure 2). In addition, the transient absorption spectra observed at nanosecond time delays, which this and other works⁵¹ have assigned to the ³ππ* state absorption of the purine free base, have very similar absorption bands around 400 nm in both purine and 9-methylpurine, whereas the long-wavelength absorption band observed in 9-methylpurine around 580/560 nm in acetonitrile/buffer solution is overshadowed in the spectra of the purine free base by a species absorbing in the spectral region from ∼450 to 500 nm (compare Figure 2 to Figure 3). It is proposed that this band originates from an N7H transient species that overlaps with the long-wavelength ³ππ* state absorption band of the N9H tautomer. Clearly, a rigorous assignment of the transient absorption spectra of the purine free base in different solvents requires a complete analysis of the quantum-chemical properties of the excited states of the N7H tautomer. This is, however, out of the scope of the present work since the primary focus is on the excited-state dynamics of 9-methylpurine and the N9H purine tautomer. Besides, the sugar moiety at the N9 position in the purine nucleosides blocks this tautomerization, making the N7H purine tautomer a less relevant biological species.

Excited-State Dynamics of 9-Methylpurine and N9H Purine Tautomer

The quantum-chemical and semiclassical dynamics calculations confirm that the deactivation mechanism is composed of three major stages (Figure 9), as extracted from the global fitting of the transient absorption experiments. The first stage is a population transfer from the S₂(ππ*) to the S₁(nπ*) state via internal conversion through the (S₂(ππ*)/S₁(nπ*))_CI conical intersection. The proximity of this funnel to the Franck–Condon region is compatible with the ultrafast lifetimes (τ₁ = 150 to 300 fs) recorded for both the purine free base and 9-methylpurine and the 25 fs lifetime estimated from the dynamics simulations. The second stage is the vibrational relaxation of the S₁(nπ*) state to the solvent. The flat shape of the potential energy surface around the conical intersection would explain the coexistence of the ¹ππ* state and an unrelaxed ¹nπ* state during the first picoseconds, as reflected in the transient absorption spectra (Figure 8, top panel). This, together with the large energy gap (∼0.7 eV) computed between the (S₂(ππ*)/S₁(nπ*))_CI conical intersection and the S₁(nπ*) minimum, supports vibrational cooling to the solvent with an average lifetime of 6–15 ps (τ₂ in Table 1). This leads to a third and final stage (τ₃ = 195 to 645 ps), where population is transferred to the T₂(ππ*) potential energy surface via the (S₁(nπ*)/T₂(ππ*))_ISC intersystem crossing funnel together with conformational relaxation to the T₁(ππ*) global minimum. In other words, it is proposed that the deactivation pathways occur sequentially: S₂(ππ*) → S₁(nπ*,hot) → S₁(nπ*,relaxed) → T₂(ππ*) → T₁(ππ*), as shown in Figure 9. We stress that the T₂(ππ*) → T₁(ππ*) conformational relaxation is an adiabatic process occurring on an ultrafast time scale (few femtoseconds), where the ππ* character is conserved, as shown in Figure 7, and supported by the dynamics simulations.

The high triplet quantum yield measured experimentally is in contrast with the 10% of the population that reaches the triplet manifold in the dynamical simulations (SI Figure S18). This discrepancy is due to the qualitatively wrong behavior of the CASSCF method, which yields a flat potential connecting the S₁(nπ*) minimum with the deactivation funnel to the ground state, instead of the barrier predicted by CASPT2. The topology of the CASPT2 potential energy profiles extracted from minimum energy path calculations is consistent with the experimental triplet quantum yield of near unity. In fact, the CASPT2 minimum energy paths are consistent with a very efficient population transfer to the singlet S₁(nπ*) minimum, from where intersystem crossing occurs. At the same time, the shape of the S₁(nπ*) potential precludes the decay of population to the ground state due to the uphill pathway calculated to access the S₁(nπ*)/S₀ conical intersection from this minimum (pathway (iiia) in Figure 7). Moreover, the very modest spin–orbit coupling calculated at the intersystem crossing region can explain the relatively slow rate of triplet-state population experimentally measured. The profile calculated for the subsequent deactivation of the system from the triplet state, via the (T₁(ππ*)/S₀)_ISC located ∼2 eV above the triplet T₁(ππ*) minimum, explains the 1.7 μs time constant measured by Quiñones and Arce for the purine free base to decay to the ground state in an O₂-free environment.⁵¹

Comparison with the Excited-State Dynamics in Other Purine Derivatives

The canonical DNA purine bases have been classified in contemporary literature as photostable systems, based primarily on the ultrafast nonradiative decays extracted from femtosecond dynamics experiments and deactivation pathways inferred from quantum mechanical and molecular dynamics simulations.^3,83−85 These bases decay primarily from the initially populated spectroscopic ¹ππ* states, the so-called ¹L_a state according to Platt’s nomenclature,⁸⁶ to the ground state following a barrierless path that directs the population through a (¹ππ*(L_a)/S₀)_CI internal conversion funnel.^36,43,83,87 The ¹L_a state is the lowest-energy excited state in guanine, whereas it is the third excited state in adenine, according to gas-phase calculations.^36,43 Along this path, two internal conversion funnels (i.e., the ¹ππ*(L_a)/¹nπ* and ¹ππ*(L_a)/¹ππ*(L_b)) in the case of adenine and two intersystem crossing funnels, namely, (¹ππ*/³nπ*)_ISC and (¹ππ*/³ππ*)_ISC, were predicted for adenine and guanine. However, the steeply descending nature of the potential energy profile along this pathway has been suggested to prevent the retention of the wavepacket at these singlet/singlet and singlet/triplet crossing regions long enough to divert the system to other regions of the singlet potential energy surface or to leak population to the triplet manifold.

The topology of the potential energy surfaces in the canonical DNA purine bases also minimizes radiative decay of the excited population. This is in contrast to the constitutional isomer of adenine, 2-aminopurine (Scheme 1), which shows a significant fluorescence quantum yield from the initially populated ¹ππ*(L_a) state that varies from 0.3 to 0.7 on going from acetonitrile to aqueous buffer solution.^81,88,89 This is consistent with the location of a minimum in the gas-phase ¹ππ* potential energy profile, which was predicted by gas-phase calculations as the most stable state, although energetically very close to the ¹nπ* state at the Franck–Condon region. In fact, relatively small energy barriers amounting to 5 and 10 kcal/mol separate the ¹ππ* minimum from the ¹ππ*(L_a)/S₀ and the ¹ππ*(L_a)/¹nπ* conical intersections, respectively.^87,90 Thus, radiative decay in 2-aminopurine competes with two other internal conversion channels: relaxation to the ¹nπ* excited state and to the S₀ state.^87,90 Hence, from these three competing relaxation pathways, fluorescence is preferred in 2-aminopurine (ϕ_F = 0.3 to 0.7) over internal conversion to the ground state (ϕ_IC = 0.3) or intersystem crossing to the T₁ state (ϕ_ISC = 0.1 to 0.4), depending on the solvent used.⁸¹

Regarding the structural elements of these purine derivatives, different authors have correlated the relative deactivation rates observed for the canonical purine nucleobases and their derivatives shown in Scheme 1 with the presence or absence of a substituent at the C2 position of the purine heterocycle,^10,11,83,91 which would hinder the puckering of the C2 carbon, characteristic of the ¹ππ*(L_a)/S₀ seam of intersection. Following this reasoning, one would expect 9-methylpurine and the purine free base, both of which lack a substituent at the position C2, to decay back to the ground state on ultrafast time scales, which is not the case. This suggests an alternative paradigm, where the group at the C6 position plays an important role in the ultrafast decay of the excited-state population to the ground state of these purine derivatives. The amino or oxo group at the C6 position inhibits access to the ¹nπ* state and facilitates access to the ¹ππ*(L_a)/S₀ conical intersection. This alters the shape and ordering of the potential energy surfaces in such a way that population of the ¹nπ* state cannot compete with the direct ground-state relaxation pathways involving puckering of the group at the C2 position in the six-membered ring. A secondary pathway, alternative to the main internal conversion via N2–C3 bond rotation and involving the puckering at the C6 position, has been proposed to play a role in the nonradiative decay of adenine and guanine.^38,47,49 Hence, our results for 9-methylpurine and the purine free base lend strong support to the idea that the functional group at the C6 position plays an important role in regulating the rate of internal conversion to the ground state in these purine derivatives. This idea is consistent with recent ultrafast measurements reported for hypoxanthine and inosine,^10,11 2-aminopurine,⁸¹ and allopurinol.⁸⁰ It might also be consistent with recent transient absorption measurements for the methylxanthine derivatives,¹² although these compounds lack the C2=N3 and N1=C6 double bonds, which are available in the other purine derivatives and play an important role in their puckering deformation pathways.

It should be noted that the C6 position in the purine bases is analogous to the C4 position in the pyrimidine derivatives. Hence, following the rationale above, it is expected that the functional group at the C4 position in the pyrimidine derivatives would also play an important role in regulating the rates of radiative and nonradiative decay to the ground state. This is consistent with the observation that the canonical pyrimidine monomers^3,9 and 4-pyrimidinone⁹² decay primarily by ultrafast internal conversion to the ground state, whereas 1-methyl-2-pyrimidinone^93,94 and 5-methyl-2-pyrimidinone⁹⁵ decay primarily by long-lived radiative and/or nonradiative decay pathways. Experimental and computational work is currently underway in our groups in order to further scrutinize this paradigm.

Returning to 9-methylpurine and the N9H purine tautomer, an alternative model for deactivation is proposed in this work that is based on both experimental and theoretical findings. Although the shape of the potential energy profile along the spectroscopic ¹ππ*(L_a) state for these two purine derivatives is very similar to the one calculated for 2-aminopurine,^87,90 the existence of the ¹nπ* state below the ¹ππ*(L_a) state at the Franck–Condon region and the proximity of the ¹ππ* minimum to the ¹ππ*(L_a)/¹nπ* internal conversion funnel propel the population to the lowest-lying ¹nπ* minimum. Deactivation to the ground state from the ¹nπ* minimum is prevented, as in other purine derivatives,^36,43 due to the existence of an energy barrier to access the ¹nπ*/S₀ internal conversion funnel. Therefore, the degeneracy of an excited triplet state in the region of the ¹nπ* minimum favors the transfer of population to the triplet manifold, resulting in the population of the ³ππ* state in near-unity yields in both 9-methylpurine and the N9H purine tautomer.

In summary, a close parallelism between the ultrafast nonradiative decay to the ground state of the canonical DNA bases and the population of the triplet states in the purine free base and 9-methylpurine can be established. In recent literature, the photostability of the DNA and RNA monomers has been rationalized in terms of a three-state model, where deactivation to the ground state is governed by nonradiative decays from ¹ππ* excited states to the ground state, with minor contributions from pathways involving the ¹ππ*(L_b) and ¹nπ* states leading to slower decays.^36,43 Conversely, this and other works^{13−15,18−21,96} have shown that population of nπ* excited states has the potential to increase the propensity for photochemical damage by acting as doorway states in the singlet-to-triplet population transfer. A three-state model involving two ππ* and one nπ* electronic states is proposed to rationalize the photophysics of the purine derivatives undergoing intersystem crossing, which is similar to the one previously suggested for the canonical purine DNA nucleobases.^36,43 In the mechanism proposed in Figure 9, however, two singlet states (¹ππ* and ¹nπ*) and one triplet state (³ππ*) are proposed to participate in the main deactivation sequence: ¹ππ* → ¹nπ* → ³ππ* → S₀.

As described above, the substitution pattern of the purine skeleton defines the Franck–Condon state ordering and the topology of the potential energy surfaces and determines the inherent relaxation pathways of the system. However, it should be noted that the solvent also plays an essential role in modulating the depth of the minima and the magnitude of the energy barriers that restrict access to key conical intersections and relevant deactivation pathways.⁹⁷⁻⁹⁹ The solvent also affects the vibronic coupling between singlet and triplet excited states.⁸¹ Therefore, the solvent used can ultimately adjust the experimental time constants and product yields for competing processes. As such, caution should be exercised when comparing calculations done in vacuum to experimental results performed in solution and vice versa.

Conclusions

In this joint experimental and theoretical contribution, it is shown that excitation at 266 nm of both the 9-methylpurine and the N9H tautomer of the purine free base populates primarily the S₂(ππ*) state in the Franck–Condon region. The excited-state population decays on an ultrafast time scale (τ₁) to populate the vibrationally excited ¹nπ* state, which cools in a few picoseconds (τ₂) to populate the relaxed ¹nπ* state. Intersystem crossing to the triplet manifold occurs with a lifetime of hundreds of picoseconds (τ₃), ultimately reaching the ³ππ* minimum. Finally, the ³ππ* state can intersystem cross back to the ground state in a time scale on the order of microseconds.

In a broader perspective, the results presented in this work indicate that the rates of nonradiative decay to the ¹nπ* state and the triplet state in the purine derivatives are regulated by (1) the energetic accessibility of internal conversion funnels to the ¹nπ* excited state, (2) the existence/absence of small singlet–triplet energy gaps at the position of singlet state minima, and (3) the occurrence of energetic barriers that hinder internal conversion from the ¹ππ*, ¹nπ*, and ³ππ* states to the ground state. It is also shown that the heterocyclic purine chromophore is not responsible for the ultrafast internal conversion to the ground state observed in the adenine and guanine monomers and in other purine derivatives. Instead, it is proposed that the functional group at the C6 position plays an important role in regulating the rates and the accessibility of radiative and nonradiative relaxation pathways in the purine derivatives in solution, whereas the substituent at the C2 position plays a secondary role.

Supporting Information Available

Experimental and computational methods; supporting experimental and computational results; Cartesian coordinates of the optimized stationary and conical intersection structures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^∥ L.M.-F., C.R., and C.R. contributed equally to this work.

The authors declare no competing financial interest.