Do Daughters Really Cause Divorce? Stress, Pregnancy, and Family Composition

Abstract

Provocative studies have reported that in the United States, marriages producing firstborn daughters are more likely to divorce than those producing firstborn sons. The findings have been interpreted as contemporary evidence of fathers' son preference. Our study explores the potential role of another set of dynamics that may drive these patterns: namely, selection into live birth. Epidemiological evidence indicates that the characteristic female survival advantage may begin before birth. If stress accompanying unstable marriages has biological effects on fecundity, a female survival advantage could generate an association between stability and the sex composition of offspring. Combining regression and simulation techniques to analyze real-world data, we ask, How much of the observed association between sex of the firstborn child and risk of divorce could plausibly be accounted for by the joint effects of female survival advantage and reduced fecundity associated with unstable marriage? Using data from the National Longitudinal Survey of Youth (NLSY79), we find that relationship conflict predicts the sex of children born after conflict was measured; conflict also predicts subsequent divorce. Conservative specification of parameters linking pregnancy characteristics, selection into live birth, and divorce are sufficient to generate a selection-driven association between offspring sex and divorce, which is consequential in magnitude. Our findings illustrate the value of demographic accounting of processes which occur before birth—a period when many outcomes of central interest in the population sciences begin to take shape.

Introduction

Provocative studies in economics and sociology, using data from the United States, have reported associations between offspring sex and marital stability (Ananat and Michaels 2008; Bedard and Deschênes 2005; Dahl and Moretti 2008; Mammen 2008; Morgan et al. 1988; Spanier and Glick 1981). Several of these studies indicate that marriages producing firstborn daughters are more likely to end in divorce than marriages producing firstborn sons. This finding has generated considerable interest within the academic literature and beyond, influencing popular discourse (Belkin 2010; Clark-Flory, 2010; Hutchison 2010; Kelly 2010; Landsburg 2003a, b).

We, like many others, are intrigued by the findings because they naturally raise the question, Whence the difference in divorce risk? Some hypotheses build from the idea that fathers exhibit a son preference: for example, they might identify more closely with sons than daughters (Dahl and Moretti 2008; Morgan et al. 1988) and thus may be more firmly drawn into a family with sons than one with daughters. Others, including Lundberg (2005), have indicated reasons for caution in interpreting associations between sex of offspring and risk of divorce as evidence of son preference; among these are publication bias and deliberate sex-specific abortion. We investigate another possible reason: namely, the dynamics of selection into live birth. We are motivated by evidence that the sex of only a subset of pregnancies is observed in data; almost nothing is known about all the pregnancies that do not end in a live birth.

Evidence in the epidemiological literature indicates that the unobserved subset of pregnancies may be large; as many as one-half or more of normal, otherwise viable pregnancies may end without a live birth (Benagiano et al. 2010; Grudzinskas and Nysenbaum 1985; Macklon et al. 2002). There is also evidence that the female survival advantage observed throughout the human life course may begin before birth, manifesting in sex ratios among early pregnancies that are substantially more male than sex ratios among live births (Pergament et al. 2002).

In the presence of a prenatal female survival advantage, any factor affecting pregnancy survival could affect the sex ratio in a birth cohort. One such factor might be the biological effects of stressors, such as relationship conflict or other characteristics associated with unstable unions (Arck et al. 2008; Maconochie et al. 2006; Nakamura et al. 2008; Nepomnaschy et al. 2008). The dynamics we investigate are an example of the classic demographic concept of survival bias. Perhaps unions producing male pregnancies are more stable than they would have been if they had produced female pregnancies; however, it may also be (or may instead be) that more male pregnancies than female pregnancies in already unstable unions disappear before being observed in data. We explicate the distinction between the former (counterfactual) types of hypotheses and the latter (selection-based) types, and then discuss what the distinction means for both for policy and for population sciences.

The absolute magnitude of effects of relationship stress on population sex ratios at birth is likely to be small (Wilcox and Baird 2011). Selection dynamics could not plausibly explain large sex-specific differences; for example, stressors would not be tenable to explain sex ratios observed in parts of contemporary Asia (Das Gupta 2005; Sen 1992, 2003). However, the magnitude of the observed association between offspring sex and divorce in the United States is itself small. Our empirical question is whether—given what is known in medicine, biology, and social science—selection dynamics could plausibly affect sex ratios at birth enough to warrant attention in this context. How much of the observed association between offspring sex and divorce could plausibly be accounted for by the joint effects of female survival advantage and adverse conditions associated with marital instability?

We take two approaches to answering this question. First, we use longitudinal data from the United States to identify time ordering between indicators of marital stability and offspring sex. If fathers' son preference alone explains the association, then sons born in the future would be unlikely to affect marital stability in the present. Second, we build a simulation tool that models links among pregnancy characteristics, survival to live birth, and marital stability. We use plausible parameter values based on existing evidence from biology and social science, and allow these parameters to vary reasonably. We find that even under conservative assumptions, these relationships combine to generate associations between offspring sex and divorce that are driven entirely by selection and that are of consequential magnitude.

Empirical social scientists drawing inferences about gender dynamics from the daughter/divorce association have relied on implicit assumptions about dynamics of selection into live birth (Dahl and Moretti 2008; Mammen 2008; Morgan et al. 1988; Spanier and Glick 1981). This study explicates some of those assumptions and illustrates the importance of testing their validity. For this study, we focus on the period beginning shortly after fertilization; we discuss that choice in our conclusion.

The association between sex of offspring and risk of divorce—and secular trends in that association—may in fact reveal important information about gender dynamics in families. Our results indicate that to learn that information, it is important to first account for selection into live birth. Innovations in measurement and modeling that integrate evidence and methods from biological and social sciences will be critical to that end. More generally, as we discuss in our conclusion, demographic analysis of selection into live birth may be valuable for advancing understanding of many questions in the population sciences.

Motivation: Sex Preference, Gender, and Parental Behavior

Population scientists have devoted substantial effort to identifying how parental investments in children are affected by social definitions and valuations of gender.¹ In the United States, social scientists have explored evidence of parental sex preference by examining the relationships between offspring sex and multiple domains of family life. The conclusions from this work are mixed. Polling data indicate that fathers (but not mothers) are more likely to express a preference for sons when presented with the hypothetical situation of having a single child (Dahl and Moretti 2008). In contrast, patterns in fertility timing (Morgan and Pollard 2002; Teachman and Schollaert 1989) and self-reported preferences (Dahl et al. 2006; Pebley and Westoff 1982) are more consistent with parental preference for mixed-sex sibships than for one sex over another.

Some parenting behaviors vary by the sex of the child, such as child-care arrangements (Hiedemann et al. 2004), choice of playtime activities (Lytton and Romney 1991), and fathers' time investments (Harris and Morgan 1991; Lundberg et al. 2007; Tucker et al. 2003). Others do not, including investments of mothers' time (Crouter et al. 1993), either parent's verbal interaction (Lytton and Romney 1991), prenatal care (Lhila and Simon 2008), parenting styles (Shumow et al. 1998), parental availability (Hofferth and Anderson 2003), and parental affection (Tucker et al. 2003).

Our study is relevant to the interpretation of all of those patterns, but is directly motivated by provocative findings indicating relationships between offspring sex and marital stability. In some surveys, parents of sons report greater marital happiness than parents of daughters and are more sanguine about the stability of their marriage (Cox et al. 1999; Katzev et al. 1994). Some studies have reported that unmarried couples with a son enter into marriage more quickly than those with a daughter (Lundberg and Rose 2003), while others have reported no evidence of a difference (Bzostek et al. 2012). Especially provocative has been work indicating that sons are more likely than daughters to live with their fathers (Dahl and Moretti 2008; Lundberg and Rose 2003; Mott 1994), in part because couples are more likely to divorce if they have daughters than if they have sons (Ananat and Michaels 2008; Bedard and Deschênes 2005; Dahl and Moretti 2008; Mammen 2008; Morgan et al. 1988; Spanier and Glick 1981).

Others have noted that the reported relationship between offspring sex and divorce is small in practical, real-world terms (Lundberg 2005; Raley and Bianchi 2006). Table 1 summarizes published findings linking survival of a first marriage and the sex of its first child. The estimated risks in the top panel come from studies that compare divorce risk in each discrete time period after the birth of a daughter versus after the birth of a son. They indicate that couples with daughters stand about a 1–2 per 1,000 higher chance of divorcing in each eight-month period after the birth of a daughter. The estimated risks in the bottom panel come from studies that sample parents at a single point in time, and compare the likelihood that their first marriage has ended if they had a firstborn daughter versus a firstborn son. They indicate differences on the order of 5 per 1,000. The differences are sufficiently small that they can be discerned only in large samples.

Table 1.

Previous studies on divorce and sex composition of offspring

Authors (year)	Comparison	t	Δ (percentage points)	Sample Size	Data Source
Longitudinal or Quasi-Longitudinal Analyses (Outcome: Risk of divorce per t month period)
Morgan et al. (1988)	Couples with 1 daughter versus 1 son	7	0.17a	178,310	CPS,b 1980
Morgan and Pollard (2002)	Couples with firstborn daughters versus sons	12	0.12c	261,759	CPS, 1985, 1990, 1995
Diekmann and Schmidheiny (2004)	Women with 1 daughter versus 1 son	1	0.0004d	5,396	FFS,e M995
Cross-sectional Analyses (Outcome: At time of survey, woman divorced from first husband)
Dahl and Moretti (2008)	Ever-married adults aged 18–40 coresiding with ≥1 child aged 0–12:		1.03	96,859	CPS, 1980, 1985, 1990, 1995
	Firstborn daughters versus sons		0.45	1,932,964	Census, 1960–1980
Ananat and Michaels (2008)	White women with a ≤17-year-old: Firstborn daughter versus son		0.63	619,499	Census, 1980
Bedard and Deschenes (2008)	U. S. born ever-married white women with birth ≤5 years into marriage: Firstborn daughter versus son		0.80	465,595	CPS, 1980, 1985, 1990

Note: See also the 11 studies cited in Morgan and Pollard (2002: table 1A).

^aOdds ratio of 1.071, on base risk that ranges 1.7 % to 2.5 %, depending on time since marriage.

^bCPS is an abbreviation for the June Marriage and Fertility Supplement to the Current Population Survey.

^cOdds ratio of 1.03, but base risk not reported in the article. Using different data, we estimated the base risk around 1 % to 4 %, depending on time since marriage.

^dOdds ratio of 1/0.88 on base risk that ranges 0.28 % to 0.34 %, depending on time since marriage.

^eFFS is an abbreviation for the Fertility and Family Survey.

Others have counseled caution in interpreting associations between offspring sex and risk of divorce as evidence of son preference in the contemporary United States, in light of period changes in the associations (Morgan and Pollard 2002), risk of publication bias (Lundberg 2005), correlations between offspring sex and needs (Hiedemann et al. 2004; Raley and Bianchi 2006), or even deliberate sex-selective abortion (Lundberg 2005). We investigate an additional possible reason: selection into live birth. Given the small magnitude of the observed association between offspring sex and divorce, even weak selection effects might still warrant caution. Whether such effects could plausibly be operating at sufficient scale to merit attention by population scientists is our empirical question.

Conceptual Framework

Associations between sex of offspring and divorce risk have been identified by using standard discrete dependent variable regression approaches. These approaches begin by positing some latent characteristic, which we call “marital fitness.” The latent fitness of a marriage (m*) may be a function of any number of measured (x) and unmeasured (η) characteristics. Among the measured characteristics might be an indication of whether the couple has a firstborn daughter (g) and whether they have a firstborn son (b):

$$m_i^{\ast }={\mathbf{x}}_i^{\prime }\beta +{\delta }_1{g}_i+{\delta }_2{b}_i+{\eta }_i.$$ (1)

Latent marital fitness is not observed in data. Rather, one observes only reflections of it, such as whether the couple is still married (m = 1) or has divorced (m = 0). In that case, latent fitness would be defined such that those couples who are observed to be married represent the more fit subset:

$$m_i=\{\begin{array}{c}1\mathrm{if}{m}_i^{\ast }\ge 0\hfill \\ 0\mathrm{if}{m}_i^{\ast }<0\hfill \end{array}\phantom{\}}.$$

Regression specifications, such as the probit or logit, use assumptions about the probability distribution of η and observations of m, x, g, and b to uncover the nature of relationships between marriage fitness and the sex composition of offspring. In many cases, researchers using various implementations of this general approach have observed that marriages producing firstborn sons tend to be slightly more “fit” than marriages producing firstborn daughters: formally, in terms of Eq. (1), they obtain estimates of δ₂ that are statistically significantly greater than δ₁.

One common interpretation of the observed patterns is counterfactual, succinctly expressed by Dahl and Moretti (2008:1090): “[Many] first-born daughters … would have had a father present in the household had they been first-born sons instead.” This interpretation holds that $({\widehat{\delta }}_2-{\widehat{\delta }}_1)>0$ because firstborn sons improve the fitness of their parents' marriages—for example, because their presence draws fathers into a shared parental commitment to child rearing (Morgan et al. 1988).

We aim to investigate the extent to which a selection-based mechanism—which is not counterfactual—could also generate $({\widehat{\delta }}_2-{\widehat{\delta }}_1)>0$. Only the sex of live births is observed in data, and not the sex of pregnancies overall. Even in population surveys that include questions about miscarriages, little is known about pregnancies that do not survive to live birth.

To explicate potential selection dynamics, we add a term to the right side of Eq. (1), thereby capturing all three possible outcomes of a pregnancy, if it occurs. Using Eq. (1), consider couple i, who have had P_i ≥ 0 pregnancies:

$$m_i^{\ast }={\mathbf{x}}_i^{\prime }\beta +{\delta }_1{g}_i+{\delta }_2{b}_i+{\delta }_3\sum _{p=0}^{P_i}{\omega }_p+{\eta }_i.$$ (1a)

In this formulation, ω_p = 0 if pregnancy number p ended in a live birth, and 1 otherwise. Consider a set of couples who have had at most one child (indicated by b + g ≤ 1); because sex of a pregnancy is observed only if it ends in live birth, the sex of a pregnancy is known only for those couples for whom ${\sum }_{p=0}^{P_i}{\omega }_p<P_i$. In light of this sample selection process, we take conditional expectations of both sides of Eq. (1a). First, we consider a set of couples who are observed to have firstborn sons:

$$E\left[m^{\ast }\mid \mathbf{x},b=1,\sum _{p=1}^{P_i}{\omega }_p<P\right]={\mathbf{x}}^{\prime }\beta +{\delta }_2+E\left[\eta \mid \mathbf{x},b=1,\sum _{p=1}^{P_i}{\omega }_p<P\right].$$

Next, we consider another set of couples who are observed as otherwise identical but who have firstborn daughters:

$$E\left[m^{\ast }\mid \mathbf{x},g=1,\sum _{p=1}^P{\omega }_p<P\right]={\mathbf{x}}^{\prime }\beta +{\delta }_1+E\left[\eta \mid \mathbf{x},g=1,\sum _{p=1}^P{\omega }_p<P\right].$$

Subtract the two to get the expected difference in underlying marriage “fitness” for the two sets of couples:

$$E\left[\Delta m^{\ast }\mid \mathbf{x},\sum _{p=1}^P{\omega }_p<P\right]=({\delta }_2-{\delta }_1)+\left\{E\left[\eta \mid \mathbf{x},b=1,\sum _{p=1}^P{\omega }_p<P\right]-E\left[\eta \mid \mathbf{x},g=1,\sum _{p=1}^P{\omega }_p<P\right]\right\}.$$ (2)

In terms of Eq. (2), the difference (δ₂ – δ₁) identifies the counterfactual marriage fitness impact of firstborn sons compared with firstborn daughters only if the difference in curly braces is zero. The first term in that difference represents unobserved marital stability characteristics, on average, among couples that have a firstborn son; the second, among couples that have a firstborn daughter. We will discuss evidence from epidemiology, biology, and medicine implying that the difference between these two averages may not be zero; the fact that a couple even has a firstborn child may contain different information about their circumstances, depending on that child's sex. (For continued mathematical discussion of these issues, see Online Resource 1, section A.1.)

A specific explication of the difference between selection-based versus counterfactual mechanisms may be warranted. Note that the sex of a pregnancy is determined by a characteristic of the sperm cell that fertilizes it: if the cell is of type Y, the pregnancy is male; if it is of type X, the pregnancy is female. Counterfactual interpretations hold that some divorced couples with a daughter would still be married if a Y-type sperm had fertilized the pregnancy instead of the X-type sperm that actually did. By contrast, selection-based interpretations hold that some of these couples would have divorced either way, no matter what type of sperm had fertilized. One observes more daughters among the divorced couples because those couples' male pregnancies tend not to reach live birth and therefore tend not to show up in data.² These types of interpretations are not mutually exclusive. Some fraction of the observed differences in marriage fitness can be driven by counterfactual mechanisms (for example, sons draw their fathers into a shared parental commitment to child rearing), while another fraction can be driven by selection (for example, male pregnancies in adverse conditions never survive to be observed in data). In this study, we ask the following: If nothing but selection mechanisms were at play, how big could the difference in divorce risk be, given what we know about the relevant processes?

Background: Biological Stress, Survival Bias, and Relationship Stability

Fecundity and Offspring Sex Composition

Throughout this study, we maintain the assumption that the sex of pregnancies is assigned as if by coin flip; we discuss this assumption further in the conclusion. We emphasize that this assumption is not sufficient to justify a counterfactual interpretation of the difference (δ₂ – δ₁) in Eq. (2). Rather, a counterfactual interpretation must also rely on additional assumptions about unobserved factors related both to marital stability and to male and female prenatal survival probabilities. For example, in Online Resource 1 (section A.1), we carry forward the simple model of sample selection from our conceptual framework, assuming that the sex of pregnancies is randomly assigned, and explicate the additional specific assumption that underlies counterfactual interpretation of equations like Eq. (1). Having explicated it, we are not aware of any evidence that would justify it.

Additional assumptions necessary for counterfactual interpretation would be trivial if almost all pregnancies—regardless of sex—were to end in live birth, or if prenatal survival probabilities were about the same regardless of the sex of the pregnancy. However, there is evidence in the epidemiological literature that neither of these is true. The evidence indicates that only one-quarter to one-half of pregnancies actually end in live birth (Benagiano et al. 2010; Macklon et al. 2002; Nepomnaschy et al. 2004; Roberts and Lowe 1975; Vitzthum et al. 2006; Wang et al. 2003; Wilcox et al. 1988),³ and that there may be a prenatal female survival advantage (Chahnazarian 1988; Kellokumpu-Lehtinen and Pelliniemi 1984; McMillen 1979; Pergament et al. 2002; Vatten and Skjaerven 2004).⁴

In the presence of a female survival advantage, a couple's fecundity—the probability that a fertilized egg will become a live birth—can end up reflected in the sex composition of their offspring. In that case, assigning a purely counterfactual interpretation to (δ₂ – δ₁) in Eq. (2) requires assumptions beyond merely that sex of pregnancies is assigned as if by coin flip. The simplest additional condition would be that no unobserved factor is associated both with fecundity and with marital stability. In the next section, we cite evidence to the contrary: biological stress may be associated both with fecundity and with marital stability.

Biological Stress, Relationship Stability, and Fecundity

Biological stress occurs when cells are exposed to corticosteroid hormones (McEwen and Wingfield 2003). High levels of these hormones predict reduced fecundity (Arck et al. 2008; Ferin 1999; Nakamura et al. 2008; Nepomnaschy et al. 2008; Parker and Douglas 2010; Waffarn and Davis 2012). The biological system that regulates corticosteroid hormones overlaps substantially with the system that regulates progesterone, a hormone critical to healthy progress from fertilization to early pregnancy (Ferin 1999; Parker and Douglas 2010). At the end of pregnancy, stress hormones are directly involved in finalizing organ development in the fetus and in inducing labor (Waffarn and Davis 2012).

In a healthy person, levels of stress hormones rise sharply in the face of an acute challenge (a stressor), such as a threat to personal safety. Major disasters (such as earthquakes) or violent conflict are likely stressors; studies have reported associations between healthy pregnancy outcomes and these types of events (Lauderdale 2006; Mansour and Rees 2012; Torche 2011). Complementing such studies, others have reported associations between a woman's self-reported emotional well-being and the probability that her pregnancy ends in live birth (Arck et al. 2008; Maconochie et al. 2006; Nakamura et al. 2008; Sugiura-Ogasawara et al. 2002).

Persistent exposure to stressors may eventually lead to high concentrations of stress hormones even without any immediately accompanying stressor or sense of arousal (Fremont and Bird 2000; McEwen and Wingfield 2003; Miller et al. 2007). Chronic hyperstimulation of the stress system is associated with adverse conditions in childhood and adolescence, including lower levels of parental support or availability (Lupien et al. 2009). These conditions are more common in the case of parental union dissolution, which is predictive of lower-quality relationships in adulthood (Sassler et al. 2009). When exposed to a stressor, a person with a chronically hyperstimulated stress system faces greater risk of extended negative affect and externalizing behavior, in part because of chemical effects of stress hormones on the brain (Gourley et al. 2013; Het et al. 2012; McEwen 2003; Ruttle et al. 2011; van Eck et al. 1996). Negative affect and externalizing behaviors may represent risk factors for divorce (Emery et al. 1999). Consistent with these patterns, psychologists have observed associations between relationship stability and biological stress responses to interpersonal conflict (Beck et al. 2013; Gunlicks-Stoessel and Powers 2009; Laurent et al. 2013; Powers et al. 2006).

Finally, in the opposite causal direction, higher-quality relationships may buffer biological response to stressors: in effect, a healthy marriage may substitute for corticosteroid hormones (Friedman et al. 2012; Hennessy et al. 2009; Meuwly et al. 2012).

Linking chronic stress to pregnancy outcomes, emerging research indicates evidence of a negative association between chronic hyperstimulation of a woman's stress system and the likelihood of having a live birth. For example, Nepomnaschy et al. (2004) collected biological samples from noncontracepting married women volunteers and found a negative association between the probability that a woman's pregnancy survived and the urinary concentration of cortisol—an important stress hormone—during the first few weeks after fertilization. Others have observed negative associations between the likelihood of pregnancy success and other indicators of chronic hyperstimulation (Nakamura et al. 2008; Sugiura-Ogasawara et al. 2002).

Dynamics linking divorce to elevated stress hormone levels, linking elevated stress hormones to adverse conditions for pregnancies, and linking the sex of a pregnancy to its likelihood of reaching live birth could interact to generate a selection-driven daughter–divorce association. In that case, it remains an open empirical question whether the relevant associations are strong enough to matter for counterfactual interpretation. Direct investigation of that question would require high-quality prospective measurement of stress hormone levels; reproductive hormone levels; fertility behavior; marital status and relationship quality; and menstrual, ovulatory, and pregnancy-related outcomes for a large population-representative sample of women. It would involve stratifying chromosomally normal, viable fertilized eggs by sex as early as possible and following them prospectively to determine whether they become clinical pregnancies and then live births. One could apply standard demographic methods to assess the selection processes. For the most part, such sampling and measurement would be technologically possible but expensive. To our knowledge, it has never been done. Given the incompleteness of sampling and measurement, in the next section, we describe a second-best approach.

Data and Methods

Adverse Conditions and Sex of Subsequent Births

We begin by revisiting the association between marital instability and offspring sex, using marital histories and indicators of stress from a longitudinal population survey. Counterfactual explanations of the association posit that after they are born, girls place greater strains on marriages than do boys; a selection-driven explanation posits that girls are more likely than boys to be born into marriages that were already strained. We use this clear distinction in time-ordering to evaluate these hypotheses by testing whether marital fitness correlates with the sex of births that occur after strain was measured.

We analyze data from the 1979 National Longitudinal Study of Youth (NLSY79), a nationally representative sample of U.S. residents born from 1957 to 1965 (those aged 14–22 years in 1979). Respondents were followed annually until 1994 and biennially thereafter. The follow-up period for our analyses ends in 2010.⁵

Following previous studies on offspring sex and divorce, we limit the sample to white women without premarital births. Given our interest in the time ordering of marital discord and the gender composition of children, we further limit the sample to women who have at least one birth in their first marriage. The sample meeting these criteria consists of 1,314 women. We use two measures to capture indicators of biological stress as well as marital fitness. The first is a marital conflict scale. Married female respondents are asked about the frequency with which they argue with husbands in nine domains. Responses range from 0 (“never”) to 3 (“all the time”). We sum these responses, producing a marital conflict scale that ranges from 0 to 24, with a mean of 7.8 and a standard deviation of 4.4 (α = .76). The second is a psychometric instrument, the Center for Epidemiological Studies Depression (CES-D) Scale (Radloff 1977), the only item capturing emotional health in the NLSY79 prior to 2000. The scale is generated by summing responses to questions about feelings or behaviors indicating chronic depression risk. Scores range from 0 to 60; higher values indicate higher levels of depression risk. Depression is associated with biological stress (McEwen 2003; Rawdin et al. 2013). The mean CES-D score in our sample was 8.1, with a standard deviation of 8.2. Both measures were first asked of childless women in 1992. Depression risk was not measured again until respondents reached age 40, but marital conflict was measured biennially after 1992.

We would have preferred to conduct a test of time ordering of marital strain and offspring sex using data collected throughout marriages. This is not feasible because by 1992, when these measures were first collected, NLSY79 respondents in this sample were 27–35 years of age and had already been married for 8.8 years, on average. Nevertheless, because many couples had not yet completed their fertility by 1992, a “second-best” approach is feasible. We focus on those marriages that survived until 1992 and that went on to have at least one more child between 1992 and 2010 in order assess whether marital conflict and/or emotional health predict the birth of daughters. The NLSY79 remains the only longitudinal U.S. data set that has collected measures of emotional health and marital conflict during reproductive years with sufficiently long follow-up that fertility and divorce can be observed.

We begin by describing the association between these measures and subsequent risk of divorce, using linear probability models (results are not sensitive to functional form). In each regression, our dependent variable is a dichotomous indicator of whether a respondent who was in her first marriage in 1992 divorced between 1993 and 2010. Covariates of interest—investigated in two separate regressions—are the respondent's 1992 CES-D score and 1992 marital conflict score. In both regressions, additional covariates include age at marriage and total number of births.

We next identify the association between the distress measures and the sex of offspring. We pool all first, second, and third births occurring within a woman's first marriage during the follow-up period. For each birth, we regress a dichotomous indicator for whether the offspring is male against his/her mother's 1992 scores on the conflict and CES-D instruments. Results are the same using the conflict score measured in the year most closely preceding the birth. Additional covariates include age at first birth, birth order, and total births after 1992; results do not change if we add indicators for educational attainment and urban/rural residence. Standard errors are estimated in a manner that accounts for possible statistical nonindependence between observations of different births to the same mother (which might arise, for example, because the psychometric scores are repeated in every observation of the same mother).

All births in our regression occurred after distress was measured. Sons are unlikely to have improved the quality of their parents' marriages before they were born; any association observed through these analyses is more likely to reflect selection into live birth. If sex-selective medical abortions were sufficiently common and sufficiently correlated with marital strain, interpretation would be more complicated. In our simulation exercise described in the next section, we explicitly rule out any direct relationship between prenatal sex selection and stress.

Simulation: Stress, Fecundity, Sex of First Birth, and Divorce

In the analysis described in the preceding subsection, we use survey data on characteristics that are associated with biological stress. Direct measures of biological stress are increasingly available in population representative data (Seeman et al. 2010), but no major U.S. cohort studies contain these indicators measured simultaneously with fertility behavior. Furthermore, in population surveys, little is observed about pregnancies that do not end in a live birth. In some surveys, respondents are asked to report past miscarriages; these almost certainly represent a small fraction of lost pregnancies. Furthermore, genetic characteristics indicating the viability and sex of a miscarriage are almost never observed in these data. In retrospective data on miscarriages, it is also difficult to reliably observe biological stress at the time of that pregnancy. In light of these gaps in measurement, we build a simulation that draws on information taken from vital statistics, population surveys, and published studies in biology and medicine, as well as our findings from the preceding subsection.

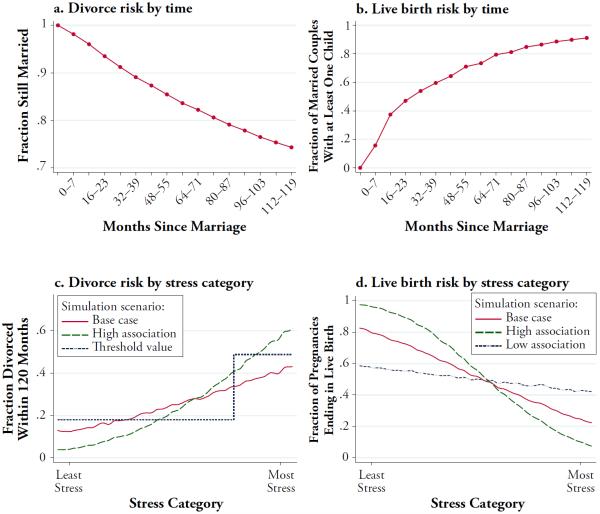
The description in this section is summarized in Table 2 and Fig. 1. Further detail is available in Online Resource 1 (section A.2).

Table 2.

Simulation inputs

Parameter Definition	Base Value	High Value	Low Value	Reference
Population Sex Ratios
Male pregnancies per 100 female pregnancies	140	170	110	Pergament et al. (2002)
Male births per 100 female births	105.88	105.88	105.88	U.S. Vital Statistics (1990–1995)
Fertility/Fecundity
Pr{≥1 child | time since marriage}		See Fig. 1b		Table 1A of MLCa
Overall % of pregnancies reaching live birth	50	70	30	Benagiano et al. (2010)
Pr{live birth | stress}		See Fig. 1d		Relationships in Table 3b
Divorce Risk
Pr{divorce | time since marriage}		See Fig. 1a		Table 1A of MLCa
Pr{divorce | stress}		See Fig. 1c		Relationships in Table 3b
Other Factors
Correlation: fertility behavior/fecundability and marriage fitness	0	0.4	0.4	Authors' conjectures

Note: These parameter values comprise those used in all 11 scenarios presented in Table 4.

^aMLC refers to Morgan et al. (1988).

^bFor details on how we used the results in Table 3 to arrive at the parameter values shown, see the section, Simulation: Stress, Fecundity, Sex of First Birth, and Divorce.

Fig. 1.

Simulation inputs: Divorce and live birth probabilities. Graphical representations of parameter values referenced in Table 2

Inputs

The simulation tool combines four pieces of information on biological and family processes, together with our findings from the analyses described in the earlier section describing adverse conditions and sex of subsequent births. Where appropriate, we test a range of values.

1. The time path of divorce risk for married couples

This path takes the form of 15 period-specific risks, where each period represents eight months (results are not sensitive to the length of these intervals). We have explored the implications of two sets of risks; one is from the June 1980 Current Population Survey (CPS80), as reported in Morgan et al. (1988); the other is from the NLSY79. Because results were similar for both sets of risks, we report only those using the CPS80 series here.

2. Sex ratios among early pregnancies and among live births

We fix the sex ratio of live births at 105.88 boys per 100 girls, which corresponds to the ratio observed in U.S. vital statistics (registered first births to married white women between 1990 and 1995).

We explore the implications of three different assumptions regarding the sex ratio in early pregnancy, all based on information in the epidemiological literature. Estimates in the literature vary from 110 to 170 early male pregnancies per 100 female (Pergament et al. 2002). Therefore, for our base case, we assume a sex ratio of 140 male pregnancies per 100 female; we also explore the implications of the ends of this range.

The extent of the prenatal female survival advantage is determined mechanically by the difference between the sex ratio early in pregnancy versus the ratio at live birth. Sex does not change in the course of a pregnancy, so a falling sex ratio implies a female survival advantage.

3. The probability that a chromosomally viable pregnancy will survive to live birth

We explore the implications of three different assumptions about this probability, all based on information in the epidemiological literature. Estimates in the literature vary from 30 % to 70 % (Benagiano et al. 2010). Therefore, we explore the implications of assuming that fertilized eggs have a 30 %, 50 %, or 70 % probability of surviving to live birth.

4. The time path of pregnancy risk for married couples

Because no population survey identifies early pregnancies, we cannot draw on any real-world study for this time path. However, population studies do report birth risks for married couples; we therefore combine those with the probability of survival to live birth (see input 3). For example, in simulation runs specifying that pregnancies have a 50 % probability of surviving to live birth, we also specify that for each live birth that occurs, two pregnancies must have begun in the previous period. We have explored the implications of using two different sets of birth risks; one is from the CPS80, as reported in Morgan et al. (1988), and the other is from the NLSY79. Because results were similar for both sets of risks, we report only those using the CPS80 here.

We use the simulation to explore implications of these factors on the divorce/offspring sex association in a cohort of 250,000 hypothetical couples during the 10 years following their formation.

The Operation of the Simulation Tool

The simulation runs in discrete time; there are 15 time periods. In each time period, the simulation tool uses the inputs in the previous subsection to assign new pregnancies to couples who are still married and not currently pregnant, new live births to couples who are currently pregnant, and new divorces to couples who are still married.

In keeping with the maintained assumption that the sex of pregnancies is randomly assigned, every new pregnancy is given equal probability of being male, as specified in input 2 in the previous subsection. A subset of pregnant couples is chosen to experience a live birth; less-stressed couples and couples carrying female pregnancies are more likely to be chosen. We do not allow stress to directly generate sex-specific mortality. Instead, because it operates against a background of female survival advantage, it indirectly influences sex ratios across the stress distribution because all pregnancies in more-stressed couples suffer a survival disadvantage, so male pregnancies in these couples bear two disadvantages: (1) they lack the female survival advantage; and (2) there is the direct effect of stress on fecundity.

At the end of each period, the simulation tool chooses a subset of still-married couples to divorce. More-stressed couples are at higher risk of being chosen. Intentionally, we allow no counterfactual effects on divorce risk, either of the presence of children or of their sex composition. This is in order to investigate the magnitude of purely selection-driven daughter–divorce associations that could be generated in plausible scenarios. If these associations are sufficiently small relative to the associations reported in the literature, then a counterfactual effect would likely be filling the difference.

The simulation explores only “mechanical” relationships between probabilistic outcomes; that is, it does not allow for any forward-looking or strategic behavior. In particular, we do not build in an opportunity for simulated couples to take into account their underlying marital stability when planning their fertility. To account for these sorts of dynamics, the simulation assigns to each couple a fertility behavior parameter and a marital stability parameter. We examine the implications of correlations between these parameters of −0.4, 0, and 0.4. The simulation rules out any form of deliberate prenatal sex selection or sex-specific parity progression.

More detail on the operation of the simulation tool is available in Online Resource 1, section A.2.

Outputs

At the end of a simulation run, we have, for the entire hypothetical cohort, a panel data set containing

• Whether and when each couple divorced: D_t for t ∈ {1, …, 15}.

• The number of children (0, 1, 2, or 3 or more) born so far to each couple, which we convert to an indicator: C_t = 1 if the couple has had a child, and 0 otherwise.

• The sex of each child born, which we convert to an indicator: S_t = 1 if the child has had a firstborn son, and 0 otherwise.

Using this panel data set, we can model relationships between fertility, offspring sex, and marital status using standard regression equations analogous to those in the literature on offspring sex and divorce.

As highlighted in the description in the earlier section on the operation of the simulation tool, the simulation is more likely to subject a couple to divorce if it is more stressed and is less likely to choose a pregnancy to end in live birth if the couple is more stressed. In order for our simulation exercise to be useful, it is critical that we choose plausible magnitudes for these stress associations. To that end, we calibrate these magnitudes in part by drawing on the results of the analyses described in the earlier section on adverse conditions and sex of subsequent births. First, we run the simulation tool using putative magnitudes for stress associations. At the end of the simulation run, we rescale our stress parameter to have the same standard deviation as the CES-D score observed in the NLSY79 sample. Then, we mimic the analyses described in the earlier section on adverse conditions and sex of subsequent births on the simulated histories. We compare the stress/divorce and stress/offspring sex associations in the simulated histories against those we observed in the NLSY79. Then, we adjust putative magnitudes of the stress associations and repeat the process. To be conservative, we calibrate putative magnitudes so that they generate associations in our NLSY79-like analyses that are one-half as strong as the associations that we actually observed in the NLSY79. We also test the implications of setting relationships that generate associations equal in strength to those we observed in the real-world data and of setting relationships that generate associations of only one-tenth the magnitude.

Is our putative stress-termination association plausible? There is little direct real-world evidence about the magnitude of associations between early pregnancy loss and biological stress. In one study shedding light on this, Nepomnaschy et al. (2008: Table 1) followed a cohort of pregnancies that was selected to be typical, and observed a 2.7 times higher risk of nonlive termination for the pregnancies that were exposed to more than the cohort median level of stress hormones. The analogous association in our base case of the simulation is 2.0, which is more conservative than the 2.7 that they reported.⁶

Analysis of Outputs

One set of regression analyses is prospective, mimicking studies like those in the top panel of Table 1. Specifically, we drop a couple from follow-up after it divorces, and then use a logistic regression specification to estimate discrete-time, proportional hazards regressions of the following form:

$$d_{i,t}={\beta }_0+{\beta }_{1}t+{\beta }_2{t}^2+{\delta }_1{C}_{i,t}+{\delta }_2{S}_{i,t}+{\beta }_3{C}_{i,t}t+{\beta }_4{C}_{i,t}{t}^2+{\epsilon }_{i,t},$$ (3)

where d_i,t represents the log odds that couple i will divorce in period t. The parameter of interest is the apparent “son effect” (δ₂) , which we convert into percentage point terms by computing marginal effects holding time constant at the period of peak divorce risk.

A second set of analyses is cross-sectional, mimicking studies such as those in the bottom panel of Table 1. Specifically, we mimic the process of drawing parents from a cross-sectional data set, such as the U.S. census. We keep only couple-periods that have children present. We then randomly draw a single period for each couple and estimate linear probability regressions of the following form:

$$D_i={\delta }_0+{\tilde{\delta }}_2{\tilde{S}}_i+{\tilde{\epsilon }}_i,$$ (4)

where D_i takes the value of 1 if the couple is observed to be divorced, and 0 otherwise. As with the prospective analyses, the parameter of interest is the apparent son effect (${\tilde{\delta }}_2$), in percentage point terms.

The objective of the simulation is to identify how much of the observed associations between offspring sex and divorce could plausibly be driven by selection into live birth. To that end, we compare estimates of δ₂ and ${\tilde{\delta }}_2$ to the real-world associations quoted in Table 1. Because the simulation allows for only selection-driven associations, if these estimates are similar, then there may be need for caution regarding counterfactual interpretations of the real-world associations.

Results and Discussion

Time-Ordering: Reported Stressors and Offspring Sex

Table 3 contains coefficient estimates from the linear probability regressions using the NLSY79 data. Column A reports the results of two regressions (a separate one for each distress measure) that describe associations between prospective risk of divorce and each of the two distress measures.

Table 3.

Reported stressors and prospective risks of divorce and male birth: First marriages intact in 1992

	(A) Divorced Between 1992 and 2010 (1 = Divorced, 0 = Not)	(B) Sex of Births 1992–2010 (1 = Male; 0 = Female)
Mother-Reported Characteristics in 1992
Marital conflict (μ = 7.8, σ = 4.4)a	0.015** (0.003)	−0.010† (0.005)
CES-Db Score (μ = 8.1, σ = 8.2)a	0.008** (0.002)	−0.006* (0.003)
Percentage With y = 1	23.7	50.3
Other Covariatesa
Age at marriage	μ = 22.4, σ = 3.8	Not included
Total births in this marriage	μ = 2.3, σ = 1.0	Not included
Birth order	Not included	μ = 2.0, σ = 0.7
Age at first birth	Not included	μ = 34.0, σ = 2.9
Total births in this marriage after 1992	Not included	μ = 1.7, σ = 0.7
Sample Sizesc
Number of mothers	1,314
Number of births		587

Notes: Data are from the National Longitudinal Survey of Youth, 1979 cohort. For all statistics except observation counts, observations are weighted to represent the population from which the regression sample was drawn.

^aμ is the mean of the characteristic; σ is the standard deviation.

^bCES-D is Center for Epidemiologic Studies–Depression, a standard psychometric indicator of depression risk (see Radloff 1977).

^cObservation counts are unweighted.

^†p < .10;

^*p < .05;

^**p < .01;

The top row indicates that women who were 1 standard deviation below the mean conflict score were 13 percentage points less likely to divorce than those who were 1 standard deviation above the mean (0.015 × 4.4 × 2 = 13.2%). The second row describes the association between the CES-D score and the subsequent 18-year risk of divorce. Women scoring 1 standard deviation below the mean on the CES-D instrument were, on average, 13 percentage points less likely to divorce over the subsequent 18 years than those who scored 1 standard deviation above the mean (0.008 × 8.2 × 2 = 13.1%). These findings are consistent with evidence in the sociological literature that depression and marital stress predict divorce (Amato 2010; Wade and Pevalin 2004).

The results in column A are unlikely to reflect a causal association; the objective of the analyses is purely descriptive. Many characteristics are likely correlated with both distress and divorce, but if distress or any associated characteristics are also correlated with fecundity, then the female prenatal survival advantage can generate selection-driven associations between divorce and sex of offspring.

The first row in column B reports coefficient estimates from regressions of the sex of children against their mothers' marital conflict score in 1992; the second row, against their mothers' CES-D score. Column B includes only births after 1992. If the sex of live births is assigned as if by coin flip, there should be no association in this column. However, the associations are large and negative. Women reporting levels of conflict in 1992 that were 1 standard deviation above the mean were 7.7 percentage points less likely (−0.010 × 4.4 × 2 = −7.7 %) to subsequently give birth to boys than women who had similar fertility but who had reported levels of conflict 1 standard deviation below the mean. This magnitude is large. For example, race is a well-known predictor of child sex (Chahnazarian 1988; Davis et al. 2007; Marcus et al. 1998; Pergament et al. 2002); black mothers are about 0.6 percentage points less likely to have a son than white mothers. The association between the likelihood of having a son and a 2 standard deviation difference in marital conflict score is 10 times that size. Given the lack of similar information in other data sets, we cannot determine whether this magnitude is anomalous. Lending credence to the result is the fact that if we restrict the follow-up period to include only births within five years after psychometric measurement, we estimate stronger associations; furthermore, restricting the analysis only to first births greatly reduces the sample size but has no effect on the magnitude of the associations. In the future, when reliable longitudinal measures of biological stress, divorce, and fertility outcomes become available in other population-representative surveys, analyses such as these should be replicated. For example, the 1997 cohort of the NLSY and the National Longitudinal Study of Adolescent Health are following these outcomes; in about a decade, these cohorts will be sufficiently far along in their marriage and fertility to facilitate such analysis. In the meantime, we treat these results conservatively by using relationships in our simulation that are one-half and one-tenth as strong (and that are separately benchmarked against pregnancy survival studies, as described in the earlier section discussing the operation of the simulation tool).

Simulation

Table 2 and upcoming Fig. 3 detail the parameters used in the simulation.

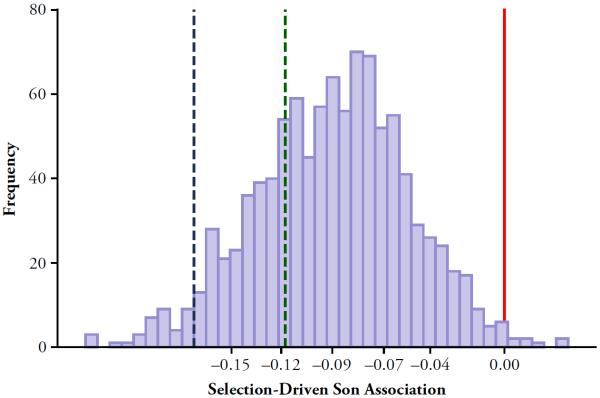
Fig. 3.

Simulation results: Cross-sectional analyses, base parameter values. We executed the simulation tool 1,000 times, using the base parameter vector outlined in Table 2 (and in the series traced by the solid lines in Fig. 1) each time. At the end of each execution, we randomly drew one time period for each couple and dropped all childless couples. This mimics the process of drawing data on parents with children from a cross-sectional data set like the census. Using a linear probability regression, we then estimated the difference in risk of having divorced as a function of sex of the first birth. The regression equation is described in the text (Eq. (4)); it mimics the analyses reported in studies such as those reported in the bottom panel of Table 1. That exercise generated 1,000 risk differences (${\tilde{\delta }}_2$ in the regression equation): one for each execution of the simulation tool. This histogram shows the distribution of the 1,000 values. The 10th percentile, 25th percentile, mean, 75th percentile, and 90th percentile are marked and labeled on the horizontal-axis, and the vertical solid line is at 0. Dotted vertical lines indicate reported effect sizes from two of the studies cited in the bottom panel of Table 1

Base Case

We begin by executing the simulation 1,000 times, each time using the parameter vector in column 3 of Table 3, but a different random number seed (and therefore, different values for all stochastic terms). At the end of each simulation run, we estimate regression Eqs. (3) and (4).

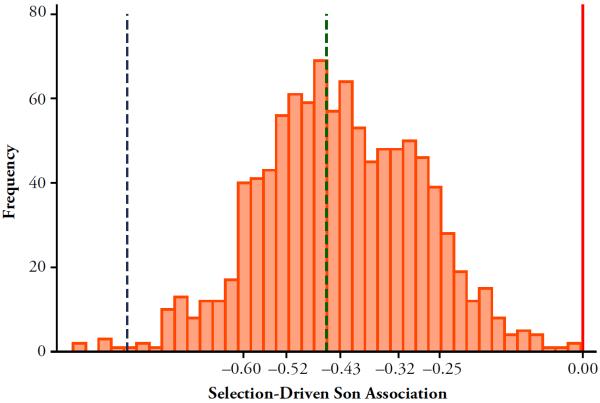
Figure 2 is a histogram of the 1,000 estimates of δ₂ from Eq. (3) (one for each simulation run), converted into percentage point marginal effects for the highest risk period for couples with children. The association between firstborn son and divorce risk is negative in all but 10 of the 1,000 runs. On average over the 1,000 runs, the apparent son effect on the risk of divorce was about 0.094 percentage points, which represents between 55 % and 23,500 % of the effect sizes quoted in the top panel of Table 1. In 561 of the 1,000 runs, the selection-driven son association exceeded 50 % of the effect size reported by Morgan et al. (1988).

Fig. 2.

Simulation results: Longitudinal analyses, base parameter values. We executed the simulation tool 1,000 times, using the base parameter vector outlined in Table 2 (and in the series traced by the solid lines in Fig. 1) each time. At the end of each execution, we estimated a discrete-time proportional hazards regression on the simulated data set. The regression equation is described in the text (Eq. (3)); it mimics the analyses reported in studies such as those cited in the top panel of Table 1. We then converted estimated log odds differences (δ₂ in the regression equation) to percentage point risk differences for the period of peak divorce risk. This exercise generated 1,000 risk differences (one for each execution of the simulation tool); this histogram shows the distribution of the 1,000 values. The 10th percentile, 25th percentile, mean, 75th percentile, and 90th percentile are marked and labeled on the horizontal-axis, and the vertical solid line is at 0. Dotted vertical lines indicate reported effect sizes from two of the studies cited in the top panel of Table 1

Figure 3 is a histogram of the 1,000 estimates of ${\tilde{\delta }}_2$ from Eq. (4) (one for each simulation run). On average over the 1,000 runs, the association of firstborn son and divorce risk was −0.43 percentage points. This association represents about 40 % to 100 % of the effect sizes reported in the studies in the bottom panel of Table 1. In about one-half the cases, the selection-driven son association was equal to or greater than the effect size reported by Dahl and Moretti (2008).

Sensitivity Tests

Table 4 summarizes results using alternative values of our key parameters. For each alternative set of values, we executed the simulation 250 times, using a different random number seed each time. At the end of each run, we estimated regression Eqs. (3) and (4). In Table 4, we report the mean and standard deviation of the selection-driven son associations across the 250 runs.

Table 4.

Simulation results: Alternative scenarios (percentage point risk differences)

Scenario	Son Effect
	Prospective (δ2)	Cross-sectional (${\tilde{\delta }}_2$)
Base Case	−0.10 (0.04)	−0.44 (0.15)
170 Male Pregnancies Per 100 Female	−0.16 (0.04)	−0.75 (0.14)
110 Male Pregnancies Per 100 Female	−0.01 (0.04)	−0.05 (0.14)
30 % of Pregnancies End in Live Birth	−0.06 (0.04)	−0.24 (0.15)
70 % of Pregnancies End in Live Birth	−0.13 (0.04)	−0.72 (0.15)
“High Association” Cases in Figs, 1c and 1d	−0.32 (0.04)	−1.92 (0.13)
“Low Association” Case in Fig. 1d	−0.02 (0.04)	0.08 (0.15)
“Threshold Value” Case in Fig. 1c	−0.09 (0.05)	−0.42 (0.14)
Positive Correlation Between Fertility and Marriage “Fitness”	−0.10 (0.04)	−0.55 (0.15)
Negative Correlation Between Fertility and Marriage “Fitness”	−0.07 (0.04)	−0.31 (0.13)

Notes: For each scenario indicated, we executed 250 simulations on 250,000 hypothetical couples each time, using base parameters given in column 3 of Table 2, except as indicated in that scenario's label. At the end of the simulation, we estimated a discrete-time, proportional-hazards survival regression on the simulated data set and converted the estimated log odds difference to a percentage-point risk difference, as described in the text and in the notes to Fig. 2. The average risk difference across the 250 simulations is what we report in column 2. We also simulated the process of drawing data on parents with children from a cross-sectional data set like the census, as described in the text and in the notes to Fig. 3, and estimated the difference in risk of having divorced as a function of sex of the first birth, using a linear probability regression. That average risk difference across the 250 simulations is what we report in column 3. In parentheses beneath each risk difference, we report the bootstrap standard error (i.e., the mean squared deviation across the 250 simulations from the reported son effect).

Rows 2 and 3 in Table 4 indicate the effect of alternative assumptions about the sex ratio of pregnancies. If the female survival advantage is at the top of the plausible range (i.e., if sex ratios fall by 60 % during pregnancy), selection-driven effects could account for all the associations reported in most of the studies cited in Table 1. On the other hand, if that survival advantage is low, selection-driven effects are likely to be trivial in size.

Rows 4 and 5 of Table 4 illustrate the effect of alternative assumptions about the likelihood that a pregnancy will survive to live birth. The results indicate that lower prenatal mortality risk implies larger selection-driven son associations, compared with the base case, especially in the cross-sectional analysis (column 2). If survival probabilities are high, selection-driven effects could fully account for the associations reported in most of the studies cited in the bottom panel of Table 1.

Row 6 illustrates the implications of stress-divorce and stress-fecundity relationships of the strength implied by the NLSY79 results (Table 3). The selection-driven son association matches or exceeds those reported in every one of the studies cited in Table 1. Row 7 illustrates that if the stress-fecundity relationship is weak, selection-driven effects are likely to be trivial.

In row 8, we explore an alternative functional form in the relationship between stress and divorce. In the NLSY79 cohort, respondents with scores indicating highest risk of depression or high levels of relationship conflict were substantially more likely to divorce compared with those in the middle of the distribution on these measures. However, those with low scores and those with scores in the middle of the distribution were nearly equally likely to divorce. In light of that pattern, we hold divorce risk constant for the bottom three quartiles of the stress distribution; it then jumps to a new, higher level. Results are similar between this alternative functional form and the base case, suggesting that selection-driven son associations may confound interpretation of results like those reported in Table 1, even if the relationship between biological stress and divorce is more complicated than we specified in our base case, as long as the best linear representation of that relationship is as specified in our base case.

The last pair of rows indicates the implications of alternative assumptions about the relationship between marital fitness and fertility behavior. In the penultimate row, couples that get a high draw in terms of marital fitness are also likely to get a high draw in terms of the likelihood of getting pregnant in any period. In that case, stable couples would be overrepresented in any cohort of pregnancies. In the last row, the correlation is specified in the opposite direction, so that unstable couples would be overrepresented in any cohort of pregnancies. The results suggest that if more unstable couples try harder than more stable couples to have children, this behavior may offset the effects of stress on fecundity and thereby reduce the selection-driven son association. This pattern further highlights important possible interrelationships between family processes that might be described as “primarily social” and those that might be described as “primarily biological.”

Conclusion

Son- preference exists in the modern world; it almost certainly affects some population and family processes. In this study, we investigate a tool that social scientists have used in efforts to uncover some of those effects: namely, the treatment of offspring sex as a natural experiment to approximate counterfactual comparisons. Drawing on evidence in the social and natural science literatures, we find that this approach may not be well-suited to its purpose when associations are small in terms of absolute magnitude. Specifically, we find that selection into live birth may account for a large proportion of the observed association between offspring sex and divorce in the United States.

Using data from a large cohort study, we find evidence that indicators of stress predict the sex of future live births and also predict future divorce. Then, using the current state of knowledge regarding patterns of fertility, marriage, and pregnancy outcomes, we investigate plausible implications of these patterns when they interact. The results indicate that female survival advantage, operating against a background of prenatal mortality risk that is correlated with marital instability, could plausibly give rise to at least one-half of the observed correlation between offspring sex and marital stability.

Our findings add one more cause for caution—in addition to those that have already been noted (for example, Lundberg 2005)—regarding the use of the association to make claims about social norms, or to make claims about secular changes in those norms, or as a source of quasi-random variation in divorce risk.

Our analysis was designed to speak to current research on offspring sex and divorce. Because marriage is no longer the dominant environment of fertility and child rearing in the United States (Kennedy and Bumpass 2007), it may be worth extending this type of inquiry to outcomes other than divorce. Extending our approach to apply to nonmarital unions or to investigate outcomes other than union stability—including, for example, sex-specific child support payment (Mammen 2008)—may be instructive.

Evidence that offspring sex might reflect unmeasured characteristics of families could also have implications that extend to other lines of inquiry in demography. Research across the empirical social sciences investigates ways in which family demographic composition and living arrangements affect and are affected by family members' individual outcomes as well as conditions in the family's social and economic environment.⁷ In some of these cases, nonrandom selection into live birth is likely to be trivial to the main inferences; in others, it might be more consequential. In order to know when we should care, it will be important to continue demographic investigation of the dynamics of selection into live birth, in a manner that is integrated with existing research on fertility behavior and other family processes.

The strength of our conclusions is naturally limited by the degree of uncertainty about the relevant parameters. Many of these parameters are difficult or expensive to measure. For the most part, our main conclusions are robust to values across ranges that are considered plausible based on the current state of knowledge, although our sensitivity tests have specifically highlighted potential value of identifying the true size of the prenatal female survival advantage and the true fraction of fertilized eggs that become live births, and of better pinning down relationships among fecundability, fecundity, and fertility behavior.

Throughout this study, we have maintained the assumption that the sex of early pregnancies is randomly assigned. Our analysis begins in the days after an embryo has formed, when it appears that sex ratios are male-skewed. However, there may be relevant selection dynamics even earlier than that; evidence suggests that sex ratios become increasingly male as a cohort of fertilized eggs develop into embryos, after which the female survival advantage begins (Boklage 2005). Questions remain about prenatal and neonatal female survival advantage (Lawn et al. 2013; Steinsaltz 2013). Tracing the time path of population sex ratios at as high a temporal resolution as possible, beginning as early as possible (perhaps even before fertilization), in as many well-characterized subpopulations as possible, is an important demographic exercise.

Valuable work in biology, medicine, and epidemiology over the past half-century has investigated sex-specific selection into live birth. However, measurement and analysis of selective mortality, group-specific survival advantage, and cohort composition are squarely in the purview of population studies (Crimmins et al. 2008; Manton et al. 1995; Vaupel and Yashin 1985). Standard components in the toolkits of empirical social scientists—including the tools of sampling design, formal demography, and behavioral modeling—offer much promise toward integrating reproductive biology with a broader understanding of social and population dynamics.