Abstract
Purpose
This paper focuses on developing a novel non-iterative fat water decomposition algorithm more robust to fat water swaps and related ambiguities.
Methods
Field map estimation is reformulated as a constrained surface estimation problem to exploit the spatial smoothness of the field, thus minimizing the ambiguities in the recovery. Specifically, the differences in the field map induced frequency shift between adjacent voxels are constrained to be in a finite range. The discretization of the above problem yields a graph optimization scheme, where each node of the graph is only connected with few other nodes. Thanks to the low graph connectivity, the problem is solved efficiently using a non-iterative graph cut algorithm. The global minimum of the constrained optimization problem is guaranteed. The performance of the algorithm is compared with that of state-of-the-art schemes. Quantitative comparisons are also made against reference data.
Results
The proposed algorithm is observed to yield more robust fat water estimates with fewer fat water swaps and better quantitative results than other state-of-the-art algorithms in a range of challenging applications.
Conclusion
The proposed algorithm is capable of considerably reducing the swaps in challenging fat water decomposition problems. The experiments demonstrate the benefit of using explicit smoothness constraints in field map estimation and solving the problem using a globally convergent graph-cut optimization algorithm.
Keywords: fat water decomposition, non-iterative, graph cut, optimal surface, minimum-cost closed set
INTRODUCTION
The separation of water and fat in MRI is an important problem, with several clinical applications (1–5). While frequency selective excitation/saturation schemes are available (6–9), multi-echo Dixon-like schemes have enjoyed a lot of attention in the past decade due to their ability to account for large B0 field inhomogeneity (10, 11). These methods acquire images at multiple echo-times and exploit the dependence of temporal variations in magnetization on the unknown fat and water concentrations, fat water chemical shift, magnetic field inhomogeneity induced frequency shift, and decay terms. The unknown parameters are then estimated by fitting the signal model to the measured data.
Classical multi-echo methods rely on voxel-by-voxel fitting of the signal model to the measured data (10–12). The voxel-by-voxel fitting approach suffers from the non-convexity of the associated maximum likelihood criterion, which makes iterative algorithms such as Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL) (12) sensitive to field map initializations. The estimation is also made difficult by the presence of phase wraps in body regions with large field inhomogeneity and ambiguities in voxels with only one metabolite (e.g. water-only voxels), which manifest as spurious fat water swaps in the decompositions. Several extensions of the IDEAL algorithm such as region growing (13), region merging (14), multi-resolution based methods (15), hybrid approaches (16), as well as multi-seed region growing algorithms (17) are introduced to overcome these ambiguities by taking advantage of the assumption of field map smoothness.
While the above methods work well most of the time, they may result in fat water swaps in challenging applications such as lung scans with multiple unconnected regions and regions of low signal to noise ratio. An alternative to the above implicit approaches to exploit field map smoothness is the global optimization scheme that relies on an explicit smoothness penalty. In (18), the estimation of the field map at all voxels is formulated as the minimization of a global criterion, which is the linear combination of the sum of the voxel-independent criteria and a field map smoothness penalty, and solve it using an iterative graph cut algorithm. Since the direct discretization of the problem results in a large graph, whose solution is computationally infeasible, the authors rely on an iterative approach. Specifically, a one-layer graph is constructed at each iteration; the vertices at each voxel correspond to the frequency value at the previous iteration and a new guess (18). The global optimum of this one-layer graph problem is obtained using efficient s-t cut algorithms (19–24). While this iterative approach is computationally efficient, the whole algorithm is not guaranteed to converge to the global minimum of the specified cost function.
The main focus of this paper is to introduce a novel non-iterative graph cut algorithm for fat water decomposition. We formulate the recovery of the field map at all the image voxels as a constrained optimization scheme. The proposed global criterion is the sum of the voxel-independent maximum likelihood criteria. While this global optimization scheme is similar to that of Hernando et al.(18), the main difference is the lack of smoothness penalty term in our global criterion. We instead rely on constraints to enforce the smoothness of the field map. Specifically, the differences in field map between adjacent voxels are constrained in a small range. The discretization of this problem yields a graph optimization problem, where each vertex of the graph is constrained to be connected with a small number of its neighbors. Thanks to the reduced connectivity, the three-dimensional graph search problem can be directly solved using an optimal surface segmentation algorithm (24) in a realistic run time. The non-iterative algorithm is guaranteed to converge to the global minimum of the constrained optimization problem. We compare the proposed algorithm against several state-of-the-art fat water decomposition algorithms available in the ISMRM fat water toolbox on several challenging cases. These datasets are made available as part of the 2012 ISMRM Challenge. The qualitative and quantitative comparisons demonstrate that the proposed scheme is capable of minimizing fat water swaps in these challenging cases.
THEORY
Background
We now briefly review the mathematical formulation that is essential for the discussion in later sections. We will also review the iterative graph cut algorithm of Hernando et al. (18) to highlight its differences from the proposed scheme. In multi-echo water and fat decomposition, a sequence of images are collected with different echo time (TE) shifts, t1, t2, …, tN. The signal at each individual voxel is described by the model in (25):
| [1] |
Here, ρwater(r) and ρfat(r) are complex-valued concentrations of water and fat, respectively. The fat signal is modelled using an M peak model, where δi is the chemical shift between the ith fat peak and water, measured in Hz, and βi > 0 is the relative weight of each peak. The relative weights add up to unity (Σβi = 1). The parameters βi and δi are assumed to be known; the decomposition process involves the estimation of the unknown concentrations ρfat, ρwater, as well as f(r) and from the measured data. The field inhomogeneity induced frequency shift and decay terms are consolidated in the parameter . Here, f(r) is the local frequency shift due to magnetic field inhomogeneity at the spatial location r = (x, y), while models the decay due to intra-voxel dephasing. The consolidation of the decays of fat and water into a single term is shown to reduce bias and improved noise stability (18, 25). This model can be expressed in the matrix form as:
| [2] |
The unknown parameters are obtained by minimizing the least-squares error between the model and the measured data:
| [3] |
Since the above minimization is dependent on many parameters, the standard practice is to decouple them using the VARPRO approach (26). Specifically, the criterion is minimized with respect to some of the variables by assuming the others to be fixed, thus eliminating them from the optimization. Minimizing the above cost function with respect to the concentrations, assuming γ to be fixed, we obtain the optimal concentration estimates as . Substituting the optimal concentrations back in [3], and solving for γ, we obtain
| [4] |
One can again minimize the expression with respect to to obtain a cost function that is only dependent on f:
| [5] |
Since the estimation of
values does not suffer from ambiguities, an exhaustive search over possible
values is used to obtain
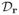 from Cr (26).
from Cr (26).
In order to address the sensitivity of the voxel-by-voxel optimization strategy specified by [5] to multiple feasible solutions and phase wrapping, Hernando et al. (18) formulated the joint recovery of the field map at all the voxels as a smoothness regularized optimization scheme. The global criterion is the linear combination of the sum of
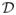 (r, f) and a smoothness penalty (18):
(r, f) and a smoothness penalty (18):
| [6] |
Here,
 (r) is the local neighborhood of the voxel at location r and wr,s are pre-defined weights that specify the relative importance of each difference term. The first term is the sum of the voxel-independent criteria in [5], while the second term promotes field map smoothness. Hernando et al., convert the above continuous problem to a discrete optimization scheme by restricting the field map to a set of discrete values.
(r) is the local neighborhood of the voxel at location r and wr,s are pre-defined weights that specify the relative importance of each difference term. The first term is the sum of the voxel-independent criteria in [5], while the second term promotes field map smoothness. Hernando et al., convert the above continuous problem to a discrete optimization scheme by restricting the field map to a set of discrete values.
The direct discrete minimization of [6] using a graph cut algorithm is computationally infeasible, since it involves a large and fully connected graph. Hence, the authors solve it iteratively by solving a sequence of binary decision problems at each iteration; these decision problems are solved efficiently using graph cut. At the (n + 1)th iteration, they consider two possible solutions at each voxel: Γn+1(r) = {fn(r), gn(r)}. Here, fn(r) is the optimal solution from the previous iteration, while gn(r) is chosen as fn(r) ± β, where β is a pre-specified constant, or picked randomly a set of local minimizers of
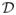 (f(r)). Each binary decision problem is efficiently solved using graph cut and is guaranteed to converge to a global minimum. However, the iterative algorithm is still not guaranteed to converge to the global minimum of the cost function. The local minima effects sometimes manifest as fat water swaps in challenging datasets
(f(r)). Each binary decision problem is efficiently solved using graph cut and is guaranteed to converge to a global minimum. However, the iterative algorithm is still not guaranteed to converge to the global minimum of the cost function. The local minima effects sometimes manifest as fat water swaps in challenging datasets
Reformulation as a smoothness constrained surface estimation problem
We formulate the estimation of the field map f(r) as the constrained optimization scheme:
| [7] |
where ex = (1, 0) and ey = (0, 1) are the unit vectors in the x and y directions, respectively. Instead of the smoothness penalty on the field map used in (18), we constrain the differences between field map values at adjacent voxels to be less than F (Hz) to minimize the ambiguities. Decreasing the maximum step size will result in a smoother field map. Note that [7] simplifies to a fully decoupled voxel-by-voxel search when the restrictions are removed (i.e, F = ∞). Since the above problem is non-convex, simple gradient descent schemes are not guaranteed to converge to the global minimum of the criterion.
We discretize the problem by restricting the possible field map values at each location to a uniform grid specified by f = n Δ. Here n = −Nmax, …, Nmax −1 is the discrete index and Δ(Hz) is the grid spacing. The discretization error can be controlled by setting Δ sufficiently small. The discrete optimization scheme is thus equivalent to fitting a smooth surface S to the 3-D discrete dataset
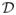 (r, f) (see Fig. 1.(a)); the height of the surface at the spatial location r is f(r). The number of discrete points in the surface is equal to NxNy, where the image is assumed to be of size Nx × Ny. The summation in [7] is essentially the sum of the values of the 3-D function
(r, f) (see Fig. 1.(a)); the height of the surface at the spatial location r is f(r). The number of discrete points in the surface is equal to NxNy, where the image is assumed to be of size Nx × Ny. The summation in [7] is essentially the sum of the values of the 3-D function
 (r, f) along the surface. The function
(r, f) along the surface. The function
 (r, f) can be interpreted as the negative of the likelihood that the surface passes through the point (r, f). The likelihood of the surface is obtained by summing the likelihoods of the points on the surface. The constraints in [7] can be conveniently expressed by representing the discrete dataset as a connected graph G(V, E) (Fig. 1.(b)), where V denotes the set of vertices and E are the edges. Correspondingly, the size of the graph is Nx × Ny × Nf, where Nf = 2Nmax is the number of layers in the graph (the number of discrete field map values). We have one vertex for each discrete point (r, n), while the edges of the graph (denoted by E) are specified by the constraints in [7]. Specifically, an edge exists between the vertex (r, n) and (r′, n′) if and only if |n−n′| ≤ α, with α is the smoothness constraint in the graph and r and r′ are neighbouring voxels; the four neighbors of the voxel r are (r + ex), (r − ex), (r + ey), and (r − ey). If we let Rf denote the complete search range of the uniform grid (Hz), then F = α Δ, Δ = Rf/Nf. It can be seen that a graph surface S is a subset of V if only if it satisfies the constraints in [7]. This enables us to rewrite [7] as
(r, f) can be interpreted as the negative of the likelihood that the surface passes through the point (r, f). The likelihood of the surface is obtained by summing the likelihoods of the points on the surface. The constraints in [7] can be conveniently expressed by representing the discrete dataset as a connected graph G(V, E) (Fig. 1.(b)), where V denotes the set of vertices and E are the edges. Correspondingly, the size of the graph is Nx × Ny × Nf, where Nf = 2Nmax is the number of layers in the graph (the number of discrete field map values). We have one vertex for each discrete point (r, n), while the edges of the graph (denoted by E) are specified by the constraints in [7]. Specifically, an edge exists between the vertex (r, n) and (r′, n′) if and only if |n−n′| ≤ α, with α is the smoothness constraint in the graph and r and r′ are neighbouring voxels; the four neighbors of the voxel r are (r + ex), (r − ex), (r + ey), and (r − ey). If we let Rf denote the complete search range of the uniform grid (Hz), then F = α Δ, Δ = Rf/Nf. It can be seen that a graph surface S is a subset of V if only if it satisfies the constraints in [7]. This enables us to rewrite [7] as
Fig. 1.
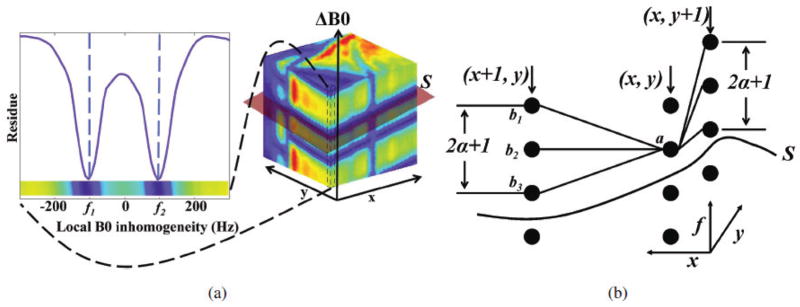
Illustration of the graph cut algorithm. (a) The residues specified by
 (r, f) are discretized on a uniform frequency grid nΔ; n = −Nmax, …, Nmax − 1. The discrete optimization is essentially a surface detection problem on a graph with 2Nmax layers, where the residues at each vertex are the vertex costs. Note that there are both local and global minimal costs in the graph. In this example the local minimal cost at f1 are very close to the global minimal cost at f2, for which voxel-independent schemes mostly fail. (b) Illustration of the constraints in graph-cut optimization. Each vertex on a specific voxel is connected with (2α + 1) neighbors. For example, the vertex a at the spatial location (x, y) is only connected with b1, b2, and b3 in the column corresponding to its neighbouring voxel (x + 1, y). Similarly, it is only connected to (2α + 1) neighbors in the voxel (x, y + 1). S is the surface that intersects one voxel at each column within the smoothness constraint. The objective of the graph cut optimization is to search for the surface with minimal costs.
(r, f) are discretized on a uniform frequency grid nΔ; n = −Nmax, …, Nmax − 1. The discrete optimization is essentially a surface detection problem on a graph with 2Nmax layers, where the residues at each vertex are the vertex costs. Note that there are both local and global minimal costs in the graph. In this example the local minimal cost at f1 are very close to the global minimal cost at f2, for which voxel-independent schemes mostly fail. (b) Illustration of the constraints in graph-cut optimization. Each vertex on a specific voxel is connected with (2α + 1) neighbors. For example, the vertex a at the spatial location (x, y) is only connected with b1, b2, and b3 in the column corresponding to its neighbouring voxel (x + 1, y). Similarly, it is only connected to (2α + 1) neighbors in the voxel (x, y + 1). S is the surface that intersects one voxel at each column within the smoothness constraint. The objective of the graph cut optimization is to search for the surface with minimal costs.
| [8] |
In the above equation, V(S) are the vertices of the surface. Note that each vertex is a point in 3-D: v = (r, f). In the next subsection, we introduce the graph cut algorithm to solve [8].
Optimal surface estimation using graph cut algorithm
In (27), Wu and Chen have shown that the optimal surface estimation problem can be transformed to the detection of a minimum-cost closed set in a transformed graph. A closed set
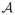 in a directed graph is a subset of graph vertices such that there is no edge from a vertex in
in a directed graph is a subset of graph vertices such that there is no edge from a vertex in
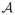 to a vertex in its complement
to a vertex in its complement
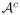 (Fig. 2.(a)). The cost of the closed set
(Fig. 2.(a)). The cost of the closed set
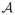 is defined as the total sum of the costs of all vertices in
is defined as the total sum of the costs of all vertices in
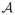 . The transformation of the original problem to minimum-cost closed set enables us to solve [8] using efficient polynomial time s-t cut schemes (28, 29). This approach is akin to transformation of a surface integral to a volume integral using Gauss theorem in the context of parametric snakes (30).
. The transformation of the original problem to minimum-cost closed set enables us to solve [8] using efficient polynomial time s-t cut schemes (28, 29). This approach is akin to transformation of a surface integral to a volume integral using Gauss theorem in the context of parametric snakes (30).
Fig. 2.
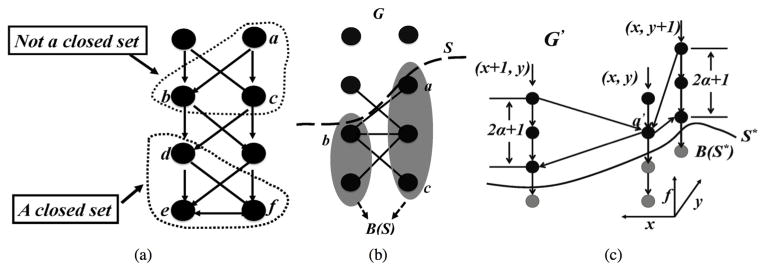
Illustration of the concepts in graph-cut optimization. (a) Closed set: vertices a, b and c do not form a closed set, because vertex d which is a successor of b and c is not in the set. Nonetheless, vertices d, e and f form a closed set. (b) An example of bottom-most neighbour. Vertex a is on the surface, b is an bottom-most neighbour of a. Similarly, c is a bottom-most neighbour of b. (c) The task of finding an optimal surface S* is transformed into finding the minimum-cost closed set B(S*) (indicated as gray vertices) beneath S* in the directed graph G′.
The key step in the graph transformation is the identification of a closed set B(S), which has a one-to-one mapping with a surface S. For a feasible surface S, we define B(S) as the set of all the vertices of G that are on or below S. It can be observed that for any feasible surface S in G, the bottom-most neighbors of every vertex in B(S) are also contained within B(S). The bottom-most neighbour of a vertex v ∈ V is the vertex in the neighboring column with the smallest f-coordinate, which can co-exist with v on a feasible surface (See Fig. 2.(b)). We also transform the cost of each vertex in the graph G (denoted by
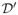 ):
):
| [9] |
Note that
 (r, n) is essentially the derivative of
(r, n) is essentially the derivative of
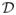 (r, n) along the frequency direction, with the appropriate boundary conditions. We can recover the value of
(r, n) along the frequency direction, with the appropriate boundary conditions. We can recover the value of
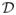 from
from
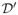 as
. Using this property (27), we can rewrite the surface sum Σv∈V
(T)
as
. Using this property (27), we can rewrite the surface sum Σv∈V
(T)
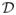 (v) in [8] as
(v) in [8] as
| [10] |
Thus, instead of finding the optimal surface S* directly, we seek the closed set B(S*) with the minimum cost E(S*), which uniquely defines the surface S*. The algorithm to solve [10] proceeds by creating a directed vertex-weighted graph G′(V′, E′) from G(V, E) (27). The vertices v′(x, y, f) ∈ G′ has a one-to-one correspondence with the vertices v(x, y, f) in G. Arcs (directed edges) are added to G′ to make sure that each closed set in G′ includes all the vertices associated to the corresponding surface vertices plus all the “lower” vertices in G. This is done by adding two types of arcs: intracolumn arcs and intercolumn arcs. The intracolumn arcs ensure that all vertices below a given vertex (within one column) are also included in the closed set. The intercolumn arcs ensure that the smoothness constraints are satisfied. As an example in Fig. 2.(c), we will consider the added arcs for one vertex v′. It will be associated with two intracolumn arcs: one directed towards the vertex immediately below it in the column and one from the vertex immediately above it. Two intercolumn arcs will also exist for each neighbouring column in the x-direction (y-direction): one directed to the bottom-most neighbour of v′ on the neighbouring column and one from the vertex on the neighbouring column whose bottom-most neighbour on the column of v′ is vertex v′. We do not show the boundary conditions to avoid cluttering the exposition of the key ideas. An outline of the algorithm is also described in the pseudo-code below.
Algorithm.
Graph surface search for optimal field map (
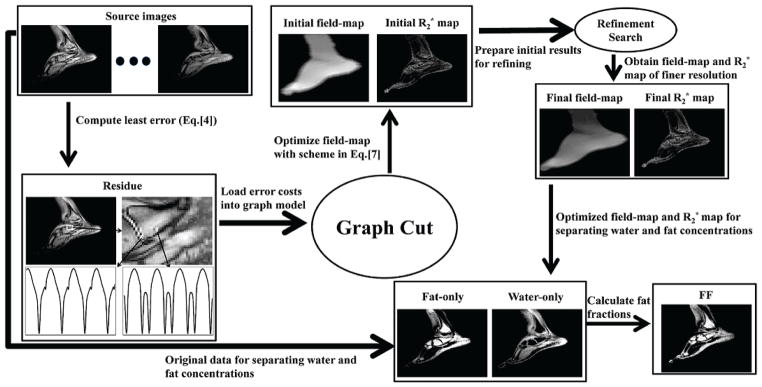
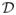 (x, y, f))
(x, y, f))
|
Once the optimal surface is determined using maximum flow/s-t cut algorithm on the transformed graph G′, the solutions are refined by searching on a finer grid in the range [f(r) − Δ, f(r) + Δ] (see Fig. 3). This search minimizes the effect of discretization. Since the search is constrained in the specified frequency range, the search is computationally inexpensive and the solution is still guaranteed to satisfy the constraints in [7]. We also determine the optimal for each frequency value by an exhaustive search.
Fig. 3.
Information flow in the proposed method. The residue specified by D(r, f) in [5] is discretized on a uniform grid. The global optimum of the proposed constrained optimization problem is obtained using a globally optimal graph cut optimization to yield the initial field map and the initial map. This solution is refined using a finer discrete search around the initial results provided by the graph cut algorithm. The refined field maps are used to estimate the fat water concentrations as .
METHODS
Implementation details
We use a six peak fat model, where the location of the peaks, denoted by δi in [1] correspond to 3.8 ppm, 3.4ppm, 2.6 ppm, 1.93 ppm, 0.39 ppm, −0.6 ppm for all the experiments. The relative weights of these peaks, denoted by βi in [1] are 0.0870, 0.693, 0.1280, 0.0040, 0.0390, 0.0480, respectively. These parameters are adopted from (25).
We use a discrete search procedure to determine
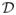 (r, f) from
(r, f) from
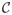 (r, γ) according to [5]. This approach similar to the one followed in (18). Specifically, for each value of f, we search over Nr discrete values of
in the range 0 s−1 to 500 s−1. This search process introduces minimal biases since the criterion is considerably smoother along the
dimension. We set the field map search range Rf to be [−8 ppm, 8 ppm]. Our experiments show that this search range is large enough to account for the range of field maps. The criterion specified is computed on a voxel-by-voxel basis. The optimal field map surface is then obtained by running the graph cut algorithm on the discretized problem. The discrete field map derived using the above algorithm is refined to minimize the effect of discretization. The refinement process involves an exhaustive search in the frequency range [f(r)−Δ, f(r)+Δ] and the
range. The range is discretized with approximately a 1 Hz spacing and exhaustively searched to obtain the minimum. The same rule applies to the refinement of
. Finally, the fat and water volumes are estimated by solving
; the fat volume fraction is then obtained from the derived concentrations. Since the proposed scheme is currently only implemented in 2-D, each of the slices in multi-slice datasets are processed separately. See Fig. 3 for the data flow in the proposed scheme.
(r, γ) according to [5]. This approach similar to the one followed in (18). Specifically, for each value of f, we search over Nr discrete values of
in the range 0 s−1 to 500 s−1. This search process introduces minimal biases since the criterion is considerably smoother along the
dimension. We set the field map search range Rf to be [−8 ppm, 8 ppm]. Our experiments show that this search range is large enough to account for the range of field maps. The criterion specified is computed on a voxel-by-voxel basis. The optimal field map surface is then obtained by running the graph cut algorithm on the discretized problem. The discrete field map derived using the above algorithm is refined to minimize the effect of discretization. The refinement process involves an exhaustive search in the frequency range [f(r)−Δ, f(r)+Δ] and the
range. The range is discretized with approximately a 1 Hz spacing and exhaustively searched to obtain the minimum. The same rule applies to the refinement of
. Finally, the fat and water volumes are estimated by solving
; the fat volume fraction is then obtained from the derived concentrations. Since the proposed scheme is currently only implemented in 2-D, each of the slices in multi-slice datasets are processed separately. See Fig. 3 for the data flow in the proposed scheme.
Metric used for the comparisons
We use the same metric as in 2012 ISMRM Challenge to evaluate the performance of the proposed algorithm as well as other state-of-the-art algorithms. Specifically, the performance of the algorithm is specified by the score
| [11] |
where FF is the fat fraction obtained from the specific algorithm and FFref is the reference fat fraction. The fat fraction is defined as the ratio of fat intensity to the sum of fat and water intensities. In the above equation, P is the mask, and Nvoxels is the total number of voxels. The multiplication factor is to obtain the scores in percent.
The decompositions obtained by the proposed scheme were also evaluated by an expert radiologist (JDN) on a four point scale. The scales were chosen as (1): too many fat water swaps & not diagnostic quality, (2): few swaps & may be clinically misleading, (3): few swaps, but not clinically misleading, (4): no swaps & good quality.
Optimization of parameters
As mentioned in theory section, the proposed algorithm is dependent on three parameters:
Nf, the number of layers used in the graph optimization,
Nr, the number of discrete values of , prior to graph optimization, and
α, the smoothness constraint assumed in the graph optimization; F = α * Rf/Nf.
We determine the optimal parameters by running the proposed algorithm with different parameter choices and comparing the scores of the resulting decompositions with the reference fat water ratios on the first four datasets.
Comparison of algorithms
We compare the proposed scheme with the implementations of the current algorithms available in the ISMRM fat water toolbox. Specifically, comparisons are performed between the proposed method and four state-of-the-art fat water algorithms: Iterative Graph Cut Algorithm (IGCA) in (18), Safest-first Region Growing Algorithm (SRGA) in (17), Golden Section Search Algorithm (GSSA) in (13), and Hierarchial IDEAL of Multiresolution Field map (HIMF) algorithm in (15). We assumed the default parameters provided in the toolbox for all the comparisons.
Datasets used for the experiments
Seventeen multi-echo datasets used in this study are distributed as part of 2012 ISMRM Challenge. The multi-slice coil-combined datasets correspond to different anatomical regions and were acquired on different institutions and different field strengths (1.5 and 3T). See Table 1 for details of these datasets. The reference fat-fractions and the masks corresponding to the image regions, where the fat fractions are compared, were downloaded from 2012 ISMRM Challenge website. The reference fat fractions were derived from larger number of echoes (typically 12–16 echoes) using the iterative graph cut algorithm (18). The masks were generated by thresholding the raw images, followed by manual segmentation and binary morphological operations to exclude isolated voxels and to erode edges which are likely to be partial volume voxels. These masks were checked by an expert for validity. The number of echoes that are used for the proposed decomposition and comparison with other methods varied between the datasets, as shown by the second row in Table 1. All datasets were processed on a desktop computer with 3.2GHz Intel Xeon CPU and 23.6GB RAM.
Table 1.
Details of the datasets used in the validation. The rows correspond to # TE: number of echoes used by the decomposition, MinTE: minimum TE value, MaxTE: maximum TE value, Field: field strength of the magnet, the anatomical region, Size/x: the matrix size in x, Size/y: matrix size in y, and #Slices: total number of slices in the dataset.
| Dataset | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| # TE | 6 | 8 | 5 | 6 | 4 | 5 | 6 | 5 | 6 | 5 | 6 | 4 | 4 | 4 | 4 | 5 | 3 |
| MinTE | 1.4 | 1.2 | 1.4 | 1.4 | 1.6 | 1.6 | 1.9 | 1.4 | 1.7 | 1.3 | 1.2 | 1.7 | 1.2 | 1.4 | 2.9 | 2.9 | 2.9 |
| MaxTE | 9.2 | 10.6 | 10.6 | 9.7 | 18.8 | 13.1 | 17.4 | 12.6 | 15.4 | 7.2 | 11.2 | 11.0 | 4.2 | 8.3 | 12.5 | 15.7 | 9.3 |
| Field | 3T | 3T | 3T | 3T | 1.5T | 1.5T | 1.5T | 1.5T | 3T | 3T | 1.5T | 1.5T | 3T | 1.5T | 1.5T | 1.5T | 1.5T |
| Anatomy | Knee | H&N | Foot | Knee | Calves | Thigh | Foot | Liver | Brain | Wrist | Liver | Liver | Thigh | H&N | Breast | Spine | Shldr |
| Size/x | 192 | 225 | 256 | 192 | 122 | 122 | 250 | 224 | 251 | 192 | 256 | 157 | 256 | 256 | 256 | 160 | 101 |
| Size/y | 192 | 227 | 256 | 192 | 242 | 244 | 175 | 248 | 201 | 192 | 256 | 257 | 131 | 256 | 55 | 208 | 101 |
| # Slices | 4 | 2 | 2 | 4 | 5 | 5 | 5 | 3 | 3 | 4 | 5 | 3 | 4 | 4 | 5 | 3 | 4 |
RESULTS
We study the effect of the parameters Nf and Nr in Fig. 4.(a) and the effect of the smoothness constraint in Fig. 4.(c). We observe that the scores vary in a small range when α ≤ 3. The performance degrades when α > 3. This is expected since the algorithm becomes similar to voxel-independent schemes with increasing α. Since the optimal performance is obtained at this value, we set α = 3 in all the experiments. Specifically, the average scores from the first four datasets are obtained for different values of Nf and Nr, assuming α = 3; the plot for different choices are shown in Fig. 4.(a). We observe that the algorithm is relatively insensitive to the choice of Nr, while the optimal performance is achieved around Nf = 100. Therefore, as we chose field map search range as [−8pm, 8pm], the grid spacing δ is approximately 10Hz for a field strength of 1.5 T and 20Hz for 3 T. Note that the constraint on the field map gets stronger as we increase Nf since F is inversely proportional to Nf. This explains why the scores drop slightly when Nf is increased beyond 100. Based on this study, we fix Nf = 100 and Nr = 20 in the rest of the paper. Note that the computational complexity of the algorithm is dependent on Nf and Nr. The refinement is conducted in two steps: a) The field map values in the range of [f(r) − Δ, f(r) + Δ] at each location are exhaustively searched with a 1 Hz resolution, assuming the values from the first pass. b) Once the optimal frequency is determined, the values are similarly searched exhaustively with a 1 ms−1 resolution. We plot the average computation time for the different choices in Fig. 4.(b). The average computation time for a 256×256 sized image is 90 seconds. These optimized parameters from the first four datasets are used for all the experiments.
Fig. 4.
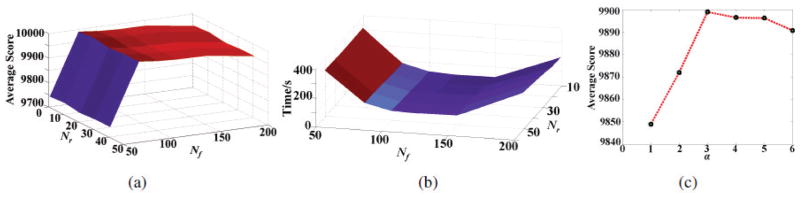
Dependence of the solution on the parameters. In (a). The number of f grid points (Nf ) and points (Nr) are varied and the resulting average scores are plotted. We observe that the results are not too sensitive to Nr, while the best scores are obtained for Nf ≈ 100. The average run times of the algorithms are shown in (b). For the optimal parameters, the average run time is approximately 90 seconds. The effect of the smoothness constraints on the scores are shown in (c). Here, we assume Nf = 100 and Nr = 20. We observe that the best results are obtained when α = 3 (i.e., 7 neighbors).
The quantitative comparisons of the GOOSE algorithm against the leading algorithms in the fat water toolbox (IGCA, SRGA, and HIMF schemes) are shown in Table 2. The GSSA algorithm often results in higher errors and hence were excluded from the studies. The SRGA algorithm is designed for uniformly spaced echoes and hence could not be run on dataset #3; the score is marked as N/A. The best score in each case is shown in bold. It is observed that the proposed scheme provides better results in most of the challenging cases. While it provides slightly lower scores in dataset #11 and dataset #14, the scores are very close to the best performing algorithm. The qualitative scores of the decompositions obtained by the proposed algorithm by the expert radiologist (JDN) are also reported in the last row of Table 2. The qualitative scores agreed with the quantitative scores overall. The main inconsistency was in the context of dataset #9, where the quantitative scores were high. The low qualitative scores were mainly due to the presence of small swaps in the trabecular bone regions with low signal intensity. None of the current algorithms were capable of avoiding these small swaps from limited number of echoes.
Table 2.
Quantitative comparison of the proposed scheme against state-of-the-art algorithms and qualitative evaluation by a radiologist. The first four rows of each algorithm GOOSE, IGCA, SRGA and HIMF correspond to quantitative scores (in percent) for the 17 datasets. Best scores are indicated by bold letters. The second row at each algorithm corresponds to the average qualitative score (out of four) assigned by the radiologist. Note that SRGA works only on uniformly sampled dataset and dataset #3 is non-uniformed sampled. Therefore no score is reported from SRGA for dataset #3.
| Method | Mean | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GOOSE | 99.27 | 99.84 | 99.81 | 96.50 | 99.87 | 99.94 | 99.88 | 99.90 | 99.94 | 99.97 | 99.72 | 99.75 | 95.58 | 99.91 | 99.87 | 99.15 | 99.13 | 98.80 |
| 3.74 | 4 | 4 | 3.5 | 4 | 4 | 4 | 4 | 4 | 2 | 4 | 4 | 1 | 4 | 4 | 4 | 4 | 4 | |
|
| ||||||||||||||||||
| IGCA | 91.85 | 99.46 | 68.29 | 95.97 | 99.71 | 91.00 | 99.88 | 95.36 | 81.58 | 91.78 | 99.68 | 99.91 | 81.28 | 94.18 | 87.71 | 81.79 | 98.84 | 94.64 |
| 2.25 | 4 | 1 | 4 | 4 | 2.5 | 4 | 1.5 | 1 | 1 | 3 | 4 | 1 | 1 | 1.2 | 1 | 3 | 1 | |
|
| ||||||||||||||||||
| SRGA | 83.05 | 91.37 | 45.36 | N/A | 96.52 | 26.47 | 99.27 | 87.92 | 99.23 | 48.94 | 93.03 | 99.60 | 51.71 | 99.23 | 99.88 | 98.73 | 96.02 | 96.43 |
| 3.06 | 4 | 1 | N/A | 4 | 1 | 3.5 | 4 | 2.5 | 1 | 4 | 3.8 | 1 | 4 | 4 | 4 | 3.2 | 4 | |
|
| ||||||||||||||||||
| HIMF | 69.72 | 97.49 | 56.38 | 42.01 | 98.07 | 63.47 | 99.55 | 46.03 | 64.14 | 58.99 | 93.79 | 99.14 | 51.23 | 90.41 | 17.86 | 58.67 | 85.44 | 62.52 |
| 2.09 | 4 | 1.5 | 1.2 | 4 | 4 | 2 | 4 | 2.1 | 1.8 | 1.5 | 4 | 1 | 1 | 1 | 1 | 2.5 | 1 | |
The decomposition obtained from the five algorithms on a foot dataset (dataset #7) is shown in Fig. 5. This is a rather challenging dataset due to the large range of field inhomogeneity. It is seen that IGCA, GSSA, HIMF suffer from fat water swaps near the ankle. Similarly, GSSA and HIMF have more swaps on both leg and toe region. The field maps derived by these algorithms (see bottom row) exhibit abrupt variations indicating convergence to local minima. We observe that the SRGA algorithm, as well as the proposed scheme, is capable of providing good estimates in this example. A noticeable difference in the field map recovered by the proposed scheme is that it takes small values outside the anatomical region. This can be attributed to the constrained formulation [7]. Specifically, the data-consistency term
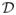 (r, f) is considerably smaller in amplitude in regions with low signal than regions with signal. Hence, many different values of f may give the same cost. The constrained formulation will pick one solution among the possible ones that satisfy the constraints. Due to the transformation [9], the solutions at these voxels often correspond the first few nodes at these voxels.
(r, f) is considerably smaller in amplitude in regions with low signal than regions with signal. Hence, many different values of f may give the same cost. The constrained formulation will pick one solution among the possible ones that satisfy the constraints. Due to the transformation [9], the solutions at these voxels often correspond the first few nodes at these voxels.
Fig. 5.
Qualitative comparisons of the algorithms on a foot dataset (2012 Challenge dataset #7). Top row: Fat; Second row: Water; Third: Field map. Fat water swaps are seen in IGCA, GSSA and HIMF indicated by arrows. The proposed and SRGA scheme are seen to provide good decompositions, which is also evident from the quantitative scores in Table 2 (also shown at the top left corner of each fat image).
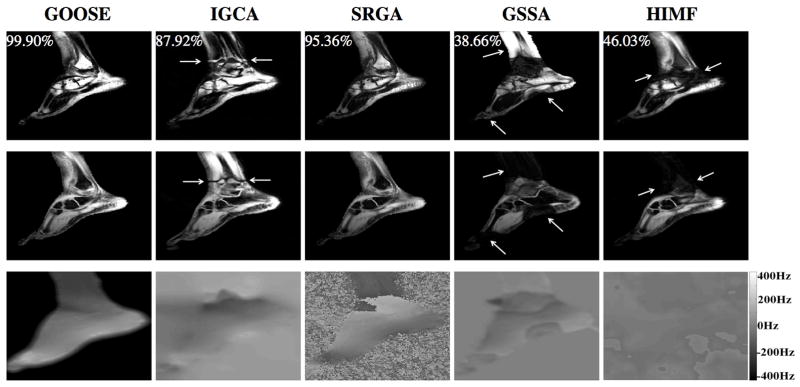
Another example, corresponding to the head/neck and upper thorax dataset (dataset #2) is shown in Fig. 6. This set is challenging due to the larger magnetic field inhomogeneity and multiple disconnected regions. From Fig. 6, we observe that all algorithms, except the proposed method, suffers from multiple fat water swaps in the region under neck. The failure of the SRGA scheme, which performed well in the other datasets, may be due to the disconnected nature of the regions and the large dynamic range; these challenges probably make the accurate seed placement in the region-growing algorithm difficult.
Fig. 6.
Qualitative comparisons on a head and neck dataset (2012 ISMRM Challenge dataset #2). Top row: Fat; Second row: Water; Third: Field map. All of the algorithms except the GOOSE scheme result in swaps between water and fat. Quantitative comparison can be seen from Table 2 (also shown at the top left corner of each fat image).
Fig. 7 shows the decomposition on an axial liver dataset (dataset #12). We observe that the existing schemes result in swaps in all the three slices, while the proposed scheme correctly recovered the fat and water in slices 1 & 3. The GOOSE algorithm also failed in slice 2, resulting in a swap. The main reason for the failure of the GOOSE algorithm in this case is that the anatomical regions are disconnected; the algorithm is not able to propagate the correct solution to the region of failure. This is a fundamental problem associated with algorithms that exploit field map smoothness.
Fig. 7.
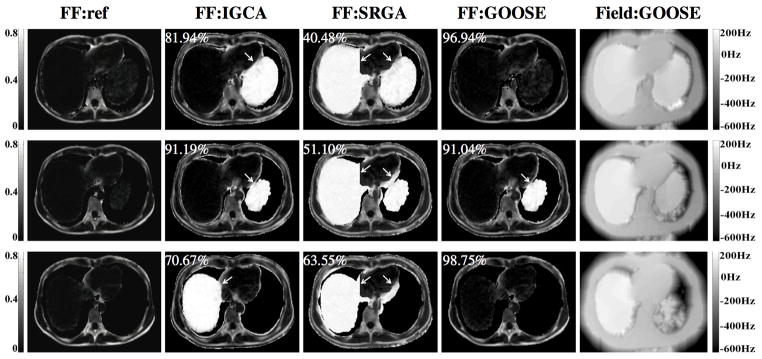
Comparison of the algorithms on 2012 ISMRM Challenge dataset #12. First column: Fat Fraction (FF) map for reference from 2012 ISMRM Challenge committee; Second: FF from SRGA; Third: FF from IGCA; Fourth: FF from GOOSE; Fifth: Field map from GOOSE. Each row corresponds to one slice in the dataset. This is a challenging example due to the disconnected regions in the dataset. We observe that all algorithms except the proposed one result in swaps in all the slices. The proposed scheme is capable of recovering the fractions correctly in slices 1 & 3 (first and third row), while it results in a swap in the second slice. Quantitative scores are shown at the top left corner of each FF map.
Fig. 8 shows the fat water decomposition of two slices of a breast dataset (dataset #15). The IGCA scheme resulted in large and obvious swaps, while the SRGA method resulted in subtle swaps, indicated by arrows. The GOOSE scheme is capable of providing results that are in good agreement with the ground truth in most regions. It resulted in a small swap in the middle, which is also indicated by arrows.
Fig. 8.
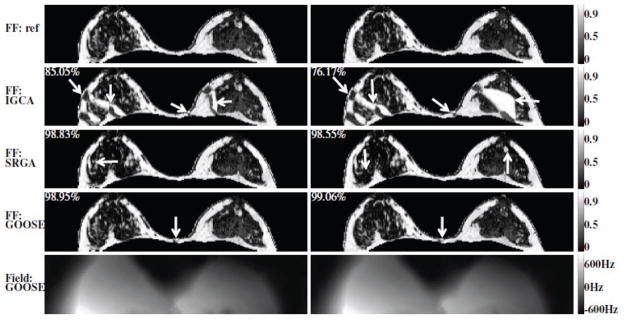
Comparison of the algorithms on a breast dataset (2012 ISMRM Challenge dataset #15). First row: Fat Fraction (FF) map for reference from 2012 ISMRM Challenge committee; Second: FF from IGCA; Third: FF from SRGA; Fourth: FF from GOOSE; Fifth: Field map from GOOSE. Each column corresponds to one slice in the dataset. IGCA results in large and obvious swaps. In contrast, the SRGA scheme results in several subtle swaps pointed by arrows. The proposed scheme is seen to agree well with the reference dataset, which is also evident from the quantitative comparisons in Table 2 (also shown at the top left corner of each FF map).
DISCUSSION & CONCLUSION
We introduced a novel fat water decomposition scheme, which we term as globally optimal surface estimation (GOOSE) algorithm. The proposed algorithm uses explicit constraints to exploit the smoothness of the field map, thus minimizing the ambiguities in maximum likelihood estimation. Specifically, the differences in the field map between adjacent voxels are constrained to be within a small range (less than 25Hz). The discretization of the criterion yields a problem that can be efficiently solved using graph cut optimization. Thanks to the considerably reduced graph connectivity, the algorithm is guaranteed to yield the global minimum of the cost function in a short computation time. While the algorithm shares some similarities with the global optimization scheme of Hernando et al. (18), the key difference is the constrained formulation. The global optimality guarantees of the algorithm are seen to be beneficial in practical settings. We have compared the proposed algorithm against some of the algorithms available in the ISMRM fat water toolbox. Overall, the comparisons show that the proposed scheme yields fewer swaps and thus better fat water decompositions. The algorithm is also evaluated independently by the 2012 ISMRM challenge committee; the decompositions using the GOOSE scheme resulted in scores that were only 0.04% lower than the winning team (31), which combined the results of several decomposition schemes in the ISMRM fat water toolbox using a perceptual quality metric (31). While the proposed scheme may be improved by combining it with other methods in a similar fashion, the resulting performance improvement is not expected to be significant.
A major limitation of the proposed implementation is that it is restricted to two dimensions. Currently, the different slices in multi-slice datasets are processed independently without considering the field map smoothness across slices. The extension of this algorithm to three dimensions can provide further improvement in performance of the current two-dimensional method. Specifically, the smoothness of the field map between the slices can enable us to resolve the ambiguities in datasets with disconnected regions. For example, we anticipate that this extension will improve the performance in the context of dataset #12 (see Fig. 7). Specifically, the 2-D scheme recovers the first and third slices accurately, while the second slice had a swap due to the disconnected regions. This will be part of our future work.
We have adopted the fat water model in [1], which is relatively established in the fat water community. Hence, our algorithm shares the benefits and drawbacks associated with the specific model. For example, the proposed algorithm is dependent on the number of fat peaks and their relative strengths in the model. This assumption considerably reduces the unknowns and offers a proportional reduction in variance. However, it is likely to result in biases when the relative strengths differ from actual values. Similarly, we have consolidated the decay parameters of fat and water into a single term. While the consolidation of the decay terms of fat and water into a single term is shown to be beneficial (18, 25), this approach may introduce biases in regions where this assumption is violated.
Acknowledgments
This work is supported by grants NSF CCF-0844812, NSF CCF-1116067, and ACS RSG-11-267-01-CCE.
The authors would like to thank the organizers and developers of the ISMRM fat water toolbox, which was used for the comparisons in this paper (http://ismrm.org/workshops/FatWater12/data.htm). The authors would also like to thank the committee of 2012 ISMRM Challenge for providing data and codes to test our algorithm (http://www.ismrm.org/challenge/). The authors also thank the anonymous reviewers, whose insightful comments considerably improved the quality of the manuscript. The implementation of the proposed algorithm using Matlab can be found at https://research.engineering.uiowa.edu/cbig/content/goose.
References
- 1.Bredella MA, Tirman PF, Peterfy CG, Zarlingo M, Feller JF, Bost FW, Belzer JP, Wischer TK, Genant HK. Accuracy of T2-weighted fast spin-echo MR imaging with fat saturation in detecting cartilage defects in the knee: comparison with arthroscopy in 130 patients. AJR Am J Roentgenol. 1999;172:1073–1080. doi: 10.2214/ajr.172.4.10587150. [DOI] [PubMed] [Google Scholar]
- 2.Bley TA, Wieben O, François CJ, Brittain JH, Reeder SB. Fat and water magnetic resonance imaging. J Magn Reson. 2010;31:4–18. doi: 10.1002/jmri.21895. [DOI] [PubMed] [Google Scholar]
- 3.Hu HH, Kim H, Nayak KS, Goran MI. Comparison of Fat–Water MRI and Single-voxel MRS in the Assessment of Hepatic and Pancreatic Fat Fractions in Humans. Obesity. 2010;18:841–847. doi: 10.1038/oby.2009.352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Reeder SB, Robson PM, Yu H, Shimakawa A, Hines CDG, McKenzie CA, Brittain JH. Quantification of hepatic steatosis with MRI: the effects of accurate fat spectral modeling. J Magn Reson. 2009;29:1332–1339. doi: 10.1002/jmri.21751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reeder SB, Markl M, Yu H, Hellinger JC, Herfkens RJ, Pelc NJ. Cardiac CINE imaging with IDEAL water-fat separation and steady-state free precession. J Magn Reson. 2005;22:44–52. doi: 10.1002/jmri.20327. [DOI] [PubMed] [Google Scholar]
- 6.Haase A, Frahm J, Hanicke W, Matthaei D. 1H NMR chemical shift selective (CHESS) imaging. Physics in Medicine and Biology. 2000;30:341. doi: 10.1088/0031-9155/30/4/008. [DOI] [PubMed] [Google Scholar]
- 7.Meyer CH, Pauly JM, Macovski A, Nishimura DG. Simultaneous spatial and spectral selective excitation. Magn Reson Med. 2005;15:287–304. doi: 10.1002/mrm.1910150211. [DOI] [PubMed] [Google Scholar]
- 8.Schick F. Simultaneous highly selective MR water and fat imaging using a simple new type of spectral-spatial excitation. Magn Reson Med. 2005;40:194–202. doi: 10.1002/mrm.1910400205. [DOI] [PubMed] [Google Scholar]
- 9.Bydder GM, Steiner RE, Blumgart LH, Khenia S, Young IR. MR imaging of the liver using short TI inversion recovery sequences. J Computer Assisted Tomography. 1985;9:1084. doi: 10.1097/00004728-198511000-00015. [DOI] [PubMed] [Google Scholar]
- 10.Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153:189–194. doi: 10.1148/radiology.153.1.6089263. [DOI] [PubMed] [Google Scholar]
- 11.Glover GH, Schneider E. Three-point Dixon technique for true water/fat decomposition with B0 inhomogeneity correction. Magn Reson Med. 2005;18:371–383. doi: 10.1002/mrm.1910180211. [DOI] [PubMed] [Google Scholar]
- 12.Reeder SB, Pineda AR, Wen Z, Shimakawa A, Yu H, Brittain JH, Gold GE, Beaulieu CH, Pelc NJ. Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): Application with fast spin-echo imaging. Magn Reson Med. 2005;54:636–644. doi: 10.1002/mrm.20624. [DOI] [PubMed] [Google Scholar]
- 13.Yu H, Reeder SB, Shimakawa A, Brittain JH, Pelc NJ. Field map estimation with a region growing scheme for iterative 3-point water-fat decomposition. Magn Reson Med. 2005;54:1032–1039. doi: 10.1002/mrm.20654. [DOI] [PubMed] [Google Scholar]
- 14.Jacob M, Sutton BP. Algebraic decomposition of fat and water in MRI. IEEE Trans Med Imaging. 2009;28:173–184. doi: 10.1109/TMI.2008.927344. [DOI] [PubMed] [Google Scholar]
- 15.Tsao J, Jiang Y. Hierarchical IDEAL: Fast, robust, and multiresolution separation of multiple chemical species from multiple echo times. Magn Reson Med. 2012;70:155–159. doi: 10.1002/mrm.24441. [DOI] [PubMed] [Google Scholar]
- 16.Lu W, Hargreaves BA. Multiresolution field map estimation using golden section search for water-fat separation. Magn Reson Med. 2008;60:236–244. doi: 10.1002/mrm.21544. [DOI] [PubMed] [Google Scholar]
- 17.Berglund J, Johansson L, Ahlstrom H, Kullberg J. Three-point Dixon method enables whole-body water and fat imaging of obese subjects. Magn Reson Med. 2010;63:1659–1668. doi: 10.1002/mrm.22385. [DOI] [PubMed] [Google Scholar]
- 18.Hernando D, Kellman P, Haldar JP, Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn Reson Med. 2010;63:79–90. doi: 10.1002/mrm.22177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to algorithms. MIT press; 2001. [Google Scholar]
- 20.Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Trans Pattern Anal. 2001;23:1222–1239. [Google Scholar]
- 21.Ishikawa H. Exact optimization for Markov random fields with convex priors. IEEE Trans Pattern Anal. 2003;25:1333–1336. [Google Scholar]
- 22.Kolmogorov V, Zabin R. What energy functions can be minimized via graph cuts? IEEE Trans Pattern Anal. 2004;26:147–159. doi: 10.1109/TPAMI.2004.1262177. [DOI] [PubMed] [Google Scholar]
- 23.Boykov Y, Veksler O. The Handbook of Mathematical Models in Computer Vision. Springer; 2006. Graph cuts in vision and graphics: Theories and applications; pp. 79–96. [Google Scholar]
- 24.Li K, Wu X, Chen DZ, Sonka M. Optimal surface segmentation in volumetric images-a graph-theoretic approach. IEEE Trans Pattern Anal. 2006;28:119–134. doi: 10.1109/TPAMI.2006.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yu H, Shimakawa A, McKenzie CA, Brodsky E, Brittain JH, Reeder SB. Multiecho water-fat separation and simultaneous R2* estimation with multifrequency fat spectrum modeling. Magn Reson Med. 2008;60:1122–1134. doi: 10.1002/mrm.21737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hernando D, Haldar JP, Sutton BP, Ma J, Kellman P, Liang ZP. Joint estimation of water/fat images and field inhomogeneity map. Magn Reson Med. 2008;59:571–580. doi: 10.1002/mrm.21522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wu X, Chen D. Optimal net surface problems with applications. Automata, Languages and Programming. 2002;2380:1029–1042. [Google Scholar]
- 28.Hochbaum DS. A new—old algorithm for minimum-cut and maximum-flow in closure graphs. Networks. 2001;37:171–193. [Google Scholar]
- 29.Picard JC. Maximal closure of a graph and applications to combinatorial problems. Management Science. 1976;22:1268–1272. [Google Scholar]
- 30.Jacob M, Blu T, Unser M. Efficient energies and algorithms for parametric snakes. IEEE Trans Image Proc. 2004;13:1231–1244. doi: 10.1109/tip.2004.832919. [DOI] [PubMed] [Google Scholar]
- 31.David SS, Johan B, Joel K, Hakan A, Malcolm JA, Brian W. Optimization of Fat-Water Separation Algorithm Selection and Options Using Image-based Metrics with Validation by ISMRM Fat-Water Challenge Datasets. Proceedings of the 21st Annual Meeting of ISMRM; Salt Lake City, UT. 2013. [Google Scholar]


