Generalized Higher Degree Total Variation (HDTV) Regularization

Abstract

We introduce a family of novel image regularization penalties called generalized higher degree total variation (HDTV). These penalties further extend our previously introduced HDTV penalties, which generalize the popular total variation (TV) penalty to incorporate higher degree image derivatives. We show that many of the proposed second degree extensions of TV are special cases or are closely approximated by a generalized HDTV penalty. Additionally, we propose a novel fast alternating minimization algorithm for solving image recovery problems with HDTV and generalized HDTV regularization. The new algorithm enjoys a ten-fold speed up compared to the iteratively reweighted majorize minimize algorithm proposed in a previous work. Numerical experiments on 3D magnetic resonance images and 3D microscopy images show that HDTV and generalized HDTV improve the image quality significantly compared with TV.

I. Introduction

The total variation (TV) image regularization penalty is widely used in many image recovery problems, including denoising, compressed sensing, and deblurring [1]. The good performance of the TV penalty may be attributed to its desirable properties such as convexity, invariance to rotations and translations, and ability to preserve image edges. However, the main challenges associated with this scheme are the undesirable patchy or staircase-like artifacts in reconstructed images, which arise because TV regularization promotes sparse gradients.

We recently introduced a family of novel image regularization penalties termed as higher degree TV (HDTV) to overcome the above problems [2]. These penalties are defined as the L₁-L_p norm (p = 1 or 2) of the nth degree directional image derivatives. The HDTV penalties inherit the desirable properties of the TV functional mentioned above. Experiments on two-dimensional (2D) images demonstrate that HDTV regularization provides improved reconstructions, both visually and quantitatively. Notably, it minimizes the staircase and patchy artifacts characteristic of TV, while still enhancing edge and ridge-like features in the image. The HDTV penalties were originally designed for 2D image reconstruction problems and were defined solely in terms of 2D directional derivatives. The direct extension of the current scheme to 3D is challenging due to the high computational complexity of our current implementation. Specifically, the iteratively reweighted majorize minimize (IRMM) algorithm that we used in [2] is considerably slower than state-of-the-art TV algorithms [3]–[5].

In this work we extend HDTV to higher dimensions and to a wider class of penalties based on higher degree differential operators, and devise an efficient algorithm to solve inverse problems with these penalties; we term the proposed scheme generalized HDTV. The generalized HDTV penalties are defined as the L₁-L_p norm, p ≥ 1, of all rotations of an nth degree differential operator. By design, the generalized HDTV penalties also inherit the desirable properties of TV and HDTV such as translation- and rotation-invariance, scale covariance, as well as convexity. Furthermore, generalized HDTV penalties allow for a diversity of image priors that behave differently in preserving or enhancing various image features—such as edges or ridges—and may be finely tuned for the specific image reconstruction task at hand. Our new algorithm is based on an alternating minimization scheme, which alternates between two efficiently solved subproblems given by a shrinkage and the inversion of a linear system. The latter subproblem is much simpler to solve if the measurement operator has a diagonal form in the Fourier domain, as is the case for many practical inverse problems, such as denosing, deblurring, and single coil compressed sensing magnetic resonance (MR) image recovery. We find that this new algorithm improves the convergence rate by a factor of ten compared to the IRMM scheme, making the framework comparable in run time to the state-of-the-art TV methods.

We study the relationship between the generalized HDTV scheme and existing second degree TV generalizations [6]–[12]. Specifically, we show that many of the second degree TV generalizations (e.g. Laplacian penalty [6]–[8], the Frobenius norm of the Hessian [9], [13], and the recently introduced Hessian-Shatten norms [12]) are special cases or equivalent to the proposed HDTV scheme, when the differential operator in the HDTV regularization is chosen appropriately. The main benefit of the generalized HDTV framework is that it extends to higher degree image derivatives (n ≥ 2) and higher dimensions easily. Furthermore, our current implementation is considerably faster than many of the existing TV generalizations. We also observe that some of the current TV generalizations may result in poor reconstructions. For example, the penalties that promote the sparsity of the Laplacian operators have a large null space [14], and inverse problems regularized with such penalties may still be ill-posed. Moreover, Laplacian-based penalties are known to preserve point-like features rather than line-like features, which is also undesirable in many image reconstruction settings.

We compare the convergence of the proposed algorithm with our previous IRMM implementation. Our results show that the proposed scheme is around ten times faster than the IRMM method. We also demonstrate the utility of HDTV and generalized HDTV regularization in the context of practical inverse problems arising in medical imaging, including deblurring and denoising of 3D fluorescence microscope images, and compressed sensing MR image recovery of 3D angiography datasets. We show that 3D-HDTV routinely outperforms TV in terms of the SNR of reconstructed images and its ability to preserve ridge-like details in the datasets. We restrict our comparisons with TV since the implementations of many of the current extensions are only available in 2D; comparisons with these methods are available in [2]. Moreover, some of the TV extensions, like total generalized variation [11], are hybrid methods that combines derivatives of different degrees. The proposed HDTV scheme may be extended in a similar fashion, but it is beyond the scope of the present work.

II. Background

A. Image Recovery Problems

We consider the recovery of a continuously differentiable d-dimensional signal f : Ω → ℂ from its noisy and degraded measurements b. Here Ω ⊂ ℝ^d is the spatial support of the image. We model the measurements as y = 𝒜(f) + η, where η is assumed to be Gaussian distributed white noise and 𝒜 is a linear operator representing the degradation process. For example, 𝒜 may be a blurring (or convolution) operator in the deconvolution setting, a Fourier domain undersampling operator in the case of compressed sensing MR images reconstruction, or identity in the case of denoising. The operator 𝒜 may be severely ill-conditioned or non-invertible, so that in general recovering f from its measurements requires some form of regularization of the image to ensure well-posedness. Hence, we formulate the recovery of f as the following optimization problem

$$\underset{f}{\text{min}}{\Vert 𝒜(f)-\mathbf{b}\Vert }^2+\lambda 𝒥(f),$$ (1)

where ‖𝒜(f) − b‖² is the data fidelity term, 𝒥 (f) is a regularization penalty, and the parameter λ balances the two terms, and is chosen so that the signal-to-error ratio is maximized.

B. Two-dimensional HDTV

In 2D, the standard isotropic TV regularization penalty is the L₁ norm of the gradient magnitude, specified as

$$\mathrm{T}\mathrm{V}(f)={\int }_{\mathrm{\Omega }}|\nabla f(\mathbf{r})|d\mathbf{r}={\int }_{\mathrm{\Omega }}\sqrt{{({\partial }_{x}f(\mathbf{r}))}^2+{({\partial }_{y}f(\mathbf{r}))}^2}d\mathbf{r}.$$

In [2] we showed that the 2D-TV penalty can be reinterpreted as the mixed L₁–L₂ norm or the L₁-L₁ of image directional derivatives. This observation led us to propose two families of HDTV regularization penalties in 2D, specified by

$$\mathrm{I}-\mathrm{H}\mathrm{D}\mathrm{T}{\mathrm{V}}_n(f)={\int }_{\mathrm{\Omega }}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }{|f_{\theta ,n}(\mathbf{r})|}^{2}d\theta \right)}^{\frac{1}{2}}d\mathbf{r},$$ (2)

$$\mathrm{A}-\mathrm{H}\mathrm{D}\mathrm{T}{\mathrm{V}}_n(f)={\int }_{\mathrm{\Omega }}(\frac{1}{2\pi }{\int }_0^{2\pi }|f_{\theta ,n}(\mathbf{r})|d\theta )d\mathbf{r},$$ (3)

where f_θ,n is the nth degree directional derivative operator in the direction u_θ = [cos(θ), sin(θ)], defined as

$$f_{\theta ,n}(\mathbf{r})=\frac{{\partial }^n}{\partial {\gamma }^n}f{(\mathbf{r}+\gamma {\mathbf{u}}_{\theta })|}_{\gamma =0}.$$

The family of penalties defined by (2) and (3) were termed as isotropic and anisotropic HDTV, respectively. It is evident from (2) and (3) that 2D-HDTV penalties preserve many of the desirable properties of the standard TV penalty, such as invariance under translations and rotations and scale covariance. Furthermore, practical experiments in [2] demonstrate that HDTV regularization outperforms TV regularization in many image recovery tasks, in terms of both SNR and the visual quality of reconstructed images. Our experiments also indicate that the anisotropic case, which corresponds to the fully separable L₁-L₁ penalty, typically exhibits better performance in image recovery tasks over isotropic HDTV.

III. Generalized HDTV Regularization Penalties

The 2D-HDTV penalties given in (2) and (3) may be described as penalizing all rotations in the plane of the nth degree differential operator ${\partial }_x^n$. This interpretation suggests an extension of HDTV to higher dimensions, and to a wider class of rotation invariant penalties based on nth degree image derivatives, by penalizing all rotations in d-dimensions of an arbitrary nth degree differential operator 𝒟 = ∑_|α|=n c_α∂^α, where α is a multi-index and the c_α are constants. Thus, given a specific nth degree differential operator 𝒟, and p ≥ 1, we define the generalized HDTV penalty for d-dimensional signals f : Ω → ℂ as

$$𝒢[𝒟,p](f)={\int }_{\mathrm{\Omega }}{\left({\int }_{SO(d)}{|{𝒟}_{\mathbf{U}}f(\mathbf{r})|}^{p}d\mathbf{U}\right)}^{\frac{1}{p}}d\mathbf{r},$$ (4)

where SO(d) = {U ∈ ℝ^d×d : U^T = U⁻¹, det U = 1} is the special orthogonal group, i.e. the group of all proper rotations in ℝ^d, and 𝒟_U is the rotated operator defined as

$${𝒟}_{\mathbf{U}}f({\mathbf{r}}_0)=𝒟{[f({\mathbf{r}}_0+\mathbf{U}\mathbf{r})]|}_{\mathbf{r}=0}.$$

By design the generalized HDTV penalties are guaranteed to be rotation and translation invariant, and convex for all p ≥ 1. It is also clear they are contrast and scale covariant, i.e. for all α ∈ ℝ, 𝒢(α · f) = |α|𝒢(f) and 𝒢(f_α) = |α|^n−d𝒢(f), where f_α(x) ≔ f(α · x). Below we discuss some particular cases for which (4) affords simplifications.

1) Generalized HDTV penalties in 2D

The 2D rotation group SO(2) can be identified with the unit circle 𝕊¹ = {(cos θ, sin θ) : θ ∈ [0,2π]}, which allows us rewrite the integral in (4) as a one-dimensional integral over θ ∈ [0,2τ]. By choosing $𝒟={\partial }_x^n$ and p = 2, 1 we recover the isotropic and anisotropic HDTV penalties specified in (2) and (3). In this work we also consider 2D-HDTV penalties for arbitrary p ≥ 1,

$$\mathrm{H}\mathrm{D}\mathrm{T}\mathrm{V}[n,p](f)={\int }_{\mathrm{\Omega }}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }{|f_{\theta ,n}(\mathbf{r})|}^{p}d\theta \right)}^{\frac{1}{p}}d\mathbf{r}.$$ (5)

For the p = 1 case we will simply write HDTVn, i.e. HDTVn = HDTV[n, 1].

For a generalized HDTV penalty in 2D, where 𝒟 is an arbitrary nth degree differential operator, we may also write

$$𝒢[𝒟,p](f)={\int }_{\mathrm{\Omega }}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }{|{𝒟}_{\theta }f(\mathbf{r})|}^{p}d\theta \right)}^{\frac{1}{p}}d\mathbf{r},$$ (6)

where 𝒟_θf(r₀) = 𝒟[f(r₀ + U_θr)]|_r=0, and U_θ is a coordinate rotation about the origin by the angle θ.

2) Generalized HDTV penalties in 3D

The 3D rotation group SO(3) has a more complicated structure so that in general we cannot simplify the integral in (4). However, all rotations in 3D of the standard HDTV operator $𝒟={\partial }_x^n$ are specified solely by the orientations u ∈ 𝕊² = {u ∈ ℝ³ : ‖u‖ = 1}. Thus, in this case the integral in (4) simplifies to

$$\mathrm{H}\mathrm{D}\mathrm{T}\mathrm{V}[n,p](f)={\int }_{\mathrm{\Omega }}{\left({\int }_{{𝕊}^2}{|f_{\mathbf{u},n}(\mathbf{r})|}^{p}d\mathbf{u}\right)}^{\frac{1}{p}}d\mathbf{r},$$ (7)

where f_u,n is the nth degree directional derivative defined as

$$f_{\mathbf{u},n}(\mathbf{r})=\frac{{\partial }^n}{\partial {\gamma }^n}f{(\mathbf{r}+\gamma \mathbf{u})|}_{\gamma =0},\mathbf{u}\in {𝕊}^2.$$

Likewise, if an operator 𝒟 is rotation symmetric about an axis, then all rotations of 𝒟 in 3D can be specified by the unit directions¹ u ∈ 𝕊². For example, the 2D Laplacian Δ = ∂_xx +∂_yy embedded in 3D is rotation symmetric about the z-axis, so that any rotation of Δ is specified solely by the u ∈ 𝕊² to which z = [0,0,1] is mapped. For this class of operator the integral in (4) simplifies to

$$𝒢[𝒟,p](f)={\int }_{\mathrm{\Omega }}{\left({\int }_{{𝕊}^2}{|{𝒟}_{\mathbf{u}}f(\mathbf{r})|}^{p}d\mathbf{u}\right)}^{\frac{1}{p}}d\mathbf{r},$$ (8)

where 𝒟_uf(r₀) = 𝒟[f(r₀ + U_r)]|_r=0 for any U ∈ SO(3) that maps the axis of symmetry of 𝒟 to u.

3) Rotation Steerability of Derivative Operators

The direct evaluation of the above integrals by their discretization over the rotation group is computationally expensive. The computational complexity of implementing HDTV regularization penalties can be considerably reduced by exploiting the rotation steerable property of nth degree differential operators. Towards this end, note that the first degree directional derivatives f_u,1 have the equivalent expression

$$f_{\mathbf{u},1}(\mathbf{r})={\mathbf{u}}^T\nabla f(\mathbf{r}).$$

Similarly, higher degree directional derivatives f_u,n(r) can be expressed as the separable vector product

$$f_{\mathbf{u},n}(\mathbf{r})=\mathbf{s}{(\mathbf{u})}^T{\nabla }_{n}f(\mathbf{r}),$$

where, s(u) is vector of polynomials in the components of u and Δ_nf(r) is the vector of all nth degree partial derivatives of f. For example, in the second degree case (n = 2) in 2D, we may choose

$$\mathbf{s}(\mathbf{u})={[u_x^2,2u_x{u}_y,u_y^2]}^T;{\nabla }_{2}f(\mathbf{r})={[f_{xx}(\mathbf{r}),f_{xy}(\mathbf{r}),f_{yy}(\mathbf{r})]}^T.$$ (9)

In the case of a general nth degree differential operator 𝒟, by repeated application of the chain rule we may write the rotated operator 𝒟_U for any U ∈ SO(d) as

$${𝒟}_{\mathbf{U}}f({\mathbf{r}}_0)=𝒟f{({\mathbf{r}}_0+\mathbf{U}\mathbf{r})|}_{\mathbf{r}=0}=\mathbf{s}{(\mathbf{U})}^T{\nabla }_{n}f({\mathbf{r}}_0),$$ (10)

where s(U) is a vector of polynomials in the components of U, whose exact expression will depend on the choice of operator 𝒟. For example, the second degree 2D operator 𝒟 = ∂_xx + α∂_yy would have

$$\mathbf{s}(\mathbf{u})={[u_x^2+\alpha u_y^2,2(1-\alpha )u_x{u}_y,u_y^2+\alpha u_x^2]}^T.$$

Note that (10) shows that the choice of differential operator 𝒟 defining a generalized HDTV penalty only amounts to a different choice of steering function s(U) as specified in (10). This property will be useful in deriving a unified discrete framework for generalized HDTV penalties.

We now study the relationship of the generalized HDTV scheme with second degree extensions of TV in the recent literature. We show that many of them are related to the second degree (n = 2) generalized HDTV penalties, when the derivative operator is chosen appropriately. Specifically, the general second degree derivative operator has the form 𝒟 = ∑_|α|=2 c_α∂^α, and we will show that different choices of the coefficients c_α and p in (4) encompass many of the proposed regularizers.

A. Laplacian Penalty

One choice of 𝒟 is the Laplacian Δ, where Δ = ∂_xx + ∂_yy in 2D and Δ = ∂_xx + ∂_yy + ∂_zz in 3D. Note that the Laplacian is rotation invariant, so that Δ_Uf = Δf for all U ∈ SO(d). Thus, for any choice of p in (4), we obtain the penalty

$${𝒢}_{\mathrm{\Delta }}(f)={\int }_{\mathrm{\Omega }}|\mathrm{\Delta }f(\mathbf{r})|d\mathbf{r},$$

which was introduced for image denoising in [6]. This penalty has two major disadvantages. First of all, it has a large null space. Specifically, any function that satisfies the Laplace equation (Δf(r) = 0) will result in 𝒢_Δ(f) = 0. As a result, the use of this regularizer to constrain general ill-posed inverse problems is not desirable. Another problem is that due to the Laplacian being isotropic, its use as a penalty results in the enhancement of point-like features rather than line-like features.

B. Frobenius Norm of Hessian

Another interesting case corresponds to the second degree 2D operator $𝒟={\partial }_{xx}-(2\sqrt{2}-3){\partial }_{yy}$. The corresponding isotropic (p = 2) generalized HDTV penalty is thus given by

$$𝒢[𝒟,2](f)={\int }_{\mathrm{\Omega }}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }{|f_{\theta ,2}(\mathbf{r})-(2\sqrt{2}-3)f_{{\theta }^{\perp },2}(\mathbf{r})|}^{2}d\theta \right)}^{\frac{1}{2}}d\mathbf{r},$$

where f_θ^⊥,2(r) is the second derivative of f along ${\theta }^{\perp }=\theta +\frac{\pi }{2}$. Using the rotation steerability of second degree directional derivatives we have f_θ,2(r) = f_xx(r) cos² θ +f_yy(r) sin² θ +2f_xy(r) cos θ sin θ, and the expression for 𝒢[𝒟, 2](f) simplifies to

$$𝒢[𝒟,2](f)=c{\int }_{\mathrm{\Omega }}\sqrt{{|f_{xx}(\mathbf{r})|}^2+{|f_{yy}(\mathbf{r})|}^2+2{|f_{xy}(\mathbf{r})|}^2}d\mathbf{r},$$ (11)

for a constant c. This functional can be expressed as 𝒢[𝒟, 2](f) = ∫_Ω ‖ℋf‖_F dr, where ℋf is the Hessian matrix of f(r) and ‖·‖_F is the Frobenius norm. This second order penalty was proposed by [9], and can also be thought of as the straightforward extension of the classical second-degree Duchon’s seminorm [14]. A similar argument shows an isotropic generalized HDTV penalty is equivalent to the Frobenius norm of the Hessian in 3D, as well.

C. Hessian-Shatten Norms

One family of second degree penalties that generalize (11) are the Hessian-Shatten norms recently introduced by Lefkimmiatis et al. in [12]. These penalties are defined as

$$\mathrm{H}\mathrm{S}p(f)={\int }_{\mathrm{\Omega }}{\Vert \mathscr{H}f(\mathbf{r})\Vert }_{{𝒮}_p},\forall 1\le p\le \infty ,$$ (12)

where ℋf is the Hessian matrix of f, and ‖·‖_𝒮p is the Shatten p-norm defined as ‖X‖_𝒮p = ‖σ(X)‖_p, where σ(X) is a vector containing the singular values of the matrix X. The Schatten norm is equal to the Frobenius norm when p = 2, thus the penalty HS2 is equivalent to the generalized HDTV penalty 𝒢[𝒟, 2] given in (11). For p ≠ 2, the Hessian-Shatten norms are not directly equivalent to a generalized HDTV penalty. However, there is a close relationship between the p = 1 case of (12) and the anisotropic second degree HDTV penalty, HDTV2. Specifically, we have the following proposition, which we prove in the Appendix:

Proposition 1

The penalties HDTV2 and HS1 are equivalent as semi-norms over 𝒞²(Ω, ℝ), Ω ⊂ ℝ^d, in dimension d = 2 or 3, with bounds

$$(1-\delta )·\mathrm{H}\mathrm{S}1(f)\le C·\mathrm{H}\mathrm{D}\mathrm{T}\mathrm{V}2(f)\le \mathrm{H}\mathrm{S}1(f),\forall f\in {𝒞}^2(\mathrm{\Omega },ℝ),$$

where δ = 0.37 for d = 2, δ = 0.43 for d = 3, and C is a normalization constant independent of f.

Note that in the Appendix we show C · HDTV2(f) = HS1(f) if the Hessian matrices of f at all spatial locations are either positive or negative semi-definite, i.e. have all non-negative eigenvalues or all non-positive eigenvalues. In natural images only a fraction of the pixels or voxels will have Hessian eigenvalues with mixed sign, thus we expect the HS1 and HDTV2 penalties to be nearly proportional and to behave very similarly in applications. Our experiments in the results section are consistent with this observation.

D. Benefits of HDTV

The preceding shows that the generalized HDTV penalties encompass many of the proposed image regularization penalties based on second degree derivatives, or in the case of certain Hessian-Shatten norms, closely approximate them. The generalized HDTV penalties have the additional benefit of being extendible to derivatives of arbitrary degree n > 2. Additionally, a wide class of image recovery problems regularized with any of the various HDTV penalties—regardless of dimension d, degree n, choice of differential operator 𝒟—can all be put in a unified discrete framework, and solved with the same fast algorithm, which we introduce in the following section.

IV. Fast Alternating Minimization Algorithm for HDTV Regularized Inverse Problems

A. Discrete Formulation

We now give a discrete formulation of the problem (1) with generalized HDTV regularization. In this setting we consider the recovery of a discrete d-dimensional image (d = 2 or 3), according to a linear observation model

$$\mathbf{b}=\mathbf{A}\mathbf{x}+\mathbf{n},$$

where matrix A ∈ ℂ^M×N represents the linear degradation operator, x ∈ ℂ^N and b ∈ ℂ^M are vectorized versions of the signal to be recovered and its measurements, respectively, and n ∈ ℂ^M is a vector of Gaussian distributed white noise.

We represent the rotated discrete derivative operators 𝒟_u for u ∈ 𝒮, where 𝒮 = SO(d) or 𝕊^d−1 where appropriate, by block-circulant² N × N matrices D_u; that is, the multiplication D_ux corresponds to the multi-dimensional convolution of x with a discrete filter approximating 𝒟_u. Thus, the image recovery problem (1) in the discrete setting with generalized HDTV regularization is given by

$$\underset{\mathbf{x}}{\text{min}}{\Vert \mathbf{A}\mathbf{x}-\mathbf{b}\Vert }^2+\lambda {\int }_{𝒮}{\Vert {\mathbf{D}}_{\mathbf{u}}\mathbf{x}\Vert }_{{\ell }_p}d\mathbf{u}.$$ (13)

In the case that p > 1, designing an efficient algorithm for solving (13) is challenging due to the non-separability of the generalized HDTV penalty. Moreover, our experiments from [2] indicate the anisotropic case p = 1 typically exhibits better performance in image recovery tasks over the p > 1 case. Accordingly, for our new algorithm we will focus on the p = 1 case:

$$\underset{\mathbf{x}}{\text{min}}{\Vert \mathbf{A}\mathbf{x}-\mathbf{b}\Vert }^2+\lambda {\int }_{𝒮}{\Vert {\mathbf{D}}_{\mathbf{u}}\mathbf{x}\Vert }_{{\ell }_1}d\mathbf{u}.$$ (14)

Note that the regularization is essentially the sum of absolute values of all the entries of the signals D_ux. Extending our algorithm to general p, including the nonconvex case 0 < p < 1, is reserved for a future work.

B. Algorithm

To realize a computationally efficient algorithm for solving (14), we modify the half-quadratic minimization method [16] used in TV regularization [3], [17] to the HDTV setting. We approximate the absolute value function inside the ℓ₁ norm with the Huber function:

$${\phi }_{\beta }(x)=\{\begin{array}{ccc}\hfill |x|-1/2\beta \hfill & \hfill \text{if}\hfill & \hfill |x|\ge \frac{1}{\beta }\hfill \\ \hfill \beta {|x|}^2/2\hfill & \hfill \text{else}.\hfill & \hfill \hfill \end{array}$$

The approximate optimization problem for a fixed β > 0 is thus specified by

$$\underset{\mathbf{x}}{\text{min}}{\Vert \mathbf{A}\mathbf{x}-\mathbf{b}\Vert }^2+\lambda {\int }_{𝒮}\sum _{j=1}^N{\phi }_{\beta }({[{\mathbf{D}}_{\mathbf{u}}\mathbf{x}]}_j)d\mathbf{u}.$$ (15)

Here, [x]_j denotes the j^th element of x. Note that this approximation tends to the original HDTV penalty as β → ∞. Our use of the Huber function is motivated by its half-quadratic dual relation [17]:

$${\phi }_{\beta }(y)=\underset{z}{\text{min}}\{\frac{\beta }{2}{|y-z|}^2+|z|\}.$$

This enables us to equivalently express (15) as

$$\underset{\mathbf{x},\mathbf{z}}{\text{min}}{\Vert \mathbf{A}\mathbf{x}-\mathbf{b}\Vert }^2+\lambda {\int }_{𝒮}\{\frac{\beta }{2}{\Vert {\mathbf{D}}_{\mathbf{u}}\mathbf{x}-{\mathbf{z}}_{\mathbf{u}}\Vert }^2+{\Vert {\mathbf{z}}_{\mathbf{u}}\Vert }_{{\ell }_1}\}d\mathbf{u},$$ (16)

where z_u ∈ ℂ^N are auxiliary variables that we also collect together as z ∈ ℂ^N × 𝒮. We rely on an alternating minimization strategy to solve (16) for x and z. This results in two efficiently solved subproblems: the z-subproblem, which can be solved exactly in one shrinkage step, and the x-subproblem which involves the inversion of a linear system that often can be solved in one step using discrete Fourier transforms. The details of these two subproblems are presented below. To obtain solutions to the original problem (14), we rely on a continuation strategy on β. Specifically, we solve the problems (15) for a sequence β_n → ∞, warm starting at each iteration with the solution to the previous iteration, and stopping the algorithm when the relative error of successive iterates is within a specified tolerance.

C. The z-subproblem: Minimization with respect to z, assuming x fixed

Assuming x to be fixed, we minimize the cost function in (16) with respect to z, which gives

$$\underset{\mathbf{z}}{\text{min}}{\int }_{𝒮}\{\frac{\beta }{2}{\Vert {\mathbf{D}}_{\mathbf{u}}\mathbf{x}-{\mathbf{z}}_{\mathbf{u}}\Vert }^2+{\Vert {\mathbf{z}}_{\mathbf{u}}\Vert }_{{\ell }_1}\}d\mathbf{u}.$$

Note that since the objective is separable in each component [z_u]_j of z_u we may minimize the expression over each [z_u]_j independently. Thus, the exact solution to the above problem is given component-wise by the soft-shrinkage formula

$${[{\mathbf{z}}_{\mathbf{u}}]}_j=\text{max}(|{[{\mathbf{D}}_{\mathbf{u}}\mathbf{x}]}_j|-\frac{1}{\beta },0)\frac{{[{\mathbf{D}}_{\mathbf{u}}\mathbf{x}]}_j}{|{[{\mathbf{D}}_{\mathbf{u}}\mathbf{x}]}_j|},$$ (17)

where we follow the convention $0·\frac{0}{0}=0$. While performing the shrinkage step in (17) is not computationally expensive, the need to store the auxiliary variables z_u ∈ ℂ^N for many u ∈ 𝒮 will make the algorithm very memory intensive. However, we will see in the next subsection that the rest of the algorithm does not need the variable z explicitly, but only its projection onto a small subspace, which significantly reduces the memory demand.

D. The x-subproblem: Minimization with respect to x, assuming z to be fixed

Assuming that z is fixed, we now minimize (16) with respect to x, which yields

$$\underset{\mathbf{x}}{\text{min}}{\Vert \mathbf{A}\mathbf{x}-\mathbf{b}\Vert }^2+\frac{\lambda \beta }{2}{\int }_{𝒮}{\Vert {\mathbf{D}}_{\mathbf{u}}\mathbf{x}-{\mathbf{z}}_{\mathbf{u}}\Vert }^{2}d\mathbf{u}.$$

The above objective is quadratic in x, and from the normal equations its minimizer satisfies

$$(2{\mathbf{A}}^T\mathbf{A}+\lambda \beta {\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{D}}_{\mathbf{u}}d\mathbf{u})\mathbf{x}=2{\mathbf{A}}^T\mathbf{b}+\lambda \beta {\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{z}}_{\mathbf{u}}d\mathbf{u}.$$ (18)

We now exploit the steerability of the derivative operators to obtain simple expressions for the operator ${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{D}}_{\mathbf{u}}d\mathbf{u}$ and the vector ${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{z}}_{\mathbf{u}}d\mathbf{u}$. The discretization of (10) yields D_u = ∑_j s_j(u)E_j, where E_j for j = 1, …, P are circulant matrices corresponding to convolution with discretized partial derivatives and s_i(u) are the steering functions. This expression can be compactly represented as S(u)E, where ${\mathbf{E}}^T=[{\mathbf{E}}_1^T,\dots ,{\mathbf{E}}_P^T]$ and S(u) = [s₁(u) I, s₂(u) I,…, s_P (u) I]. Here, I denotes the N × N identity matrix, where N is the number of pixels (x ∈ ℂ^N). Thus,

$${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{D}}_{\mathbf{u}}d\mathbf{u}={\mathbf{E}}^T\underset{\mathbf{C}}{\underbrace{{\int }_{𝒮}\mathbf{S}{(\mathbf{u})}^T\mathbf{S}(\mathbf{u})d\mathbf{u}}}\mathbf{E}.$$

The C matrix is essentially the tensor product between Q = ∫_𝒮 s(u)^T s(u) du and I_N×N. Hence we may write ${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{D}}_{\mathbf{u}}d\mathbf{u}={\sum }_{i,j}{q}_{i,j}{\mathbf{E}}_i^T{\mathbf{E}}_j$, where q_i,j is the (i, j) entry of Q. Note that the matrix Q can be computed exactly using expressions for the steering functions s(u). For example, with 2D-HDTV2 regularization (i.e. s(u) as given in (9)) one can show that up to a scaling factor,

$$\mathbf{Q}=\left[\begin{array}{ccc}\hfill 3\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 4\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 3\hfill \end{array}\right],$$

which gives ${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{D}}_{\mathbf{u}}d\mathbf{u}=3{\mathbf{E}}_1^T{\mathbf{E}}_1+4{\mathbf{E}}_2^T{\mathbf{E}}_2+3{\mathbf{E}}_3^T{\mathbf{E}}_3+{\mathbf{E}}_3^T{\mathbf{E}}_1+{\mathbf{E}}_1^T{\mathbf{E}}_3.$.

Similarly, we rewrite

$${\int }_{𝒮}{\mathbf{D}}_{\mathbf{u}}^T{\mathbf{z}}_{\mathbf{u}}d\mathbf{u}={\mathbf{E}}^T\underset{q}{\underbrace{{\int }_{𝒮}\mathbf{S}{(\mathbf{u})}^T{\mathbf{z}}_{\mathbf{u}}d\mathbf{u}}}=\sum _{j=1}^P{\mathbf{E}}_j^T{\mathbf{q}}_{j.}$$ (19)

To compute q we may use a numerical quadrature scheme to approximate the integral over 𝒮, i.e. we approximate $\mathbf{q}\approx {\sum }_{i=1}^K{w}_i\mathbf{S}({\mathbf{u}}_i){\mathbf{z}}_{{\mathbf{u}}_i}$, where the samples u_i ∈ 𝒮 and weights w_i, i = 1, …, K, are determined by the choice of quadrature; more details on the choice and performance of specific quadratures are given below. Note that the above equation implies that we only need to store P images specified by the vector q, which is much smaller than the number of samples K required to ensure a good approximation of the integral. This considerably reduces the memory demand of the algorithm.

In general, the linear equation (18) may be readily solved using a fast matrix solver such as the conjugate gradient algorithm. Note that the matrices E_j are circulant matrices and hence are diagonalizable with the discrete Fourier transform (DFT). When the measurement operator A is also diagonalizable with the DFT³, (18) can be solved efficiently in the DFT domain, as we now show in a few specific cases:

1) Fourier Sampling

Suppose A samples some specified subset of the Fourier coefficients of an input image x. If the Fourier samples are on a Cartesian grid, then we may write A = Sℱ, where ℱ is the d-dimensional discrete Fourier transform and S ∈ ℝ^M×N is the sampling operator. Then (18) can be simplified by evaluating the discrete Fourier transform of both sides. We obtain an analytical expression for x as:

$$\mathbf{x}={ℱ}^{-1}\left\{\frac{2{\mathbf{S}}^T\mathbf{b}+\lambda \beta ℱ[{\mathbf{E}}^T\mathbf{q}]}{2{\mathbf{S}}^T\mathbf{S}+\lambda \beta ℱ[{\mathbf{E}}^T\mathbf{C}\mathbf{E}]}\right\}.$$ (20)

Here, ℱ [E^TCE] is the transfer function of the convolution operator E^TCE. When the Fourier samples are not on the Cartesian grid (for example, in parallel imaging), where the one step solution is not applicable, we could still solve (18) using preconditioned conjugate gradient iterations.

2) Deconvolution

Suppose A is given by a circular convolution, i.e. Ax = h * x, then ℱ[Ax] = H · ℱ[x] and ℱ[A^T y] = H̄ · ℱ[y], where H = ℱ[h] and H̄ denotes the complex conjugate of H. Taking the discrete Fourier transform on both sides, (18) can be solved as:

$$\mathbf{x}={ℱ}^{-1}\left\{\frac{2\overline{\mathbf{H}}·ℱ[\mathbf{b}]+\lambda \beta ℱ[{\mathbf{E}}^T\mathbf{q}]}{2{|\mathbf{H}|}^2+\lambda \beta ℱ[{\mathbf{E}}^T\mathbf{C}\mathbf{E}]}\right\}.$$ (21)

The denoising setting corresponds to the choice A = I, the identity operator, in which case H = 1, the vector of all ones.

E. Discretization of the derivative operators

The standard approach to approximate the partial derivatives is using finite difference operators. For example, the derivative of a 2D signal along the x dimension is approximated as q[k₁, k₂] = f[k₁ +1, k₂] − f[k₁, k₂] = Δ₁ * f. This approximation can be viewed as the convolution of f by ${\mathrm{\Delta }}_1[k]=\phi (k+\frac{1}{2})$, where φ(x) = ∂B₁(x)/∂x and B₁(x) is the first degree B-spline [18]. However, this approximation does not possess rotation steerability, i.e. the directional derivative can not be expressed as the linear combination of the finite differences along x and y directions.

To obtain discrete operators that are approximately rotation steerable, in the 2D case we approximate the nth order partial derivatives, ${\partial }^{n_1,n_2}≔{\partial }_x^{n_1}{\partial }_y^{n_2}$ for all n₁ + n₂ = n, as the convolution of the signal with the tensor product of derivatives of one-dimensional B-spline functions:

$${\partial }^{n_1,n_2}f[k_1,k_2]=[B_n^{(n_1)}(k_1+\delta )\otimes B_n^{(n_2)}(k_2+\delta )]*f[k_1,k_2],$$ (22)

for all k₁, k₂ ∈ ℕ, where $B_n^{(m)}(x)$ denotes the mth order derivative of a nth degree B-spline. In order to obtain filters with small spacial support, we choose the δ according to the rule

$$\delta =\{\begin{array}{ccc}\hfill \frac{1}{2}\hfill & \hfill \text{if}\hfill & \hfill n\text{is old}\hfill \\ \hfill 0\hfill & \hfill \text{else}.\hfill & \hfill \hfill \end{array}$$

The shift δ implies that we are evaluating the image derivatives at the intersection of the pixels and not at the pixel midpoints. This scheme will result in filters that are spatially supported in a (n+1)×(n+1) pixel window. Likewise, in the 3D case we approximate the nth order partial derivatives, ${\partial }^{n_1,n_2,n_3}≔{\partial }_x^{n_1}{\partial }_y^{n_2}{\partial }_z^{n_3}$ for all n₁ +n₂ +n₃ = n, as

$${\partial }^{n_1,n_2,n_3}f[k_1,k_2,k_3]=[B_n^{(n_1)}(k_1+\delta )\otimes B_n^{(n_2)}(k_2+\delta )\otimes B_n^{(n_3)}(k_3+\delta )]*f[k_1,k_2,k_3],$$ (23)

for all k₁, k₂, k₃ ∈ ℕ with the same rule for choosing δ which results in filters supported in a (n + 1)³ volume.

While the tensor product of B-spline functions are not strictly rotation steerable, B-splines approximate Gaussian functions as their degree increases, and the tensor product of Gaussians is exactly steerable. Hence, the approximation of derivatives we define above is approximately rotation steerable; see Fig. 1. However, the support of the filters required for exact rotation steerability is much larger than the B-spline filters. These larger filters were observed to provide worse reconstruction performance than the B-spline filters. Thus the B-spline filters represent a compromise between filters that are exactly steerable but have large support, and filters that have small support but are poorly steerable.

Figure 1.

2D and 3D B-spline directional derivative operators at different angles. Note that the operators are approximately rotation steerable.

F. Numerical quadrature schemes for SO (d) and 𝕊^d−1

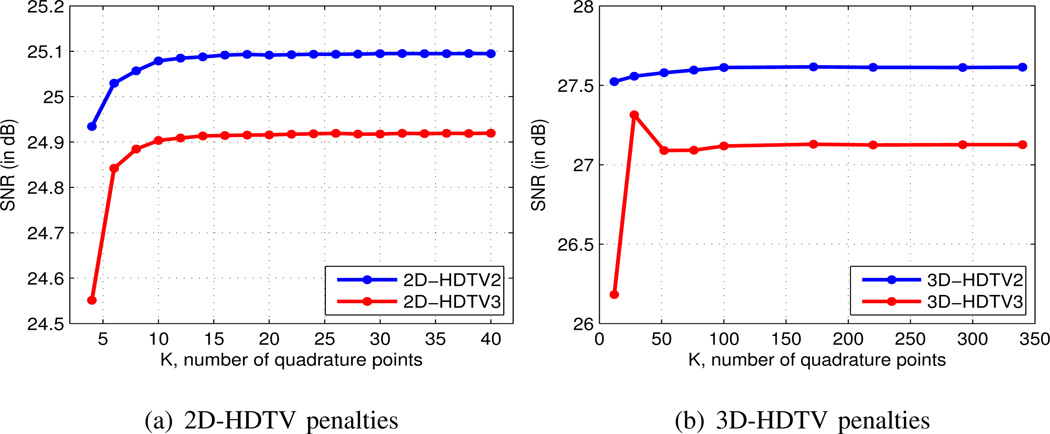
Our algorithm requires us to compute the projected shrinkage q in (19), which is defined as an integral over 𝒮 = SO(d) or 𝕊^d−1. We approximate this quantity using various numerical quadrature schemes depending on the space 𝒮. In the 2D case, we may simply parameterize u ∈ 𝕊¹ as u_θ = [cos(θ), sin(θ)], then approximate with a Riemann sum by discretizing the parameter θ as ${\theta }_i=i\frac{2\pi }{K}$, for i = 1, …, K, where K is the specified number of sample points. In this case we find K ≥ 16 samples yields a suitable approximation, in the sense that the optimal SNR of reconstructions obtained under various generalized HDTV penalties are unaffected by increasing the number of samples; see plot (a) in Fig. 2.

Figure 2.

Performance of proposed quadrature schemes. In (a) and (b) we display the SNR (as defined in (24)) in a denoising experiment as a function of the number of quadrature points K used to approximate the integral in (14). The same inputs were used for each K, except for the regularization parameter λ was tuned in each case to optimize the resulting SNR. In both the 2D and 3D case we observe an initial gain in SNR, demonstrating the value in better approximating the integral, but the change in SNR slows after a certain threshold. Namely, in the 2D experiment (a) we see that the change in SNR is within 0.01 dB after K ≈ 16 for both the HDTV2 and HDTV3 penalties. Likewise, in the 3D experiment (b), the change in SNR is within 0.05 dB after K ≈ 76.

In higher dimensions the analgous Riemann sum approximations become inefficient, and instead we make use of more sophisticated numerical quadrature rules. To approximate integrals over the sphere 𝕊² we apply Lebedev quadrature schemes [19]. These schemes exactly integrate all polynomials on the sphere up to a certain degree, while preserving certain rotational symmetries among the sample points. This is advantageous because the number of sample points can be significantly reduced if the derivative operators D_u obey any of the same rotational symmetries. In general, we find that Lebedev schemes with K ≥ 76 sample points provide a suitable approximation; see plot (b) in Fig. 2. Additionally, we note that for integrals over SO(3) we may design efficient quadrature schemes by taking the product of a 1D uniform quadrature scheme and a Lebedev scheme. We refer the interested reader to [20] for more details.

G. Algorithm Overview

Algorithm.

FAST HDTV(A, b, λ)

M ← 1
β ← βinit, x ← ATb
while M < MaxOuterIterations
do		m ← 1
		while m < MaxInnerIterations
		do		Compute partial derivatives using (22) or (23)
				Compute rotated operator outputs Duix using (10)
				Update zui based on [Duix]j using shrinkage rule (17)
				Compute projected shrinkage q using (19)
				Update x based on q using (20), (21)
				m ← m + 1
		β ← β * βincfactor
		M ← M + 1
return (x)

The pseudocode for the fast alternating HDTV algorithm is shown above. In our experiments we use the continuation scheme β_n+1 = β_inc · β_n for some constant β_inc > 1 and initial β₀. We warm start each new iteration with the estimate from the previous iteration, and stop when a given convergence tolerance has been reached; we evaluate the performance of the algorithm under different choices of β₀ and β_inc in the results section. We typically use 10 outer iterations (MaxOuterIterations = 10) and a maximum of 10 inner iterations (MaxInnerIterations = 10). The algorithm is terminated when the relative change in the cost function is less than a specified threshold.

V. Results

We compare the performance of the proposed fast 2D-HDTV algorithm with our previous implementation based on IRMM. We also study the improvement offered by the proposed 2D- and 3D-HDTV schemes over classical TV methods in the context of applications such as deblurring and recovery of MRI data from under sampled measurements. We omit comparisons with other 2D-TV generalizations since extensive comparisons were performed in our previous paper [2]. In each case, we optimize the regularization parameters to obtain the optimized SNR to ensure fair comparisons between different schemes. The signal to noise ratio (SNR) of the reconstruction is computed as:

$$\mathrm{S}\mathrm{N}\mathrm{R}=-10{\text{log}}_{10}\left(\frac{{\Vert {\mathbf{x}}_{\text{orig}}-\hat{\mathbf{x}}\Vert }_F^2}{{\Vert {\mathbf{x}}_{\text{orig}}\Vert }_F^2}\right),$$ (24)

where x̂ is the reconstructed image, x_orig is the original image, and ‖·‖_F is the Frobenius norm.

A. Two-dimensional HDTV using fast algorithm

1) Convergence of the fast HDTV algorithm

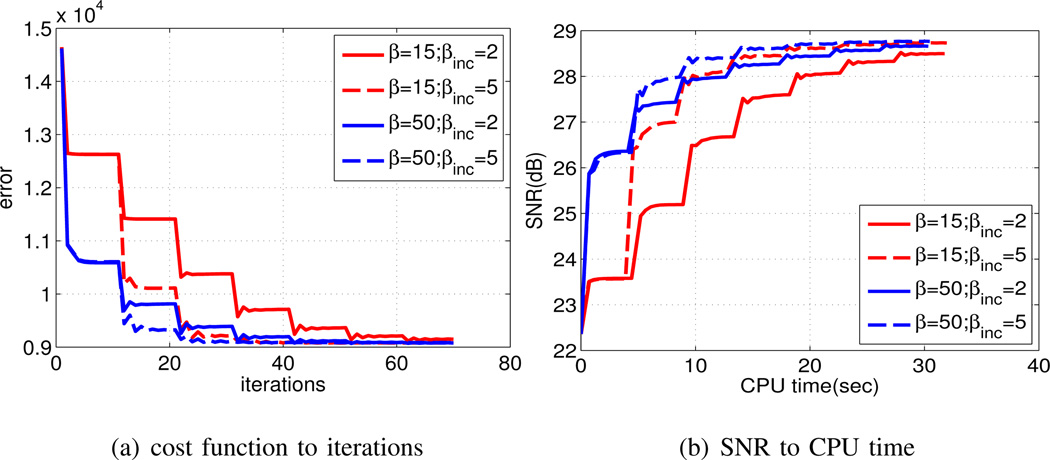
We investigate the effect of the continuation parameter β and the increment rate β_inc on the convergence and the accuracy of the algorithm. For this experiment, we consider the reconstruction of a MR brain image with acceleration factor 1.65 using the fast HDTV algorithm. The cost as a function of the number of iterations and the SNR as a function of the CPU time is plotted in Fig. 3. We observe that with different combinations of starting values of β and increment rate β_inc, the convergence rates of the algorithms are approximately the same and the SNRs of the reconstructed images are around the same value. However, when we choose the parameters as β = 15 and β_inc = 2, which are the smallest among the parameters chosen in the experiments, the SNR of the recovered image is comparatively lower than the others. This implies that in order to enforce full convergence the final value of β needs to be sufficiently large.

Figure 3.

Performance of the continuation scheme. We plot the cost as a function of the number of iterations in (a) and SNR as a function of CPU time in (b). We investigate four different combinations of the parameters β and β_inc. It is shown in (a) that the convergence rates of different combinations are approximately the same. We also observe in (b) that the SNR’s of the reconstructed images in four settings are similar except that when the final value of β is not large enough (β = 15, β_inc = 2) the SNR is comparatively lower than the others.

2) Comparison of the fast HDTV algorithm with iteratively reweighted HDTV algorithm

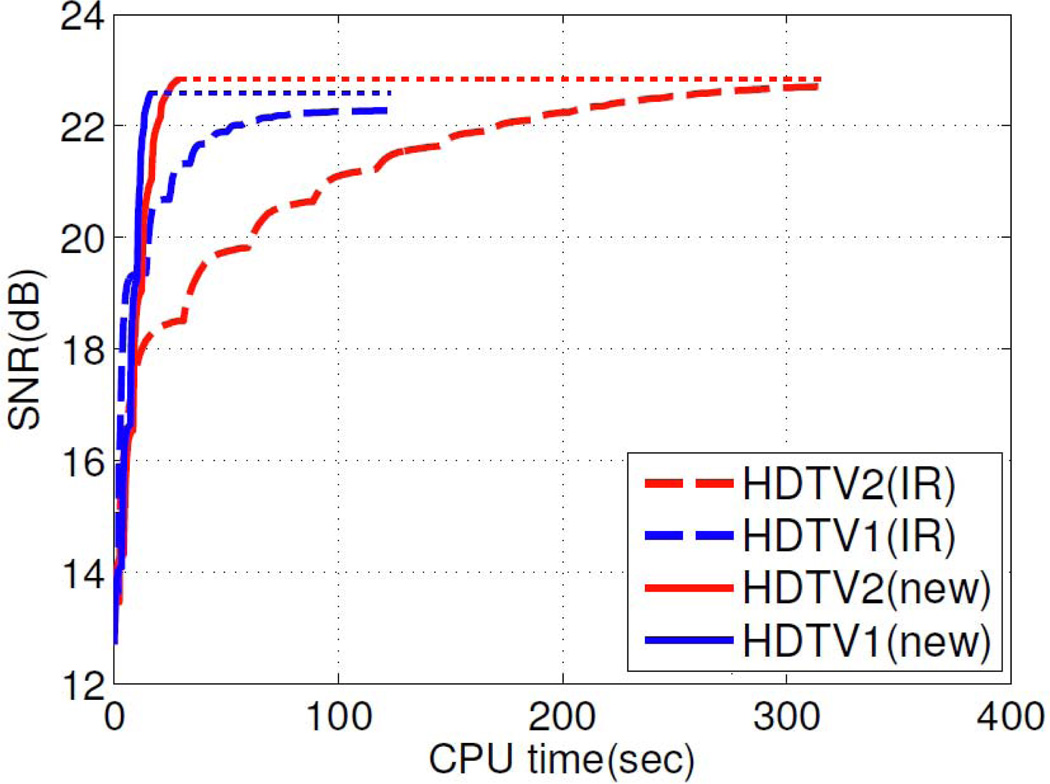
In this experiment, we compare the proposed fast HDTV algorithm with the IRMM algorithm in the context of the recovery of a brain MR image with acceleration factor of 4 in Fig. 4. Here we plot the SNR as a function of the CPU time using TV and second degree HDTV with the IRMM algorithm and the proposed algorithm, respectively. We observe that the proposed algorithm (blue curve) takes around 20 seconds to converge compared to 120 seconds by IRMM algorithm (blue dotted curve) using TV penalty, and 30 seconds (red curve) compared to 300 seconds (red dotted curve) using second degree HDTV regularization. Thus, we see that the proposed algorithm accelerates the problem significantly (ten-fold) compared to IRMM method.

Figure 4.

IRMM algorithm versus proposed fast HDTV algorithm in different settings. The blue, blue dotted, red, red dotted curves correspond to HDTV1 using proposed algorithm, HDTV1 using IRMM, HDTV2 using proposed algorithm, HDTV2 using IRMM algorithm, respectively. We extend (solid lines) the original plot by dotted lines for easier comparisons of the final SNRs. We see that the proposed algorithm takes 1/6 of the time taken by IRMM for HDTV1, and 1/10 of the time taken by IRMM for HDTV2.

3) Comparison of related algorithms

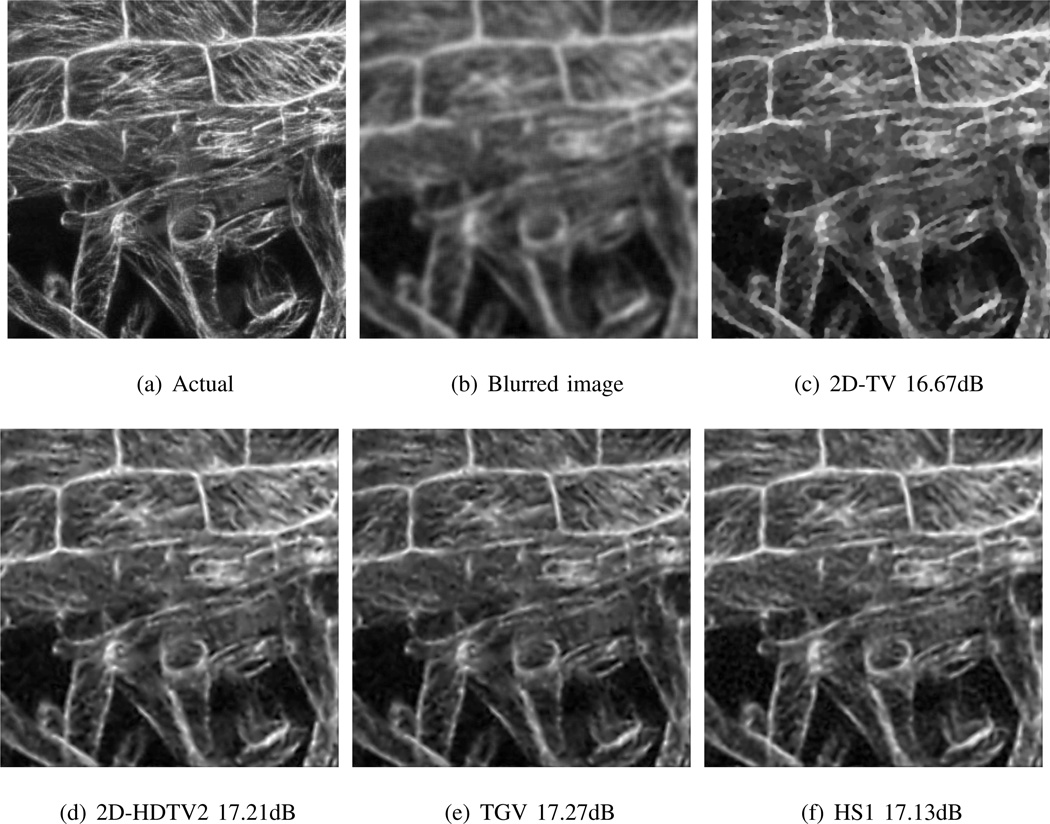
In order to demonstrate the utility of HDTV, we compare its performance with standard TV and two state-of-the-art schemes using higher order image derivatives, i.e, 1) the Hessian-Shatten norm p = 1 regularization penalty [12], which we refer to as HS1 regularization; 2) the total generalized variation scheme [11], referred to as TGV regularization. In Fig. 5, we have compared second and third degree HDTV with TV, HS1, and TGV regularization in the context of deblurring of a microscopy cell image of size 450×450. The original image is blurred with a 5×5 Gaussian filter with standard deviation 1.5, with additive Gaussian noise of standard deviation 0.05. We observe that the TV deblurred image has patchy artifacts and washes out the cell textures, while the higher degree schemes, including HDTV2, HDTV3, and HS1, gave very similar results (shown from (c) to (f)) with more accurate reconstructions, improving the SNR over standard TV by approximately 0.5 dB.

Figure 5.

Deblurring of a microscopy cell image. (a) is the actual cell image. (b) is the blurred image. (c)–(f) show the deblurred images using TV, HDTV2, TGV, and HS1 schemes, respectively. The results show that TV brings in patchy artifacts, while higher degree TV schemes preserve more details. HDTV2, TGV, and HS1 methods provide almost similar results both visually and in SNR, with a 0.5 dB SNR improvement over standard TV.

In Table I we present quantitative comparisons of the performance of the regularization schemes on six test images, in the context of compressed sensing, denoising, and deblurring. We observe that HDTV regularization provides the best SNR among schemes that only rely on single degree derivatives. The comparison of the proposed methods against TGV, which is a hybrid method involving first and second degree derivatives, show that in some cases the TGV scheme provides slightly higher SNR than the HDTV methods. However, we did not observe significant perceptual differences between the images. All higher degree schemes routinely outperform standard TV.

TABLE I.

Comparison of 2D TV-related methods (SNR)

		CS-brain	CS-wrist	Denoise-brain	Denoise-Lena	Deblur-cell1	Deblur-cell2
	2D-TV	22.77	20.96	27.60	27.35	15.66	16.67
single-degree	2D-HDTV2	22.82	21.20	28.05	27.65	16.19	17.21
	2D-HDTV3	22.53	21.02	28.30	27.45	16.17	17.20
	HS1	22.50	20.51	28.08	27.51	16.17	17.13
multiple-degree	TGV	22.80	21.25	28.17	27.78	16.25	17.27

We also note that in Proposition 1 we demonstrated a theoretical equivalence between HDTV2 and HS1 regularization penalties in a continuous setting. These experiments confirm that the discrete versions of these penalties perform similarly in image reconstruction tasks.

B. Three-dimensional HDTV

In the following experiments we investigate the utility of HDTV regularization in the context of compressed sensing, denoising, and deconvolution of 3D datasets. Specifically, we compare image reconstructions obtained using the second and third degree 3D-HDTV penalty versus the standard 3D-TV penalty.

1) Compressed Sensing

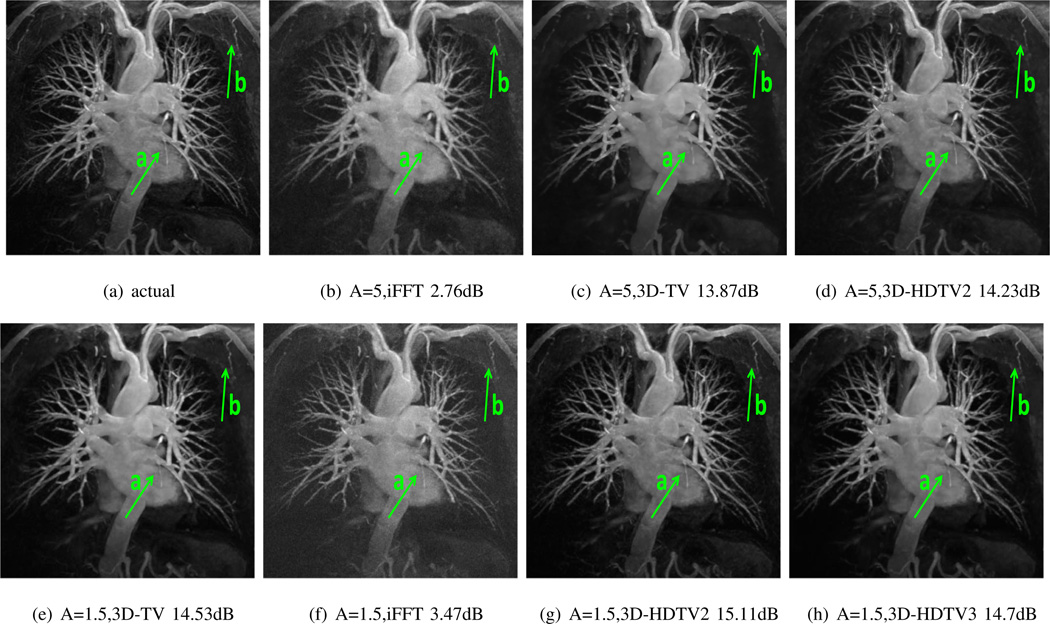
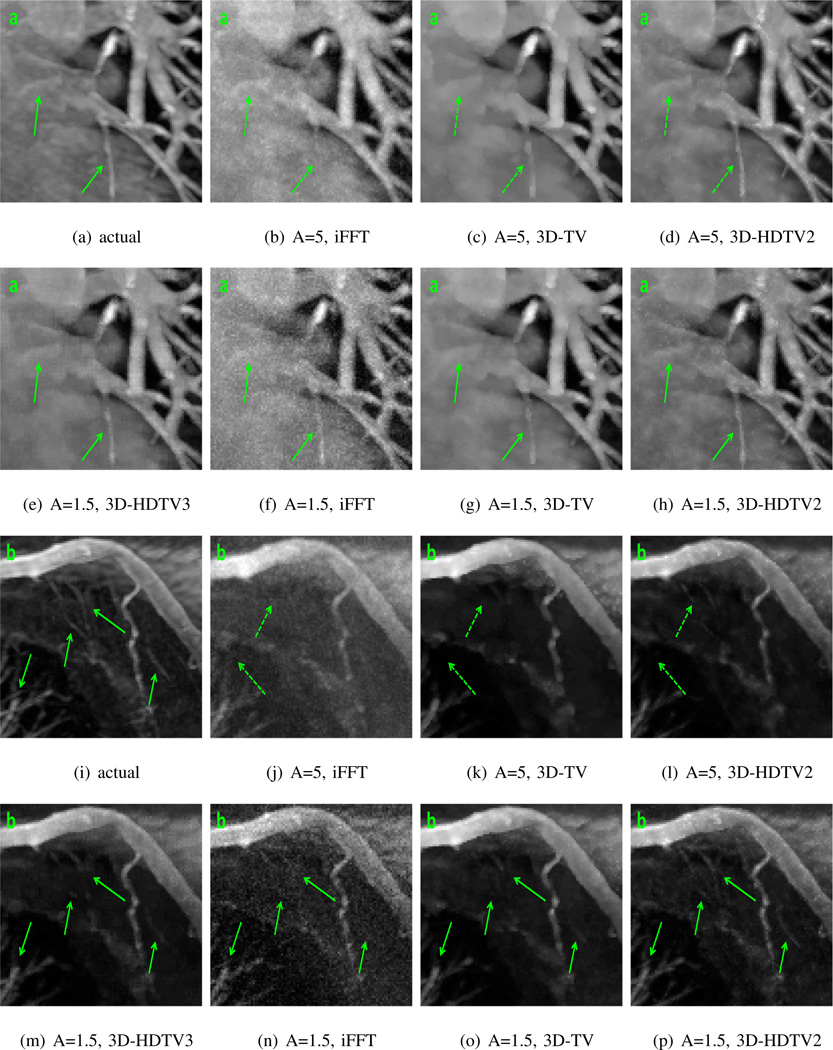
In these experiments we consider the compressed sensing recovery of a 3D MR angiography dataset from noisy and undersampled measurements. We experiment on a 512×512×76 MR dataset obtained from [21], which we retroactively undersampled using a variable density random Fourier encoding with acceleration factor of 1.5. To these samples we also added 5 dB Gaussian noise with standard deviation 0.53. Shown in Fig. 6 are the maximum intensity projections (MIP) of the reconstructions obtained using various schemes. We observe that there is a 0.4 dB improvement in 3D-HDTV over standard 3D-TV, and we also note that 3D-HDTV preserves more line details compared with standard 3D-TV. In Fig. 7 we present zoomed details of the two marked regions in Fig. 6. We observe that 3D-HDTV provides more accurate and natural-looking reconstructions, while 3D-TV result has some patchy artifacts that blur the details in the image.

Figure 6.

Compressed sensing recovery of MR angiography data from noisy and undersampled Fourier data (acceleration of 1.5 with 5dB additive Gaussian noise). (a) through (h) are the maximum intensity projection images of the dataset. (a) is the original image. (b) to (d) show the reconstructions with acceleration of 5, using direct iFFT, 3D-TV, 3D-HDTV2, separately. (e) to (h) indicate the reconstructed images with acceleration of 1.5, using 3D-TV, direct iFFT, 3D-HDTV2, 3D-HDTV3, separately. We observe that 3D-HDTV method preserves more details that are lost in 3D-TV reconstruction. The arrows highlight two regions that are shown in zoomed detail in Fig. 7.

Figure 7.

The zoomed images of the two regions highlighted in Fig. 6. The first two rows display the zoomed region (a) of the reconstructions with acceleration of 1.5 and 5 using direct inverse Fourier transform, 3D-TV, 3D-HDTV, separately. The third and fourth rows display the zoomed region (b) of the reconstructions. We observe that 3D-HDTV methods preserve more line-like features compared with 3D-TV (indicated by green arrows).

2) Deconvolution

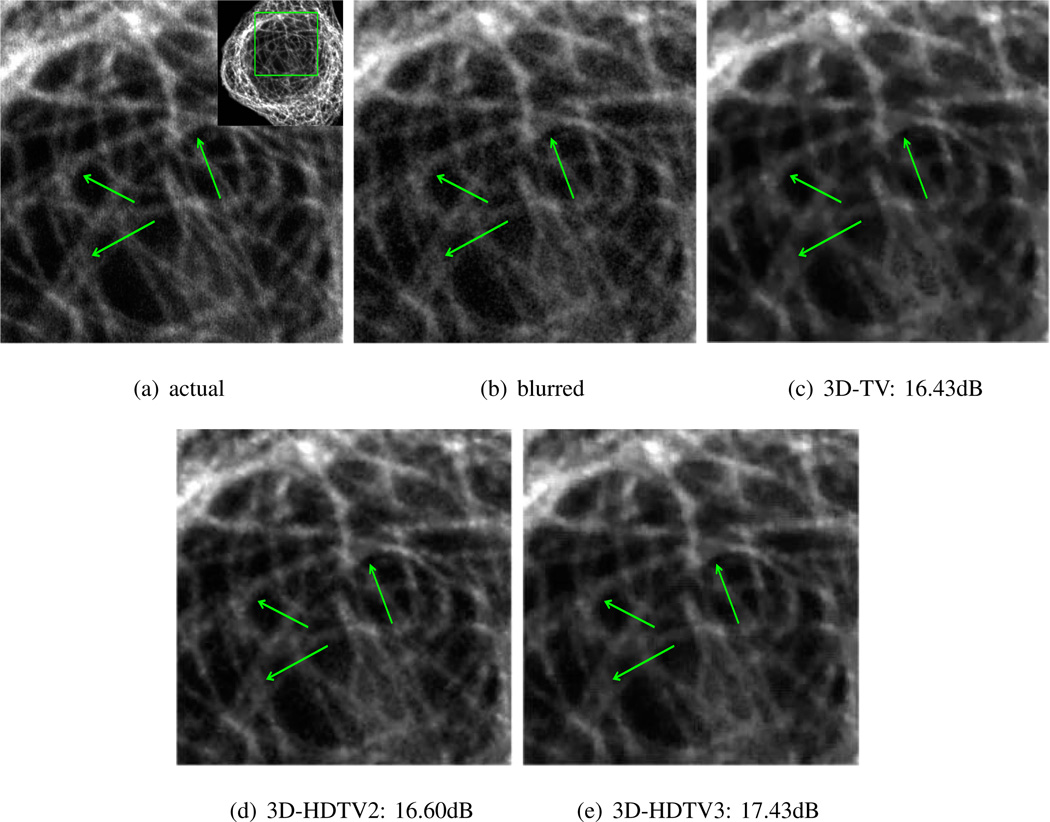
We compare the deconvolution performance of the 3D-HDTV with 3D-TV. Fig. 8 shows the decovolution results of a 3D fluorescence microscope dataset (1024 × 1024 × 17). The original image is blurred with a Gaussian filter of size 5 × 5 × 5 with standard deviation of 1, with additive Gaussian noise of standard deviation 0.01. The results show that 3D-HDTV scheme is capable of recovering the fine image features of the cell image, resulting in a 0.3 dB improvement in SNR over 3D-TV.

Figure 8.

Deconvolution of a 3D fluorescence microscope dataset. (a) is the original image. (b) is the blurred image using a Gaussian filter with standard deviation of 1 and size 5 × 5 × 5 with additive Gaussian noise (σ = 0.01). (c) to (e) are deblurred images using 3D-TV, 3D-HDTV2, 3D-HDTV3, separately. We observe that the 3D-TV recovery is very patchy and some small details are lost, while the HDTV methods preserve the line-like features (indicated by green arrows) with a 0.2 dB improvement in SNR.

The SNRs of the recovered images in the context of different applications are shown in Table. II. We observe that the HDTV methods provide the best overall SNR for all of the cases, in which 3D-HDTV2 gives the best SNR for compressed sensing settings, and the 3D-HDTV3 method provides the best SNR for denoising and deblurring cases. Compared with 3D-TV scheme, the 3D-HDTV schemes improve the SNR of the reconstructed images by around 0.5 dB.

TABLE II.

Comparison of 3D methods (SNR)

	CS-MRA(A=5)	CS-MRA(A=1.5)	CS-Cardiac	Denoise-1	Denoise-2	Deblur-1	Deblur-2	Deblur-3
3D-TV	13.87	14.53	18.37	17.12	16.25	19.02	16.43	14.50
3D-HDTV2	14.23	15.11	18.56	17.25	16.70	19.15	16.60	14.87
3D-HDTV3	14.01	14.70	18.50	17.68	17.14	19.73	17.43	15.23

VI. Discussion and Conclusion

We introduce a family of novel image regularization penalties called generalized higher degree total variation (HDTV). These penalties are essentially the sum of ℓ_p, p ≥ 1, norms of the convolution of the image by all rotations of a specific derivative operator. Many of the second degree TV extensions can be viewed as special cases of the proposed penalty or are closely related. We also introduce an alternating minimization algorithm that is considerably faster than our previous implementation for HDTV penalties; the extension of the proposed scheme to three dimensions is mainly enabled by this speedup. Our experiments demonstrate the improvement in image quality offered by the proposed scheme in a range of image processing applications.

This work could be further extended to account for other noise models. We assumed the quadratic data-consistency term in (1) for simplicity. Since it is the negative log-likelihood of the Gaussian distribution, this choice is only optimal for measurements that are corrupted by Gaussian noise. However, the proposed framework can be easily extended to other noise distributions by replacing the data fidelity term by the negative log-likelihood of the specified noise distribution. We do not consider these extensions in this work since our focus is only on modifying the regularization penalty.

Another direction for future research is to futher improve on our algorithm. The proposed version is based on a half-quadratic minimization method, which requires the parameter β to go infinity to ensure the equivalence of the auxiliary variables z_u to D_u (see (16)). It is shown by several authors that high β values are often associated with slow convergence and stability issues; augmented Lagrangian (AL) methods or the split Bregman methods were introduced to avoid these problem in the context of total variation and ℓ₁ minimization schemes [22], [23]. These methods introduce additional Lagrange multiplier terms to enforce the equivalence, thus avoiding the need for large β values. However, these schemes are infeasible in our setting since we need as many Lagrange multiplier terms as the number of directions u_i needed for accurate discretization; the associated memory demand is large. We implemented AL schemes in the 2D setting, but the improvement in the convergence was very small and did not justify the significant increase in memory demand. The challenge then is to design an algorithm for HDTV that exhibits the enhanced convergence properties of the AL method while maintaining a low memory footprint. This is something we hope to explore in a future work.

APPENDIX

A. Proof of Proposition 1

The HDTV2 penalty can be expressed using the Hessian matrix as

$$\mathrm{H}\mathrm{D}\mathrm{T}\mathrm{V}2(f)={\int }_{\mathrm{\Omega }}\mathrm{\Phi }(\mathscr{H}f(\mathbf{r}))d\mathbf{r},$$

where Φ(ℋf(r)) ≔ ∫_𝕊^d−1 |u^Tℋf(r)u| du. Since the Hessian is a real symmetric matrix, it has the eigenvalue decomposition ℋf(r) = Udiag(λ_f (r))U^T where U = U(r) is a unitary matrix, and λ_f (r) is a vector of the Hessian eigenvalues. Thus, by a change of variables

$$\mathrm{\Phi }(\mathscr{H}f(\mathbf{r}))={\int }_{{𝕊}^{d-1}}|{\mathbf{u}}^T\text{diag}({\lambda }_f(\mathbf{r}))\mathbf{u}|d\mathbf{u}.$$ (25)

Because the singular values of a symmetric matrix are the absolute value of its eigenvalues, we have ‖ℋf(r)‖_𝒮1 = ‖λ_f (r)‖₁, and together with (25) this gives the factorization

$$\mathrm{\Phi }(\mathscr{H}f(\mathbf{r}))=\underset{{\mathrm{\Phi }}_0({\lambda }_f(\mathbf{r}))}{\underbrace{\frac{{\int }_{{𝕊}^{d-1}}|{\mathbf{u}}^T\text{diag}({\lambda }_f(\mathbf{r}))\mathbf{u}|d\mathbf{u}}{{\Vert {\lambda }_f(\mathbf{r})\Vert }_1}}}{\Vert \mathscr{H}f(\mathbf{r})\Vert }_{{𝒮}_1}.$$ (26)

To prove the claim it suffices to establish bounds for Φ₀. By the triangle inequality we have

$${\int }_{{𝕊}^{d-1}}|{\mathbf{u}}^T\text{diag}({\mathit{\lambda }}_f(\mathbf{r}))\mathbf{u}|d\mathbf{u}\le {\int }_{{𝕊}^{d-1}}{\mathit{u}}^T\text{diag}(|{\mathit{\lambda }}_f(\mathbf{r})|)\mathbf{u}d\mathbf{u}=V_d{\Vert {\mathit{\lambda }}_f(\mathbf{r})\Vert }_1.$$

If we further suppose the Hessian eigenvalues λ_f (r) = (λ₁(r), …, λ_d(r)) are all non-negative, then u*diag(λ_f (r))u ≥ 0 for all u ∈ 𝕊^d−1, and so we may remove the absolute value from the integrand in Φ₀. Consider the vector-valued function F(v) = diag(λ_f (r))v defined on the unit ball B^d = {v ∈ ℝ^d : |v| ≤ 1}. Note that for u ∈ 𝕊^d−1, the surface normal n(u) = u, hence we have

$$\mathbf{F}(\mathbf{u})·\mathbf{n}(\mathbf{u})={\mathbf{u}}^T\text{diag}({\mathit{\lambda }}_f(\mathbf{r}))\mathbf{u},\forall \mathbf{u}\in {𝕊}^{d-1},$$

and so by the divergence theorem

$${\int }_{{𝕊}^{d-1}}{\mathbf{u}}^T\text{diag}({\mathit{\lambda }}_f(\mathbf{r}))\mathbf{u}d\mathbf{u}={\int }_{{𝕊}^{d-1}}\mathbf{F}·\mathbf{n}d\mathbf{u}={\int }_{B^d}\nabla ·\mathbf{F}d\mathbf{v}={\int }_{B^d}\sum _{k=1}^n{\lambda }_k(\mathbf{r})d\mathbf{v}=V_d{\Vert {\mathit{\lambda }}_f(\mathbf{r})\Vert }_1,$$

where V_d is the volume of B^d. A similar argument holds when the Hessian eigenvalues λ_f (r) are all non-positive. Thus, for Φ₀ (re-scaled by V_d) we have

$${\mathrm{\Phi }}_0({\mathit{\lambda }}_f(\mathbf{r}))=\frac{{\int }_{{𝕊}^{d-1}}|{\mathbf{u}}^T\text{diag}({\lambda }_f(\mathbf{r}))\mathbf{u}|d\mathbf{u}}{V_d{\Vert {\lambda }_f(\mathbf{r})\Vert }_1}\le 1,$$

where equality holds when the Hessian eigenvalues λ_f (r) are all non-negative or non-positive. We now derive lower bounds for Φ₀ in the 2D and 3D cases.

1) 2D Bound

Fix r, and let λ_f (r) = (λ₁, λ₂). In 2D we have

$${\mathrm{\Phi }}_0({\lambda }_1,{\lambda }_2)=\frac{{\int }_{{𝕊}^1}|{\lambda }_1{x}^2+{\lambda }_2{y}^2|d\mathbf{u}}{\pi (|{\lambda }_1|+|{\lambda }_2|)}=\frac{{\int }_0^{2\pi }|{\lambda }_1{\text{cos}}^2(\theta )+{\lambda }_2{\text{sin}}^2(\theta )|d\theta }{\pi (|{\lambda }_1|+|{\lambda }_2|)}.$$

We have Φ₀(λ₁, λ₂) < 1 only when λ₁ and λ₂ are both non-zero and differ in sign. By a scaling argument, it suffices to look at the case where λ₁ = 1 and λ₂ = −α, for some α with 0 < α ≤ 1. Thus, the minimum of Φ₀ coincides with the function

$$\mathrm{\Psi }(\alpha )=\frac{{\int }_0^{2\pi }|{\text{cos}}^2(\theta )-\alpha {\text{sin}}^2(\theta )|d\theta }{\pi (1+\alpha )},0<\alpha \le 1.$$

By the identity ${\text{cos}}^2(\theta )-\alpha {\text{sin}}^2(\theta )=(\frac{1-\alpha }{2})+(\frac{1+\alpha }{2})\text{cos}(2\theta )$ we have $\mathrm{\Psi }(\alpha )=\frac{1}{2\pi }{\int }_0^{2\pi }|\frac{1-\alpha }{1+\alpha }+\text{cos}(2\theta )|d\theta$. Setting Ψ′ (α) = 0 gives the necessary condition ${\int }_0^{2\pi }\text{sgn}[\frac{1-\alpha }{1+\alpha }+\text{cos}(2\theta )]d\theta =0$, which is true only if α = 1. Therefore, we obtain the bound ${\mathrm{\Phi }}_0({\lambda }_1,{\lambda }_2)\ge \frac{1}{2\pi }{\int }_0^{2\pi }|\text{cos}(2\theta )|d\theta =\frac{2}{\pi }\approx 0.63$.

B. 3D Bound

In the 3D case we have

$${\mathrm{\Phi }}_0({\lambda }_1,{\lambda }_2,{\lambda }_3)=\frac{3}{4\pi }\frac{{\int }_{{𝕊}^2}|{\lambda }_1{x}^2+{\lambda }_2{y}^2+{\lambda }_3{z}^2|d\mathbf{u}}{|{\lambda }_1|+|{\lambda }_2|+|{\lambda }_3|}=\frac{3}{4\pi }{\int }_0^{2\pi }{\int }_0^{\pi }\frac{|{\lambda }_1{x}^2+{\lambda }_2{y}^2+{\lambda }_3{z}^2|}{|{\lambda }_1|+|{\lambda }_2|+|{\lambda }_3|}\text{sin}\varphi d\varphi d\theta ,$$

where we use spherical coordinates (x, y, z) = (cos θ sin ϕ sin θ sin ϕ, cosϕ), with 0 ≤ θ ≤ 2π, 0 ≤ ϕ ≤ π. Note that Φ₀(λ₁, λ₂, λ₃) < 1 only if for some i ≠ j, λ_i and λ_j are both non-zero and differ in sign. By a scaling argument, it suffices to look at the case where λ₁ = −α, λ₂ = −β, and λ₃ = 2 for some α and β with 0 ≤ α, β ≤ 2. Thus, it is equivalent to minimize the function

$$\mathrm{\Psi }(\alpha ,\beta )=\frac{3}{4\pi }{\int }_0^{2\pi }{\int }_0^{\pi }\frac{|2z^2-\alpha x^2-\beta y^2|}{2+\alpha +\beta }\text{sin}\varphi d\varphi d\theta ,0\le \alpha ,\beta \le 2.$$

Using the identity x² + y² + z² = 1, one can show that

$$2z^2-\alpha x^2-\beta y^2=\left(\frac{\beta -\alpha }{2}\right)(x^2-y^2)+\left(\frac{4+\alpha +\beta }{6}\right)(3z^2-1)+\frac{2-\alpha -\beta }{3}=\frac{a}{2}{\text{sin}}^2(\varphi )\text{cos}(2\theta )+\left(\frac{4+b}{6}\right)(3{\text{cos}}^2(\varphi )-1)+\frac{2-b}{3},$$

where we have set a = β − α and b = α + β. We may write this as A cos(2θ)+B, where $A=A(a,\varphi )=\frac{a}{2}{\text{sin}}^2(\varphi )$ and B = B(b, ϕ) is given by the above equation. Then the minimum of Ψ coincides with the minimum of the function

$$\tilde{\mathrm{\Psi }}(a,b)=\frac{3}{4\pi (2+b)}{\int }_0^{\pi }{\int }_0^{2\pi }|A\text{cos}(2\theta )+B|d\theta d\varphi ,-2\le a\le 2;0\le b\le 4.$$

Observe that

$${\int }_0^{2\pi }|A\text{cos}(2\theta )+B|d\theta \ge {\int }_0^{2\pi }|B|d\theta ,$$

which implies Ψ̃ (a, b) ≥ Ψ̃ (0, b), and so a necessary condition for a minimum is a = 0, or equivalently α = β. Thus, we evaluate

$$\mathrm{\Psi }(\alpha ,\alpha )=\frac{3}{8\pi (1+\alpha )}{\int }_{{𝕊}^2}|2z^2-\alpha (x^2+y^2)|d\mathbf{u}=\frac{3}{4(1+\alpha )}{\int }_0^{\pi }|2{\text{cos}}^2\varphi -\alpha {\text{sin}}^2\varphi |\text{sin}\varphi d\varphi =\frac{1}{1+\alpha }(2\alpha \sqrt{\frac{\alpha }{2+\alpha }}-\alpha +1),$$

which can be shown to have a minimum of ≈ 0.57 at α ≈ 1.1.