Adaptive gain control during human perceptual choice

Abstract

Neural systems adapt to background levels of stimulation. Adaptive gain control has been extensively studied in sensory systems, but overlooked in decision-theoretic models. Here, we describe evidence for adaptive gain control during the serial integration of decision-relevant information. Human observers judged the average information provided by a rapid stream of visual events (samples). The impact that each sample wielded over choices depended on its consistency with the previous sample, with more consistent or expected samples wielding the greatest influence over choice. This bias was also visible in the encoding of decision information in pupillometric signals, and in cortical responses measured with functional neuroimaging. These data can be accounted for with a new serial sampling model in which the gain of information processing adapts rapidly to reflect the average of the available evidence.

INTRODUCTION

Optimal choices require information to be evaluated appropriately and combined without loss (Ernst and Banks, 2002; Gold and Shadlen, 2001; Wald and Wolfowitz, 1949). For example, an accurate medical diagnosis is made by considering all of the relevant symptoms, weighting each by the reliability with which it predicts a suspected condition. This intuition forms a mainstay of philosophical reflections on decision-making (Peirce, 1878) and is formalised in mathematically optimal models of choice behaviour, such as those based on serial integration of likelihoods (Ma et al., 2006; Wald and Wolfowitz, 1949; Yang and Shadlen, 2007). Empirically, this ideal observer framework accounts for choices, response latencies and neural activity observed during psychophysical tasks involving integrating noisy information over time, such as the random dot motion (RDM) paradigm (Beck et al., 2008; Gold and Shadlen, 2007).

However, unlike psychophysical judgments of stationary sensory signals, real-world choices (such as those faced by medical practitioners) often require the integration of variable, heterogenous or otherwise incommensurable information. Linear integration of highly variable information on an absolute scale poses a challenge for the nervous system, because it requires coding units to represent information across a broad dynamic range. One efficient solution is to encode information relative to the local context, by adapting the gain of neuronal firing to the range of information available over the short or long term (Barlow, 1961; Carandini and Heeger, 2012; Webb et al., 2003). For example, the visual system adapts to light levels over the diurnal cycle (Bartlett, 1965) or to stimulus contrast over the recent trial history (Greenlee and Heitger, 1988). In cortical neurons, adaptation is mediated both by habituation (Carandini and Ferster, 1997) and by normalisation mechanisms that scale the response of a neuron by that of its neighbours (Carandini and Heeger, 2012; Heeger, 1992). Beyond the sensory cortices, adaptive mechanisms may allow relative coding of utility, leaving economic choices vulnerable to the influence of local context (Louie and Glimcher, 2012; Padoa-Schioppa, 2009; Tremblay and Schultz, 1999), and provoking preference reversals and other violations of axiomatic rationality (Louie et al., 2013; Soltani et al., 2012). However, adaptive gain control has been overlooked in canonical models of information integration during perceptual choice (Bogacz et al., 2006; Ratcliff and McKoon, 2008).

Here, we describe a new serial sampling model of perceptual choice in which the gain of information processing adapts rapidly to the changing statistics of environment. We used this adaptive gain model to understand the behaviour of humans categorising a rapid stream of visual gratings on the basis of their angle of orientation. Humans performing this task exhibited two suboptimal biases in choice behaviour, visible in the impact that each grating (‘sample’) wielded over the eventual decision. Firstly, samples that carried similar decision information to their predecessor wielded greater influence on choice, even independent of their physical appearance (consistency bias). Secondly, samples that occurred later in the stream were also more diagnostic of choice (recency bias) (Tsetsos et al., 2012b). Simulations reveal that these two biases are both predicted by the adaptive gain model. Moreover, the gain of encoding of decision information in pupil diameter and in cortical brain responses followed tightly the predictions of the model. These findings provide evidence for remarkably rapid and flexible gain control during decision-making, define limits on the optimality of human judgment, and place a strong new constraint on computational models of perceptual choice.

RESULTS

Adaptive gain model

Consider a task in which observers view a fixed number of discrete samples of evidence occurring in succession (see Fig. 1b), with each sample k characterised by decision update DU_k that can vary continuously between −1 and +1. The observers’ task is to judge whether the aggregate information ∑DU_k is greater or less than zero. This ‘expanded judgment’ task is sometimes known as the Weather Prediction task (Poldrack et al., 2001; Yang and Shadlen, 2007). In this task, the optimal policy is to integrate the log-likelihood ratio associated with each sample, which is equivalent to basing choices on the sum of decision values ∑DU_k. The adaptive gain model proposes that each decision update passes through a nonlinear (sigmoidal) transfer function f:

$${\widehat{\mathrm{D}\mathrm{U}}}_{\mathrm{k}}=f({\mathrm{DU}}_{\mathrm{k}}\mid x_{\mathrm{k}-1},\sigma )$$ [eq.1]

where x_k corresponds to the point of maximal gain during processing of sample k, and σ corresponds to the shallowness of the non-linearity (step-like for σ => 0, linear for σ => ∞). A formal description of the transfer function is given in the Supplemental Information (S2).

Figure 1.

Experimental Design and Model. A. Category-level averaging task. Rapid visual streams of eight oriented Gabor patterns were presented at 4 Hz. Participants reported whether, on average, the tilt of the eight elements fell closer to the cardinal or diagonal axis. B. Schematic illustration of the adaptive transfer function for an example trial. Left panel: samples (blue dots, shaded by their order of occurrence from light to dark) are drawn from a distribution (inverted blue Gaussian) and characterised by a decision update value (position on x-axis). With each new sample, the transfer function (grey lines) shifts fractionally in the direction of the latest sample. Right panel: illustrative gain (difference on y-axis) from two samples (red lines) under two different transfer functions (light and dark grey lines). Gain is maximal when the inflection point of the transfer function coincides with the expectation of the sampling distribution (inverted blue Gaussian), i.e. given the dark grey curve. See also Supplemental Information, Fig. S1.

In the adaptive gain model, after each sample k the point of maximal gain x_k is updated according to the feature information provided by sample k using a delta rule with learning rate α:

$$x_{\mathrm{k}}=x_{\mathrm{k}-1}+\alpha \cdot \left({\mathrm{DU}}_{\mathrm{k}}-x_{\mathrm{k}-1}\right)$$ [eq.2]

Thus, after each sample k, the inflection point x_k of the transfer function f is progressively adjusted towards the current expectation of the sampling distribution (Fig. 1b). Because the gradient of the transfer function is steepest at this point, samples arriving at, or close to, this point will be most diagnostic of choice. One important corollary of this model is that across samples, observers become most influenced by information with the highest probability of occurrence. Supplementary figure S1a displays how the shape of the transfer function adapts for changes in inflection point x_k, and σ.

Finally, the output decision updates are subjected to a noisy sum with signal-to-noise ratio β and compared to a fixed category boundary falling at -β₀ (zero for the ideal observer):

$$\mathrm{P}\phantom{)}(\text{respond}>0)\phantom{(}=\Phi \left(\beta \cdot \sum _{\mathrm{k}=1}^8{\widehat{\mathrm{D}\mathrm{U}}}_{\mathrm{k}}+{\beta }_0\right)$$ [eq.3]

where P(respond > 0) corresponds to the model-predicted probability of responding that the sequence is greater than zero, and Φ( ) corresponds to the probit decision rule, i.e., the Gaussian cumulative density function. The choice of this decision rule is motivated by the idea that each sample of evidence DU_k is corrupted by additive Gaussian noise whose standard deviation relates inversely to the corresponding β parameter.

Adaptive gain model: simulations

We generated simulated streams of 8 samples of evidence (range: −1:1) and asked the model to classify them. For illustration, we began with an arbitrary set of parameters (β = 1, σ = 0.5, α = 0.5). The point of maximal gain x_k was initialised to zero and updated according to equation 2.

When decisions are made on the basis of multiple samples of evidence, decisions may rely more heavily on the information provided by some samples than others. We thus used logistic regression to characterise the impact that each sample had on binary choices made by the model (and subsequently, humans). Our regression model comprised a total of 15 predictors in addition to an intercept term. The first eight predictors encoded the decision information for each of the eight samples (DU_k) in order of occurrence, with the resulting coefficients (we call these ‘sample’ coefficients) w_k reflecting the weight that each of the 8 successive samples wielded over the choice. The subsequent predictors and resulting coefficients w_k^δ were aimed at identifying how information in samples 2-8 was up-weighted or down-weighted as a function of its disparity with previous information. To this end we defined a new quantity δ(DU)_k that encoded the absolute dissimilarity in decision information between each sample (excluding the first) and its predecessor (we set δ(DU)₀ = 0):

$$\delta {\left(\mathrm{DU}\right)}_{\mathrm{k}}=\mid {\mathrm{DU}}_{\mathrm{k}}-{\mathrm{DU}}_{\mathrm{k}-1}\mid$$ [eq.4]

Predictors 9-15 encoded the interaction between DU_k and δ(DU)_k. The coefficients associated with these predictors (we call these ‘consistency’ coefficients) would be positive if dissimilarity between successive samples led to up-weighting and negative if dissimilarity led to down-weighting.

Thus, the full regression model, including the two per-sample predictors described above, was defined as follows

$$\mathrm{P}\phantom{)}(\text{respond}>0)\phantom{(}=\Phi \left(\sum _{\mathrm{k}=1}^8\left(w_{\mathrm{k}}+w_{\mathrm{k}}^{\delta }\cdot \delta {\left(\mathrm{DU}\right)}_{\mathrm{k}}\right)\cdot {\mathrm{DU}}_{\mathrm{k}}+{\beta }_0\right)$$ [eq.5]

For the simulated data, the estimated sample coefficients w_k and consistency coefficients w^δ_k, are plotted against their corresponding sample k in Fig. 2a (left panel). These simulations reveal two clear predictions made by the adaptive gain model. First, although ‘sample’ coefficients are all positive, indicating that each contributed to the decision, those for later samples are more positive than those for earlier samples – a ‘recency’ bias (Fig. 2a, left panel; blue circles). The adaptive gain model thus predicts that later-occurring evidence will carry more weight in the decision. In the model, this occurs because the inflection point of the transfer function takes some time to converge to the mean of the sampling distribution, and so later-occurring samples will, on average, be more likely to fall in zone of maximum gain, where samples are more diagnostic of choice. Secondly, ‘consistency’ coefficients were all negative (Fig. 2a, left panel; green circles). Thus, the model predicts that observers will tend to disregard samples that differ strongly from their predecessor, because on average these will fall further from the inflection point of the adapting likelihood function. We call this a ‘consistency bias’, as it reflects the difficulty of evaluating successive samples with respect to a common standard.

Figure 2.

A. Model predictions using a simulation with arbitrary parameters. Estimated sample coefficients (blue), and consistency coefficients (green), for both an adaptive (top panel / circles) and static (bottom panel / triangles) version of the model. B. Strength of recency (top panel) and consistency (bottom panel) biases, shown for both the adaptive (α = 0.5, filled circles) and static (α = 0, filled triangles) version of the model, for a range of σ values controlling the gain of the nonlinear transfer function. C. Heatmaps showing predicted biases under a broad range of transfer function slope (σ) and learning rate (α) values. Red/yellow colouring shows positive values, blue/cyan shows negative values. Left panel: recency bias (DU_5-8-DU_1-4) is positive for learning rates greater than 1. Right panel: consistency bias is mostly negative for learning rates greater than 1.

For comparison, in Fig. 2a (right panel) we include the predictions of a ‘static’ model, which is identical in all respects except that the learning rate α is set to zero (β = 1, σ = 0.5, α = 0). This model reduces to a standard psychophysical model with a nonlinear transfer function (Naka and Rushton, 1966). As can be seen, the coefficients w_k associated with DU_k (encoding the weight given to each sample; blue triangles) are positive but do not increase over time, yielding no recency bias. Moreover, the coefficients w^δ_k associated with DU_k · δ(DU)_k (encoding the up- or down-weighting of samples 2-8; green triangles) are close to zero, revealing no consistency bias. Thus, the effects described in Fig. 2a (left panel) depend on the adaptation of the transfer function across samples.

Next, we verified that these predictions are not specific to the parameterisation chosen above. In Fig. 2c, we summarise these two biases for values of σ and α in the range −1:1, setting the signal-to-noise level (β) to 1 (adding different levels of noise had no qualitative effect on these predictions). In the left panel, we calculate the recency bias as the difference between sample coefficients for late (DU_5-8) and early (DU_1-4) samples, and plot this summary measure for differing values of σ and α. Of note, these are positive for values of α > 0 (red/yellow shading), showing that the recency bias holds whenever the transfer function is updated towards the current expectation. By contrast, they are negative (showing a primacy effect) for values of α < 0, i.e. when the transfer function is updated away from the current expectation. This ability to predict primacy and recency shows the generality of the model and potential to capture a range of different weighting profiles, under distinct parameterisations. In the right panel we show the average of the 7 consistency coefficients under different parameterizations. Similarly, these are all negative for values of α > 0 (blue/cyan shading). The adaptive model displays both recency and consistency biases for a range of σ values, maximal as σ approaches 0 (i.e. when the transfer function is most step-like), whereas the static model fails to display either of these biases (Fig 2b). Together, these simulations show that the recency and consistency biases do not depend on specific values of σ or α (α > 0), and that both biases can be reversed via the introduction of a negative learning rate, which shifts the point of maximum gain away from the expectation of the sampling distribution.

Experiment 1: human behavioural data

We tested the predictions of the adaptive gain model by asking 23 healthy human observers to classify a stream of eight visual gratings (presented at 4 Hz) as more ‘cardinal’ or ‘diagonal’, providing feedback according to their aggregate decision update value (Fig. 1a). The decision update for each sample k (the quantity that we term DU_k) depended nonlinearly on angle of orientation, with gratings whose orientation was closer to 0° or 90° providing evidence for one response, and those closer to 45° or −45° contributing evidence in favour of the opposite response (Fig. S1b and Supplemental Information). This task has the appealing property that decision updates are orthogonal to perceptual information, because very different angles (e.g. 10° and 80°) offer the same decision information, allowing us to distinguish any sequential effects in decision-making from low-level perceptual priming (Wyart et al., 2012a) (the independence of DU_k from perceptual information is shown in Fig. S1b). Participants responded with a key press following presentation of all eight samples, allowing us to test (using the regression-based approach described in eq 5) for the presence of recency and consistency biases predicted by the adaptive gain model.

Using the regression approach described above to assess the impact that each sample had on human decisions, coefficients were less positive for early (k < 5) than late (k > 4) samples (Fig. 3a, left panel, blue circles; t₍₂₂₎ = 5.38, p < 0.001). Consistency coefficients for items 2-8 were on average negative-going (Fig.3a, left panel, green circles; t₍₂₂₎ = 2.05, p < 0.05). Thus human participants showed both the recency and consistency biases predicted by the model. Furthermore, the human data also reveal the existence of a ‘belief compatibility’ bias, reflecting the compatibility with the running average of the sequence, which displays the same qualitative pattern as the consistency bias, and which is also predicted by the adaptive gain model (see Supplemental Information for details and Fig. S3). Additionally, the recency and consistency biases displayed by human participants were present in both early and late periods of the experiment (Fig. S3), and did not depend on knowledge of the sequence length, as demonstrated in an additional behavioural experiment (Fig. S3).

Figure 3.

Behavioural results and model predictions. A. Experiment 1 B. Experiment 2. Regression coefficients from behavioural data (filled colour circles), together with adaptive model predictions (lines), estimated using a multivariate logistic regression of choice against a linear combination of factors. Blue dots and lines: sample coefficients w_k for the eight sample decision updates (w_k). Green dots and lines: consistency coefficients w^δ_k indicating the influence of disparity between samples. Solid lines plot model predictions based on analytically derived parameter values, fitting against choice data. Dashed lines plot model predictions based on an exhaustive search over parameter space, minimising the mean squared error between behavioural and model parameter estimates. Error bars indicate +-1 S.E. See also Supplemental Information, Fig. S3.

We fit the adaptive gain model to the data by searching for the parameterisation that best predicted human choices given the input sequence (values of DU_k), i.e. maximising the model log-likelihood corresponding to the probability of a model using a set of generative parameters β, σ, α to have produced the observed behavioural data. Details of this Bayesian model fitting approach are described in full in the Supplemental Information. Model choices obtained using the resulting maximum likelihood parameters (β = 0.63, σ = 0.67, and α = 0.26) were then subjected to the same regression analyses as human data, and are overlaid on Fig. 3a (solid blue and green lines). As can be seen, the model is able to capture the recency and consistency biases both qualitatively and quantitatively. The regression analysis yields 15 parameter estimates (Fig. 3a) and model predictions fall within the 95% confidence intervals produced by the human behavioural data for all but four of them. Additionally, we searched exhaustively over different values of the three parameters σ, β and α for the model parameterisation that minimised the difference with the human regression coefficients (dashed blue and green lines in Fig. 3a). The resulting parameters (β = 0.7, σ = 0.63, and α = 0.2) provided an equally good fit to the human data.

The statistically significant recency and consistency biases in human behaviour militate in favour of the adaptive gain model over its static counterparts. However, to compare these models more formally, fitting the static model to the data using the same maximum likelihood criteria described above produced a poorer fit compared to its adaptive model counterpart (shown in Fig. S3 Supplemental information) even when the extra parameter was taken into account by using the Bayesian Information Criterion (BIC) (see Experimental Procedures). In addition, directly comparing the residual mean squared error (MSE) between behavioural parameter estimates for each subject and model predictions, we found that the adaptive model was a significantly better fit to the data than its static counterpart (t₍₂₂₎ = 4.12, p < 0.0005). This comparison shows that the adjustment of the slope of the transfer function alone is not sufficient to account for the biases observed in human choice behaviour. The failure of the static model to account for human performance also demonstrates the suboptimality of integration in our task, because the static model describes the performance of a Bayesian ideal observer with or without input noise (Fig. S2 and text).

Experiment 1: pupillometry

Traditional theories (Aston-Jones and Cohen, 2005) and recent evidence (Cohen and Aston-Jones, 2005; Eldar et al., 2013; Gilzenrat et al., 2002; Nassar et al., 2012) have pointed to pupil diameter as a correlate of the gain of information processing during decision-making. Pupil diameter is partly driven by arousal-linked changes in the neural response of the locus coeruleus, which in turn modulates cortical activity via diffuse noradrenergic projections (Usher et al., 1999). We thus turned to pupillometric data recorded during experiment 1 to investigate how moment-by-moment changes in pupil diameter following the presentation of sample k were predicted by its decision information DU_k, and how this correlation was modulated by consistency between current and previous sample δ(DU)_k.

Pupil diameter changes slowly in response to cognitive and attentional factors, typically peaking 1-2 seconds post-stimulus, but its sub-second fluctuations can be disambiguated using a linear regression approach similar to that often employed to model the sluggish BOLD response (Nassar et al., 2012; Wierda et al., 2012; Zylberberg et al., 2012). Having successfully recorded pupil diameter from 20 of the 23 participants we created a regression model in which the pupil response at each time point t following sample k was modelled as a linear combination of ∣DU_k∣ (reflecting the strength of the current evidence sample, associated with coefficients w_k,dt) and ∣DU_k∣ · δ(DU)_k (reflecting how the neural encoding of evidence strength depends on its consistency with the previous evidence sample, associated with coefficients w_k,dt ^δ):

$$\text{pupil}\phantom{)}({\mathrm{t}}_{\mathrm{k}}+\mathrm{dt})\phantom{(}=\left(w_{\mathrm{k},\mathrm{dt}}+w_{\mathrm{k},\mathrm{dt}}^{\delta }\cdot \delta {\left(\mathrm{DU}\right)}_{\mathrm{k}}\right)\cdot \mid {\mathrm{DU}}_{\mathrm{k}}\mid +w_{\mathrm{dt}}^{\mathrm{sum}}\cdot \mid \sum _{\mathrm{j}=1}^8{\mathrm{DU}}_{\mathrm{j}}\mid +{\in }_{\mathrm{dt}}$$ [eq.6]

where pupil(t_k + dt) is the normalized and base-lined pupil size at time dt following the onset of sample k (the final term encodes the mean decision information on that trial, ensuring that fluctuations in pupil diameter reflect sample-specific changes in DU_k and not the global difficulty of the trial). The coefficients of this regression across time provide the time course of encoding of decision information in pupillometric signals (w_k,dt) and the modulation of this encoding by the consistency of decision information contained in consecutive samples (w^δ_k,dt). The evidence contained in the first sample (DU₁) was excluded from the analysis to avoid interference from possible transient responses at the beginning of the sequence, unrelated to the decision update. These encoding functions, averaged across samples, are plotted in blue and green respectively in Fig. 4b. Pupil diameter tended to grow with increasing decision information, with a peak in encoding at about 1000 ms post-stimulus (blue trace; maximum significance at 1140 ms after sample onset, t₍₁₉₎ = 3.5, p < 0.001). Critically however, and consistent with behavioural findings, this encoding was negatively modulated by the difference to the previous sample δ(DU)_k – samples whose predecessor provided very different decision information were encoded more weakly in pupillary signals. This is shown by plotting the coefficients (w^δ_k,dt) associated with DU_k · δ(DU)_k, which diverged negatively from zero (Fig. 4b, green trace; maximum significance at 2000ms after sample onset, t₍₁₉₎ = 3.0, p < 0.004). In other words, pupillary responses track fluctuations in the strength of decision evidence, and the reduced gain of information processing when evidence is inconsistent with its predecessor, that mirror those observed in behaviour, and are predicted by the adaptive gain model. Demonstrating this effect another way, in Fig. 4c we plotted the encoding of DU_k in pupil responses separately for samples with small and large values of δ(DU)_k, i.e. that were similar/dissimilar to the previous sample based on a median split. Encoding was stronger when samples were more similar (full blue line) than when they were different (faded blue line).

Figure 4.

Pupil dilation in response to decision information. A. Pupil dilation over the course of a trial expressed as the proportion change relative to a pre-sequence baseline level. Vertical lines represent the onset of the 8 decision-relevant samples. B. Regression coefficents showing the encoding of decision information in pupil diameter (eq. 6) for the time window −500 to +2500ms relative to the onset of each sample. Blue curves - coefficents for decision update w_k. Green coefficients for disparity interaction w^δ_k. Each curve reflects coefficients averaged across samples 2 – 8. Coloured horizontal bars indicate regions of significance against baseline at the level p<0.05 uncorrected (light) and corrected (dark) for multiple comparisons. C. Pupil dilation encoding timecourse of decision update DU_k divided into conditions of either small or large δ(DU)_k – i.e. large or small shifts in decision space between the preceding (k-1) and current (k) sample – divided on the basis of a median split on δ(DU)_k. Coloured horizontal bars indicate regions of significant difference between low and high δ(DU)_k at p<0.05 uncorrected (light) and corrected (dark) for multiple comparisons. D. Pupil encoding timecourse of decision update DU_k, for early (position 2-4) vs late (position 5-8) occurring samples. See also Supplemental Information, Fig. S4.

Previous models have accounted for recency effects in perceptual categorisation by assuming that integration is leaky, with information dissipating gradually across the choice period (Usher and McClelland, 2001; Wang, 2002). Our model of behaviour provides an alternative explanation for the recency bias, suggesting that it is (at least in part) due to dampened information gain for earlier samples, rather than exclusively by a subsequent leak of the information. If this is indeed the case, then momentary encoding of DU_k in pupil_k,t should be heightened for later samples. We thus averaged encoding curves for early (samples 2-4) and late (samples 5-8) occurring samples separately (see Experimental Procedures), and plotted them separately (Fig. 4d). Statistical comparison indicated that they diverged reliably at about 1 s post-stimulus, with stronger encoding for later samples (t₍₁₉₎ = 1.78, one-tailed p < 0.05), as predicted by the adaptive gain model.

Experiment 2: human behavioural data

Changes in pupil diameter offer a proxy for variations in the gain of cortical processing, but a more direct measure of brain activity can be obtained using functional neuroimaging. We thus asked a new cohort of 18 participants to perform the same task whilst undergoing functional magnetic resonance imaging (fMRI). Once again, observers viewed streams of 8 visual gratings presented at 4 Hz, and judged whether the angles of orientation were (on average) more ‘cardinal’ or more ‘diagonal’. Regression coefficients for w_k and w^δ_k are shown in figure 3b. As can be seen, behavioural data once again revealed a recency bias (t₍₁₈₎ = 3.9, p < 0.001) and a consistency bias (green circles; t₍₁₈₎ = 4.6, p < 0.001), similar to those observed in experiment 1. The best fits to human choices (solid lines) and regression parameters themselves (dashed lines) reveal that the adaptive gain model can approximate these very closely (parameters of the best-fitting model were β = 0.5, σ = 0.92, and α = 0.65). Model predictions for 13 out of 15 parameter estimates fell within the 95% confidence intervals of the behavioural data. Once again the adaptive model outperformed its static counterpart, in which the learning rate was fixed at zero. Replicating the results of experiment 1, the static model demonstrated significantly larger residuals (t₍₁₈₎ = 4.67 p < 0.0002) and poorer fits to the data even after taking into account the extra parameter using the BIC.

Experiment 2: fMRI data

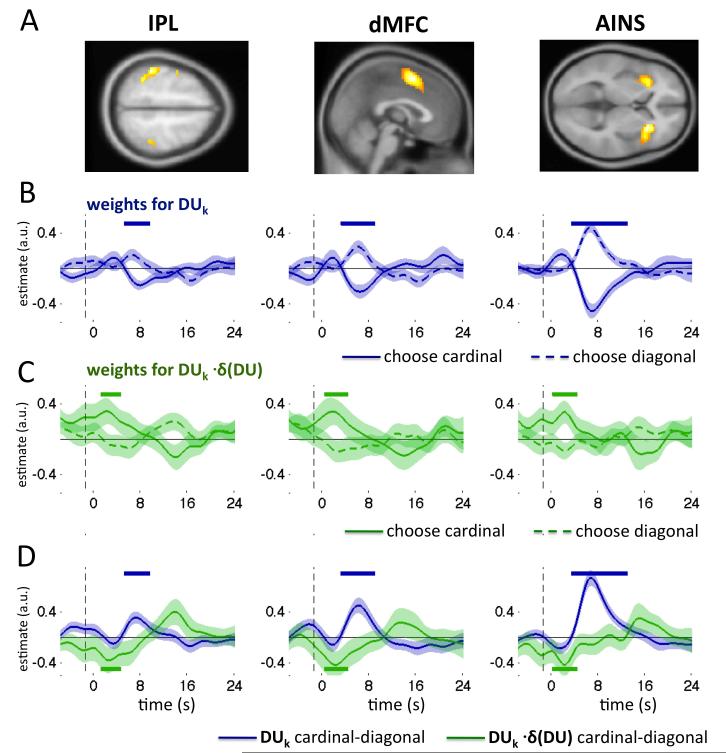
The main effect of stimulus onset in experiment 2 evoked positive-going BOLD responses in a number of cortical regions, including visual cortical zones, the lateral parietal and prefrontal cortices, the pre-supplementary motor area and anterior insular cortex (Fig. S5 and Tables S1-S3, Supplemental Information). The main purpose of our experiment was to determine how BOLD signals encoded information provided by each stimulus (i.e. DU_k) and how this encoding was modulated by the consistency between current and previous sample δ(DU)_k. To this end, we focussed on three cortical clusters that have been implicated in perceptual category judgments in previous neuroimaging studies (Filimon et al., 2013; Grinband et al., 2006; Heekeren et al., 2008; Ho et al., 2009; Liu and Pleskac, 2011): the lateral parietal cortex (falling principally on the inferior parietal lobule; IPL); a region of the dorsal medial prefrontal cortex comprising mainly the pre-supplementary motor area stretching inferiorly to the anterior cingulate cortex (dMFC); and the anterior insular cortex (figure 5a, left, middle and right panels respectively).

Figure 5. fMRI data.

A. Clusters selected as regions of interest: IPL, dMFC and AINS, rendered onto axial/sagittal slices of the template brain of the Montreal Neurological institute at a threshold of p < 0.00001 uncorrected. B. Encoding of DU_k (i.e. evidence favouring cardinal) in BOLD signals as a function of time in seconds (x-axis) for trials on which cardinal (solid blue line) or diagonal (dashed blue line) were chosen. Shading around each line shows standard error of the mean. Upper blue bars denote timepoints where encoding curves diverge significantly, at p<0.05. C. As for B, but plotting consistency coefficients w^δ_k for BOLD signals. Green bars denote significant timepoints. D. Plot of the difference between encoding for each choice in A and B. Blue lines: divergence between encoding of DU_k for the two choices. Green lines: divergence between encoding of DU_k · δ(DU)_k for the two choices. See also Supplemental Information, Fig. S5 and Tables S1-S3.

We analysed imaging data for each region using a comparable approach to that adopted for the eyetracking data: extracting fMRI timeseries aligned to stimulus onset for each trial allowed us to regress the decision information for each sample DU_k onto the post-stimulus BOLD signals, yielding one parameter estimate per sample for each timepoint following the stimulus. We then averaged these timecourses across samples, and plotted separately for trials on which each of the two options (cardinal vs. diagonal) was chosen (blue lines in figure 5b; see Experimental Procedures). The resulting curves plot the extent to which decision information (e.g. relative evidence favouring cardinal over diagonal) was encoded in BOLD signals, both when participants chose cardinal and when they chose diagonal.

$$\text{BOLD}\phantom{)}({\mathrm{t}}_{\mathrm{k}}+\mathrm{dt})\phantom{(}=\left(w_{\mathrm{k},\mathrm{dt}}+w_{\mathrm{k},\mathrm{dt}}^{\delta }\cdot \delta {\left(\mathrm{DU}\right)}_{\mathrm{k}}\right)\cdot {\mathrm{DU}}_{\mathrm{k}}+w_{\mathrm{dt}}^{\mathrm{sum}}\cdot \mid \sum _{\mathrm{j}=1}^8{\mathrm{DU}}_{\mathrm{j}}\mid +{\in }_{\mathrm{dt}}$$ [eq.7]

This approach parallels that frequently employed to identify regions encoding action values in reward-guided decision tasks (Boorman et al., 2009). In equation 7, BOLD(t_k + dt) is the normalized and base-lined BOLD response in each region at time dt following the onset of sample k. The resulting coefficients are shown in figure 5b. Strong encoding of DU_k as a function of choice was observed in each of the three regions of interest, as demonstrated by the divergence between w_k,dt in BOLD signals for trials with opposing choices (peak statistics, at 8-10 s post-stimulus: IPL, t₍₁₈₎ = 2.78, p < 0.007; dMFC t₍₁₈₎ = 4.06, p < 0.001; AINS t₍₁₈₎ = 7.22, p < 0.000001; blue traces and bars in fig. 5b). In other words, BOLD signals in these regions encoded decision-relevant activity in a fashion that predicted choices.

Next, building upon the analyses described above, we assessed how the encoding of DU_k in BOLD signals was modulated by the recent history of stimulation. To this end, we estimated regression coefficients for the interaction between DU_k and δ(DU)_k, i.e. the extent to which this encoding of DU_k was heightened or dampened according to consistency with the previous sample. Coefficients for this regression were reversed with respect to those for w_k,dt (green traces in Fig. 5c), consistent with the negative coefficients observed for w^δ_k,dt in the behavioural and eyetracking data. This finding thus reveals a reliable mitigation of DU_k encoding in all three regions when information diverges between samples (peak statistics, at 2-5 s post-stimulus: IPL, t₍₁₈₎ = 1.87, p < 0.05; dMFC t₍₁₈₎ = 2.02, p < 0.03; AINS t₍₁₈₎ = 2.38, p < 0.02; green bars in Fig. 5c). Indeed, plotting the relative encoding (for the two responses) of DU_k and DU_k ·δ(DU) in the two choices revealed reliable positive- and negative-going coefficients that matched those obtained for behavioural data (blue and green bars in Fig. 5d). In other words, encoding of decision information in the BOLD signal is modulated by the consistency between current and previous decision information.

Experiment 3. Reanalysis of EEG recordings

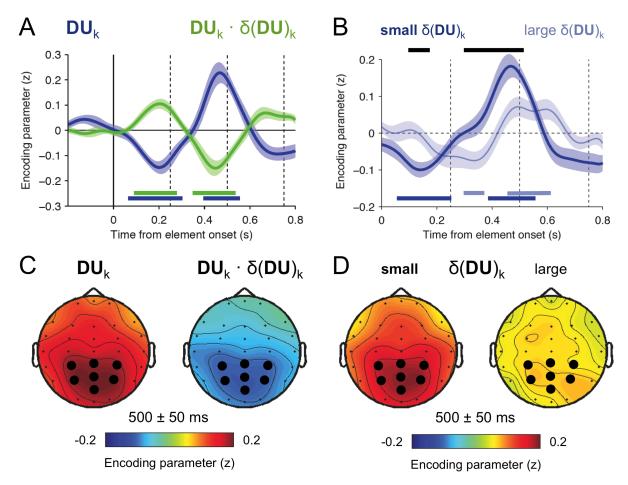
In an earlier published study (Wyart et al., 2012a), we recorded EEG data whilst participants performed the same cardinal/diagonal task. In these data, DU_k was encoded in EEG signals peaking at 500ms post-stimulus over the parietal cortex. These data afforded the opportunity to test how the encoding of DUk was modulated by δ(DU)_k. We found strong modulation between 400 and 500ms post-stimulus (t₍₁₄₎ = 4.7, p < 0.001), consistent with the encoding timecourse for DU_k. These results are described in figure 6 and Supplemental information figure S6.

Figure 6.

EEG response to decision information. A. EEG encoding timecourse of decision information. Blue - decision update coefficients w_k. Green – disparity interaction coefficients w^δ_k. Curves display parameter coefficients from the multivariate regression of EEG signal amplitude against a linear combination of decision factors (eq. S4) for the time window −200 to +800ms relative to the onset of each sample. Each curve reflects coefficients averaged across samples 2 – 8. Coloured horizontal bars indicate regions of significance at the level p<.05 uncorrected for both w_k (blue) and w^δ_k (green). B. Timecourse of decision update DU_k divided into conditions of either small (dark blue) or large (light blue) inter-item disparity across decision space (δ(DU)_k), divided on the basis of a median split. Coloured horizontal bars indicate significance against baseline and black bars indicate regions of significant difference between low and high δ(DU)_k, both at p<0.05 uncorrected. C. EEG encoding topographies of decision information at 500 ms following the corresponding element. Blue - decision update DU_k. Green - disparity interaction DU_k · δ(DU)_k. Large dots indicate parietal electrodes of interest (CP3, CPz, CP4, P3, Pz, P4, POz). D. EEG encoding topographies for DU_k divided into conditions of either small (left) or large (right) inter-item disparity across decision space, divided on the basis of a median split. Same conventions as in C. See also Supplemental Information, Fig. S6.

Experiment 4. Manipulation of presentation order

Statistical comparison strongly supported the view that the gain function adapts rapidly over time. Nevertheless, we decided to pit the static and adaptive versions of the model against each other in a further experiment for which the two models made different predictions. We created a version of the cardinal/diagonal discrimination task on which each trial consisted of just 4 samples, with 2 favouring cardinal and 2 favouring diagonal. This allowed us to systematically manipulate the order of presentation of the samples drawn from either category (cardinal [C] or diagonal [D]) in three discrete conditions: alternating (C-D-C-D or D-C-D-C), pairs (C-C-D-D or D-D-C-C) and sandwich (C-D-D-C or D-C-C-D). The adaptive and static gain models make very different predictions about how the weights associated with decision information on samples 1-4 should vary as a function of the three conditions, with static gain predicting no difference as a function of position in any of the three conditions (Fig. 7b, blue dots), and the adaptive gain model predicting different patterns in each (Fig. 7a, red dots). These predictions are shown in Fig. 7a alongside the values obtained from a new cohort of human participants (n = 16) performing the task (filled grey bars). Comparing the mean squared error (MSE) between behavioural parameter estimates and those for the two models produced significantly better fits for the adaptive compared to the static model (t₍₁₄₎ = 3.0, p < 0.001). Strikingly, the adaptive model is able to capture the large shifts in weighting associated with each condition (Fig. 7a). Subjecting these 4-item task data to the same analyses as experiments 1 and 2, we also observed the same recency (t₍₁₄₎ = 2.9, p < 0.02) and consistency (t₍₁₄₎ = 3.9, p < 0.003). See also Supplemental Information Fig. S7, for further behavioural results and model predictions from the 4-item task.

Figure 7.

Adaptive (A) and static (B) model predictions for different sequence classes. Decision weighting profiles based on four item sequences (experiment 4), estimated using a multivariate logistic regression of choice against a linear combination of the four decision updates. Behavioural weighting coefficients (filled grey bars) are displayed for three cardinal (C) - diagonal (D) sequence types, alternating (C-D-C-D or D-C-D-C), pairs (C-C-D-D or D-D-C-C) and sandwich (C-D-D-C or D-C-C-D).. Adaptive gain model parameter estimates from twenty separate runs are plotted for both adaptive (A, red circles) and static (B, blue circles), based on exhaustively searching over parameter space, minimising the MSE between behavioural and model parameter estimates. See also Supplemental Information, Fig. S7.

DISCUSSION

We used impact analyses in conjunction with an expanded judgment task and functional neuroimaging to assess how humans weighted decision-relevant information arriving in a rapid stream. We observed evidence for two suboptimal biases. Firstly, humans are unduly swayed by the samples that occurred shortly prior to choice (recency bias). Secondly, their decisions are less influenced by samples that carry dissimilar decision information to their predecessor (consistency bias). These two biases, and their neural expression in pupillometric and imaging data, are accounted for by a model in which the gain of information processing is adapted rapidly – within the timespan of a single trial – to coincide with the expectation of the distribution from which information is sampled. This ‘adaptive gain’ model thus describes a gain control mechanism by which categorical inferences become tuned to local statistics of decision-relevant information, much as low-level sensory systems maximise gain by adapting to background levels of stimulation (Bartlett, 1965; Carandini and Heeger, 2012; Fairhall et al., 2001).

The adaptive gain model makes two critical assumptions. The first is that categorical responses involve a nonlinear transformation of decision information. This assumption is common to standard psychophysical models of detection (Naka and Rushton, 1966) and cognitive models of categorical perception (Shepard, 1987; Tenenbaum and Griffiths, 2001), but has not hitherto been a prominent feature of the serial sampling approach. In categorisation, the well-known heightened sensitivity of observers close to a category boundary, and the consequent emergence of prototypical representations (perceptual ‘magnet’ effects) is naturally modelled with a sigmoidal transfer function of the sort adopted here (Bonnasse-Gahot and Nadal, 2008; Feldman et al., 2009). We have previously shown that perceptual averaging of multiple, simultaneously-occurring visual items is best described with a model in which decision information is transformed sigmoidally, leading to ‘robust averaging’ – reduced impact for samples of evidence that diverge from the central tendency of the information (de Gardelle and Summerfield, 2011).

The second assumption is that the point of maximal gain of evidence processing (i.e the steepest portion of the nonlinear transfer function, f) adapts to the local statistics of stimulation. As this happens, divergent or otherwise surprising evidence will tend to fall in a portion of decision space with lower gain (i.e. the shallower part of the transfer function), and thus contribute more weakly to choice. It should be noted that expected evidence will lead to a weaker transduced signal in absolute terms, consistent with the finding that expected stimuli elicit globally reduced neural signals (Summerfield and Egner, 2009; Summerfield et al., 2008; Todorovic et al., 2011). The biases that we report are not merely due to perceptual priming, because our cardinal/diagonal task carefully orthogonalises the magnitude of the perceptual update (perceptual similarity between adjacent samples) and decision update (difference in decision value between two adjacent samples).

The adaptive gain mechanism ensures that information that confirms (rather than disconfirms) the current belief will fall at the point of maximal gain and come to have more impact on the eventual choice. This furnishes the prediction – recently confirmed – that observers should exhibit heightened sensitivity to information that is more likely to occur, even when it is cued as irrelevant to the task at hand (Wyart et al., 2012b). Moreover, the stronger gain of processing of belief-congruent evidence provides a mechanism for understanding the confirmation bias, by which belief-consistent evidence is given more credence, with inconsistent evidence often downplayed or ignored (Nickerson, 1998). One study in which participants integrate discrete binary samples of evidence reported that belief-consistent evidence tends to be under-rather than over-weighted, but as noted by the authors of that study, this may reflect the fact that once a criterial level of evidence was achieved (i.e. 3 out of 5 successes), the decision could already be made with full certainty (de Lange et al., 2011). During speeded decision-making, the presence of a confirmatory bias may help to bring decisions about weak or ambiguous evidence to a close, avoiding prolonged deliberation and contributing to a maximisation of overall reward rate (Bogacz et al., 2006; Deneve, 2012; Drugowitsch et al., 2012).

In the current experiment, we provide evidence that gain adaptation occurs within the timeframe of a single trial. This means that information occurring at the end of the trial is (on average) processed with higher gain than information presented early on. Our model thus provides one explanation for the recency bias, whereby later-occurring evidence often holds more sway over decisions, at least over the timescale of integration required here (Ossmy et al., 2013). However, whereas past accounts of recent have invoked a forgetting process by which information is lost over time (Usher and McClelland, 2001), the adaptive gain model predicts that early samples should be processed with weaker gain at the point of occurrence. Accordingly, we found that pupillary signals, proposedly a generic index of the gain of cortical processing, encoded decision information more steeply for later relative to earlier samples. Nevertheless, our model does not rule out leak as an additional contributor to the recency bias, in particular where integration occurs over several seconds (Tsetsos et al., 2012a).

Psychophysical judgments made by well-trained humans and other primates have frequently been found to approach the standard of an ideal observer, i.e. one whose performance is limited only by the variability in the stimulus (Bogacz et al., 2006; Gold and Shadlen, 2001; Ma et al., 2006). Our model predicts that when input signals have low variance, for example when the evidence is a fixed quantity corrupted by noise, then performance will approach optimality. This occurs because all of the evidence falls within the narrow range for which gain is maximal, where the transfer function is approximately linear. In other words, our model makes the strong prediction that optimality in perceptual choice will depend directly on the variability of the input signal. This may help explain an long-standing discrepancy in the decision sciences, as to why humans appear to perform optimally in perceptual classification tasks (Bogacz et al., 2006) but are often inconsistent in their subjective preferences or economic choices (Kahneman et al., 1982; Vlaev et al., 2011). Unlike most psychophysical judgments, real-world choices often involve comparisons between dissimilar goods or incommensurable options, which the adaptive gain model predicts will be deviate from optimality. Indeed, recent theories have appealed to another form of adaptive control – divisive normalisation – as a source of contextual bias driving decoy effects and other preference instabilities (Louie et al., 2013). More generally, adaptive gain mechanisms may have evolved to ensure that, in world in which the decision-relevant information can change rapidly and unpredictably, the most probable information is processed with the highest gain, sacrificing optimality for computational efficiency (Carandini and Heeger, 2012). We have previously shown that rapid adaptation to the information on the previous trial guides decision-making when classification judgments are on nonstationary information (Summerfield et al., 2011).

One plausible mechanism by which adaptive gain control could be implemented is by adjustments to the tuning of neurons coding for expected information (Eldar et al., 2013). In the Supplemental Information (S2) we describe how our psychophysical model could be implemented in a biologically plausible fashion as population coding model in which the tuning profile across a population of neurons is adjusted in so that the tuning of neurons sensitive to expected information is sharpest. In this population model, the consistency and recency biases fall out of a very simple assumption: that sensory tuning, hence the gain with which the next sample is processed, is determined by the current state of activation in a subsequent layer that integrates sensory information in an additive fashion. This model not only predicts both the consistency and recency biases, but also correctly predicts that the encoding of decision information (e.g. the correlation between DU_k and neurophysiological measures described here) will depend positively on the gain of information processing, and that fulfilled predictions per se would elicit weaker neural responses, because a more select group of sharply tuned neurons is activated by the input (Wiggs and Martin, 1998). This theory is consistent with the repeated finding that BOLD signals to expected information tend to be suppressed, rather than enhanced (Summerfield and Egner, 2009; Summerfield et al., 2008; Todorovic et al., 2011) as well as with a recent report that despite this ‘expectation suppression’, more probable signals can be decoded with heightened fidelity from appropriate visual regions (Kok et al., 2012). As such, our model bears close resemblance to ‘predictive coding’ accounts of perception, in which expectations constrain the space over which perceptual inferences can be made (Friston, 2005).

In conclusion, we describe evidence for adaptive gain control during human decision-making. Adaptive gain control provides a mechanism for neural systems to adjust their range of sensitivity to suit the information that is most likely to occur in the current environment. During serial integration of decision information, this mechanism prompts us to give most credence to expected information, and to downplay that which is outlying or unanticipated. This leads to maximal sensitivity to likely events, but gives rise to previously-described suboptimalities, such as the recency bias and consistency bias. This work unites two literatures on priming and decision-making and provides a framework for understanding decision-making in a changing world.

EXPERIMENTAL PROCEDURES

Participants

Healthy human volunteers (n=23, n=18, n=16, and n=16 in experiments 1-4 respectively) gave informed consent to participate in the study. All reported normal or corrected-to-normal vision and no history of neurological or psychiatric impairment.

Task

In all four experiments, participants viewed a stream of successive, centrally presented Gabor patches (‘samples’) with variable angle of orientation, and judged whether, on average, the orientation of the Gabors fell closer to the cardinal axes or diagonal axes. Each sample k was assigned a decision value DU_k which mapped orientation onto decision value according to a “sawtooth” function, whose output ranged between +1 (−90°, 0°, +90°) and −1 (−45°, +45°) with decision values of zero at the category boundaries (22.5°, 67.5°, 112.5°, and 157.5°). The sawtooth function is shown in Supplemental information figure S1. Participants received fully informative feedback according to whether they correctly classified the stream as more cardinal (i.e. where ∑DU_k > 0) or diagonal (where ∑DU_k < 0).

Stimuli

Each stream consisted of 8 samples (exp 1-3) or 4 samples (exp 4). Each sample was a high contrast Gabor patch (spatial frequency 2 cycles per degree; standard deviation of Gaussian envelope 1 degree) presented against a uniform grey background. Samples were presented with an onset asynchrony of 250 ms (i.e. at 4 Hz). Sequences were preceded and succeeded by a mask created from the linear superposition of the four cardinal and diagonal Gabor patterns.

We collected response data differently in experiments 1/4 and 2/3. In experiments 2 and 3, responses followed the onset of a centrally-occuring green dot that succeeded the backward mask, and were made with a button (exp 2) or key (exp 3) press with the left or right hand (category-response mappings were counterbalanced across participants). Auditory feedback consisted of an ascending (400 Hz/800 Hz, 100 ms/100ms) or descending (800 Hz/400 Hz, 100 ms/100ms) tone signalling correct and incorrect responses respectively that onset 250 ms after response. In experiments 1 and 4, we used a different approach in which participants reported the integrated decision value on a continuous scale, allowing precise feedback to be administered. Responses were cued by a screen divided vertically at the centre, and the response was made by clicking the mouse on the left or right of the screen at a position corresponding to the integrated decision value. Immediately following response, visual feedback in the form of a vertical red line was presented along the scale indicating the position corresponding to the objective average of all elements. Trials were separated by a blank inter-stimulus interval of 1500 ms (exp 1 and 3), 1500-4500 ms (exp 2), or 600 ms (exp 4). Experiments consisted of 400 trials in blocks of 50 (exp 1 and 4), 450 trials in blocks of 90 (exp 2), or 672 trials in blocks of 96 (exp 3).

Design

In experiments 1 and 4, samples were drawn from one of two bimodal distributions, thereby ensuring an equal number of samples with more cardinal and more diagonal orientation. Bimodal distributions were shifted positively or negatively by a fixed value to control whether the sum of decision values ∑DU_k favoured a cardinal or diagonal response. In experiment 2, sample orientations were drawn from one of two sigmoidal distributions over decision values (range −1 to +1). In experiment 4, the order of presentation of the 4 Gabors was manipulated to create three discrete conditions: alternation (i.e. C-D-C-D or D-C-D-C, 50% of trials), pairs (C-C-D-D or D-D-C-C, 25% of trials) and sandwich (C-D-D-C and D-C-C-D, 25% of trials), where C and D represent samples favouring the cardinal or diagonal categories. Because decision values were sampled from normal or bi-model distributions, orientations (perceptual values) were also drawn from distributions containing a subset of all possible angles.

Apparatus and recordings

Visual stimuli were generated, and behavioural responses recorded using Psychophysics-3 Toolbox (Brainard, 1997; Pelli, 1997) in addition to custom scripts written for MATLAB (The MathWorks, Natick, MA, USA). Data from experiment 2 were obtained in the fMRI scanner. Images were rear-projected into the scanner bore via a custom shielded Samsung 40 inch LCD screen (LTA400HF) with a 60 Hz refresh rate. For all other experiments observers viewed a standard cathode ray tube (CRT) monitor set to a display refresh rate of either 85Hz (exp 1) or 60Hz (exp 3 and 4) with a resolution of 1024 × 768, from a distance of 60 - 80cm in a darkened room.

Eye-tracking

In experiment 1 pupil diameter was measured continuously throughout the experiment using an Eyelink 1000 eye-tracking system, recording monocularly at a sampling rate of 250Hz. Calibration was performed twice, both before the start of the experiment and after 200 trials. Subjects were instructed to minimize head movement with the use of a chinrest. Data from three subjects was discarded due to poor calibration.

Preprocessing and encoding analysis of pupillometry data

Blink artifacts were removed from the data using a custom interpolation method in which spline fitting was performed based on pupil diameter 200ms prior to blink onset, and 200ms after offset. Subsequently, high frequency components were removed (data smoothing) using a 50ms sliding window. Pupil measures were z-scored within trials, expressed relative to a pre-trial baseline period (−280 to 0ms relative to sequence onset), and trimmed using cutoffs of ±3. Finally, the data was z-scored across trials before being entered into a general linear model (GLM). Three regressors were included in the GLM (equation 7, main text): the decision update DU_k for each sample, the mean DU for the 8 samples comprising each sequence, and the interaction between DU_k and the absolute difference in decision update between each sample and its predecessor DU_k ·δ(DU_k). Regressions were performed on a sample by sample basis for pupil measures from −500 to +2000ms relative to sample onset. Following this, parameter estimates were then averaged across samples. Significance testing of the pupil encoding curves was carried out using a mass univariate approach, corrected for multiple comparisons using a nonparametric random permutation test: after point estimate t-values had been obtained at all timepoints, values of DU_k and dilation traces were shuffled 1000 times to produce randomly paired datasets. We then performed t-tests across the entire sequence time-course (−500 to 2000ms peristimulus time, in steps of 20ms) for each shuffled dataset, recording the maximum test statistic from the entire time-course. Point estimate statistics that fell within the 95th percentile (p < 0.025 or p > 0.975) of this null distribution based on shuffled values, were deemed significant. For further detail on the procedure see (Summerfield and Mangels, 2005).

Preprocessing and analysis of fMRI data

Images were acquired in a 3 Tesla (Siemens TRIO) with a 32 –channel head coil using a standard echo-planar imaging (EPI) sequence. Images were 64×64×36 volumes with voxel size 3×3×3 mm; acquired with a 2s repetition time (TR) and 30ms echo time. Five runs of 300 volumes were obtained, each of which lasted approximately 10 minutes and corresponded to one experimental block of 90 trials.

Preprocessing of the imaging data was carried out in SPM8 and included correction for head motion and slice acquisition timing, followed by spatial normalization to the standard template brain of the Montreal Neurological Institute (MNI brain). Images were resampled to 4mm cubic voxels and spatially smoothed with a 10mm full width at half-maximum isotropic Gaussian kernel. A 128s temporal high-pass filter was applied in order to exclude low-frequency artifacts. Temporal correlations were estimated using restricted maximum likelihood estimates of variance components using a first-order autoregressive model. The resulting nonsphericity was used to form maximum likelihood estimates of the activations.

All statistical analyses were first conducted at the level of individual subjects and the resulting estimates were carried forward for a second stage involving group-level inferences. We identified regions of interest (ROIs) using a simple design matrix in which a finite impulse response (FIR) was used to model each timepoint after stimulus onset for all trials. We then plotted voxels that responded significantly (p < 0.00001, uncorrected) in the third bin (6 s) post-stimulus. We chose to focus on IPL, dMFC and AINS because these regions have all been implicated in perceptual decision-making in recent fMRI studies. The purpose of our study was not to make strong claims about the localisation of regions involved in decision-making, but to use previously-described regions to test hypotheses pertaining to adaptive gain control.

BOLD timeseries were extracted from each region and averaged across voxels. We then extracted overlapping epochs from −4 s to 24 s around the onset of each stimulus, and used a GLM approach similar to that for the pupil and EEG data to assess how decision information was encoded in BOLD signals. Segregating trials into those where the participants’ choice was cardinal vs. diagonal, we regressed decision information [8 regressors encoding Du_k associated with each sample, and 7 regressors encoding DU_k · δ(DU)_k] on the resulting BOLD signals at each timepoint separately. This resulted in an intercept and 15 parameter estimates for each timepoint per choice condition. We averaged across the 8 estimates for DU_k and the 7 estimates for DU_k · δ(DU)_k and plotted the resulting average estimates for each timepoint and choice (cardinal vs. diagonal; Fig. 5b-c). These plots thus demonstrate the extent to which BOLD signals in each region covaried with decision information (e.g. the extent to which the information favoured cardinal), and how this covariation was dampened by difference to the previous sample, separately for trials on which the participants chose cardinal and where they chose diagonal.