Abstract
Sibling studies have become increasingly popular because they provide better control over confounding by unmeasured family-level risk factors than can be obtained in standard cohort studies. However, little attention has been devoted to the development of efficient design strategies for sibling studies in terms of optimizing power. We here address this issue in commonly encountered types of sibling studies, allowing for continuous and binary outcomes and varying numbers of exposed and unexposed siblings. For continuous outcomes, we show that in families with sibling pairs, optimal study power is obtained by recruiting discordant (exposed–control) pairs of siblings. More generally, balancing the exposure status within each family as evenly as possible is shown to be optimal. For binary outcomes, we elucidate how the optimal strategy depends on the variation of the binary response; as the within-family correlation increases, the optimal strategy tends toward only recruiting discordant sibling pairs (as in the case of continuous outcomes). R code for obtaining the optimal strategies is included.
Keywords: design, power, sample size, sibling studies
1 Introduction
In recent years, epidemiological studies involving siblings have become increasingly common [1–7], and this design has now also been recognized in popular textbooks [8]. Sibling designs can provide better control over confounding by unmeasured family-level risk factors shared by the siblings (e.g. genetic, environmental, or socioeconomic) compared to other sampling strategies [9]. In addition, they can enhance study efficiency by reducing extraneous variability. Sibling studies are sometimes limited to two individuals per family, as in the case of twin studies [10], but more commonly comprise sibships of varying sizes, including singletons [11].
To estimate exposure effects with correlated data, two popular approaches are generalized linear models (or marginal models) using generalized estimating equations (GEE) to handle within-family correlations and random effects models (or mixed effects models). Marginal models have a population-average interpretation, whereas mixed effects models capture variation across families and allow for a family-specific interpretation. There has been extensive discussion in the literature of the relative merits of marginal models compared with mixed effects models [12, 13]. A recent study by Hubbard et al. [14] advises that mixed effects models should be approached with caution as they rely on unverifiable distributional assumptions. Specifically for sibling studies, a number of approaches have been employed to date including between–within (BW) models with fixed or random intercepts [15], conditional logistic regression models [16] for binary outcomes, and marginal models [9, 17]. Several review articles [9, 15, 18] provided detailed comparisons of the various approaches. In the context of fixed effect BW models and marginal models, Sjölander et al. [18] and Frisell [9] pointed out that the estimation and interpretation of the model parameters depends on the shared and non-shared confounders of sibling sets. Specifically, within-sibling estimates from BW models have larger bias in the presence of non-shared confounders relative to those from marginal models [9]. Furthermore, within-sibling estimates will have larger bias if the within-family correlation of exposure is higher than that of confounders.
Still missing from the literature, however, is a comprehensive treatment of optimal design strategies for sibling studies and easy access to the calculation of study power in specific settings. Ideally, study power should be readily available for any combination of exposed and unexposed individuals in sibships of varying sizes, and take within-family correlations into account, for either continuous or discrete study outcomes. To address this need, we here present design strategies to optimize study power based on marginal models using GEE to handle the within-family correlations. GEE provides an explicit way of handling within-family correlation, which for the purpose of power calculation is especially convenient. As far as we know, explicit power calculation methods for mixed effects models in the case of binary outcomes have only been developed under fixed alternatives [19], or rely on simulation [20] and the use of unverifiable distributional assumptions [14]. In the GEE setting we are able to explicitly calculate the asymptotic power (based on results in Li and McKeague [21]) and avoid the use of simulation methods. Throughout this paper, we use E and C to denote exposed and control (where “control” refers to unexposed) status, respectively. So an EC sibling pair (or an EC family) denotes two siblings with opposite exposure status, and an EE (or CC) sibling pair denotes two exposed (or unexposed) siblings.
The paper is organized as follows. Preliminary materials setting up the statistical model appear in Section 2. The proposed design strategies are developed in Sections 3 and 4. Section 5 contains discussion.
2 Statistical model
In this section, we formulate the statistical model that is used throughout the paper. Let yij be the outcome, xij the exposure of interest for the jth sibling in the ith family, and μij = E(yijjxij) be the conditional mean of yij given xij. A marginal model [9, 12] to estimate the effect of exposure can be written as
| (1) |
where g(.) is logit link for binary outcome and identity link for continuous outcomes, parameter λ is the intercept and parameter β measures the association between exposure and outcome. The parameters associated with this model are estimated by the GEE approach [21, 22] which requires specifying a working correlation matrix. We assume that siblings have positive correlations in terms of the outcome of interest.
We are interested in testing the hypothesis that a specific exposure is associated with a specific outcome of interest, i.e. H0 : β = 0 vs H1 : β ≠ 0. Our results are based on the use of a quasi-score test (rather than a Wald test) [21]. Quasi-score tests under marginal models have been studied extensively [23, 24] and provide a sound alternative to the score test when a score function is not available (the likelihood function is often intractable for correlated data). Unlike a score statistic, a quasi-score test is constructed from an estimating equation and an associated sandwich-type variance estimator, which results in a test that is asymptotically equivalent to a quasi-likelihood ratio test. The Wald test is a popular test, but Hauck and Donner [25] reported that the Wald statistic in logistic regression decreases under the alternative with increasing effect size because of increasing variance of the estimator of the regression parameter. This “aberrant” behavior of the Wald statistic raises difficulties for the study of optimal design strategies and is beyond the scope of the present paper.
Let m be the number of families in the study, α the type I error rate, and the 100(1 − α)th percentile of the chi-square distribution with 1 degree of freedom. According to Li and McKeague [21], the test statistic asymptotically follows a chi-square distribution with 1 degree of freedom and the power of detecting a specific β = β1 is the probability , where is a non-central chi-squared random variable with 1 degree of freedom and the non-centrality parameter νm is given in eq. (2) in the Appendix. It is straightforward to see that the statistical power increases with the non-centrality parameter. With this formula, we can calculate study power for family studies with varying sibship sizes and allocation schemes. As study power is uniquely determined by the non-centrality parameter, a comparison of noncentrality parameters will provide the differences in statistical power for alternative design strategies. In the following sections, various common design issues that arise in sibling studies will be explored to provide recommendations for optimizing power.
3 Optimal design strategies for studies with a continuous outcome
We first evaluate optimal design strategies for studies with a continuous outcome for the following scenarios: (1) studies including families with one singleton or two siblings; (2) studies adding siblings to existing families; and (3) studies in which all families have the same number of siblings. The within-family correlation of the outcome is denoted by ρ throughout this paper. R code for calculating statistical power and minimum detectable effect size is provided in Sections S3, S5, S8, and S10 of the Supplemental Materials.
3.1 Studies including families with one singleton or two siblings
We start with a simple situation where up to two subjects are available from a single family and identify exposed individuals in each family by the letter “E” and unexposed (control) individuals by the letter “C”. With this notation, the study may include the family structures EC, EE, CC, E, and C. A first question then is whether to recruit one or two individuals per family. As mentioned earlier, the idea is simply to compare the non-centrality parameter νm for the two competing strategies. Let mec, mee, mcc, me, and mc denote the number of EC, EE, CC, E, and C families in a study, respectively. For continuous outcomes, the link function g(.) in model (1) is the identity link. That is μij = λ + βxij, and the conditional variance is given by var(yijjxij) = σ2 which does not depend on the mean μij. Notice that the conditional variance σ2 is assumed to be constant across the exposure levels. The non-centrality parameter in this case is given in eq. (3) in the Appendix. This allows for the comparison of various design strategies with different combinations of EE, CC, EC, E, and C families. These comparisons (in section “Non-centrality parameter for continuous outcomes involving EE, CC, EC, E and C families” in the Appendix) show that for a given number of subjects, the non-centrality parameter νm will be maximized when only EC families are included for the study. If this ideal design strategy is fully implemented, the non-centrality parameter reduces to
where β1 is the alternative value and 1 – ρ is the “design effect” in this case. As νm is an increasing function of ρ, study power will increase as ρ increases; largest study power is therefore obtained when outcomes are most highly correlated within sibships.
Sometimes in practice, not every exposed subject will have an unexposed sibling, in which case the above “ideal design strategy” cannot be implemented. However, from comparisons of the non-centrality parameter, it can be seen that recruiting two E (or C) families will be more efficient than recruiting a single EE (or CC) family. This also makes sense intuitively given that the positively correlated EE (or CC) siblings include redundant information whereas E (or C) singletons are independent.
From these observations, the following recruiting principles can be distilled:
-
(a)
Recruit EC sibling pairs whenever possible,
-
(b)
When (a) is not possible, recruit an equal number of individuals from E and C families.
If these recruiting principles are followed, a mixture of E, C, and EC families will be recruited for study (unless the ideal recruiting strategy is possible and the study can be limited to EC families). The non-centrality parameter νm is then given by
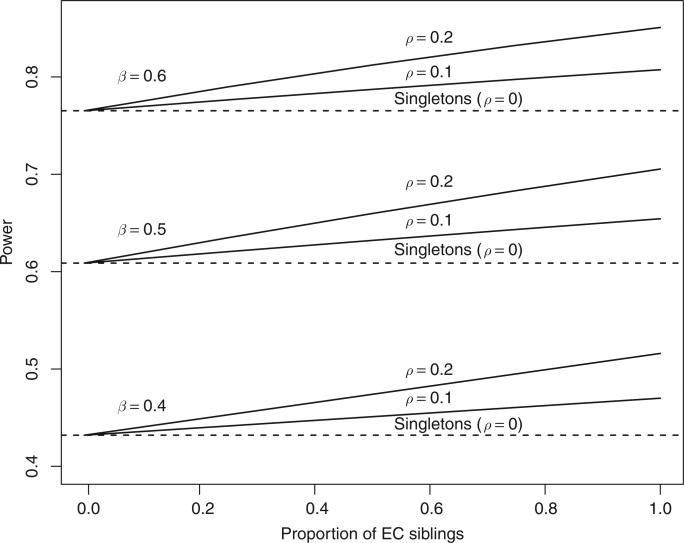
Notice that νm is still an increasing function of the correlation ρ, associated with the benefit gain from EC sibling pairs. Figure 1 illustrates the ideal strategies in relation to other strategies in terms of statistical power for a specific situation with an example of 80 subjects.
Figure 1.
Power of sibling (solid) and singleton (dashed) designs; n = 80 individuals with 40 exposed, 40 unexposed, as the number of exposure–control sib pairs increases from 0 to 40
3.2 Adding siblings to available families
In typical epidemiologic studies, the number of exposed subjects is limited, but the number of unexposed controls is not. Let us therefore consider the situation in which some EC, E, and C families have been recruited for the study, and it is feasible to recruit additional control subjects. We could then recruit sibling controls either (a) from E families to form EC families, or (b) from EC families to form ECC families, or (c) to add C families.
Following the principles outlined above, attempts should first be made to recruit additional unexposed controls from existing E families to form EC sibling pairs. This will give a better within-sibship exposure contrast than forming ECC families or adding C families.
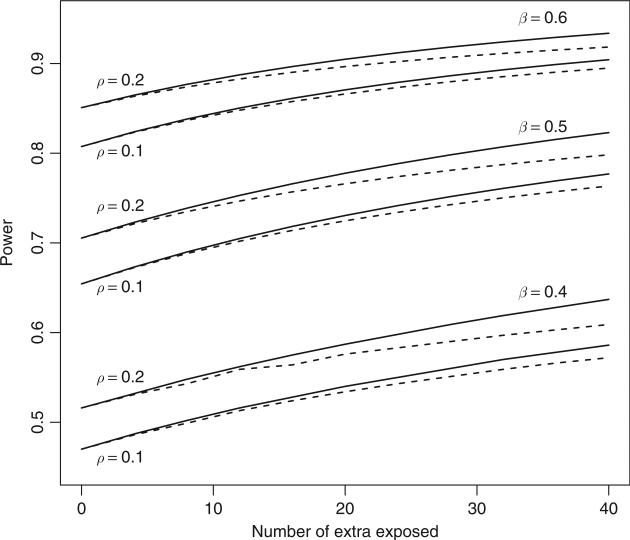
However, if additional controls are not available for E families, then should the extra controls be recruited from existing EC families to form ECC families or should C families be added? To compare the latter two scenarios we compare the corresponding values of νm. The expression of the non-centrality parameter is given in eq. (4) in the Appendix. The comparison shows that recruiting additional controls to form ECC families will generate greater statistical power than recruiting new C families, as illustrated in Figure 2, where extra controls are added to 40 EC pairs.
Figure 2.
Additional power from adding extra unexposed individuals to existing EC families (solid) and as singletons (dashed) starting from 40 exposure-control sib pairs
3.3 Studies in which all families have the same number of siblings
Next we consider the situation in which an identical number of siblings are recruited from each family. Let n be the number of siblings recruited from each family, ne of which are exposed and nc = n – ne are unexposed. The non-centrality parameter is given by
Notice that when ne is closest to one half of n, the non-centrality parameter νm is maximized. This means study power is largest when the exposure status within each family in the study is balanced. When n is an even number, power is maximized for ne = n/2. Then the above formula becomes where N is the total number of subjects in the study.
4 Optimal design strategies for studies with a binary outcome
It suffices to consider binary outcomes (e.g., a disease outcome) with a prevalence of less than 0.5 in both the exposed and unexposed groups because if the disease prevalence is greater than 0.5, “non disease” status can be used as the outcome with a prevalence less than 0.5 for mathematical equivalence. R code for deriving optimal design strategies and calculating power and minimum detectable relative risk is provided in Sections S1, S2, S4, S6, S7, and S9 of the Supplemental Materials.
4.1 Studies including families with one singleton or two siblings
Consider the scenario with up to two available siblings per family. This corresponds to family structures EC, EE, CC, E, and C. For binary outcomes, the link function in model (1) is taken as logit.
As mentioned earlier, recruiting two E (or C) families will be more efficient than recruiting a single EE (or CC) family because the positively correlated EE (or CC) siblings include redundant information, whereas E (or C) singletons are independent and provide additional information. Therefore an optimal recruiting strategy will involve a combination of EC, E, and C families. To find the optimal allocation scheme for such families, numerical methods are required to maximize νm given in eq. (5) in the Appendix. There is no closed-form solution for the maximization; the R code designed to find the optimal allocation scheme is provided in Section S1 of the Supplemental Materials.
The optimal strategy for a binary outcome differs from the approach taken for continuous outcomes. In the extreme case of ρ = 0, where there is no within-family correlation of study outcomes (or when only E or C families are recruited), the number of recruited E and C families should be proportional to the standard deviations of the binary response in the two groups, where ν0 = p0(1 – p0) and v1 = p1(1 – p1). Here p0 and p1 denote the prevalence of the outcome in the unexposed and exposed groups, respectively. The reason for this change in strategy is that the variance of a binary outcome depends on its mean or prevalence. In this case of ρ = 0, the best strategy will be to have , and such that , where pe and pc denote the proportions of E and C families, respectively. If however , as when the proportions p0 and p1 are close, the numbers of exposed and unexposed subjects should be balanced. This is consistent with results of Demidenko [26].
When ρ > 0, the recruiting strategy should include EC families. Examples are given in Table 1 for optimal design strategies for selected values of ρ, p0, and p1, where pec denotes the proportion of EC families. As the correlation ρ increases, recruiting more EC families will provide larger benefits compared to selecting E and C families in proportion to the standard deviations of the binary outcome. In this scenario, the proportion pe will decrease as ρ increases.
Table 1.
Optimal design strategy based on a binary outcome
|
p0 = 0.10 and p1 = 0.20 |
p0 = 0.10 and p1 = 0.30 |
|||||
|---|---|---|---|---|---|---|
| ρ = 0 | ρ = 0.2 | ρ = 0.4 | ρ = 0 | ρ = 0.2 | ρ = 0.4 | |
| Optimal proportions of siblings and singletons | pe = 57% | pe = 7% | pe = 0% | pe = 60% | pe = 15% | pe = 8% |
| pc = 43% | pc = 0% | pc = 0% | pc = 40% | pc = 0% | pc = 0% | |
| pec = 0% | pec = 93% | pec = 100% | pec = 0% | pec = 85% | pec = 92% | |
When the correlation exceeds a critical value depending on p0 and p1, the best strategy will be to only recruit EC families. As an example, with ρ = 0:4, p0 = 0:1, and p1 = 0:2, only EC siblings should be recruited (Table 1).
The effect size (i.e. the difference between p1 and p0) also matters. As illustrated in Table 1, the optimal proportion of exposed pe will be larger as the difference between p1 and p0 increases. This follows from the change in the ratio of the two standard deviations which also increases.
4.2 Adding siblings to available families
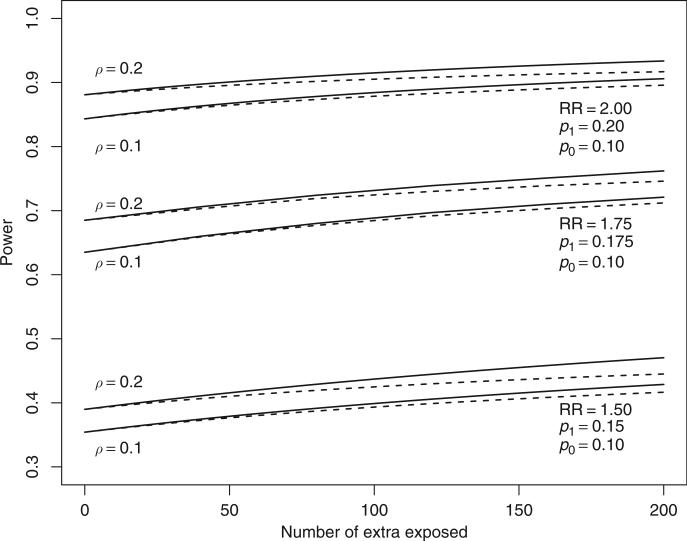
We next consider for binary outcomes the scenario with a fixed number of exposed study subjects available from EC, C, and E families and the possibility to recruit additional unexposed control subjects. Again, our options will be to recruit sibling controls either (a) from EC families to form ECC families, or (b) from E families to form EC families, or (c) to add C families. From the principles above it follows that one should first try to recruit additional unexposed controls from existing E families to form EC families. This will provide a better contrast of exposure status compared with adding C families or forming ECC families. The explicit formula of the non-centrality parameter is given in eq. (6) in the Appendix. With this formula, different recruitment strategies can be compared. As shown in Figure 3, where extra controls are added to 200 EC pairs, recruiting sibling controls from EC families will provide more statistical power compared to recruiting additional C families.
Figure 3.
Additional power from adding extra unexposed individuals to existing EC families (solid) and as singletons (dashed) starting from 200 exposure-control sib pairs
4.3 Studies in which all families have the same number of siblings
In the scenario where the same number of siblings are recruited from each family, the non-centrality parameter is given by
In this case, vm is maximized when . Therefore the most efficient strategy is to assign the exposed and control study subjects according to the ratio rather than balancing the numbers of exposed and unexposed siblings, unless (i.e. p0 and p1 are close to each other).
5 Discussion
In this paper, we have investigated the design efficiency of sibling studies with binary exposures using a novel GEE-based [21] approach to calculate study power and estimate required sample sizes. Correlations of (continuous or binary) study outcomes between siblings are taken into account. Our results are obtained by maximizing explicit expressions for the non-centrality parameters of the (chi-squared) limiting distributions of quasi-score test statistics under local alternatives. The optimal design strategies for continuous and binary study outcomes are found to differ while sharing some common elements.
For studies with at most two siblings per family and a continuous study outcome, the optimal design strategy is to recruit EC sibling pairs. When the same number (more than two) of siblings is to be recruited from all families, the optimal strategy is to balance the exposure status within each family as evenly as possible. However, for studies with a binary outcome, the variation of the outcome is different across the two exposure groups due to its dependence on the mean (or prevalence). This needs to be taken into account and results in a more complex form for the optimal design strategies. Unknown values of p0 and p1 will make implementation of the proposed optimal strategies challenging. In practice, the underlying prevalence will almost always be unknown and will have to be estimated from the literature. In the absence of any empirical estimates, design strategies could be evaluated for a plausible range of values and then conservative estimates selected. Besides the aforementioned differences, studies with continuous and binary outcomes also share some common elements. Recruiting an EE or a CC sibling pair is less efficient in terms of study power compared to recruiting two E singletons or two C singletons. Furthermore, adding an additional control to E or EC families to form EC or ECC families is more efficient than adding a new C family with only a singleton.
Our results show that all study subjects in family studies contribute to study power, albeit in different degrees in different settings. The efficiency of a family study will therefore be compromised by the exclusion of any study subjects, even if these subjects are not easily compared to siblings who differ in exposure status. As pointed out by Frisell [9], even results from sibling designs have to be interpreted with caution as they can be biased by confounders not shared by the siblings. Given the availability of analytic techniques that account for correlated and non-paired data, approaches that do not include all available study subjects [5, 6, 27, 28] should be avoided in the interests of validity and study power.
We have limited our focus to scenarios involving families with no more than three siblings, or the same number of siblings in each family; this should be sufficient for evaluating the most commonly used sibling designs. R code is included. Optimal recruiting strategies for settings with more complex family structures are not presented, because the maximization of the non-centrality parameter becomes highly computer intensive, and it would be beyond the scope of the article to present the results in any detail.
Our approach was developed and illustrated for cross-sectional sibling studies without repeated measurements. In a longitudinal sibling study with repeated measures, the key difference is that the correlation structure will be more complex because of the added within-subject correlation. The theoretical basis for the approach developed here [21] does not assume a specific correlation structure, so the formula provided in section “General formula for the non-centrality parameter” in the Appendix could potentially be used to provide guidelines for longitudinal sibling studies as well.
We have focused on the quasi-score test, but in practice the Wald test is popular, despite its limitations for binary outcomes mentioned earlier. The optimal strategies proposed in this paper also apply to the Wald test in the case of continuous outcomes. An interesting topic for future research would be to compare the quasi-score, quasi-likelihood, and Wald tests in terms of optimal design strategies for binary outcomes.
Our analysis defines study efficiency in terms of statistical power, ignoring any considerations relating to the relative cost of recruiting either exposed or unexposed siblings in different family settings. It can already be seen, however, that in common situations where study outcomes are positively correlated between siblings, the recruiting of EE or CC families might be easier and more cost effective compared to the recruiting of EC or E or C families, although this will be less efficient in terms of statistical power alone for a given sample size. When required, the trade-off between study cost and statistical efficiency could further be explored using the formulas in this paper given the costs of recruiting siblings and singletons.
Supplementary Material
Acknowledgments
The work of Zhigang Li was partially supported by NIH Grant 1R03NR014915-01. The work of Ian McKeague was partially supported by NIH Grant R01GM095722-01 and NSF Grant DMA-307838. The work of L.H. Lumey was partly supported by NIH grant R01AG042190-03.
Appendix
General formula for the non-centrality parameter
Let ψ = (λ, β), B = (0, 1), and Ri(α) denote the working correlation matrix for the ith family. The working covariance can be written as which may not equal the true variance, where Δi = diag[var(yi1), . . . , var(yini)]. When the working correlation R(α) is the true correlation, the working variance equals the true variance denoted by . Suppose there are L possible combinations of exposure patterns and family sizes denoted by (ul, sl), l = 1, . . . , L. Let then ωl, l = 1, . . . , L denote the proportion of the lth pattern. We can view this distribution as a particular allocation scheme given at the design stage. The general formula for non-centrality parameter is given by
| (2) |
with ψ1 = (λ0, β1), ψ0 = (λ0, 0), Dl = Di = ∂ui/∂ψ, and Vl = Vi evaluated under ψ = ψ0 and (xi, ni) = (ul, sl) and evaluated under ψ = ψ1 and (xi, ni) = (ul, sl). Here λ0 denotes the value of the intercept.
Non-centrality parameter for continuous outcomes involving EE, CC, EC, E, and C families
According to eq. (2), the explicit expression of the non-centrality parameter νm for continuous outcomes involving EE, CC, EC, E, and C families in a study is given by
| (3) |
where A1 = 2(mec + mee + mcc)=(1 + ρ) + me + mc, and
To show that the non-centrality parameter νm in eq. (3) is maximized when only EC families are included for the study, it suffices to show that recruiting one EC family generates a larger νm compared with recruiting one E and one C singletons, or recruiting two E singletons, or recruiting two C singletons, or recruiting one EE family or recruiting one CC family.
For the first case comparing recruiting one EC family with recruiting one E and one C singletons, we need to show that the νm increases if we change me, mc, and mec to me — 1, mc – 1, and mec + 1, respectively. If we do so, after some fundamental calculations, it is straightforward to see that the new A1 in eq. (3), say , becomes A1 – 2ρ=(1 + ρ) indicating that the denominator in eq. (3) decreases, and the new B1, say , becomes indicating the numerator in eq. (3) increases and consequently the non-centrality parameter νm in eq. (3) increases. Thus, recruiting one EC family does result in a larger non-centrality parameter compared with recruiting one E and one C singletons.
Using a similar approach, it can be shown that recruiting one EC family also generates a larger noncentrality parameter compared with recruiting one EE family or recruiting one CC family. Therefore, the non-centrality parameter in eq. (3) is maximized when only EC families are included for the study for a given number of subjects. If the given number of subjects is an odd number say 2k + 1, then it is straightforward to see that νm is maximized when there are k EC siblings and one E singleton (or equivalently one C singleton).
Non-centrality parameter for continuous outcomes involving ECC, EC, E, and C families
Let mecc denote the number of ECC families. According to eq. (2), the explicit expression of the noncentrality parameter νm for continuous outcomes involving ECC, EC, E, and C families in a study is given by
| (4) |
where , and
Non-centrality parameter for binary outcomes involving EC, E, and C families
According to eq. (2), the explicit expression of the non-centrality parameter νm for binary outcomes involving EC, E, and C families in a study is given by
| (5) |
where , v0 = p0(1 – p0), v1(1 – p1), and
Non-centrality parameter for binary outcomes involving ECC, EC, E, and C families
According to eq. (2), the explicit expression of the non-centrality parameter νm for binary outcomes involving ECC, EC, E, and C families in a study is given by
| (6) |
where
and θ is defined in the display following eq. (5).
Footnotes
Supplemental Material: The online version of this article (DOI: 10.1515/ijb-2014-0015) offers supplementary material, available to authorized users.
Contributor Information
Zhigang Li, Section of Biostatistics and Epidemiology, Department of Community and Family Medicine, Geisel School of Medicine at Dartmouth, One Medical Center Drive, 7927 Rubin Building, Hanover, NH 03755, USA.
Ian W. McKeague, Department of Biostatistics, Columbia University, 722 West 168th Street, New York, NY 10032, USA im2131@columbia.edu
Lambert H. Lumey, Department of Epidemiology, Columbia University, 722 West 168th Street, New York, NY 10032, USA lumey@columbia.edu
References
- 1.Dabelea D, Hanson RL, Lindsay RS, Pettitt DJ, Imperatore G, Gabir MM, et al. Intrauterine exposure to diabetes conveys risks for type 2 diabetes and obesity: a study of discordant sibships. Diabetes. 2000;49:2208–11. doi: 10.2337/diabetes.49.12.2208. [DOI] [PubMed] [Google Scholar]
- 2.Dabelea D, Pettitt DJ. Intrauterine diabetic environment confers risks for type 2 diabetes mellitus and obesity in the offspring, in addition to genetic susceptibility. J Pediatr Endocrinol Metab. 2001;14:1085–91. doi: 10.1515/jpem-2001-0803. [DOI] [PubMed] [Google Scholar]
- 3.Dwyer T, Blizzard L, Morley R, Ponsonby AL. Within pair association between birth weight and blood pressure at age 8 in twins from a cohort study. BMJ. 1999;319:1325–9. doi: 10.1136/bmj.319.7221.1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dwyer T, Morley R, Blizzard L. Twins and fetal origins hypothesis: within-pair analyses. Lancet. 2002;359:2205–6. doi: 10.1016/S0140-6736(02)09083-9. [DOI] [PubMed] [Google Scholar]
- 5.Lawlor DA, Bor W, O'Callaghan MJ, Williams GM, Najman JM. Intrauterine growth and intelligence within sibling pairs: findings from the mater-university study of pregnancy and its outcomes. J Epidemiol Community Health. 2005;59:279–82. doi: 10.1136/jech.2004.025262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lawlor DA, Clark H, Smith GD, Leon DA. Intrauterine growth and intelligence within sibling pairs: findings from the Aberdeen children of the 1950s cohort. Pediatrics. 2006;117:e894–902. doi: 10.1542/peds.2005-2412. [DOI] [PubMed] [Google Scholar]
- 7.Saelens BE, Ernst MM, Epstein LH. Maternal child feeding practices and obesity: a discordant sibling analysis. Int J Eat Disord. 2000;27:459–63. doi: 10.1002/(sici)1098-108x(200005)27:4<459::aid-eat11>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 8.Rothman KJ, Greenland S. Modern epidemiology. Lippincott Williams & Wilkins; Philadelphia, PA: 2008. [Google Scholar]
- 9.Frisell T, Öberg S, Kuja-Halkola R, Sjölander A. Sibling comparison designs: bias from non-shared confounders and measurement error. Epidemiology. 2012;23:713–20. doi: 10.1097/EDE.0b013e31825fa230. [DOI] [PubMed] [Google Scholar]
- 10.Morley R, Dwyer T. Studies of twins: what can they tell us about the fetal origins of adult disease? Paediatr Perinat Epidemiol. 2005;19:2–7. doi: 10.1111/j.1365-3016.2005.00608.x. [DOI] [PubMed] [Google Scholar]
- 11.Lumey LH, Stein AD, Kahn HS, Bruin KM, van der P, Blauw GJ, Zybert PA, et al. Cohort profile: the Dutch hunger winter families study. Int J Epidemiol. 2007;36:1196–204. doi: 10.1093/ije/dym126. [DOI] [PubMed] [Google Scholar]
- 12.Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G. Longitudinal data analysis. Chapman & Hall/CRC Press; Florida: 2008. [Google Scholar]
- 13.Diggle P, Heagerty P, Liang K-Y, Zeger S. Analysis of longitudinal data. Oxford University Press; Oxford: 2002. [Google Scholar]
- 14.Hubbard AE, Ahern J, Fleischer NL, Van der Laan M, Lippman SA, Jewell N, et al. To GEE or not to GEE: comparing population average and mixed models for estimating the associations between neighborhood risk factors and health. Epidemiology. 2010;21:467–74. doi: 10.1097/EDE.0b013e3181caeb90. [DOI] [PubMed] [Google Scholar]
- 15.Neuhaus JM, McCulloch CE. Separating between- and within-cluster covariate effects by using conditional and partitioning methods. J R Stat Soc Ser B. 2006;68:859–72. [Google Scholar]
- 16.Carlin JB, Gurrin LC, Sterne JA, Morley R, Dwyer T. Regression models for twin studies: a critical review. Int J Epidemiol. 2005;34:1089–99. doi: 10.1093/ije/dyi153. [DOI] [PubMed] [Google Scholar]
- 17.Dwyer T, Blizzard L. A discussion of some statistical methods for separating within-pair associations from associations among all twins in research on fetal origins of disease. Paediatr Perinat Epidemiol. 2005;19:48–53. doi: 10.1111/j.1365-3016.2005.00615.x. [DOI] [PubMed] [Google Scholar]
- 18.Sjölander A, Frisell T, Öberg S. Causal interpretation of between-within models for twin research. Epidemiol Methods. 2012;1:217–37. [Google Scholar]
- 19.Dang Q, Mazumdar S, Houck PR. Sample size and power calculations based on generalized linear mixed models with correlated binary outcomes. Comput Methods Programs Biomed. 2008;91:122–7. doi: 10.1016/j.cmpb.2008.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Moineddin R, Matheson FI, Glazier RH. A simulation study of sample size for multilevel logistic regression models. BMC Med Res Methodol. 2007;7:34. doi: 10.1186/1471-2288-7-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li Z, McKeague IW. Power and sample size calculations for generalized estimating equations via local asymptotics. Stat Sin. 2013;23:231–50. doi: 10.5705/ss.2011.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 23.Rotnitzky A, Jewell NP. Hypothesis testing of regression parameters in semiparametric generalized linear models for cluster correlated data. Biometrika. 1990;77:485–97. [Google Scholar]
- 24.Boos DD. On generalized score tests. Am Stat. 1992;46:327–33. [Google Scholar]
- 25.Hauck WW, Donner A. Wald's test as applied to hypotheses in logit analysis. J Am Stat Assoc. 1977;72:851–3. [Google Scholar]
- 26.Demidenko E. Sample size determination for logistic regression revisited. Stat Med. 2007;26:3385–97. doi: 10.1002/sim.2771. [DOI] [PubMed] [Google Scholar]
- 27.Nelson MC, Gordon-Larsen P, Adair LS. Are adolescents who were breast-fed less likely To Be overweight? Analyses of sibling pairs to reduce confounding. Epidemiology. 2005;16:247–53. doi: 10.1097/01.ede.0000152900.81355.00. [DOI] [PubMed] [Google Scholar]
- 28.Matte TD, Bresnahan M, Begg MD, Susser E. Influence of variation in birth weight within normal range and within sibships on IQ at age 7 years: cohort study. BMJ. 2001;323:310–14. doi: 10.1136/bmj.323.7308.310. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.