Incorporating temporal features of repeatedly measured covariates into tree-structured survival models

Abstract

Tree-structured survival methods empirically identify a series of covariate-based binary split points, resulting in an algorithm that can be used to classify new patients into risk groups and subsequently guide clinical treatment decisions. Traditionally, only fixed-time (e.g. baseline) values are used in tree-structured models. However, this manuscript considers the scenario where temporal features of a repeated measures polynomial model, such as the slope and/or curvature, are useful for distinguishing risk groups to predict future outcomes. Both fixed- and random-effects methods for estimating individual temporal features are discussed, and methods for including these features in a tree model and classifying new cases are proposed. A simulation study is performed to empirically compare the predictive accuracies of the proposed methods in a wide variety of model settings. For illustration, a tree-structured survival model incorporating the linear rate of change of depressive symptomatology during the first four weeks of treatment for late-life depression is used to identify subgroups of older adults who may benefit from an early change in treatment strategy.

1 Introduction

Late-life depression can lead to serious health consequences, including disability associated with comorbid medical and cognitive disorders and increased mortality due to suicide (Reynolds et al., 1999). When treating late-life depression with antidepressants, it can be of considerable interest to identify the likelihood of success for each patient as they progress throughout the clinical course, thereby allowing clinicians to tailor each patient's treatment accordingly. For example, Mulsant et al. (2006) showed that, after only four weeks of acute treatment for late-life depression, one could identify which patients would benefit from treatment modification based on their initial percent decrease in depressive symptomatology.

As an extension of this work, our aim was to develop methodology that incorporates temporal features (e.g. slope and curvature) of repeatedly measured depression scores, as well as additional baseline clinical and demographic characteristics, to identify subgroups that may benefit from a change in acute treatment strategy after only four weeks. For these types of clinical questions, a tree-structured survival modeling framework, such as those proposed by LeBlanc and Crowley (1992, 1993) or Hothorn et al. (2006), is useful because it is easily interpreted and can be used to classify new patients into prognostic groups, thereby facilitating the selection of an appropriate treatment regime.

Traditionally, only fixed-time (e.g. baseline) covariates are included in tree-structured models. Proposed methods for incorporating repeatedly measured covariates in tree-structured survival models (Bacchetti and Segal, 1995; Huang et al., 1998) allow for subgroups to be identified based on updated covariate values, as opposed to only baseline covariate values. However, these methods are not sufficient for addressing the aim of this manuscript because our interest lies specifically in how temporal features of repeatedly measured covariates can be used to identify an individual's risk for a future event.

In this manuscript, we propose to quantify temporal features of each individual's trajectory up to a given time point t_s and, subsequently, include these features as possible covariates in a tree-structured survival model to predict outcomes occurring after time t_s. To this end, we first discuss two possible methods for estimating individual temporal features of repeatedly measured covariates for use in tree-structured survival models: (i) fitting a separate fixed-effects polynomial regression model for each individual and (ii) fitting one two-stage random-effects polynomial regression model for the entire cohort. Methods for including these estimated individual temporal features in a tree-structured survival model and classifying new individuals into the resulting prognostic groups are proposed.

Results from a simulation study performed to empirically evaluate the accuracy of the fixed- and random-effects methods in a variety of model scenarios are presented. Because these methods may require the use of a computer to classify new cases, this simulation study also evaluated a simpler approach that includes the last fixed-time observation as a proxy for the temporal feature. The predictive accuracies of these methods were compared to a naive method that ignores the temporal feature and also a hypothetical method where the true temporal feature is known. Finally, the methodology is applied to a subset of the late-life depression data used by Mulsant et al. (2006) to identify groups of patients that may require a change in treatment regime after only four weeks.

2 Tree-structured survival modeling

Although tree-structured models were introduced as early as 1963 by Morgan and Sonquist in the field of Automated Interaction Detection (AID), the first comprehensive tree-growing algorithm was developed by Breiman et al. (1984). This algorithm, “Classification and Regression Trees” (CART), allows users to generate tree models with both continuous and categorical outcomes. Gordon and Olshen (1985), Segal (1988), and LeBlanc and Crowley (1992, 1993) extended the CART algorithm to generate tree models with censored time-to-event outcomes.

The conditional inference framework, developed by Hothorn et al. (2006), is an alternative to CART-based recursive partitioning algorithms. Similar to CART-based methods, conditional inference trees can also accommodate several types of outcomes, including continuous, categorical, multivariate, and censored time-to-event. However, an advantage of the conditional inference framework when developing prognostic models is that they are specifically designed to address the problems of overfitting and selection bias for which CART-based recursive partitioning methods have been criticized (Hothorn et al., 2006). Because our primary interest in this manuscript is developing clinically relevant tree-structured models, the proposed methods will be discussed in the context of conditional inference trees for survival outcomes; however, these methods can be directly extended to other types of recursive partitioning methods and outcomes as well.

Consider a time to an event Y , a censoring time C, and an observed outcome Y * = min(Y,C). Conditional inference survival trees seek to describe the conditional distribution of the outcome, Y *, given the status of m covariates X = (X₁, . . . , X_m) through recursive partitioning. As discussed by Hothorn et al. (2006), this algorithm begins by first testing the global null hypothesis of independence between the m covariates and the response. If this hypothesis cannot be rejected, the algorithm stops. If this hypothesis can be rejected, the association between Y * and each covariate X_j, j = 1, . . . , m, is determined by test statistics incorporating log-rank scores or p-values that quantify the deviation from the covariate-specific hypotheses of independence. Once the best splitting covariate $X_j^{\ast }$ has been determined, the specific splitting value on that covariate can be identified using two-sample log-rank scores. After executing this split, the process is repeated for the resulting discrete subgroups, also called nodes. Any nodes for which the global null hypothesis of independence is not rejected are called terminal nodes. An example of a recursive partitioning tree with four terminal nodes (h₄ − h₇) is shown in Fig. 1. See Hothorn et al. (2006) for additional details of the conditional inference algorithm.

Figure 1.

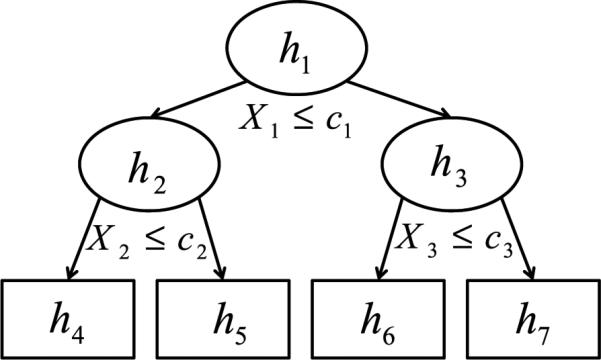
An example of a conditional inference tree. At each of the nodes h₁–h₃, cases with X ≤ c are sent to the left child node and cases with X > c are sent to the right child node. Nodes h–h₇ are terminal nodes.

3 Proposed methodology

Consider an individual i with repeated covariate measurements W_i = (W_i(t_i1), . . . ,W_i(t_iJi))′ observed prior to a prespecified landmark time point t_s, such that t_iJi ≤ t_s. The set of unique discrete time points on which an individual i has observed measurements is denoted by ${\mathcal{M}}_i$. Follow-up continues until either the time of the event Y_i or the time of censoring from the study C_i. Thus, the observed outcome for i is denoted by ($Y_i^{\ast }$, δ_i), where $Y_i^{\ast }=\min (Y_i,C_i)$ and δ_i = 1(Y_i ≤ C_i).

The proposed methodology uses temporal features observed up to a landmark time point t_s to predict a future event. If individuals with $Y_i^{\ast }\le t_s$ are used to estimate the temporal features and, subsequently, to fit the predictive model, the resulting estimates may be biased because future information is being used to predict a past event. Thus, only individuals with $Y_i^{\ast }>t_s$ are included in the sample of size N. The set of unique discrete time points on which repeatedly measured covariate data are observed for all N individuals is denoted by $\mathcal{M}$, such that ${\mathcal{M}}_i\subseteq \mathcal{M}$, i = 1, . . . , N.

3.1 Estimating temporal features

Although there are several types of temporal features that could be incorporated into tree-structured models, of particular interest in this manuscript are temporal features that can be modeled with a polynomial function of time. The general shape of the trajectory over time, most often a straight line (modeled with a first degree polynomial) or a quadratic curve (modeled with a second degree polynomial), can be identified based on study design, prior knowledge of the clinical and biological behavior of the repeatedly measured data, or direct observation of the plotted observed values. However, within this general shape, each individual is assumed to have his or her own unique trajectory as he or she progresses through the clinical course.

We discuss two methods for estimating individual temporal features to be used in tree-structured models: (i) fitting a separate fixed-effects polynomial regression model for each individual, and (ii) fitting one two-stage random-effects polynomial regression model for all N individuals in the cohort.

3.1.1 Fixed-effects method

A fixed-effects polynomial regression model

$${\mathbf{W}}_i={\mathbf{X}}_i{\mathbf{B}}_i+{∊}_i$$ (1)

is fit for each individual i, where X_i is a J_i × P fixed design matrix of the form

$${\mathbf{X}}_i=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill {(t_{i1}-{\stackrel{‒}{t}}_i)}^1\hfill & \hfill \cdots \hfill & \hfill {(t_{i1}-{\stackrel{‒}{t}}_i)}^p\hfill & \hfill \cdots \hfill & \hfill {(t_{i1}-{\stackrel{‒}{t}}_i)}^{P-1}\hfill \\ \hfill 1\hfill & \hfill {(t_{i2}-{\stackrel{‒}{t}}_i)}^1\hfill & \hfill \cdots \hfill & \hfill {(t_{i2}-{\stackrel{‒}{t}}_i)}^p\hfill & \hfill \cdots \hfill & \hfill {(t_{i2}-{\stackrel{‒}{t}}_i)}^{P-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill {(t_{i{J}_i}-{\stackrel{‒}{t}}_i)}^1\hfill & \hfill \cdots \hfill & \hfill {(t_{i{J}_i}-{\stackrel{‒}{t}}_i)}^p\hfill & \hfill \cdots \hfill & \hfill {(t_{i{J}_i}-{\stackrel{‒}{t}}_i)}^{P-1}\hfill \end{array}\right],$$ (2)

with ${\stackrel{‒}{t}}_i={\sum }_{j=1}^{J_i}{t}_{ij}∕J_i$. The first column of X_i represents the intercept and each subsequent column represents the centered time points for each polynomial feature. The P × 1 vector of individual temporal features (e.g. slope, curvature) is denoted by B_i = (B_i0, . . . , B_i(P−1))′. The vector of residual errors is denoted by ε_i = (ε_i1, . . . , ε_iJ)′, with ${∊}_{ij}\sim (0,{\sigma }_{∊}^2)$. The estimates of B_i are calculated as

$${\widehat{\mathbf{B}}}_i={\left({\mathbf{X}}_j^{\prime }{\mathbf{X}}_i\right)}^{-1}{\mathbf{X}}_i^{\prime }{\mathbf{W}}_i$$

given ${\mathbf{X}}_i^{\prime }{\mathbf{X}}_i$ is of full rank (Searle, 1997). After fitting all N individual fixed polynomial regression models, the N × P matrix of temporal features is denoted by B̂* = (B̂₁, . . . , B̂_N)′.

3.1.2 Random-effects method

The two-stage random-effects approach is different from the fixed-effects approach because it allows for each individual's trajectory to be uniquely modeled while still borrowing information from those with more information. Specifically, when the within-subject variability is large relative to the between-subject variability, the individual estimates are weighted more toward the population-averaged effect than toward their own observed responses. This model characteristic helps to ensure that the individual estimates will not be artificially extreme or unstable, even in the presence of large within-subject variability (Laird and Ware, 1982; Brown and Prescott, 1999; Fitzmaurice et al., 2004; Hedeker and Gibbons, 2004).

One two-stage random-effects polynomial model is fit for all N individuals in the cohort. For an individual i with J_i repeated observations W_i, the two-stage random-effects model as proposed by Laird and Ware (1982) can be represented as

$${\mathbf{W}}_i={\mathbf{X}}_i\beta +{\mathbf{Z}}_i{\mathbf{b}}_i+{∊}_i,$$ (3)

where β is a P × 1 vector of unknown population parameters, X_i is a known J_i × P design matrix linking β to W_i, b_i is a Q × 1 vector of unknown individual parameters, and Z_i is a known J_i × Q design matrix linking b_i to W_i. The design of the fixed-effects matrix, X_i, is given in Eq. (2). The random-effects matrix, Z_i, is equivalent to X_i if all fixed parameters are also considered to vary randomly. If only some of the fixed parameters are considered to vary randomly, Z_i is a subset of the columns in X_i.

Following Laird and Ware (1982), we assume that the individual random-effects are distributed as b_i ~ N(0, G), where G is the Q × Q matrix containing the set of between-subject variance/covariance parameters, denoted by γ_G when arranged as a vector. The vector of residual errors ε_i = (ε ₁, . . . , ε_J)′ is assumed to be independent of b_i and distributed as ε_i ~ N_Ji (0, R_i), where R_i is a J_i × J_i matrix containing the set of within-subject variance/covariance parameters, denoted by γ_R when arranged as a vector. The dimensions of γ_G and γ_R depend on constraints in the covariance structure. The repeatedly measured covariate is distributed as W_i ~ N_Ji (X_iβ, V_i), where ${\mathbf{V}}_i={\mathbf{Z}}_i{\mathbf{GZ}}_i^{\prime }+{\mathbf{R}}_i$. Any mising observations in W_i are assumed to be either missing completely at random or missing at random (Little and Rubin, 2002).

Given that all assumptions outlined above are met, the estimates for parameters in γ_G and γ_R can be obtained based on the entire cohort of size N through an estimation method such as restricted maximum likelihood, which reduces the likelihood to include only the variance/covariance parameters. The resulting parameter estimates ${\widehat{\gamma }}_G$ and ${\widehat{\gamma }}_R$ are substituted into G and R_i to obtain ${\widehat{\mathbf{V}}}_i={\mathbf{Z}}_i\widehat{\mathbf{G}}{\mathbf{Z}}_i^{\prime }+{\widehat{\mathbf{R}}}_i$. The estimated matrices V̂_i, i = 1, . . . , N, can then be substituted into the generalized least squares estimator to calculate the fixed population effects as

$$\widehat{\beta }={\left(\sum _{i=1}^N{\mathbf{X}}_i^{\prime }{\widehat{\mathbf{V}}}_i^{-1}{\mathbf{X}}_i\right)}^{-1}\sum _{i=1}^N{\mathbf{X}}_i^{\prime }{\widehat{\mathbf{V}}}_i^{-1}{\mathbf{W}}_i,$$

The fixed population and variance/covariance estimates are then used to calculate the individual estimates as

$${\widehat{\mathbf{b}}}_i=\widehat{\mathbf{G}}{\mathbf{Z}}_i^{\prime }{\widehat{\mathbf{V}}}_i^{-1}({\mathbf{W}}_i-{\mathbf{X}}_i\widehat{\beta }).$$ (4)

These individual random-effects are commonly referred to as the “Empirical Best Linear Unbiased Predictors” or the “Empirical Bayes Estimates” (Brown and Prescott, 1999; Fitzmaurice et al., 2004).

After estimating the fixed and random-effects parameters, the set of temporal features for each individual is calculated as

$${\widehat{\mathbf{B}}}_i={\widehat{\beta }}^{\left(Z\right)}+{\widehat{\mathbf{b}}}_i,$$

where ${\widehat{\beta }}^{\left(Z\right)}=\widehat{\beta }$ when Z_i = X_i. When Z_i is a subset of X_i, the fixed-effects parameters ${\widehat{\beta }}^{\left(Z\right)}$ make up the subset of β corresponding to the Q columns in Z, such that X = [Z X*] and $\beta ={({\widehat{\beta }}^{{\left(Z\right)}^{\prime }},{\beta }^{{\ast }^{\ast }})}^{\ast }$. Thus, a single temporal feature of interest for individual i, denoted by B_iq, is composed of the population estimate ${\widehat{\beta }}_q^{\left(Z\right)}$ and the additional deviation of the i^th individual from the population estimate b̂_iq. The N × Q matrix of all temporal features is denoted by B̂* = (B̂₁, . . . , B̂_N )′. Henceforth, we assume that all fixed effects also vary randomly, letting P = Q.

3.2 Fitting a tree-structured model incorporating temporal features

Regardless of whether the fixed- or random-effect approach is used, and assuming that P = Q, each column in B̂*, denoted ${\widehat{\mathbf{B}}}_0^{\ast }$, ${\widehat{\mathbf{B}}}_1^{\ast },\dots ,{\widehat{\mathbf{B}}}_{Q-1}^{\ast }$, represents a temporal feature that could be included in the tree-structured model. In a first-order polynomial model, the estimated slope ${\widehat{\mathbf{B}}}_1^{\ast }$ represents the linear rate of change from baseline to time t_s. In a second-order polynomial model, both the slope ${\widehat{\mathbf{B}}}_1^{\ast }$ and curvature ${\widehat{\mathbf{B}}}_2^{\ast }$ contribute to the characterization of the trajectory from baseline to time t_s. Similarly, in higher order polynomial models (Q > 2), temporal features ${\widehat{\mathbf{B}}}_q^{\ast }$, q 1, . . . , (Q − 1) contribute to the characterization of the trajectory. Because one of the benefits of tree-structured methods is that they empirically select the most important variables for building the model, it may be useful to at least include all possible features ${\widehat{\mathbf{B}}}_1^{\ast },\dots ,{\widehat{\mathbf{B}}}_{(Q-1)}^{\ast }$ so that the entire trajectory can be characterized. The intercept ${\widehat{\mathbf{B}}}_0^{\ast }$, which represents the average at the midpoint of follow-up, can also be included in the model; however, it may not be essential if the observed baseline value or other fixed time values observed on or prior to time t_s are also used as covariates. The resulting tree model is denoted by H*.

3.3 Classifying new individuals

Consider a new individual k not in the original sample of size N. A repeatedly measured covariate W_k(t_{k j}) is observed for individual k on multiple discrete ordered times t_{k j}, j = 1, . . . , J_k, with t_Jk ≤ t_s. Assuming he or she comes from the same population as the original sample, the final tree model H* can be used to classify him or her into a risk group h ∈ H*.

When the fixed-effects method is used for estimation, it should also be used for classification; the same holds true for the random-effects method. This consistency in method selection is important because the features estimated using the random-effects method are shrunken toward the population mean, while the features estimated using the fixed-effects method do not exhibit this property.

3.3.1 Fixed-effects method

The temporal features for a new individual k are estimated by fitting a new fixed-effects polynomial regression model, as detailed in Section 3.1.1. The resulting estimated features B̂_k and other covariates of interest observed on or prior to time t_s can be used to classify individual k into a terminal node h ∈ H̃*.

3.3.2 Random-effects method

The true temporal features for a new individual k are denoted by B_k = β^(Z) + b_k. One possible method for obtaining estimates of these parameters for classification of a new individual into a terminal node h ∈ H* is to fit a random-effects model that incorporates the data from individual k into the original dataset of size N used to create H*. However, for investigators who have interest in predictive classification, such an approach would not be feasible unless they had access to the original data used to fit the random-effects model. To obtain estimates of β^(z) and b_k without access to the original database, we assume that the fixed-effects and variance/covariance estimates from the original polynomial regression model are equivalent to those that would have resulted if the new individual k had been included. This assumption is reasonable given that individual k is believed to have come from the same population as the original sample.

Given the above assumptions are met, b̂_k is estimated as

$${\widehat{\mathbf{b}}}_k=\widehat{\mathbf{G}}{\mathbf{Z}}_k^{\prime }{\widehat{\mathbf{V}}}_k^{-1}({\mathbf{W}}_k-{\mathbf{X}}_k\widehat{\beta }),$$

where ${\widehat{\mathbf{V}}}_k={\mathbf{Z}}_k\widehat{\mathbf{G}}{\mathbf{Z}}_k^{\prime }+{\widehat{\mathbf{R}}}_k$. The between-subject matrix, Ĝ, and the vector of population averaged estimates, $\widehat{\beta }$, are equivalent in both content and dimension to those estimated in the original two-stage random-effects model. The design matrices, Z_k and X_k, have dimensions J_k × Q and J_k × P, respectively, and can be created using Eq. (2) as a reference. The estimated within-subject error matrix, R̂_k, has rows and columns corresponding to the observed time points in ${\mathcal{M}}_k$ and incorporates the within-subject estimates in ${\widehat{\gamma }}_R$. When the within-subject error is assumed to be independent of time (e.g. takes the form ${\sigma }_{∊}^2{I}_{k\times k}$), it is not necessary that ${\mathcal{M}}_k\subseteq \mathcal{M}$ in order to create R̂_k. However, when time-based constraints are assumed (e.g. autocorrelated within-subject error) it may be necessary that ${\mathcal{M}}_k\subseteq \mathcal{M}$.

The temporal features for individual k are calculated as ${\widehat{\mathbf{B}}}_k={\widehat{\beta }}^{\left(Z\right)}+{\widehat{\mathbf{b}}}_k$. These estimates and other fixed covariate values observed on or prior to time t_s that were included in H* are used to classify individual k into a terminal node h ∈ H̃*.

4 Simulation study

A simulation study was performed to assess the predictive abilities of the fixed- and random-effects methods. Because both of these methods may require the use of a computer and/or knowledge of variance/covariance estimates from the original model, a simpler, alternative method that includes the last fixed-time observation in the tree model as a proxy for the temporal feature was also evaluated. These three methods were compared to the naive scenario where the temporal feature is ignored, as well as the hypothetical scenario where the true temporal feature is known. Because the levels of between- and within-subject variability and the number of repeatedly measured observations were expected to influence predictive accuracy, the methods were evaluated under a wide variety of data generation scenarios. The statistical package R version 2.12.0 (R Development Core Team, 2008) was used to perform the simulation study.

4.1 Data generation

Data were generated based on two primary scenarios: (A) the presence of a linear temporal feature in a tree-structured survival model, and (B) the presence of linear and quadratic temporal features in a tree-structured survival model. Thus, in scenario A, the rate of change of a repeatedly measured covariate was associated with the survival outcome. In scenario B, the combination of both the rate of change and the curvature were associated with the survival outcome. Within each scenario, we varied the levels of within-subject variability, between-subject variability, and the number of repeated measures to provide a range of data scenarios. The survival function for each case was identified through a tree-structured survival model that included the true temporal feature(s), the baseline value of the repeatedly measured covariate, and the fixed model covariates.

Parameter values for data generation were selected based on estimates from linear and quadratic random-effects polynomial regression models of the Hamilton Rating Scale for Depression (HRSD) in the Maintenance Therapies in Late-Life Depression (MTLD) data. Inspection of these data showed a small quadratic effect after four weeks. Thus, we fit a linear random-effects polynomial regression model to only the first four weeks of data to get approximate parameter values for the linear data generation scenario. The estimated within- and between-subject variances were used as approximate medians of the ranges of within- and between-subject error parameter values.

We fit a quadratic random-effects polynomial regression model to only the first 12 weeks of MTLD data to get parameter values for the quadratic data generation scenario. This time period was selected because we aimed to use quadratic temporal features to identify subgroups that might require an early change in treatment strategy, and week 12 is the last week prior to the second half of acute treatment. Although the quadratic effect was significant, its coefficient and associated between-subject variance were very small. Thus, in order to simulate data that would be more reflective of scenarios in which a quadratic feature might influence the survival outcome, we inflated the quadratic coefficient and associated between-subject variance values until plots of the simulated data resembled a more relevant scenario. For consistency, the ranges of within-subject error were set equal to those the linear data generation scenario. The range of the between-subject variance was selected to span the inflated model estimate.

For both the linear and quadratic data generation scenarios, we expected that the within-subject variance would differentiate the models’ performances more than the between-subject variability. This is largely because the random-effects method uses information from other observations to stabilize observations with larger within-subject variability, while the fixed-effects method does not. Thus, we selected a larger range of within-subject variances than between-subject variances.

4.1.1 Scenario A: Linear temporal feature

Random-effects were distributed as b_i = (b_i0, b_i1)′ ~ N₂(0, G_2×2), with variances $\{{\sigma }_0^2,{\sigma }_1^2\}$ and covariance ρσ₀σ₁. Repeatedly measured covariates were distributed as ${\mathbf{W}}_{i1}\mid {\mathbf{b}}_i\sim N_J({\mathbf{X}}_i\beta +{\mathbf{Z}}_i{\mathbf{b}}_i,{\sigma }_{∊}^2{\mathbf{I}}_{J\times J})$, with β = (β₀, β₁)′ and

$${\mathbf{X}}_i={\mathbf{Z}}_i=1({\mathbf{t}}_i-{\stackrel{‒}{t}}_i)],$$

where 1 is a J × 1 vector of ones, t_i = [1, . . . , J]′, and ${\stackrel{‒}{t}}_i={\sum }_{j=1}^J{t}_{ij}∕J$.

These data were generated with two levels of between-subject error $({\sigma }_1^2=\{2,.5\})$, five levels of within-subject error $({\sigma }_{∊}^2=\{40,20,10,1,0.1\})$, and three follow-up time periods (J = {4, 8, 12}), resulting in 30 different data generation scenarios. Additional parameters were fixed at ${\{\beta }_0,{\beta }_1,{\sigma }_0^2,\rho \}=\{16,-1.6,11,0.26\}$.

4.1.2 Scenario B: Linear and quadratic temporal features

Random-effects were distributed as b = (b_i0, b_i1, b_i2)′ ~ N₃(0, G_{3 × 3}), with variances $\{{\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2\}$ and covariances {ρ₀₁σ₀σ₁, ρ₀₂σ₀σ₂, ρ₁₂σ₁σ₂}. Repeatedly measured covariates were distributed as ${\mathbf{W}}_{i1}{\mathbf{b}}_i\sim N_J({\mathbf{X}}_i\beta +{\mathbf{Z}}_i{\mathbf{b}}_i,{\sigma }_{∊}^2{\mathbf{I}}_{J\times J})$, with β = (β₀, β₁, β₂)′ and

$${\mathbf{X}}_i={\mathbf{Z}}_i=\left[1({\mathbf{t}}_i-{\stackrel{‒}{t}}_i){({\mathbf{t}}_i-{\stackrel{‒}{t}}_i)}^2\right].$$

These data were generated with two levels of between-subject error $({\sigma }_2^2=\{0.5,0.01\})$, five levels of within-subject error $({\sigma }_{∊}^2=\{40,20,10,1,0.1\})$, and two follow-up time periods (J = {8, 12}), resulting in 20 different data generation scenarios. Although the follow-up time period J= 4 was included in scenario A, it was not included in scenario B because the quadratic effect was not perceptible with only four time points. Additional parameters were fixed as {β₀, β₁, β₂} = {15, 0.6, 0.03} and $\{{\sigma }_0^2,{\sigma }_1^2,{\rho }_{01},{\rho }_{02},{\rho }_{12}\}=\{10,0.5,-0.01,0.05,-0.3,0.2\}$.

4.1.3 Fixed-time covariates and outcome

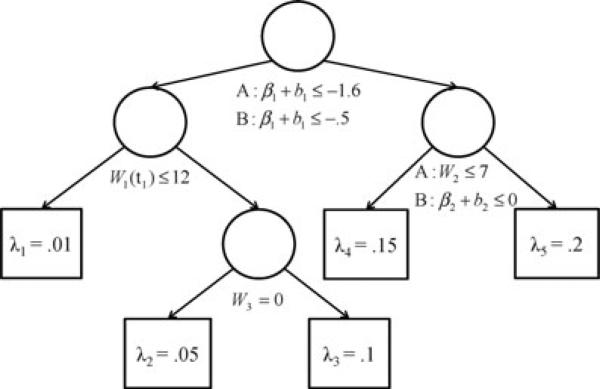
Two fixed-time covariates to be used in the true tree-structured model were generated as W_i2 ~ Normal(7, 2) and W_i3 ~ Bernoulli(0.4). Three fixed-time noise covariates were generated as W_i4 ~ Normal(20, 5), W_i5 ~ Bernoulli(0.7), and W_i6 ~ Bernoulli(0.5). True event times were generated as T ~ exp(λ_h), where λ_h was determined by the tree model in Fig. 2. Censoring times were generated as C ~ Unif(0, 21). Observed outcomes were computed as $Y_i^{\ast }=\min (Y_i,C_i)$, with δ_i = 1(Y_i ≤ C_i).

Figure 2.

True survival tree models for scenarios A (linear temporal feature only) and B (linear and quadratic temporal features). In scenario A, the tree splits first on the slope, β₁ + b₁, followed by the observed baseline value of the repeatedly measured covariate, W₁ (t₁), and fixed-time covariates W₂ and W₃. In scenario B, the tree splits first on the slope, followed by splits on the baseline value of the repeatedly measured covariate, the curvature, β₂ + b₂, and fixed-time covariate W₃. Time-to-event outcomes of cases classified into each of the five terminal nodes follow exponential distributions with parameters λ_h, h = 1, . . . , 5.

The true survival tree structures for scenarios A and B are shown in Fig. 2. In scenario A, the survival tree structure split first on the slope B₁ = β₁ + b₁ followed by the baseline value of the repeatedly measured covariate W₁(t₁) and the fixed model covariates W₂ and W₃. In scenario B, the tree structure split first on the slope, followed by the baseline value W₁(t₁), the curvature B₂ = β₂ + b₂, and the fixed model covariate W₃.

4.2 Computing and model assessment

For each data scenario, 1000 pairs of training and testing datasets, each containing N = 500 samples, were generated. The ctree function (Hothorn et al., 2006) was used to fit a conditional inference survival tree model to each of the 1000 training datasets with each of five methods: (i) including the true temporal feature in the set of possible predictors (“true”), (ii) including no temporal feature estimate in the set of possible predictors (“naive”), (iii) including the last observed value in the set of possible predictors (“last value”), (iv) estimating the temporal feature using the fixed-effects approach and subsequently including it in the set of possible predictors (“fixed-effects”), and (v) estimating the temporal feature using the random-effects approach and subsequently including it in the set of possible predictors (“random-effects”). Each of the five methods included the same base set of possible predictor variables to fit the tree model, consisting of the baseline value of the repeatedly measured covariate W₁(t₁) and model and noise covariates W₂ to W₆. In scenario A, the estimated linear feature was included; in scenario B, both the linear and quadratic features were included.

After a tree model H* was fit based on a training dataset, the Nelson Aalen cumulative hazard estimates were calculated for each terminal node, h ∈ H̃*. Subsequently, each of the cases in the paired testing dataset was classified into one of these terminal nodes. For the true, naive, and last value methods, each case could be directly classified using the simulated test data. For the fixed- and random-effects methods, the methodology given in Section 7 was used to estimate the temporal feature(s) for each case in the testing dataset prior to classification into a terminal node. The time-dependent area under the curve (AUC) (Heagerty et al., 2000), implemented with the SurvivalAUC function and package (Heagerty and Saha, 2006), was then used to calculate the accuracy with which the tree model H* was able to predict each observation's actual survival outcome at 21 weeks of follow-up based on the estimated cumulative hazards. This time frame was selected because it was similar to the time frame used in the MTLD study.

4.3 Results

4.3.1 Scenario A: Linear temporal feature

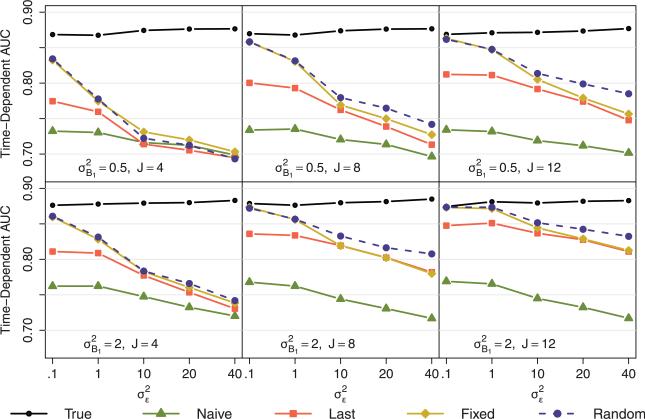
Results for the linear temporal feature are shown in Fig. 3 and in Table S1 of the supplementary web-based material. As expected, the accuracy of the hypothetical scenario assuming a known temporal feature (true method) was highest across all the data scenarios. Among the methods reflecting actual scenarios (fixed- and random-effects, naive, and last), the accuracies tended to decrease with higher within-subject variability, lower between-subject variability, and fewer repeated measures.

Figure 3.

Simulation results from scenario A (linear temporal feature). The plotted values represent the median time-dependent AUC for 1000 simulations of training and testing samples of N = 500 each. The top and bottom rows display results from data generation scenarios with smaller and larger between-subject variability, respectively. The first, second, and third columns, display results from data generation scenarios with 4, 8, and 12 repeatedly measured covariates, respectively. Within each line graph, the five different methods are compared across data generation scenarios ranging from small to large within-subject variability.

With lower within-subject variability, the fixed- and random-effects methods performed similarly, both showing an advantage over the last and naive methods. As the within-subject error increased, the random-effects method began to show an advantage over the fixed-effects method, particularly with more repeated measures, while the fixed-effects and last methods began to perform more similarly. The fixed- and random-effects and last methods had greater accuracies than the naive method in all scenarios except for large within-subject error, small between-subject error, and only four repeated measurements.

4.3.2 Scenario B: Quadratic temporal feature

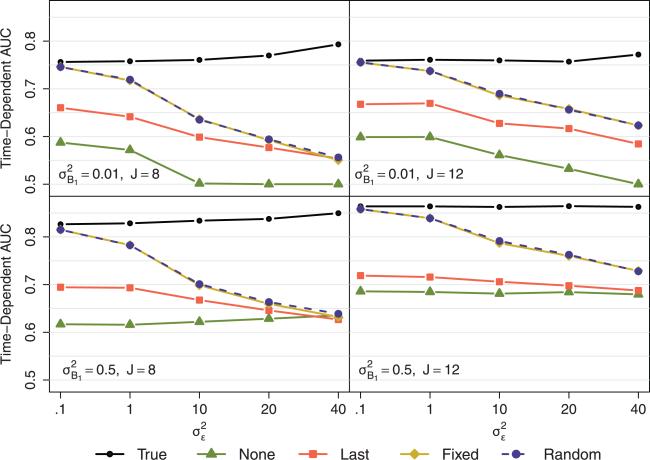
Results for the quadratic temporal feature are shown in Fig. 4 and in Table S2 of the supplementary web-based material. As expected, the predictive accuracy of the hypothetical scenario assuming a known temporal feature (true method) was highest. Overall, the accuracies of the methods reflecting actual scenarios (fixed- and random-effects, naive, and last) tended to decrease with higher within-subject variability, lower between-subject variability, and fewer repeated measures. The fixedand random-effects methods performed almost identically throughout all data scenarios.

Figure 4.

Scenario B: Quadratic temporal feature. Plotted values represent the median time-dependent AUC for 1000 simulations of training and testing samples of N = 500 each. The top and bottom rows display results from data generation scenarios with smaller and larger between-subject variability, respectively. The first and second columns display results from data generation scenarios with 8 and 12 repeatedly measured covariates, respectively. Within each line graph, the five different methods are compared across data generation scenarios ranging from small to large within-subject variability.

With eight repeated measures, the fixed- and random-effects methods were more accurate than the last and naive methods except for high levels of within-subject error; the last method was also more accurate than the naive method except for with higher between- and within-subject variability. With 12 repeated measures, the fixed- and random-effects methods consistently performed better than the naive and last methods. The last method performed better than the naive method with smaller between-subject variability but was more similar to the naive method with larger between-subject variability.

5 Application

We applied our proposed methodology to data from the MTLD I clinical trial (Reynolds et al., 1999) to identify subgroups of older adults who might benefit from a change in acute treatment strategy after only four weeks. Participants in this clinical trial were required to be older than 59 and to meet expert clinical judgment and diagnostic criteria for recurrent, nonpsychotic, nondysthymic, unipolar major depression. During the acute treatment phase of the trial, 180 patients were given a combination therapy of nortriptyline with steady-state levels from 80 to 120 ng/mL and weekly interpersonal therapy. After remission from depression, they were observed in a continuation phase, and as long as they did not relapse, they were randomized to maintenance therapies with a 2 × 2 randomized block design using placebo drug versus nortriptyline and a medical clinic versus interpersonal therapy.

Our analysis included data from the first 26 weeks of acute treatment; however, only the N = 158/180 (88.88%) individuals who did not experience depression remission during the first four weeks were included in this analysis. Our outcome of interest, remission from depression, was defined as occurring when the 17-item HRSD (HRSD-17) score was ≤ 10 for at least three consecutive weeks. Baseline predictors of interest are summarized in Table 1. The statistical package R version 2.12.0 (R Development Core Team, 2008) was used for all analyses.

Table 1.

Baseline clinical and demographic characteristics of a subset of patients in the Maintenance Therapies in Late-Life Depression (MTLD) clinical trial.

Continuous measures	N	Median (IQR)
Baseline Hamilton 17-Item Rating Scale for Depression (HRSD)	158	19 (17–22)
Brief Symptom Inventory (BSI) Anxiety Subscale	157	0.833 (0.167–1.333)
Interpersonal Support and Evaluation List Self Esteem Score (ISEL-SE)	155	4 (2–7)
Cumulative Illness Rating Scale for Geriatrics (CIRS-G)	154	7 (5–9)
Pittsburgh Sleep Quality Index (PSQI)	113	11 (8–14)
Education (years)	157	12 (12–14)
Age (years)	158	67 (63–71)
Depression Duration (years since first episode)	158	15.5 (4–34.75)

Categorical measures	N	% (n)
Female	158	74.05 (117)
White	158	94.30 (149)

5.1 Modeling rate of change of depression symptomatology

To estimate individual rates of change in depression symptomatology during the first four weeks of acute treatment, the lme function in the nlme package (Pinheiro et al., 2010) was used to fit a linear random-effects model, as given in Eq. 3, where β = (β₀, β₁)′, b_k = (b₀, b₁)′, and

$${\mathbf{X}}_i={\mathbf{Z}}_i=[1{\mathbf{t}}_i-{\stackrel{‒}{t}}_i],$$ (5)

with t_i = (t_i1, . . . , t_iJ )′, ${\stackrel{‒}{t}}_i={\sum }_{i=1}^{J_i}{t}_{ij}∕J_i$.

After fitting the model, the fixed-effects parameters and the between- and within-subject variance/covariance matrices were estimated as $\widehat{\beta }={(16.24,-1.59)}^{\prime }$, ${\widehat{\sigma }}_e^2=9.36$, and

$$\widehat{\mathbf{G}}=\left[\begin{array}{cc}\hfill 10.99\hfill & \hfill 1.34\hfill \\ \hfill 1.34\hfill & \hfill .77\hfill \end{array}\right],$$ (6)

respectively. The N = 158 estimated rates of change were calculated as ${\widehat{\mathbf{B}}}_1={\widehat{\beta }}_1+{\widehat{\mathbf{b}}}_1$. These slopes had a median of −1.60 and an interquartile range (−1.99, −1.24). Thus, the majority of individuals had decreasing rates of change in depressive symptomatology, as would be expected during acute treatment.

5.2 Fitting a tree-structured model incorporating rate of change of depressive symptomatology

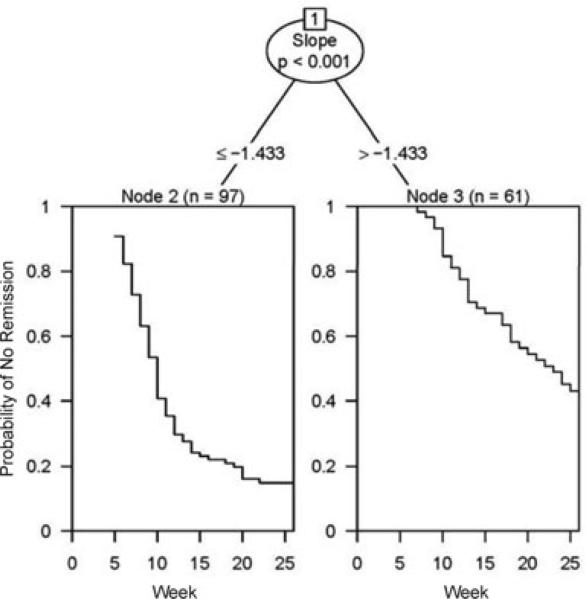
The ctree function (Hothorn et al., 2006) was used to fit a conditional inference tree-structured survival model using the estimated slopes and fixed time covariates shown in Table 1 as possible predictors. The resulting tree, displayed in Fig. 5, identified two risk groups based on the random-effects rate of change in depressive symptomatology during the first four weeks of treatment. The median survival time for node 2 was 10 weeks, with a 95% confidence interval of (9, 11). The median survival time for node 3 was 23 weeks, with a 95% confidence interval of (18, 26 +). Thus, the individuals with slower decreases in depression symptomatology during the first four weeks (slope > 1.−433) were at significantly higher risk of not remitting from depression by the end of acute treatment. Although our initial interest was in identifying additional baseline covariates in addition to the temporal features that might define these subgroups, none of the baseline variables appeared in the final model.

Figure 5.

Tree-structured survival model for depression remission using a two-stage random-effects model to estimate the individual linear rates of change in depression symptomatology during the first four weeks of acute treatment. The tree splits on the rate of change of depressive symptomatology across the first four weeks of acute treatment. Individuals with a more negative slope (n = 97) have faster time to remission compared to individuals with a less negative slope (n = 61).

5.3 Classifying new cases

To classify a new patient k using the tree model in Fig. 5, it is first necessary to estimate his or her individual HRSD-17 slope B_k1 based on observations W_k(t_{k j}), j = 1, . . . , J_k, over the first four weeks of treatment. Because a random-effects approach was used for the original model, this estimate is calculated as ${\widehat{B}}_{k1}={\widehat{\beta }}_1+{\widehat{b}}_{k1}$, where ${\widehat{\beta }}_1=-1.59$ is the estimated population averaged slope from the original random-effects model. The individual deviation from the population averaged slope b̂_k1 is calculated as

$${\widehat{\mathbf{b}}}_k=\widehat{\mathbf{G}}{\mathbf{Z}}_k^{\prime }{\widehat{\mathbf{V}}}_k^{-1}({\mathbf{W}}_k-{\mathbf{X}}_k\widehat{\beta }),$$ (7)

where V̂_k = Z_kĜZ_k + R̂_k,Ĝ is equal to the estimated between-subject variance/covariance matrix given in Eq. 6, and ${\widehat{\mathbf{R}}}_k={\widehat{\sigma }}_{∊}^2{\mathbf{I}}_{J_k\times J_k}$, with ${\widehat{\sigma }}_{∊}^2=9.36$. The fixed- and random-effects design matrices are constructed as

$${\mathbf{X}}_k={\mathbf{Z}}_k=[\mathbf{t}{\mathbf{t}}_k-{\stackrel{‒}{t}}_k],$$

where t_k = (t_k1, . . . , t_kJk)′ and ${\stackrel{‒}{t}}_k={\sum }_{k=1}^{J_k}{t}_{kj}$. The estimated HRSD-17 slope ${\widehat{\beta }}_1+{\widehat{b}}_{k1}$ is then used to classify the new individual k into a risk group in Fig. 5.

6 Conclusions

Temporal features, such as slope and curvature of a trajectory over time, can be important predictors of future survival events. In this manuscript, we proposed to model these features through fixedand random-effects polynomial regression models and incorporate them into tree-structured survival models. We also proposed methods for using the resulting models to predict survival outcomes for new cases not in the original cohort.

To illustrate our proposed methods, data from a late-life depression study were used to develop a tree-structured model to identify individuals who would benefit from a modification in their treatment after only four weeks. The rate of change in depression symptomatology over the first four weeks of acute treatment was estimated using the random-effects approach and, subsequently, included in a tree model with other baseline covariates of interest, including baseline depression severity. The tree-structured model split on the slope, such that individuals with slower decreases in their depression symptomatology had a significantly longer median time to remission. Thus, although baseline depression severity was included as a possible predictor, it was “trumped” by the rate of change of depression over the first four weeks.

A simulation study was conducted to assess the accuracy of the proposed methods for predicting survival outcomes. Because the proposed fixed- and random-effects methods may require a computer for classification of new individuals, the accuracy of a simpler method that uses the last observed value as a proxy for the temporal feature was also evaluated. These methods were compared to a naive method assuming no temporal feature and a hypothetical method where the true temporal feature was known. We assessed two scenarios: (A) a linear feature related to the survival outcome, and (B) linear and quadratic features related to the survival outcome.

When a linear temporal feature was related to the outcome, the accuracy of the random-effects method was similar to or greater than the accuracies of the fixed-effects, last value, and naive methods. The random-effects method showed a particular advantage over the fixed-effects, last value, and naive methods when larger between- and within-subject variability was present. This finding may be explained by the fact that only the random-effects method incorporates information from other observations to stabilize individual estimates in the presence of large within-subject variability (Brown and Prescott, 1999). Unlike the random-effects method, the fixed-effects method does not incorporate information from other individuals’ observations. However, it does incorporate multiple time points to estimate the temporal feature, making it more stable than the last value and naive methods. Thus, in scenario A, the accuracy of the fixed-effects method was greater than that of the last value method when the within-subject variability was small. The naive method only incorporated information about the trajectory from the baseline value, which had a low correlation with the slope in scenario A. Thus, the accuracy of the naive method was only similar to the accuracies of other methods when they had little available trajectory information (i.e. very large within-subject variability and only four repeated measures).

When both linear and quadratic temporal features were related to the outcome of interest, the accuracy of the random- and fixed-effects were very similar. These methods were comparable to the true method with very small levels of within-subject variability. However, with larger within-subject variability, the accuracies of the fixed- and random-effects methods dropped to a much lower level than was seen in the scenario A. The accuracies of the naive and last methods were more similar to the accuracies of the fixed- and random-effects methods when more repeated measures were available. This finding may be explained by the fact that the quadratic term was centered, and thus, the first and last values represented the most extreme points of the curve. As the number of observations increases, these extreme values are able to provide more information about the amount of curvature in the trajectory.

Overall, the simulation results suggest that if only linear features are included in the tree model, the random-effects method should be preferred if classification using a computer is practical and estimates of within- and between-subject variability from the original tree model are available. If these estimates are not available, the fixed-effects method may still provide results that are clinically comparable (i.e. a similar effect size) to the random-effects method, albeit less statistically accurate with larger within-subject variability. When classification using a computer is not practical, tree models created using the last value as a proxy for the linear feature may result in accuracies comparable to those of the fixed- or random-effects method when large within-subject variability is present or when few repeated observations are available. For quadratic features, it may be best to only use repeatedly measured data with smaller levels of within-subject variability. In these scenarios the fixed- and random-effects methods performed relatively well, but their accuracies quickly decreased with larger within-subject error.

Further simulation studies should be performed to identify situations that may yield differential results. In particular, it would be informative to investigate how larger or smaller linear and quadratic effects impact the accuracies of the various methods. Additionally, because the random-effects model is known for its ability to accommodate missing data (Brown and Prescott, 1999), it would be of interest to run further simulation studies to determine the extent to which this method is preferable under various percentages of missing data. Finally, our simulations were set up so that the linear temporal feature was the first split on the tree, thus playing a critical role in the prediction of subsequent events. However, if the design of the true tree model had incorporated the linear temporal feature further down the tree, implying a weaker relationship between the outcome and the temporal feature, the proposed methods may not have shown such an advantage over the naive method. If the true tree model in scenario B had split first on the quadratic feature instead of on the linear feature, the simulation results may also have been different.

Our proposed approach has many advantages that can lead to an accurate and reliable tree-structured model. However, there are also a number of limitations to consider. One such limitation is that it is necessary to identify a landmark time point t_s prior to the use of the proposed methodology. In the application to late-life data, a landmark time point of four weeks was selected due to prior research identifying four weeks as a critical decision point in acute treatment of late-life depression (Mulsant et al., 2006). When prior knowledge is not available, it may be necessary to identify a landmark time point that will allow for the largest number of individuals to be included in the model while still providing enough repeated measures to accurately estimate the temporal feature.

Additional limitations are related to the selection and use of the polynomial regression model for estimating temporal features. First, the use of the polynomial regression model requires that the temporal features have a linear relationship with time. Either functional mixed-effects models or nonlinear mixed-effects models could be used if more flexibility is required. Second, the proposed polynomial regression model does not include covariates, possibly leading to estimation error when covariates affect the true shape of the trajectory. Third, all individuals in the sample are required to have the same functional form when using this model. For situations where latent or covariate-based subgroups are expected to have different functional forms, multiple polynomial regression models could be used. However, this would require a priori identification of these subgroups. To address this challenge, we are developing tree-structured methods for longitudinal outcomes, such as those proposed by Segal (1992), to identify empirically based subgroups that exhibit trajectories with different functional forms.