Abstract
Activity patterns of neural population are constrained by underlying biological mechanisms. These patterns are characterized not only by individual activity rates and pairwise correlations but also by statistical dependencies among groups of neurons larger than two, known as higher-order interactions (HOIs). While HOIs are ubiquitous in neural activity, primary characteristics of HOIs remain unknown. Here, we report that simultaneous silence (SS) of neurons concisely summarizes neural HOIs. Spontaneously active neurons in cultured hippocampal slices express SS that is more frequent than predicted by their individual activity rates and pairwise correlations. The SS explains structured HOIs seen in the data, namely, alternating signs at successive interaction orders. Inhibitory neurons are necessary to maintain significant SS. The structured HOIs predicted by SS were observed in a simple neural population model characterized by spiking nonlinearity and correlated input. These results suggest that SS is a ubiquitous feature of HOIs that constrain neural activity patterns and can influence information processing.
Information in the brain is represented by the collective spiking activity of multiple neurons1. Activity patterns of observed neurons are highly structured due to various underlying biological mechanisms including direct anatomical connections2,3, indirect connections mediated by unobserved neurons4,5, and intrinsic nonlinearity of individual neurons6,7. However, exploration of this structure is non-trivial due to limited data size in comparison to possible combinations of activity patterns that grow exponentially with population size.
To infer the structure of neural activity patterns from limited amount of data, the maximum entropy principle has been successfully applied8,9. Under this principle, the probability distribution of activity patterns is estimated to be the least structured distribution that is consistent with a set of observed activity statistics. Conventionally this maximum entropy distribution is statistically characterized by parameters of different orders, where the orders refer to the numbers of subset neurons that these parameters constrain. The model with the first-order parameters fits to the observed activity rates of individual neurons. The model that additionally includes the second-order parameters further adjusts the observed deviations of pairwise correlations from the chance coincidence expected from the individual activity rates. The second-order parameters are referred to as pairwise interactions. More generally, the model that includes up to the k-th (k = 3, 4, . . . ) order interactions adjusts simultaneous activation rates of k neurons from the expectation based on interactions up to the (k-1)-th order. Interactions beyond the pairwise interactions (k> 2) are collectively termed higher-order interactions (HOIs)10,11. Notably, these interactions refer to statistical dependency of neurons, and do not necessarily involve anatomical connections.
In earlier studies, individual activity rates and pairwise correlations alone could explain ~ 90% of variability in activity patterns of small populations of retinal ganglion cells8,9 and cortical neurons12,13. However, this does not exclude the existence of HOIs or limit their contribution to information processing. Indeed, the addition of HOIs to a statistical model significantly improved the goodness-of-fit to neural activities obtained from multi unit activity14,15, single unit activity5,16,17,18,19,20, and local field potential21,22 in both in vivo and in vitro preparations. Furthermore, HOIs are relevant in neural information coding14,16,18,23. However, previous studies have not identified a key feature in HOIs that summarizes the principal role of seemingly diverse HOIs.
One of the most striking features of neural population activity is simultaneous silence (SS). The spiking activity of individual neurons is known to be sparse24. As a result, the most commonly observed activity pattern in typical networks is the pattern in which all neurons are silent. Does SS involve HOIs? Indeed, departures from the level of expected SS from individual activity rates and pairwise correlations (excess SS) were empirically reported previously16,17,18,19,20. However, the significance of SS in characterizing HOIs of the population activity is not well understood.
Here, we examine SS in population activity of the hippocampal CA3 networks in cultured slices. Previous studies demonstrated that CA3 pyramidal cells in the organotypic slice cultures are wired with an in vivo-like connection probability of 15–30%3, and their spontaneous spike rates are closer to those of in vivo hippocampal neurons25, compared to neurons in acute slice preparations. We demonstrate that most local groups of hippocampal neurons that possess HOIs express excess SS. A single parameter that quantifies SS accounts for about 20% of the variability in population activity patterns that is produced by numerous HOIs. We then confirm specific oscillatory structure of HOIs at successive interaction orders predicted from the SS. Through modeling, we also demonstrate that correlated population activity caused by spiking nonlinearity and correlated input exhibits the same structure of HOIs, and that this structure conveys information of input. These results suggest that neurons are operating in a unique regime where they are constrained to be silent simultaneously.
Results
Simultaneous silence and HOIs of hippocampal neurons
We analyzed the spontaneous spiking activity of putative neurons in the
hippocampal CA3 area of organotypic slice cultures, measured by the Calcium
imaging method. Slices were prepared from postnatal day 7, and then
cultivated from day 7 to 14 (see Methods). Neuronal activity was detected by
onsets of calcium transients3,26,27,28, which provided
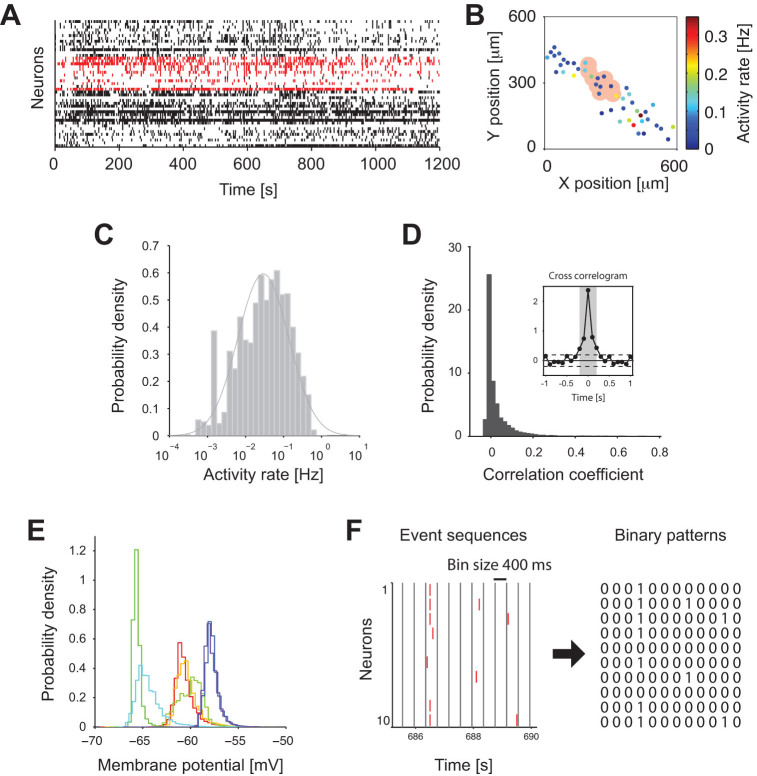
event-timing data with a resolution of 100 ms. Fig. 1A
and B display an example of population event activity of a single
slice culture, and spatial positions and activity rates of individual neurons.
We analyzed 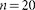 slices in total, and found
the following features. First, activity rates of the neurons from all slices
were distributed close to a log-normal distribution (Fig.
1C), similarly to spike rates of in vivo hippocampal CA3
neurons of awake rodents29,30. The rates of calcium events in
individual cells computed from 2122 neurons in 20 slices were 0.073 ±
0.097 (mean ± standard deviation (SD) events/s; median 0.035,
interquartile range 0.01–0.097 events/s). Notably, activity rates of
neurons in cultured slices were close to those under an awake in vivo
condition25. Second, the activity of pairs of neurons was
only weakly correlated (Fig. 1D). Average correlation
coefficient was 0.033 ± 0.065 SD (detection in a 100 ms
window). A cross-correlogram revealed that, on average, the activity of pairs of
neurons was not correlated after a ~ 400 ms timelapse (Fig. 1D inset). Third, intracellular voltage recordings under the
same experimental conditions all reveal uni-modal distributions of membrane
potentials (Fig. 1E). Hence, no obvious sign of a
superposition of UP and DOWN states was detected.
slices in total, and found
the following features. First, activity rates of the neurons from all slices
were distributed close to a log-normal distribution (Fig.
1C), similarly to spike rates of in vivo hippocampal CA3
neurons of awake rodents29,30. The rates of calcium events in
individual cells computed from 2122 neurons in 20 slices were 0.073 ±
0.097 (mean ± standard deviation (SD) events/s; median 0.035,
interquartile range 0.01–0.097 events/s). Notably, activity rates of
neurons in cultured slices were close to those under an awake in vivo
condition25. Second, the activity of pairs of neurons was
only weakly correlated (Fig. 1D). Average correlation
coefficient was 0.033 ± 0.065 SD (detection in a 100 ms
window). A cross-correlogram revealed that, on average, the activity of pairs of
neurons was not correlated after a ~ 400 ms timelapse (Fig. 1D inset). Third, intracellular voltage recordings under the
same experimental conditions all reveal uni-modal distributions of membrane
potentials (Fig. 1E). Hence, no obvious sign of a
superposition of UP and DOWN states was detected.
Figure 1. Ensemble activity of CA3 putative neurons detected by Calcium imaging.
(A) Ensemble activity of 45 neurons from a single hippocampal slice. Small vertical ticks indicate events detected from calcium imaging signals. Ensemble activity of an example group of 10 neurons is marked in red. (B) Spatial distribution of neurons in the CA3 area of the slice in A. Each filled circle represents a position of a neuron. The color indicates activity rate of each neuron. The pink area corresponds to the example group highlighted in A. (C) Distribution of activity rates from neurons in all 20 slices. Solid line is a fitted log-normal distribution. (D) Distribution of correlation coefficients calculated from the event sequences (within a 100 ms window) from all the pairs of neurons in 1000 neighboring groups from 20 slices. The inset shows an average cross-correlogram from all the pairs of neurons. Dashed lines indicate ± 2 SD of the correlogram at 1–2 sec lags. The gray shading (−0.2 ms to + 0.2 ms) indicates the interval where the correlgoram exceeded the dashed lines. (E) Distributions of membrane potentials recorded from neurons (n = 7) in hippocampal slice cultures under the same condition as described in Methods. Different colors indicate different neurons. In all cases, the densities of the membrane potentials were characterized by a unimodal profile. (F) Construction of binary patterns from event sequences. The event sequences are binned using a window of 400 ms. In each bin, we denote ‘0’ if there is no event, and ‘1’ if there is at least one event.
To analyze the correlated activity of multiple neurons, 50 groups of 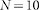 neighboring neurons were selected from
each of 20 slices (see an example group of neurons shaded in pink in Fig. 1B and events marked in red in Fig.
1A), for a total of 1000 groups of 10 nearest-neighbor cells. The
centers of groups were sampled according to the spatial density of cells in the
CA3 area (See Methods). The average ‘radius’ of the 1000
groups was 36.6 (±13.4 SD) μm, where the radius of a group
was computed as the mean Euclidean distance of its cell positions from the
group's center position. We then represented the activity of the
ith neuron
neighboring neurons were selected from
each of 20 slices (see an example group of neurons shaded in pink in Fig. 1B and events marked in red in Fig.
1A), for a total of 1000 groups of 10 nearest-neighbor cells. The
centers of groups were sampled according to the spatial density of cells in the
CA3 area (See Methods). The average ‘radius’ of the 1000
groups was 36.6 (±13.4 SD) μm, where the radius of a group
was computed as the mean Euclidean distance of its cell positions from the
group's center position. We then represented the activity of the
ith neuron 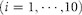 in a time window
by a binary variable
in a time window
by a binary variable 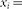 {0,1}, where
‘1’ denotes an active state in which at least one event
occurred, and ‘0’ represents an inactive, or
‘silent’, state in which no events occurred (Fig. 1F). We used a 400 ms time-window in the
subsequent analyses to incorporate the temporal correlation observed in the
cross-correlogram (c.f. the shaded interval in Fig. 1D
inset).
{0,1}, where
‘1’ denotes an active state in which at least one event
occurred, and ‘0’ represents an inactive, or
‘silent’, state in which no events occurred (Fig. 1F). We used a 400 ms time-window in the
subsequent analyses to incorporate the temporal correlation observed in the
cross-correlogram (c.f. the shaded interval in Fig. 1D
inset).
To examine if hippocampal neurons exhibit collective activity beyond what can be
explained by pairwise interactions, we compared the activity patterns of a group
of observed neurons with those predicted from a pairwise maximum entropy
model8,9,31, 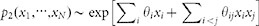 .
This model provides the least structured probability distribution that is
consistent with the observed activity rates of individual neurons and
correlations between pairs of neurons. The parameters
.
This model provides the least structured probability distribution that is
consistent with the observed activity rates of individual neurons and
correlations between pairs of neurons. The parameters 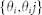 were adjusted to fit these statistics. We call this
model a pairwise model hereafter. First, we examined if the neurons exhibited SS
beyond that predicted by the pairwise correlations. To this end, we compared the
observed probability of the pattern in which all of 10 neurons are
simultaneously silent with its probability according to the pairwise model.
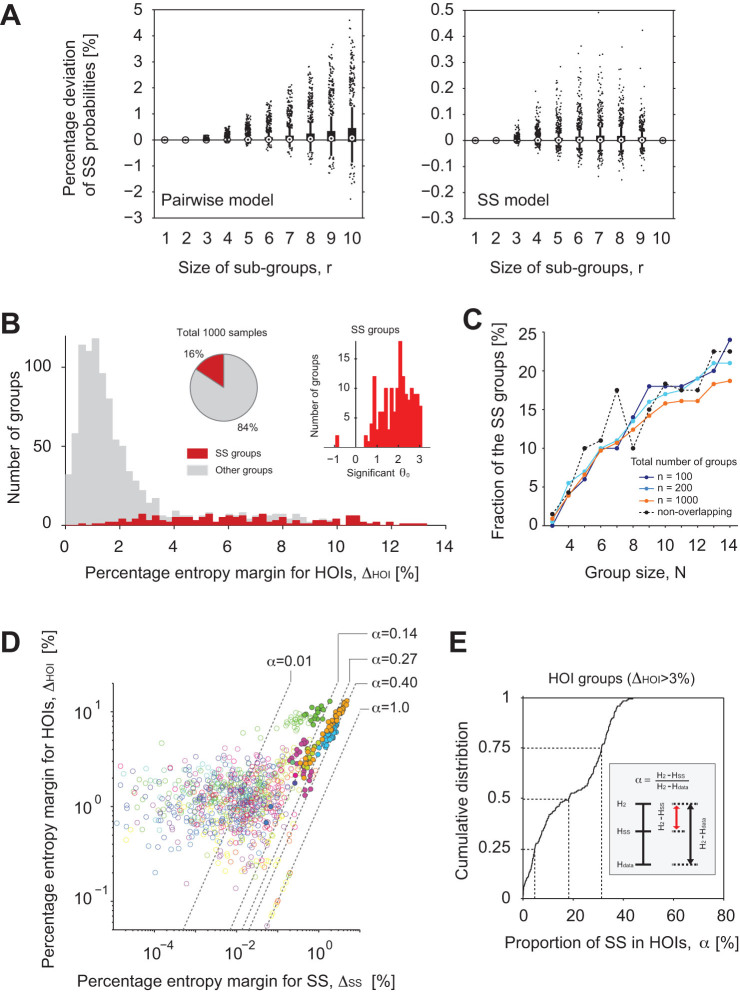
Figure 2A displays a distribution of percentage
deviation of observed SS probabilities from the prediction of the pairwise
model,
were adjusted to fit these statistics. We call this
model a pairwise model hereafter. First, we examined if the neurons exhibited SS
beyond that predicted by the pairwise correlations. To this end, we compared the
observed probability of the pattern in which all of 10 neurons are
simultaneously silent with its probability according to the pairwise model.
Figure 2A displays a distribution of percentage
deviation of observed SS probabilities from the prediction of the pairwise
model, 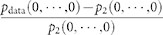 , where
, where 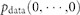 is the observed probability of SS. In some groups,
the pairwise model tended to underestimate the occurrence probability of SS of
10 neurons. This discrepancy has to be explained by HOIs in the data.
is the observed probability of SS. In some groups,
the pairwise model tended to underestimate the occurrence probability of SS of
10 neurons. This discrepancy has to be explained by HOIs in the data.
Figure 2. Sub-groups of 10 hippocampal neurons exhibit longer periods of SS than predicted from pairwise interactions.
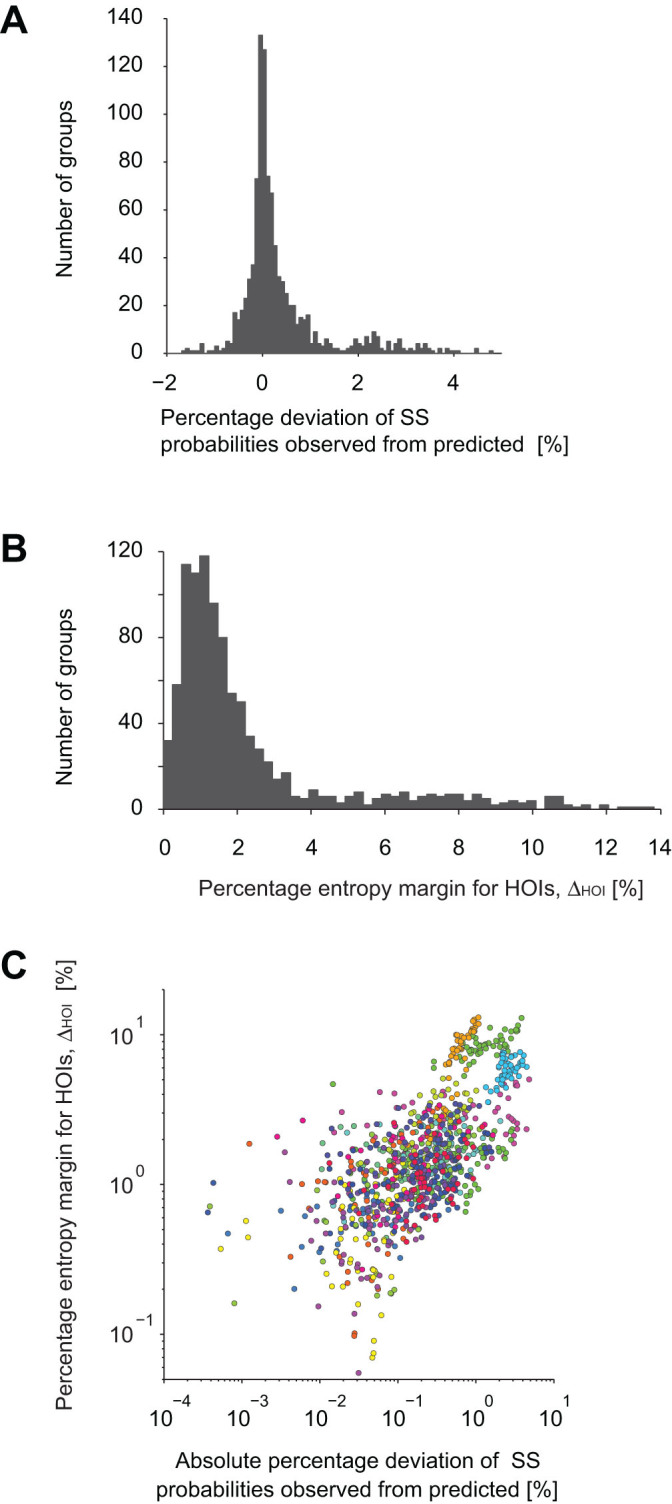
(A) Distribution of the percentage deviation of the observed probability of
SS of 10 neurons from the prediction of the pairwise model, 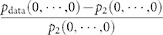 . Positive values indicate more
frequent SS in the data than predicted by the pairwise model. (B) Histogram
of percentage entropy margins for HOIs computed as
. Positive values indicate more
frequent SS in the data than predicted by the pairwise model. (B) Histogram
of percentage entropy margins for HOIs computed as 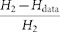 . (C) Dependency of the percentage
entropy margin for HOIs on the percentage deviation of the observed from
predicted probabilities of SS. The same color indicates groups selected from
the same slice culture. 5 outliers were excluded from the plots.
. (C) Dependency of the percentage
entropy margin for HOIs on the percentage deviation of the observed from
predicted probabilities of SS. The same color indicates groups selected from
the same slice culture. 5 outliers were excluded from the plots.
To examine the contribution of HOIs to population activity, we computed the
fraction of entropy that is explained by HOIs. This fraction, referred to as the
percentage entropy margin for HOIs, is quantified as  , where
, where 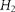 is
the entropy of the pairwise model and
is
the entropy of the pairwise model and 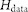 is the entropy of the observed histogram of population activity patterns. We
call
is the entropy of the observed histogram of population activity patterns. We
call 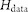 the data entropy in the
following. The data entropy is characterized by all of the first, second, and
HOIs. Therefore, the difference between
the data entropy in the
following. The data entropy is characterized by all of the first, second, and
HOIs. Therefore, the difference between 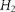 and
and 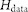 must be explained by
HOIs. We found that the distribution of
must be explained by
HOIs. We found that the distribution of 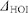 exhibited a long tail (Fig. 2B). This indicates
that there were a noticeable number of groups in which HOIs played a much
stronger role in shaping population activity. Finally, we explored the relation
between the contributions of HOIs to the probability of SS. We found that the
groups expressing higher/lower probabilities of SS than the pairwise model
coincided with the groups possessing large entropy margins for HOIs (Fig. 2C). The positive correlation between these two values
in Fig. 2C (Spearman's rank correlation
coefficient 0.69, p <0.001) implies that a significant
portion of the HOIs of the CA3 neurons may be explained by the SS. The rank
correlation coefficient was higher (0.92) and statistically significant
(p < 0.001) if we analyze non-overlapping groups.
exhibited a long tail (Fig. 2B). This indicates
that there were a noticeable number of groups in which HOIs played a much
stronger role in shaping population activity. Finally, we explored the relation
between the contributions of HOIs to the probability of SS. We found that the
groups expressing higher/lower probabilities of SS than the pairwise model
coincided with the groups possessing large entropy margins for HOIs (Fig. 2C). The positive correlation between these two values
in Fig. 2C (Spearman's rank correlation
coefficient 0.69, p <0.001) implies that a significant
portion of the HOIs of the CA3 neurons may be explained by the SS. The rank
correlation coefficient was higher (0.92) and statistically significant
(p < 0.001) if we analyze non-overlapping groups.
Simultaneous silence is a ubiquitous feature of HOIs
To directly examine the contribution of the SS to the entropy explained by HOIs, we constructed a maximum entropy model that augments the pairwise model with a single additional term to account for the probability of SS observed in the data. We refer to this model as the SS model:
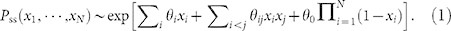 |
Here a single parameter, 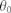 ,
was introduced to account for the probability of SS of
,
was introduced to account for the probability of SS of 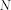 neurons. Positive or negative
neurons. Positive or negative 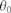 indicates that the probability of SS of all neurons
is more or less than predicted by the pairwise model, respectively. Importantly,
this new SS term is equivalent to adding specific structured HOIs into the
pairwise model. By expanding the SS term into the standard HOI-coordinates, we
obtain
indicates that the probability of SS of all neurons
is more or less than predicted by the pairwise model, respectively. Importantly,
this new SS term is equivalent to adding specific structured HOIs into the
pairwise model. By expanding the SS term into the standard HOI-coordinates, we
obtain  Hence, increasing or decreasing
the total period of quiescence is equivalent to introducing a single parameter
to the HOIs with alternating signs for different orders of interaction. In
addition to capturing individual activity rates and pairwise correlations, the
SS model explores this 1-dimensional structure in the high-dimensional space of
HOIs to fit the rate of SS. We fitted the SS model to the same 1000 groups of
10 hippocampal neurons obtained from 20 slices. Note that, in each
group, the fitted first and second order parameters of the SS model are
generally different from those of the pairwise model because of the newly
introduced SS term.
Hence, increasing or decreasing
the total period of quiescence is equivalent to introducing a single parameter
to the HOIs with alternating signs for different orders of interaction. In
addition to capturing individual activity rates and pairwise correlations, the
SS model explores this 1-dimensional structure in the high-dimensional space of
HOIs to fit the rate of SS. We fitted the SS model to the same 1000 groups of
10 hippocampal neurons obtained from 20 slices. Note that, in each
group, the fitted first and second order parameters of the SS model are
generally different from those of the pairwise model because of the newly
introduced SS term.
We compared goodness-of-fit of the SS model with that of the pairwise model
(Fig. 3A). The ordinate of the panels represents
percentage differences between observed and predicted SS probabilities of
sub-groups of 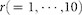 neurons by the two
models (Left, the pairwise model; Right, the SS model). By definition, the
pairwise model adjusts the silence rates of individual neurons (equivalent to 1
minus activity rates,
neurons by the two
models (Left, the pairwise model; Right, the SS model). By definition, the
pairwise model adjusts the silence rates of individual neurons (equivalent to 1
minus activity rates, 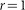 ) and pairs (
) and pairs (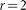 ) (Fig. 3A Left
panel). However, the pairwise model fitted to the data underestimated
probabilities of SS for larger sub-groups of neurons. This means that many
sub-groups of hippocampal neurons expressed SS more often than chance as
predicted from their activity rates and the pairwise correlations. In contrast,
the SS model additionally accounts for the probability of SS of all 10 neurons
in a group (see the complete match of the data and prediction at
) (Fig. 3A Left
panel). However, the pairwise model fitted to the data underestimated
probabilities of SS for larger sub-groups of neurons. This means that many
sub-groups of hippocampal neurons expressed SS more often than chance as
predicted from their activity rates and the pairwise correlations. In contrast,
the SS model additionally accounts for the probability of SS of all 10 neurons
in a group (see the complete match of the data and prediction at 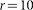 in addition to
in addition to 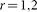 in Fig. 3A Right panel).
Order of magnitude reductions in the differences were observed in the SS of many
sub-groups (
in Fig. 3A Right panel).
Order of magnitude reductions in the differences were observed in the SS of many
sub-groups (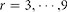 ). (Note the scale
difference in the Left and Right panels.).
). (Note the scale
difference in the Left and Right panels.).
Figure 3. Significant SS is observed in the groups of 10 neurons exhibiting HOIs.
(A) (Left) Comparison of the observed SS probabilities of sub-groups of  neurons with predictions of the
pairwise model. Abscissa, the size
neurons with predictions of the
pairwise model. Abscissa, the size  of sub-groups. Ordinate, the percentage deviation of observed
from predicted average SS probabilities of sub-groups of neurons, where the
normalization divides the difference by SS probability predicted from a
pairwise model. The comparison was performed for all possible sub-groups of
of sub-groups. Ordinate, the percentage deviation of observed
from predicted average SS probabilities of sub-groups of neurons, where the
normalization divides the difference by SS probability predicted from a
pairwise model. The comparison was performed for all possible sub-groups of
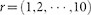 neurons in the 1000 groups
of 10 neurons. Whiskers represent 1.5 times the distance from
25th to 75th percentile. Dots are outliers. (Right) Comparison of the
observed SS probabilities of the sub-groups with predictions of the SS
model. Note the difference in the scales of the ordinates in the Left and
Right panels. (B) Distribution of percentage entropy margins for HOIs for
the SS groups (red, 16%), i.e. groups for which the SS model showed
significantly better fit than the pairwise model, and the rest of the groups
(gray, 84%). The right inset shows distribution of the parameter
neurons in the 1000 groups
of 10 neurons. Whiskers represent 1.5 times the distance from
25th to 75th percentile. Dots are outliers. (Right) Comparison of the
observed SS probabilities of the sub-groups with predictions of the SS
model. Note the difference in the scales of the ordinates in the Left and
Right panels. (B) Distribution of percentage entropy margins for HOIs for
the SS groups (red, 16%), i.e. groups for which the SS model showed
significantly better fit than the pairwise model, and the rest of the groups
(gray, 84%). The right inset shows distribution of the parameter 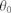 of the SS groups. The
distribution was heavily biased toward positive
of the SS groups. The
distribution was heavily biased toward positive 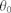 , indicating prevalent excess SS. (C) Group
size dependency of the number of SS groups. Solid lines with different
colors indicate different numbers of groups selected from each slice: 5, 10,
50 groups per slice, for a total of
, indicating prevalent excess SS. (C) Group
size dependency of the number of SS groups. Solid lines with different
colors indicate different numbers of groups selected from each slice: 5, 10,
50 groups per slice, for a total of 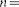 100, 200, and 1000 groups of size
100, 200, and 1000 groups of size 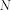 from 20 slices, respectively. The dashed black
line is the result of selecting non-overlapping groups from each slice (see
Methods). Thus, the fraction of SS groups and its group size dependency were
robust to the degree of overlap between sampled groups in each slice. (D)
Scatter plots of entropy margins for HOIs versus entropy margins for SS. The
same color indicates groups selected from the same slice culture. Filled
circles indicate SS groups. Dashed lines represent different proportions of
HOI entropy margin explained by the SS term,
from 20 slices, respectively. The dashed black
line is the result of selecting non-overlapping groups from each slice (see
Methods). Thus, the fraction of SS groups and its group size dependency were
robust to the degree of overlap between sampled groups in each slice. (D)
Scatter plots of entropy margins for HOIs versus entropy margins for SS. The
same color indicates groups selected from the same slice culture. Filled
circles indicate SS groups. Dashed lines represent different proportions of
HOI entropy margin explained by the SS term, 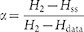 . We excluded 13 outliers from the plots. (E)
Cumulative distribution function of the proportion of SS,
. We excluded 13 outliers from the plots. (E)
Cumulative distribution function of the proportion of SS,  , in the groups exhibiting HOIs (
, in the groups exhibiting HOIs (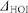 > 3%).
> 3%).
We tested the excess or paucity of SS using the SS model against a null
hypothesis of no such activity (i.e., the hypothesis that the pairwise model is
sufficient to characterize the data). Here, we used 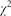 -tests11 with multiple comparison
correction using the Benjamini-Hochberg-Yekutieli method with a false discovery
rate of 0.05 to assess if the SS term significantly improved the fitting in each
group (See Methods). Of 1000 groups, 156 groups (16%) from 10 slices rejected
the null hypothesis (Fig. 3B). We call these groups that
exhibit excess or paucity of SS the SS groups. Statistical properties of the SS
as well as non-SS groups were summarized in Table 1.
Indeed, most of the groups (68%, 133 groups out of 197) that exhibited
relatively large margins of entropy for HOIs (
-tests11 with multiple comparison
correction using the Benjamini-Hochberg-Yekutieli method with a false discovery
rate of 0.05 to assess if the SS term significantly improved the fitting in each
group (See Methods). Of 1000 groups, 156 groups (16%) from 10 slices rejected
the null hypothesis (Fig. 3B). We call these groups that
exhibit excess or paucity of SS the SS groups. Statistical properties of the SS
as well as non-SS groups were summarized in Table 1.
Indeed, most of the groups (68%, 133 groups out of 197) that exhibited
relatively large margins of entropy for HOIs (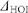 > 3%) were the SS groups. Note that, at
this point, each of the SS groups could have had either significantly positive
or negative
> 3%) were the SS groups. Note that, at
this point, each of the SS groups could have had either significantly positive
or negative 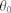 . It turned out that 154
out of the 156 SS groups exhibited significantly positive
. It turned out that 154
out of the 156 SS groups exhibited significantly positive 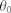 (Fig. 3B Right inset). Thus,
virtually all the SS groups expressed significantly larger probability of SS
than the corresponding pairwise model. In these groups, the total number of bins
for which all neurons were quiet was larger than expected by the corresponding
pairwise model. In other words, activity was confined to a smaller number of
bins. Hence, we conclude that the population activity of most groups exhibiting
HOIs (
(Fig. 3B Right inset). Thus,
virtually all the SS groups expressed significantly larger probability of SS
than the corresponding pairwise model. In these groups, the total number of bins
for which all neurons were quiet was larger than expected by the corresponding
pairwise model. In other words, activity was confined to a smaller number of
bins. Hence, we conclude that the population activity of most groups exhibiting
HOIs (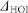 > 3%) was
significantly sparse in time. Note that the observed fraction of SS groups was
robust to the number of groups sampled from each slice but typically increased
with the size of these groups (Fig. 3C).
> 3%) was
significantly sparse in time. Note that the observed fraction of SS groups was
robust to the number of groups sampled from each slice but typically increased
with the size of these groups (Fig. 3C).
Table 1. Activity rates, correlation coefficients, and probabilities of SS computed from binary sequences using 400 ms window under control and PTX conditions. Values are expressed as Mean (± SD).
| Activity rate | Correlation coefficient | Prob. SS | |
|---|---|---|---|
| Control | 0.039 (± 0.042) | 0.060 (± 0.108) | 0.728 (± 0.152) |
| SS groups | 0.032 (± 0.035) | 0.172 (± 0.122) | 0.831 (± 0.103) |
| Non-SS gropus | 0.040 (± 0.043) | 0.040 (± 0.092) | 0.706 (± 0.151) |
| PTX | 0.027 (± 0.017) | 0.920 (± 0.108) | 0.965 (± 0.021) |
Finally, we examined the relation between the percentage entropy margin for HOIs,
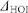 , and the percentage of the HOI
entropy explained by the SS. The latter entropy was computed as
, and the percentage of the HOI
entropy explained by the SS. The latter entropy was computed as 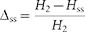 , where
, where 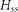 is the entropy of the SS model. Figure 3D displays scatter plots of these values for all groups. As
predicted from Fig. 2C, we observe significant positive
correlation between
is the entropy of the SS model. Figure 3D displays scatter plots of these values for all groups. As
predicted from Fig. 2C, we observe significant positive
correlation between 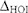 and
and 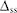 (Spearman's rank correlation
coefficient 0.52, p <0.001). The dashed lines are isoclines of a
constant ratio
(Spearman's rank correlation
coefficient 0.52, p <0.001). The dashed lines are isoclines of a
constant ratio 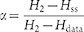 . This ratio describes
the fraction of entropy explained by the SS in the entropy margin for HOIs. As
expected, the SS groups (filled circles) typically had large
. This ratio describes
the fraction of entropy explained by the SS in the entropy margin for HOIs. As
expected, the SS groups (filled circles) typically had large  . Figure 3E displays
a distribution of
. Figure 3E displays
a distribution of  for the groups that
expressed large margin for HOIs (197 groups with
for the groups that
expressed large margin for HOIs (197 groups with 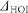 > 3%). In these groups, the single
higher-order parameter of the SS explained 18.3% (interquartile range,
4.7–31%) of the entropy for HOIs (Fig. 3C).
Since we have only added a single parameter in the high-dimensional space of
HOIs, this result implies that the SS comprises one important characteristic of
the HOIs.
> 3%). In these groups, the single
higher-order parameter of the SS explained 18.3% (interquartile range,
4.7–31%) of the entropy for HOIs (Fig. 3C).
Since we have only added a single parameter in the high-dimensional space of
HOIs, this result implies that the SS comprises one important characteristic of
the HOIs.
In order to assess biases that may be caused by limited samples in our data sets, we repeated our analysis using two alternative data sets (Supplementary Fig. S1 online). First, we analyzed only one half of the data by taking every other bin of the original population activity patterns for each slice. Second, we analyzed bootstrapped population activity patterns, where the same number of patterns as the original data were resampled with replacement in each slice. These two data sets contain less variations of population activity patterns than the original data. For the both data sets, the fraction of SS groups was smaller than the 16% found in Fig. 3B. The fraction of the HOIs explained by SS also decreased to less than a half of 18% found in Fig. 3E. Because we did not overestimate these quantities after subsampling and resampling, it is unlikely that our original estimation (16% exhibits significant SS; 18% of HOIs is explained by SS) overestimated the fractions expected from a larger number of samples. In sum, the analyses confirm significant SS in the data, and predict the presence of the alternating signs of HOIs, a possibility we directly test now.
Alternating signs of HOIs predicted by SS
If SS is a major feature of the HOIs, we expect to find HOIs whose signs alternate depending on the orders of interaction (c.f. the expansion of the SS term). In order to directly examine the structure of HOIs, we consider a simple maximum entropy model that includes a single global parameter for each order of HOIs:
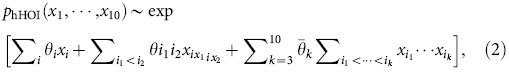 |
where 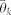 (
(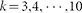 ) is a
single parameter for the
) is a
single parameter for the 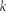 th order HOIs.
The term for the
th order HOIs.
The term for the 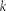 th order interaction
parameterized by a parameter
th order interaction
parameterized by a parameter 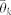 sums all
combinatorial interactions of
sums all
combinatorial interactions of 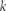 neurons
among 10 neurons. We call this model the homogeneous HOI (hHOI) model. The hHOI
model fitted to the data reproduces the histogram of the number of active
neurons in each time bin14,19,20,32.
neurons
among 10 neurons. We call this model the homogeneous HOI (hHOI) model. The hHOI
model fitted to the data reproduces the histogram of the number of active
neurons in each time bin14,19,20,32.
In these data sets (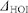 > 3%),
the hHOI model explained 24% of the variability in population activity due to
HOIs (interquartile range 11–34%) as assessed by
> 3%),
the hHOI model explained 24% of the variability in population activity due to
HOIs (interquartile range 11–34%) as assessed by 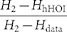 , where
, where 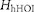 is
the entropy of the hHOI model. This result indicates prevalent heterogeneity in
the HOIs. The result also upper bounds the fraction of entropy for HOIs that
could be explained by the single SS term. We then investigated how
much of this entropy is actually explained by the SS term. Figure
4A displays relations between the percentage entropy
margin explained by the hHOI model,
is
the entropy of the hHOI model. This result indicates prevalent heterogeneity in
the HOIs. The result also upper bounds the fraction of entropy for HOIs that
could be explained by the single SS term. We then investigated how
much of this entropy is actually explained by the SS term. Figure
4A displays relations between the percentage entropy
margin explained by the hHOI model, 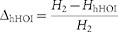 ,
and by the SS model,
,
and by the SS model, 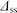 . Similarly to
Fig. 3D, the dashed lines are isoclines of
. Similarly to
Fig. 3D, the dashed lines are isoclines of 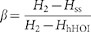 , which quantifies the fraction of entropy
explained by the SS in the entropy margin for the homogenous HOIs. Figure 4B shows a distribution of
, which quantifies the fraction of entropy
explained by the SS in the entropy margin for the homogenous HOIs. Figure 4B shows a distribution of 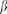 for the groups exhibiting HOIs (
for the groups exhibiting HOIs (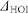 > 3%). In these groups, the
single SS term explained 80% of the entropy for homogeneous HOIs (interquartile
range 48–92%). From this result, we conclude that SS constitutes the
dominant structure of the homogeneous HOIs.
> 3%). In these groups, the
single SS term explained 80% of the entropy for homogeneous HOIs (interquartile
range 48–92%). From this result, we conclude that SS constitutes the
dominant structure of the homogeneous HOIs.
Figure 4. The groups that express HOIs exhibited alternating signs of homogenous HOIs at successive orders of interaction.
(A) Scatter plots of entropy margins for hHOIs versus entropy margins for SS.
The same color indicates groups selected from the same slice culture. Filled
circles indicate groups exhibiting HOIs (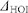 > 3%). Dashed lines represent
different proportions of homogenous HOI entropy margin explained by the SS
term,
> 3%). Dashed lines represent
different proportions of homogenous HOI entropy margin explained by the SS
term, 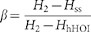 . We excluded 9 outliers
from the plots. (B) Cumulative distribution function of this proportion,
. We excluded 9 outliers
from the plots. (B) Cumulative distribution function of this proportion, 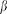 , for the groups exhibiting HOIs
(
, for the groups exhibiting HOIs
(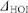 > 3%). (C) The
homogeneous HOI parameters up to the 6th order of the hHOI model. Each box
covers 25th to 75th percentile, and whiskers represent 1.5 times
the distance from the 25th to 75th percentile. Dots are outliers. The
distributions at the 3rd, 4th, and 5th order deviated significantly from
zero (two tailed sign test, *** and * represent significance level 0.001 and
0.05, respectively). (D) (Left) 3-dimensional plots of the homogeneous HOIs
of the hHOI model. Outliers with elements larger than 10 or less than
−10 were excluded. (Right) A histogram of the number of groups
that fell in 8 quadrants of the
> 3%). (C) The
homogeneous HOI parameters up to the 6th order of the hHOI model. Each box
covers 25th to 75th percentile, and whiskers represent 1.5 times
the distance from the 25th to 75th percentile. Dots are outliers. The
distributions at the 3rd, 4th, and 5th order deviated significantly from
zero (two tailed sign test, *** and * represent significance level 0.001 and
0.05, respectively). (D) (Left) 3-dimensional plots of the homogeneous HOIs
of the hHOI model. Outliers with elements larger than 10 or less than
−10 were excluded. (Right) A histogram of the number of groups
that fell in 8 quadrants of the 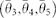 parameter space. The same color marks the same slice culture. The dotted
horizontal line is the chance level (12.5%) with random HOIs.
parameter space. The same color marks the same slice culture. The dotted
horizontal line is the chance level (12.5%) with random HOIs.
We next directly visualize the structure of homogeneous HOIs. Figure 4C displays distributions of the homogeneous HOI parameters,
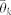 of the hHOI models. (We only show
the parameters for
of the hHOI models. (We only show
the parameters for 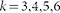 although we fitted
hHOIs up to the 10th order). The homogeneous HOI parameters up to the fifth
order but not higher were significantly different from zero (two tailed sign
test). The set of the homogeneous HOI parameters,
although we fitted
hHOIs up to the 10th order). The homogeneous HOI parameters up to the fifth
order but not higher were significantly different from zero (two tailed sign
test). The set of the homogeneous HOI parameters, 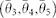 , from each group fell in a particular quadrant in
the 3-dimensional space (negative triple-wise, positive quadruple-wise, and
negative quintuple-wise interactions, Fig. 4D), exhibiting
an obviously biased direction. (If the set of homogeneous HOI parameters
randomly fell in any quadrant, the probability that the observed number of
groups (~ 54% of the groups) would fall in any single quadrant would be less
than
, from each group fell in a particular quadrant in
the 3-dimensional space (negative triple-wise, positive quadruple-wise, and
negative quintuple-wise interactions, Fig. 4D), exhibiting
an obviously biased direction. (If the set of homogeneous HOI parameters
randomly fell in any quadrant, the probability that the observed number of
groups (~ 54% of the groups) would fall in any single quadrant would be less
than 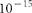 ). Thus the structured homogeneous
HOIs found up to the 5th order contributed to the excess SS found in 68% of the
groups with
). Thus the structured homogeneous
HOIs found up to the 5th order contributed to the excess SS found in 68% of the
groups with 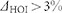 . These results demonstrate
that the structured HOIs with alternating signs are an attribute of excess SS in
local networks of hippocampal neurons.
. These results demonstrate
that the structured HOIs with alternating signs are an attribute of excess SS in
local networks of hippocampal neurons.
Simultaneous silence relies on network inhibition
Several different biological mechanisms may underlie the observed structure of HOIs. One such mechanism may be the inhibitory networks in the hippocampal CA3 area. To test this hypothesis, we examined population activity under bath application of GABAA receptor antagonist picrotoxin (PTX) (Fig. 5A). When fast GABAA mediated inhibitory networks were blocked by PTX, activities of observed neurons nearly completely synchronized with each other (Fig. 5B). The cross-correlogram exhibited a sharper peak (Fig. 5B inset) than that in the control (cf. Fig. 1C), much shorter than the 400 ms time window used to analyze the control condition. Nonetheless, we used the same window-size, 400 ms, to test for the deviation of SS from the pairwise model, except in Fig. 6D, where we explored the dependency on bin sizes. Table 1 summarizes activity rates, correlation coefficients, and probabilities of SS computed using the 400 ms bin under control and PTX conditions. The average probability of SS under the PTX conditions was much larger than that under the control condition. However, this frequent SS is expected from the high pairwise correlation coefficients observed under the PTX conditions. Indeed, the entropy explained by HOIs was greatly diminished in the PTX data, indicating that the pairwise model adequately explained population activity in almost all groups under blockade of inhibition (Fig. 5C). Accordingly, the percentage of groups that exhibited significant SS beyond the pairwise model was considerably reduced from 16% down to 4% (Fig. 5C, red). The considerable reduction of SS groups was observed whenever the window size larger than 200 ms was used in order to thoroughly cover the synchronous events (Fig. 5D). We thus concluded that an inhibitory network is necessary for neurons to produce both frequent SS and weak pairwise correlations; the conjunction of both can only be explained by HOIs.
Figure 5. Blocking inhibitory networks by PTX eliminated HOIs.
The panels retain the same presentation format as in Fig. 1A, D and Fig. 3B. (A) Ensemble activity of 76 neurons in the CA3 area of a single hippocampal slice under bath application of PTX. (B) Distribution of correlation coefficients between two event sequences (resolution of 100 ms) of all the pairs of neurons in 450 groups from 9 slices. Inset shows an average cross-correlogram. (C) Distribution of percentage entropy margin for HOIs. The groups that showed improved fitting with the SS term are marked in red (the SS groups, 4%). Others (96%) are in gray. (D) The number of the SS groups with respect to the bin size for the analysis.
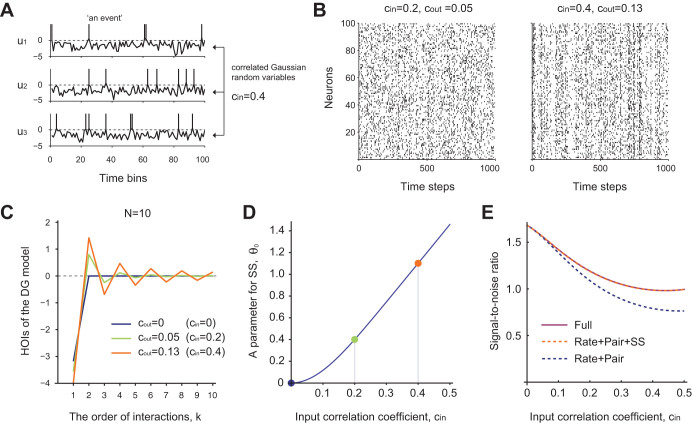
Figure 6. The ensemble activity simulated by the Dichotomized Gaussian (DG) model exhibits alternating signs of HOIs depending on successive orders of interaction.
(A) Illustration of a DG model of 3 neurons. The traces in each panel
represent correlated input variables, 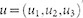 at different time steps. The inputs are sampled from a
multivariate Gaussian distribution,
at different time steps. The inputs are sampled from a
multivariate Gaussian distribution, 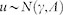 , with mean vector
, with mean vector  and
covariance
and
covariance 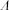 (See Methods). Here
we assume that the mean vector contains the same scalar element,
(See Methods). Here
we assume that the mean vector contains the same scalar element, 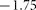 , in order to yield the activity
probability
, in order to yield the activity
probability 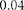 , a value close to
the empirically observed average activity rate (0.039 per 400 ms
window). The off-diagonal elements of
, a value close to
the empirically observed average activity rate (0.039 per 400 ms
window). The off-diagonal elements of 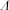 are all fixed at
are all fixed at 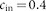 . The
vertical lines above 0 in each panel mark the time steps at which an input
crosses the threshold. (B) Simulation of the DG model with 100 neurons with
weak (Left) and strong (Right) input correlations. The weak input
correlation (
. The
vertical lines above 0 in each panel mark the time steps at which an input
crosses the threshold. (B) Simulation of the DG model with 100 neurons with
weak (Left) and strong (Right) input correlations. The weak input
correlation (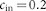 ) in the Left panel
yields a weak correlation coefficient (
) in the Left panel
yields a weak correlation coefficient (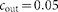 ) of output binary variables, whereas the strong input correlation
(
) of output binary variables, whereas the strong input correlation
(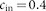 ) in the Right panel yields
a stronger correlation coefficient (
) in the Right panel yields
a stronger correlation coefficient (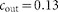 ) of output binary variables. (C) The HOIs of a small population
) of output binary variables. (C) The HOIs of a small population
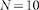 from the DG model shows
clear alternation of signs as the order of interaction
from the DG model shows
clear alternation of signs as the order of interaction 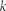 increases except for
increases except for 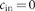 . Negative interactions occur at odd
. Negative interactions occur at odd 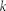 and positive interactions occur
at even
and positive interactions occur
at even 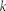 . (D) The parameter of
SS,
. (D) The parameter of
SS, 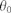 , as a function of input
correlation coefficient,
, as a function of input
correlation coefficient, 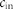 . The
dots marked in color represent
. The
dots marked in color represent 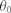 at
at 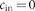 , 0.2, and 0.4. (E) The
signal-to-noise ratio of the input correlation coefficient,
, 0.2, and 0.4. (E) The
signal-to-noise ratio of the input correlation coefficient, 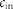 , as a function of
, as a function of 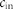 in the population activity of the DG
model (The solid purple line). The dotted lines are signal-to-ratios in the
subset features of the population activity (blue: the activity rates of
individual and pairwise neurons; orange: the activity rates of individual
and pairwise neurons plus the SS rate).
in the population activity of the DG
model (The solid purple line). The dotted lines are signal-to-ratios in the
subset features of the population activity (blue: the activity rates of
individual and pairwise neurons; orange: the activity rates of individual
and pairwise neurons plus the SS rate).
Simultaneous silence emerges in a population of thresholding units that receive correlated input
Finally, we demonstrated that a simple model of neural population reproduces the
structured HOIs with alternating signs with respect to different orders of
interaction observed in the spontaneous activity of hippocampal neurons under
the control conditions. A population model known as the Dichotomized Gaussian
(DG) model33,34,35,36 simulates a population of neurons that
receive correlated Gaussian inputs, where each neuron produces a binary output
in response to its input by simple thresholding (Fig. 6A,
See Methods). Despite the substantial simplification, the spiking mechanism is
similar to the one assumed in networks of balanced excitatory and inhibitory
neurons: the mean input to each neuron is typically smaller than the threshold
and, therefore, spikes are induced by fluctuations in the input. The DG model
has been reported to reproduce neural activity patterns better than the pairwise
model22. Figure 6B displays simulated
DG models using different strengths of input correlations (Fig.
6B), including one that produces output correlations similar to those
found in experimental observations (see Table 1). The
population exhibited asynchronous spiking activity. We numerically computed the
HOIs of the DG model for 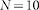 (See
Methods). The HOIs showed clear alternation in signs with respect to the
successive orders of interaction (Fig. 6C) and
demonstrated excess SS (Fig. 6D). These results show that
the experimentally observed SS with structured HOIs can arise from the
conjunction of two ubiquitous biological features, i.e., correlated input and
spiking nonlinearity. Further, we demonstrate that SS can contain rich
information of inputs provided to the observed population of neurons. Figure 6E compares the signal-to-noise ratio for estimating
the input correlation based on specific features of population activities
– activity rates and pairwise correlations (Rate + Pair), SS in
addition to activity rates and correlations (Rate + Pair + SS), and joint
activity rates of all orders (Full). The signal-to-noise ratio, which is also
called the linear Fisher information37,38,39, quantifies the
accuracy of estimating a small change in an input parameter by an optimal liner
decoder (see Methods). The result shows that measuring SS in addition to
activity rates and correlations can provide nearly full information available
from the observation of all statistics. The results were qualitatively the same
when an input mean (or a threshold level) was estimated instead of input
correlation.
(See
Methods). The HOIs showed clear alternation in signs with respect to the
successive orders of interaction (Fig. 6C) and
demonstrated excess SS (Fig. 6D). These results show that
the experimentally observed SS with structured HOIs can arise from the
conjunction of two ubiquitous biological features, i.e., correlated input and
spiking nonlinearity. Further, we demonstrate that SS can contain rich
information of inputs provided to the observed population of neurons. Figure 6E compares the signal-to-noise ratio for estimating
the input correlation based on specific features of population activities
– activity rates and pairwise correlations (Rate + Pair), SS in
addition to activity rates and correlations (Rate + Pair + SS), and joint
activity rates of all orders (Full). The signal-to-noise ratio, which is also
called the linear Fisher information37,38,39, quantifies the
accuracy of estimating a small change in an input parameter by an optimal liner
decoder (see Methods). The result shows that measuring SS in addition to
activity rates and correlations can provide nearly full information available
from the observation of all statistics. The results were qualitatively the same
when an input mean (or a threshold level) was estimated instead of input
correlation.
Discussion
We investigated the structure of HOIs in spontaneous activity of neurons in the CA3
area of organotypic hippocampal slice cultures. Most groups (~ 70%) of neurons that
expressed significant HOIs (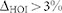 ) also
exhibited excess SS (Fig. 3), and SS alone could account for ~
20% of the entropy explained by HOIs in these groups. This result predicts
significantly biased homogeneous HOIs with alternating signs at successive orders of
interaction and our data analysis confirmed this prediction (Fig.
4). We also found that SS explained 80% of the entropy due to structured
homogeneous HOIs.
) also
exhibited excess SS (Fig. 3), and SS alone could account for ~
20% of the entropy explained by HOIs in these groups. This result predicts
significantly biased homogeneous HOIs with alternating signs at successive orders of
interaction and our data analysis confirmed this prediction (Fig.
4). We also found that SS explained 80% of the entropy due to structured
homogeneous HOIs.
SS was robustly observed across a range of time-bins (Fig. 5D) and sizes of neural populations (Fig. 3C). Moreover, SS and the resulting structure of HOIs arise in the simplest model of a neural population that possesses a spiking nonlinearity and correlated inputs (the DG model), where additional observation of SS is sufficient to decode most information of input conveyed by different orders of HOIs. These results suggest that excess SS is an important and ubiquitous characteristic of neural population activity that summarizes its low-dimensional structure in the combinatorial space of HOIs. We identified alternating signs of HOIs up to the 5th order with statistical significance in the analyzed data (Fig. 4C and D), and the DG model displayed the predicted structure up to the highest order of interaction (Fig. 6C). Based on these observations, we speculate that the predicted structure of HOIs beyond the 5th order should be identifiable in future, given longer experimental recordings. We also speculate that appropriate models5,15,21 of neural population activity implicitly include excess SS as well as the resulting structure of HOIs, as demonstrated in the DG model.
Multiple biological mechanisms may underlie the high SS probability observed and alternating signs of HOIs. While we have shown that even simple thresholding units with correlated inputs can reproduce this structure, we do not exclude contributions from other mechanisms. Indeed, we demonstrated the involvement of inhibitory input in generating SS (Fig. 5). Under the blockade of GABAA receptors, activities of neurons were almost completely synchronized. Therefore HOIs of the population activity were significantly diminished. It is expected that neurons are almost fully synchronized and fire regularly if inhibition is removed40. However, it may require additional neuronal mechanisms with slow dynamics41,42 to robustly account for the sparse synchronous activity observed in the current data sets. While this result may simply indicate that inhibition is necessary to place a network of neurons in a fluctuation-driven regime43,44 for them to be sensitive to correlated input (c.f. Fig. 6), it may alternatively suggest the existence of clustered inhibitory input that simultaneously shuts down a group of local neurons and produces excess SS. Inhibitory interneurons in the hippocampus have diverging connections to principal neurons45 and show powerful control over timing and rhythms of their spiking activity46,47. Such inhibitory circuits are ideally suited to implement a winner-take-all-like competition among groups of neurons, which are common in models of hippocampal circuits aiming to reproduce place fields48,49. Similar operations of hippocampal inhibitory circuits have also been suggested for cellular assemblies50 and memory consolidation51. Thus the excess SS in spontaneous activity reported here might be related to functions requiring sparse information representation with a small fraction of active neurons. It is therefore interesting to see if the same experimental manipulation of inhibition that influences, for example, the sparse place field representation, also influences SS during spontaneous activity.
Our study demonstrates that excess SS explains a large fraction of the variability
caused by complex HOIs in neural populations. Although it was previously reported
that HOIs fitted to several representative activity patterns explain occurrence
probabilities of other general patterns18, this study did not
normalize the model probability distribution because of the computational complexity
associated with the normalization step. As a drawback, it was previously unknown how
much of the variability associated with HOIs was explained by a small number of
representative activity patterns. In contrast, the entropy maximization approach we
have taken was suitable to evaluate these quantities. More generally, virtually all
previous studies of HOIs14,19,20 attempted to fit multiple model
parameters to the data rather than to extract the most prominent feature in the
space of HOIs. Note that the hHOI model fitted to the data reproduces an observed
histogram of the number of active neurons in time bins (i.e., a population
spike-count histogram). Thus the hHOI model is equivalent to the K-pairwise model
proposed in Tkačik et al.20 although the two
models utilize different features of activity patterns to represent homogenous HOIs.
We have found that SS can parsimoniously summarize 80% of the specific structure of
hHOIs. Furthermore, successive orders of interaction have alternating signs. This
resulting structure extends the negative triple-wise interactions previously found
in local (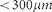 ) populations of 3 neurons17.
) populations of 3 neurons17.
In sum, we demonstrate that representing HOIs using “silence” provides a much more concise description than the canonical representation based on “activity”. We conclude that significant SS is a ubiquitous feature in neural population activity that expresses apparently diverse HOIs across different orders.
Methods
Recording method
Hippocampal slice cultures were prepared from postnatal day 7 Wistar/ST rats (SLC) (either male or female). Entorhino-hippocampal stumps were cultivated on membrane filters using 50% minimal essential medium, 25% Hanks' balanced salt solution, 25% horse serum, and antibiotics in a humidified incubator at 37°C in 5% CO2 and were used for experiments on days 7 to 14 in vitro. On experimental days, slices were washed with oxygenated artificial cerebrospinal fluid (aCSF) consisting of (mM) 127 NaCl, 26 NaHCO3, 3.3 KCl, 1.24 KH2PO4, 1.2 MgSO4, 1.2 CaCl2, and 10 glucose and bubbled with 95% O2 and 5% CO2. They were then transferred to a 35-mm dish filled with 2 ml of dye solution and incubated for 40 min in a humidified incubator at 37°C in 5% CO2 with 0.0005% Oregon Green 488 BAPTA-1 (OGB-1) AM (Invitrogen), 0.01% Pluronic F-127 (Invitrogen), and 0.005% Cremophor EL (Sigma-Aldrich). They were recovered in aCSF for> 30 min and mounted in a recording chamber at 32°C and perfused with aCSF at a rate of 1.5–2.0 ml/min for > 15 min. Hippocampal CA3 pyramidal cell layer was imaged at 10 Hz using a Nipkow-disk confocal microscopy (CSU-X1; Yokogawa Electric), a cooled CCD camera (iXonEM+ DV897; Andor Technology), an upright microscope with a water-immersion objective lens (16 ×, 0.8 numerical aperture, Nikon). Fluorophores were excited at 488 nm with a laser diode and visualized with a 507-nm long-pass emission filter. The recording lengths varied from 600 sec to 3300 sec (600 sec (n = 9); 1200 sec (n = 4); 310, 610, 700, 900, 1100, 1800, 3300 s (n = 1)). Picrotoxin was bath-applied at a concentration of 50 µM to 9 slices (600 sec (n = 7) and 350 s (n = 2)). After identification of cell types, the regions of interest (ROIs) were carefully placed onto the cell bodies. The fluorescence change (ΔF/F) was calculated as ΔF/F = (Ft–F0)/F0, where Ft is the fluorescence intensity at time t, and F0 is the baseline averaged for 50 s before and after time t. For neurons, event times were reconstructed from the onsets of Ca2+ transients3,27,28. The signals were then inspected by eye to remove erroneously detected noise. The data is available online (http://gaya.jp/data). Under the same condition as described above, membrane potentials were whole-cell recorded at I = 0 from pyramidal cells (n = 7) visually identified under infrared differential interference contrast microscopy. Patch pipettes (3−6 MΩ) were filled with a solution consisting of (in mM) 120 K-gluconate, 10 KCl, 10 HEPES, 10 creatine phosphate, 4 MgATP, 0.3 Na2GTP, and 0.2 EGTA. The signal was digitized at 10 kHz and filtered with a band of 1–2000 Hz. Liquid junction potentials were not corrected. Experiments were performed with the approval of the animal experiment ethics committee at the University of Tokyo (approval No. P24-6) and according to the University of Tokyo guidelines for the care and use of laboratory animals. All efforts were made to minimize the animals' suffering and the number of animals used.
Selection of groups of neighboring neurons
From each slice, we selected 50 distinct overlapping groups, each consisting of
10 nearest-neighbor neurons, based on the following procedure. In each slice, we
estimated the density of spatial distribution of the cells in the recorded area
of CA3 by an optimized 2-dimensional kernel density estimation method52. We then sampled a spatial point from the estimated density, and
selected the 10 neurons nearest to the point. We repeated this procedure until
we obtained 50 distinct groups (we discarded groups of neurons if the exactly
same group of 10 was previously selected). The neurons with low activity rates
(less than 0.01 Hz) were excluded from this analysis. In addition, we
changed the number of neurons in a group from 3 to 14 to investigate effect of
the group size (Fig. 3C). We sampled up to 50 groups per
slice following the same sampling procedure described above. Finally, we sampled
non-overlapping groups of 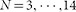 neurons.
Note that we can sample only a small number of groups from each slice if groups
are stochastically sampled by the above-mentioned method. Thus, we took the
following procedure to efficiently select non-overlapping groups from each
slice. First, we fitted a 2-dimensional Gaussian density function to the spatial
distribution of cells in each slice. We then determined the first principle
component, and scored the positions of neurons along the first principle axis.
We selected neurons that are nearest neighbors in terms of this score as a
group. To determine the number of groups sampled from each slice, we computed
the maximum number of non-overlapping groups that can be sampled from each of
all slices. We used the smallest number of groups among them to sample an equal
number of groups from each slice.
neurons.
Note that we can sample only a small number of groups from each slice if groups
are stochastically sampled by the above-mentioned method. Thus, we took the
following procedure to efficiently select non-overlapping groups from each
slice. First, we fitted a 2-dimensional Gaussian density function to the spatial
distribution of cells in each slice. We then determined the first principle
component, and scored the positions of neurons along the first principle axis.
We selected neurons that are nearest neighbors in terms of this score as a
group. To determine the number of groups sampled from each slice, we computed
the maximum number of non-overlapping groups that can be sampled from each of
all slices. We used the smallest number of groups among them to sample an equal
number of groups from each slice.
Model fitting and a test of simultaneous silence
First, we fit to binary population activity data (see Fig.
1F in Results) the pairwise maximum entropy model8,9,31, 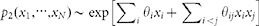 , where
, where  is a binary variable of 0 or 1. Here
the parameters of the model,
is a binary variable of 0 or 1. Here
the parameters of the model, 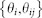 , were
fitted by a maximum likelihood principle,
, were
fitted by a maximum likelihood principle, 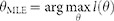 , where
, where 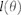 is the log
likelihood of the data under the model. The nonlinear fitting was performed
using a custom convex optimization program in Matlab. We then fit to the same
data a maximum entropy model that augments the pairwise model with a single term
to account for the observed probability of SS in addition (the SS model, see
Eq. 1 in Results). The increase in likelihood over the
pairwise model seen after adding a parameter for the SS is related to the
reduction in entropy by
is the log
likelihood of the data under the model. The nonlinear fitting was performed
using a custom convex optimization program in Matlab. We then fit to the same
data a maximum entropy model that augments the pairwise model with a single term
to account for the observed probability of SS in addition (the SS model, see
Eq. 1 in Results). The increase in likelihood over the
pairwise model seen after adding a parameter for the SS is related to the
reduction in entropy by 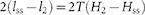 , where
, where 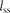 and
and  are the log likelihood of the data under the SS
model and the pairwise model respectively, and
are the log likelihood of the data under the SS
model and the pairwise model respectively, and 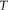 is the number of observed patterns (bins). Under
the null hypothesis of no such SS term, the variability in the model estimation
due to finite samples make the difference in log likelihood following a
is the number of observed patterns (bins). Under
the null hypothesis of no such SS term, the variability in the model estimation
due to finite samples make the difference in log likelihood following a 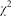 -distribution with one degree of
freedom as
-distribution with one degree of
freedom as 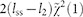 11. The
p-value of the observed likelihood increase was computed using this null
distribution. The p-values were further corrected by the
Benjamini-Hochberg-Yekutieli multiple comparison correction method that is
applicable to dependent tests, using Matlab code written by Groppe
et al.53,54 This method controls the proportion
of tests that incorrectly declare significant SS (the false discovery rate).
11. The
p-value of the observed likelihood increase was computed using this null
distribution. The p-values were further corrected by the
Benjamini-Hochberg-Yekutieli multiple comparison correction method that is
applicable to dependent tests, using Matlab code written by Groppe
et al.53,54 This method controls the proportion
of tests that incorrectly declare significant SS (the false discovery rate).
A dichotomized gaussian (DG) model
The DG model is a threshold neuron model with Gaussian input signals33,34,35,36. The binary output of the  -th neuron (
-th neuron (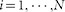 ) is given by
) is given by 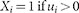 or
or 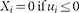 , where
, where 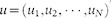 is drawn from a multivariate Gaussian distribution
with mean
is drawn from a multivariate Gaussian distribution
with mean 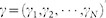 and a covariance matrix
and a covariance matrix 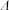 whose diagonal is 1 as
whose diagonal is 1 as 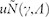 . Note that
. Note that  describes matrix (or vector) transpose. Here we
consider a homogenous neuron pool: the mean is all fixed at
describes matrix (or vector) transpose. Here we
consider a homogenous neuron pool: the mean is all fixed at 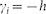 and the off-diagonal elements of
and the off-diagonal elements of 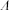
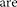 all fixed at
all fixed at 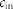 . The probability that individual output neurons are
in an active state is given by
. The probability that individual output neurons are
in an active state is given by 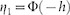 , where
, where
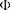 is the one-dimensional cumulative
distribution function (CDF) of a zero-mean, unit variance Gaussian distribution.
The probability of simultaneous activity of 2 neurons is given by
is the one-dimensional cumulative
distribution function (CDF) of a zero-mean, unit variance Gaussian distribution.
The probability of simultaneous activity of 2 neurons is given by 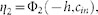 where
where 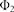 is the 2-dimensional Gaussian CDF with zero-means, unit variances,
and a off-diagonal correlation coefficient
is the 2-dimensional Gaussian CDF with zero-means, unit variances,
and a off-diagonal correlation coefficient 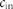 . The correlation coefficient between 2 output neurons is given by
. The correlation coefficient between 2 output neurons is given by 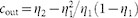 .
.
The probability distribution of population activity has a simple analytical
expression in this model. Note that the correlated inputs can be written as 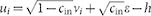 , where
, where  is a unit variance white Gaussian noise
is a unit variance white Gaussian noise 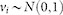 specific to each neuron, and
specific to each neuron, and 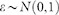 is an input noise that is common
across all neurons. The conditional probability of a single neuron spiking given
the common input
is an input noise that is common
across all neurons. The conditional probability of a single neuron spiking given
the common input  is given by33
is given by33
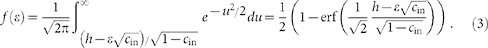 |
The probability that
exactly  neurons are active and
neurons are active and  neurons are inactive is given
neurons are inactive is given
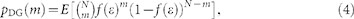 |
where the expectation is performed with
respect to the common input noise,  .
Note that the binomial factor
.
Note that the binomial factor 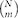 sums
all possible combinations of population activity patterns with
sums
all possible combinations of population activity patterns with  active neurons. In order to obtain the
probability mass function for the finite population size
active neurons. In order to obtain the
probability mass function for the finite population size 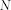 , we numerically computed the above equation. On
the other hand, the same population-count probabilities are described by
, we numerically computed the above equation. On
the other hand, the same population-count probabilities are described by
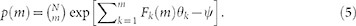 |
Here 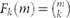 (
(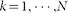 ) is
the k-th order feature of the hHOI model, which counts all combinations
of choosing k neurons out of m active neurons, and
) is
the k-th order feature of the hHOI model, which counts all combinations
of choosing k neurons out of m active neurons, and 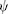 is a normalization factor. Thus, by
solving linear equations,
is a normalization factor. Thus, by
solving linear equations, 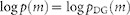 for
for 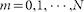 , we obtain the parameters,
, we obtain the parameters, 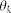 (
(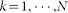 ), and the normalization factor
), and the normalization factor 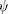 .
.
We quantify the signal-to-noise ratio for estimating the input correlation, 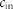 , based on the population activity
of the homogenous DG model as follows. A small change in
, based on the population activity
of the homogenous DG model as follows. A small change in 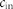 is inferred from a vector of observation,
is inferred from a vector of observation, 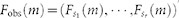 , where indices
, where indices 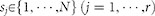 specify a subset of r features
that are taken into account for the inference. The signal for detecting the
input correlation is given by
specify a subset of r features
that are taken into account for the inference. The signal for detecting the
input correlation is given by 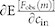 and
the noise of the observation is quantified by
and
the noise of the observation is quantified by 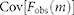 , where
, where 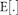 is the expectation and
is the expectation and 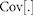 is the
is the 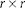 covariance matrix calculated using
covariance matrix calculated using
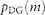 defined above. Together, the
signal-to-noise ratio is given by
defined above. Together, the
signal-to-noise ratio is given by 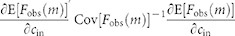 38,39. In the paper, we specifically consider three
types of observations as
38,39. In the paper, we specifically consider three
types of observations as 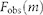 : the full
observation
: the full
observation 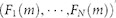 , the activity rates of
individual and pairwise neurons
, the activity rates of
individual and pairwise neurons 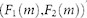 , and
these activity rates plus the SS rate
, and
these activity rates plus the SS rate 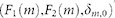 , where
, where 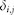 represents
Kronecker's delta. Notably, when all the features
represents
Kronecker's delta. Notably, when all the features 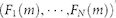 are observed, the above signal-to-noise
ratio becomes equivalent to the Fisher information55 of the input
correlation, i.e.,
are observed, the above signal-to-noise
ratio becomes equivalent to the Fisher information55 of the input
correlation, i.e., 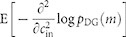 , and thus
upper-bounds the accuracy of unbiased estimators of
, and thus
upper-bounds the accuracy of unbiased estimators of 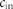 based on the population activity. See56,57 for information in subset features achieved by a general
optimal nonlinear decoder as assessed by the Fisher information.
based on the population activity. See56,57 for information in subset features achieved by a general
optimal nonlinear decoder as assessed by the Fisher information.
Author Contributions
H.S.: Conception and design; Analysis and interpretation of data; Drafting and revising the article. K.S.: Drafting and revising the article. T.I.: Acquisition of data; Revising the article. Y.I.: Acquisition of data; Drafting and revising the article. T.T.: Conception and design; Analysis and interpretation of data; Drafting and revising the article.
Supplementary Material
Supplementary Figure S1
Acknowledgments
We thank Takuya Sasaki for his help in providing picrotoxin data, and Charles Yokoyama and Alexandra V Terashima for their critical reading of our manuscript. This work was supported by RIKEN Brain Science Institute (HS and TT), Kakenhi 22115003 (YI), and Health and Labour Sciences Research Grants for Research on Regulatory Science of Pharmaceuticals and Medical Devices from MHLW (iNCENS: iPS-Non Clinical Experiments for Nervous System) (YI).
References
- Salinas E. & Sejnowski T. J. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci 2, 539–550 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes A. D. Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat Neurosci 6, 593–599 (2003). [DOI] [PubMed] [Google Scholar]
- Takahashi N., Sasaki T., Matsumoto W., Matsuki N. & Ikegaya Y. Circuit topology for synchronizing neurons in spontaneously active networks. Proc Natl Acad Sci USA 107, 10244–102499 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidne M. et al. Modeling the impact of common noise inputs on the network activity of retinal ganglion cells. J Comput Neurosci 33, 97–121 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köster U., Sohl-Dickstein J., Gray C. M. & Olshausen B. A. Modeling higher-order correlations within cortical microcolumns. PLoS Comput Biol 10, e1003684 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- De la Rocha J., Doiron B., Shea-brown E. & Reyes A. Correlation between neural spike trains increases with firing rate. Nature 448, 802–807 (2007). [DOI] [PubMed] [Google Scholar]
- Pitkow X. & Meister M. Decorrelation and efficient coding by retinal ganglion cells. Nat Neurosci 15, 628–635 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman E., Berry M. J., Segev R. & Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shlens J. et al. The structure of multi-neuron firing patterns in primate retina. J Neurosci 26, 8254–8266 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martignon L. et al. Neural coding: higher-order temporal patterns in the neurostatistics of cell assemblies. Neural Comput 12, 2621–2653 (2000). [DOI] [PubMed] [Google Scholar]
- Nakahara H. & Amari S. Information-geometric measure for neural spikes. Neural Comput 14, 2269–2316 (2002). [DOI] [PubMed] [Google Scholar]
- Tang A. et al. A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. J Neurosci 28, 505–518 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu S., Huang D., Singer W. & Nikolic D. A small world of neuronal synchrony. Cereb Cortex 18, 2891–2901 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montani F. et al. The impact of high-order interactions on the rate of synchronous discharge and information transmission in somatosensory cortex. Philos Trans. A Math Phys Eng Sci 367, 3297–3310 (2009). [DOI] [PubMed] [Google Scholar]
- Montani F., Phoka E., Portesi M. & Schultz S. R. Statistical modelling of higher-order correlations in pools of neural activity. Physica A 392, 3066–3086 (2013). [Google Scholar]
- Ohiorhenuan I. E. et al. Sparse coding and high-order correlations in fine-scale cortical networks. Nature 466, 617–621 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohiorhenuan I. E. & Victor J. D. Information-geometric measure of 3-neuron firing patterns characterizes scale-dependence in cortical networks. J Comput Neurosci 30, 125–141 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganmor E., Segev R. & Schneidman E. Sparse low-order interaction network underlies a highly correlated and learnable neural population code. Proc Natl Acad Sci USA 108, 9679–9684 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tkačik G. et al. The simplest maximum entropy model for collective behavior in a neural network. J Stat Mech Theor Exp P03011 (2013). [Google Scholar]
- Tkačik G. et al. Searching for collective behavior in a large network of sensory neurons. PLoS Comput Biol 10, e1003408 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santos G. S., Gireesh E. D., Plenz D. & Nakahara H. Hierarchical interaction structure of neural activities in cortical slice cultures. J Neurosci 30, 8720–8733 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu S. et al. Higher-order interactions characterized in cortical activity. J Neurosci 31, 17514–17526 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimazaki H., Amari S., Brown E. N. & Grün S. State-space analysis of time-varying higher-order spike correlation for multiple neural spike train data. PLoS Comput Biol 8, e1002385 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy W. B. & Baxter R. A. Energy efficient neural codes. Neural Comput 8, 531–543 (1996). [DOI] [PubMed] [Google Scholar]
- Okamoto K. et al. Ex vivo cultured neuronal networks emit in vivo-like spontaneous activity. J Physiol Sci 64, 421–431 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikegaya Y., Aaron G. & Cossart R. Synfire chains and cortical songs: Temporal modules of cortical activity. Science 304, 559–564 (2004). [DOI] [PubMed] [Google Scholar]
- Sasaki T., Matsuki N. & Ikegaya Y. Metastability of active CA3 networks. J Neurosci 27, 517–528 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi N., Sasaki T., Usami A., Matsuki N. & Ikegaya Y. Watching neuronal circuit dynamics through functional multineuron calcium imaging (fMCI). Neurosci Res 58, 219–225 (2007). [DOI] [PubMed] [Google Scholar]
- Mizuseki K. & Buzsáki G. Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep. 4, 1010–1021 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G. & Mizuseki K. The log-dynamic brain: how skewed distributions affect network operations. Nat Rev Neurosci 15, 264–278 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocco S., Leibler S. & Monasson R. Neuronal couplings between retinal ganglion cells inferred by efficient inverse statistical physics methods. Proc Natl Acad Sci USA 106, 14058–14062 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M. et al. Population rate dynamics and multineuron firing patterns in sensory cortex. J Neurosci 32, 17108–17119 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amari S., Nakahara H., Wu S. & Sakai Y. Synchronous firing and higher-order interactions in neuron pool. Neural Comput 15, 127–142 (2003). [DOI] [PubMed] [Google Scholar]
- Bethge M. & Berens P. Near-maximum entropy models for binary neural representations of natural images. Adv NIPS 20, 97–104 (2008). [Google Scholar]
- Macke J. H., Opper M. & Bethge M. Common input explains higher-order correlations and entropy in a simple model of neural population activity. Phys Rev Lett 106, 208102 (2011). [DOI] [PubMed] [Google Scholar]
- Montangie L. & Montani F. Quantifying higher-order correlations in a neuronal pool. Physica A 421, 388–400 (2015). [Google Scholar]
- Seriès P., Latham P. E. & Pouget A. Tuning curve sharpening for orientation selectivity: coding efficiency and the impact of correlations. Nat Neurosci 7, 1129–1135 (2004). [DOI] [PubMed] [Google Scholar]
- Beck J., Bejjanki V. R. & Pouget A. Insights from a simple expression for linear fisher information in a recurrently connected population of spiking neurons. Neural Comput 23, 1484–1502 (2011). [DOI] [PubMed] [Google Scholar]
- Moreno-Bote R. et al. Information-limiting correlations. Nat Neurosci 17, 1410–1417 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci 8, 183–208 (2000). [DOI] [PubMed] [Google Scholar]
- Mongillo G., Barak O. & Tsodyks M. Synaptic theory of working memory. Science 319, 1543–1546 (2008). [DOI] [PubMed] [Google Scholar]
- Curto C., Sakata S., Marguet S., Itskov V. & Harris K. D. A simple model of cortical dynamics explains variability and state dependence of sensory responses in urethane-anesthetized auditory cortex. J Neurosci 29, 10600–10612 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Vreeswijk C. & Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726 (1996). [DOI] [PubMed] [Google Scholar]
- Shadlen M. N. & Newsome W. T. The variable discharge of cortical neurons: Implications for connectivity, computation, and information coding. J Neurosci 18, 3870–3896 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freundl T. F. and Buzsaki G. Interneurons of the hippocampus. Hippocampus 6, 347–470 (1996). [DOI] [PubMed] [Google Scholar]
- Royer S. et al. Control of timing, rate and bursts of hippocampal place cells by dendritic and somatic inhibition. Nat Neurosci 15, 769–75 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M., Vida I. & Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci 8, 45–56 (2007). [DOI] [PubMed] [Google Scholar]
- Rolls E. T., Stringer S. M. & Elliot T. Entorhinal cortex grid cells can map to hippocampal place cells by competitive learning. Network 17, 447–465 (2006). [DOI] [PubMed] [Google Scholar]
- Cheng S. & Frank L. M. The structure of networks that produce the transformation from grid cells to place cells. Neuroscience 197, 293–306 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger T. & Somogyi P. Neuronal diversity and temporal dynamics: the unity of hippocampal circuit operations. Science 321, 53–57 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez P. & Squire L. R. Memory consolidation and the medial temporal lobe: a simple network model. Proc Natl Acad Sci USA 91, 7041–7045 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimazaki H. & Shinomoto S. Kernel bandwidth optimization in spike rate estimation. J Comput Neurosci 29, 171–182 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y. & Yekutieli D. The control of the false discovery rate in multiple testing under dependency. 29, 1165–1188 (2001).
- Groppe D. M., Urbach T. P. & Kutas M. Mass univariate analysis of event-related brain potentials/fields I: a critical tutorial review. Psychophysiology 48, 1711–1725 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover T. M. & Thomas J. A. Elements of Information Theory. (John Wiley & Sons, Inc., 1991). [Google Scholar]
- Oizumi M., Okada M., Amari S. Information loss associated with imperfect observation and mismatched decoding. Front Comput Neurosci. 5, 9 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyama S. On the relation between encoding and decoding of neuronal spikes. Neural Comput. 1425, 1408–1425 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure S1