Computational Modeling of Flow-Altering Surgeries in Basilar Aneurysms

Abstract

In cases where surgeons consider different interventional options for flow alterations in the setting of pathological basilar artery hemodynamics, a virtual model demonstrating the flow fields resulting from each of these options can assist in making clinical decisions. In this study, image-based computational fluid dynamics (CFD) models were used to simulate the flow in four basilar artery aneurysms in order to evaluate postoperative hemodynamics that would result from flow-altering interventions. Patient-specific geometries were constructed using MR angiography and velocimetry data. CFD simulations carried out for the preoperative flow conditions were compared to in vivo phase-contrast MRI measurements (4DFlowMRI) acquired prior to the interventions. The models were then modified according to the procedures considered for each patient. Numerical simulations of the flow and virtual contrast transport were carried out in each case in order to assess postoperative flow fields and estimate the likelihood of intra-aneurysmal thrombus deposition following the procedures. Postoperative imaging data, when available, were used to validate computational predictions. In two cases, where the aneurysms involved vital pontine perforator arteries branching from the basilar artery, idealized geometries of these vessels were incorporated into the CFD models. The effect of interventions on the flow through the perforators was evaluated by simulating the transport of contrast in these vessels. The computational results were in close agreement with the MR imaging data. In some cases, CFD simulations could help determine which of the surgical options was likely to reduce the flow into the aneurysm while preserving the flow through the basilar trunk. The study demonstrated that image-based computational modeling can provide guidance to clinicians by indicating possible outcome complications and indicating expected success potential for ameliorating pathological aneurysmal flow, prior to a procedure.

INTRODUCTION

Cerebral aneurysms account for approximately 10% of all strokes.^1,7,23,30 Rupture leads to subarachnoid hemorrhage, with a mortality rate of 50% and morbidity rate of 50% for those who survive.^14,24 Untreated giant intracranial aneurysms, those greater than 25 mm in diameter, present a particularly grave danger of hemorrhage, mass effect, and thromboembolism, ^11,12,17,18 resulting in a mortality rate of 68% after 2 years and 85% after 5 years.¹⁷ Wide-necked saccular and fusiform aneurysms are often not amenable to a treatment by surgical clipping or endovascular coiling, since such aneurysms cannot be completely excluded from the circulation without sacrificing the flow to the distal vasculature. Particular challenges are involved with basilar artery non-saccular aneurysms, as any intervention compromising perfusion of the pons is not compatible with patient survival. In some cases, treatment has been attempted by performing surgeries that aim to reduce the flow through the aneurysm in hope that this would inhibit disease progression. This can be achieved by clipping some of the proximal or distal arteries, typically accompanied by a bypass providing flow to distal vasculature.^13,26 Despite their advantages, these treatments introduce complications related to undesired thrombotic occlusion of the vital branch arteries. A computational model predicting regions that are likely to become occupied with thrombus following a flow altering procedure could help evaluate various treatment options. Previous studies have indicated that intra-aneurysmal regions with elevated thrombus formation potential are characterized by low flow velocities and wall shear stresses as well as by increased flow residence time.^21,22 In this study an image-based computational fluid dynamics (CFD) modeling methodology was used to model postoperative flow fields and identify thrombus-prone regions resulting from flow-altering interventions in four basilar artery aneurysms.

There is an extensive literature describing numerical simulations of blood flow in patient-specific aneurysmal geometries.^{4,5,8,10,15,25,29} The exact role of hemodynamics in aneurysm progression and rupture remains uncertain, however some of the reports elucidated the importance of aneurysm morphology and biomechanical factors in the disease.^3,19,28,31 Image-based modeling of vascular interventions can help understand how the flow patterns influence vessel remodeling, as the exact time and type of the flow alteration is known, and the response to intervention can be monitored. It is recognized that a central benefit of numerical modeling is the capability to simulate postoperative flows prior to a planned procedure. ^16,26,27 Several recent studies addressed the flow in patient-specific models of intracranial aneurysms of the posterior circulation.^2,6,27 While elucidating the hemodynamics in these lesions, previous studies excluded pontine perforators from the analyses. The typical size of the perforators is in the range of 200–300 μm, which is below the resolution of commonly employed non-invasive clinical imaging modalities. This makes it impossible to acquire patient-specific geometries of these vessels or measure the flow through them with phase-contrast MRI methods. Nevertheless, without an understanding of the flow in the perforators, it is not possible to evaluate alternative surgical options, as it is precisely the effect of a surgery on the flow to the brainstem that must be assessed prior to the procedure. The current report is a first attempt to conduct CFD simulations in basilar aneurysm models that incorporate idealized pontine perforator artery geometries.

The four cases modeled in this study will be presented starting from a simpler case, where only one surgical option was evaluated, and then proceed to more complicated cases, with two or more alternative procedures considered and simulated numerically. In the later cases, it was important to assess how the proposed interventions would affect the flow through vital perforators and therefore the computational models included an idealized representation of these smaller vessels.

METHODS

Patients

In this report we present computational analysis for four basilar artery aneurysm patients recruited to this study using institutionally approved IRB consent. A brief description of their vascular pathology and treatment options is provided below.

Patient 1

A 65-year-old male presented with a giant aneurysm of the basilar apex (Fig. 1a). Note that while the remaining patients are oriented according to the radiological convention, “facing the viewer” or “right is left”, this image is shown from the posterior view to match the orientation of MRI-measured flow fields presented later in the text. In order to reduce the flow into the aneurysm while preserving the flow to the pontine perforator branches, the basilar artery was clipped proximal to the superior cerebellar arteries (SCAs). To provide the flow to the vessels of the basilar apex, a bypass was performed from the left middle cerebral artery (MCA) to the ipsilateral posterior cerebral artery (PCA).

FIGURE 1.

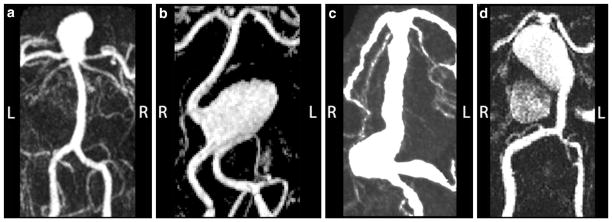
Contrast-enhanced MRA images of the preoperative geometries in 4 basilar artery aneurysm patients. (a) Patient 1: basilar apex aneurysm; (b) Patient 2: proximal basilar artery aneurysm; (c) Patient 3: fusiform basilar trunk aneurysm; and (d) Patient 4: fusiform basilar trunk aneurysm. The orientation of the images is shown with letters “L” (left) and “R” (right).

Patient 2

A 66-year-old female presented with a giant, partially thrombosed aneurysm of the proximal basilar artery (Fig. 1b). A surgical or endovascular occlusion of one of the supplying vertebral arteries was considered in order to reduce the flow into the aneurysmal sac and induce its thrombotic occlusion. This resulted in two alternatives: occluding the left vertebral (option 1) or the right vertebral artery (option 2). Following the evaluation of postoperative conditions that would result from each surgical option, the aneurysm was treated by stent-assisted coiling, rather than by an occlusion of a vertebral artery.

Patient 3

In this case of a 69-year-old male, the aneurysm involved the whole vertebrobasilar system (Fig. 1c). Additional MRI studies revealed a large mass of intraluminal thrombus located in the mid-basilar trunk as well as in one of the vertebral arteries. Several surgical options, involving occlusions of the vertebrals and basilar trunk as well as adding bypasses supplying the basilar apex were considered in this exceptionally complicated case in the hope that flow reduction could inhibit further progression of the disease. The basilar trunk was occluded distal to the anterior inferior cerebellar arteries (AICAs); an MCA to PCA bypass was performed to supply the vessels of the basilar apex as well as the brainstem perforators of the basilar artery distal to the occlusion.

Patient 4

A 50-year-old male presented with a giant aneurysm of the basilar trunk (Fig. 1d). Additional MRI data demonstrated a large mass of intra-luminal thrombus. For several years this patient was monitored with MR imaging and a steady growth of the aneurysm was observed in the distal part of the sac. Following a surveillance study which indicated substantial growth, a clinical decision was made to intervene by clipping the basilar apex proximal to the superior cerebellars and supplying the vessels of the apex from the anterior circulation through an MCA to PCA bypass.

MR Angiography and Velocimetry

High-resolution, contrast-enhanced MR angiography (CE-MRA) images of the cerebral vessels were obtained with an injection of gadolinium (Gd-DTPA, 20 cc intravenous injection at 2 cc/s). Patients 1 and 4 were imaged on a 1.5T scanner (Achieva, Phillips, Best, the Netherlands), while the images for Patients 2 and 3 were obtained on a 3T scanner (Skyra, Siemens Healthcare, Erlangen, Germany). The maximum intensity projection (MIP) images of the preoperative vascular geometries are shown in Fig. 1. A Balanced Fast Field Echo sequence was used to visualize the surrounding soft tissues and determine the presence of intra-lumenal thrombus. For Patient 3, a novel, black-blood MRI sequence “SPACE” was employed for vessel wall and intra-lumenal thrombus imaging. For 3 patients, in vivo, time-resolved 3D velocity fields were acquired for the preoperative conditions using phase-contrast MRI (4D Flow MRI). 4D MRI with prospective gating was used to measure 3 velocity components at all points within field of view, including within the aneurysmal vessel (FOV = 192 mm × 114 mm, 128 × 76 matrix, 1.5 mm isotropic resolution, temporal window = 25.52 ms/pulsatile phase, TE = 3.26 ms, Flip angle = 15°, velocity encoding (VENC) = 160 cm/s for each component, 1 segment, prospective gating). The measured, three-dimensional flow fields were visualized using post-processing software EnSight (CEI Inc., Apex, NC) by emitting streamlines at different time points within the cardiac cycle from a manually positioned plane.

In order to obtain the inlet flow conditions for the CFD models, the velocities in the supplying vertebral arteries were measured with 2D PC-MRI. A 5 mm imaging slice transverse to the vertebral arteries, with a velocity encoding (VENC) of 125 cm/s was used to measure the through-plane component of velocity. Retrospective gating was used resulting in a temporal resolution of 27 ms and an in-plane resolution of 0.6 mm × 0.6 mm. These measurements were used to prescribe time-dependent inlet velocity boundary conditions for numerical simulation.

Model Construction

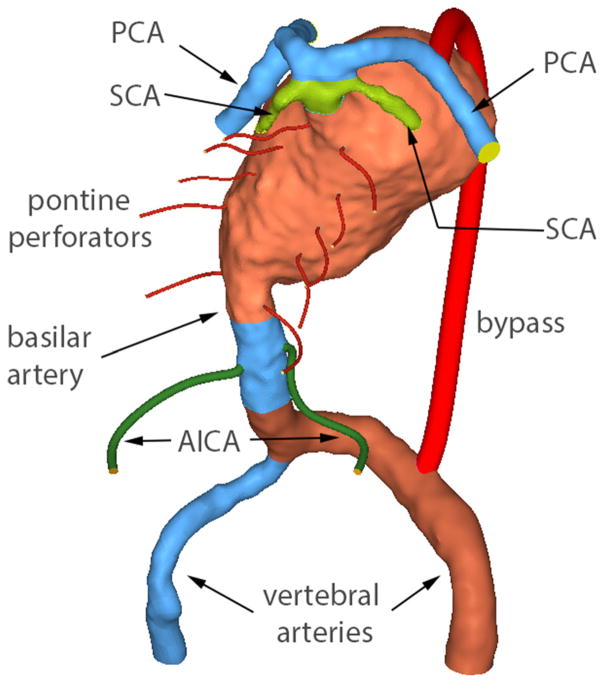
Patient-specific luminal geometries of the aneurysms were generated from CE-MRA data. In-house software was used to form a three-dimensional iso-surface from a set of MRA slices. In order to obtain this iso-surface, a threshold intensity value was selected that defined the intra-luminal volume of the vessels. The three-dimensional surface was co-registered with the two-dimensional MR slices and the threshold level was then adjusted to ensure that the segmented surface coincided with the luminal boundaries of the MR gray-scale data. The surface was then transferred into 3D modeling software, Rapidform XOR3 (3D Systems, Rock Hill, SC), where the volume of interest, which included the aneurysm with the proximal and distal vessels, was selected and background noise was removed. Remaining artifactual defects were then manually eliminated and holes in the surface were filled. In the cases of Patient 3 and Patient 4, the aneurysms involved the smaller branches of the basilar artery, feeding the cerebellum and brainstem. In order to simulate the flow through these vessels, AICAs and pontine perforators were added to the patient-specific models of the basilar artery. Since these smaller vessels were not discernable on the MR angiography images, their geometries were based on anatomy atlas drawings. Perforators and AICAs were constructed by creating a circular opening in the basilar wall, then creating 3D spline representing a typical path for the vessel, and finally, generating a surface by sweeping the opening circumference along the spline. Thus, a constant diameter was assumed for each branch vessel, based on a nominal diameter. The resulting geometries were imported into the pre-processing software package Hypermesh (Altair Engineering, Troy, MI), where an unstructured tetrahedral mesh was generated over the computational domains. The mesh density for these models was the same as that used in our previous studies, where mesh independence was verified for similar basilar aneurysm geometries.^3,20–22

In order to simulate the flow resulting from alternative surgical options, the preoperative geometries were modified by adding bypasses or truncating vessel segments which represented surgical clipping. A much finer mesh was generated for the smaller vessels, with an element size of 0.07 mm used for pontine perforators. In order to be consistent with the mesh used for the models representing alternative surgical options, as well as to minimize the amount of work required for meshing numerous vessels, the models were constructed from components corresponding to different vessels or their segments. An example showing the components used for the meshing of patient’s 4 model is presented in Fig. 2. The model is shown in posterior view so that all basilar branches included in the analysis could be labeled. In this modular approach, each vessel was meshed as a separate computational domain which could be added or removed (turned on and off) depending on the considered postoperative configuration. For example, a vertebral artery could be removed and a bypass joining the contralateral vertebral with a posterior cerebral artery (PCA) could be added to simulate one of the options, without remeshing the aneurysmal basilar artery and all the perforators. All 3D components are stored in a Hypermesh model, but only components participating in a given flow configuration are exported as a CFD mesh for each simulation. The surface elements for each component are exported along with the tetrahedral elements inside the volume. Since removing or clipping a vessel component results in a gap in the model’s surface, interior boundary surfaces were created at the interfaces between the 3D components. The interface elements are exported as an interior mesh if both components are active or as a surface (wall) mesh if one of the components is removed.

FIGURE 2.

Components of the model meshed as separate computational domains. The model includes AICAs and pontine perforators, as well as a vertebral-to-PCA bypass. Posterior view is shown (unlike the MRA image in Fig. 1) in order to show the perforators.

Numerical Solution of the Flow Equations

The incompressible Navier–Stokes equations were solved using a finite-volume solver, Fluent (ANSYS, Inc, Canonsburg, PA). The flow was assumed to be Newtonian, with a dynamic viscosity of 0.0035 Pa s. Rigid walls were assumed for all simulations conducted in this study. A pressure-based coupled algorithm was used to solve a coupled system of the momentum and pressure-based continuity equations. A second-order scheme was used in time discretization and a third-order, MUSCL scheme was used for discretization of the momentum equations. The number of time steps per cardiac cycle matched the number of cardiac phases acquired with 4D MRI for the same patient (about 33 intervals per cardiac cycle). For the initial, preoperative flow simulations, patient-specific flow waveforms obtained from the through-plane PC-MRI measurements were prescribed at the inlets. The outlet pressure was set to zero for all outlets.

In order to prescribe the boundary conditions for the postoperative flow simulations, the preoperative inlet flow rates were adjusted assuming that the distal vascular territories would require the same amount of flow before and after the procedure. For example, in the case where a vertebral artery was occluded, the flow through the collateral vertebral was increased to maintain the same total inlet flow. The flow through a bypass feeding the basilar apex was equal to the cumulative outflow of the basilar apex branches in the preoperative flow conditions. In the case where a clip above the SCAs was modeled, the flow through the MCA to PCA bypass was set to the sum of the pre-operative flow rates through the PCAs, while the same amount of flow was subtracted from the inlet wave-forms prescribed for the vertebral inlets.

Modeling Contrast Agent Transport

In order to assess the effect of surgery on the flow residence time, a contrast agent injection was numerically simulated using a “virtual ink” technique, described in a previous report.²¹ This method provides an Eulerian approach for estimation of the flow residence time (RT). The technique is based on solving the advection–diffusion equation to compute the transport of a passive scalar. The velocities obtained in the numerical solution of the Navier–Stokes equations are used to calculate the advection of the virtual contrast, while the contrast has no effect on the velocity field. The flow is advection-dominated, so the diffusion coefficient is set to zero. A third-order MUSCL scheme is used for spatial discretization. The injection of virtual contrast is simulated for a number of cardiac cycles and then followed by contrast-free flow simulation that is carried on until the contrast is completely washed-out from the geometries. The value of the scalar at the inlets is set to 1 during the contrast injection and zero otherwise; therefore, the regions where the scalar value is 1 are filled with contrast, while the regions where its value is zero are contrast-free. It should be noted that, due to the Eulerian nature (which represents the concentration as the volume average over the control volume) of this method and a finite amount of numerical diffusion, the value of the scalar obtained in the numerical solution is not always 0 or 1 but can assume values in between. The flow regions with the scalar value above 0.5, that are considered to be filled with the contrast, can be numerically highlighted in the post-processing analysis. An animation showing the propagation of virtual contrast can be generated by combining contrast maps obtained at different time steps of the simulation.

RESULTS

Preoperative Flow Fields Measured with 4D Flow MRI and Computed with CFD

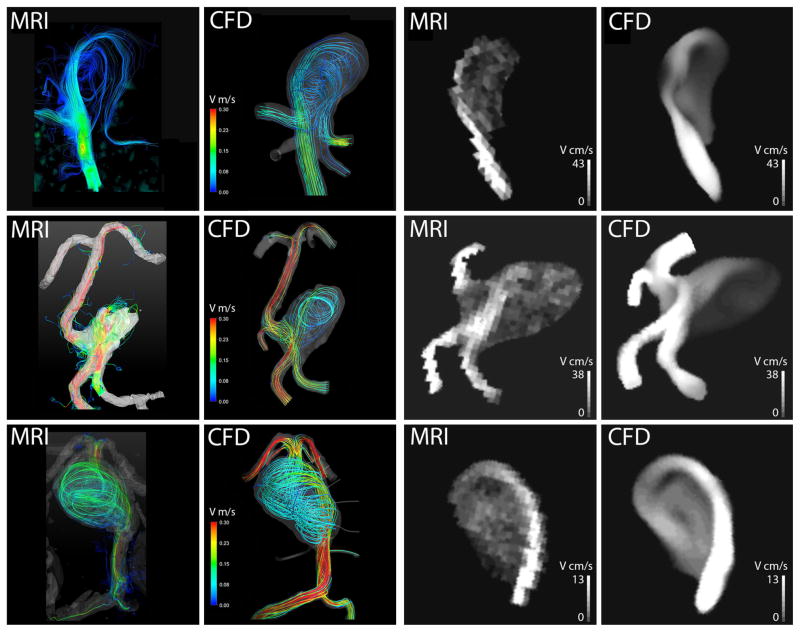
In vivo 4D Flow MRI measurements were obtained for three patients prior to surgery. For patient 3 only through-plane (two-dimensional) PC-MRI measurements were available, providing time-resolved flow rates through the supplying vertebral arteries. For the remaining patients (1, 2 and 4), the measured and calculated preoperative flow fields were compared both qualitatively and quantitatively. Each row in Fig. 3 shows the flow fields obtained for one of these patients. Preoperative flow streamlines are shown in the left half of the figure (first two columns). In each case, the flow field measured with 4D MRI is shown on the left (first column) while those obtained with CFD are shown on the right (second column). Since flow streamlines can be misleading because of their dependence on location and number of seed points, we also compared velocity magnitude maps obtained for cross-sectional planes through the aneurysms. These velocity cut-planes are shown in the right of Fig. 3 (last two columns) with the velocities measured by 4D Flow MRI shown on the left (third column) and those computed with CFD on the right (last column). For patient 1 both methods show that the flow coming up the basilar artery enters the lesion and forms a strong vortex in the aneurysm dome. While some fraction of the flow enters one of the PCAs prior to entering the aneurysm, the other PCA receives most of its blood from the flow exiting the aneurysm. For patient 2 (center row), the aneurysmal flow is determined by a complex interaction of the jets entering from the vertebral arteries. A region of slow, recirculating flow is observed in the lower part of the aneurysmal sac. This low flow region is adjacent to the intra-aneurysmal thrombus detected with additional MRI studies. The last row is showing the MRI measurements and CFD simulations for preoperative flow conditions in patient 4. Both methods show a high-velocity jet propagating along the posterior wall of the basilar trunk and a strong recirculation region in the aneurysmal sac.

FIGURE 3.

Comparison of preoperative flow fields obtained in 3 patients. Patient 1: top row, Patient 2: center row, Patient 4: bottom row. The color images show 3D streamlines; the black and white images show velocity magnitude maps calculated for cross-sectional planes through the aneurysms.

A quantitative comparison of the MRI and CFD results obtained in these 3 patients is presented in Table 1. The mean and maximum velocities as well as the standard deviation were obtained for the 4D Flow MRI measurements and CFD simulations. The velocities were measured on a cross-sectional plane (2D) with an up-sampling of the 4D MRI dataset to match the resolution of the CFD data. In each case the flow was characterized by a high-velocity jet entering the aneurysm and a large area of slow, recirculating flow. Since velocity values in these distinct flow regions were substantially different, the mean and maximum velocities in them were calculated and compared separately. In each case, approximately one hundred data points were used in the jet region and 130 data points in the slow flow region. An average error in the jet regions is about 20%, while larger discrepancies were observed in the slow flow regions. This can be explained by the MRI velocity encoding settings that were optimized for capturing higher velocities observed in the jet regions.

TABLE 1.

Comparison of velocities measured in vivo with 4D Flow MRI and computed with CFD.

	High-velocity jet		Low-velocity region
	CFD	4D MRI	CFD	4D MRI
Patient 1
Mean	29.86	31.79	9.34	8.35
SD	10.41	15.92	3.33	3.46
Max	43	68	18	19
Patient 2
Mean	25.8	20.67	4.2	7.6
SD	11.55	10.06	1.05	3.77
Max	51	53	7	19
Patient 4
Mean	16.77	13.14	6.36	4.22
SD	6.14	5.44	1.87	1.42
Max	27	28	10	8

For each patient, the mean and maximum velocities were computed for the high-velocity jet and slow recirculating flow regions.

Postoperative Flow Simulations

Patient 1

Following the procedure, the jet entering the aneurysm was eliminated. The postoperative streamlines, originating in the bypass supplying the flow from the ipsilateral MCA, are shown in Fig. 4b. Following the clipping of the basilar artery, the flow from the bypass splits between the two PCAs, while the flow in the aneurysm remains essentially stagnant. This reduction of the flow predicted by CFD indicates that the aneurysm is likely to clot off following the procedure. The transport of virtual contrast computed for the preoperative and postoperative flow conditions is shown in Figs. 4c and 4d. In the preoperative flow, the contrast enters the aneurysm through the basilar artery and quickly fills the aneurysmal volume, propagating along its walls. In the postoperative case, the contrast enters through a bypass and flows through the PCAs, while only a small amount enters the aneurysm at a later time. By the time the aneurysm is completely filled with contrast in the preoperative flow, the volume is still almost empty in the postoperative case. Thus, the modeling predicts that the surgery would result in increased flow residence time in the aneurysmal volume, which is likely to facilitate thrombotic occlusion. The region filled with contrast in the postoperative model (d) is similar to the volume which remained patent following the thrombotic occlusion observed in vivo (e).

FIGURE 4.

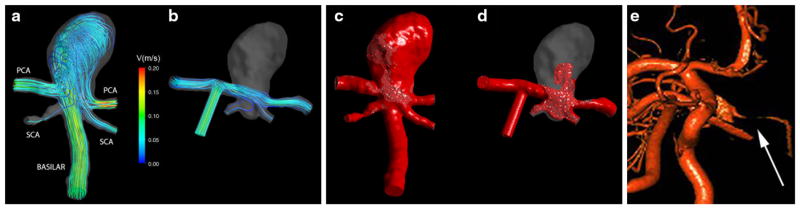
Patient 1: (a) Preoperative streamlines obtained with CFD; (b) Postoperative streamlines obtained with CFD; Comparison of virtual contrast transport for preoperative (c) and postoperative (d) flow conditions. Postoperative imaging (e), demonstrating the thrombotic occlusion of the aneurysmal sac (shown by the arrow).

Patient 2

Two alternative interventions were simulated: occlusion of either the left vertebral artery (option 1) or right vertebral artery (option 2). The CFD simulations predicted dramatically different postoperative flow fields resulting from these options. In option 1 (Fig. 5a), a high-velocity jet enters the aneurysm impinging on its opposite wall; then the jet reverses direction, causing a strong recirculation in the lesion. In option 2 (Fig. 5b), the jet flows into the basilar trunk, while a part of it is deflected by the wall into the aneurysmal sac, resulting in a slowly rotating vortex. The virtual contrast simulations carried out for both options show that clipping the left vertebral (Fig. 5c) would result in quick filling of the aneurysm, while filling of the basilar trunk is delayed. If the right vertebral is clipped (Fig. 5d), the contrast quickly flows into the basilar, while the flow residence time in the aneurysm is increased. The latter scenario is relatively more likely to promote aneurysm clotting.

FIGURE 5.

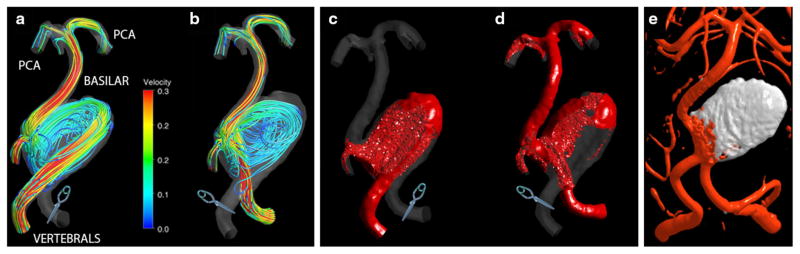
Patient 2: Two postoperative flow scenarios: (a) left vertebral occlusion and (b) right vertebral occlusion. The virtual contrast simulations: (c) quick filling of the aneurysm in the first option; (d) increased flow RT in the in the second option. Postoperative imaging (e), demonstrating the thrombotic occlusion of the aneurysmal sac following stent-assisted coiling.

This aneurysm was treated by stent-coiling, rather than by an occlusion of a vertebral artery. A stent was placed through the left vertebral and into the basilar trunk and a then endovascular coils were deployed through the stent, filling the aneurysmal sac. The stent ensured the coils would stay in place in the sac, thus eliminating the jets entering the aneurysm. The flow from the left vertebral proceeded into the basilar trunk, while the aneurysm was essentially excluded from the circulation. Postoperative images demonstrated thrombotic occlusion of the aneurysm following this procedure (Fig. 5e). These postoperative results cannot be used for a direct comparison with CFD predictions, since the intervention was different from the options simulated with CFD. Nevertheless, this was the only case where postoperative CFD simulations were conducted prior to the procedure and the results were used to inform the clinicians.

Patient 3

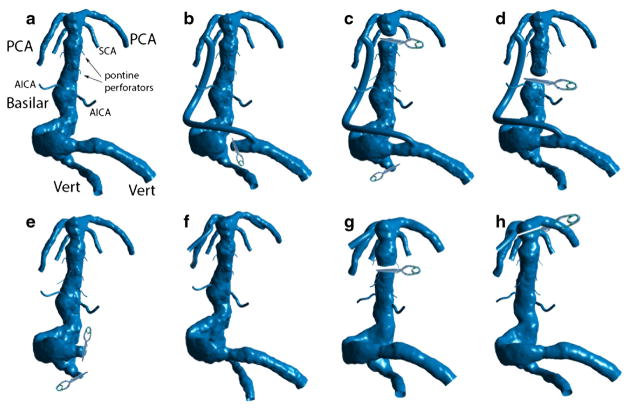
Seven alternative flow scenarios were simulated for this patient, as shown in Fig. 6 and will be briefly described here: (a) the preoperative geometry; (b) occlusion of the dominant vertebral and placement of a bypass from this vertebral, immediately proximal to the site of occlusion, to the ipsilateral PCA; (c) occlusion of the smaller vertebral and clipping the basilar proximal to the SCAs with a bypass from the dominant vertebral to the PCA; (d) mid-basilar occlusion immediately distal to AICAs accompanied by a bypass from the dominant vertebral to the PCA; (e) occlusion of both vertebrals with the flow provided by a bypass from a vertebral artery to one of the AI-CAs; (f) adding posterior communicating arteries in order to connect the apex to the anterior circulation; (g) mid-basilar occlusion with a bypass supplying the apex from the MCA; and finally (h) clipping the basilar apex distal to the SCAs with a bypass from the MCA supplying the PCAs. Numerical simulations were carried out for each of these flow scenarios. In order to keep the excessive details out of this report, we will discuss only three of these options: (b), (c), and (h) that we will refer to as Options 1, 2, and 3 respectively.

FIGURE 6.

Surgical options simulated for patient 3. (a) Preoperative geometry; (b) Dominant vertebral artery occlusion with a dominant vertebral-to-PCA bypass; (c) Occlusion of the smaller vertebral and clipping the basilar artery below the apex with a bypass from the dominant vertebral to the PCA; (d) Mid-basilar occlusion with dominant vertebral-to-PCA bypass; (e) Occlusion of both vertebrals with the flow provided by a bypass to AICA; (f) Adding PCOM arteries to connect with anterior circulation; (g) Actual procedure: mid-basilar occlusion with an MCA-to-PCA bypass; and (h) Clipping the basilar artery at the apex above the SCAs with an MCA-to-PCA bypass.

For this patient, we were not able to obtain 4D Flow MRI measurements. A novel “SPACE” technique, however, was very useful in determining the regions occupied by intra-luminal thrombus. The angiography images showed that one of the vertebral arteries was substantially larger than the other. The thrombus deposition in the aneurysmal vertebral indicated that further decrease of the flow through this vessel could cause its complete occlusion. In addition a large thrombus was found in the mid-basilar region, as shown in Fig. 7a. Flow streamlines are not particularly helpful in showing how different procedures affect the flow through the pontine perforator arteries, since depending on their seeding point they may or may not enter these tiny vessels. The images showing the computations of the virtual contrast advection can provide a better visualization of the flow and, particularly, of the flow separations regions where contrast filling is delayed. All images shown in Fig. 7 from (b) to (e) correspond to the same time interval after starting the contrast injection. This is the time step when the preoperative geometry was completely filled with the contrast (Fig. 7b). In option 1 (Fig. 7c), the contrast is flowing up the bypass to the basilar apex and fills the basilar trunk in a retrograde fashion. The flow residence time (RT) in the distal basilar is increased, indicating inadequate flow to some of the perforators above the AICAs. In option 2 (Fig. 7d), it was assumed that the bypass provides all the flow required by the apex and that the vertebrals are supplying only the AICA’s and pontine perforators, which amounts to less than 10% of the preoperative flow. These flow conditions caused substantial increase of the RT in the basilar trunk, compromising the flow to all smaller branches. In option 3 (Fig. 7e), approximately 50% of the flow is diverted to the PCAs via the bypass, while the remaining half is flowing through the basilar trunk towards the superior cerebellars. In this case the contrast eventually fills the perforators after several cardiac cycles; however such an increase in the flow RT relative to the preoperative conditions could potentially lead to the perforators’ occlusion. The actual intervention in this case corresponded to option (g) and resulted in severe perforators infarction not compatible with patient’s survival.

FIGURE 7.

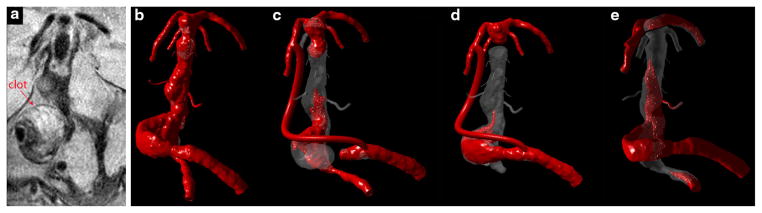
Patient 3: (a) MRI SPACE sequence showing intra-luminal thrombus; Virtual contrast simulations: (b) Preoperative flow conditions; (c) Option 1. Dominant vertebral clip with a vertebral-to-PCA bypass; (d) Option 2.Clipping smaller vertebral and basilar apex with a bypass from dominant vertebral to PCA; (e) Option 3.MCA-to-PCA bypass and clipping the basilar apex distal to SCAs. The simulations show inadequate flow through the perforators for all considered options.

Patient 4

The aneurysm was treated surgically, by clipping the basilar artery proximal to the SCAs and performing a bypass from an MCA to PCA in order to supply the basilar apex. In addition to this procedure, which will be referred to as “option 1”, two alternative surgical options were modeled with CFD. Both alternative models included a clipping of the smaller vertebral and the distal basilar, accompanied with a bypass from the dominant vertebral to the ipsilateral PCA. The difference between the two was that in one case, “option 2”, the distal basilar was clipped proximal to the SCAs, completely separating the basilar apex, while in the other, “option 3”, the clip was placed across the SCAs, leaving one of the superior cerebellar arteries with the basilar apex and the other with the basilar trunk. The results showing the filling of these geometries with virtual contrast at the same time interval following the injection are presented in Figs. 8a, 8b, 8c, and 8d. The model is viewed from the posterior direction in order to show the perforators. At the time when the preoperative geometry was completely filled with the contrast (a), the postoperative geometries still had large regions that remained free of contrast. In option 1 (b), it was assumed that the basilar apex was adequately supplied by a bypass from the MCA, while the same amount of flow was subtracted from the vertebrals. This resulted in very slow flow in the basilar trunk with substantially increased flow residence time in the aneurysm. Similarly, in option 2, almost 80% of the inlet flow proceeded through the bypass to the apex, leaving only a fraction to flow through the basilar trunk (Fig. 8c). The contrast failed to reach the perforators even after 5 cardiac cycles, indicating sluggish and inadequate supply to these vessels. In the last option (d), the slanted clip across the SCAs resulted in a quick filling of the basilar apex with the flow diverted to the PCAs through the bypass, while preserving a relatively vigorous flow through the basilar trunk toward the remaining SCA outlet. After 5 cycles, both AICAs and the perforators were filled with the contrast. The flow residence time in the aneurysm was increased relative to the preoperative flow conditions, which could facilitate thrombus deposition in the area adjacent to the initial thrombus mass.

FIGURE 8.

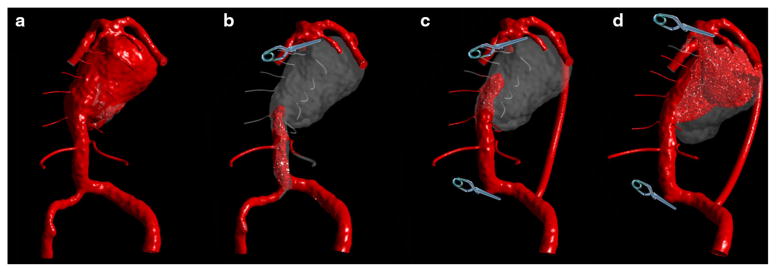
Patient 4: Virtual contrast simulations (note that the aneurysm is shown in posterior view) for various flow scenarios: (a) Preoperative conditions; (b) Basilar apex is clipped below the SCAs and supplied by a bypass from the MCA. (c) Basilar apex is clipped below the SCAs, smaller vertebral is occluded and bypass is performed from the dominant vertebral to PCA; (d) Basilar apex is clipped across the SCAs, smaller vertebral is occluded and bypass is performed from the dominant vertebral to PCA.

DISCUSSION

Numerical results obtained from CFD models of the four basilar aneurysms considered in the study were in good qualitative agreement with available imaging data. A quantitative comparison showed that while the MR measurements and numerical results were similar in the regions with relatively high velocities, the differences were larger for the low flow zones. The velocity encoding settings used in PC-MRI studies were determined by higher velocities observed in the posterior arteries. This could lead to less accurate results in the intra-aneurysmal regions characterized by low velocities, where MRI measurements were more affected by noise. This makes the verification of numerical results in disturbed flow regions more difficult, but also highlights the advantage of CFD in capturing these flow patterns.

In the first two cases, the aneurysms affected either a proximal or distal segment of the basilar artery. It is thus likely that, while being very large in size, these aneurysms did not involve the brainstem perforators. The numerical models constructed in these cases thus did not include the perforators on the assumption that an intervention altering the flow in the aneurysm would not affect the flow through these vessels. In the other two cases, the aneurysms involved the basilar trunk and therefore it was necessary to assess the postoperative flow through the perforators. The resolution that could be obtained for CE-MRA on our 3T SIEMENS scanner was 0.7 mm isotropic, which is barely sufficient for observing the AICAs and inadequate to visualize the 200–300 μm perforators. Therefore, idealized geometries of these smaller vessels were incorporated into the image-based models. Adding the perforators substantially increased the number of computational cells and therefore the computational cost of these more complex models. It should be noted that computational results depend on the location of the perforators added to the model. For example, the perforators modeled for Patient 4 were assumed to emanate from the posterior wall of the basilar artery, which was the area adjacent to the brainstem and also least affected by the aneurysmal disease (Fig. 8). The perforators on left side of the basilar were in line with the direction of the high-velocity jet and were quickly filled with the contrast. The perforators on the other side were located in the flow recirculation region and were filled by a retrograde flow, which delayed their contrast arrival time. It is not clear whether this difference would have a major effect on the patency of these vessels, as from the limited number of simulations conducted in this study it is not possible to determine a universal residence time threshold. It is hoped that by modeling the flow in a number of similar aneurysms and comparing CFD predictions to available clinical data we would be able to determine the range of flow residence time that would correlate with thrombus layering.

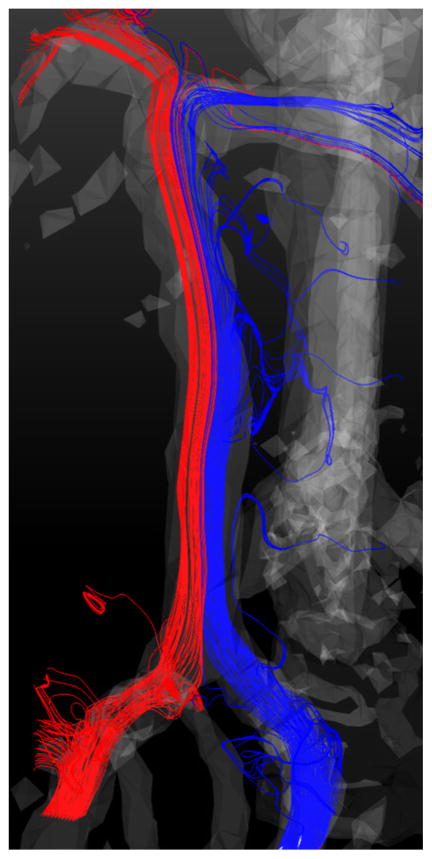
Prescribing the flow boundary conditions for the perforators is even more challenging, as PC-MRI methods also lack resolution for measuring the flow through them in vivo. An attempt was made to assess the total amount of flow exiting through the perforators and AICAs by calculating a difference between the flow rates in the proximal and distal basilar artery. A healthy basilar artery was imaged with 4D Flow MRI and velocity fields were obtained through the cardiac cycle. The flow field is shown in Fig. 9, where the streamlines are colored according to the originating vertebral artery. Cross-sectional planes were placed above the junction of the vertebral arteries and below the superior cerebellar arteries and the flow rates were computed for each cardiac phase of the cycle. The data analysis showed that the amount of flow exiting through the branches is similar to the error of this technique, which is about 10% of the flow. It should be noted that little mixing is observed in the basilar artery; thus each vertebral artery predominantly supplies distal vasculature on the ipsilateral side. These results are consistent with a study by Bockman et al., where the flow and mixing in four healthy vertebrobasilarsystems were studied with CFD as well as arterial spin labeling MRI measurements.² For Patient 4, the effect of alternative procedures on the flow distribution among the outlets was quantified by measuring the total flow exiting through the AICAs and brainstem perforators. The results obtained for each surgical option as well as for the preoperative conditions are summarized in Table 2. Separating the PCAs and SCAs from the basilar trunk resulted in substantial increase of the flow through the perforators, as they became the only outlets available for the basilar flow. This increase, however, was not uniformly distributed among the perforators, but strongly depended on their location. The uncertainties related to flow boundary conditions and their postoperative changes are likely to have a larger effect on CFD predictions than numerical errors that could result from limited resolution in the smaller branches.

FIGURE 9.

Flow streamlines in a healthy basilar artery measured with 4D Flow MRI. The streamlines are colored by the originating vertebral artery.

TABLE 2.

Patient 4: changes in the total flow rate in the brainstem perforators resulting from alternative surgical options.

	Preoperative		Option 1		Option 2		Option 3
	mL/s	%	mL/s	%	mL/s	%	mL/s	%
Total basilar flow	6.558	100.0	6.400	100.0	5.697	100.0	5.697	100.0
Outlet flow in perforators	0.322	4.9	0.640	10.0	1.318	23.1	0.161	16.1

In the case of Patient 3, all postoperative flow models showed inadequate flow to the perforators. The aneurysmal disease caused almost a uniform dilation of the basilar, resulting in a very slow flow even in the preoperative conditions. Apparently the low preoperative velocities and high flow residence time were near a physiologic threshold, as extensive thrombus layering was observed in the aneurysm prior to the intervention. Any procedure diverting some part of the flow from the basilar trunk would exacerbate these conditions, promoting further obstruction of the perforators with thrombus. In the other cases, in particular Patient 4 where the perforators were also incorporated into the model, the presence of high-velocity jets allowed redirection of the flow in order to reduce the impact on the aneurysmal wall. Based on these few cases, the results indicate that for aneurysms with “still water” preoperative flow conditions any procedure aiming at reducing the flow through the basilar artery is likely to further compromise the flow to the pontine perforators. Considering alternative interventional options for the models with perforators, it can be concluded that placing a clip across the superior cerebellar arteries ensured that almost half of the flow goes through the basilar trunk supplying the perforators. This advantage in the postoperative flow conditions should be balanced by the technical challenge of implementing this option.

In this study the arterial walls were assumed rigid. This assumption is reasonable for modeling the flow in cerebral arteries, as cine MR images show no appreciable movements of these vessels over the cardiac cycle.³ In addition, the aneurysmal disease results in reduced elasticity of the arterial wall.⁹ The Newtonian flow assumption, typical for the flow in large arteries, may be not ideal for modeling the flow through pontine perforators or in regions with very low shear rates. Nevertheless, our previous simulations show that this would have a secondary effect on the flow, considering the uncertainty in the flow boundary conditions and in idealized geometries of the smaller vessels. We think that a more important limitation of this study is the lack of patient-specific information on the flow through the pontine perforators and the changes caused by the flow redistribution following a procedure. Another assumption on the boundary conditions was prescribing a zero pressure at the outlets. In one of our unpublished preliminary studies, in vivo 4D MRI measurements of the flow in a basilar aneurysm were compared to CFD results obtained with different outlet conditions. In one simulation, the outlet flow rates were prescribed based on generalized assumptions about the distal territories (e.g., equal flow through the PCAs since the left and right hemispheres demand equal posterior flow); in the other run the outlet pressure was set to zero for all branches. The model with zero-pressure outlet conditions was found to be much closer to the in vivo measurements. It is possible that the distal resistance is similar for different basilar branches, unlike the branches of the aorta, where the vessels can run for longer distances before they reach the internal organs. The study limitations and assumptions considered above could potentially lead to some inaccuracies in the prediction of postoperative flows, however the clinical data obtained following the procedures seem to verify the numerical results. The inherent limitation of such validation is that it is not possible to implement alternative interventional options on the same patient.

CONCLUSION

Image-based numerical models were generated in order to evaluate alternative surgical options considered for four basilar artery aneurysm patients. In two cases, where the aneurysms affected pontine perforator vessels, idealized perforator geometries were incorporated into the patient-specific models. A transport of virtual contrast was simulated and the results were used to assess the changes in the flow residence time resulting from each of the modeled interventions. CFD results were in close agreement with available MR imaging data. The study indicates that computational models constructed from medical imaging data can be used to predict postoperative flow in cerebral aneurysms. This information, available prior to surgery, may help improve the outcome of surgical procedures.