Persistent Residual Errors in Motor Adaptation Tasks: Reversion to Baseline and Exploratory Escape

Abstract

When movements are perturbed in adaptation tasks, humans and other animals show incomplete compensation, tolerating small but sustained residual errors that persist despite repeated trials. State-space models explain this residual asymptotic error as interplay between learning from error and reversion to baseline, a form of forgetting. Previous work using zero-error-clamp trials has shown that reversion to baseline is not obligatory and can be overcome by manipulating feedback. We posited that novel error-clamp trials, in which feedback is constrained but has nonzero error and variance, might serve as a contextual cue for recruitment of other learning mechanisms that would then close the residual error. When error clamps were nonzero and had zero variance, human subjects changed their learning policy, using exploration in response to the residual error, despite their willingness to sustain such an error during the training block. In contrast, when the distribution of feedback in clamp trials was naturalistic, with persistent mean error but also with variance, a state-space model accounted for behavior in clamps, even in the absence of task success. Therefore, when the distribution of errors matched those during training, state-space models captured behavior during both adaptation and error-clamp trials because error-based learning dominated; when the distribution of feedback was altered, other forms of learning were triggered that did not follow the state-space model dynamics exhibited during training. The residual error during adaptation appears attributable to an error-dependent learning process that has the property of reversion toward baseline and that can suppress other forms of learning.

Introduction

When a motor command is produced but the result is other than expected, the brain partially compensates for the error by altering the commands on the next attempt (Shadmehr and Mussa-Ivaldi, 1994; Krakauer et al., 2000; Thoroughman and Shadmehr, 2000). As a result, when a perturbation is presented repeatedly, the changes in motor commands accumulate, mostly compensating for the perturbation. A puzzling feature of this process of adaptation is that the compensation is often incomplete: after many trials of training, subjects still exhibit small, sustained errors in their performance (Krakauer et al., 2000, 2006; Tseng et al., 2007; Rabe et al., 2009; Galea et al., 2011; Taylor et al., 2014). It appears that, even with extended training, there are persistent steady-state errors that the brain does not correct. Why should this be?

State-space models of learning provide a mathematical description of adaptation that can account for these persistent residual errors (Smith et al., 2006; Kording et al., 2007). In these models, it is assumed that the brain learns to estimate the state of the environment, updating its estimate after each trial based on the experienced error. In addition, the estimated state partially reverts toward baseline after each trial. That is, error-dependent learning is balanced with trial-to-trial forgetting (or reversion toward a baseline state). These two opposing effects eventually reach equilibrium in which learning from error balances reversion toward baseline. This trial-to-trial reversion is thought to be directly observable by using trials in which errors are constrained to zero, called error-clamp trials (Scheidt et al., 2000; Smith et al., 2006; Criscimagna-Hemminger and Shadmehr, 2008; Pekny et al., 2011; Ingram et al., 2013; Kitago et al., 2013).

However, recent work has revealed that reversion to baseline in adaptation paradigms is not inevitable. Close inspection of behavior in error-clamp trials reveals that subjects persist in their asymptotic actions over several trials before beginning to revert to baseline (Vaswani and Shadmehr, 2013). Reversion to baseline in error-clamp trials can be prevented altogether by reinforcing an action performed at asymptote or by imposing variable errors in clamp trials (Shmuelof et al., 2012; Vaswani and Shadmehr, 2013). If reversion to baseline is not obligatory, why is it that subjects cannot close their residual error?

We suggested previously that the attenuation of reversion to baseline reflected the engagement of an alternative reinforcement-based learning process, which is usually mostly suppressed in regular adaptation paradigms (Shmuelof et al., 2012). This alternative process deviates from the dynamics of the state-space model and, in particular, may not be susceptible to reversion to baseline. Here, we asked whether such an alternative learning process could also be used to overcome the persistent residual errors seen during adaptation. We used a novel kind of error clamp that imposed constant, small, nonzero errors. We posited that the ensuing decorrelation of visual feedback from a subjects' actions might create sufficient contextual change (Vaswani and Shadmehr, 2013) to provoke subjects to break free from error-based learning and respond to the residual error with another kind of learning.

Materials and Methods

Participants.

Fifty-seven healthy, right-handed subjects (34 females, aged 20–41 years) participated in the experiments. All subjects were naive to the purpose of the experiment and were paid to participate. The experiments took place at Columbia University, and the work was approved by the Columbia University Institutional Review Board.

Paradigm.

Subjects sat at a table with their right hand supported on a lightweight sled. Air jets in the sled generated air cushions that facilitated frictionless planar movements. Subjects could not see their hand but were provided with continuous visual feedback throughout the experiment. Custom routines, courtesy of Dr. R. L. Sainburg (Pennsylvania State University, State College, PA), controlled the real-time visual display.

Subjects performed movements with their right arm from a starting circle to a circular target (0.5 cm diameter) positioned 8 cm away at 135° (Fig. 1A). Hand and arm positions were recorded at 120 Hz using a Flock of Birds magnetic system (Ascension Technology). If the cursor hit the target, a pleasant tone was played. Subjects also received numerical feedback indicating their speed and were told that this score indicated solely their speed. Subjects were told that the object of the task was to hit the target while maintaining a quick speed; they were not required to stop at the target. Subjects took 118 ms to reach the target extent, on average.

Figure 1.

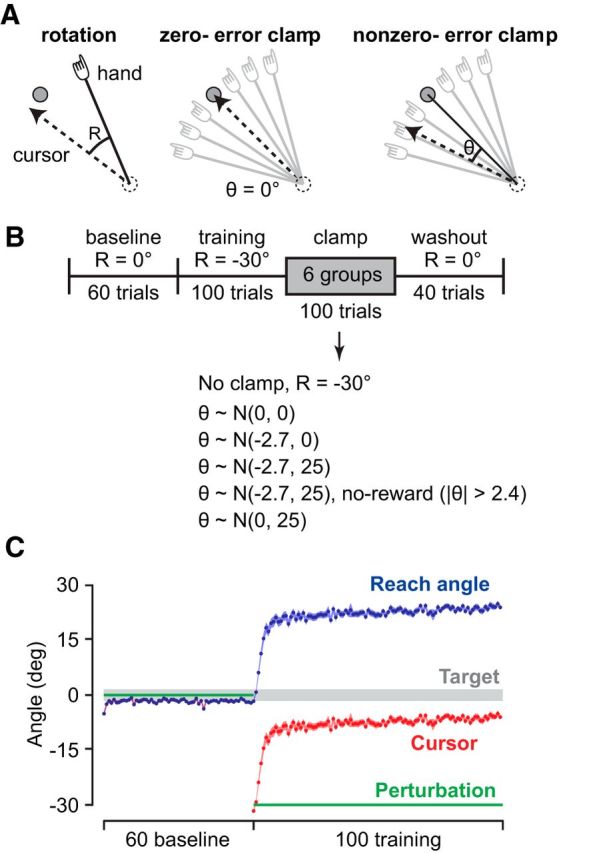
Paradigm. A, Subjects made 8 cm reaching movements to a target at 135°. Visual feedback was perturbed by a rotation (left) or clamp (middle and right). In clamp trials, the cursor (dashed lines) moved directly to the target (middle) or to an endpoint, independent of the reach angle (solid lines). B, Subjects completed 60 trials of baseline training with veridical visual feedback, followed by 100 trials of a 30° visuomotor rotation. Then, subjects were exposed to 100 clamp trials, in which visual feedback was presented along a line at a fixed angle in each trial. C, Each group received a different clamp angle (θ) distribution. We denote these distributions by N(x, y), indicating that the feedback was normally distributed with mean x and variance y. A control group (no-clamp) received additional rotation trials instead of clamps. One group was always clamped to the target [N(0, 0)]. Three groups received feedback with a distribution that was similar in mean and/or variance to their movements during the training period [N(0, 25), N(−2.7, 0), N(−2.7, 25)]. A last group received feedback with similar mean and variance, but trajectories to the target (|θ| < 2.4°) resampled so no trials were rewarded (N(−2.7, 25), no-reward group). In each of these groups, the distribution of feedback was pseudorandom.

Our primary concern was to expose the subjects to a visuomotor perturbation and test whether behavior after adaptation exhibited steady-state errors. To understand the reason for these errors, we then probed how subjects learned from error by following the perturbation with error-clamp trials in which we decoupled visual feedback from reach angles, controlling for error on each trial.

All subjects first completed 40 baseline trials, in which cursor position was veridical, followed by a short break. They then completed 20 additional baseline trials, followed by 100 trials of training in which the cursor was rotated 30° counterclockwise. Each group then completed a group-specific pattern of clamp trials in which we controlled the trial-to-trial distribution of visual feedback, followed by 40 trials of washout in which veridical feedback was provided (Fig. 1B).

Subjects were told that, during the experiment, they would find themselves making errors and that they should not think about what was causing them but continue to aim for the target. Subjects were told explicitly that, if they notice anything weird, they should tell the experimenter.

We tested six groups of subjects (Fig. 1C). In the first group (no-clamp), subjects received 100 additional perturbation trials without an error-clamp block. In the next five conditions, subjects were presented with error-clamp trials, in which cursor position was decoupled from hand position, but we modulated the distribution of cursor feedback. We use the notation N(x, y) to indicate that subjects received visual feedback drawn from a normal distribution with mean x and variance y. The N(0, 0) group (n = 7) received traditional error-clamp trials, in which the cursor moved toward the center of the target on every trial. That is, the cursor feedback had a distribution with mean zero and variance zero. In pilot experiments, after 100 trials of training in a 30° clockwise rotation, subjects were receiving feedback with a distribution with mean ± SD of −2.7° ± 5° (variance, 25 deg²). Accordingly, the N(−2.7, 25) group (n = 10) received cursor feedback drawn pseudorandomly from this distribution. These parameters were similar to the mean and variance of the distribution of visual feedback these subjects received at the end of the training block. To examine the role of reward, we considered a condition in which the distribution of feedback resembled that during training but without any successful trials. In the N(−2.7, 25) no-reward group (n = 8), any trials in which the cursor would end in the target were resampled pseudorandomly from the distribution. That is, in this condition, subjects never hit the target and never received the pleasant tone but still received feedback about the speed of their movements. To dissociate the roles of mean and variance of the feedback distribution on behavior, in two groups, we used a distribution in which one of these parameters was similar to that of subjects at the end of training, but the other changed. The N(0, 25) group (n = 10) received visual feedback with a distribution with mean zero and variance 25 deg², a variance similar to the variance of subjects' movements at the end of the training block but with a different mean. The N(−2.7, 0) group (n = 15) received feedback with a bias (−2.7°) but no variance. In each group that received error-clamp trials, all subjects received the same sequence of feedback.

State-space model.

We fit a two-state model to the behavior of subjects during the training block and assessed to what degree the model fit could predict behavior during the clamp and washout blocks of the experiment (Smith et al., 2006). In this model, the perturbation was estimated via two internal states: (1) one of which learns quickly from prediction error but also reverts to baseline quickly, called the “fast” state; and (2) the other of which learns slowly and reverts to baseline slowly, termed the “slow” state. On each trial, the state estimate x⁽ⁿ⁾ is updated from the error e⁽ⁿ⁾ as follows:

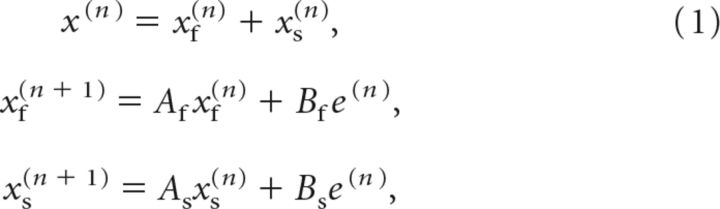where x_f and x_s are the fast and slow states, respectively. The learning rates are 0 < B_s < B_f < 1, and the retention rates are 0 < A_f < A_s < 1. For each subject, we fit the learning and retention rates of the model to the behavior during the baseline and training block, minimizing the least squared error between the data and model output. Then we fixed the parameters and, using the feedback provided in the clamp block, predicted the reach angles during the clamp and washout blocks for each subject. To evaluate the ability of the model to accurately predict behavior, we computed the variance accounted for (VAF) by the model in the fit and prediction periods, as well as the square root of the mean squared error (RMSE) of the model predictions. We also computed the predicted trial-to-trial retention at the end of training. To do so, we calculated the retention in the state estimate at the end of training if a trial without error were presented: (A_fx_f⁽ⁿ⁾ + A_sx_s⁽ⁿ⁾)/x⁽ⁿ⁾.

To assess whether noise could account for some of our observations, we also simulated the behavior of subjects using a state-space model with noise:

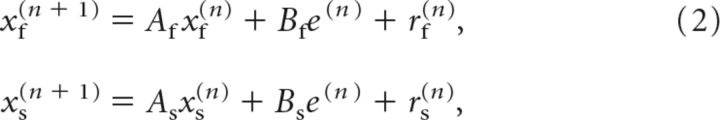where r_f⁽ⁿ⁾ and r_s⁽ⁿ⁾ are state noise applied to the learning process. In our simulations, r_f⁽ⁿ⁾ and r_s⁽ⁿ⁾ were independent normally distributed random variables with mean of 0° and variance of 5 deg². The learning and retention rates were set to the average parameters from the two-state model fit to the behavior during the baseline and training blocks for each subject: A_f = 0.920, B_f = 0.131, A_s = 0.969, and B_s = 0.060.

Data analysis.

Data were analyzed offline using custom routines written in MATLAB (R2013a; MathWorks). The angle of the hand at the target extent, relative to the target direction, was used to assess direction of the movement. Movements in the wrong direction (>120° from the goal direction) were eliminated (0.04% of trials). All measures are reported as mean ± SEM.

Statistical analyses were conducted using MATLAB or SPSS (version 21; IBM). We used Student's t test (paired when appropriate) to compare performance. Because the VAF by the state-space model is bounded and not normally distributed, Mann–Whitney U and Kruskal–Wallis tests was used to compare the VAF across groups.

Exploration.

Previous work has shown that, when subjects receive limited feedback about their movements, substantial trial-to-trial variability in behavior can be observed (Izawa and Shadmehr, 2011). Recent work has further suggested that subjects can make use of variability to arrive at a successful solution when a perturbation is applied (Wu et al., 2014). We sought to identify exploratory behavior in clamp trials, in which subjects might increase their trial-to-trial variability in the face of altered feedback. Because subjects differ in their behavior, we compared the variability of each subject's behavior in clamp trials with the variability of their behavior in the training block. We first calculated the SD of the hand direction in an 11 trial (current ± 5 trials) sliding window across the experiment to find the variability of behavior around each trial. By finding the mean and SD of this distribution in the last half of the training block, we could evaluate the typical variability for each subject. Then, we identified windows in the clamp block about which subjects had a high variability, >2 SDs from the mean for that subject. For a given trial, if >80% of the 15 nearby trials (current ± 7 trials) were considered to have a high variability, we labeled the point as representative of exploration. This second criteria was used to prevent a single, potentially erroneous movement from causing several trials to be labeled as exploratory, by requiring a sustained increase in the trial-to-trial variability in behavior.

Results

We asked six groups of volunteers to make 8 cm reaching movements. In the baseline block, the motion of the cursor was an identity transformation of the motion of the hand, and the participants reached to place the cursor in the target. In the training block, the motion of the cursor (Fig. 1C, red dots) was a −30° (counterclockwise) rotation of the motion of the hand (Fig. 1C, blue dots). Participants learned to alter their reach angle by an average of 25.5 ± 0.5° (last 20 trials of the training block compared with the last 20 trials of the baseline block, across all groups), resulting in 85% compensation for the perturbation, producing a residual error of −6.3 ± 0.5°, a value significantly different from zero (t test, t₍₅₆₎ = −12.0, p = 4E-17). However, the target radius was only 1.8°. Why did participants exhibit a residual error, on average missing the target?

A state-space model of adaptation provides one account of this behavior (Smith et al., 2006; Kording et al., 2007). According to this model, in the training block, the subject notes that, as they generate a motor command, the cursor does not go where they had expected. The difference between the expected sensory consequence and the observed consequence is a prediction error, inducing learning in a forward model relating motor commands to their expected sensory consequences. State-space models assume that this internal model is parameterized via a set of states and that these states learn from prediction error. Critically, these states also partially revert toward their baseline state after each trial. Consequently, subjects will converge on a nonzero error at the end of training when incomplete retention from one trial to the next, pulling behavior toward the baseline, balances new learning from the residual error. A two-state model fitted to the data for all subjects in the baseline and training block estimated that trial-to-trial retention at the end of training was 0.95 ± 0.01. That is, the model predicted that, without errors, motor output will decay at the rate of ∼5% per trial at the end of training. We used zero-error-clamp trials (trials in which motion of the cursor always hit the target, regardless of subjects' actions) to quantitatively test this prediction. We then used nonzero-error clamps, in which the errors were drawn from various distributions similar to subjects' behavior at asymptote. We hypothesized that presenting errors that were decorrelated from subjects' actions might trigger subjects to abandon their steady-state behavior (Vaswani and Shadmehr, 2013) and lead them to overcome this residual error.

Persistent residual error after prolonged training was accounted for by a state-space model

In the no-clamp group, the visuomotor rotation was maintained for 200 trials. With this group, we wanted to answer two questions: (1) would performance exhibit residual error even with this extended amount of training; and (2) if so, would the state-space model from the first 100 training trials predict performance in the second 100 training trials?

Performance of a typical subject is shown in the left column of Figure 2A, and the group data are summarized in the right column of the same figure. With extended training, the reach angles changed, resulting in partial compensation for the perturbation and placement of the cursor near the target. Indeed, by the end of the extended training, the cursor position exhibited a nonzero error (last 20 trials, error of −4.2 ± 0.8°, t₍₇₎ = −5.2, p = 0.001). We fit a state-space model to each participant's data in the baseline and first 100 training trials and then fixed the model parameters and used it to predict performance in the remaining 100 training trials, as well as in the washout trials (Fig. 2A, black dots). The model fit the baseline and training data well, accounting for 87 ± 2% of the variance, with an RMSE of 4.9 ± 0.3°. The model estimated that trial-to-trial retention after 100 trials of training was 0.95 ± 0.02. Overall, the model predicted behavior in the extended training and washout block of the experiment quite accurately (VAF, 86 ± 2%; RMSE, 4.5 ± 0.2°).

Figure 2.

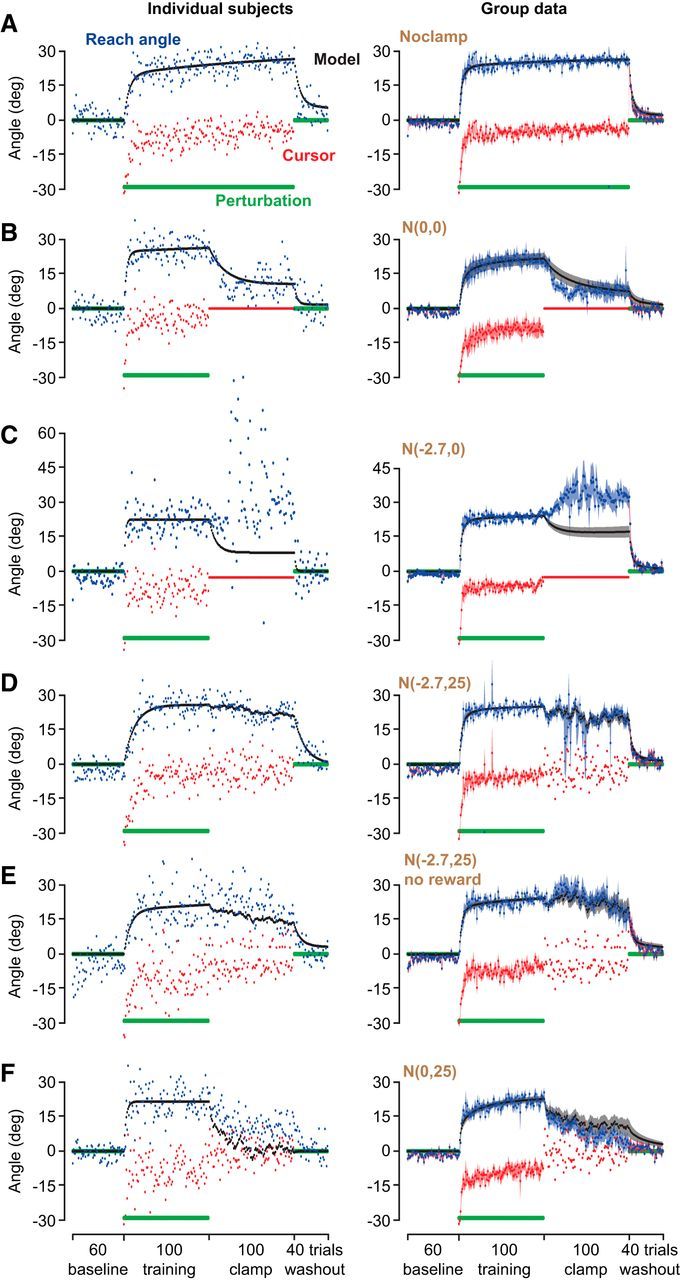
Behavior of typical subjects (left) and groups (mean ± SEM across subjects; right) for the No clamp (A), N(0, 0) (B), N(−2.7, 0) (C), N(−2.7, 25) (D), N(−2.7, 25) (E) no reward, and N(0, 25) (F) groups. Green lines indicate the rotation angle. Red points indicate cursor feedback. Blue points indicate the reach angle. A state-space model was fit to the baseline and training data for each subject. The parameters from that fit were fixed and used to predict behavior in the clamp and washout periods. Black lines indicate the predictions of the model (mean ± SEM across subjects).

Therefore, in extended training, participants continued to exhibit significant residual errors, and these errors could be captured by a model in which there was a small but significant trial-to-trial reversion toward baseline.

Reversion to baseline in zero-error-clamp trials was incompletely predicted by a state-space model

If the residual error is attributable to trial-to-trial reversion to baseline, then in the absence of error the reach angles should decay toward the baseline precisely as predicted by the model. To test for this, we presented a second group of subjects with traditional error-clamp trials in which, regardless of the reach angle, the cursor moved toward the center of the target. We label this kind of error clamp as having a mean zero, variance zero distribution associated with error, N(0, 0). Performance of a typical subject that experienced this condition is illustrated in the left column of Figure 2B. In the training block, the reach angles changed (blue dots), resulting in partial compensation for the perturbation and placement of the cursor near the target. Importantly, by near the end of training, the cursor positions exhibited both a residual mean error (−3.4°) and variance (11.6 deg²). At the onset of the N(0, 0) error clamp, the cursor position became decoupled from reach angles. Consequently, the reach angles exhibited a change toward baseline.

We fit a state-space model to the data in the baseline and training trials and then fixed the model parameters and used it to predict performance in the error clamp. The model accounted for 91% of the variance in the reach angle of this subject over the range of trials fitted, with an RMSE of 4.2°, and produced an estimate of trial-to-trial retention of 0.96 ± 0.02 across subjects. The model predicted that, at the onset of the error-clamp trials, the reach angles should gradually revert toward baseline and that this reversion would not be complete by the end of the block, resulting in a nonzero bias (Fig. 2B, black dots, left column). We observed both of these predictions in the data collected from this subject. However, it appeared that the actual decay in reach angles was somewhat faster than predicted (Fig. 2B, blue vs black dots, left column).

To analyze the group data, we again fit a state-space model to the baseline and training data of each subject and then computed the predictions of the model for the error-clamp and washout blocks. By the end of the training block, the reach angles exhibited residual error of −9.1 ± 2.6°, an amount significantly different from zero (t₍₆₎ = 3.5, p = 0.01). The model fit the baseline and training data well (VAF, 84 ± 4%; RMSE, 4.2 ± 0.1°) and then predicted a decay in reach angles during the N(0, 0) error clamp, producing a predicted bias of 7.8 ± 2.6° at the end of that block (Fig. 2B, black line, right column). Indeed, in the measured data, we found that reach angles in the error-clamp block declined (end of training vs end of clamp, paired t test, t₍₆₎ = 6.17, p < 0.001), resulting in a bias of 8.4 ± 2.9° at the end of the block. This bias at the end of the error-clamp block was a fraction (32 ± 15%) of the reach angles achieved during the training block, a fraction that was similar to that observed in our previous work in a force-field learning task (26 ± 5%, Experiment 1 in the study by Vaswani and Shadmehr, 2013). Therefore, exposure to the N(0, 0) error clamp resulted in a reversion of the reach angles toward baseline, with an endpoint that was well predicted by the model.

However, the model predictions and measurements differed in one aspect. After introduction of the error-clamp trials, the reach angles changed more rapidly than was predicted by the model (paired t test, first 20 trials of clamps, t₍₆₎ = −2.5, p < 0.05). Overall, the model did a modest job predicting the data in the clamp and washout blocks (VAF, 42 ± 8%; RMSE, 7.0 ± 0.9°).

In summary, the results of the N(0, 0) group illustrated that, in the error-clamp block, the motor output decayed toward baseline with an endpoint that was well predicted by the model but with a decay rate that was significantly faster than predicted. The inability of the model to fully predict the data is important because it puts in doubt the applicability of the state-space model and the interpretation that it provides for residual errors at the end of training. However, another possibility is that the state-space model does provide an accurate description of one kind of learning that occurs in adaptation tasks, but that this specific form of error-clamp trial is not an innocuous probe, instead transitioning behavior to an alternative learning process evidenced by, in this case, a faster reversion to baseline.

A nonzero-error clamp led to exploratory behavior

We next considered an error clamp in which, instead of zero error, subjects were presented with a small constant nonzero error [N(−2.7, 0) group]. Importantly, the error in the error-clamp block was smaller than the participants' residual error in the training block. Our hypothesis was that a sudden decorrelation between actions and errors in the setting of a residual error might trigger processes sensitive to residual target error and overcome the steady state reached by adaptation. As we will show, the state-space model predicted partial reversion to baseline. However, behavior was dramatically different from predicted.

After the training block, volunteers in this group were exposed to a distribution of visual feedback in which the mean error was −2.7°, with zero variance. Performance of a typical subject in the N(−2.7, 0) group is shown in the left column of Figure 2C. By the end of the training block, this participant's reach angles produced a residual error of −7.2°. Note that the magnitude of this error was larger than the errors presented in the error-clamp block. As a consequence, the state-space model predicted that the reach angles would revert partially toward baseline (Fig. 2C, black dots). However, the participant's behavior was qualitatively different from that predicted: reach angles did not monotonically revert toward baseline but instead varied dramatically from trial to trial. It appeared that the participant was searching for a reach angle that would place the cursor in the target.

The group data are shown in the right column of Figure 2C. By the end of the training block, movements exhibited a residual error of −5.8 ± 0.6°. Remarkably, when presented with a smaller error in the error-clamp block, rather than maintaining their performance or reverting toward baseline, the subjects increased their reach angle (end of training vs end of clamp, t₍₁₄₎ = 2.6, p = 0.02), attempting to close the small but persistent error. By the end of the clamp block, they reached on average 32.1 ± 3.4° from the target. This behavior in the N(−2.7, 0°) error-clamp trials was interesting because it was quite different from expected from the standpoint of the behavior in the training trials. Subjects maintained a persistent error of −5.8°, on average, in the training trials but attempted to remove a smaller −2.7° error in the clamp trials.

We fit the state-space model to each participant's data in the training trials and then used the model to predict behavior in the error-clamp and washout trials. The model estimated a trial-to-trial retention of 0.95 ± 0.01 and predicted that reach angles should decrease in clamp trials because of the reduction in mean error size. However, this did not occur because, on average, reach angles increased (Fig. 2C). Indeed, the model was a poor predictor of behavior in the error-clamp block (fit period, VAF, 83 ± 2% and RMSE, 5.4 ± 0.3°; prediction period, VAF, 51 ± 4% and RMSE, 17.1 ± 2.5°). Behavior in this group appears to reflect a transition toward using an alternative learning mechanism to close the constant residual error. As we will show later, instead of learning from error, soon after the start of the error-clamp block, some subjects in this group behaved in a way that suggested exploration.

Learning from error continued only when error clamps presented nonzero mean and nonzero variance

To further ascertain what it was about the nonzero-error clamp that led to the exploratory behavior, we tested a new N(−2.7, 25) group, in which subjects were presented with the same constant, small bias, on average, but also with a variance similar to the subject's own performance in the training block. In previous work, we have shown that giving an error clamp with variance similar to that seen during initial adaptation slows the reversion to baseline (Vaswani and Shadmehr, 2013). Thus, if the exploratory behavior seen in the N(−2.7, 0) group was the result of detecting the change to nonzero clamp with zero variance, perhaps detection would be more difficult with a more naturalistic variance of errors in the nonzero-error clamp. Performance of a typical subject in the N(−2.7, 25) group is shown in the left column of Figure 2D. At the end of the training block, the subject had a −4.1° residual mean error and 12.0 deg² variance of error. We fit the model to the data in the baseline and training blocks of this subject and found that it well predicted that subject's performance in the ensuing error-clamp and washout blocks (Fig. 2C, left column; fit period, VAF, 92% and RMSE, 4.3°; prediction period, VAF, 84% and RMSE, 3.8°).

This excellent prediction ability was true in the group data as well. In the N(−2.7, 25) group data, by the end of the training block, the movements exhibited a residual error of mean of −4.9 ± 0.5° and variance of 19.3 ± 1.5 deg². When we fit the model to the training trials for each subject in the N(−2.7, 25) group and then used the model to predict behavior in the remaining trials, we found that, in the error-clamp and washout blocks, the measured behavior was well predicted by the state-space model (Fig. 2D; fit period, VAF, 85 ± 3% and RMSE, 5.6 ± 0.6°; prediction period, VAF, 67 ± 8% and RMSE, 9.4 ± 2.8°). Indeed, the model did a better job of predicting behavior in the N(−2.7, 25) error-clamp block compared with N(−2.7, 0) group (Mann–Whitney U test, U_(9,15) = 26, p < 0.02), as well as better than the N(0, 0) group (Mann–Whitney U test, U_(7,9) = 9, p < 0.02). That is, it appeared that, when the feedback distribution in the error-clamp block had a nonzero mean and variance, a state-space model that accounted for a subject's behavior during training could also account for behavior in clamp trials. This was the case even when the distribution of feedback had a reduced bias compared with the training block. The exploratory behavior seen in the N(−2.7, 0) group, in which there was a small nonzero error with zero variance, was not seen in the setting of normal variance. This suggests that error-dependent learning described by the state-space model is the default learning system during adaptation, unless a change in the statistics of movements is detected.

The state-space model assumes that changes in behavior are driven by prediction errors in sensory outcomes of motor commands. We have shown previously that adaptation based on sensory prediction errors will proceed at the expense of decreasing task success (hitting the target goal; Mazzoni and Krakauer, 2006). This led us to conclude that cerebellar-based sensory-prediction error-dependent adaptation is indifferent to reward (Krakauer et al., 2006; Krakauer and Mazzoni, 2011; Izawa et al., 2012; Haith and Krakauer, 2013). If this is true, then it predicts that behavior predicted by a state-space model in a nonzero-error clamp should proceed in the absence of task success (hitting the target).

In the N(−2.7, 25) group, the cursor hit the target on 16% of the clamp trials. To test whether these rewarded movements were affecting behavior, we considered an error-clamp condition in which the distribution of feedback had both a variance and a small bias, but none of the trials produced a rewarding outcome during the error-clamp block (Fig. 2E). In this N(−2.7, 25) no-reward group, any randomly generated cursor position in the error-clamp block that would land in the target was discarded and resampled from the N(−2.7, 25) distribution. For each subject, we fit the model to the data in the baseline and training blocks and then used the model to predict behavior in the remaining trials. We found that, despite the absence of rewarding trials, performance in the error clamp was again well predicted (fit period, VAF, 83 ± 2% and RMSE, 5.4 ± 0.4°; prediction period, VAF, 70 ± 5% and RMSE, 7.1 ± 0.5°). That is, even without task success, error-based learning in the training trials was essentially maintained in the N(−2.7, 2.5) no-reward group as in the N(−2.7, 2.5) group.

Finally, we considered a scenario in which the feedback had a variance similar to subjects' own movements but no bias: N(0, 25) group. In this group, by the end of the training block, the movements exhibited a bias of 8.1 ± 1.8° and variance of 23.4 ± 3.3 deg². We fit the model to the baseline and training trials for each subject and then used it to predict behavior in the error-clamp block. The model predicted decay in the error-clamp block, but the observed decay was again faster (Fig. 2F). Indeed, the model did a poor job of predicting behavior in the error-clamp and washout blocks (fit period, VAF, 78 ± 3% and RMSE, 5.8 ± 0.3°; prediction period, VAF, 33 ± 5% and RMSE, 10.6 ± 1.0°). As in the N(0, 0) group, the measured behavior exhibited a decay that was faster than predicted by the model, suggesting that a change in policy also occurred when the bias of the distribution of feedback was altered in clamp trials.

Overall, the results suggest that, when sensory feedback is decoupled from the motor commands of the subject, a condition that is met in all error-clamp trials, the error-dependent learning policy in the training trials is essentially maintained if the distribution of errors in the error-clamp trials (including mean and variance) are similar to subjects' own patterns in the preceding training trials. To statistically test this idea, we used a nonparametric ANOVA to test the effect of error distribution on the ability of the state-space model to account for behavior in the clamp and washout blocks. There was no difference in the mean or variance of the distribution of error during the end of the training period across groups (ANOVA: mean, F₍₅₎ = 1.9, p = 0.1; variance, F₍₅₎ = 1.7, p = 0.1). However, when we varied the distribution of feedback in clamp trials, there was a significant difference in the prediction period VAF across groups (Kruskal–Wallis test, χ²₍₅₎ = 32.4, p < 0.00001). We compared the prediction period VAF for each group with the VAF in the no-clamp group. Post hoc tests of mean rank revealed no significant reduction in the ability of the model to account for behavior in the N(−2.7, 25) and N(−2.7, 25) no-reward error-clamp blocks compared with the no-clamp group. Therefore, the learning policy that was present in the training trials was essentially maintained in the N(−2.7, 25) and N(−2.7, 25) no-reward error-clamp blocks. However, the prediction period VAF in the N(0, 0), N(−2.7, 0), and N(0, 25) groups was significantly different from that in the extended training group.

Therefore, when the error-clamp block presented an error distribution that was similar to errors during training, behavior appeared consistent with the training trials, exhibiting learning from error and partial reversion to baseline. When the error-clamp block presented an error distribution that was different from the training trials, new behavior appeared that was different from the training trials.

Quantifying exploration

As mentioned above, participants in the N(−2.7, 0) group showed behavior that was quite different from what would be expected by a state-space model: in clamp trials, they dramatically increased their trial-to-trial variability (Fig. 3A). This increased variability appeared to us to be a form of exploration. We attempted to quantify this behavior.

Figure 3.

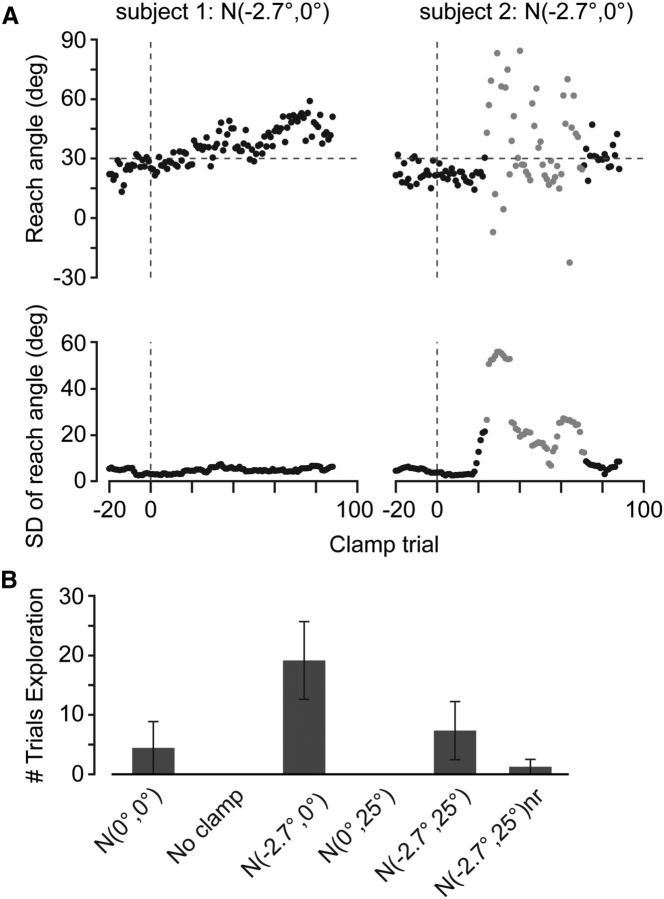
Exploration in clamp trials. A, In the N(−2.7, 0) group, some subjects tried to close the error gradually (top left), whereas some dramatically increased the trial-to-trial variability of their movements (top right). We identified these trials in which subjects were exploring (gray) by comparing the variance of subjects' movements with their variance during the training period (bottom). B, The number of trials identified as exploration (mean ± SEM across subjects) in the six groups. Subjects in the N(−2.7, 0) group explored more than any other group, including three subjects who explored for >50 trials. nr, No reward.

Because subjects can have very different variability in their reach direction across movements, we defined exploration as a sustained increase (persistently >2 SD above the mean) in the trial-to-trial variability of a subject's movements compared with the typical trial-to-trial variability observed in the training block for that subject (Fig. 3A, bottom row). This metric appeared to capture successfully the trials in which subjects were exploring. Subjects in the N(−2.7, 0) group explored an average of 19 ± 6.5 trials. This group included three subjects who explored for more than half of the 100 clamp trials. No subjects in the no-clamp group and only one subject in the N(0, 0) group showed any evidence of exploration (Fig. 3B).

Why did subjects change their behavior so dramatically from that observed in training? During the training block, errors had a nonzero mean and a nonzero variance. In the N(−2.7, 0) error-clamp block, the cursor was placed 2.7° away from the center of the target, regardless of the movement produced by the subjects. Therefore, the onset of the N(−2.7, 0) error-clamp block produced four kinds of change in the feedback: (1) a reduction in the mean of the distribution associated with the position of the cursor; (2) a change in the variance of this distribution; (3) a change in the rate of success, in terms of accurately bringing the cursor to the target; and (4) a change in the correlation between reach angles and cursor position (in error-clamp blocks, the two become decoupled). Perhaps in the N(−2.7, 0) group, the sudden change in the feedback from the training block to the error-clamp block was instrumental in altering the learning policy.

We used the number of exploration trials as our proxy for a change in the learning policy. At the group level, we found that the probability of change in policy was largest for the N(−2.7, 0) group and smallest in the N(0, 25) and N(−2.7, 25) no-reward groups. We also examined whether there were any differences between individuals in the N(−2.7, 0) group. If all individuals were equally sensitive to changes in the feedback distribution, subjects who experience a greater change in feedback might be expected to be more likely to change their policy. However, among subjects in the N(−2.7, 0) group, there was no relationship between the bias at the end of training and the number of trials of exploration observed in clamp trials (p = 0.4). Subjects may differ in their sensitivity to changes in the feedback distribution. However, as a group, when a change in the distribution of feedback was presented, subjects were more likely to exhibit a change in policy.

The selective exploratory behavior we observed in the N(−2.7, 0) group could not be accounted for simply by noise in the learning process. We simulated the behavior of 100 subjects in each group using a state-space model with state noise (Eq. 2; van Beers et al., 2013). With this state noise present, a small number of trials were classified as exploratory (less than five trials on average), critically with no difference between groups in the amount of exploration (ANOVA, F₍₅₎ = 0.92, p = 0.5).

The engagement of an exploratory policy may rely, in part, on cognitive awareness of a change in the task in clamp trials. All participants were instructed to report whether they noticed anything “weird” during the experiment. One participant in the N(−2.7, 0) group who showed exploratory behavior noticed a change in the experiment during the clamp period and asked whether the goal was still to hit the target. Although this evidence is anecdotal, it lends support to the idea that the exploratory behavior is distinct from what is engaged during initial learning.

Discussion

When movements are perturbed, resulting in errors, the motor system rapidly adapts its output to reduce these errors (Shadmehr and Brashers-Krug, 1997; Krakauer et al., 1999, 2000; Thoroughman and Shadmehr, 2000). However, when a visual perturbation is presented repeatedly, subjects do not completely adapt. Instead, subjects sustain a residual error in their movements. What is the reason for these residual errors?

Here, we demonstrated that, even with extended training, subjects sustained a residual error when learning to compensate for a visuomotor rotation. In the framework of a state-space model, this residual error can be attributed to a balance between learning from error and incomplete trial-to-trial retention. To test this idea, we used the state-space model to fit the data during training and then fixed model parameters and used it to predict behavior during conditions in which we controlled the error distribution, named error-clamp trials (Scheidt et al., 2000). We found that, in error-clamp trials with a smaller error than the residual error and no variance, subjects changed their policy dramatically and acted to close the error, exhibiting exploratory behavior while doing so. In error-clamp trials with zero bias, subjects also changed their policy and exhibited a faster reversion to baseline than expected. However, these changes in policy were prevented if the distribution of feedback in the error-clamp block had a bias and variance similar to that in the training block (even when feedback precluded successful trials and was unrelated to subjects' own motor commands). In these cases, the error-dependent process that accounted for learning in the training block also accounted for behavior in the error-clamp block. Therefore, it appears that the residual errors during training are indeed attributable to a balance between learning from error and incomplete trial-to-trial retention.

Our results show that trial-to-trial retention and error-dependent learning processes that can describe behavior during adaptation can also mostly predict behavior when errors are imposed artificially. However, the key new result is that this is only the case if the overall distribution of imposed errors is similar to that generated by subjects themselves. In contrast, when experiencing feedback that lacked realistic trial-to-trial bias and variability, subjects demonstrated changes in behavior that were qualitatively different from state-space model predictions from the training period. In particular, subjects tried to overcome a fixed imposed error that was in fact smaller than the mean residual error they had sustained during the training block and exhibited a faster reversion to baseline when the distribution of imposed error had zero bias.

We and others have suggested that, in addition to error-based learning, other learning processes may operate in motor adaptation tasks (Diedrichsen et al., 2010; Huang et al., 2011; Izawa and Shadmehr, 2011). In particular, we have suggested that state-space models are good fits for error-based learning and that deviation from state-space predictions does not imply falsification of the model but rather that additional learning processes are at play (Huang et al., 2011; Herzfeld et al., 2014). Similarly, the current and previous experiments suggest that error clamps can serve as both readouts for processes captured by state-space models and a trigger for additional learning processes. Zero-error-clamp trials, in which feedback is constrained to zero and decoupled from subjects' behavior, have led to insights into learning processes that are well captured by state-space models (Hwang et al., 2006; Criscimagna-Hemminger and Shadmehr, 2008; Tanaka et al., 2009). However, an increasing body of evidence has demonstrated that zero-error clamps are not innocuous but can induce subjects to actively change their learning policy (Pekny et al., 2011; Shmuelof et al., 2011; Vaswani and Shadmehr, 2013). Recent work suggests that the distribution and type of feedback available might determine the nature of the behavior elicited in clamp trials (Pekny et al., 2011; Shmuelof et al., 2011, 2012; Vaswani and Shadmehr, 2013).

Here, instead of presenting clamps in which error was zero on every trial, we parameterized the distribution of errors. Using a state-space model, we fit the behavior during training and assayed the degree to which the process of learning during the training block predicted behavior during the clamp block.

We found that the state-space model failed to predict behavior in the clamp trials in which the error distribution was very different from subjects' performance in the training trials. The reason, we suggest, is that subjects are likely to alter their behavior when they detect a change in the distribution of errors (Shmuelof et al., 2011; Vaswani and Shadmehr, 2013). In Vaswani and Shadmehr (2013), we presented subjects with a distribution of feedback that had a similar mean and variance to that during training. Here, we saw a qualitative change in the response to errors when either the mean or variance of the feedback distribution changed. In some cases, subjects exhibited a faster reversion to baseline than was predicted by their behavior during training. In other cases, subjects dramatically increased the trial-to-trial variability in their movements in response to an error; this exploratory behavior could not be described by state-space models of learning. It is striking that, despite the availability of this alternate strategy, subjects did not use it to reduce residual error during the training block or when variability of feedback in clamp trials matched that seen at asymptote. We only observed exploratory behavior when errors during the clamp block had a fixed mean and zero variance.

In a previous study, we showed that, when feedback was altered to provide only binary information at the asymptote of the training block, there was a qualitative change in behavior in subsequent (zero-error) clamp trials (Shmuelof et al., 2012) compared with subjects who received both binary and full cursor feedback. Our explanation for this effect was that providing only binary feedback promoted engagement of an alternative learning system to maintain behavior at asymptote. Therefore, the availability of vector error information from full cursor feedback must have led to a suppression of this alternative learning mechanism. A similar selective suppression of a secondary learning process could explain the failure to overcome residual error at asymptote. Like the switch to binary error in our previous study (Shmuelof et al., 2012), a change in the distribution of feedback to a persistent residual error triggered engagement of a secondary learning process (exploration) that was capable of reducing the residual error. This secondary learning process was not engaged when the distribution of feedback was similar to that during training, even when the bias of the distribution was the same and successful outcomes were withheld, perhaps because subjects perceived that they were in control of the errors and therefore persisted with behavior similar to when veridical feedback was provided (Bhanji and Delgado, 2014).

We suggest that the secondary learning process observed in the N(−2.7, 0) group is reinforcement-based (Huang et al., 2011; Izawa and Shadmehr, 2011; Haith and Krakauer, 2013), which is consistent with the exploratory nature of the behavior. Furthermore, the lack of sensitivity to removal of reward when subjects received a realistic distribution of feedback in clamp trials suggests that this reinforcement-based component of learning plays little role in the behavior of the majority of the groups we considered. Providing endpoint feedback alone appears to be another way to promote engagement of reinforcement-based learning (Izawa and Shadmehr, 2011). Notably, when subjects adapt given only endpoint feedback, they show more exploratory behavior early on and less asymptotic residual error (Taylor et al., 2014), further supporting the view that residual errors and reversion to baseline are not universal limitations to human motor learning but are a characteristic feature of error-based learning.

Therefore, state-space models may capture a particular form of learning that dominates in typical adaptation tasks, in which errors are related to the actions one produces. This form of learning leads to rapid reduction of errors, at the expense of a residual asymptotic error. What is the underlying learning mechanism that the state-space model captures so effectively? The error-driven component of the state-space model appears to relate to prediction errors driving an update to an internal forward model in the cerebellum (Mazzoni and Krakauer, 2006; Tseng et al., 2007; Taylor et al., 2010; Izawa and Shadmehr, 2011). The reversion to baseline during training could reflect passive decay in time of the parameters of this forward model. When experiments are conducted with longer intertrial intervals, monkeys exhibit reduced learning and reduced complex spike-induced long-term depression of Purkinje cells, indicating that cerebellar learning is affected by the passage of time between trials (Yang and Lisberger, 2014). Passive decay may be advantageous because environmental processes themselves tend to dissipate over time (Kording et al., 2007). Alternatively, reversion to baseline could reflect competition between a weakly and a strongly reinforced action (Shmuelof et al., 2012).

Conclusion

Residual errors in adaptation tasks reflect the operation of a single learning process (forward model-based, cerebellar-dependent) that, when provided with strong vector error, suppresses alternative forms of learning and is well captured by a state-space model. This suppression can be overcome through changes in the distribution of feedback provided either during acquisition (Izawa and Shadmehr, 2011; Shmuelof et al., 2012) or during error-clamp trials, as was done here. These changes in feedback lead to recruitment of an exploratory, possibly reinforcement-based, mechanism that is capable of reducing residual asymptotic errors. We conclude that error clamps can be “neutral” and capture the predicted retention behavior of state-space models when vector feedback is provided and when the distribution of errors matches those during acquisition. When these aspects of feedback are altered, other forms of learning are triggered that do not follow state-space model dynamics.