Abstract
Transcriptional regulation plays vital roles in many fundamental biological processes. Reverse engineering of genome-wide regulatory networks from high-throughput transcriptomic data provides a promising way to characterize the global scenario of regulatory relationships between regulators and their targets. In this review, we summarize and categorize the main frameworks and methods currently available for inferring transcriptional regulatory networks from microarray gene expression profiling data. We overview each of strategies and introduce representative methods respectively. Their assumptions, advantages, shortcomings, and possible improvements and extensions are also clarified and commented.
Keywords: Gene expression data, Genome-wide inference, Computational model, Transcriptional regulatory network, Reverse engineering
1. INTRODUCTION
Transcriptional regulation plays crucial roles in protein synthesis and its dynamical responses to internal and external signals, such as development processes and environmental stimuli [1, 2]. The temporal and spatial levels of mRNA and ultimately protein abundance are actually controlled by transcriptional regulations in a cell [3]. A regulation system consisting of genes, RNAs, proteins, and other molecules constructs the complicated regulatory interactions during sequentially transcriptional, post-transcriptional, translational and post-translational processes, which structure into multiplex networks [4]. A transcriptional regulatory network generally refers to regulatory activities between regulators, e.g. transcription factors (TFs), and their targets, e.g. genes [1, 5]. A gene’s transcription will be initialized or terminated by the TF proteins binding to its promoter region generally at the 5’ upstream of the transcription start site. To some degree, the final expression abundance is mainly determined by the activation or repression of their regulatory relationships [2, 6, 7]. Without distinguishably considering the physical regulations, a gene regulatory network refers to a collection of gene-gene interactions corresponding to such regulatory relationships through their products, and the interactions in gene regulatory network denote this kind of regulations. In contrast, a transcriptional regulatory network represents the physical bindings and direct regulatory interactions between regulators and their targets [8]. It contains more concrete and specific regulatory information between TFs and genes. From a systematic perspective, genome-wide transcriptional regulatory networks in cells control gene expression dynamically and precisely in response to biological context specificities [9].
Identifying transcriptional regulatory networks is of paramount importance from deciphering transcriptional mechanisms to uncovering potential drug targets [10, 11]. Various network reconstruction methods have been proposed and they can be generally categorized as ‘bottom-up’ and ‘top-down’ methods. The traditional gene knockout experiments can be categorized as bottom-up methods, which firstly identify the detailed regulations between TFs and targets individually, and then summarize all these regulations to form a regulatory network. The genetic relationships between genes can be detected from the effected genes after knocking out some gene [12-14]. And a global gene regulatory network can be built up after collecting these experimentally identified genetic interactions. Alternatively, top-down methods refer to the emerging systems biology approaches of identifying the global regulatory interactions systematically and in parallel. They firstly acquire many potentially regulatory interactions and then validate each of them by additional experiments. For instance, ChIP-Seq technology makes the genome-wide identification of protein-DNA interactions possible [15, 16]. The regulatory elements of DNA-binding proteins such as TFs are identified from massively parallel sequencing [17]. A genome-wide regulatory network is then drafted from these identifications. The details of TF-target binding event in specific conditions are often checked by further experiments [18]. Microarrays are another type of systematic expression monitoring technologies, which measures the amount of mRNA produced during transcription by hybridization [19, 20]. The reconstruction or inference of regulatory network from microarray gene expression data is often called a reverse engineering process, which backwardly reasons the regulatory system from its observational behavior [21]. Recently, the reverse engineering of transcriptional control network from microarray data becomes very popular to revealing genome-wide regulations [21-25]. Numerous computational strategies have been proposed to reconstruct large-scale gene regulatory relationships from expression profiles [26-29]. Several papers [30-33] have summarized and compared the available strategies from different perspectives. For instance in [30], Emmert-Streib and colleagues presented a systematic overview and comparison study of the network inference methods. They conceptually categorized the existing methods from statistical learning perspective. In this review, we focus on these available computational methods by highlighting their assumptions, advantages, weaknesses, possible improvements and future research directions individually.
Computational methods of inferring transcriptional regulatory networks from expression data are highly motivated by the availability of genome-wide expression profiling data [34-37]. The activities of gene regulation are closely related to gene expression levels [6, 38]. Gene expression profiles of time series or perturbations indicate the dynamics and differences of genes and then imply the causal regulatory possibilities between them. Moreover, the individual gene pairs between regulators and target genes should also be considered with cooperative and systematic perspectives, such as co-regulations, competitive regulations of activators and repressors, and indirect genetic regulations [9, 37, 39]. A global transcriptional regulatory network is embedded with high interacting affinities between regulators and targets, which can be learned from transcriptomic data. And the details of individual regulatory events are hypothesized to be validated by further experiments [13, 40]. The top-down method generates a global view of regulatory relationships in form of network illustrating the context-dependent scenario of regulations. Existing computational methods of inferring regulatory networks are all to formulate the regulations into certain models with these measured expression values [23, 26, 27].
In this review, we firstly formulate the reverse engineering of transcriptional regulatory networks from transcriptomic profiles into a general framework, and then review the major available strategies developed to address this problem, e.g., correlation-based methods, Boolean network methods, Bayesian network methods, differential equation methods, and knowledge-based methods of integrating and evaluating prior regulations. We focus on introducing the assumptions and main ideas behind these strategies and their approximations in the modeling of regulatory systems. Then the current research directions and alternatives of deciphering regulatory network from expression data are discussed. A brief vision of reconstructing transcriptional regulatory networks from high-throughput expression profiling dataset is then concluded.
2. FRAMEWORK OF REVERSE ENGINEERING
The surge of microarray technologies provides unprecedented opportunities to measure genome-wide gene expression simultaneously [19]. Various strategies have been developed to infer the regulatory architectures from their corresponding gene expression profiles for transforming experimental data into regulatory knowledge [22]. The inferred networking linkages represent the regulatory relationships among these measured genes.
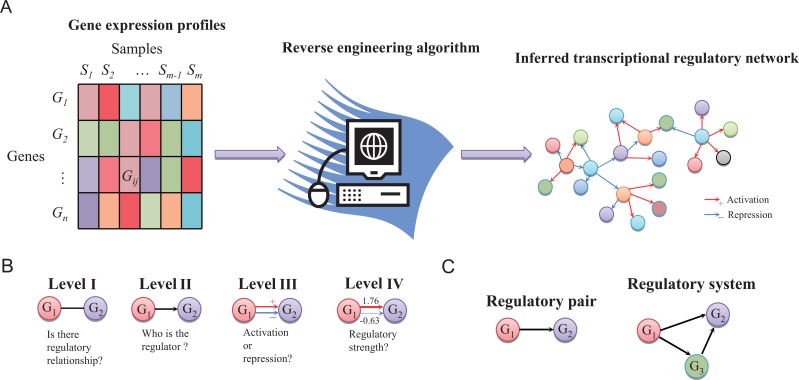
(Fig. 1) illustrates the general framework of the reverse engineering of transcriptional regulatory networks from gene expression
data. Essentially, transcriptional regulatory network reconstruction is to identify physical and genetic regulatory relationships between TFs and
target genes from their expression profiles. Without distinguishing the difference between TF and its own gene, gene regulatory network is often used
as an approximation to the transcriptional regulatory system. Since the abundance of TF protein is often not available, it is approximated by its
gene s expression. Specifically, a transcriptional regulatory system is represented by a network, whose nodes refer to regulators and target genes and
whose edges indicate their regulatory interactions. As shown in (Fig. 1A), from microarray gene expression data, such as profiles of
time-series physiological processes or perturbation experiments of gene knockout or RNA interface, we reversely engineer the network structures and
parameters, e.g., regulatory logic, causality and strength, from the measured gene expressions by developing models and algorithms. The measured genes
are those nodes in the regulatory network, and the linkages and related parameters can be identified from the patterns underlying the gene
measurements. The regulatory network and expression data are often represented by regulatory matrix
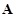 and expression matrix
and expression matrix
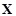 , respectively, i.e.,
, respectively, i.e.,
Fig. (1).
The general framework of reverse engineering transcriptional regulatory networks. (A) The framework of inferring regulatory network from gene expression profiles. There are various sample types of gene expression data, such as condition-specific, perturbation and time series data. A reverse engineering algorithm takes the input of the gene expression profiles and outputs the inferred gene regulatory relationships in form of a network. (B) The interrelated four levels of regulatory parameter information should be determined in the reverse engineering. The algorithm addresses the gene regulatory questions at one or several combined levels. (C) The regulatory pair and system in the modeling. The decision-making of regulatory relationship of an individual pair is in an isolated manner. However, the regulatory system consists of complicated regula-tions of combination and cooperation, such as the indirect regulation from gene G1 to gene G2 conditioned upon gene G3, which needs to be modeled in a systematic manner.
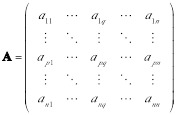 ,
,
 ,
,
where entry
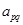 is the regulatory interactions between the
is the regulatory interactions between the
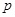 -th gene and the
-th gene and the
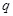 -th gene (
-th gene (
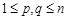 ), and entry
), and entry
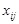 represents the gene expression value of the
represents the gene expression value of the
 -th gene (
-th gene (
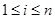 ) at the
) at the
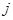 -th experiment (
-th experiment (
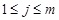 ). It is noted that
). It is noted that
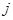 refers to a sample or a time point with specific phenotype meaning. The process of reverse engineering is to determine the unknown elements of matrix
refers to a sample or a time point with specific phenotype meaning. The process of reverse engineering is to determine the unknown elements of matrix
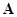 from the known
from the known
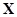 , which is a reverse strategy for reconstructing the underlying regulatory relationships of the system.
, which is a reverse strategy for reconstructing the underlying regulatory relationships of the system.
As illustrated in (Fig. 1B), there are four levels of clarity for the elements of
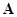 , which answer different questions about the regulatory parameters respectively. Suppose there are two genes,
, which answer different questions about the regulatory parameters respectively. Suppose there are two genes,
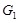 and
and
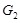 . From the available gene expression data
. From the available gene expression data
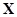 , Level I inference is to determine whether there is a regulatory connection between
, Level I inference is to determine whether there is a regulatory connection between
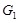 and
and
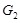 from data
from data
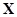 . Let
. Let
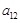 and
and
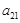 represent the regulatory interactions from
represent the regulatory interactions from
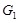 to
to
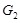 and that from
and that from
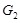 to
to
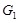 , respectively. Level I is to determine whether
, respectively. Level I is to determine whether
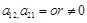 . The binary decision makings build the fundamental architecture of these regulations from gene expression data. Then, when we identify the causal
influence from the regulator of TF
. The binary decision makings build the fundamental architecture of these regulations from gene expression data. Then, when we identify the causal
influence from the regulator of TF
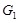 to its target gene
to its target gene
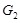 , Level II inference determines the edge direction and causality in the regulatory network, i.e.,
, Level II inference determines the edge direction and causality in the regulatory network, i.e.,
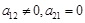 . In certain conditions or states, TF might activate or repress the transcription of a target gene, and the concentration of the target is then
increased or decreased accordingly. The edge orientation underlying the Level Ⅲ regulatory relationship contains the type information of activation and
repression, i.e.,
. In certain conditions or states, TF might activate or repress the transcription of a target gene, and the concentration of the target is then
increased or decreased accordingly. The edge orientation underlying the Level Ⅲ regulatory relationship contains the type information of activation and
repression, i.e.,
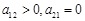 when
when
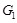 activates
activates
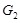 , and
, and
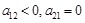 when
when
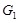 represses
represses
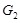 . More specifically, when we identify the regulation strength from
. More specifically, when we identify the regulation strength from
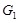 to
to
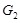 in the Level IV inference, such as
in the Level IV inference, such as
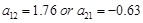 , it provides concrete regulatory weight of its transcriptional dynamics. Level I inference is to reconstruct gene regulatory interactions, while the
other inference levels contain more detailed information about transcriptional regulatory interactions, such as regulator and target, activation and
repression, and concrete regulatory strength. The strong or weak regulation can then be relatively assessed when all the real numbers of regulatory
strengths are determined. (Fig. 1C) shows the direct modeling of the regulation in an isolated gene pair and in a simple regulatory
system respectively. The left graph refers to the regulation between
, it provides concrete regulatory weight of its transcriptional dynamics. Level I inference is to reconstruct gene regulatory interactions, while the
other inference levels contain more detailed information about transcriptional regulatory interactions, such as regulator and target, activation and
repression, and concrete regulatory strength. The strong or weak regulation can then be relatively assessed when all the real numbers of regulatory
strengths are determined. (Fig. 1C) shows the direct modeling of the regulation in an isolated gene pair and in a simple regulatory
system respectively. The left graph refers to the regulation between
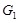 and
and
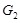 , while the right one shows the direct causality from
, while the right one shows the direct causality from
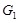 to
to
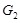 and the indirect influence transferring from
and the indirect influence transferring from
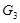 . When the system contains a large number of genes, it is apparent that they are needed to be modeled in a systematic manner.
. When the system contains a large number of genes, it is apparent that they are needed to be modeled in a systematic manner.
The intrinsic difficulties of transcriptional regulatory network reverse engineering come from several sources. Mathematically, one difficulty is the
so-called curse of dimensionality, i.e.,
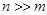 in the formation of expression matrix
in the formation of expression matrix
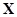 . For intensive cost, there are often a few samples (
. For intensive cost, there are often a few samples (
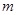 ) of microarray that have been experimented, while thousands of genes (
) of microarray that have been experimented, while thousands of genes (
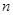 ) have been tested simultaneously in each experiment [41]. From the statistical learning perspective, it is hard to infer a reliable solution of gene
regulations from expression data [27]. Moreover, genome-wide regulatory networks tend to be sparse [34-36, 42], all of which result in the high
likelihoods to achieve false positive regulations or low likelihoods to achieve false negative regulations [34-36]. Biologically, gene regulation is a
complicated physiological process that contains some important steps, such as TF selectively binds to the upstream of the transcription start sites of
certain genes to initialize the transcription. Thus, we often model the regulatory system by simplifying some mechanisms, such as cooperation or
competition of the TF regulators [43]. Furthermore, the real environment of gene regulation is very dynamic with respect to temporal and spatial
features. For example, the up-regulation of one gene encoding a TF can sequentially affect its downstream targets and some regulations can only take
place in particular cell types [44, 45].
) have been tested simultaneously in each experiment [41]. From the statistical learning perspective, it is hard to infer a reliable solution of gene
regulations from expression data [27]. Moreover, genome-wide regulatory networks tend to be sparse [34-36, 42], all of which result in the high
likelihoods to achieve false positive regulations or low likelihoods to achieve false negative regulations [34-36]. Biologically, gene regulation is a
complicated physiological process that contains some important steps, such as TF selectively binds to the upstream of the transcription start sites of
certain genes to initialize the transcription. Thus, we often model the regulatory system by simplifying some mechanisms, such as cooperation or
competition of the TF regulators [43]. Furthermore, the real environment of gene regulation is very dynamic with respect to temporal and spatial
features. For example, the up-regulation of one gene encoding a TF can sequentially affect its downstream targets and some regulations can only take
place in particular cell types [44, 45].
The reconstructed regulatory network is a graphical representation of transcriptional topology of both trans- and cis-regulations [46]. The static network structure is usually not efficient to describe the three-dimensional regulatory contexts in cells [47]. Moreover, the epigenetic regulations, such as DNA methylation [48], histone modification and nucleosome positioning [49], strongly influence transcriptional concentrations [50]. miRNAs are also regarded as crucial regulators in the post-transcriptional regulations [51]. The multiplex, hierarchical, heterogeneous regulatory processes are intensely cooperative to generate gene expression levels of mRNA abundance detected by microarray. At the same time, the microarray technique of measuring gene expression is still in its maturing period. The sample preparation, such as cell numbers [52], as well as data preprocessing alternatives including probeset design, background correction and normalization [53, 54], highly affect the quantitatively measured values. Furthermore, the cognate mRNA level is used to represent TF activity in the reverse engineering. The abundance mismatch between mRNA and protein also interfere with the inference of the regulation system [55]. These obstacles challenge the perfect reconstruction of regulatory relationship from expression data.
To address these difficulties of reverse engineering regulatory networks, numerous efforts have been devoted and many substantial regulations have been discovered by in silico methods and validated by traditional experiments [30-33, 56]. An international competition named DREAM (Dialogue for Reverse Engineering Assessments and Methods) has been initialized to catalyze the quantitative modeling of transcriptional network inferences [57, 58]. For evaluating the reconstruction performances, several types of measures have often been utilized, e.g., general statistical measures, functional consistency measures and network-based measures [30]. For widely-used statistical measures, the evaluations are often implemented by opening the expression profiling dataset and blinding the benchmarked network structure. After the transcriptional regulatory interactions are inferred from the data by some proposed method, the assessments are performed by comparing the identification results with the benchmarked network [23]. Compared to true regulations, these measures are employed to evaluate the predictions, e.g., sensitivity, specificity, accuracy, F-measure, and Matthews correlation coefficient [30, 59]. The tradeoffs between sensitivity and specificity are often presented by the receiver operating characteristic (ROC) curve. The area under the ROC curve (AUC) is often calculated for assessment [60]. Currently, many methods for reverse engineering regulatory networks have been available [22, 27, 30]. Instead of introducing them individually, we categorize them into several main streams of strategies and introduce their main ideas and philosophies.
3. EXISTING METHODS
Due to the difficulties mentioned above, the transcriptional regulatory network inferences are far from accurate and perfect [61], and almost all available methods have their own advantages and drawbacks [27, 61]. We summarize them into the following five categories, namely correlation-based methods, Boolean network methods, Bayesian network methods, differential equation methods, and integrative prior knowledge-based methods.
3.1. Correlation-based Methods
The first endeavor to identify the regulatory relationships in thousands genes measured in microarray is to investigate their pairwise correlations. If
gene
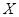 highly coexpresses with gene
highly coexpresses with gene
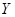 , that is to say, when gene
, that is to say, when gene
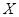 s expression grows up, gene
s expression grows up, gene
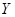 s expression grows up or down simultaneously, then the association between the two genes can be detected and modeled by some methods. The regulation
can be inferred according to their transcriptional dependence. For multiple genes, clustering is often employed to identify the coexpressed genes [62,
63]. The genes in the same clusters or groups characterize similar expression patterns during physiological processes. They are often assumed to be
regulated by the same or related TFs. Two correlation measures are widely used to detect the associated gene pairs, i.e., correlation coefficient [64]
and mutual information [65].
s expression grows up or down simultaneously, then the association between the two genes can be detected and modeled by some methods. The regulation
can be inferred according to their transcriptional dependence. For multiple genes, clustering is often employed to identify the coexpressed genes [62,
63]. The genes in the same clusters or groups characterize similar expression patterns during physiological processes. They are often assumed to be
regulated by the same or related TFs. Two correlation measures are widely used to detect the associated gene pairs, i.e., correlation coefficient [64]
and mutual information [65].
The most popular linear correlation between two variables is Pearson s correlation coefficient (PCC). Suppose gene
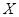 and gene
and gene
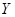 have a series of
have a series of
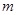 measurements
measurements
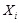 and
and
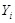 , where
, where
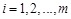 , then the PCC
, then the PCC
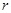 between
between
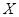 and
and
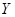 is estimated by the sample correlation coefficient, i.e.,
is estimated by the sample correlation coefficient, i.e.,
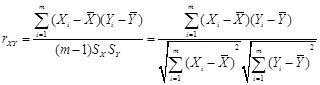 ,
,
where
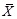 and
and
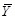 are the sample means of
are the sample means of
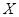 and
and
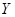 , and
, and
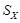 and
and
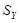 are the sample standard deviations of
are the sample standard deviations of
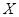 and
and
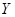 . WGCNA (Weighted Gene Coexpression Network Analysis) is a representative method of building the gene coexpression regulatory network by employing PCC
[66]. (Fig. 2) shows its general framework [67]. Firstly, a clustering method such as hierarchical clustering is implemented to group
thousands of genes into some clusters. In each cluster, the highly coexpressed genes are linked by correlation values. For example, when
. WGCNA (Weighted Gene Coexpression Network Analysis) is a representative method of building the gene coexpression regulatory network by employing PCC
[66]. (Fig. 2) shows its general framework [67]. Firstly, a clustering method such as hierarchical clustering is implemented to group
thousands of genes into some clusters. In each cluster, the highly coexpressed genes are linked by correlation values. For example, when
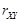 exceeds a defined threshold such as
exceeds a defined threshold such as
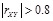 , a functional linkage between
, a functional linkage between
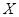 and
and
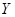 is created in the resulting coexpression network. After the pairwise functional implications between any two genes are identified, a genome-wide
network is built up. The simplicity underlies the method that makes it popular to analyze gene expression data, especially to build gene coexpression
relationships [68]. Beyond the linear correlation metric of PCC, some rank-based correlations such as Spearman s correlation are also employed to
detect the relationship between genes [69]. These correlations replace gene expression values to their relative ranks and then calculate the
correlation coefficient between the two ranking lists.
is created in the resulting coexpression network. After the pairwise functional implications between any two genes are identified, a genome-wide
network is built up. The simplicity underlies the method that makes it popular to analyze gene expression data, especially to build gene coexpression
relationships [68]. Beyond the linear correlation metric of PCC, some rank-based correlations such as Spearman s correlation are also employed to
detect the relationship between genes [69]. These correlations replace gene expression values to their relative ranks and then calculate the
correlation coefficient between the two ranking lists.
Fig. (2).
The framework of building gene coexpression regulatory network [67]. (A) The array data. (B) The correlation analysis of these genes. (C) Pairwise gene correlation matrix. The bold numbers are those over a defined threshold 0.80. (D) The built gene coexpression network.
Mutual information (MI) is often employed to measure the non-linear gene expression associations between pairs of genes [65, 70]. Generally, MI is an
information-theoretic measure of the mutual dependence between two random variables. For two genes
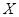 and
and
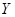 , it is defined as
, it is defined as
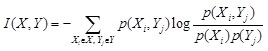 ,
,
where two gene expression values construct two vectors, in which the elements
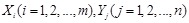 denote their expression values in different samples respectively.
denote their expression values in different samples respectively.
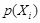 and
and
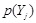 are the marginal probabilities of each discrete value
are the marginal probabilities of each discrete value
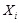 in
in
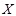 and
and
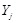 in
in
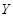 , respectively.
, respectively.
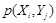 is the joint probability of
is the joint probability of
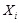 and
and
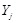 . High MI value indicates that there may be a close relationship between the two genes, while low MI value implies their independence [60].
. High MI value indicates that there may be a close relationship between the two genes, while low MI value implies their independence [60].
MI has been widely used to identify transcriptional regulatory relationships from gene expression data [71]. The quick and accurate estimation of MI is a crucial step in the reverse engineering because computing pairwise MI is nontrivial and quite time-consuming [72]. Similar to the PCC-based framework shown in (Fig. 2), the available approaches compute the pairwise MI between all gene pairs and construct an association matrix. RN (Relevant Network) chooses the gene pairs when its MI value exceeds a given threshold of significant value [65, 70]. ARACNE (Algorithm for the Reconstruction of Accurate Cellular Networks) implements the data processing inequality on each connected gene triplet to remove the least significant edge in the MI relevant networks [73]. CLR (Context Likelihood of Relatedness) transforms the MI values into z-scores and connects the genes by employing a background sensitive estimator [74]. MRNET (Maximum Relevance Network) is built on the MI-based mRMR (minimum redundancy maximum relevance) feature selection method [75]. MINET presents a software package of MI estimators for inferring large-scale transcriptional regulatory networks [76]. By implementing these MI-based methods, some important transcriptional regulations have been revealed and validated [77, 78].
Unlike PCC and MI, maximum information correlation (MIC) is proposed to detect the strength of any type of linear or nonlinear correlations between genes [79]. MIC adopts binning as a scheme to apply MI to calculate the association between gene variables. It is defined as
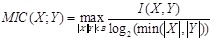 ,
,
where
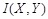 is the MI of
is the MI of
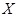 and
and
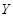 .
.
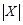 ,
,
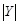 are the numbers of
are the numbers of
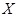 bins and
bins and
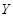 bins divided, and the total number of bins
bins divided, and the total number of bins
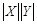 is constrained to be less than some number
is constrained to be less than some number
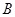 . MIC defaults
. MIC defaults
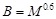 and
and
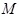 is the sample size [79]. Although the effectiveness of MIC is controversial [80], it devotes an effort to identifying diverse types of gene
relationships and indicates the importance of an association metric to identify genetic relationships [81].
is the sample size [79]. Although the effectiveness of MIC is controversial [80], it devotes an effort to identifying diverse types of gene
relationships and indicates the importance of an association metric to identify genetic relationships [81].
The correlation or coexpression is a fundamental strategy to identify the regulatory relationships at the former Level I and Level IV inferences (Fig. 1) and should be improved to be more reasonable in the reverse engineering [82]. Although it is found that the genes in the same grouped clusters tend to have similar functions, these genes might have no direct interactions with each other, and there is no any information to distinguish causal regulators and responsive targets. The built network is not directed (Level II) and without the causality of functional linkages (Level Ⅲ) [83], though it can be determined by additional information, such as annotated TFs [77]. Moreover, the clustering methods such as hierarchical clustering are highly dependent on the threshold chosen to cut the hierarchical tree (dendrogram). The number of clusters and chosen distance metrics also highly affect the resulting networks [81]. It is often assumed that there is modularity property in coexpression regulatory networks, which means dense connections between the genes within the same modules but sparse connections between genes in different modules [68]. The clusters form the building blocks of genome-wide regulatory networks. The linkages between these modules are often omitted in these available methods [84]. These functional linkages indicate the crosstalk and functional cooperation between these modules upon certain conditions [67, 85-87].
Another important issue of this type of methods is the isolated modeling of individual gene pairs as shown in (Fig. 1C). The
regulatory effect from
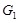 to
to
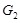 can also be transferred from
can also be transferred from
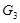 . The indirect regulations highly bias the inferred results [88, 89]. We should consider the degree of association with the removal of the effects from
indirect regulations by controlling one or several other genes. Partial correlation coefficient can be employed to quantify the association between two
genes when conditioning on other gene or genes [88]. For instance, conditioning on a gene or gene set
. The indirect regulations highly bias the inferred results [88, 89]. We should consider the degree of association with the removal of the effects from
indirect regulations by controlling one or several other genes. Partial correlation coefficient can be employed to quantify the association between two
genes when conditioning on other gene or genes [88]. For instance, conditioning on a gene or gene set
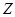 , partial correlation
, partial correlation
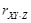 between gene
between gene
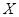 and gene
and gene
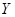 is to measure the exact correlation between the parts of
is to measure the exact correlation between the parts of
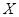 and
and
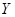 that have no relationship with
that have no relationship with
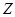 . The order of partial correlation coefficient is determined by the number of conditioned genes. Obviously, the mentioned PCC is the zeroth-order
partial correlation coefficient. Theoretically, it can be raised to any arbitrary order. The first-order and second-order partial correlation is
defined as
. The order of partial correlation coefficient is determined by the number of conditioned genes. Obviously, the mentioned PCC is the zeroth-order
partial correlation coefficient. Theoretically, it can be raised to any arbitrary order. The first-order and second-order partial correlation is
defined as
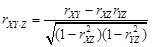 and
and
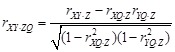 ,
,
respectively. In practice, it is difficult to calculate high-order partial correlation coefficient because of the curse of dimensionality. It is often estimated by developing some specific computation techniques in the reverse engineering of regulatory networks [89].
Similarly, conditional mutual information (CMI) measures the conditional dependency between two genes given other gene or gene set. The CMI of genes
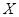 and
and
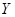 given
given
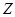 is defined as
is defined as
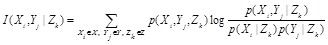
CMI has been applied to reconstruct genome-wide regulatory networks [90-92]. The recently proposed MIC is also expected to be extended to calculate the conditional and partial versions for detecting more delicate and meaningful associations between genes [93].
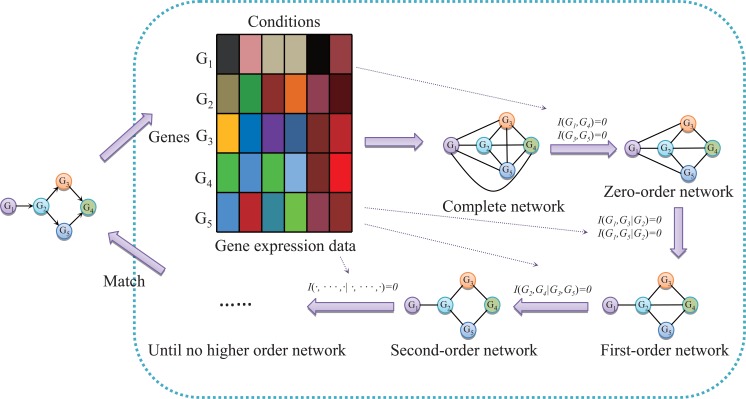
Based on CMI, we proposed a reverse engineering method [60] by utilizing path consistency algorithm [94] to remove the edges with conditional
independent correlation from the network. (Fig. 3) shows the general framework of our PCA-CMI method. The main idea of PCA-CMI is to
eliminate the edges with independent correlations recursively, i.e., from low to high order independent correlation until there is no edge that can be
removed. Firstly, we began with a complete graph, in which all the possible regulations among these genes are contained. Secondly, for adjacent gene
pair
 and
and
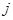 , we calculated MI
, we calculated MI
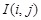 , i.e., zeroth-order CMI. We removed the edges between genes
, i.e., zeroth-order CMI. We removed the edges between genes
 and
and
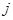 if they have low or zero MI values. Thirdly, for adjacent gene pair
if they have low or zero MI values. Thirdly, for adjacent gene pair
 and
and
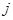 , we computed the first-order CMI
, we computed the first-order CMI
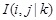 conditioned on their adjacent gene
conditioned on their adjacent gene
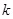 . We removed the edge between them if they have low or zero CMI. The next step is to identify higher order CMI until there are no more adjacent edges
to be eliminated [60]. Since it is also time-consuming to calculate CMI [60, 90], in our proposed algorithm, with the assumption of Gaussian
distribution, CMI is estimated with Gaussian kernel probability density estimator [56].
. We removed the edge between them if they have low or zero CMI. The next step is to identify higher order CMI until there are no more adjacent edges
to be eliminated [60]. Since it is also time-consuming to calculate CMI [60, 90], in our proposed algorithm, with the assumption of Gaussian
distribution, CMI is estimated with Gaussian kernel probability density estimator [56].
Fig. (3).
The reverse engineering diagram of PCA-CMI (path consistency algorithm based on conditional mutual information) [60]
From a regulatory system perspective, linear regression methods identify the associations among genes comprehensively [95, 96]. Compared to the former
correlation or partial correlation based methods, the regression methods model each gene by multiple predictors. They associate the expression of one
gene to all the genes in the whole system and then identify these predictors by variable selection. So the cooperative regulatory relationships among
genes can be identified simultaneously. Let
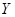 denote a gene and
denote a gene and
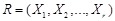 be the gene set potentially regulate gene
be the gene set potentially regulate gene
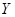 . Their relationship is modeled by a linear function, i.e.,
. Their relationship is modeled by a linear function, i.e.,
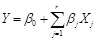 . The ordinary least squares, partial least squares and maximum likelihood methods can then be used to estimate the parameters of the linear system
[97, 98]. Under the parsimony assumption, a regulatory network tends to be sparse [34, 36, 42]. Some variable selection method such as LASSO [99] and
elastic net [100] are often employed to recognize the crucial regulators by the regularization techniques [101]. Specifically, LASSO minimizes the
residual sum of squares subject to a bound on the
. The ordinary least squares, partial least squares and maximum likelihood methods can then be used to estimate the parameters of the linear system
[97, 98]. Under the parsimony assumption, a regulatory network tends to be sparse [34, 36, 42]. Some variable selection method such as LASSO [99] and
elastic net [100] are often employed to recognize the crucial regulators by the regularization techniques [101]. Specifically, LASSO minimizes the
residual sum of squares subject to a bound on the
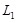 -norm of the coefficients, i.e.,
-norm of the coefficients, i.e.,
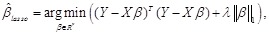
where
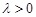 and
and
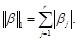 Obviously, some coefficients may be shrunken to zero and the global linkages (coefficients) between these genes can be then inferred. We can find that
the causal relationships or directions between these genes are embedded in the regression model. Regression combined with variable selection formulates
the regulations into a systems biology approach to reconstructing the underlying genetic interactions from expression profiles. Apparently,
regression-based methods achieve a sparse regulatory network and perform the four levels of regulation inferences shown in (Fig. 1B).
For time course expression data, the vector autoregressive model is also employed to specify the gene expression value by a linear regression of those
of earlier time points [97]. Similarly, Granger causality is modeled to learn time-lagged regulatory networks from time-course gene expression data
[102, 103].
Obviously, some coefficients may be shrunken to zero and the global linkages (coefficients) between these genes can be then inferred. We can find that
the causal relationships or directions between these genes are embedded in the regression model. Regression combined with variable selection formulates
the regulations into a systems biology approach to reconstructing the underlying genetic interactions from expression profiles. Apparently,
regression-based methods achieve a sparse regulatory network and perform the four levels of regulation inferences shown in (Fig. 1B).
For time course expression data, the vector autoregressive model is also employed to specify the gene expression value by a linear regression of those
of earlier time points [97]. Similarly, Granger causality is modeled to learn time-lagged regulatory networks from time-course gene expression data
[102, 103].
3.2. Boolean Network Methods
One of the main-stream strategies to reverse engineering transcriptional regulatory networks is based on Boolean networks. Boolean models treat the genes in a regulation system as logical elements [104]. It assumes that a single gene can be represented by a Boolean variable denoting whether it is expressed or not. The wiring of an element to one another corresponds to functional linkages between genes, and the Boolean rules determine the result of a regulatory signaling transduction given a set of input values [105, 106]. Boolean network provides a simple decision-making model of describing the regulatory mechanisms in a transcriptional system [104, 107, 108].
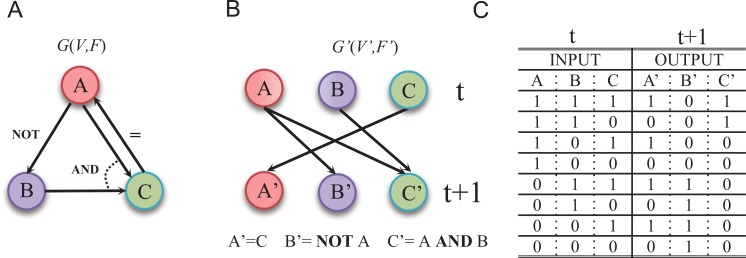
Specifically, a Boolean network is a directed graph
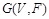 , where the set
, where the set
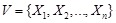 of nodes representing genes. (Fig. 4A) shows a simple example. For each node
of nodes representing genes. (Fig. 4A) shows a simple example. For each node
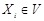 ,
,
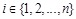 , a Boolean function
, a Boolean function
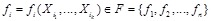 is associated with it individually. The inputs of
is associated with it individually. The inputs of
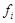 are from the specified parent nodes
are from the specified parent nodes
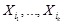 in
in
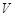 to each node
to each node
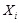 . The variable
. The variable
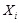 is Boolean and its value is often denoted as 0 or 1 which corresponds to the logical value True or False respectively. The logic operators AND , OR ,
and NOT are employed to define the Boolean operations in these genes [107]. At any given time
is Boolean and its value is often denoted as 0 or 1 which corresponds to the logical value True or False respectively. The logic operators AND , OR ,
and NOT are employed to define the Boolean operations in these genes [107]. At any given time
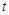 , an expression pattern of
, an expression pattern of
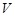 names a state of a Boolean network, i.e.,
names a state of a Boolean network, i.e.,
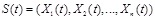 . The state at time point
. The state at time point
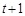 is determined by Boolean functions
is determined by Boolean functions
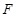 from the state
from the state
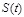 , i.e.,
, i.e.,
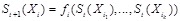 . The states of all nodes are updated according to their respective Boolean functions and all states transitions together correspond to a state
transition of the regulatory network.
. The states of all nodes are updated according to their respective Boolean functions and all states transitions together correspond to a state
transition of the regulatory network.
Fig. (4).
An example of Boolean network. (A) A Boolean network G(V,F). (B) The corresponding wiring graph of G(V,F) (C) The logic operations and state transition table. The possible input at time point and the corresponding output at time t+1 are listed in the table. Boolean network models the regulatory relationships in the logical operating scheme [106].
For representing the state transition, it is convenient to build a corresponding wiring diagram
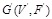 of a Boolean network
of a Boolean network
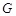 as shown in (Fig. 4B) [106, 109]. For each node
as shown in (Fig. 4B) [106, 109]. For each node
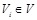 , let
, let
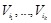 be the parent nodes of
be the parent nodes of
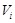 in
in
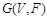 . By introducing an additional node
. By introducing an additional node
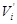 , we link an edge from
, we link an edge from
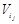 (
(
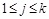 ) to
) to
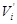 . Then
. Then
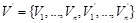 in the resulting network. Apparently, the expression pattern of the additional node set
in the resulting network. Apparently, the expression pattern of the additional node set
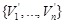 is determined by
is determined by
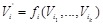 individually and corresponds to the regulatory network state at the next time point. If we regard the expression patterns of the set
individually and corresponds to the regulatory network state at the next time point. If we regard the expression patterns of the set
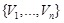 as the input of
as the input of
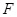 , the expression patterns of
, the expression patterns of
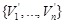 are the output as shown in (Fig. 4C).
are the output as shown in (Fig. 4C).
The reverse engineering of a Boolean network is to infer the Boolean functions
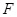 at these nodes from expression data. When
at these nodes from expression data. When
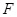 is known, the underlying network topology of regulations can be built spontaneously. An exhaustive search is to try out all Boolean functions on all
is known, the underlying network topology of regulations can be built spontaneously. An exhaustive search is to try out all Boolean functions on all
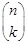 combinations of
combinations of
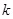 out of
out of
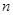 genes. It is known to be an NP-complete problem and takes exponential time in the inference [105, 106]. So it is often tractable by employing certain
computational techniques to avoid exponentially searching a consistent network structure with the observational data. When multiple network structures
are found to be consistent with the gene expression data, more scoring metrics and assumptions can be defined to select one suitable regulatory
architecture [26, 110].
genes. It is known to be an NP-complete problem and takes exponential time in the inference [105, 106]. So it is often tractable by employing certain
computational techniques to avoid exponentially searching a consistent network structure with the observational data. When multiple network structures
are found to be consistent with the gene expression data, more scoring metrics and assumptions can be defined to select one suitable regulatory
architecture [26, 110].
Boolean network is a fundamental model of genetic system which identifies the network structure from a systematic perspective. It fulfills the Levels I, II and Ⅲ inferences of gene regulatory networks. The dynamic property and the simplicity in understanding and analyzing make it an attractive model of regulatory network reverse engineering. However, the binary and synchronous (i.e., the state of all genes updates to the next one at the same time) assumptions are not consistent with the true biological system [111]. To address these limitations, the discretization strategies and Boolean models have been extended in various ways to make them more biologically realistic and computationally tractable [26]. With the availability of gene expression data with larger sample size and higher quality, there have been approaches to introducing stochasticity to these models, such as probabilistic Boolean networks [112-114] in which the state transition diagram is stochastic. The generalized Boolean network models also try to cope with the shortcomings by enabling more sophisticated forms of logical update which allows asynchronous transition of elements [115].
3.3. Bayesian Network Methods
Definition. Bayesian network is a directed acyclic graph (DAG) representing a set of random variables and their joint probability distribution together with the family of conditional probabilities induced by the graph [116, 117].
Bayesian network is a typical probabilistic graphical model of causal inference in statistics. The general idea of learning Bayesian network structure
from data is to evaluate each network structure with respect to the given data by defining a scoring function and to identify the optimal one according
to the score [118]. The structure represents the conditional independence of these variables that facilitate their joint distribution to be decomposed.
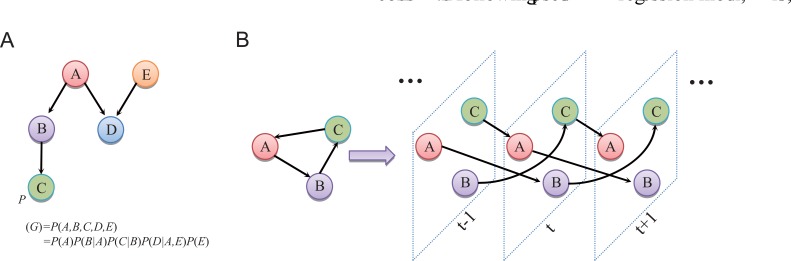
The graph
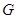 is often assumed to follow the Markov property that each gene
is often assumed to follow the Markov property that each gene
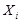 is independent of its non-descendents, given its parents in
is independent of its non-descendents, given its parents in
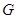 . By applying the chain rules of probability and the properties of conditional independency, the joint distribution on genes
. By applying the chain rules of probability and the properties of conditional independency, the joint distribution on genes
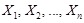 can be uniquely represented by the product form
can be uniquely represented by the product form
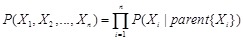 ,
,
where
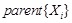 is the set of parents of
is the set of parents of
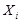 in
in
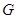 . In this way, each Bayesian network specifies the joint probability distribution over all genes down to the conditional distributions of the genes
. In this way, each Bayesian network specifies the joint probability distribution over all genes down to the conditional distributions of the genes
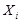 given their parents. As shown in (Fig. 5A), gene D is dependent on gene A and gene E, and independent on
the other gene or genes. The global network probability is determined by the dependence structure between multiple interacting components.
given their parents. As shown in (Fig. 5A), gene D is dependent on gene A and gene E, and independent on
the other gene or genes. The global network probability is determined by the dependence structure between multiple interacting components.
Fig. (5).
The graphical representation of Bayesian network and dynamic Bayesian network. (A) An example of a Bayesian network. By recursive de-composition, the joint probability distribution of the network is . The condi-tional independence simplifies the conditional probability distributions of these nodes in the decomposition. (B) The graphical representation of a dynamic Bayesian network (DBN). The static and dynamic representations are shown respectively. Assuming the temporal regulations are from time t+1 to , cyclic structures are apparently permitted in the DBN framework.
The graphical representation consists of two distinct parts in reverse engineering transcriptional regulatory networks. The first component
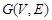 is a DAG representing the causal relationships of regulations (i.e., edges of set
is a DAG representing the causal relationships of regulations (i.e., edges of set
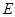 ) among a set of genes (i.e., nodes of set
) among a set of genes (i.e., nodes of set
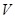 ). An edge exists from gene A to gene B if and only if A is a direct regulator of B. The second component is a set
of parameter
). An edge exists from gene A to gene B if and only if A is a direct regulator of B. The second component is a set
of parameter
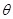 , which describes a conditional probability distribution of each gene, given its parent regulators. Taken together, the two components specify a
probability distribution over the set of genes in
, which describes a conditional probability distribution of each gene, given its parent regulators. Taken together, the two components specify a
probability distribution over the set of genes in
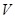 , i.e., the network structure of regulations. Often, Bayesian scoring metric is derived to evaluate the posterior probability of a graph
, i.e., the network structure of regulations. Often, Bayesian scoring metric is derived to evaluate the posterior probability of a graph
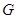 given the gene expression data
given the gene expression data
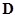 , i.e.,
, i.e.,
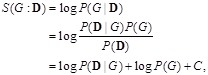
where
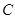 is a constant which can be ignored [119]. In a Bayesian network framework, the calculation of the log marginal likelihood
is a constant which can be ignored [119]. In a Bayesian network framework, the calculation of the log marginal likelihood
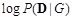 involves the probability of the data over all possible parameters
involves the probability of the data over all possible parameters
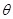 assigned to
assigned to
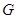 . It is an NP-hard problem to select the maximum scored network structure given the data [117, 118]. Thus, the most probable network structure is
generally implemented by approximating the posterior probabilities of the regulatory combinations heuristically [37, 118]. Bayesian network model
becomes appealing for modeling causal relationships between these genes by selecting the most likely causalities in form of a DAG [9, 29, 119]. Some
techniques have been developed to narrow down the search space to a tractable size. As an assumption, the basic form of Bayesian network cannot handle
cyclic regulations and the temporal dynamic regulatory relationships [117]. Other alternatives have been proposed to extend the applicability of
Bayesian network modeling, such as dynamic Bayesian network [120-124], module network [84] and state-space model [121, 125].
. It is an NP-hard problem to select the maximum scored network structure given the data [117, 118]. Thus, the most probable network structure is
generally implemented by approximating the posterior probabilities of the regulatory combinations heuristically [37, 118]. Bayesian network model
becomes appealing for modeling causal relationships between these genes by selecting the most likely causalities in form of a DAG [9, 29, 119]. Some
techniques have been developed to narrow down the search space to a tractable size. As an assumption, the basic form of Bayesian network cannot handle
cyclic regulations and the temporal dynamic regulatory relationships [117]. Other alternatives have been proposed to extend the applicability of
Bayesian network modeling, such as dynamic Bayesian network [120-124], module network [84] and state-space model [121, 125].
Based on the framework of Bayesian network, dynamic Bayesian network (DBN) introduces the time concept and models a stochastic temporal process of a
set of random variables over time series [121-123]. It has been employed to describe the qualitative nature of the dependencies that exist between
genes in a temporal process. The structure of a DBN is assumed to perform regulatory functions over discrete time points indexed by
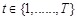 . Similar to the assumptions in Bayesian network, let
. Similar to the assumptions in Bayesian network, let
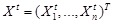 be the gene expression vector of
be the gene expression vector of
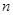 genes at time
genes at time
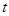 . For the time points
. For the time points
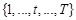 , under the first-order Markovian assumption, i.e.,
, under the first-order Markovian assumption, i.e.,
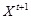 is independent of
is independent of
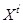 for
for
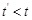 given
given
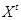 , we thus have
, we thus have
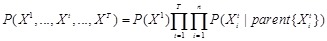
in the time-course gene expression data [123]. As illustrated in (Fig. 5B), the underlying acyclic graph in Bayesian network can now be permitted to contain cycles. DBN model can explore the general network structure of gene regulations and overcome the shortcomings of the acyclic assumption and static network structure in Bayesian network learning models. A more complicated time-varying DBN model of describing the time-evolving network structures underlying the time series is also developed [126].
3.4. Differential Equation Methods
Differential equation formalisms including ordinary and partial differential equations have been widely used to describe and simulate dynamical systems in science and engineering. The powerful mathematical methods have been implemented to model the biochemical systems of metabolic processes and kinetic dynamics of genetic regulation processes [25, 26]. The regulatory interactions in form of network are revealed by the differential and functional relations between the time-dependent concentration variables [36, 127]. Here, we mainly introduce the ordinary differential equation (ODE) models in modeling transcriptional regulatory network. Partial differential equation (PDE) models contain the similar framework as ODE with more dynamic dimensions beyond the time in ODE [26]. ODE models directly consider the time differentiation and then the dynamics and causal relationships can be simultaneously identified in the four inference levels (Fig. 1) of reverse engineering regulatory network.
In ODE models, the change rate of gene expression of a component in a regulatory system is modeled as a function of the concentrations of all the components. Mathematically, the general ODE model can be formulated as
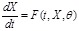 ,
,
where
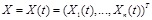 represents the gene expression values of genes
represents the gene expression values of genes
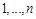 at time point
at time point
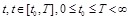 . The causal effects of gene expressions are embedded in the ODE system [128, 129]. Function
. The causal effects of gene expressions are embedded in the ODE system [128, 129]. Function
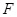 describes the relationship between the first order derivative of X and the concentration of genes in the regulatory system. It is a linear or
nonlinear function that describes the relationships between the change rate concentration of genes and their causal regulators. Specifically, a linear
ODE model can be written as
describes the relationship between the first order derivative of X and the concentration of genes in the regulatory system. It is a linear or
nonlinear function that describes the relationships between the change rate concentration of genes and their causal regulators. Specifically, a linear
ODE model can be written as
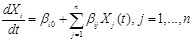 ,
,
where
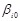 is the intercept and
is the intercept and
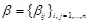 denotes the regulation effects of genes in the regulatory system on the rate of expression change of the
denotes the regulation effects of genes in the regulatory system on the rate of expression change of the
 -th gene.
-th gene.
The problem of network reconstruction from data is then transformed to identify the parameters in the ODE system. Traditionally, the least squares
method and likelihood-based methods are implemented to find these parameters [27, 34]. Various techniques have also been employed to evaluate them [41,
130]. However, these methods are not effective for reverse engineering genome-wide regulatory networks. We and Lu et al. [128, 129] proposed
an integrative pipeline to address the problem by introducing a two-step paradigm to identify these parameters effectively. The first step is to fit
the mean curves of the gene expressions and then to estimate the derivative value
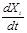 respectively, i.e.,
respectively, i.e.,
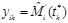 ,
,
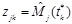 ,
,
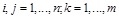 , where
, where
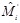 is estimated continuously from the mean curve,
is estimated continuously from the mean curve,
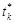 is one of the
is one of the
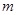 set time points in range
set time points in range
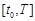 . Thus, the regulatory system becomes the following pseudo-regression model, i.e.,
. Thus, the regulatory system becomes the following pseudo-regression model, i.e.,
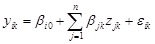 ,
,
where
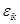 is the error term of estimation. Based on the parsimony assumption, the second step is to conduct the variable selection and estimation procedure by a
regularization framework, such as LASSO [99] and SCAD [131], to shrink the variables as optimally as possible. The regulatory network is then
reconstructed from the data when we identify the parameters of the formulated linear regression system. Original methods [128, 129] include a
clustering procedure to divide these genes into groups with similar expression profiles, which helps to build a genome-wide network and simultaneously
avoid the identifiability problem [132].
is the error term of estimation. Based on the parsimony assumption, the second step is to conduct the variable selection and estimation procedure by a
regularization framework, such as LASSO [99] and SCAD [131], to shrink the variables as optimally as possible. The regulatory network is then
reconstructed from the data when we identify the parameters of the formulated linear regression system. Original methods [128, 129] include a
clustering procedure to divide these genes into groups with similar expression profiles, which helps to build a genome-wide network and simultaneously
avoid the identifiability problem [132].
ODE is a directed network model and the dynamic feature of regulations is automatically and naturally quantified. In ODE models, gene regulations are
modeled by derivative equations, which quantify the change rate of gene expression of one gene (dependent variable) in the system as a function of
expressions of all related genes (independent variables) that refer to its regulators. In a transcriptional regulatory system, it is TFs that regulate
the gene transcriptional processes. The abundance of TF proteins is the real independent variables. We usually have no such information and simply use
the TF genes expression as approximation. Under such assumption, the reverse engineering of regulatory network becomes inferring the parameters of
some specified functions such as the former linear function from gene expression data [128]. According to the differences between a mathematical
modeling perspective and a statistical perspective lying in the network inference [133], ODE is to model the regulatory system but not to directly
infer the regulatory network. The derivation equations are firstly assumed to describe the functional relationships among genes and their products.
Then, the statistical techniques such as parameter estimation and variable selection are implemented to infer the regulatory architectures [128]. The
resulting nonzero regulatory linkages construct a regulatory network. Time delay of the activation and self-degradation can also be flexibly integrated
in the dynamical system by introducing certain terms in the differential equations, such as
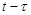 , where
, where
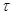 denotes a time delay and
denotes a time delay and
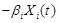 for the
for the
 -th gene s self-regulation [26]. Compared to the former regression methods of modeling the mRNA concentrations of individual components in the system,
ODE describes the derivatives of their concentrations. The strategies of parameter estimation are similar to each other.
-th gene s self-regulation [26]. Compared to the former regression methods of modeling the mRNA concentrations of individual components in the system,
ODE describes the derivatives of their concentrations. The strategies of parameter estimation are similar to each other.
3.5. Knowledge-based Methods
With the essential difficulties in the reverse engineering of regulatory networks, purely data-driven method is very difficult to identify genuine transcriptional regulations. It is hard to promise the effectiveness and efficiency of the reverse engineering only from gene expression profiles [22, 27, 134]. There are urgent requirements to develop novel methods that can utilize expression data in some alternative manners. At the same time, various prior knowledge of gene regulations from literature and genomic datasets can provide additional functional linkage information between genes, such as documented regulations [135, 136], TF binding sequence motifs in promoter region [45], ChIP-Seq data of protein-DNA binding [137] and protein-protein interactions [59]. These prior knowledge can be integrated together with gene expression data to identify transcriptional regulatory networks. Theoretically, the resolution space can be narrowed down to improving the identification significantly [138-140]. So it guides the inference in right direction and helps remove false positives in the predictions [141, 142]. Knowledge-based methods fall into two subcategories, the combination of prior knowledge and the evaluation of prior knowledge. We review them individually as follows.
3.5.1.
The combination of prior knowledge is often implemented on the former reviewed reverse engineering methods. Bayesian network is one of the rational models to integrate prior knowledge in a principled manner to increase the inference reliability [140, 142]. According to the Markov assumption, the probability of a network structure can be decomposed as
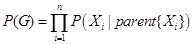 ,
,
where
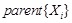 is the parents of
is the parents of
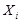 in the DAG. The probability of a local regulatory structure
in the DAG. The probability of a local regulatory structure
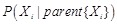 is then calculated according to the structural knowledge priors,
is then calculated according to the structural knowledge priors,
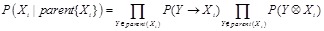 .
.
The decomposition facilitates to incorporate the prior knowledge about regulatory structure into the network inference. Various techniques have been
proposed to calculate these probabilities, i.e.,
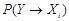 and
and
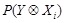 , as accurately and effectively as possible. Following a framework of statistical physics, [139] and [143] proposed an energy function to introduce the
prior knowledge from multiple sources into the reverse engineering of regulatory network. Their main idea is to express the available prior knowledge
in terms of network energy. Specifically, the prior knowledge about the regulatory relationship between gene
, as accurately and effectively as possible. Following a framework of statistical physics, [139] and [143] proposed an energy function to introduce the
prior knowledge from multiple sources into the reverse engineering of regulatory network. Their main idea is to express the available prior knowledge
in terms of network energy. Specifically, the prior knowledge about the regulatory relationship between gene
 and gene
and gene
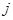 is represented by
is represented by
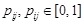 . Network energy of a network is then defined on the biological prior knowledge matrix. Then, a prior distribution over network structures is obtained
by means of a Gibbs distribution [139]. The parameter of this distribution represents the weight associated with the prior knowledge relative to the
gene expression profiles. In this way, the prior knowledge is integrated into a Bayesian network framework to learn the regulatory network structure.
They achieved higher performance of inference in both simulated and real data [139, 143].
. Network energy of a network is then defined on the biological prior knowledge matrix. Then, a prior distribution over network structures is obtained
by means of a Gibbs distribution [139]. The parameter of this distribution represents the weight associated with the prior knowledge relative to the
gene expression profiles. In this way, the prior knowledge is integrated into a Bayesian network framework to learn the regulatory network structure.
They achieved higher performance of inference in both simulated and real data [139, 143].
Based on an ODE model, we proposed a method of linear programming (LP) to integrate prior knowledge in the reverse engineering of regulatory network [138]. The main idea is to build an LP model to minimize the association gap between gene expression data and network structure with constraints of the priori of regulatory relationships, and then to solve the LP to obtain the integrated regulatory network.
Specifically, given an experiment with
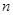 genes and
genes and
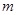 samples, the gene expression matrix is
samples, the gene expression matrix is
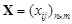 , where
, where
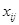 is the expression level of the
is the expression level of the
 -th gene in the
-th gene in the
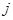 -th sample. We employed an ODE model to quantify the rate of change of gene expression as a function of the expression of other genes [138]. Due to the
unclear structures of regulatory system and data scarcity [41, 95, 138], we used the simplest linear additive models:
-th sample. We employed an ODE model to quantify the rate of change of gene expression as a function of the expression of other genes [138]. Due to the
unclear structures of regulatory system and data scarcity [41, 95, 138], we used the simplest linear additive models:
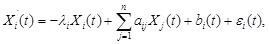
for
 , where the state variable
, where the state variable
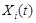 is the mRNA concentrations of gene
is the mRNA concentrations of gene
 at time point
at time point
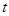 ,
,
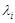 is the self-degradation coefficient,
is the self-degradation coefficient,
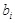 is the external stimuli, which is set to 0 when there is no external input, and
is the external stimuli, which is set to 0 when there is no external input, and
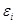 represents the error and noise.
represents the error and noise.
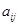 describes the type and strength of the effect of gene
describes the type and strength of the effect of gene
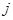 on gene
on gene
 , whose positive, zero or negative values indicate the activation, naught or repression regulatory relationships between them respectively. For
simplicity, we set
, whose positive, zero or negative values indicate the activation, naught or repression regulatory relationships between them respectively. For
simplicity, we set
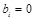 . Hence, the equations can be described as:
. Hence, the equations can be described as:
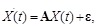
where
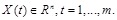 After we approximated
After we approximated
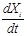 by
by
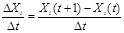 and neglected the error part, the linear additive model becomes
and neglected the error part, the linear additive model becomes
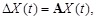
where
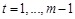 . Instead of solving the equations by singular value decomposition (SVD) technique [41, 95, 127, 138], we derived a sparse regulation network [36, 56]
based on an LP model. At the same time, more and more prior knowledge of gene regulatory network can be obtained from various sources. For example, if
we know that gene
. Instead of solving the equations by singular value decomposition (SVD) technique [41, 95, 127, 138], we derived a sparse regulation network [36, 56]
based on an LP model. At the same time, more and more prior knowledge of gene regulatory network can be obtained from various sources. For example, if
we know that gene
 and gene
and gene
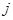 are interactive with the rule that
are interactive with the rule that
 activates
activates
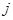 , such priori should be guaranteed in the inference procedure and the inferred network should contain such information as
, such priori should be guaranteed in the inference procedure and the inferred network should contain such information as
 activates
activates
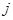 .
.
In our LP model [138], the objective function is to minimize the number of gene connections to realize the sparseness of the inferring network, and the constraints are the linear additive equations and the prior knowledge of some local network structures. The model is described as
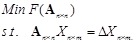
There are
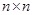 variables
variables
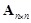 and
and
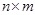 constraints. It is equivalent to solve a canonical LP:
constraints. It is equivalent to solve a canonical LP:
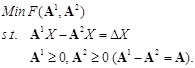
Clearly, there are
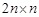 variables and
variables and
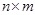 constraints. In the canonical form, the linear objective function can be defined as:
constraints. In the canonical form, the linear objective function can be defined as:
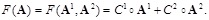
The sparseness and the prior knowledge for regulatory network are represented in the objective function and in the constraints of the LP model,
respectively. When we let
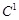 =1
and
=1
and
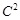 =1
, the objective function becomes
=1
, the objective function becomes
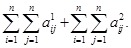
Hence, a sparse regulatory network is achieved from gene expression data by minimizing these regulatory strength coefficients with the constraints of
the prior knowledge about the gene relationships. Generally, there are three kinds of the prior knowledge about the functional relationship between
gene
 and gene
and gene
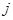 ;
;
 activates/represses
activates/represses
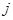 (
(
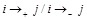 ),
),
 has no any relationship with
has no any relationship with
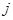 (
(
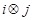 ), and
), and
 has some relationship with
has some relationship with
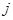 , but unclear of positive or negative regulation (
, but unclear of positive or negative regulation (
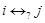 ). These prior knowledge are reflected in the constraints by the defined rules. If gene
). These prior knowledge are reflected in the constraints by the defined rules. If gene
 is an activator of gene
is an activator of gene
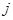 (
(
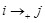 ), we set
), we set
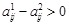 as a constraint in our LP model. Conversely, if gene
as a constraint in our LP model. Conversely, if gene
 represses gene
represses gene
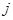 (
(
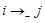 ), we set
), we set
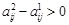 . If gene
. If gene
 has no any relationship with gene
has no any relationship with gene
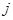 (
(
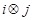 ), we set
), we set
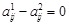 as a constraint. If it is unclear which one is an activator or repressor (
as a constraint. If it is unclear which one is an activator or repressor (
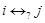 ), we set the constraint as
), we set the constraint as
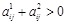 and
and
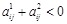 . By solving the two LP models with the two constraints respectively, we selected the sparser solution as the inferred network [138].
. By solving the two LP models with the two constraints respectively, we selected the sparser solution as the inferred network [138].
3.5.2. Evaluating Prior Regulations
Due to the complexity of gene regulation and the difficulty of network inference from expression profiles, reverse engineering cannot easily identify genuine regulatory relationships [27, 134]. An amount of knowledge about gene regulations has been deciphered by decades of endeavors [41, 144]. Alternatively, we can evaluate the knowledge-based gene regulations documented in literature and databases and filter out the activated regulations in certain biological conditions and phenotypes. The screening evaluation procedure provides direct evidence for highlighting the condition-specific regulatory network in biological system [91, 134, 144]. Based on the available or predefined regulatory networks, the consistency between architecture and expression are measured, and the most rational network structure with the expression data can be revealed [145, 146]. In the evaluation strategy, each of the reference networks is assessed by measuring the correspondence between network structures and gene expression profiles. The comparison of matching significance in these knowledge-based regulatory networks can identify the responsive regulatory networks of certain conditions and phenotypes.
Network structure determines the regulatory functionality and robustness [147, 148]. The new forward-like engineering of matching network structure with gene expression data provides more alternatives to investigate the regulatory relationships. The original paper in this direction was published in [144]. The authors proposed a Gaussian graphical model to represent the causal relationships of regulatory network architecture and defined a graph consistency probability to measure the goodness of fitting between network and data. However the directed acyclic graph assumption limits its generality and applicability. Collaborating with the senior author of the original work, we introduced a DBN model to handle general regulatory networks [134]. Specifically, by recursive factorization, the joint probability distribution of a certain directed network architecture is represented as a product of the individual density functions conditioned on their parent variables [134, 144], i.e.
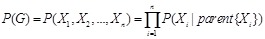 in graph
in graph
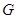 . Let
. Let
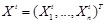 be the gene expression of
be the gene expression of
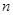 genes at time point
genes at time point
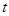 . Thus, for
. Thus, for
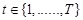 , under the first-order Markovian assumption that
, under the first-order Markovian assumption that
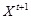 is independent of
is independent of
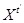 for
for
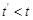 given
given
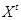 , we have
, we have
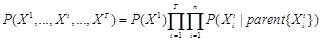 in the time course data. Assume
in the time course data. Assume
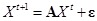 ,
,
where

where
 is the regulatory coefficient of
is the regulatory coefficient of
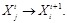
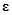 is the error vector and
is the error vector and
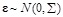 with
with
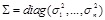 . According to linear assumption [125, 134], the log-likelihood function
. According to linear assumption [125, 134], the log-likelihood function
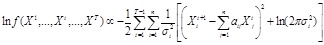 .
.
Although the binary regulatory relationship between gene
 and gene
and gene
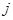 is available in the priori, the details of activation (
is available in the priori, the details of activation (
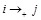 ), repression (
), repression (
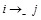 ), no regulation (
), no regulation (
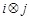 ), as well as the Level IV of regulatory strength are unknown, especially in specific conditions. So we employed a quadratic programming (QP) to
calculate the likelihood value by optimizing the coefficients
), as well as the Level IV of regulatory strength are unknown, especially in specific conditions. So we employed a quadratic programming (QP) to
calculate the likelihood value by optimizing the coefficients
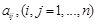 , i.e.,
, i.e.,
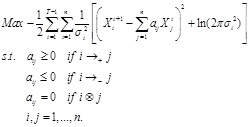
The constraints in the QP represent the regulatory strength between
 and
and
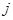 . Based on the log-likelihood value, the significance of a network architecture was evaluated by a random sampling process [134, 145, 146]. For each
regulatory network, we randomly generated
. Based on the log-likelihood value, the significance of a network architecture was evaluated by a random sampling process [134, 145, 146]. For each
regulatory network, we randomly generated
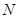 (e.g. 2000) networks by rewiring the same number of regulations in the nodes of the evaluating network. An empirical p-value is calculated to
evaluate its statistical significance, i.e.,
(e.g. 2000) networks by rewiring the same number of regulations in the nodes of the evaluating network. An empirical p-value is calculated to
evaluate its statistical significance, i.e.,
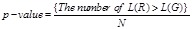 ,
,
where
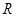 is a random network,
is a random network,
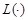 is the maximum log-likelihood value of the random network
is the maximum log-likelihood value of the random network
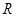 and the evaluating network
and the evaluating network
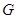 . The evaluation provides a powerful alternative to identify responsive regulatory networks in certain dynamics of environment and condition [134].
. The evaluation provides a powerful alternative to identify responsive regulatory networks in certain dynamics of environment and condition [134].
Apparently, the knowledge-based regulatory relationships among these genes are not complete and the reference network library should be as complete as possible. To the ends, [149] and [150] have developed methods to integrate inference and evaluation in the same framework by completing the gene network with modifications so that the resultant network achieves more consistency with the gene expression data. The missing regulations can be identified from initial incomplete prior network. Due to the difficulties of pure data-driven inference of regulatory network, the alternatives of combining prior knowledge and evaluating prior gene regulations show promising research directions to investigate transcriptional regulatory network from gene expression data [134].
4. DISCUSSION AND CONCLUSION
In this review, we summarized the state-of-the-art methods of reverse engineering transcriptional regulatory networks from gene expression data and categorized them into several general frameworks, i.e., correlation-based methods, Boolean network methods, Bayesian network methods, differential equation methods and knowledge-based methods. (Table 1) lists these strategies and their typical methods. Some methods implement hybrid models and employ several computational techniques to reversely engineer regulatory networks [41, 83]. These methods such as REVEAL [105], BC3NET [151] and GENIE3 [152] can be classified into multiple categories. For simplicity, we only categorized
Table 1.
Some available strategies and their representative methods for inferring regulatory networks from gene expression profiles. Their supporting websites and original publications are also shown. Some R packages (http://cran.r-project.org) for Bayesian learning and differential equation parameter identification are also shown. In each category, the methods are ordered alphabetically.
| Category | Method | Website | Reference |
|---|---|---|---|
| Correlation-based methods | ANOVA | http://www2.bio.ifi.lmu.de/˜kueffner/anova.tar.gz | [155] |
| ARACNE | http://wiki.c2b2.columbia.edu/califanolab/ index.php/Software/ARACNE | [56, 73] | |
| CLR | http://cran.r-project.org/web/packages/parmigene | [74] | |
| C3NET | http://cran.r-project.org/web/packages/c3net/index.html | [71] | |
| GLMNET | http://cran.r-project.org/web/packages/glmnet/ | [99, 100] | |
| grangerTlasso | http://www.biostat.washington.edu/~ashojaie/ | [103] | |
| MINET | http://cran.r-project.org/web/packages/minet/ | [76] | |
| MRNET | http://penglab.janelia.org/proj/mRMR/ | [75] | |
| ParCorA | http://www.comp-sys-bio.org/software.html | [88] | |
| PCA-CMI | http://csb.shu.edu.cn/subweb/grn.htm | [60] | |
| Relevance Network | http://buttelab.stanford.edu/start | [65, 70] | |
| Schafer and Strimmer | http://strimmerlab.org/software.html | [89] | |
| Simone | http://cran.r-project.org/web/packages/simone/ | [156] | |
| Stuart et al. | http://cmgm.stanford.edu/~kimlab/multispecies/ | [64] | |
| WGCNA | http://labs.genetics.ucla.edu/horvath/ CoexpressionNetwork/Rpackages/ WGCNA | [66, 68] | |
| Boolean network methods | Akutsu et al. | http://www.bic.kyoto-u.ac.jp/takutsu/members/takutsu/ | [106, 109] |
| Antelope | http://turing.iimas.unam.mx:8080/AntelopeWEB/content/about.jsp | [157] | |
| BoolNet | http://cran.r-project.org/web/packages/BoolNet | [158] | |
| BooleSim | https://github.com/matthiasbock/BooleSim | [159] | |
| Handorf and Klipp | http://code.google.com/p/libscopes/wiki/Paper2011 | [160] | |
| Modent | http://acgt.cs.tau.ac.il/modent/ | [161] | |
| REVEAL | Not available | [105] | |
| Shmulevich et al. | http://shmulevich.systemsbiology.net/ | [112, 113, 115] | |
| Bayesian network methods | ARTIVA | http://cran.r-project.org/web/packages/ARTIVA/index.html | [162] |
| BC3NET | http://cran.r-project.org/web/packages/bc3net/index.html | [151] | |
| Beal et al. | http://www.cse.buffalo.edu/faculty/mbeal/ | [125] | |
| BNFinder | http://bioputer.mimuw.edu.pl/software/bnf | [163] | |
| BNLEARN | http://cran.r-project.org/web/packages/bnlearn | [164] | |
| BNT | http://code.google.com/p/bnt/ | [120] | |
| Frideman et al. | http://www.cs.huji.ac.il/labs/compbio/expression/ | [117, 119] | |
| GeneNet | http://cran.r-project.org/web/packages/GeneNet | [83] | |
| G1DBN | http://cran.r-project.org/web/packages/G1DBN/index.html | [165] | |
| GlobalMIT | https://code.google.com/p/globalmit | [166] | |
| Module network | http://ai.stanford.edu/~erans/module_nets/ | [84] | |
| TESLA | http://sailing.cs.cmu.edu/tesla/index.html | [126] | |
| SSM | http://www.chems.msu.edu/groups/chan/ssm.zip | [167] | |
| Differential equation methods | Chen et al. | Not available | [127] |
| deSolve | http://cran.r-project.org/web/packages/deSolve | [168] | |
| D'haeseleer et al. | Not available | [95] | |
| D-NetWeaver | https://cbim.urmc.rochester.edu/software/d-netweaver/ | [128, 129] | |
| GRNInfer | http://doc.aporc.org/wiki/Software | [41] | |
| Inferelator | http://bonneaulab.bio.nyu.edu/software.html | [154] | |
| Tegner et al. | http://www.bu.edu/bme/people/primary/collins/ | [34, 36] | |
| TRNInfer | http://www.sysbio.ac.cn/cb/chenlab/software.htm | [153] | |
| Wahde and Hertz | http://www.nbi.dk/~hertz/ | [169] | |
| Knowledge-based methods | Banjo | http://www.cs.duke.edu/~amink/software/banjo | [142] |
| BNP | http://research.bioe.bilgi.edu.tr/bnp/ | [170] | |
| Greenfield et al. | http://bonneaulab.bio.nyu.edu/software.html | [171] | |
| Hill et al. | http://mukherjeelab.nki.nl/DBN | [172] | |
| Linear programming | http://doc.aporc.org/wiki/Software | [138] | |
| Liu et al. | http://doc.aporc.org/wiki/Software | [134] | |
| Network energy | Not available | [139, 143] | |
| Network Screening | http://www.molprof.jp/~horimoto/ | [144] | |
| PLASSO | http://nba.uth.tmc.edu/homepage/liu/pLasso | [173] | |
| Miscellaneous methods | GENIE3 | http://homepages.inf.ed.ac.uk/vhuynht/software.html | [152] |
| Neural network | http://www.me.chalmers.se/~mwahde | [174] | |
| Petri net | http://dnagarden.hgc.jp/en/doku.php/software | [175] | |
| Supervised learning | http://cbio.ensmp.fr/sirene | [167, 177] | |
| TIGRESS | http://cbio.ensmp.fr/tigress | [178] | |
| Differential equation methods | Chen et al. | Not available | [127] |
| deSolve | http://cran.r-project.org/web/packages/deSolve | [168] | |
| D'haeseleer et al. | Not available | [95] | |
| D-NetWeaver | https://cbim.urmc.rochester.edu/software/d-netweaver/ | [128, 129] | |
| GRNInfer | http://doc.aporc.org/wiki/Software | [41] | |
| Inferelator | http://bonneaulab.bio.nyu.edu/software.html | [154] | |
| Tegner et al. | http://www.bu.edu/bme/people/primary/collins/ | [34, 36] | |
| TRNInfer | http://www.sysbio.ac.cn/cb/chenlab/software.htm | [153] | |
| Wahde and Hertz | http://www.nbi.dk/~hertz/ | [169] | |
| Knowledge-based methods | Banjo | http://www.cs.duke.edu/~amink/software/banjo | [142] |
| BNP | http://research.bioe.bilgi.edu.tr/bnp/ | [170] | |
| Greenfield et al. | http://bonneaulab.bio.nyu.edu/software.html | [171] | |
| Hill et al. | http://mukherjeelab.nki.nl/DBN | [172] | |
| Linear programming | http://doc.aporc.org/wiki/Software | [138] | |
| Liu et al. | http://doc.aporc.org/wiki/Software | [134] | |
| Network energy | Not available | [139, 143] | |
| Network Screening | http://www.molprof.jp/~horimoto/ | [144] | |
| PLASSO | http://nba.uth.tmc.edu/homepage/liu/pLasso | [173] | |
| Miscellaneous methods | GENIE3 | http://homepages.inf.ed.ac.uk/vhuynht/software.html | [152] |
| Neural network | http://www.me.chalmers.se/~mwahde | [174] | |
| Petri net | http://dnagarden.hgc.jp/en/doku.php/software | [175] | |
| Supervised learning | http://cbio.ensmp.fr/sirene | [176, 177] | |
| TIGRESS | http://cbio.ensmp.fr/tigress | [178] |
them into one of them. For instance, REVEAL also employs mutual information technique beyond Boolean network, so it can also belong to correlation-based methods. In (Table 1), some methods such as TRNInfer [153] and Inferelator [154] reconstruct the four levels of transcriptional regulatory relationships, while others such as PCA-CMI [60] and WGCNA [68] generally identify gene regulations without direction information.
After the emergence of high-throughput microarray techniques, great efforts have been undertaken to infer transcriptional regulatory networks from gene expression profiles. Because of the complexity of gene regulations, it is still a challenging task to infer genome-wide regulatory networks from expression data by mathematical modeling [179]. Various computational methods have been proposed to interpret gene expression data and decipher the regulation mechanism of controlling gene expression. The reviewed methods are very useful for providing the quantitative models of harnessing the perturbation and time series of gene expression datasets and identifying the causal relationship of transcriptional regulations. In turn, the endeavors of coupling the regulatory interaction between genes imply the paramount importance of gene regulations in the study of genomics and genetics. It is difficult to assess these methods and select the best one that supersedes all the others by defining some benchmark standards [23]. The details and assumptions in the modeling of real regulation systems as well as the gene expressions in specific conditions and phenotypes determine the superiority of each method. The simple model as Boolean network can reveal critical implications in transcriptional regulation systems [107].
Besides the methods reviewed above, some other methods such as supervised learning [176, 177], feature selection [152, 178], neural network [174] and Petri net [175] methods have also been proposed to address the problem of learning transcriptional regulatory network from gene expression data. Most of these miscellaneous methods are heuristic for mining the relationship between genes from expression profiles. The availability next generation sequencing (NGS) technologies, e.g., RNA-Seq [180], can generate transcriptomic data of higher quality. Theoretically, these reviewed methods can be extended easily to reverse engineering transcriptional regulatory networks from RNA-Seq data. At the same time, identification of the causal regulatory mechanism of gene expression dynamics from gene expression data is constrained from the assumptions and approximations in the models. For instance, time delay between the activation of a TF and its downstream target genes widely exists in the regulatory relationships, which has not been well considered in the available methods [123, 181]. Also, the dynamics of regulation has not been modeled sufficiently, i.e., the regulation strength between TF and targets are always time-varying with temporal features [126]. The reviewed methods can be extended to integrate these important regulatory features into the models of causal regulatory relationships between genes. The reverse engineering methods will become more and more sophisticated for modeling transcriptional regulatory systems as comprehensively as possible.
Beyond utilizing gene expression data, an important research direction in building transcriptional regulatory network is to predict the interaction between TF protein and DNA by machine learning methods. Currently, one of the most important problems in the predictions is how to effectively formulate a biological sequence with a discrete model or a vector, yet still keep considerable sequence order information. All the existing operation engines, such as covariance discriminant (CD) [182, 183], neural network [184], support vector machine (SVM) [185, 186], random forest [187], conditional random field [188], nearest neighbor (NN) [189]; OET-KNN [190], Fuzzy K-nearest neighbor [191, 192], ML-KNN algorithm [193], and SLLE algorithm [183], can only handle vector but not sequence samples. However, a vector defined in a discrete model may completely lose all of the sequence-order information [194]. To avoid completely losing the sequence-order information for proteins, the pseudo amino acid composition or Chou’s PseAAC was proposed [194, 195]. Ever since the concept of PseAAC was proposed in 2001 [194], the approach of representing protein/peptide sequences has been widely used in all the areas of computational genomics [196]. Moreover, the concept of PseKNC (Pseudo K-tuple Nucleotide Composition) was introduced to deal with DNA/RNA sequences in computational genomics, such as for identifying nucleosome positioning [182] and predicting recombination spots [197]. The development of PseAAC for protein sequences and PseKNC for DNA sequences will highly facilitate the prediction of transcriptional regulatory interactions between TF protein and DNA only from sequence information [187, 198, 199].
The challenges of reverse engineering are not only from the information availability, but also from the complexity of regulation system [200]. The measured gene expression levels are not merely determined by the activity of its transcriptional regulators. Post-transcriptional regulations (microRNA silencing [51]) as well as epigenetic modifications (DNA methylation [48] and histone modification [201]) on the gene sequences also highly affect the levels of gene expression. The sequential and combinatorial regulations of gene expression among epigenetic factors, TFs, microRNAs should be considered systematically in reverse engineering regulatory systems when these genomic datasets are available [202]. In the future, the heterogeneous regulatory system with multiple genetic and epigenetic factors should be modeled to integrate transcriptional and post-transcriptional regulations. The integration of genomics, transcriptomics, proteomics datasets, such as ChIP-Seq, protein-binding motifs, gene expression, miRNA abundance, ratios of DNA methylation and chromatin modification, and prior knowledge of regulation, from multiple levels and various aspects of gene regulations provides a possible solution to reconstruct context-specific gene regulations [47]. The networks inferred from various levels can crossly validate each other for accurately identifying gene regulations underlying the whole system. Furthermore, the contradicted identifications in these inferences should be analyzed carefully. They might be caused by the noisy datasets, unrevealed regulatory mechanisms, and specific phenotype associations. Reverse engineering of transcriptional regulatory networks by integrating multiple datasets is a very important research direction [41, 153]. Consistent regulatory relationships at multiple levels shed a brilliant light on the gene expression dynamics in response to various internal signals and external stimuli.
In conclusion, a genome-wide inference of transcriptional regulatory networks from gene expression data provides a promising way to decipher the large-scale causal regulatory relationships among genes. Model-based computational methods of harnessing genomic data facilitate the discovery and revolutionize the research of gene regulation. We summarized the advantages and commented on the improvement possibilities of addressing the disadvantages of these methods individually. The assumptions of modeling the spatial and temporal gene regulations will become more and more reasonable with the accumulation of knowledge about gene regulations. The models will also become more and more close to the real complexity of gene regulation when we obtain better gene expression data with enough sample size and dedicated experiment design, multilevel biological processes, higher quality of expression signals, and systematic perspectives. Knowledge-based methods of integrating existing priori and gene expression seem to be powerful and flexible to decipher the genuine transcriptional control circuits in regulatory systems.
ACKNOWLEDGEMENTS
Thanks are due to Drs Songyot Nakariyakul, Xiaoxu Han, Rui-Sheng Wang, Xianwen Ren and Jiguang Wang for their critical comments. This work was partially supported by the National Natural Science Foundation of China (NSFC) under Grant No. 31100949 and the Fundamental Research Funds of Shandong University under Grant No. 2014TB006.
CONFLICT OF INTEREST
The author(s) confirm that this article content has no conflict of interest.
References
- 1.Spitz F., Furlong E.E. Transcription factors: from enhancer binding to developmental control. Nat. Rev. Genet. 2012;13(9):613–626. doi: 10.1038/nrg3207. [DOI] [PubMed] [Google Scholar]
- 2.Chen K., Rajewsky N. The evolution of gene regulation by transcription factors and microRNAs. Nat. Rev. Genet. 2007;8(2):93–103. doi: 10.1038/nrg1990. [DOI] [PubMed] [Google Scholar]
- 3.Levine M., Davidson E.H. Gene regulatory networks for development. Proc. Natl. Acad. Sci. USA. 2005;102(14):4936–4942. doi: 10.1073/pnas.0408031102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Orphanides G., Reinberg D. A unified theory of gene expression. Cell. 2002;108(4):439–451. doi: 10.1016/s0092-8674(02)00655-4. [DOI] [PubMed] [Google Scholar]
- 5.Babu M.M., Luscombe N.M., Aravind L., Gerstein M., Teichmann S.A. Structure and evolution of transcriptional regulatory networks. Curr. Opin. Struct. Biol. 2004;14(3):283–291. doi: 10.1016/j.sbi.2004.05.004. [DOI] [PubMed] [Google Scholar]
- 6.Beer M.A., Tavazoie S. Predicting gene expression from sequence. Cell. 2004;117(2):185–198. doi: 10.1016/s0092-8674(04)00304-6. [DOI] [PubMed] [Google Scholar]
- 7.Kim H.D., O’Shea E.K. A quantitative model of transcription factor-activated gene expression. Nat. Struct. Mol. Biol. 2008;15(11):1192–1198. doi: 10.1038/nsmb.1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.de Matos Simoes R., Dehmer M., Emmert-Streib F. Interfacing cellular networks of S. cerevisiae and E. coli: connecting dynamic and genetic information. BMC Genomics. 2013;14:324. doi: 10.1186/1471-2164-14-324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Amit I., Garber M., Chevrier N., Leite A.P., Donner Y., Eisenhaure T., Guttman M., Grenier J.K., Li W., Zuk O., Schubert L.A., Birditt B., Shay T., Goren A., Zhang X., Smith Z., Deering R., McDonald R.C., Cabili M., Bernstein B.E., Rinn J.L., Meissner A., Root D.E., Hacohen N., Regev A. Unbiased reconstruction of a mammalian transcriptional network mediating pathogen responses. Science. 2009;326(5950):257–263. doi: 10.1126/science.1179050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Blais A., Dynlacht B.D. Constructing transcriptional regulatory networks. Genes Dev. 2005;19(13):1499–1511. doi: 10.1101/gad.1325605. [DOI] [PubMed] [Google Scholar]
- 11.Lee T.I., Rinaldi N.J., Robert F., Odom D.T., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Zeitlinger J., Jennings E.G., Murray H.L., Gordon D.B., Ren B., Wyrick J.J., Tagne J.B., Volkert T.L., Fraenkel E., Gifford D.K., Young R.A. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298(5594):799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- 12.Bogarad L.D., Arnone M.I., Chang C., Davidson E.H. Interference with gene regulation in living sea urchin embryos: transcription factor knock out (TKO), a genetically controlled vector for blockade of specific transcription factors. Proc. Natl. Acad. Sci. USA. 1998;95(25):14827–14832. doi: 10.1073/pnas.95.25.14827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pe’er D., Regev A., Elidan G., Friedman N. Inferring subnetworks from perturbed expression profiles. Bioinformatics. 2001;17(Suppl. 1):S215–S224. doi: 10.1093/bioinformatics/17.suppl_1.s215. [DOI] [PubMed] [Google Scholar]
- 14.Hu Z., Killion P.J., Iyer V.R. Genetic reconstruction of a functional transcriptional regulatory network. Nat. Genet. 2007;39(5):683–687. doi: 10.1038/ng2012. [DOI] [PubMed] [Google Scholar]
- 15.Workman C.T., Mak H.C., McCuine S., Tagne J.B., Agarwal M., Ozier O., Begley T.J., Samson L.D., Ideker T. A systems approach to mapping DNA damage response pathways. Science. 2006;312(5776):1054–1059. doi: 10.1126/science.1122088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Park P.J. ChIP-seq: advantages and challenges of a maturing technology. Nat. Rev. Genet. 2009;10(10):669–680. doi: 10.1038/nrg2641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Johnson D.S., Mortazavi A., Myers R.M., Wold B. Genome-wide mapping of in vivo protein-DNA interactions. Science. 2007;316(5830):1497–1502. doi: 10.1126/science.1141319. [DOI] [PubMed] [Google Scholar]
- 18.Marson A., Kretschmer K., Frampton G.M., Jacobsen E.S., Polansky J.K., MacIsaac K.D., Levine S.S., Fraenkel E., von Boehmer H., Young R.A. Foxp3 occupancy and regulation of key target genes during T-cell stimulation. Nature. 2007;445(7130):931–935. doi: 10.1038/nature05478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schena M., Shalon D., Davis R.W., Brown P.O. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science. 1995;270(5235):467–470. doi: 10.1126/science.270.5235.467. [DOI] [PubMed] [Google Scholar]
- 20.Hughes T.R., Marton M.J., Jones A.R., Roberts C.J., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Kidd M.J., King A.M., Meyer M.R., Slade D., Lum P.Y., Stepaniants S.B., Shoemaker D.D., Gachotte D., Chakraburtty K., Simon J., Bard M., Friend S.H. Functional discovery via a compendium of expression profiles. Cell. 2000;102(1):109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 21.Hartemink A.J. Reverse engineering gene regulatory networks. Nat. Biotechnol. 2005;23(5):554–555. doi: 10.1038/nbt0505-554. [DOI] [PubMed] [Google Scholar]
- 22.Marbach D., Costello J.C., Küffner R., Vega N.M., Prill R.J., Camacho D.M., Allison K.R., Kellis M., Collins J.J., Stolovitzky G., DREAM5 Consortium Wisdom of crowds for robust gene network inference. Nat. Methods. 2012;9(8):796–804. doi: 10.1038/nmeth.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marbach D., Prill R.J., Schaffter T., Mattiussi C., Floreano D., Stolovitzky G. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA. 2010;107(14):6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Csete M.E., Doyle J.C. Reverse engineering of biological complexity. Science. 2002;295(5560):1664–1669. doi: 10.1126/science.1069981. [DOI] [PubMed] [Google Scholar]
- 25.Kaern M., Blake W.J., Collins J.J. The engineering of gene regulatory networks. Annu. Rev. Biomed. Eng. 2003;5:179–206. doi: 10.1146/annurev.bioeng.5.040202.121553. [DOI] [PubMed] [Google Scholar]
- 26.de Jong H. Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 2002;9(1):67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- 27.Bansal M., Belcastro V., Ambesi-Impiombato A., di Bernardo D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007;3:78. doi: 10.1038/msb4100120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hecker M., Lambeck S., Toepfer S., van Someren E., Guthke R. Gene regulatory network inference: data integration in dynamic models-a review. Biosystems. 2009;96(1):86–103. doi: 10.1016/j.biosystems.2008.12.004. [DOI] [PubMed] [Google Scholar]
- 29.Karlebach G., Shamir R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008;9(10):770–780. doi: 10.1038/nrm2503. [DOI] [PubMed] [Google Scholar]
- 30.Emmert-Streib F., Glazko G.V., Altay G., de Matos Simoes R. Statistical inference and reverse engineering of gene regulatory networks from observational expression data. Front. Genet. 2012;3:8. doi: 10.3389/fgene.2012.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Werhli A.V., Grzegorczyk M., Husmeier D. Comparative evaluation of reverse engineering gene regulatory networks with relevance networks, graphical gaussian models and bayesian networks. Bioinformatics. 2006;22(20):2523–2531. doi: 10.1093/bioinformatics/btl391. [DOI] [PubMed] [Google Scholar]
- 32.Li H., Xuan J., Wang Y., Zhan M. Inferring regulatory networks. Front. Biosci. 2008;13:263–275. doi: 10.2741/2677. [DOI] [PubMed] [Google Scholar]
- 33.Lee W.P., Tzou W.S. Computational methods for discovering gene networks from expression data. Brief. Bioinform. 2009;10(4):408–423. doi: 10.1093/bib/bbp028. [DOI] [PubMed] [Google Scholar]
- 34.Yeung M.K., Tegnér J., Collins J.J. Reverse engineering gene networks using singular value decomposition and robust regression. Proc. Natl. Acad. Sci. USA. 2002;99(9):6163–6168. doi: 10.1073/pnas.092576199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gardner T.S., Faith J.J. Reverse-engineering transcription control networks. Phys. Life Rev. 2005;2(1):65–88. doi: 10.1016/j.plrev.2005.01.001. [DOI] [PubMed] [Google Scholar]
- 36.Tegner J., Yeung M.K., Hasty J., Collins J.J. Reverse engineering gene networks: integrating genetic perturbations with dynamical modeling. Proc. Natl. Acad. Sci. USA. 2003;100(10):5944–5949. doi: 10.1073/pnas.0933416100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nachman I., Regev A., Friedman N. Inferring quantitative models of regulatory networks from expression data. Bioinformatics. 2004;20(Suppl. 1):i248–i256. doi: 10.1093/bioinformatics/bth941. [DOI] [PubMed] [Google Scholar]
- 38.Luscombe N.M., Babu M.M., Yu H., Snyder M., Teichmann S.A., Gerstein M. Genomic analysis of regulatory network dynamics reveals large topological changes. Nature. 2004;431(7006):308–312. doi: 10.1038/nature02782. [DOI] [PubMed] [Google Scholar]
- 39.Kim H.D., Shay T., O’Shea E.K., Regev A. Transcriptional regulatory circuits: predicting numbers from alphabets. Science. 2009;325(5939):429–432. doi: 10.1126/science.1171347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Amit I., Regev A., Hacohen N. Strategies to discover regulatory circuits of the mammalian immune system. Nat. Rev. Immunol. 2011;11(12):873–880. doi: 10.1038/nri3109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang Y., Joshi T., Zhang X.S., Xu D., Chen L. Inferring gene regulatory networks from multiple microarray datasets. Bioinformatics. 2006;22(19):2413–2420. doi: 10.1093/bioinformatics/btl396. [DOI] [PubMed] [Google Scholar]
- 42.Leclerc R.D. Survival of the sparsest: robust gene networks are parsimonious. Mol. Syst. Biol. 2008;4:213. doi: 10.1038/msb.2008.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kato M., Hata N., Banerjee N., Futcher B., Zhang M.Q. Identifying combinatorial regulation of transcription factors and binding motifs. Genome Biol. 2004;5(8):R56. doi: 10.1186/gb-2004-5-8-r56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fairfax B.P., Makino S., Radhakrishnan J., Plant K., Leslie S., Dilthey A., Ellis P., Langford C., Vannberg F.O., Knight J.C. Genetics of gene expression in primary immune cells identifies cell type-specific master regulators and roles of HLA alleles. Nat. Genet. 2012;44(5):502–510. doi: 10.1038/ng.2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pilpel Y., Sudarsanam P., Church G.M. Identifying regulatory networks by combinatorial analysis of promoter elements. Nat. Genet. 2001;29(2):153–159. doi: 10.1038/ng724. [DOI] [PubMed] [Google Scholar]
- 46.Emmert-Streib F., de Matos Simoes R., Mullan P., Haibe-Kains B., Dehmer M. The gene regulatory network for breast cancer: integrated regulatory landscape of cancer hallmarks. Front. Genet. 2014;5:15. doi: 10.3389/fgene.2014.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gibcus J.H., Dekker J. The context of gene expression regulation. F1000 Biol. Rep. 2012;4:8. doi: 10.3410/B4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bock C. Analysing and interpreting DNA methylation data. Nat. Rev. Genet. 2012;13(10):705–719. doi: 10.1038/nrg3273. [DOI] [PubMed] [Google Scholar]
- 49.Segal E., Widom J. What controls nucleosome positions? Trends Genet. 2009;25(8):335–343. doi: 10.1016/j.tig.2009.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jaenisch R., Bird A. Epigenetic regulation of gene expression: how the genome integrates intrinsic and environmental signals. Nat. Genet. 2003;33(Suppl.):245–254. doi: 10.1038/ng1089. [DOI] [PubMed] [Google Scholar]
- 51.Bartel D.P. MicroRNAs: target recognition and regulatory functions. Cell. 2009;136(2):215–233. doi: 10.1016/j.cell.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lovén J., Orlando D.A., Sigova A.A., Lin C.Y., Rahl P.B., Burge C.B., Levens D.L., Lee T.I., Young R.A. Revisiting global gene expression analysis. Cell. 2012;151(3):476–482. doi: 10.1016/j.cell.2012.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Canales R.D., Luo Y., Willey J.C., Austermiller B., Barbacioru C.C., Boysen C., Hunkapiller K., Jensen R.V., Knight C.R., Lee K.Y., Ma Y., Maqsodi B., Papallo A., Peters E.H., Poulter K., Ruppel P.L., Samaha R.R., Shi L., Yang W., Zhang L., Goodsaid F.M. Evaluation of DNA microarray results with quantitative gene expression platforms. Nat. Biotechnol. 2006;24(9):1115–1122. doi: 10.1038/nbt1236. [DOI] [PubMed] [Google Scholar]
- 54.Irizarry R.A., Hobbs B., Collin F., Beazer-Barclay Y.D., Antonellis K.J., Scherf U., Speed T.P. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4(2):249–264. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- 55.Kao K.C., Yang Y.L., Boscolo R., Sabatti C., Roychowdhury V., Liao J.C. Transcriptome-based determination of multiple transcription regulator activities in Escherichia coli by using network component analysis. Proc. Natl. Acad. Sci. USA. 2004;101(2):641–646. doi: 10.1073/pnas.0305287101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Basso K., Margolin A.A., Stolovitzky G., Klein U., Dalla-Favera R., Califano A. Reverse engineering of regulatory networks in human B cells. Nat. Genet. 2005;37(4):382–390. doi: 10.1038/ng1532. [DOI] [PubMed] [Google Scholar]
- 57.Stolovitzky G., Monroe D., Califano A. Dialogue on reverse-engineering assessment and methods: the DREAM of high-throughput pathway inference. Ann. N. Y. Acad. Sci. 2007;1115:1–22. doi: 10.1196/annals.1407.021. [DOI] [PubMed] [Google Scholar]
- 58.Schaffter T., Marbach D., Floreano D. GeneNetWeaver: in silico benchmark generation and performance profiling of network inference methods. Bioinformatics. 2011;27(16):2263–2270. doi: 10.1093/bioinformatics/btr373. [DOI] [PubMed] [Google Scholar]
- 59.Liu Z.P., Chen L. Proteome-wide prediction of protein-protein interactions from high-throughput data. Protein Cell. 2012;3(7):508–520. doi: 10.1007/s13238-012-2945-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhang X., Zhao X.M., He K., Lu L., Cao Y., Liu J., Hao J.K., Liu Z.P., Chen L. Inferring gene regulatory networks from gene expression data by path consistency algorithm based on conditional mutual information. Bioinformatics. 2012;28(1):98–104. doi: 10.1093/bioinformatics/btr626. [DOI] [PubMed] [Google Scholar]
- 61.Marbach D., Prill R.J., Schaffter T., Mattiussi C., Floreano D., Stolovitzky G. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA. 2010;107(14):6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ben-Dor A., Shamir R., Yakhini Z. Clustering gene expression patterns. J. Comput. Biol. 1999;6(3-4):281–297. doi: 10.1089/106652799318274. [DOI] [PubMed] [Google Scholar]
- 63.Eisen M.B., Spellman P.T., Brown P.O., Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA. 1998;95(25):14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Stuart J.M., Segal E., Koller D., Kim S.K. A gene-coexpression network for global discovery of conserved genetic modules. Science. 2003;302(5643):249–255. doi: 10.1126/science.1087447. [DOI] [PubMed] [Google Scholar]
- 65.Butte A.J., Kohane I.S. Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements. Pac. Symp. Biocomput. 2000;5:418–429. doi: 10.1142/9789814447331_0040. [DOI] [PubMed] [Google Scholar]
- 66.Langfelder P., Horvath S. WGCNA: an R package for weighted correlation network analysis. BMC Bioinformatics. 2008;9:559. doi: 10.1186/1471-2105-9-559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.He D., Liu Z.P., Honda M., Kaneko S., Chen L. Coexpression network analysis in chronic hepatitis B and C hepatic lesions reveals distinct patterns of disease progression to hepatocellular carcinoma. J. Mol. Cell Biol. 2012;4(3):140–152. doi: 10.1093/jmcb/mjs011. [DOI] [PubMed] [Google Scholar]
- 68.Zhang B., Horvath S. A general framework for weighted gene co-expression network analysis. 2005. [DOI] [PubMed]
- 69.Fujita A., Sato J.R., Demasi M.A., Sogayar M.C., Ferreira C.E., Miyano S. Comparing Pearson, Spearman and Hoeffding’s D measure for gene expression association analysis. J. Bioinform. Comput. Biol. 2009;7(4):663–684. doi: 10.1142/s0219720009004230. [DOI] [PubMed] [Google Scholar]
- 70.Butte A.J., Tamayo P., Slonim D., Golub T.R., Kohane I.S. Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proc. Natl. Acad. Sci. USA. 2000;97(22):12182–12186. doi: 10.1073/pnas.220392197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Altay G., Emmert-Streib F. Inferring the conservative causal core of gene regulatory networks. BMC Syst. Biol. 2010;4:132. doi: 10.1186/1752-0509-4-132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Olsen C., Meyer P.E., Bontempi G. On the impact of entropy estimation on transcriptional regulatory network inference based on mutual information. EURASIP J. Bioinform. Syst. Biol. 2009;•••:308959. doi: 10.1155/2009/308959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Margolin A.A., Nemenman I., Basso K., Wiggins C., Stolovitzky G., Dalla Favera R., Califano A. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7(Suppl. 1):S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Faith J.J., Hayete B., Thaden J.T., Mogno I., Wierzbowski J., Cottarel G., Kasif S., Collins J.J., Gardner T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007;5(1):e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ding C., Peng H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005;3(2):185–205. doi: 10.1142/s0219720005001004. [DOI] [PubMed] [Google Scholar]
- 76.Meyer P.E., Lafitte F., Bontempi G. minet: A R/Bioconductor package for inferring large transcriptional networks using mutual information. BMC Bioinformatics. 2008;9:461. doi: 10.1186/1471-2105-9-461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Carro M.S., Lim W.K., Alvarez M.J., Bollo R.J., Zhao X., Snyder E.Y., Sulman E.P., Anne S.L., Doetsch F., Colman H., Lasorella A., Aldape K., Califano A., Iavarone A. The transcriptional network for mesenchymal transformation of brain tumours. Nature. 2010;463(7279):318–325. doi: 10.1038/nature08712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Wang K., Saito M., Bisikirska B.C., Alvarez M.J., Lim W.K., Rajbhandari P., Shen Q., Nemenman I., Basso K., Margolin A.A., Klein U., Dalla-Favera R., Califano A. Genome-wide identification of post-translational modulators of transcription factor activity in human B cells. Nat. Biotechnol. 2009;27(9):829–839. doi: 10.1038/nbt.1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Reshef D.N., Reshef Y.A., Finucane H.K., Grossman S.R., McVean G., Turnbaugh P.J., Lander E.S., Mitzenmacher M., Sabeti P.C. Detecting novel associations in large data sets. Science. 2011;334(6062):1518–1524. doi: 10.1126/science.1205438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kinney J.B., Atwal G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA. 2014;111(9):3354–3359. doi: 10.1073/pnas.1309933111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Song L., Langfelder P., Horvath S. Comparison of co-expression measures: mutual information, correlation, and model based indices. BMC Bioinformatics. 2012;13:328. doi: 10.1186/1471-2105-13-328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.D’haeseleer P., Liang S., Somogyi R. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics. 2000;16(8):707–726. doi: 10.1093/bioinformatics/16.8.707. [DOI] [PubMed] [Google Scholar]
- 83.Opgen-Rhein R., Strimmer K. From correlation to causation networks: a simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Syst. Biol. 2007;1:37. doi: 10.1186/1752-0509-1-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Segal E., Shapira M., Regev A., Pe’er D., Botstein D., Koller D., Friedman N. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat. Genet. 2003;34(2):166–176. doi: 10.1038/ng1165. [DOI] [PubMed] [Google Scholar]
- 85.Liu Z.P., Wang Y., Zhang X.S., Chen L. Identifying dysfunctional crosstalk of pathways in various regions of Alzheimer’s disease brains. BMC Syst. Biol. 2010;4(Suppl. 2):S11. doi: 10.1186/1752-0509-4-S2-S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.He D., Liu Z.P., Chen L. Identification of dysfunctional modules and disease genes in congenital heart disease by a network-based approach. BMC Genomics. 2011;12:592. doi: 10.1186/1471-2164-12-592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Liu K.Q., Liu Z.P., Hao J.K., Chen L., Zhao X.M. Identifying dysregulated pathways in cancers from pathway interaction networks. BMC Bioinformatics. 2012;13(1):126. doi: 10.1186/1471-2105-13-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.de la Fuente A., Bing N., Hoeschele I., Mendes P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics. 2004;20(18):3565–3574. doi: 10.1093/bioinformatics/bth445. [DOI] [PubMed] [Google Scholar]
- 89.Schäfer J., Strimmer K. An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics. 2005;21(6):754–764. doi: 10.1093/bioinformatics/bti062. [DOI] [PubMed] [Google Scholar]
- 90.Liang K.C., Wang X. Gene regulatory network reconstruction using conditional mutual information. EURASIP J. Bioinform. Syst. Biol. 2008;•••:253894. doi: 10.1155/2008/253894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Saito S., Hirokawa T., Horimoto K. Discovery of chemical compound groups with common structures by a network analysis approach (affinity prediction method). J. Chem. Inf. Model. 2011;51(1):61–68. doi: 10.1021/ci100262s. [DOI] [PubMed] [Google Scholar]
- 92.Frenzel S., Pompe B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett. 2007;99(20):204101. doi: 10.1103/PhysRevLett.99.204101. [DOI] [PubMed] [Google Scholar]
- 93.Speed T. Mathematics. A correlation for the 21st century. Science. 2011;334(6062):1502–1503. doi: 10.1126/science.1215894. [DOI] [PubMed] [Google Scholar]
- 94.Kalisch M., Buhlmann P. Estimating high-dimensional directed acyclic graphs with the pc-algorithm. J. Mach. Learn. Res. 2005;7:613–636. [Google Scholar]
- 95.D’haeseleer P., Wen X., Fuhrman S., Somogyi R. Linear modeling of mRNA expression levels during CNS development and injury. Pac. Symp. Biocomput. 1999;4:41–52. doi: 10.1142/9789814447300_0005. [DOI] [PubMed] [Google Scholar]
- 96.Kim H., Lee J.K., Park T. Inference of large-scale gene regulatory networks using regression-based network approach. J. Bioinform. Comput. Biol. 2009;7(4):717–735. doi: 10.1142/s0219720009004278. [DOI] [PubMed] [Google Scholar]
- 97.Opgen-Rhein R., Strimmer K. Learning causal networks from systems biology time course data: an effective model selection procedure for the vector autoregressive process. BMC Bioinformatics. 2007;8(Suppl. 2):S3. doi: 10.1186/1471-2105-8-S2-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Pihur V., Datta S., Datta S. Reconstruction of genetic association networks from microarray data: a partial least squares approach. Bioinformatics. 2008;24(4):561–568. doi: 10.1093/bioinformatics/btm640. [DOI] [PubMed] [Google Scholar]
- 99.Tibshirani R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Series B Stat. Methodol. 1996;58:267–288. [Google Scholar]
- 100.Zou H., Trevor H. Regularization and variable selection via the Elastic Net. J. R. Stat. Soc. Series B Stat. Methodol. 2005;67:301–320. [Google Scholar]
- 101.Shojaie A., Michailidis G. Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs. Biometrika. 2010;97(3):519–538. doi: 10.1093/biomet/asq038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Lozano A.C., Abe N., Liu Y., Rosset S. Grouped graphical Granger modeling for gene expression regulatory networks discovery. Bioinformatics. 2009;25(12):i110–i118. doi: 10.1093/bioinformatics/btp199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Shojaie A., Michailidis G. Discovering graphical Granger causality using the truncating lasso penalty. Bioinformatics. 2010;26(18):i517–i523. doi: 10.1093/bioinformatics/btq377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Thomas R. Boolean formalization of genetic control circuits. J. Theor. Biol. 1973;42(3):563–585. doi: 10.1016/0022-5193(73)90247-6. [DOI] [PubMed] [Google Scholar]
- 105.Liang S., Fuhrman S., Somogyi R. Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pac. Symp. Biocomput. 1998;3:18–29. [PubMed] [Google Scholar]
- 106.Akutsu T., Miyano S., Kuhara S. Identification of genetic networks from a small number of gene expression patterns under the Boolean network model. Pac. Symp. Biocomput. 1999;4:17–28. doi: 10.1142/9789814447300_0003. [DOI] [PubMed] [Google Scholar]
- 107.Wang R.S., Saadatpour A., Albert R. Boolean modeling in systems biology: an overview of methodology and applications. Phys. Biol. 2012;9(5):055001. doi: 10.1088/1478-3975/9/5/055001. [DOI] [PubMed] [Google Scholar]
- 108.Ivanov I. Boolean models of genomic regulatory networks: reduction mappings, inference, and external control. Curr. Genomics. 2009;10(6):375–387. doi: 10.2174/138920209789177584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Akutsu T., Miyano S., Kuhara S. Inferring qualitative relations in genetic networks and metabolic pathways. Bioinformatics. 2000;16(8):727–734. doi: 10.1093/bioinformatics/16.8.727. [DOI] [PubMed] [Google Scholar]
- 110.Ideker T.E., Thorsson V., Karp R.M. Discovery of regulatory interactions through perturbation: inference and experimental design. Pac. Symp. Biocomput. 2000;5:305–316. doi: 10.1142/9789814447331_0029. [DOI] [PubMed] [Google Scholar]
- 111.Garg A., Di Cara A., Xenarios I., Mendoza L., De Micheli G. Synchronous versus asynchronous modeling of gene regulatory networks. Bioinformatics. 2008;24(17):1917–1925. doi: 10.1093/bioinformatics/btn336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Shmulevich I., Dougherty E.R., Kim S., Zhang W. Probabilistic Boolean Networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics. 2002;18(2):261–274. doi: 10.1093/bioinformatics/18.2.261. [DOI] [PubMed] [Google Scholar]
- 113.Shmulevich I., Lähdesmäki H., Dougherty E.R., Astola J., Zhang W. The role of certain Post classes in Boolean network models of genetic networks. Proc. Natl. Acad. Sci. USA. 2003;100(19):10734–10739. doi: 10.1073/pnas.1534782100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Faryabi B., Vahedi G., Datta A., Chamberland J.F., Dougherty E.R. Recent advances in intervention in markovian regulatory networks. Curr. Genomics. 2009;10(7):463–477. doi: 10.2174/138920209789208246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Shmulevich I., Dougherty E.R., Zhang W. From Boolean to probabilistic Boolean networks as models of genetic regulatory networks. Proc. IEEE. 2002;90(11):1778–1792. [Google Scholar]
- 116.Pearl J. Probabilistic Reasoning in Intelligent Systems. San Francisco: Morgan Kaufmann; 1988. [Google Scholar]
- 117.Friedman N., Linial M., Nachman I., Pe’er D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000;7(3-4):601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- 118.Heckerman D., Chickering D.M. Learning Bayesian networks: the combination of knowledge and statistical data. Mach. Learn. 1995;20:197–243. [Google Scholar]
- 119.Friedman N. Inferring cellular networks using probabilistic graphical models. Science. 2004;303(5659):799–805. doi: 10.1126/science.1094068. [DOI] [PubMed] [Google Scholar]
- 120.Murphy K.P., Milan S. Modelling gene expression data using dynamic Bayesian networks. Tech. Rep. MIT Artificial Intelligence Lab; 1999. [Google Scholar]
- 121.Perrin B.E., Ralaivola L., Mazurie A., Bottani S., Mallet J., d’Alché-Buc F. Gene networks inference using dynamic Bayesian networks. Bioinformatics. 2003;19(Suppl. 2):ii138–ii148. doi: 10.1093/bioinformatics/btg1071. [DOI] [PubMed] [Google Scholar]
- 122.Husmeier D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics. 2003;19(17):2271–2282. doi: 10.1093/bioinformatics/btg313. [DOI] [PubMed] [Google Scholar]
- 123.Zou M., Conzen S.D. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics. 2005;21(1):71–79. doi: 10.1093/bioinformatics/bth463. [DOI] [PubMed] [Google Scholar]
- 124.Kim S., Imoto S., Miyano S. Dynamic Bayesian network and nonparametric regression for nonlinear modeling of gene networks from time series gene expression data. Biosystems. 2004;75(1-3):57–65. doi: 10.1016/j.biosystems.2004.03.004. [DOI] [PubMed] [Google Scholar]
- 125.Beal M.J., Falciani F., Ghahramani Z., Rangel C., Wild D.L. A Bayesian approach to reconstructing genetic regulatory networks with hidden factors. Bioinformatics. 2005;21(3):349–356. doi: 10.1093/bioinformatics/bti014. [DOI] [PubMed] [Google Scholar]
- 126.Ahmed A., Xing E.P. Recovering time-varying networks of dependencies in social and biological studies. Proc. Natl. Acad. Sci. USA. 2009;106(29):11878–11883. doi: 10.1073/pnas.0901910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Chen T., He H.L., Church G.M. Modeling gene expression with differential equations. Pac. Symp. Biocomput. 1999;4:29–40. [PubMed] [Google Scholar]
- 128.Wu S., Liu Z.P., Qiu X., Wu H. Modeling genome-wide dynamic regulatory network in mouse lungs with influenza infection using high-dimensional ordinary differential equations. PLoS One. 2014;9(5):e95276. doi: 10.1371/journal.pone.0095276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Lu T., Liang H., Li H., Wu H. High dimensional ODEs coupled with mixed-effects modeling techniques for dynamic gene regulatory network identification. J. Am. Stat. Assoc. 2011;106(496):1242–1258. doi: 10.1198/jasa.2011.ap10194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Bonneau R. Learning biological networks: from modules to dynamics. Nat. Chem. Biol. 2008;4(11):658–664. doi: 10.1038/nchembio.122. [DOI] [PubMed] [Google Scholar]
- 131.Fan J., Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001;96(45):1348–1360. [Google Scholar]
- 132.Miao H., Xia X., Perelson A.S., Wu H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev Soc Ind Appl Math. 2011;53(1):3–39. doi: 10.1137/090757009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Emmert-Streib F., Dehmer M., Haibe-Kains B. Untangling statistical and biological models to understand network inference: the need for a genomics network ontology. Front. Genet. 2014;5:299. doi: 10.3389/fgene.2014.00299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Liu Z.P., Zhang W., Horimoto K., Chen L. Gaussian graphical model for identifying significantly responsive regulatory networks from time course high-throughput data. IET Syst. Biol. 2013;7(5):143–152. doi: 10.1049/iet-syb.2012.0062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Salgado H., Peralta-Gil M., Gama-Castro S., Santos-Zavaleta A., Muñiz-Rascado L., García-Sotelo J.S., Weiss V., Solano-Lira H., Martínez-Flores I., Medina-Rivera A., Salgado-Osorio G., Alquicira-Hernández S., Alquicira-Hernández K., López-Fuentes A., Porrón-Sotelo L., Huerta A.M., Bonavides-Martínez C., Balderas-Martínez Y.I., Pannier L., Olvera M., Labastida A., Jiménez-Jacinto V., Vega-Alvarado L., Del Moral-Chávez V., Hernández-Alvarez A., Morett E., Collado-Vides J. RegulonDB v8.0: omics data sets, evolutionary conservation, regulatory phrases, cross-validated gold standards and more. Nucleic Acids Res. 2013;41(Database issue):D203–D213. doi: 10.1093/nar/gks1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Bernstein B.E., Birney E., Dunham I., Green E.D., Gunter C., Snyder M., ENCODE Project Consortium An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489(7414):57–74. doi: 10.1038/nature11247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Ren B., Robert F., Wyrick J.J., Aparicio O., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Volkert T.L., Wilson C.J., Bell S.P., Young R.A. Genome-wide location and function of DNA binding proteins. Science. 2000;290(5500):2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- 138.Liu Z.P., Zhang X.S., Chen L. Inferring gene regulatory networks from expression data with prior knowledge by linear programming.; 2010. [Google Scholar]
- 139.Werhli A.V., Husmeier D. Reconstructing gene regulatory networks with bayesian networks by combining expression data with multiple sources of prior knowledge. 2007. [DOI] [PubMed]
- 140.Mukherjee S., Speed T.P. Network inference using informative priors. Proc. Natl. Acad. Sci. USA. 2008;105(38):14313–14318. doi: 10.1073/pnas.0802272105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Steele E., Tucker A., ’t Hoen P.A., Schuemie M.J. Literature-based priors for gene regulatory networks. Bioinformatics. 2009;25(14):1768–1774. doi: 10.1093/bioinformatics/btp277. [DOI] [PubMed] [Google Scholar]
- 142.Bernard A., Hartemink A.J. Informative structure priors: joint learning of dynamic regulatory networks from multiple types of data. Pac. Symp. Biocomput. 2005;10:459–470. [PubMed] [Google Scholar]
- 143.Imoto S., Higuchi T., Goto T., Tashiro K., Kuhara S., Miyano S. Combining microarrays and biological knowledge for estimating gene networks via bayesian networks. J. Bioinform. Comput. Biol. 2004;2(1):77–98. doi: 10.1142/s021972000400048x. [DOI] [PubMed] [Google Scholar]
- 144.Saito S., Aburatani S., Horimoto K. Network evaluation from the consistency of the graph structure with the measured data. BMC Syst. Biol. 2008;2:84. doi: 10.1186/1752-0509-2-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Zhou H., Saito S., Piao G., Liu Z.P., Wang J., Horimoto K., Chen L. Network screening of Goto-Kakizaki rat liver microarray data during diabetic progression. BMC Syst. Biol. 2011;5(Suppl. 1):S16. doi: 10.1186/1752-0509-5-S1-S16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Piao G., Saito S., Sun Y., Liu Z.P., Wang Y., Han X., Wu J., Zhou H., Chen L., Horimoto K. A computational procedure for identifying master regulator candidates: a case study on diabetes progression in Goto-Kakizaki rats. BMC Syst. Biol. 2012;6(Suppl. 1):S2. doi: 10.1186/1752-0509-6-S1-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Stelling J., Klamt S., Bettenbrock K., Schuster S., Gilles E.D. Metabolic network structure determines key aspects of functionality and regulation. Nature. 2002;420(6912):190–193. doi: 10.1038/nature01166. [DOI] [PubMed] [Google Scholar]
- 148.Barkai N., Leibler S. Robustness in simple biochemical networks. Nature. 1997;387(6636):913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 149.Nakajima N., Tamura T., Yamanishi Y., Horimoto K., Akutsu T. Network completion using dynamic programming and least-squares fitting. 2012. [DOI] [PMC free article] [PubMed]
- 150.Saito S., Zhou X., Bae T., Kim S., Horimoto K. Identification of master regulator candidates in conjunction with network screening and inference. Int. J. Data Min. Bioinform. 2013;8(3):366–380. doi: 10.1504/ijdmb.2013.056077. [DOI] [PubMed] [Google Scholar]
- 151.de Matos Simoes R., Emmert-Streib F. Bagging statistical network inference from large-scale gene expression data. PLoS One. 2012;7(3):e33624. doi: 10.1371/journal.pone.0033624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Huynh-Thu V.A., Irrthum A., Wehenkel L., Geurts P. Inferring regulatory networks from expression data using tree-based methods. PLoS One. 2010;5(9):e12776. doi: 10.1371/journal.pone.0012776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Wang R.S., Wang Y., Zhang X.S., Chen L. Inferring transcriptional regulatory networks from high-throughput data. Bioinformatics. 2007;23(22):3056–3064. doi: 10.1093/bioinformatics/btm465. [DOI] [PubMed] [Google Scholar]
- 154.Bonneau R., Reiss D.J., Shannon P., Facciotti M., Hood L., Baliga N.S., Thorsson V. The Inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. Genome Biol. 2006;7(5):R36. doi: 10.1186/gb-2006-7-5-r36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Küffner R., Petri T., Tavakkolkhah P., Windhager L., Zimmer R. Inferring gene regulatory networks by ANOVA. Bioinformatics. 2012;28(10):1376–1382. doi: 10.1093/bioinformatics/bts143. [DOI] [PubMed] [Google Scholar]
- 156.Charbonnier C., Chiquet J., Ambroise C. Weighted-LASSO for structured network inference from time course data. Stat. Appl. Genet. Mol. Biol. 2010;9:15. doi: 10.2202/1544-6115.1519. [DOI] [PubMed] [Google Scholar]
- 157.Arellano G., Argil J., Azpeitia E., Benítez M., Carrillo M., Góngora P., Rosenblueth D.A., Alvarez-Buylla E.R. “Antelope”: a hybrid-logic model checker for branching-time Boolean GRN analysis. BMC Bioinformatics. 2011;12:490. doi: 10.1186/1471-2105-12-490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Müssel C., Hopfensitz M., Kestler H.A. BoolNet--an R package for generation, reconstruction and analysis of Boolean networks. Bioinformatics. 2010;26(10):1378–1380. doi: 10.1093/bioinformatics/btq124. [DOI] [PubMed] [Google Scholar]
- 159.Bock M., Scharp T., Talnikar C., Klipp E. BooleSim: an interactive Boolean network simulator. Bioinformatics. 2014;30(1):131–132. doi: 10.1093/bioinformatics/btt568. [DOI] [PubMed] [Google Scholar]
- 160.Handorf T., Klipp E. Modeling mechanistic biological networks: an advanced Boolean approach. Bioinformatics. 2012;28(4):557–563. doi: 10.1093/bioinformatics/btr697. [DOI] [PubMed] [Google Scholar]
- 161.Karlebach G., Shamir R. Constructing logical models of gene regulatory networks by integrating transcription factor-DNA interactions with expression data: an entropy-based approach. J. Comput. Biol. 2012;19(1):30–41. doi: 10.1089/cmb.2011.0100. [DOI] [PubMed] [Google Scholar]
- 162.Lèbre S., Becq J., Devaux F., Stumpf M.P., Lelandais G. Statistical inference of the time-varying structure of gene-regulation networks. BMC Syst. Biol. 2010;4:130. doi: 10.1186/1752-0509-4-130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Wilczyński B., Dojer N. BNFinder: exact and efficient method for learning Bayesian networks. Bioinformatics. 2009;25(2):286–287. doi: 10.1093/bioinformatics/btn505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Scutari M. Learning Bayesian Networks with the bnlearn R Package. J. Stat. Softw. 2010;35(3):1–22. [Google Scholar]
- 165.Lebre S. Inferring dynamic genetic networks with low order independencies. 2009. [DOI] [PubMed]
- 166.Vinh N.X., Chetty M., Coppel R., Wangikar P.P. GlobalMIT: learning globally optimal dynamic bayesian network with the mutual information test criterion. Bioinformatics. 2011;27(19):2765–2766. doi: 10.1093/bioinformatics/btr457. [DOI] [PubMed] [Google Scholar]
- 167.Li Z., Shaw S.M., Yedwabnick M.J., Chan C. Using a state-space model with hidden variables to infer transcription factor activities. Bioinformatics. 2006;22(6):747–754. doi: 10.1093/bioinformatics/btk034. [DOI] [PubMed] [Google Scholar]
- 168.Soetaert K., Petzoldt T., Setzer R.W. Solving differential equations in R: package deSolve. J. Stat. Softw. 2010;33(9):1–25. [Google Scholar]
- 169.Wahde M., Hertz J. Modeling genetic regulatory dynamics in neural development. J. Comput. Biol. 2001;8(4):429–442. doi: 10.1089/106652701752236223. [DOI] [PubMed] [Google Scholar]
- 170.Isci S., Dogan H., Ozturk C., Otu H.H. Bayesian network prior: network analysis of biological data using external knowledge. Bioinformatics. 2014;30(6):860–867. doi: 10.1093/bioinformatics/btt643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Greenfield A., Hafemeister C., Bonneau R. Robust data-driven incorporation of prior knowledge into the inference of dynamic regulatory networks. Bioinformatics. 2013;29(8):1060–1067. doi: 10.1093/bioinformatics/btt099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Hill S.M., Lu Y., Molina J., Heiser L.M., Spellman P.T., Speed T.P., Gray J.W., Mills G.B., Mukherjee S. Bayesian inference of signaling network topology in a cancer cell line. Bioinformatics. 2012;28(21):2804–2810. doi: 10.1093/bioinformatics/bts514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Wang Z., Xu W., San Lucas F.A., Liu Y. Incorporating prior knowledge into Gene Network Study. Bioinformatics. 2013;29(20):2633–2640. doi: 10.1093/bioinformatics/btt443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Wahde M., Hertz J. Coarse-grained reverse engineering of genetic regulatory networks. Biosystems. 2000;55(1-3):129–136. doi: 10.1016/s0303-2647(99)00090-8. [DOI] [PubMed] [Google Scholar]
- 175.Matsuno H., Doi A., Nagasaki M., Miyano S. Hybrid Petri net representation of gene regulatory network. Pac. Symp. Biocomput. 2000;5:341–352. doi: 10.1142/9789814447331_0032. [DOI] [PubMed] [Google Scholar]
- 176.Soinov L.A., Krestyaninova M.A., Brazma A. Towards reconstruction of gene networks from expression data by supervised learning. Genome Biol. 2003;4(1):R6. doi: 10.1186/gb-2003-4-1-r6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Mordelet F., Vert J.P. SIRENE: supervised inference of regulatory networks. Bioinformatics. 2008;24(16):i76–i82. doi: 10.1093/bioinformatics/btn273. [DOI] [PubMed] [Google Scholar]
- 178.Haury A.C., Mordelet F., Vera-Licona P., Vert J.P. TIGRESS: Trustful Inference of Gene REgulation using Stability Selection. BMC Syst. Biol. 2012;6:145. doi: 10.1186/1752-0509-6-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Wyrick J.J., Young R.A. Deciphering gene expression regulatory networks. Curr. Opin. Genet. Dev. 2002;12(2):130–136. doi: 10.1016/s0959-437x(02)00277-0. [DOI] [PubMed] [Google Scholar]
- 180.Wang Z., Gerstein M., Snyder M. RNA-Seq: a revolutionary tool for transcriptomics. Nat. Rev. Genet. 2009;10(1):57–63. doi: 10.1038/nrg2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Bar-Joseph Z., Gitter A., Simon I. Studying and modelling dynamic biological processes using time-series gene expression data. Nat. Rev. Genet. 2012;13(8):552–564. doi: 10.1038/nrg3244. [DOI] [PubMed] [Google Scholar]
- 182.Chen W., Lin H., Feng P.M., Ding C., Zuo Y.C., Chou K.C. iNuc-PhysChem: a sequence-based predictor for identifying nucleosomes via physicochemical properties. PLoS One. 2012;7(10):e47843. doi: 10.1371/journal.pone.0047843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Wang M., Yang J., Xu Z.J., Chou K.C. SLLE for predicting membrane protein types. J. Theor. Biol. 2005;232(1):7–15. doi: 10.1016/j.jtbi.2004.07.023. [DOI] [PubMed] [Google Scholar]
- 184.Feng K.Y., Cai Y.D., Chou K.C. Boosting classifier for predicting protein domain structural class. Biochem. Biophys. Res. Commun. 2005;334(1):213–217. doi: 10.1016/j.bbrc.2005.06.075. [DOI] [PubMed] [Google Scholar]
- 185.Feng P.M., Chen W., Lin H., Chou K.C. iHSP-PseRAAAC: Identifying the heat shock protein families using pseudo reduced amino acid alphabet composition. Anal. Biochem. 2013;442(1):118–125. doi: 10.1016/j.ab.2013.05.024. [DOI] [PubMed] [Google Scholar]
- 186.Chen W., Feng P.M., Lin H., Chou K.C. iRSpot-PseDNC: identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Res. 2013;41(6):e68. doi: 10.1093/nar/gks1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Lin W.Z., Fang J.A., Xiao X., Chou K.C. iDNA-Prot: identification of DNA binding proteins using random forest with grey model. PLoS One. 2011;6(9):e24756. doi: 10.1371/journal.pone.0024756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Xu Y., Ding J., Wu L.Y., Chou K.C. iSNO-PseAAC: predict cysteine S-nitrosylation sites in proteins by incorporating position specific amino acid propensity into pseudo amino acid composition. PLoS One. 2013;8(2):e55844. doi: 10.1371/journal.pone.0055844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Cai Y.D., Chou K.C. Predicting subcellular localization of proteins in a hybridization space. Bioinformatics. 2004;20(7):1151–1156. doi: 10.1093/bioinformatics/bth054. [DOI] [PubMed] [Google Scholar]
- 190.Shen H.B., Chou K.C. A top-down approach to enhance the power of predicting human protein subcellular localization: Hum-mPLoc 2.0. Anal. Biochem. 2009;394(2):269–274. doi: 10.1016/j.ab.2009.07.046. [DOI] [PubMed] [Google Scholar]
- 191.Xiao X., Wang P., Chou K.C. GPCR-2L: predicting G protein-coupled receptors and their types by hybridizing two different modes of pseudo amino acid compositions. Mol. Biosyst. 2011;7(3):911–919. doi: 10.1039/c0mb00170h. [DOI] [PubMed] [Google Scholar]
- 192.Xiao X., Min J.L., Wang P., Chou K.C. iCDI-PseFpt: identify the channel-drug interaction in cellular networking with PseAAC and molecular fingerprints. J. Theor. Biol. 2013;337:71–79. doi: 10.1016/j.jtbi.2013.08.013. [DOI] [PubMed] [Google Scholar]
- 193.Wu Z.C., Xiao X., Chou K.C. iLoc-Plant: a multi-label classifier for predicting the subcellular localization of plant proteins with both single and multiple sites. Mol. Biosyst. 2011;7(12):3287–3297. doi: 10.1039/c1mb05232b. [DOI] [PubMed] [Google Scholar]
- 194.Chou K.C. Prediction of protein cellular attributes using pseudo-amino acid composition. Proteins. 2001;43(3):246–255. doi: 10.1002/prot.1035. [DOI] [PubMed] [Google Scholar]
- 195.Chou K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics. 2005;21(1):10–19. doi: 10.1093/bioinformatics/bth466. [DOI] [PubMed] [Google Scholar]
- 196.Shen H.B., Chou K.C. PseAAC: a flexible web server for generating various kinds of protein pseudo amino acid composition. Anal. Biochem. 2008;373(2):386–388. doi: 10.1016/j.ab.2007.10.012. [DOI] [PubMed] [Google Scholar]
- 197.Qiu W.R., Xiao X., Chou K.C. iRSpot-TNCPseAAC: identify recombination spots with trinucleotide composition and pseudo amino acid components. Int. J. Mol. Sci. 2014;15(2):1746–1766. doi: 10.3390/ijms15021746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Fang Y., Guo Y., Feng Y., Li M. Predicting DNA-binding proteins: approached from Chou’s pseudo amino acid composition and other specific sequence features. Amino Acids. 2008;34(1):103–109. doi: 10.1007/s00726-007-0568-2. [DOI] [PubMed] [Google Scholar]
- 199.Zhao X.W., Li X.T., Ma Z.Q., Yin M.H. Identify DNA-binding proteins with optimal Chou’s amino acid composition. Protein Pept. Lett. 2012;19(4):398–405. doi: 10.2174/092986612799789404. [DOI] [PubMed] [Google Scholar]
- 200.Cheng C., Yan K.K., Hwang W., Qian J., Bhardwaj N., Rozowsky J., Lu Z.J., Niu W., Alves P., Kato M., Snyder M., Gerstein M. Construction and analysis of an integrated regulatory network derived from high-throughput sequencing data. PLOS Comput. Biol. 2011;7(11):e1002190. doi: 10.1371/journal.pcbi.1002190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Mendenhall E.M., Williamson K.E., Reyon D., Zou J.Y., Ram O., Joung J.K., Bernstein B.E. Locus-specific editing of histone modifications at endogenous enhancers. Nat. Biotechnol. 2013;31(12):1133–1136. doi: 10.1038/nbt.2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Gerstein M.B., Kundaje A., Hariharan M., Landt S.G., Yan K.K., Cheng C., Mu X.J., Khurana E., Rozowsky J., Alexander R., Min R., Alves P., Abyzov A., Addleman N., Bhardwaj N., Boyle A.P., Cayting P., Charos A., Chen D.Z., Cheng Y., Clarke D., Eastman C., Euskirchen G., Frietze S., Fu Y., Gertz J., Grubert F., Harmanci A., Jain P., Kasowski M., Lacroute P., Leng J., Lian J., Monahan H., O’Geen H., Ouyang Z., Partridge E.C., Patacsil D., Pauli F., Raha D., Ramirez L., Reddy T.E., Reed B., Shi M., Slifer T., Wang J., Wu L., Yang X., Yip K.Y., Zilberman-Schapira G., Batzoglou S., Sidow A., Farnham P.J., Myers R.M., Weissman S.M., Snyder M. Architecture of the human regulatory network derived from ENCODE data. Nature. 2012;489(7414):91–100. doi: 10.1038/nature11245. [DOI] [PMC free article] [PubMed] [Google Scholar]