The human sex ratio from conception to birth

Significance

The human sex ratio has long interested cell biologists, developmental biologists, demographers, epidemiologists, evolutionary biologists, gynecologists, and statisticians. Nonetheless, the trajectory of the human sex ratio from conception to birth has been poorly characterized. We present the most comprehensive analysis of this trajectory ever done. Our dataset is the largest ever assembled to estimate the sex ratio at conception and is the first, to our knowledge, to include data from 3- to- 6-d-old embryos, induced abortions, chorionic villus sampling, amniocentesis, and fetal deaths and live births. Our results indicate that the sex ratio at conception is unbiased, the proportion of males increases during the first trimester, and total female mortality during pregnancy exceeds total male mortality; these are fundamental insights into early human development.

Abstract

We describe the trajectory of the human sex ratio from conception to birth by analyzing data from (i) 3- to 6-d-old embryos, (ii) induced abortions, (iii) chorionic villus sampling, (iv) amniocentesis, and (v) fetal deaths and live births. Our dataset is the most comprehensive and largest ever assembled to estimate the sex ratio at conception and the sex ratio trajectory and is the first, to our knowledge, to include all of these types of data. Our estimate of the sex ratio at conception is 0.5 (proportion male), which contradicts the common claim that the sex ratio at conception is male-biased. The sex ratio among abnormal embryos is male-biased, and the sex ratio among normal embryos is female-biased. These biases are associated with the abnormal/normal state of the sex chromosomes and of chromosomes 15 and 17. The sex ratio may decrease in the first week or so after conception (due to excess male mortality); it then increases for at least 10–15 wk (due to excess female mortality), levels off after ∼20 wk, and declines slowly from 28 to 35 wk (due to excess male mortality). Total female mortality during pregnancy exceeds total male mortality. The unbiased sex ratio at conception, the increase in the sex ratio during the first trimester, and total mortality during pregnancy being greater for females are fundamental insights into early human development.

The sex ratio at conception in humans is unknown, despite hundreds of years of speculation and research. Investigations of the sex ratio date back at least as far as Graunt (1) who described a net excess of male births (2). By the late 1800s, it was clear that more males than females die during later pregnancy (3). Beyond these facts, the demographic and genetic dynamics of the sex ratio from conception to birth are poorly resolved.

The claim that the conception or primary sex ratio (PSR) is more male-biased than the birth sex ratio appears often in textbooks (4, 5) and in the scientific literature (e.g., refs. 6–11), usually with little or no description of evidence. Estimates of the PSR in these studies are typically 0.56 (proportion males) or greater. Many fewer researchers have claimed that the PSR is unbiased or slightly male-biased (12–16). A handful of researchers has claimed or implied that the PSR is female-biased (17–19) or claimed that the PSR cannot be estimated due to lack of appropriate data and/or methodological problems (20–22).

Previous estimates of the PSR have no meaningful basis in data from the time of conception (or within at least a month of it). At best, the PSR has been estimated via backward extrapolation from data on induced or spontaneous abortions, fetal deaths, or live births; most of the non–live-birth data stems from the second or third trimester of pregnancy. In addition, even if one ignores the fallibility of extrapolation, biased estimates of the PSR based on spontaneous abortions and fetal deaths have usually been regarded as arising from unbiased samples of a population of embryos or fetuses having a biased PSR. The alternative possibility that the estimates arise from biased samples of a population having an unbiased PSR has received little attention. The most likely source of bias is the differential tendency of the two sexes to die during pregnancy, which has long been recognized (see above), although its implications for the estimation of the PSR have usually been ignored.

Here, we estimate the trajectory of the sex ratio from conception to birth by analyzing 3- to 6-d-old embryos derived from assisted reproductive technology (ART) procedures, induced abortions, fetuses that have undergone chorionic villus sampling (CVS) or amniocentesis, and US census records of fetal deaths and live births. Our assemblage of data is the most comprehensive and largest ever assembled to estimate the PSR and the sex ratio trajectory and is the first, to our knowledge, to include all of these types of data.

Materials and Methods

We measured gestation time as elapsed time since conception (syngamy) or conception age (CA). CA estimates were inferred from the date of the last menstrual period (LMP) or the clinical estimate (based on an ultrasound scan or the assessment of the birth attendant) by subtracting 2 wk from the original estimate. This approximation captures the central tendency of the distribution of days since the date of conception; the modal time is 15 d, and more than 50% of conceptions are estimated to occur between 12 and 16 d after LMP (23).

We defined the cohort sex ratio (CSR) at a given CA as the sex ratio of the cohort of embryos (fetuses) inside mothers. CSR is directly calculated from amniocentesis, CVS, and induced-abortion data and inferred from ART and fetal-death and live-birth data. By definition, the PSR is equal to the CSR at conception. We further defined the abnormal CSR and the normal CSR as the cohort sex ratio of embryos (fetuses) that were karyotypically abnormal and karyotypically normal, respectively.

We analyzed five kinds of data.

Three- to 6-d-Old Embryos.

We used FISH or array comparative genomic hybridization (aCGH) to karyotype embryos. See ref. 24 for an overview of FISH and refs. 25 and 26 for reviews of its use for karyotypic assessment. FISH may overestimate the incidence of aneuploidy (27). There is no indication that this would influence sex ratio estimates. Chromosomes X, Y, 8, 9, 13, 14, 15, 16, 17, 18, 20, 21, and 22 were scored. The number of chromosomes scored for a given embryo ranged from 2 (X and Y) to 13. The FISH probes are shown in the SI Text. Embryos analyzed by FISH were at least 3 d old and were at the blastomere stage; almost all were 3 d old. See refs. 28 and 29 for an overview of aCGH. All chromosomes were scored. Embryos analyzed by aCGH were between 3 and 6 d old; ∼30% were 3 d old (blastomere stage), with most of the remainder being 5 d old (blastocyst stage). FISH and aCGH produce functionally equivalent screens of karyotypic abnormality (30); further cross-validation is needed.

Most embryos had one cell analyzed; results for embryos with multiple cells analyzed are aggregated over the cells. Embryos analyzed by FISH included all submitted for analysis, even if developmentally arrested by day 3. Embryos analyzed by aCGH included only those that were not arrested at the time of sampling (days 3–6).

An embryo was scored as a male if it had a Y chromosome in at least one cell and as a female if it had no Y chromosome and at least two X chromosomes. An embryo was scored as normal if cells were identically XX or XY and had exactly two copies of each autosome scored. Other sexable karyotypes were scored as abnormal. There were 139,704 sexable embryos (94,535 FISH and 45,169 aCGH).

Induced Abortions.

To our knowledge, there are only 41 studies of the sex of fetuses from induced abortion (SI Text); these data have never before been assembled and analyzed. It is almost certain that all fetuses were naturally conceived (most analyses were published before 1978, when ART was introduced) and virtually all were sampled randomly with respect to fetal health and sex. The methods used to assign sex were histology (1 study), karyotype (20 studies), morphology (3 studies), and sex chromatin (17 studies). Thirty-nine studies specify trimester for each fetus; of these, 12 studies provide data allowing a CSR estimate for trimester 1 and for trimester 2. Twenty-four studies specify gestational age in weeks.

CVS.

The procedures used to process and assess each sample are shown in SI Text. The use of CVS is reviewed in refs. 31 and 32.

The CVS data provided estimates of the CSR from 6 to 25 wk CA. In our analysis of the relationship between CSR and CA, we used data from 6 to 12 wk (97% of the sample) to avoid possible overrepresentation of troubled pregnancies. In almost all cases, CA estimates were based on the LMP.

Amniocentesis.

The procedures used to process and assess each sample were identical to those for CVS (SI Text). The use of amniocentesis is reviewed in refs. 31 and 32.

The amniocentesis data provided estimates of the CSR from 10 to 39 wk CA. In our analysis of the relationship between CSR and CA, we used data from 10 to 20 wk (96% of the sample) to avoid possible overrepresentation of troubled pregnancies and because the cohort of fetuses is increasingly influenced by birth after 24 wk (so that mortality is not the sole influence on the CSR). In almost all cases, CA estimates were based on the LMP.

Our ART, CVS, and amniocentesis data were based on similar criteria for scoring karyotypes and therefore provide comparable insights into the CSR from the beginning of pregnancy to the end.

Fetal Deaths and Live Births.

We created a dataset containing sex and CA for all US fetal deaths and live births for 1995–2004 using data from www.cdc.gov/nchs/data_access/Vitalstatsonline.htm. Reporting is poor before 18 wk CA, and it is nearly complete only after 25 wk (33). We included CA estimates derived from the LMP and from the clinical estimate. We omitted records with imputed sex or gestational age (SI Text).

Statistical Approach.

We estimated sex ratios using mixed-effect analyses (34) or fixed-effect analyses on the logit scale. All model comparisons involved nested models. We provide two ways of assessing a given model comparison. First, we present the absolute difference (ΔAIC) between the model with lowest Akaike information criterion (AIC) value and the other model(s). A ΔAIC value of 2 or more is often taken to indicate that two models differ in their level of support (35, pp. 70–71). Second, we present the Akaike weight for each model. The evidence ratio (ER) for a pair of models is the ratio of their weights (larger/smaller), which is equivalent to the ratio of their model likelihoods. An ER between 100 and 1,000 denotes strong support for the model with the larger weight (36). [An Akaike weight is also controversially interpreted as an approximate Bayesian posterior probability that the model is true given the assumption that the true model is contained in the set of models considered (37–39).] One can also assume that the simplest model among those considered is a true null hypothesis and estimate the probability that a ΔAIC value could have arisen via random sampling (40–43). Critical values of ΔAIC depend on the difference, k, in the number of model parameters between the null and alternative hypotheses (43). For example, for k = 5 (all model comparisons in Tables 1–4 and Tables S3–S5), critical values for ΔAIC are 1.07 (α = 0.05), 5.09 (α = 0.01), 6.75 (α = 0.005), and 10.52 (α = 0.001). Model comparisons here differ in k, but the critical value of ΔAIC for α = 0.05 is at most 1.84 and for α = 0.01 it is at most 5.34. In all tables, N denotes sample size.

Table 1.

Mixed-effect analyses of the association between the karyotypic state of all ART embryos and the CSR

Scoring	Embryos	CSR	N	ΔAIC	Akaike weight
Any	All	0.502	139,704	22.870	<0.001
	Abnormal	0.508	84,881	0	>0.999
	Normal	0.493	54,823

Scoring denotes the chromosomes used to assess karyotypic state. Any denotes assessment based on any number of chromosomes scored (between 2 and 23).

Table 4.

Mixed-effect analyses of the association between MA and the CSR, as estimated from ART embryos analyzed by FISH

Model	Fitted model	ΔAIC	Akaike weight
I	Logit(CSR) = 0.012	0	0.971
I + MA	Logit(CSR) = -0.075 + 0.002MA	7.043	0.029

I denotes intercept. n = 92,037.

Results

Analysis of ART Data.

We assigned random effects to women and to procedures within women and treated karyotypic state as a factor.

We first estimated the PSR. For all embryos (Any) in Table 1, the CSR estimate of 0.502 (95% CI: 0.499–0.505) suggests that the PSR is unbiased or slightly male-biased. This estimate derives from the largest amount of data ever assembled from a known time close to conception; an estimate closer to conception is likely impossible.

The model stratified with karyotypic state (Abnormal and Normal) had substantially more support than a model without stratification (Any); the ER for the stratified and unstratified models is greater than 1,000 (≥0.999/<0.001). The abnormal CSR estimate is 0.508 (95% CI: 0.505–0.512), and the normal CSR estimate is 0.493 (95% CI: 0.488–0.497). These estimates suggest that very early development is more hazardous for males than for females. Nature’s filter against abnormalities such as aneuploidy must be similar to our filter because the frequency of such abnormalities among newborns is 1% at most. This frequency implies that most abnormalities cause embryonic death [although embryos may self-correct (44)]; the timing of mortality may be such that the CSR is temporarily female-biased soon after conception.

We assessed if CSR estimates depended on whether one cell or more than one cell was scored (Table 2) because it is possible that mosaic embryos were falsely scored as normal because abnormal cells were not scored; only FISH data were analyzed (few aCGH analyses involved more than one cell). Most had one cell (90,580 embryos) or two cells (2,567 embryos) scored. The CSR estimates based on one cell qualitatively match those based on more than one cell. When one cell was scored, the stratified model had greater support. When multiple cells were scored, the nonstratified and stratified models had similar support; this is likely due to a small sample size. These results suggest that the false scoring of abnormal embryos as normal has little influence on our observation that the normal CSR is female-biased (Table 1).

Table 2.

Mixed-effect analyses of the association between the karyotypic state of ART embryos analyzed by FISH and the CSR when one cell was scored and when more than one cell was scored

Number of cells scored	Embryos	CSR	N	ΔAIC	Akaike weight
1	All	0.503	90,580	27.107	<0.001
	Abnormal	0.511	56,354	0	>0.999
	Normal	0.491	34,226
>1	All	0.502	3,955	0	0.731
	Abnormal	0.513	3,170	2.374	0.269
	Normal	0.458	785

We assessed the association of each target chromosome and the CSR in two ways. In the first, the embryo could be normal or abnormal for any other chromosome (Table 3); FISH and aCGH data are presented separately. Estimates of the CSR for FISH and aCGH based on any chromosome are 0.503 (95% CI: 0.500–0.507, n = 94,535) and 0.500 (95% CI: 0.495–0.505, n = 45,169), respectively. The CSR estimate “all” is ∼0.500 for each target chromosome assayed by FISH. This similarity suggests that the embryos chosen for analysis of a given target chromosome were chosen randomly from the assemblage. (There is only one CSR estimate “all” for the aCGH analyses because the same embryos provided all of the target chromosome estimates.)

Table 3.

Mixed-effect analyses of the association between the overall state of the embryo (Any) or the state of individual chromosomes and the CSR

Chromosome	Embryos	FISH				aCGH
		CSR	N	ΔAIC	Akaike weight	CSR	N	ΔAIC	Akaike weight
Any	All	0.503	94,535	31.275	<0.001	0.500	45,169	0	0.953
	Abnormal	0.511	59,524	0	>0.999	0.502	24,357	6.004	0.047
	Normal	0.490	35,011			0.498	19,812
XY	All	0.503	94,535	533.156	<0.001	0.500	45,169	850.311	<0.001
	Abnormal	0.589	16,282	0	>0.999	0.840	1,874	0	>0.999
	Normal	0.486	78,253			0.486	43,295
1	All	—	—	—	—	0.500	45,169	0	0.942
	Abnormal	—	—	—	—	0.481	2,972	5.571	0.058
	Normal	—	—	—	—	0.502	42,197
2	All	—	—	—	—	0.500	45,169	0	0.784
	Abnormal	—	—	—	—	0.478	2,856	2.579	0.216
	Normal	—	—	—	—	0.502	42,313
3	All	—	—	—	—	0.500	45,169	0	0.982
	Abnormal	—	—	—	—	0.486	2,255	7.898	0.018
	Normal	—	—	—	—	0.501	42,914
4	All	—	—	—	—	0.500	45,169	0	0.948
	Abnormal	—	—	—	—	0.484	2,459	5.704	0.052
	Normal	—	—	—	—	0.501	42,710
5	All	—	—	—	—	0.500	45,169	1.460	0.325
	Abnormal	—	—	—	—	0.468	2,547	0	0.675
	Normal	—	—	—	—	0.502	42,622
6	All	—	—	—	—	0.500	45,169	0	0.959
	Abnormal	—	—	—	—	0.483	2,365	6.300	0.041
	Normal	—	—	—	—	0.501	42,804
7	All	—	—	—	—	0.500	45169	4.400	0.100
	Abnormal	—	—	—	—	0.466	2,637	0	0.900
	Normal	—	—	—	—	0.502	42,532
8	All	0.505	22,113	0	0.984	0.500	45,169	0	0.983
	Abnormal	0.503	4,119	8.274	0.016	0.488	2,638	8.102	0.017
	Normal	0.506	17,994			0.501	42,531
9	All	0.524	3,678	0	0.947	0.500	45,169	0	0.845
	Abnormal	0.516	655	5.780	0.053	0.478	3,010	3.394	0.155
	Normal	0.526	3,023			0.502	42,159
10	All	—	—	—	—	0.500	45,169	0	0.951
	Abnormal	—	—	—	—	0.481	2,683	5.930	0.049
	Normal	—	—	—	—	0.501	42,486
11	All	—	—	—	—	0.500	45,169	0	0.962
	Abnormal	—	—	—	—	0.484	2,748	6.438	0.038
	Normal	—	—	—	—	0.501	42,421
12	All	—	—	—	—	0.500	45,169	0	0.978
	Abnormal	—	—	—	—	0.486	2,360	7.583	0.022
	Normal	—	—	—	—	0.501	42,809
13	All	0.503	89,263	0	0.976	0.500	45,169	0	0.936
	Abnormal	0.505	23,598	12.075	0.024	0.482	3,133	5.361	0.064
	Normal	0.503	65,665			0.502	42,036
14	All	0.503	18,378	0	0.992	0.500	45,169	0	0.936
	Abnormal	0.500	4,727	9.542	0.008	0.485	3,078	5.366	0.064
	Normal	0.504	13,651			0.501	42,091
15	All	0.500	78,437	42.555	<0.001	0.500	45,169	0	0.963
	Abnormal	0.518	24,120	0	>0.999	0.490	4,209	6.512	0.037
	Normal	0.492	54,317			0.501	40,960
16	All	0.504	79,589	0	0.881	0.500	45,169	0	0.990
	Abnormal	0.508	24,097	7.213	0.119	0.497	5,187	9.164	0.010
	Normal	0.502	55,492			0.501	39,982
17	All	0.502	76,327	9.821	0.007	0.500	45,169	0	0.889
	Abnormal	0.517	18,489	0	0.993	0.480	2,755	4.154	0.111
	Normal	0.498	57,838			0.502	42,414
18	All	0.503	88,607	0	0.796	0.500	45,169	0	0.927
	Abnormal	0.510	23,587	2.717	0.204	0.481	3,168	5.080	0.073
	Normal	0.500	65,020			0.502	42,001
19	All	—	—	—	—	0.500	45,169	0	0.995
	Abnormal	—	—	—	—	0.492	4,499	10.459	0.005
	Normal	—	—	—	—	0.501	40,670
20	All	0.502	17,866	0	0.969	0.500	45,169	0	0.975
	Abnormal	0.497	4,896	6.910	0.031	0.486	3,213	7.332	0.025
	Normal	0.504	12,970			0.501	41,956
21	All	0.503	89,669	0	0.973	0.500	45,169	0	0.987
	Abnormal	0.510	25,434	7.151	0.027	0.496	4,362	8.624	0.013
	Normal	0.500	64,235			0.501	40,807
22	All	0.504	80,548	0	0.992	0.500	45,169	1.441	0.327
	Abnormal	0.503	25,218	9.567	0.008	0.480	5,098	0	0.673
	Normal	0.504	55,330			0.503	40,071

As noted, the FISH sample included arrested and nonarrested embryos and the aCGH sample contained only nonarrested embryos (most had undergone blastocyst formation). Comparison of the two samples provides insight into the early association between chromosome abnormality and the attainment of a critical developmental milestone.

For the FISH sample, there was greater support for the nonstratified model for all but three of the chromosomes, which suggests that there is no sex bias in the expression of abnormality for most chromosomes. For XY, 15, and 17, there was greater support for the stratified model. The ER is ∼140 for chromosome 17 and is >1,000 for XY and for chromosome 15. Thus, there is strong to very strong support for a sex bias in the abnormality of these chromosomes. For these cases, the abnormal CSR estimate is male-biased and the normal CSR estimate is female-biased. Note that the abnormal CSR estimate (0.589) for the embryos with abnormal sex chromosomes (XY) is biased upward because XO embryos are not included (Discussion).

For the aCGH sample, there was greater support for the nonstratified model for all but 4 of the 23 chromosomes, which suggests that there is no sex bias in the expression of abnormality for most chromosomes. For chromosomes 5 and 22, there was marginally greater support for the stratified model. The ER is ∼2 for both. For chromosomes XY and 7, there is moderate to very strong support for a sex bias of abnormality. The ER is >1,000 for XY and is ∼9 for chromosome 7. As noted above, the abnormal CSR estimate (0.840) for the embryos with abnormal sex chromosomes is biased upward. The abnormal CSR estimate for chromosome 7 is female-biased.

The male bias among FISH embryos abnormal for chromosome 15 (0.518) and for 17 (0.517) and the female bias among abnormal aCGH embryos (15: 0.490; 17: 0.480) are consistent with excess death of male embryos before the time of blastocyst formation. We lack data on chromosome 7 among FISH embryos, but the support for the stratified model among aCGH embryos suggests that this chromosome may also play an important role in blastocyst formation.

In the second way we assessed the association of each target chromosome and the CSR, all scored chromosomes were normal except the target chromosome, which could be normal or abnormal (SI Text). This analysis allowed us to assess whether the association between the state of a target chromosome and the CSR was a consequence of the target chromosome by itself or of an ensemble of chromosomes (in which only the target chromosome has a known state). There are relatively few embryos that are abnormal for just one chromosome. Only the analysis for XY suggests substantially greater support for the stratified model. For chromosome 15, the abnormal CSR estimate is female-biased compared with the normal CSR estimate, which is reversed compared with when other chromosomes could be normal or abnormal; reasons for this other than reduced sample size are unclear. For chromosome 17, the abnormal CSR estimate is male-biased compared with the normal CSF estimate, which is the same as when other chromosomes were normal or abnormal.

Taken together, these results indicate that abnormalities occur more frequently in male embryos than in female embryos and suggest that the female bias of the normal CSR estimate (0.493; Table 1) is associated with abnormality of just a few autosomes. However, the role of each of these autosomes by itself is ambiguous. See Discussion for the possible cause of the association of chromosome 15 and the abnormal CSR. The decrease in the abnormal CSR estimate pre- and postarrest (Table 3; Any: 0.511 vs. 0.502) is consistent with embryonic mortality before blastocyst formation being male-biased. The normal CSR estimate is female-biased, which implies that the CSR may temporarily become female-biased due to the death of karyotypically abnormal embryos.

There were differences among chromosomes in frequency of abnormalities. The frequency of karyotypic abnormality is greater in the FISH sample compared with the aCGH sample, the likely reason being that most abnormalities are incompatible with continuing development. The average frequency of abnormality for FISH is 25.39% (low: 17.22% for XY, high: 31.31% for chromosome 22), and for CGH, it is 6.94% (low: 4.15% for XY, high: 11.48% for chromosome 16). There is significant heterogeneity among chromosomes for frequency of abnormality (FISH: χ² = 7,679.748, 11 df, P « 0.001; CGH: χ² = 6,193.179, 22 df, P « 0.001). (There is also significant heterogeneity when the sex chromosomes are omitted; as noted, their frequency of abnormality is underestimated.) These statistical tests have the probably incorrect assumption that abnormality for a chromosome occurs independently of abnormality for other chromosomes.

Additional analyses of the association between karyotype and the CSR are shown in SI Text (blastomere aCGH data vs. blastocyst aCGH data and blastomere FISH data vs. blastocyst aCGH data).

We analyzed maternal age (MA) as a metric predictor of the CSR (Table 4). The model without age has strong support (ER ∼ 33), which suggests that there is no association between the CSR and maternal age; most studies indicate that maternal age has little or no influence on the sex ratio at birth (45–46).

Analysis of limited data (n = 819) suggested that there is no association between mother’s race and the CSR. We compared an overall model, a model stratified between black and nonblack mothers, and a model stratified between white and nonwhite mothers. The overall model had substantially greater support than either stratified model.

Analysis of Induced-Abortion Data.

We assessed the effect of trimester on the CSR by using a mixed-effect analysis in which random effects were assigned to each study (Table 5); we analyzed only the data from the 12 studies that each provided a first and second trimester estimate. We did not distinguish between diagnostic methods or between abnormal and normal sex ratios because karyotypic information for aborted fetuses is limited. The stratified model had greater support (ER ∼ 10.6). The associated estimates suggest that the CSR increases with trimester (first: 0.511 vs. second: 0.559). This increase is consistent with greater net female mortality during the first and second trimesters (see below).

Table 5.

Mixed-effect analyses of the influence of trimester on the CSR estimated from induced-abortion data

Sample of fetuses	CSR	N	ΔAIC	Akaike weight
All with known trimester	0.524	4,999	4.737	0.086
First trimester	0.511	3,392	0	0.914
Second trimester	0.559	1,607

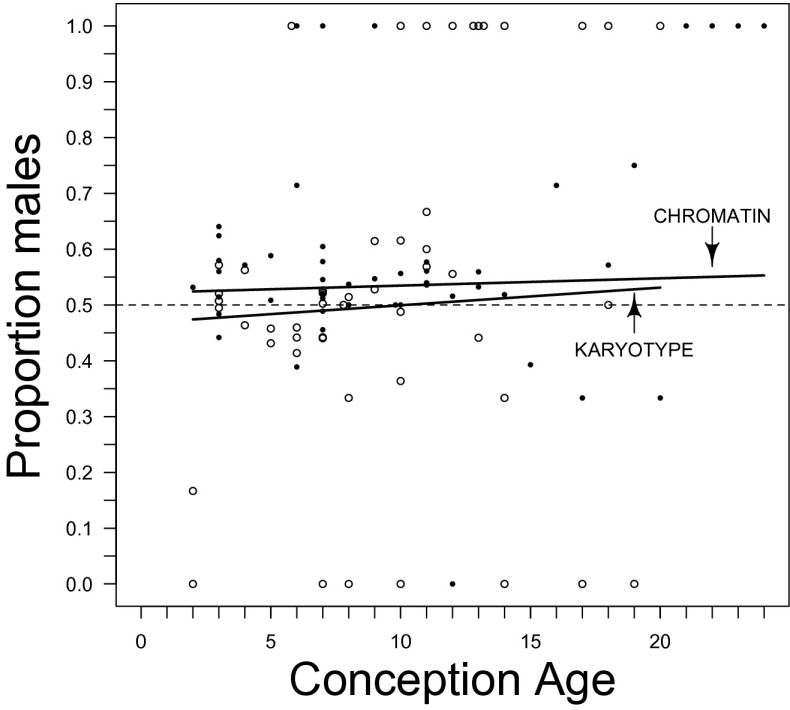
We also assessed the relationship between the CSR and CA by using a mixed-effect logistic regression analysis in which random effects were assigned to each study. The sole study based on histology was omitted because it contained fetuses of a single age. Fourteen of the remaining 23 studies present a several-week range of CA for some or all fetuses. We fit separate models for the early CA estimates and for the late estimates. A model with no influence of CA as a metric predictor had the most support. In keeping with the increased CSR estimate in the second trimester compared with the first trimester (see above), we present the CSR estimates based on the early CA estimates (Table 6; the CSR estimates based on late CA estimates are qualitative identical). The model with most support was diagnostic method specific (ER ∼ 39). We focus on the chromatin and karyotype studies because the diagnosis of sex from morphology likely overestimates the CSR, especially in early pregnancy (47, 48), due to the difficulty of distinguishing between female and male genitalia of early fetuses. We regard the chromatin estimate and especially the karyotype estimate as much more accurate; for these, CSR increases with CA (Fig. 1), which is consistent with greater net mortality for female fetuses during the first two trimesters. The male bias of the chromatin trend compared with the karyotype trend is consistent with the claim that the former method overestimates the CSR because female cells with poor staining of the Barr body are falsely classified as male.

Table 6.

Mixed-effect analyses of the influence of CA on the CSR estimated from induced-abortion data

Model	Fitted model	N	ΔAIC	Akaike weight
I + CA	Logit(CSR) = 0.063 + 0.006CAearly	14,839	7.322	0.025
I + CA method-specific	Logit(CSR)C = 0.086 + 0.005CAearly	8,373	0	0.975
	Logit(CSR)K = -0.157 + 0.013CAearly	4,872
	Logit(CSR)M = 0.852–0.044CAearly	1,594

I denotes intercept, _C denotes chromatin, _K denotes karyotype, and _M denotes morphology. _early denotes analyses based on early conception ages (see text).

Fig. 1.

The relationship between conception age and cohort sex ratio estimated from induced-abortion data. Observed sex ratios and estimated regression for chromatin (●) and for karyotype (○) data (Table 6). A dashed line denotes a sex ratio of 0.5.

Analysis of CVS Data.

We assessed whether the abnormal and the normal CSR differed by using a fixed-effect analysis because there was only one sample per mother (Table 7). The stratified and unstratified models have similar support (ER ∼ 1.61). The CSR is more male-biased (0.514) compared with the CSR among embryos (0.502; Table 1). Approximately 9% of fetuses were abnormal during this period compared with ∼61% among embryos (Table 1).

Table 7.

Fixed-effect analyses of the influence of karyotypic state on the CSR estimated from CVS data

Fetuses	CSR	N	ΔAIC	Akaike weight
All	0.514	61,769	0	0.617
Abnormal	0.521	5,481	0.956	0.383
Normal	0.513	56,288

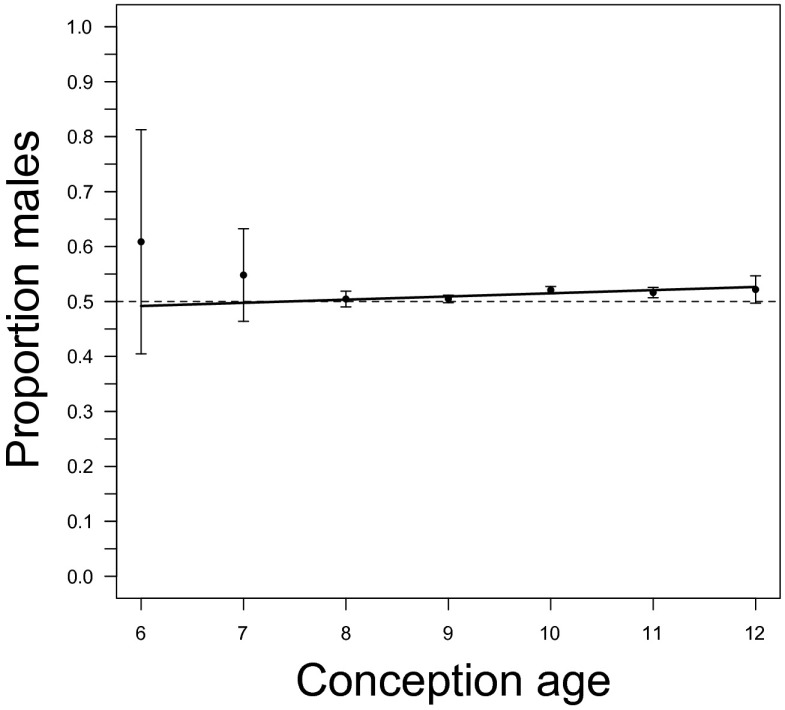
We also used a fixed-effect regression analysis to assess the relationship between the CSR and CA (Table 8). The model without CA as predictor has greater support (ER ∼ 8.52); this model indicates that the CSR increases between 6 and 12 wk (Fig. 2).

Table 8.

Fixed-effect analyses of the influence of CA on the CSR estimated from CVS data

Model	Fitted model	ΔAIC	Akaike weight
I	Logit(CSR) = 0.053	4.294	0.105
I + CA	Logit(CSR) = -0.218 + 0.023CA	0	0.895

I denotes intercept. n = 60,081.

Fig. 2.

The relationship between conception age and cohort sex ratio estimated from CVS data. Observed cohort sex ratio (with 95% confidence limits) and the estimated regression (Table 8). Fractional ages are rounded to the nearest integer. A dashed line denotes a sex ratio of 0.5.

Analysis of Amniocentesis Data.

We assessed whether the abnormal and the normal CSR differed by using a fixed-effect analysis because there was only one sample per mother (Table 9). The stratified model has much greater support (ER > 1,000), which suggests that the abnormal and normal CSRs are distinct. The CSR is less male-biased (0.506) compared with the CSR among CVS fetuses (0.514). Approximately 3.5% of embryos are abnormal; the abnormal CSR estimate is male-biased.

Table 9.

Fixed-effect analyses of the influence of karyotypic state on the CSR estimated from amniocentesis data

Fetuses	CSR	N	ΔAIC	Akaike weight
All	0.506	839,590	44.814	<0.001
Abnormal	0.523	36,833	0	>0.999
Normal	0.505	802,757

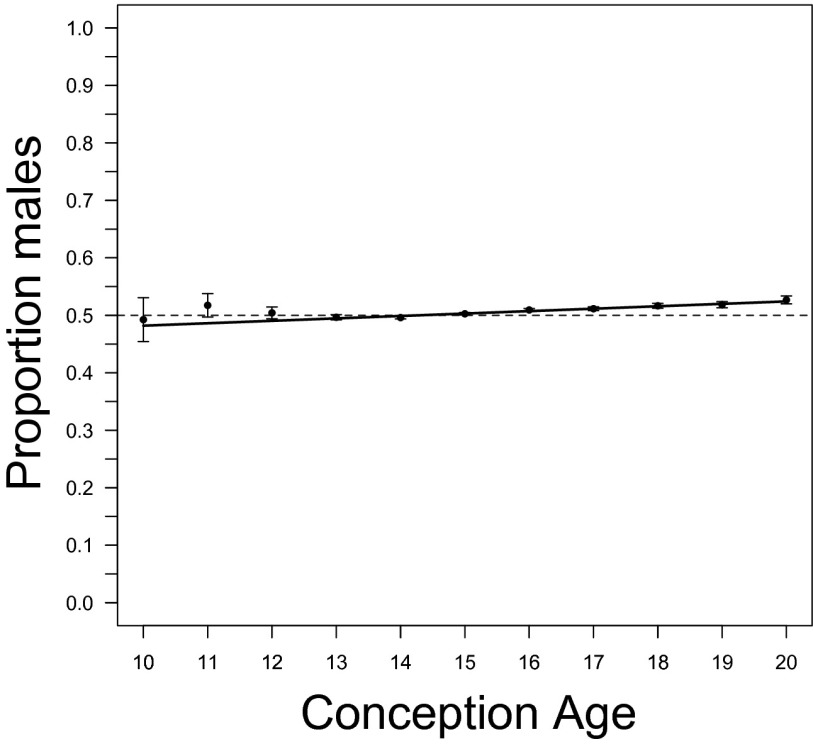
We also used a fixed-effect regression analysis to assess the relationship between the CSR and CA (Table 10). The model with CA as predictor has much greater support (ER > 1,000); this model indicates that the CSR increases between 10 and 20 wk (Fig. 3).

Table 10.

Fixed-effect analyses of the influence of CA on the CSR estimated from amniocentesis data

Model	Fitted model	ΔAIC	Akaike weight
I	Logit(CSR) = 0.022	168.522	<0.001
I + CA	Logit(CSR) = -0.241 + 0.017CA	0	>0.999

I denotes intercept. n = 809,274.

Fig. 3.

The relationship between conception age and cohort sex ratio estimated from amniocentesis data. Observed cohort sex ratio (with 95% confidence limits) and the estimated regression (Table 10). Fractional conception ages are rounded to the nearest integer. A dashed line denotes a sex ratio of 0.5.

There could be an overrepresentation of females among the fetuses undergoing amniocentesis, especially among early procedures, because there is a higher false-positive rate among females in tests for chromosome 21 aneuploidy based on maternal serum levels of α-fetoprotein (AFP) and free β-human CG (β-hCG) (49). Such a bias could generate an increasing relationship between the CSR and CA. The CSR of screened pregnancies in our sample is less male-biased than for unscreened pregnancies. However, the CSR increases between 10 and 20 wk for screened pregnancies and for unscreened pregnancies. We conclude that maternal screening does not distort our qualitative understanding of the CSR.

Analysis of Fetal-Death and Live-Birth Data.

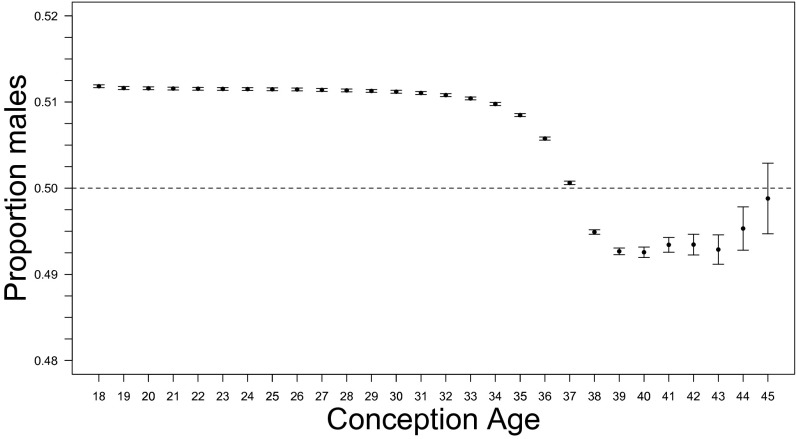
Karyotypic information for fetuses and babies is very limited. We did not distinguish between the abnormal CSR and the normal CSR. The CSR declines markedly after 35 wk CA (Fig. 4) due to the tendency of males to be born earlier. The birth sex ratio can be viewed as an admixture of an earlier male-biased wave followed by a female-biased wave. This shift is no fluke of sampling; there were 17,309,547 births and fetal deaths during weeks 35–37 and 14,010,729 thereafter.

Fig. 4.

The relationship between conception age and cohort sex ratio estimated from US fetal deaths and live births for 1995–2004 (combined). Observed cohort sex ratio (with 95% confidence limits). Conception age is based on the date of the last menstrual period; 18 denotes ≤18 wk. A dashed line denotes a sex ratio of 0.5.

The trend of the CSR estimates when CA is based on the clinical estimate is virtually identical to that shown in Fig. 4 up to 33 wk. The CSR then declines until week 38, but it never becomes female-biased. The estimates for later CAs are very variable, perhaps because there are many fewer pregnancies with late clinical estimates, especially those greater than or equal to 41 wk (clinical: n = 27,567; LMP: n = 1,309,690). We do not view the greater stability of late LMP-based CSR estimates as a reason to prefer this dating method; we urge further research to resolve the controversy over dating methods (50–52).

Discussion

Analysis of ART Embryos.

Sex-biased mortality may have occurred before assay, although this is unlikely. Such mortality could be caused by disrupted expression of maternally inherited mRNA or of RNA synthesized by the embryo. The ART embryos had at least eight cells when assayed. Some gene expression starts at the one-cell stage, and some X- or Y-linked loci are expressed before the eight-cell stage (53–58); embryonic genome activation is reviewed by refs. 59 and 60. It is implausible that any such differential mortality just happens to produce an assemblage of embryos whose CSR is statistically coincident with 0.5, a value expected given unbiased segregation of sex chromosomes during spermatogenesis and unbiased fertilization. An exact a posteriori power calculation provides additional insight. Assume that the (false) null hypothesis is that the CSR is 0.5 and that the (true) alternative hypothesis is that the CSR is, say, 0.505. For n = 139,704, when α = 0.05, there is an ∼59% statistical power to reject the false hypothesis that the CSR is 0.5. If the true CSR is 0.510, there is an ∼98% power to reject the false hypothesis.

There are nine reasons why ART embryos provide a meaningful estimate of the CSR and why our unbiased estimate of the PSR is plausible; we list them in rough order of their importance. Details are provided in SI Text.

• i)The birth sex ratio of babies conceived via ART matches the birth sex ratio of babies conceived naturally.
• ii)The birth sex ratio for ART with in vivo conception and the birth sex ratio for ART with in vitro conception appear to be identical.
• iii)Our estimate of the PSR matches the value expected given unbiased segregation of sex chromosomes during spermatogenesis and unbiased fertilization.
• iv)Analyses of data from other species do not provide conclusive evidence that the mammalian PSR is male-biased.
• v)The method of in vitro conception does not appear to influence the ART estimate of the CSR.
• vi)A high proportion of early naturally conceived embryos may be abnormal (as in our ART sample).
• vii)Typical methods for collection and preparation of gametes appear to have little or no influence on the ART birth sex ratio.
• viii)The average age difference between women who use ART and women who conceive naturally does not imply that ART embryos are unsuitable as a basis for an estimate of the PSR.
• ix)Ionic strength, pH, and temperature during fertilization and early development vary across ART protocols but are not grossly different from in vivo conditions as far as they are known.

Analysis of XO Embryos.

ART embryos with one X chromosome and no Y chromosome (XO) were not included in our CSR estimate because their sex is ambiguous; the many fewer YO embryos were included. Each XO embryo may never have had a maternal and a paternal sex chromosome or it may have lost one. The latter kind of embryo should contribute to a CSR estimate. We calculated their potential influence on the CSR estimate derived from the FISH analyses as follows. The percentage of XO embryos having a maternal X chromosome may be similar to the live-born frequency, which is at least 75% (61) [there is only one study of XO embryos known to us; all had a maternal X chromosome, n = 10]. If true and XO embryos had equal probabilities of resulting from X- and Y-bearing sperm, one expects that 62.5% of XO embryos were female (XX) and 37.5% were male (XY). There were 11,372 XO samples in our ART sample. The argument above implies that there are more “hidden” females (at most 7,107.5) than hidden males (at most 4,264.5). Accordingly, any correction for the missing embryos will leave unchanged or reduce the CSR estimate. For example, if h is the proportion of hidden zygotes in the XO sample, when h = 0 (no hidden zygotes), the CSR estimate is 0.502 [=70,171/(70,171 + 69,533)], which is the CSR estimate in Table 1. When h = 0.5, the CSR estimate is 0.497 {=[70,171 + 0.5(4,264.5)]/[70,171 + 69,533 + 0.5(11,372)]}. When h = 1.0, the CSR estimate is 0.493 = (70,171 + 4,264.5)/(70,171 + 69,533 + 11,372). We believe that the value of h for our sample is closer to 1.0 than to 0.0; most XO embryos had two copies of at least several chromosomes. No matter what the value of h, these estimates demonstrate that inclusion of hidden zygotes from among the XO sample does not generate a male bias in the CSR estimate.

This argument implies that our abnormal CSR estimate in Table 1 (0.508, n = 84,881) is based on a sample from which abnormal females were 66% (=62.5/37.5) more likely than abnormal males to be excluded. When h = 0, the abnormal CSR estimate is 0.508 [=43,144/(43,144 + 41,737)], which is the estimate in Table 1. When h = 0.5, the abnormal estimate is 0.500 {=[43,144 + 0.5(0.375)(11,372)]/[43,144 + 0.5(0.375)(11,372) + 41,737 + 0.5(0.625)(11,372)]}. When h = 1.0, the estimate is 0.493 {=[43,144 + (0.375)(11,372)]/[43,144 + (0.375)(11,372) + 41,737 + (0.625)(11,372)]}. The normal CSR estimate remains female-biased (0.493 in Table 1). None of the corrections of the CSR or of the abnormal CSR suggest that there is a substantial male bias of the PSR or of the CSR during early pregnancy.

Possible Causes of the Influence of Specific Chromosomes.

The association between CSR estimates and the state of the sex chromosomes and of chromosome 15 (Table 3, FISH) may be caused by entanglement of the bivalents of the Y chromosome and those of chromosome 15 at the pachytene stage of meiosis I. There is sequence homology between repetitive DNA in the heterochromatin of chromosome 15 and the heterochromatin of the q arm of the Y chromosome (62, 63). Such homology likely generates a physical association between the sex vesicle or “XY body” (64, 65) and the short arm of chromosome 15; physical association likely also occurs during metaphase (66). Sequence homology between repetitive DNA in chromosome 15 (and the other acrocentric chromosomes: 13, 14, 21, and 22) and in the X chromosome may also help generate a physical association (67); this may cause the excess of translocations involving the X chromosome and chromosomes 15, 21, and 22 (68). Entanglement may underlie the susceptibility of chromosome 15 to karyotypic abnormalities (69).

Karyotypic abnormalities generated in spermatogenesis, although rarer than those generated during oogenesis, may have a special influence on early development (70). Chromosomes 7 (Table 3, aCGH) and 17 (Table 3, FISH) may also exhibit this influence, although we lack possible causal explanations at the molecular level. Abnormality involving chromosome 7 (uniparental disomy that may disrupt imprinting; polysomy) is known or suspected to be associated with male-biased pathology after birth (71, 72), but the association of this chromosome with sex-specific prenatal morbidity and mortality appears not to have been investigated. An association between the Y chromosome and disomy for chromosome 21 has been described in sperm by ref. 73, although its cause is unknown (74, 75). This association is consistent with the decrease in the male bias of the abnormal CSR estimate for chromosome 21 (Table 3, FISH: 0.510 vs. aCGH: 0.496), although there is equivocal support for either stratified model. The apparent lack of influence of the state of chromosomes 13 and 18 on the CSR suggests that sex ratio biases among newborns aneuploid for these chromosomes are due to mortality during later development, as suggested by refs. 76 and 77.

Our assessments of the association between specific chromosomes and the abnormal and normal CSR estimates are based on Akaike weights (Table 3). For the FISH data, these assessments are identical to those based on adjusted P values derived from the change in deviance between nonstratified and stratified models [adjustments were based on a Bonferroni correction that controls in the weak sense the familywise type 1 error rate at 0.05 or on a correction that controls the false-discovery rate (78, 79) at 0.05]. For the aCGH data, Akaike weights, a Bonferroni correction, and a correction of the false discovery rate underwrite identical conclusions for all chromosomes except chromosome 7 (ΔAIC = 4.400, P_Bonferroni = 0.305, P_{False-discovery-rate} = 0.152).

Analysis of Induced-Abortion Data.

Our analysis suggests that female-biased mortality causes the CSR to increase between 2 and 20 wk CA. This increase is consistent with the inference from the ART analysis that the early CSR could be female-biased. Induced-abortion studies reporting female-biased first-trimester CSR estimates appear to be carefully done (17, 80–85). In addition, refs. 48 and 86–88 described female-biased CSRs for first trimester spontaneous abortions, but see ref. 89.

Analysis of CVS Data.

Our analysis suggests that the CSR is female-biased early in pregnancy and that female-biased mortality causes it to increase between 6 and 12 wk CA.

Analysis of Amniocentesis Data.

Our analysis suggests that the CSR increases between 10 and 20 wk due to female-biased mortality and that it surpasses 0.5 at ∼15 wk CA.

Analysis of Fetal-Death and Live-Birth Data.

Male-biased mortality during the second half of the second trimester and during the third trimester has little influence on the CSR (Fig. 4); the small size of this influence appears to be underappreciated.

The biphasic nature of the sex ratio of births (Fig. 4) has not been investigated thoroughly (90–92), although it has important implications for how to define a “premature” birth. One proximate cause of the sex ratio change may be that males typically attain a critical fetal weight earlier than do females (the average weight of newborn males is ∼100 g greater than females in the US data). Birth initiation is discussed in refs. 93 and 94.

James claimed that there is “a [positive] association of male births with long gestations” (95, p. 264) and that there is an “excess of males among post-term births” (92). A postterm birth is defined as one having a CA of 38 wk (40 wk LMP) or greater. For the US data, the CSR estimate for all post–38-wk births is 0.493 (95% CI: 0.493–0.493, n = 6,573,562), which is lower than the estimate for week 38 (0.497, 95% CI: 0.497–0.497, n = 7,437,167), suggesting an opposite trend, if any, to the one posited by James.

Overview.

Our analysis suggests that the PSR is unbiased. Analysis of the ART data suggests that the CSR could become female-biased within a week or two of conception because more male embryos are abnormal (assuming that the death rate of abnormal male embryos during this period is at least equal to that of abnormal female embryos). The CSR then increases early in pregnancy (due to higher female mortality) and decreases later in pregnancy (due to higher male mortality). Three independent datasets (induced abortions, CVS, and amniocentesis) suggest that the CSR increases until the latter half of the second trimester. If the PSR is 0.5, total female mortality must be greater than total male mortality during pregnancy because the sex ratio of all births is male-biased.

Female-biased mortality during the second trimester is likely not caused by gross karyotypic abnormalities such as monosomy and trisomy, because these probably cause earlier death. A female bias has been reported among apparently karyotypically normal spontaneous abortions during the first two trimesters (86–88). The apparent increase in female mortality occurs despite gene expression by two X chromosomes (although most loci on one or the other X chromosome are not expressed in a given cell). The expression of deleterious mutations is thought to be masked when the two X chromosomes have equal inactivation probabilities (96). Sex differences in gene expression are known later in pregnancy and later in life (97–99), but we lack information on how sex differences in gene expression earlier in pregnancy might contribute to female-biased mortality. One possible mechanism is that a paternal X chromosome retards development in such a way that female mortality rate increases; this has been confirmed in the mouse (100). Another possible mechanism is skewed X-inactivation (usually defined as >75% of cells sampled having, say, the paternal X chromosome inactivated), which can unmask recessive deleterious alleles (101, 102); it can also mask them (103). Skewed inactivation is associated with female-biased pathology later in life (104–106) and also with an elevated risk of spontaneous abortion (107, 108), although the sex ratio of the abortions appears to be unknown.

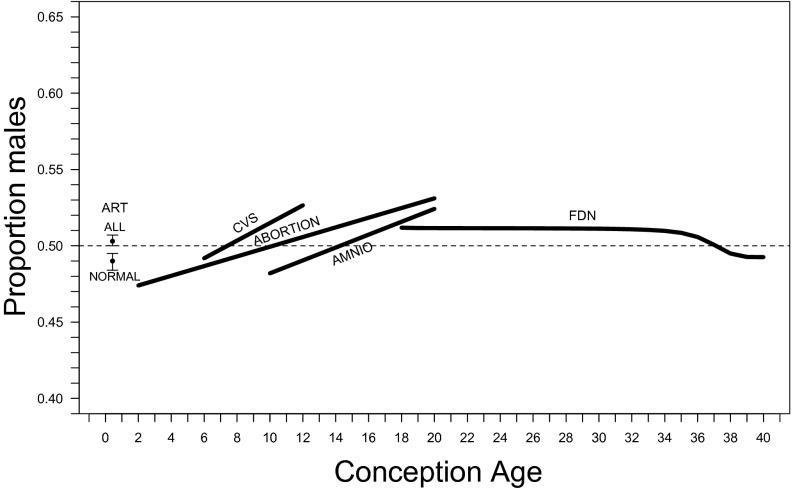
There are ambiguities in regard to our estimate of the trajectory of the CSR from conception to birth (Fig. 5). One is the discrepancy among the quantitative estimates of the CSR between 10 and 20 wk. A likely cause of the female bias of the amniocentesis estimates compared with the induced-abortion estimates is the presence of more than 200,000 fetuses in our sample that have undergone amniocentesis due to elevated AFP and total hCG levels (see above). When such fetuses are excluded, CSR estimates are higher than those in Fig. 3 and are consistent with those from induced abortions. For example, among fetuses whose rounded conception age is 20 wk, the CSR for those with elevated AFP and total hCG levels is 0.492 (n = 8,598) and 0.552 (n = 11,873) for the others. The latter estimate is close to the CSR at 20 wk inferred from the induced-abortion data.

Fig. 5.

The trajectory of the cohort sex ratio from conception to birth. ALL and NORMAL denote the total and normal sex ratio estimates based on ART embryos (Table 1), respectively, CVS denotes the estimated sex ratio trend based on CVS data (Table 8), ABORTION denotes the estimated trend based on induced abortions sexed via karyotype (Table 6), AMNIO denotes the estimated trend based on amniocentesis data (Table 10), and FDN denotes the trend of cohort sex ratio based on US fetal deaths and live births. A dashed line denotes a sex ratio of 0.5.

We now address James’ causally explicit claim (109, 110) that more males than females are conceived due to the interaction between the timing of fertilization and fluctuations of estrogen, testosterone, gonadotrophins, and progesterone during the menstrual cycle. The key assumption of this hypothesis is that the male-biased birth sex ratio is the result of a male-biased PSR. Such backward extrapolation is potentially misleading, and in this instance, the analysis of the induced-abortion data indicates that the CSR is female-biased during the first trimester of pregnancy and only later becomes male-biased. We do not deny the reality of the hormonal fluctuations and the nonuniformity of fertilization times, although whether the birth sex ratio depends on hormonal fluctuations is controversial (111–115). Even if there is such a dependency, the birth sex ratio does not have any necessary implication for the PSR; perhaps, for example, the timing of conception has a differential effect on the fate of male and female embryos (116). We conclude that James’ claim is incorrect, given our results that the PSR is unbiased, that the CSR may be female-biased during the first trimester, that the CSR increases during the first trimester, and that the predicted male bias among postterm births is absent.

Our results are also inconsistent with the hypothesis that the male-biased birth sex ratio arises from male-biased implantation of blastocysts after unbiased conception (117). The CSR early in the first trimester (after implantation) could be female-biased and the CSR increases during the first two trimesters. To this extent, male-biased implantation cannot by itself explain the male-biased birth sex ratio. In addition, the normal CSR estimate for the aCGH embryos is not male-biased (Table 3, Any = 0.498). Most of these embryos had undergone blastocyst formation, which may indicate competency for implantation.

We now consider the implications of our results for understanding of the evolution of the human sex ratio.

Extending the argument of Düsing (118), Fisher (8) claimed that the sex ratio had evolved via a process of natural selection and that the equilibrium outcome of this process is equal investment in the two sexes at “the end of the period of parental expenditure.” Fisher implied that there is a monotonic trajectory of the CSR towards this equilibrium; this is contradicted by our results (see Fig. 5 and SI Text).

We address two specific claims as to the sex ratio associated with this equal investment equilibrium (see SI Text). First, many scientists believe that 0.5 is the equilibrium sex ratio, although Fisher did not make this specific claim. We show using US data that the sex ratio for the 1900 cohort at age 40 is consistent with 0.5. However, the evolutionary implications of this result are ambiguous given the lack of real data on the sex specificity and timing of investment. This ambiguity is an important cautionary lesson, which is underscored by our result that female mortality during pregnancy may be greater than male mortality. All other things being equal, this greater female mortality implies that the sex ratio at investment equilibrium should be male-biased. Second, we show that Charlesworth’s (119) prediction that the equilibrium sex ratio is female-biased (p. 356) by “the end of the first year of postnatal life” for populations with little or no post-birth investment is not consistent with the data from the 1900 cohort or with data from hunter-gatherer, horticultural, and pastoral societies (120).

Finally, we suggest (see SI Text) that it is not self-evident that the sex ratio of a human cohort attains any fixed value (apart from sampling error) before only one sex remains. Static idealization of a trait can be misleading if dynamic expression is a central component of a trait’s evolutionary response to natural selection (121, 122). Determining the validity of this static idealization that the ultimate target of natural selection is a single sex ratio (as opposed to the target being, say, an age-specific sequence of sex ratios) will require data on the sex specificity and timing of parental investment, statistical assessment of the age-specific sex ratios to determine whether they are reasonably regarded as age invariant, and a comparison of the predictive accuracy of relevant static and dynamic adaptive models.