Ideal probe single-molecule experiments reveal the intrinsic dynamic heterogeneity of a supercooled liquid

Significance

Supercooled liquids are believed to exhibit spatially heterogeneous dynamics, where molecular mobility within a given spatial region may differ from that of a neighboring region, potentially by orders of magnitude. If supercooled liquids are ergodic, such that the spatial average of all regions with distinct dynamics equals the time average of a given region, these regions of distinct dynamics must interchange over time. With an appropriate probe, similar in size and mobility to the host, single-molecule measurements can provide direct access to these spatial and temporal variations. Here, such a probe is used, revealing how relaxation dynamics are distributed in time and space and directly demonstrating ergodicity of a prototypical glass former down to the glass transition temperature.

Abstract

The concept of dynamic heterogeneity and the picture of the supercooled liquid as a mosaic of environments with distinct dynamics that interchange in time have been invoked to explain the nonexponential relaxations measured in these systems. The spatial extent and temporal persistence of these regions of distinct dynamics have remained challenging to identify. Here, single-molecule fluorescence measurements using a probe similar in size and mobility to the host o-terphenyl unambiguously reveal exponential relaxations distributed in time and space and directly demonstrate ergodicity of the system down to the glass transition temperature. In the temperature range probed, at least 200 times the structural relaxation time of the host is required to recover ensemble-averaged relaxation at every spatial region in the system.

Despite decades of intensive study, a full theory of the glass transition is lacking; so too is a full understanding of the causal relationships between the unusual phenomena displayed by glass-forming liquids in the supercooled regime and the glass transition. One such phenomenon is the onset of nonexponential relaxations in the supercooled regime. Consistent with such relaxations, a variety of experiments have suggested the presence of dynamic heterogeneity, where—over a given time—molecular mobility in a given region may differ by orders of magnitude from that in another region, potentially just nanometers away (1, 2). While some experiments have sought to quantify the size of these regions, others have sought to quantify their persistence in time, as supercooled liquids are assumed to be ergodic, requiring that over long times, all dynamic environments are sampled (3–5). Precise description of dynamic heterogeneity in glass formers remains challenging due to the ensemble, subensemble, and/or time averaging inherent in most experimental techniques. However, such description remains of significant interest given the poorly understood causal relationship between dynamic heterogeneity and the glass transition as well as the need for experimental observations that may distinguish between various theories of the glass transition (6, 7).

Typically, putative dynamic heterogeneity has been recognized in experiments through the shape of the ensemble relaxation, which is well described by a stretched exponential (exp[−(t/τ_fit)^β]) where the deviation of β below 1 describes the degree of stretching and has been interpreted as a barometer of dynamic heterogeneity. Multiple scenarios are consistent with an ensemble stretched exponential relaxation, and two limiting cases can be straightforwardly described: The ensemble stretched exponential emerges from (i) a superposition of exponentials with different relaxation times or (ii) identical stretched exponentials with the same relaxation time. The former limit describes a system with variation of time scales distributed in space but not time, while the latter represents the opposite extreme. The former case describes a system that is not ergodic over times accessed in the experiment, while the latter suggests a system that has fully randomized on that time scale. The concept of dynamic heterogeneity and particular experimental findings on the spatial extent and temporal persistence of putative regions of distinct dynamics can be found in reviews in the literature (3–5, 8).

Given the possibility of nanometer-scale regions of distinct dynamics, single-molecule measurements have been considered an ideal tool for scrutinizing dynamic heterogeneity in supercooled liquids and distinguishing between scenarios consistent with a stretched exponential decay (8). While such experiments have shown potential in probing dynamic heterogeneity in glass-forming systems including molecular (9–13) and polymeric glass formers (14–18), limitations related to characteristics of the single-molecule fluorescent probes have substantially hindered these experiments and interpretation thereof (8, 19).

To mirror dynamic heterogeneity in a host system, fluorescent probe molecules need to be sufficiently small to reside within distinct dynamic regions, sufficiently fast to report dynamic exchange on the time scale of host structural relaxation, and sufficiently long-lived to capture potential longer-lived heterogeneities and to avoid artifacts associated with finite trajectory length (19, 20). Fluorescent molecules with suitable photophysical properties including high quantum yield and photostability are typically large and slow compared with host molecules, potentially obscuring host heterogeneities by averaging over them in space and/or time. Most single-molecule experiments in supercooled liquids thus far have revealed individual probe relaxations that are nearly exponential, but it has been unclear whether this supported the view of dynamic heterogeneity as dominated by variations in space—suggesting very long-lived heterogeneities or that supercooled liquids are nonergodic—or reflected limitations of the probe in reporting host dynamic heterogeneity (8).

Here, we report a single-molecule study of the well-studied molecular glass former o-terphenyl that employs a new, ideal probe close in size and rotational correlation time to o-terphenyl itself. On average, these probes report stretched exponential relaxations with comparable β values to those measured in probe-free ensemble studies of o-terphenyl. From these measurements, we demonstrate how relaxation time distributions are spread in space and time, directly demonstrate ergodicity recovery, and estimate the dynamic exchange time of the system down to the glass transition temperature.

Materials and Methods

Sample Preparation.

O-terphenyl (Sigma-Aldrich) was recrystallized at least three times in methanol and dissolved in toluene at the concentration of 5 mg/mL. The solution was photobleached in a home-built, high-power light-emitting diode (LED) based photobleaching setup for 48 h to achieve a fluorescent-free host matrix (21). The substrate, a silicon wafer, was cut into ∼ 6.5 × 6.5 mm pieces and cleaned with piranha solution (H₂SO₄:H₂O₂ = 3:1). To avoid dewetting of the film during sample preparation at room temperature, cleaned substrates were treated with trichloro(phenethyl)silane, which results in a hydrophobic surface. The fluorescent probe, BODIPY268 (SI Materials and Methods and Fig. S1), was dissolved in toluene and mixed with the o-terphenyl solution and solvent-casted onto the hydrophobically treated silicon wafer. Typical film thickness was 300–500 nm, as confirmed by ellipsometry (alpha-SE; J.A. Woollam). The concentration of the probe in the host o-terphenyl was on the order of 10⁻¹⁰ M, which results in 100–200 molecules per field of view.

Data Collection.

Single-molecule rotation was studied using a home-built microscope in a wide-field configuration equipped with a vacuum cryostat (ST-500; Janis) for temperature control. Light from a continuous wave laser (Nd:Vanadate 532-nm diode laser) was coupled into a multimode fiber (F-MCB-T-1FC; Newport), and the fiber was shaken by a piezoelectric buzzer (500−4,700 Hz) to eliminate speckles and create a randomly polarized and homogeneously illuminated field of view. The laser light was focused onto the primary image plane on the back of the objective lens (LD Plan-Neofluar; Zeiss; air 63×, N.A. = 0.75, working distance = 1.5 mm) creating an illuminated field of view of ∼100 μm diameter. The fluorescence was collected by the same objective lens and passed through a dichroic mirror followed by long-pass and band-pass filters. A Wollaston prism split the image into two orthogonal polarizations that were imaged onto an electron multiplying charge-coupled device camera (Andor iXon DV887) (10).

Excitation power varied with data set from 5 mW to 30 mW at the back of the objective lens, corresponding to power density of 50–300 W/cm² at the sample. Possible sample heating during excitation was assessed and corrected (SI Materials and Methods). Movies with frame rate >5 Hz were collected continuously, whereas slower frame rate movies were collected with 0.2-s constant exposure time, with illumination shuttered between frames to limit photobleaching. For each data set, several movies at each temperature were collected, and typically >1,000 single molecules were analyzed at each temperature for each data set (Table S1).

Data Analysis.

From the two orthogonal images, polarized fluorescence intensities (I_s, I_p) of each single molecule were extracted, and single-molecule linear dichroism was calculated via LD(t) = (I_s − I_p)/(I_s + I_p). An autocorrelation of LD(t) was constructed via [Σ_t′a(t′) ⋅ a(t′+t)]/[ Σ_t′a(t′) ⋅ a(t′)] where a(t) = LD(t) − <LD(t)> and was fit to a stretched exponential function, C(t) = C(0) ⋅ exp[-(t/τ_fit)^β]. τ_c was calculated from the fit values of τ_fit and β [τ_c = (τ_fit/β) ⋅ Γ(1/β), where Γ is the gamma function]. Each autocorrelation function (ACF) was fit with least squares fitting until the correlation function decayed to 0.1, and β and C(0) values were constrained to 0.2 < β < 2.0 and 0.3 < C(0) < 2.0. For single frame rate data, median frame rate was chosen to be ∼ 15 frames per median τ_fit and only molecules with (number of frames)/τ_fit >2 and trajectory length >10 τ_fit were analyzed. Data analysis was performed using IDL software (ITT Visual Information Solutions) as described previously (10, 22).

Results and Discussion

Movies capturing the rotational dynamics of the fluorescent probe, BODIPY268, in supercooled o-terphenyl from T_g (243 K) to T_g + 6 K were collected as described above. This probe, designed and synthesized for this study, has a molecular weight of 268.1 g/mol, comparable to that of the host, o-terphenyl (230.3 g/mol), and photophysical properties that meet the requirements for this single-molecule study (SI Materials and Methods and Figs. S1 and S2).

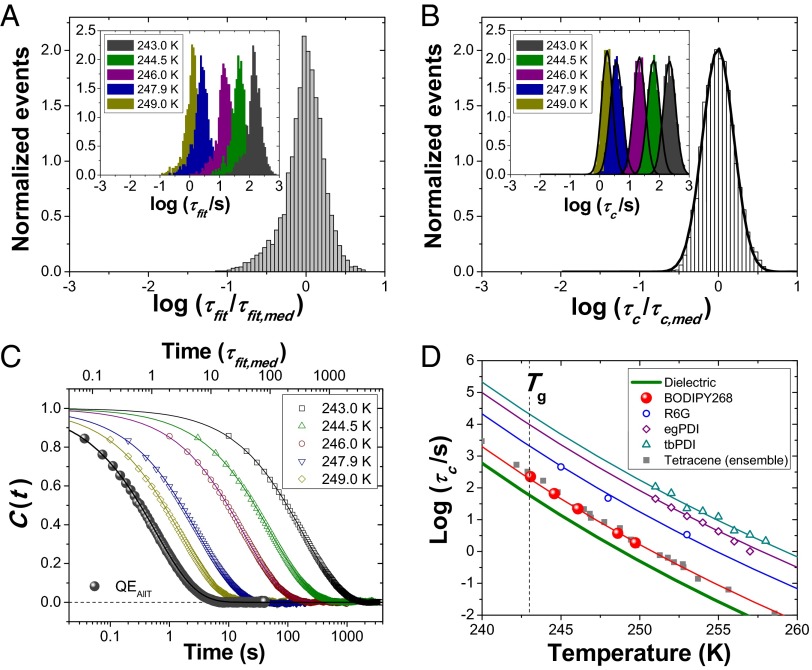
Individual probe linear dichroism trajectories were analyzed as described in Materials and Methods. Fig. 1 shows distributions of (Fig. 1A) τ_fit and (Fig. 1B) τ_c as obtained from fitting linear dichroism ACFs of each single molecule. τ_fit describes the time scale on which the ACF initially decays, while τ_c represents the average rotational correlation time, taking into account possible dynamic exchange experienced by the probe molecule. As in previous single-molecule reports in supercooled liquids, no change in distribution shape was apparent (in τ_fit or τ_c) as a function of temperature in the range probed (Fig. 1 A and B, Insets). This remained true when multiple frame rates were used to assure dynamic range was sufficient to capture the fastest and slowest molecules present in the system at a given temperature (SI Results and Discussion and Fig. S3). Temperature-combined histograms were therefore prepared by dividing individual single-molecule τ_fit and τ_c values by the median τ_fit and τ_c values at each temperature normalized by the area under the distribution (Fig. 1 A and B). In addition to assessing individual single-molecule ACFs, quasi-ensemble (QE) ACFs that are the average of all single-molecule ACFs were constructed and fit to stretched exponentials at each temperature, yielding QE values τ_fit,QE, τ_c,QE and β_QE (Fig. 1C). A temperature-combined QE ACF was created by dividing lag times by the median τ_fit value for each temperature before averaging (Fig. 1C). The temperature-combined QE ACF yielded a best-fit β of ∼0.65.

Fig. 1.

(A and B) Temperature reduced (A) τ_fit and (B) τ_c distributions for BODIPY268 in o-terphenyl for a data set of median trajectory length of 173τ_fit normalized by the area under the distributions. Insets show distributions at each temperature. Solid curves in B are fits to Gaussians with FWHM = 0.47. (C) QE ACFs for each temperature (open symbols) with solid lines the best fits to stretched exponential functions. Filled circles show the QE ACF for all temperatures combined. This curve is shifted to the left for clarity (upper axis). (D) Temperature dependence of τ_c for BODIPY268 (red filled circles) and other single-molecule (open symbols) (9, 10) and ensemble (filled squares) (24) probes in o-terphenyl. The thick solid line is the Volgel−Fulcher−Tammann fit to the temperature dependence of dielectric relaxation times of neat o-terphenyl, and thin lines are vertical shifts of this line (23).

To confirm that the probe follows the dynamics of the host, a minimum requirement for a probe that reports dynamic heterogeneity of the host, the temperature dependence of the rotational correlation time for BODIPY268 was compared with that of dielectric relaxation (23) as well as those of other single-molecule measurements in the literature and an ensemble measurement using tetracene (Fig. 1D) (9, 10, 24). Tetracene is a fluorescent probe that is not suitable for single-molecule measurements due to poor photophysical properties but can be measured via ensemble experiments and has a similar molecular weight (228.3 g/mol) to o-terphenyl (230.1 g/mol). Each probe displays dynamics that follow the temperature dependence of the host system, although probe relaxation times are shifted, generally scaling with the relative size of the probe to the host molecule. This result is consistent with previous work on both single-molecule and ensemble probe studies in o-terphenyl and other supercooled liquids (9, 10, 24–27). In o-terphenyl, the vertical shifts are 2.6 decades, 2.2 decades, and 1.6 decades for N,N′-bis(2,5-tert-butylphenyl)-3,4,9,10-perylenedicarboximide (tbPDI), N,N′-bis(triethylglycol)-3,4,9,10-perylenedicarboximide (egPDI), and Rhodamine 6G, respectively. The relaxation of BODIPY268 is shifted 0.5 decades relative to the dielectric relaxation. However, BODIPY268 rotates at the same rate as tetracene, which is reported to rotate at the same rate as o-terphenyl itself as determined by self-diffusion NMR measurements (24, 28).

The identification and employment of a probe very similar in size and rotational time scale to the host molecules of the supercooled liquid presents a critical advance in single-molecule experiments investigating dynamic heterogeneity. The BODIPY268 probe is expected to eliminate spatial and/or temporal averaging over heterogeneity in the supercooled liquid; such averaging has been inferred from probe-dependent ensemble and single-molecule experiments previously (8, 27). This probe’s ability to report the full breadth of dynamic heterogeneity in o-terphenyl rather than averaging over a proportion of it is supported by the similarity between the β value reported by tetracene in o-terphenyl in ensemble experiments and the QE β value (∼0.65) of BODIPY268 measured in this study (24). It is thus reasonable to conclude that BODIPY268 is an ideal single-molecule probe, one that can accurately report the dynamic characteristics, including dynamic heterogeneity, of the host system.

The concept of dynamic heterogeneity has been invoked to explain the stretched exponential relaxation in glass-forming liquids (3–5, 8, 29). Formally, a stretched exponential function is a superposition of a distribution of exponential relaxations with different relaxation times and can be written as Eq. 1, the inverse Laplace transform (ILT) of the function (SI Results and Discussion). The distribution P(log τ; τ_fit, β) can be numerically obtained for any τ_fit and β value (30, 31), with this distribution the underlying set of relaxation times associated with a given stretched exponential decay.

$$\exp \left[-{\left(t/{\tau }_{fit}\right)}^{\beta }\right]={\displaystyle {\int }_{-\infty }^{\infty }P(\log \tau ;{\tau }_{fit},\beta )\cdot \exp }\left(-t/\tau \right)d\log \tau .$$ [1]

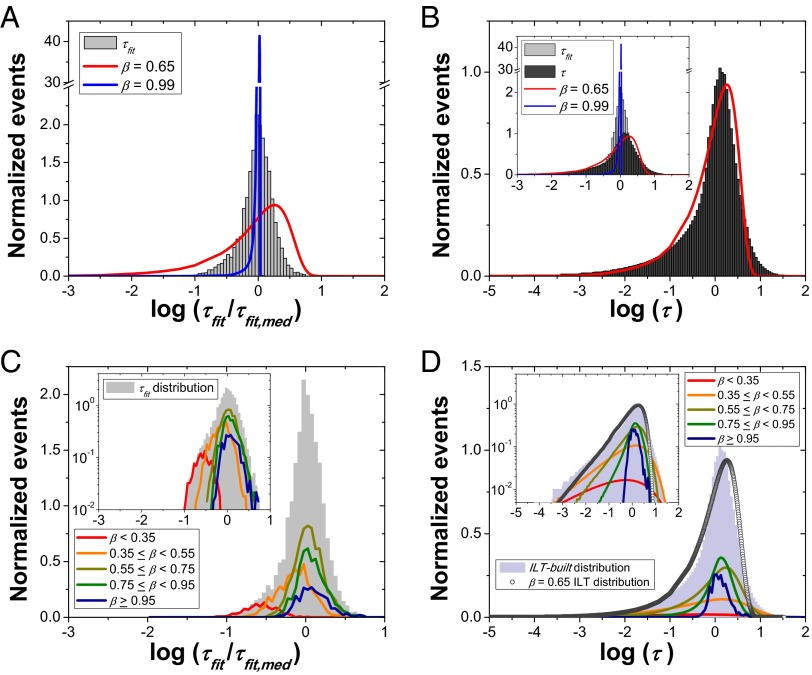
Fig. 2A shows the measured τ_fit distribution combined for all temperatures (also shown in Fig. 1A) compared with the expected distributions from ILTs of stretched exponentials with β = 0.65 (the measured QE β) and 0.99. β = 0.99 was plotted instead of β = 1 for ease of representation, as the distribution associated with β = 1 is a delta function, with infinite height.

Fig. 2.

(A) τ_fit distribution for the 173τ_fit,med trajectory length data set also shown in Fig. 1A (gray histogram) and distributions from ILT of stretched exponentials with β of 0.65 (QE β, red line) and 0.99 (blue line). (B) ILT-built distribution (dark gray) from the experiment and that of a stretched exponential with β = 0.65 (red line). Inset is reproduction of A with the ILT-built distribution included. (C and D) Contribution of single molecules with particular stretching exponents to the (C) measured τ_fit and (D) constructed ILT-built distributions. Insets are log−log versions of C and D.

In the context of dynamic heterogeneity, these two distributions represent two limits. In one limit, all measured single molecules would have the same relaxation time scale (blue line) and the same β < 1. This is the temporal heterogeneity limit or “homogenous” scenario. In the other limit, each single molecule would have a single exponential relaxation with a different time scale, consistent with the distribution associated with the ILT of the QE result (red line). In principle, no broader distribution is allowed unless the stretched exponential is not a good representation of the ensemble relaxation. This is the spatial heterogeneity or “heterogeneous” scenario.

The τ_fit distribution measured from the single molecules falls between these two limiting cases, and the degree of the deviation represents the interplay of spatial and temporal heterogeneity in the system, with the width of the measured distribution primarily a measure of how spatial and temporal heterogeneities are distributed rather than a measure of the degree of overall dynamic heterogeneity, which is reported instead by the single-molecule QE β value.

The ILT of a stretched exponential function yields a distribution of single-exponential relaxation times. As such, to test whether the measured QE stretched relaxation can be described as a sum of exponentials spread in time and space, an attempt was made to recover the distribution predicted by the ILT of the QE ACF. This test can also validate that the breadth of the measured τ_fit distribution reflects dynamic heterogeneities rather than experimental limitations such as finite trajectory length (19).

First, a set of reference distributions of τ_fit = 1 and β ranging from 0.20 to 0.99 in 0.01 steps was built (SI Results and Discussion and Fig. S4). In brief, for each measured single-molecule τ_fit and β, a distribution was chosen from the reference set based on the β value and shifted by the measured τ_fit. This process is meant to “unwrap” temporal heterogeneity reported by a given molecule; thus, following this procedure, the distribution of exponential relaxations experienced by a given single molecule over the course of the experiment is obtained. This process was repeated for all single molecules, and the distributions were combined, leading to an ILT-built distribution, the full distribution of exponential relaxations reported by the probe molecules in space and time during the experiment.

Fig. 2B shows the ILT-built distribution from the experiment compared with the ILT distribution associated with a stretched exponential function with β = 0.65. The match is clearly superior to that of either of the limiting cases shown in Fig. 2A and Fig. 2B, Inset, with the area mismatch between the distributions ≈ 10%. This shows that the single-molecule correlation functions report the full breadth of relaxation times present in the system and indicates that temporal heterogeneity is responsible for narrowing the measured τ_fit distribution from the predicted distribution associated with β = 0.65.

Fig. 2 C and D shows where molecules with different β values fall within the τ_fit distribution, with Fig. 2C showing the raw reduced τ_fit distribution over all temperatures and Fig. 2D showing the corresponding ILT-built distribution. From Fig. 2C, it can be appreciated that molecules with low β values preferentially have small τ_fit values. The ILT-built distribution, in turn, shows that contributions from single molecules with low β are spread over the entire τ_fit distribution while those with high β are concentrated in the slower part of the distribution. Additional analysis of the single molecule contributions to the ILT-built distribution is presented in SI Results and Discussion and Fig. S5. The finding that single molecules with high β values tend to be in the slower part of the distribution is consistent with the picture that slower molecules may report less temporal heterogeneity than faster ones due to temporal averaging, as was seen in previous single-molecule experiments with probes exhibiting slow rotations relative to the host molecules (10, 12). However, because the faster molecules in the data set experience more rotations than the slower ones, such an observation is also consistent with exchange time being correlated with local relaxation time and longer-lived molecules experiencing more dynamic environments. This encouraged close investigation of the trajectory length dependence of the character of the stretched exponential decays.

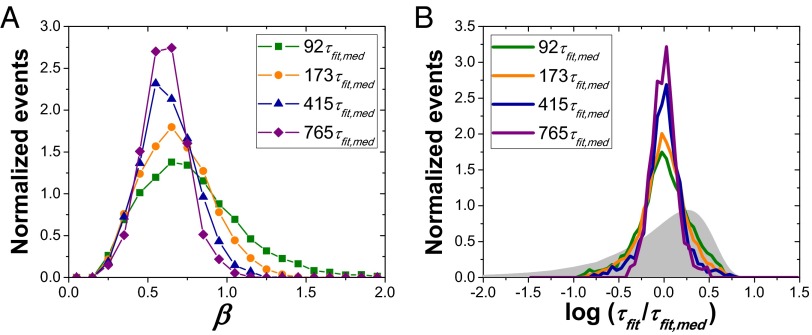
Given an ergodic system, monitoring a single molecule for long enough should return the same β value as obtained via an ensemble measurement over shorter times. Fig. 3A shows how β distributions change with median data set trajectory length obtained by varying excitation power. Higher excitation power leads to better signal-to-noise at the expense of time to probe photobleaching. Data sets with median trajectory lengths of 92τ_fit,med, 173τ_fit,med, 415τ_fit,med, and 765τ_fit,med were acquired. The 92τ_fit,med and 173τ_fit,med median trajectory length data sets were obtained from five different temperatures from 243 K to 249 K, whereas 415τ_fit,med and 765τ_fit,med data sets were obtained at the single temperature of 248 K. As median trajectory length increases, the β distribution exhibits a shift to lower values and significant narrowing. The shape of the distribution is reasonably symmetric for the 415τ_fit,med and 765τ_fit,med trajectory length data sets, whereas shorter trajectory length data sets display tails at high β, likely due to statistical fluctuations and poor fits associated with short trajectories (19). Fig. 3B shows the τ_fit distribution for each data set, which also narrows as median trajectory lengths increases.

Fig. 3.

Distributions of (A) β and (B) τ_fit for four data sets of varied median trajectory length. Filled gray distribution in B is the ILT distribution associated with a β = 0.65 stretched exponential, the expected distribution given only spatial heterogeneity.

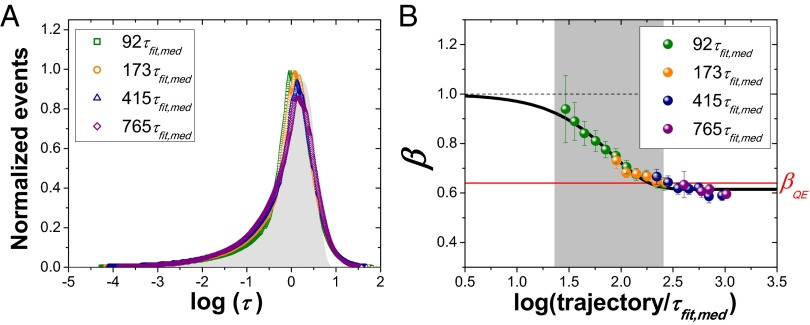
Fig. 4A shows ILT-built distributions of each median trajectory length data set; these collapse well and are similar to the ILT distribution of β = 0.65 independent of median trajectory length of the data sets. This collapse shows that the inherent underlying relaxation time distribution in the system is independent of trajectory length and that this set of underlying relaxations is exponential, a validation of the picture of dynamic heterogeneity. The difference in τ_fit distributions (Fig. 3B) but similarity in ILT-built distributions (Fig. 4A) shows that at short and long trajectory length, the experiment reports the same degree of dynamic heterogeneity in the system. That heterogeneity is, however, apportioned differently between spatial and temporal components. The narrowing of the β and τ_fit distributions with increasing trajectory length and the similarity of the ILT-built distributions at all trajectory lengths directly demonstrate ergodicity of the system down to the lowest temperature probed, the glass transition temperature.

Fig. 4.

(A) ILT-built distributions for four data sets of varied median trajectory length. Filled gray distribution is the ILT distribution associated with a β = 0.65 stretched exponential. (B) The dependence of β on the molecule specific trajectory length for the indicated median trajectory length data sets. Error bars are 99% confidence intervals.

Within each data set, a range of single-molecule trajectory lengths is present. Assessing median β value across all data sets as a function of trajectory length reveals that as trajectory length increases, β decreases (Fig. 4B), consistent with the view that molecules experience more temporal heterogeneity with longer trajectories. The data collapse to a single curve, which can be used to estimate the range of time scales on which dynamic environments are interchanging. Fig. 4B shows that the β value deviates from 1 by ∼25τ_fit,med and approaches a value near the QE β value by ∼ 200τ_fit,med. This trend, together with the trends in width of the τ_fit and β distributions (SI Results and Discussion and Fig. S6), shows that the time averaging required to recover ensemble averaged relaxation at every spatial region in the system is hundreds to thousands of times the host structural relaxation time.

These time scales can be compared with previous estimates of exchange time obtained from a variety of experiments in o-terphenyl (9, 32, 33). Given the similarity in relaxation time scales between tetracene and BODIPY268 (Fig. 1D), comparison between experiments using these probes is most straightforward. Our findings are consistent with the result from the tetracene study over a portion of the temperature range probed. However, that measurement showed a strong decrease of exchange time relative to overall relaxation time of the system with increasing temperature (32) [and a previous single-molecule result showed the opposite trend (9)], while we find no temperature dependence of exchange time relative to structural relaxation time as a function of temperature in the range investigated. This discrepancy may be related to the tetracene experiment’s selection of a slow subensemble of the probe molecules, whereas our approach does no such subensemble selection.

Conclusion

Design and synthesis of a fluorescent probe of similar chemical structure, size, and mobility to the supercooled liquid host molecules has allowed single-molecule fluorescence measurements that directly access the spatial and temporal components of dynamic heterogeneity in the prototypical supercooled liquid o-terphenyl. Through trajectory-length-dependent studies and ILT treatment of the measured data, it is unambiguously shown that observed stretched exponential decays emerge from sets of exponential relaxations distributed in space and time. While the measured single-molecule relaxation time (τ_fit) and stretching exponent (β) distributions evolve with trajectory length, the underlying relaxation time distribution (τ) obtained through the ILT remains stable, demonstrating the ergodicity of system. At short times (<25 times the median relaxation time of the supercooled liquid), the system appears completely spatially heterogeneous, with distinct dynamic regions displaying different exponential relaxations. At longer times, at least 200 times the median relaxation time, the system recovers ergodicity, and every spatial region in the system shows the same nonexponential relaxation dynamics.