Iterative adaptive radiations of fossil canids show no evidence for diversity-dependent trait evolution

Significance

Many of the most diverse lineages of animals and plants are hypothesized to have arisen via the process of adaptive radiation. Most modern definitions of adaptive radiation focus on the role of ecological opportunity in regulating rates of morphological diversification. Using the rich fossil record of North American canids (wolves, foxes, and their relatives), I found no relationship between past diversity and rates of body size or tooth shape evolution. Instead, phenotypic evolution is directed toward adaptively optimal morphologies, such as large size or broad molars, without changes in the rate at which diversity accumulates. If these kinds of processes are common, we may need to rethink many of our ideas about the origins of morphological diversity.

Abstract

A long-standing hypothesis in adaptive radiation theory is that ecological opportunity constrains rates of phenotypic evolution, generating a burst of morphological disparity early in clade history. Empirical support for the early burst model is rare in comparative data, however. One possible reason for this lack of support is that most phylogenetic tests have focused on extant clades, neglecting information from fossil taxa. Here, I test for the expected signature of adaptive radiation using the outstanding 40-My fossil record of North American canids. Models implying time- and diversity-dependent rates of morphological evolution are strongly rejected for two ecologically important traits, body size and grinding area of the molar teeth. Instead, Ornstein–Uhlenbeck processes implying repeated, and sometimes rapid, attraction to distinct dietary adaptive peaks receive substantial support. Diversity-dependent rates of morphological evolution seem uncommon in clades, such as canids, that exhibit a pattern of replicated adaptive radiation. Instead, these clades might best be thought of as deterministic radiations in constrained Simpsonian subzones of a major adaptive zone. Support for adaptive peak models may be diagnostic of subzonal radiations. It remains to be seen whether early burst or ecological opportunity models can explain broader adaptive radiations, such as the evolution of higher taxa.

A central prediction of modern adaptive radiation theory is that rates of diversification and phenotypic evolution are fastest early in clade history and subsequently slow as niches become saturated (1). This prediction is derived in large part from the writings of Simpson (2, 3), who suggested that fast rates of phenotypic evolution are required during the early phases of adaptive radiation to move lineages rapidly through inadaptive phases of the adaptive landscape to a new peak. Although the fossil record provides many examples of rapid early accumulation of morphological disparity (4–10), direct evidence for early rapid rates of phenotypic evolution, a so-called “early burst,” has proved rare in phylogenetic comparative data (11). There are several plausible explanations for why early bursts are seldom observed. For example, temporally declining rates are difficult to detect in datasets comprising only extant taxa, and comparative methods are extremely sensitive to noise from convergence or measurement error (11, 12). Incorporation of fossil taxa in phylogenetic tests for early bursts can improve detection of these patterns (13), although isolated analyses of subclades within a larger adaptive radiation may fail to show evidence of declining disparity with time if rates have already significantly decreased, even when fossil species are sampled (14).

An alternative explanation for the lack of early bursts in comparative data is that ecological opportunity, not time, is the key determinant of rates of morphological evolution. If opportunity is the dominant force driving rates of morphological evolution in adaptive radiation, then the early burst model should be a particularly poor fit when clade age is a weak predictor of species richness. Patterns of diversity through time in the fossil record strongly suggest that diversity-dependent speciation and extinction dynamics are common (15–17) and weak or negative relationships between clade age and species richness are increasingly recognized in molecular phylogenies (18–20). To test the role of ecological opportunity in driving the morphological component of adaptive radiation more explicitly, Mahler et al. (21) developed a novel approach to model rates of morphological evolution as function of estimated past diversity at nodes of a time-calibrated molecular phylogeny (a similar method can be found in ref. 22). Using estimated lineage diversity as a proxy for past ecological opportunity in island communities of Anolis lizards, they found strong support for diversity dependence of evolutionary rates for body size and limb bone lengths, both of which influence habitat use and performance (21). This result would seem to lend support to a primary role for ecological opportunity in regulating rates of morphological evolution during adaptive radiation. It remains to be tested, however, whether diversity dependence can provide a compelling mechanism to explain patterns of morphological disparity through time in more general contexts, such as on continents, or over longer geological times scales.

In this article, I test for diversity dependence of rates of body size and dental evolution in living and fossil members of the dog family, Canidae. Canids are an attractive system for such a study. Living canids exhibit a range of dietary and predatory behaviors that can be readily diagnosed for fossil species on the basis of craniodental traits (23, 24). The canid fossil record is also well sampled, yielding a diverse radiation of ∼140 species (25–27) that spans the Late Eocene (40 Mya) through present day. Perhaps most importantly, however, for the first 35 My of their evolutionary history, canids were restricted to and diversified exclusively within North America. If ecological opportunity plays a prominent role in regulating rates of morphological diversification over geological time scales, we should expect to find support for a link between diversity and the tempo of ecomorphological diversification in continental radiations with excellent fossil records, such as Canidae.

Results and Discussion

Canids have traditionally been divided into three sequential, subfamilial radiations: Hesperocyoninae (Late Eocene–Middle Miocene), Borophaginae (Early Oligocene–Late Pliocene), and Caninae (Late Oligocene–present). Phylogenetic analysis of a morphological character matrix representing 120 species of living and fossil North American canids using Bayesian inference (28, 29) recovered all three clades, although only Caninae was strongly supported as monophyletic [posterior probability (PP) = 1; Supporting Information]. Time calibration of canid phylogeny using a relaxed, uncorrelated morphological clock calibrated by tip last appearance dates and 16 informative node age priors (29) yielded a maximum clade credibility tree that was highly unresolved toward the base of each subfamily (Supporting Information). I therefore used 500 randomly sampled trees from the Bayesian PP distribution, as well as the tree with the highest natural log likelihood [ln(likelihood)] (hereafter, the “best” tree; Fig. 1) for subsequent macroevolutionary analyses.

Fig. 1.

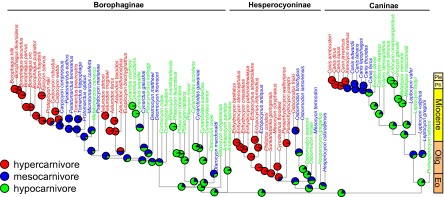
Reconstruction of ancestral diet under a model of symmetrical transition rates on the time-calibrated tree with the highest log-likelihood from the Bayesian PP distribution. Eo, Eocene; Olig, Oligocene; Ple, Pleistocene; Pli, Pliocene.

To understand how ecological opportunity may have influenced rates of morphological evolution, I estimated dietary diversity through time, using the method of Mahler et al. (21). Hypercarnivorous canids are those canids for which large-vertebrate prey comprise >70% of their diet, mesocarnivorous canids have diets composed of 50–70% vertebrate material, and hypocarnivorous canids consume <30% vertebrate materials and may heavily use invertebrate or plant material instead. Based on a series of linear discriminant function analyses (LDAs), I was able to classify 91 fossil canids to one of these categories. A symmetrical model, where transitions directly between hypercarnivory and hypocarnivory are predicted to be extremely rare, is the best-supported model of dietary evolution [median small sample-corrected Akaike information criterion weight (AICcW) = 0.69; Supporting Information], although model-averaged rates indicate less frequent transitions from hypercarnivory into mesocarnivory than vice versa (Supporting Information). Ancestral state estimation under the symmetrical model on the best tree from the Bayesian posterior distribution suggests that the most recent common ancestor of living and fossil canids was most likely a hypocarnivore but that transitions to mesocarnivory and hypercarnivory occurred relatively rapidly and multiple times (Fig. 1).

To determine whether morphological diversification in canids was influenced by ecological opportunity, clade age, or other factors, I fit a series of macroevolutionary models to two ecomorphological traits that have been shown previously to associate with resource use in carnivores. Body mass is positively correlated with maximum prey size in extant canids, and it is widely viewed as an important predictor of ecological niche in vertebrates. For ln(body mass), a model where evolutionary rates decline as a function of increasing diversity within dietary regimes (median ψ = −0.001, range = −0.012–0.049) received slightly higher support than models allowing for time- or diet-dependent variation in rates but received lower relative support than a constant-rate Brownian motion (BM) model (Table 1). An Ornstein–Uhlenbeck (OU) model with separate adaptive body mass peaks for the three dietary categories is preferred over all models, including diversity-dependent rates (median AICcW over all models compared = 0.73, Table 1). Based on the need to balance energy expended during foraging with energy obtained from prey, carnivores are predicted to switch to obligate hypercarnivory at sizes of 14.5–21 kg (30). The hypercarnivore optimum is here inferred to be 20.7 kg (median, range = 14.5–35.8 kg), in agreement with these predictions. Smaller optimal masses of 4.7 kg (2.9–9 kg) and 3.2 kg (2.6–4.8 kg) were estimated for mesocarnivorous and hypocarnivorous species, respectively (Table 1).

Table 1.

Median results from macroevolutionary models fitted to 500 trees sampled at random from the Bayesian posterior distribution

Trait	Model	lnLk	AICc	AICcW	${\sigma }^2$	Scalar	Hypercarnivore	Mesocarnivore	Hypocarnivore
ln(mass)	BM	−43.46	91.06	<0.01	0.018	—	—	—	—
	ACDC	−43.40	93.08	<0.01	0.020	−0.002	—	—	—
	Diversity dependence	−43.35	92.96	<0.01	0.017	0	—	—	—
	Diversity-dependent diet	−42.65	91.56	<0.01	0.024	−0.001	—	—	—
	BMV	−42.72	93.89	<0.01	—	—	0.016	0.023	0.016
	Trend	−34.56	75.39	0.25	0.015	0.041	—	—	—
	OU	−31.33	73.34	0.73	0.014	7.4 × 10−5	3.03	1.55	1.16
RLGA	BM	57.73	−111.32	<0.01	0.002	—	—	—	—
	ACDC	61.93	−117.59	<0.01	5.7 × 10−4	0.052	—	—	—
	Diversity dependence	61.33	−116.37	<0.01	0.001	1 × 10−5	—	—	—
	Diversity-dependent diet	58.69	−111.11	<0.01	0.002	−8 × 10−5	—	—	—
	BMV	66.27	−124.08	<0.01	—	—	0.001	0.001	0.0035
	Trend	57.73	−109.19	<0.01	0.002	−0.001	—	—	—
	OU	77.01	−143.32	>0.99	0.004	0.182	0.63	0.80	0.97

Relative support is indicated by small sample AICcWs. The evolutionary rate is given by ${\sigma }^2$, whereas scalar refers to model-specific parameters [accelerating/decelerating rate (ACDC) = r; diversity dependent models = ψ, trended random walk (Trend) = μ, OU = α]. For variable rate (BMV) and multipeak OU models, diet-specific values are provided in the final three columns. AICc, corrected Akaike information criterion; lnLk, ln(likelihood).

Further dissection of these results lends support to the view that body size plays an unpredictable role in macroevolutionary pattern (31), and casts doubt on its general utility in studying adaptive radiation. The α-parameter of the OU model describes the strength with which traits are attracted to their associated optima. It is often more intuitive, however, to reparameterize an OU model in terms of the phylogenetic half-life, t_1/2 = ln(2)/α, which describes the time required for adaptation to a new selective regime to become more influential than constraints implied by an ancestral regime (32). For body mass, the median estimated α-parameter of 0.00074 leads to a t_1/2 of 936 My. Even α estimated on the best tree, an order of magnitude larger at 0.008, leads to a t_1/2 of 86 My. Such weak attraction suggests that canid body size evolution might be better explained as a slow sustained trend toward larger body sizes across the three dietary categories (32). Indeed, a trended random walk, albeit with a single trend for all species regardless of diet, provides the second best fit to these data (Table 1).

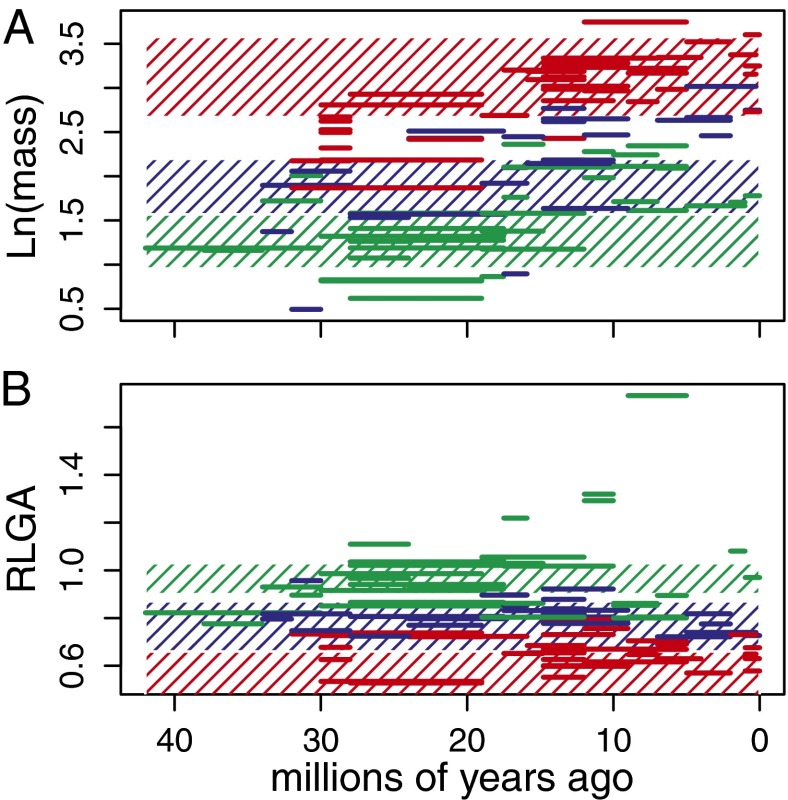
The true picture of body size evolution is likely much more complex. A plot of canid body masses through time in relation to the putative adaptive optima (Fig. 2A and Supporting Information) reveals two striking patterns. First, although a large optimal mass of >20 kg is inferred for hypercarnivores, no canid achieves this size until the Middle Miocene, with Osbornodon fricki being the only hesperocyonine to do so. Second, there is a general increase in both mean and minimum canid body sizes toward the present that affects the size distribution of species within all three niches (33, 34). This pattern is indicative of a driven (35) or active (36) trend, Cope’s rule in its strictest sense (37), and suggests that canid body size niches have themselves been shifting over the past 40 My (2, 3). The differences in maximum size of hypercarnivores before and after the Middle Miocene, combined with an apparent increase in minimum sizes through the Cenozoic (Fig. 2A), possibly represent environmentally induced changes in optimal body mass associated with post-Oligocene cooling and the expansion of grasslands, similar to the pattern found for North American horses (38). Regardless of the cause, overlaying of adaptive trends on simultaneously evolving niches complicates simple interpretation of macroevolutionary dynamics for canid body sizes. Many previous studies of adaptive radiation models (21, 39, 40) have examined patterns of body size evolution with the justification that it is a significant predictor of ecological niche (41). Although this claim may have physiological or biomechanical justification in some specific contexts, the incorporation of fossil data here, as in other studies (34, 42, 43), highlights that more complex and temporally variable patterns are common for body size, and serves as a warning against using it to draw general conclusions about the tempo and mode of ecological diversification within a clade, particularly when only extant members are sampled.

Fig. 2.

Trait values through time for ln(body mass) (A) and RLGA (B). Hatched areas correspond to the range of optimal values estimated for a random sample of 500 trees from the Bayesian posterior distribution.

The second trait, relative lower grinding area (RLGA), is the combined areas of the talonid basin of the lower first molar (m1) and of the entire lower second molar, relative to body size (represented by m1 length) (23, 24). Hypercarnivorous canids should exhibit lower values of RLGA as the slicing function of the m1 trigonid is emphasized over grinding, whereas hypocarnivorous canids should exhibit large grinding areas for processing tough materials, such as plant matter and arthropod exoskeletons (23, 24). Considering rate models only, diversity-dependent models received low support (median AICcW < 0.01 for diversity and dietary diversity-dependent models) and models allowing for time-dependent increases (median AICcW = 0.02) or diet-specific rates (median AICcW = 0.95) were preferred. Considering the entire suite of models, RLGA is also best explained by an adaptive peak model (median AICcW > 0.99; Table 1). This model predicts a median optimal relative grinding area of 0.63 (range = 0.37–0.7) for hypercarnivorous canids, whereas hypocarnivorous canids are attracted to a larger area of 0.97 (0.90–1.03). Mesocarnivorous species are again intermediate, with optimal grinding areas of 0.8 (0.66–0.87).

In contrast to the results for body mass, the median estimated α-parameter over the posterior sample of trees (α = 0.18) implies strong and rapid attraction of RLGA toward these peaks (t_1/2 = 3.85 My). Furthermore, these zones remained remarkably stable throughout canid history and seem to have been unaffected by the biotic and abiotic factors that promoted macroevolutionary increases in canid body sizes. Despite the evolution of a few morphologically extreme hypocarnivores in the Middle to Late Miocene (Cynarctus species; Fig. 2B), most species cluster about their inferred optimal trait values. Presumably, the properties of vertebrate flesh have not changed much over the Cenozoic, and the functional demands of processing meat are the same now as they were in the Late Eocene.

Selection of a multipeak OU process with a relatively strong attraction parameter for RLGA suggests that the 40-My radiation of North American canids might be best viewed as an iterative set of replicated ecological radiations (1, 23, 44, 45) occurring in and among at least three constant and bounded dietary zones. The concept of replicate adaptive radiation is generally viewed as being at odds with classic predictions of temporally declining or diversity-dependent rates of morphological evolution (46, 47). Their expected outcomes, at least in terms of the rate at which morphospace is filled, are remarkably consistent, however. Simulations show that early peak disparity is consistent with expectations of both early rapid evolutionary rates and evolution occurring at a constant rate but within a bounded morphospace (14). Under this second scenario, a limited range of morphological outcomes, due to developmental, ecological, or functional constraints (45), cause diversifying clades to saturate morphospace rapidly, after which disparity ceases to increase, regardless of subsequent increases in taxonomic diversity (6, 48, 49). Temporally declining rates and time-homogeneous rates in a bounded space cannot be distinguished based on disparity patterns alone (14), but if our attempts to interpret patterns of disparity through time focus on rate variation as the explanatory factor, as we have tended to do (1, 50, 51), then variation in evolutionary rates will seem all too prevalent (49, 52).

Simpson suggested the concept of subzones to differentiate fine-scale ecological diversification within adaptive zones from that among major [“totally distinct, essentially discontinuous” (ref. 2, p. 189)] adaptive zones. To the extent that subzones represent a highly restricted and narrowly circumscribed set of niches relative to the broader adaptive zone of the parent clade, then iterative or replicated patterns of deterministic ecomorphological evolution are perhaps to be expected. The fossil record of North American canids, along with many classic examples of adaptive radiation from the biological literature, such as anole ecomorphs, fits well within this definition, and support for multipeak OU processes may be diagnostic of subzonal diversification. If this hypothesis is correct, then much of what we have learned from empirical studies about the macroevolutionary dynamics of quantitative traits during adaptive radiation has come from a focus on deterministic subzonal radiations that may or may not scale to higher level processes. If early burst- or diversity-dependent–like patterns are to be found in comparative data, they may be restricted to higher level clades (2, 3, 14, 53–55). A renewed focus on understanding patterns of morphological diversification in the fossil record using phylogenetic methods provides our best hope of resolving this question.

It is possible that preference for a multipeak OU model is an artifact of correlations between RLGA and some of the variables used to classify fossil canids to dietary groups (Supporting Information). High convergence rates are expected for univariate traits evolving under BM-like processes (56, 57), and a worst-case scenario in which species are simply divided into regimes based on trait values simulated under BM results in false-positive rates of 100% in favor of a multipeak OU model (Supporting Information). Furthermore, predictive tests suggest that fitted model parameter estimates do not allow BM evolution to be ruled out for RLGA (Supporting Information). I suspect such an artifact is not driving the results obtained here. A large body of ecomorphological work indicates that RLGA convergently responds to macroevolutionary changes in diet among carnivores (58), providing a crucial phenotype environment correlation upon which an adaptive hypothesis can be based (45). Furthermore, the asymmetry of model-averaged rates between hypercarnivory and mesocarnivory (Supporting Information) would not be expected under a Brownian model. Nonetheless, this situation presents a particular challenge for modeling adaptive evolution in the fossil record, where ecological habits must often be inferred directly from traits of macroevolutionary interest or from alternative traits that show substantial correlations with them.

Even if the preferred multipeak OU models are discounted, time-homogeneous or diet-specific rate scenarios receive greater weight than traditional adaptive radiation models for body mass and RLGA. My results therefore add to a growing body of work that provides little support for the generality of time- or diversity-dependent controls on quantitative trait variation (11, 47, 59). There are reasonable explanations for why diversity-dependent regulation of evolutionary rates might go undetected in North American canids. An implicit assumption in this study is that ecological opportunity is determined only by the number of coexisting canid species. The fossil record of North American carnivorans is exceptionally diverse, and species from several clades, including Amphicyonidae, Ursidae, Felidae, and Procyonidae, almost certainly competed with fossil canids for dietary resources (23). Consideration of rates of ecomorphological evolution in a broader phylogenetic context could generate alternative interpretations to those made here. Similarly, the methods used in this study assume a relatively stable environment where the effect of variation in ecological opportunity on evolutionary rate is uniform across dietary groups and through time. This assumption seems questionable, given the trends observed for body size, and more refined models that allow for variation in these parameters would be useful for future tests.

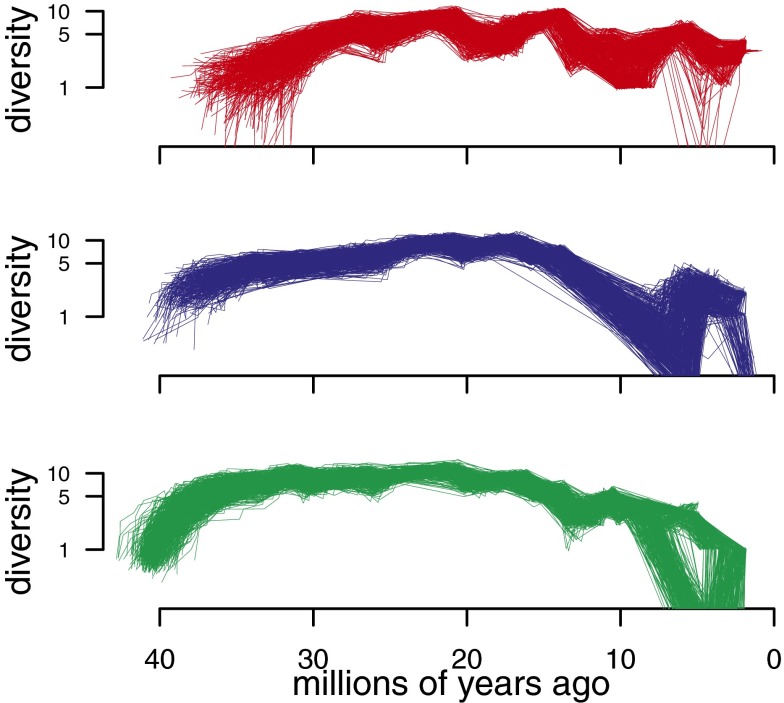
More broadly, ecological opportunity could exert controls on the generation of morphological disparity in subzonal adaptive radiations without acting directly on trait evolutionary rates by regulating transitions between niches. Although I did not directly test for a signal of diversity-dependent transition rates, there is some evidence to suggest that such a process may have been operating. Semilog plots of reconstructed dietary diversity through time show that for most of the Cenozoic, dietary diversity in the North American canid guild remained relatively constant (Fig. 3), despite substantial turnover at the subfamilial and tribal levels (23) (Fig. 1). The most striking example of replicate adaptive radiation, Caribbean anoles, shows exactly this signal, in fact, with strong evidence for diversity-dependent diversification rates on different islands (60) but support for multipeak OU models over diversity-dependent rates or early burst models for ecomorphological traits (47). Tests for diversity-dependent controls on niche occupancy, rather than underlying ecomorphological traits, would be a fruitful avenue for further tests of adaptive radiation in the fossil record.

Fig. 3.

Plots of diversity through time for hypercarnivores (Top), mesocarnivores (Middle), and hypocarnivores (Bottom), estimated using the method of Mahler et al. (21). Diversity is computed from marginal ancestral state estimates, and is therefore more conservative than are raw species counts with respect to uncertainty in dietary history. Trajectories are computed for 500 trees from the Bayesian posterior distribution to accommodate the effects of phylogenetic uncertainty. Note the logarithmic scale on the ordinate, rendering semilog plots.

Materials and Methods

Phylogenetic Inference.

I assembled a matrix of 123 morphological characters coded for 121 canid species plus one outgroup (SI Text). The matrix was largely based on characters described elsewhere (25–27, 61). Although there is some overlap in characters among these sources, character states and codings often differed. I redefined character states, where possible, after merging similar characters and recoded taxa to fit with the new scheme. Some remaining gaps in the matrix were filled in based on primary examination of specimens or by reference to descriptions in the literature. For the final matrix, 30.9% of cells were coded as “?”.

I used fossil tip dating (29) with an independent gamma rate (IGR) uncorrelated relaxed clock model, as implemented in MrBayes version 3.2 (28), to produce a distribution of time-calibrated canid phylogenies for comparative analyses. The stratigraphic range of each species was recorded from work by Wang and coworkers (25–27), and the last appearance date was assigned as a point constraint on occurrence time. I placed a relatively broad exponential prior (λ = 127) on the variance of the gamma distribution for the IGR model, and a log-normal prior on the clock rate (mean = −6, SD = 0.1). Tip dating neglects information from species’ stratigraphic ranges, and preliminary analyses revealed that not accounting for first appearance dates resulted in unreasonably old divergence times (e.g., a Cretaceous origin for Canidae). I used a topology-only analysis before time calibration to identify unambiguous (PP = 1) nodes that could be constrained. The oldest first appearance date for members of each of the 15 clades, plus the root node, was used to define the offset for an exponential age prior on that node. The mean of each exponential distribution was chosen to generate a reasonable age range, typically with a mean of ∼2 My older and a 95% upper bound within 5 My of the first appearance date. I imposed slightly narrower priors on younger divergences. For both analyses, I used the default Markov model for morphological data, with coding set to variable and gamma-distributed rates. Two runs with four chains (three heated and one cold) were run for 1 million (topology only) and 5 million (time calibration) generations, sampling from the chain every 100 generations. After ensuring convergence using MrBayes diagnostics and trace plots of posterior sample values, I discarded the first 25% of samples. For the topology search, node support was assessed from a maximum clade credibility tree produced from the retained sample.

Morphological Data and Analyses.

I collected morphological measurements from fossil and living canid specimens housed in the collections of the American Museum of Natural History and National Museum of Natural History. Measurements were taken using Mitutoyo digital calipers to 0.01-mm precision. I estimated body masses for fossil canids from lower m1 lengths, using Van Valkenburgh’s regression equation (62). Mass estimates were ln-transformed before computing species means. Sample sizes ranged from 1 to 96 individuals per species for m1 length (median = 4) and 1–77 individuals per species for RLGA (median = 4).

I classified fossil canids to one of three dietary categories (hypercarnivore, mesocarnivore, or hypocarnivore) using LDA implemented in the Modern Applied Statistics with S (MASS) (63) package for R (64). The training set consisted of five well-represented and informative craniodental variables (relative blade length, blade size relative to jaw length, relative size of the lower second molar, mechanical advantage of the temporalis muscle, and robustness of the lower fourth premolar) measured for 21 extant canid species, nine procyonids (representing all genera except Nasuella), and Ailurus fulgens. Noncanid species were included because fossil canids exhibit more extreme adaptions to hypocarnivory than is realized in the extant radiation (25). This suite of craniodental traits permitted classification of fossil canid species without direct reference to the traits analyzed for evolutionary pattern (i.e., body size, RLGA), although correlations among all traits should be borne in mind when interpreting results (SI Text). Due to the fragmentary nature of much fossil material, I performed a series of discriminant analyses, iteratively reducing the number of variables to maximize species coverage. Two taxa, Enhydrocyon stenocephalus and Urocyon galushi, were classified using alternative variables. The classifications for these taxa were consistent with expectations based on congeners.

I estimated transition rates between dietary regimes under a Markov model using the fitDiscrete() function in geiger version 2.0 (65). Five hundred trees were sampled at random, without replacement, from the Bayesian posterior distribution, and models were fitted under equal (k = 1), symmetrical (k = 3), and all different (k = 6) rates models. Model fit was assessed by computing small sample AICcWs, which give a measure of relative support for each model, given the candidate pool. I also computed model-averaged rates (SI Text). To visualize the evolution of dietary strategy, I computed marginal ancestral state probabilities (66) on the best tree using the phytools library (67).

To understand the dynamics of body mass and RLGA evolution, I fit models of continuous trait evolution to the random sample of 500 trees. Constant-rate BM, temporally accelerating/decelerating rate, and trended random walk models were fitted using the fitContinuous() function in geiger. I fit diversity-dependent rate models using the fitDiversityModel() function in the phytools library (67). The ψ-parameter of the diversity-dependent models determines the magnitude and direction of change in rate per unit change in diversity, and is expected to be negative for a classic diversity-dependent process (21). I fit two permutations of the diversity-dependent rate model. In the first, I assumed a single regime, corresponding to a general lineage diversity dependence. For the second, lineage diversity was estimated based on dietary regimes, thereby allowing rates to vary as a function of dietary diversity through time. I fit multipeak OU and diet-specific Brownian rate (BMV) models using the OUwie library (68). Although it is possible to fit multipeak OU models that also allow α and ${\sigma }^2$ to vary across selective regimes, simulations show that parameter estimates are unreliable unless the number of terminals in the tree is exceptionally large (68). Because I was specifically interested in estimating the parameters of the OU model, I therefore restricted my analyses to models constraining α and ${\sigma }^2$ to be constant over states. I based model selection on computation of AICcW.