Synaptic diversity enables temporal coding of coincident multi-sensory inputs in single neurons

Abstract

The ability of the brain to rapidly process information from multiple pathways is critical for reliable execution of complex sensory-motor behaviors, yet the cellular mechanisms underlying a neuronal representation of multimodal stimuli are poorly understood. Here we explored the possibility that the physiological diversity of mossy fiber (MF) to granule cell (GC) synapses within the mouse vestibulocerebellum may contribute to the processing of coincident multisensory information at the level of individual GCs. We found that the strength and short-term dynamics of individual MF-GC synapses can act as biophysical signatures for primary vestibular, secondary vestibular and visual input pathways. The majority of GCs receive inputs from different modalities, which when co-activated, produced enhanced GC firing rates and distinct first spike latencies. Thus, pathway-specific synaptic response properties permit temporal coding of correlated multisensory input by single GCs, thereby enriching sensory representation and facilitating pattern separation.

In order to represent and process information from complex natural events, the brain must integrate signals from multiple senses¹, as well as those arising from self-generated actions². Several studies have shown that convergence of functionally distinct inputs occurs at the level of single neurons in the neocortex^3-5, superior colliculus⁶, striatum⁷, and cerebellum⁸. To date the primary neuronal computation reported for multimodal integration is to increase firing rate upon coincident cross-modal stimulus (either subadditive, additive, or superadditive), thus enhancing saliency of a particular event^1,9. Short-term plasticity can provide an additional non-linearity that can contribute to neuronal computations of unisensory feature-selectivity^10,11, but it remains to be determined how individual synaptic response properties could contribute to multimodal processing. Thus a pertinent question is how the diversity of synaptic efficacy and dynamics, observed throughout the brain^3,12-14, can be exploited to encode spike representations of multi-sensory information.

Cerebellar granule cells (GCs) are the most numerous neurons in the brain and relay rich contextual information from mossy fibers (MFs) to Purkinje cells (PCs) in order to fine tune motor behaviors with tens of milliseconds precision¹⁵. Theoretical models suggest that large divergent connectivity of single MF to many GCs, and the mixing of different input features onto single GCs, support expansion recoding in the GC layer. This network property is thought to enhance pattern decorrelation and thus increase the number of distinct input activity patterns to be “learned” by PCs^16-18. However these models neglect the contribution of MF-GC synaptic diversity that may substantially influence the formation of not only spatial, but also temporal patterns of active GCs¹⁹.

Their short dendrites (~ 15 μm) and small numbers of synaptic inputs make GCs ideally suited for 1) examining the diversity of synaptic behavior²⁰, 2) identifying the type of information conveyed by different synaptic inputs^21,22, and 3) establishing the direct influence of synaptic behavior (without dendritic filtering or nonlinearities) on the output firing of single neurons²³. We found that input-specific synaptic behaviors and mixed sensory innervation of single GCs provide a mechanism for coding multi-sensory events by their response onset.

Results

Diversity of MF-GC synaptic behavior

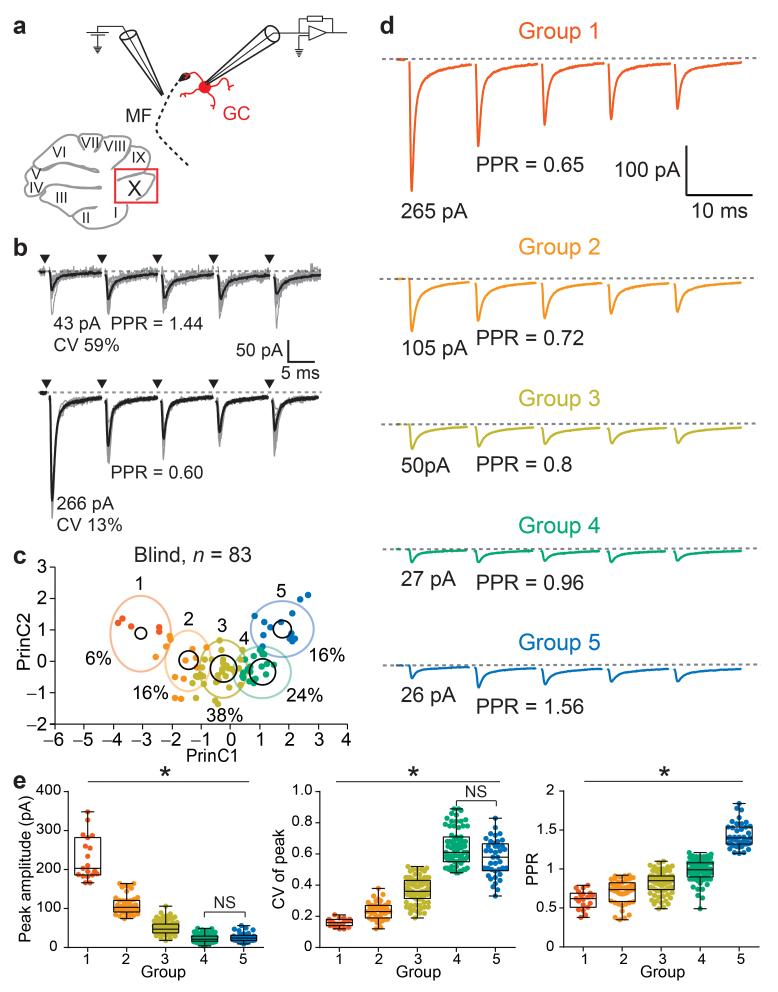
MF-GC synapses exhibit a striking diversity in strength and short-term plasticity across connections^20,24. We investigated the functional properties of MF-GC synapses within nodulus (lobule X), a region of the vestibulocerebellum in which the origins of MF projections have been well characterized²⁵. This region of the vestibulocerebellum receives projections primarily from medial vestibular nucleus (MVe), nucleus prepositus hypoglossi (PrH; optokinetic²⁶ and object motion⁸, referred to as “visual”), and direct projections from the vestibular ganglion (VG)²⁵. Unitary AMPAR-mediated synaptic currents (EPSCs) were evoked from single MFs using a blind, minimal stimulation protocol²⁰ (Fig. 1a). MF-GC EPSCs were highly heterogeneous across connections (Fig. 1b): initial mean amplitude varied from 10-290 pA, the within input trial-to-trial variability (coefficient of variation, CV) varied from 0.1-0.7, and the paired-pulse ratio (PPR) varied from 0.4-1.8 (n = 83; Supplementary Fig. 1a). Since we observed striking correlations between these EPSC metrics (Supplementary Fig. 1b), we performed a K-Means clustering analysis (KMC), leading to the identification of five groups of inputs (Fig. 1c), which accounted for nearly 80 % of the variance of EPSC metrics across the entire population of inputs (Supplementary Fig. 2). MF input groups were numbered and arranged in descending order according to the peak amplitude of their average EPSC (Fig. 1d). The mean CV and PPR for each group were larger for smaller inputs (Fig. 1e), consistent with a potential source of diversity arising from the different properties of vesicular release of neurotransmitter.

Figure 1.

Identification of MF-GC input types using K-Means clustering analysis of EPSC properties. (a) Diagram of a parasagittal slice of cerebellar vermis, showing the vestibular region (lobule X) where single MF-GC connections were studied using extracellular stimulation and postsynaptic whole-cell voltage-clamp recording of unitary EPSCs. (b) Unitary EPSCs from individual trials (gray traces) and mean (black trace) from two example MF-GC synapses (arrowheads indicate timing of stimulation). EPSC peak amplitude, coefficient of variation of the peak amplitude (CV), and paired-pulse ratio (PPR) were used for cluster analysis. (c) Plot of the two principal components (PrinC) calculated using the K-Means clustering algorithm on 259 inputs. Data points are experiments in which blind stimulation was performed (n = 83 inputs). Black circles are the cluster centers with an area proportional to the number of points inside the cluster. The percentage of inputs in each cluster are indicated (%). Color-code is used throughout all figures referring to input groups. (d) Averaged traces, calculated from each cluster or “Group” (n inputs are 19, 44, 81, 74, and 41 for groups 1-5). (e) Summary plots of EPSC metrics according to group for all 259 inputs. Box plots represent quantiles (minimum, 25 %, median, 75 % and maximum values).

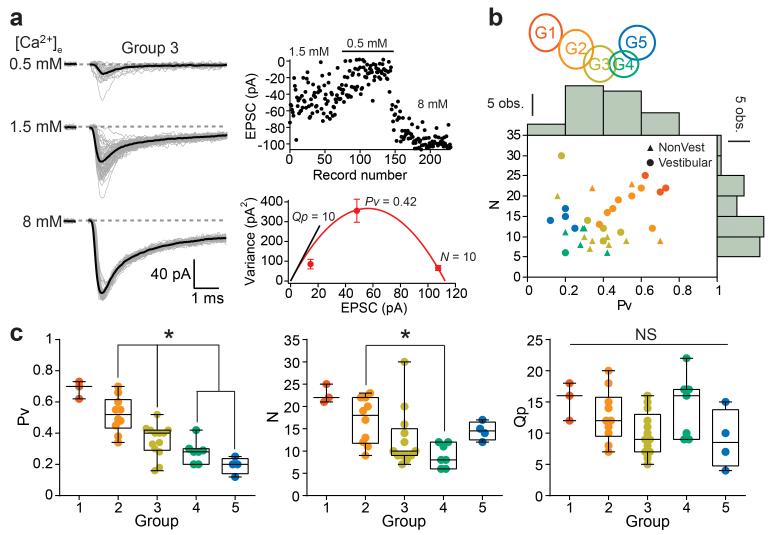
Using multiple probability fluctuation analysis²⁰ (Fig. 2a) we observed significant differences across groups in the number of release sites (N) and release probability per vesicle (Pv), but did not detect a difference in quantal size (Fig. 2b,c). Large inputs with low CV required both high Pv and N, while small inputs comprised low Pv and N. The PPR was not always correlated with Pv: notably input groups 4 and 5 have a similarly low Pv, but only inputs from group 5 exhibit short-term facilitation. Thus we identified several functionally distinct classes of MF-GC synapses, which differ primarily in their presynaptic properties, suggesting they might belong to distinct MF input pathways.

Figure 2.

Multiple probability fluctuation analysis reveals the origin of synaptic diversity (a) Unitary EPSCs recorded in three different extracellular [Ca²⁺] ([Ca²⁺]_e). (Top right) Peak amplitudes of EPSCs. (Bottom right) Variance versus mean plot and a fit with a multinomial model (eq. 1, red trace) in order to estimate the release probability per vesicle (Pv, 1.5 mM [Ca²⁺]_e), number of release sites (N, x-intercept) and quantal amplitude (Qp, slope of black line). Error bars represent errors in estimating the variance (eq. 3). (b) KMC schematic indicates color code for different clusters or groups. Distribution of N and Pv with histograms displayed at the edge of the plot. Data were pooled from inputs recorded both in vestibular (circles, n = 20 inputs) and non-vestibular regions (triangles, n = 17 inputs) of the cerebellar vermis. (c) Cross group comparison of Pv, N, and Qp (n = 3, 10, 13, 7, and 4 inputs, respectively), with only Qp not showing a co-variance with synapse type.

Input pathway-specific synaptic behavior

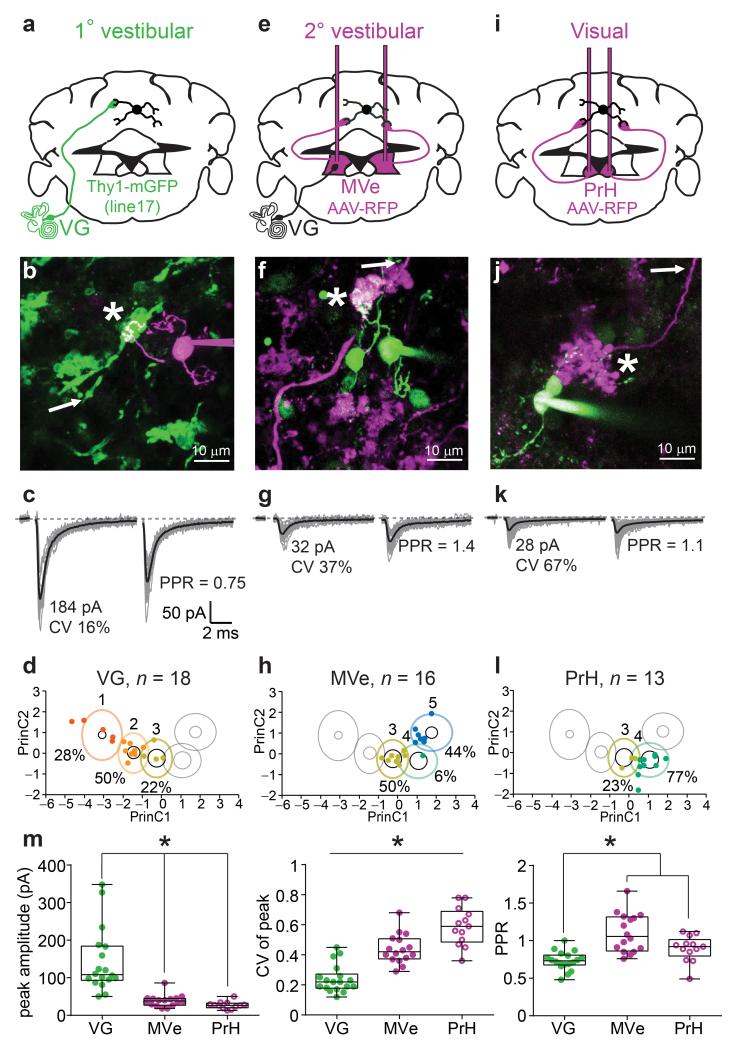
In order to examine whether different precerebellar projections comprise different functional classes of MF synapses, we identified single MFs for targeted stimulation in acute brain slices using various strategies of genetic expression of fluorescent proteins. Of the three principal precerebellar structures projecting to the vestibulocerebellum, we found that only the VG expressed GFP in a Thy1-GFP transgenic mouse line (Supplementary Fig. 3). MVe and PrH neurons were fluorescently labeled by stereotaxic injection of an adeno-associated virus expressing turbo red fluorescent protein (TurboRFP; Supplementary Fig. 4). We then used simultaneous two-photon fluorescence imaging and Dodt contrast to selectively stimulate fluorescently labeled MFs (Supplementary Fig. 5). EPSCs evoked from VG MFs were large, and exhibited a low CV and strong short-term depression, with 80 % of the synaptic responses being classified (using KMC) as group 1 or 2 (Fig. 3a-d). EPSCs evoked from MVe and PrH MFs had small mean amplitudes, large CV, and short-term plasticity ranging from little depression to strong facilitation (Fig. 3e-l). Ninety four percent of inputs from MVe MFs were categorized as groups 3 and 5 (Fig. 3h), while 82 % of PrH MF inputs were categorized as group 4 (Fig. 3l). The results of KMC were corroborated by statistical differences for EPSC mean amplitude and CV between the different MF projections (Fig. 3m). The PPR of VG MF inputs were significantly smaller than either of the other projections types, but because MVe MFs conveyed both depressing and facilitating inputs (groups 3 and 5) we did not detect a difference in PPR as compared to MF inputs arising from PrH. These data demonstrate that visual, primary and secondary vestibular pathways utilize distinct classes of MF inputs with distinct synaptic behaviors.

Figure 3.

Pathway-specific MF-GC synaptic properties. (a) Schematic diagram showing the vestibular ganglion (VG), origin of labeled MFs in a transgenic mouse line (green, Thy1-mGFP (line 17)). (b) 2PLSM image of identified connection (star) between a GFP-expressing MF (green) and a GC filled with Alexa 594 (magenta) during whole-cell recording (the arrow indicates the position of the stimulation pipette placed using simultaneous Dodt contrast). (c) Unitary EPSCs recorded from the synaptic connection in b. (d) Cluster identification of inputs evoked from all 1° vestibular MFs (n = 18 inputs). (e,i) Same as in a, except MFs expressed turboRFP (magenta) following AAV9 injections in medial vestibular (MVe) and prepositus hypoglossi nucleus (PrH), respectively. (f,j), same as in b, except GCs were filled with Alexa 488 (green). Note, previously patched GCs are still apparent. (h,l) same as in d, for MVe (n = 16 inputs) and PrH inputs (n = 13), respectively. (m) Summary plots of EPSC metrics across MF-GC pathways. Only statistically significant differences are indicated.

Sensory-specific EPSC properties in vivo

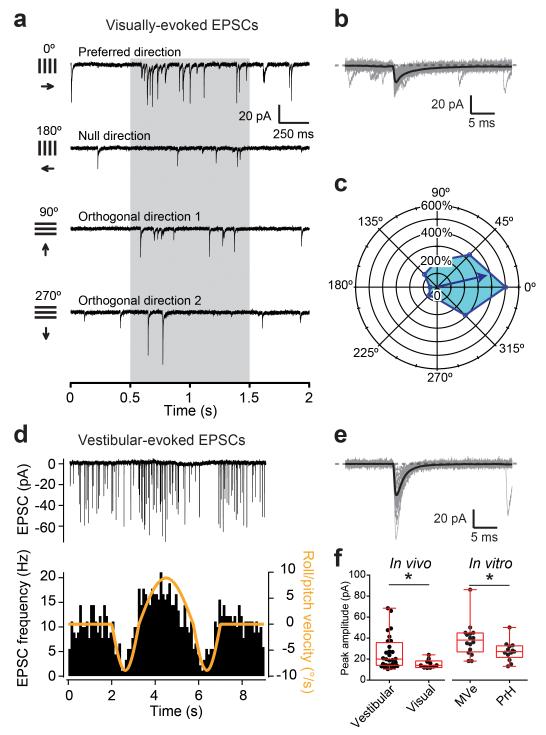
To directly examine whether MF-GC synaptic properties differ according to the sensory modalities they convey, we recorded sensory-evoked EPSCs from GCs in the vestibulocerebellum (flocculus) in vivo from anesthetized mice²¹. Visual pathways were stimulated using drifting gratings of different orientations (Fig. 4a-c), and vestibular pathways were stimulated by whole-body rotation (Fig. 4d,e). Spontaneous EPSC rates were 9.1 ± 6.0 vs. 5.5 ± 5.2 Hz (mean and SD), for cells in which vestibular (n = 28) and visual inputs (n = 10) could be evoked, respectively. We found that EPSCs evoked by moving gratings in the preferred direction were smaller by a ratio of 1:1.7-fold on average than those evoked by vestibular stimulation (Fig. 4f, left), and did not depress significantly during the stimulus presentation (Supplementary Fig. 6). The ratio of amplitudes of vestibular versus visual-evoked responses were consistent with in vitro results, provided that we pooled only MVe inputs as the “vestibular” population, since flocculus does not receive primary vestibular afferents²⁵, and considered PrH as the “visual” population of MF inputs (PrH inputs were 1.4 times smaller than MVe inputs, Fig. 4f, right). Taken together both our in vitro and in vivo findings demonstrate that the MF-GC synaptic behavior is input pathway-specific and thus acts as a biophysical signature of input modality.

Figure 4.

In vivo demonstration of sensory-specific MF-GC synaptic properties. (a) Example of current traces recorded from GCs in voltage-clamp in vivo during the presentation of visual gratings of different orientations. The grey shaded areas indicate the periods when the gratings moved. (b) Visual motion-evoked EPSCs (gray) and average EPSC waveform (black) for the cell in a. (c) Polar plot showing the direction tuning of the cell shown in a. (d) (Top) evoked EPSCs in GCs in response to an in vivo vestibular stimulation around the roll/pitch axis. (Bottom) EPSC frequency modulation follows the velocity stimulus waveform. (e) Evoked EPSCs (gray) and average EPSC waveform (black) for the cell in d. (f) (Left) vestibular (n = 28 inputs) and visual (n = 10) EPSCs have different peak amplitudes in vivo. (Right) the same trend is observed in EPSC recordings from acute slices (in vitro) when stimulating MVe (n = 16 inputs) and PrH MFs (n = 13).

Convergence of multimodal inputs onto single GCs

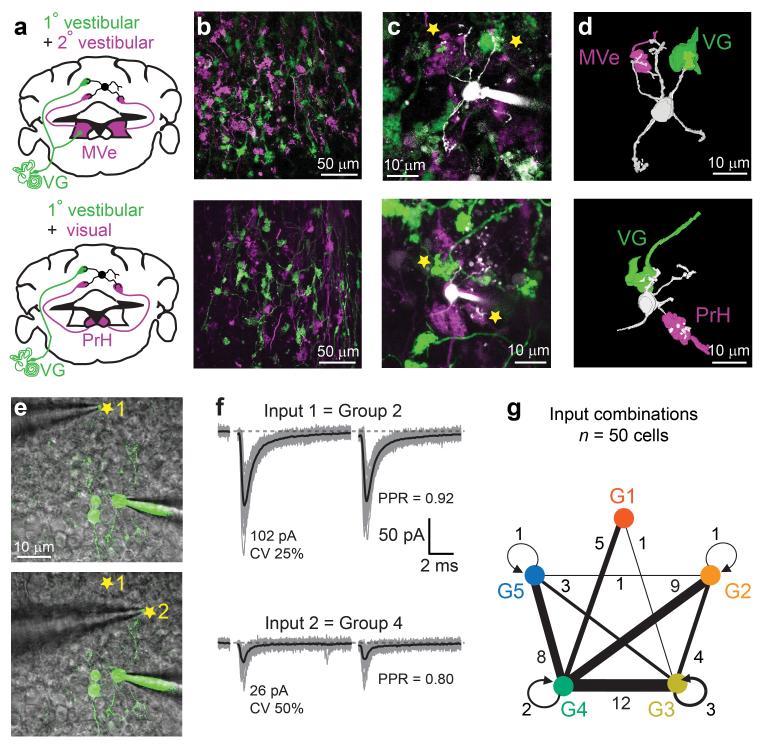
To determine how input-specific synaptic properties might facilitate multi-modal integration, we examined whether single GCs were innervated by multiple MF inputs carrying different sensory signals, which has been shown to occur for efferent inputs in a cerebellar-like structure in weakly electric fish²⁷, and in other regions of the rodent cerebellum²⁸. We therefore performed stereotaxic viral injections in Thy1-GFP mice (labeling VG) in order to express turboRFP in either MVe or PrH MFs (Fig. 5a,b). Innervation patterns were then determined by labeling single GCs in acute slices using whole-cell loading of Alexa 594, then examining if GC dendrites contacted GFP or turboRFP-positive MFs. We found that GCs were frequently contacted by VG and MVe (27 %; n = 43 labeled GCs; Fig. 5c,d), as well as VG and PrH MFs (15 %; n = 35 GCs). These data indicate that mixed-modal innervation is a prominent wiring feature in the GC layer, allowing single GCs to integrate synaptic inputs carrying primary and secondary vestibular (VG vs. MVe), as well as vestibular and visual modalities (VG vs. PrH).

Figure 5.

Multimodal convergence onto single GCs. (a) Double labeling of primary and secondary vestibular afferents, or primary vestibular and visual afferents. AAV9-RFP was injected in MVe or PrH (magenta) of transgenic animals (green, Thy1-mGFP (line 17)). (b) Example 2PLSM images of fluorescent MFs in VC. (c) Example GCs filled with Alexa 594 (white) which were found to be connected to VG and MVe or PrH MFs (stars). (d) 3D reconstructions of the connected GCs and MFs shown in c. (e) Blind stimulation of two MF inputs in single GCs. Superimposition of a 2PLSM image of a GC filled with Alexa 594 (green) and an infrared Dodt contrast image showing the positions of the stimulation electrode (stars) where two different inputs were evoked. Other labeled GCs are from previous attempts. (f) EPSCs evoked from locations shown in e. KMC was used to identify input type. (g) Summary of MF inputs type pairs observed in single GCs. Thickness of connecting lines between groups indicates frequency that a pair was observed (values are number of observations per pair). Circular arrows represent GCs where the two evoked inputs belonged to the same group.

Because the functional properties of many synapses are target cell-dependent²⁹, we next examined whether different MF-GC synapses impinging on the same GC preserve their pathway-specific synaptic behavior. Blind stimulation of two different MF inputs onto single GCs (n = 50), followed by a post-hoc KMC (Fig. 5e,f), indicated that a vast majority of GCs received MF inputs belonging to at least two different input groups (n = 43/50 input pairs; Fig. 5g). Moreover, MF inputs characteristic of VG and MVe (i.e. groups 1 and 2 or groups 3 and 5) were often associated with the PrH input group 4 (34/50). These results corroborate the anatomical findings and demonstrate that 1) the functional properties of MF-GC synapses are determined by the input pathway, 2) GCs are generally contacted by MFs originating from different input pathways, and 3) mixed innervation of single GCs often involves different sensory modalities.

GC integration of pathway-specific synaptic inputs

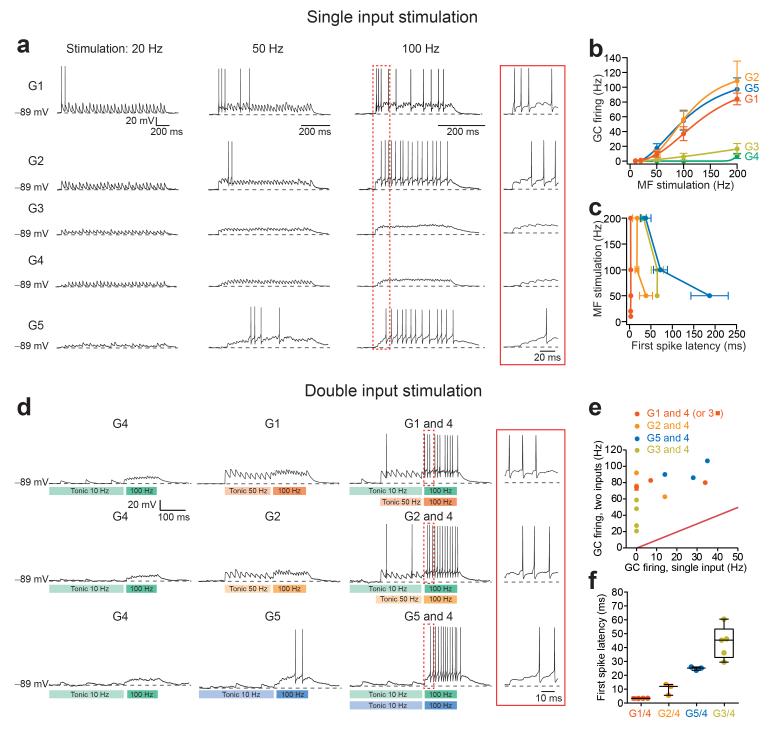
To investigate whether the convergence of different MF pathways could support distinct GC spike representations, we first examined how GCs integrate the different MF input types. We performed blind stimulation of MF-GC synapses at different frequencies and monitored GC membrane voltage in whole-cell current-clamp mode. For these experiments, NMDARs were not blocked since they are known to participate in synaptic integration²³. It should be noted that in order to examine MF transmission and integration in isolation, GABA_ARs were blocked, which also blocked their tonic activation³⁰ and thereby increased the apparent excitability of GCs. Each input was first characterized in voltage-clamp, and then classified offline, using KMC. As expected from their large synaptic conductance, single MFs from groups 1 and 2 produced robust GC firing for stimulation frequencies above 50 Hz, with short first spike latencies (Fig. 6a-c). Regardless of frequency, the first EPSP of group 1 inputs exhibited a high probability of firing (79%, n = 7 cells). On the other hand, MF inputs from groups 3 and 4 produced little, if any, GC firing for stimulation frequencies up to 200 Hz. Interestingly, group 5 MF inputs also produced robust firing, despite the small amplitude of single EPSCs. This was due to synaptic facilitation and temporal integration of EPSPs, which in turn resulted in longer first spike latencies (Fig. 6a,c). The differences in EPSC amplitude and short-term plasticity are reminiscent of “driver” and “modulatory” synaptic input types within thalamus and cortex¹⁴. In the remaining sections we will refer to inputs from groups 1, 2, and 5 as driver inputs because they induced GC firing alone. Inputs from groups 3, and 4 we will refer to as supporting inputs, rather than “modulatory inputs,” which unlike MF inputs, activate mGluRs¹⁴.

Figure 6.

Input-specific synaptic integration in single GCs. (a) Representative current-clamp traces showing GC EPSP trains and resulting action potentials evoked with trains of 30 stimuli at 20, 50, and 100 Hz of each MF input type. Inset shows early EPSP summation, illustrating the relative delays of 1^st spike from the onset of stimulation. (b) Input/output (I/O) relationships for MF types from groups 1-5 (n = 3, 6, 8, 5 and 7 inputs, respectively). (c) Delays between 1^st evoked spike and onset of stimulation vary between input groups. Note that for G1 1^st spike timing rapidly follows stimulation onset at all frequencies. (d) Voltage responses of single GCs evoked from individual and simultaneous stimulation of supporting and driver MF inputs. In vivo-like baseline and stimulus-driven activity are indicated in the underlying boxes. Early EPSP summation shown inside the inset, demonstrates combination-specific delays, akin to those obtained with single driver MF input stimulation without baseline tonic activity (see a). (e) Comparison of single inputs driving GC firing (groups 1, 2, 5, and 3; n = 4, 3, 3, and 4 cells, respectively) vs. when combined with input group 4 (note in one case a group 1 input was paired with a group 3 input). (f) Summary plot of combination-specific first spike latencies (within the category labeled G1/4 we included a combination between group 1 and group 3).

GC integration represents mixed-modal activation

We next set out to determine how GCs transformed coincident activation of different combinations of MF input types. Because vestibular MFs exhibit tonic firing rates that allow encoding of preferred and non-preferred direction of head movements by bidirectional modulation²¹, MFs stimulation included an initial train of 10 pulses delivered at a frequency corresponding to the tonic firing of each afferent type in vivo: input groups 1 and 2 (primary vestibular) were set to 50 Hz³¹, and input groups 3-5 were set to 10 Hz according to our in vivo measurements. The stimulation onset for input groups 3, 4, and 5 was delayed by 3 ms to account for polysynaptic delays. Following the tonic firing period, all MFs were stimulated 10 times at 100 Hz, a firing frequency in the range of vestibular neuron activity³², as well as of eye movement-related stimuli (saccades) in PrH²⁶. Tonic MF firing dramatically reduced the ability of input groups 1 and 2 to engage GC firing because of synaptic depression, while the 10 Hz tonic MF firing did not appreciably change the impact of group 5 inputs (Fig. 6d). Vestibular driver inputs (groups 1, 2, and 5) were often found to co-innervate single GCs with visual supporting input (group 4, PrH). Simultaneous stimulation of driver and supporting inputs produced a robust enhancement of GC firing rate (Fig. 6d,e), reminiscent of super-additive multi-sensory integration observed in superior colliculus⁹. Moreover, the first spike latencies of GCs responses from the onset of 100 Hz stimulation were markedly different across the different input combinations (Fig. 6d,f), and mirrored the firing onset delays of the individual driver inputs when stimulated without spontaneous activity (Fig. 6c). Combinations of inputs from groups 1 and 4 produced spikes on the first simultaneous synaptic stimulation, resulting in a delay of less than 4 milliseconds. Combinations of inputs from groups 2 and 4 and from groups 5 and 4, produced spikes on the first or second (delay: 10 ms) and third synaptic stimulation (25 ms), respectively. Additionally, we recorded GC output in response to simultaneous stimulations of group 3 and 4 inputs. Neither input drove GC firing on its own, however the combination of the two was sufficient to produce a few action potentials (Fig. 6e), and interestingly, with longer latencies (44 ms) than in response to combined group 5 and 4 inputs (Fig. 6f).

In order to examine the effect of a wide range of stimulation frequencies on GCs output and the effect of tonic inhibition³⁰ we used an established synaptic and integrate-and-fire (sIAF) model²³. The synaptic parameters were adjusted to mirror the mean EPSC and short-term plasticity for each input group. First, we verified that indeed the model could replicate recorded GC input-output curves (I/Os) and first spike latencies (Supplementary Fig. 7a-c). We then simulated co-activation of vestibular driver inputs (groups 1, 2, or 5) and visual supporting input (group 4, PrH) as in experiments (Fig. 6). The simulations corroborated our experimental results, namely that tonic firing activity induces steady-state synaptic depression of groups 1 and 2 inputs, that input combinations greatly increase GC responses, and that first-spike latencies were combination-specific (Supplementary Fig. 7d,e).

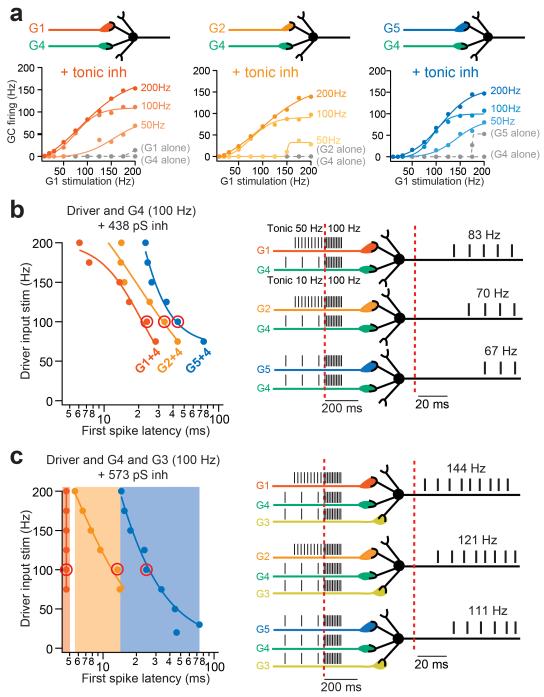
Under physiological conditions, GCs receive Golgi cell-mediated inhibition, 98 % of which is thought to be mediated by tonic activation of GABA_ARs³⁰. Moreover, it is thought that a minimum of 3 active MF inputs are necessary to drive GC firing^{17, 22}in the presence of tonic inhibition. Because these two parameters are difficult to implement in situ we used our sIAF model to examine their impact on GC integration of co-activation of modality-specific inputs. The combination of synaptic depression and tonic inhibition prevented single driver inputs from evoking GC firing for MF stimulation rates below 175 Hz (Fig. 7a, gray traces). However, when one driver and one supporting input were combined, GC output was again strongly enhanced, exhibiting increase in gain and dynamic range, but required higher frequency from the supporting input, as compared to without tonic inhibition (Fig. 7a vs. Supplementary Fig. 7f). Thus synaptic depression and tonic inhibition ensure that only co-activated inputs induce significant GC firing.

Figure 7.

Model GCs respond to co-activation of multiple sensory pathways with specific onset delays. (a) Simulated GC I/O curves in response to combinations of different MF types in the presence of 438 pS tonic inhibition using a synapse-based integrate-and-fire model (sIAF). Driver inputs (G1, 2, and 5) were combined with the supporting input (G4) driven at different frequencies (indicated on the right hand side). sIAF I/Os from individual input groups are plotted as dashed gray curves. (b) (Left) combination-specific first spike latencies for different simulated driver input frequencies. Red circles indicate example delays for each input combination shown in right schematic, in response to co-activation of both inputs at 100 Hz, on background spontaneous MF firing rates observed in vivo (50 Hz for primary vestibular and 10 Hz for secondary vestibular and visual afferents). (c) Similar simulation as in b, except with co-activation of a third MF input (group 3) and a 30 % increased tonic inhibition. Note that combinations of three inputs produce distinct delays according to the type of driver input (shaded area, left).

The simulations also predict that in the presence of tonic inhibition each input combination elicits a characteristic frequency-dependent range of delays in GC firing, relative to the time of cross-modal stimulus presentation (Fig. 7b). Combinations of inputs from groups 1 and 4 produce spikes with delays from 6 to 28 ms, groups 2 and 4 from 14-44 ms, and finally groups 5 and 4 from 24-74 ms. In order to examine the influence of a third input we chose the other supporting input, group 3 (secondary vestibular), which often combines with driver inputs (Fig. 5g). Tonic inhibition was also increased by 30 % in order to account for the increase in MF drive to Golgi cells¹⁷. With 3 co-activated inputs, GCs first spike latencies uniquely represented the type of driver input by distinct first spike latencies, with no frequency dependence for group 1 (5 ms across frequencies vs. 6-14 ms for group 2, and 15-74 ms for group 5; Fig. 7c). Thus the sIAF model predicts that under physiological conditions delays in GC firing from the start of concomitant MF activation can be used as a temporal signature of the specific combinations of MF inputs.

Model GC response latencies enhance pattern decorrelation

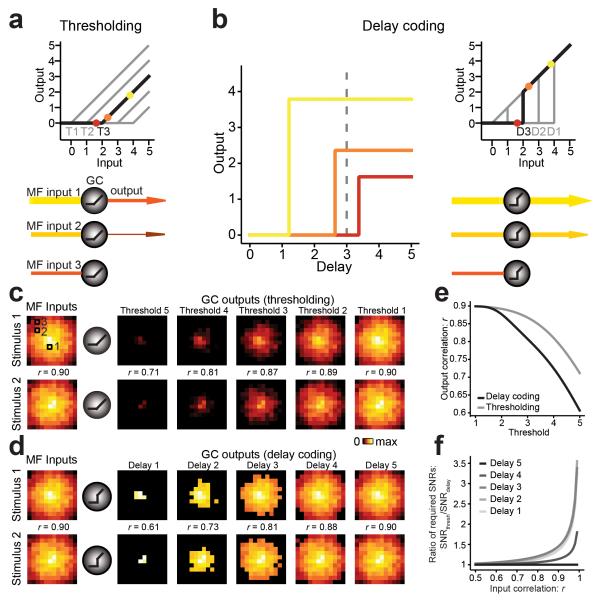
One proposed function of the GC layer is to reduce pattern overlap between representations of similar stimuli to facilitate their discrimination by PCs^{16-18, 33}. We explored potential benefits of differential GC response delays in enhancing the discriminability of stimulus representations using a simplified computer model of an array of GCs receiving similar but not identical patterns of MF inputs. One mechanism of reducing pattern overlap originally proposed by Marr¹⁸ is sparsening of representations by applying a threshold such that only strongly activated GCs will fire. In the thresholding model, once the threshold is crossed the GC output linearly increases with input strength (Fig. 8a). We implemented a simplified delay coding model, where the output strength (represents firing rate in arbitrary units) is equal to the input strength (represents total synaptic current in arbitrary units), but only after a delay, which itself depends on the input strength (Fig. 8b). This property of the model mimics the inverse relationship between net synaptic input (sum of active MFs) and output response delays observed at the MF-GC synapse. At short delays, therefore, only strongly activated GCs cross threshold (Fig. 8b). The I/O function at a fixed delay D is therefore characterized by a discontinuity in GC output when the delay-dependent threshold is crossed. GCs were set to maintain their firing rate during the duration of the input, akin to what we observed experimentally (Fig. 6d).

Figure 8.

Delay coding enhances pattern decorrelation. (a,b) Schematic diagrams of thresholding and delay coding models. Color code refers to open squares in c. In both models GCs only generate output if their input exceeds a certain threshold (T). In the thresholding model this output is proportional to the difference between input and threshold. In the delay coding model the output follows the input after a delay (D) that is shorter for stronger inputs. The input-output transform at a fixed delay expresses a discontinuity (“jump”) in the GC output at the delay-dependent threshold. The resulting GC output exceeds that of the thresholding model for any suprathreshold input strength. (c) Left of schematic GCs is an image map of MF inputs (equivalent to net synaptic current, coded as pixel intensity) for two similar patterns. Right of schematic GCs is the GC output response maps (equivalent to firing frequency) for the thresholding model. Each panel shows the same random subset of 144 cells. Cells are arranged by decreasing average input intensity from center to periphery. Pattern overlap as quantified by Pearson correlation r is indicated for each pair. (d) Same as c but output patterns are calculated using the delay coding model. (e) Pattern decorrelation (r) in the large N limit as a function of the threshold. Delay coding (black) achieves substantially stronger decorrelation (lower r values) than thresholding (gray). (f) Relative improvement of delay coding model, estimated from the ratio of output SNRs required for reliable pattern discrimination by a linear classifier. Note the delay coding model can improve the decorrelation by up to 3-fold. The largest value graphed corresponds to input correlation r = 0.99.

We compared the decorrelation performance of the threshold model to that of the delay coding model. Overlapping pairs of input patterns of net synaptic input strengths were created using a correlated joint normal distribution with a mean ± SD of 2 ± 1 across N = 1,000,000 GCs. For a random subset of model GCs, inputs and their corresponding outputs are shown as images where pixel intensity is either input strength or output response for a particular GC (Fig. 8c,d). To determine the decorrelation performance of each model we quantified the overlap between pairs of input and corresponding output patterns by calculating the Pearson product moment correlation coefficient r. We found that the I/O transformations resulting from both models were able to generate substantial decorrelation (i.e. output r values are smaller than input values; Fig. 8c,e). However, for short delays the decorrelation obtained with delay coding was substantially more pronounced than decorrelation achieved by thresholding (r = 0.61 vs. 0.71 for delay 1 and threshold 5 respectively). Intuitively, this is explained by the jump in the GC I/O function, which enhances “contrast” between active and non-active GCs compared to the continuous threshold model. Delay coding provided better pattern decorrelation for strongly correlated inputs (r > 0.5), but not when paired inputs were already dissimilar (Supplementary Fig. 8). With longer delays, the decorrelation performance became gradually more similar between delay coding and thresholding as the discontinuity in the delay coding model became less pronounced. To estimate the relative contribution of delay coding to pattern separation, we quantified the pattern discriminability using an optimal linear classifier in the presence of output noise. Specifically, we asked how much noise could be added to the decorrelated patterns before the percentage of misclassifications exceeded a preset threshold (e.g. 5 %). Then we calculated a signal to noise ratio (SNR). The delay coding model routinely detected small differences in patterns with lower SNRs than the thresholding model, suggesting improved discriminability. For difficult discriminations the delay coding model reached classification criterion at 3-fold lower SNR than the threshold model (Fig. 8f). This measure of relative improvement was insensitive to the specific threshold chosen. Taken together, the experimental results and delay coding simulations show that variable GC spiking delays support enhanced decorrelation of input activity patterns relative to the standard thresholding model proposed by Marr, and thus can better represent rich spatiotemporal patterns of MF activity.

Discussion

Diversity in synaptic strength and short-term plasticity is ubiquitous across excitatory connections. Here we demonstrate that the diversity within a single anatomical class of inputs (cerebellar MFs) reflects the heterogeneity in synaptic signatures representing different MF input pathways. In the case of the vestibulocerebellum, we found that different sensory modalities (primary vestibular, secondary vestibular, and visual) converge onto single GCs and preserve their functional signatures. Integration of these inputs by single GCs results in distinct output firing representations of specific correlated multimodal input combinations. This temporal coding strategy is a novel basis for single neuron computation of multi-modal information. Within the input layer of the cerebellar cortex, the delay coding strategy can also contribute to enhanced pattern separation, allowing a more robust classification of input activity patterns by PCs than originally predicted by Marr and Albus^16,18.

Origin of MF-GC synaptic diversity

Using variance-mean analysis of EPSCs, we established that the diversity in the MF-GC input pathways arises from differences in the presynaptic properties of vesicular release. Presynaptic mechanisms therefore ensure that each MF pathway is capable of maintaining its functional specificity, even when co-innervating single GCs. As well, the predominance of presynaptic mechanisms determining short-term plasticity³⁴ supports a flexible strategy for establishing synaptic diversity. To date, the molecular underpinnings of this release diversity are unknown. Nevertheless synaptic diversity could be established by genetic, developmental, or activity-dependent mechanisms. Consistent with the latter, long-term potentiation of MF-GC synapses is expressed presynaptically³⁵. Moreover, other long-term or homeostatic changes in release properties may result from the differences in the basal firing rates of primary versus secondary vestibular inputs^21,31.

It is interesting to consider the possibility that input-specific synaptic behaviors may be tuned to the inherent temporal response of the sensory modality they convey. Within the primary vestibular pathway, group 1 and 2 MFs could arise from regular and irregular vestibular nerve afferents³⁶, or from semicircular canal and otolith afferents. The large MF-GC EPSC amplitude and short-term depression of primary vestibular afferents may underlie the short, high frequency bursts of single unit GC recordings in nodulus during initiation of body movements³⁷. We speculate that PCs could use this information as a time stamp of the initiation of body movement. Moreover, PCs have been shown to encode body acceleration in the nodulus⁸, which may also require short GC response latencies. Secondary vestibular afferents have been shown to linearly report self-motion velocity in the flocculus²¹, which is consistent with the mean PPR of MVe afferents (Fig. 3d). It is interesting to note that the combination of input groups 5 and 4 was the most efficient at driving GC firing (at low frequency of MF activity, Fig. 7a), despite their small initial synaptic response. This is due to the synaptic facilitation of group 5 inputs, and the relative insensitivity of non-depressing synapses to tonic inhibition²³. These results highlight the importance and sometimes counter-intuitive influence of short-term plasticity in information processing.

Multimodal processing by single GCs

Our results show that GC responses to vestibular driver inputs are greatly enhanced when the visual supporting input is concurrently activated (Fig. 6 and 7). This phenomenon, termed multisensory enhancement, has been reported in superior colliculus⁶ and neocortex⁴ as a mechanism to enhance saliency of stimuli as well as generating a unified percept from senses with inherently different psychophysical responses⁹. In the cerebellum our data suggests that multimodal integration subserves both strategies for detecting correlations of sensory features³⁸ in the complex sensory-motor environment (Fig. 6 and 7), similar to what has been found in the weakly electric fish²⁷. The convergence of multiple primary and secondary vestibular afferents onto single GCs could participate in cerebellar computations observed in monkeys, such as estimation of orientation relative to gravity³⁹, which require the integration of information from multiple vestibular channels (e.g. semicircular canals and otoliths). Proprioceptive inputs originating from the spinal cord could also be integrated along with vestibular and visual inputs, however we have not characterized their input properties and wiring.

The vestibulocerebellum is crucial for the elaborate computation of self-motion through the integration of allocentric and egocentric cues (vestibular and optic flow vs. proprioception and copies of motor commands) both in mice³² and monkeys^8,40. Fundamental to this computation is the ability of the cerebellum to predict and cancel the sensory consequences of self-motion^2,40. By analogy to the circuit computation in the cerebellar-like structure of the electric fish⁴¹, the multisensory consequences of expected motion are transmitted via MFs to GCs, and then onto PCs, where synaptic weights can be tuned by supervised learning rules under the control of climbing fibers, such that the PC output can cancel expected sensory information^2,32. Indeed biophysical models of PCs have shown that supervised learning rules allow PCs to encode learned patterns of GC synaptic activity by the temporal structure of their firing⁴². Here we show that mixed input pathway convergence occurs in the majority of vestibulocerebellar GCs (Fig. 5), with the pairing of one driver and two supporting inputs producing 3 distinct sets of GC response delays corresponding to each driver input. Thus the network of delay coding GCs could be responsible for relaying the temporal structure of the vestibular and/or visual reafference (self-generated sensory response), thereby allowing efficient sensory cancellation by PC activity.

Synaptic diversity enhances pattern decorrelation

Single GCs have been shown to integrate proprioceptive information and motor command copies^27,28. Our finding that GCs can be innervated by MFs carrying information from different senses, reveal a more general wiring principle that is consistent with the long-standing theory of expansion-recoding within the GC layer^16,18 (except see²²). We propose here that the input-specific synaptic behaviors and mixed innervation together contribute to a novel temporal coding scheme that effectively enhances the differences between output patterns in response to similar input patterns, thereby enhancing their discriminability. The spike onset delays represent distinct input combinations for co-activation of 3 or more MF inputs (Fig. 7c), consistent with recent theoretical findings that 3-4 synaptic inputs is optimal for sparse coding and information transmission¹⁷. Our simple delay coding model provides an additional dimension for performing pattern decorrelation in the GC layer^16,18,43.

Although it is difficult to predict how PCs will read out the different GC activity patterns, simple linear discriminators show several fold improvement in the ability to classify similar patterns (Fig. 8f). The orthogonal function, as described above, is that different GC delays may provide a repertoire of temporal waveforms to PCs in order to integrate and sculpt precise temporal response⁴¹. A scenario combining pattern decorrelation and temporal response sculpting would arise when two similar sensory contexts would require a PC to respond with two distinct temporal response waveforms. Our modeling suggests that this task would be facilitated by GC delay coding but more work is required to demonstrate this possibility explicitly. Nevertheless, spatio-temporal pattern decorrelation supports the notion that the GC network can present complex sensory contexts to PCs using variable temporal delays, which can be independently associated with the “teaching” signals conveyed by climbing fibers, as hypothesized for the timing-dependent learning mechanism necessary for predictive motor control³³. But such a mechanism can also be used to tune PC sensitivity to spatio-temporal parallel fiber activity patterns in order to cancel expect sensory inputs.

It has recently shown that unipolar brush cells provide the late component of GC response delays necessary for cancelling sensory consequences of self-generated stimulation in the cerebellar like structure of the eclectic fish⁴¹. In mammals, expected sensory cancellation could take advantage of input-specific synaptic behaviors to provide GC response delays of up to 100 ms, while unipolar brush cells could provide the longer delays⁴⁴. Intrinsic differences in the temporal activation of MFs within an input pathway^45,46 might also contribute to differential GC delays.

Expansion-recoding and sparse representations of incoming inputs are common features of several sensory systems⁴³. As in the cerebellar cortex, sensory afferents diverge onto a cortical layer containing numerous neurons that convey a sparse representation of the sensory information to a second layer made of readout units. Given the known functional synaptic diversity of thalamocortical (visual¹³, auditory¹⁴, or somatosensory^14,47), intracortical projections¹⁴, and the cross-feature/modal innervation of cortical³, and hippocampal neurons⁴⁸, input-specific delay coding could serve as a ubiquitous strategy to enhance pattern separation of complex time-varying input stimuli¹⁹.

Finally, whether input-specific synaptic diversity constitutes a fundamental component of sensory processing (e.g. feature extraction) for neurons is an area of active research⁴⁹. We speculate that the temporal coding strategies imparted by driver and supporting inputs in GCs may provide the much needed insight into how thalamic and cortical circuits might process type I (driver) inputs, which are strong inputs carrying the primary sensory information, and type II (modulatory) synaptic inputs¹⁴. How input-specific synaptic diversity could also underpin feature selection is exemplified by strong synaptic weights between recurrently connected layer 2/3 Pyramidal neurons with similar orientation preferences⁵⁰.

Methods

Cerebellar slice preparation and synaptic recordings

All animal experimental procedures were approved by the ethics committee for animal experimentation at the Pasteur Institute. Acute parasagittal slices (200 μm) of cerebellum were prepared from F1 and F2 mice (cross of BALB/cJ and C57BL/6J), both males and females, aged between 30-60 days postnatal (mean = 46 days), except for mice injected with viral constructs (see below) which were between 60 and 90 days old. Transgenic mice expressing mGFP under the Thy1 promoter (line 17, gift from Prof. Pico Caroni) were bred on a C57BL/6J background, and maintained as heterozygotes. Mice were swiftly decapitated and the brain quickly removed and placed in ice-cold slicing solution containing (in mM): 2.5 KCl, 0.5 CaCl₂, 4 MgCl₂, 1.25 NaH₂PO₄, 24 NaHCO₃, 25 glucose, and 230 sucrose. Slices were cut from the dissected cerebellar vermis using a vibratome (Leica VT1200S) and directly transferred to an incubation chamber containing (in mM): 85 NaCl, 2.5 KCl, 0.5 CaCl₂, 4 MgCl₂, 1.25 NaH₂PO₄, 24 NaHCO₃, 25 glucose, and 75 sucrose, maintained at 32 °C for 30 minutes. Subsequently the slices were transferred to an external recording solution kept at room temperature and containing (in mM): 125 NaCl, 2.5 KCl, 1.5 CaCl₂, 1.5 MgCl₂, 1.25 NaH₂PO₄, 25 NaHCO₃, and 25 glucose. All solutions were saturated with 95 % O₂ and 5 % CO₂.

Whole-cell patch-clamp recordings of cerebellar granule cells (GCs) were performed using a Multiclamp 700B amplifier (Axon Instruments) with fire-polished thick-walled glass patch electrodes (1.5 mm OD/0.75 mm ID, Sutter Instruments; 5-10 MΩ tip resistance) filled with the following K⁺-based solution (in mM): 110 KOH, 110 MeSO3, 6 NaOH, 4.6 MgCl2, 5 EGTA-K, 1.78 CaCl2, 4 NaATP, 0.3 NaGTP (280 mOsm, pH 7.3). Cells with series resistances above 30 MΩ were discarded from analysis. A liquid junction potential of 6 mV²⁰ was used to correct all membrane voltage values (subtracted from measured value).

For voltage-clamp recordings, GCs were held at −87 mV and single mossy fiber transmission was evoked with 10 μsec voltage pulses 5 V above threshold (Digitimer Ltd, Letchworth Garden City, UK) using a second patch pipette (typically with tip resistance of 4-6 MΩ) filled with ACSF and placed in the GC layer (typically 50-100 μm from the soma of the GC). Activation of a single MF was routinely confirmed by verifying that increasing the stimulus intensity did not evoke an increase in EPSC amplitude⁵¹. MFs were stimulated by random placement of the stimulus electrode within the GC layer (blind stimulation). AMPARs mediated EPSCs were isolated using the following drug mix: SR 95531 [2-(3-carboxypropyl)-3-amino-6-(4-methoxyphenyl) pyridazinium bromide] (10 μM) to block GABA_ARs, D-AP5 (D-(−)-2-Amino-5-phosphonopentanoic acid) (10 μM) and 7-chlorokynurenic acid (7-Chloro-4-hydroxyquinoline-2-carboxylic acid) (20 μM) to block NMDARs, and strychnine (0.3 μM) to block glycineRs (all drugs were purchased from Abcam, Cambridge, UK).

For current-clamp recordings, patch electrode tips were coated with wax. The resting membrane potential (Vm) was maintained at −89 mV, if necessary, using small amounts of injected current (typically < 10 pA). This potential corresponds to the average resting Vm measured immediately following formation of whole-cell (−89 ± 0.5 mV, n = 37 cells). EPSPs were recorded in the presence of GABA_A and glycineRs blockers, but without NMDARs antagonists. Trains of 30 stimulations at 10, 20, 50, 100 and 200 Hz were delivered to single MFs with 1 minute intervals to prevent long-term changes in synaptic efficacy⁵². Because the action potential (AP) threshold decreases rapidly after establishing whole-cell, we discarded recordings where threshold changed by more than 3 mV. The mean AP threshold was −55 ± 0.5 mV (n = 26 cells). Although our resting Vm and AP threshold values are lower than those reported in the literature, we find that the difference of potential between them is in the range reported^{23, 53}.

All recordings were performed at 35-37 °C, low-pass filtered at 10 kHz and digitized at 100 kHz using an analog to digital converter (model NI USB 6259, National Instruments, Austin, TX, USA) and acquired with Nclamp (www.neuromatic.thinkrandom.com) running in Igor PRO (Wavemetrics, Lake Oswego, OR, USA).

Analysis of EPSCs and GC firing

Analysis was performed with Neuromatic in Igor PRO (v. 6.2). Traces were filtered off-line at 4 kHz. Data points during the extracellular stimulus artifact were blanked, and the capacitive response subtracted using a double exponential fit to its decay. All EPSC traces were corrected for series resistance error using an algorithm written in Igor based on⁵⁴. EPSC were baseline-subtracted using a 1 ms window ending immediately before the stimulus and the mean peak amplitude and relative variability (CV) were measured from the average inside a 100 μsec window around the peak. The synaptic variance was corrected for background noise by subtracting the variance measured over a 100 μsec window preceding the baseline window by an amount equal to the time between the baseline window and the EPSC peak²⁰. The CV was estimated with a minimum of 30 consecutive traces. Paired-pulse ratio between the 2^nd and 1^st EPSCs (PPR) was calculated by subtracting the average of single EPSCs from the trials in which a pair was delivered. PPRs were calculated from a minimum of 20 trials per pulse train. For EPSC traces displayed in figures, peak amplitude, CV and PPR values were calculated from the displayed traces (i.e. trials with paired stimulation only).

GCs firing rates were measured inside a time window starting from the onset of the 1^st MF stimulation and ending 10 ms (twice the average membrane time constant measured from the decay of a voltage response to a 100 ms long 4 pA square pulse; n = 6 cells) after the last stimulus. AP threshold and onset of firing were measured at the first point of the AP upstroke.

Statistical tests and K-Means cluster analysis

Statistical tests were performed using non-parametric methods. The Wilcoxon rank sums test was used to compare EPSC metrics between two samples. For multiple comparisons we used the non-parametric Steel-Dwass test that corrects for error rate. In the figures statistical significance (p < 0.05) is indicated by an asterisk (*) or noted otherwise non-significant (NS). All error bars are standard error of the mean unless otherwise indicated. Box plots show minimum, median, and maximum values, the top and bottom of the box are first and third quartile.

An unsupervised K-Means clustering (KMC) method (JMP software, SAS, NC, USA) was used to identify putative input groups inside the whole population of inputs obtained from all experiments (n = 259 inputs). We used the EPSC mean amplitude, CV and PPR as metrics for the cluster analysis, as they yielded the strongest correlations. We chose to use the PPR between the 2^nd and 1^st EPSCs because it revealed short-term facilitation in a subset of synapses which was rapidly counteracted by short-term depression during the subsequent pulses (see Fig. 1d). In brief, the KMC algorithm uses an iterative refinement technique that alternates between assigning each observation to the closest mean and updating the means to be the centroids of the observations in one cluster⁵⁵. Sets of correlated variables (our multidimensional data points) are converted to principal components, and the principal component subspace is used as the cluster centroid subspace. Because the KMC results depend on the ordering of the input data set, we randomly shuffled our data points and repeated the analysis a hundred times. The number of clusters (k means) is an input parameter and was determined using the elbow method in which the percentage of variance explained by the number of clusters is plotted against the number of clusters for each individual EPSC metric (Supplementary Fig. 2). The plot allowed us to determine that five clusters is the minimum number needed to account for the maximum amount of variance across all three EPSC metrics.

Estimating synaptic quantal parameters with multiple probability fluctuation analysis

MF-GC EPSCs were consecutively recorded in 0.5/5, 1.5/1.5 and 8/0 mM of Ca²⁺/Mg²⁺. Some inputs recorded in non-vestibular regions of the vermal cerebellum (n = 17/37 of all inputs) were added to the data to increase the sample size. Mean peak current amplitude ($\overline{I}$) and background-corrected variance (${\sigma }_I^2$) were calculated from a minimum of 30 EPSCs during stable epochs (Spearman’s rank order stability test). The mean and variance at each [Ca²⁺]_e were fit with a multinomial model accounting for time course and quantal variance⁵⁶

$${\sigma }_I^2=\left[Q_p\overline{I}-\frac{{\overline{I}}^2}{N}\right]\left(1+C{V}_{QII}^2\right)+Q_p\overline{I}C{V}_{QI}^2$$ Equation 1:

where Qp is the mean quantal size, N is the number of release sites and CV_QI and CV_QII are the coefficients of variation of intrasite and intersite quantal variability⁵⁶. CV_QI is composed of CV_QS, the quantal variability at single sites and CV_QL the variability arising from stochastic release latency. As our data did not contain MF-GC connections with single synapses we could not estimate CV_QS and we therefore used the value from²⁰: 0.26. We calculated CV_QL from the difference in variability between stimulus-aligned (0.51, n = 7) and rise time-aligned quantal currents (0.35) to be 0.17. The total quantal variance CV_QT can be calculated as follows:

$$C{V}_{QT}=\sqrt{C{V}_{QI}^2+C{V}_{QII}^2}=\sqrt{C{V}_{QS}^2+C{V}_{QL}^2+C{V}_{QII}^2}$$ Equation 2:

CV_QT was measured from stimulus-aligned EPSCs (n = 37 inputs): 0.44. CV_QI was calculated to be 0.31 from CV_QS and CV_QL. Thus CV_QII was 0.32 in good agreement with previous estimates²⁰. Errors in estimating the variance were calculated using the following equation⁵⁶:

$${\sigma }_{\mathrm{samplevariance}}=\sqrt{\frac{2{\sigma }^4}{n-1}}$$ Equation 3:

where σ² is the population variance and n is the number of observations. Errors in estimating the variance are represented by error bars in (Fig. 2). Mean and variance fits were weighted according to errors.

GFP expression in Thy1-mGFP (line 17) mice

Expression of GFP in vestibular ganglion (VG) neurons was verified in Thy1-mGFP (line 17) mice aged from postnatal day 7 to 10 before the inner ear gets too hard to extract the ganglion (n = 4 mice). Mice were swiftly decapitated and the temporal bone was dissected out of the rest of the head in ice-cold ACSF under a stereo microscope (Leica Microsystems). The VG, which is situated in the upper part of the outer end of the internal auditory meatus, was extracted by carefully breaking the bone around it using fine forceps and gently pulling it from the nerve end cut from the brainstem during the dissection. The VG was then put into a chamber under a confocal microscope and held in place with a slice anchor holder.

To verify GFP expression in brainstem nuclei, 100 micron thick coronal slices of cerebellum with brainstem were cut from fixed brains of adult Thy1-mGFP (line 17) mice (n = 5). Simultaneous contrast and fluorescence images were acquired using the microscopy system described below, to visualize neuronal somata and eventual GFP expression, respectively. About 30% of neurons were found to express GFP in the spinal vestibular nucleus (SpVe; Supplementary Fig. 3). The following structures also known to project to VC⁵⁷ were devoid of labeled neurons: medial vestibular (MVe), prepositus hypoglossi (PrH), superior vestibular nuclei, and reticular formation. Images are only shown for MVe and PrH (Supplementary Fig. 3).

Relative contribution of MFs arising from different precerebellar pathways within cerebellar nodulus

Quantification of MF afferent types were estimated from⁵⁷, which excluded primary vestibular afferents. In this study MFs arising from the MVe, PrH and SpVe nuclei represented around 50 %, 20 % and 5 % of all extrinsic MFs (eMfs) from the brainstem, respectively. We found that GFP MFs contacted 14% of GC dendritic claws (n = 58 cells) and 48 % of GCs, 89 % of which were contacted by only one GFP MF. Thus, regarding the contribution of SpVe to GFP MFs an upper estimate gave 30 % of 5 % = 1.5 % and therefore GFP MF from VG represented 12.5 % of all MFs and 89 % of GFP MFs. Our study concerning MFs arising from MVe, PrH and VG represented 43 %, 17 % and 12.5 % of eMFs, respectively, and thus together accounted for 72.5 % of all eMFs.

Stereotaxic injections

In order to fluorescently label different MF pathways, we performed stereotaxic injections of viral vectors expressing fluorescent protein into precerebellar nuclei. We used the following vectors: AAV2/9.hSyn.ChR2(H134R).mCherry.WPRE provided by Karl Deisseroth (Stanford University) and produced by the INSERM UMR1089 platform (used in 9/16 recordings from MVe MFs; Fig. 3e-h), or an AAV9.hSyn.TurboRFP.WPRE.rBG vector purchased from Penn Vector Core (Philadelphia, PA, USA). Mice aged between 40-50 days were deeply anesthetized prior to surgery with a mixture of hypnotic (ketamine 1.5 %, Mérial) and analgesic (xylazine 0.05 %, Bayer) anesthetics mixed in phosphate buffer and injected in the peritoneum. A local anesthetic (xylocaine 2 % gel, Newpharma) was applied on top of the location of the cranial incision. The anesthetized mouse was then placed on a stereotaxic frame adaptor comprising adjustable ear bars and tooth holder. The skull was then perforated at the injection site with a surgical drill. The injection of viral constructs in the MVe (120 nl; virus titer, 6.6 e10¹² GC/ml; bregma −6 mm, lateral 1 mm, ventral 4.3 mm) or the PrH (60 nl; bregma −6.48 mm; lateral – 0.37 mm; ventral 5.1 mm) was performed by slow infusion (200 nl/min) with steel needles (26G × 50 mm and 36G × 70 mm, Phymep) connected to a pump via a catheter and a Hamilton syringe. Injected mice were then kept 2 to 4 weeks to allow for transgene expression.

To verify the correct location of stereotaxic injections and that viral transduction did not spill out of the targeted nuclei we examined fluorescent protein (XFP) expression in 100 microns thick coronal slices of fixed cerebellum and brainstem (Supplementary Fig. 4). The concentrations of viral vectors and the volume of injection were adjusted in order to restrict viral transduction to the targeted structures. Images were acquired with a confocal microscope (LSM700, Zeiss) equipped with an air objective (10×, 0.45 NA, Zeiss) and a laser (555 nm) and running with the Zen 2009 v.5.5 software (Zeiss). In all cases where viral injection was successfully achieved, XFP expression was specifically found in neurons of the targeted nuclei (n = 4/7 and 3/4 mice for MVe and PrH respectively). Nuclei were identified using the Franklin and Paxinos mouse brain atlas. In the other brains (n = 3/7 and 1/4 for MVe and PrH respectively) we found no expression of XFP throughout the entire cerebellum and brainstem suggesting the viral injection failed.

Targeted stimulation of fluorescent mossy fibers guided by two-photon scanning microscopy

GCs were identified and whole-cell patch-clamped using infrared Dodt-gradient contrast and a QlClick digital CCD camera (QImaging, Surrey, BC, Canada) mounted on an Ultima multiphoton microscopy system (Bruker Nano Surfaces Division, Middleton, WI, USA), and based on an Olympus BX61W1 microscope, equipped with a water-immersion objective (60×, 1.1 NA, Olympus Optical, Tokyo, Japan). Two-photon excitation was performed with a Ti-sapphire laser (Spectraphysics). To visualize GCs contacting GFP-labeled MFs, Alexa Fluor 594 (10 μM) was dialyzed via the patch electrode. Two-photon excitation of GFP and Alexa 594 was performed at 810 nm. To visualize GCs contacting MFs labeled with a red fluorescent protein, we dialyzed them via the patch electrode with Alexa 488, and used an excitation wavelength of 1000 nm. Simultaneous Dodt-gradient contrast and fluorescence imaging was used to position the stimulation pipette near a labeled axon whose MF connected to the patched GC. Connections were confirmed if co-localization of XFP (MF) and Alexa fluorescence were observed over several focal planes spanning at least 3 microns. We then performed minimal stimulation as described for the blind stimulation protocol (see above). As expected for fluorescence-guided targeting of MFs, low levels of voltage (typically 2-5 V) were needed to evoke transmission as compared to blind stimulation. To insure that we were stimulating the intended MFs we performed a set of experiments where we carefully withdrew the stimulation pipette away from the proximity of the axon until we lost transmission, and repeated minimal stimulation by gradually adjusting voltage (Supplementary Fig. 5). The rationale is that the initial proximity to the stimulated axon would be demonstrated if stimulation voltage had to be consistently increased with further distance from the targeted axon. Our results show that stimulus voltage was always positively correlated with distance from the targeted axon (n = 3 cells). Moreover, minimal stimulations (5 V above threshold) covered an area no more than 5 μm wide demonstrating the spatial precision of our method. Individual dendrites of GCs extending apart substantially further than 5 μm, this method is very unlikely to stimulate more than one MF connecting the same GC, and rather specifically the fluorescence-labeled MF.

Estimating MF pathway convergence onto single GCs

In order to examine possible convergence of primary vestibular with secondary vestibular or PrH afferents in single GCs we performed stereotaxic injections in Thy1-mGFP (line 17) mice (n = 6 and 5, respectively). Acute slices were then prepared and GCs were filled with a fluorescent dye to visualize connections with afferent types. Because the emission spectrum of our fluorescent dyes (Alexa 488 or 594) overlap with those of XFPs we resorted to use the dual single and two-photon ability of our microscopy system. GCs were filled with Alexa 594, excited with a 594 nm diode laser (Omicron Lasers), which did not excite the far-red RFP, and imaged with confocal microscopy while fluorescent MFs were imaged under 2PLSM excitation at 1000 nm. Connections between GCs and fluorescent MFs were verified offline using the Fiji software (www.fiji.sc). 3D reconstructions of GCs and connected MFs were performed with Fiji-TrakEM2.

Synaptic behavior of different MF inputs converging on single GCs

Blind minimal stimulation protocol (see above) was used to evoke synaptic transmission, successively, from two independent MFs innervating the same GC. Independent connections were first ascertained using KMC, whereby different connections were confirmed if their inputs belonged to different clusters. In the case where the two inputs belonged to the same cluster, we calculated the averaged differences between the EPSCs mean amplitude, CV, PPR and waveform (10-90% rise time and weighted decay) of the two inputs. In 6/8 cells the mean difference between EPSC metrics was greater than 20%, and the two inputs were thus considered coming from different synapses. In the two other cases, inputs could not be differentiated with those metrics (mean differences < 10%) and were therefore rejected and not analyzed further.

Animals and surgical preparations for in vivo recordings

All experiments were performed on 4-6 week old C57BL/6 mice, of either sex, anaesthetized with either ketamine / xylazine (100 mg/kg / 10 mg/kg body weight, respectively) or a mix of fentanyl / midazolam / medetomidine (0.05 mg/kg / 5.0 mg/kg / 0.5 mg/kg, respectively) and topped-up throughout the experiment as required, indicated by the recovery of the toe-withdrawal reflex. We did not find significant differences between the two anesthetic conditions in mean EPSC peak amplitude: 23.3 ± 3.9 pA with ketamine / xylazine vs. 29.3 ± 4.9 pA with fentanyl / midazolam / medetomidine (mean and SEM; n = 16 and 12 vestibular recordings, respectively; p = 0.30) and frequency of spontaneous EPSCs: 9.4 ± 1.4 vs. 8.7 ± 1.9 Hz (p = 0.36). Experiments performed with the two different anaesthetic conditions were therefore pooled.

Mice were head-fixed with a head holder consisting of ear bars and a mouth clamp (Narishige, modified) in the prone position, with the head angled nose-down by 32.6 °. Mice were freely breathing and maintained at a body temperature of 37 °C with a heating blanket (FHC), controlled with a rectal thermometer. To access the flocculus, a small craniotomy was performed in the left petrosal bone over the paraflocculus. The dura mater was removed with fine forceps (Dumont No. 5). The brain was kept moist with phosphate-buffered saline (PBS, Sigma). All experiments were in compliance with UK Home Office regulations.

In vivo electrophysiology

Whole-cell patch-clamp recordings were performed from GCs in the left cerebellar flocculus using the blind patch-clamp technique⁵⁸ as previously described²¹. Recordings were performed in the flocculus rather than in the nodulus because the mechanical support provided by the cranium facilitates whole-cell recordings. Electrodes were pulled on a vertical electrode puller (Narishige) to show a resistance of 7-10 MΩ when filled with intracellular solution containing (in mM): 110 K-MeSO3, 6 NaOH, 3 MgCl₂, 0.02 CaCl₂, 40 Hepes, 0.15 BAPTA, 4 Na₂ATP, 0.3 Na₂GTP plus 0.4 % biocytin, adjusted to pH 7.3 with KOH; 290 mOsm. Electrodes were advanced through the paraflocculus into the flocculus to a depth of 1200 to 2000 μm from the pial surface of the paraflocculus. GCs showed a capacitance of 3.6 ± 0.1 pF. Recordings with series resistances over 55 MΩ were discarded (average series resistance = 41.0 ± 1.2 MΩ).

Excitatory postsynaptic currents (EPSCs) were recorded in voltage-clamp at −70 mV, close to the reversal potential of Cl⁻ to isolate excitatory postsynaptic currents, with an Axon Multiclamp 700 B amplifier (Molecular Devices), low-pass filtered at 8 kHz, digitized at 33.3 kHz with an ITC-18 ADC/DAC board (HEKA), acquired with an Apple Power Mac computer running Igor Pro (Wavemetrics) with Neuromatic/Nclamp (www.neuromatic.thinkrandom.com/), and stored digitally for offline analysis.

Vestibular stimulation

For vestibular stimulation the mouse and head holder were fixed on a custom-built computer controlled motion device (rotational stages by Newport) allowing separate and combined rotations about a horizontal and a vertical axis. The axes of rotation were centered between the vestibular organs. With the head tilted 32.6 ° nose-down and the anterior-posterior axis of the mouse oriented 45 ° to the axis of vertical rotation, horizontal rotation primarily stimulated the horizontal semi-circular canals (SCCs), while vertical rotation stimulated almost exclusively the left anterior and right posterior SCCs⁵⁹. The mouse was rotated in the dark following a discontinuous compound sinusoidal position/velocity profile, controlled by custom-written routines in Igor Pro (Wavemetrics). For horizontal rotations, maximum velocities of 38 °/s were presented. For reasons of recording stability, vertical rotations were usually limited to maximum velocities of 9 °/s.

Visual motion stimulation

Visual stimuli were presented to the ipsilateral or contralateral eye on a LCD monitor (Dell) using an Apple Mac Mini running the psychophysics toolbox in Matlab, triggered by the electrophysiological recording software. The LCD monitor (screen size 17 inch diagonal) was positioned at a distance of 21 cm to the eye of the mouse at an angle of 45 ° to the animal’s anterior-posterior axis, thus covering approximately 79 ° in azimuth and 63 ° in elevation. Motion stimulation consisted of drifting black and white square-wave gratings at full screen contrast with a spatial frequency of 0.04 cycles/° moving with a temporal frequency of 2 cycles/s. Each trial consisted of 8 blocks of equally spaced directions of motion, with stripes stationary for 1 s, drifting at constant speed for 1 s, and being stationary for 1 s before the orientation was changed by 225 °.

Analysis of in vivo data

Data analysis was performed using Igor Pro with Neuromatic. EPSCs were detected using a −3 to −5 pA threshold criterion from the recorded traces after binomial smoothing over 6 points and subsequently confirmed by visual inspection. EPSCs were aligned on the event onset and baselined over a window of 1 ms ending 0.1 ms before the event onset. EPSC traces were corrected for series resistance error as described above for in vitro recordings. Peri-stimulus time histograms (PSTHs) were calculated for 100 ms time bins. To determine the presence of a vestibular response, the EPSC rate was tested for correlations to the stimulus parameters position, velocity, and acceleration. Visual-motion evoked responses were calculated from the average EPSC frequency over the period of visual-motion stimulation for each of the 8 stimulus directions measured and normalized to the average baseline rate calculated from the 8 1 second-intervals preceding the visual motion stimuli. Polar plots show these baseline-normalized responses according to their direction of stimulation. Visual-motion tuning vectors were calculated as the vector sum of these response vectors from all 8 directions measured, divided by 2, the number of stimulus directions per quadrant. Spontaneous activity was assessed by analyzing all EPSC occurring in a 1 second epoch before stimulus presentation. GCs that received 2 or more separable inputs²¹ were excluded from analysis. For visual evoked EPSCs (preferred direction), stability of EPSCs amplitude over the stimulus epoch was examined using Spearman’s rank order stability test routine written in Neuromatic (www.neuromatic.thinkrandom.com/) with a 1^st pass mean search window of 10 points, a 2^nd pass window with fraction 0.5, and a significance level of 0.05.

Numerical simulations of synaptic integration in GCs

GC voltage responses to MF inputs were simulated as in²³. Briefly, AMPAR and NMDAR conductances (G_AMPAR and G_NMDAR) were injected into an integrate-and-fire model written in Igor Pro. Membrane voltage (V) was calculated with the following differential equation:

$$\begin{array}{cc}\hfill & -C_m{V}^{\prime }=Gm(V-Em)+{\Sigma }_i{G}_{AMPAR,i}•{\Delta }_{AMPAR,i}\left(t\right)•(V-E_{AMPAR})\hfill \\ \hfill & +G_{NMDAR,i}•{\Delta }_{NMDAR,i}\left(t\right)•m\left(V\right)•(V-E_{NMDAR})\hfill \end{array}$$ Equation 4:

where V’ is the time derivative of V, Cm is the membrane capacitance, Gm and Em are the membrane leak conductance and its reversal potential, respectively, and i is the index for different sets of conductances representing different MFs. E_AMPAR and E_NMDAR are the AMPAR and NMDAR reversal potentials, Δ_AMPAR(t) and Δ_NMDAR(t) indicate the spike trains convolved with the unitary synaptic conductance waveforms and m(V) is the fraction of GluN2C-containing NMDARs not blocked by Mg²⁺⁶⁰. C_m was set to 5 pF as calculated from the membrane time constant (4.71 ± 0.07 ms) measured from the decay of voltage in response to a current step of 4 pA and 100 ms duration (n = 6 cells). Gm was set to 1.1 nS and Em to −89 mV as measured from recorded cells (1.1 ± 0.04 nS and −82 ± 0.9 mV, n = 29). E_AMPAR and E_NMDAR were set to 0 mV. The action potential threshold was set to −55 mV as measured (see above).

The time course of synaptic conductances was modeled with the following multiple-exponential equation:

$$A\left(t\right)={(1-e^{-\tau ∕{\tau }_r})}^n(d_1{e}^{-\tau ∕{\tau }_{d1}}+d_2{e}^{-\tau ∕{\tau }_{d2}}+d_3{e}^{-\tau ∕{\tau }_{d3}})∕a_{norm},\tau =t-t_e$$ Equation 5:

where t_e is the synaptic event time, τ_r is the rise time constant, τ_d1, τ_d2 and τ_d3 are the decay time constants, d₁, d₂, d₃ are the percentage amplitudes of the different components, and a_norm is a normalization scale factor.

AMPAR direct and spillover conductances waveform parameters were adjusted to match the G_AMPARs obtained from recorded AMPAR EPSCs divided by the driving force. The AMPAR spillover component peak amplitude was set to 0.34 of the direct component peak amplitude, as described in⁶¹. G_NMDARs waveform parameters were taken from⁵³ and the G_NMDAR to G_AMPAR ratio was adjusted so that simulated EPSPs fitted the recorded AMPAR+NMDAR-mediated EPSPs. A G_NMDAR/G_AMPAR ratio of 0.1 produced good fits of EPSPs for all different input groups, consistent with the low ratio measured in adult GCs⁵³. The unblocked G_NMDARs was then calculated from the NMDAR I-V relation in²³. Depression and facilitation of the AMPAR (direct and spillover) and NMDAR synaptic conductances were modeled as single exponential functions. We adjusted both the time constants (τ_D and τ_F) and their amplitudes (D and F) in order to fit the train of AMPAR conductances estimated from EPSCs for each group. G_NMDAR dynamics were subsequently adjusted to reproduce summating EPSPs recorded in current-clamp. Values for simulated synaptic conductances time courses and short-term dynamics for each input group are displayed in the supplemental tables 1&2.

Tonic activation of a6-containing GABA_ARs was model as in²³. Briefly, a constant inhibitory conductance of 438 pS and reversal potential of −79 mV was added when 2 MF inputs were simulated. For the 3 MF input condition we increased inhibitory conductance by 30 % (573 pS) to mimic the network-activity-dependent inhibition described in¹⁷.

Simplified GC layer model for pattern decorrelation

In the thresholding model the GC output is given by the formula

$$y_i={[x_i-k]}_{+}$$ Equation 6:

^18,62-64 where x_i and y_i are the input and output of the i^th GC, k is the threshold and subscript “+” denotes half-wave rectification. In the delay coding model, the output replicates the input after a delay d that depends on the strength of the input. The output as a function of the delay can thus be expressed by the formula

$$y_i\left(d\right)=\{\begin{array}{c}{x}_i,x_i\ge k\left(d\right)\hfill \\ 0,else\hfill \end{array}\phantom{\}}$$ Equation 7:

with a delay-dependent threshold k(d). We used a range of delays denoted from 1 to 5, the threshold k being set at 4 at delay 1 and reduced to 0 at delay 5 in equidistant steps.

Output pattern correlations in the large N limit of the simplified GC model were calculated by numerical integration. Double integrals of the form

$$M_{nm}(k,l;\rho )={\int }_k^{\infty }dx{\int }_l^{\infty }dy\frac{{(x-k)}^n{(y-l)}^m}{n!m!2\pi \sqrt{1-{\rho }^2}}{e}^{-\frac{x^2+y^2-pxy}{2(1-\rho 2)}}$$ Equation 8:

were computed as described⁶⁴. Output correlation of the thresholding model was computed as [M₁₁(k-2,k-2;r)- M₁₁(k-2,k-2;0)]/ [M₁₁(k-2,k-2;1)- M₁₁(k-2,k-2;0)]. Output correlation of the delay coding model was computed as [C(k(d),2;r)- C(k(d),2;0)]/[C(k(d),2;1)- C(k(d),2;0)] with

$$C(k,l;\rho )=M_{11}(k-l,k-l;\rho )+2K{M}_{10}(k-l,k-l;\rho )+k^2{M}_{00}(k-l,k-l;\rho )$$ Equation 9:

Calculation of minimum SNRs tolerated by linear classifier

We assumed that the patterns to discriminate have equal mean and variance. Then, using elementary trigonometry and the fact that the scalar product of unit length vectors equals the cosine of the angle subtended by these vectors, the Euclidean distance between the patterns in units of pattern SD equals:

$$d_{decorrelator}=\sqrt{2(1-r_{decorrelatoror})}$$ Equation 10:

where decorrelator is either thresholding or delay coding.

Assuming isotropic noise the maximum permissible noise variance equals

$$1∕2f{d}_{decorrelator}^2$$ Equation 11:

where f depends on the level of acceptable misclassifications (if, e.g., 5 % misclassifications are just acceptable and noise is Gaussian then f ≈ 0.37). The ratio of minimum required SNRs is thus (1-r_{delay_coding})/(1-r_thresholding).