Selecting Spatial Scale of Covariates in Regression Models of Environmental Exposures

Abstract

Environmental factors or socioeconomic status variables used in regression models to explain environmental chemical exposures or health outcomes are often in practice modeled at the same buffer distance or spatial scale. In this paper, we present four model selection algorithms that select the best spatial scale for each buffer-based or area-level covariate. Contamination of drinking water by nitrate is a growing problem in agricultural areas of the United States, as ingested nitrate can lead to the endogenous formation of N-nitroso compounds, which are potent carcinogens. We applied our methods to model nitrate levels in private wells in Iowa. We found that environmental variables were selected at different spatial scales and that a model allowing spatial scale to vary across covariates provided the best goodness of fit. Our methods can be applied to investigate the association between environmental risk factors available at multiple spatial scales or buffer distances and measures of disease, including cancers.

Introduction

In public health research, it is acknowledged that both compositional (individual-level) and contextual (neighborhood-level) variables are important for explaining variation in health outcomes.^1–7 For example, the role of contextual variables continues to be a key focus of investigators studying potential risk factors for obesity,^8–10 where neighborhood variables such as fast-food density and green-space presence are thought to be important factors that contribute to obesity status. Neighborhood- or area-level variables can also have an important role in explaining variation in environmental chemical exposures. One example is found with modeling variation in polychlorinated biphenyls (PCBs) measured in carpet dust using percentage of developed land, population density, and number of industrial facilities within 2 km of residences, where total PCB levels are significantly associated with either the percentage of developed land or the population density.¹¹

Through the use of geocoding and geographic information systems (GIS), researchers can link an individual residential address to an external database containing numerous area-level or environmental variables, where the number of variables is denoted by p. Typically, each of the area-level variables is available at multiple geographic scales. Thus, the p number of area-level variables available to consider when explaining variation in a health outcome can quickly multiply. Many socioeconomic status (SES) variables, including race, education, household income, and housing tenure, are available from the U.S. Census at the census block group, census tract, and county level. To clarify, we use the word “level” as a general term for spatial unit. Level is synonymous with region size, which, as will be seen later in our case example, denotes a buffer size. In addition to geopolitical areas, researchers can also create a set of geographic areas of varying size to summarize environmental variables using circular buffers or rings centered at observed data points. As an example, population density can be calculated at distances of 1, 2, and 3 mi from a residential location by intersecting spatial buffers of these sizes with census block group data.

With the abundance of socioeconomic and environmental data available at multiple spatial scales, a natural question arises for researchers who wish to investigate environmental effects: at what spatial scale (geographic areal unit) should each area-level variable be modeled in order to explain a fixed health outcome or environmental exposure of interest? Area-level covariates used as contextual variables in regression models are often in practice modeled at the same spatial scale, where, generally, a smaller spatial unit (ie, census block group versus a county) is thought to better capture heterogeneity in regression relationships. Krieger et al.⁴ model area-based socioeconomic measures at three spatial scales (census block group, census tract, and ZIP Code) to study mortality outcomes and cancer incidence and find that the effect estimates for the smaller spatial units (census block group and census tract) are similar, while the effect estimates for the larger spatial unit (ZIP Code) differ and are sometimes in the opposite direction. Krieger et al.⁴ conclude that the level of geography is important and recommend the use of SES variables at a smaller spatial scale, namely census block group or census tract.

The selection of spatial scale for environmental variables is a problem typically encountered in modeling groundwater quality. A variable that is often incorporated into statistical models of groundwater quality is area land use, as it is known to be one of the factors that can affect water quality. Barringer et al.¹² find that the use of a circular buffer around a water table well is a simple and effective method for correlating water quality and land use. Regional and national groundwater studies have associated land use near a well with water quality using a fixed circular buffer distance, with 500 m a common choice and 1 km a less common choice.^13–17 Some researchers have evaluated the univariate correlation of land use variables with groundwater quality. Ferrari and Ator¹⁸ find correlations between agricultural land use and nitrate concentrations using circular buffers of 400 and 800 m. Kolpin¹⁹ correlates the concentrations of nitrate, alachlor, and atrazine detected in wells with a variety of land use variables using circular buffers ranging in size from 200 m to 2 km. Johnson and Belitz²⁰ evaluate a range of circular buffer and wedge sizes in a univariate correlation analysis of urban land use and the occurrence of volatile organic compounds (VOCs) in groundwater using Kendall’s tau (τ). They find that the values of τ are within 10% of one another for circles and wedges ranging in size from 500 m to 2 km, with statistically significant correlations for all sizes, and conclude that the popular choice of a 500-m circular buffer is adequate for assigning land use variables to a well.

Other researchers have evaluated the buffer distance to select each type of land use variable to be used in a regression model of groundwater quality. Rupert²¹ selects the circular buffer size for land use variables to explain the detection of elevated atrazine or desethyl-atrazine (atrazine/DEA) concentrations and elevated concentrations of nitrate using univariate logistic regression. The optimal buffer size is 2 km for agricultural land use variables and 500 m for urban land use variables according to McFadden’s ρ², which is a transformation of the log-likelihood statistic that is designed to imitate the r² of linear regression for univariate regression models.²¹ The buffer distances of 2 km for agricultural land use variables and 500 m for urban land use variables are then used in multiple logistic regression models of the probability of elevated atrazine/DEA detection and the probability of elevated nitrate detection.

An important question is whether all area-level variables should be modeled at the same spatial scale, as recent studies have shown that different area-level covariates are associated with health outcomes at different spatial scales.^2,6,7 Root⁶ finds that the relationship between area-level SES variables and orofacial cleft risk varies when using different spatial scales to define neighborhoods. The study results indicate that poverty has a stronger association with risk for cleft palate at smaller geographic scales, while unemployment has a stronger association at larger scales, thus providing evidence that neighborhood effects operate at different spatial scales. In addition, Flowerdew et al.² demonstrate in a British study of limiting long-term illness (LLTI) that the correlation strength between area-level variables and LLTI can vary depending on the spatial scale. Stronger correlations are present for LLTI and age group at the smaller enumeration district (ED) scale, while stronger correlations exist for LLTI and unemployment at the larger ward scale. In another study, Block et al.⁸ examine the relationship between fast-food restaurant density (FFRD) and black and low-income neighborhoods while controlling for various neighborhood variables such as commercial activity and presence of highways, which, in addition to FFRD, are available at two spatial scales (0.5- and 1-mi buffer sizes). They find that, while the results for both buffer analyses are similar, the 1-mi buffer analysis leads to a statistically significant association for median household income, perhaps due to a better capturing of how far people are willing to travel to buy food. In light of these findings, it is important to consider spatial scale for each area-level covariate when studying relationships between environmental variables and a particular outcome variable.

In this paper, we present a novel approach for modeling area-based variables at different spatial scales using four model selection approaches. To demonstrate these methods, we use a nitrate dataset containing numerous geologic and land use variables at different buffer sizes to investigate potential associations with nitrate concentrations in drinking well water. Contamination of drinking water by nitrate is a growing problem in agricultural areas of the United States, as ingested nitrate can lead to the endogenous formation of N-nitroso compounds, which are potent carcinogens. Our methods are not limited to the case example we present, but can be applied to other area-based variables that are related to cancer.

Methods

Statistical methods

We review four established methods used in model selection: forward stepwise regression, incremental forward stagewise regression, least angle regression (LARS), and the lasso.²⁴ Next, we introduce our modified versions of these algorithms to select the spatial scale. Lastly, we present an application of our methods to model groundwater nitrate concentrations in Iowa.

Model selection approaches

Forward stepwise regression

Forward stepwise regression is a common approach used for model selection. A description of the forward stepwise regression algorithm detailed by Berk²² and Wheeler²³ is as follows:

1. Initialize all regression coefficients ${\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_p=0$, and let r = y, where r denotes the residual vector and y denotes the response vector.

2. Of the candidate variables, find the predictor x_j that has the greatest absolute correlation with the residuals r, and add x_j to the working design matrix X_in.

3. Let $\widehat{\mathit{\beta }}={({\mathit{X}}_{in}^T{\mathit{X}}_{in})}^{-1}{\mathit{X}}_{in}^T\mathit{y}$.

4. Compute the residuals r = y − ŷ, where ŷ is the vector of fitted values.

5. Iterate steps (2)–(4) until there is an inadequate improvement in the performance of the model or until all predictors have been added to the model.

For step (5), we consider there to be an inadequate improvement in the model’s performance if the difference in the Akaike information criterion (AIC) between the current model and the proposed model is less than ε, for some ε > 0.

Incremental forward stagewise regression

Incremental forward stagewise regression is another common approach used for model selection. Hastie et al.²⁴ and Hastie et al.²⁵ describe the incremental forward stagewise regression algorithm as follows:

1. Initialize all regression coefficients ${\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_p=0$, and let r = y, where r denotes the residual vector and y denotes the response vector.

2. Find the predictor x_j that has the greatest absolute correlation with the residuals r.

3. Let ${\widehat{\beta }}_j\leftarrow {\widehat{\beta }}_j+{\delta }_j$, where δ_j = τ·sign[corr(r,x_j)] for some step size τ>0.

4. Let r ← r − δ_jx_j.

5. Iterate steps (2)–(4) until none of the predictors are correlated with the residuals r.

For step (5), we consider none of the predictors to be correlated with the residuals if max|corr(r, X)| is less than a specified tolerance, where the tolerance is some small, positive number.

Least angle regression

Following the notation of Yuan and Lin,²⁶ the LARS algorithm is described as follows:

1. Initialize all regression coefficients ${\widehat{\beta }}_1^{[0]},\dots ,{\widehat{\beta }}_p^{[0]}=0$, and let r^[0] = y, where r^[0] denotes the residual vector at index 0 and y denotes the response vector. Set i = 1, where i is the index for the current iteration count.

2. Find the predictor x_c among the p possible predictors that has the greatest absolute correlation with the residuals r^[i−1].

3. Let the active set ${\mathit{A}}_i$be equal to the corresponding column index of X associated with the predictor x_c, and add x_c to the working design matrix ${\mathit{X}}_{{\mathit{A}}_i}$.

4. Let γ be a p-dimensional vector where all values are set equal to 0. Calculate the current least squares direction γ by updating

   $$\mathit{\gamma }[{\mathit{A}}_i]={({\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{X}}_{{\mathit{A}}_i})}^{-1}{\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{r}}^{[i-1]}.$$
5. For every j in X that is not an element of the active set ${\mathit{A}}_i$, calculate α_j, the minimum distance needed to move the active regression coefficient(s) in direction γ until another predictor x_j has as much correlation with the current residuals as the variables in the active set. That is, find α_j ∊ (0,1) such that

   $${\Vert {\mathit{x}}_j^T({\mathit{r}}^{[i-1]}-{\alpha }_j\mathit{X}\mathit{\gamma })\Vert }^2={\Vert {\mathit{x}}_{j^{\prime }}^T({\mathit{r}}^{[i-1]}-{\alpha }_j\mathit{X}\mathit{\gamma })\Vert }^2,$$

   where j′ is arbitrarily chosen from ${\mathit{A}}_i$.

6. If ${\mathit{A}}_i\ne \{1,\dots ,p\}$, set $\mathit{\alpha }=\underset{{\mathit{\alpha }}_j>0}{\underset{j\notin {\mathit{A}}_i}{\min }}({\mathit{\alpha }}_j)={\mathit{\alpha }}_{j*}$, update the current active set ${\mathit{A}}_{i+1}={\mathit{A}}_i\cup \{j*\}$, where j* denotes the corresponding column index of X associated with the predictor x_j*, and add x_j* to the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$; else, set α = 1.

7. Let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\mathit{\alpha }\mathit{\gamma }$.

8. Let ${\mathit{r}}^{[i]}=\mathit{y}-\mathit{X}{\widehat{\mathit{\beta }}}^{[i]}$.

9. Set i = i + 1, and iterate steps (4)–(8) until α = 1, when all predictors have been added to the model.

For step (5), for ease of computation, we select j′ to always be the first value of the active set ${\mathit{A}}_i$. Thus, for each iteration, x_j′ corresponds to the first column of the design matrix ${\mathit{X}}_{{\mathit{A}}_i}$. After p iterations, the ordinary least squares (OLS) solution is reached.²⁵

Lasso

The lasso, which stands for least absolute shrinkage and selection operator,²⁷ is a shrinkage method that is good for dealing with high-dimensional data and correlated covariates by placing a constraint on the magnitude of the regression coefficients.^23,24 Hastie et al.²⁴ define the lasso estimate as follows: ${\widehat{\beta }}^{\mathrm{lasso}}=\underset{\beta }{\arg \min }{\displaystyle \sum _{i=1}^n{\left(y_i-{\beta }_0{\displaystyle \sum _{j=1}^p{X}_{ij}{\beta }_j}\right)}^2}$, such that ${\displaystyle \sum _{j=1}^p\left|{\beta }_j\right|\le t}$, where t is a tuning parameter that determines the shrinkage extent. Efron et al.²⁸ discover that the LARS algorithm can be modified to obtain the lasso solutions. As with LARS, the lasso adds variables to the active set. However, unlike LARS, the lasso does not permit active nonzero coefficients to cross zero, and in cases where a nonzero coefficient reaches zero, that variable is dropped from the active set.²⁴

Following the notation of Efron et al.²⁸, Shi²⁹ describes the lasso algorithm as follows:

1. Initialize all regression coefficients ${\widehat{\mathit{\beta }}}_1^{[0]},\dots ,{\widehat{\mathit{\beta }}}_p^{[0]}=0$, and let r^[0] = y, where r^[0] denotes the residual vector at index 0 and y denotes the response vector. Set i = 1, where i is the index for the current iteration count.

2. Find the predictor x_j among the p possible predictors that has the greatest absolute correlation with the residuals r^[i−1], and let the active set ${\mathit{A}}_i$ be equal to the corresponding column index of X associated with the predictor x_j.

3. Add x_j to the working design matrix ${\mathit{X}}_{{\mathit{A}}_i}$ such that ${\mathit{X}}_{{\mathit{A}}_i}={(\dots {\mathit{s}}_j{\mathit{x}}_j\dots )}_{j\in {\mathit{A}}_i}$, where s_j = sign{corr(x_j,r^[i−1])} = ±1.

4. Compute the following:

   • ĉ = corr(X,r^[r−1]),
   • Ĉ =max{|ĉ|},
   • ${\mathrm{A}}_{{\mathit{A}}_i}={(1_{\left|{\mathit{A}}_i\right|}^T{\mathit{G}}_{{\mathit{A}}_i}^{-1}{1}_{\left|{\mathit{A}}_i\right|})}^{-1/2}$, where $\left|{\mathit{A}}_i\right|$ is the length of ${\mathit{A}}_i$ and ${\mathit{G}}_{{\mathit{A}}_i}={\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{X}}_{{\mathit{A}}_i}$, and
   • $\mathit{a}={\mathit{X}}^T{\mathit{u}}_{{\mathit{A}}_i}$, where ${\mathit{u}}_{{\mathit{A}}_i}={\mathit{X}}_{{\mathit{A}}_i}{\mathit{w}}_{{\mathit{A}}_i}$ and ${\mathit{w}}_{{\mathit{A}}_i}={\mathrm{A}}_{{\mathit{A}}_i}{\mathit{G}}_{{\mathit{A}}_i}^{-1}{1}_{\left|{\mathit{A}}_i\right|}$.

5. Find $\widehat{\gamma }=\min \left\{\underset{j\notin {\mathit{A}}_i}{{\min }^{+}}\left(\frac{\widehat{C}-{\widehat{c}}_j}{{\mathrm{A}}_{{\mathit{A}}_i}-{\alpha }_j},\frac{\widehat{C}+{\widehat{c}}_j}{{\mathrm{A}}_{{\mathit{A}}_i}-{\alpha }_j}\right)\right\}={\widehat{\gamma }}_{\widehat{j}}$, where “min^+” specifies that, for every j not in the active set ${\mathit{A}}_i$, the minimum is found over only the positive elements, and ĵ denotes the corresponding column index of X associated with the predictor x_ĵ.

6. Let $\widehat{\mathit{d}}$ be a p-dimensional vector where all values are set equal to 0. For every $j\in {\mathit{A}}_i$, update $\widehat{\mathit{d}}$ by calculating

   $$\widehat{\mathit{d}}[{\mathit{A}}_i]=s_j{(w_{{\mathit{A}}_i})}_j.$$

7. Find $\tilde{\gamma }=\underset{j\in {\mathit{A}}_i}{{\min }^{+}}\left(-\frac{{\widehat{\beta }}_j}{{\widehat{d}}_j}\right)={\tilde{\gamma }}_{\tilde{j}}$, where $\tilde{j}$ denotes the corresponding column index of X associated with the predictor ${\mathit{x}}_{\tilde{j}}$. If $\tilde{\gamma }<\widehat{\gamma }$,.let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\tilde{\gamma }\widehat{\mathit{d}}$, update ${\mathit{A}}_{i+1}={\mathit{A}}_i-\left\{\tilde{j}\right\}$, and update the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$; else, let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\tilde{\gamma }\widehat{\mathit{d}}$, update ${\mathit{A}}_{i+1}={\mathit{A}}_i\cup \left\{\widehat{j}\right\}$, and update the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$.

8. Let ${\mathit{r}}^{[i]}=\mathit{y}-\mathit{X}{\widehat{\mathit{\beta }}}^{[i]}$.

9. Set i = i + 1, and iterate steps (4)–(8) until all predictors have been added to the model and $\tilde{\gamma }<\widehat{\gamma }$.

Notice that step (7) is the lasso modification to the LARS algorithm. At the final iteration, the OLS solution is reached.²⁸

Modifications of Model Selection Approaches to Select Spatial Scale

Spatial scale forward stepwise regression

We propose a modified forward stepwise regression algorithm that selects each area-level variable at only one spatial scale in order to build regression models to explain variation in a continuous outcome variable. We use the basic forward stepwise algorithm with adjustments to select the scale for variables available at more than one spatial level. In the algorithm, all variables are considered at all available spatial scales as potential candidates to enter a model. However, due to potentially high correlations present across different scales for a given variable, we constrain the algorithm to select each area-level variable at a single spatial scale.

Our modeling approach uses a 3-D or stacked matrix, where each stack represents a particular level of covariates, including spatial scale. As an example, we might have several individual-level covariates, an area-level covariate available at 1, 2, and 3 mi, and another area-level covariate available at 4 and 6 mi. In this case, the first stack would contain the individual-level variables; the second, third, and fourth stacks would contain the area-level variable at the 1-, 2-, and 3-mi levels; and the fifth and sixth stacks would contain the area-level variable at the 4- and 6-mi levels, respectively. In cases where values are only present for a covariate at certain levels, that covariate is assigned missing values at all other levels. The spatial scale forward stepwise regression algorithm is as follows:

1. Construct an n × p × S stacked matrix X, where n = the number of observations, p = the number of variables, and S = the number of levels of covariates.

2. Initialize all regression coefficients ${\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_p=0$, and let r = y, where r denotes the residual vector and y denotes the response vector.

3. For each stack s, s = 1,…,S: Of the candidate variables, find the predictor x_js that has the greatest absolute correlation with the residuals r.

4. Of the s correlations, select the predictor x_js that has the maximum correlation, and add that predictor to the working design matrix X_in.

5. Let $\widehat{\mathit{\beta }}={({\mathit{X}}_{in}^T{\mathit{X}}_{in})}^{-1}{\mathit{X}}_{in}^T\mathit{y}$.

6. Compute the residuals r = y – ŷ, where ŷ is the vector of fitted values.

7. Iterate steps (3)–(6) until there is an inadequate improvement in the performance of the model or until all predictors have been added to the model.

For step (4), it is important to note that, once an overall maximum is determined, we select the corresponding variable at the best spatial scale and remove all other versions (or spatial scales) of that variable from further consideration for model selection. In this way, we constrain the algorithm to select each area-based variable at a single spatial scale. For step (7), we consider there to be an inadequate improvement in the model’s performance if the difference in the AIC between the current model and the proposed model is less than ε, for some ε > 0.

Spatial scale incremental forward stagewise regression

We spatially modify the basic forward stagewise algorithm to select each area-level variable at a single spatial scale. We use the same matrix data structure as with the spatial scale forward stepwise algorithm. The spatial scale incremental forward stagewise regression algorithm is as follows:

1. Construct an n × p × S stacked matrix X, where n = the number of observations, p = the number of variables, and S = the number of levels of covariates.

2. Initialize all regression coefficients ${\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_p=0$, and let r = y, where r denotes the residual vector and y denotes the response vector.

3. For each stack s, s = 1,…,S: Find the predictor x_js that has the greatest absolute correlation with the residuals r.

4. Of the s correlations, select the predictor x_js that has the maximum correlation.

5. Let ${\widehat{\beta }}_j\leftarrow {\widehat{\beta }}_j+{\delta }_j$, where δ_j = τ·sign[corr(r,x_js)] for some step size τ > 0.

6. Let r ← r − δ_jx_js.

7. Iterate steps (3)–(6) until none of the predictors are correlated with the residuals r.

For step (4), once an overall maximum is determined, we select the corresponding variable at the best spatial scale and remove all other versions (or spatial scales) of that variable from further consideration. In this way, we constrain the algorithm to select each area-level variable at a single spatial scale. For step (7), we state that none of the predictors are correlated with the residuals if the overall maximum is less than a specified tolerance, where the tolerance is some small positive number.

Spatial scale least angle regression

Our approach for the spatial modification of the LARS algorithm involves the use of a block diagonal matrix ${\mathrm{A}}_{\mathit{cand}}=\left(\begin{array}{ccc}{a}_1& & 0\\ & \ddots & \\ 0& & a_p\end{array}\right)$, where each a_j,,for j = 1,…, p, is an s_j × s_j identity matrix such that each column indicates a particular level or spatial scale, where p is the total number of predictor variables disregarding spatial scale and s_j is the number of levels of covariates for the jth variable. A_cand is a square matrix with $p*={\displaystyle \sum _{j=1}^p{s}_j}$ rows. Every time a variable enters the active set ${\mathit{A}}_i$, A_cand is updated by removing all other versions (or spatial scales) of the winning variable. When X is post-multiplied by A_cand, we get the candidate design matrix X_cand, which keeps track of variables in the active set as well as candidate variables. Through this updating of X_cand, we modify the basic LARS algorithm to select each area-level variable at a single spatial scale.

Adopting the notation of Yuan and Lin,²⁶ the spatial scale LARS algorithm is as follows:

1. Initialize all regression coefficients ${\widehat{\beta }}_1^{[0]},\dots ,{\widehat{\beta }}_{p*}^{[0]}=0$, and let r^[0] = y, where r^[0] denotes the residual vector at index 0 and y denotes the response vector. Let A_cand be a preprocessed p* × p* block diagonal matrix. Set i = 1, where i is the index for the current iteration count.

2. Find the predictor x_c among the p* possible predictors that has the greatest absolute correlation with the residuals r^[i−1].

3. Let the active set ${\mathit{A}}_i$ be equal to the corresponding column index of X associated with the predictor x_c, and add x_c to the working design matrix ${\mathit{X}}_{{\mathit{A}}_i}$.

4. Update A_cand by removing all other versions of the winning predictor variable x_c, and update the candidate design matrix X_cand = X · A_cand.

5. Let γ be a p*-dimensional vector, where all values are set equal to 0. Calculate the current least squares direction γ by updating

   $$\mathit{\gamma }[{\mathit{A}}_i]={({\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{X}}_{{\mathit{A}}_i})}^{-1}{\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{r}}^{[i-1]}$$

   .
6. For every j in X_cand that is not an element of the active set ${\mathit{A}}_i$ calculate α_j, which is the minimum distance needed to move the active regression coefficient(s) in direction γ until another predictor x_j has as much correlation with the current residuals as the variables in the active set. That is, find α_j ∊ (0,1) such that

   $$\begin{array}{l}{\Vert {\mathit{x}}_j^T({\mathit{r}}^{[i-1]}-{\alpha }_j{\mathit{X}}_{\mathit{cand}}{({\mathit{\gamma }}^T{\mathit{A}}_{\mathit{cand}})}^T)\Vert }^2\\ ={\Vert {\mathit{x}}_{j^{\prime }}^T({\mathit{r}}^{[i-1]}-{\alpha }_j{\mathit{X}}_{\mathit{cand}}{({\mathit{\gamma }}^T{\mathit{A}}_{\mathit{cand}})}^T)\Vert }^2,\end{array}$$

   where j′ is arbitrarily chosen from ${\mathit{A}}_i$

7. If $\left|{\mathit{A}}_i\right|\ne p$, set $\mathit{\alpha }=\underset{{\mathit{\alpha }}_j>0}{\underset{j\notin {\mathit{A}}_i}{\min }}({\mathit{\alpha }}_j)={\mathit{\alpha }}_{j*}$, update the current active set ${\mathit{A}}_{i+1}={\mathit{A}}_i\cup \{j*\}$, where j* denotes the corresponding column index of X associated with the predictor x_j*, add x_j* to the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$, update A_cand, and update the candidate design matrix X_cand = X · A_cand; else, set α = 1.

8. Let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\mathit{\alpha }\mathit{\gamma }$.

9. Let ${\mathit{r}}^{[i]}=\mathit{y}-{\mathit{X}}_{\mathit{cand}}{({({\widehat{\mathit{\beta }}}^{[i]})}^T{\mathit{A}}_{\mathit{cand}})}^T$.

10. Set i = i + 1, and iterate steps (5)–(9) until α = 1, when all predictors have been added to the model.

For steps (4) and (7), once a predictor variable is chosen to enter the model, we select that variable at the best spatial scale and remove all other versions (or spatial scales) of that variable from further consideration from the candidate design matrix X_cand. In this way, we constrain the algorithm to select each area-level variable at a single spatial scale. For step (6), for ease of computation, we select j′ to always be the first value of the active set ${\mathit{A}}_i$ Thus, for each iteration, x_j′ corresponds to the first column of the design matrix ${\mathit{X}}_{{\mathit{A}}_i}$. After p iterations, the OLS solution is reached.²⁵

Spatial scale lasso

As with the spatial modification of LARS, our modeling approach for the spatial modification of the lasso algorithm involves the use of a p* × p* block diagonal matrix ${\mathrm{A}}_{\mathit{cand}}=\left(\begin{array}{ccc}{a}_1& & 0\\ & \ddots & \\ 0& & a_p\end{array}\right)$, where each a_j, for j = 1,…,p, is an s_j × s_j identity matrix such that each column indicates a particular level or spatial scale, where p is the total number of predictor variables disregarding spatial scale, s_j is the number of levels of covariates for the jth variable, and p* is the total number of predictor variables at all available levels such that $p*={\displaystyle \sum _{j=1}^p{s}_j}$. As with the spatially modified LARS method, every time a variable enters the active set ${\mathit{A}}_i$, A_cand is updated by removing all other versions (or spatial scales) of the winning variable. When X is post-multiplied by A_cand, we get the candidate design matrix X_cand, which keeps track of variables in the active set as well as candidate variables. Through this updating of X_cand, we modify the basic lasso algorithm to select each area-level variable at a single spatial scale.

Adopting the notation of Efron et al.²⁸, the spatial scale lasso algorithm is as follows:

1. Initialize all regression coefficients ${\widehat{\beta }}_1^{[0]},\dots ,{\widehat{\beta }}_{p*}^{[0]}=0$, and let r^[0] = y, where r^[0] denotes the residual vector at index 0 and y denotes the response vector. Let A_cand be a preprocessed p* × p* block diagonal matrix. Set i = 1, where i is the index for the current iteration count.

2. Find the predictor x_j among the p* possible predictors that has the greatest absolute correlation with the residuals r^[i−1], and let the active set ${\mathit{A}}_i$ be equal to the corresponding column index of X associated with the predictor x_j.

3. Add x_j to the working design matrix ${\mathit{X}}_{{\mathit{A}}_i}$ such that ${\mathit{X}}_{{\mathit{A}}_i}={(\dots {\mathit{s}}_j{\mathit{x}}_j\dots )}_{j\in {\mathit{A}}_i}$, where s_j =sign{corr(x_j,r^[i−1])} = ±1.

4. Update A_cand by removing all other versions of the winning predictor variable x_j, and update the candidate design matrix X_cand = X · A_cand.

5. Compute the following:

   • ĉ = corr(X_cand,r^[r−1]),
   • Ĉ =max{|ĉ|},
   • ${\mathrm{A}}_{{\mathit{A}}_i}={(1_{\left|{\mathit{A}}_i\right|}^T{\mathit{G}}_{{\mathit{A}}_i}^{-1}{1}_{\left|{\mathit{A}}_i\right|})}^{-1/2}$, where $\left|{\mathit{A}}_i\right|$ is the length of ${\mathit{A}}_i$ and ${\mathit{G}}_{{\mathit{A}}_i}={\mathit{X}}_{{\mathit{A}}_i}^T{\mathit{X}}_{{\mathit{A}}_i}$, and
   • $\mathit{a}={\mathit{X}}_{\mathit{cand}}^T{\mathit{u}}_{{\mathit{A}}_i}$, where ${\mathit{u}}_{{\mathit{A}}_i}={\mathit{X}}_{{\mathit{A}}_i}{\mathit{w}}_{{\mathit{A}}_i}$ and ${\mathit{w}}_{{\mathit{A}}_i}={\mathrm{A}}_{{\mathit{A}}_i}{\mathit{G}}_{{\mathit{A}}_i}^{-1}{1}_{\left|{\mathit{A}}_i\right|}$.

6. Find $\widehat{\gamma }=\min \left\{\underset{j\notin {\mathit{A}}_i}{{\min }^{+}}\left(\frac{\widehat{C}-{\widehat{c}}_j}{{\mathrm{A}}_{{\mathit{A}}_i}-{\alpha }_j},\frac{\widehat{C}+{\widehat{c}}_j}{{\mathrm{A}}_{{\mathit{A}}_i}-{\alpha }_j}\right)\right\}={\widehat{\gamma }}_{\widehat{j}}$, where “min⁺” specifies that, for every j not in the active set ${\mathit{A}}_i$ the minimum is found over only the positive elements, and ĵ denotes the corresponding column index of X associated with the predictor x_ĵ.

7. Let $\widehat{\mathit{d}}$ be a p*-dimensional vector where all values are set equal to 0. For every $j\in {\mathit{A}}_i$, update $\widehat{\mathit{d}}$ by calculating

   $$\widehat{\mathit{d}}[{\mathit{A}}_i]=s_j{(w_{{\mathit{A}}_i})}_j.$$

8. Find $\tilde{\gamma }=\underset{j\in {\mathit{A}}_i}{{\min }^{+}}\left(-\frac{{\widehat{\beta }}_j}{{\widehat{d}}_j}\right)={\tilde{\gamma }}_{\tilde{j}}$, where $\tilde{j}$ denotes the corresponding column index of X associated with the predictor ${\mathit{x}}_{\tilde{j}}$. If $\tilde{\gamma }<\widehat{\gamma }$,.let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\tilde{\gamma }\widehat{\mathit{d}}$, update ${\mathit{A}}_{i+1}={\mathit{A}}_i-\left\{\tilde{j}\right\}$, and update the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$; else, let ${\widehat{\mathit{\beta }}}^{[i]}={\widehat{\mathit{\beta }}}^{[i-1]}+\tilde{\gamma }\widehat{\mathit{d}}$, update ${\mathit{A}}_{i+1}={\mathit{A}}_i\cup \left\{\widehat{j}\right\}$, update the working design matrix ${\mathit{X}}_{{\mathit{A}}_{i+1}}$, update A_cand, and update the candidate design matrix X_cand = X · A_cand.

9. Let ${\mathit{r}}^{[i]}=\mathit{y}-{\mathit{X}}_{\mathit{cand}}{({({\widehat{\mathit{\beta }}}^{[i]})}^T{\mathit{A}}_{\mathit{cand}})}^T$.

10. Set i = i + 1, and iterate steps (5)–(9) until all predictors have been added to the model and $\tilde{\gamma }<\widehat{\gamma }$.

Step (8) is the lasso modification. For steps (4) and (8), once a predictor variable is chosen to enter the model, we select that variable at the best spatial scale and remove all other versions (or spatial scales) of that variable from further consideration from the candidate design matrix X_cand. In this way, we constrain the algorithm to select each area-level variable at a single spatial scale. At the final iteration, the OLS solution is reached.²⁸

Application to Groundwater Nitrate

Study data

To model the variation in nitrate in drinking well water in Iowa, we used data for private wells sampled from 1984 to 2011 by the following programs: the Iowa Grants to Counties Water Well Program (GTC), the Iowa Private Well Tracking System, the Iowa Statewide Rural Well Water Survey, the Iowa Community Private Well Study, and the U.S. Geological Survey (USGS). We used only those wells with the most accurate locations as determined by GPS measurements, topographic quad maps, and geocoded residence addresses. Seventy-five percent of the well locations were based on geocoded residential street addresses. Nitrate data were reported either as nitrate or nitrite-plus-nitrate as NO₃⁻, and the latter were converted to nitrate-nitrogen (hereafter referred to as “nitrate”). Values below the detection limit were imputed from a log-normal distribution of uncensored data.³⁰ Same-day samples at the same well location and depth were excluded if their standard deviation was 5 mg/L nitrate-N or more; otherwise the average of such samples was used. Nitrate data were natural-log-transformed prior to modeling. There were 11,931 well measurements in the analysis dataset.

We considered a set of 115 explanatory variables in the statistical analysis (Table 1). Variables were available for characteristics at the individual well location and for characteristics of the surrounding environment over different distance buffers. Variables at the individual well level include longitude, latitude, elevation, well depth, bedrock status, and bedrock depth, among others. A geographic information system was used to calculate the surrounding environmental variables. Most of the environmental variables were calculated using more than one distance buffer to assess the importance of spatial scale. An exception was for counts of animal feeding operations (AFOs) by type (Confined, Open Feedlot, Mixed), which were only calculated at 10 km. The AFO type of the closest AFO was also recorded, along with the number of animals at the nearest AFO (NearAFO_AnimalUnits). Most of the other area-based variables were calculated at distances of 500 m and 1 km. These area-based covariates include average percent sand, average percent clay, average slope length, and mean population density, among others. Only fine-grain thickness (FnGrn_Logs) was calculated at 4- and 6-mi distances. Additional details on the variables are available in Wheeler et al.³⁰ To account for missing data, we excluded 9.3% of the observations that were missing values for any of the covariates and used 10,824 nitrate measurements in our analysis.

Table 1.

Variable definitions for the variables considered in the spatial scale forward stepwise, forward stagewise, LARS, and lasso models. The horizontal dashed line separates the individual-level variables and the area-based variables available at more than one buffer distance. Any variable that falls below the dashed line has a suffix indicating the associated spatial scale.

VARIABLE NO.	NAME	DESCRIPTION
1	Latitude	Latitude value of well location (degrees)
2	Longitude	Longitude value of well location (degrees)
3	SampleYr	Well sample year
4	Well_Depth	Depth of measurement well (ft)
5	Elevation	Land-surface elevation at well point (ft)
6	Bdrk_Dpth	Depth (ft) to bedrock at well point
7	Bdrk_Flag	Flag indicating if well is within or above bedrock. 0 = Above bedrock; 1 = Within bedrock
8	NearAFO_Dist	Distance to nearest AFO (Animal Feeding Operation) facility (m)
9	NearAFO_Type_1	Type of nearest AFO facility: Open Feedlot
10	NearAFO_Type_2	Type of nearest AFO facility: Confined/Open (ie, mixed)
11	NearAFO_AnimalUnits	Total Animal Units at the nearest AFO facility
12	Count_10 kmConfmnts	Number of confinement-only AFOs within 10 km of the well point
13	Count_10 kmFeedlots	Number of feedlot-only AFOs within 10 km of the well point
14	Count_10 kmMixed	Number of mixed-only AFOs within 10 km of the well point
15	Count_10 kmHogs	Number of hog facilities within 10 km of the well point
16	precip	Estimated mean annual precipitation at well point for the time period 1981–2010 (millimeters times 100)
17	mintemp	Estimated mean annual minimum temperature at well point for the time period 1981–2010 (°C times 100)
18	maxtemp	Estimated mean annual maximum temperature at well point for the time period 1981–2010 (°C times 100)
19	SinkholeDist_m	Distance from well point to nearest sinkhole point (m)
20	K	Average horizontal hydraulic conductivity of all glacial deposits at well point (ft/day)
21	AvgK	Average horizontal hydraulic conductivity of all glacial deposits within a 4 × 4-mile square around the well point (ft/day)
22	Kz	Average vertical hydraulic conductivity of all glacial deposits at the well point (ft/day)
23	AvgKz	Average vertical hydraulic conductivity of all glacial deposits within a 4 × 4-mile square around the well point (ft/day)
24	Trans	Transmissivity of all glacial deposits at the well point (ft2/day)
25	AvgTrans	Average transmissivity of all glacial deposits within a 4 × 4-mile square around the well point (ft2/day)
26	MaxKz	Maximum kz within the 4 × 4-mile square around the well point (ft/day)
27	KKzT_Logs	Number of USGS water well logs within a 4 × 4-mile square around the well point (count)
28–29	Sand	Average percent sand within a 500-m/1-km buffer
30–31	Silt	Average percent silt within a 500-m/1-km buffer
32–33	Clay	Average percent clay within a 500-m/1-km buffer
34–35	OM	Average percent organic matter within a 500-m/1-km buffer
36–37	Db033	Average bulk density at 1/3 bar within a 500-m/1-km buffer (g/cm3)
38–39	Dbovendry	Average oven dry bulk density at 1/3 bar within a 500-m/1-km buffer (g/cm3)
40–41	Ksat	Average saturated hydraulic conductivity within a 500-m/1-km buffer (μm/s)
42–43	AWC	Average available water capacity within a 500-m/1-km buffer (cm H2O/cm soil)
44–45	H2O15	Average water content at 15 bar within a 500-m/1-km buffer (percent by weight)
46–47	AASHTOGr	Average AASHTO group classification within a 500-m/1-km buffer
48–49	Kw	Average K factor for whole soil within a 500-m/1-km buffer
50–51	Kf	Average K factor for rock free soil within a 500-m/1-km buffer
52–53	CaCO3	Average calcium carbonate within a 500-m/1-km buffer (percent by weight)
54–55	CEC7	Average cation-exchange capacity within a 500-m/1-km buffer (milliequivalents per 100 g)
56–57	pHH2O	Average pH (1 to 1 water) within a 500-m/1-km buffer
58–59	Slope	Average percent slope within a 500-m/1-km buffer
60–61	SlopeLength	Average slope length within a 500-m/1-km buffer (ft)
62–63	Runoff	Average runoff potential within a 500-m/1-km buffer (Scale: 1–6; negligible to very high)
64–65	T	Average soil loss tolerance within a 500-m/1-km buffer (tons/acre/year)
66–67	WEI	Average wind erodibility index within a 500-m/1-km buffer
68–69	Aspect	Average aspect (direction the surface of the soil faces) within a 500-m/1-km buffer (degrees)
70–71	MAP	Average mean annual precipitation within a 500-m/1-km buffer (mm)
72–73	FrostFDays	Average number of frost free days per year within a 500-m/1-km buffer
74–75	FrostAction	Average degree of frost action within a 500-m/1-km buffer (Scale: 0–3; none to high)
76–77	CorrosionCon	Average risk of concrete corrosion within a 500-m/1-km buffer (Scale: 1–3; low to high)
78–79	CorrosionSt	Average risk of steel corrosion within a 500-m/1-km buffer (Scale: 1–3; low to high)
80–81	IACSR	Average Iowa corn suitability rating within a 500-m/1-km buffer (Scale: 0–100)
82–83	WaterDepth	Average depth to water within a 500-m/1-km buffer (cm)
84–85	FloodingFreq	Average flooding frequency within a 500-m/1-km buffer (Scale: 0–4, none to very frequent)
86–87	PondingFreq	Average ponding frequency within a 500-m/1-km buffer (%)
88–89	DrainClass	Average drainage classification within a 500-m/1-km buffer (Scale: 1–7, very poorly drained to excessively drained)
90–91	FarmClass	Percent “not prime farmland” within a 500-m/1-km buffer
92–93	HELWater	Percent “not highly water erodable land” within a 500-m/1-km buffer
94–95	HELWind	Percent “not highly wind erodable land” within a 500-m/1-km buffer
96–97	Basements	Percent “very limited and somewhat limited” basement limitations within a 500-m/1-km buffer
98–99	SewageLag	Percent “very limited and somewhat limited” sewage lagoon limitations within a 500-m/1-km buffer
100–101	Trails	Percent “very limited and somewhat limited” path and trail limitations within a 500-m/1-km buffer
102–103	HydricClas	Percent “all hydric and partially hydric” hydric classifications within a 500-m/1-km buffer
104–105	TileDrn_USGS	Mean “estimated percent tile drainage on agricultural lands” within a 500-m/1-km buffer
106–107	TileDrn_IADNR	Mean “estimated percent tile drainage” within a 500-m/1-km buffer
108–109	PopDen90	Mean population density within a 500-m/1-km buffer derived from U.S. Census 1990 (persons per km2)
110–111	PopDen00	Mean population density within a 500-m/1-km buffer derived from U.S. Census 2000 (persons per km2)
112–113	Recharge	Estimated mean annual natural ground-water recharge within a 500-m/1-km buffer (millimeters per year)
114–115	FnGrn_Logs	Number of well logs within a 4 × 4-mile/6 × 6-mile square around the well point used to generate an interpolated total fine-grain thickness grid

Statistical analysis

We modeled the natural log of nitrate concentrations in well water using our four spatial scale selection algorithms. We built spatial scale forward stepwise regression, spatial scale incremental forward stagewise regression, spatial scale LARS, and spatial scale lasso models to explain variation in log nitrate concentration while allowing any individual-level variable to enter the model and any area-based variable to enter the model at a single spatial scale, considering all available spatial scales. For spatial scale forward stepwise and spatial scale stagewise, we used a stacked data matrix where the first stack contained individual-level variables or area-level variables available at only one spatial scale, the second and third stacks contained area-level variables at the 500-m and 1-km levels, and the fourth and fifth stacks contained area-level variables at the 4- and 6-mi levels, respectively. Given that variables available at multiple spatial scales were limited to enter a model at a single spatial scale, the total number of variables possible for model inclusion was 71 instead of 115. More specifically, the total number of individual-level variables and area-level variables available at one spatial scale possible for model inclusion was 27, and the total number of area-level variables possible was 44.

For spatial scale forward stagewise, spatial scale LARS, and spatial scale lasso, we fitted OLS regression models with the selected covariates to obtain approximate p-values and AIC measures. For ease of computation, approximate significance levels were determined when the covariates selected from the spatial scale stagewise, LARS, and lasso algorithms were plugged into OLS regression models to obtain standard error estimates. Because LARS and lasso yield a sequence of solutions, for each algorithm we selected as the final model the one that had the minimum OLS-based AIC. The outcome and predictor variables were standardized to have a mean of 0 and a standard deviation of 1. We used a significance level of α = 0.05. For the spatial scale forward stepwise algorithm, we set ε = 1 because the rule of thumb for a meaningful difference in AIC is 2 to 3.³¹ Decreasing the value of ε leads to larger models and better goodness of fit. For the spatial scale forward stagewise algorithm, we used a commonly accepted increment or step size of 0.001²² and set the tolerance = 0.01. Increasing the step size leads to larger coefficient estimates and a decreased number of algorithm iterations, and increasing the tolerance leads to models with fewer selected covariates and decreased goodness of fit. All analyses were performed using R version 3.1.0.³²

Evaluation metrics

To evaluate the success of our spatial scale algorithms, we examined our methods using three criteria. First, for each of the four algorithms, we checked to see whether different spatial scales were selected and enumerated the number of selected variables that fell into each spatial scale category. Second, we looked at the agreement in sign and spatial scale for significant variables that were selected across various groupings of the algorithms. Third, in order to evaluate the rationale of including different variables at different spatial scales within the same model, for each algorithm we compared AIC measures across three different scenarios: 1) when limiting all selected area-based variables to be at the smallest available spatial scale, 2) when limiting all selected area-based variables to be at the largest available spatial scale, and 3) when using all selected area-based variables at the spatial scales originally selected by the model.

Results

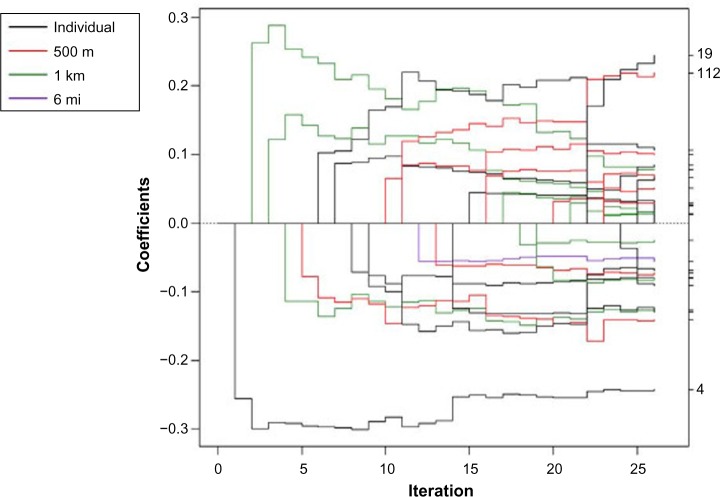
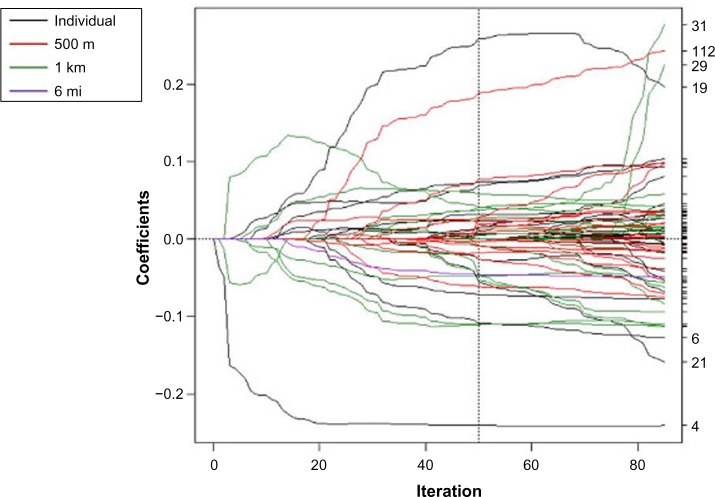
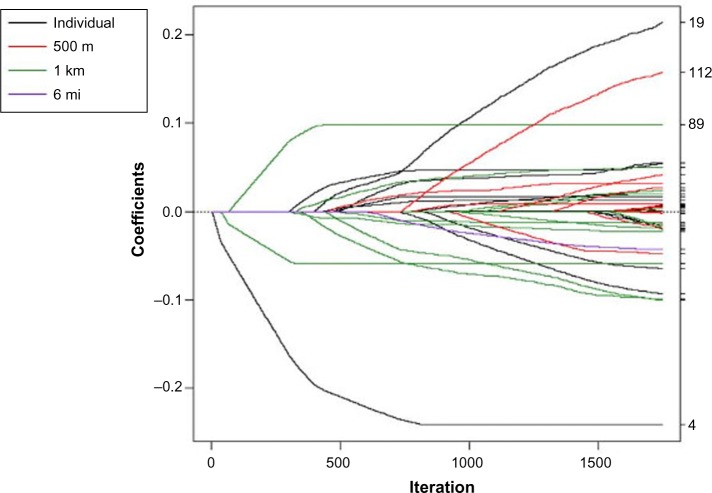
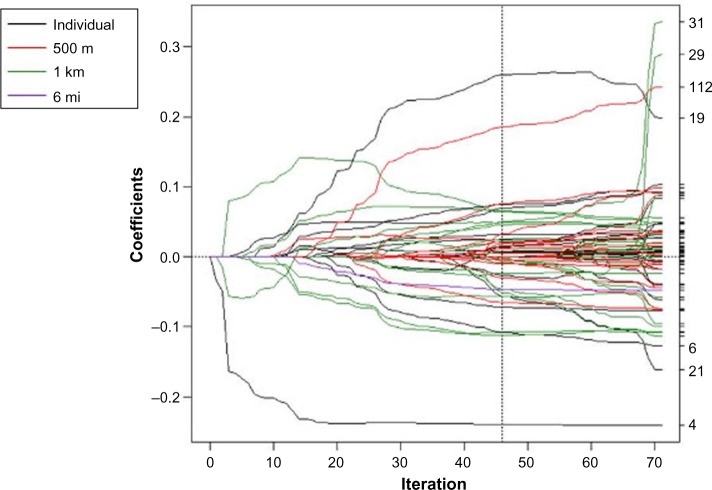
Different variables were selected at different spatial scales using the spatial scale forward stepwise, spatial scale incremental forward stagewise, spatial scale LARS, and spatial scale lasso algorithms (Figs. 1–4). In each coefficient path plot, iterations of the respective algorithm are shown as the model-building progresses, where the coefficient estimates at each iteration change as variables enter or leave a model. Black lines represent individual-level variables, red lines indicate area-based variables at the 500-m level, green lines denote area-based variables at the 1-km level, and purple lines represent area-based variables at the 6-mi level. The forward stepwise algorithm converged after 26 iterations (Fig. 1), and the forward stagewise algorithm converged after 1,747 iterations (Fig. 2). Not surprisingly, it took a large number of iterations before the stagewise algorithm converged because of the incremental updating of the beta coefficient estimates. The LARS algorithm converged to the OLS estimates after 71 iterations (Fig. 3). The dotted vertical line in Figure 3 indicates the chosen model that had the minimum OLS-based AIC. The lasso algorithm converged to the OLS estimates after 85 iterations (Fig. 4). It took more iterations for the lasso algorithm to converge than for the LARS due to lasso’s ability to add and drop variables. The dotted vertical line in Figure 4 indicates the chosen model that had the minimum OLS-based AIC.

Figure 1.

Coefficient paths for spatial scale forward stepwise regression to explain log nitrate concentration in drinking wells in Iowa. The scale the variable entered the model is indicated by the legend.

Figure 4.

Coefficient paths for spatial scale lasso to explain log nitrate concentration in drinking wells in Iowa. The scale the variable entered the model is indicated by the legend. The dotted vertical line indicates the chosen model that had the minimum OLS-based AIC.

Figure 2.

Coefficient paths for spatial scale incremental forward stagewise regression to explain log nitrate concentration in drinking wells in Iowa. The scale the variable entered the model is indicated by the legend.

Figure 3.

Coefficient paths for spatial scale LARS to explain log nitrate concentration in drinking wells in Iowa. The scale the variable entered the model is indicated by the legend. The dotted vertical line indicates the chosen model that had the minimum OLS-based AIC.

The coefficient estimates for each of the covariates selected in each of the algorithms are shown in Table 2, where the horizontal dashed line separates the individual-level variables and the area-based variables that have multiple spatial scales. Across all four algorithms, there were significant positive associations between log nitrate concentration and the following covariates: elevation, number of mixed-only AFOs within a 10-km buffer (Count_10 kmMixed), number of hog facilities within a 10-km buffer (Count_10 kmHogs), distance from well point to nearest sinkhole point (SinkholeDist_m), average transmissivity (AvgTrans), average wind erodibility index within a 500-m buffer (WEI_500 m), and estimated mean annual natural ground-water recharge within a 500-m buffer (Recharge_500 m). There were significant negative associations between log nitrate concentration and the following covariates: latitude, well depth, bedrock depth, bedrock status, average horizontal hydraulic conductivity (AvgK), average soil loss tolerance within a 1-km buffer (T_1 km), percent “not prime farmland” within a 500-m buffer (FarmClass_500 m), mean population density within a 1-km buffer from the U.S. Census 2000 (PopDen00_1 km), and fine-grain thickness at the 6-mi distance (FnGrn_Logs_6 mi).

Table 2.

Estimated coefficients from spatial scale (SS) forward stepwise, forward stagewise, LARS, and lasso models. The blank cells indicate variables not selected for a particular model. The horizontal dashed line separates the individual-level variables and the area-based variables considered at multiple spatial scales.

VARIABLE NO.	EXPLANATORY VARIABLE	SS-STEPWISE	SS-STAGEWISE	SS-LARS	SS-LASSO
1	Latitude	−0.069 (*)	−0.015 (*)	−0.027 (*)	−0.026 (*)
4	Well_Depth	−0.243 (*)	−0.242 (*)	−0.240 (*)	−0.241 (*)
5	Elevation	0.107 (*)	0.055 (*)	0.075 (*)	0.074 (*)
6	Bdrk_Dpth	−0.129 (*)	−0.093 (*)	−0.109 (*)	−0.108 (*)
7	Bdrk_Flag	−0.080 (*)	−0.065 (*)	−0.072 (*)	−0.072 (*)
11	NearAFO_AnimalUnits		0.003	0.006	0.006
12	Count_10 kmConfmnts		0.001
13	Count_10 kmFeedlots		0.013	0.008	0.007
14	Count_10 kmMixed	0.026 (*)	0.020 (*)	0.024 (*)	0.024 (*)
15	Count_10 kmHogs	0.026 (*)	0.006 (*)	0.014 (*)	0.016 (*)
19	SinkholeDist_m	0.244 (*)	0.214 (*)	0.260 (*)	0.259 (*)
21	AvgK	−0.091 (*)	−0.021 (*)	−0.056 (*)	−0.056 (*)
22	Kz	0.067 (*)	0.008	0.032	0.032
23	AvgKz		0.017 (+)	0.016 (*)	0.015 (*)
25	AvgTrans	0.084 (*)	0.055 (*)	0.069 (*)	0.070 (*)
31	Silt_1 km			0.050 (*)	0.038 (+)
32	Clay_500 m			0.013 (+)	0.012 (+)
35	OM_1 km	−0.079 (*)	−0.023 (+)	−0.057 (*)	−0.047 (*)
39	Dbovendry_1 km		0.024 (*)	0.025 (*)	0.028 (*)
41	Ksat_1 km		0.020 (*)	0.046 (*)	0.041 (*)
42	AWC_500 m			0.019 (*)	0.018 (*)
46	AASHTOGr_500 m		0.032	0.020	0.020
47	AASHTOGr_1 km	0.012
49	Kw_1 km			−0.004
52	CaCO3_500 m	−0.141 (*)
53	CaCO3_1 km		−0.099 (*)	−0.108 (*)	−0.110 (*)
55	CEC7_1 km		−0.017 (*)	−0.047 (*)	−0.053 (*)
56	pHH2O_500 m		−0.002	−0.030 (*)	−0.026 (*)
58	Slope_500 m		−0.019 (*)	−0.007 (+)	−0.009 (+)
60	SlopeLength_500 m		0.009	−0.004
63	Runoff_1 km			0.021	0.011
65	T_1 km	−0.126 (*)	−0.100 (*)	−0.112 (*)	−0.110 (*)
66	WEI_500 m	0.100 (*)	0.042 (*)	0.076 (*)	0.077 (*)
71	MAP_1 km			−0.009	−0.009 (+)
74	FrostAction_500 m	0.052 (*)	0.027 (*)	0.020	0.025
76	CorrosionCon_500 m	0.066 (*)
77	CorrosionCon_1 km		0.050 (*)	0.064 (*)	0.058 (*)
78	CorrosionSt_500 m		0.007
81	IACSR_1 km			−0.003
82	WaterDepth_500 m			0.005	−0.003
83	WaterDepth_1 km		−0.013
85	FloodingFreq_1 km	0.013
86	PondingFreq_500 m	0.029 (*)	0.005 (+)	0.011	0.009
89	DrainClass_1 km	0.078 (*)	0.098 (*)	0.066 (+)	0.041
90	FarmClass_500 m	−0.073 (*)	−0.048 (*)	−0.065 (*)	−0.061 (*)
94	HELWind_500 m		−0.001	−0.010	−0.009 (+)
97	Basements_1 km		0.003
99	SewageLag_1 km	0.012		0.007 (+)	0.005
100	Trails_500 m				−0.017
101	Trails_1 km			−0.024
107	TileDrn_IADNR_1 km		−0.059	0.049 (+)
108	PopDen90_500 m			0.033 (*)	0.029 (*)
111	PopDen00_1 km	−0.026 (*)	−0.020 (*)	−0.051 (*)	−0.047 (*)
112	Recharge_500 m	0.219 (*)	0.158 (*)	0.186 (*)	0.189 (*)
115	FnGrn_Logs_6 mi	−0.055 (*)	−0.043 (*)	−0.047 (*)	−0.046 (*)

Notes: Values marked with (*) have a P-value <0.05, and values marked with (+) have an associated P-value <0.1 (when covariates selected from the SS-Stagewise, SS-LARS, and SS-Lasso algorithms are plugged into OLS regression models).

Multiple spatial scales of 500 m and 1 km were selected for variables by each of the algorithms (Table 3). All four models selected fine-grain thickness (FnGrn_Logs) to enter at the 6-mi level. For the spatial scale forward stepwise model, 26 of the 71 individual- and area-level covariates were selected. With seven variables selected at the 500-m level and seven variables selected at the 1-km level, there was an even split between the number of variables selected at the 500-m level versus the 1-km level. For the spatial scale forward stagewise model, 39 of the 71 individual- and area-level covariates were selected. Again, there was a fairly even split with 11 variables selected at the 500-m level and 12 variables selected at the 1-km level. For the spatial scale LARS model, 46 of the 71 individual- and area-level covariates were selected. More variables were chosen to enter at the 1-km level than the 500-m level, with 14 variables selected for the latter and 17 variables for the former. For the spatial scale lasso model, 42 of the 71 individual- and area-level covariates were selected. There was a fairly even split, with 14 variables selected at the 500-m level and 13 variables selected at the 1-km level.

Table 3.

Number of variables selected at each spatial scale for spatial scale (SS) forward stepwise, forward stagewise, LARS, and lasso models. The last row gives the total number of possible variables at each spatial scale.

	INDIVIDUAL-LEVEL	AREA-LEVEL						NUMBER OF VARIABLES SELECTED
		500 m		1 km	4 mi		6 mi
SS-Stepwise	11	7		7	0		1	26
SS-Stagewise	15	11		12	0		1	39
SS-LARS	14	14		17	0		1	46
SS-Lasso	14	14		13	0		1	42
Number of available variables	27		43			1		71

Overall, there was consistency across the spatial scale algorithms in terms of the coefficient signs and spatial scale for the significant selected variables (Table 4). For various groupings of the algorithms, it is evident that, of the commonly selected covariates, the majority of them were significant. There were no instances of significant variables having different signs across algorithms, and only two instances of significant variables being selected at different spatial scales across algorithms. Average calcium carbonate (CaCO3) and average risk of concrete corrosion (CorrosionCon) were selected at the 500-m level by spatial scale stepwise and at the 1-km level by spatial scale stagewise, spatial scale LARS, and spatial scale lasso.

Table 4.

Number of shared significant variables with the same sign and spatial scale and total number of shared variables for spatial scale (SS) forward stepwise, forward stagewise, LARS, and lasso models. The frequency of shared significant variables with the same sign and spatial scale is given along with the total number of shared variables in parentheses.

	INDIVIDUAL-LEVEL	AREA-LEVEL
		500 m	1 km	4 mi	6 mi
SS-Stepwise, SS-Stagewise, SS-LARS, SS-Lasso	10	3	2	0	1
No. of shared variables	(11)	(5)	(4)	(0)	(1)
SS-Stepwise, SS-Stagewise, SS-LARS	10	3	2	0	1
No. of shared variables	(11)	(5)	(4)	(0)	(1)
SS-Stepwise, SS-Stagewise, SS-Lasso	10	3	2	0	1
No. of shared variables	(11)	(5)	(4)	(0)	(1)
SS-Stepwise, SS-LARS, SS-Lasso	10	3	3	0	1
No. of shared variables	(11)	(5)	(5)	(0)	(1)
SS-Stagewise, SS-LARS, SS-Lasso	10	3	7	0	1
No. of shared variables	(14)	(9)	(9)	(0)	(1)
SS-Stepwise, SS-Stagewise	10	4	3	0	1
No. of shared variables	(11)	(5)	(4)	(0)	(1)
SS-Stepwise, SS-LARS	10	3	3	0	1
No. of shared variables	(11)	(5)	(5)	(0)	(1)
SS-Stepwise, SS-Lasso	10	3	3	0	1
No. of shared variables	(11)	(5)	(5)	(0)	(1)
SS-Stagewise, SS-LARS	10	3	7	0	1
No. of shared variables	(14)	(10)	(10)	(0)	(1)
SS-Stagewise, SS-Lasso	10	3	7	0	1
No. of shared variables	(14)	(9)	(9)	(0)	(1)
SS-LARS, SS-Lasso	11	6	8	0	1
No. of shared variables	(14)	(13)	(13)	(0)	(1)
Significant but with different signs	0	0	0	0	0
Significant but with different SS*	–	2	0	0	0

Notes: Variables with a P-value <0.05 are considered significant (when covariates selected from the SS-Stagewise, SS-LARS, and SS-Lasso algorithms are plugged into OLS regression models).

^*In comparing SS-Stepwise with SS-Stagewise, SS-LARS, and SS-Lasso.

For spatial scale stepwise, spatial scale stagewise, spatial scale LARS, and spatial scale lasso, we fitted OLS regression models based upon the selected covariates to obtain AIC measures for the three different scenarios mentioned previously. The table of AIC measures is shown in Table 5. For all methods, the model using the model-selected spatial scales (Model 3) resulted in the smallest AIC, indicating a better goodness of fit. Thus, we saw a significant improvement in goodness of fit with the spatial scale models in which we used the area-based variables at the spatial scales originally selected by each model. Across all scenarios, the spatial scale lasso had the best goodness of fit.

Table 5.

OLS-based Akaike information criterion (AIC) comparisons across spatial scale (SS) forward stepwise, forward stagewise, LARS, and lasso models.

	SS-STEPWISE	SS-STAGEWISE	SS-LARS	SS-LASSO
Model 1: Smallest SS available	28,193.57	28,196.73	28,183.15	28,178.17
Model 2: Largest SS available	28,144.05	28,143.04	28,133.79	28,131.90
Model 3: Model-selected SS	28,130.90	28,135.15	28,100.19	28,096.65

Using the final model provided by the spatial scale lasso, 26 of the 42 selected variables were significant (Table 2). Of the significant variables, several variables had larger magnitudes and stood out as being important for explaining the variation in nitrate. There were significant positive associations between log nitrate concentration and the following covariates: distance from well point to nearest sinkhole point (SinkholeDist_m) and estimated mean annual natural ground-water recharge within a 500-m buffer (Recharge_500 m). In addition, there were significant negative associations between log nitrate concentration and the following covariates: bedrock depth, well depth, average calcium carbonate within a 1-km buffer (CaCO3_1 km), and average soil loss tolerance within a 1-km buffer (T_1 km).

Discussion and Conclusions

To consider the problem of spatial scale selection for area-based variables available at more than one spatial scale in a regression model, we modified the forward stepwise, forward stagewise, LARS, and lasso algorithms to select the best spatial scale for each area-level covariate. Our algorithms allow for any number of spatial scales of covariates to be considered and also enable the inclusion of individual-level covariates or covariates with only one possible spatial scale. We constrained the four algorithms to select each area-based variable to enter the model at a single spatial scale to avoid collinearity effects. When applying the algorithms to model groundwater nitrate exposure in Iowa, we found that not all environmental variables were selected at the same spatial scale. For all four spatial scale algorithms, the regression model that used the model-selected spatial scales had the best model fit. Furthermore, there was an overall agreement in coefficient sign and spatial scale for significant variables that were selected across the algorithms. The selection of area-level variables at different spatial units gives evidence for the environmental effects operating at different spatial scales and demonstrates the importance of considering the spatial scale when modeling environmental exposures.

Other researchers have developed approaches to address the problem of spatial scale selection in regression modeling. For example, rather than choosing the best available scale for each area-level covariate, Root et al.⁷ use the variance of the outcome variable (eg, disease rates) to select a buffer distance at which to conduct the regression analysis and then use the area-level variables at the selected buffer distance. They propose the Brown–Forsythe (F_BF) test of homogeneity of variance to select the optimal neighborhood or buffer size for modeling disease rates. In their approach, Root et al.⁷ use circular buffers to create a collection of “neighborhoods” of different sizes around each subject and then use the F_BF statistical test to select the ideal buffer distance. This approach assumes that small neighborhoods will have high variances (reflective of an individualistic data structure) and large neighborhoods will have low variances (reflective of a global data structure). The goal is to select an “optimal” neighborhood that adequately captures the global characteristics of the neighborhood environment in which a person lives without being so large as to lose applicability to the individual.⁷

Using the F_BF test as a method to choose the optimal neighborhood has its merits. First, it is robust to deviations from the normal distribution in the outcome variables, which can occur when disease rates are modeled as normally distributed outcomes.⁷ Second, it allows researchers to more specifically define geographic areas that may be more relevant for a particular health outcome, as opposed to using predefined geopolitical spatial scales such as census block groups or counties, which may not adequately capture the proximal environment of an individual.^7,33 The F_BF approach for selecting spatial scale also has its limitations. First, it may not be suitable for researchers who wish to select neighborhoods other than those defined by using buffers.⁷ Second, the buffer-based estimates of neighborhood SES variables have measurement error (in addition to the measurement error present in the census data) by assuming that people are equally distributed within a census block group, but this is generally common to buffering approaches. Third, and most importantly, area-level variables are not involved in the selection of the optimal buffer size for calculating disease rates. The buffer distance is selected based on finding a spatial scale with a moderate variance for disease rates, and then the SES variables are modeled at the selected buffer size. Thus, the F_BF test does not directly select the spatial scale for area-level covariates.

The strategies for the selection of spatial scale of environmental variables have been primarily univariate, at least in the context of the analysis of groundwater quality. Buffer shape sizes for land use variables have typically been selected independently from one another, as well as from variables measured at the well level.^20,21 However, the magnitude of the effect measure and the significance of relationships between area-level variables and the outcome could change when other important variables are considered simultaneously.

Our methods provide a novel approach to the problem of spatial scale selection and have several strengths. First, rather than making an assumption about the appropriate spatial scale at which to model area-based variables, our spatial scale algorithms directly allow the data to drive the selection of spatial scale and permit different spatial scales to be present within a model. Second, our approach to spatial scale selection is multivariate and permits the simultaneous consideration of individual-level variables and area-level variables available at multiple spatial scales to be included in a model. Third, due to the potentially high correlations present across different spatial scales for a given variable, our algorithms constrain each variable to enter the model at a single spatial scale. That is, if a variable is available at two spatial scales, it can enter the model only at one of the two scales. Crowder and South³⁴ permit a variable to enter a regression model at both available spatial scales, and their results show that these variables have opposite signs, suggesting the possibility of collinearity effects. Fourth, to address correlations present across variables, one of our algorithms constrains the regression coefficients in the presence of correlated covariates. Fifth, our methods are scalable and can be extended to accommodate high-dimensional datasets with a large number of covariates at a variety of different spatial scales.

While our initial results when applying our algorithms are encouraging, our analysis of groundwater nitrate has limitations. First, because of limited resources we were unable to consider more buffer distances in our analysis. Second, our analysis of nitrate used fixed buffer sizes for area-level variables across the study area, but adaptive buffer sizes based on population density may be more appropriate. Third, we excluded some observations due to missing values for some of the covariates. Regarding limitations of the algorithms, in the case of the spatial scale lasso, the spatial scale of a variable is fixed once it enters the model. That is, even if a variable is dropped, we constrain that variable to reenter the model at the same spatial scale as was originally selected. This is done to ensure that the correlation between the current residuals and the candidate variables does not exceed the maximum correlation achieved between the current residuals and the variables in the active set. Another limitation is the lack of standard errors for the algorithms, which necessitated our use of OLS models to obtain the P-values. The algorithms we present are for modeling a continuous outcome variable. We are currently working on developing versions of our spatial scale algorithms to model a binary outcome variable. In addition, we plan to run a simulation study to compare model performance across our four algorithms and also aim to evaluate a random effect at different spatial scales.

In the case study of groundwater nitrate exposure, we used our spatial scale algorithms to select area-based variables available at multiple buffer distances in order to explain variation in groundwater nitrate, a known risk factor for cancer. Our methods can be applied to other research problems, where it is of interest to select environmental or area-based risk factors available at multiple spatial scales that are associated with a health outcome of interest such as cancer.