VFMA: Topographic Analysis of Sensitivity Data From Full-Field Static Perimetry

Abstract

Purpose:

To analyze static visual field sensitivity with topographic models of the hill of vision (HOV), and to characterize several visual function indices derived from the HOV volume.

Methods:

A software application, Visual Field Modeling and Analysis (VFMA), was developed for static perimetry data visualization and analysis. Three-dimensional HOV models were generated for 16 healthy subjects and 82 retinitis pigmentosa patients. Volumetric visual function indices, which are measures of quantity and comparable regardless of perimeter test pattern, were investigated. Cross-validation, reliability, and cross-sectional analyses were performed to assess this methodology and compare the volumetric indices to conventional mean sensitivity and mean deviation. Floor effects were evaluated by computer simulation.

Results:

Cross-validation yielded an overall R² of 0.68 and index of agreement of 0.89, which were consistent among subject groups, indicating good accuracy. Volumetric and conventional indices were comparable in terms of test–retest variability and discriminability among subject groups. Simulated floor effects did not negatively impact the repeatability of any index, but large floor changes altered the discriminability for regional volumetric indices.

Conclusions:

VFMA is an effective tool for clinical and research analyses of static perimetry data. Topographic models of the HOV aid the visualization of field defects, and topographically derived indices quantify the magnitude and extent of visual field sensitivity.

Translational Relevance:

VFMA assists with the interpretation of visual field data from any perimetric device and any test location pattern. Topographic models and volumetric indices are suitable for diagnosis, monitoring of field loss, patient counseling, and endpoints in therapeutic trials.

Perimetry is a time-established test used in patients with glaucoma¹ and retinal degenerations, such as retinitis pigmentosa (RP)^2–4 for screening, disease detection, and classification, monitoring for progression, correlation with activities of daily life, and, more recently, structure-function studies. Because the earliest and most disabling features of many forms of inherited retinal degeneration involve visual field loss, most often in the periphery, testing the entire visual field is crucial for the evaluation and monitoring of these patients. The most common means of full-field testing is kinetic perimetry, which can efficiently locate the borders of seeing areas. In comparison, static perimetry can better define small sensitivity levels, and detect subtle sensitivity gradients and emerging scotomas. In the absence of a fast, full-thresholding algorithm, previous full-field static perimetry studies have used the standard full-threshold staircase strategy and limited the number of test points to avoid long exam durations.^5,6 A new, fast full-threshold algorithm, GATE-i⁷ has enabled full-field static perimetry with more test locations and practical test durations (Weleber RG, et al. IOVS 2009;50:ARVO E-Abstract 3813; Schiefer U, et al. IOVS 2009;50:ARVO E-Abstract 5354).

Clinicians currently have several options to aid in the assessment of static visual field tests. Among them are visual appraisals of the test results for emerging scotomas and disease regionality, and the quantification of defects and the remaining field by performance metrics or indices. Current visualization techniques include charts of individual sensitivity levels, grayscale and color representations in which the spatial distribution of the sensitivity levels are quantized with large interval, and deviation plots showing comparisons with average age-matched healthy normal controls. These display methods typically generate flat, 2-D illustrations where the spatial and sensitivity dimensions can appear pixelated. An early form of 3-D display of sensitivity has been used to illustrate the progression of field loss in patients with retinitis pigmentosa from mutation of RP1.⁸ Other mathematical models have been developed to study the effects on the visual field of neurological disease, trauma, retinal degenerations,^9,10 and glaucoma.^11,12

Perimetry data can be condensed into global indices of visual function. These indices quantify and distill trends in the visual field into simple numerical summary measures, and are important as endpoints in therapeutic trials, longitudinal analyses, and patient assessments. Conventional indices include mean sensitivity (MS) and mean deviation (MD),¹³ which are based on the average sensitivity value. These indices are appropriate for rectilinear grids with uniform spacing; however, for grids with radial patterns, central condensation, and unequal spacing, these indices become weighted averages. The weighting biases the indices to the regions of higher sampling density, which alters their interpretation and limits their comparison among grids with different sampling patterns. Furthermore, these indices are global measures and can be insensitive to local spatial or regional behavior.

To improve the interpretation and assessment of static perimetry data, we introduce a topographic approach to Visual Field Modeling and Analysis (VFMA). Topographic methods are currently used in photokeratoscopy to map the surface of the cornea and in the analysis of retinal layers with optical coherence tomography. A similar approach has been used to present topographic assessment of the optic disc.¹⁴ In this study, we perform topographic modeling, interactive visualization, and data distillation of visual field sensitivity data using a custom software application we developed called VFMA. VFMA renders 3-D surface models of the hill of vision (HOV)¹⁵ and its defects, and also provides quantitative functional measures. We focus on several visual function indices that are derived from the HOV volume, or the volume beneath the sensitivity surface. These indices capture the visual field magnitude and extent at all states of disease without weighting bias, and are more meaningful when comparing exams acquired with different grids than indices based on simple averaging, such as MS and MD. The volumetric indices are conceptually similar to the kinetic visual field global volume,¹⁶ but VFMA allows measurements from the entire visual field as well as specific regions of interest. Furthermore, VFMA provides contour analysis and comparisons with normative data, supports perimeter test grids of any size and arrangement, and performs peripheral field modeling with minimal cartographic distortion. In this study, we used VFMA to demonstrate the clinical use of HOV volume analysis in patients with retinitis pigmentosa.

We also investigated the effects of perimeter hardware limitations on the visual function indices. The maximum luminance for a stimulus, which is set by the perimeter manufacturer, determines the minimum sensitivity value (MSV) measurable. In this work, the term “floor effect” is used to describe sensitivity values that are near the MSV or are clipped by the MSV, which occurs when the subject cannot detect the perimeter's maximum intensity stimulus. Floor effects can have a significant influence on the outcome and interpretation of a perimetry exam.^17,18 We performed a post hoc analysis of floor effects and their impact on the visual function indices. Progressively larger MSVs were imposed on the perimetry data we collected to simulate the floor effects induced by perimeters with smaller maximum stimuli.

Methods

Subjects

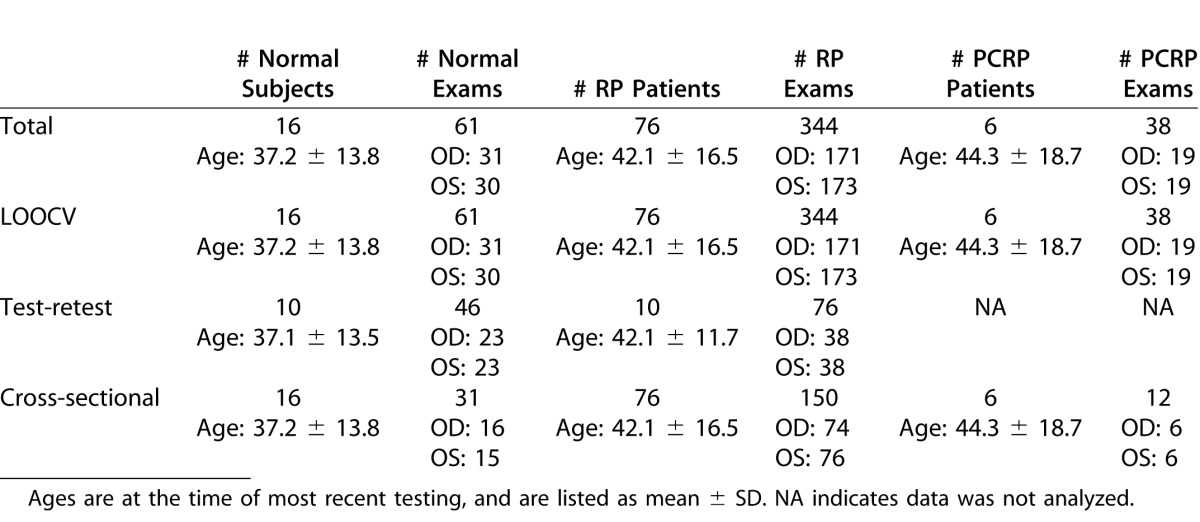
The 98 subjects in this study, summarized in the first row of Table 1, included 16 normal volunteers (age range, 18.5–62.7 years) and 82 patients with retinitis pigmentosa (RP). Among the patients, 76 (range, 12.6–75.6 years) had inherited forms of typical RP and six (range, 22.4–70.3 years) had pericentral RP (PCRP). For normal subjects, the exclusion criteria were history of migraines, uveitis, glaucoma, retinal, or other disease that would influence visual field testing; ocular surgery for reasons other than cataracts (a minimum of 6 months following cataract surgery was required); medication known to affect vision; or refractive error > ±6 diopters (spherical) or > 2 diopters (cylindrical). One control required a +4.75 sphere and 4 RP patients required spherical corrections for the more hyperopic eye of +3.25, +4.00, +4.50, and +6.00. Approval adhering to the tenets of the Declaration of Helsinki was obtained from the Oregon Health and Science University (OHSU) Institutional Review Board, and written, informed consent was provided by all subjects.

Table 1.

Summary of the Data Used in Each Analysis

Visual Field Testing

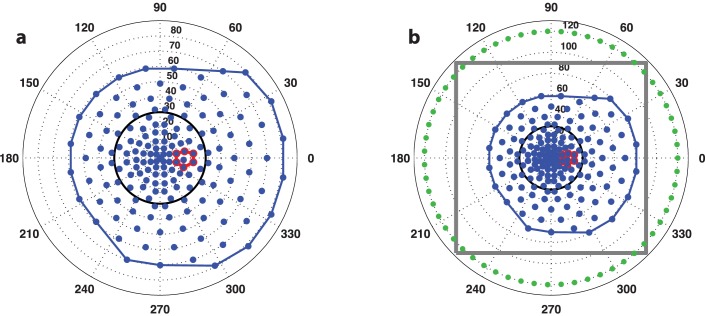
Full-field automated static testing was performed on all subjects with either an Octopus 101 or an Octopus 900 perimeter (Haag-Streit AG, Köniz, Switzerland) using a 10 cd/m² (31.5 apostilbs) background, the GATE-i strategy,⁷ and Goldmann stimulus size V. Fixation was monitored by the technician during the entire testing session. Subjects were tested with the radially oriented, centrally condensed, binocularly symmetric grid pattern shown in Figure 1. This grid consisted of N_t = 164 points spanning a solid angle, or angular footprint, of 3.69 steradians (sr). Measured threshold values from the Octopus 101 were exported and converted¹⁹ to differential luminance sensitivity (DLS) in decibels (dB); for the Octopus 900, this conversion was performed automatically by the manufacturer's EyeSuite software. The quality of each subject's exam was assessed by a reliability factor (RF), defined as the percentage of total catch trials resulting in either a false-positive or false-negative. Any exam with an RF > 15% for normal subjects or 25% for patients was excluded; based on this criterion, three normal and nine patient exams were excluded.

Figure 1.

The binocularly symmetric 164-point grid pattern used in all static perimetry exams in this study, shown in angular coordinates for the right-eye. (a) The test points and convex hull footprint are in blue, the blind spot search region is outlined in red, and the 30° central circle is black. (b) A wider view showing the zero-sensitivity boundary constraints in green and the gray outline of the interpolation grid used for surface modeling.

HOV Modeling With Thin Plate Spline (TPS) Interpolation

Topographic surface models of the HOV were created for each exam with TPS interpolation²⁰ of the perimetry data. The surface was constrained outside the subject's field-of-view by adding N_z = 60 artificial points with zero sensitivity along a circle with radius 120°, as shown in Figure 1b. The set of points 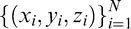defined the data from one static visual field exam, where N = N_t + N_z = 224, (x_i,y_i) is location of the i^th grid point in angular coordinates and z_i is the corresponding DLS value in dB. The HOV surface model was defined at location (x,y) by

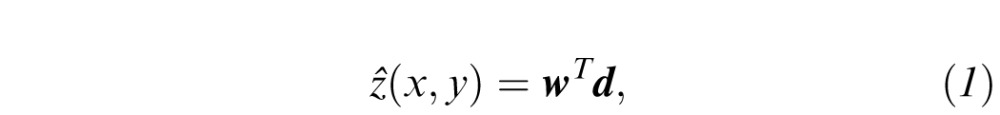where w = [w_x w_y w₀ w₁ w₂…w_N]^T and d = [x y 1 φ(‖x−x_i‖)]^T are (N+3) × 1 vectors of weights and displacements, respectively.²¹ Here, φ(r) = r²log(r) is the infinitely differentiable TPS radial basis function, and x = [x y]^T and x_i = [x_i y_i]^T are 2 × 1 coordinate vectors. The weight vector was found by solving the matrix equation

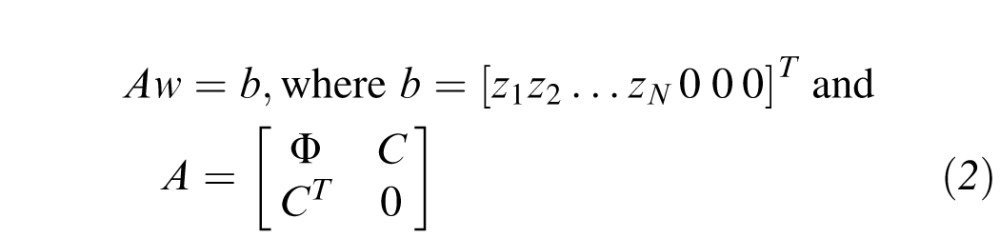The ij^th element of the N × N submatrix Φ is Φ_ij = φ(‖x_i−x_j‖), and the i^th row of the N × 3 submatrix C is [1 x_i y_i]. Once the weight vector w was calculated, the surface was interpolated at an arbitrary location (x,y) by updating d with the location coordinates and evaluating Equation 1. In this study, we interpolated the data from each exam onto a dense 501 × 501 point rectilinear grid with 0.36° spacing along each dimension, which is outlined in Figure 1b.

The blind spot was detected automatically from a group of candidate locations in the testing grid, shown in red in Figure 1. These seven points were separated into two clusters with combinatorial optimization by maximizing the separation between the mean DLS values in each cluster. The grid locations belonging to the cluster with the smaller mean were labeled as the blind spot. To mitigate the clustering error caused by a large spurious DLS value, the blind spot cluster was constrained to a maximum of five samples.

For visualization and interactive examination, VFMA generated a 3-D rendering of the interpolated HOV surface color-coded by DLS value. User-controllable rotation, panning, and zooming operations enabled interactive inspection of the HOV surface model. In addition, geographic and topographic selections of the HOV were made through the VFMA interface. For example, region-of-interest (ROI) analyses were possible by defining boundaries, such as a circle centered at the origin or an iso-sensitivity contour around the base of a scotoma.

Volumetric Visual Function Indices

We developed a class of visual function indices based on the volume within the interpolated HOV surface. Whereas a conventional index like mean sensitivity conveys only visual sensitivity information, a volumetric measure is more general, and captures the sensitivity and the topographic footprint over which the sensitivity is assessed. This makes it more appropriate for comparisons among irregular grids and grids of different sizes and topographic footprints. It also represents the visual field function with a unit of quantity, the volume of sensitivity, which can be useful when describing how much sensitivity has been lost or gained over time.

The volume represents the total sensitivity across solid angle, and is reported in units of decibel-steradians (dB-sr). The decibel was chosen to indicate the magnitude of sensitivity because it is a logarithmic unit and corresponds well to perceptual differences. The steradian was chosen to define the angular extent because it is the International System of Units (SI) measure of solid angle. To minimize cartographic distortions, especially in the peripheral visual field, all mathematical operations are executed on a spherical surface representing the interior of the perimeter cupola. In spherical coordinates, the volume is

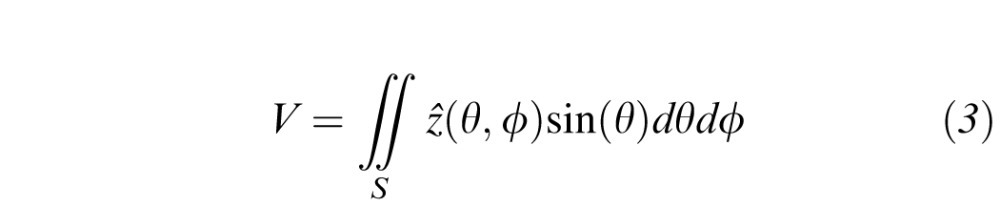where θ is the co-latitude angle, ϕ is the azimuth angle, and S is the selection region defined by the user. Here, V represents the volume of the solid defined by ẑ(θ, ϕ) and ẑ = 0 over the angular region S. The VFMA calculates volumes by the midpoint integration rule wherein the finely interpolated surface is summed and scaled by the pixel extent.²²

The volume can be customized according to what region S is selected for investigation. When the selection region is the entire grid, the result is the total volume, V_TOT. In this study, we analyzed V_TOT and the central field volume, V_30°, defined by a setting the selection region S to be a circle with a radius of 30° centered on the point of fixation. The footprints of these volumes are depicted in Figure 1. We also examined the normalized index V_30°/V_TOT, which approaches zero as central sensitivity is lost and approaches one as peripheral sensitivity is lost. The blind spot was not removed before surface fitting and calculation of these volumes.

We also analyzed topographic surface models of visual field defect. Because Equation 2 is linear in the z_i sensitivity values, an HOV model of the defect was created by replacing each z_i value with the DLS difference between the subject and an age-adjusted normal.²³ The resulting interpolated surface depicts the visual field in defect space, as opposed to the native DLS space. The defect space surface models are three-dimensional, finely sampled analogues of total deviation plots, and are useful for quantifying patterns for field loss. For example, a scotoma appears as a recession in the DLS surface and as an elevated ridge in the defect surface. In defect space, the volume is

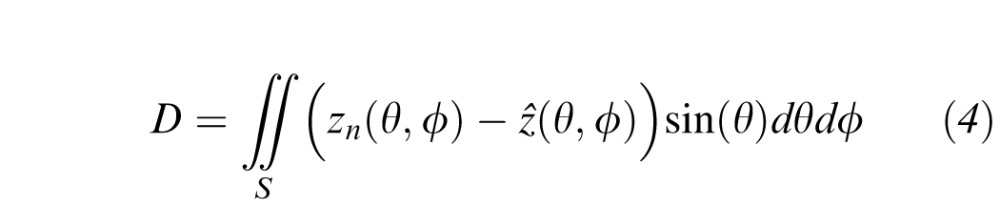where z_n is the age-adjusted normative DLS. These volumes measure the net defect volume in the selection region. In this study, we analyzed the defect space volumes D_TOT and D_30°. For defect space measures, the blind spot was removed before volume calculation.

Validation and Analyses

The accuracy of the HOV modeling was assessed using leave-one-out cross-validation (LOOCV).^20,24 LOOCV measures the residual DLS error at each of the test locations by reinterpolating the surface using all data except that location, and then accumulates the errors from all test locations. The error for the k^th location is e_k = ẑ_k (x_k, y_k) – z_k, where ẑ_k (x_k, y_k) is the HOV surface interpolated at location (x_k,y_k) using the set of points 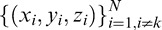in Equation 2. Errors are measured only at the locations of the 164 test points and not at the 60 boundary constraints. Table 1 provides a summary of the data used in the LOOCV analysis. Only the most recent perimetry exam for each subject's eye was used. For comparison with the TPS interpolation in VFMA, we also performed LOOCV on HOV models generated with nearest-neighbor (NN) interpolation. Being a zeroth-order strategy, NN interpolation served as a reference for benchmarking the higher-order TPS method. Performance was assessed by the coefficient of determination (R²)²⁴ and the index of agreement (d),^25,26 as given by

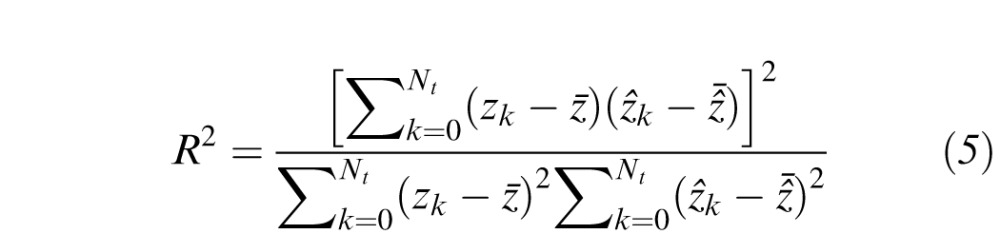and

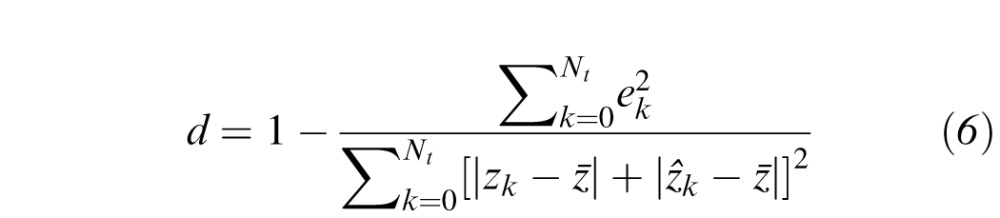Here, 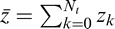is the mean sensitivity and 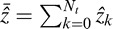is the mean interpolated value during LOOCV. Better performance is indicated by larger R² and d. The R², which specifies the proportion of the data variation captured by the topographic model, is commonly used as a goodness-of-fit metric. The d is an alternative metric ranging from 0.0 (no agreement between the model and observation) and 1.0 (perfect agreement).

Repeatability analysis was performed on the visual function indices derived from test–retest data from 10 normals and 10 RP patients. All subjects had an initial visual field test and between 1 and 5 additional tests. Repeated tests were included only if obtained within 90 days of the initial test. Table 1 summarizes the data used for this analysis. We analyzed the volumetric measures V_TOT, V_30°, V_30°/V_TOT, D_TOT, and D_30° from VFMA as well as the conventional indices MS and MD. Repeatability performance was assessed by the coefficient of variation (CV), where CV = σ/μ, σ is the within-subject deviation estimated via 1-way ANOVA and μ is the corresponding mean. We also estimated the repeatability coefficient (RC) = 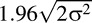, which is the value below which lies with 95% probability the difference between any two measures from the same subject. Smaller values for CV and RC indicate higher reliability.

A cross-sectional analysis was performed to obtain descriptive information for each visual function index for the three subject groups. Groups were compared with a linear mixed-effects model, allowing for unequal variances in different groups, and adjusting for age at exam and the perimeter device used. The outcome variable was the average of each index over both eyes. Examination of residual plots suggested that a transformation of the indices was unnecessary for this comparison. Estimated mean index values and standard errors for each group were obtained from the regression analyses, averaging over covariates. Estimated mean differences between index values for each pair of groups and 95% confidence intervals also were obtained.

Floor Effects

The impact of floor effects on the visual function indices was simulated by artificially elevating the MSV and recalculating the indices. The MSV was elevated to a new value M by setting all measured DLS values z_i that were less than M to M, as in

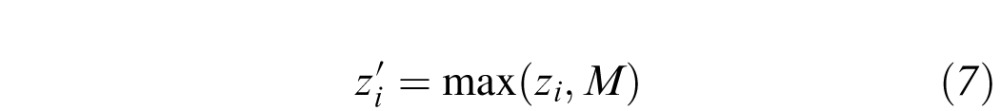This modification was applied to all N_t test locations in each perimetry exam in this study, and to all age-adjusted normative sensitivity values. With this approach, the dynamic range of the sensitivity data monotonically decreases as M increases, although the DLS values retain the same reference point. We simulated MSVs of M = 4, 6, 9, 12, 15, and 18 dB. For each simulated MSV, all visual function indices were recalculated. and the LOOCV and repeatability analyses were repeated. The cross-sectional analyses were repeated for M = 4 and 18 dB.

All analyses were performed with SAS 9.2 (SAS Institute, Cary, NC, USA) STATA 11.3 (StataCorp LP, College Station, TX, USA), and MATLAB 8.2 (MathWorks, Natick, MA, USA), and a level of 0.05 was used for all significance tests.

Results

HOV Modeling and Visualization

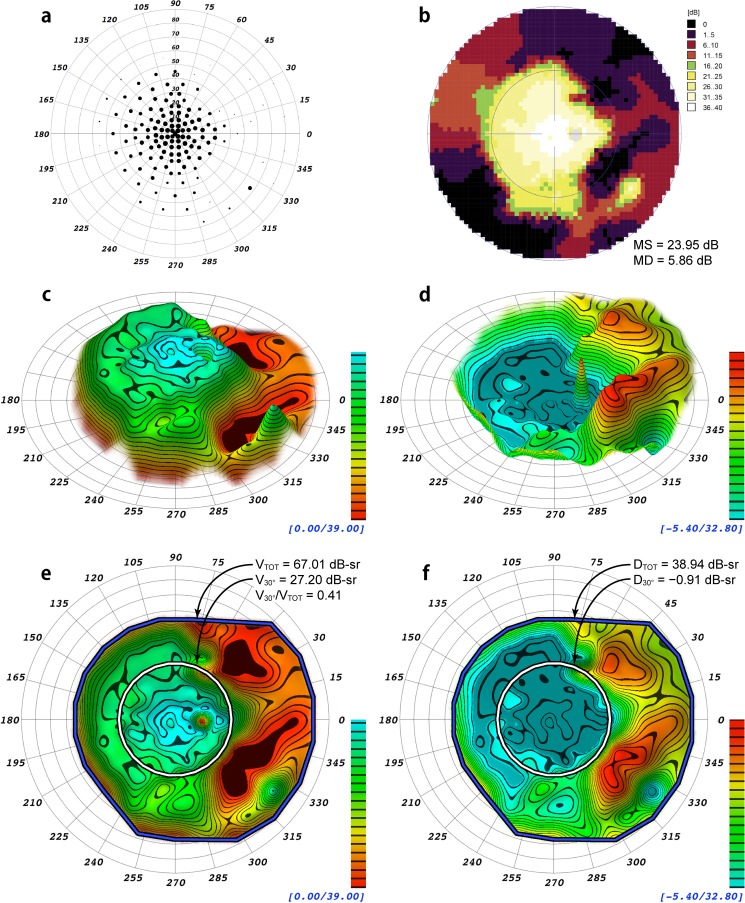
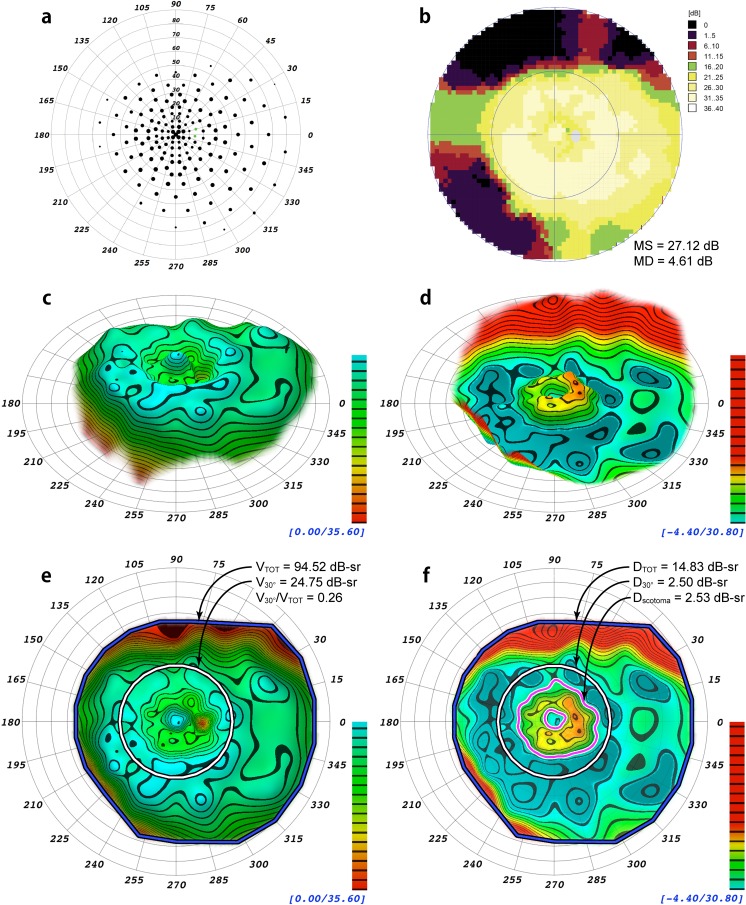
Displayed in Figures 2 and 3 are example renderings of the HOV surface models for two patients with different distributions of field loss, one with peripheral field loss from RP and the other with a ring scotoma from early PCRP. Models in the DLS and defect spaces are shown. For comparison, data from each patient's visual field exam also are depicted using conventional display methods. The conventional indices MS and MD, the volumetric indices V_TOT, V_30°, D_TOT, D_30°, and the ratio V_30°/V_TOT are presented in Figures 2 and 3, and a volumetric measurement of the ring scotoma is presented for the field in Figure 3. The 3-D topographic representations generated by VFMA show the HOV contours and enhance the subtle variations in the visual fields.

Figure 2.

Comparison of different visualizations and indices of a static perimetry exam from a 63-year-old patient with mild autosomal dominant retinitis pigmentosa from the frameshift mutation, NM_006,269.1:c.3157delT(P.Tyr1053ThrfsX4) of RP1⁸ in association with a second, novel heterozygous mutation in RP9, NM_203,288.1:c664delT, which is predicted to eliminate a stop codon and add 28 amino acids to the RP9 protein. (a) Scaled-point plot in which each grid location is scaled in size to reflect the DLS value. (b) Incremental color-scale plot generated by the Octopus 900 (Haag-Streit). (c) Oblique view of the 3-D hill of vision model generated by VFMA, with iso-sensitivity contours at 2 dB intervals. (d) Oblique view of the 3-D defect space model generated by VFMA showing peripheral field loss. (e) En face view with the selection boundaries for the total volume (blue/black) and the central 30° volume (white/black). (f) En face view of the defect space created by subtraction of the patient DLS values from those of an age-matched normal. The D_TOT and D_30° indices for this eye indicate substantial loss of peripheral field with minimal loss of central field. The blind spot and its inverted peak can be seen in (c), (d), and (e); the blind spot was removed in (f) to mitigate its effects on the defect space volumetric measurements.

Figure 3.

Comparison from a patient with autosomal dominant pericentral retinitis pigmentosa in association with a reported heterozygous mutation in NR2E3,²⁷ NM_014,249.2: c.166G>A(P.G56R), and a second heterozygous variation, NM_005,802.3:c.2643C>G(P.H881Q), of unknown significance in TOPORS.²⁹ (a) Scaled-point plot of DLS values. (b) Incremental color-scale plot generated by the Octopus 900 (Haag-Streit). (c) Oblique topographical view generated by VFMA. (d) Defect space model generated by VFMA depicting pericentral field loss. (e) En face view with the selection boundaries for the total volume (blue/black) and the central 30° volume (white/black). (f) En face view of the defect space. The volume of the pericentral scotoma defect (the region between the magenta/white contour lines) is shown. Because of the existence of negative values (the patient had greater than normal sensitivity in some regions) between the outer boundary of the scotoma and the 30° circle, the pericentral scotoma volume is slightly larger than that of D_30°.

The cross-validation results are presented in Table 2. The TPS interpolator showed good performance with large d values indicating high accuracy, and also good consistency with similar R² values and similar d values in each subject group. By comparison, the performance of the NN interpolator was lower and less consistent among groups. The R² and d values from the VFMA TPS interpolator were significantly larger than those from the NN interpolator, overall (P < 0.001) and within each subject group (P < 0.001 in each case). The standard deviations for R² and d were largest in the RP group, which is likely a reflection of the diversity of visual field patterns within this group.

Table 2.

Cross-Validation Results Showing the Coefficient of Determination (R²) and Index of Agreement (d), Listed as Mean ± SD, for the Two Interpolation Methods Tested in This Study

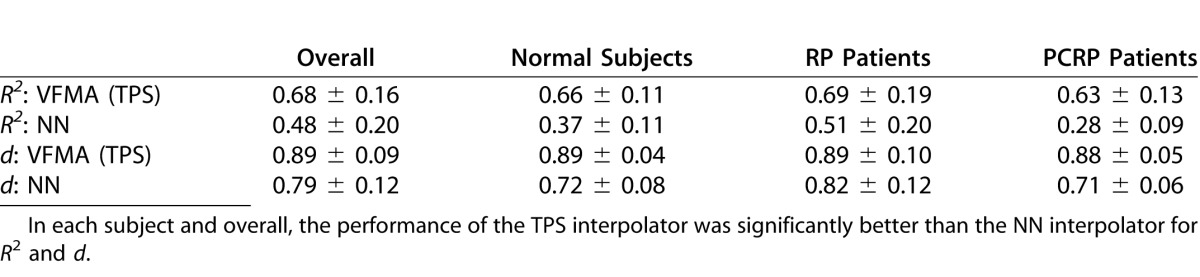
The complete cross-validation results for each simulated MSV are presented in Supplementary Tables S1 through S6. As the simulated MSV increases and floor effects become more pronounced, the R² and d values changed only slightly, getting worse in the RP and PCRP groups and better in the normal group. The improvement in the normal group is due to the increased uniformity and spatial autocorrelation of the far peripheral fields where the floor effects are more likely to occur. The worsening in the patient groups is a result of the floor effects causing abruptly increased sensitivity values at isolated test locations, which reduces the local autocorrelation and the accuracy of any neighborhood-based interpolation scheme. At every simulated MSV, the R² and d values from VFMA remained significantly larger than the NN interpolator.

Visual Function Indices

In terms of test–retest variability, the volumetric visual function indices were comparable to the conventional indices in both subject groups and generally showed good repeatability performance. The results of the repeatability analysis are summarized in Table 3. The CVs were similar for V_TOT and MS, and also for D_TOT and MD, although among normals the D_TOT coefficient was somewhat larger than that for MD. For the indices in DLS space, the variation was larger among RP patients than normal subjects. The CVs of the regional volumetric indices V_30° and D_30° were similar to their global counterparts V_TOT and D_TOT. The largest CVs were found in the defect space indices of normal subjects; because normal subjects have negligible field loss, the visual function indices in defect space had mean values near zero which elevated the CVs. Similarly, the normalized index V_30°/V_TOT in RP patients had a mean near zero and, consequently, a relatively large CV. For the defect space measures of RP subjects, however, the CVs remained small. Although the repeatability coefficients in Table 3 are not comparable across indices, they provide useful summary information for a given index regarding how similar two observations on the same individual are likely to be.

Table 3.

Repeatability Results Showing the Repeatability Coefficient (RC) and the Coefficient of Variation (CV) for the Conventional and Volumetric Visual Function Indices

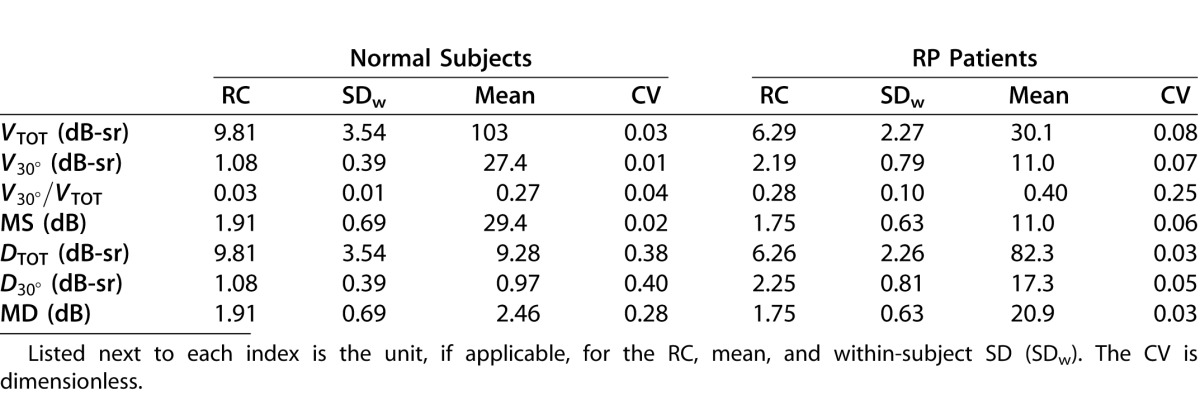
The complete test–retest results for each simulated MSV are presented in Supplementary Tables S7 through S14. Compared to the original, unadjusted data, the simulated floor effects produced increased sensitivity values. Consequently, the DLS-space indices V_TOT, V_30° and MS grew with MSV while the defect–space indices D_TOT, D_30° and MD and the normalized index V_30°/V_TOT correspondingly shrank (Supplementary Tables S9 and S10). These indices changed considerably more in the RP group due to the greater impact of severe floor effects in regions with visual field loss. The within-subject standard deviations (Supplementary Tables S11 and S12) tended to decrease because the dynamic range was being reduced as the simulated MSV became larger. Accordingly, the CVs (Supplementary Tables S7 and S8) generally improved for the indices in DLS space. The changes in defect-space indices were less predictable, but were quite small for the range of MSVs considered.

The results from the cross-sectional analysis are presented in Table 4. It is apparent that the three groups are distinct with regard to each visual function index. There was little to no overlap among groups for any index, and the means were significantly different between groups for every index. Compared to normal subjects, RP patients had elevated V_30°/V_TOT values, indicating a loss of peripheral field. For the PCRP group, V_30°/V_TOT was smaller compared to the RP and normal groups, while V_TOT was larger than RP and smaller than normal. This corresponds to more relative central field loss and some peripheral field loss, although not as much as seen in the RP group.

Table 4.

Cross-Sectional Results Comparing the Mean Visual Function Indices in Each Subject Group Based on Regression Models

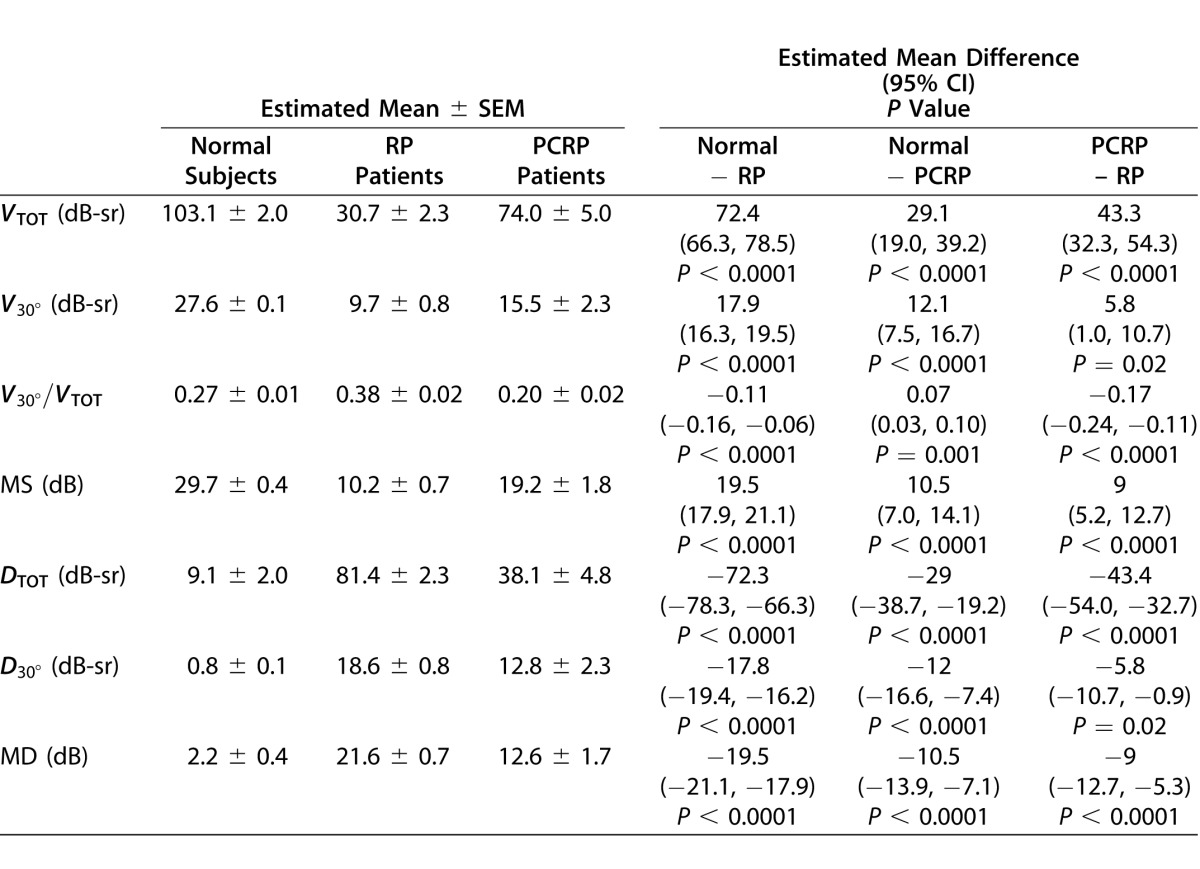
As reported in Supplementary Table S15, a simulated MSV of 4 dB resulted in relatively small changes to the mean and standard errors in the visual function indices for each subject group as compared to the unadjusted values in Table 4. In particular, the mean differences between the RP and PCRP group indices were generally smaller, and hence the P values comparing these groups tended to be larger. This impact is most apparent in comparisons of the regional volumetric measures V_30° and D_30°, since these are the indices for which the original P values in Table 4 were substantially larger than 0.0001. When more severe floor effects are simulated at an MSV of 18 dB, as shown in Supplementary Table S16, the mean differences between groups decreased for all indices, which impacted the statistical comparisons between the subject groups. Again, this is most apparent when comparing V_30° and D_30° between the RP and PCRP groups.

Discussion

HOV Analysis With VFMA

The LOOCV results demonstrate that the choice of interpolator is important. A higher-order method with smooth kernels like TPS interpolation is more accurate than a piecewise constant method when interpolating static visual field data.

The volumetric visual function indices tested in this study are comparable in performance to the conventional indices mean sensitivity and mean deviation. The test–retest analysis indicates that the volumetric indices have similar reliability as the conventional ones, and the cross-sectional analysis confirms that the volumetric indices are as discriminative among subject groups.

The volumetric measurements from the visual field in Figure 2 are consistent with the visual field phenotype reported in autosomal dominant RP from mutation of RP1⁸ and are in agreement with a prior report of the central visual field in RP being more robust and intact compared to that of the periphery.⁴ The visual field loss with a pericentral distribution seen in Figure 3 is consistent with autosomal dominant RP associated with a heterozygous mutation of NR2E3²⁷ and an autosomal dominant mutation of TOPORS.^28,29

The magnitudes of the volumetric visual function indices depend on the topographic angular footprint of the testing grid and the stimulus size. The total volume V_TOT is a function of the grid extent and, because DLS values are non-negative, is monotonically nondecreasing with grid solid angle. Regional indices like V_30° have a fixed topographic footprint and do not have this dependency. Depending on the grid extent, the field may be truncated, especially in normal subjects. Compared to stimulus size III, size V has been shown to have a larger dynamic range³⁰ and smaller variability³¹ in glaucoma patients. In RP patients, use of stimulus size V yields more seeing locations whereas use of size III has been suggested for early disease to allow access to statistical analyses of progression that are not available for size V.³² Based on the concept of spatial summation, we predict that stimulus size is positively correlated with volume. Studies are currently underway to characterize the sensitivity of the volumetric measures to these factors.

Floor effects due to the perimeter manufacturer's design decisions can alter the variability, sensitivity, and validity of any quantitative index of visual function derived from a perimetry exam. Our simulation of floor effects through post hoc increments of the MSV showed no negative impact on the repeatability of either the volumetric or the conventional indices. The mean index values in each subject group were affected, sometimes considerably, which is expected given the severity of the floor effects that were simulated. However, the volumetric and conventional indices appeared to react similarly as the simulated MSV was increased, which reinforces the comparable performance between these different types of measures that was observed in the original analysis with no simulated floor effects. Even relatively severe floor effects did not disrupt the discrimination of the three subject groups with most indices. The exception to this is the ability of the regional volumetric indices V_30° and D_30° to discriminate between the RP and PCRP groups. This result is somewhat expected, since increasing the MSV will artificially improve the sensitivities in the central fields of typical RP and PCRP patients, making them appear more similar and more difficult to discriminate.

Translation to the Clinic

In a clinical setting, VFMA has been a useful tool for illustrating to the patient the appearance of his/her visual fields and comparisons with expected results for normals. With a binocularly symmetric test grid, the visual fields for each eye can be fused using best location or spatial probability summation to simulate vision with binocular viewing for the patient.³³ Demonstrating the effects of visual field loss on how one sees, monocularly and with binocular viewing, has become an integral part of the care of patients with retinitis pigmentosa and allied disorders at the Oregon Retinal Degeneration Center. Such visual presentations are very helpful when explaining how field loss creates impairment, the concept of compensation of seeing field between the two eyes, and in discussing issues surrounding driving and disability.

The conventional global visual function indices of mean sensitivity and mean defect are valuable to clinicians, particularly for standard rectilinear grids, but can present difficult concepts for patients to understand. In our experience with patients, we have found that describing the visual field as a hill of vision in the literal sense facilitates their comprehension, and the volume of the hill is a more intuitive functional measure than indices based on the average hill height such as mean sensitivity.

VFMA also enables localized volumetric measurements that quantify visual function in specific regions of the hill of vision, which otherwise could not be achieved easily with currently available techniques. Of importance is the ability to measure volumetric visual function indices correlating to a specific area of retina undergoing genetic or stem cell therapy intervention. Repeated measurements in this same area provide a functional assessment of the effects, positive and negative, of regional therapeutic interventions, measurements that are difficult to obtain in any other manner.

The defect space is useful for volumetric measurement of central, pericentral, or regional scotomas, particularly for follow-up test sessions and comparisons among patient cohorts. Defect space volumes also are useful for measuring field loss in patients with retinal degenerations, macular dystrophies, including Stargardt disease, optic atrophies, and other causes of central or paracentral scotomas.

Summary

We have developed a topographic methodology and software application, VFMA, for processing and visualizing static perimetry data. It is applicable to any static perimetric sensitivity data, including standard automated perimetry and microperimetry. VFMA generates a 3-D model of the hill of vision, allowing detailed topographic examinations of visual fields in DLS and defect spaces, and the creation of global and regional visual function indices for quantitative assessments. We believe this new methodology will aid examinations of pathologic changes in macular degenerations and other diseases of the visual system, improve the analysis of structure-function relationships, and provide more refined outcome measures for clinical trials.