Antibiotic resistance as collateral damage: the tragedy of the commons in a two-disease setting

Abstract

We propose a simple two-disease epidemic model where one disease exhibits only a drug-sensitive strain, while the other exhibits both drug-sensitive and drug-resistant strains. Treatment for the first disease may select for resistance in the other. We model antibiotic use as a mathematical game through the study of individual incentives and community welfare. The basic reproduction number is derived and the existence and local stability of the model equilibria are analyzed. When the force of infection of each disease is unaffected by the presence of the other, we find that there is a conflict of interest between individual and community, known as a tragedy of the commons, under targeted treatment towards persons infected by the single strain disease, but there is no conflict under mass treatment. However, we numerically show that individual and social incentive to use antibiotics may show disaccord under mass treatment if the restriction on the transmission ability of the dually infected people is removed, or drug resistant infection is worse than drug sensitive infection, or the uninfected state has a comparative disutility over the infected states.

1 Introduction

In recent years, the problem of bacterial antibiotic resistance has led to suggestions that antibiotics are overprescribed [8, 27], and that decreasing the use of antibiotics could benefit society as a whole by minimizing the emergence of drug-resistance [36, 12]. It has been argued that antibiotic efficacy should be considered as a common good [7], and that collective action may be needed to preserve this common good against overuse. Some authors believe that individual incentives may drive overuse of antibiotics, leading to a “tragedy of the commons” [1]. The concept of the tragedy of the commons originated from an example on population control proposed by Lloyd [29] in 1833 and later developed by Hardin [18] in the 1960s. One example of this is seen in simple mathematical models of drug resistance, where increasing treatment of mild or early disease may benefit the individual, despite the fact that such an outcome may lead to an increase in drug-resistant bacteria and thus a decrease in the overall efficacy of antibiotic treatment [38].

An important example of how drug-resistance occurs is the use of broad spectrum antibiotics [20]. In this case, treatment of one infection or disease may select for resistance in other organisms which are present [50]. This phenomenon has been observed during the use of mass azithromycin to eliminate trachoma due to Chlamydia trachomatis, a leading cause of infectious blindness in the world [52]. The World Health Organization promotes antibiotic treatment for trachoma control, using mass administration of single-dose oral azithromycin [44, 52]. While Chlamydia trachomatis has never exhibited epidemiologically important drug resistance [49, 21], the emergence of macrolide-resistant pneumococcus due to mass administration of azythromycin has been observed [28, 47], though such resistance has declined after cessation of treatment [47, 19]. Fears of increased mortality have proven unfounded, e.g. [39, 17, 24, 25].

In this paper, based on the pattern seen for pneumococcus and Chlamydia trachomatis, we propose and analyze a simple model of coinfection and cotransmission of two infectious agents in order to determine whether antibiotic resistance is a tragedy of the commons in a two diseases setting. For one infectious agent, we assume that both sensitive and resistant strains are possible, while for the other, only drug sensitive strains are present. Both are modeled as simple SIS (susceptible-infectious-susceptible) processes [23]. Coinfection by multiple pathogens or diseases is a global challenge for public health. It has attracted increasing attention in the field of mathematical epidemiology since the pioneering works by Dietz [14], Bremermann and Thieme [5], and others. For example, a number of mathematical models for HIV/TB coninfection [32, 45, 2, 43], HIV/malaria coinfection [34], HIV/gonorrhea coinfection [35], malaria and meningitis coinfection [26], and CA-MRSA/HA-MRSA co-colonization [11, 40] have been developed in recent years.

Our model assumes that treatment is targeted to the agent that only has sensitive strains, but can select for resistance in the other infectious agent (as a type of “collateral damage”). We will assume that the population as a whole has a particular treatment rate, which gives rise to an equilibrium prevalence of both infections. A single individual in the population who changes her or his treatment rate will then experience either more or less infection. When increasing infection rate for an individual causes that individual to spend less time infected, that individual has an incentive to increase treatment. However, if increasing the population rate of treatment causes a higher population cost, a tragedy of the commons results. Previously we used this method to analyze the tragedy of the commons resulting from incentives to treat early or mild disease ([38]; see [42] for a general exposition), and in this paper we will apply the same method to a simple model of cotransmission.

2 The model

We recently analyzed a simple SIS model (susceptible-infective-susceptible) of drug resistance [38] for one disease, denoted by P. The state of a single individual may be completely susceptible, infected with drug-susceptible organisms only, or infected with drug-resistant organisms only. We consider a single individual in a large population, subject to constant forces of infection. Let X⁽ⁱ⁾, $X^{(i)},Y_S^{(i)}$, and $Y_R^{(i)}$ denote the probability the individual is susceptible, infected with the sensitive strain, or infected with the resistant strain, respectively. Treatment, occurring at rate ${\theta }_P^{(i)}$, may lead to a new clinical appearance of drug resistance with probability δ ∈ (0, 1). Let ρ_P denote the recovery rate. Denoting the force of infection (only dependent on the number of individuals infected, and independent of individual choice of treatment) due to sensitive strains by λ_S and due to resistant strains by λ_R, a single individual follows the Markov chain

$$\frac{d{X}^{(i)}}{dt}=-({\lambda }_S+{\lambda }_R)X^{(i)}+({\rho }_P{Y}_S^{(i)}+{\rho }_P{Y}_R^{(i)})+{\theta }_P^{(i)}(1-\delta )Y_S^{(i)},$$

$$\frac{d{Y}_S^{(i)}}{dt}={\lambda }_S{X}^{(i)}-{\rho }_P{Y}_S^{(i)}-{\theta }_P^{(i)}{Y}_S^{(i)},$$

$$\frac{d{Y}_R^{(i)}}{dt}={\lambda }_R{X}^{(i)}-{\rho }_P{Y}_R^{(i)}+{\theta }_P^{(i)}\delta Y_S^{(i)},$$

which is Model 1 in the previous paper ([38]).

We now extend this model to include a second disease, denoted by C. Motivated by the example of Chlamydia, we again assume a simple SIS process for the second disease, and assume no drug resistance is possible for this second disease. Nevertheless, treating individuals with this disease may select for drug resistance in the first disease (since this first disease might be present). We now denote the recovery rate for the second disease by ρ_C, and the force of infection by λ_C. Let X⁽ⁱ⁾ denote the probability that a single individual in a large population is infected with no infectious agent, $Y_S^{(i)}$ the probability the individual is infected by the drug-sensitive strain of the first agent (and not infected with the second agent), $Y_R^{(i)}$ the probability the individual is infected by the drug-resistant strain of the first agent (and not infected with the second agent), $Y_C^{(i)}$ the probability the individual is infected by the second agent (and not infected with either strain of the first agent), $Y_{SC}^{(i)}$ the probability the individual is infected by the drug-sensitive strain of the first agent and also by the second agent, and finally $Y_{RC}^{(i)}$ the probability the individual is infected by the drug-resistant strain of the first agent and also by the second agent. The treatment rate for individuals infected by the second infectious agent only is ${\theta }_C^{(i)}$; the treatment rate for individuals infected simultaneously by both agents is denoted ${\theta }_{PC}^{(i)}$. Here, a susceptible individual who contacts a dually infected person could become infected only with the first, the second or both agents as a result of the single contact; we thus have infection rates of λ_SC→S, λ_SC→C and λ_SC→SC (or λ_RC→R, λ_RC→C and λ_RC→RC), correspondingly. Then, we have

$$\frac{d{X}^{(i)}}{dt}=-({\lambda }_S+{\lambda }_R+{\lambda }_C+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}+{\lambda }_{SC\to C}+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC}+{\lambda }_{RC\to C})X^{(i)}+({\rho }_P{Y}_S^{(i)}+{\rho }_P{Y}_R^{(i)}+{\rho }_C{Y}_C^{(i)})+({\theta }_C^{(i)}{Y}_C^{(i)}+{\theta }_{PC}^{(i)}(1-\delta )Y_{SC}^{(i)}+{\theta }_P^{(i)}(1-\delta )Y_S^{(i)}),$$

$$\frac{d{Y}_S^{(i)}}{dt}=({\lambda }_S+{\lambda }_{SC\to S})X^{(i)}-({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_S^{(i)}+({\rho }_C{Y}_{SC}^{(i)}-{\rho }_P{Y}_S^{(i)})-{\theta }_P^{(i)}{Y}_S^{(i)},$$

$$\frac{d{Y}_R^{(i)}}{dt}=({\lambda }_R+{\lambda }_{RC\to R})X^{(i)}-({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_R^{(i)}+({\rho }_C{Y}_{RC}^{(i)}-{\rho }_P{Y}_R^{(i)})+({\theta }_{PC}^{(i)}{Y}_{RC}^{(i)}+{\theta }_{PC}^{(i)}\delta Y_{SC}^{(i)}+{\theta }_P^{(i)}\delta Y_S^{(i)}),$$ (2.1)

$$\frac{d{Y}_C^{(i)}}{dt}=({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{RC\to C})X^{(i)}-({\lambda }_S+{\lambda }_R+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC})Y_C^{(i)}+({\rho }_P{Y}_{SC}^{(i)}+{\rho }_P{Y}_{RC}^{(i)}-{\rho }_C{Y}_C^{(i)})-{\theta }_C^{(i)}{Y}_C^{(i)},$$

$$\frac{d{Y}_{SC}^{(i)}}{dt}={\lambda }_{SC\to SC}{X}^{(i)}+({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_S^{(i)}+({\lambda }_S+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC})Y_C^{(i)}-({\rho }_P+{\rho }_C)Y_{SC}^{(i)}-{\theta }_{PC}^{(i)}{Y}_{SC}^{(i)},$$

$$\frac{d{Y}_{RC}^{(i)}}{dt}={\lambda }_{RC\to RC}{X}^{(i)}+({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_R^{(i)}+({\lambda }_R+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC})Y_C^{(i)}-({\rho }_P+{\rho }_C)Y_{RC}^{(i)}-{\theta }_{PC}^{(i)}{Y}_{RC}^{(i)}.$$

We omit human migration, birth, natural and disease-induced death; the total probability satisfies $X^{(i)}+Y_S^{(i)}+Y_R^{(i)}+Y_C^{(i)}+Y_{SC}^{(i)}+Y_{RC}^{(i)}=1$. For any given set of forces of infection, these linear equations can be solved for the equilibrium values of the probabilities of being in each state. We denote the equilibrium by ${Ē}^{(i)}=({\overline{X}}^{(i)},{Ȳ}_S^{(i)},{Ȳ}_R^{(i)},{Ȳ}_C^{(i)},{Ȳ}_{SC}^{(i)},{Ȳ}_{RC}^{(i)})$.

As indicated above, we wish to consider a particular individual who chooses treatment rates ${\theta }_P^{(i)},{\theta }_C^{(i)}$ or ${\theta }_{PC}^{(i)}$, faced by a unanimous choice θ_P, θ_C or θ_PC made by all other individuals. The following system of equations describing the corresponding community-level transmission dynamics:

$$\frac{dX}{dt}=-({\lambda }_S+{\lambda }_R+{\lambda }_C+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}+{\lambda }_{SC\to C}+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC}+{\lambda }_{RC\to C})X+({\rho }_P{Y}_S+{\rho }_P{Y}_R+{\rho }_C{Y}_C)+({\theta }_C{Y}_C+{\theta }_{PC}(1-\delta )Y_{SC}+{\theta }_P(1-\delta )Y_S),$$

$$\frac{d{Y}_S}{dt}=({\lambda }_S+{\lambda }_{SC\to S})X-({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_S+({\rho }_C{Y}_{SC}-{\rho }_P{Y}_S)-{\theta }_P{Y}_S,$$

$$\frac{d{Y}_R}{dt}=({\lambda }_R+{\lambda }_{RC\to R})X-({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_R+({\rho }_C{Y}_{RC}-{\rho }_P{Y}_R)+({\theta }_{PC}{Y}_{RC}+{\theta }_{PC}\delta Y_{SC}+{\theta }_P\delta Y_S),$$ (2.2)

$$\frac{d{Y}_C}{dt}=({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{RC\to C})X-({\lambda }_S+{\lambda }_R+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC})Y_C+({\rho }_P{Y}_{SC}-{\rho }_P{Y}_{RC}-{\rho }_C{Y}_C)-{\theta }_C{Y}_C,$$

$$\frac{d{Y}_{SC}}{dt}={\lambda }_{SC\to SC}X+({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_S+({\lambda }_S+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC})Y_C-({\rho }_P+{\rho }_C)Y_{SC}-{\theta }_{PC}{Y}_{SC},$$

$$\frac{d{Y}_{RC}}{dt}={\lambda }_{RC\to RC}X+({\lambda }_C+{\lambda }_{SC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{RC\to C}+{\lambda }_{RC\to RC})Y_R+({\lambda }_R+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC})Y_C-({\rho }_P+{\rho }_C)Y_{RC}-{\theta }_{PC}{Y}_{RC},$$

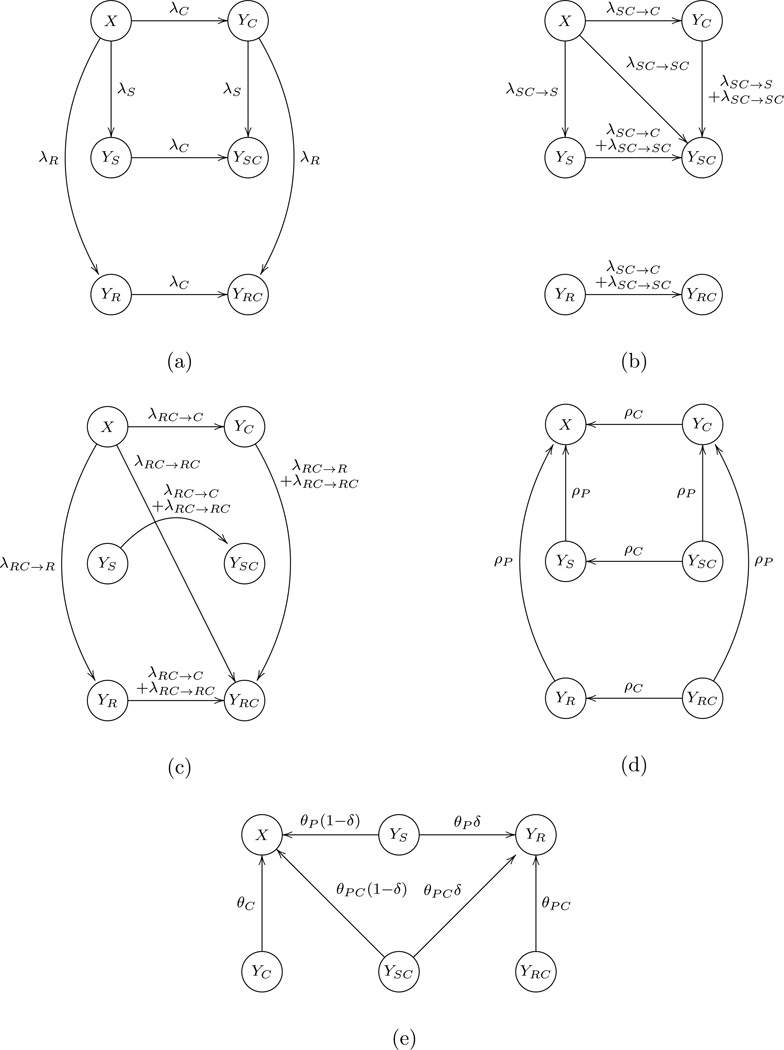
where X, Y_S, Y_R, Y_C, Y_SC, and Y_RC are the proportion of each disease state in the whole population; X + Y_S + Y_R + Y_C + Y_SC + Y_RC = 1. A state transition diagram for the disease transmission is shown in Figure 1. We assume that the forces of infection are proportional to the prevalence fractions and the force of infection of one agent is not affected by the presence of the other:

• (A1)λ_S = β_SY_S, λ_R = β_RY_R where β_R < β_S; λ_C = β_CY_C;
• (A2)λ_SC→SC = β₁₁Y_SC, λ_SC→S = β₁₀Y_SC, λ_SC→C = β₀₁Y_SC,

  ${\lambda }_{RC\to RC}={\beta }_{11}^{\prime }{Y}_{RC},{\lambda }_{RC\to R}={\beta }_{10}^{\prime }{Y}_{RC},{\lambda }_{RC\to C}={\beta }_{01}^{\prime }{Y}_{RC}$;

• (A3)β₁₁ + β₁₀ = β_S and β₁₁ + β₀₁ = β_C, ${\beta }_{11}^{\prime }+{\beta }_{10}^{\prime }={\beta }_R$ and ${\beta }_{11}^{\prime }+{\beta }_{01}^{\prime }={\beta }_C$.

Figure 1.

Flow diagram of the model. Infection process: (a) encounter Y_S, Y_R and Y_C, respectively, and get infected; (b) encounter Y_SC and get infected; (c) encounter Y_RC and get infected. (d) Recovery process. (e) Treatment process.

Here β_S, β_R, and β_C are transmission coefficients of the drug-sensitive strain of the first agent, drug-resistant strain of the first agent, and the second agent, respectively. Note that an individual in a large population is subject to constant exogenous forces of infection (unaffected by the decision of that single individual), while the forces of infection at the population level are determined by the overall disease prevalence in the community. In many cases the emergence of drug resistance is indeed associated with a fitness cost [31], i.e., β_R < β_S, but a fitness cost of resistance may not be universally exhibited (e.g. [13]). Also, we do not assume that both infections in dually infected people are simply transmitted independently. Cotransmission from dually infected people is assumed possible, as a single infectious contact could contain a sufficient dose of both infectious agents. It is assumed that all model parameters are positive, with the exception of treatment rates ${\theta }_P^{(i)},{\theta }_C^{(i)},{\theta }_{PC}^{(i)}$, θ_P, θ_C, θ_PC and parts of transmission coefficients β₁₁, β₁₀, β₀₁, ${\beta }_{11}^{\prime },{\beta }_{10}^{\prime },{\beta }_{01}^{\prime }$ which can be zero.

In general, we let D_P and D_C be an average health state disutility of infection or colonization by the first or second agent, respectively; we assume no difference in disutility between drug susceptible and drug resistant strains. Rather, individuals who are infected with a drug resistant strain are at a disadvantage because we assume treatment will be less effective (leading to longer mean durations of infection). We also assume no interaction between the agents, so that the disutility of being infected by both agents is the sum of the separate disutilities. Thus, for a single individual we wish to minimize

$$J^{(i)}=D_P{J}_P^{(i)}+D_C{J}_C^{(i)},$$

where $J_P^{(i)}={Ȳ}_S^{(i)}+{Ȳ}_R^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)}$ and $J_C^{(i)}={Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)}$ represent the probabilities being infected by the first or second agent, respectively, and ${Ē}^{(i)}=({\overline{X}}^{(i)},{Ȳ}_S^{(i)},{Ȳ}_R^{(i)},{Ȳ}_C^{(i)},{Ȳ}_{SC}^{(i)},{Ȳ}_{RC}^{(i)})$ is the stable equilibrium of the individual equations. Analogously, for a community we can define its average disutility as

$$J=D_P{J}_P+D_C{J}_C,$$

where J_P = Ȳ_S + Ȳ_R + Ȳ_SC + Ȳ_RC and J_C = Ȳ_C + Ȳ_SC + Ȳ_RC represent the fractions being infected by the first or second agent, respectively, and Ē = (X̄, Ȳ_S, Ȳ_R, Ȳ_C, Ȳ_SC, Ȳ_RC) is the stable steady state of the community equations.

We will examine these equations under two treatment strategies: (a) mass treatment, and (b) treatment targeted towards persons infected by disease C. In the first case, we assume θ_P = θ_C = θ_PC = θ, so that all individuals are equally likely to be treated, regardless of their infection status, as would be the case during mass administration of azithromycin to eliminate trachoma. In the second case, we assume θ_P = 0 and θ_C = θ_PC = θ. Here, targeting infectives with the second agent may select for drug resistance in the first agent. Similarly, we assume ${\theta }_P^{(i)}={\theta }_C^{(i)}={\theta }_{PC}^{(i)}={\theta }^{(i)}$, and ${\theta }_P^{(i)}=0$ and ${\theta }_C^{(i)}={\theta }_{PC}^{(i)}={\theta }^{(i)}$, respectively, for an individual under the two treatment strategies.

The disutility to each individual is determined not only by that individual’s choice of treatment, but also by all other individuals’ average choice. We followed standard methods ([42, 38]) to calculate the disutility of an individual, and determined whether individual incentives always parallel to community outcomes. To analyze individual incentives for treatment, we first determined the equilibrium dynamics of infection. We then examined a single individual whose forces of infection (for each agent that is circulating) are determined by the overall treatment rate in the entire population, and determined the expected amount of time that would be spent infected in each disease if this individual chose a different treatment rate rather than the population as a whole.

3 Main results

In this section, we derive the basic reproduction number for the population-level model, and then study the existence and local stability of feasible equilibria. The possibility of the occurrence of a tragedy of the commons under mass treatment or targeted treatment is analytically investigated.

3.1 The basic reproduction number

We consider the community equations (2.2) in which the forces of infection are not exogenous, but determined by the disease prevalence. It is clear that E₀ = (1, 0, 0, 0, 0, 0) is the unique disease free equilibrium of system (2.2). Following the method and notations of van den Driessche and Watmough [51], we find

$$F=\left(\begin{array}{ccccc}\hfill {\beta }_S\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_S-{\beta }_{11}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_R\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_R-{\beta }_{11}^{\prime }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_C\hfill & \hfill {\beta }_C-{\beta }_{11}\hfill & \hfill {\beta }_C-{\beta }_{11}^{\prime }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_{11}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_{11}^{\prime }\hfill \end{array}\right)$$

and

$$V=\left(\begin{array}{ccccc}\hfill {\rho }_P+{\theta }_P\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\rho }_C\hfill & \hfill 0\hfill \\ \hfill -{\theta }_P\delta \hfill & \hfill {\rho }_P\hfill & \hfill 0\hfill & \hfill -{\theta }_{PC}\delta \hfill & \hfill -{\rho }_C-{\theta }_{PC}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_C+{\theta }_C\hfill & \hfill -{\rho }_P\hfill & \hfill -{\rho }_P\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_P+{\rho }_C+{\theta }_{PC}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_P+{\rho }_C+{\theta }_{PC}\hfill \end{array}\right).$$

The basic reproduction number ℛ₀ of model (2.2) is defined as the spectral radius of the next generation matrix F · V⁻¹, i.e., ${ℛ}_0=\underset{1\le i\le 5}{\text{max}}{ℛ}_{i0}$ where

$${ℛ}_{10}=\frac{{\beta }_S}{{\rho }_P+{\theta }_P},{ℛ}_{20}=\frac{{\beta }_R}{{\rho }_P},{ℛ}_{30}=\frac{{\beta }_C}{{\rho }_C+{\theta }_C},{ℛ}_{40}=\frac{{\beta }_{11}}{{\rho }_P+{\rho }_C+{\theta }_{PC}}\text{and}{ℛ}_{50}=\frac{{\beta }_{11}^{\prime }}{{\rho }_P+{\rho }_C+{\theta }_{PC}}.$$

For i = 1, …, 5, ℛ_i0 is the reproduction number corresponding to epidemiological classes Y_S, Y_R, Y_C, Y_SC, and Y_RC, respectively. In case of mass treatment or targeted treatment, we know ℛ₄₀ < min{ℛ₁₀, ℛ₃₀}, ℛ₅₀ < min{ℛ₂₀, ℛ₃₀}, and hence ${ℛ}_0=\underset{1\le i\le 3}{\text{max}}{ℛ}_{i0}$. Moreover, E₀ is locally asymptotically stable if ℛ₀ < 1 and unstable if otherwise.

3.2 The equilibria

For an individual subject to constant exogenous forces of infection (unaffected by the treatment strategy that person chooses), the coefficient matrix of its individual equations (2.1), denoted by A = (a_ij)_6×6, is (or can be reduced to) a constant irreducible matrix (or submatrix) with nonnegative off-diagonal entries and zero column sums. It follows from Corollary 4.3.2 in Smith [48] or Lemma 1 in Cosner et al. [10] that (2.1) has a unique nonnegative equilibrium ${Ē}^{(i)}=({\overline{X}}^{(i)},{Ȳ}_S^{(i)},{Ȳ}_R^{(i)},{Ȳ}_C^{(i)},{Ȳ}_{SC}^{(i)},{Ȳ}_{RC}^{(i)})$ which is globally stable in the hyperplane

$$\{(X^{(i)},Y_S^{(i)},Y_R^{(i)},Y_C^{(i)},Y_{SC}^{(i)},Y_{RC}^{(i)})\in {ℝ}_{+}^6:X^{(i)}+Y_S^{(i)}+Y_R^{(i)}+Y_C^{(i)}+Y_{SC}^{(i)}+Y_{RC}^{(i)}=1\}.$$

Direct computations find that the community model equations (2.2) can have up to four types of steady states as follows. The detailed derivation and stability analysis appear in Appendix A.

Theorem 3.1

Let ℜ(z) be the real part of a complex number z. For system (2.2) under mass treatment or targeted treatment, we have

1. The no-disease or disease free equilibrium E₀ = (1, 0, 0, 0, 0, 0) always exists and it is stable if ℛ₀ < 1 and unstable otherwise.

2. One-strain equilibrium:

   1. $E_1=(\frac{1}{{ℛ}_{10}},1-\frac{1}{{ℛ}_{10}},0,0,0,0)$ exists if and only if ℛ₁₀ > 1 and θ_P = 0 (targeted treatment). E₁ is stable if and only if ℛ₁₀ > max{1, ℛ₂₀, ℛ₅₀} and ℛ₃₀ < 1.
   2. $E_2=(\frac{1}{{ℛ}_{20}},0,1-\frac{1}{{ℛ}_{20}},0,0,0)$ exists if and only if ℛ₂₀ > 1. E₂ is stable if and only if ℛ₂₀ > max{1, ℛ₁₀, ℛ₄₀} and ℛ₃₀ < 1.
   3. $E_3=(\frac{1}{{ℛ}_{30}},0,0,1-\frac{1}{{ℛ}_{30}},0,0)$ exists if and only if ℛ₃₀ > 1. Targeted treatment: E₃ is stable if and only if ℛ₃₀ > 1, ℛ₂₀ < 1, $\Re {\lambda }_3^{+}<0$ and $\Re {\lambda }_3^{-}<0$. Mass treatment: E₃ is stable if and only if ℛ₁₀ < 1, ℛ₂₀ < 1, and ℛ₃₀ > 1. Here ${\lambda }_3^{\pm }$ denote the roots of λ² + M₁λ + M₀ = 0 with

      $$M_1=(1-{ℛ}_{10}){\rho }_P+(1-\frac{{ℛ}_{40}}{{ℛ}_{30}})({\rho }_P+{\rho }_C+\theta )+{\beta }_C(1-\frac{1}{{ℛ}_{30}}),$$

      $$M_0=(1-{ℛ}_{10}){\rho }_P+\left(\right(1-\frac{{ℛ}_{40}}{{ℛ}_{30}})({\rho }_P+{\rho }_C+\theta )+{\beta }_C(1-\frac{1}{{ℛ}_{30}}\left)\right)+\theta ({\beta }_C+{\beta }_S)(1-\frac{1}{{ℛ}_{30}}).$$
3. Two-strain equilibrium:

   1. $E_{12}=(\frac{1}{{ℛ}_{10}},Y_{12},1-\frac{1}{{ℛ}_{10}}-Y_{12},0,0,0)$ exists if and only if ℛ₁₀ > ℛ₂₀, ℛ₁₀ > 1, and θ_P > 0. E₁₂ is stable if and only if ℛ₃₀ < 1. Here

      $$Y_{12}=\frac{(1/{ℛ}_{20}-1/{ℛ}_{10})(1-1/{ℛ}_{10})}{1/{ℛ}_{20}-1/{ℛ}_{10}+\delta {\theta }_P/{\beta }_R}\in (0,\frac{1}{{ℛ}_{10}}).$$
   2. $E_{13}=(X_{13},\frac{1}{{ℛ}_{30}}-X_{13},0,\frac{1}{{ℛ}_{10}}-X_{13},\frac{({\beta }_S+{\beta }_C)(\frac{1}{{ℛ}_{10}}-X_{13})(\frac{1}{{ℛ}_{30}}-X_{13})}{({\beta }_S+{\beta }_C-{\beta }_{11})X_{13}},0)$ exists if and only ℛ₁₀ > 1, ℛ₃₀ > 1 and θ_P = θ_C = θ_PC = 0 (no treatment). E₁₃ is stable if and only if β_S > β_R. Here X₁₃ ∈ [1/(ℛ₁₀ℛ₃₀), min{1/ℛ₁₀, 1/ℛ₃₀}) is the smaller root to

      $${\beta }_{11}{X}^2-\left(\right(\frac{1}{{ℛ}_{10}}+\frac{1}{{ℛ}_{30}}-1){\beta }_{11}+({\beta }_S+{\beta }_C))X+({\beta }_S+{\beta }_C)\frac{1}{{ℛ}_{10}{ℛ}_{30}}=0$$

      if β₁₁ > 0 and equals 1/(ℛ₁₀ℛ₃₀) if β₁₁ = 0.
   3. $E_{23}=(X_{23},0,\frac{1}{{ℛ}_{30}}-X_{23},\frac{1}{{ℛ}_{20}}-X_{23},0,\frac{({\beta }_R+{\beta }_C)(\frac{1}{{ℛ}_{20}}-X_{23})(\frac{1}{{ℛ}_{30}}-X_{23})}{({\beta }_R+{\beta }_C-{\beta }_{11}^{\prime })X_{23}})$ exists if and only if ℛ₂₀ > 1 and ℛ₃₀ > 1. Mass treatment: E₂₃ is stable if and only if ℛ₁₀ < ℛ₂₀. Targeted treatment: E₂₃ is stable if and only if $\Re {\lambda }_{23}^{+}<0$ and $\Re {\lambda }_{23}^{-}<0$. Here X₂₃ ∈ [1/(ℛ₂₀ℛ₃₀), min{1/ℛ₂₀, 1/ℛ₃₀}) is the smaller root to

      $${\beta }_{11}^{\prime }{X}^2-\left(\right(\frac{1}{{ℛ}_{20}}+\frac{1}{{ℛ}_{30}}-1){\beta }_{11}^{\prime }+({\beta }_R+{\beta }_C))X+({\beta }_R+{\beta }_C)\frac{1}{{ℛ}_{20}{ℛ}_{30}}=0$$

      if ${\beta }_{11}^{\prime }>0$ and equals 1/(ℛ₂₀ℛ₃₀) if ${\beta }_{11}^{\prime }=0$. Here ${\lambda }_{23}^{\pm }$ are solutions to λ² + H₁λ + H₀ = 0 with

      $$H_1=(1-\frac{{ℛ}_{10}}{{ℛ}_{20}}){\rho }_P+({\beta }_C+{\rho }_P-{\beta }_{11}{X}_{23}),$$

      $$H_0=(1-\frac{{ℛ}_{10}}{{ℛ}_{20}}){\rho }_P({\beta }_C+{\rho }_P-{\beta }_{11}{X}_{23})+\theta (({\beta }_C-{\rho }_C-\theta )+{\beta }_S(\frac{1}{{ℛ}_{20}}-X_{23}\left)\right).$$

4. Coexistence equilibrium of the form Ẽ = (X̃, Ỹ_S, Ỹ_R, Ỹ_C, Ỹ_SC, Ỹ_RC) in which all the components are positive. Ẽ exists only if ℛ₁₀ > 1, ℛ₃₀ > 1, ℛ₁₀ > ℛ₂₀ and θ_C > 0.

Remark 3.2

Note that if ℛ₁₀ < 1 and ℛ₃₀ > 1 then M₁ > 0 and M₀ > 0. Thus E₃ is stable if ℛ₃₀ > 1, ℛ₂₀ < 1 and ℛ₁₀ < 1. In particular, when θ = 0, E₃ is stable if and only if ℛ₃₀ > 1, ℛ₂₀ < 1 and ℛ₁₀ < 1. However, for a non-zero targeted treatment rate θ, E₃ can remain stable even if ℛ₁₀ > 1. For example, given β_S = 1.1, β_R = 0.5, β_C = 3, ρ_P = 1, ρ_C = 0.5, θ = 1, β₁₁ = 0.5, we have ℛ₃₀ = 2 > 1, ℛ₂₀ = 0.5 < 1, ℛ₁₀ = 1.1 > 1, but M₁ = 3.65 and M₀ = 1.675. In addition, if β₁₁ = 0 then M₀ > 0 implies M₁ > 0.

Remark 3.3

Under targeted treatment, E₂₃ is stable if ℛ₁₀ < ℛ₂₀. However, it is possible that E₂₃ remains stable even if ℛ₁₀ > ℛ₂₀. For example, given β_S = 2, β_R = 1.5, β_C = 3, ρ_P = 1, ρ_C = 1, θ = 1, β₁₁ = 0, ${\beta }_{11}^{\prime }=0$, we have ℛ₁₀ = 2 > ℛ₂₀ = 1.5 > 1 and ℛ₃₀ = 1.5 > 1, but H₁ = 11/3 and H₀ = 1/9. In addition, if ${\beta }_{11}={\beta }_{11}^{\prime }=0$ then H₀ > 0 implies H₁ > 0.

Remark 3.4

By comparing the existence and stability condition of equilibria, we find that there exists at most one stable equilibrium under mass treatment, or under targeted treatment if ℛ₁₀ < 1 or ℛ₁₀ < ℛ₂₀. In particular, when the coexistence equilibrium exists under mass treatment, it is the only possibly stable equilibrium.

Moreover, numerical calculations suggest that there exists exactly one stable equilibrium for any parameter setting and the coexistence equilibrium is stable whenever it exists.

3.3 The tragedy of the commons

Given a set of parameter values, we first solve for the stationary solutions of (2.2) and substitute the stable solution into the exogenous forces of infection of the individual model (2.1), and then find the proportion in each infected state. From these proportions, we can then compute the disutility of an individual. An individual has an incentive to increase antibiotic treatment if the individual disutility J⁽ⁱ⁾ is decreasing in terms of θ⁽ⁱ⁾, i.e., more treatment produces less disutility. A community benefits from treatment if the community disutility J is decreasing in θ. Locally, a tragedy of the commons occurs when the goal of the individual conflicts with that of the community. Mathematically, this means that for a fixed parameter set, we have

$${(\frac{\partial J^{(i)}}{\partial {\theta }^{(i)}}·\frac{\partial J}{\partial \theta })|}_{{\theta }^{(i)}=\theta ={\theta }_0}<0\text{for some}{\theta }_0>0.$$

Let ${\lambda }_S^{*}={\lambda }_S+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}={\beta }_S({Ȳ}_S+{Ȳ}_{SC}),{\lambda }_R^{*}={\lambda }_R+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC}={\beta }_R({Ȳ}_R+{Ȳ}_{RC})$ and ${\lambda }_C^{*}={\lambda }_{RC\to RC}+{\lambda }_{RC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{SC\to C}+{\lambda }_C={\beta }_C({Ȳ}_C+{Ȳ}_{SC}+{Ȳ}_{RC})$. Recall that under mass treatment, we assume all infected people are treated at the same rate (θ_P = θ_PC = θ_C = θ and ${\theta }_P^{(i)}={\theta }_{PC}^{(i)}={\theta }_C^{(i)}={\theta }^{(i)}$), while under targeted treatment, that individuals with C are treated, whether or not they exhibit the other infection (θ_P = 0, θ_PC = θ_C = θ and ${\theta }_P^{(i)}=0,{\theta }_{PC}^{(i)}={\theta }_C^{(i)}={\theta }^{(i)}$). The proof of the following is postponed to Appendix B.

Theorem 3.5

Modeling a single individual according to (2.1) implies

$$J_P^{(i)}=\frac{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})}{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})+{\rho }_P({\rho }_P+{\theta }^{(i)})}$$

under mass treatment, and

$$J_C^{(i)}=\frac{{\lambda }_C^{*}}{{\lambda }_C^{*}+{\rho }_C+{\theta }^{(i)}}$$

under mass treatment or targeted treatment, respectively.

The community model (2.2) implies that

$$J_P=\text{max}\{1-\frac{{\rho }_P+\theta }{{\beta }_S},0\}=\text{max}\{1-\frac{1}{{ℛ}_{10}},0\}$$

under mass treatment, and

$$J_C=\text{max}\{1-\frac{{\rho }_C+\theta }{{\beta }_C},0\}=\text{max}\{1-\frac{1}{{ℛ}_{30}},0\}$$

under mass treatment or targeted treatment, respectively.

In addition, under targeted treatment, there exist some parameter sets such that $J_P^{(i)}$ (or J_P) is increasing in θ⁽ⁱ⁾ (or θ).

Thus, under mass treatment, both $J^{(i)}=D_P{J}_P^{(i)}+D_C{J}_C^{(i)}$ and J = D_PJ_P + D_CJ_C are decreasing in θ⁽ⁱ⁾ and θ, respectively, for any D_P > 0 and D_C > 0. This indicates that increasing mass treatment increases the utility of both the individual and community, and there is no tragedy of the commons in two diseases setting under mass treatment.

However, J = D_PJ_P + D_CJ_C can increase in θ for some D_P > 0 and D_C > 0 (e.g. D_P ≫ D_C) under targeted treatment. For this reason, the incentives for the individual and community do not always coincide, and a tragedy of the commons may occur provided that only infectives with the second agent receive treatment.

Theorem 3.6

For system (2.2) under targeted treatment, assume that there always exists a globally stable equilibrium. If ℛ₁₀ > 1, ℛ₁₀ > ℛ₂₀ and ℛ₃₀ > 1 at θ = 0, then J_P < 1 − 1/ℛ₁₀ for θ ∈ (0, β_C − ρ_C), and J_P = 1 − 1/ℛ₁₀ for θ ∈ {0} ∪ [β_C − ρ_C, ∞).

Proof

No treatment (θ = 0): E₁₃ is the unique stable equilibrium and J_P = 1 − 1/ℛ₁₀.

Small treatment (0 < θ < β_C − ρ_C): one of E₃, E₂₃ and Ẽ is stable. If E₃ is stable, then J_P = 0; else if E₂₃ is stable, then J_P = 1 − (X₂₃ + 1/ℛ₂₀ − X₂₃) = 1 − 1/ℛ₂₀ < 1 − 1/ℛ₁₀; else if Ẽ is stable then, J_P < 1 − 1/ℛ₁₀ due to (ρ_P − β_S(X̃ + Ỹ_C))(Ỹ_S + Ỹ_SC) = −θỸ_SC < 0.

High values for the treatment rate (θ ≥ β_C − ρ_C): disease C disappears. E₁ is stable and J_P = 1 − 1/ℛ₁₀.

Remark 3.7

Under targeted treatment, we define Q(θ) = θȲ_SC/(Ȳ_S + Ȳ_SC) as the treatment rate for the sensitive strain of disease P at a stable equilibrium Ē (θ). Assume that there always exists a globally stable equilibrium, it follows from the proof of Theorem 3.6 that

$$\frac{dQ}{d\theta }=-{\beta }_S\frac{d{J}_P}{d\theta }$$

which implies that max_θ≥0 Q(θ) = min_θ≥0 J_P, namely, the fraction of population being infected with the first agent is minimized (or maximized) whenever the treatment rate for the first infectious agent reaches its maximum (or minimum).

However, if there is no cotransmission from Y_RC, i.e., ${\beta }_{11}^{\prime }=0$, then $J_P^{(i)}$ is decreasing in θ⁽ⁱ⁾, which implies that J⁽ⁱ⁾ is decreasing in θ⁽ⁱ⁾ for any D_P > 0 and D_C > 0 (see Appendix B). In addition, if disease C has higher disutility than disease P, i.e., D_C ≥ D_P, then J⁽ⁱ⁾ is constantly decreasing in θ⁽ⁱ⁾. We omit the straightforward but tedious proof.

4 Numerical simulations

The above analysis shows that a tragedy of the commons does not exist under mass treatment. However, as defined above, a tragedy of the commons can appear for the case of targeted treatment. In this case, individuals who choose treatment rates which are larger than those adopted by the community achieve lower disutility, even though the entire community will experience more disease if everyone increases their treatment rates in the same way. But in this case—targeted treatment—the treatment rates apply only to dual infection; as the treatment rate increases, eventually the second disease is completely eliminated, and with it, all opportunity to treat the first infection. In a sense, this is not a classical tragedy of the commons, because it is removable after a change of treatment strategy from targeted treatment to mass treatment. However, the same two-disease model can exhibit a conflict of interest between individual and society under mass treatment if (i) assumption (A3) is not required, namely, the force of infection of dually infected hosts is different from singly infected hosts, or (ii) drug sensitive and drug resistant strains of the first disease have different disutility, or (iii) the uninfected has significant disutility.

In general, the relationship between antimicrobial resistance and virulence is not straight-forward (e.g. [6]). While in some cases, a clear fitness cost of resistance is believed to apply, it cannot be assumed that drug resistant strains are less virulent (e.g. [13], but see [15]). In some cases, drug resistance genes are present on a plasmid which also includes virulence factors (e.g. [33]), but in other cases evolution of drug resistance may simply alter expression of virulence factors [22]. To explore this possibility in our model, we assume the resistant infection could have higher disutility than the sensitive infection. One disadvantage of the use of broad-spectrum antibiotics in general, including azithromycin, is the disruptive effect such treatments have on the normal microbiome, which may permit the overgrowth of other harmful organisms [3]. This is particularly true in the case of Clostridium difficile in the gastrointestinal tract for example (e.g. [37]). Could colonization (though of course not infection) by pneumococcus have benefits in preventing the growth of other organisms? While some literature supports the notion that pneumococcal colonization is not beneficial [46], we explore the consequences of assuming that individuals in the susceptible state for pneumococcus have a comparative disutility over the colonized (infectious) states. In these two cases, we can define the individual and community disutility as

$$J^{(i)}=D_U{X}^{(i)}+D_S({Ȳ}_S^{(i)}+{Ȳ}_{SC}^{(i)})+D_R({Ȳ}_R^{(i)}+{Ȳ}_{RC}^{(i)})+D_C({Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)})$$

and

$$J=D_{U}X+D_S({Ȳ}_S+{Ȳ}_{SC})+D_R({Ȳ}_R+{Ȳ}_{RC})+D_C({Ȳ}_C+{Ȳ}_{SC}+{Ȳ}_{RC}),$$

respectively, where D_U, D_S, D_R and D_C are, respectively, the average disutility of the uninfected, the sensitive and resistant infections of the first disease, and the infections of the second disease. In what follows, we will give numerical examples to consolidate our analytical arguments.

Example 4.1

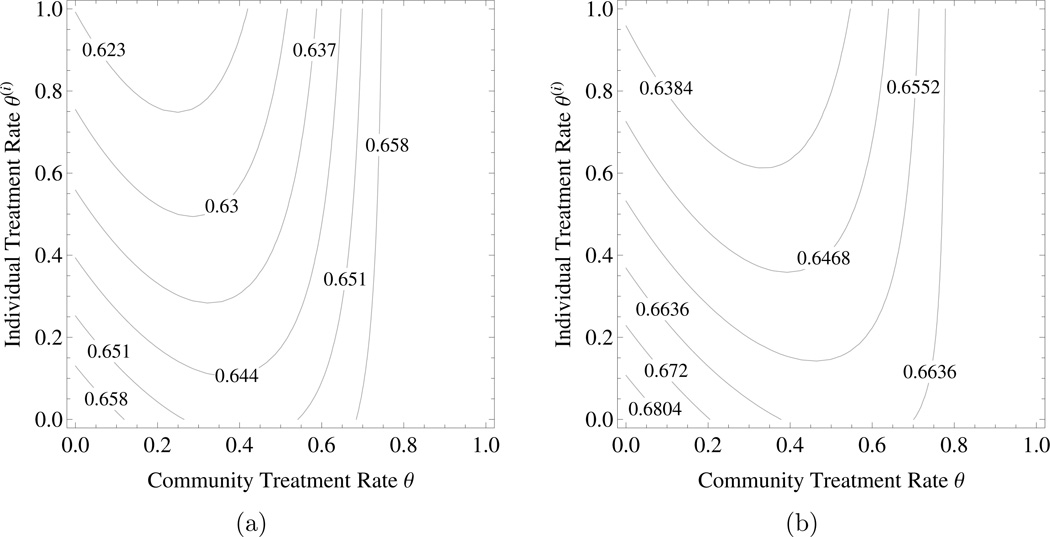
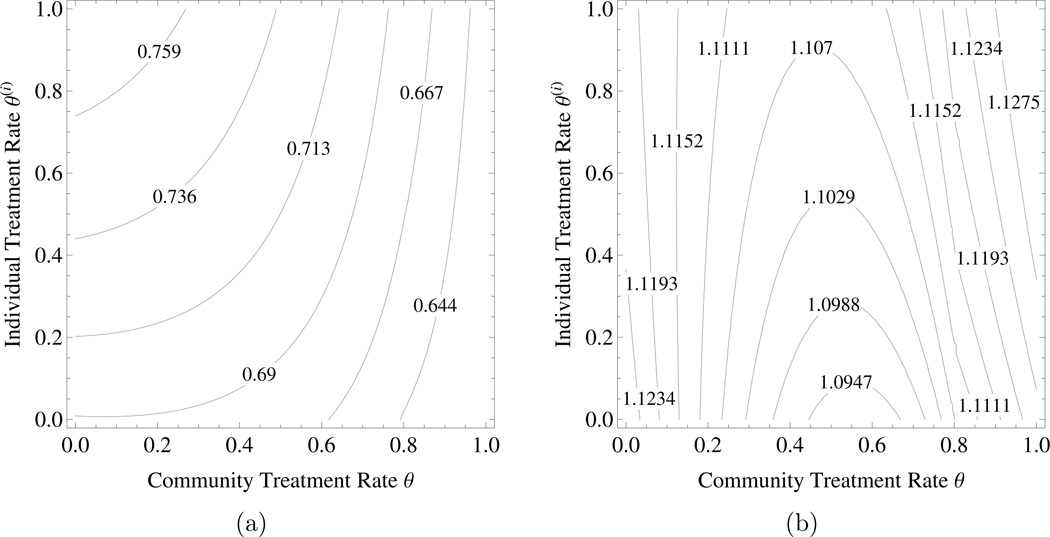
The tragedy of the commons under targeted treatment. Consider community model (2.2) with β_S = 3, β_R = 1.2, β_C = 1.8, β₁₁ = 1, ${\beta }_{11}^{\prime }=1$, δ = 0.3, ρ_P = 1, ρ_C = 1, and θ ∈ [0, 1]. β₁₀, β₀₁, ${\beta }_{10}^{\prime },{\beta }_{01}^{\prime }$ can be determined accordingly by (A3). Figures 2a shows the probability of an individual being infected by agent P and Figure 2b represents the individual disutility under targeted treatment with D_P = 1 and D_C = 0.05. Here an individual gets better if s/he departs from the community strategy and treats more, but things are worse if everyone does that. For the same parameter values, the tragedy of the commons under targeted treatment remains even if there is no cotransmission, i.e., ${\beta }_{11}={\beta }_{11}^{\prime }=0$. However, the tragedy of the commons disappears when the ratio D_P: D_C decreases below a certain threshold value.

Figure 2.

The tragedy of the commons under targeted treatment. a) The probability of an individual being infected by agent $P-J_P^{(i)}$, b) the individual disutility due to both diseases – $J^{(i)}=D_P{J}_P^{(i)}+D_C{J}_C^{(i)}$. The parameter values are as in the text. The horizontal axis is the community level of targeted treatment rate and the vertical axis is the level of targeted treatment rate chosen by an individual within the community.

Example 4.2

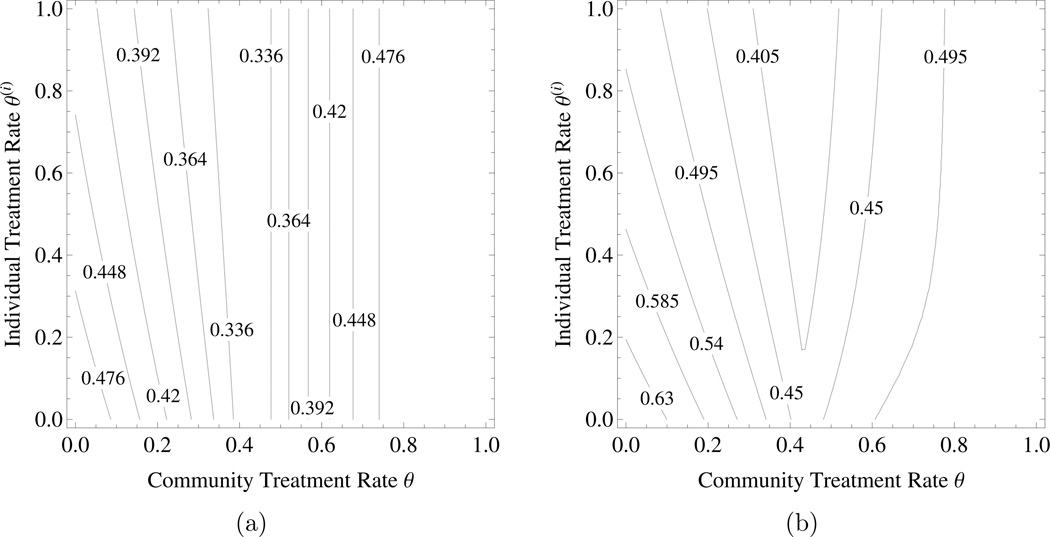
The tragedy of the commons under mass treatment without (A3). The values of parameters are β_S = 2.1, β_R = 2, β_C = 1.2, β₁₁ = 0.6, β₁₀ = 1.4, β₀₁ = 0.6, ${\beta }_{11}^{\prime }=0.1,{\beta }_{10}^{\prime }=0.1,{\beta }_{01}^{\prime }=1.1$, δ = 0.5, ρ_P = 1, ρ_C = 0.4, and θ ∈ [0, 1]. Figures 3a shows the probability of an individual being infected by agent P and Figure 3b represents the individual disutility under mass treatment with D_P = 1 and D_C = 0.25. Here disease C is assumed to differentially suppresse the resistant strain of disease P, namely, the transmission of the resistant strain of disease P from Y_RC is much lower than the transmission of the sensitive strain of disease P from $Y_{SC}({\beta }_R/{\beta }_S>({\beta }_{11}^{\prime }+{\beta }_{10}^{\prime })/({\beta }_{11}+{\beta }_{10}))$. Note that the formulae for $J_C^{(i)}$ and $J_P^{(i)}$ are the same as the case of mass treatment with assumption (A3) (see Theorem 3.5). As θ > 0.43, the sensitive strain of disease P goes extinct in the community which leads to ${\lambda }_S^{*}=0$. Thus $J_P^{(i)}={\lambda }_R^{*}/({\lambda }_R^{*}+{\rho }_P)$ and it is independent of personal choice of treatment when θ > 0.43. In this scenario, a higher treatment rate for the sensitive strain of the first infectious agent, Q(θ) = θ, could cause a larger proportion of people being infected with the first agent, J_P.

Figure 3.

The tragedy of the commons under mass treatment without assumption (A3). a) The probability of an individual being infected by agent $P-J_P^{(i)}$, b) the individual disutility due to both diseases – $J^{(i)}=D_P{J}_P^{(i)}+D_C{J}_C^{(i)}$. Parameters are as in the text. The horizontal axis is community level of mass treatment rate and the vertical axis is the level of mass treatment rate chosen by an individual within the community.

Example 4.3

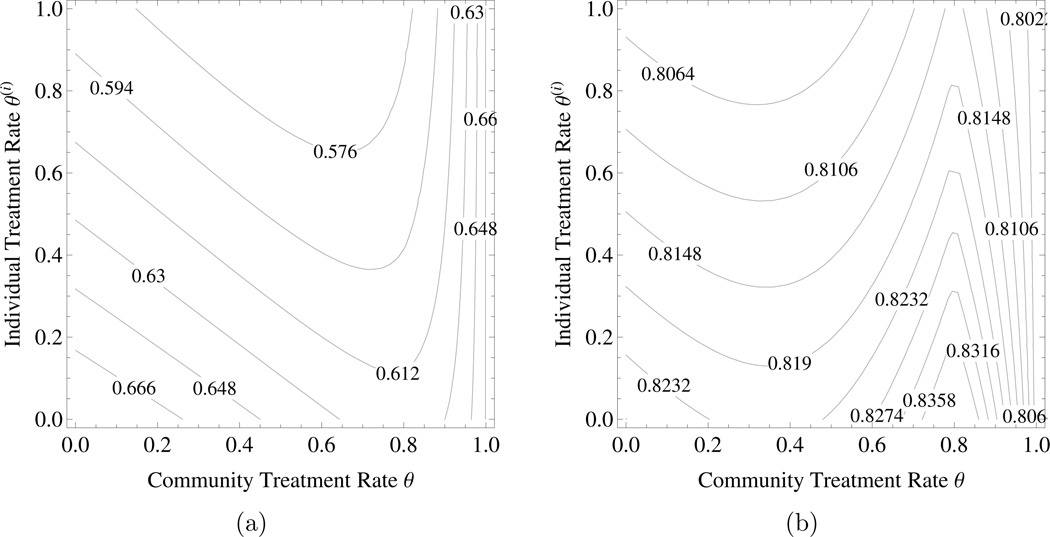
The tragedy of the commons under mass treatment with D_S ≠ D_R or D_U > 0. Choose the same parameter as in Example 4.1 except that β_R = 1.5, δ = 0.1, and the average disutility of infection/noninfection are different. Figures 4a and 4b represent the individual disutility under mass treatment with D_U = 0, D_S = 1 < D_R = 2 and D_C = 0.05, and D_U = 0.7, D_S = D_R = 1 and D_C = 0.05, respectively. In both cases there is a conflict of interest between individual and society: good for individual but bad for community.

Figure 4.

The tragedy of the commons under mass treatment with D_S ≠ D_R or D_U > 0. a) the individual disutility J⁽ⁱ⁾ when resistant infection has higher disutility than sensitive infection, b) the individual disutility J⁽ⁱ⁾ when the uninfected has significant disutility. Parameters are as in the text. The horizontal axis is community level of mass treatment rate and the vertical axis is the level of mass treatment rate chosen by an individual within the community.

It is worth noting that under certain circumstance individual incentives may favor under-treatment while increasing treatment will benefit community. Again choose the same parameter as in Example 4.1 except the average disutility of infection/noninfection. Figures 5a and 5b represent the individual disutility under mass treatment with D_U = 0, D_S = 1 < D_R = 2.5 and D_C = 0.05, and D_U = 1.2, D_S = D_R = 1 and D_C = 0.5, respectively. In both cases an increasing in treatment rate could be bad for individual but good for community.

Figure 5.

Individual incentives which may favor undertreatment in case of mass treatment with D_S ≠ D_R or D_U > 0. a) the individual disutility J⁽ⁱ⁾ when resistant infection has higher disutility than sensitive infection, b) the individual disutility J⁽ⁱ⁾ when the uninfected state has a lower utility than the infected states. Parameters are as in the text. The horizontal axis is community level of mass treatment rate and the vertical axis is the level of mass treatment rate chosen by an individual within the community.

5 Discussion

Rational antibiotic policy must consider the possibility that individual incentives to use antibiotics may drive overtreatment. Such overtreatment may lead to increasing drug resistance in other organisms, yielding a tragedy of the commons [1]. In a previous paper [38], we studied two single disease models of drug resistance: a simple SIS model and a two-stage (mild and severe) model, and found that a conflict of interest between individual and society does not occur for the former but is possible for the later under certain circumstances—individual incentives can favor overtreatment of mild infection leading to a worse outcome for society. However, mass administration of azithromycin during trachoma control provides a possible example of second mechanism for a conflict of interest between individual and society: treatment of one disease can lead to drug resistance in another organism.

In this paper, we extend previous game theory models of antibiotic policy to a setting of two infectious diseases which are cocirculating. In this model, treatment of one disease selects for resistance in the other, mimicking the behavior of induced resistance in pneumococcus caused by treatment of chlamydia. Mass antibiotic distributions for trachoma elimination are known to select for macrolide resistance in pneumococcus [47], although the prevalence of such resistance has been seen to rapidly decline after cessation of mass distribution [19]. Our model was designed to reflect specific features of chlamydia and pneumoccus in this setting, but we did not restrict the analysis to parameters reflecting the biology of pneumococcus and chlamydia. In this specific setting, for a base case scenario, we assumed that the two infections do not interact competitively (the presence of one organism does not reduce transmission of the other). In our model, treatment induces drug resistance in one organism (pneumococcus) but not in the other. We examined two scenarios: mass treatment, in which individual treatment is not based on knowledge of chlamydial infection status, and targeted treatment, in which individuals without chlamydia are not treated. The occurrence of a tragedy of the commons resulting from individual incentives to be treated is strongly influenced by the choice of mass versus targeted treatment, as well as by the health state utility of the various epidemiological states of individuals.

More specifically, we find that the model can imply conflicting individual and social incentives to use antibiotics. Such discord arises for a given population rate of treatment when individuals who diverge from it do better (or worse), while if all individuals make the same choice, all do worse (or better). Moreover, for a given parameter set, such discord may arise for some treatment values but not others. Also, individual incentives can favor underuse as well as overuse. We identified four different examples of discord between the individual and the community in our model.

First, suppose that infection or colonization by drug resistant pneumococcus is worse than infection or colonization by drug sensitive pneumococcus (the health state utility is lower for drug resistant infection or colonization). For specific parameter values, it is possible that individuals who choose rates higher than the population lower their health state utility because of the acquisition of drug resistance during treatment. Yet if the entire population chooses this new, higher treatment rate, the overall prevalence of infection is lower and the population benefits.

However, this example is far from the only way that individual incentives can lead to socially undesirable outcomes. Suppose now that the uninfected state has a lower utility than the infected states, because pneumococcal colonization is protecting the individual against infection by a third organism (whose presence is not explicitly modeled). Numerical scenarios reveal that for low treatment rates, the individual and community incentives can favor increased treatment, due to the benefits of curing chlamydia. But for higher treatment rates, individuals who choose higher rates than the community begin to experience worse outcomes, because the assumed disadvantage of curing pneumococcal colonization outweighs the benefits of clearing chlamydial infection. It is possible for individual incentives to favor lower treatment rates despite the fact that the population as a whole could continue to benefit from higher treatment, leading to another example of individual incentives leading to underuse of antibiotics.

These examples aside, in our model, a true tragedy of the commons can arise in which individual incentives can drive overuse of antibiotics. In our base case scenario, we assumed that for pneumococcus, drug susceptible and drug resistant infection (or colonization) have the same health state utility, and that it is better to be uninfected or uncolonized. While pneumococcus and chlamydia themselves are unlikely to interact competitively—each is unlikely to reduce the transmission of the other—infectious agents of course can be in competition, and we considered the following example in which the drug resistant strain of pneumococcus is less fit in the presence of chlamydia than the drug sensitive strain of pneumococcus. In other words, a fitness cost of drug resistance in pneumococcus is manifested by reduced ability to spread in the presence of chlamydia. Under these assumptions, under mass treatment, a tragedy of the commons may arise. Population level treatment rates can be found for which individuals do better if they exceed the population treatment rate. If the entire population, however, chooses a higher rate of treatment, the resulting reduction in chlamydia leads to an overcompensating degree of drug resistant pneumococcus, because (in this hypothetical scenario) chlamydia is no longer inhibiting drug resistant pneumococcus to the same degree. We found that for mass treatment, such a tragedy of the commons is impossible if the two organisms do not interact competitively.

If we depart from the assumption of mass treatment and allow targeted treatment, individual incentives can again drive socially disadvantageous treatment rates, but for a different reason. Under this assumption, individuals are only treated if they show signs of chlamydia (unlike in a mass administration campaign). Pneumococcus is only treated for individuals who are coinfected with chlamydia, so that the effective rate of pneumococcal treatment becomes smaller as the prevalence of chlamydia drops. Even when we assume identical health utility of drug sensitive and drug resistant pneumococcal colonization and infection, that either is worse than being uncolonized or uninfected, and that chlamydia and pneumococcus do not interact competitively, a kind of tragedy of the commons arises. Here, individual incentives favor increased treatment, but if the population as a whole chooses a larger rate of treatment, the declining prevalence of chlamydia reduces opportunities to treat pneumococcus. Individual incentives drive overuse, but this mathematical tragedy of the commons is unrelated to drug resistance and can be avoided by a different choice of antibiotic policy.

Our model does not reflect all features of trachoma mass drug administration in practice. Specifically, we did not include cocirculation of multiple pneumococcal strains, the role of strain-specific immunity in pneumococcus [9], the presence of pneumococcal vaccination, or the timing of mass drug administration. We only included a single organism for which resistance can be induced, and we have ignored age structure, demography, latency, multiple chlamydial strains, chlamydial cross immunity, and network effects. We also observe that the mathematical analysis of the current model has not revealed explicit criteria for the existence, uniqueness, and stability of the coexistence equilibrium. Numerical simulations suggest that under the base scenario there always exists exactly one (globally) stable equilibrium and the coexistence equilibrium is (globally) stable whenever it exists. Finally, the relationship between antibiotic use and drug resistance may be more complex than simple selection models would imply [30]. We cannot conclude that a tragedy of the commons is impossible in a more general setting.

Recent recommendations to improve antibiotic stewardship include efforts to avoid overuse of broad spectrum antibiotics (e.g. [4]), in part because of a belief that broad spectrum antibiotic use promotes drug resistance [41]. Simple game theory models as we present here can be our first step in understanding the forces which shape the epidemiology of drug resistance. If antibiotic use exceeds the socially optimal level, it is important to understand whether such excessive antibiotic use really benefits the individuals who use them. Overuse of antibiotics based on a mistaken belief that they are helpful does not reflect a true conflict of interest between the individual and society, but a true conflict of interest does arise if individuals have genuine health incentives to use antibiotics at a level exceeding the socially optimal value. This work suggests that a tragedy of the commons does not arise in simple models of trachoma control through the use of mass treatment. More realistic models of the population biology of drug resistant strains may provide examples of the tragedy of the commons due to treatment of unrelated organisms.

Highlights.

• A two-disease epidemic model with drug-resistance is proposed.

• Treatment for one disease may select for resistance in the other.

• Antibiotic use is modeled as a mathematical game between individual and society.

• The tragedy of the commons for mass treatment and targeted treatment are discussed.

• A conflict of interest between individual and society can occur in several cases.

Appendix

A. Proof of Theorem 3.1

The calculation of boundary equilibria for the community equations (2.2) is straightforward and simple except that of E₁₃ and E₂₃ which can be found in Gao et al. [16]. So we will only focus on the stability analysis. By substituting X = 1 − (Y_S + Y_R + Y_C + Y_SC + Y_RC) into the last five equations of (2.2), we obtain a qualitatively equivalent 5-dimensional ODEs system, denoted by (2.2)′, with respect to Y_S, Y_R, Y_C, Y_SC, and Y_RC. We represent the equilibria corresponding to the reduced system by $E_0^{\prime },E_1^{\prime },E_2^{\prime },E_3^{\prime },E_{12}^{\prime },E_{13}^{\prime },E_{23}^{\prime }$, and Ẽ′, where the first component of E₀, E₁, E₂, E₃, E₁₂, E₁₃, E₂₃, and Ẽ is removed, respectively. The Jacobian matrix of (2.2)′ at an equilibrium $E\prime \in \{E_0^{\prime },E_1^{\prime },E_2^{\prime },E_3^{\prime },E_{12}^{\prime },E_{13}^{\prime },E_{23}^{\prime },Ẽ\prime \}$ and that of (2.2) at the corresponding equilibrium E ∈ {E₀, E₁, E₂, E₃, E₁₂, E₁₃, E₂₃, Ẽ} have the same set of nonzero eigenvalues.

Local stability of E₀

The Jacobian matrix of (2.2)′ at $E_0^{\prime }$ is $J(E_0^{\prime })=F-V$ and the set of its eigenvalues is

$$\{{\beta }_S-{\rho }_P-{\theta }_P,{\beta }_R-{\rho }_P,{\beta }_C-{\rho }_C-{\theta }_C,{\beta }_{11}-{\rho }_P-{\rho }_C-{\theta }_{PC},{\beta }_{11}^{\prime }-{\rho }_P-{\rho }_C-{\theta }_{PC}\}.$$

The no-disease equilibrium E₀ is stable if ℛ₀ < 1 and unstable otherwise.

Local stability of E₁

The Jacobian matrix of system (2.2)′ at $E_1^{\prime }$ is $J(E_1^{\prime })$ and the set of its eigenvalues is

$$\{(1-{ℛ}_{10}){\rho }_P,(\frac{{ℛ}_{20}}{{ℛ}_{10}}-1){\rho }_P,({ℛ}_{30}-1)({\rho }_C+\theta ),(\frac{{ℛ}_{40}}{{ℛ}_{10}}-1)({\rho }_P+{\rho }_C+\theta )+{\beta }_S(\frac{1}{{ℛ}_{10}}-1),(\frac{{ℛ}_{50}}{{ℛ}_{10}}-1)({\rho }_P+{\rho }_C+\theta )\}.$$

under targeted treatment. Recall that $E_1^{\prime }$ (or E₁) exists if and only if ℛ₁₀ > 1 and θ_P = 0 which means that $E_1^{\prime }$ (or E₁) does not exist under mass treatment.

Targeted treatment: since ℛ₁₀ > 1 and ℛ₁₀ > ℛ₄₀, the first and fourth eigenvalues of $J(E_1^{\prime })$ are negative. E₁ is stable if and only if ℛ₁₀ > max{1, ℛ₂₀, ℛ₅₀} and ℛ₃₀ < 1.

Local stability of E₂

The Jacobian matrix of system (2.2)′ at $E_2^{\prime }$ is $J(E_2^{\prime })$ and the set of its eigenvalues is

$$\left\{\right(\frac{1}{{ℛ}_{20}}-\frac{1}{{ℛ}_{10}}){\beta }_S,(1-{ℛ}_{20}){\rho }_P,({ℛ}_{30}-1)({\rho }_C+\theta ),(\frac{{ℛ}_{40}}{{ℛ}_{20}}-1)({\rho }_P+{\rho }_C+\theta ),(\frac{{ℛ}_{50}}{{ℛ}_{20}}-1)({\rho }_P+{\rho }_C+\theta )+(1-{ℛ}_{20}){\rho }_P\}.$$

under either targeted treatment or mass treatment.

Since ℛ₂₀ > 1 and ℛ₂₀ > ℛ₅₀, the second and last eigenvalues of $J(E_2^{\prime })$ are negative. E₂ is stable if and only if ℛ₂₀ > max{1, ℛ₁₀, ℛ₄₀} and ℛ₃₀ < 1.

Local stability of E₃

The Jacobian matrix of system (2.2)′ at $E_3^{\prime }$ is J(E₃) and the set of its eigenvalues is

$$\{{\lambda }_3^{+},({ℛ}_{20}-1){\rho }_P,(1-{ℛ}_{30})({\rho }_C+\theta ),{\lambda }_3^{-},(\frac{{ℛ}_{50}}{{ℛ}_{30}}-1)({\rho }_P+{\rho }_C+\theta )+{\beta }_C(\frac{1}{{ℛ}_{30}}-1\left)\right\}$$

under targeted treatment, where ${\lambda }_3^{+}$ and ${\lambda }_3^{-}$ denote the roots of λ² + M₁λ + M₀ = 0, or

$$\{({ℛ}_{10}-1)({\rho }_P+\theta ),({ℛ}_{20}-1){\rho }_P,(1-{ℛ}_{30})({\rho }_C+\theta ),(\frac{{ℛ}_{40}}{{ℛ}_{30}}-1)({\rho }_P+{\rho }_C+\theta )+{\beta }_C(\frac{1}{{ℛ}_{30}}-1),(\frac{{ℛ}_{50}}{{ℛ}_{30}}-1)({\rho }_P+{\rho }_C+\theta )+{\beta }_C(\frac{1}{{ℛ}_{30}}-1\left)\right\}$$

under mass treatment.

• Targeted treatment: E₃ is stable if and only if ℛ₃₀ > 1, ℛ₂₀ < 1, $\Re {\lambda }_3^{+}<0$ and $\Re {\lambda }_3^{-}<0$.

• Mass treatment: E₃ is stable if and only if ℛ₁₀ < 1, ℛ₂₀ < 1, and ℛ₃₀ > 1.

Local stability of E₁₂

Recall that E₁₂ exists if and only if ℛ₁₀ > ℛ₂₀, ℛ₁₀ > 1, and θ_P > 0 (mass treatment). The Jacobian matrix of system (2.2)′ at $E_{12}^{\prime }$ is $J(E_{12}^{\prime })$ and the set of its eigenvalues is

$$\{({ℛ}_{30}-1)({\rho }_C+\theta ),{\lambda }_{12}^{+},{\lambda }_{12}^{-},{\tilde{\lambda }}_{12}^{+},{\tilde{\lambda }}_{12}^{-}\},$$

where ${\lambda }_{12}^{\pm }$ and ${\tilde{\lambda }}_{12}^{\pm }$ are solutions to

$${\lambda }^2+K_1\lambda +K_0=0\text{and}{\lambda }^2+L_1\lambda +L_0=0,$$

respectively. Here

$$K_1=\frac{{\beta }_R({\rho }_P+\theta )({ℛ}_{10}-1)+{\rho }_P({\rho }_P+\theta )({ℛ}_{10}-{ℛ}_{20})}{{\beta }_S}+({\beta }_S-{\beta }_R)Y_{12}>0,$$

$$K_0=({\rho }_P({\rho }_P+\theta )({ℛ}_{10}-{ℛ}_{20})+{\beta }_S\delta \theta )Y_{12}>0,$$

$$L_1=({\rho }_P+{\rho }_C+\theta )(({ℛ}_{10}-{ℛ}_{40})+({ℛ}_{10}-{ℛ}_{50}))/{ℛ}_{10}+{\beta }_R({ℛ}_{10}-1)/{ℛ}_{10}+({\beta }_S-{\beta }_R)Y_{12}>0,$$

$$L_0={\beta }_R({\rho }_P+{\rho }_C+\theta )({ℛ}_{10}-{ℛ}_{40})(1-1/{ℛ}_{10}-Y_{12})/{ℛ}_{10}+({\rho }_P+{\rho }_C+\theta )({ℛ}_{10}-{ℛ}_{50})(({\rho }_P+{\rho }_C+\theta )({ℛ}_{10}-{ℛ}_{40})/{ℛ}_{10}^2+({\rho }_P+\theta )Y_{12})>0,$$

which imply that E₁₂ is stable if and only if ℛ₃₀ < 1.

Local stability of E₁₃

Recall that E₁₃ exists if and only if ℛ₁₀ > 1, ℛ₃₀ > 1 and θ = 0 (no treatment). The Jacobian matrix of system (2.2)′ at $E_{13}^{\prime }$ is $J(E_{13}^{\prime })$ and the set of its eigenvalues is

$$\{-{\beta }_S+{\rho }_P,({\beta }_R-{\beta }_S){\rho }_P/{\beta }_S,-{\beta }_C+{\rho }_C,-({\beta }_C-{\beta }_{11}^{\prime }{X}_{13})-{\rho }_P,)-({\beta }_S+{\beta }_C-{\beta }_{11})-{\beta }_{11}({\rho }_P/{\beta }_S+{\rho }_C/{\beta }_C-2X_{13}).\}$$

It follows from X₁₃ < min{ρ_P/β_S, ρ_C/β_C} and β_S > β_R that E₁₃ is stable when it exists.

Local stability of E₂₃

Recall that E₂₃ exists if and only if ℛ₂₀ > 1 and ℛ₃₀ > 1. The Jacobian matrix of system (2.2)′ at $E_{23}^{\prime }$ is $J(E_{23}^{\prime })$ and the set of its eigenvalues is

$$\{({ℛ}_{10}/{ℛ}_{20}-1)({\rho }_P+\theta ),-{\beta }_R+{\rho }_P,-{\beta }_C+{\rho }_C+\theta ,-({\beta }_C-{\beta }_{11}{X}_{23})-{\rho }_P,-({\beta }_R+{\beta }_C-{\beta }_{11}^{\prime })-{\beta }_{11}^{\prime }({\rho }_P/{\beta }_R+({\rho }_C+\theta )/{\beta }_C-2X_{23})\}$$

under mass treatment or

$$\{{\lambda }_{23}^{+},-{\beta }_R+{\rho }_P,-{\beta }_C+{\rho }_C+\theta ,{\lambda }_{23}^{-},-({\beta }_R+{\beta }_C-{\beta }_{11}^{\prime })-{\beta }_{11}^{\prime }({\rho }_P/{\beta }_R+({\rho }_C+\theta )/{\beta }_C-2X_{23})\}$$

under targeted treatment where ${\lambda }_{23}^{\pm }$ are solutions to λ² + H₁λ + H₀ = 0.

• Mass treatment: E₂₃ is stable if and only if ℛ₁₀ < ℛ₂₀.

• Targeted treatment: E₂₃ is stable if and only if $\Re {\lambda }_{23}^{\pm }<0$.

Existence of Ẽ

It follows from (2.2) that the equilibrium Ẽ satisfies

$$({\rho }_C+\theta -{\beta }_C(\tilde{X}+{Ỹ}_S+{Ỹ}_R))({Ỹ}_C+{Ỹ}_{SC}+{Ỹ}_{RC})=0,$$

$$({\rho }_P+\theta -{\beta }_S(\tilde{X}+{Ỹ}_C))({Ỹ}_S+{Ỹ}_{SC})=0,$$

$$({\rho }_P-{\beta }_R(\tilde{X}+{Ỹ}_C))({Ỹ}_R+{Ỹ}_{RC})=\delta \theta ({Ỹ}_S+{Ỹ}_{SC})>0$$

under mass treatment or

$$({\rho }_C+\theta -{\beta }_C(\tilde{X}+{Ỹ}_S+{Ỹ}_R))({Ỹ}_C+{Ỹ}_{SC}+{Ỹ}_{RC})=0,$$

$$({\rho }_P-{\beta }_S(\tilde{X}+{Ỹ}_C))({Ỹ}_S+{Ỹ}_{SC})=-\theta {Ỹ}_{SC}<0,$$

$$({\rho }_P-{\beta }_R(\tilde{X}+{Ỹ}_C))({Ỹ}_R+{Ỹ}_{RC})=\delta \theta {Ỹ}_{SC}>0.$$

under targeted treatment. Hence, in both cases, a necessary condition for the existence of Ẽ is that: ℛ₁₀ > 1, ℛ₃₀ > 1, ℛ₁₀ > ℛ₂₀ and θ > 0. For a simple case: ${\beta }_{11}={\beta }_{11}^{\prime }=0$ under mass treatment, we can solve the equilibrium equations by substitution and rigorously prove that there exists at most one positive equilibrium. In addition, ρ_C + θ − β_C is an eigenvalue of the Jacobian J(Ẽ′) (or J(Ẽ)).

B. Proof of Theorem 3.5

Denote the k-th equilibrium equation of the individual equations (2.1) and community equations (2.2) as eq_k and EQ_k, respectively. Let ${\lambda }_S^{*}={\lambda }_S+{\lambda }_{SC\to S}+{\lambda }_{SC\to SC}={\beta }_S({Ȳ}_S+{Ȳ}_{SC}),{\lambda }_R^{*}={\lambda }_R+{\lambda }_{RC\to R}+{\lambda }_{RC\to RC}={\beta }_R({Ȳ}_R+{Ȳ}_{RC})$ and ${\lambda }_C^{*}={\lambda }_{RC\to RC}+{\lambda }_{RC\to C}+{\lambda }_{SC\to SC}+{\lambda }_{SC\to C}+{\lambda }_C={\beta }_C({Ȳ}_C+{Ȳ}_{SC}+{Ȳ}_{RC})$.

Community model under mass treatment (θ_P = θ_PC = θ_C = θ)

The sum of EQ₄, EQ₅ and EQ₆ gives

$$-({\rho }_C+\theta -{\beta }_C(\overline{X}+{Ȳ}_S+{Ȳ}_R))({Ȳ}_C+{Ȳ}_{SC}+{Ȳ}_{RC})=0$$

Since X̄ + Ȳ_S + Ȳ_R + Ȳ_C + Ȳ_SC + Ȳ_RC = 1, we have

$$J_C={Ȳ}_C+{Ȳ}_{SC}+{Ȳ}_{RC}=1-({\rho }_C+\theta )/{\beta }_C=1-1/{ℛ}_{30}\text{if}{ℛ}_{30}>1\text{or}0\text{if}{ℛ}_{30}\le 1.$$

The sums of EQ₂ and EQ₅, and, EQ₃ and EQ₆ give

$$-({Ȳ}_S+{Ȳ}_{SC})({\rho }_P+\theta -{\beta }_S(\overline{X}+{Ȳ}_C))=0,$$

$$-{\rho }_P({Ȳ}_R+{Ȳ}_{RC})+\delta \theta ({Ȳ}_S+{Ȳ}_{SC})+{\beta }_R(\overline{X}+{Ȳ}_C)({Ȳ}_R+{Ȳ}_{RC})=0.$$

Direct calculations yield

$$\overline{X}+{Ȳ}_C=\frac{{\rho }_P+\theta }{{\beta }_S}=\frac{1}{{ℛ}_{10}},$$

$${Ȳ}_S+{Ȳ}_{SC}=\frac{({\beta }_S-{\rho }_P-\theta )({\beta }_S{\rho }_P-{\beta }_R({\rho }_P+\theta ))}{{\beta }_S({\beta }_S({\rho }_P+\delta \theta )-{\beta }_R({\rho }_P+\theta ))}=\frac{(1-1/{ℛ}_{10})(1-{ℛ}_{20}/{ℛ}_{10}){\rho }_P}{\delta \theta +{\rho }_P(1-{ℛ}_{20}/{ℛ}_{10})},$$ (5.1)

$${Ȳ}_R+{Ȳ}_{RC}=\frac{\delta \theta ({\beta }_S-{\rho }_P-\theta )}{{\beta }_S({\rho }_P+\delta \theta )-{\beta }_R({\rho }_P+\theta )}=\frac{\delta \theta (1-1/{ℛ}_{10})}{\delta \theta +{\rho }_P(1-{ℛ}_{20}/{ℛ}_{10})},$$

and hence

$$J_P=1-({\rho }_P+\theta )/{\beta }_S=1-1/{ℛ}_{10}\text{if}{ℛ}_{10}>1\text{or}0\text{if}{ℛ}_{10}\le 1.$$

Community model under targeted treatment (θ_P = 0, θ_PC = θ_C = θ)

The derivation of J_C for community model under targeted treatment is exactly the same as that for community model under mass treatment. J_P is not always a decreasing function of community treatment rate θ. For example, given a parameter set under targeted treatment: β_S = 3, β_R = 1.2, β_C = 1.8, β₁₁ = 1, ${\beta }_{11}^{\prime }=1$, δ = 0.3, ρ_P = 1, ρ_C = 1, we have ∂J_P/∂θ ≈ 0.121952 > 0 at θ = 0.7. For the same parameter values except that ${\beta }_{11}={\beta }_{11}^{\prime }=0$, we still have ∂J_P/∂θ ≈ 0.113367 > 0 at θ = 0.7.

Individual model under mass treatment $({\theta }_P^{(i)}={\theta }_{PC}^{(i)}={\theta }_C^{(i)}={\theta }^{(i)})$

The sum of eq₄, eq₅ and eq₆ gives

$${\lambda }_C^{*}({\overline{X}}^{(i)}+{Ȳ}_S^{(i)}+{Ȳ}_R^{(i)})-({\rho }_C+{\theta }^{(i)})({Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)})=0.$$

Since ${\overline{X}}^{(i)}+{Ȳ}_S^{(i)}+{Ȳ}_R^{(i)}+{Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)}=1$, we have

$$J_C^{(i)}={Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)}={\lambda }_C^{*}/({\lambda }_C^{*}+{\rho }_C+{\theta }^{(i)}).$$

The sums of eq₂ and eq₅, and, eq₃ and eq₆ give

$$-({\rho }_P+{\theta }^{(i)})({Ȳ}_S^{(i)}+{Ȳ}_{SC}^{(i)})+{\lambda }_S^{*}({\overline{X}}^{(i)}+{Ȳ}_C^{(i)})=0,$$

$$-{\rho }_P({Ȳ}_R^{(i)}+{Ȳ}_{RC}^{(i)})+\delta {\theta }^{(i)}({Ȳ}_S^{(i)}+{Ȳ}_{SC}^{(i)})+{\lambda }_R^{*}({\overline{X}}^{(i)}+{Ȳ}_C^{(i)})=0.$$

Again since ${\overline{X}}^{(i)}+{Ȳ}_S^{(i)}+{Ȳ}_R^{(i)}+{Ȳ}_C^{(i)}+{Ȳ}_{SC}^{(i)}+{Ȳ}_{RC}^{(i)}=1$, we get three linear equations with respect to ${\overline{X}}^{(i)}+{Ȳ}_C^{(i)},{Ȳ}_S^{(i)}+{Ȳ}_{SC}$ and ${Ȳ}_R^{(i)}+{Ȳ}_{RC}^{(i)}$. Direct calculations yield

$${\overline{X}}^{(i)}+{Ȳ}_C^{(i)}=\frac{{\rho }_P({\rho }_P+{\theta }^{(i)})}{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})+{\rho }_P({\rho }_P+{\theta }^{(i)})},$$

$${Ȳ}_S^{(i)}+{Ȳ}_{SC}=\frac{{\rho }_P{\lambda }_S^{*}}{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})+{\rho }_P({\rho }_P+{\theta }^{(i)})},$$

$${Ȳ}_R^{(i)}+{Ȳ}_{RC}^{(i)}=\frac{({\rho }_P+{\theta }^{(i)}){\lambda }_R^{*}+\delta {\theta }^{(i)}{\lambda }_S^{*}}{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})+{\rho }_P({\rho }_P+{\theta }^{(i)})},$$

and hence

$$J_P^{(i)}=\frac{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})}{{\lambda }_R^{*}({\rho }_P+{\theta }^{(i)})+{\lambda }_S^{*}({\rho }_P+\delta {\theta }^{(i)})+{\rho }_P({\rho }_P+{\theta }^{(i)})}.$$

Moreover, it follows (5.1) that $J_C^{(i)}$ and $J_P^{(i)}$ can be explicitly written in terms of model parameters and we can study an individual’s disutility in community treatment rate.

Individual model under targeted treatment $({\theta }_P^{(i)}=0,{\theta }_{PC}^{(i)}={\theta }_C^{(i)}={\theta }^{(i)})$

The derivation of $J_C^{(i)}$ for individual model under targeted treatment is exactly the same as that for individual model under mass treatment.

Now we give an outline of the proof to the statement: $J_P^{(i)}$ is not necessarily decreasing in θ⁽ⁱ⁾. First, we solve the individual equations and simplify the derivative of $J_P^{(i)}$ with respect to θ⁽ⁱ⁾. We find that the sign of $\partial J_P^{(i)}/\partial {\theta }^{(i)}$ is the same as a polynomial in θ⁽ⁱ⁾ of the form

$$h({\theta }^{(i)})=-(c_4*{({\theta }^{(i)})}^4+c_3*{({\theta }^{(i)})}^3+c_2*{({\theta }^{(i)})}^2+c_1*({\theta }^{(i)})+c_0),$$

where

$$c_4=c_4({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_S,{\lambda }_C,{\rho }_P,{\rho }_C),$$

$$c_3=c_{30}({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\lambda }_C,{\rho }_P,{\rho }_C)-c_{31}({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_S,{\lambda }_C,{\rho }_P)\delta ,$$

$$c_2=c_{20}({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\lambda }_C,{\rho }_P,{\rho }_C)-c_{20}^{\prime }({\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\rho }_P)-c_{21}({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\lambda }_C,{\rho }_P,{\rho }_C)\delta ,$$

$$c_1=c_1({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\lambda }_C,{\rho }_P,{\rho }_C),$$

$$c_0=c_0({\lambda }_{SC\to SC},{\lambda }_{SC\to C},{\lambda }_{SC\to S},{\lambda }_{RC\to RC},{\lambda }_{RC\to C},{\lambda }_{RC\to R},{\lambda }_S,{\lambda }_R,{\lambda }_C,{\rho }_P,{\rho }_C),$$

and $c_{20}^{\prime }={\lambda }_{RC\to RC}({\lambda }_{SC\to S}+{\lambda }_S){\rho }_P^2({\lambda }_{SC\to S}+{\lambda }_{RC\to R}+{\lambda }_S+{\lambda }_R+{\rho }_P)$. Here c₀, c₁, c₂₀, c₂₁, c₃₀, c₃₁ and c₄ are the addition of some positive terms. Furthermore, we find that c₂₀ > c₂₁ and c₃₀ > c₃₁ which imply that $c_2>-c_{20}^{\prime }$ and c₃ > 0. In particular, if cotransmission of R and C is rare, i.e., ${\beta }_{11}^{\prime }=0$, then $c_{20}^{\prime }=0$ and h(θ⁽ⁱ⁾) < 0 for any θ⁽ⁱ⁾.

Nevertheless, it is possible that h(θ⁽ⁱ⁾) > 0 for some θ⁽ⁱ⁾ when ${\beta }_{11}^{\prime }>0$. To construct such a counterexample, we observe that λ_SC→SC, λ_SC→C, λ_RC→C, λ_C, ρ_C do not appear in $c_{20}^{\prime }$ but in other coefficients. Let λ_SC→SC = λ_SC→C = λ_RC→C = λ_C = ρ_C = 0 and then h(θ⁽ⁱ⁾) takes the form

$$ĥ({\theta }^{(i)})=-{\lambda }_{SC\to SC}^2({ĉ}_4*{({\theta }^{(i)})}^4+{ĉ}_3*{({\theta }^{(i)})}^3+{ĉ}_2*{({\theta }^{(i)})}^2+{ĉ}_1*({\theta }^{(i)})+{ĉ}_0),$$

where

$${ĉ}_2={ĉ}_{20}-c_{20}^{\prime }/{\lambda }_{RC\to RC}\text{and}{ĉ}_4={\lambda }_{SC\to S}+{\lambda }_S+{\rho }_P({\lambda }_{SC\to S}+{\lambda }_S)/{\lambda }_{RC\to RC}.$$

Here ĉ₀, ĉ₁, ĉ₂₀, ĉ₃ are polynomials. Thus, $c_{20}^{\prime }$ can dominate the sign of ĥ(θ⁽ⁱ⁾) as λ_RC→RC → 0. For example, given a parameter set under targeted treatment: λ_SC→SC = 0.0001, λ_SC→C = 0.0001, λ_SC→S = 1, λ_RC→RC = 0.001, λ_RC→C = 0.0001, λ_RC→R = 1, λ_S = 1, λ_R = 1, λ_C = 0.0001, ρ_P = 1, ρ_C = 0.0001, δ = 0.5, we have $\partial J_P^{(i)}/\partial {\theta }^{(i)}=6.55516\times {10}^{-7}>0$ at θ⁽ⁱ⁾ = 1.

However, if D_C ≥ D_P, then we find that ∂J⁽ⁱ⁾/∂θ⁽ⁱ⁾ is constantly negative and hence an individual always benefits from increasing his/her treatment.